Физика формулы перемещения: Перемещение при прямолинейном равномерном движении — урок. Физика, 9 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Открытая Физика. Равноускоренное движение

В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения a→ остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения g→. Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости υ→ и ускорения a→ направлены вдоль прямой движения.

Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

Проекции векторов скорости υ→ и ускорения a→ на координатные оси. a_x = 0, a_y = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой υ = υ₀ + at.

В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Графики скорости равноускоренного движения

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC: a=υ-υ0t=|BC||AC|.

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ₀ = –2 м/с, a = 1/2 м/с².

Для графика II: υ₀ = 3 м/с

, a = –1/3 м/с².

Скорость и ускорение

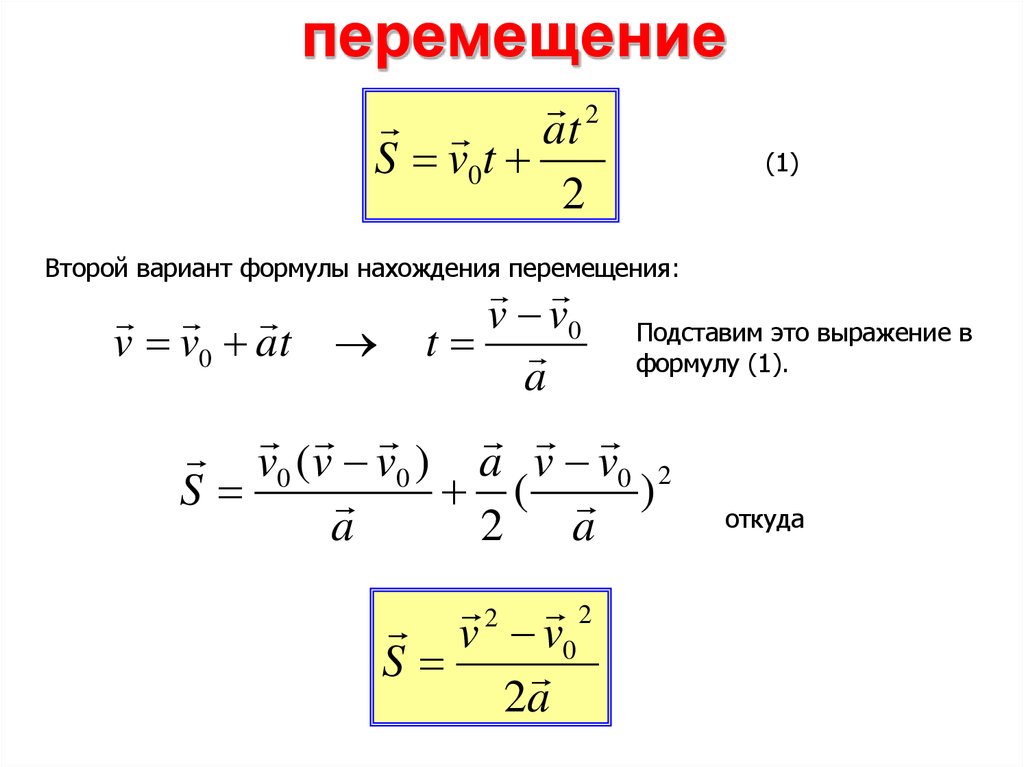
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от

0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF.

Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с. s=(|OD|+|EF|)2|OF|=υ0+υ2t=2υ0+(υ-υ0)2t.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде: s=υ0t+at22.

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t: y=y0+υ0t+at22.

Это выражение называют законом равноускоренного движения.

Графики равноускоренного движения

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t.

Результат записывается в виде s=υ2-υ022a.

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s: υ=υ02+2as.

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид s=υ22a; υ=2as.

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Равноускоренное движение тела

Равномерное прямолинейное движение в физике

Содержание:

Равномерное прямолинейное движение:

Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?

Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?

Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за

Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.

В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: Это отношение показывает, как быстро движется тело, но ничего не говорит о направлении движения.

Чтобы скорость характеризовала и быстроту движения, и его направление, ее определяют через перемещение.

Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:

Из равенства (1) следует, что скорость — векторная физическая величина. Ее модуль численно равен модулю перемещения за единицу времени, а направление совпадает с направлением перемещения (т. к. ).

Отношение для всех участков движения на рисунке 43 одинаково: Значит, скорость равномерного прямолинейного движения постоянна:

с течением времени не изменяется ни ее модуль, ни ее направление.

Из формулы (1) легко найти перемещение:

и путь (равный модулю перемещения ):

А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени Рассмотрим пример. Автомобиль движется с постоянной скоростью по прямолинейному участку шоссе (рис. 44).

Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время автомобиль совершил перемещение Подставляя в равенство (4), получим:

Приняв запишем формулу для координаты автомобиля:

Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.

Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.

Для любознательных:

Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.

Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!

Главные выводы:

При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.

Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Пример решения задачи:

Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением где

Определите: 1) проекцию скорости лодки 2) координату лодки в момент времени 3) проекцию перемещения лодки на ось Ох и путь, пройденный лодкой за время от момента до момента

Решение

Сделаем рисунок к задаче.

По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив получим

Найдем

Из рисунка 49: проекция перемещения

Ответ:

Графическое представление равномерного прямолинейного движения

Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.

Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.

В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.

Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши Тани Как представить графически характеристики их движения?

Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при координата Леши Тани

Построим графики зависимости проекции скорости проекции перемещения пути S и координаты X от времени t.

График проекции скорости

Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: Так как проекции постоянны, то графики их зависимости от времени t — прямые, параллельные оси времени (прямые I и II на рисунке 52).

Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.

График проекции перемещения

Проекция перемещения совершенного за время t, определяется формулой (см. § 6).

Зависимость проекции перемещения от времени для Леши или График — наклонная прямая I (рис. 53).

Для Тани или График — наклонная прямая II, изображенная на рисунке 53.

Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.

График пути

Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: Поэтому при график пути совпадает с графиком проекции перемещения (прямая I), а при график пути (прямая III) является «зеркальным отражением» графика II (проекции перемещения) от оси времени.

Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.

График координаты

Его называют также графиком движения.

По формуле , используя данные из условия задачи и рисунок 51, находим зависимости координаты Леши и Тани от времени Графики этих зависимостей — прямые I и II на рисунке 54. Они параллельны соответствующим графикам проекций перемещения на рисунке 53.

Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.

По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.

Что еще можно определить по графикам?

По графику проекции скорости можно найти проекцию перемещения и пройденный путь

Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна а основание — времени t. Значит, площадь прямоугольника равна Таким образом, проекция перемещения численно равна площади прямоугольника между графиком проекции скорости и осью времени. При проекция перемещения отрицательна, и площадь надо брать со знаком «минус».

Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.

По углу наклона графика проекции перемещения можно оценить скорость движения

Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.

Главные выводы:

Для равномерного прямолинейного движения:

График проекции скорости — прямая, параллельная оси времени.
Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется скоростью движения.
Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.

Пример №1

Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью Через время после проезда перекрестка он встречает едущего в город велосипедиста, движущегося равномерно со скоростью Определите расстояние между участниками движения через время после их встречи, если Запишите кинематические законы движения мотоциклиста и велосипедиста, постройте графики проекции и модуля скорости, проекции перемещения, координаты и пути для обоих участников движения.

Решение

Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.

В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:

Найдем координату велосипедиста в начальный момент времени. Пусть точка С на оси Ох — место встречи участников движения (рис. 56).

Тогда

Кинематический закон движения велосипедиста имеет вид:

Расстояние между мотоциклистом и велосипедистом через время после их встречи равно сумме путей, которые они проделают за это время. Значит,

Пример №2

Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости совпадают (рис. 56). Для велосипедиста график проекции скорости — прямая 2, а модуля скорости — прямая Объясните причину несовпадения.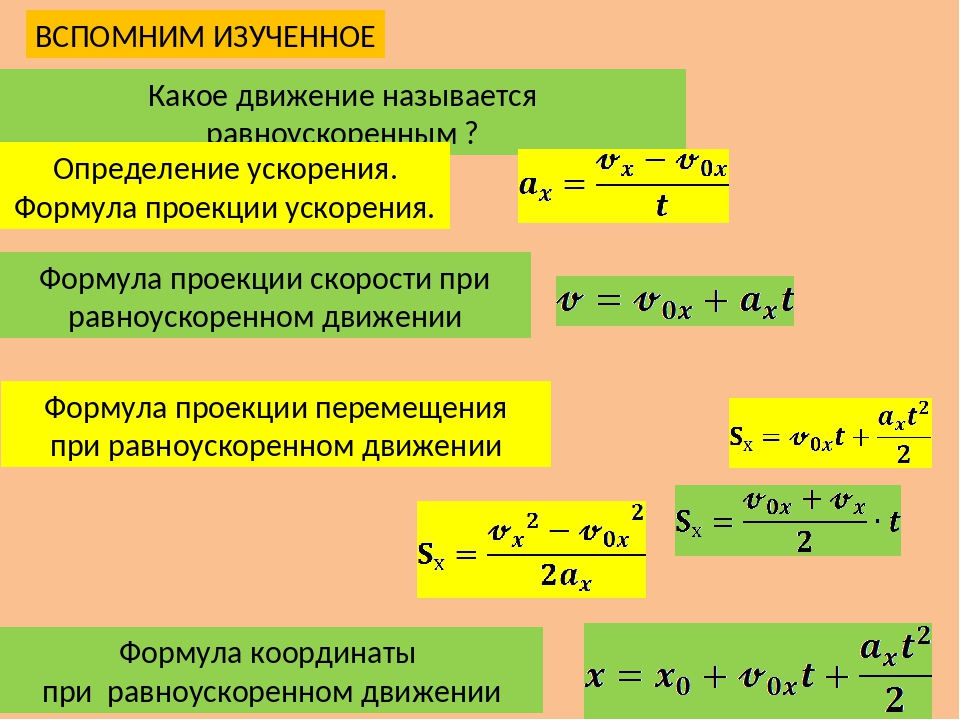

Графиками пути s, проекции и модуля перемещения (рис. 57) будут прямые, выражающие прямую пропорциональную зависимость от времени t.

Для мотоциклиста:

Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).

Для велосипедиста:

Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая — графиком проекции его перемещения.

Графики координат представлены на рисунке 58. Они выражают зависимости (прямая 1) и (прямая 2). Точка А определяет время встречи и координату места встречи.

Ответ:

Прямолинейное равномерное движение и скорость

Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.

Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.

При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:

Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено:

Так как отношение в формуле является положительной скалярной величиной, то направление вектора скорости совпадает с направлением вектора перемещения Единица измерения скорости в СИ – метр в секунду:

Если скорость известна, то можно определить перемещение s материальной точки за промежуток времени при прямолинейном равномерном движении:

При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:

Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:

Можно получить формулу для вычисления координаты точки в произвольный момент времени (см.: тема 1.2):

Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).

Из формулы (1.5) определяется выражение для проекции скорости:

Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.

Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость – время будет представлять собой линию, параллельную оси времени — скорость такого движения не зависит от времени (е):

График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f):

Пример №3

Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста скорость второго велосипедиста (g)?

Определите: а) координату и время встречи велосипедистов; b) пройденные велосипедистами пути и совершенные ими перемещения к моменту встречи; с) время прошедшее с начала движения до момента, когда расстояние между ними стало 10 км.

Дано:

Решение:

a) При решении задачи соблюдается следующая последовательность действий:

I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).

II действие. Уравнение движения записывается в общем виде:

III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде:

IV действие. Координаты велосипедистов при встрече равны: Это равенство решается для

V действие. Для определения координат и встречи велосипедистов необходимо решить уравнения их движения для времени

Так как то

b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:

c) Время прошедшее с начала движения до момента, когда между ними осталось 10 км, вычисляется по нижеприведенному равенству:

или

Скорость при равнопеременном прямолинейном движении

Из формулы (1. 14) видно, что если известны ускорение и начальная скорость тела то можно определить его скорость в любой момент времени:

или ее проекцию на ось

Если начальная скорость равна нулю то:

Из этих выражений видно, что скорость при равнопеременном движении является линейной функцией от времени. График зависимости скорости от времени – прямая линия, проходящая через начало координат (или через Эта линия, в соответствии с увеличением или уменьшением скорости, направлена вверх или вниз (с).

Перемещение при равнопеременном прямолинейном движении

Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком и осью времени.

На приведенных графиках — это заштрихованная фигура трапеции (см: с):

или в векторной форме:

Если в последнюю формулу вместо подставить выражение (1. 18), то получим

обобщенную формулу перемещения для равнопеременного движения:

Таким образом, формула проекции перемещения (например, на ось при равнопеременном прямолинейном движении будет:

а формула координаты:

(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя то:

Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени и его график представляет собой параболу, проходящую через начало координат (d).

В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время прошедшее от начала движения. Такую задачу можно решить тогда, когда известны ускорение, начальное и конечное значения скорости. Для получения этой формулы из выражения (1. 19) получаем

Это выражение подставляется в формулу (1.21):

После простых преобразований получаем:

Для проекции конечной скорости получаем: Если движение начинается из состояния покоя то проекции перемещения и скорости будут равны:

Равноускоренное и равнозамедленное движения

Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.

При равноускоренном движении векторы и имеют одинаковые направления. В этом случае знаки у обеих проекций и или положительные, или же отрицательные. Если материальная точка начнет движение из состояния покоя то независимо от направления движения, оно во всех случаях будет равноускоренным.

При равнозамедленном движении векторы и имеют противоположные направления. В этом случае проекции и имеют противоположные знаки, если один из них отрицательный, то другой – положительный.

В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.

Таблица 1.3.

Кинематика прямолинейного движения

Физические величины бывают скалярные и векторные. Скалярные физические величины характеризуются только численным значением, тогда как векторные определяются и числом (модулем), и направлением. Скалярными физическими величинами являются время, температура, масса, векторными — скорость, ускорение, сила.
Мир вокруг нас непрерывно изменяется, или движется, т. е. можно сказать, что движение (изменение) есть способ существования материи.

Простейшая форма движения материи — механическое движение — заключается в изменении взаимного расположения тел или их частей в пространстве с течением времени. Наука, изучающая механическое движение, называется механикой (от греческого слова — подъемная машина).

Даже самое простое движение тела оказывается достаточно сложным для изучения и исследования. Соответственно, для того чтобы в сложном явлении «увидеть» главное, в физике строится его адекватная упрощенная модель.

В механике широко используется простейшая модель реального тела, называемая материальной точкой (МТ). Под материальной точкой понимают тело, размерами и формой которого можно пренебречь при описании данного движения. Хотя МТ представляет собой абстрактное понятие, упрощающее изучение многих физических явлений, она, подобно реальному телу, «имеет» массу, энергию и т. д.

Кроме материальной точки, в механике используется модель абсолютно твердого тела. Под абсолютно твердым телом понимают модель реального тела, в которой расстояние между его любыми двумя точками остается постоянным. Это означает, что размеры и форма абсолютно твердого тела не изменяются в процессе его движения. В противном случае говорят о модели деформируемого тела.

В классической (ньютоновской) механике рассматривается движение тел со скоростями, намного меньшими скорости света в вакууме
Классическая механика состоит из трех основных разделов: кинематики, динамики и статики. В кинематике (от греческого слова — движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова — сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова — искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.

Всякое движение тела можно представить в виде двух основных видов движения — поступательного и вращательного.

Поступательным называется движение тела, при котором прямая, соединяющая в этом теле любые две точки, при перемещении остается параллельной самой себе (рис. 1).

Вращательным называется движение абсолютно твердого тела вокруг неподвижной прямой, называемой осью вращения, при котором все точки тела движутся по окружностям, центры которых лежат на этой оси (рис. 2).

Основными задачами кинематики являются:

описание совершаемого телом движения с помощью математических формул, графиков или таблиц;

определение кинематических характеристик движения (перемещения, скорости, ускорения).

Движение тела можно описать только относительно какого-либо другого тела. Тело, относительно которого рассматривается исследуемое движение, называют телом отсчета (ТО). Для описания движения используются формулы, графики и таблицы, выражающие зависимость координат, скоростей и ускорений от времени.

Основным свойством механического движения является его относительность: характер движения тела зависит от выбора системы отсчета (СО).

Систему отсчета, выбираемую для описания того или иного движения, образуют: тело отсчета, связанные с ним система координат (СК) и прибор для измерения времени (часы) (рис. 3).

Система координат и часы необходимы для того, чтобы знать, как с течением времени изменяется положение тела относительно выбранного тела отсчета.

Для описания движения материальной точки в пространстве вводятся такие понятия, как траектория, перемещение, путь.

Линию, которую описывает материальная точка в процессе движения по отношению к выбранной СО, называют траекторией (от латинского слова trajectorus — относящийся к перемещению). Если траектория является прямой линией, то движение называется прямолинейным, в противном случае — криволинейным.

Длина участка траектории, пройденного МТ в процессе движения, называется путем (s).

Термин «скаляр», происходящий от латинского слова scalarus — ступенчатый, введен У. Гамильтоном в 1843 г.

Термин «вектор» произошел от латинского слова vector — несущий и введен У. Гамильтоном в 1845 г.
Перемещением называют вектор направленный из точки, заданной радиус-вектором где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором где МТ находится в рассматриваемый момент времени (рис. 4):

Для количественного описания механического движения тел (МТ) вводятся физические величины, характеризующие пространство и время: длина l, время t.

Длина l определяется как расстояние между двумя точками в пространстве. Основной единицей длины в Международной системе единиц (СИ) является метр (1м).

Время t между двумя событиями в данной точке пространства определяется как разность показаний прибора для измерения времени, например часов. В основе работы прибора для измерения времени лежит строго периодический физический процесс. В СИ за основную единицу времени принята секунда (1с).
В зависимости от вида движения могут выбираться следующие системы координат: одномерная (на прямой линии) (рис. 5), двухмерная (на плоскости) (рис. 6), трехмерная (в пространстве) (рис. 7).

Произвольное движение материальной точки может быть задано одним из трех способов: векторным, координатным, траекторным (естественным).

При векторном способе описания положение движущейся МТ по отношению к выбранной системе отсчета определяется ее радиус-вектором

Радиус-вектор всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением

При координатном способе описания положение точки относительно СО определяется координатами х, у, z, а закон движения — уравнениями х = х(t), у = y(t), z = z(t) (см. рис. 8). Исключив из этих уравнений время /, можно найти уравнение траектории движения точки.

Траекторный (естественный) способ описания движения применяется, когда известна траектория движения материальной точки по отношению к выбранной СО (рис. 9).

Текущее положение материальной точки в данном случае определяется расстоянием s, измеренным вдоль траектории от выбранного на ней начала отсчета (точка О на рисунке 9). Кинематический закон движения МТ при этом задается уравнением s = s(t).

Если положить в основу классификации движений характер изменения скорости, то получим равномерные и неравномерные движения, а если вид траектории, то — прямолинейные и криволинейные.

Для того чтобы описать быстроту изменения положения тела (МТ) и направление движения относительно данной СО, используют векторную физическую величину, называемую скоростью

Чтобы охарактеризовать неравномерное движение тела (МТ), вводят понятие средней скорости движения как отношение перемещения тела к промежутку времени за который это перемещение произошло (рис. 10):

Средней путевой скоростью называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени его прохождения:

Средняя путевая скорость в отличие от средней скорости является скалярной величиной.

Однако средняя скорость характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.

Для того чтобы отразить характер движения в данной точке траектории или в данный момент времени, вводится понятие мгновенной скорости — это скорость тела (МТ), равная производной перемещения по времени:

Вектор мгновенной скорости в любой точке траектории направлен по касательной к ней (см. рис. 10).

В СИ основной единицей скорости является метр в секунду

Простейший вид движения — равномерное. Равномерным называется движение МТ, при котором она за любые равные промежутки времени совершает одинаковые перемещения.

При прямолинейном движении в одном направлении модуль перемещения равен пройденному пути s. Скорость равномерного движения равна отношению перемещения тела ко времени за которое это перемещение произошло:

При равномерном движении скорость постоянна и равна средней скорости определяемой выражением (2).

Зависимость перемещения от времени имеет вид Вследствие того, что — радиус-вектор, задающий положение МТ в начальный

момент времени получаем кинематическое уравнение движения в векторном виде

При проецировании радиус-вектора, например, на ось Ох получаем кинематическое уравнение для координаты при равномерном движении:

Здесь — координата тела (МТ) в начальный момент времени Если начальный момент времени уравнение принимает вид

Для наглядности описания механического движения удобно представлять зависимости между различными кинематическими величинами графически.

Скорость МТ при равномерном движении постоянна, поэтому график зависимости проекции скорости от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис.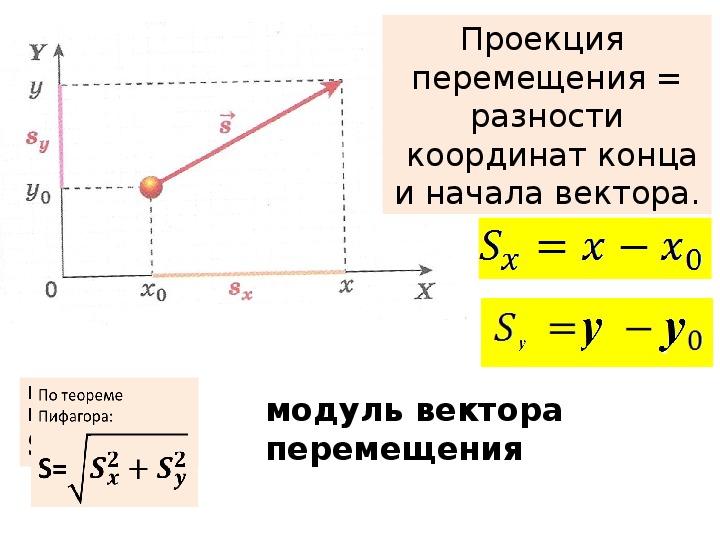 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси а 2 — в отрицательном Площади закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей за промежуток времени

График зависимости координаты материальной точки, движущейся равномерно прямолинейно, от времени x(t) — линейная функция (рис. 12).
На рисунке отрезок / прямой соответствует равномерному движению в положительном направлении оси Ох; отрезок 2 прямой — покою материальной точки; отрезок 3 прямой — равномерному движению в отрицательном направлении оси Ох.

Проекция скорости движения численно равна угловому коэффициенту этой прямой линии:

т. е. тангенсу угла наклона (tga) этой прямой к оси времени.

График зависимости пути (модуля перемещения| от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).

Угловой коэффициент (tga) этой прямой численно равен модулю скорости движения v. Поэтому на рисунке большей скорости у, соответствует больший угловой коэффициент (tg).

Для тел (МТ), участвующих в нескольких движениях одновременно, справедлив принцип независимости движений:

если тело (МТ) участвует в нескольких движениях одновременно, то его результирующее перемещение равно векторной сумме перемещений за то же время в отдельных движениях:

Как следует из принципа независимости движений, конечное перемещение тела не зависит от порядка (последовательности) суммирования перемещений при отдельных движениях.

Пусть, например, при переправе через реку, скорость течения которой мы движемся на лодке со скоростью относительно воды. В этом случае результирующее перемещение (рис. 14) лодки относительно берега будет складываться из собственного перемещения относительно воды и перемещения вместе с водой вследствие течения реки:

На основе принципа независимости движений формулируется классический закон сложения скоростей:

результирующая скорость тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей отдельных движений (рис. 15):

Этот закон справедлив только при условии, что скорость каждого отдельного движения мала по сравнению со скоростью света

Так, для рассмотренного примера (см. рис. 14) результирующая скорость лодки

Равномерное движение по прямой линии в повседневной жизни встречается сравнительно редко. Например, различные транспортные средства (автомобиль, автобус, троллейбус и т. д.) равномерно и прямолинейно движутся лишь на небольших участках своего пути, в то время как на остальных участках их скорость изменяется как по величине, так и по направлению.

Для измерения мгновенной скорости движения на транспортных средствах устанавливается прибор — спидометр.

Физика – 10

Так как отношение 1
t в формуле является положительной скалярной величиной, то направление вектора скорости совпадает с направлением вектора перемещения . Единица измерения скорости в СИ – метр в секунду:

[v] = [s]
[t] = 1м
1с = 1м
с

Если скорость известна, то можно определить перемещение материальной точки за промежуток времени t при прямолинейном равномерном движении:

= ⋅ t. (1.2)

•При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:

l = s = vt. (1.3)

s_x = v_xt. (1.4)

Можно получить формулу для вычисления координаты точки х в произвольный момент времени (см. : тема 1.2):

x = x₀ + s_x , x = x₀ + v_xt. (1.5)

Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если

материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (c).
Из формулы (1.5) определяется выражение для проекции скорости:

v_x = x-x₀
t. (1.6)

Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость – время будет представлять собой линию, параллельную оси времени – скорость такого движения не зависит от времени (e):

Урок по физике в 9 классе “Перемещение тела при прямолинейном равноускоренном движении”

Физика 9 класс

УМК А.В. Пёрышкин

Тема урока. Перемещение при прямолинейном равноускоренном движении

Цель урока: создать условия для восприятия формулы перемещения, формировать навыки решения задач различных типов, используя формулы равноускоренного прямолинейного движения, развивать логическое мышление обучающихся

Тип урока: изучение нового материала, закрепление полученных знаний

Оборудование: компьютер, проектор, презентация, карточки с задачами и тестами.

Ход урока

Организационный момент

Девиз урока: «Я буду умным,

Я буду мудрым,

Я буду стараться…

У нас все получится!”

Проверка домашнего задания

1)Устный опрос.

-Какой вид механического движения мы изучаем?

-Какой вид движения мы изучили?

-Что называют механическим движением?

-В чем отличие равномерного от равноускоренного движения?

-Какая величина не меняется при равномерном движении?

-Какая величина не меняется при равноускоренном движении?

-Запишите на доске формулы скорости и ускорения равноускоренного движения

2)Решение задач различных видов

Задача 1. О какой скорости – средней или мгновенной – идет речь: пуля вылетает из винтовки со скоростью 800 м/с; самолет летит из Киева в Москву со скоростью 800 км/ч; спидометр в автомобиле показывает 75 км/ч?

Задача 2. Скорость зайца 15 м/с , а скорость волка 54 км/ч. Кто из них имеет большую скорость?

Задача 3. Автомобиль движется со скоростью 36 км/ч, и в течение 10 с тормозит с ускорением 0,5 м/с². Необходимо определить его скорость в конце

торможения

Задача 4. На графике представлены 4 зависимости скорости от времени, и необходимо определить, у какого из этих тел максимальное, а у какого минимальное ускорения.

Изучение нового материала

На доске два графика.

-Какой из них соответствует равномерному движению? Равноускоренному движению?

-Как найти перемещение при равномерном движении?

-Каков геометрический смысл перемещения при равномерном движении?

-Как найти площадь прямоугольника? Треугольника?

-Как найти площадь фигуры, расположенной под графиком проекции скорости?

Вывод формулы перемещения записывает на доске один ученик, остальные работают в тетрадях, учитель корректирует записи.

Закрепление полученных знаний

Опрос

-Равноускоренному или равнозамедленному движению соответствует полученная формула?

-Как записать формулу для расчета перемещения, если тело движется с уменьшающейся по модулю скоростью?

-Каковы единицы измерения скорости, ускорения, перемещения в СИ?

2) Решение текстовых задач

Задача № 1. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5с. Найти тормозной путь.

Задача № 2. Зависимость скорости материальной точки от времени задана формулой υ_х= 6t. Написать уравнение координаты и найти путь за 10 c.

3)Решение графических задач по материалам ОГЭ

1.Какой из графиков (рис.1) соответствует равноускоренному движению тела, при котором вектор ускорения направлен противоположно вектору скорости?

А. 1. Б. 2. В. 3.

2.По графику зависимости скорости от времени (рис.2) определите ускорение тела в момент времени t = 4 c.

А.0,5 м/с². Б. 4 м/с². В. 0,8 м/с².

3.На каком из графиков (рис3) представлено движение тела, имеющего наибольшее ускорение?

А. 1. Б. 2. В. 3

Рис. 1 Рис. 2 Рис. 3

Проверка полученных знаний

Самостоятельная работа. Тест

1 .По графику зависимости скорости от времени (рис.1) определите модуль ускорения тела.

А. 4 м/с². Б. 1 м/с². В. 32 м/с²

2.На рисунке 2 приведен график зависимости скорости движения тела от времени. Какое уравнение соответствует этому графику?

А. v=3+t . Б. v=3-t. В. v=3-3t.

3.Какой из графиков (рис.3) соответствует уравнению скорости v=2-t?

А. 1. Б. 2. В. 3.

4.Вагонетка, имеющая скорость 2 м/с, начинает двигаться с ускорением 0,25 м/с². На каком расстоянии она окажется через 20 с?

А. 30 м. Б. 50 м. В. 90 м.

5. Подъезжая к уклону, лыжник имел скорость 5 м/с. Найти длину спуска, если движение по нему происходило с ускорением 0, 5 м/с² в течение 4 с.

А. 9 м. Б. 24 м. В. 36 м.

Рис. 1 Рис. 2 Рис. 3

Ответы: 1-Б, 2-Б, 3-А, 4-В, 5-Б

Итог урока.

-Какие виды движения мы рассматривали на уроке?

-Формулу какой физической величины вы вывели?

-Чем отличаются между собой формулы равноускоренного и равнозамедленного движения?

Домашнее задание: выучить формулы из п. 7, выполнить упр.7(1-3)

Скорость, ускорение и смещение – Описание движения с помощью графиков и уравнений – Eduqas – GCSE Physics (Single Science) Revision – Eduqas

$0″> Это уравнение применимо к объектам с постоянным ускорением:

Это когда:

конечная скорость (v) измеряется в метрах в секунду (м/с)
начальная скорость (u) измеряется в метрах в секунду (м/с)
ускорение (a) измеряется в метрах в секунду в квадрате (м/с²)
перемещение (x) измеряется в метрах (м)

Расчет конечной скорости

Приведенное выше уравнение можно использовать для расчета конечной скорости объекта, если известны его начальная скорость, ускорение и перемещение.{2}}{2a}\]

kbf8kdmli8.0.0.0.1:0.1.0.$0.$1.$23″> Эти уравнения движения:

\[ускорение = \frac{изменение\ скорости}}{время\затраченное}\]
\[скорость = \frac{расстояние \ пройденное {время}\]

можно переставить, чтобы сформировать другие полезные уравнения, которые помогут решить.

Если объект меняет скорость, то это уравнение

\[пройденное расстояние\ = скорость \умножить на время\]

становится

\[пройденное расстояние\ = средняя\ скорость \умножить на время\]

\[расстояние\ пройдено = \frac{1}{2} (начальная\ скорость + конечная\ скорость) \times time\]

{2}\]

Вопрос

Игрушечная ракета летит вертикально вверх против силы тяжести с начальной скоростью 20 м/с.{2} = \text{-}5 \]

\[x = 20\text{-}5=15~м\]

Какая формула для скорости?

Далеко не стоит критиковать штрафы за превышение скорости как инструмент общественной безопасности (и источник муниципальных доходов), но, возможно, правоохранительным органам следует подумать о том, чтобы переименовать их в «штрафы за превышение скорости».

Позвольте нам сделать наше дело. Видите ли, хотя эти два понятия связаны, слова «скорость» и «скорость» в физике не относятся к одному и тому же.

Скорость, определенная

Скорость — это общее расстояние, которое проходит объект за определенный интервал времени.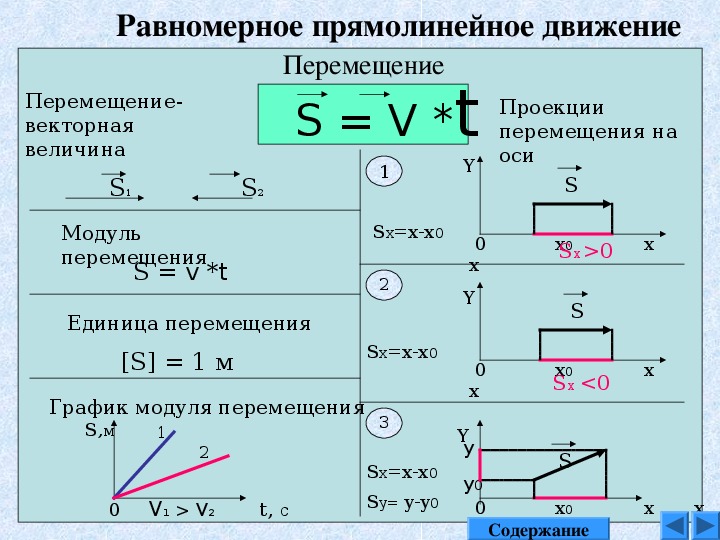

Velocity добавляет в разговор кое-что еще. Будучи тем, что физики называют «векторной величиной», скорость включает в себя как величину, так и направление. С другой стороны, скорость — это «скалярная величина», явление, связанное с величиной, но , а не направлением .

Майкл Ричмонд, доктор философии, профессор Школы физики и астрономии Рочестерского технологического института, определил скорость как «скорость изменения смещения во времени».

Покрытие земли

Что, скажите на милость, такое “перемещение”? По сути, это отмечает изменение положения объекта или разницу между тем, где он физически начинается, и тем, где он заканчивается.

Обратите внимание, что изменение положения объекта не всегда равно пройденному расстоянию. Это может показаться нелогичным, но потерпите нас.

Пробегите один круг по идеальному 8-футовому (2,4-метровому) кругу, и вы преодолеете расстояние в 8 футов.

Однако , вы также вернетесь к исходной начальной точке. Таким образом, это означает, что ваше смещение будет равно 0 футам (т. е. 0 метрам), даже если вы преодолели большее расстояние .

Обучение на примере

Время для другой гипотезы.

Допустим, вы находитесь в спортзале и ведете светскую беседу. Если бы другой посетитель сказал вам: «Сегодня Гэри пробежал 39,3 фута (12 метров) за три секунды», он бы дал вам его скорость , но не его скорость .

Чтобы рассчитать скорость Гэри, нам нужно больше информации.

Если бы наш приятель по спортзалу сказал: «Сегодня Гэри пробежал 39,3 фута (12 метров) на запад за три секунды», то мы бы знали о направлении его движения и хорошо начали.

Формула для расчета скорости объекта выглядит следующим образом:

Здесь буквы “v”, “d” и “t” обозначают соответственно “скорость”, “смещение” и “время”. Другими словами, скорость = смещение деленное на время .

При использовании этой формулы важно измерять перемещение в метрах и время в секундах. Для простоты предположим, что старый Гэри бежал на запад по совершенно прямой линии длиной 12 метров (32,8 фута), поэтому его перемещение равно пройденному им расстоянию.

Мы также знаем, что ему потребовалось три секунды, чтобы преодолеть разрыв между начальной и конечной точками.

Таким образом, подставив числа, мы получим следующее:

Следовательно, Гэри двигался на запад со средней скоростью 4 метра в секунду (13,12 фута в секунду).

(Фразировка имеет значение. Все, что мы сделали, это рассчитали среднюю скорость Гэри; мы не обращались к теме мгновенной скорости, явлению, которое вносит свой собственный поворот в формулу, разбитую выше.)

Заключительные комментарии

Теперь… о так называемых штрафах за превышение скорости. Если вы когда-либо получали его, то направление, в котором двигался ваш автомобиль в то время, должно быть фактором. Сознательно или нет, об этом думали и вы, и полицейский.

Знаете, что может быть хуже слишком быстрой езды? Еду слишком быстро в неправильном направлении . (Рассмотрите улицы с односторонним движением. Или даже дороги с двумя полосами движения, которые заставляют автомобилистов с одной стороны двигаться медленнее.)

Так что да, учитывая все, что мы узнали сегодня, мы думаем, вы могли бы доказать, что “штрафы за превышение скорости” действительно должны называться “штрафами за превышение скорости”. Или что-то подобное. Всем спокойной ночи.

Первоначально опубликовано: 5 января 2022 г.

3.6 Определение скорости и смещения по ускорению – University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

Выведите кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
Использовать интегральную формулировку кинематических уравнений при анализе движения.
Найдите функциональную форму зависимости скорости от времени по заданной функции ускорения.
Найдите функциональную форму зависимости положения от времени по заданной функции скорости.

В этом разделе предполагается, что у вас достаточно знаний в области исчисления, чтобы быть знакомым с интеграцией. В разделах «Мгновенная скорость и скорость» и «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с помощью производной.Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.

Кинематические уравнения интегрального исчисления

Начнем с частицы с ускорением a (t) — известная функция времени.Поскольку производная по времени от функции скорости есть ускорение,

[латекс]\frac{d}{dt}v(t)=a(t),[/latex]

мы можем взять неопределенный интеграл от обеих частей, найдя

[латекс]\int \frac{d}{dt}v(t)dt=\int a(t)dt+{C}_{1},[/latex]

где C ₁ — постоянная интегрирования. Поскольку [latex]\int \frac{d}{dt}v(t)dt=v(t)[/latex], скорость равна

[латекс]v(t)=\int a(t)dt+{C}_{1}.[/latex]

Точно так же производная по времени от функции положения является функцией скорости,

[латекс]\frac{d}{dt}x(t)=v(t).[/латекс]

Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти

[латекс] х (т) = \ int v (т) dt + {C} _ {2}, [/латекс]

, где C ₂ — вторая постоянная интегрирования.

Используя эти интегралы, мы можем вывести кинематические уравнения для постоянного ускорения. С a ( t ) = a константа, и выполняя интегрирование на рисунке, мы находим

[латекс]v(t)=\int adt+{C}_{1}=at+{C}_{1}.[/латекс]

Если начальная скорость v (0) = v ₀ , то

[латекс]{v}_{0}=0+{C}_{1}.[/латекс]

Тогда С ₁ = v ₀ и

[латекс]v(t)={v}_{0}+at,[/латекс]

, что (Уравнение). {2}+{C}_{2}.{2}[/латекс]. а) Какова функция скорости моторной лодки? б) В какой момент времени скорость достигает нуля? в) Какова функция положения моторной лодки? г) Каково водоизмещение моторной лодки с момента начала торможения до момента, когда скорость равна нулю? (e) Нарисуйте график функций скорости и положения.

Стратегия

(a) Чтобы получить функцию скорости, мы должны проинтегрировать и использовать начальные условия, чтобы найти постоянную интегрирования. (b) Мы устанавливаем функцию скорости равной нулю и находим t .(c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальная позиция принимается равной нулю, нам нужно только оценить функцию позиции при [latex]t=0[/latex].

Решение

Примем t = 0 за время, когда лодка начинает замедляться.

Показать ответ
Из функциональной формы ускорения мы можем решить рисунок, чтобы получить v ( t ):
[латекс]v(t)=\int a(t)dt+{C}_{1}=\int -\frac{1}{4}tdt+{C}_{1}=-\frac{1} {8}{t}^{2}+{C}_{1}. {3}=21,1\,\текст{м}\текст{.}[/латекс]

Рис. 3.30 (a) Скорость моторной лодки как функция времени. Моторная лодка уменьшает скорость до нуля за 6,3 с. В моменты времени, превышающие это значение, скорость становится отрицательной, то есть лодка меняет направление. (b) Положение моторной лодки в зависимости от времени. В момент времени t = 6,3 с скорость равна нулю, и лодка остановилась. В моменты времени, превышающие это, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, где она возникла.
Значение
Функция ускорения линейна во времени, поэтому при интегрировании используются простые полиномы. На рисунке мы видим, что если мы расширим решение за точку, где скорость равна нулю, скорость станет отрицательной, и лодка изменит направление. Это говорит нам о том, что решения могут дать нам информацию, выходящую за рамки нашего непосредственного интереса, и мы должны быть осторожны при их интерпретации. {2}[/латекс].{3}.[/латекс]
Скорость можно записать как v ( t ) = 5 t (1 – t ), что равно нулю при t = 0 и t = 1 с.
Определение, различия, формулы с примерами
Расстояние и перемещение — это основные физические величины, используемые для измерения длины, пройденной телом. Разница между Distance и Displacement делает их важными и особенными в использовании.Это тема, в которой многие студенты путаются между двумя понятиями. Мы постарались упростить концепции вместе с примерами для вашего удобства. В этой статье мы поймем две величины, их различия и сходства. Расстояние и перемещение — важная концепция для всех кандидатов, сдающих экзамен JEE. Читайте дальше, чтобы узнать больше о Distance и Displacement.
Прочтите о звуковых волнах здесь.
Расстояние
Расстояние — это фактическая длина, пройденная телом.Его также называют длиной пути.
Например, объект движется из точки O в P, тогда длина пути будет равна расстоянию OP = 360 м.
Расстояние является скалярной величиной. Он имеет только величину и не имеет направления.
Перемещение
Перемещение кратчайшее расстояние между начальным и конечным положением движения. Смещение обычно обозначается S или Δ x.
Пусть x1 — это положение объекта в момент времени t1, а x2 — это положение объекта в момент времени t2.
Тогда перемещение (Δx) определяется как:
Перемещение (Δx) = конечное положение – исходное положение = (x2 – x1) Затраченное время (ΔT) = (t2 – t1)
Например, объект путешествие из точки A в B, здесь длина пути ACDB — это расстояние, пройденное объектом, а длина пути AB — смещение.

Смещение — это векторная величина, которая имеет как величину, так и направление.
Подробнее об электромагнитной индукции см. здесь.
Например, частица движется из точки Q в O, тогда перемещение частицы определяется как:
Перемещение (S) = положение точки O – Положение точки Q = 0 – 240 = – 240 м
Знак минус показывает направление смещения.
Следует помнить:
Смещение может быть как положительным, так и отрицательным. Расстояние не может быть отрицательным.
Пример: Может быть смещение -20 м.Поскольку отрицательный знак указывает на обратное направление, но не может быть пройденного расстояния -20 м
Пройденное расстояние является величиной смещения. Так что это всегда позитив.
Смещение объекта может быть равно нулю, если начальное и конечное положение совпадают, но пройденное расстояние может быть не равно нулю.
Подробно о магнитном эффекте электрического тока.
Пример
Q1 . Во время рыбалки Джастин проезжает 12 км на юг.2}=11,7 км (юго-запад)\)
Подробнее о колебаниях см. в статье по ссылке.
Q2. Круглая площадка имеет радиус 1,2 м. Бегун пробегает два круга по земле, начиная и заканчивая в одном и том же месте. Какое расстояние он преодолел? Сколько было его водоизмещения?
А2. Пройденное расстояние = 2 x длина окружности земли = 15,08 м
Перемещение = 0
Поскольку начальная и конечная точки совпадают.
Надеюсь, эта статья дала вам подробное объяснение расстояний и перемещений.Попрактикуйтесь в этой теме с помощью бесплатных пробных тестов в приложении Testbook.
Часто задаваемые вопросы о расстоянии и смещении᠎
В.1 Что такое расстояние?
Ответ 1 Расстояние – это фактическая длина, пройденная телом.
Q.2 Что такое водоизмещение?
Ответ 2 Перемещение – это кратчайшее расстояние между начальным и конечным положением движения.
Q.3 Каковы единицы измерения расстояния и смещения?
Ответ.3 Единица измерения расстояния и перемещения в метрах (м).
Q.4 Является ли смещение векторной величиной?
Ответ 4 Да, перемещение является векторной величиной.
Q.5 Является ли расстояние векторной величиной?
Ответ 5 Нет, расстояние не является векторной величиной.
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получайте мгновенные оповещения о вакансиях бесплатно!
Получите Daily GK и текущие события Capsule и PDF-файлы
Получите более 100 бесплатных пробных тестов и викторин

Подпишитесь бесплатно У вас уже есть аккаунт? Войти
Следующее сообщение
Функция смещения: определение – исчисление Как
Функция смещения сообщает нам, как далеко частица ушла от начальной точки (начала координат) в данный момент времени.
Обратите внимание, что перемещение не совпадает с пройденным расстоянием ; в то время как частица может двигаться вперед и назад или по кругу, смещение представляет собой только разницу между начальным и конечным положением. Это векторная величина, что означает, что она имеет как значение, так и направление (например, 20 м на север или минус 50 футов). Оно равно пройденному расстоянию только в том случае, если движение прямолинейное в постоянном направлении.
Нахождение функции смещения в (относительно) простых ситуациях
Пример вопроса: Предположим, мяч движется вниз по склону с начальной скоростью 11 м/с и ускорением 2 м/с.Чему равно перемещение при t = 2?
Формула для нахождения смещения (Δ с):
Шаг 1: Определите части уравнения (из вопроса):
v ₀ = 11 м/с
т = 2 с
а = 2 м/с
Шаг 2: Вставьте значения в формулу и решите.
По приведенному выше уравнению перемещение при t = 2 будет:
( 11 м/с · 2 с) + (½ · 2 м/с · 2 с ² ),
Давая ответ как 22 м + 4 м = 26 м.
Как выводится формула?
Допустим, двумерная частица совершает движение в каком-то постоянном направлении (представьте себе точку на числовой прямой).
Скорость частицы может изменяться, но для упрощения вычислений предположим, что ускорение постоянно.
Ускорение определяется как изменение скорости в единицу времени , поэтому, если у вас есть начальная скорость и постоянное ускорение, вы можете записать ускорение в любой момент времени через скорость:
или
Используя немного алгебры, можно записать скорость через ускорение:
Скорость — это изменение положения в единицу времени, поэтому скорость частицы — это первая производная положения.
и
С небольшой перестановкой и алгебраической подстановкой вы получите:

Установив начальное расстояние равным 0, вы получите уравнение, которое дает вам смещение или изменение положения.

Каталожные номера
Расстояние, перемещение и положение. Получено с https://washingtonlee.apsva.us/wp-content/uploads/sites/38/2017/02/Distance-Displacement-and-Position-Notes. pdf 26 февраля 2019 г.
Элерт, Гленн. Уравнения движения.Гипертекст физики. Получено с https://physics.info/motion-equations/ 27 февраля 2019 г.
————————————————– ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Какова формула смещения и расстояния? – Рестораннорман.ком
Какая формула смещения и расстояния?
Формула смещения. Смещение — это изменение положения объекта относительно начала координат. Смещение является векторной величиной и поэтому имеет как величину, так и направление. Смещение = (конечная позиция) – (исходная позиция) = изменение позиции. D = Xf-Xi.
Какая формула 9 класса водоизмещения?
Общее пройденное расстояние d = 3 м + 5 м + 6 м = 14 м. Величину смещения можно получить, визуализируя ходьбу. Фактический путь от A до B равен 3 м, затем от B до D равен 5 м и, наконец, от D до E равен 6 м. |С| =√92+52 = 10,29 м.
Что такое символ смещения?
Δ x \Delta x Δx — это символ, используемый для обозначения смещения.
В чем сходство и различие между расстоянием и перемещением?
В физике расстояние и смещение используются для обозначения расстояния между двумя точками. Однако это не одно и то же. В то время как расстояние — это длина фактического пути между двумя местоположениями, смещение, с другой стороны, — это длина кратчайшего пути между двумя местоположениями.
Каковы три различия между расстоянием и перемещением?
Расстояние — это полный путь, пройденный телом, а перемещение — кратчайший путь, пройденный телом. Расстояние никогда не может быть нулевым, но смещение может быть. Расстояние никогда не может быть отрицательным, а смещение может быть как положительным, так и отрицательным. Расстояние не уменьшается со временем, тогда как перемещение уменьшается.
Что означает смещение?
1 : акт или процесс перемещения: состояние перемещения шторм, вызвавший перемещение тысяч людей.2а физика: объем или вес жидкости (например, воды), вытесненной (см. смысл 2а смещения) плавающим телом (например, кораблем) равного веса.
Пример смещения?
Перемещение определяется как акт перемещения кого-либо или чего-либо из одного положения в другое или измерение объема, замененное чем-либо другим. Примером водоизмещения является вес воды, которую заменяет океанский лайнер.
Что такое смещение на примере?
Что понимается под водоизмещением?
Что такое смещение краткий ответ?
Перемещение (обозначается символом d или s), также называемое длиной или расстоянием, представляет собой одномерную величину, представляющую расстояние между двумя определенными точками.Стандартной единицей перемещения в Международной системе единиц (СИ) является метр (м). Смещение обычно измеряется или определяется по прямой линии.
Какое определение смещения лучше всего?
Слово «смещение» означает, что объект сдвинулся или был смещен. Смещение определяется как изменение положения объекта.
Каковы характеристики водоизмещения?
1) Это векторная величина, поэтому она имеет величину и направление.2) Он может быть положительным или отрицательным в зависимости от его направления. 3) Если вы начали и закончили в одной и той же точке, то смещение равно нулю. 4) Оно может быть равно или меньше расстояния, но не больше расстояния.
Что такое 9 класс водоизмещения?
Смещение: Кратчайшее расстояние между начальным и конечным положением движущегося объекта в заданном интервале времени от начального до конечного положения объекта называется смещением объекта.
Что такое расстояние и перемещение для класса 9?
Расстояние — фактическая длина пути, пройденного объектом. Смещение — это кратчайшее расстояние между начальным и конечным положением объекта. Это скалярная величина. Это векторная величина. Перемещение тела может быть равно нулю.
В чем разница между расстоянием и перемещением для класса 9?
Расстояние является скалярной величиной, поскольку зависит только от величины, а не от направления.Смещение является векторной величиной, так как зависит как от величины, так и от направления. Расстояние можно измерить по непрямому пути. Смещение можно измерить только по прямому пути.
Что такое единица смещения СИ?
Единицей перемещения в СИ является метр (м). Расстояние — это величина смещения между двумя положениями.
Какова формула смещения и его единица СИ?
Кратчайшее расстояние между начальной и конечной точками называется смещением.S.I единица смещения = м.
Что такое скорость в системе СИ?
метров в секунду
Определение, вывод и примеры решения
Что такое смещение?
Перемещение — это термин, который используется для описания перемещения из одного места в другое. Если человек встает со стула, чтобы пойти на кухню, то это называется перемещением. Он определяется как изменение положения объекта. Когда тело перемещается из одного положения в другое, кратчайшее расстояние между начальным положением и конечным положением тела вместе с направлением называется смещением.
также читал:
Вывод смещения
формула и как смещение рассчитано:
Δx = x _F – x _I
где x — конечное положение
X _i — начальное положение, т.е. откуда объект начинает движение
Δx — изменение положения объекта.
Если объект движется в двух разных направлениях x и y, то перемещение будет
S = √x ² + y ²
S = ut + ½ at ²
3 Здесь
u = начальная скорость
v = конечная скорость
a = ускорение
t = затраченное время
Подробнее:
Разница между перемещением и расстоянием
Разница между расстоянием и перемещением. Для расстояния направление не нужно, но для вычисления перемещения нужно направление. Смещение можно измерить; таким образом, это физическая величина, но здесь также задано направление, что делает ее векторной величиной.
Подробнее:
Решенные примеры
Q.1. Велосипедист едет на своем велосипеде из точки А в точку В. Расстояние между точками А и В равно 5 км. Он повернул назад и затем едет из положения B в положение C. Расстояние B и C равно 4 км.какое смещение.

Решение: Формула и как рассчитывается смещение:
Δx = x _F – x _I

Расстояние между A и B- 4 км
Таким образом, перемещение, которое равно
D= конечное положение – исходное положение
= 4км – 2км
= 2км
Q.2. Рам проехал 3 км из точки А в точку В, а затем прошел расстояние 4 км под прямым углом к точке АВ. Каково будет результирующее смещение?
Решение: Здесь баран сначала двигался из точки A в точку B по прямой линии, а затем под прямым углом, который может быть как вверх, так и вниз. Таким образом, получается прямоугольный треугольник.
Таким образом, теорема Пифагоры будет применяться:
AC ² = AB ² = BC ² + BC ² + BC ²
AC = √ab ² + BC ²
AC = √ 3 ² +4 ²
=√25
= 5 км
Подробнее:
Q.3. Автомобиль проезжает 4 м на восток, а затем поворачивает, чтобы проехать еще 3 м на юг. Что такое водоизмещение автомобиля?
Решение: Здесь указаны направления,
от A до B- 4 м
от B до C- 3 м
Здесь расстояние будет
4 км + 3 км = 7 км )
Для смещения мы должны помнить, что было начальным и конечным положением, и поэтому мы должны видеть кратчайшее расстояние, которое равно AC.
Таким образом, теорема Пифагоры будет применяться:
AC ² = AB ² = BC ² + BC ² + BC ²
AC = √ab ² + BC ²
AC = √ 4 ² +4 ²
AC= =√3 ²
= 5,65 км
Таким образом, полное перемещение составит 5,65 км
Q.403. Автомобиль движется из пункта А в пункт В 4 км, затем из пункта В в пункт С под прямым углом 3 км, а затем возвращается из пункта С в пункт А 5 км.Какими будут расстояние и перемещение?
Решение: Расстояние = AB + BC + AC
= 4+3 +5
= 12 км
Расстояние между начальным и начальным положением равно смещению
Конечное положение и начальное положение совпадают, т.е. , смещение здесь будет равно 0.
Читайте также:
На что следует обратить внимание
При расчете смещения следует помнить о некоторых вещах:
Смещение — это изменение положения объекта.
Смещение измеряется векторной величиной, потому что оно зависит от того, насколько далеко простирается объект.
Перемещение может быть нулевым, если пройдено расстояние, но нет изменения положения.
Перемещение прямо пропорционально скорости .
Подробнее:
Примеры вопросов
Вопросы: Дайте простое определение смещения.
Ответ: Когда тело перемещается из одного положения в другое, кратчайшее расстояние между начальным и конечным положением тела вместе с направлением называется перемещением.Смещение также описывается как относительное положение, возникающее в результате движения.
Вопрос: Как смещение можно описать уравнением?
ANS:
ANS: Формула и как рассчитывается смещение:
Δx = x _F – x ^I

, где xf – это конечное положение, где объект достигает
X ⁱ — начальное положение, т.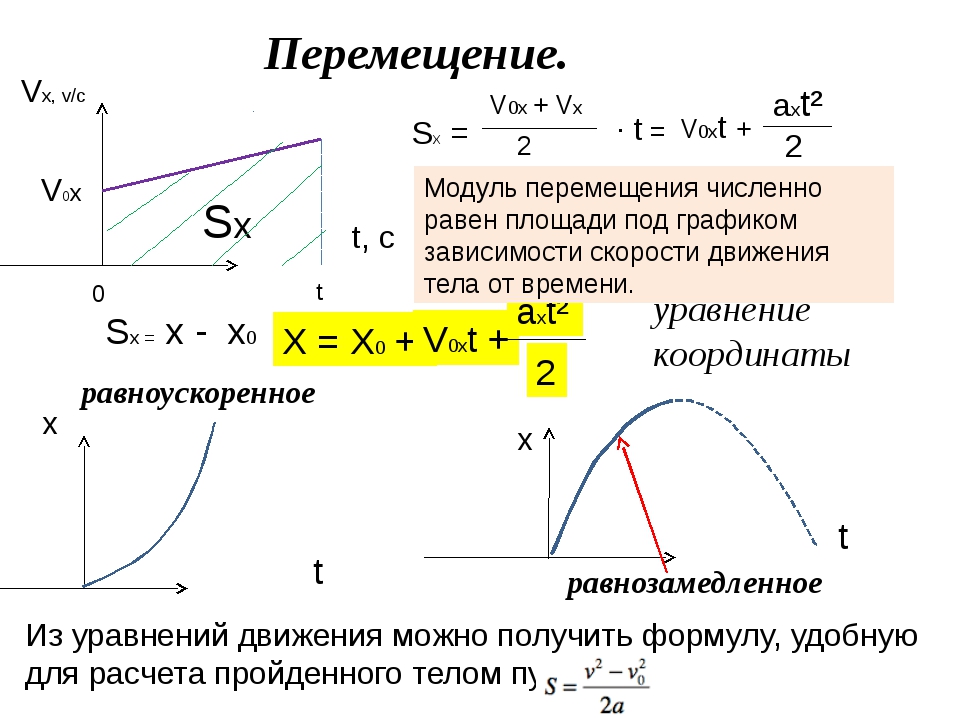 е. откуда объект начинает движение
Δx — изменение положения объекта.
Вопрос: От чего зависит смещение?
Ответ: Перемещение зависит от начального и конечного положения пути, который проходит объект. Дельта x или дельта y — это символ смещения, а дельта — изменение положения. Таким образом, скорость зависит от пройденного пути, а скорость зависит от перемещения.
Подробнее:
Вопрос: Является ли смещение скалярной или векторной величиной?
Ответ: Расстояние — это скалярная величина, указывающая, какой путь прошел объект во время своего движения, а смещение — это векторная величина, которая зависит от того, как далеко объект достигает.Это относится к изменению общей позиции. Это физическая величина, но это физическая векторная величина.
Вопрос: Может ли смещение быть равным нулю?
Ответ: Ответ на этот вопрос — да, смещение может быть равно нулю, поскольку смещение известно как изменение положения.
Например,
Когда объект стартует из точки А, проходит через точки В и С и снова возвращается в точку А. Здесь смещение будет равно нулю.
Объект завершает путешествие по круговой траектории, смещение будет равно нулю.
Вопрос: Чем расстояние отличается от смещения?
Ответ: Разница между расстоянием и перемещением заключается в направлении. Для расстояния направление не нужно, но для вычисления перемещения нужно направление. Смещение можно измерить; таким образом, это физическая величина, но здесь также задано направление, что делает ее векторной величиной.
Подробнее:
Вопрос: Может ли смещение быть отрицательным?
Ответ: Как правило, смещение может быть отрицательным, поскольку смещение относится к изменению положения при рассмотрении направления.При расчете смещения необходимо направление. Например,
Если начальное положение 8 м, а конечное положение 2 м
Тогда здесь перемещение будет 2 м – 6 м = -4 м
Вопрос: Пропорционально ли перемещение скорости? Объяснять?
Ответ: Да, смещение может быть прямо пропорционально скорости при постоянном времени.