Физика формулы прд: Прямолинейное равномерное движение :: Класс!ная физика

Кинематика. Прямолинейное движение

Средняя скорость движения
Уравнение скорости при ПРмД
Перемещение при ПРмД
Уравнение ПРмД
Сложение скоростей
Сложение перемещений
Определение ускорения
Средняя скорость при ПРуД
Уравнение скорости при ПРуД
Перемещение при ПРуД
Уравнение координаты при ПРуД
Путь за одну n-ю секунду при ПРуД

Движение по окружности

Связь между периодом и частотой
Угловая скорость по определению
Связь между угловой скоростью и частотой и периодом
Ускорение при движении по окружности (центростремительное)
Связь между линейной и угловой скоростями
Связь между ускорением и периодом

Динамика

Первый закон Ньютона
Второй закон Ньютона
Третий закон Ньютона
Закон Гука
Сила трения скольжения
Сила трения покоя
Сила трения скольжения на наклонной плоскости
Сила трения покоя на наклонной плоскости
Закон всемирного тяготения
Сила тяжести на поверхности Земли и на высоте Н
Ускорение свободного падения на поверхности Земли и на высоте Н
Первая космическая скорость
Скорость ИСЗ на высоте Н
Период обращения ИСЗ

Работа и мощность.

Импульс, энергия. Законы сохранения

Импульс тела (по определению)
Cвязь между импульсом силы и изменением импульса тела
Закон сохранения импульса тел
Механическая работа (по опр.)	A = Fs cosα
Кинетическая энергия
Потенциальная энергия тела, поднятого над Землей	Ep = mgh
Потенциальная энергия упруго деформированного тела
Закон сохранения энергии в отсутствие трения	Ек1 + Ер1 = Ек2 + Ер2
Закон сохранения энергии при наличии трения	Ек1 + Ер1 = Ек2 + Ер2 +
Работа силы трения	Атр = – F трs
Мощность (по определению)
Мощность тела при равномерном движении (или мгновенная)
КПД

Статика

Первое условие равновесия
Вращающий момент силы
Второе условие равновесия

МКТ идеального газа

Количество вещества в молях
Число молекул в массе m
Молярная масса (масса моля)
Масса вещества
Масса одной молекулы
Плотность вещества
Связь между средней квадратичной скоростью и температурой
Связь между температурой Цельсия t и Кельвина T	T = t + 273
Связь между средней кинетической энергией и температурой
Концентрация молекул
Основное уравнение МКТ идеального газа
Давление (по определению)
Связь между давлением газа и средней кинетической энергией
Связь между давлением газа и T
Уравнение состояния идеального газа Менделеева-Клапейрона
Объединенный газовый закон Клапейрона
Закон Бойля-Мариотта (изотермич. )
Закон Гей-Люсака (изобарный)
Закон Шарля (изохорный)

Параболическое движение: горизонтальное, под углом к горизонту. Формулы, график, тесты

Тестирование онлайн

Движение тела, брошенного горизонтально

Рассмотрим движение тела, брошенного в горизонтальном направлении с некоторой высоты h и начальной скоростью v₀. Траектория такого движения имеет вид спадающей ветви параболы.

Для описания движения тела необходимо задать координатные оси. Ось Оy направим вертикально вверх, горизонтальную ось Оx – вдоль полета. Такое движение по криволинейной траектории рассматривают как сумму двух движений, протекающих независимо друг от друга – движение с ускорением свободного падения вдоль оси Оy и равномерного прямолинейного движения вдоль оси Оx.

Движение вдоль горизонтальной оси Оx равномерное.

Движение вдоль вертикальной оси ОУ – свободное падение тела с некоторой высоты h (на графике y

0).

Реальная скорость тела в некоторый момент времени – это векторная сумма горизонтальной составляющей скорости v_x и вертикальной скорости v_y.

Движение тела, брошенного под углом к горизонту

Угол броска определяет траекторию движения, дальность полета, максимальную высоту подъема тела.

Аналогично движению тела, брошенного горизонтально, это движение рассматривают как сумму независимых движений: равномерного движения вдоль горизонтальной оси ОХ и свободного падения тела вдоль вертикальной оси ОУ.

Движение вдоль горизонтальной оси ОХ равномерное.

Движение вдоль вертикальной оси ОУ – свободное падение тела, брошенного вертикально вверх с некоторой начальной скоростью v_0y. Тело поднимается на максимальную высоту h, затем возвращается вниз.

Действительная скорость, с которой движется тело.

Упражнения

При каком угле бросания достигается максимальная дальность полета?

При угле бросания 45⁰, так как можно вывести формулу для дальности полета . Максимальная дальность полета будет при

Неделя литовской культуры-2015

Дни литовской культуры проходят в гимназии с 2003 года, и это стало доброй традицией. За это время реализован не один образовательный проект, гимназия принимала видных деятелей культуры, искусства и литературы Литвы.

Гостями церемонии открытия Недели стали заместитель председателя ассоциации учителей литовского языка в Калининградской области Альгирдас Кормилавичус, фольклорный коллектив «Рутяле» (г. Гурьевск) под руководством Ирены Тирюбы, фольклорный коллектив (художественный руководитель Ирма Куркова) из пос. Переславское «Куполите». Ирена Тирюба рассказала о народных литовских инструментах и особенностях национального костюма.

В рамках реализации гимназического проекта «Неделя литовской культуры» состоялась открытая лекция Б. Н. Адамова для учащихся гимназии. Борис Николаевич Адамов – член правления и один из организаторов Калининградского клуба краеведов, автор книги «Кристионас Донелайтис. Время. Люди. Память». В лекции об известных литовцах Кёнигсберга он особое внимание уделил Людвигу Резе – литовскому поэту, критику, переводчику, профессору и ректору Кёнигсбергского университета.

Тренер баскетбольной команды БФУ им.И. Канта Гедиминас Мелунас провел мастер-класс для баскетбольной команды 5«А» класса. Ребятам были показаны новые техники и приемы игры в баскетбол, которые многому  их научили. Время пролетело очень быстро, но тренер обещал встретиться еще раз.

Учащиеся 10-х классов, слушатели Школы юного дипломата, совершили визит в Генеральное консульство Республики Литва. Это событие стало частью программы Дней литовской культуры в гимназии № 40. Учащихся встречали Генеральный консул господин Витаутас Умбрасас и атташе по культуре господин Романас Сенапедис, которые очень тепло и радушно отнеслись к гостям. На встрече обсуждались такие вопросы, как путь дипломата в профессию. Другой интересующей всех участников темой был вопрос молодежного международного сотрудничества. Учащиеся поделились своим впечатлениями от проектов с литовскими школами и гимназиями. Другим вопросом обсуждения стала деятельность консульства в сфере обмена культур на территории Калининградской области. 

10-я юбилейная Неделя Литовской культуры в гимназии № 40 завершилась 20 февраля 2015 г. Почетными гостями церемонии стали руководитель представительства МИД России в Калининграде Павел Анатольевич Мамонтов, Витаутас УМБРАСАС, министр-советник, исполняющий обязанности генерального консула Литовской Республики, заместитель председателя ассоциации учителей литовского языка в Калининградской области Альгирдас Кормилавичус, руководитель общественной кафедры «Образование и дипломатия» гимназии №40, главный специалист-эксперт Представительства МИД России в Калининграде Юлия Изидоровна Матюшина. Были подведены итоги Недели, награждены участники и победители различных конкурсов.  В конкурсе чтецов «По следам  литовских поэтов» среди учащихся 5-11 классов победителями стали Булаев Дмитрий, ученик 6«С» класса, Балесная Мария, ученица 7«Б» класса, Даудова Деши, читавшая стихотворения на литовском языке. В фотоконкурсе «Путешествие по Литве» победителем конкурса стала творческая группа 8«О» класса (Волошина Тамара, Громазина Арина, Рубцова Лариса Владимировна). Дипломы победителям вручали руководитель представительства МИД России в Калининграде Павел Анатольевич Мамонтов и Витаутас Умбрасас, министр-советник, исполняющий обязанности генерального консула Литовской Республики. Ярким украшением Церемонии закрытия стало выступление народного коллектива лицея № 35 «Жюгелис (žiogelis)» (руководитель Альгирдас Кормилавичус) и музыкального коллектива гимназии № 40 «Канцона» (руководитель Н.В. Литвинова).

Список альбомов пуст.

Как решать задачи по физике легко

Предмет “Физика” дается с легкостью не каждому ученику. Некоторые задачи вызывают изумления и трудности даже у преподавателей. Существует несложная система, придерживаясь которой решить любую задачу будет реально, сомневаться в ответе не придется, а у педагога отпадут поводы “придраться”. И подготовка к ЕГЭ по физике будет даваться легче.

Решение задач по физике без затруднений

Перед тем как приступить к мозговому штурму, стоит успокоиться и вдумчиво прочитать задачу полностью. Иногда она может быть простой, однако непонятные слова могут создать впечатление безвыходности. Ознакомившись, стоит перечитать еще раз. Вникли? Записываем условия.

Записываем условия

1. Пишем “дано”. С этого шага начинается решение любой задачи. В этом блоке записываем все известные условия, чтобы с легкостью можно было к ним обратиться.
2. Таблица “СИ”. Сведения вписываются справа от “Дано”, требуются, когда нужно перевести какое-то значение (например, сантиметры в метры).

Рисуем схему

Большинство задач подразумевает наличие схемы, даже если этот шаг необязателен, составление схемы облегчит их понимание. Рисунок должен содержать все известные величины, требующиеся для решения. Иногда за добровольное включение схемы начисляются дополнительные баллы к решению задачи.

Определяем неизвестные величины

• Вопрос задачи. Выписав все известные сведения, проводим черту, а затем вписываем, что еще неизвестно.
• Вопрос себе. Чтобы убедиться, что все вопросы заданы, стоит еще раз вчитаться, а затем спросить себя: “Что я ищу?”

Подбираем формулы

1. Формулы. Выпишите все формулы, способствующие решению задачи.
2. Преобразования. Здесь происходят сокращения, если им есть место.
3. Уравнения. Из полученного результата составляется одно или система уравнений.

Решаем уравнения и ищем все неизвестные величины

Под получившееся уравнения нужно написать известные математические величины. Шаг повторяется под все величины под знаком “неизвестно”. Стоит начать с переменных, значение которых определяется проще. Когда все неизвестные найдены, получается ответ. Он обводится прямоугольником. Готово!

Советы

• Некоторые задачи даются к решению непросто. Множество из них требуют повышенного внимания, однако некоторые ученики не питают любви к предмету. Изучать его все же придется. Придерживаясь советов по решению уравнений из курса физики, решение задач покажется несложной процедурой, а понимать программу станет интереснее.
• Внимательно читайте условия. Чтобы понимать способы решения, стоит несколько раз пройтись по условиям, обращая внимание на детали. Чтобы понимать, усвоились ли данные, стоит оторваться от учебника и воспроизвести ее в голове. Совпадает с написанным в учебнике? Нет? Перечитайте еще раз, представив ситуацию наглядно, словно в кино – так картинка станет реальнее!
• Решайте для себя. Чтобы развить интерес к ходу работы, следует погрузиться в нее, понимая, что вы делаете это прежде всего для себя, а не ради оценки, репетитора, преподавателя. Так вы избавляетесь Плот того, что приходится заставлять себя возвращаться к работе.
• Полюбите то, что делаете. Решать, чтобы решить – неправильный путь. Чтобы процесс работы был интересен, нужно полюбить физику. Как развить интерес к тому, что сложно понимать? Помните, что все неизведанное – повод к саморазвитию, а каждая новая решенная задача – новый опыт!
• Повторения. Чтобы каждый следующий раз давался проще, желательно хотя бы раз в день решать по одной задаче. Так выработается привычка, улучшится память и восприятие условий, что в дальнейшем поможет решать новые системы уравнений в считанные минуты!
• Задавайте вопросы. Важно задавать вопрос всякий раз, когда он возникает, не взирая на реакцию. Чем больше ответов вы получите, тем лучше будете ориентироваться в физике.
• Берите перерывы. Иногда на задачу нужен “новый взгляд”. Если ответ не поддается вычислениям уже длительное время, следует переключить свое внимание, а затем снова приступить к работе. Свежие мысли нередко моментально выдают способ решения!
• Помните, что главное – подбор формул. Остальное – лишь подключение знаний математики. Выпишите все формулы, который на ваш взгляд могут подойти, а затем подробно разбирайте, что именно нужно в вашем случае!

Тест по физике «Основные формулы» 9 класс.

Тест по физике «Основные формулы» 9 класс.

1. Если Δr есть перемещение тела за интервал времени Δt, то какая величина определяется отношением Δr/Δt?

1. путь

2. перемещение

3. средняя скорость

2. Какое из уравнений описывает равномерное движение?

1. x = v_oxt + a_xt²/2

2. x = x_o + v_xt

3. v_x = v_ox + a_xt

3. Центростремительное ускорение материальной точки при движениях по окружности с постоянной по модулю скоростью выражается формулой:

1. a = Δr/Δt

2. a = (v² − v_o²)/2S

3. a = v²/R

4. Угловая скорость при движении материальной точки по окружности с постоянной по модулю скоростью выражается формулой:

1. ω = πν

2. ω = π/T

3. ω = Δφ/Δt

5. По какой из представленных формул можно определить силу упругости?

1. F = mg

2. F = μN

3. F = kΔl

6. Какая из приведенных формул выражает закон всемирного тяготения?

1. F = GMm/R²

2. F = kq₁q₂/r²

3. F = GM/R²

7. По какой из приведенных формул можно определить модуль ускорения свободного падения?

1. g = GM₃/(2R₃²)

2. g = GM₃/R₃²

3. g = 2GM₃/R₃²

8. По какой из формул определяется реактивная сила?

1. F = u∙|dm/dt|

2. F = kΔl

3. F = am

9. По какой формуле следует рассчитывать работу силы F, направленной под углом α к перемещению?

1. A = (F/Δr)cos α

2. A = FΔr∙sin α

3. A = FΔr∙cos α

10. Какое из приведенных выражений соответствует закону сохранения механической энергии?

1. A_mp = mgh₂ − mgh₁

2. FΔt = mv₂ − mv₁

3. mgh = mv²/2

как сдать часть 2 ЕГЭ по математике — Учёба.ру

Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Татьяна Петрова,

аспирантка механико-математического факультета МГУ им. Ломоносова,

преподаватель математики учебного центра Challenge

Задание № 9

Что требуется

Выполнить вычисления и преобразования.

Особенности

Это задача на вычисление значения числового или буквенного выражения. Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.

Советы

Нужно знать базовые формулы и уметь их применять.

Задание № 10

Что требуется

Решить задачу с прикладным содержанием.

Особенности

Здесь предлагаются задачи прикладного характера, связанные с такими областями науки, как физика, химия, биология. В этом задании можно встретить все типы уравнений и неравенств: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические и тригонометрические. Ваша задача — выразить требуемую величину из заданной формулы.

Советы

Внимательно читайте условие и старайтесь его понять. Следите, чтобы единицы измерения были приведены к одному виду. Выражайте ту или иную переменную в общем виде и только потом подставляйте числовые значения. Не спешите считать в лоб, пробуйте сокращать.

Задание № 11

Что требуется

Решить текстовую задачу.

Особенности

Всего существует шесть типов текстовых задач. Они могут быть на движение, на совместную работу, на проценты, на смеси, растворы и сплавы, на прогрессии, на оптимальный выбор и целые числа. Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.

Задачи на движение	\(S = V \cdot t\)
Задачи на совместную работу	\(A = p \cdot t\)
Задачи на смеси, растворы и сплавы	\(C = \frac{V_{1}}{ V} \cdot 100\%\)

Советы

Обратите внимание, что формулы в задачах на движение и на работу очень похожи. Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.

Задание № 12

Что требуется

Найти наибольшее или наименьшее значение функции.

Особенности

Здесь требуется уметь находить производную функции, а также исследовать функцию с помощью производной. Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.

Советы

Выучите базовую таблицу производных, а также формулы производной произведения, частного и композиции функций. Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.

Задание № 13

Что требуется

Решить тригонометрическое, рациональное, показательное, логарифмическое уравнение, уравнение с радикалом или смешанное уравнение, содержащее одновременно логарифмы, модули, радикалы.

Особенности

Для решения любого уравнения существует два основных правила. Во-первых, решение всегда должно начинаться с нахождения ОДЗ — области допустимых значений, то есть всех значений переменной, при которых это уравнение имеет смысл. Во-вторых, нужно помнить основные методы решения уравнений и уметь применять их. Как правило, решение данной задачи требует замены, позволяющей свести уравнение к квадратному.

Советы

Для решения тригонометрических уравнений важно знать формулы приведения и знаки тригонометрических функций на четвертях окружности. Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).

Задание № 14

Что требуется

Решить стереометрическую задачу.

Особенности

Это задача на построение сечения многогранника и нахождение его площади, а также на нахождение расстояний и углов в пространстве, нахождение объемов различных многогранников и круглых тел (цилиндр, конус, шар). Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).

Советы

В этой задаче, как правило, два пункта. В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.

Задание № 15

Что требуется

Решить тригонометрическое, рациональное, показательное, логарифмическое (в том числе с переменным основанием) неравенство, неравенство с радикалом, смешанное неравенство, содержащее одновременно логарифмы, модули, радикалы.

Особенности

Здесь необходимо свести сложное неравенство к простейшему. Часто для этого используются замены показательных и тригонометрических функций (не забывайте про ограничения!). Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.

Советы

Метод решения логарифмических неравенств опирается на монотонность логарифмической функции. Помните, что если у логарифма переменное основание, то нужно рассматривать два случая: а) основание лежит в диапазоне от 0 до 1 (функция убывает), б) основание больше единицы (функция возрастает). Если основание переменное, то можно избавиться от перебора случаев, перейдя к новому, постоянному основанию.

В логарифмических неравенствах внимательно следите за областью допустимых значений, применяя формулы действий с логарифмами, она может как расширяться, так и сужаться. И если первую ситуацию легко исправить, то вторая приведет к потере решений, что недопустимо.

Задание № 16

Что требуется

Решить планиметрическую задачу.

Особенности

Под этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.

Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.

Советы

Необходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.

Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.

И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.

Площадь треугольника через высоту и основание	\(S = \frac{1}{2}a \cdot h_{a}\)
Площадь треугольника через две стороны и угол между ними	\(S = \frac{1}{2}a \cdot b \cdot \sin \alpha\)
Площадь треугольника через радиус вписанной окружности	\(S = p \cdot r\), где \(p = \frac{a+b+c}{2}\), \(r\) – радиус вписанной окружности
Площадь треугольника через радиус описанной окружности	\(S = \frac{a \cdot b \cdot c}{4R}\), где \(R\) – радиус описанной окружности
Формула Герона	\(S = {\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p = \frac{a+b+c}{2}\)

Задание № 17

Что требуется

Решить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор.

Особенности

Задача на злобу дня, которая появилась на ЕГЭ только в последние годы. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.

Советы

Внимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтоб подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.

Задание № 18

Что требуется

Решить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.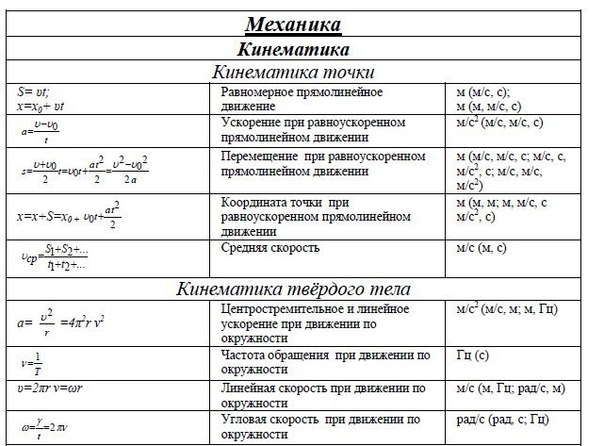

Особенности

Эти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика.

Советы

Чтобы подготовиться к заданиям с параметрами, я рекомендую решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов». Также хочется дать лайфхак для уравнений с двумя неизвестными: как правило, там спрятана геометрическая фигура, построй ее и получишь честное графическое решение.

Задание № 19

Что требуется

Решить задачу на числа и их свойства.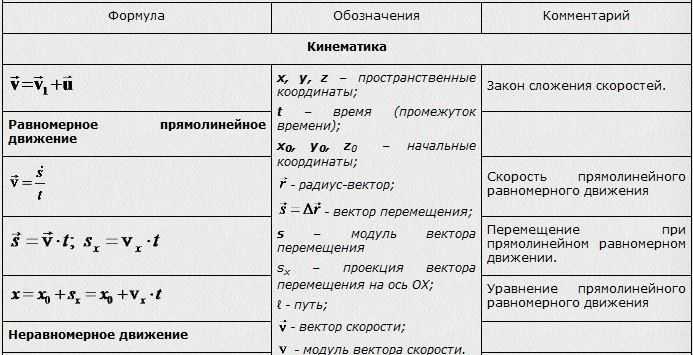

Особенности

Это самая сложная задача экзамена, олимпиадного уровня, она оценивается в четыре первичных балла. Тем не менее материал для ее решения школьники проходят еще в 6-8 классе. Задание требует хорошего логического мышления и математической культуры.

Советы

Повторите основные признаки делимости целых чисел, вспомните понятия «НОК/НОД», выучите формулы арифметической и геометрической прогрессии. «Прорешайте» типовые задания из сборника Г.И. Вольфсона и М.Я. Пратусевича «Арифметика и алгебра». Последние два задания (№ 18 и № 19) — это прямая заявка на 100 баллов.

Движение под действием силы тяжести

Движение под действием силы тяжести.

Основной задачей механики, является определение положения тела в любой момент времени. Решением задачи для частиц, движущихся в поле тяжести Земли являются, уравнения, в проекциях на оси OX и OY :

Этих формул достаточно, чтобы решить любую задачу о движении тела под действием силы тяжести.

А) Тело брошено вертикально вверх

В этом случае v_0x = 0, g_x = 0, v_0y = v_0, g_y = – g_.

Движение тела в этом случае будет происходить по прямой линии, причем сначала вертикально вверх до точки, в которой скорость обратится в нуль, а затем вертикально вниз.

Б) Тело брошено горизонтально

При этом v_0x = v₀ , g_x = 0, v_0y = 0, g_y = – g , х₀ = 0, и, следовательно,

Чтобы определить вид траектории, по которой тело будет дви­гаться в этом случае, выразим время t из первого уравнения и подставим его во второе уравнение. В результате мы получим квадратичную зависимость у от х:

Это означает, что тело при этом будет двигаться по ветви параболы.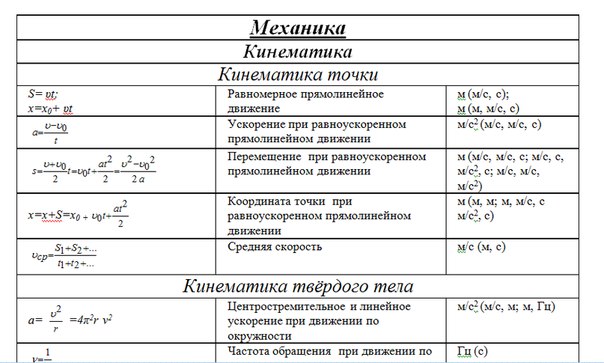

 

В) Тело брошено под углом к горизонту

В этом случае v _{0 x} = v₀ с osα , g_x = 0, v_0y = v₀ sin α , g_y = – g , х₀ = y₀ =  0,   и потому

 

Во всех рассмотренных примерах на тело действовала одна и та же сила тяжести. Однако движения при этом выглядели по-разному. Объясняется это тем, что характер движения любого тела в заданных условиях определяется его начальным состоянием. Недаром все по­лученные нами уравнения содержат начальные координаты и на­чальные скорости. Меняя их, мы можем заставить тело подниматься вверх или опускаться вниз по прямой линии, двигаться по параболе, достигая ее вершины, или опускаться по ней вниз; дугу параболы мы можем изогнуть сильнее или слабее и т. д. И в то же время все это многообразие движений можно выразить одной простой фор­мулой:

Редкие уравнения и формулы современной физики PDF

Замедление времени t ‘= t √ (1 – v 2 / c 2 )

Уменьшение длины ℓ ‘= ℓ √ (1 – v 2 / c 2 )

Релятивистская масса м ‘ = м √ (1 – v 2 / c 2 )

Относительная скорость u ‘= u + v 1 + uv / c 2

Релятивистская энергия E = mc 2 √ (1 – v 2 / c 2 )

Релятивистский моментум p = м v √ (1 – v 2 / c 2 )

Энергия-Импульс E 2 = p 2 c 2 + m 0 2 c 4

Релятивистский эффект Доплера

Фотоэффект K макс = E – ϕ = h (- 0 )

Уравнение Шредингера i ℏ ∂ Ψ ( r , т ) = – ℏ 2 ∇ 2 Ψ ( r , t ) + V ( r ) Ψ ( r , t ) ∂t 2 m E ψ ( r ) = – ℏ 2 ∇ 2 ψ ( r ) + V ( r ) ψ ( r ) 2 м

Принцип неопределенности Гейзенберга Уравнение Ридберга 1 = – R ∞ ⎛ 1 – 1 ⎞ ⎠ λ n 2 n 0 2

Период полураспада Н = Н 0 2 – т / τ

индекс-оф.

es /

 Название Размер
 Android / -
 Галерея искусств/                  -
 Атаки / -
 Переполнение буфера / -
 C ++ / -
 CSS / -
 Компьютер / -
 Конференции / -
 Растрескивание / -
 Криптография / -
 Базы данных / -
 Глубокая сеть / -
 Отказ в обслуживании/            -
 Электронные книги / -
 Перечисление / -
 Эксплойт / -
 Техники неудачной атаки / -
 Судебная экспертиза / -
 Галерея / -
 HTML / -
 Взломать / -
 Взлом-веб-сервер / -
 Взлом беспроводных сетей / -
 Взлом / -
 Генератор хешей / -
 JS / -
 Ява/                         -
 Linux / -
 Отмыкание/                  -
 Журналы / -
 Вредоносное ПО / -
 Метасплоит / -
 Разное / -
 Разное / -
 Протоколы сетевой безопасности / -
 Сеть / -
 ОПЕРАЦИОННЫЕ СИСТЕМЫ/                           -
 Другое / -
 PHP / -
 Perl / -
 Программирование / -
 Python / -
 RSS / -
 Rdbms / -
 Разобрать механизм с целью понять, как это работает/          -
 Рубин/                         -
 Сканирование сетей / -
 Безопасность/                     -
 Захват сеанса / -
 Снифферы / -
 Социальная инженерия/           -
 Поддерживает / -
 Системный взлом / -
 Инструменты/                        -
 Учебники / -
 UTF8 / -
 Unix / -
 Вариос-2 / -
 Варианты / -
 Видео/                       -
 Вирусы / -
 Окна / -
 Беспроводная связь / -
 Xml / -
 z0ro-Репозиторий-2 / -
 z0ro-Репозиторий-3 / -
 

[PDF] Кембриджский справочник по физическим формулам

Кембриджский справочник по физическим формулам Грэма Воана – это краткий справочник для студентов и специалистов в области физики, инженерии, прикладной математики и других физических наук. Он содержит коллекцию из более чем 2000 часто используемых формул и уравнений, изучаемых на курсах физики бакалавриата, охватывающих следующие основные темы – базовая математика, динамика и механика, квантовая физика, физика твердого тела, термодинамика, электромагнетизм, оптика и астрофизика. Исчерпывающий указатель позволяет быстро и просто найти искомые формулы, а уникальная табличная форма четко определяет все задействованные величины.

В книге всесторонне освещены основные темы программ бакалавриата по физике.Это была компактная и портативная книга, подходящая для решения задач, повседневной работы и пересмотра экзаменов. Это обязательный справочник для студентов и специалистов в области физики, инженерии, прикладной математики и других физических наук. Эта страница содержит ссылку для загрузки одним щелчком PDF-файла «Кембриджского справочника по физическим формулам Грэма Воана».

Охваченные темы

Книга «Кембриджский справочник по физическим формулам» содержит обширный список важных формул и уравнений по следующим основным темам курсов физики бакалавриата.

• Единицы, константы и преобразования
• Основы математики
• Динамика и механика
• Квантовая физика
• Термодинамика
• Физика твердого тела
• Электромагнетизм
• Оптика
• Астрофизика

PDF СКАЧАТЬ ССЫЛКУ

Вы можете просмотреть или загрузить PDF-файл книги «Кембриджский справочник по физическим формулам Грэма Воана», просто щелкнув ссылку для загрузки, представленную ниже.Электронная копия состоит из 230 страниц, а размер pdf составляет 1,6 МБ (прибл.).

СКАЧАТЬ PDF (1,6 MB)

ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ

Этот веб-сайт был создан для того, чтобы помочь соискателям JEE бесплатно загрузить учебные материалы (PDF, электронные книги). www.iitjeephysics4u.com постоянно пытается помочь студентам, которые не могут позволить себе покупать учебные материалы и книги. Если вы считаете, что материалы полезны, мы рекомендуем вам приобрести их на законных основаниях у оригинальных издателей или владельцев. www.iitjeephysics4u.com вообще не владеет этими материалами, они не создавали и не сканировали. Мы просто предоставляем здесь ссылки, которые уже доступны в Интернете. Мы никоим образом не несем ответственности за правильность и актуальность содержания или информации, представленной в этих учебных материалах и книгах. По вопросам и предложениям, не стесняйтесь обращаться к нам по адресу [email protected], мы делаем все возможное, .

Мы вообще не поддерживаем пиратство . Эти копии были предоставлены только нуждающимся студентам, которые финансово слабы, но заслуживают большего, чтобы учиться.Спасибо.

Физические формулы – определение, уравнения, примеры

Изучение физики – это реализация концепций и их выводов для решения проблем. Что ж, в этой статье вы найдете именно то, что вам нужно для решения физических задач. Вопросы по физике всегда будут сложными для учащихся, и это будет бросать вызов вашим навыкам и знаниям физики. Некоторые из основных задач, с которыми студенты должны столкнуться при решении вопросов по физике, – это изучить, какие числа задаются и задаются в задаче, применять правильную физическую формулу или уравнение и вводить значения и производить правильные вычисления.

Чтобы добиться успеха в подобных задачах, каждый хочет иметь адекватное понимание физических формул и их концепций. Следовательно, в этой статье мы предоставляем исчерпывающий список физических формул , который будет служить промежуточным справочником при решении физических задач. Кроме того, вы можете использовать этот список физических уравнений в качестве быстрого пересмотра перед экзаменом.

Список физических формул и уравнений

Физика – это самый базовый предмет из всех наук, и к тому же, кажется, очень трудным для освоения.По сути, изучение физики – это не что иное, как изучение основных законов, управляющих нашей Вселенной. Можно овладеть физикой, если они хорошо разбираются в теориях, а также они могут легко определить связь между величинами или числами, с помощью которых они могут составлять формулы, выводить их и просто учиться.

Студенты, которые ищут формулы физики, могут взять список с этой страницы и использовать его для ежедневного пересмотра перед экзаменом. При запоминании физических формул, прежде всего, постарайтесь понять, что формула говорит и означает, а затем, какое физическое отношение она описывает.Если вы понимаете темы физики, лежащие в основе этих формул, вам будет легко вывести и запомнить их. Итак, используйте список физических уравнений, доступный здесь, и решайте основные физические задачи очень легко и быстро.

1) Формула средней скорости:

Средняя скорость – это средняя скорость движущегося тела за все пройденное им расстояние.

S = \ (\ frac {d} {t} \)

Где,

Ю	Средняя скорость
д	Пройденное расстояние
т	Общее время занято

2) Формула ускорения:

Ускорение определяется как скорость изменения скорости к изменению во времени.Обозначается символом а.

а = \ (\ frac {v-u} {t} \)

где,

а	Разгон
в	Конечная скорость
u	Начальная скорость
т	Затраченное время

3) Формула плотности:

Плотность материала показывает его плотность в определенной области.

\ (\ rho = \ frac {m} {V} \)

Где,

ρ ρ	Плотность
м	Масса корпуса
В	Объем кузова

4) Второй закон Ньютона:

Согласно второму закону движения Ньютона, сила может быть выражена произведением массы и ускорения тела.

F = м ×

Где,

Ф	Force
м	Масса корпуса
а	Доступное ускорение

5) Формула мощности:

Способность выполнять некоторую работу называется Энергией. Энергия, затрачиваемая на выполнение работы за единицу времени, называется Силой.

P = \ (\ frac {W} {t} \)

Где,

п.	Мощность
Вт	Работа выполнена
т	Затраченное время

6) Формула веса:

Вес – это не что иное, как сила, которую объект испытывает под действием силы тяжести.

W = мг

Где,

Вт	Масса
м	Масса корпуса
г	Ускорение свободного падения

7) Формула давления:

Давление определяется как сила, приложенная к единице площади объекта.

P = \ (\ frac {F} {A} \)

Где,

п.	Давление
ф.	Приложенная сила
А	Общая площадь объекта

8) Формула кинетической энергии:

Кинетическая энергия – это энергия, которой обладает тело благодаря своему состоянию движения.2 \)

Где,

E	Кинетическая энергия
м	Масса корпуса
в	Скорость, с которой движется тело

9) Формула закона Ома: Закон

Ом гласит, что ток, протекающий через какой-либо материал проводника, прямо пропорционален разности потенциалов между двумя конечными точками проводника.

V = I × R

Где,

В	Напряжение измеряется в вольтах
я	Электрический ток, протекающий по проводнику, в амперах.
R	Сопротивление материала в Ом.

10) Формула частоты:

Частота – количество оборотов в секунду или количество волновых циклов.

f = \ (\ frac {V} {\ lambda} \)

Где,

из	Частота волны
В	Скорость или скорость волны
λ λ	Длина волны

Заключительные слова

Это список некоторых из важных физических формул , которые используются всеми учащимися в основном для решения физических задач.Каждый раздел теории физики заменяется бесчисленным множеством формул. Если вы поймете теорию, лежащую в основе формул, вам будет легче заниматься физикой. Так что не просто набирайте упомянутые здесь формулы физики для экзаменов, разбирайтесь в них и соотносите их с каждой концепцией физики и будьте творческим учеником в своем классе.

Если вам нужен список формул по математике и химии , чтобы легко решать задачи и набирать более высокие оценки на итоговых экзаменах, посетите наш сайт и получите обновленный список формул и уравнений для лучшей подготовки.

Часто задаваемые вопросы по физическим формулам

1. Где найти все формулы физики?

Вы можете найти все основные и часто используемые формулы физики из приведенного выше списка, представленного здесь, и когда они вам понадобятся, вы можете использовать их бесплатно в кратчайшие сроки.

2. Какие основные формулы в физике?

Основные формулы по физике приведены ниже для студентов. Итак, давайте получим от них добычу, прежде чем решать задачи по физике:

• v = u + при
• с = ut + 1 / 2at ^ 2
• v ^ 2-u ^ 2 = 2 как
• F = ma
• P = сила / площадь

3. Как я могу узнать научные формулы?

Один из лучших способов понять и изучить физические формулы – это практиковаться и запоминать их вывод. Решите примерные суммы с помощью формулы и бегло прочитайте формулы через день. Используйте дворец памяти и запишите все формулы доступным языком и легко запомните их.

4. Как запоминать физические формулы?

Есть четыре трех шага, которые вы должны выполнить, чтобы запомнить все формулы физики.Они как под

1. Использование мнемонических устройств
2. Понимание каждой формулы
3. Забота о своем теле

5. Какие советы по изучению физических формул?

Ниже приведены основные советы по быстрому изучению нескольких формул физики :

• Практическая концентрация
• Расслабьте мозг
• Практикуйтесь как можно больше
• Минимизируйте контрольные чеки
• Разберитесь в основной концепции формулы
• Держитесь подальше от всех отвлекающих факторов
• Узнайте, как выводятся все формулы
• Используйте приемы запоминания

Физические формулы | Важная физическая формула Pdf Sheet

Список физических формул

Физика – один из таких предметов, который больше связан с пониманием предмета, а не с запоминанием. В целом физика – один из таких предметов, требующий большего внимания. Студенты, стремящиеся достичь больших высот в своей карьере, должны хорошо владеть предметом. Формулы физики, предоставленные командой Entrancei, впитывают новые способности и расширяют возможности мышления.

Формулы по физике, предоставленные командой, помогают студентам в достижении концептуальной ясности. Физические формулы помогут студентам решать сложные задачи на экзамене.Поскольку физика является преобладающим предметом, решающим задачи NCERT, выполните упражнения NCERT с помощью решений NCERT для класса 11 по физике и решений NCERT для класса 12 по физике.

Глава мудрые формулы физики

Физические формулы Класс-11

Физические формулы, класс 12

Физические формулы Класс-10

Почему важны физические формулы?

Основное использование формул физики

Отличное владение физикой помогает студентам получить более высокие места на конкурсных экзаменах. Формулы физики выводятся и объясняются в деталях. Основная цель нашей команды – построить прочный фундамент концепций.

Формулы физики используйте перед вопросами

Формулы физики подготовлены с учетом экзаменов и их уровня сложности. Физика состоит из различных типичных числовых формул, основанных на формулах длины. Большинство учеников игнорируют большинство числовых, поскольку они не могут запомнить формулы. В формулах по физике учащимся предлагаются выводы, основанные на формулах.Формулы по физике подготовлены после глубокого изучения предыдущих вопросов.

Для облегчения изучения формулы физики раздваиваются на различные фрагменты. Студенты могут найти формулы для классификации по главам. Подготовка к экзамену становится очень простой. У одного студента есть полный список формул по физике вместе с ними, так как все числа имеют свою основу в формулах. Подтверждение с помощью формул не только помогает студентам решать сложные числовые решения, но и помогает им набирать более высокие баллы на экзаменах.

Как эффективно изучать концепции физики?

Крайне важно быть готовым к полной подготовке прямо перед экзаменами. Мы в Entrancei предоставляем студентам полный набор заметок для 12 класса физики. Эти заметки облегчили бы подготовку наших студентов. Поскольку физика является одним из таких предметов, программа обучения которого очень разнообразна. Чтобы упростить процесс пересмотра, команда предоставила учебный материал, который можно использовать для доработки.

Физические формулы очень эффективны с точки зрения последнего пересмотра.В учебном материале все предельно ясно изложено. Все ненужное в учебниках NCERT удалено, и предоставлен краткий список полного класса 12 по физике. Наши факультеты сделали все возможное, чтобы предоставить студентам необходимую информацию. Все формулы по физике подготовлены после тщательного изучения вопросников предыдущего года.

Почему Entrancei лучше всего подходит для изучения физических концепций?

1. Специалисты нашей команды имеют значительный многолетний опыт чтения лекций.
2. Команда Entrancei уже сдала экзамены.
3. Физические формулы всегда были на первом месте среди топперов.
4. Так как учебные материалы в Entrancei были подготовлены в очень разнообразной манере. Студенты всегда могут найти в экзаменах разное количество общих вопросов. Всем учащимся предоставляется стратегия достижения определенных отметок.
5. Все формулы по физике подготовлены в формате Pdf.Это делает его легко доступным для студентов.
6. Каждая тема объясняется в самых разных областях. Все учебные материалы доступны бесплатно. Студентам нужно только зарегистрироваться у нас.

Как эффективно использовать физические формулы

Основное применение физики начинается в 11 классе. Начните с механики, для изучения которой потребовалось много вещей. В этой части вы узнаете, как применять формулы физики в числовом выражении и как использовать множественные концепции.Решая численное решение, является ли оно объективным или субъективным, вам потребовалось два размышления, это ясность концепции, а во-вторых, использование физических формул в этих темах.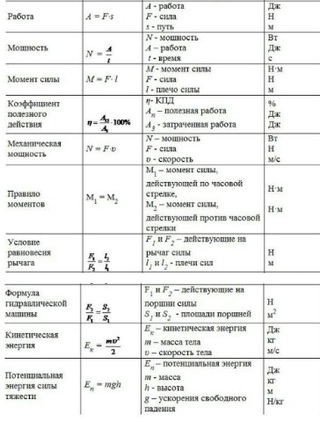 Если вы помните, как использовались физические формулы в этой теме, весь вопрос будет упрощен, и вы сможете перейти к нескольким концепция в данный период времени.

Лучший способ использовать физическую формулу – сначала прочитать главу и загрузить таблицу формул физики входной главы и попытаться запомнить всю формулу сразу после этого начните решать числовые и попытайтесь сформулировать свою концепцию по предмету и понять приложение формулы физики.Во-вторых, таблица в формате pdf с формулами физики будет настоятельно рекомендована в последнюю редакцию минут, то есть незадолго до экзаменационной недели. Перед заключительным экзаменом прочтите всю таблицу формул по физике, это поможет вам быстро завершить программу, и весь процесс пересмотра будет быстрее. Последняя минута может значительно улучшить ваши оценки, поэтому настоятельно рекомендуется сделать свою заметку с помощью справка по листу формул физики, когда вы напишете формулу и концепцию, это поможет вам сохранить концепцию.

Решение задач по физике

Физика является предметом числовых, вы можете изучить концепцию физики с помощью числовых. Чтобы понять концепцию, необходимо решить числовую физику. Студенты сталкиваются с множеством трудностей при решении физических задач, и существует другой подход к решению вопросов. спросили теперь в физике, каков правильный метод? Чтобы ответить на этот вопрос, нужно построить свою концепцию, прежде чем перейти к вопросу, а затем попытаться запомнить все важные физические формулы, использованные в этой главе.Начните с субъективных вопросов, если вы столкнулись с проблемой при решении числовых решений, попробуйте решить вопросы физики из решенной книги. Но не пытайтесь понять числовое значение решения, попробуйте хотя бы 5-6 раз использовать числовое значение, прежде чем прибегать к помощи решения. Или, если вы понимаете вопрос из решения, вам будет трудно решить новый вопрос. Этот лист поможет вам улучшить навыки численного решения. Используйте учебник NCERT для большей концептуальной ясности и решайте вопросы, заданные в упражнении, воспользуйтесь ссылками из решений NCERT для класса 12 по физике.

FAQ (Часто задаваемые вопросы) по физическим формулам

Q-1. Как пользоваться физическими формулами?

Ans- Физика – это предмет концептуального применения, и формулы физики могут вам очень помочь. Лучший способ использовать формулы физики – это делать заметки из учебника. Примечания к каждой главе должны быть резюме на последней странице и записывать все важные формулы и интеллектуальные карты. Используйте приведенный выше лист на этой странице для дополнительных формул на одной странице, это поможет вам подготовить эффективный лист физических формул.

Q-2. Достаточно ли формулы Entrancei Physics для вступительного экзамена?

Ans- Да, физических формул, загруженных экспертом Entrancei, достаточно для конкурсных экзаменов, таких как JEE, NEET, NTSE и вступительных экзаменов на олимпиады. Вы можете записать все физические уравнения по главам для эффективных пересмотров.

Q-3. Каковы лучшие стратегии для численного решения физики?

Ans- Лучший способ решить физические численные задачи – это принять правильный подход, и он начинается с правильного понимания главы. Прочтите теорию и попытайтесь понять формулы, прежде чем переходить к числовому решению. Запишите интеллект-карту и кратко опишите концепцию, использованную в этой главе. Прежде чем задавать вопросы, запомните все формулы и уравнения на листе выше. Попробуйте приступить к формированию решаемых примеров.

Q-4. Какие самые важные главы физики необходимы для хорошего концептуального понимания?

Ans- Каждая глава физики важна, но немногим требовалось дополнительное внимание для создания хороших основ, таких как механика, волны, включая волновую оптику, тепло и термодинамику, электрические и магнитные явления, современную физику.

Q-5. Как развить навыки численного решения?

Ans- Чтобы построить численное решение, нужно постоянно работать. Прочтите теоретический раздел своего учебника, там есть раздел, посвященный отработанным примерам. Эти числовые примеры соответствуют различным уровням мышления и часто используют несколько концепций, представленных в этой главе или даже в предыдущих главах.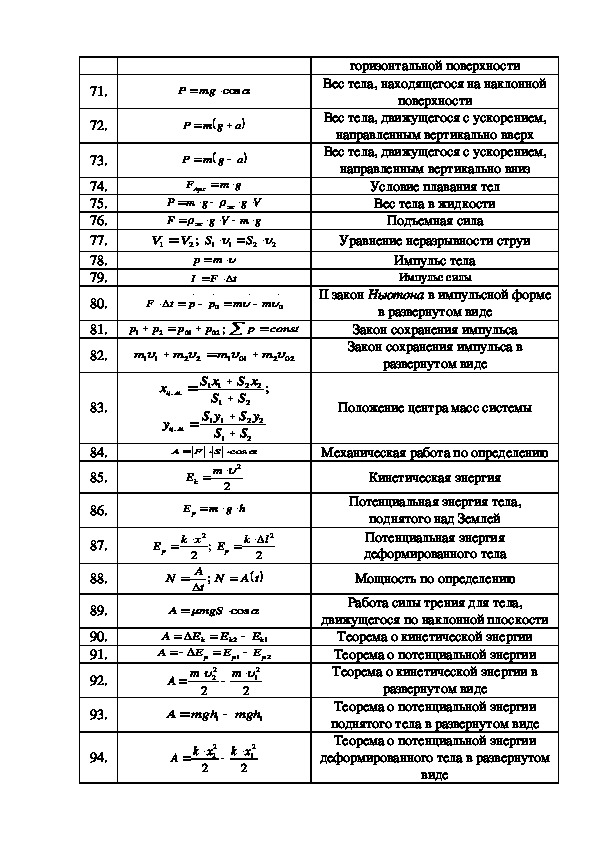 Вам следует прочитать постановку задачи и попытаться решить ее самостоятельно. В случае затруднений посмотрите решение, данное в книге.Даже если вы успешно решите проблему, вам следует изучить решение, чтобы сравнить его с вашим методом решения. Возможно, вы подумали о лучшем методе, но знание нескольких методов всегда полезно.

Q-6. Как я могу легко запоминать формулы физики?

Ans – Изучение формул физики очень важно для любого студента, поскольку он готовится к экзаменам совета директоров и другим экзаменам. Однако наиболее частый вопрос, который задают ученики, – как легко выучить формулы.Для этого нет ярлыка. Единственный способ – практиковать максимальное количество, на которое вы способны. Это может показаться очень распространенной идеей, но это единственный эффективный способ запомнить формулы физики. Чем больше вы занимаетесь задачами числовой физики с необходимыми формулами, тем больше вероятность, что вы их все запомните.

Вы можете записать все важные формулы в одном месте, чтобы просматривать их в свободное время.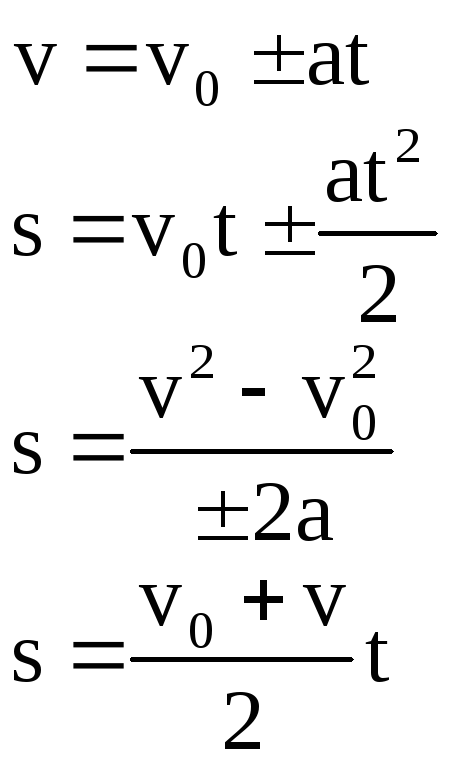 Это также еще один способ просмотреть и запомнить все формулы.

Q-7. Можно ли собрать все важные физические формулы в одном месте?

Ans -Да, можно собрать все основные формулы физики в одном месте, зайдя на сайт Entrancei, одной из ведущих компаний Индии. На Entrancei вы найдете список всех важных физических формул на одной странице. Вы можете просмотреть эти формулы на нашем официальном сайте, и все учебные материалы доступны в формате PDF бесплатно.

Q-8.Почему важны формулы физики?

Ans -Физика – один из таких предметов, который требует множества формул. Соответствующее изучение формул физики поможет студентам оценить свои сильные и слабые стороны. Студенты, которые хотят подготовиться к экзаменам, могут использовать формулы физики. Сохранение формул может быть до некоторой степени затруднительным. Считается, что подготовка с правильными учебными материалами может быть полезна.

Q-9. Почему необходимо изучать формулы физики?

Ans -Важно выучить и понять формулы физики в соответствии с вашей учебной программой. С помощью этих формул вы легко решите любую проблему. Если вы хотите стать ученым в будущем или если вы хотите конкретно заниматься этой областью, чрезвычайно важно эффективно выучить все формулы. И решать уравнения, когда вы хотите работать ученым или в другой области, которая использует физику, или когда вы хотите стать учителем физики или учителем в области, которая использует физику.

Q-10.Как пользоваться физическими формулами?

Ans -Физика – это предмет концептуального приложения, и формулы физики могут облегчить вам жизнь.Лучший способ использовать формулы физики – делать заметки из учебника. Примечания к каждой главе должны быть резюме на последней странице и содержать все важные формулы и интеллектуальные карты. Используйте лист выше на этой странице для дополнительных формул на одной странице. Это отличный способ составить эффективный лист формул физики.

Q-11. Почему Entrancei лучше всего подходит для физических формул?

Ans – Эксперты нашей академии Entrancei имеют многолетний опыт проведения конференций и уже сдали экзамены. Физические формулы всегда имеют наивысшее предпочтение для ботинок. С тех пор учебные материалы Энтранси были подготовлены самым разнообразным образом. Студенты всегда могут найти разное количество часто задаваемых вопросов во время экзаменов. Всем ученикам дается стратегия нацеливания на определенные точки. Все формулы физики находятся в формате PDF и доступны бесплатно; это делает его легко доступным для студентов.

Глава Мудрая викторина по физике

Таблицы формул по физике для 9-го класса

Формулы физики – одна из самых сложных вещей для запоминания при изучении книги или перелистывании уроков один за другим, чтобы найти, какая формула относится к какой главе.Приближаются экзамены 9-го класса CBSE, и студенты уже начали подготовку к ключевому экзамену в своей жизни. Формулы по физике – это общие формулы, которые не только важны для подготовки к 9-му классу, но и образуют основу для концепций физики более высокого уровня. Формулы по физике также играют важную роль в таких областях, как инженерия, медицина, информатика, механика, электричество, программное обеспечение, оборудование и т. Д.

Таблицы формул по физике для класса 9 – Глава Мудрые формулы

Запоминание всех формул физики может быть непростым , но с вручную подобранными Таблицами формул по физике для класса 9 от Gradeup вы можете легко запомнить все формулы из всех глав, которые помогут вам успешно сдать экзамен по физике CBSE Class 9 2021.

Формулы по физике 9-го класса CBSE включают формулы, относящиеся к движению, силе и законам движения, гравитации и звуку. Эти формулы по физике для 9-го класса будут чрезвычайно полезны для учащихся, чтобы они могли быстрее и точнее решать вопросы.

Пожалуйста, перейдите по следующей ссылке, чтобы загрузить PDF-файл с таблицами физических формул для 9-го класса:

Загрузите таблицы с физическими формулами для 9-го класса здесь

Преимущества физических формул для 9-го класса:

Физическая формула Таблицы могут помочь студентам в мгновение ока решить сложную задачу. Запоминание каждой формулы из каждой главы может считаться большой проблемой для студентов, которым просто необходимы некоторые стратегии для легкого запоминания формул. На этом этапе Gradeup предлагает Таблицы формул по физике для класса 9, чтобы учащиеся могли легко загрузить PDF-файл со всеми формулами с веб-сайта или приложения без каких-либо проблем.

• Этот PDF-файл с формулами полезен для предстоящего 10-го экзамена CBSE Class 2021.
• Очень важно хорошо знать формулы и короткие трюки по физике.
• Это также улучшит ваши методы и навыки решения физических задач.
• Эти таблицы физических формул для класса 9 содержат важные формулы из каждой главы.
• Студенты могут загрузить эти формулы в формате PDF и использовать их в будущем.

Если у вас есть какие-либо вопросы или предложения, не стесняйтесь писать их в разделе комментариев ниже.

Часто задаваемые вопросы:

(PDF) Значение физических уравнений и физическое образование

-146- Журнал Корейского физического общества, Vol. 73, No. 2, July 2018

расстояние s и получение связи между двумя переменными

. Однако в типичном обучении уравнениям и обучении

такой контекст исследования редко обсуждается.

Уравнения физики выражают взаимосвязь между

концепциями физики с помощью символов, которые представляют концепции физики

[6]. Уравнение физики связывает

физическое мышление и математическое мышление, а

помогает применять концепции физики к проблемным ситуациям.В этом смысле уравнение физики

является посредником, соединяющим

концептуальное знание и процессное знание физики. Физическое уравнение

,

можно разделить на атомное уравнение

, представляющее физический принцип, закон и определение,

и составное уравнение, которое является синтезом атомарных уравнений

. Например, F = ma, который выражает 2-й закон движения New-

тонн, и F = −kx, представляющий

закон Хука, являются атомарными уравнениями. С другой стороны,

ma = −kx, уравнение движения для простого гармонического колебания

, полученное комбинацией двух атомных уравнений

, является составным уравнением. Эта статья фокусируется на

значении уравнения атомной физики и его

образовательном значении.

Поскольку физическое уравнение – это среда, которая соединяет

физику и математику, обучение физическому уравнению

должно быть средством понимания концепций физики,

, а не просто способом решения проблем.Чтобы предоставить

теоретическую основу для работы, в этом исследовании были собраны тезисы обсуждения физического образования, относящиеся к значению

уравнений физики. При этом средние

физических уравнений делятся на физические средние

значений и математические значения. Также рассмотрены различные дискуссии, относящиеся к физическим значениям. В частности,

, исследования онтологических категорий физики

понятий, исследования типов семантических отношений между понятиями, содержащимися в уравнениях физики,

и исследования их функций и концептуального статуса в

обсуждается использование физических уравнений. Наконец, обсуждались

образовательных последствий этих исследований.

II. ВЗАИМОДЕЙСТВИЕ ФИЗИЧЕСКОЙ КОНЦЕПЦИИ

И МАТЕМАТИЧЕСКИХ ФОРМ В УРАВНЕНИЯХ ФИЗИКИ

Физика и математика взаимозависимы. В его истории математика – очень мощный инструмент физики, а

, наоборот, процесс решения таких физических проблем, как кинематика, термодинамика, электромагнетизм,

и квантовая механика

, также повлиял на разработку

понятия математики [7].Сегодня уравнения физики

являются основным посредником между физикой и математикой

, но они не играли своей текущей роли с начала

. Геометрия использовалась вместо уравнений, чтобы

представляли законы и принципы науки [8,9]. Для примера

Галилей использовал геометрическое соотношение, а не

алгебраическое уравнение, чтобы обсудить концепцию равномерного движения

и равноускоренного движения [10]. В

16 и 17 веков Кеплер предложил уравнение

T2 = kR3, касающееся периода (T) орбитального движения планет

и большой полуоси (R) эллиптического или

бит. Ферма также объяснил принцип наименьшего действия с помощью

уравнений. После успеха математической систематизации механики, основанной на исчислении, использование

уравнений в физике резко возросло.

С использованием уравнений развитие физики

включало как математическую формализацию, так и предварительную

формулировку и концептуализацию формализма. Формализация и концептуализация

повлияли друг на друга

[11].Даже после завершения формализации можно продолжить интерпретацию

и обсуждение деталей концепции

. Например, после формализации законов механики Ньютоном

продолжились споры, касающиеся инерциальной системы отсчета [12]. После формулировки квантовой механики

, различные дебаты по интерпретации квантовой механики

все еще продолжаются

[13]. С другой стороны, поскольку физические уравнения определяют взаимосвязь между концепциями, пониманию

физического уравнения должно предшествовать более глубокое понимание соответствующей концепции. Например, чтобы получить коэффициент «1/2»

в форме кинетической энергии 1

2 мв2,

, мы должны понять форму тео энергии работы-

бэр [5].

III. МАТЕМАТИЧЕСКИЕ И ФИЗИЧЕСКИЕ

ЗНАЧЕНИЯ ФИЗИКИ

УРАВНЕНИЯ

Способ использования уравнений в физике демонстрирует

особенностей, которые отличаются от математических.

Символы физического уравнения соответствуют объектам,

, тогда как математические уравнения не требуют соответствия

отвечающих объектам.В результате, уравнения физики

применимы не во всех ситуациях из-за подчеркнутых допущений, ограничений и ограниченного охвата

. Таким образом,

, применяя физическое уравнение, может быть или не подходить

priate в зависимости от контекста.

Эти особенности, касающиеся применения уравнения физики

, следует учитывать при преподавании и обучении.

Таким образом, изучение уравнений физики должно выходить за рамки понимания математических соотношений уравнений.