Скорость при РПД
Урок 2. Физика 9 класс
На этом уроке вспоминаем, какое движение называется равномерным. А также повторим понятие скорости тела при прямолинейном равномерном движении, рассмотрим зависимость знаков проекций скорости и перемещения.
Конспект урока “Скорость при РПД”
Известно что, для того чтобы найти положение тела в какой-то момент времени, нужно знать вектор перемещения, потому что именно он связан с изменением координат движущегося тела. Как же найти вектор перемещения? Ответ на этот вопрос зависит от того, какое движение совершает тело.
Рассмотрим равномерное движение тела.
Равномерное движение — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Стоит отметить, что равномерное движение может быть как прямолинейным, когда траекторией движения тела является прямая линия, так и криволинейным

Равномерное прямолинейное движение – самый простой вид движения, так как траекторией является прямая линия.
При движении тела вдоль прямой в одном направлении перемещение тела непрерывно возрастает. Чтобы найти перемещение за некоторый промежуток времени, надо знать, как быстро оно возрастает. Быстроту этого возрастания определяют отношением перемещения к значению промежутка времени, в течение которого оно произошло. Это отношение называют скоростью равномерного прямолинейного движения тела и обозначают греческой буквой υ.
Таким образом, скорость равномерного прямолинейного движения тела
Т.е. скорость показывает, какое перемещение тело совершает в единицу времени.
Важно помнить, что единицей скорости в системе СИ
является м/с.
Значит, для того чтобы найти перемещение тела заданное время t, надо знать его скорость υ. Тогда перемещение тела можно вычислить по формуле:
По формулам, написанным в векторной виде, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия. Тогда, в проекциях на ось
sх = υхt
Это уравнение называют уравнением перемещения.
Остановимся более подробно на определении знака проекции скорости и перемещения.
– Проекция скорости и перемещения будет положительной, если тело движется в положительном направлении оси координат

– Проекция скорости и перемещения будет отрицательной, если тело движется в отрицательном направлении оси координат (х<x0).
– Проекция скорости и перемещения будет равна нулю, если тело покоится или движется в направлении, перпендикулярном оси координат (х = х0).
Получим формулу для вычисления координаты тела х в любой момент времени.
Пусть в момент времени
Тогда
x – x0= υхt
Или
х = х0+ υхt
Это уравнение называют кинематическим уравнением
равномерного движения.
Полученная формула может видоизменяться в зависимости от знака проекции скорости и значения начальной координаты.
Если тело движется вдоль оси х в положительном направлении, то формула принимает вид
x = х1+ υ1t
Если тело движется вдоль оси х в отрицательном направлении, то формула принимает вид:
если начальная координата равна нулю
х = –υ2t
или
х = х3 – υ3t.
Так как, при равномерном прямолинейном движении направление скорости тела не изменяется, то путь равен модулю перемещения.
Тогда
s = |υx|t
Это выражение называют уравнением пути.
Если же направление движения тела меняется, то пройденный путь окажется больше модуля вектора перемещения.
Основные выводы:
·
Равномерное прямолинейное
движение — это движение, при котором тело за любые равные промежутки времени совершает
одинаковые перемещения.
· Основной характеристикой равномерного движения является скорость.
· Единицей скорости в системе СИ является м/с.
· Скорость показывает, какое перемещение тело совершает в единицу времени.
· х = х0+ υхt — кинематическое уравнение равномерного движения
· Проекция скорости на ось х будет положительной, если тело движется вдоль оси х в положительном направлении. При этом проекция вектора перемещения так же будет положительной.
·
Проекция
скорости на ось х будет отрицательной, если тело движется вдоль оси х в отрицательном
направлении. При этом проекция вектора перемещения так же будет отрицательной.
· Скорость тела и перемещение будут равны нулю, если тело покоится или движется в направлении, перпендикулярном оси координат.
Предыдущий урок 1 Механическое движение. СО. Траектория, путь и перемещение
Следующий урок 3 Прямолинейное равноускоренное движение. Ускорение
Получите полный комплект видеоуроков, тестов и презентаций Физика 9 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Уравнение РПД
Мы знаем, что в каждый
момент времени, положение точки задаётся радиус-вектором. Пусть в момент
времени t0,
начальное положение точки задаёт радиус-вектор .
Исходя из определения скорости равномерного прямолинейного движения, запишем:
Как правило, начальный момент времени — это точка отсчёта, поэтому примем t0 = 0. Если мы теперь выразим из полученного выражения, то получим функцию зависимости радиус-вектора от времени:
Это и есть уравнение равномерного прямолинейного движения. То есть, если нам известно начальное положение точки и скорость её движения, то мы сможем найти радиус-вектор в каждый момент времени.
Вместо векторного уравнения можно использовать уравнение для каждой из координат:
Поскольку пройденный путь
— это изменение координаты х в данном случае, мы можем найти его,
используя модуль скорости. Заметим, что числовые значения пройденного пути и
перемещения будут совпадать при прямолинейном движении. Только не стоит
забывать, что пройденный путь — это скалярная величина, которая не может быть
отрицательной.
Только не стоит
забывать, что пройденный путь — это скалярная величина, которая не может быть
отрицательной.
Перемещение же, легко может быть отрицательным, если точка двигается в направлении, противоположном направлению координатной оси.
Итак, мы выяснили, что для описания равномерного прямолинейного движения достаточно получить уравнение для одной координаты. Давайте рассмотрим, как будут выглядеть графики функций зависимости скорости и координаты от времени. Начнём с простого: при равномерном движении скорость постоянна. Поэтому график зависимости скорости от времени будет представлять собой прямую горизонтальную линию.
Иными словами, при
равномерном движении скорость не зависит от времени, так как является
константой. Заметим, что если мы рассмотрим конечный промежуток времени, то получим
ограниченную область, имеющую форму прямоугольника. Площадь этого
прямоугольника будет являться ничем иным, как изменением координаты х. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а
длина другой — это время.
Действительно, ведь длина одной из сторон прямоугольника — это скорость, а
длина другой — это время.
Рассмотрим теперь несколько графиков зависимости координаты от времени. На рисунке вы видите три прямых, каждая из которых описывается одним и тем же уравнением.
Точки пересечения этих
графиков с осью х соответствуют значениям начального положения х0.
Как видно из графика, для зелёной прямой х0 = 0, для синей
прямой х0 > 0, а для красной — х0 <
0. На графике видно, что скорость для красной и зелёной прямых больше нуля.
Действительно, ведь значение координаты х увеличивается с течением
времени. Значит, тело двигается в направлении, совпадающем с направлением оси х.
Это соответствует положительному перемещению, а, значит, положительной скорости.
В случае с синей прямой, мы видим противоположную картину: значит, тело
двигается в обратном направлении, поэтому скорость отрицательная. Из графика
также видно, что конечная координата для синей прямой будет отрицательной, а
для красной и зелёной прямых — положительной. И ещё, исходя из графиков, мы
можем судить о модуле скорости. Очевидно, что тело, движение которого описано
красной прямой двигается быстрее остальных. Ведь за тот же промежуток времени
оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что
для синей прямой модуль скорости больше, чем для зелёной. Из этих наблюдений
можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем
больше скорость движения. Действительно: представьте на минуту график
зависимости координаты от времени, который представляет собой вертикальную
прямую. Это будет означать, что скорость бесконечно большая, т.к. тело
перемещается на любое расстояние за промежуток времени, равный нулю.
Разумеется, в классической механике такие перемещения невозможны.
Из графика
также видно, что конечная координата для синей прямой будет отрицательной, а
для красной и зелёной прямых — положительной. И ещё, исходя из графиков, мы
можем судить о модуле скорости. Очевидно, что тело, движение которого описано
красной прямой двигается быстрее остальных. Ведь за тот же промежуток времени
оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что
для синей прямой модуль скорости больше, чем для зелёной. Из этих наблюдений
можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем
больше скорость движения. Действительно: представьте на минуту график
зависимости координаты от времени, который представляет собой вертикальную
прямую. Это будет означать, что скорость бесконечно большая, т.к. тело
перемещается на любое расстояние за промежуток времени, равный нулю.
Разумеется, в классической механике такие перемещения невозможны.
Примеры решения задач.
Задача 1. Точка,
равномерно двигаясь вдоль оси X,
переместилась из координаты в
координату за 5 с. Определите
модуль и направление скорости этой точки.
Точка,
равномерно двигаясь вдоль оси X,
переместилась из координаты в
координату за 5 с. Определите
модуль и направление скорости этой точки.
Задача 2. Две машины равномерно двигаются по одной прямой. Опишите условия, при которых столкновение невозможно.
Движения и того, и
другого автомобиля описываются одним и тем же общим уравнением. Обозначим одну
машину за грузовик, а другую за легковую. На графике обозначим грузовик синей
точкой, а легковую машину — красной точкой. Итак, рассмотрим первый случай:
машины двигаются в разные стороны. Тогда, скорость одной машины должна быть
положительной, а скорость другой — отрицательной (например, легковая машина
будет двигаться в положительном направлении). Чтобы машины не столкнулись, начальная
координата машины с отрицательной скоростью, должна быть меньше, чем начальная
координата машины с положительной скоростью. В противном случае, они будут
двигаться навстречу друг другу и столкнуться. Графически это можно изобразить
так:
Графически это можно изобразить
так:
Скорость красного графика положительная, поскольку координата х увеличивается с течением времени, а скорость синего графика — отрицательная, поскольку координата х уменьшается с течением времени. Эти графики никогда не пересекутся, поэтому столкновения не произойдёт. Заметим, что при таком раскладе, скорости не имеют значения. Имеет значение только знак (то есть направление движения). Конечно, вы можете сказать, что если мы продолжим графики, то они всё же пересекутся. Но для этого машинам нужно переместиться в прошлое, потому что координата времени, соответствующая точке пересечения, отрицательная.
Рассмотрим теперь второй случай: когда машины двигаются в одном направлении, и при этом, машина, идущая впереди, едет быстрее. Что значит, машина, идущая впереди? Это значит, что её начальная координата должна быть больше.
То есть условие таково:
машина, начальная координата которой больше, должна двигаться со скоростью не
меньше, чем скорость второй машины. Опять же, если мы изобразим это графически,
то увидим, что графики не пересекаются.
Опять же, если мы изобразим это графически,
то увидим, что графики не пересекаются.
Начальная координата красного графика больше и скорость тоже больше. Если же скорости будут одинаковы, то это будет означать одинаковый наклон синей и красной линий по отношению к оси времени. В этом случае, графики будут представлять собой параллельные прямые, а такие прямые, как известно, не пересекаются.
Формула равноускоренного движения в физике
Содержание:
- Определение и формула равноускоренного движения
- Основные кинематические величины при равноускоренном движении
- Примеры решения задач
Определение и формула равноускоренного движения
Определение
Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным. Если скорость при этом увеличивается, то такое движение носит название равноускоренного движения.
Равноускоренное движение можно определить еще как движение, при котором модуль касательного ускорения
($a_{\tau}=$ const $>0$). {2}}{l}$
{2}}{l}$
Читать дальше: Формула силы Лоренца.
Равномерное прямолинейное движение – презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. П.3 Равномерное прямолинейное движение
Прямолинейное движение – видмеханического движения, траектория
которого прямая линия.
Криволинейное движение – вид
механического движения, траектория
которого кривая линия.
3. Равномерное движение
Движениеназывается
равномерным,
если тело за любые равные промежутки
времени
совершает
одинаковое
перемещение.

X
Равномерное
прямолинейное движение
Движение при котором тело, двигаясь
по прямолинейной траектории, за
любые равные промежутки времени
совершает одинаковые перемещения
называется равномерным
прямолинейным (РПД)
X
X
Скорость характеризует
быстроту изменения
координаты со временем
x
x
t
7. Скорость –это
векторная величина, равная отношениюперемещения ко времени, в течение
которого произошло это перемещение.
ИЛИ
Перемещение, совершенное в единицу
времени
S
t
S t
– скорость
S – перемещение
t
– время
Закон изменения
перемещения со
временем (для РПД)
0
x
0
x
x
Проекция вектора скорости
положительная
0
x
0
x
x
Проекция вектора скорости
отрицательная
Формула в скалярной форме
для скорости
Sx
x
t
Единицы измерения скорости
СИ:
м/с
(метр в секунду)
Дополнительно:
км/ч, м/мин,
см/мин, мм/с
1 м/с – это скорость такого движения, при
котором движущееся тело за 1 с совершает
перемещение, равное 1 м.
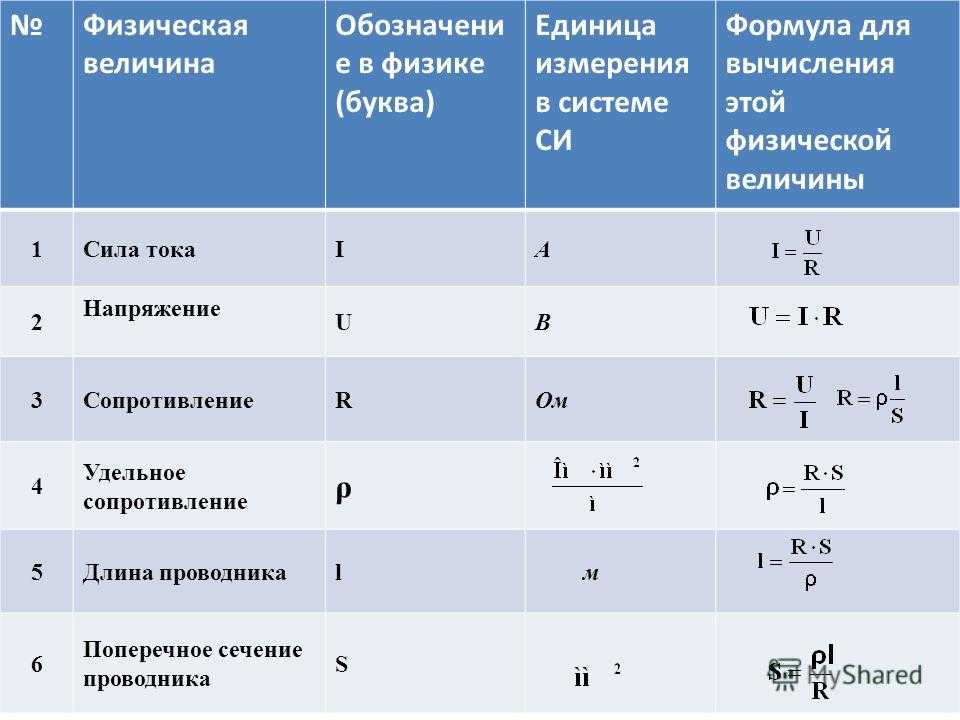
Перевод м/с в км/ч и обратно
м
1 км
3600 км
км
1 1
1
3,6
1000 ч
с
1000 ч
ч
3600
км
1000 м
1 м
1
1
ч
3600 с 3,6 с
S
t
const
X
X
υх, м/с
График проекции
скорости
1
t, с
0
2
Проекция перемещения
y
S
Sx
x0
0
x
x
– вектор перемещения
S
S x – проекция вектора
перемещения
x0 – начальная координата
x – координата через
определенный интервал времени
18. Решение ОЗМ для РПД;
x x0 SxSx x t
x x0 x t
x x0 x (t t 0)
S
x0
0
Sx
x
Решение ОЗМ для РПД;
Зависимость
координаты от
времени при РПД;
Закон РПД;
Уравнение РПД;
x
x x0 x (t t 0)
x x0 x (t t 0)
x x0
x
(t t 0)
x
x
t
Проекция скорости на координатную ось
равна изменению координаты в единицу
времени, т.е. скорость показывает как
быстро
изменяются
при
движении
координаты тела.

Задача № 1
Напишите уравнение движения лыжника.
Определите через какое время координата
лыжника будет равна – 225 м.
2,5 м с
x
0
x0 = 25 м
Задача 2 :
Движение двух велосипедистов
описывается уравнениями: х1 = 12t и х2
= 120 – 10t. Найдите начальную
координату, модуль и направление
вектора их скоростей, постройте
графики движения х(t), определите
графически и аналитически время и
место их встречи.
22. Задача 3 Тело движется равномерно и прямолинейно, за 10 с перемещается из точки А с координатами (0;2) в точку В с координатами
(4;-1). Чему равен модульскорости?
23. Задача 4 Координата тела изменяется с течением времени согласно формуле х=15-3t. Чему равен модуль скорости тела через 3 с
после началадвижения?
24. Задача 5 Координата тела изменяется с течением времени согласно формуле х=10-4t. Чему равен модуль скорости тела через 5 с
после началадвижения?
25. Задача 6 Движение грузового автомобиля описывается уравнением х1 = -270+12t, а движение пешехода по обочине шоссе – уравнением
х2 = -1,5t. С
Скакой скоростью они
движутся и в каком
направлении?
26. Задача 7 Движение двух велосипедистов описывается уравнениями: х1 = 5t и х2 = 150 – 10t. Найдите начальную координату, модуль и
направление вектора ихскоростей, постройте графики
движения х(t), определите
графически и аналитически время
и место их встречи.
27. Задача 8 Движение двух велосипедистов описывается уравнениями:х1=2t и х2 = -5 + 10t. Найдите начальную координату, модуль и
направление вектора ихскоростей, постройте графики
движения х(t), определите
графически и аналитически
время и место их встречи.
28. Д/з 1. Учить П 1- 3 2. решить задачи № 3,16, 23, 22, 57. 3. дополнительно: Задачи 20, 23
English Русский Правила
Перемещение при прямолинейном равномерном движении 9 класс онлайн-подготовка на Ростелеком Лицей
Равномерное прямолинейное движение
Равномерным движением называется такое движение, при котором тело за любые равные промежутки времени проходит одинаковые расстояния.
Необходимо отметить то, что равномерным может быть не только прямолинейное, но и криволинейное движение.
Равномерное прямолинейное движение (РПД) – движение, при котором тело движется вдоль прямой и за любые равные промежутки времени совершает одинаковые перемещения (рис. 1).
Рис. 1. Равномерное прямолинейное движение
Точное определение равномерного движения
Задача. Велосипедист за каждую секунду проезжает 10 м. Будет ли такое движение равномерным?
Рис. 2. Иллюстрация к задаче
На первый взгляд, кажется, что да, так как за равные промежутки времени (1 с) совершается равное перемещение, равное 10 м. Но что мы знаем о движении тела за промежутки времени меньше 1 с?
За первую секунду велосипедист проехал 10 м. Однако может оказаться, что за первые полсекунды велосипедист проехал 3 м, а за вторые – 7 м, то есть движение было неравномерным (рис. 3).
Рис. 3. Неравномерное движение велосипедиста
Казалось бы, выход в том, чтобы в определении уточнить, что не только за каждую секунду совершаются равные перемещения, но и за каждые полсекунды.
При рассмотрении отдельно движения каждые полсекунды может оказаться, что первую четверть секунды велосипед проезжал 4 м, а вторые – 1 м (или другие любые перемещения). То есть, опять-таки, движение неравномерное. Соответственно, необходимо в определение добавить слово «любой» промежуток времени (1 с; 0,5 с; 0,25 с и т. д.)
Корректное определение:
Равномерное движение – движение, при котором тело за любые равные промежутки времени проходит равные расстояния.
Скорость
Важная характеристика такого движения – скорость. Из 7-го класса вам известно, что скорость – это физическая величина, которая характеризует быстроту движения. При равномерном прямолинейном движении скорость – величина постоянная.
Скорость – векторная величина. Единицей измерения скорости является .
Если вектор скорости направлен по направлению оси, то тогда проекция скорости будет . Если скорость направлена против выбранной оси, то проекция этого вектора будет отрицательной.
Рис. 4. Знак проекции скорости в зависимости от ее направления
Единицы измерения скорости. Перевод из одних единиц в другие
Как известно, скорость в СИ измеряется в м/с. 1 м/с – это такая скорость, при которой тело, двигаясь равномерно прямолинейно, за 1 с совершает перемещение, равное 1 м.
В повседневной жизни не всегда удобно скорость измерять в . Например, скорость автомобиля мы привыкли измерять в км/ч, ученые измеряют скорость ракеты в км/с. Рассмотрим перевод от внесистемных единиц измерения в системные на примере задачи.
Задача.
Поезд метро движется со скоростью . Выразите эту скорость в .
Решение.
Переведем километры в метры. Приставка кило- (к-), согласно СИ, обозначает 1000:
Переведем часы в секунды: . Тогда для того чтобы перевести в , нужно умножить значение скорости на 1000 и разделить на 3600 или же разделить значение скорости на 3,6:
Аналогично
Определение скорости, пути и перемещения
Перейдем к формуле для расчета скорости. Скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло:
Скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло:
Обращаем ваше внимание на то, что при прямолинейном движении длина вектора перемещения равна пути, пройденному этим телом. Поэтому мы можем сказать, что модуль перемещения равен пройденному пути. Чаще всего вы эту формулу встречали в 7 классе и в математике. Она записывается просто: . Но важно понимать, что это лишь частный случай (рис. 5).
Рис. 5. Формула для расчета скорости
Систему отсчет мы можем выбирать произвольно, то есть направлять координатные оси так, как нам удобно. Главное – проекции всех векторов в дальнейшем рассматривать в одной и той же выбранной системе координат.
Уравнение движения
Рис. 6. Проекция вектора перемещения
Если вспомнить, что проекция вектора определяется как разность конечной и начальной координат (рис. 6), т. е. , то можно получить закон движения при прямолинейном равномерном движении:
где – это проекция скорости, которая может быть как отрицательной, так и положительной, в зависимости от направления скорости относительно выбранной оси (рис. 7).
7).
Рис. 7. Проекция скорости
График скорости
Рис. 8. График зависимости проекции скорости от времени для РПД
График зависимости проекции скорости от времени, представленный на рис. 8, – непосредственная характеристика равномерного движения. По горизонтальной оси откладывается время, по вертикальной оси – проекция скорости. Если график проекции скорости располагается над осью абсцисс, то это означает, что тело будет двигаться вдоль оси Ох в положительном направлении. В обратном случае направление движения противоположно направлению оси.
Геометрическое толкование пути
Рис. 9. Геометрический смысл графика скорости от времени
Пройденный путь будет численно равен площади, ограниченной осью времени, перпендикуляром на эту ось, осью проекции скорости и графиком проекции скорости (рис. 9).
График для РПД
При изучении РПД особый интерес представляет график зависимости координаты тела от времени.
Закон зависимости координаты от времени (уравнение движения)
где – текущая координата, – начальная координата, – проекция перемещения тела, – проекция скорости тела, – время.
В математике вы уже встречались с подобной зависимостью, а именно с уравнением прямой , где – свободный член, – коэффициент при (рис. 10).
Рис. 10. График функции
Это значит, что зависимость координаты от времени при РПД также будет прямой линией (рис. 11).
Рис. 11. Зависимость координаты от времени при РПД
Обратим внимание на важные моменты при построении графиков:
1. Оси, на которых мы будем откладывать соответствующие значения величин, должны быть подписаны вместе с единицами измерения.
2. Правильный выбор масштаба.
На рис. 12 представлены два графика равномерного прямолинейного движения тел. Точка пересечения с осью ординат – это точка, в которой , а это значит, что , .
Точка пересечения двух графиков – это место встречи двух тел.
График для первого тела устремлен вверх. Это значит, что проекция скорости первого тела положительна. График второго тела устремлен вниз, то есть проекция скорости второго тела отрицательна.
Рис. 12. Два графика РПД
Пользуясь графиком, запишем закон движения для первого тела:
За время тело переместилось на 6 м, то есть . Подставляем все данные в закон движения первого тела:
Навыки работы с графиками позволяют существенно упростить решения физических задач.
Заключение
На этом уроке мы рассмотрели зависимость пройденного пути от скорости. Скорость – это векторная величина.
Список литературы
- Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. – М.: Просвещение.
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009.
 – 300.
– 300. - Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «mnogoformul.ru» (Источник)
Домашнее задание
- Что такое равномерное движение? Приведите примеры, какое движение можно считать равномерным.
- Запишите формулу, по которой можно найти проекцию вектора перемещения тела при прямолинейном равномерном движении, если известна проекция вектора скорости.
- Как графически определить модуль вектора перемещения тела, если есть график зависимости скорости тела от времени?
Карта сайта
|
Калькулятор процентной разницы
Создано Альваро Диесом и Домиником Черниа, докторантами
Отзыв от Jack Bowater
Последнее обновление: 18 июня 2022 г.
- Что такое процентная разница?
- Как найти процентную разницу?
- Формула процентной разницы
- Когда процентная разница полезна, а когда она сбивает с толку?
- Значение процентной разницы в реальной жизни
- Как лгать с данными, не лгая?
- Часто задаваемые вопросы
Калькулятор процентной разницы поможет вам сравнить два числа. Здесь мы покажем вам, как рассчитать процентную разницу между двумя числами и, надеюсь, , чтобы правильно объяснить, что такое процентная разница , а также некоторые распространенные ошибки. В следующей статье мы также покажем вам формулу процентной разницы. Кроме того, мы объясним различия между различными процентными калькуляторами и то, как данные могут быть представлены вводящими в заблуждение, но технически верными способами для доказательства различных аргументов.
Если вы хотите рассчитать процентную разницу между процентными пунктами, воспользуйтесь нашим калькулятором процентных пунктов.
Что такое процентная разница?
Чтобы ответить на вопрос “что такое процентная разница?” сначала нам нужно понять , что такое процент . Процент — это просто еще один способ говорить о дроби. Процент также является способом описания отношения между двумя числами. Например, мы можем сказать, что 5 — это 20% от 25, или 2 — это 5% от 40. Когда мы говорим о процентах, мы можем думать о знаке % как о значении 1/100 . Возвращаясь к нашему последнему примеру, если мы хотим узнать, что составляет 5% от 40, мы просто перемножаем все переменные следующим образом:
5 * 1/100 * 40 = 200/100 = 2
Если вы будете следовать этой формуле, вы должны получить результат, который мы предсказывали ранее: 2 — это 5% от 40, или, другими словами, 5% от 40 — это 2. Если хотите, теперь вы можете попробовать проверить, равно ли 5 20. % от 25.
Теперь, если мы хотим поговорить о разнице в процентах , нам сначала понадобится разница, то есть нам нужны два, не идентичных, числа.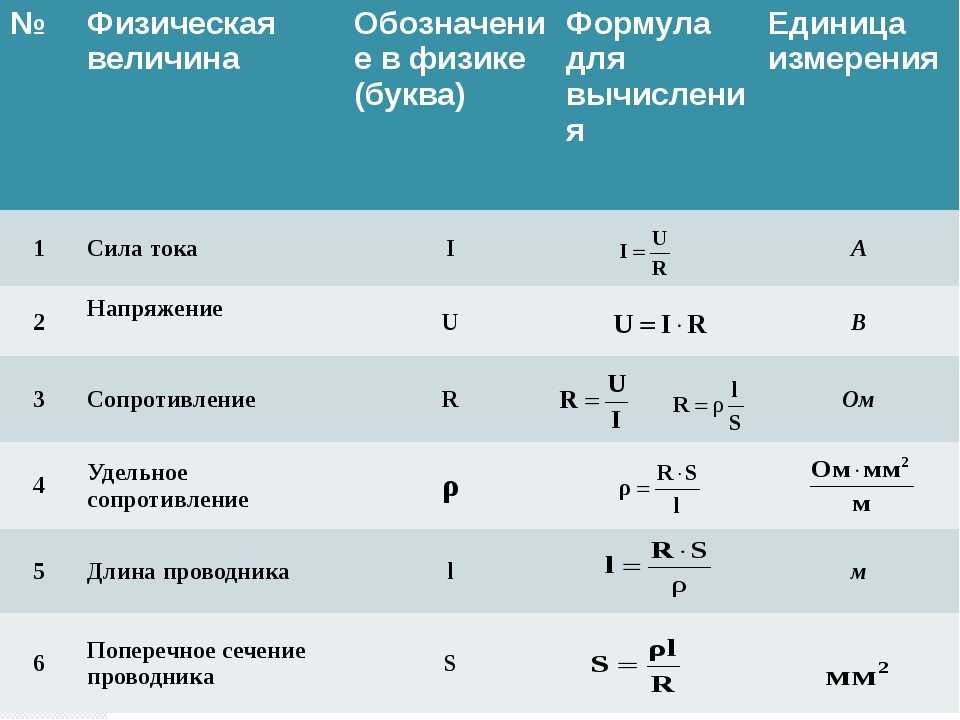 Возьмем, например, 23 и 31; их разница равна 8. Теперь нам нужно перевести 8 в проценты, а для этого нам нужна точка отсчета, и вы, возможно, уже задавались вопросом: Должен ли я использовать 23 или 31? Поскольку мы не предоставили никакого контекста для этих чисел, ни одно из них не является надлежащей точкой отсчета, поэтому самым честным ответом было бы использовать среднее или середина этих двух чисел.
Возьмем, например, 23 и 31; их разница равна 8. Теперь нам нужно перевести 8 в проценты, а для этого нам нужна точка отсчета, и вы, возможно, уже задавались вопросом: Должен ли я использовать 23 или 31? Поскольку мы не предоставили никакого контекста для этих чисел, ни одно из них не является надлежащей точкой отсчета, поэтому самым честным ответом было бы использовать среднее или середина этих двух чисел.
Напоминаем, что, хотя мы и дали точный ответ на вопрос «что такое процентная разница?», точность не так распространена, как мы все надеемся, что это будет . Очень часто (преднамеренно или непреднамеренно) называют процентную разницу, которая на самом деле является процентным изменением. Это еще больше затрудняет определение процентной разницы без надлежащего точного поиска.
Мы рассмотрим эту проблему вместе с недобросовестным представлением данных в следующих разделах . Мы надеемся, что это поможет вам отличить хорошие данные от плохих данных, чтобы вы могли определить, какая процентная разница есть, а какая нет. А пока, , давайте посмотрим, как использовать этот калькулятор и как найти процентную разницу двух заданных чисел.
Мы надеемся, что это поможет вам отличить хорошие данные от плохих данных, чтобы вы могли определить, какая процентная разница есть, а какая нет. А пока, , давайте посмотрим, как использовать этот калькулятор и как найти процентную разницу двух заданных чисел.
Как найти процентную разницу?
Чтобы вычислить процентную разницу между двумя числами, a и b , выполните следующие вычисления:
- Найдите абсолютную разницу между двумя числами:
|a - b| - Найдите среднее из этих двух чисел:
(a + b) / 2 - Разность разделить на среднее:
|a - b| / ((а + б) / 2) - Выразите результат в виде процентов , умножив его на
100 - Или вместо этого используйте калькулятор процентной разницы Omni 😃
Вот как найти процентную разницу! Вы можете извлечь из этих расчетов формулу процентной разницы, но если вам лень, просто продолжайте читать, потому что в следующем разделе мы сделаем это за вас. Просто помните, что знание того, как рассчитать процентную разницу, не равно пониманию того, что такое процентная разница.
Просто помните, что знание того, как рассчитать процентную разницу, не равно пониманию того, что такое процентная разница.
Ранее мы упоминали, что люди иногда путают процентную разницу с процентным изменением, которое является отличной (хотя и очень интересной) величиной, которую можно рассчитать с помощью другого из наших Омни-калькуляторов. Если вы читали, как рассчитать процентное изменение, вы должны знать, что у нас есть изменение либо на 50%, либо на -33,3333%, в зависимости от того, какое значение является начальным, а какое — конечным.
Формула процентной разницы
Прежде чем мы углубимся в более сложные темы, касающиеся процентной разницы, нам, вероятно, следует поговорить о конкретной формуле, которую мы используем для расчета этого значения. Формула процентной разницы выглядит следующим образом:
процентная разница = 100 * |a - b| / ((a + b) / 2)
Чтобы быть еще более конкретным, вы можете говорить о процентном увеличении или процентном уменьшении. Чтобы просто сравнить два числа, используйте калькулятор процентов. Или, если вы хотите рассчитать относительную ошибку, используйте калькулятор процентной ошибки.
Чтобы просто сравнить два числа, используйте калькулятор процентов. Или, если вы хотите рассчитать относительную ошибку, используйте калькулятор процентной ошибки.
Теперь вы знаете формулу процентной разницы и как ее использовать . Имейте в виду, что, поскольку в формуле присутствует абсолютное значение, калькулятор процентной разницы не будет работать в обратном порядке. Вот почему вы не можете ввести число в последние два поля этого калькулятора.
Когда разница в процентах полезна, а когда сбивает с толку?
Теперь пришло время углубиться в полезность процентной разницы в качестве измерения . Вас не должно удивлять, что полезность процентной разницы лучше всего проявляется при сравнении двух чисел; но это не всегда так. Возможно, нам следует воздержаться от разговора о разнице в процентах, когда мы имеем в виду одно и то же значение во времени. Мы думаем, что так и должно быть, потому что в повседневной жизни мы склонны думать о процентном изменении , а не о процентной разнице.
А пока давайте посмотрим пару примеров, где полезно говорить о процентной разнице . Допустим, вы хотите сравнить размер двух компаний с точки зрения их сотрудников. В этом примере в компании C работает 93 сотрудника, а в компании B — 117. Чтобы сравнить разницу в размере между этими двумя компаниями , разница в процентах является хорошей мерой. В этом случае, используя калькулятор процентной разницы, мы видим, что разница составляет 22,86%. Одной из ключевых особенностей процентной разницы является то, что она останется прежней, если вы поменяете количество сотрудников между компаниями. Как мы уже установили, 9Разница в процентах 0025 — это сравнение без направления.
Однако неверно утверждать, что компания C на 22,86% меньше, чем компания B , или что B на 22,86% больше, чем C . В этом случае мы будем говорить о процентном изменении , что не совпадает с процентной разницей . Другая проблема, с которой вы можете столкнуться при выражении сравнения с использованием разницы в процентах, заключается в том, что если сравниваемые числа не похожи, разница в процентах может ввести в заблуждение. Почему?
Другая проблема, с которой вы можете столкнуться при выражении сравнения с использованием разницы в процентах, заключается в том, что если сравниваемые числа не похожи, разница в процентах может ввести в заблуждение. Почему?
Представьте себе, что компания C объединяется с компанией A , в которой работает 20 000 сотрудников. Теперь в новой компании CA работает 20 093 сотрудника, а процентная разница между CA и B составляет 197,7%. Давайте поднимем его на ступеньку выше. Теперь новая компания T со 180 000 сотрудников объединяется с CA и образует компанию CAT . Мы не совсем уверены, чем занимается эта компания, но думаем, что это что-то связанное с кошачьими. CAT сейчас насчитывает 200 093 сотрудника. Теперь процентная разница между B и CAT увеличивается только до 199,8%, несмотря на то, что CAT на 895,8% больше, чем CA с точки зрения процентного увеличения.
” Как это вообще возможно? ” Хороший вопрос. Причина здесь в том, что, несмотря на увеличение абсолютной разницы между этими двумя числами, изменение процентной разницы резко уменьшается. Эти два числа настолько далеки друг от друга, что такое большое увеличение на самом деле довольно мало с точки зрения их текущей разницы. Следовательно, если мы хотим сравнить числа, сильно отличающиеся друг от друга, с использованием разницы в процентах вводит в заблуждение . Если вы хотите избежать каких-либо из этих проблем, мы рекомендуем сравнивать только числа, которые отличаются не более чем на один порядок (два, если вы хотите подтолкнуть его). Если вы хотите узнать больше о порядках и о том, что означает этот термин, мы рекомендуем наш калькулятор научной записи.
Как и во всем, что вы делаете, вы должны быть осторожными при использовании калькулятора процентной разницы , а не просто использовать его вслепую. В нашем примере процентная разница не была хорошим инструментом для сравнения компаний
В нашем примере процентная разница не была хорошим инструментом для сравнения компаний CAT и B . В конце концов, может быть несколько способов снять кожу с CAT , но не все способы одинаковы.
Значение процентной разницы в реальной жизни
И вот мы, наконец, подошли к проблеме с процентной разницей и как она используется в реальной жизни, а точнее в СМИ . Разница в процентах представляет собой ненаправленную статистику между любыми двумя числами. Однако когда статистические данные представляются в СМИ, они очень редко преподносятся точно и точно. Даже при правильных намерениях использование неправильных инструментов сравнения может ввести в заблуждение и дать неверное представление о данной проблеме.
Что касается процентной разницы, проблема возникает, когда путают с процентным увеличением или процентным уменьшением. Мы видели, насколько обманчивыми могут быть эти меры, когда неверный расчет применяется к крайнему случаю, например, при сравнении количества сотрудников между CAT против B . Но теперь, мы надеемся, вы знаете лучше и можете видеть сквозь эти различия и понимать, что означают настоящие данные.
Но теперь, мы надеемся, вы знаете лучше и можете видеть сквозь эти различия и понимать, что означают настоящие данные.
Еще одна проблема с данными заключается в том, что когда они представлены определенным образом, это может привести к тому, что зритель сделает неверные выводы или создаст неправильное впечатление. Давайте рассмотрим еще один пример и увидим, как изменение предоставленной статистики может явно повлиять на то, как мы рассматриваем проблему , даже если данные одинаковы.
Как лгать с данными, не лгая?
Первое, что вы должны признать, это то, что сами по себе данные (при условии, что они правильно собраны) не заботятся о том, что вы думаете, что является этическим или моральным ; это просто эмпирическое наблюдение мира. Это означает, что сила данных заключается в их интерпретации , в том, как мы их понимаем и как мы можем использовать их в своих интересах.
Давайте рассмотрим пример того, как представлять одни и те же данные по-разному для доказательства противоположных аргументов.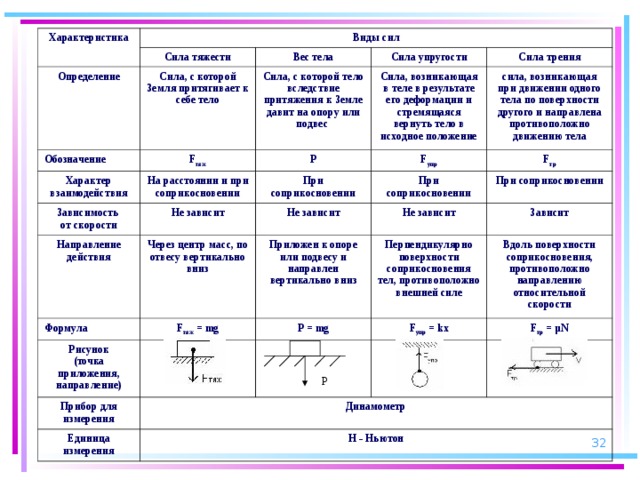 Взяв, к примеру, уровень безработицы в США, мы можем изменить влияние представленных данных, просто изменив используемый инструмент сравнения или представив вместо этого необработанные данные. Уровень безработицы в США в 2018 году составлял около 90 025 4%, тогда как в 2010 году он составлял около 10 %. Оставив в стороне определения безработицы и , предполагая, что эти цифры верны , мы собираемся посмотреть, как эти статистические данные могут быть представлены.
Взяв, к примеру, уровень безработицы в США, мы можем изменить влияние представленных данных, просто изменив используемый инструмент сравнения или представив вместо этого необработанные данные. Уровень безработицы в США в 2018 году составлял около 90 025 4%, тогда как в 2010 году он составлял около 10 %. Оставив в стороне определения безработицы и , предполагая, что эти цифры верны , мы собираемся посмотреть, как эти статистические данные могут быть представлены.
Для первого примера можно сказать, что было уровень безработицы в целом снизился на 6% ( 10% - 4% = 6% ). В качестве альтернативы, мы могли бы сказать, что произошло процентное снижение на 60% , так как это процентное снижение между 10 и 4. Наконец, мы могли бы говорить о процентной разнице около 85% , которая произошла между безработицей в 2010 и 2018 годах. ставки.
Если же мы предпочитаем остаться с необработанными числами , мы можем сказать, что в настоящее время в США насчитывается примерно на 17 миллионов активных работников по сравнению с 2010 годом. Или мы могли бы сказать, что, поскольку рабочая сила сокращается за последние годы, существует около 9 миллионов безработных меньше человек, и это было бы столь же верно. Просто взглянув на представленные вам цифры, вы, вероятно, начали понимать истинные масштабы проблемы с данными и статистикой и то, насколько по-разному они могут выглядеть в зависимости от того, как они представлены.
Или мы могли бы сказать, что, поскольку рабочая сила сокращается за последние годы, существует около 9 миллионов безработных меньше человек, и это было бы столь же верно. Просто взглянув на представленные вам цифры, вы, вероятно, начали понимать истинные масштабы проблемы с данными и статистикой и то, насколько по-разному они могут выглядеть в зависимости от того, как они представлены.
Важным выводом из всего этого является то, что мы не можем свести данные только к одному числу , так как это становится бессмысленным. Вы должны знать, как было получено это число, , что оно представляет собой и почему оно может дать неверное представление о ситуации. Так что просто помните, люди могут заставить числа говорить все, что они хотят, так что будьте начеку и сохраняйте критическое мышление, когда сталкиваетесь с информацией .
Часто задаваемые вопросы
Равна ли процентная разница процентному изменению?
Нет , это два разных понятия . В процентной разнице точка отсчета представляет собой среднее из двух данных нам чисел, а в процентном изменении одно из этих чисел принимается за точку отсчета. Более того, в отличие от процентного изменения, процентная разница представляет собой сравнение без направления .
В процентной разнице точка отсчета представляет собой среднее из двух данных нам чисел, а в процентном изменении одно из этих чисел принимается за точку отсчета. Более того, в отличие от процентного изменения, процентная разница представляет собой сравнение без направления .
Какова процентная разница между 20 и 30?
Давайте пошагово определим процентную разницу между 20 и 30:
- Вычислите абсолютную разницу между нашими числами:
|20 - 30| = |-10| = 10 - Вычислите также их среднее значение:
(20 + 30) / 2 = 50 / 2 = 25 - Разделите разницу на среднее значение:
10/25 = 0,4 - Выразите результат в процентах:
0,4 * 100 = 40%
Когда процентная разница равна 100%?
Разница в процентах равна 100% тогда и только тогда, когда одно из чисел в три раза больше другого числа . Доказать это не сложно! Смотри:
Процентная разница между
aиbравна 100% тогда и только тогда, когда мы имеемa - b = (a + b) / 2.
Не ограничивая общности, мы предполагаем, что
a ≥ b, поэтому мы можем опустить абсолютное значение в левой части. Отсюда следует, что2a - 2b = a + bСледовательно,
a = 3b, как и утверждалось!
Альваро Диэз и Доминик Черния, кандидат доктора философии
Значение
Значение B
Процентная разница
Разница
Advanced Mode
Если вы хотите рассчитать один процентный разница после другого, нажима Advanced Depode
. ниже.
Ознакомьтесь с 9 похожими процентными калькуляторами.0001
Введение
Коды переноса излучения являются ключевым инструментом для многих исследований и практических приложений, связанных с взаимодействием излучения с веществом. Существует множество кодов, включая FLUKA, Geant4, MCNP, PHITS или TOPAS [1–5]; недавние обзоры, посвященные применениям лучевой терапии, можно найти в [6, 7]. В большинстве случаев приходится сталкиваться с общей проблемой: поле излучения и результирующее распределение дозы должны быть захвачены в довольно большом пространственном масштабе, например, в человеческом теле, в детекторе физики высоких энергий или в экранирующем слое. в космической среде обитания. В то же время, однако, радиационное воздействие осуществляется посредством событий энерговклада (в основном ионизации и возбуждения атомов мишени), распределенных в пространстве с интервалом ∼нм. Объединение этих пространственных масштабов и работа с ними в общей моделирующей структуре, без сомнения, является сложной задачей. Существуют два основных подхода, а именно подход сжатой истории, подходящий для макроскопического моделирования, и подход с последовательной структурой треков, предназначенный для микроскопического и наноскопического моделирования. В подходе сжатой истории алгоритм моделирования переноса излучения имеет дело с кумулятивными эффектами множественных столкновений частиц, аппроксимированных за один «шаг».
В большинстве случаев приходится сталкиваться с общей проблемой: поле излучения и результирующее распределение дозы должны быть захвачены в довольно большом пространственном масштабе, например, в человеческом теле, в детекторе физики высоких энергий или в экранирующем слое. в космической среде обитания. В то же время, однако, радиационное воздействие осуществляется посредством событий энерговклада (в основном ионизации и возбуждения атомов мишени), распределенных в пространстве с интервалом ∼нм. Объединение этих пространственных масштабов и работа с ними в общей моделирующей структуре, без сомнения, является сложной задачей. Существуют два основных подхода, а именно подход сжатой истории, подходящий для макроскопического моделирования, и подход с последовательной структурой треков, предназначенный для микроскопического и наноскопического моделирования. В подходе сжатой истории алгоритм моделирования переноса излучения имеет дело с кумулятивными эффектами множественных столкновений частиц, аппроксимированных за один «шаг». Шаг моделируется как путь, свободный от взаимодействий, а в его конце рассматривается общее изменение энергии частицы (с помощью функций тормозной способности) и направления движения. Фактическая длина свободного пробега, потери энергии и отклонение измеряются стохастически. Ядерные реакции, приводящие к образованию различных частиц после того, как произошло взаимодействие, также могут быть смоделированы. Коды, использующие такой подход, широко и успешно применяются и позволяют точно рассчитывать, например, дозу облучения в мишенях разных размеров. Напротив, трековые коды [8, 9] разработаны для моделирования всех одиночных столкновений с атомными электронами в мишени в пособытийной манере. Результатом моделирования является набор пространственных координат ионизации и возбуждения, индуцированных первичной частицей и ее вторичными электронами, и энерговыделений в каждом событии, формирующих трек частицы. Что касается различных материалов мишени, перенос излучения с использованием подхода сжатой истории в основном требует знания тормозной способности частиц (а также данных о сечениях ядерных реакций), в то время как моделирование событий за событием требует точного знания всех сечений взаимодействия.
Шаг моделируется как путь, свободный от взаимодействий, а в его конце рассматривается общее изменение энергии частицы (с помощью функций тормозной способности) и направления движения. Фактическая длина свободного пробега, потери энергии и отклонение измеряются стохастически. Ядерные реакции, приводящие к образованию различных частиц после того, как произошло взаимодействие, также могут быть смоделированы. Коды, использующие такой подход, широко и успешно применяются и позволяют точно рассчитывать, например, дозу облучения в мишенях разных размеров. Напротив, трековые коды [8, 9] разработаны для моделирования всех одиночных столкновений с атомными электронами в мишени в пособытийной манере. Результатом моделирования является набор пространственных координат ионизации и возбуждения, индуцированных первичной частицей и ее вторичными электронами, и энерговыделений в каждом событии, формирующих трек частицы. Что касается различных материалов мишени, перенос излучения с использованием подхода сжатой истории в основном требует знания тормозной способности частиц (а также данных о сечениях ядерных реакций), в то время как моделирование событий за событием требует точного знания всех сечений взаимодействия. с атомными электронами [10]. Поэтому расчеты гусеничной конструкции в основном выполняются только в воде.
с атомными электронами [10]. Поэтому расчеты гусеничной конструкции в основном выполняются только в воде.
Для медицинских применений ионизирующего излучения, а также для защиты от радиации интерес представляет макроскопический масштаб всего поля излучения, воздействующего на человека. Необходимы точные расчеты физической поглощенной дозы в органах и тканях облученного человека, даже для применения лучевой терапии не только в лечебном объеме, но и в окружающих областях [11, 12]. Необходимо учитывать различные элементные составы и неоднородности тканей. В то же время радиационные эффекты с точки зрения, например, уничтожения раковых клеток или индуцирования геномных аберраций или мутаций могут быть прослежены до радиационных взаимодействий, происходящих в масштабе чувствительных субклеточных мишеней, таких как ядерная ДНК или хромосомные домены. Описание и, насколько это возможно, прогнозирование этих эффектов требует инструментов моделирования с подходом трековой структуры в сочетании с программной копией целевого геномного содержимого. Также, помимо взаимодействий с молекулой ДНК (прямое повреждение), необходимо учитывать, что энерговыделение воды в клетке может привести к радиолизу воды, с образованием свободных радикалов, которые могут диффундировать, химически реагировать друг с другом и повреждение ДНК (косвенное повреждение). В этом смысле были разработаны усовершенствованные коды трековой структуры, такие как PARTRAC [8], которые в настоящее время позволяют полностью моделировать цепочку событий от прохождения излучения одноклеточной модели (с использованием жидкой воды в качестве суррогатного материала) до индукции начальное повреждение ДНК (а также, в некоторой степени, эволюция и репарация повреждений).
Также, помимо взаимодействий с молекулой ДНК (прямое повреждение), необходимо учитывать, что энерговыделение воды в клетке может привести к радиолизу воды, с образованием свободных радикалов, которые могут диффундировать, химически реагировать друг с другом и повреждение ДНК (косвенное повреждение). В этом смысле были разработаны усовершенствованные коды трековой структуры, такие как PARTRAC [8], которые в настоящее время позволяют полностью моделировать цепочку событий от прохождения излучения одноклеточной модели (с использованием жидкой воды в качестве суррогатного материала) до индукции начальное повреждение ДНК (а также, в некоторой степени, эволюция и репарация повреждений).
В этом общем контексте в настоящее время предпринимаются усилия по разработке инструментов биофизического моделирования, которые могут одновременно обеспечивать макроскопическое описание радиационного поля и его последствий с точки зрения повреждений на клеточном/субклеточном уровне, например, Geant4/Geant4 -проект ДНК [13].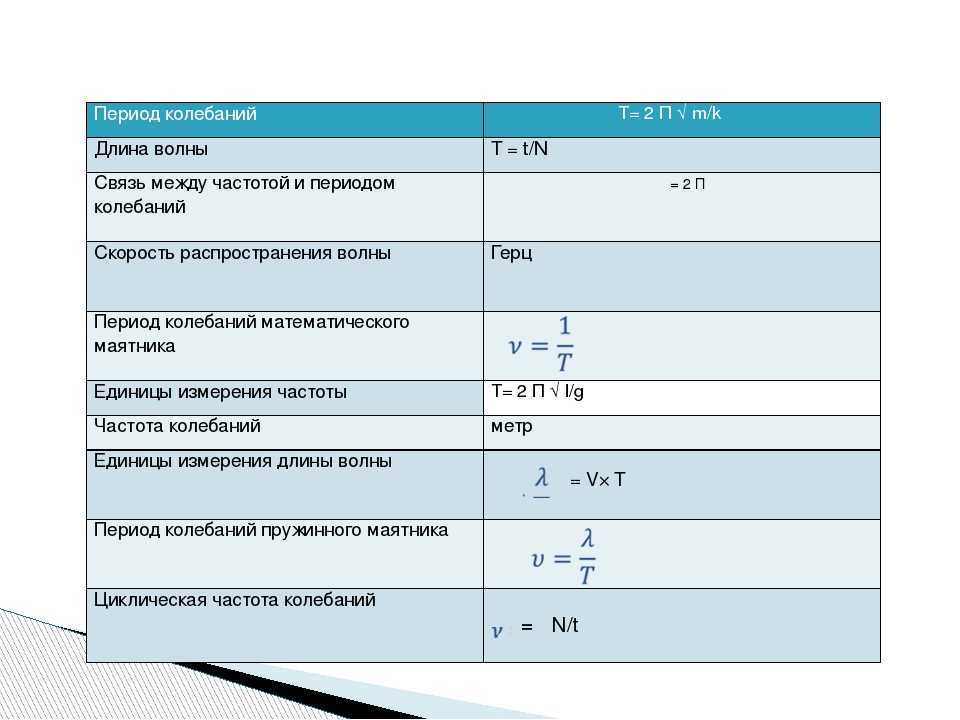 Однако можно использовать различные стратегии для объединения существующих кодов переноса излучения с использованием подхода сжатой истории с кодами трековой структуры. Это привело бы к лучшему использованию имеющихся инструментов, расширению применимости транспортных кодов к биологическим конечным точкам и кодов трековой структуры к большим объемам и включению вторичных частиц, образующихся в результате ядерных реакций. Простой подход к соединению с большим потенциалом состоит во внедрении в коды переноса излучения аналитических формул или справочных таблиц, которые фиксируют результаты моделирования трековой структуры индуцированного повреждения ДНК. Такой подход дает ряд важных преимуществ: существующие коды переноса излучения либо уже предоставляют информацию, необходимую для сопряжения, либо могут быть легко разработаны для этого; Связывание также может выполняться пользователями в автономном режиме, что не требует реальной разработки транспортного кода; Внедрение формул или таблиц в транспортный код также приводит к значительной экономии вычислительного времени по сравнению с запуском новых симуляций.
Однако можно использовать различные стратегии для объединения существующих кодов переноса излучения с использованием подхода сжатой истории с кодами трековой структуры. Это привело бы к лучшему использованию имеющихся инструментов, расширению применимости транспортных кодов к биологическим конечным точкам и кодов трековой структуры к большим объемам и включению вторичных частиц, образующихся в результате ядерных реакций. Простой подход к соединению с большим потенциалом состоит во внедрении в коды переноса излучения аналитических формул или справочных таблиц, которые фиксируют результаты моделирования трековой структуры индуцированного повреждения ДНК. Такой подход дает ряд важных преимуществ: существующие коды переноса излучения либо уже предоставляют информацию, необходимую для сопряжения, либо могут быть легко разработаны для этого; Связывание также может выполняться пользователями в автономном режиме, что не требует реальной разработки транспортного кода; Внедрение формул или таблиц в транспортный код также приводит к значительной экономии вычислительного времени по сравнению с запуском новых симуляций.
Тогда возникает вопрос, какая информация лучше всего подходит для создания моста между выходным сигналом переноса излучения и кодом структуры пути. Код переноса излучения должен уметь описывать характеристики поля излучения с широким выбором наблюдаемых (типы частиц, распределение энергии, распределение ЛПЭ, направление движения и т. д.) в целях различных размеров, в идеале вплоть до длины шага используется для расчетов в методе сжатой истории. Конечно, полная характеристика поля в пространственном масштабе, который соответствует объему одной клетки, непрактична и нецелесообразна с точки зрения вычислительного времени при рассмотрении макроскопической цели. Например, в сценарии вокселизированной мишени типичный размер кубического вокселя составляет порядка ~1 мм, и для извлечения параметров, описывающих поле излучения в вокселе, можно использовать процедуры усреднения. Интересно, что аналитические формулы реализованы, например, в программе PHITS, которые позволяют рассчитывать распределение микродозиметрических величин в макроскопических областях мишени [5]. По определению, микродозиметрические величины, такие как линейная энергия, строятся с учетом стохастичности энерговыделения излучением в чувствительных участках микрометрового размера. Таким образом, можно утверждать, что они идеально подходят для характеристики поля излучения в ядре отдельной клетки, которое можно рассматривать как квазисферический объем с линейным размером ~10 мкм. Эти соображения лежат в основе наших предыдущих работ, в которых мы предложили полную связь между PHITS и PARTRAC для получения ОБЭ нейтронов различной энергии [14, 15], а также полный набор аналитических функций [16], воспроизводящих PARTRAC дает результаты по различным типам повреждений ДНК в зависимости от оценки LET, когда ядро клетки облучают различными легкими ионами при энергиях, соответствующих лучевой терапии, вплоть до остановки. Такая оценка ЛПЭ, полученная путем деления дозы, доставленной в ядро клетки, на флюенс частиц (с соответствующим преобразованием единиц), действительно аналогична понятию средней линейной энергии дозы в микродозиметрии.
По определению, микродозиметрические величины, такие как линейная энергия, строятся с учетом стохастичности энерговыделения излучением в чувствительных участках микрометрового размера. Таким образом, можно утверждать, что они идеально подходят для характеристики поля излучения в ядре отдельной клетки, которое можно рассматривать как квазисферический объем с линейным размером ~10 мкм. Эти соображения лежат в основе наших предыдущих работ, в которых мы предложили полную связь между PHITS и PARTRAC для получения ОБЭ нейтронов различной энергии [14, 15], а также полный набор аналитических функций [16], воспроизводящих PARTRAC дает результаты по различным типам повреждений ДНК в зависимости от оценки LET, когда ядро клетки облучают различными легкими ионами при энергиях, соответствующих лучевой терапии, вплоть до остановки. Такая оценка ЛПЭ, полученная путем деления дозы, доставленной в ядро клетки, на флюенс частиц (с соответствующим преобразованием единиц), действительно аналогична понятию средней линейной энергии дозы в микродозиметрии. Тем не менее, существуют некоторые ограничения для этого связанного подхода с использованием функций на основе ЛПЭ: средняя доза линейной энергии (или определение ЛПЭ, которое согласуется с определением, принятым в расчетах PARTRAC) может быть недоступно для всех транспортных кодов. Кроме того, одно и то же значение ЛПЭ дважды пересекается по мере замедления частицы в ее дистальной и проксимальной частях пика Брэгга, но характеристики трека, включая его биологическую эффективность, различны. Следовательно, при построении графика повреждения ДНК в зависимости от LET появляются крючки, и однозначные математические функции не могут воспроизвести полный набор результатов, включая самые низкие энергии частиц. Вместо этого для решения этой проблемы можно предложить представление повреждения ДНК как функции энергии частиц. Это также имеет то преимущество, что распределение энергии частиц может быть легко извлечено из транспортных кодов.
Тем не менее, существуют некоторые ограничения для этого связанного подхода с использованием функций на основе ЛПЭ: средняя доза линейной энергии (или определение ЛПЭ, которое согласуется с определением, принятым в расчетах PARTRAC) может быть недоступно для всех транспортных кодов. Кроме того, одно и то же значение ЛПЭ дважды пересекается по мере замедления частицы в ее дистальной и проксимальной частях пика Брэгга, но характеристики трека, включая его биологическую эффективность, различны. Следовательно, при построении графика повреждения ДНК в зависимости от LET появляются крючки, и однозначные математические функции не могут воспроизвести полный набор результатов, включая самые низкие энергии частиц. Вместо этого для решения этой проблемы можно предложить представление повреждения ДНК как функции энергии частиц. Это также имеет то преимущество, что распределение энергии частиц может быть легко извлечено из транспортных кодов.
Исходя из этих соображений, мы предоставляем в этой работе набор новых аналитических функций, исследующих, как результаты PARTRAC по повреждению ДНК зависят от энергии частицы для легких ионов вплоть до Ne, с энергиями на нуклон (удельные энергии, далее называемые просто энергиями) от 0,5 ГэВ/н до остановки. Новые формулы воспроизводят количество повреждений ДНК на единицу дозы или трек частиц и дополняют предыдущие результаты по количеству повреждений в зависимости от ЛПЭ частиц. Таким образом, пользователи транспортного кода, желающие внедрить такие формулы в код переноса излучения, получают возможность выбора по-разному. Далее мы обсудим, как доступность этих формул закладывает основу для эффективной стратегии выполнения связи между переносом излучения и кодами трековой структуры. Мы обсуждаем ограничения такой стратегии и способы их преодоления, в частности, в отношении проблемы электронного равновесия. Результаты полной связи между транспортными кодами и кодами структуры пути для конкретных тематических исследований должны быть представлены в другом месте, эта работа расширяет потенциал применения результатов PARTRAC и их использование для расширения существующих транспортных кодов для получения основанных на повреждениях ДНК оценок биологическая эффективность.
Новые формулы воспроизводят количество повреждений ДНК на единицу дозы или трек частиц и дополняют предыдущие результаты по количеству повреждений в зависимости от ЛПЭ частиц. Таким образом, пользователи транспортного кода, желающие внедрить такие формулы в код переноса излучения, получают возможность выбора по-разному. Далее мы обсудим, как доступность этих формул закладывает основу для эффективной стратегии выполнения связи между переносом излучения и кодами трековой структуры. Мы обсуждаем ограничения такой стратегии и способы их преодоления, в частности, в отношении проблемы электронного равновесия. Результаты полной связи между транспортными кодами и кодами структуры пути для конкретных тематических исследований должны быть представлены в другом месте, эта работа расширяет потенциал применения результатов PARTRAC и их использование для расширения существующих транспортных кодов для получения основанных на повреждениях ДНК оценок биологическая эффективность.
Материалы и методы
Моделирование трековой структуры PARTRAC
PARTRAC [8, 17–21] представляет собой семейство инструментов биофизического моделирования для моделирования биологических эффектов ионизирующего излучения на субклеточном и клеточном уровнях. Он имеет модульную структуру, отражающую лежащие в его основе механизмы и процессы. Отдельные модули объединяют знания из радиационной физики, химии, биофизики ДНК и ее радиационных повреждений и радиационной биологии. Модульная структура инструмента облегчает уточнение модели, интеграцию новых функций, а также расширение для дополнительных конечных точек.
Он имеет модульную структуру, отражающую лежащие в его основе механизмы и процессы. Отдельные модули объединяют знания из радиационной физики, химии, биофизики ДНК и ее радиационных повреждений и радиационной биологии. Модульная структура инструмента облегчает уточнение модели, интеграцию новых функций, а также расширение для дополнительных конечных точек.
Моделирование начинается с модуля, описывающего физические процессы взаимодействия излучения с проходимым веществом. Код способен обрабатывать фотоны, электроны, протоны и легкие ионы в широком диапазоне энергий, что важно для естественных, медицинских и технических приложений. Обычно в качестве заменителя биологического материала используется жидкая вода. Для фотонов пользователь может указать однородную среду с произвольным атомным составом. Для каждого типа частиц реализованы установленные данные о поперечном сечении. Соответствующий набор данных подвергается стохастической выборке для создания in silico представление картины взаимодействия, в пособытийном режиме, т. е. моделирующее отдельные ионизации, возбуждения и дальнейшие процессы (кроме ядерных реакций). За первичной частицей следят до тех пор, пока она не остановится или пока не покинет заданный интересующий объем, который обычно окружает клетку. Кроме того, отслеживаются все вторичные электроны, освобожденные первичными частицами, а также все частицы более высокого порядка. Каждый такой сгенерированный трек отличается, но они имеют некоторые общие черты, например, плотные области ядра в треках ионов, окруженные полутенями с редкими треками вторичных электронов.
е. моделирующее отдельные ионизации, возбуждения и дальнейшие процессы (кроме ядерных реакций). За первичной частицей следят до тех пор, пока она не остановится или пока не покинет заданный интересующий объем, который обычно окружает клетку. Кроме того, отслеживаются все вторичные электроны, освобожденные первичными частицами, а также все частицы более высокого порядка. Каждый такой сгенерированный трек отличается, но они имеют некоторые общие черты, например, плотные области ядра в треках ионов, окруженные полутенями с редкими треками вторичных электронов.
В последующем модуле, который представляет дохимические и химические процессы развития трека, отдельные события ионизации и возбуждения преобразуются в реактивные частицы или релаксируются в молекулы воды. Реализованы коэффициенты ветвления, выходы различных видов и их диффузионные свойства. Диффузия видов прослеживается вместе с их взаимными реакциями в пошаговом режиме. В дополнение к взаимным реакциям виды удаляются при атаке клеточной ДНК, гистонов или в неспецифических реакциях, определяемых их временем жизни.
Реализованы многомасштабные модели ДНК и хроматина. Они варьируются от атомной модели двойной спирали ДНК до ее связывания с нуклеосомами, образования хроматинового волокна размером около 30 нм, его петель и доменов до хромосомных территорий внутри клеточных ядер. В настоящее время в PARTRAC доступны две такие многомасштабные модели: сферическая для лимфоцитов человека и эллиптическая для фибробластов человека.
Путем наложения этих моделей ДНК и хроматина на следы радиации с точки зрения распределения энергии (так называемые прямые радиационные эффекты) и атаки реактивных видов (косвенные эффекты) оценивается повреждение ДНК. Запасы энергии в сахаро-фосфатном остове, а также атаки гидроксильных радикалов стохастическим образом преобразуются в разрывы нитей ДНК. Разрывы на обеих цепях в пределах геномного расстояния в 10 пар оснований (п.н.) оцениваются как двухцепочечные разрывы (DSB). Даже DSB могут группироваться, особенно для частиц с высокой ЛПЭ. Кластеры DSB оцениваются всякий раз, когда два или более DSB появляются в пределах 25 п. н. Кластеры DSB являются примером кластерных поражений (локально множественных поврежденных участков), которые, вероятно, создают критические проблемы для систем клеточной репарации и могут представлять собой начальное повреждение, в конечном итоге приводящее к хромосомным аберрациям и гибели клеток. Термин сайты DSB включает как изолированные сайты DSB, так и их кластеры: изолированный сайт DSB образует сайт DSB, и кластер, например, из трех DSB, разделенных менее чем на 25 п.н. друг от друга, также оценивается как один сайт DSB. Помимо этой простой схемы классификации, PARTRAC включает еще один модуль, который позволяет пользователю оценивать паттерны фракционирования ДНК по многочисленным шкалам, начиная от очень коротких фрагментов (десятки пар оснований) до фрагментов хромосом (сотни миллионов пар оснований).
н. Кластеры DSB являются примером кластерных поражений (локально множественных поврежденных участков), которые, вероятно, создают критические проблемы для систем клеточной репарации и могут представлять собой начальное повреждение, в конечном итоге приводящее к хромосомным аберрациям и гибели клеток. Термин сайты DSB включает как изолированные сайты DSB, так и их кластеры: изолированный сайт DSB образует сайт DSB, и кластер, например, из трех DSB, разделенных менее чем на 25 п.н. друг от друга, также оценивается как один сайт DSB. Помимо этой простой схемы классификации, PARTRAC включает еще один модуль, который позволяет пользователю оценивать паттерны фракционирования ДНК по многочисленным шкалам, начиная от очень коротких фрагментов (десятки пар оснований) до фрагментов хромосом (сотни миллионов пар оснований).
Наконец, в последнее десятилетие большое внимание уделялось разработке модуля ремонта в PARTRAC [17, 18, 22–25]. Он представляет собой негомологичный путь соединения концов репарации DSB, доминирующей репарации DSB в клетках человека в фазах клеточного цикла G0 и G1. Модуль явно объясняет действие ферментов репарации, а также подвижность разрывов хроматина. Это было распространено и на хромосомные аберрации. Обнадеживающие предварительные результаты были получены и для конечной точки уничтожения клеток.
Модуль явно объясняет действие ферментов репарации, а также подвижность разрывов хроматина. Это было распространено и на хромосомные аберрации. Обнадеживающие предварительные результаты были получены и для конечной точки уничтожения клеток.
Результаты PARTRAC были подтверждены имеющимися большими наборами экспериментальных данных в области радиационной физики, химии и биологии, ср. [8] и ссылки. в нем. Инструмент послужил эталоном для других кодов. Его недавние приложения включали модель, обеспечивающую механистическую интерпретацию биологической эффективности нейтронов [14, 15], модель радиационно-индуцированных эффектов свидетеля [26–30] или исследование воздействия радиации на митохондриальную ДНК [31].
В этой работе мы проанализировали ранее опубликованную обширную базу данных моделирования PARTRAC повреждений ДНК, индуцированных легкими ионами [20, 21]. Ядра модельных клеток облучали 1 H, 4 HE, 7 LI, 9 BE, 11 B, 12 C, 14 N, 16 O или 14 N, 16 O или 14 . , 0,5, 1, 2, 4, 8, 16, 32, 64, 128, 256 или 512 МэВ/нуклид. Ионы стартовали полностью лишенными электронов. Источником ионов служила окружность 2 диаметром 80 мкм, расположенная тангенциально к модельному ядру лимфоцита (сфера диаметром 10 мкм, содержащая 6,6 Гб ДНК в 23 парах хромосом). Взаимодействия оценивались в интересующей сферической «мировой» области диаметром 14,22 мкм, концентричной с моделью ядра. Для каждого типа иона и энергии было смоделировано не менее 1280 частиц (до 3,2 миллиона протонов высокой энергии). Симуляции были разделены на 256–8,192 прогона с 5–3200 частицами за прогон. Статистические погрешности представлены как ± 1,96-кратное стандартное отклонение, следовательно, охватывают 95% доверительные интервалы для смоделированных выходов повреждений ДНК, рассчитанных на основе распределений Пуассона.
, 0,5, 1, 2, 4, 8, 16, 32, 64, 128, 256 или 512 МэВ/нуклид. Ионы стартовали полностью лишенными электронов. Источником ионов служила окружность 2 диаметром 80 мкм, расположенная тангенциально к модельному ядру лимфоцита (сфера диаметром 10 мкм, содержащая 6,6 Гб ДНК в 23 парах хромосом). Взаимодействия оценивались в интересующей сферической «мировой» области диаметром 14,22 мкм, концентричной с моделью ядра. Для каждого типа иона и энергии было смоделировано не менее 1280 частиц (до 3,2 миллиона протонов высокой энергии). Симуляции были разделены на 256–8,192 прогона с 5–3200 частицами за прогон. Статистические погрешности представлены как ± 1,96-кратное стандартное отклонение, следовательно, охватывают 95% доверительные интервалы для смоделированных выходов повреждений ДНК, рассчитанных на основе распределений Пуассона.
DSB, кластеры DSB и сайты DSB были подсчитаны. Из абсолютного количества поражений и осевшей дозы были рассчитаны выходы повреждений на Гр на Гбит/с. В данной работе это называется дозовым подходом. В качестве альтернативы учитывались коэффициенты повреждения на дорожку на Гбит/с, что может служить основой для подхода, основанного на плотности потока. Эти два подхода могут быть использованы для объединения переноса излучения с моделированием трековой структуры с использованием различных стратегий. Пользователь транспортного кода должен выбрать соответствующий код в зависимости от наличия результатов переноса излучения и конкретного изучаемого случая. Это рассматривается позже в обсуждении.
В данной работе это называется дозовым подходом. В качестве альтернативы учитывались коэффициенты повреждения на дорожку на Гбит/с, что может служить основой для подхода, основанного на плотности потока. Эти два подхода могут быть использованы для объединения переноса излучения с моделированием трековой структуры с использованием различных стратегий. Пользователь транспортного кода должен выбрать соответствующий код в зависимости от наличия результатов переноса излучения и конкретного изучаемого случая. Это рассматривается позже в обсуждении.
Аналитическое представление результатов повреждения ДНК
Чтобы сделать возможным переход от подхода, основанного на дозе, к подходу, основанному на флюенсе, результаты моделирования по дозе, осаждаемой в ядре на трек D трек (в Гр ) были подогнаны в зависимости от начальной энергии иона E (в МэВ/нуклон):
Dtrack=p1Ep2(1+exp(p3)Ep4)p5.(1)
мотивировано формой результатов моделирования в логарифмическом масштабе (ср. Результаты раздел). Эта функция объединяет два члена степенной зависимости, Ep2 и Ep2-p4p5, с плавным логистическим переходом между ними. Параметры p 3 (используются в экспоненциальной форме, чтобы гарантировать положительность результирующих степенных коэффициентов) и p 5 влияют на переходную область, а p 1 масштабируют величину функции.
Результаты раздел). Эта функция объединяет два члена степенной зависимости, Ep2 и Ep2-p4p5, с плавным логистическим переходом между ними. Параметры p 3 (используются в экспоненциальной форме, чтобы гарантировать положительность результирующих степенных коэффициентов) и p 5 влияют на переходную область, а p 1 масштабируют величину функции.
Выходы Y DSB, DSB-кластеров и DSB-сайтов (выраженные в Гр на Гбп) были подогнаны как функция начальной энергии ионов E (выражено в МэВ/нуклон) по:
Y=p0+p111+(E exp(p2))p3(1−11+(E exp(p4))p5)+p611+(E exp(p7)) p8.(2)
Эти функции объединяют три степенных члена с логистическими переходами между ними. При параметрах p > 0 первый и последний члены уменьшаются, а второй увеличивается с ростом энергии. Параметры p 2 , p 4 и p 7 управляют положением этих логистических степенных функций; р 3 , р 5 и р 8 их откосов; p 1 и p 6 величина эффектов; и p 0 изображает асимптотическое поведение при высоких энергиях. Поведение при высоких энергиях (т. е. с низкой ЛПЭ) было взято из работы [3]. 16, используя следующие значения: p 0 = 6,8 DSB, 0,07 кластеров DSB и 6,8 сайтов DSB на Гр на Гбит/с.
Поведение при высоких энергиях (т. е. с низкой ЛПЭ) было взято из работы [3]. 16, используя следующие значения: p 0 = 6,8 DSB, 0,07 кластеров DSB и 6,8 сайтов DSB на Гр на Гбит/с.
Параметры этих тестовых функций были адаптированы к результатам моделирования путевой структуры с использованием нелинейной подгонки модели в Matlab (The MathWorks Inc., США). Это было сделано для каждого типа повреждения и каждого иона в отдельности, а также для доз на трек. Некоторые термины или параметры в некоторых случаях были не нужны и поэтому не включались (ср. 9).0051 Результаты ). Несколько значений параметров были исправлены вручную (в частности, параметр p 8 для DSB и их сайтов, ср. Результаты ), чтобы помочь избежать переобучения, особенно во избежание локальных минимумов или максимумов, которые в противном случае могли бы возникнуть как простые артефакты процедуры подгонки, не подтвержденные результатами моделирования. Выходы повреждений на дорожку на Гбит затем получали произведением формулы (2) для выходов на Гр на Гбит и формулы (1) для дозы на дорожку.
Расчеты аморфной трековой структуры
При заданной настройке моделирования трековой структуры PARTRAC учитывались только те ионы, области ядра трека которых попадали в ядро. Ионы, проходящие рядом и попадающие в ядро только своими областями полутени, не учитывались. Этот подход был выбран для ограничения вычислительных затрат на моделирование структуры треков для высокоэнергетических ионов, которые создают очень широкие области полутени с низкой плотностью, например, протоны с энергией 512 МэВ/нуклон, высвобождающие вторичные электроны с пробегом в воде и, следовательно, радиусом трека в несколько единиц. миллиметров, но общая ЛПЭ (включая ядро трека) составляет всего около 0,2 кэВ/мкм. Чтобы оценить ограничения этого подхода, были выполнены дополнительные расчеты с использованием модели аморфной структуры пути [32], которая предполагает радиальное распределение дозы: 9где Радиус трека R TR (в мкм) дается R TR = 0,062 E 1. 7 , с E (Mev/u) Denoting yoniting the y). ], а λ — постоянная интегрирования, пропорциональная ЛПЭ дорожки. Доля ЛПЭ, осевшая во внутренней части дорожки (до определенного расстояния R от оси трека, например, радиус клеточного ядра) затем рассчитывали по формуле:
7 , с E (Mev/u) Denoting yoniting the y). ], а λ — постоянная интегрирования, пропорциональная ЛПЭ дорожки. Доля ЛПЭ, осевшая во внутренней части дорожки (до определенного расстояния R от оси трека, например, радиус клеточного ядра) затем рассчитывали по формуле:
)=1 иначе (4)
, где ln обозначает натуральный логарифм. Среднюю долю ЛПЭ, откладываемую в сферическом ядре клетки треками, попадающими в ядро своими центральными областями (и, альтернативно, соседними треками), рассчитывали в программе Matlab (The MathWorks Inc., США) путем численного интегрирования радиального распределения дозы, перекрывающегося с ядра клетки и усреднение по прицельным параметрам (т. е. расстоянию ядра трека от центра ядра клетки).
Результаты
Средние дозы, поступившие на трек в сферическом ядре клетки, представлены в зависимости от начальной энергии частиц на рисунке 1. Результаты на рисунке 1 не включают треки, ядра которых не пересекают ядро, но чья полутень все еще может отдавать там энергию. Результаты моделирования структуры трека PARTRAC для каждого события показаны символами. Линии показывают их соответствие формуле (1) с параметрами, перечисленными в таблице 1. Поскольку дозы, осаждаемые на частицу, охватывают очень широкий диапазон: от 0,44 мГр для протонов с энергией 512 МэВ (ионы H) до 3,03 Гр для ионов Ne с энергией 1 МэВ/нуклон. , мы показываем график как в логарифмическом, так и в линейном масштабе. За исключением 512 МэВ/н, аналитические формулы хорошо воспроизводят результаты моделирования. В частности, они фиксируют общее степенное увеличение осажденной дозы с уменьшением энергии примерно до 0,5–1 МэВ/нуклон. Также воспроизводится уменьшение осажденной дозы с дальнейшим уменьшением энергии. Обратите внимание, что нанесенные на график дозы являются средними значениями по всем смоделированным трекам. Фактическое выделение энергии треком зависит от длины его пути внутри ядра и, следовательно, сильно отличается от треков, ядра которых попадают в ядро в центре, от тех, которые поражают его только по периферии.
Результаты моделирования структуры трека PARTRAC для каждого события показаны символами. Линии показывают их соответствие формуле (1) с параметрами, перечисленными в таблице 1. Поскольку дозы, осаждаемые на частицу, охватывают очень широкий диапазон: от 0,44 мГр для протонов с энергией 512 МэВ (ионы H) до 3,03 Гр для ионов Ne с энергией 1 МэВ/нуклон. , мы показываем график как в логарифмическом, так и в линейном масштабе. За исключением 512 МэВ/н, аналитические формулы хорошо воспроизводят результаты моделирования. В частности, они фиксируют общее степенное увеличение осажденной дозы с уменьшением энергии примерно до 0,5–1 МэВ/нуклон. Также воспроизводится уменьшение осажденной дозы с дальнейшим уменьшением энергии. Обратите внимание, что нанесенные на график дозы являются средними значениями по всем смоделированным трекам. Фактическое выделение энергии треком зависит от длины его пути внутри ядра и, следовательно, сильно отличается от треков, ядра которых попадают в ядро в центре, от тех, которые поражают его только по периферии. Еще большие вариации были бы получены, если бы учитывались также треки, перекрывающие ядро только своей полутенью (ср. 9).0051 Обсуждение ). Стохастический характер индивидуальных взаимодействий играет лишь незначительную роль из-за большого количества событий на дорожку.
Еще большие вариации были бы получены, если бы учитывались также треки, перекрывающие ядро только своей полутенью (ср. 9).0051 Обсуждение ). Стохастический характер индивидуальных взаимодействий играет лишь незначительную роль из-за большого количества событий на дорожку.
РИСУНОК 1 . Средняя доза, поступающая в ядро лимфоцита на один трек ионов H–Ne с начальной энергией от 0,25 до 512 МэВ/нуклон, смоделированная с помощью пошагового моделирования трековой структуры PARTRAC (символы) и подогнанная по аналитическим формулам (уравнение 1 (линии) с параметрами, указанными в таблице 1. Панель (A) в логарифмическом масштабе для выделения широкого диапазона значений и качества подгонки; панель (B) в линейной шкале.
ТАБЛИЦА 1 . Параметры аналитических функций (уравнение 1), описывающих дозу облучения ядра клетки (в Гр) в расчете на одну стартовую частицу в зависимости от ее стартовой энергии (в МэВ/нуклон).
Паттерны повреждения ДНК в значительной степени, но не полностью соответствуют дозе на трек. Действительно, когда выходы DSB, кластеров DSB или сайтов DSB нанесены на дорожку (рис. 2–4, панели A и B), общие закономерности напоминают те, что на рис. 1: индукция каждого из этих классов повреждений увеличивается с уменьшением энергии, примерно по степенному закону примерно до 0,5–1 МэВ/н, а затем уменьшается. Однако при анализе выходов повреждений на единицу дозы обнаруживается более тонкая структура: общий выход DSB (рис. 2C) увеличивается примерно с 6,8 DSB на Гр на Гбит/с при высоких энергиях до примерно в три раза более высоких значений при около 1 МэВ/нуклон для легких ионов. и насыщаются на уровне около 16 DSB на Гр на Гбит/с для ионов B-Ne ниже примерно 10 МэВ/нуклон. Имеются систематические указания на волнообразное поведение относительно тяжелых ионов при этих низких энергиях. Гораздо более выраженные вариации наблюдаются для кластеров DSB: их выходы (рис. 3C,D) увеличиваются с таких низких значений, как 0,07 на Гр на Гбит/с при высоких энергиях, примерно до 1 для H, 2,6 для He и 1,9.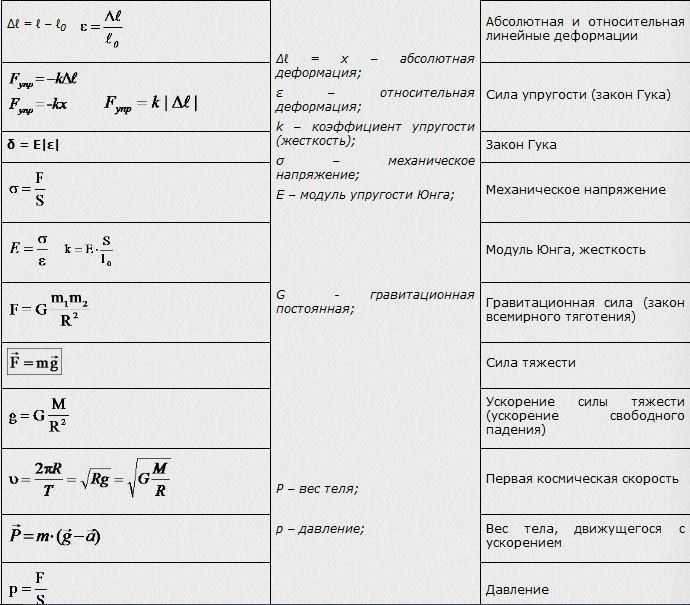 –2,8 на Гр на Гбп для более тяжелых ионов при энергиях 1–10 МэВ/н. Как и в случае с DSB, моделирование также предсказывает для кластеров волнообразное поведение с локальными минимумами около 1 МэВ/нуклон для ионов от C до Ne. Выходы сайтов DSB (рис. 4C) при высоких энергиях примерно равны общему количеству DSB, поскольку подавляющее большинство DSB образуются как изолированные. Однако при низких энергиях выходы DSB-узлов падают, для самых тяжелых изучаемых ионов приближаясь или даже ниже значений высоких энергий. Это происходит по мере того, как все большая доля DSB образует кластеры, которые учитываются только как отдельные сайты, но как несколько DSB. Моделирование предполагает, что выходы кластеров могут дополнительно увеличиваться при энергиях <0,5 МэВ/н. Для всех классов повреждений результаты моделирования гусеничной конструкции хорошо воспроизводятся настоящими аналитическими формулами. Это верно не только для выхода повреждений на Гр (панели C), которые были подобраны по формулам, но также и для выходов на дорожку (панели A и B), которые не были подобраны напрямую.
–2,8 на Гр на Гбп для более тяжелых ионов при энергиях 1–10 МэВ/н. Как и в случае с DSB, моделирование также предсказывает для кластеров волнообразное поведение с локальными минимумами около 1 МэВ/нуклон для ионов от C до Ne. Выходы сайтов DSB (рис. 4C) при высоких энергиях примерно равны общему количеству DSB, поскольку подавляющее большинство DSB образуются как изолированные. Однако при низких энергиях выходы DSB-узлов падают, для самых тяжелых изучаемых ионов приближаясь или даже ниже значений высоких энергий. Это происходит по мере того, как все большая доля DSB образует кластеры, которые учитываются только как отдельные сайты, но как несколько DSB. Моделирование предполагает, что выходы кластеров могут дополнительно увеличиваться при энергиях <0,5 МэВ/н. Для всех классов повреждений результаты моделирования гусеничной конструкции хорошо воспроизводятся настоящими аналитическими формулами. Это верно не только для выхода повреждений на Гр (панели C), которые были подобраны по формулам, но также и для выходов на дорожку (панели A и B), которые не были подобраны напрямую. Даже широкие диапазоны выходов кластеров DSB представлены правильно (см. Логарифмический график на рисунке 3D).
Даже широкие диапазоны выходов кластеров DSB представлены правильно (см. Логарифмический график на рисунке 3D).
РИСУНОК 2 . Моделирование PARTRAC выхода двухцепочечных разрывов ДНК (DSB) в лимфоцитах человека ионами H – Ne с начальными энергиями от 0,25 до 512 МэВ / u (символы), подогнанное аналитическими формулами (линии). Столбики погрешностей отображают предполагаемые 95% доверительные интервалы смоделированных результатов. Там, где планки погрешностей не видны, они меньше символов. Панели (A,B) : доходность на дорожку на Гбит/с в логарифмическом и линейном масштабах, рассчитанная как произведение уравнений 1 и 2, подробности в тексте; панель C: выход на Гр на Гбит/с, в линейной шкале, соответствует уравнению. 2 с параметрами из таблицы 2.
РИСУНОК 3 . Моделирование PARTRAC (символы) и их аппроксимация аналитическими формулами (линии) для выходов кластеров двухцепочечных разрывов ДНК (кластеров DSB) в лимфоцитах человека ионами H–Ne с начальными энергиями от 0,25 до 512 МэВ/нуклон.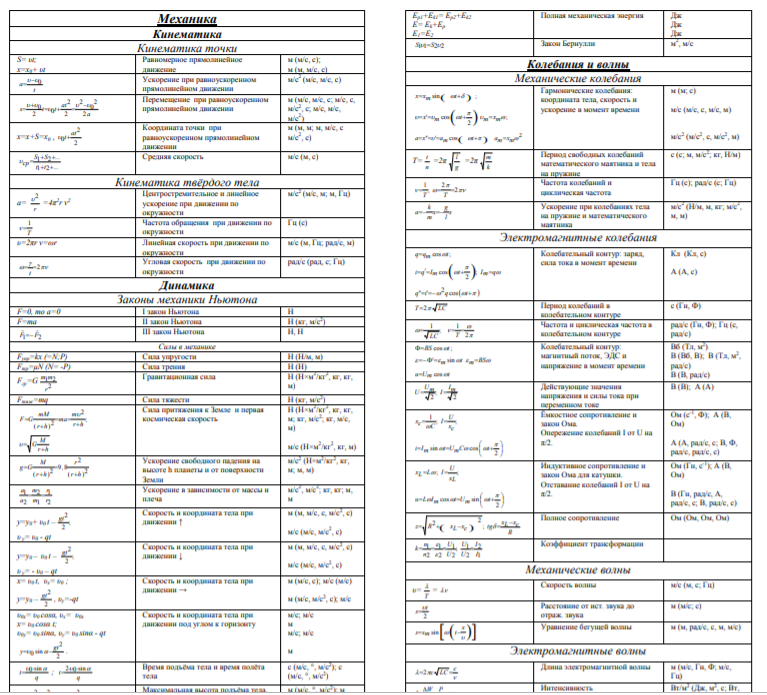 Столбики погрешностей отображают предполагаемые 95% доверительные интервалы смоделированных результатов. Там, где планки погрешностей не видны, они меньше символов. Панели (A,B) : выход на дорожку на Гбит/с в логарифмическом и линейном масштабах, рассчитанный как произведение уравнений 1 и 2, подробности в тексте; панели (C,D) : выход на Гр на Гбит/с, в линейной и логарифмической шкалах, подогнанный по уравнению. 2 с параметрами из таблицы 2.
Столбики погрешностей отображают предполагаемые 95% доверительные интервалы смоделированных результатов. Там, где планки погрешностей не видны, они меньше символов. Панели (A,B) : выход на дорожку на Гбит/с в логарифмическом и линейном масштабах, рассчитанный как произведение уравнений 1 и 2, подробности в тексте; панели (C,D) : выход на Гр на Гбит/с, в линейной и логарифмической шкалах, подогнанный по уравнению. 2 с параметрами из таблицы 2.
РИСУНОК 4 . Моделирование PARTRAC на сайтах двухцепочечных разрывов ДНК (сайты DSB), индуцированных в лимфоцитах человека ионами H–Ne с начальными энергиями от 0,25 до 512 МэВ/нуклон (символы), подобранными аналитическими формулами (линии). Столбики погрешностей отображают примерно 95% доверительные интервалы смоделированных результатов. Там, где планки погрешностей не видны, они меньше символов. Панели (A,B) : доходность на дорожку на Гбит/с в логарифмическом и линейном масштабах, рассчитанная как произведение уравнений 1 и 2, подробности в тексте; панели (C) : выход на Гр на Гбит/с, в линейной шкале, соответствует уравнению. 2 с параметрами из таблицы 2.
2 с параметрами из таблицы 2.
ТАБЛИЦА 2 . Параметры аналитических функций (уравнение 2), описывающих выходы DSB, DSB-кластеров или DSB-сайтов (выраженные в Гр на Гбп) в зависимости от начальной энергии частиц (в МэВ/нуклон).
Оценки выделенной энергии, которые не отражены в настоящем моделировании трековой структуры, показаны на рисунке 5 с использованием модели аморфной трековой структуры. При высоких энергиях только часть ионной ЛПЭ фактически оседает на пройденное ядро (черные кружки). Например, для ионов с энергией 512 МэВ/нуклон эта доля падает примерно до 60 %, так что можно ожидать, что представленные модели PARTRAC пропустят почти 40 % общей энергии, выделяемой треком. Однако эта недостающая доля быстро уменьшается с уменьшением энергии ионов, например, до 23% для треков с энергией 64 МэВ/н, и еще больше уменьшается (почти до нулевой доли) для треков, более узких, чем ядро клетки (энергии ниже примерно 14 МэВ/нуклон). ). Чтобы уменьшить недостающую долю при заданной энергии, необходимо было бы включить треки, проходящие вблизи ядра (цветные кружки). Однако источник и область моделирования должны быть значительно увеличены, вплоть до миллиметровых областей для высокоэнергетических ионов, с высокими вычислительными затратами на моделирование трековой структуры. К счастью, результаты простой формулы, уравнение. 4, для дозы во внутренней части трека (черные звездочки) обеспечивают полезную аппроксимацию доли энергии, выделенной ядру, и, следовательно, также доли, которая отсутствует в моделировании структуры трека высокоэнергетических ионов, и может быть используется вместе с уравнениями 1 и 2 в стратегии связи на основе плотности потока энергии (см. 9).0051 Обсуждение ).
Однако источник и область моделирования должны быть значительно увеличены, вплоть до миллиметровых областей для высокоэнергетических ионов, с высокими вычислительными затратами на моделирование трековой структуры. К счастью, результаты простой формулы, уравнение. 4, для дозы во внутренней части трека (черные звездочки) обеспечивают полезную аппроксимацию доли энергии, выделенной ядру, и, следовательно, также доли, которая отсутствует в моделировании структуры трека высокоэнергетических ионов, и может быть используется вместе с уравнениями 1 и 2 в стратегии связи на основе плотности потока энергии (см. 9).0051 Обсуждение ).
РИСУНОК 5 . Энергия, выделяемая ядру клетки, когда учитываются только треки, которые непосредственно поражают ядро своим ядром (черные кружки), как в настоящих симуляциях структуры треков, или включая вклад всех треков в пределах большей области (цветные символы) при заданном значении. флюенс. Вложенная энергия выражается как доля LET частицы (линейная передача энергии). Среднее значение вклада на трек, попадающий непосредственно в ядро (черные кружки), может быть аппроксимировано энерговыделением внутренней части трека того же размера, уравнение 4 (черные звезды). Расчеты на основе модели аморфной трековой структуры.
Среднее значение вклада на трек, попадающий непосредственно в ядро (черные кружки), может быть аппроксимировано энерговыделением внутренней части трека того же размера, уравнение 4 (черные звезды). Расчеты на основе модели аморфной трековой структуры.
Обсуждение
Были предоставлены аналитические формулы, которые представляют общий выход двухцепочечных разрывов ДНК, их кластеров и сайтов DSB в зависимости от начальной энергии частиц. Следует уточнить, что целью данной работы не было ни создание теоретической модели повреждения ДНК ионными пучками, ни разработка оптимальной модели для воспроизведения данных моделирования с использованием строго ограниченного числа параметров. Цель состояла исключительно в том, чтобы воспроизвести данные моделирования феноменологическим образом, но с высокой степенью точности, чтобы облегчить их использование в рамках кода переноса излучения.
Были проанализированы три класса повреждений ДНК, во всех случаях рассматривая общее повреждение, т. е. возникающее в результате повреждений ДНК, индуцированных как непосредственно ( посредством прямого энерговыделения ДНК), так и опосредованно (опосредовано свободными радикалами). Мы решили включить в это исследование только избранные классы повреждений ДНК, что обосновано следующим: DSB обычно рассматриваются как ключевые начальные повреждения, связанные с биологическими эффектами ионизирующего излучения. Тем не менее, даже большинство DSB можно отремонтировать. Кластерные повреждения ДНК, в частности кластеры DSB, вероятно, создают серьезные проблемы для системы клеточной репарации и обычно могут приводить к летальным исходам [34]. Когда паттерны, полученные для различных классов повреждений ДНК, сравнивают с паттернами, наблюдаемыми для гибели клеток в зависимости от ЛПЭ частиц, наблюдается удивительно близкое совпадение для сайтов DSB [20], что позволяет предположить, что эта конечная точка является хорошим индикатором результатов воздействия в Условия инактивации репликации клеток.
е. возникающее в результате повреждений ДНК, индуцированных как непосредственно ( посредством прямого энерговыделения ДНК), так и опосредованно (опосредовано свободными радикалами). Мы решили включить в это исследование только избранные классы повреждений ДНК, что обосновано следующим: DSB обычно рассматриваются как ключевые начальные повреждения, связанные с биологическими эффектами ионизирующего излучения. Тем не менее, даже большинство DSB можно отремонтировать. Кластерные повреждения ДНК, в частности кластеры DSB, вероятно, создают серьезные проблемы для системы клеточной репарации и обычно могут приводить к летальным исходам [34]. Когда паттерны, полученные для различных классов повреждений ДНК, сравнивают с паттернами, наблюдаемыми для гибели клеток в зависимости от ЛПЭ частиц, наблюдается удивительно близкое совпадение для сайтов DSB [20], что позволяет предположить, что эта конечная точка является хорошим индикатором результатов воздействия в Условия инактивации репликации клеток.
Основное механистическое допущение, лежащее в основе настоящей стратегии связывания, состоит в том, что анализируемые повреждения ДНК являются аддитивными, т. е. что выходы изучаемых классов повреждений при облучении смешанным полем представляют собой сумму выходов отдельных треков. В связи с локальным характером ДР, их скоплений и мест это предположение выполняется до доз порядка нескольких сотен Гр [16, 35]: вероятность того, что, например, два ДР, индуцированных разными первичными частицами, Кластер DSB незначителен, поскольку два DSB должны были бы происходить в пределах 25 п.н. Тот же аргумент еще более силен для комбинации двух разрывов нити в DSB, которая должна произойти в пределах 10 п.н. Обратите внимание, что отклонения от аддитивности (и линейности) появляются при гораздо меньших дозах для крупномасштабных эффектов, таких как фрагментация по шкале Mbp или хромосомные аберрации, которые обычно происходят на микрометровых расстояниях.
Важно отметить, что установка, использованная при моделировании структуры гусеницы, которая была выполнена для получения результатов, подогнанных в этой работе, не обеспечивает условий электронного равновесия как в продольном, так и в поперечном направлении. Это связано с тем, что ионы исходили из источника, непосредственно примыкающего к ядру клетки и имеющего площадь, равную площади сечения ядра. Эта установка отличается от типичного моделирования с транспортным кодом, где, за исключением начальной области накопления, условия равновесия выполняются во всем интересующем объеме. К счастью, продольная разница не накладывает серьезного ограничения на применимость настоящей стратегии связи, по крайней мере, в схеме, основанной на дозе, как показано экспериментальным моделированием трековой структуры с постепенным увеличением расстояния от источника до ядра [21]: Как осаждаемая доза, так и количество повреждений (в виде абсолютного количества поражений) занижены современным моделированием по сравнению со случаем электронного равновесия, с различиями, которые могут достигать 20% для высокоэнергетических ионов. Однако эти эффекты почти нивелируются выходами классов DSB на единицу дозы, которые различаются между двумя установками всего на несколько процентов.
Это связано с тем, что ионы исходили из источника, непосредственно примыкающего к ядру клетки и имеющего площадь, равную площади сечения ядра. Эта установка отличается от типичного моделирования с транспортным кодом, где, за исключением начальной области накопления, условия равновесия выполняются во всем интересующем объеме. К счастью, продольная разница не накладывает серьезного ограничения на применимость настоящей стратегии связи, по крайней мере, в схеме, основанной на дозе, как показано экспериментальным моделированием трековой структуры с постепенным увеличением расстояния от источника до ядра [21]: Как осаждаемая доза, так и количество повреждений (в виде абсолютного количества поражений) занижены современным моделированием по сравнению со случаем электронного равновесия, с различиями, которые могут достигать 20% для высокоэнергетических ионов. Однако эти эффекты почти нивелируются выходами классов DSB на единицу дозы, которые различаются между двумя установками всего на несколько процентов.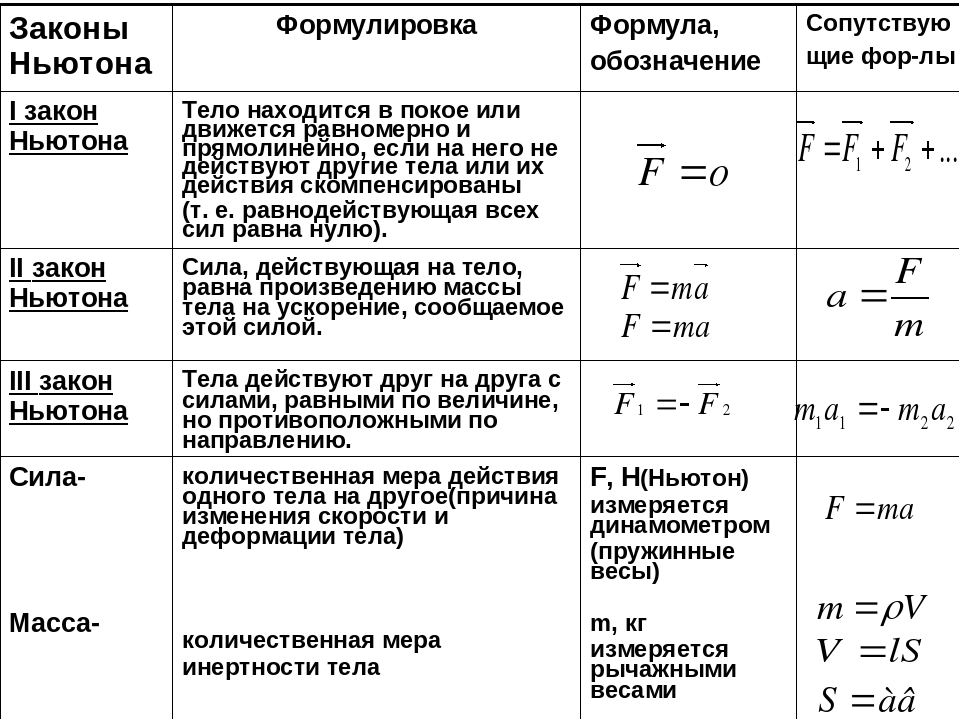 Точно так же латеральная разность также почти не влияет на применимость основанной на дозе схемы, поскольку значительные доли энергии, выделяемой треком, не отражаются настоящей установкой только для высокоэнергетических треков с низкой плотностью. В настоящей установке с ионным источником, не превышающим поперечное сечение ядра клетки, не учитывается энергия, вкладываемая в ядро за счет треков, проходящих не непосредственно через ядро, а только в его окрестности (до нескольких миллиметров при самых высоких энергиях), т.е. треки, перекрывающиеся с ядром только своей полутенью. Когда рассматриваются дозы на трек и выходы классов DSB (схема на основе флюенса), для высокоэнергетических ионов следует добавить вклад электронов, не включенный в результаты, представленные здесь, но присутствующие в равновесных условиях. Как в продольном, так и в поперечном направлении это может соответствовать пространственным масштабам в несколько миллиметров. В поперечном направлении, хотя даже высокоэнергетические следы содержат центральную область с плотностью энерговыделения намного выше, чем в области полутени (где она падает обратно пропорционально квадрату расстояния от оси следа), заметные доли энергии могут выделяться в больших внешних областях.
Точно так же латеральная разность также почти не влияет на применимость основанной на дозе схемы, поскольку значительные доли энергии, выделяемой треком, не отражаются настоящей установкой только для высокоэнергетических треков с низкой плотностью. В настоящей установке с ионным источником, не превышающим поперечное сечение ядра клетки, не учитывается энергия, вкладываемая в ядро за счет треков, проходящих не непосредственно через ядро, а только в его окрестности (до нескольких миллиметров при самых высоких энергиях), т.е. треки, перекрывающиеся с ядром только своей полутенью. Когда рассматриваются дозы на трек и выходы классов DSB (схема на основе флюенса), для высокоэнергетических ионов следует добавить вклад электронов, не включенный в результаты, представленные здесь, но присутствующие в равновесных условиях. Как в продольном, так и в поперечном направлении это может соответствовать пространственным масштабам в несколько миллиметров. В поперечном направлении, хотя даже высокоэнергетические следы содержат центральную область с плотностью энерговыделения намного выше, чем в области полутени (где она падает обратно пропорционально квадрату расстояния от оси следа), заметные доли энергии могут выделяться в больших внешних областях.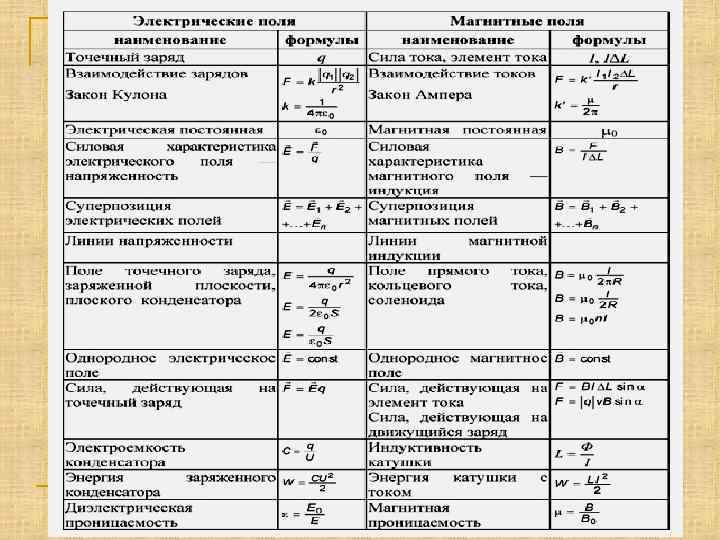 трека. Важно отметить, что энерговыделение во внешней области очень мало, а возникающее в результате повреждение ДНК соответствует нижнему пределу ЛПЭ настоящего подхода, т. е. выходам p 0 = 6,8 DSB, 0,07 кластеров DSB и 6,8 сайтов DSB на Гр на Гбит/с. Тем не менее, дозы и выходы повреждений должны быть добавлены при использовании подхода, основанного на флюенсе, для самых высоких энергий частиц. Уравнение 4, используемое в сочетании с нашими значениями параметров p 0 , обеспечивает первое быстрое средство для этого. Дальнейшие исследования, включая полное моделирование треков с помощью PARTRAC, включение больших расстояний от трека до ядра и получение профилей радиального распределения дозы, дадут возможность проверки достоверности и дальнейшего уточнения этой поправки с использованием того же подхода.
трека. Важно отметить, что энерговыделение во внешней области очень мало, а возникающее в результате повреждение ДНК соответствует нижнему пределу ЛПЭ настоящего подхода, т. е. выходам p 0 = 6,8 DSB, 0,07 кластеров DSB и 6,8 сайтов DSB на Гр на Гбит/с. Тем не менее, дозы и выходы повреждений должны быть добавлены при использовании подхода, основанного на флюенсе, для самых высоких энергий частиц. Уравнение 4, используемое в сочетании с нашими значениями параметров p 0 , обеспечивает первое быстрое средство для этого. Дальнейшие исследования, включая полное моделирование треков с помощью PARTRAC, включение больших расстояний от трека до ядра и получение профилей радиального распределения дозы, дадут возможность проверки достоверности и дальнейшего уточнения этой поправки с использованием того же подхода.
Результаты, представленные в этой работе, заложили основу стратегии объединения переноса излучения и моделирования трековой структуры, как обсуждается ниже.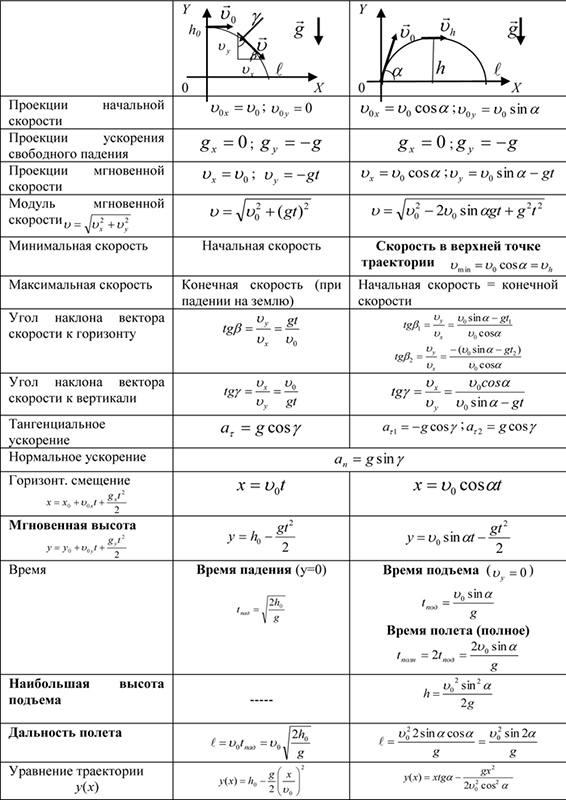 Связывание может быть выполнено по схеме, основанной на дозе или на основе плотности потока, с только что обсужденным ограничением. Основная часть информации, которую необходимо извлечь из кода переноса излучения, — это тип частиц и распределение энергии в интересующем месте. Это означает характеристику типов частиц и их энергий на входной плоскости, касательной к ядру клетки. В большинстве приложений характеристики поля излучения вряд ли будут различаться в нескольких соседних ячейках, поэтому использование вокселя размером ~10 мкм, содержащего только одну ячейку, было бы излишне подробным. Однако типичные размеры вокселя в кодах переноса излучения около 1 мм могут быть слишком крупными. Более тонкая вокселизация может потребоваться в областях с сильно меняющимися в пространстве характеристиками поля, таких как узкие области пика Брэгга в методах активного сканирования в адронной лучевой терапии или при работе с альфа-частицами ближнего действия от внутренних излучателей или терапией с захватом бора.
Связывание может быть выполнено по схеме, основанной на дозе или на основе плотности потока, с только что обсужденным ограничением. Основная часть информации, которую необходимо извлечь из кода переноса излучения, — это тип частиц и распределение энергии в интересующем месте. Это означает характеристику типов частиц и их энергий на входной плоскости, касательной к ядру клетки. В большинстве приложений характеристики поля излучения вряд ли будут различаться в нескольких соседних ячейках, поэтому использование вокселя размером ~10 мкм, содержащего только одну ячейку, было бы излишне подробным. Однако типичные размеры вокселя в кодах переноса излучения около 1 мм могут быть слишком крупными. Более тонкая вокселизация может потребоваться в областях с сильно меняющимися в пространстве характеристиками поля, таких как узкие области пика Брэгга в методах активного сканирования в адронной лучевой терапии или при работе с альфа-частицами ближнего действия от внутренних излучателей или терапией с захватом бора. По сравнению с моделированием только (физического) осаждения дозы, это может потребовать некоторых дополнительных шагов интерполяции (или даже экстраполяции) или процедур усреднения.
По сравнению с моделированием только (физического) осаждения дозы, это может потребовать некоторых дополнительных шагов интерполяции (или даже экстраполяции) или процедур усреднения.
Стратегия объединения кодов переноса с моделированием структуры пути на основе использования формализма, основанного на дозе, потребует явного расчета дозы, доставленной в целевое место для каждого типа частиц, с кодом переноса излучения. В идеале следует затем рассчитать взвешенное по дозе распределение энергий частиц в одном и том же месте и просуммировать все выходы повреждений, соответствующие различным энергетическим интервалам, рассчитанным по аналитической формуле уравнения (1). 2, чтобы, наконец, получить общий урон. Другой возможностью было бы оценить первый момент взвешенного по дозе распределения энергии частиц (в основном, значение энергии, при котором в среднем данный вид частиц доставляет дозу) и применить уравнение 2 к этому единственному значению энергии. Эта аппроксимация концептуально аналогична связыванию, выполненному с применением формул на основе ЛПЭ, использующих ЛПЭ средней дозы в целевом участке в качестве единственного значения ЛПЭ для данного вида, как это было сделано в нашей предыдущей работе [14]. Его достоверность должна быть проверена с помощью специальных симуляций.
Его достоверность должна быть проверена с помощью специальных симуляций.
В рамках подхода, основанного на флюенсе, доступны как доза для ядер-мишеней (уравнение 1), так и повреждение ДНК, вызванное треком частицы (уравнение 1, умноженное на уравнение 2). Стратегия, основанная на использовании такого подхода, потребует расчета флюенса частиц (распределение в энергетических бункерах) для всех видов частиц на входе в целевую площадку. Как обсуждалось выше, полное распределение энергий частиц, возможно, можно было бы заменить одним средним значением, но и в этом случае использование среднего значения, взвешенного по дозе, кажется более подходящим, чем взвешенного по плотности потока энергии. Степень, в которой использование средних значений энергии представляет собой хорошее приближение, следует исследовать в конкретном случае. Вообще говоря, использование справочных таблиц с коэффициентами преобразования плотности энергии в дозу является распространенным решением, предлагаемым, например, в публикациях МКРЗ для приложений радиационной защиты. Предложенный в данной работе подход на основе флюенса с аналитическими функциями представляет собой аналогичное решение. Он дополняет коэффициенты преобразования флюенса в дозу коэффициентами флюенса в повреждение, которые в конечном итоге можно использовать для добавления биологического «веса» к (физической) поглощенной дозе.
Предложенный в данной работе подход на основе флюенса с аналитическими функциями представляет собой аналогичное решение. Он дополняет коэффициенты преобразования флюенса в дозу коэффициентами флюенса в повреждение, которые в конечном итоге можно использовать для добавления биологического «веса» к (физической) поглощенной дозе.
Настоящая работа дополняет анализ нашего предыдущего исследования [16], в котором выходы повреждений ДНК были параметризованы как функция ЛПЭ частиц в ядре клетки. Параметризация повреждения ДНК с точки зрения энергии частиц, а не LET, имеет несколько преимуществ: во-первых, энергию частиц легче получить из транспортных кодов, чем LET в узком смысле, полученном при моделировании трековой структуры PARTRAC, т. е. как энергию, переданную ядру клетки. на единицу длины пути. Эта оценка LET имеет большое сходство с микродозиметрической линейной энергией, но доступность микродозиметрических величин ограничена несколькими транспортными кодами, такими как PHITS. Во-вторых, использование энергии позволяет обойти проблему одинакового значения ЛПЭ, возникающего при двух разных энергиях при замедлении частицы. Таким образом, параметризация на основе энергии позволяет использовать единую математическую функцию для описания эффективности частиц в индукции повреждения ДНК от быстрых до останавливающих частиц. В-третьих, не только самые стабильные изотопы, рассматриваемые в данной работе, но и другие, такие как 2 H, 3 He или 11 C присутствуют в смешанных полях, возникающих при облучении, например, пучком 12 C. Индукция повреждения ДНК различными изотопами одного и того же вида до сих пор явно не рассматривалась моделированием PARTRAC. Однако можно предвидеть, что, возможно, за исключением области пика Брэгга (энергии ниже нескольких МэВ/нуклон), электронные взаимодействия очень похожи для изотопов с одним и тем же атомным номером и зарядом при одной и той же скорости, т. е. при одной и той же энергии на единицу.
Во-вторых, использование энергии позволяет обойти проблему одинакового значения ЛПЭ, возникающего при двух разных энергиях при замедлении частицы. Таким образом, параметризация на основе энергии позволяет использовать единую математическую функцию для описания эффективности частиц в индукции повреждения ДНК от быстрых до останавливающих частиц. В-третьих, не только самые стабильные изотопы, рассматриваемые в данной работе, но и другие, такие как 2 H, 3 He или 11 C присутствуют в смешанных полях, возникающих при облучении, например, пучком 12 C. Индукция повреждения ДНК различными изотопами одного и того же вида до сих пор явно не рассматривалась моделированием PARTRAC. Однако можно предвидеть, что, возможно, за исключением области пика Брэгга (энергии ниже нескольких МэВ/нуклон), электронные взаимодействия очень похожи для изотопов с одним и тем же атомным номером и зарядом при одной и той же скорости, т. е. при одной и той же энергии на единицу. нуклон (удельная энергия). Однако их значения ЛПЭ различаются из-за разной массы. Таким образом, для каждого изотопа необходимо использовать специальную функцию на основе LET, отражающую эффективность индукции повреждения ДНК, энергетическая параметризация, представленная в этой работе, должна быть в значительной степени общеприменимой. Моделирование, направленное на проверку этой гипотезы, должно быть выполнено в будущем.
нуклон (удельная энергия). Однако их значения ЛПЭ различаются из-за разной массы. Таким образом, для каждого изотопа необходимо использовать специальную функцию на основе LET, отражающую эффективность индукции повреждения ДНК, энергетическая параметризация, представленная в этой работе, должна быть в значительной степени общеприменимой. Моделирование, направленное на проверку этой гипотезы, должно быть выполнено в будущем.
В заключение, настоящие результаты обеспечивают основу для связывания кодов переноса излучения с моделированием структуры пути PARTRAC. Такая связь сочетает в себе сильные стороны обоих подходов. Транспортные коды дают возможность работать с макроскопическими масштабами, а моделирование трековой структуры обеспечивает подробное представление лежащих в основе механизмов от выделения энергии излучением до индукции повреждения ДНК. Выбор фактической стратегии соединения через подход, основанный на дозе или флюенсе, и характеристика поля излучения с помощью распределения энергии или ЛПЭ или средневзвешенных значений зависит от конкретного транспортного кода и конкретной изучаемой ситуации. Предоставленные аналитические формулы представляют собой довольно простое решение, открывающее путь ко многим будущим приложениям, включая, помимо прочего, моделирование биологических эффектов ионно-лучевой терапии, бор-захватной терапии и бор-нейтронозахватной терапии.
Предоставленные аналитические формулы представляют собой довольно простое решение, открывающее путь ко многим будущим приложениям, включая, помимо прочего, моделирование биологических эффектов ионно-лучевой терапии, бор-захватной терапии и бор-нейтронозахватной терапии.
Заявление о доступности данных
Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующим авторам.
Вклад авторов
PK, WF, AO и GB разработали исследование. WF, PK и GB выполнили моделирование PARTRAC. П.К. предложил аналитические формулы и выполнил подгонку. PK, WF и GB интерпретировали результаты. PK и GB составили рукопись. Все авторы критически прочитали и рассмотрели рукопись.
Финансирование
Исследование, приведшее к этим результатам, было поддержано институциональным финансированием Института ядерной физики CAS, Helmholtz Zentrum München и Университета Павии, а также частично Чешским научным фондом (номер проекта 21-06451S).
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Примечание издателя
Все претензии, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Ссылки
1. Battistoni G, Bauer J, Boehlen TT, Cerutti F, Chin MPW, Dos Santos Augusto R, et al. Код FLUKA: инструмент точного моделирования для терапии частицами. Фронт Онкол (2016) 6:116. doi:10.3389/fonc.2016.00116
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
2. Эллисон Дж., Амако К., Апостолакис Дж., Арсе П., Асаи М., Асо Т.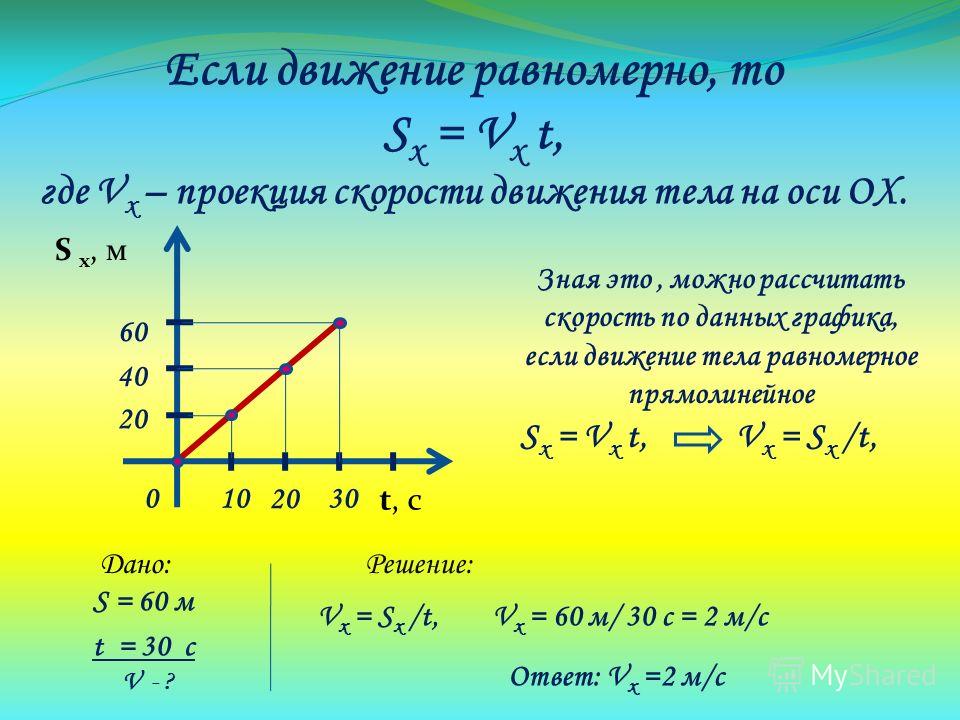 и др. Последние разработки в Geant4. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125
и др. Последние разработки в Geant4. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125
Полный текст CrossRef | Google Scholar
3. Werner CJ, Bull JS, Solomon CJ, Brown FB, McKinney GW, Rising ME и другие. Примечания к выпуску MCNP версии 6.2. В: Примечания к выпуску MCNP6.2 . Лос-Аламос: Лос-Аламосская национальная лаборатория, отчет LA-UR-18-20808 (2018 г.). doi:10.2172/1419730
CrossRef Полный текст | Google Scholar
4. Faddegon B, Ramos-Méndez J, Schuemann J, McNamara A, Shin J, Perl J, et al. Инструмент TOPAS для моделирования частиц, инструмент моделирования Монте-Карло для физики, биологии и клинических исследований. Physica Med (2020) 72:114–21. doi:10.1016/j.ejmp.2020.03.019
Полный текст CrossRef | Академия Google
5. Сато Т., Ивамото Ю., Хашимото С., Огава Т., Фурута Т., Абэ С-и и др. Особенности системы кодов переноса частиц и тяжелых ионов (PHITS) версии 3. 02. J Nucl Sci Technol (2018) 55:684–90. doi:10.1080/00223131.2017.1419890
02. J Nucl Sci Technol (2018) 55:684–90. doi:10.1080/00223131.2017.1419890
CrossRef Full Text | Google Scholar
6. Бруалла Л., Родригес М., Лаллена А.М. Системы Монте-Карло, используемые для планирования лечения и проверки дозы. Strahlenther Onkol (2017) 193:243–59. doi:10.1007/s00066-016-1075-8
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
7. Мураро С., Баттистони Г., Краан А.С. Проблемы моделирования Монте-Карло как клинического и исследовательского инструмента в терапии частицами: обзор. Front Phys (2020) 8:567800. doi:10.3389/fphy.2020.567800
Полный текст CrossRef | Google Scholar
8. Фридланд В., Дингфельдер М., Кундрат П., Джейкоб П. Структуры дорожек, ДНК-мишени и радиационные эффекты в коде биофизического моделирования Монте-Карло PARTRAC. Mutat Research/Fundamental Mol Mech Mutagenesis (2011) 711:28–40. doi:10.1016/j.mrfmmm.2011.01.003
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
9. Nikjoo H, Emfietzoglou D, Liamsuwan T, Taleei R, Liljequist D, Uehara S. Отслеживание радиации, повреждение ДНК и реакция — обзор. Rep Prog Phys (2016) 79:116601. doi:10.1088/0034-4885/79/11/116601
Nikjoo H, Emfietzoglou D, Liamsuwan T, Taleei R, Liljequist D, Uehara S. Отслеживание радиации, повреждение ДНК и реакция — обзор. Rep Prog Phys (2016) 79:116601. doi:10.1088/0034-4885/79/11/116601
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
10. Дингфельдер М. Моделирование трековой структуры заряженных частиц. Health Phys (2012) 103:590–5. doi:10.1097/HP.0b013e3182621292
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
11. Hall EJ, Giaccia AJ. Радиобиология для рентгенолога . 8-е изд. 9781496335418. Филадельфия: Уолтерс Клювер (2019).
12. Фридланд В., Кундрат П. Моделирование радиационных эффектов в клетках и тканях. В: Браме А, редактор. Комплексная биомедицинская физика , Vol. 9. Амстердам: Эльзевир (2014). п. 105–42. дои: 10.1016/b978-0-444-53632-7.00906-0
CrossRef Полный текст | Google Scholar
13.Geant4-ДНК. Geant4-DNA: расширение набора инструментов Geant4 для моделирования методом Монте-Карло для радиобиологии (2021 г. ). Доступно по адресу: http://geant4-dna.org/ (по состоянию на 20 мая 2021 г.).
). Доступно по адресу: http://geant4-dna.org/ (по состоянию на 20 мая 2021 г.).
Google Scholar
14. Baiocco G, Barbieri S, Babini G, Morini J, Alloni D, Friedland W, et al. Происхождение биологической эффективности нейтронов как функции энергии. Научный представитель (2016) 6:34033. дои: 10.1038/srep34033
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
15. Baiocco G, Barbieri S, Babini G, Morini J, Friedland W, Kundrát P, et al. На стыке физики и биологии: нейтронное дело. Радиационная дозиметрия (2018) 180:278–81. doi:10.1093/rpd/ncx222
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
16. Кундрат П., Фридланд В., Беккер Дж., Эйдемюллер М., Оттоленги А., Байокко Г. Аналитические формулы, представляющие моделирование трековой структуры повреждений ДНК, вызванных протонами и легкими ионами при энергиях, соответствующих радиотерапии. Научный представитель (2020) 10:15775. doi:10.1038/s41598-020-72857-z
doi:10.1038/s41598-020-72857-z
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
17. Фридланд В., Джейкоб П., Кундрат П. Стохастическое моделирование восстановления двухцепочечных разрывов ДНК путем негомологичного соединения концов на основе расчетов трековой структуры. Radiat Res (2010) 173:677–88. doi:10.1667/RR1965.1
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
18. Фридланд В., Кундрат П. Моделирование хромосомных аберраций на основе трековой структуры после облучения фотонами и альфа-частицами. Mutat Res (2013) 756:213–23. doi:10.1016/j.mrgentox.2013.06.013
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
19. Шмитт Э., Фридланд В., Кундрат П., Дингфельдер М., Оттоленги А. Масштабирование поперечного сечения для моделирования структуры треков низкоэнергетических ионов в жидкой воде. Радиационная дозиметрия (2015) 166:15–8. doi:10.1093/rpd/ncv302
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
20. Friedland W, Schmitt E, Kundrát P, Dingfelder M, Baiocco G, Barbieri S, et al. Всесторонняя оценка повреждения ДНК легкими ионами на основе трековой структуры от энергий, связанных с радиотерапией, до остановки. Научный представитель (2017) 7:45161. doi:10.1038/srep45161
Friedland W, Schmitt E, Kundrát P, Dingfelder M, Baiocco G, Barbieri S, et al. Всесторонняя оценка повреждения ДНК легкими ионами на основе трековой структуры от энергий, связанных с радиотерапией, до остановки. Научный представитель (2017) 7:45161. doi:10.1038/srep45161
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
21. Фридланд В., Кундрат П., Шмитт Э., Беккер Дж., Ли В. Моделирование повреждения ДНК фотонами и легкими ионами в диапазонах энергий, используемых в медицинских приложениях. Радиационная дозиметрия (2019) 183:84–8. doi:10.1093/rpd/ncy245
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
22. Фридланд В., Кундрат П., Шмитт Э. Моделирование сгустков протонов, сфокусированных до субмикрометровых масштабов: радиационное повреждение с низкой ЛПЭ в пространственной структуре, подобной высокой ЛПЭ. Радиационная дозиметрия (2015) 166:34–7. doi:10.1093/rpd/ncv146
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
23.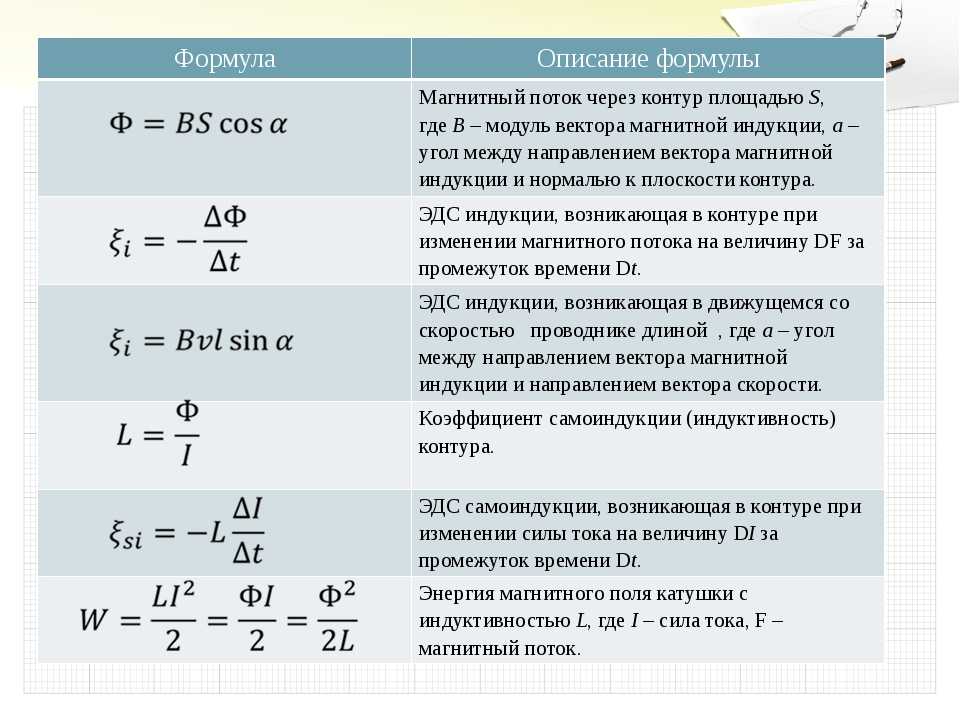 Фридланд В., Кундрат П. Модель хромосомной аберрации, сочетающая следы излучения, структуру хроматина, восстановление DSB и подвижность хроматина. Радиационная дозиметрия (2015) 166:71–4. doi:10.1093/rpd/ncv174
Фридланд В., Кундрат П. Модель хромосомной аберрации, сочетающая следы излучения, структуру хроматина, восстановление DSB и подвижность хроматина. Радиационная дозиметрия (2015) 166:71–4. doi:10.1093/rpd/ncv174
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
24. Schmid TE, Friedland W, Greubel C, Girst S, Reindl J, Siebenwirth C, et al. Субмикронные протоны 20 МэВ или 45 МэВ точечное облучение литием увеличивают выход дицентрических хромосом из-за кластеризации двухцепочечных разрывов ДНК. Mutat Res Genet Toxicol Environ Mutagen (2015) 793:30–40. doi:10.1016/j.mrgentox.2015.07.015
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
25. Friedland W, Kundrát P, Schmitt E, Becker J, Ilicic K, Greubel C, et al. Моделирование исследований индукции дицентриков после облучения сетки субмикронными сфокусированными ионными пучками. Радиационная дозиметрия (2019) 183:40–4. doi:10.1093/rpd/ncy266
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
26.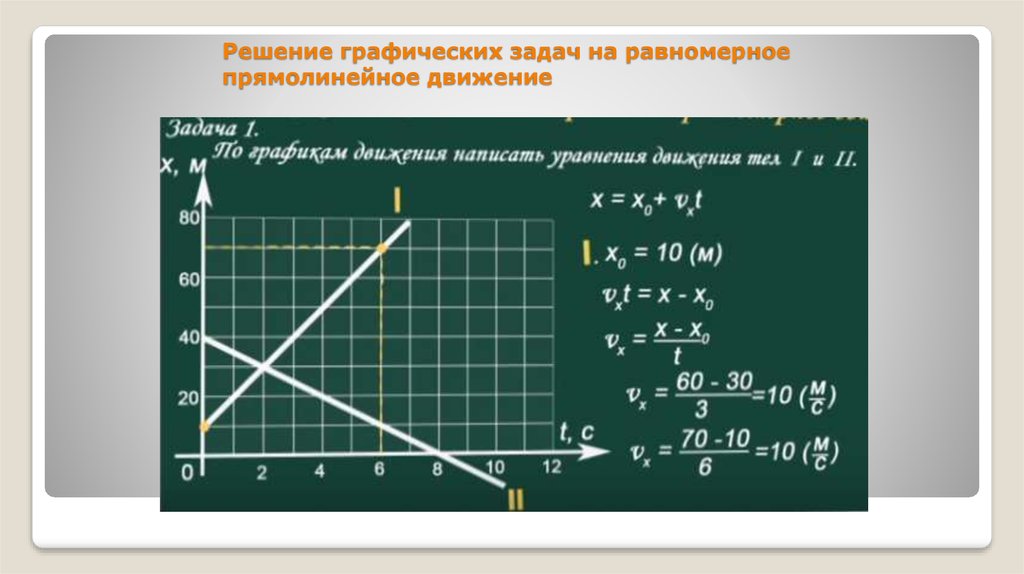 Friedland W, Kundrát P, Jacob P. Расчеты трековой структуры на гипотетических субклеточных мишенях для высвобождения сигналов, убивающих клетки, в экспериментах с наблюдателем с переносом среды. Радиационная дозиметрия (2011) 143:325–9. doi:10.1093/rpd/ncq401
Friedland W, Kundrát P, Jacob P. Расчеты трековой структуры на гипотетических субклеточных мишенях для высвобождения сигналов, убивающих клетки, в экспериментах с наблюдателем с переносом среды. Радиационная дозиметрия (2011) 143:325–9. doi:10.1093/rpd/ncq401
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
27. Kundrát P, Friedland W. Расчеты трековой структуры внутриклеточных мишеней, ответственных за высвобождение сигнала, в экспериментах с наблюдателем с переносом облученной среды, кондиционированной клеткой. Int J Radiat Biol (2012) 88:98–102. doi:10.3109/09553002.2011.595874
CrossRef Full Text | Google Scholar
28. Кундрат П., Фридланд В. Нелинейная реакция клеток на сигналы приводит к пересмотру характеристик эффектов свидетелей, полученных на основе их моделирования. Int J Radiat Biol (2012) 88:743–50. doi:10.3109/09553002.2012.698029
Полный текст CrossRef | Google Scholar
29. Кундрат П., Фридланд В. Механистическое моделирование радиационно-индуцированных эффектов свидетеля. Радиационная дозиметрия (2015) 166:148–51. doi:10.1093/rpd/ncv170
Кундрат П., Фридланд В. Механистическое моделирование радиационно-индуцированных эффектов свидетеля. Радиационная дозиметрия (2015) 166:148–51. doi:10.1093/rpd/ncv170
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
30. Кундрат П., Фридланд В. Усиленное высвобождение первичных сигналов может сделать межклеточную передачу сигналов неэффективной из-за пространственных аспектов. Научный представитель (2016) 6:33214. doi:10.1038/srep33214
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
31. Фридланд В., Шмитт Э., Кундрат П., Байокко Г., Оттоленги А. Моделирование трековой структуры паттернов отложения энергии в митохондриях и повреждения их ДНК. Int J Radiat Biol (2019) 95:3–11. doi:10.1080/09553002.2018.1450532
CrossRef Full Text | Google Scholar
32. Elsässer T, Cunrath R, Krämer M, Scholz M. Влияние расчетов трековой структуры на планирование биологического лечения при ионной лучевой терапии.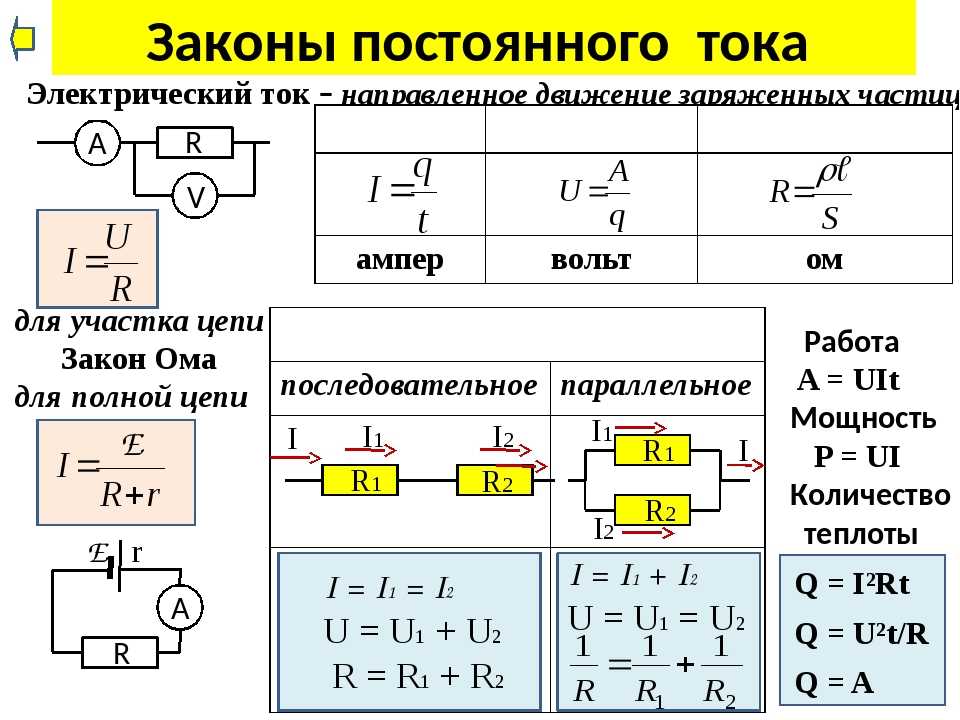 New J Phys (2008) 10:075005. doi:10.1088/1367-2630/10/7/075005
New J Phys (2008) 10:075005. doi:10.1088/1367-2630/10/7/075005
CrossRef Full Text | Google Scholar
33. Кифер Дж., Страатен Х. Модель структуры ионных треков, основанная на классической динамике столкновений (приложение для радиобиологии). Phys Med Biol (1986) 31:1201–9. doi:10.1088/0031-9155/31/11/002
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
34. Николофф Дж. А., Шарма Н., Тейлор Л. Двойные разрывы кластерных ДНК: биологические эффекты и значение для лучевой терапии рака. Гены (2020) 11:99. doi:10.3390/genes11010099
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
35. Крайпл М.С., Фридланд В., Парецке Х.Г. Взаимодействие ионных треков в пространственной и временной близости. Radiat Environ Biophys (2009) 48:349–59. doi:10.1007/s00411-009-0234-z
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Неопределенности прогнозируемых концентраций радионуклидов в наземных пищевых продуктах и пероральных дозах | Дозиметрия радиационной защиты
Фильтр поиска панели навигации Дозиметрия радиационной защитыЭтот выпускЯдерная химия, фотохимия и радиацияКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Дозиметрия радиационной защитыЭтот выпускЯдерная химия, фотохимия и радиацияКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
К.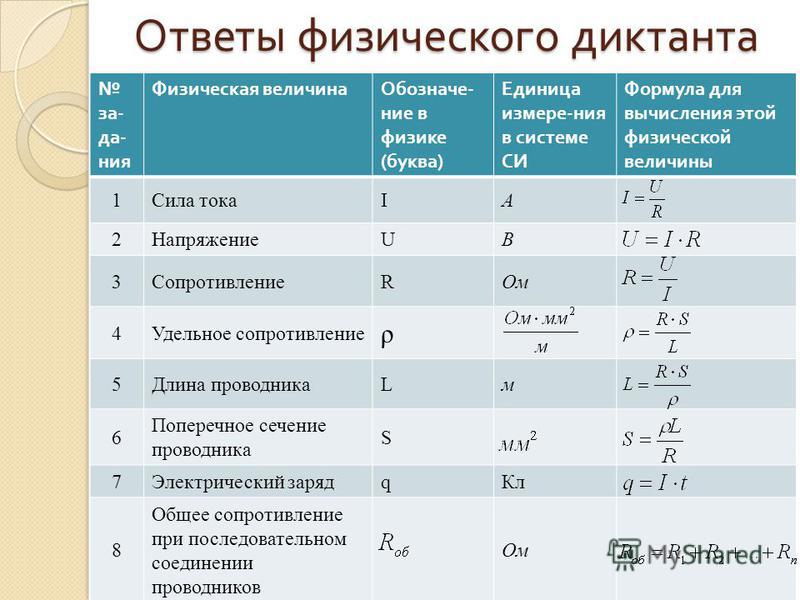 Р. Смит,
Р. Смит,
К. Р. Смит
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Дж. Браун,
Дж. Браун
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Дж. А. Джонс,
Дж. А. Джонс
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
П. Мэнсфилд,
П. Мэнсфилд
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Дж.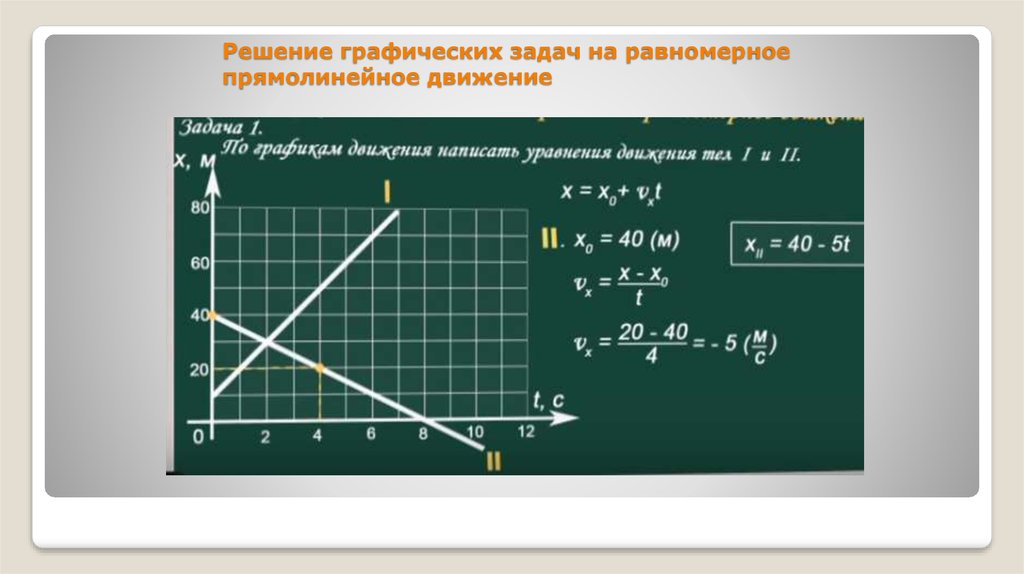 Г. Смит,
Г. Смит,
Дж. Г. Смит
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
С. М. Хейвуд,
С. М. Хейвуд
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
К. Б. Уолтерс
CB Уолтерс
Ищите другие работы этого автора на:
Оксфордский академический
пабмед
Google ученый
Дозиметрия радиационной защиты , том 98, выпуск 3, 1 марта 2002 г., стр.
- Содержание статьи
- Рисунки и таблицы
- видео
- Аудио
- Дополнительные данные
Цитировать
Cite
К. Р. Смит, Дж. Браун, Дж. А. Джонс, П. Мэнсфилд, Дж. Г. Смит, С. М. Хейвуд, К. Б. Уолтерс, Неопределенности прогнозируемых концентраций радионуклидов в наземных пищевых продуктах и дозах при приеме внутрь, Дозиметрия радиационной защиты , том 98, выпуск 3, 1 марта 2002 г., страницы 313–328, https://doi.org/10.1093/oxfordjournals.rpd.a006723
Р. Смит, Дж. Браун, Дж. А. Джонс, П. Мэнсфилд, Дж. Г. Смит, С. М. Хейвуд, К. Б. Уолтерс, Неопределенности прогнозируемых концентраций радионуклидов в наземных пищевых продуктах и дозах при приеме внутрь, Дозиметрия радиационной защиты , том 98, выпуск 3, 1 марта 2002 г., страницы 313–328, https://doi.org/10.1093/oxfordjournals.rpd.a006723
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Разрешения
- Электронная почта
- Твиттер
- Фейсбук
- Подробнее
Фильтр поиска панели навигации Дозиметрия радиационной защитыЭтот выпускЯдерная химия, фотохимия и радиацияКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Дозиметрия радиационной защитыЭтот выпускЯдерная химия, фотохимия и радиацияКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Модели обычно используются для расчета доз после обычных и потенциальных аварийных выбросов радионуклидов. Эти модели содержат ряд параметров. Значения многих из них точно не известны. Основная цель этого исследования заключалась в определении уровня неопределенности прогнозируемых концентраций радионуклидов в пищевых продуктах и доз облучения людей, потребляющих эти продукты, возникающих из-за неопределенностей значений входных параметров модели. Второстепенная цель состояла в том, чтобы определить те входные параметры, неопределенность которых вносит основной вклад в общую неопределенность предсказанных конечных точек. Принятая методология и полученные результаты представлены для следующих радионуклидов: 90 Sr, 131 I, 137 Cs и 239 Pu. Расчетные коэффициенты неопределенности (отношение 95-го процентиля к 5-му) часто очень велики, часто на два-три порядка. Результаты этого исследования могут быть использованы для определения областей, в которых дальнейшие исследования могут улучшить возможности оценки.
Эти модели содержат ряд параметров. Значения многих из них точно не известны. Основная цель этого исследования заключалась в определении уровня неопределенности прогнозируемых концентраций радионуклидов в пищевых продуктах и доз облучения людей, потребляющих эти продукты, возникающих из-за неопределенностей значений входных параметров модели. Второстепенная цель состояла в том, чтобы определить те входные параметры, неопределенность которых вносит основной вклад в общую неопределенность предсказанных конечных точек. Принятая методология и полученные результаты представлены для следующих радионуклидов: 90 Sr, 131 I, 137 Cs и 239 Pu. Расчетные коэффициенты неопределенности (отношение 95-го процентиля к 5-му) часто очень велики, часто на два-три порядка. Результаты этого исследования могут быть использованы для определения областей, в которых дальнейшие исследования могут улучшить возможности оценки.
Этот контент доступен только в формате PDF.
Дозиметрия радиационной защиты
Дозиметрия радиационной защиты
Раздел выдачи:
Артикул
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.
У вас еще нет учетной записи Oxford Academic? регистр
Неопределенности прогнозируемых концентраций радионуклидов в наземных пищевых продуктах и дозах при проглатывании – доступ 24 часа
ЕВРО €30,00
22 фунта стерлингов
39 долларов США.
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Диагностические эталонные уровни рентгенографических и компьютерных исследований в Саудовской Аравии: систематический обзор
Фантомное экспериментальное исследование доз пациентов, полученных с помощью 320-мультидетекторной компьютерной томографии при сканировании перфузии всего мозга
Диагностические референтные уровни для обычных КТ-обследований: результаты обследования доз в масштабе штата
Разработка систем на месте для 13 CO 2 Экспозиция и определение 13 C Чистая скорость ассимиляции с плодотворными побегами и целое дерево и камеру для точности 13 CO 2 Воздействие для молодых.
АДАПТИВНЫЙ ОТВЕТ У МЫШЕЙ, НЕПРЕРЫВНО ОБЛУЧАЕМЫХ ИЗЛУЧЕНИЕМ НИЗКОЙ МОЩНОСТИ
Реклама
Принципы радиобиологической модели клеточно-трековой структуры Каца
. 2015 сен; 166 (1-4): 49-55.
doi: 10.1093/rpd/ncv201. Epub 2015 22 апр.
М. П. Р. Валигурски 1 , Л Гржанка 2 , М Корцил 2
Принадлежности
- 1 Институт ядерной физики Польской академии наук, Радзиковского 152, Краков 31-342, Польша Онкологический центр им. Марии-Склодовской-Кюри, Краковское отделение, Гарнцарска 11, Краков 31-115, Польша z5waligo@cyfronet.
 pl.
pl. - 2 Институт ядерной физики Польской академии наук, Радзиковского 152, Краков 31-342, Польша.
- PMID: 254
- DOI: 10.1093/рпд/нкв201
MPR Waligórski et al. Радиационная дозиметрия. 2015 Сентябрь
. 2015 сен; 166 (1-4): 49-55.
doi: 10.1093/rpd/ncv201. Epub 2015 22 апр.
Авторы
М. П. Р. Валигурски 1 , Л Гржанка 2 , М Корцил 2
Принадлежности
- 1 Институт ядерной физики Польской академии наук, Радзиковского 152, Краков 31-342, Польша Онкологический центр им.
 Марии Склодовской-Кюри, Краковское отделение, Гарнцарска 11, Краков 31-115, Польша z5waligo@cyfronet .пл.
Марии Склодовской-Кюри, Краковское отделение, Гарнцарска 11, Краков 31-115, Польша z5waligo@cyfronet .пл. - 2 Институт ядерной физики Польской академии наук, Радзиковского 152, Краков 31-342, Польша.
- PMID: 254
- DOI: 10.1093/рпд/нкв201
Абстрактный
Теория структуры сотовых дорожек (TST), представленная Кацем в 1968 году, применяет концепцию поперечного сечения действия как вероятность того, что мишени в детекторе излучения будут активированы для выявления наблюдаемой конечной точки (например, гибели клеток). Поле излучения ионного пучка определяется зарядом Z, скоростью β (или энергией), плотностью энергии и линейной передачей энергии (ЛПЭ) иона, а не его общей поглощенной дозой или усредненной по дозе ЛПЭ. Детектор представлен радиочувствительными элементами размером a0 и радиочувствительностью D0, а его гамма-отклик представлен выражениями c-hit или multi-target, а не линейно-квадратичной формулой. Ключом к TST является формула Dδ(r), описывающая радиальное распределение дозы дельта-излучения (RDD) вокруг пути иона. Эта формула, сложенная с дозозависимой характеристикой детектора и проинтегрированная по радиусу, дает значение поперечного сечения действия «точечной цели», σPT. Усредненное значение поперечного сечения σ получается путем радиального интегрирования RDD, усредненного по a0. В режиме «ширины трека», который может иметь место на дистальном конце пути иона, значение σ может значительно превышать его геометрическое значение, [формула: см. текст]. В TST применяется несколько принципов масштабирования, что приводит к его простой аналитической формулировке. Многоцелевые детекторы, такие как клетки, представлены в TST как m, D0, σ0 («значение насыщения» поперечного сечения, которое заменяет a0) и κ («индекс насыщения детектора») в качестве четвертого параметра модели.
Детектор представлен радиочувствительными элементами размером a0 и радиочувствительностью D0, а его гамма-отклик представлен выражениями c-hit или multi-target, а не линейно-квадратичной формулой. Ключом к TST является формула Dδ(r), описывающая радиальное распределение дозы дельта-излучения (RDD) вокруг пути иона. Эта формула, сложенная с дозозависимой характеристикой детектора и проинтегрированная по радиусу, дает значение поперечного сечения действия «точечной цели», σPT. Усредненное значение поперечного сечения σ получается путем радиального интегрирования RDD, усредненного по a0. В режиме «ширины трека», который может иметь место на дистальном конце пути иона, значение σ может значительно превышать его геометрическое значение, [формула: см. текст]. В TST применяется несколько принципов масштабирования, что приводит к его простой аналитической формулировке. Многоцелевые детекторы, такие как клетки, представлены в TST как m, D0, σ0 («значение насыщения» поперечного сечения, которое заменяет a0) и κ («индекс насыщения детектора») в качестве четвертого параметра модели. С увеличением ЛПЭ иона двухкомпонентная формулировка ТКП позволяет осуществлять последовательный переход от плечевых кривых выживания при низких значениях ЛПЭ к экспоненциальным кривым при максимуме радиобиологической эффективности (БРЭ) с последующим «утончением» в конце ионного трека. Для данной клеточной линии, лучше всего подогнав четыре параметра модели (m, D0, σ0 и κ) к доступному набору данных измеренных кривых выживаемости, TST может количественно предсказать выживаемость клеток и ОБЭ для этой клеточной линии после любого другого ионное облучение.
С увеличением ЛПЭ иона двухкомпонентная формулировка ТКП позволяет осуществлять последовательный переход от плечевых кривых выживания при низких значениях ЛПЭ к экспоненциальным кривым при максимуме радиобиологической эффективности (БРЭ) с последующим «утончением» в конце ионного трека. Для данной клеточной линии, лучше всего подогнав четыре параметра модели (m, D0, σ0 и κ) к доступному набору данных измеренных кривых выживаемости, TST может количественно предсказать выживаемость клеток и ОБЭ для этой клеточной линии после любого другого ионное облучение.
© The Author 2015. Опубликовано Oxford University Press. Все права защищены. Чтобы получить разрешения, отправьте электронное письмо по адресу: [email protected].
Похожие статьи
Исследование параметров клеточной радиочувствительности.
Кац Р., Захария Р., Кучинотта Ф.
 А., Чжан С.
Кац Р. и соавт.
Радиационное разрешение 1994 г., декабрь; 140 (3): 356–65.
Радиационное разрешение 1994.
PMID: 7972688
А., Чжан С.
Кац Р. и соавт.
Радиационное разрешение 1994 г., декабрь; 140 (3): 356–65.
Радиационное разрешение 1994.
PMID: 7972688Ядро TPS для расчета выживаемости в зависимости от глубины: распределения в луче углеродной лучевой терапии на основе теории клеточной трековой структуры Каца.
Валигурски М.П., Гржанка Л., Корцил М., Олко П. Валигорски М.П. и др. Радиационная дозиметрия. 2015 сен; 166 (1-4): 347-50. doi: 10.1093/rpd/ncv202. Epub 2015 24 апр. Радиационная дозиметрия. 2015. PMID: 25
3Биологические эффекты тяжелых ионов с позиций теории мишеней.
Кац Р. Кац Р. Adv Space Res. 1986;6(11):191-8. doi: 10.1016/0273-1177(86)
- -9. Adv Space Res. 1986 год. PMID: 11537221
Микродозиметрико-кинетическая теория зависимости ОБЭ гибели клеток от ЛПЭ.

Хокинс РБ. Хокинс РБ. мед. физ. 1998 июля; 25 (7 часть 1): 1157-70. дои: 10.1118/1.598307. мед. физ. 1998. PMID: 9682201 Обзор.
Радиационная физика и радиобиология.
Росси HH. Росси Х.Х. Здоровье физ. 1996 г., июнь; 70 (6): 828-31. doi: 10.1097/00004032-199606000-00007. Здоровье физ. 1996. PMID: 8635907 Обзор.
Посмотреть все похожие статьи
Цитируется
Математическая радиобиологическая модель (MRM) для прогнозирования комплексного повреждения ДНК и выживания клеток при излучении ионизирующих частиц различного качества.
Калоспирос С.А., Никитаки З., Кириаку И., Коккорис М., Эмфиецоглу Д., Георгакилас АГ.
 Калоспирос С.А. и др.
Молекулы. 2021 5 февраля; 26 (4): 840. doi: 10.3390/молекулы26040840.
Молекулы. 2021.
PMID: 33562730
Бесплатная статья ЧВК.
Калоспирос С.А. и др.
Молекулы. 2021 5 февраля; 26 (4): 840. doi: 10.3390/молекулы26040840.
Молекулы. 2021.
PMID: 33562730
Бесплатная статья ЧВК.Прямое измерение трехмерного распределения повреждений ДНК, вызванных энергичными заряженными частицами, в модельной ткани мыши.
Мирш Дж., Томмазино Ф., Фронс А., Конрад С., Дуранте М., Шольц М., Фридрих Т., Лебрих М. Мирш Дж. и соавт. Proc Natl Acad Sci U S A. 6 октября 2015 г .; 112 (40): 12396-401. doi: 10.1073/pnas.1508702112. Epub 2015 21 сентября. Proc Natl Acad Sci U S A. 2015. PMID: 26392532 Бесплатная статья ЧВК.
термины MeSH
вещества
Монте-Карло Расчет линейных коэффициентов затухания и свойств рассеяния фотонов новых бетонов с наночастицами осмия, иридия и барита
Польский журнал медицинской физики и техники
- Подробности журнала
- Format
- Magazine
- eISSN
- 1898-0309
- Première parution
- 30 Dec 2008
- Périodicité
- 4 fois par an
- Langues
- Anglais
1. Tekin Х, Сайед М, Исса С.А. Гамма-защитные свойства гематит-серпентинового бетона, смешанного с микро- и наночастицами WO 3 и Bi 2 O 3 , с использованием кода MCNPX. Радиационная физика и химия. 2018;150:95-100. https://doi.org/10.1016/j.radphyschem.2018.05.00210.1016/j.radphyschem.2018.05.002Search in Google Scholar
Tekin Х, Сайед М, Исса С.А. Гамма-защитные свойства гематит-серпентинового бетона, смешанного с микро- и наночастицами WO 3 и Bi 2 O 3 , с использованием кода MCNPX. Радиационная физика и химия. 2018;150:95-100. https://doi.org/10.1016/j.radphyschem.2018.05.00210.1016/j.radphyschem.2018.05.002Search in Google Scholar
2. Янкович К., Станкович С., Бойович Д., Стоянович М., Антич Л. Влияние нанокремнезема и баритового заполнителя на свойства бетона со сверхвысокими характеристиками. Строительство и строительные материалы. 2016;126:147-156. https://doi.org/10.1016/j.conbuildmat.2016.09.02610.1016/j.conbuildmat.2016.09.026Поиск в Google Scholar
3. Месбахи А., Мансури Э., Чанджу А.Г., Текин Х.О. Характеристики радиационной защиты нанобетонов от фотонных и нейтронных лучей. Умные нанобетоны и материалы на основе цемента: Elsevier; 2020: 447-460. https://doi.org/10.1016/B978-0-12-817854-6.00019-210.1016/B978-0-12-817854-6.00019-2Поиск в Google Scholar
4. Malekzadeh R, Mehnati P, Sooteh MY, Mesbahi A. Влияние размера нано- и влияние микрочастиц и энергии фотонов на массовые коэффициенты ослабления висмут-кремниевых экранов в диагностической радиологии. Радиологическая физика и техника. 2019;12(3):325-334. https://doi.org/10.1007/s12194-019-00529-310.1007/s12194-019-00529-331385155Поиск в Google Scholar
Malekzadeh R, Mehnati P, Sooteh MY, Mesbahi A. Влияние размера нано- и влияние микрочастиц и энергии фотонов на массовые коэффициенты ослабления висмут-кремниевых экранов в диагностической радиологии. Радиологическая физика и техника. 2019;12(3):325-334. https://doi.org/10.1007/s12194-019-00529-310.1007/s12194-019-00529-331385155Поиск в Google Scholar
5. Забихзаде М., Ай М.Р., Аллахверди М., Месбахи А., Махдави С.Р., Шахриари М. Оценка Монте-Карло загрязнения фотонейтронами от высокоэнергетических рентгеновских медицинских ускорителей в процедурном кабинете и лабиринте: упрощенная модель. Дозиметрия радиационной защиты. 2009 г.;135(1):21-32. https://doi.org/10.1093/rpd/ncp09710.1093/rpd/ncp09719483207Search in Google Scholar
6. Juste B, Morató S, García C, Miró R, Verdú G. Применение кода Монте-Карло для изучения 3D распределение нейтронов в бункере лучевой терапии и подтверждение экспериментальными измерениями. Ядерные приборы и методы в физических исследованиях Раздел A: Ускорители, спектрометры, детекторы и сопутствующее оборудование. 2020;954:161248. https://doi.org/10.1016/j.nima.2018.09.08310.1016/j.nima.2018.09.083Search in Google Scholar
2020;954:161248. https://doi.org/10.1016/j.nima.2018.09.08310.1016/j.nima.2018.09.083Search in Google Scholar
7. Халдари Р., Месбахи А., Кара У. Расчет методом Монте-Карло экранирующих свойств недавно разработанных тяжелых бетонов для мегавольтных спектров фотонных пучков, используемых в лучевой терапии. Иранский журнал медицинской физики. 2016;13(4):250-260. https://dx.doi.org/10.22038/ijmp.2017.19206.1175Поиск в Google Scholar
8. Ахмад И., Шахзада К., Ахмад М.И. и др. Уплотнение бетона с использованием барита в качестве мелкого заполнителя и его влияние на механические и радиационные свойства бетона. Журнал инженерных исследований. 2019;7(4):81-95.Поиск в Google Scholar
9. Мортазави С., Мослех-Ширази М., Рошан-Шомал П., Раадпей Н., Барадаран-Гахфарохи М. Высокоэффективный тяжелый бетон как многоцелевой щит . Дозиметрия радиационной защиты. 2010;142(2-4):120-124. https://doi.org/10.1093/rpd/ncq26510.1093/rpd/ncq26521036811Search in Google Scholar
10. Tekin H, Sayyed M, Altunsoy E, Manici T. Экранирующие свойства и эффекты WO 3 и PbO на массовые коэффициенты затухания с использованием кода MCNPX. Копать землю. Дж. Наноматер. Биоструктур. 2017;12(3):861-867.Поиск в Google Scholar
Tekin H, Sayyed M, Altunsoy E, Manici T. Экранирующие свойства и эффекты WO 3 и PbO на массовые коэффициенты затухания с использованием кода MCNPX. Копать землю. Дж. Наноматер. Биоструктур. 2017;12(3):861-867.Поиск в Google Scholar
11. Агар О., Текин Х.О., Сайед М., Коркмаз М.Е., Кульфа О., Эртугай С. Экспериментальное исследование поведения затухания фотонов для бетонов, содержащих природный минерал перлит. Результаты по физике. 2019;12:237-243. https://doi.org/10.1016/j.rinp.2018.11.05310.1016/j.rinp.2018.11.053Search in Google Scholar
12. Rajavikraman R. Новый метод радиационной защиты с использованием нанобетонных композитов. Int J Mater Sci Eng. 2013;1:20-23. https://doi.org/10.12720/ijmse.1.1.20-2310.12720/ijmse.1.1.20-23Поиск в Google Scholar
13. Кришна Б.Г., Прасад П., Саху В., Саху Дж.П., Агарвал А. Характеристики обратного рассеяния бета-излучения и поглощения гамма-излучения углеродными наночастицами, содержащимися в бетонном композите. Документ представлен на: Nano Hybrids and Composites 2017. https://doi.org/10.4028/www.scientific.net/NHC.17.3110.4028/www.scientific.net/NHC.17.31Search in Google Scholar
Документ представлен на: Nano Hybrids and Composites 2017. https://doi.org/10.4028/www.scientific.net/NHC.17.3110.4028/www.scientific.net/NHC.17.31Search in Google Scholar
14. Tekin HO, Singh VP, Manici T. Влияние микро- и наноразмеров WO 3 на массовые коэффициенты затухания бетона с использованием кода MCNPX. Прикладное излучение и изотопы. 2017;121:122-125. https://doi.org/10.1016/j.apradiso.2016.12.04010.1016/j.apradiso.2016.12.040Поиск в Google Scholar
15. Verdipoor K, Alemi A, Mesbahi A. Массовые коэффициенты ослабления фотонов кремниевой смолы, наполненной WO 3 , PbO и Bi 2 O 3 Микро- и наночастицы для радиационной защиты. Радиационная физика и химия. 2018;147:85-90. 16. Facure A, Silva A, Rivera J, Falcao R. Рассеяние нейтронов в бетоне и дереве. : Часть II-косое падение. Дозиметрия радиационной защиты. 2008;128(3):367-374. https://doi.org/10.1093/rpd/ncm37810.1093/rpd/ncm378Поиск в Google Scholar
17. Абдо А.Е.-С. Расчет сечений для быстрых нейтронов и гамма-квантов в бетонных экранах. Анналы ядерной энергетики. 2002;29(16):1977-1988. https://doi.org/10.1016/S0306-4549(02)00019-110.1016/S0306-4549(02)00019-1Search in Google Scholar
Абдо А.Е.-С. Расчет сечений для быстрых нейтронов и гамма-квантов в бетонных экранах. Анналы ядерной энергетики. 2002;29(16):1977-1988. https://doi.org/10.1016/S0306-4549(02)00019-110.1016/S0306-4549(02)00019-1Search in Google Scholar
бетоны высокой плотности, используемые для защиты от лучевой терапии. Анналы ядерной энергетики. 2011;38(12):2752-2756. https://doi.org/10.1016/j.anucene.2011.08.02310.1016/j.anucene.2011.08.023Поиск в Google Scholar
19. Месбахи А., Азарпейванд А.-А., Хосрави Х.Р. Влияет ли состав бетона на выработку фотонейтронов внутри бункеров для лучевой терапии? Японский журнал радиологии. 2012;30(2):162-166. https://doi.org/10.1007/s11604-011-0030-y10.1007/s11604-011-0030-y22180187Поиск в Google Scholar
20. Choi CH, Park S-Y, Park JM, Chun M, Kim J-i. Моделирование методом Монте-Карло эквивалента дозы нейтронов за счет образования фотонейтронов внутри первичных барьеров хранилища для лучевой терапии. Физика Медика. 2018;48:1-5. https://doi. org/10.1016/j.ejmp.2018.03.00910.1016/j.ejmp.2018.03.00929728220Поиск в Google Scholar
org/10.1016/j.ejmp.2018.03.00910.1016/j.ejmp.2018.03.00929728220Поиск в Google Scholar
21. Месбахи А., Ализаде Г., Сейед-Оское Г., Азарпейванд А-А. Новый барит-колеманитовый бетон с пониженным образованием нейтронов в бункерах лучевой терапии. Анналы ядерной энергетики. 2013;51:107-111. https://doi.org/10.1016/j.anucene.2012.07.03910.1016/j.anucene.2012.07.039Search in Google Scholar
22. Месбахи А., Халдари Р. Свойства рассеяния нейтронов и фотонов бетонами высокой плотности, используемыми в радиационных условиях. терапевтические учреждения: исследование Монте-Карло. Польский журнал медицинской физики и техники. 2017;23(3):61. https://doi.org/10.1515/pjmpe-2017-001110.1515/pjmpe-2017-0011Поиск в Google Scholar
23. Пеловиц Д.Б. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ MCNPX Версия 2.7. 0-LA-CP-11-00438. Лос-Аламосская национальная лаборатория. 2011. Поиск в Google Scholar
24. Шейх-Багери Д., Роджерс Д. Расчет методом Монте-Карло девяти мегавольтных фотонных пучков с использованием кода BEAM. Медицинская физика. 2002;29(3):391-402. https://doi.org/10.1118/1.144541310.1118/1.144541311930914Search in Google Scholar
Медицинская физика. 2002;29(3):391-402. https://doi.org/10.1118/1.144541310.1118/1.144541311930914Search in Google Scholar
25. Mansouri E, Mesbahi A, Malekzadeh R, Mansouri A. Экранирующие характеристики нанокомпозитов для защиты от рентгеновского и гамма-излучения в медицинских целях : влияние размера частиц, энергии фотонов и концентрации наночастиц. Радиационная и экологическая биофизика. 2020:1-18. https://doi.org/10.1007/s00411-020-00865-810.1007/s00411-020-00865-832780196Поиск в Google Scholar
26. Waly E-SA, Bourham MA. Сравнительное исследование бетонов разного состава в качестве материалов для защиты от гамма-излучения. Анналы ядерной энергетики. 2015;85:306-310. https://doi.org/10.1016/j.anucene.2015.05.01110.1016/j.anucene.2015.05.011Search in Google Scholar
наночастицы включали первичные барьеры и влияние наночастиц на аспекты экранирования. Отчеты практической онкологии и лучевой терапии. 2019;24(4):363-368. https://doi.org/10.1016/j.rpor.2019.05. 00910.1016/j.rpor.2019.05.009655448731194189Search in Google Scholar
00910.1016/j.rpor.2019.05.009655448731194189Search in Google Scholar
28. Un A, Demir F. Определение массовых коэффициентов ослабления, эффективных атомных номеров и эффективного электрона номера для тяжелых и нормальных бетонов. Прикладное излучение и изотопы. 2013;80:73-77. https://doi.org/10.1016/j.apradiso.2013.06.01510.1016/j.apradiso.2013.06.01523838359Поиск в Google Scholar
29. Норхасри М.М., Хамида М., Фадзил А.М. Применение наноматериалов в бетоне: обзор. Строительство и строительные материалы. 2017;133:91-97. https://doi.org/10.1016/j.conbuildmat.2016.12.00510.1016/j.conbuildmat.2016.12.005Поиск в Google Scholar
30. Swanson WP. Аспекты радиационной безопасности при эксплуатации линейных ускорителей электронов. 1979.Поиск в Google Scholar
31. Raso DJ. Расчеты методом Монте-Карло отражения и пропускания рассеянных гамма-лучей. Ядерная наука и техника. 1963;17(3):411-418. https://doi.org/10.13182/NSE63-A1739010.13182/NSE63-A17390Поиск в Google Scholar
Prekopa webpage
Андрс Пркопа опубликовал свою первую статью, когда он был студентом бакалавриата Дебреценского университета, Венгрия. В статье решалась вероятностная задача, являющаяся обобщением задачи Банаха о спичечном коробке, когда случайные количества из случайно выбранных контейнеров конечной емкости последовательно берутся для удовлетворения требований до тех пор, пока не произойдет первое исчерпание. Вопрос в том, каковы ожидаемые, еще доступные количества в оставшихся контейнерах? Проблема Банаха — это частный случай, когда есть два контейнера, и каждый раз из случайно выбранного контейнера берется единица.
В статье решалась вероятностная задача, являющаяся обобщением задачи Банаха о спичечном коробке, когда случайные количества из случайно выбранных контейнеров конечной емкости последовательно берутся для удовлетворения требований до тех пор, пока не произойдет первое исчерпание. Вопрос в том, каковы ожидаемые, еще доступные количества в оставшихся контейнерах? Проблема Банаха — это частный случай, когда есть два контейнера, и каждый раз из случайно выбранного контейнера берется единица.
Стохастические функции множества и смежные темы
В те годы, когда он работал над докторской диссертацией, он работал над процессами Пуассона, их обобщениями, случайными функциями множества и стохастическими интегралами. Он принадлежит к тем, кто впервые разработал теорию случайных мер и случайных функций множеств в 50-х годах: шведский математик Х. Крамр, польские математики Э. Марчевский, К. Рылль-Нардзевский и венгерский математик А. Пркопа. Результаты Пкопы идут дальше всех. Он определил понятие случайной (стохастической) функции множества независимых приращений в общем абстрактном пространстве. Одним из основных результатов было расширение полностью аддитивной функции случайного множества, определенной на кольце или алгебре, до σ -кольцо или -алгебра. Полученные теоремы о расширении являются стохастическими аналогами теорем Каратодори о расширении меры. Кроме того, он ввел понятие характеристического функционала, доказал теоремы типа Радона-Никодима, определил стохастические интегралы Лебега со случайными мерами и детерминированными измеримыми подынтегральными выражениями. Одним из основных моментов его теории является доказательство теоремы о пространстве произведений, в которой он доказал, что для заданного основного распределения случайных точек (р.п.д.) типа Пуассона в абстрактном пространстве X , с неатомарной мерой параметра, где случайные точки независимо порождают дополнительные случайные величины со значениями из другого абстрактного пространства Y , тогда r.
Он определил понятие случайной (стохастической) функции множества независимых приращений в общем абстрактном пространстве. Одним из основных результатов было расширение полностью аддитивной функции случайного множества, определенной на кольце или алгебре, до σ -кольцо или -алгебра. Полученные теоремы о расширении являются стохастическими аналогами теорем Каратодори о расширении меры. Кроме того, он ввел понятие характеристического функционала, доказал теоремы типа Радона-Никодима, определил стохастические интегралы Лебега со случайными мерами и детерминированными измеримыми подынтегральными выражениями. Одним из основных моментов его теории является доказательство теоремы о пространстве произведений, в которой он доказал, что для заданного основного распределения случайных точек (р.п.д.) типа Пуассона в абстрактном пространстве X , с неатомарной мерой параметра, где случайные точки независимо порождают дополнительные случайные величины со значениями из другого абстрактного пространства Y , тогда r. p.d. в пространстве произведения X × Y также является пуассоновским. Параметр-мера результирующего r.p.d. задается интегральной формулой. В статье, в которой опубликован указанный выше результат, содержится еще одна заслуживающая внимания теорема: если параметрическая мера н.п.п. с независимыми приращениями неатомарна, то она пуассоновского типа. В то же время статья положила начало теории отмеченных пуассоновских процессов. Когда Прокопа получил вышеупомянутые результаты, венгерским ученым не разрешили публиковаться за границей. Так, его статьи появились в местных журналах, но были написаны на английском языке, поэтому они доступны для международной читательской аудитории.
p.d. в пространстве произведения X × Y также является пуассоновским. Параметр-мера результирующего r.p.d. задается интегральной формулой. В статье, в которой опубликован указанный выше результат, содержится еще одна заслуживающая внимания теорема: если параметрическая мера н.п.п. с независимыми приращениями неатомарна, то она пуассоновского типа. В то же время статья положила начало теории отмеченных пуассоновских процессов. Когда Прокопа получил вышеупомянутые результаты, венгерским ученым не разрешили публиковаться за границей. Так, его статьи появились в местных журналах, но были написаны на английском языке, поэтому они доступны для международной читательской аудитории.
Копии этих старых документов, а также некоторые из новых можно найти на его домашней странице: rutcor.rutgers.edu/~prekopa/.
Управление запасами
В начале 1960-х годов он разработал новую модель управления запасами, которая стала широко использоваться в Венгрии и других странах. В Венгрии это привело к экономии миллиардов (в долларовом выражении). Задача состояла в том, чтобы определить начальные уровни страховых запасов основных материалов и полуфабрикатов на промышленных предприятиях, чтобы обеспечить непрерывное производство на заданном уровне безопасности. Модель была сформулирована совместно с его бывшим коллегой М. Цирманном. Они определили статистику заказов как методологию решения проблем. Прокопа пошел дальше. Он обобщил теоремы Смирнова, используя глубокий математический аппарат теории мер в функциональных пространствах, что позволило ему вывести довольно общие и практически полезные формулы для определения уровней страхового запаса. Приведенные выше результаты являются прекрасными примерами решения задач, в которых сочетаются глубокая математика и важные практические приложения. В следующей работе с П. Келле он сформулировал и решил варианты оптимизационного типа задач страхового запаса, где решения больше не даются алгоритмами, а формулами. Недавно он опубликовал еще более общие решения проблем, которые появились в EJOR, и написал еще одну статью с Н.
В Венгрии это привело к экономии миллиардов (в долларовом выражении). Задача состояла в том, чтобы определить начальные уровни страховых запасов основных материалов и полуфабрикатов на промышленных предприятиях, чтобы обеспечить непрерывное производство на заданном уровне безопасности. Модель была сформулирована совместно с его бывшим коллегой М. Цирманном. Они определили статистику заказов как методологию решения проблем. Прокопа пошел дальше. Он обобщил теоремы Смирнова, используя глубокий математический аппарат теории мер в функциональных пространствах, что позволило ему вывести довольно общие и практически полезные формулы для определения уровней страхового запаса. Приведенные выше результаты являются прекрасными примерами решения задач, в которых сочетаются глубокая математика и важные практические приложения. В следующей работе с П. Келле он сформулировал и решил варианты оптимизационного типа задач страхового запаса, где решения больше не даются алгоритмами, а формулами. Недавно он опубликовал еще более общие решения проблем, которые появились в EJOR, и написал еще одну статью с Н. Нояном в Journal of Production Economics. Последние две работы в значительной степени основаны на классических результатах Колмогорова, Дуба и Донскера о распределении функционалов, определенных на траекториях гауссовских случайных процессов.
Нояном в Journal of Production Economics. Последние две работы в значительной степени основаны на классических результатах Колмогорова, Дуба и Донскера о распределении функционалов, определенных на траекториях гауссовских случайных процессов.
Стохастическое программирование и логарифмическая вогнутость
В 1960-х годах интерес Пркопы обратился к стохастическому программированию. В своей первой статье на эту тему он доказал при некоторых условиях, что распределение вероятностей оптимального значения случайной задачи линейного программирования является нормальным. Результат позволяет построить доверительный интервал для оптимального значения в этих LP. В другой работе он доказал, что если случайность заложена в технологической матрице, размеры которой неограниченно растут, то при некоторых мягких условиях разница между случайным оптимальным значением и детерминированным оптимальным значением ЛП, записанной с ожиданиями , стремится к нулю с вероятностью один или с вероятностью, в зависимости от предположений. Результаты получили приложения также в теории игр и динамике населения.
Результаты получили приложения также в теории игр и динамике населения.
Что касается моделей принятия решений стохастического программирования, Чарнс и Купер были первыми, кто сформулировал один из трех основных типов моделей и назвал его программированием с ограничениями случайности. Однако они наложили вероятностное ограничение индивидуально на каждое стохастическое ограничение, пренебрегая стохастической зависимостью между задействованными случайными величинами, поэтому их формулировка была неполной. Общая формулировка, учитывающая стохастическую зависимость, была дана Пркопой и тем самым заслужила себе место как одного из инициаторов стохастического программирования. Один из его основных результатов в этой области касается теории выпуклости вероятностных задач стохастического программирования с ограничениями. Однако его результаты имеют более общее значение. Он ввел понятие логарифмических вогнутых мер и доказал основные теоремы. В одном из них говорится, что если мера вероятности генерируется логарифмически вогнутой функцией плотности вероятности (точечной), то мера является логарифмически вогнутой. Другой утверждает, что если мы проинтегрируем многомерную логарифмически вогнутую функцию по некоторым переменным во всем их пространстве, то результирующая функция других переменных будет логарифмически вогнутой. В то время как логарифмическая выпуклость является относительно простой математической теорией, логарифмическая вогнутость глубока и широко применима. Эти прорывные результаты предоставили доказательство выпуклости широкого класса вероятностных задач стохастического программирования с ограничениями. Они также стали известными и широко применяемыми результатами в физике, статистике, экономике, выпуклой геометрии, математическом анализе и ряде других областей. Неравенство, выражающее результат первой теоремы, иногда неправильно цитируется как неравенство Пркопа-Лейндлера. После того, как Прокопа опубликовал свою теорему, Лейндлер заинтересовался одной из своих вспомогательных теорем и дал ей различные обобщения, но не самой теореме. Теория логарифмической вогнутости во многом помогла теории выпуклости стохастического программирования.
Другой утверждает, что если мы проинтегрируем многомерную логарифмически вогнутую функцию по некоторым переменным во всем их пространстве, то результирующая функция других переменных будет логарифмически вогнутой. В то время как логарифмическая выпуклость является относительно простой математической теорией, логарифмическая вогнутость глубока и широко применима. Эти прорывные результаты предоставили доказательство выпуклости широкого класса вероятностных задач стохастического программирования с ограничениями. Они также стали известными и широко применяемыми результатами в физике, статистике, экономике, выпуклой геометрии, математическом анализе и ряде других областей. Неравенство, выражающее результат первой теоремы, иногда неправильно цитируется как неравенство Пркопа-Лейндлера. После того, как Прокопа опубликовал свою теорему, Лейндлер заинтересовался одной из своих вспомогательных теорем и дал ей различные обобщения, но не самой теореме. Теория логарифмической вогнутости во многом помогла теории выпуклости стохастического программирования. Он же положил начало формулировке понятия и развитию теории r-вогнутых вероятностных мер. Несмотря на то, что это хорошие математические построения, большинство известных и практически важных распределений вероятностей являются логарифмически вогнутыми, и очень немногие известные распределения вероятностей являются r – вогнутый для некоторых r , но не вогнутый.
Он же положил начало формулировке понятия и развитию теории r-вогнутых вероятностных мер. Несмотря на то, что это хорошие математические построения, большинство известных и практически важных распределений вероятностей являются логарифмически вогнутыми, и очень немногие известные распределения вероятностей являются r – вогнутый для некоторых r , но не вогнутый.
Результаты Пркопы очень впечатлили Авраама Чарнса. В 1970-х годах Чарнс был секретарем по иностранным делам Национальной инженерной академии Мексики, а в 1977 году он предложил Пркопе иностранного члена-корреспондента этой академии. В своем письме к Пркопе от 23 февраля 1977 г. он писал: «Для того, чтобы представить эту честь в перспективе, я также назначаю профессора Л. Канторовича, российского лауреата Нобелевской премии, в члены».
Пркопа дал первый алгоритм и множество других для решения вероятностной задачи стохастического программирования с ограничениями. Он также сформулировал и решил много практических задач такого типа для водных ресурсов, энергетических систем, экономики, проблем надежности сетей и т.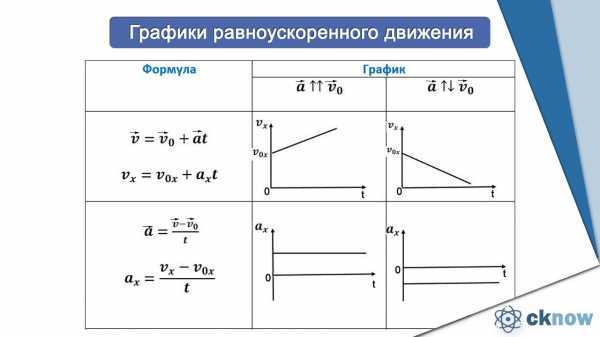 д. Заслуживает внимания его модель, которую он сформулировал для пятилетнего плана электроэнергетического сектора венгерской экономики вместе с Дек, Ганцер и Пати. При работе с ожиданиями случайных величин, появившихся в модели, результирующая ЛП давала оптимальное значение, которое не было значительно меньше (функция стоимости должна была быть минимизирована), чем оптимальное значение вероятностной задачи с ограничениями, используя 95% уровень надежности. Однако детерминистическое оптимальное решение обеспечивает только 10-процентную надежность при включении в ограничивающую функцию в вероятностном ограничении. Таким образом, без существенного удорожания было получено высоконадежное решение вместо ненадежного. Однако оптимальное решение было существенно другим. Приведенный выше пример показывает силу стохастического программирования в решении важных задач реальной жизни.
д. Заслуживает внимания его модель, которую он сформулировал для пятилетнего плана электроэнергетического сектора венгерской экономики вместе с Дек, Ганцер и Пати. При работе с ожиданиями случайных величин, появившихся в модели, результирующая ЛП давала оптимальное значение, которое не было значительно меньше (функция стоимости должна была быть минимизирована), чем оптимальное значение вероятностной задачи с ограничениями, используя 95% уровень надежности. Однако детерминистическое оптимальное решение обеспечивает только 10-процентную надежность при включении в ограничивающую функцию в вероятностном ограничении. Таким образом, без существенного удорожания было получено высоконадежное решение вместо ненадежного. Однако оптимальное решение было существенно другим. Приведенный выше пример показывает силу стохастического программирования в решении важных задач реальной жизни.
Решения вероятностных задач стохастического программирования с ограничениями с непрерывными распределениями вероятностей требуют больших вычислительных ресурсов и требуют многомерного численного интегрирования при вычислении значений функции и градиента вероятности в вероятностном ограничении. Несколько проще решение, если случайные величины в задаче дискретны, что часто встречается на практике. Чтобы эффективно решать такие проблемы, Пркопа ввел концепцию p – уровень действующий, или кратко p – действующий пункт. Он дал три алгоритмических решения этой проблемы: одно сам, одно с Визври и Бадичем и одно с Денчевой и Рущиски. Использование p-эффективных точек получило широкое распространение в литературе с момента их введения в 1990 году и породило множество статей в этой области. В одной из недавних работ Пркопы, где обсуждаются как дискретная, так и непрерывная модели, представлена взаимосвязь между вероятностным стохастическим программированием с ограничениями, дизъюнктивным и многокритериальным программированием, а также новые теоремы двойственности и новый способ решения представленных проблем, где в любой момент итерации мы получаем нижнюю и верхнюю границы оптимального значения такие, что их разности монотонно стремятся к нулю.
Несколько проще решение, если случайные величины в задаче дискретны, что часто встречается на практике. Чтобы эффективно решать такие проблемы, Пркопа ввел концепцию p – уровень действующий, или кратко p – действующий пункт. Он дал три алгоритмических решения этой проблемы: одно сам, одно с Визври и Бадичем и одно с Денчевой и Рущиски. Использование p-эффективных точек получило широкое распространение в литературе с момента их введения в 1990 году и породило множество статей в этой области. В одной из недавних работ Пркопы, где обсуждаются как дискретная, так и непрерывная модели, представлена взаимосвязь между вероятностным стохастическим программированием с ограничениями, дизъюнктивным и многокритериальным программированием, а также новые теоремы двойственности и новый способ решения представленных проблем, где в любой момент итерации мы получаем нижнюю и верхнюю границы оптимального значения такие, что их разности монотонно стремятся к нулю.
Граничные вероятности и математические ожидания, проблемы дискретных моментов
В середине 1980-х годов он инициировал разработку новых методов получения точных границ вероятности для вероятности объединения и других булевых функций случайных событий. Эти результаты привели его к открытию, что точные границы вероятностей вероятностей различных булевых функций событий, которые используют несколько членов из формулы включения-исключения, являются оптимальными значениями LP, которые представляют собой проблемы моментов с известными дискретными носителями участвуют случайные величины. Несмотря на то, что проблемы этого типа уже упоминались в книгах о проблемах моментов, Пркопа был первым, кто исследовал структуру этих проблем с помощью теории линейного программирования как в одномерном, так и в многомерном случаях. В одномерном случае он полностью описал структуру двойственных допустимых базисов для трех специальных целевых функций. Результаты позволили вывести формулы для решения задач малого масштаба, а также сформулировать эффективные алгоритмы двойного типа для больших задач. Также он вместе с Э. Боросом представил различные закрытые формы границ. Следует отметить, что любой дуально допустимый базис дает точную оценку, если этот базис также изначально допустим.
Эти результаты привели его к открытию, что точные границы вероятностей вероятностей различных булевых функций событий, которые используют несколько членов из формулы включения-исключения, являются оптимальными значениями LP, которые представляют собой проблемы моментов с известными дискретными носителями участвуют случайные величины. Несмотря на то, что проблемы этого типа уже упоминались в книгах о проблемах моментов, Пркопа был первым, кто исследовал структуру этих проблем с помощью теории линейного программирования как в одномерном, так и в многомерном случаях. В одномерном случае он полностью описал структуру двойственных допустимых базисов для трех специальных целевых функций. Результаты позволили вывести формулы для решения задач малого масштаба, а также сформулировать эффективные алгоритмы двойного типа для больших задач. Также он вместе с Э. Боросом представил различные закрытые формы границ. Следует отметить, что любой дуально допустимый базис дает точную оценку, если этот базис также изначально допустим. Линейное программирование оказалось эффективным инструментом для получения наилучших оценок. Три специальные целевые функции позволили получить оценки вероятности объединения и вероятности того, что по крайней мере r или ровно r из n событий. Многомерный случай более сложен, здесь используется многомерная интерполяция Лагранжа, но обнаружено множество двойственных допустимых базисов с оптимальными значениями, т. е. границами, полученными в виде формул и алгоритмов. Некоторые многомерные результаты были получены совместно с Г. Мди-Надь. Если использовать биномиальные моменты числа происходящих событий, то соответствующая ЛП называется агрегированной. Если мы используем по отдельности совместные вероятности событий, то ЛП называется дезагрегированным. Дезагрегированная задача чрезвычайно велика, но дает нам более точные границы, чем агрегированные задачи. На основе дезагрегированной проблемы Пркопа дал дальнейшие оценки вероятности объединения и других функций событий с Дж.
Линейное программирование оказалось эффективным инструментом для получения наилучших оценок. Три специальные целевые функции позволили получить оценки вероятности объединения и вероятности того, что по крайней мере r или ровно r из n событий. Многомерный случай более сложен, здесь используется многомерная интерполяция Лагранжа, но обнаружено множество двойственных допустимых базисов с оптимальными значениями, т. е. границами, полученными в виде формул и алгоритмов. Некоторые многомерные результаты были получены совместно с Г. Мди-Надь. Если использовать биномиальные моменты числа происходящих событий, то соответствующая ЛП называется агрегированной. Если мы используем по отдельности совместные вероятности событий, то ЛП называется дезагрегированным. Дезагрегированная задача чрезвычайно велика, но дает нам более точные границы, чем агрегированные задачи. На основе дезагрегированной проблемы Пркопа дал дальнейшие оценки вероятности объединения и других функций событий с Дж. Буксзром и Л. Гао в качестве соавторов. Совсем недавно он опубликовал статью вместе с X. Хоу, в которой свойство Монжа пересматривается с точки зрения теории LP и устанавливаются границы для функций распределения вероятностей. В нескольких недавних работах, опубликованных совместно с Э. Субаси и М. Субаси, границы создаются при дополнительных ограничениях: форма распределения вероятностей задана. Наконец, Пркопа также показал, как использовать одномерные и многомерные оценки для приближенного решения вероятностной задачи стохастического программирования с ограничениями. Успешные практические применения вышеупомянутых оценок были осуществлены Пркопой и его соавторами для надежности телекоммуникационных и транспортных сетей, ограничения распределения вероятностей критического пути в PERT, решения проблемы выполнимости и т. д. Отметим, что стохастический метод (вероятность оценки) были применены для решения проблемы детерминированной выполнимости Численные результаты показывают, что описанные выше оценки очень эффективны и просты в применении.
Буксзром и Л. Гао в качестве соавторов. Совсем недавно он опубликовал статью вместе с X. Хоу, в которой свойство Монжа пересматривается с точки зрения теории LP и устанавливаются границы для функций распределения вероятностей. В нескольких недавних работах, опубликованных совместно с Э. Субаси и М. Субаси, границы создаются при дополнительных ограничениях: форма распределения вероятностей задана. Наконец, Пркопа также показал, как использовать одномерные и многомерные оценки для приближенного решения вероятностной задачи стохастического программирования с ограничениями. Успешные практические применения вышеупомянутых оценок были осуществлены Пркопой и его соавторами для надежности телекоммуникационных и транспортных сетей, ограничения распределения вероятностей критического пути в PERT, решения проблемы выполнимости и т. д. Отметим, что стохастический метод (вероятность оценки) были применены для решения проблемы детерминированной выполнимости Численные результаты показывают, что описанные выше оценки очень эффективны и просты в применении.
Результаты по экономике и финансам
Здесь также следует упомянуть документ о пятилетнем плане электроэнергетического сектора венгерской экономики. Недавно, вместе с Г. Мди-Надь, Пркопа опубликовал статью о классе многоатрибутных функций полезности, которые имеют аналитические формы, их производные полного порядка чередуются по знаку и соединяют одноатрибутные функции полезности, которые имеют схожие свойства. Если значения атрибутов случайны, также даются границы ожидаемой полезности, основанные на моментальной информации. В одной статье, совместно с Т. Шнтаи, представлен новый и, вероятно, очень точный метод оценки бермудских и американских опционов. Модели динамического программирования формулируются для опционов пут и колл с дивидендами, а решения представлены в формулах рекурсии, которые, в свою очередь, оцениваются численно с использованием сложной техники интегрирования для многомерной нормальной функции плотности распределения. Статья появилась в журнале Quantitative Finance; больше результатов вычислений можно найти в отчете Rutcor Research тех же авторов. В другой статье, представленной на конференции INFORMS в Питтсбурге в 2006 г., Пркопа дал оценки стоимости производных финансовых инструментов, основанные на дискретных и непрерывных проблемах моментов, которые не являются частными случаями проблем моментов, обсуждавшихся выше. Помимо результатов по финансам, статья содержит другие важные результаты: дальнейшее развитие ЛП и полубесконечной ЛП техники решения задач моментов. В недавней статье, представленной на встрече ЕВРО в Праге в 2007 г., сформулирована и решена новая модель выбора оптимального портфеля с условной средней и условной дисперсией, дополняющая методологию VaR и CVaR с использованием условной дисперсии. Наконец, он только что опубликовал статью о многомерной ценности под угрозой и смежных темах, которая была представлена в качестве пленарного доклада на встрече APMOD 2008 в Братиславе. Статья открывает широкий простор для современных и очень важных с точки зрения практического применения финансовых исследований.
В другой статье, представленной на конференции INFORMS в Питтсбурге в 2006 г., Пркопа дал оценки стоимости производных финансовых инструментов, основанные на дискретных и непрерывных проблемах моментов, которые не являются частными случаями проблем моментов, обсуждавшихся выше. Помимо результатов по финансам, статья содержит другие важные результаты: дальнейшее развитие ЛП и полубесконечной ЛП техники решения задач моментов. В недавней статье, представленной на встрече ЕВРО в Праге в 2007 г., сформулирована и решена новая модель выбора оптимального портфеля с условной средней и условной дисперсией, дополняющая методологию VaR и CVaR с использованием условной дисперсии. Наконец, он только что опубликовал статью о многомерной ценности под угрозой и смежных темах, которая была представлена в качестве пленарного доклада на встрече APMOD 2008 в Братиславе. Статья открывает широкий простор для современных и очень важных с точки зрения практического применения финансовых исследований.
Водоснабжение, электроэнергетика, телекоммуникации и другие прикладные результаты
Несмотря на то, что результаты, упомянутые в этом разделе, называются «прикладными», они также представляют теоретический интерес, поскольку представлена либо новая модель, либо некоторые новые теоретические разработки в каждом из них. Что касается водных ресурсов, Пркопа создал новые модели проектирования систем резервуаров типа стохастического программирования, которые, как было показано, представляют собой выпуклые программы и решаются алгоритмически. В отношении энергосистем результаты частично относятся к стохастическому дизайну сети, частично к типу надежности транспортной сети. Он также разработал детерминированную модель оптимального суточного планирования для производства электроэнергии во взаимосвязанной системе с тепловыми электростанциями, в которой проблема распределения единиц решается одновременно с сетевыми ограничениями. Это привело к крупномасштабной задаче оптимизации с невыпуклой, нелинейной, смешанной (0 − 1) переменной, которая была почти мгновенно решена для венгерской энергосистемы. Даже сегодня это заслуживающая внимания и применимая методология. 200-страничный документ о результатах, первоначально написанный на венгерском языке, теперь доступен на английском языке. Он также опубликовал статьи по проектированию и надежности телекоммуникационных сетей.
Что касается водных ресурсов, Пркопа создал новые модели проектирования систем резервуаров типа стохастического программирования, которые, как было показано, представляют собой выпуклые программы и решаются алгоритмически. В отношении энергосистем результаты частично относятся к стохастическому дизайну сети, частично к типу надежности транспортной сети. Он также разработал детерминированную модель оптимального суточного планирования для производства электроэнергии во взаимосвязанной системе с тепловыми электростанциями, в которой проблема распределения единиц решается одновременно с сетевыми ограничениями. Это привело к крупномасштабной задаче оптимизации с невыпуклой, нелинейной, смешанной (0 − 1) переменной, которая была почти мгновенно решена для венгерской энергосистемы. Даже сегодня это заслуживающая внимания и применимая методология. 200-страничный документ о результатах, первоначально написанный на венгерском языке, теперь доступен на английском языке. Он также опубликовал статьи по проектированию и надежности телекоммуникационных сетей. Другие области применения включают области химии, диетологии, медицины и области, упомянутые в других разделах этого отчета 9.0003
Другие области применения включают области химии, диетологии, медицины и области, упомянутые в других разделах этого отчета 9.0003
История науки
Пркопа также публикует важные статьи по истории науки. Он открыл истоки теории нелинейной оптимизации и опубликовал статьи о ней. Им написаны статьи о жизни и творчестве выдающегося венгерского математика и физика 19-20 – гг. Й. Фаркаша, разработавшего теорию линейных неравенств и опубликовавшего фундаментальные работы по механическому равновесию. Последние упомянутые результаты инициировали нелинейную оптимизацию. Он почтил память жизни и творчества Фаркаша 5 ноября 2006 года на ежегодном собрании INFORMS в Питтсбурге, штат Пенсильвания, когда впервые была присуждена премия Фаркаша. Недавно в томе, посвященном памяти всемирно известного венгерского математика Йноша Бойяи, он рассказал об открытии неевклидовой геометрии в первой половине XIX в.-й -й век, изменивший ход развития математики, а также оказавший влияние на историю человеческой культуры. В дальнейших статьях он обсуждал взаимосвязь между математикой и историей культуры.
В дальнейших статьях он обсуждал взаимосвязь между математикой и историей культуры.
Книги Пркопа
Среди книг, упомянутых в его списке публикаций, мы обращаем внимание на его вводную книгу по линейному программированию, вышедшую только на венгерском языке, и его книгу по стохастическому программированию, вышедшую на английском языке. Первая вышла в 1968 (Пркопа прочитал свой первый курс по этому предмету в Будапештском университете в 1958 г.). Книга представляет линейное программирование математически точным, элегантным и дидактическим способом, и она до сих пор используется в Венгрии на курсах для выпускников (она расширяется и переводится на английский язык). В начале 1970-х профессор Оксфорда использовал эту книгу для своих курсов с помощью венгерско-английского словаря. Книга «Стохастическое программирование» — это очень информативная книга высокого уровня, которую можно использовать для преподавания предмета, но она также является отличным источником знаний для проведения исследований и/или применения.

 – 300.
– 300. 08.2020 №831, постановлением Правительства Российской Федерации от 20 октября 2021 г. №1802, методическими рекомендациями представления информации об образовательной организации высшего образования в открытых источниках с учетом соблюдения требований законодательства в сфере образования.
08.2020 №831, постановлением Правительства Российской Федерации от 20 октября 2021 г. №1802, методическими рекомендациями представления информации об образовательной организации высшего образования в открытых источниках с учетом соблюдения требований законодательства в сфере образования. На основании Лицензии на право ведения образовательной деятельности № 1751 от 10 ноября 2015 года, Свидетельства о государственной аккредитации №1922 от 06 мая 2016 года и Свидетельства о государственной аккредитации №3619 от 09 июля 2021 года университет реализует широкий спектр образовательных программ.
На основании Лицензии на право ведения образовательной деятельности № 1751 от 10 ноября 2015 года, Свидетельства о государственной аккредитации №1922 от 06 мая 2016 года и Свидетельства о государственной аккредитации №3619 от 09 июля 2021 года университет реализует широкий спектр образовательных программ.
 Персиановский)
Персиановский) 2.014.01
2.014.01
 pl.
pl. Марии Склодовской-Кюри, Краковское отделение, Гарнцарска 11, Краков 31-115, Польша z5waligo@cyfronet .пл.
Марии Склодовской-Кюри, Краковское отделение, Гарнцарска 11, Краков 31-115, Польша z5waligo@cyfronet .пл. А., Чжан С.
Кац Р. и соавт.
Радиационное разрешение 1994 г., декабрь; 140 (3): 356–65.
Радиационное разрешение 1994.
PMID: 7972688
А., Чжан С.
Кац Р. и соавт.
Радиационное разрешение 1994 г., декабрь; 140 (3): 356–65.
Радиационное разрешение 1994.
PMID: 7972688
 Калоспирос С.А. и др.
Молекулы. 2021 5 февраля; 26 (4): 840. doi: 10.3390/молекулы26040840.
Молекулы. 2021.
PMID: 33562730
Бесплатная статья ЧВК.
Калоспирос С.А. и др.
Молекулы. 2021 5 февраля; 26 (4): 840. doi: 10.3390/молекулы26040840.
Молекулы. 2021.
PMID: 33562730
Бесплатная статья ЧВК.