Урок 19. температура. энергия теплового движения молекул – Физика – 10 класс
Физика, 10 класс
Урок №19. Температура. Энергия теплового движения молекул
На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.
Глоссарий по теме:
Макроскопические параметры – величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.
Температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).
Абсолютный нуль – предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.
Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.
Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.
Кельвин – единица абсолютной температуры в Международной системе измерений (СИ).
Постоянная Больцмана – коэффициент, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
Абсолютная температура
Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.
Дополнительная литература:
- Смородинский Я.А. Температура. – 3-е издание. – М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
- Рымкевич А.
 П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67. - Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
Теоретический материал для самостоятельного изучения
Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.
Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.
Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
В 1597 году Галилей создал термоскоп
Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.
Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры.
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).
На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.
Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.
Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.
Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.
При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.
Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:
; ; ; ;
 Подтвердить или опровергнуть данное предположение может только опыт.
Подтвердить или опровергнуть данное предположение может только опыт.Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.
Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:
Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ0 (тета нулевое):
Обозначим это отношение через Θ0 (тета нулевое):
Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение
Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего
Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.
А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности
Так как , то тогда
По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.
В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).
На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.
Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле:
Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)
k = 1,38 • 10-23 Дж/К – постоянная Больцмана.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:
значение абсолютной температуры.
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:
Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры
Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры
Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.
Отсюда следует закон Авогадро, известный нам из курса химии.
Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Рассмотрим задачи тренировочного блока урока.
1. При температуре _______ (370C; 2830C; 270C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10-21Дж.
Дано:
k = 1,38 • 10-23 Дж/К – постоянная Больцмана
t -?
Решение:
Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:
Отсюда выразим Т:
Соотношение между абсолютной температурой и температурой в градусах Цельсия:
Подставим значение абсолютной температуры:
Правильный вариант ответа:
2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м-3.
Дано:
Т = 290К
р = 0,8 МПа =0,8·106 Па
k = 1,38 • 10-23 Дж/К – постоянная Больцмана
Ек -? n – ?
Решение:
Значение средней кинетической энергии хаотического поступательного движения молекул:
Подставив значение абсолютной температуры, найдём ответ:
Определим концентрацию газа из соотношения:
Правильный вариант ответа: 6·10-21; 2·1026 м-3.
Средняя удельная теплоемкость формула. Вспоминаем физику – что такое теплоемкость воды
Удельная теплоёмкость – это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.
Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.
Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.
Формула для расчёта удельной теплоёмкости имеет следующий вид:
Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:
ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.
ΔT = t2–t1, где
- t1 – первичная температура;
- t2 – конечная температура после изменения.

m – масса вещества используемого при нагреве (гр).
Q – количество теплоты (Дж/J)
На основании Цр можно вывести и другие уравнения:
- Q = m*цp*ΔT – количество теплоты;
- m = Q/цр*(t2 — t1) – массы вещества;
- t1 = t2–(Q/цp*m) – первичной температуры;
- t2 = t1+(Q/цp*m) – конечной температуры.
Инструкция по расчёту параметра
- Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
- Выписать исходные данные.
- Подставить их в формулу.
- Провести расчёт и получим результат.
В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.
Согласно инструкции приведённой выше производим следующие действия:
Выписываем исходные данные:
- Q = 35 тыс. Дж;
- m = 480 г;
- ΔT = t2–t1 =250–15 = 235 ºC.
Берём формулу, подставляем значения и решаем:
с=Q/(m*∆T)=35тыс. Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.
Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.
Расчёт
Выполним расчёт C P воды и олова при следующих условиях:
- m = 500 грамм;
- t1 =24ºC и t2 = 80ºC – для воды;
- t1 =20ºC и t2 =180ºC – для олова;
- Q = 28 тыс. Дж.
Для начала определяем ΔT для воды и олова соответственно:
- ΔТв = t2–t1 = 80–24 = 56ºC
- ΔТо = t2–t1 = 180–20 =160ºC
Затем находим удельную теплоёмкость:
- с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
- с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.
Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.
Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.
Как рассчитать теплоемкость продуктов питания
При расчёте емкости питания уравнение примет следующий вид:
с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908 *a), где:
- w – количество воды в продукте;
- p – количество белков в продукте;
- f – процентное содержание жиров;
- c – процентное содержание углеводов;
- a – процентное содержание неорганических компонентов.
Определим теплоемкость плавленого сливочного сыра Viola . Для этого выписываем нужные значения из состава продукта (масса 140 грамм):
- вода – 35 г;
- белки – 12,9 г;
- жиры – 25,8 г;
- углеводы – 6,96 г;
- неорганические компоненты – 21 г.
Затем находим с:
- с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.
Всегда помните, что:
- процесс нагревания металла проходит быстрее, чем у воды, так как он обладает C P в 2,5 раза меньше;
- по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
- в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
- при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.

Приборы и принадлежности, используемые в работе:
2. Разновесы.
3. Термометр.
4. Калориметр.
6. Калориметрическое тело.
7. Плитка бытовая.
Цель работы:
Научиться опытным путем определять удельную теплоемкость вещества.
I. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.
Теплопроводность – передача теплоты от более нагретых частей тела к менее нагретым в следствии столкновений быстрых молекул с медленными, в результате этого быстрые молекулы передают часть своей энергии медленным.
Изменение внутренней энергии какого- либо тела прямо пропорционально его массе и изменению температуры тела.
DU = cmDT (1)
Q = cmDT (2)
Величина с, характеризующая зависимость изменения внутренней энергии тела при нагревании или охлаждении от рода вещества и внешних условий называется удельной теплоемкостью тела.
(4)
Величина C, характеризующая зависимость тела поглощать теплоту при нагревании и равная отношению количества теплоты сообщенной телу, к приращению его температуры, называется теплоемкостью тела .
C = c × m. (5)
(6)
Q = CDT (7)
Молярной теплоемкостью C m , называют количество теплоты, которое необходимо для нагревания одного моля вещества на 1 Кельвин
C m = сM. (8)
C m = (9)
Удельная теплоемкость зависит от характера процесса, при котором происходит его нагревание.
Уравнение теплового баланса.
При теплообмене суммы количеств теплоты, отданных всеми телами, у которых внутренняя энергия уменьшается, равна сумме количеств теплоты, полученных всеми телами, у которых внутренняя энергия увеличивается.
SQ отд = SQ получ (10)
Если тела образуют замкнутую систему и между ними происходит только теплообмен, то алгебраическая сумма полученных и отданных количеств теплоты равна 0.
SQ отд + SQ получ = 0.
Пример:
В теплообмене участвуют тело, калориметр, жидкость. Тело отдает теплоту, калориметр и жидкость принимают.
Q т = Q к + Q ж
Q т = c т m т (T 2 – Q)
Q к = c к m к (Q – T 1)
Q ж = c ж m ж (Q – T 1)
Где Q(тау) – общая конечная температура.
с т m т (T 2 -Q) = с к m к (Q- T 1) + с ж m ж (Q- T 1)
с т = ((Q – Т 1)*(с к m к + с ж m ж)) / m т (Т 2 – Q)
Т = 273 0 + t 0 С
2. ХОД РАБОТЫ.
ВСЕ ВЗВЕШИВАНИЯ ПРОВОДИТЬ С ТОЧНОСТЬЮ ДО 0,1 г.
1. Определите взвешиванием массу внутреннего сосуда, калориметра m 1 .
2. Налейте во внутренний сосуд калориметра воды, взвесьте внутренний стакан вместе с налитой жидкостью m к.
3. Определите массу налитой воды m = m к – m 1
4. Поместите внутренний сосуд калориметра во внешний и измерьте начальную температуру воды Т 1 .
5. Выньте из кипящей воды испытуемое тело, быстро перенесите его в калориметр, определив Т 2 -начальную температуру тела, она равна температуре кипящей воды.
6. Перемешивая жидкость в калориметре, выждите, когда перестанет повышаться температура: измерьте окончательную (установившуюся) температуру Q.
7. Выньте из калориметра испытуемое тело, высушите его фильтровальной бумагой и взвешиванием на весах определите его массу m 3 .
8. Результаты всех измерений и вычислений занесите в таблицу. Вычисления производить до второго знака после запятой.
9. Составьте уравнение теплового баланса и найдите из него удельную теплоемкость вещества с .
10. По полученным результатам в приложении определить вещество.
11. Вычислите абсолютную и относительную погрешность полученного результата относительно табличного результата по формулам:
;
12. Вывод о проделанной работе.
ТАБЛИЦА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ВЫЧИСЛЕНИЙ
Физика и тепловые явления – это довольно обширный раздел, который основательно изучается в школьном курсе. Не последнее место в этой теории отводится удельным величинам. Первая из них — удельная теплоемкость.
Однако толкованию слова «удельный» обычно уделяется недостаточно внимания. Учащиеся просто запоминают его как данность. А что оно значит?
Если заглянуть в словарь Ожегова, то можно прочесть, что такая величина определяется как отношение. Причем оно может быть выполнено к массе, объему или энергии. Все эти величины обязательно полагается брать равными единице. Отношение к чему задается в удельной теплоемкости?
Причем оно может быть выполнено к массе, объему или энергии. Все эти величины обязательно полагается брать равными единице. Отношение к чему задается в удельной теплоемкости?
К произведению массы и температуры. Причем их значения обязательно должны быть равными единице. То есть в делителе будет стоять число 1, но его размерность будет сочетать килограмм и градус Цельсия. Это обязательно учитывается при формулировке определения удельной теплоемкости, которое дано немного ниже. Там же находится формула, из которой видно, что в знаменателе стоят именно эти две величины.
Что это такое?
Удельная теплоемкость вещества вводится в тот момент, когда рассматривается ситуация с его нагреванием. Без него невозможно узнать, какое количество теплоты (или энергии) потребуется затратить на этот процесс. А также вычислить ее значение при охлаждении тела. Кстати, эти два количества теплоты равны друг другу по модулю. Но имеют разные знаки. Так, в первом случае она положительная, потому что энергию нужно затратить и она передается телу. Вторая ситуация с охлаждением дает отрицательное число, потому что тепло выделяется, и внутренняя энергия тела уменьшается.
Вторая ситуация с охлаждением дает отрицательное число, потому что тепло выделяется, и внутренняя энергия тела уменьшается.
Обозначается эта физическая величина латинской буквой c. Определяется она как некоторое количество теплоты, необходимое для нагревания одного килограмма вещества на один градус. В курсе школьной физики в качестве этого градуса выступает тот, что берется по шкале Цельсия.
Как ее сосчитать?
Если требуется узнать, чему равна удельная теплоемкость, формула выглядит так:
с = Q / (m * (t 2 – t 1)), где Q — количество теплоты, m — масса вещества, t 2 – температура, которую тело приобрело в результате теплообмена, t 1 — начальная температура вещества. Это формула № 1.
Исходя из этой формулы, единица измерения этой величины в международной системе единиц (СИ) оказывается Дж/(кг*ºС).
Как найти другие величины из этого равенства?
Во-первых, количество теплоты. Формула будет выглядеть таким образом: Q = с * m * (t 2 – t 1). Только в нее необходимо подставлять величины в единицах, входящих в СИ. То есть масса в килограммах, температура — в градусах Цельсия. Это формула № 2.
Только в нее необходимо подставлять величины в единицах, входящих в СИ. То есть масса в килограммах, температура — в градусах Цельсия. Это формула № 2.
Во-вторых, массу вещества, которое остывает или нагревается. Формула для нее будет такой: m = Q / (c * (t 2 – t 1)). Это формула под № 3.
В-третьих, изменение температуры Δt = t 2 – t 1 = (Q / c * m). Знак «Δ» читается как «дельта» и обозначает изменение величины, в данном случае температуры. Формула № 4.
В-четвертых, начальную и конечную температуры вещества. Формулы, справедливые для нагревания вещества, выглядят таким образом: t 1 = t 2 – (Q / c * m), t 2 = t 1 + (Q / c * m). Эти формулы имеют № 5 и 6. Если в задаче идет речь об охлаждении вещества, то формулы такие: t 1 = t 2 + (Q / c * m), t 2 = t 1 – (Q / c * m). Эти формулы имеют № 7 и 8.
Какие значения она может иметь?
Экспериментальным путем установлено, какие она имеет значения у каждого конкретного вещества. Поэтому создана специальная таблица удельной теплоемкости. Чаще всего в ней даны данные, которые справедливы при нормальных условиях.
Чаще всего в ней даны данные, которые справедливы при нормальных условиях.
В чем заключается лабораторная работа по измерению удельной теплоемкости?
В школьном курсе физики ее определяют для твердого тела. Причем его теплоемкость высчитывается благодаря сравнению с той, которая известна. Проще всего это реализуется с водой.
В процессе выполнения работы требуется измерить начальные температуры воды и нагретого твердого тела. Потом опустить его в жидкость и дождаться теплового равновесия. Весь эксперимент проводится в калориметре, поэтому потерями энергии можно пренебречь.
Потом требуется записать формулу количества теплоты, которое получает вода при нагревании от твердого тела. Второе выражение описывает энергию, которую отдает тело при остывании. Эти два значения равны. Путем математических вычислений остается определить удельную теплоемкость вещества, из которого состоит твердое тело.
Чаще всего ее предлагается сравнить с табличными значениями, чтобы попытаться угадать, из какого вещества сделано изучаемое тело.
Задача № 1
Условие. Температура металла изменяется от 20 до 24 градусов Цельсия. При этом его внутренняя энергия увеличилась на 152 Дж. Чему равна удельная теплоемкость металла, если его масса равна 100 граммам?
Решение. Для нахождения ответа потребуется воспользоваться формулой, записанной под номером 1. Все величины, необходимые для расчетов, есть. Только сначала необходимо перевести массу в килограммы, иначе ответ получится неправильный. Потому что все величины должны быть такими, которые приняты в СИ.
В одном килограмме 1000 граммов. Значит, 100 граммов нужно разделить на 1000, получится 0,1 килограмма.
Подстановка всех величин дает такое выражение: с = 152 / (0,1 * (24 – 20)). Вычисления не представляют особой трудности. Результатом всех действий является число 380.
Ответ: с = 380 Дж/(кг * ºС).
Задача № 2
Условие. Определить конечную температуру, до которой остынет вода объемом 5 литров, если она была взята при 100 ºС и выделила в окружающую среду 1680 кДж тепла.
Решение. Начать стоит с того, что энергия дана в несистемной единице. Килоджоули нужно перевести в джоули: 1680 кДж = 1680000 Дж.
Для поиска ответа необходимо воспользоваться формулой под номером 8. Однако в ней фигурирует масса, а в задаче она неизвестна. Зато дан объем жидкости. Значит, можно воспользоваться формулой, известной как m = ρ * V. Плотность воды равна 1000 кг/ м 3 . Но здесь объем потребуется подставлять в кубических метрах. Чтобы перевести их из литров, необходимо разделить на 1000. Таким образом, объем воды равен 0,005 м 3 .
Подстановка значений в формулу массы дает такое выражение: 1000 * 0,005 = 5 кг. Удельную теплоемкость потребуется посмотреть в таблице. Теперь можно переходить к формуле 8: t 2 = 100 + (1680000 / 4200 * 5).
Первым действием полагается выполнить умножение: 4200 * 5. Результат равен 21000. Второе — деление. 1680000: 21000 = 80. Последнее — вычитание: 100 – 80 = 20.
Ответ. t 2 = 20 ºС.
Задача № 3
Условие. Имеется химический стакан массой 100 г. В него налито 50 г воды. Начальная температура воды со стаканом равна 0 градусам Цельсия. Какое количество теплоты потребуется для того, чтобы довести воду до кипения?
Имеется химический стакан массой 100 г. В него налито 50 г воды. Начальная температура воды со стаканом равна 0 градусам Цельсия. Какое количество теплоты потребуется для того, чтобы довести воду до кипения?
Решение. Начать стоит с того, чтобы ввести подходящее обозначение. Пусть данные, относящиеся к стакану, будут иметь индекс 1, а к воде — индекс 2. В таблице необходимо найти удельные теплоемкости. Химический стакан сделан из лабораторного стекла, поэтому его значение с 1 = 840 Дж/ (кг * ºС). Данные для воды такие: с 2 = 4200 Дж/ (кг * ºС).
Их массы даны в граммах. Требуется перевести их в килограммы. Массы этих веществ будут обозначены так: m 1 = 0,1 кг, m 2 = 0,05 кг.
Начальная температура дана: t 1 = 0 ºС. О конечной известно, что она соответствует той, при которой вода кипит. Это t 2 = 100 ºС.
Поскольку стакан нагревается вместе с водой, то искомое количество теплоты будет складываться из двух. Первой, которая требуется для нагревания стекла (Q 1), и второй, идущей на нагревание воды (Q 2). Для их выражения потребуется вторая формула. Ее необходимо записать два раза с разными индексами, а потом составить их сумму.
Для их выражения потребуется вторая формула. Ее необходимо записать два раза с разными индексами, а потом составить их сумму.
Получается, что Q = с 1 * m 1 * (t 2 – t 1) + с 2 * m 2 * (t 2 – t 1). Общий множитель (t 2 – t 1) можно вынести за скобку, чтобы было удобнее считать. Тогда формула, которая потребуется для расчета количества теплоты, примет такой вид: Q = (с 1 * m 1 + с 2 * m 2) * (t 2 – t 1). Теперь можно подставить известные в задаче величины и сосчитать результат.
Q = (840 * 0,1 + 4200 * 0,05) * (100 – 0) = (84 + 210) * 100 = 294 * 100 = 29400 (Дж).
Ответ. Q = 29400 Дж = 29,4 кДж.
Количество тепла, при получении которого температура тела повышается на один градус, называется теплоемкостью. Согласно этому определению.
Теплоемкость, отнесенная к единице массы, называется удельной теплоемкостью. Теплоемкость, отнесенная к одному молю, называется моляpной теплоемкостью.
Итак,
теплоемкость опpеделяется чеpез понятие
количества теплоты. Но последнее, как
и pабота, зависит от пpоцесса. Значит и
теплоемкость зависит от пpоцесса.
Сообщать теплоту – нагpевать тело – можно
пpи pазличных условиях. Однако пpи
pазличных условиях на одно и то же
увеличение темпеpатуpы тела потpебуется
pазличное количество теплоты. Следовательно,
тела можно хаpактеpизовать не одной
теплоемкостью, а бесчисленным множеством
(столько же, сколько можно пpидумать
всевозможных пpоцессов, пpи котоpых
пpоисходит теплопеpедача). Однако на
пpактике обычно пользуются опpеделением
двух теплоемкостей: теплоемкости пpи
постоянном объеме и теплоемкости пpи
постоянном давлении.
Но последнее, как
и pабота, зависит от пpоцесса. Значит и
теплоемкость зависит от пpоцесса.
Сообщать теплоту – нагpевать тело – можно
пpи pазличных условиях. Однако пpи
pазличных условиях на одно и то же
увеличение темпеpатуpы тела потpебуется
pазличное количество теплоты. Следовательно,
тела можно хаpактеpизовать не одной
теплоемкостью, а бесчисленным множеством
(столько же, сколько можно пpидумать
всевозможных пpоцессов, пpи котоpых
пpоисходит теплопеpедача). Однако на
пpактике обычно пользуются опpеделением
двух теплоемкостей: теплоемкости пpи
постоянном объеме и теплоемкости пpи
постоянном давлении.
Теплоемкость различается в зависимости от того, при каких условиях происходит нагревание тела – при постоянном объеме или при постоянном давлении.
Если
нагревание тела происходит при постоянном
объеме, т. е. dV = 0, то работа
равна нулю. В этом случае передаваемое
телу тепло идет только на изменение его
внутренней энергии, dQ = dE ,
и в этом случае теплоемкость равна
изменению внутренней энергии при
изменении температуры на 1 К, т. е.
е.
.Поскольку
для газа
,
то
.Эта
формула определяет теплоемкость 1 моля
идеального газа, называемую молярной.
При нагревании газа при постоянном
давлении его объем меняется, сообщенное
телу тепло идет не только на увеличение
его внутренней энергии, но и на совершение
работы, т.е.dQ = dE + PdV .
Теплоемкость при постоянном давлении
.
Для идеального газа PV = RT и поэтому PdV = RdT .
Учитывая
это, найдем
.Отношение
представляет собой величину, характерную
для каждого газа и определяемую числом
степеней свободы молекул газа. Измерение
теплоемкости тела есть, таким образом,
способ непосредственного измерения
микроскопических характеристик
составляющих его молекул.
Ф
ормулы
для теплоемкости идеального газа
приблизительно верно описывают
эксперимент, причем, в основном, для
одноатомных газов. Согласно формулам,
полученным выше, теплоемкость не должна
зависеть от температуры. На самом деле
наблюдается картина, изображенная на
рис. , полученная опытным путем для
двухатомного газа водорода. На участке
1 газ ведет себя как система частиц,
обладающих лишь поступательными
степенями свободы, на участке 2 возбуждается
движение, связанное с вращательными
степенями свободы и, наконец, на участке
3 появляются две колебательные степени
свободы. Ступеньки на кривой хорошо
согласуются с формулой (2.35), однако между
ними теплоемкость растет с температурой,
что соответствует как бы нецелому
переменному числу степеней свободы.
Такое поведение теплоемкости указывает
на недостаточность используемого нами
представления об идеальном газе для
описания реальных свойств вещества.
, полученная опытным путем для
двухатомного газа водорода. На участке
1 газ ведет себя как система частиц,
обладающих лишь поступательными
степенями свободы, на участке 2 возбуждается
движение, связанное с вращательными
степенями свободы и, наконец, на участке
3 появляются две колебательные степени
свободы. Ступеньки на кривой хорошо
согласуются с формулой (2.35), однако между
ними теплоемкость растет с температурой,
что соответствует как бы нецелому
переменному числу степеней свободы.
Такое поведение теплоемкости указывает
на недостаточность используемого нами
представления об идеальном газе для
описания реальных свойств вещества.
Связь молярной теплоёмкости с удельной теплоёмкостью С =M с, где с – удельная теплоёмкость , М – молярная масса .Формула Майера.
Для любого идеального газа справедливо соотношение Майера:
,где
R –
универсальная
газовая постоянная,
–
молярная
теплоемкость при постоянном давлении,
–
молярная
теплоемкость при постоянном объёме.
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
– это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q .
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах – джоулях (Дж ), как и всякий вид энергии.
В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии – калория (кал ), равная количеству теплоты, необходимому для нагревания 1 грамма воды на 1 градус Цельсия (точнее, от 19,5 до 20,5 °С). Данную единицу, в частности, используют в настоящее время при расчетах потребления тепла (тепловой энергии) в многоквартирных домах. Опытным путем установлен механический эквивалент теплоты – соотношение между калорией и джоулем: 1 кал = 4,2 Дж .
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.
Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
– это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.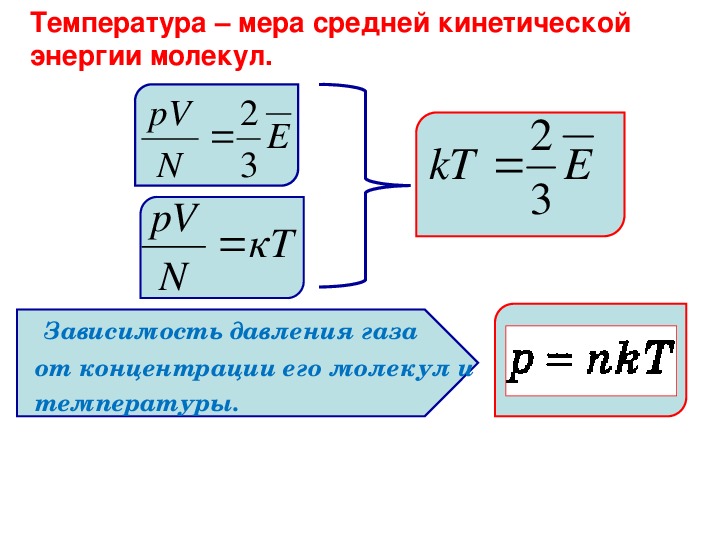
Удельная теплоёмкость обозначается буквой с . Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С . В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Q , необходимое для нагревания тела массой m от температуры t 1 °С до температуры t 2 °С , равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е. Q = c ∙ m (t 2 — t 1)По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
Это конспект по теме «Количество теплоты. Удельная теплоёмкость» . Выберите дальнейшие действия:
- Перейти к следующему конспекту:
АБСОЛЮТНАЯ ТЕМПЕРАТУРА – Методология – Большая книга физики
Необходимостью применения абсолютной температуры и, соответственно абсолютной шкалы, является неудобство применения для проведения экспериментов и решения задач, используемых в быту шкал Цельсия и Фаренгейта. Неудобство заключается в том, что когда температура опускается ниже точки замерзания воды, температуру приходится выражать отрицательным числом. Это приводит к путанице или необходимости уточнений и внесения корректировок в формулы при вычислениях.
Понятие абсолютной температуры было введено У. Томсоном (Кельвином), всвязи с чем, шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — Кельвин (К). Абсолютный ноль определён как 0 K, что равно −273.15 °C. С другой стороны, 273.15 К соответствует 0 °C.
Единица абсолютной температуры — Кельвин (К). Абсолютный ноль определён как 0 K, что равно −273.15 °C. С другой стороны, 273.15 К соответствует 0 °C.
Уильям Томсон лорд Кельвин
26 июня 1824 г – 17 декабря 1907 г
Исходя из этого соответствия, цена одного деления по шкале Кельвина равна цене деления шкалы Цельсия. Поэтому, несмотря на отличие температур состояний тела по шкале Цельсия и по шкале Кельвина, разность температур в этих шкалах одинакова.
Абсолютный ноль, является наиболее низкой возможной температурой, при которой прекращается тепловое движение молекул и атомов. Однако при абсолютном нуле частицы, входящие в состав атомов, могут совершать так называемые нулевые колебания. Но энергию этих частиц нельзя передать непосредственно при контакте тел.
Для идеального газа средняя кинетическая энергия движения молекул пропорциональна температуре:
Е = 3/2 kT .
При температуре Т=0 средняя кинетическая энергия молекул Е также будет равна нулю. Что в принципе невозможно. Откуда следует недостижимость абсолютного нуля. И не только для идеального газа (при такой температуре реальные газы могут находиться только в жидком или твёрдом состоянии), но и при любом состоянии вещества.
Справедливость этого утверждения доказывает тот факт, что температуры −273 °C и ниже просто не зафиксированы. Практически достигнуты температуры отличающиеся от абсолютного нуля на порядок 10-6 К. Есть сведения, что в Ланкастерском университете (Англия) была достигнута температура, превышающая абсолютный ноль всего лишь на 2,8 · 10-10 К. Но тем не менее порог ещё не преодолён. При температуре близкой к абсолютному нулю существенно изменяются свойства многих тел. Некоторые упругие материалы становятся хрупкими, а некоторые металлы становятся сверхпроводящими.
Что будет, если состояние вещества при такой температуре будет всё-таки достигнуто? То же, что и всегда: возникнет необходимость пересмотреть теорию на основе новых экспериментальных фактов. Но это только, если…
Но это только, если…
Физика — сборник таблиц
Формулы и т.пУниверсальная газовая постоянная R ( Ru у англосаксов) в различных системах измерения, в различных размерностях.
Удельная теплота парообразования (сводная таблица) при давлении 101,3 кПа и справочная температура кипения в град С для этого давления.
Увлажнение воздуха водяным паром, таблица. Количество (масса) воды во влажном воздухе. Кг/100м3 vs относительная влажность воздуха в %. Температуры фазовых переходов для некоторых неорганических веществ. Температуры плавления, кипения, возгонки, разложения.
Температуры плавления, кипения, возгонки, разложения.
Температуры кипения водных растворов неорганических веществ – солей, оснований в зависимости от концентрации при атмосферном давлении 101,3 кПа
Температуры кипения (oK) и Удельные теплоемкости жидкого состояния (кал/гoC) и (кДж/кгoC). Жидкие металлы.
Температура высыхания и его время для некоторых распространенных продуктов и материалов, таких как: кофе, фрукты, древесина и т.д.
В засуху огород и газон следует поливать холодной водой ночью, ибо если получится локальное падение температуры ниже точки росы вы получите еще огромное количество влаги из воздуха за счет конденсации. Температуру воздуха и относительную влажность в % можно узнать в любом прогнозе погоды.
Температуру воздуха и относительную влажность в % можно узнать в любом прогнозе погоды.Таблица указывает “абсолютную влажность” в г/м3 (верхняя строчка) и температуру точки росы воздуха в °C (нижняя строчка) для различных температур окружающего воздуха в зависимости от относительной влажности.
Сжатие и расширение газов. Изотермический, адиабатический и политропный процессы.
Связь между давлением, температурой, объемом и количеством молей газа (“массой” газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
Страницы: 1 2 3 … 19 20
Расчеты температуры и давления – Расчеты температуры и газа – GCSE Physics (Single Science) Revision
eeujvevyy2.0.0.0.1:0.1.0.$0.$1.$0″> энергии, которая заставит их двигаться быстрее.Температура газа пропорциональна средней кинетической энергии его молекул. Более быстро движущиеся частицы будут сталкиваться со стенками контейнера чаще и с большей силой.Это приводит к увеличению силы, действующей на стенки сосуда, и, следовательно, к увеличению давления.
Если температура газа измеряется по шкале Кельвина, давление пропорционально температуре.
Отсюда мы можем вывести уравнение
\[\frac{P_{1}}{T_{1}} = \frac{P_{2}}{T_{2}}\]
где:
P 1 — начальное давление
eeujvevyy2.0.0.0.1:0.1.0.$0.$1.$7″> T 1 — начальная температураP 2 — конечное давление
T 2 — конечная температура
Все температуры температура.
Это уравнение верно, пока объем и масса газа постоянны
- Вопрос
Автомобильная шина содержит воздух в количестве 1,25 × 10 5 Па при температуре 27°C. После того как автомобиль поработает какое-то время, температура воздуха в шинах поднимается до 42°C.
 Если объем шины не изменился, каково новое давление воздуха в шине?
Если объем шины не изменился, каково новое давление воздуха в шине?- Показать ответ
Сначала переведите температуру в кельвины.5 \times 315)}{300}\]
Новое давление 1,31 × 10 5 Па. .
Температура тела измеряется термометром.Отрасль Термометрия, тепло.
Фундаментальный интервал=верхняя фиксированная точка – нижняя фиксированная точка.
Верхняя фиксированная точка – чистая вода под давлением в 1 атмосферу кипит при 100°C.Нижняя фиксированная точка – чистый лед под давлением в 1 атмосферу тает 0°C
Индивидуальная пересчет температуры из одной шкалы в другую
100\C=180\F-32=100\K-273 =80\R
Преобразование разницы температур из одной шкалы в другую
5\∆C=9\∆F=5\∆K=4\∆R
ОЧЕНЬ ВАЖНО ПРИМЕЧАНИЕ;
Пирометр: чувствительные к инфракрасному излучению устройства, используемые для обнаружения инфракрасного излучения.
 Тройная точка воды – 273,16 к. Удельное сопротивление материала, нечувствительного к температуре, – нихром . Температура солнца, определяемая пирометром . При постоянном объеме газовый термометр работает по закону Шарля.
Тройная точка воды – 273,16 к. Удельное сопротивление материала, нечувствительного к температуре, – нихром . Температура солнца, определяемая пирометром . При постоянном объеме газовый термометр работает по закону Шарля.Дробное увеличение удельного сопротивления на единицу повышения температуры равно температуре коэффициент удельного сопротивления.
Примеры:
1)При какой температуре тела совпадают его температуры, измеренные в °С или °F?
SOL: пусть ° C = ° F = x 5 \ C = 9 \ F-32 5 \ x = 9 \ x-32 9x = 5x-160 4x = -160 x = -40
2) Что такое температура, при которой показания шкалы Кельвина и Фаренгиета совпадают?
Сол: Пусть K=F=x=? 5 \ k-273 = 9 \ F-32 5 \ x-273 = 9 \ x-32 5x-160 = 9x-2457 -4x = -2457 + 160 -4x = -2297 x = -4 \ -2297 x = -4 \ -2297 x = -4 \ -2297 x = 574.25
3) Температура тела увеличилась с 32°R до 373K.
 Найдите изменение температуры тела в °C,°F, по шкале Кельвина и Ремера??
Найдите изменение температуры тела в °C,°F, по шкале Кельвина и Ремера??Солнце: t1=32°R
5\C=4\R. 5\К-273\=5\С. 5\С=4\32. Отмена 5 с обеих сторон 5\C=1\8. 373-273=С. С=40°С. 100°С=t2. t1=40°С.
∆t=t2-t1. ∆t=100-40=60°С. 9\∆F=5\∆С. 5\∆К=5\∆С 9\∆F=5\60.∆К=60°С. ∆F=108°F.
4\∆R=5\∆С. 4\∆R=5\60. ∆R=48R
Имп формула:
Принцип работы термометров при 102°С. Если эта мера измерения температуры тела равна 49°С. Найдите?
а) Правильная температура тела.
b)Ошибка показаний и необходима ли коррекция?
Sol: √ × L.F.P. 0°С. -4°С. U.F.P 100°C 102°C. рупий ? 49°С. (UFP-LFP\Rs-LFP)√=(UFP-LFP\Rs-LFP)x
Rs= Показания, отображаемые любой температурой
(100-0\Rs-0)√=(102-(-4) \49-(-4). )× ( 100\Rs)√=(106\53)× Rs√=2\100=50
Ошибка=xизмеренное значение-xистинное значение
= 49C-50°C=- 1°C
Поправка=+1°C
Также читайте Математические хитрости для быстрого расчета
Это также касается тепла
Температурный коэффициент сопротивления | Физика проводников и изоляторов
Вы могли заметить, что в таблице удельных сопротивлений все значения указаны для температуры 20° Цельсия.
 Если вы подозревали, что это означает, что удельное сопротивление материала может меняться в зависимости от температуры, вы были правы!
Если вы подозревали, что это означает, что удельное сопротивление материала может меняться в зависимости от температуры, вы были правы!Значения сопротивления проводников при любой температуре, отличной от стандартной температуры (обычно указывается при 20 градусах Цельсия) в таблице удельных сопротивлений, должны определяться по еще одной формуле:
Константа «альфа» (α) известна как температурный коэффициент сопротивления и символизирует коэффициент изменения сопротивления на градус изменения температуры.Так как все материалы имеют определенное удельное сопротивление (при 20°С), они также изменяют сопротивление в зависимости от температуры на определенные величины. Для чистых металлов этот коэффициент является положительным числом, означающим, что сопротивление увеличивается на с повышением температуры. Для элементов углерода, кремния и германия этот коэффициент является отрицательным числом, а это означает, что сопротивление уменьшается на с повышением температуры.
 Для некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, а это означает, что сопротивление почти не меняется при изменении температуры (хорошее свойство, если вы хотите построить прецизионный резистор из металлической проволоки!).В следующей таблице приведены температурные коэффициенты сопротивления для нескольких распространенных металлов, как чистых, так и легированных:
Для некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, а это означает, что сопротивление почти не меняется при изменении температуры (хорошее свойство, если вы хотите построить прецизионный резистор из металлической проволоки!).В следующей таблице приведены температурные коэффициенты сопротивления для нескольких распространенных металлов, как чистых, так и легированных:Температурные коэффициенты сопротивления при 20 градусах Цельсия
Материал Элемент/сплав «альфа» на градус Цельсия Никель Элемент 0,005866 Железо Элемент 0,005671 Молибден Элемент 0.004579 Вольфрам Элемент 0,004403 Алюминий Элемент 0,004308 Медь Элемент 0,004041 Серебро Элемент 0,003819 Платина Элемент 0,003729 Золото Элемент 0,003715 Цинк Элемент 0.  003847
003847Сталь* Сплав 0,003 Нихром Сплав 0,00017 Нихром V Сплав 0,00013 Манганин Сплав +/- 0,000015 Константан Сплав -0,000074 * = Стальной сплав с содержанием железа 99,5%, углерода 0,5% тыс
Давайте посмотрим на пример схемы, чтобы увидеть, как температура может повлиять на сопротивление провода и, следовательно, на производительность схемы:
Суммарное сопротивление проводов этой цепи (провод 1 + провод 2) составляет 30 Ом при стандартной температуре.Настроив таблицу значений напряжения, тока и сопротивления получаем:
При 20 °С мы получаем 12,5 Вольт на нагрузке и всего 1,5 Вольта (0,75 + 0,75) на сопротивлении провода. Если бы температура поднялась до 35° по Цельсию, мы могли бы легко определить изменение сопротивления для каждого отрезка провода.
 Предполагая использование медной проволоки (α = 0,004041), получаем:
Предполагая использование медной проволоки (α = 0,004041), получаем:Пересчитав значения нашей схемы, мы видим, какие изменения принесет это повышение температуры:
Как видите, напряжение на нагрузке упало (с 12.5 вольт до 12,42 вольт) и падение напряжения на проводах увеличилось (с 0,75 вольт до 0,79 вольт) в результате повышения температуры. Хотя изменения могут показаться небольшими, они могут быть значительными для линий электропередач, протянувшихся на километры между электростанциями и подстанциями, подстанциями и нагрузками. На самом деле энергетическим компаниям часто приходится учитывать изменения сопротивления линий, возникающие в результате сезонных колебаний температуры, при расчете допустимой нагрузки системы.
ОБЗОР:
- Удельное сопротивление большинства проводящих материалов изменяется при изменении температуры.Поэтому значения удельного сопротивления всегда указываются при стандартной температуре (обычно 20° или 25° по Цельсию).

- Коэффициент изменения сопротивления на градус Цельсия изменения температуры называется температурным коэффициентом сопротивления . Этот фактор обозначается строчной греческой буквой «альфа» (α).
- Положительный коэффициент для материала означает, что его сопротивление увеличивается с повышением температуры. Чистые металлы обычно имеют положительный температурный коэффициент сопротивления.Коэффициенты, приближающиеся к нулю, можно получить путем сплавления некоторых металлов.
- Отрицательный коэффициент для материала означает, что его сопротивление уменьшается с повышением температуры. Полупроводниковые материалы (углерод, кремний, германий) обычно имеют отрицательные температурные коэффициенты сопротивления.
- Формула, используемая для определения сопротивления проводника при температуре, отличной от указанной в таблице сопротивлений, выглядит следующим образом:
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Второй закон термодинамики
Термодинамика — раздел физики который имеет дело с энергией и работой системы.
 Термодинамика сделок
только с крупномасштабной реакцией системы, которую мы можем наблюдать
и измерить в опытах.
В аэродинамике термодинамика
газа, очевидно, играет важную роль в анализе
двигательные системы.
То
первый закон
термодинамики определяет соотношение между различными формами
кинетическая и потенциальная энергия, присутствующая в системе,
Работа
какая система
может выполнять и передачу
нагревать.Закон гласит, что энергия сохраняется во всех термодинамических процессах.
Термодинамика сделок
только с крупномасштабной реакцией системы, которую мы можем наблюдать
и измерить в опытах.
В аэродинамике термодинамика
газа, очевидно, играет важную роль в анализе
двигательные системы.
То
первый закон
термодинамики определяет соотношение между различными формами
кинетическая и потенциальная энергия, присутствующая в системе,
Работа
какая система
может выполнять и передачу
нагревать.Закон гласит, что энергия сохраняется во всех термодинамических процессах.Однако мы можем представить себе термодинамические процессы, которые сохраняли бы энергию. но которые никогда не встречаются в природе. Например, если мы принесем горячий предмет в контакт с холодным предметом, горячий предмет остывает, а холодный предмет нагревается до тех пор, пока не будет достигнуто равновесие. Передача тепла идет от горячий предмет к холодному предмету. Мы могли бы представить себе систему, в которой вместо этого тепло будет передаваться от холодного объекта к горячему, и такая система не нарушила бы первый закон термодинамики.
 Холод
объект станет холоднее, а горячий объект станет горячее, но энергия будет
быть сохранены. Очевидно, что в природе мы не встречаем такой системы, и
объяснить это и подобные наблюдения, термодинамики предложили второй
закон термодинамики. Клазиус, Кельвин и Карно предложили различные формы
второго закона, чтобы описать конкретную физическую проблему, которую каждый
изучение. Описание второго закона, представленное на этом слайде, было взято
из учебника Холлидея и Резника «Физика».Он начинается с определения
новой переменной состояния, называемой
энтропия.
Энтропия имеет множество
физические интерпретации, включая статистический беспорядок системы,
но для наших целей давайте будем считать энтропию просто еще одним свойством
системы, как
энтальпия
или
температура.
Холод
объект станет холоднее, а горячий объект станет горячее, но энергия будет
быть сохранены. Очевидно, что в природе мы не встречаем такой системы, и
объяснить это и подобные наблюдения, термодинамики предложили второй
закон термодинамики. Клазиус, Кельвин и Карно предложили различные формы
второго закона, чтобы описать конкретную физическую проблему, которую каждый
изучение. Описание второго закона, представленное на этом слайде, было взято
из учебника Холлидея и Резника «Физика».Он начинается с определения
новой переменной состояния, называемой
энтропия.
Энтропия имеет множество
физические интерпретации, включая статистический беспорядок системы,
но для наших целей давайте будем считать энтропию просто еще одним свойством
системы, как
энтальпия
или
температура.Второй закон гласит, что существует полезная переменная состояния, называемая энтропией. Изменение энтропии (дельта S) равно теплопередаче (дельта Q), деленной на по температуре (Т).
дельта S = (дельта q) / T
Для данного физического процесса энтропия система и окружающая среда останутся постоянными, если процесс можно перевернутый.
 Если обозначить начальное и конечное состояния системы через «i» и «f»,
тогда:
Если обозначить начальное и конечное состояния системы через «i» и «f»,
тогда:Sf = Si (обратимый процесс)
Примером обратимого процесса было бы идеальное принуждение протекать через суженную трубу.(Идеальный вариант означает отсутствие потерь в пограничном слое). При движении потока через сужение давление, температура и скорость изменится, но эти переменные вернутся к своим первоначальным значения после сужения. То государство газа вернется в исходное состояние, а изменение энтропии системы будет равно нулю. Второй закон гласит, что если физический процесс необратим , энтропия системы и окружающая среда должна увеличиваться; конечная энтропия должна быть больше начальная энтропия.
Sf > Si (необратимый процесс)
Примером необратимого процесса является проблема обсуждалось во втором абзаце, когда горячий предмет соприкасается с холодным предметом. В конце концов, они оба достигают одинаковой равновесной температуры.
 Если мы тогда
разделять объекты, которые они
не возвращаются естественным образом к своим первоначальным (другим) температурам. То
процесс приведения их к одинаковой температуре необратим.
Если мы тогда
разделять объекты, которые они
не возвращаются естественным образом к своим первоначальным (другим) температурам. То
процесс приведения их к одинаковой температуре необратим.Применение второго закона описывает, почему тепло передается от горячий предмет к холодному предмету. Предположим, что тепло передается от горячий объект (объект 1) при температуре T1 к холодному объекту (объект 2) при температуре T2. Количество переданного тепла равно Q, а конечное равновесие температуру для обоих объектов обозначим Tf. Температура горячего объекта меняется по мере отвода тепла от объекта.Средняя температура горячего объекта во время процесс, который мы назовем Th, и это будет среднее значение T1 и Tf.
Th = (T1 + Tf) / 2
Точно так же для холодного объекта конечная температура равна Tf, а среднее температура во время процесса равна Tc, которая является средним значением Tf и T2.
Тс = (Т2 + Тф) / 2
Th всегда будет больше, чем Tc, потому что T1 больше, чем T2.

Т > Тс
Изменение энтропии горячего объекта будет (-Q/Th) со знаком минус применяется, потому что тепло передается от объекта.
дельта Sh = -Q/Th
Для холодного объекта изменение энтропии (Q/Tc) положительно, потому что тепло передается объекту.
дельта Sc = Q / Tc
Таким образом, полное изменение энтропии для всей системы будет определяться уравнением
Sf = Si – Q/Th + Q/Tc
где Si и Sf являются конечными и начальными значениями энтропии.Член (Q/Tc) всегда будет больше, чем (-Q/Th), потому что Th больше, чем тк. Следовательно, Sf будет больше, чем Si, как и предсказывает второй закон. Если бы вместо этого мы имели предположили, что тепло передается от холодного тела к горячему. окончательное уравнение будет
Sf = Si + Q/Th – Q/Tc
Знаки на терминах будут быть изменены из-за направления теплопередачи.Это приведет к тому, что Sf будет меньше Si, а энтропия системы уменьшится, что нарушит второй закон термодинамики.

Виды деятельности:Навигация..
- Возрождение пути Райта
- Руководство для начинающих по аэронавтике
- Домашняя страница НАСА
- http://www.nasa.gov
Температура поверхности Земли
Средняя температура поверхности земли составляет около $T = 288 \,\text{K}$. [1] Можно ли вывести это число с помощью простой модели?
Теплообмен с окружающей средой
Взгляд на недавнюю историю климата Земли показывает, что средняя температура поверхности была относительно постоянной. В течение последних 40 миллионов лет глобальная средняя температура изменялась всего на 10 градусов по Кельвину, а за последние 10 000 лет изменение составляло всего около 1 градуса. [2]
Таким образом, даже в больших временных масштабах температуру Земли можно считать постоянной.{-2} \end{выравнивание} Поскольку Земля, по существу, окружена вакуумом, единственный способ теплообмена с окружающей средой — это электромагнитное излучение, потому что, в отличие от теплопроводности и конвекции, этот процесс не требует среды для распространения.
 [5] [6] Действительно, геотермальная активность вносит незначительный дополнительный вклад, но в дальнейшем этим пренебрегают из-за его относительной слабости по сравнению с солнечным излучением.
[5] [6] Действительно, геотермальная активность вносит незначительный дополнительный вклад, но в дальнейшем этим пренебрегают из-за его относительной слабости по сравнению с солнечным излучением.Излучение черного тела
Однако мы должны указать выражения для входящего и исходящего лучистого потока.Очевидно, что падающее излучение исходит в основном от солнца с его высокой температурой поверхности, тогда как уходящее излучение должно быть каким-то образом связано с температурой земли.
Происхождение теплового излучения
Каково происхождение теплового излучения? На микроскопическом уровне температура объекта является мерой кинетической энергии его составляющих (в конечном итоге заряженных частиц). Таким образом, тепловое излучение возникает в результате теплового движения заряженных частиц, что приводит к излучению электромагнитных волн.Кинетическая энергия этих частиц статистически распределяется вокруг среднего значения, то же самое относится и к спектру их излучения.
 2 .2 \метка{pOut}
\end{выравнивание}
2 .2 \метка{pOut}
\end{выравнивание}Возможно, вам интересно, почему мы сначала использовали площадь проекции Земли, а теперь — общую площадь сферы. Объяснение состоит в том, что в первом случае мы рассматривали параллельное излучение и в этом случае перпендикулярная поверхность плоская. Наоборот, теперь мы рассмотрели радиально испускаемые лучи, и в этом случае перпендикулярная поверхность имеет криволинейную сферическую форму.
Результат
Теперь можно вставить уравнения. \eqref{pIn} и \eqref{pOut} в ур.2 \\[2экс] \Leftrightarrow \quad T_\text{e} &= \sqrt[4]{\frac{(1-a) \cdot S}{4\sigma}} \end{выравнивание} [10] [11]
При вставке значений, приведенных в предыдущих разделах, этот расчет дает температуру поверхности около $T_\text{e} = 255\,\text{K}$. Хотя это значение неплохо для очень простой модели, оно все же значительно отклоняется от фактического значения $T_\text{e} = 288\,\text{K}$.
Каковы основные недостатки этой модели? Предполагалось, что Земля представляет собой замкнутую систему с острой поверхностью, окруженную вакуумом.
 Однако это не относится к земной поверхности, так как есть еще атмосфера, которая значительно влияет на радиационный баланс. В следующей статье будет рассмотрена более сложная модель воздействия атмосферы.
Однако это не относится к земной поверхности, так как есть еще атмосфера, которая значительно влияет на радиационный баланс. В следующей статье будет рассмотрена более сложная модель воздействия атмосферы.Физика для науки и техники II
6.8 Зависимость удельного сопротивления от температуры из Office of Academic Technologies на Vimeo.
6.08 Температурная зависимость удельного сопротивления
Как и в случае с большинством физических свойств, удельное сопротивление также зависит от температуры как изменение удельного сопротивления от температуры.Когда мы наблюдаем различные проводящие среды, мы видим, что удельное сопротивление изменяется почти линейно с температурой. Другими словами, удельное сопротивление увеличивается с повышением температуры.

Для таких линейных отношений можно написать эмпирическую аппроксимацию, которая достаточно хороша для большинства инженерных целей. И это эмпирическое уравнение для удельного сопротивления имеет вид ρ минус ρ 0 равно ρ 0 умножить на некоторую постоянную, α , умножить на T минус T 0 0 — выбранная эталонная температура, и обычно мы выбираем эту температуру в качестве комнатной.
Посмотрим, T 0 это комнатная температура и равна 293 Кельвина. ρ 0 представляет удельное сопротивление при температуре Тл 0 при этой базовой температуре, и, следовательно, ρ представляет удельное сопротивление при температуре Тл . Здесь температуры выражены в Кельвинах, а константа α называется «температурным коэффициентом удельного сопротивления». Эта величина указана для различных проводящих сред в таблицах, чтобы можно было легко найти соответствующее удельное сопротивление для этой конкретной среды.

Например, удельное сопротивление меди, скажем так, температурный коэффициент удельного сопротивления меди равен 4,3 умножить на 10 в -3, обратно Кельвину. А удельное сопротивление меди при комнатной температуре, 0,0, составляет 1,69 х 10-19 Ом-метр. Аналогичным образом температурный коэффициент и удельное сопротивление при комнатной температуре для различных проводящих сред или различных материалов приведены в таблицах, чтобы их можно было найти для расчета удельного сопротивления этой среды при другой температуре.
Теперь, поскольку удельное сопротивление и сопротивление прямо пропорциональны, можно также записать эмпирическое уравнение для сопротивления или температурной зависимости сопротивления, просто заменив ρ и ρ 0 на R и Р 0 . Поэтому мы также можем легко рассчитать, насколько сопротивление объекта будет меняться в зависимости от температуры.
Температура
Температура измеряет, насколько горячим или холодным является тело по отношению к стандартному объекту.
 Для обсуждения изменений температуры важны два основных понятия: тепловой контакт и тепловое равновесие. Два объекта находятся в тепловом контакте , если они могут влиять на температуру друг друга. Тепловое равновесие существует, когда два объекта в тепловом контакте больше не влияют на температуру друг друга. Например, если на кухонную столешницу поставить пакет молока из холодильника, два объекта находятся в тепловом контакте. Через несколько часов их температуры становятся одинаковыми, и тогда они находятся в тепловом равновесии.
Для обсуждения изменений температуры важны два основных понятия: тепловой контакт и тепловое равновесие. Два объекта находятся в тепловом контакте , если они могут влиять на температуру друг друга. Тепловое равновесие существует, когда два объекта в тепловом контакте больше не влияют на температуру друг друга. Например, если на кухонную столешницу поставить пакет молока из холодильника, два объекта находятся в тепловом контакте. Через несколько часов их температуры становятся одинаковыми, и тогда они находятся в тепловом равновесии.Осязание дает некоторую информацию о температуре объекта, но это ненадежно. Например, металлическая полка в холодильнике кажется холоднее, чем продукты, лежащие на полке, даже если они находятся в тепловом равновесии. Металл кажется более холодным, потому что металл более эффективно отводит тепло от вашей руки.
Термометры — это приборы, которые определяют и измеряют температуру системы.
 Обычный термометр состоит из объема ртути, который при нагревании расширяется в капиллярную трубку.Когда термометр находится в тепловом равновесии с объектом, температуру можно считать по шкале термометра.
Обычный термометр состоит из объема ртути, который при нагревании расширяется в капиллярную трубку.Когда термометр находится в тепловом равновесии с объектом, температуру можно считать по шкале термометра.Обычно используются три температурные шкалы: Цельсия, Фаренгейта и Кельвина (также называемые абсолютными ). Сравнение термометров Цельсия и Фаренгейта показано на рисунке 1.
Рисунок 1
Сравнение термометров Цельсия и Фаренгейта.
По шкале Цельсия точка льда равна 0, а точка пара равна 100.Интервал между этими температурами делится на 100 равных частей, называемых градусов . Как показано на рисунке, по шкале Фаренгейта точка льда составляет 32 градуса, а точка пара — 212 градусов. Интервал между этими температурами делится на 180 равных частей. Следующие уравнения связывают температуру в градусах Цельсия (C) и Фаренгейта (F):
Шкала Кельвина (К) имеет градусы того же размера, что и шкала Цельсия, но ноль сдвинут к тройной точке воды .
 Тройная точка воды существует, когда вода в закрытом сосуде находится в равновесии во всех трех состояниях: лед, вода и пар. Эта точка определяется как 273,16 Кельвина и равна 0,01 градуса Цельсия; поэтому, чтобы преобразовать градусы Цельсия в Кельвины, просто прибавьте 273,15. Обратите внимание, что, поскольку градусы одинаковы в двух шкалах, разница температур одинакова как в градусах Цельсия, так и в Кельвинах.
Тройная точка воды существует, когда вода в закрытом сосуде находится в равновесии во всех трех состояниях: лед, вода и пар. Эта точка определяется как 273,16 Кельвина и равна 0,01 градуса Цельсия; поэтому, чтобы преобразовать градусы Цельсия в Кельвины, просто прибавьте 273,15. Обратите внимание, что, поскольку градусы одинаковы в двух шкалах, разница температур одинакова как в градусах Цельсия, так и в Кельвинах.Ртутный термометр использует тепловое расширение: явление, при котором большинство веществ увеличиваются в объеме при повышении их температуры.Длина стержня при нагревании изменится (Δ L ) в соответствии с Δ L = α L 0 Δ T , где L 0 — исходная длина и (дельта T ) изменение температуры. Константа α (греческая буква альфа) – это средний коэффициент линейного расширения. Это значение находится в таблицах коэффициентов для различных материалов и измеряется в единицах (градусы Цельсия) -1 .

С изменением температуры изменяется не только длина, но также площадь и объем.Таким образом, Δ A = γ A 0 Δ T , где Δ A — изменение исходной площади A 0 . Греческая буква гамма (γ) — это средний коэффициент расширения площади, равный 2α. Для изменения объема Δ В = β В 0 , Δ T , где Δ В — изменение первоначального объема В 0 . Греческая буква бета (β) — это средний коэффициент объемного расширения, который равен 3α.
Пример 1: В качестве примера применения этих уравнений рассмотрим нагрев стальной шайбы. Какова будет площадь отверстия под шайбу при исходной площади поперечного сечения 10 мм 2 , если сталь имеет α = 1,1 × 10 −5 на °С и нагрета от 20 до 70 градусов С?
Решение: Отверстие будет расширяться так же, как кусок материала с такими же размерами. Уравнение увеличения площади приводит к следующему:
Таким образом, новая площадь отверстия будет равна 10.
 011 мм 2 .
011 мм 2 .Вода является исключением из обычного увеличения объема при повышении температуры. Обратите внимание на рисунок 2 , что максимальная плотность воды достигается при температуре 4 градуса Цельсия.
Рисунок 2
Плотность воды изменяется при изменении температуры.
Эта характеристика воды объясняет, почему озеро замерзает на поверхности. Чтобы убедиться в этом, представьте, что воздух охлаждается с 10 градусов по Цельсию до 5 градусов по Цельсию. Поверхностная вода, находящаяся в равновесии с воздухом при этих температурах, плотнее, чем немного более теплая вода под ней; поэтому более холодная вода опускается, а более теплая вода снизу выходит на поверхность.Это происходит до тех пор, пока температура воздуха не упадет ниже 4 градусов, когда поверхностная вода менее плотная, чем более глубокая вода примерно на 4 градуса; затем перемешивание прекращается. Поскольку температура воздуха продолжает падать, поверхностные воды замерзают.

- Удельное сопротивление большинства проводящих материалов изменяется при изменении температуры.Поэтому значения удельного сопротивления всегда указываются при стандартной температуре (обычно 20° или 25° по Цельсию).

 П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.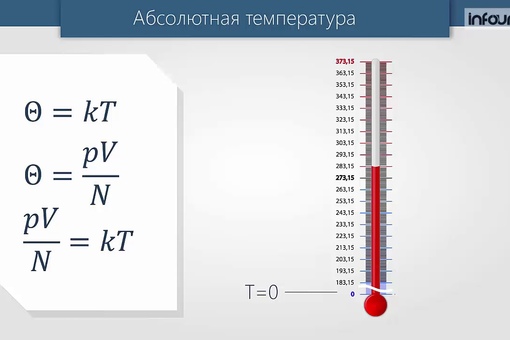

 Если объем шины не изменился, каково новое давление воздуха в шине?
Если объем шины не изменился, каково новое давление воздуха в шине? Тройная точка воды – 273,16 к. Удельное сопротивление материала, нечувствительного к температуре, – нихром . Температура солнца, определяемая пирометром . При постоянном объеме газовый термометр работает по закону Шарля.
Тройная точка воды – 273,16 к. Удельное сопротивление материала, нечувствительного к температуре, – нихром . Температура солнца, определяемая пирометром . При постоянном объеме газовый термометр работает по закону Шарля. Найдите изменение температуры тела в °C,°F, по шкале Кельвина и Ремера??
Найдите изменение температуры тела в °C,°F, по шкале Кельвина и Ремера?? Если вы подозревали, что это означает, что удельное сопротивление материала может меняться в зависимости от температуры, вы были правы!
Если вы подозревали, что это означает, что удельное сопротивление материала может меняться в зависимости от температуры, вы были правы! Для некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, а это означает, что сопротивление почти не меняется при изменении температуры (хорошее свойство, если вы хотите построить прецизионный резистор из металлической проволоки!).В следующей таблице приведены температурные коэффициенты сопротивления для нескольких распространенных металлов, как чистых, так и легированных:
Для некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, а это означает, что сопротивление почти не меняется при изменении температуры (хорошее свойство, если вы хотите построить прецизионный резистор из металлической проволоки!).В следующей таблице приведены температурные коэффициенты сопротивления для нескольких распространенных металлов, как чистых, так и легированных: 003847
003847 Предполагая использование медной проволоки (α = 0,004041), получаем:
Предполагая использование медной проволоки (α = 0,004041), получаем: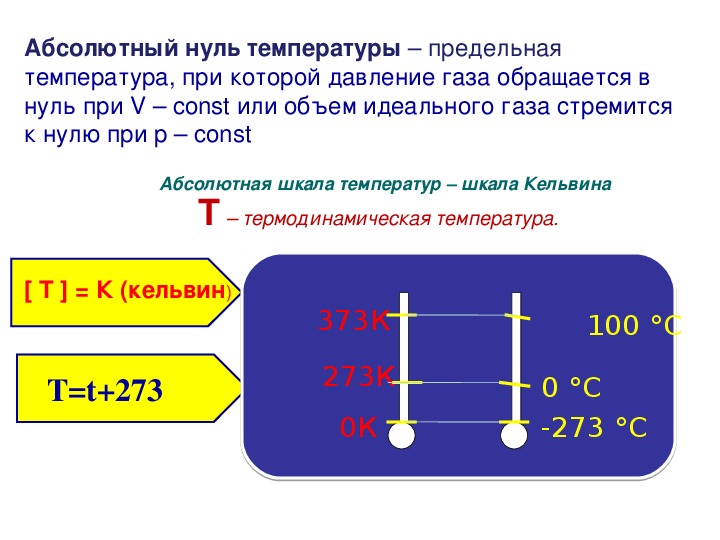
 Термодинамика сделок
только с крупномасштабной реакцией системы, которую мы можем наблюдать
и измерить в опытах.
В аэродинамике термодинамика
газа, очевидно, играет важную роль в анализе
двигательные системы.
То
первый закон
термодинамики определяет соотношение между различными формами
кинетическая и потенциальная энергия, присутствующая в системе,
Работа
какая система
может выполнять и передачу
нагревать.Закон гласит, что энергия сохраняется во всех термодинамических процессах.
Термодинамика сделок
только с крупномасштабной реакцией системы, которую мы можем наблюдать
и измерить в опытах.
В аэродинамике термодинамика
газа, очевидно, играет важную роль в анализе
двигательные системы.
То
первый закон
термодинамики определяет соотношение между различными формами
кинетическая и потенциальная энергия, присутствующая в системе,
Работа
какая система
может выполнять и передачу
нагревать.Закон гласит, что энергия сохраняется во всех термодинамических процессах. Холод
объект станет холоднее, а горячий объект станет горячее, но энергия будет
быть сохранены. Очевидно, что в природе мы не встречаем такой системы, и
объяснить это и подобные наблюдения, термодинамики предложили второй
закон термодинамики. Клазиус, Кельвин и Карно предложили различные формы
второго закона, чтобы описать конкретную физическую проблему, которую каждый
изучение. Описание второго закона, представленное на этом слайде, было взято
из учебника Холлидея и Резника «Физика».Он начинается с определения
новой переменной состояния, называемой
энтропия.
Энтропия имеет множество
физические интерпретации, включая статистический беспорядок системы,
но для наших целей давайте будем считать энтропию просто еще одним свойством
системы, как
энтальпия
или
температура.
Холод
объект станет холоднее, а горячий объект станет горячее, но энергия будет
быть сохранены. Очевидно, что в природе мы не встречаем такой системы, и
объяснить это и подобные наблюдения, термодинамики предложили второй
закон термодинамики. Клазиус, Кельвин и Карно предложили различные формы
второго закона, чтобы описать конкретную физическую проблему, которую каждый
изучение. Описание второго закона, представленное на этом слайде, было взято
из учебника Холлидея и Резника «Физика».Он начинается с определения
новой переменной состояния, называемой
энтропия.
Энтропия имеет множество
физические интерпретации, включая статистический беспорядок системы,
но для наших целей давайте будем считать энтропию просто еще одним свойством
системы, как
энтальпия
или
температура. Если обозначить начальное и конечное состояния системы через «i» и «f»,
тогда:
Если обозначить начальное и конечное состояния системы через «i» и «f»,
тогда: Если мы тогда
разделять объекты, которые они
не возвращаются естественным образом к своим первоначальным (другим) температурам. То
процесс приведения их к одинаковой температуре необратим.
Если мы тогда
разделять объекты, которые они
не возвращаются естественным образом к своим первоначальным (другим) температурам. То
процесс приведения их к одинаковой температуре необратим.

 [5] [6] Действительно, геотермальная активность вносит незначительный дополнительный вклад, но в дальнейшем этим пренебрегают из-за его относительной слабости по сравнению с солнечным излучением.
[5] [6] Действительно, геотермальная активность вносит незначительный дополнительный вклад, но в дальнейшем этим пренебрегают из-за его относительной слабости по сравнению с солнечным излучением. 2 .2 \метка{pOut}
\end{выравнивание}
2 .2 \метка{pOut}
\end{выравнивание} Однако это не относится к земной поверхности, так как есть еще атмосфера, которая значительно влияет на радиационный баланс. В следующей статье будет рассмотрена более сложная модель воздействия атмосферы.
Однако это не относится к земной поверхности, так как есть еще атмосфера, которая значительно влияет на радиационный баланс. В следующей статье будет рассмотрена более сложная модель воздействия атмосферы.

 Для обсуждения изменений температуры важны два основных понятия: тепловой контакт и тепловое равновесие. Два объекта находятся в тепловом контакте , если они могут влиять на температуру друг друга. Тепловое равновесие существует, когда два объекта в тепловом контакте больше не влияют на температуру друг друга. Например, если на кухонную столешницу поставить пакет молока из холодильника, два объекта находятся в тепловом контакте. Через несколько часов их температуры становятся одинаковыми, и тогда они находятся в тепловом равновесии.
Для обсуждения изменений температуры важны два основных понятия: тепловой контакт и тепловое равновесие. Два объекта находятся в тепловом контакте , если они могут влиять на температуру друг друга. Тепловое равновесие существует, когда два объекта в тепловом контакте больше не влияют на температуру друг друга. Например, если на кухонную столешницу поставить пакет молока из холодильника, два объекта находятся в тепловом контакте. Через несколько часов их температуры становятся одинаковыми, и тогда они находятся в тепловом равновесии. Обычный термометр состоит из объема ртути, который при нагревании расширяется в капиллярную трубку.Когда термометр находится в тепловом равновесии с объектом, температуру можно считать по шкале термометра.
Обычный термометр состоит из объема ртути, который при нагревании расширяется в капиллярную трубку.Когда термометр находится в тепловом равновесии с объектом, температуру можно считать по шкале термометра. Тройная точка воды существует, когда вода в закрытом сосуде находится в равновесии во всех трех состояниях: лед, вода и пар. Эта точка определяется как 273,16 Кельвина и равна 0,01 градуса Цельсия; поэтому, чтобы преобразовать градусы Цельсия в Кельвины, просто прибавьте 273,15. Обратите внимание, что, поскольку градусы одинаковы в двух шкалах, разница температур одинакова как в градусах Цельсия, так и в Кельвинах.
Тройная точка воды существует, когда вода в закрытом сосуде находится в равновесии во всех трех состояниях: лед, вода и пар. Эта точка определяется как 273,16 Кельвина и равна 0,01 градуса Цельсия; поэтому, чтобы преобразовать градусы Цельсия в Кельвины, просто прибавьте 273,15. Обратите внимание, что, поскольку градусы одинаковы в двух шкалах, разница температур одинакова как в градусах Цельсия, так и в Кельвинах.
 011 мм 2 .
011 мм 2 .