Физика как найти работу формула: Механическая работа — урок. Физика, 9 класс.

Механическая работа. Мощность. | Объединение учителей Санкт-Петербурга

Основные ссылки

CSS adjustments for Marinelli theme

Объединение учителей Санкт-Петербурга

Форма поиска

Поиск

Вы здесь

Главная » Механическая работа. Мощность.

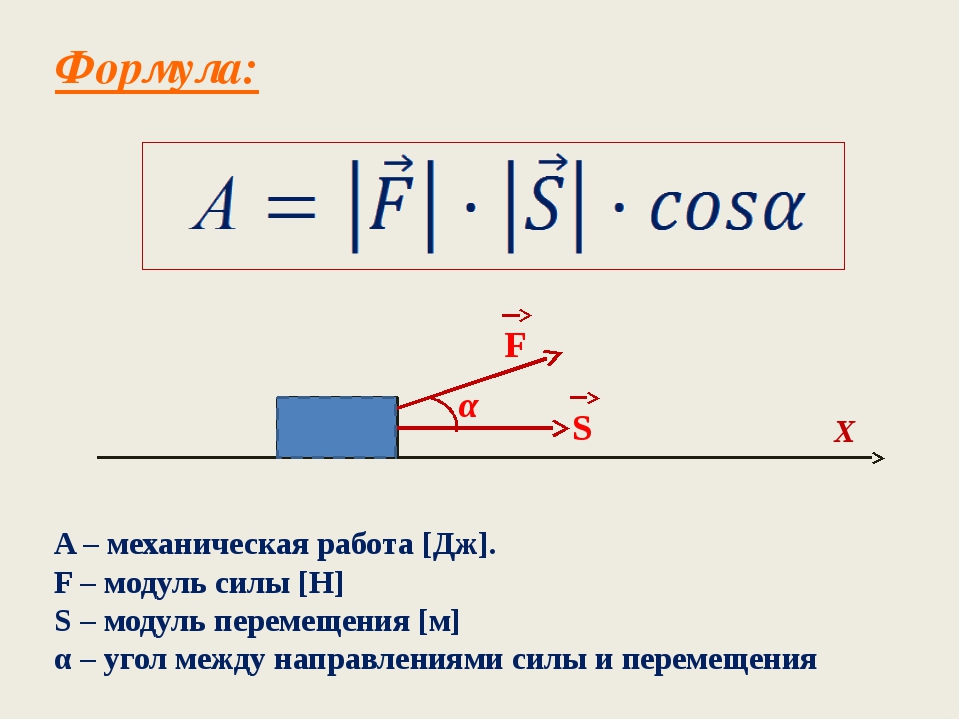
Механическая работа (А)
Физическая величина, характеризующая результат действия силы и численно равная скалярному произведению вектора силы и вектора перемещения, совершенного под действием этой силы.
A=Fscosα	A=Fscosα
Работа не совершается, если: 1.Сила действует, а тело не перемещается. Например: мы действуем с силой на шкаф, но не можем сдвинуть.
2.Тело перемещается, а сила равна нулю или все силы скомпенсированы. Например: при движении по инерции работа не совершается.
3. Угол между векторами силы и перемещения (мгновенной скорости) равен 900(cosα=0). Например: центростремительная сила работу не совершает.
Если вектора силы и перемещения сонаправлены (α=00, cos0=1), то  A=Fs
Если вектора силы и перемещения направлены противоположно (α=1800, cos1800 = -1), то A= -Fs  (например, работа силы сопротивления, трения).
Если угол между векторами силы и перемещения 00 < α < 1800, то работа положительна.
Если угол между векторами силы и перемещения 00 < α < 1800, то работа положительна.
Если на тело действует несколько сил, то полная работа (работа всех сил) равна работе результирующей силы.
Если тело движется не по прямой, то можно разбить все движение на бесконечно малые участки, которые можно считать прямолинейными, и просуммировать работы.
Графическое представление работы.
Рассмотрим движение тела под действием постоянной силы вдоль прямой Ох. График зависимости силы от координаты изображен на рисунке. Площадь заштрихованного прямоугольника на рисунке численно равна работе силы Fпри перемещении из точки х1 в точку х2.
Если сила меняется с расстоянием (координатой), то необходимо разбить все движение на такие малые участки, на которых силу можно считать неизменной, сосчитать работы на каждом элементарном участке пути, и сложить все элементарные работы. Таким образом: работа численно равна площади фигуры под графиком зависимости силы от координаты  F(x).
Единицы работы.
В международной системе единиц (СИ): [А] = Дж = Н • м Механическая работа равна одному джоулю, если под действием силы в 1 Н оно перемещается на 1 м в направлении действия этой силы.	1Дж = 1Н • 1м
Мощность
Мощность – физическая величина, характеризующая скорость совершения работы и численно равная отношению работы к интервалу времени, за который эта работа совершена . Мощность показывает, какая  работа совершается за единицу времени.
Единицы мощности В международной системе единиц (СИ):   Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.	1 л.с. (лошадиная сила) ≈ 735 Вт

Теги: 

конспект

Физика Работа силы тяжести. Работа силы упругости. Потенциальная энергия

Материалы к уроку

Конспект урока

Вычислим работу силы, используя зависимость сил взаимодействия между телами от расстояния между ними. Это позволит узнать зависимость работы силы не от скорости тела, а от расстояний между взаимодействующими телами.
Вычислим сначала работу силы тяжести при падении тела, например, камня, вертикально вниз. Найдем модуль перемещения тела: это разность между высотой, на которой находится камень над поверхностью Земли, в начальный момент времени и высотой в конечный момент времени. Сила тяжести направлена вертикально вниз, так же, как и вектор перемещения камня. Тогда по определению работа равна произведению модуля вектора силы тяжести на модуль вектора перемещения и косинус угла ноль градусов. Подставим в формулу работы выражение, полученное  выражение для модуля вектора перемещения, и используем формулу силы тяжести. Произведем математические преобразования и  получим, что работа силы тяжести равна разности произведения массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли в начальной точке и произведения массы на ускорение свободного падения и на высоту в конечной точке.

Рассмотрим теперь тело, брошенное вертикально вверх. Начальное положение тела на высоте h2, над поверхностью Земли, конечное –   на высоте h3. Векторы силы тяжести и перемещения направлены в противоположные стороны, а модуль перемещения равен разности конечной высоты и начальной. Тогда работа силы тяжести будет равна произведению модуля вектора силы тяжести на модуль вектора перемещения и на косинус угла 180 градусов. Подставляем вместо модуля вектора силы тяжести произведение массы тела на ускорение свободного падения и модуля вектора перемещения полученное для него выражение, косинус угла 180 градусов равный 1. Получаем, что работа силы тяжести и в этом случае равна разности произведения массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли в начальной точке и произведения массы на ускорение свободного падения и на высоту в конечной точке.
Если же тело перемещается под углом  к направлению силы тяжести, то работа силы тяжести равна произведению массы тела на ускорение свободного падения на модуль вектора перемещения ВС и на косинус угла между направлением перемещения и направлением силы тяжести.  
Из прямоугольного треугольника BCD видно, что произведение модуля вектора перемещения на косинус угла α разности между начальной и конечной высотой.
В этом случае так же работа силы тяжести равна разности произведения массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли в начальной точке и произведения массы на ускорение свободного падения и на высоту в конечной точке.
Во всех трех рассмотренных случаях – одинаковый результат и одна и та же формула работы силы тяжести. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела в начальный и конечный моменты времени. Эти положения определяются начальной и конечной высотами тела над поверхностью Земли.
Более того, работа силы тяжести при перемещении из одного положения в другое не зависит от формы траектории, по которой движется тело. 
Работа при перемещении вдоль кривой ВС равна разности произведений массы тела на ускорение свободного падения и на высоту, на которой находится тело в начальный и конечный моменты времени.

При движении тела по замкнутой траектории работа силы тяжести равна нулю. Например, тело движется по замкнутому контуру ВСDМВ. На участках ВС и DМ сила тяжести совершает работы, равные по абсолютной величине, но противоположные по знаку. Сумма этих работ равна нулю. Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.
Силы, обладающие такими свойствами, называют консервативными.
Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, возьмем пружину, один конец закрепим неподвижно, а к другому концу прикрепим шар. Если пружину растянуть, то она будет действовать на шар с силой упругости, направленной к положению равновесия шара, в котором пружина не деформирована. Вычислим работу силы упругости при перемещении шара. Она равна разности полупроизведения жесткости пружины на квадрат начального удлинения и полупроизведения жесткости пружины на квадрат конечного удлинения пружины.
Работа сил упругости зависит лишь от деформаций пружины в начальный момен времени и в конечный момент времени в начальном и конечном состояниях.
Работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.
Работу консервативных сил можно представить в виде разности двух значений некоторой величины, зависящей от взаимного расположения тел.
Для силы тяжести начальная высота  и конечная высота определяют взаимное расположение тела и Земли. При вычислении работы силы упругости начальное и  конечное  удлинения   – взаимное расположение витков деформированной пружины или значения деформаций другого упругого тела.
Величину, равную произведению массы тела  на ускорение свободного падения  и на высоту  тела над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.
Величину, равную половине произведения коэффициента упругости  тела на квадрат деформации, называют  потенциальной энергией упруго деформированного тела.
В обоих случаях потенциальная энергия определяется расположением тел системы или частей одного тела относительно друг друга.
Понятие потенциальной энергии дает возможность выразить работу любых консервативных сил через изменение потенциальной энергии. Работа консервативной силы равна разности потенциальной энергии в начальный момент времени и потенциальной энергии в конечный момент времени. Или   изменение потенциальной энергии тела равно работе консервативной силы, взятой с обратным знаком.
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальная энергия – это величина, которая зависит от положения взаимодействующих тел. Изменение потенциальной энергии при переходе из одного состояния в другое равно работе внутренних консервативных сил системы, взятой с противоположным знаком. Потенциальной энергией обладают любые взаимодействующие тела.
Знак «-» в формуле не означает, что работа консервативных сил всегда отрицательна. Он означает лишь то, что изменение потенциальной энергии и работа сил в системе всегда имеют противоположные знаки.
Например, при падении камня на Землю его потенциальная энергия убывает, но сила тяжести совершает положительную работу. Следовательно, работа силы тяжести и изменение энергии  имеют противоположные знаки в соответствии с формулой.
Работа консервативных сил взаимодействия определяет не саму потенциальную энергию, а ее изменение.
Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому можно произвольно выбрать состояние системы, в котором ее потенциальная энергия  считается равной нулю. Этому состоянию соответствует нулевой уровень потенциальной энергии. Ни одно явление в природе или  технике  не определяется значением самой потенциальной энергии. Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел.
Выбор нулевого уровня производится по-разному и диктуется исключительно соображениями удобства.
Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальной энергией. Тогда потенциальная энергия всегда положительна или равна нулю.
У пружины потенциальная энергия минимальна в отсутствие деформации, а у системы «камень – Земля» нулевой уровень энергии будет тогда, когда камень лежит на поверхности Земли. К данным выражениям можно добавить любую постоянную величину, и это ничего не изменит.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Работа, мощность и энергия в физике

Содержание:

Работа, мощность и энергия:

Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?

В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.

Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.

Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.

Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.

Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,

Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.

1 джоуль = 1 ньютон • 1 метр.

Для измерения большой работы используют кратные джоулю единицы:

В случае малой работы применяются дольные единицы:

Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.

Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.

Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги  а силы сопротивления Сумма же их равна 0, т. е.

Главные выводы:

1. Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
2. Силы, ускоряющие движение тела; совершают положительную работу.
3. Силы, замедляющие движение тела, совершают отрицательную работу.
4. Единица работы в СИ — 1 джоуль (1 Дж).

Пример решения задачи:

Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа Чему равна работа равнодействующей сил, приложенных к плите? Коэффициент  примите равным 

Дано:

Решение:

При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту: 

Работа силы упругости  Высота подъема  – число этажей. Тогда 

Отсюда  

Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней,  и работа 

Ответ: плита поднята на 6-й этаж; работа равнодействующей сил 

Полезная и совершённая работа

Оценивая работу машины, механизма и др. , говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?

Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например,  = 2,0 кг и картофель массой m = 10,0 кг на высоту h = 1,5 м. Какая работа здесь является полезной?

Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: А вот работа но подъему самого ведра не является полезной: Вся же совершенная (полная работа) равна:

Какую долю составляет полезная работа от совершенной?

Обозначим отношение  буквой  (эта) и назовем коэффициентом полезного действия (КПД). Тогда

КПД, как правило, выражают в процентах. 

Таким образом, КПД (эффективность работы) в данном случае равен 83 %.

Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь Цель детей — увеличить скорость движения санок. Но на санки действует еще сила трения скольжения  Она тормозит движение санок. Значит, работа детей по преодолению силы трения не является полезной:

Полезной же работой была

Тогда доля полезной работы (КПД)

Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.

А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?

Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.

Главные выводы:

1. Совершенная (т. е. полная) механическая работа всегда больше полезной.
2. КПД показывает, какую долю составляет полезная работа от всей совершенной.
3. Чем больше полезная работа, тем выше КПД.
4. КПД всегда меньше 100 %.

Пример решения задачи:

При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД  = 90 % совершена работа  = 40 кДж. Сколько мешков картофеля массой  = 40 кг каждый было поднято из хранилища? Примите

Дано:

Решение:

Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:

Полезная работа – это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:

Масса  где N – число мешков картофеля.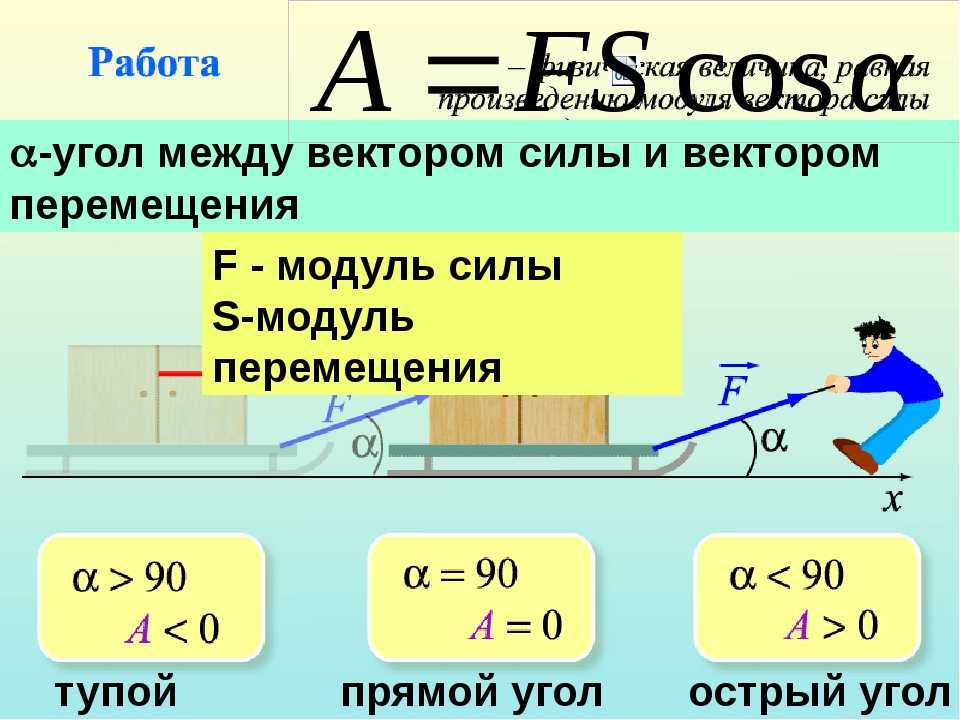 Тогда  откуда

Ответ: N = 25 мешков.

Мощность и единицы мощности

Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?

Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.

Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.

За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:

Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт): 

В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа из чего следует, что единицей работы может быть только киловатт-час (кВт • ч), но не киловатт (кВт). Выразим мощность через другие единицы — силу и скорость. Мощность но работа путь Тогда

Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.

Главные выводы

1. Мощность — физическая величина, характеризующая быстроту совершения работы.
2. Единицей мощности в СИ является 1 ватт.
3. Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.

Для любознательных

В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.

Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.

В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.

Пример решения задачи:

На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент

Дано:

Решение:

При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.

Тогда 

Ответ: P = 0, 20 кВт.

Кинетическая энергия

Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?

Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.

Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или ) и измеряется в СИ в тех же единицах, что и работа, т. е. в джоулях.

Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.

Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?

Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:

Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.

Главные выводы:

1. Кинетическая энергия выражает способность движущихся тел совершать работу.
2. Кинетическая энергия, как и работа, измеряется в джоулях.
3. Кинетическая энергия тела зависит от его массы и скорости.
4. Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).

Пример решения задачи:

Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от до  на пути s = 25 м. Определите силу тяги двигателя автомобиля и работу, которую совершила эта сила. Сопротивление движению не учитывать.

Дано:

Решение:

Чтобы увеличить кинетическую энергию от  до  сила тяги должна была совершить работу:

Но работа  Отсюда 

Ответ: 

Потенциальная энергия

При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?

Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны  и не обладают кинетической энергией. Но и у гири, и у пружины есть возможность совершить работу. Для этого достаточно в обоих случаях пережечь нить. В физике говорят, что тела (поднятая гиря, взаимодействующая с Землей, и сжатая пружина) обладают потенциальной энергией (от лат. potentia — скрытая способность). Потенциальную энергию в СИ измеряют в тех же единицах, что и работу, — в джоулях.

Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или ).

Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).

Главные выводы:

1. Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
2. Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
3. Потенциальная энергия изменяется только при совершении работы.

Расчет потенциальной энергии

Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой Данная формула справедлива и для планеты Земля, мчащейся со скоростью по орбите вокруг Солнца, и для невидимого нашему глазу атома. Существует ли единая формула для расчета потенциальной энергии?

Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.

В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести может совершить работу:

Это и есть потенциальная энергия поднятого тела:

Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте  от пола, равна:

Относительно потолка  она равна:

Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).

Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.

Главные выводы:

1. Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
2. Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
3. Потенциальная энергия деформированного тела зависит от величины деформации.

Пример решения задачи:

Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте  = 0,80 м от пола. Определите потенциальную энергию кубика относительно поверхностей: а) пола; б) стола. Какую работу нужно совершить, чтобы поднять кубик с пола на стол? Коэффициент 

Дано:

Решение:

Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):

Масса кубика  объем  тогда:

Потенциальная энергия кубика относительно поверхности стола:

Работа по подъему кубика на высоту  равна изменению его потенциальной энергии. Получаем:

Ответ: 

Закон сохранения механической энергии

Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?

Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: ). В верхней точке скорость и кинетическая энергия шарика равны нулю, а потенциальная максимальна. Значит, в рассмотренном примере происходит превращение энергии из одного вида (кинетической) в другой (потенциальную). При возвращении шарика обратно снова будет идти превращение энергии: с уменьшением высоты (и потенциальной энергии) увеличивается скорость движения шарика (и кинетическая энергия).

Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.

А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте  (рис. 243)? При подъеме шарика на высоту  его кинетическая энергия уменьшилась, но при этом появилась потенциальная энергия. А чему равна их сумма, т. е. полная механическая энергия? Данный и подобные опыты и расчеты показывают, что если сил сопротивления нет, то полная механическая энергия тела (системы тел), равная сумме кинетической и потенциальной энергий сохраняется. Данное утверждение о постоянстве механической энергии в физике называют законом сохранения механической энергии.

Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.

В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.

Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.

Главные выводы:

1. Кинетическая и потенциальная энергии взаимо-превращаемы.
2. При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
3. Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.

• Заказать решение задач по физике

Пример решения задачи:

Камень бросили вертикально вверх со скоростью На какой высоте от точки бросания кинетическая энергия камня будет в 4 раза меньше его потенциальной энергии? Сопротивлением движению камня пренебречь. Коэффициент

Дано:

Решение:

За нулевой уровень потенциальной энергии примем уровень O – O, проходящий через точку бросания камня (рис. 247). Значит, 

Полная механическая энергия камня в точке бросания 1:

 

Полная механическая энергия камня в точке 2:

По условию Значит,

Ответ: 

Энергия и работа

Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.

Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой .

Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е. 

Здесь: – угол между силой  и перемещением s (рисунок 3.1). 
Если учитывать, что , то уравнение (3. 1) примет вид:

Здесь – проекция силы в направлении смещения.
Основываясь на выражении (3.2), можно сделать следующий вывод:
если , то – работа силы положительна, направление силы и смещение совпадают;
если , то – работа силы отрицательная, направления силы и смещения противоположны;
если , то – работа, выполненная силой, равна нулю, направление силы будет перпендикулярным к направлению смещения.
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:

тогда полная работа равна работе, выполненной равнодействующей сил.

или

Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):

В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная . При перемещении тела из точки на высоте от поверхности Земли в точку на высоте от поверхности Земли, смещение тела равно: (рис. 3.2).

Здесь выполненная силой тяжести работа выражается следующей формулой:

Здесь: – вес тела, – его масса, – ускорение свободного падения, – расстояние между уровнями и  по вертикали.
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы  траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.

При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.

Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой , двигающегося со скоростью  относительно Земли на высоте от поверхности Земли:

Полная механическая энергия системы остается неизменной с течением времени:
 

Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.

Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии. 
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.

Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой. 

В закрытых системах полная энергия сохраняется.

Например, потенциальная энергия тела, падающего с высоты , зависит от его веса и абсолютно не зависит от времени проведения экспериментов.
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.

Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой . 
Если полезную работу обозначить , полную работу , тогда формулу КПД можно записать в виде:

КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.

Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх.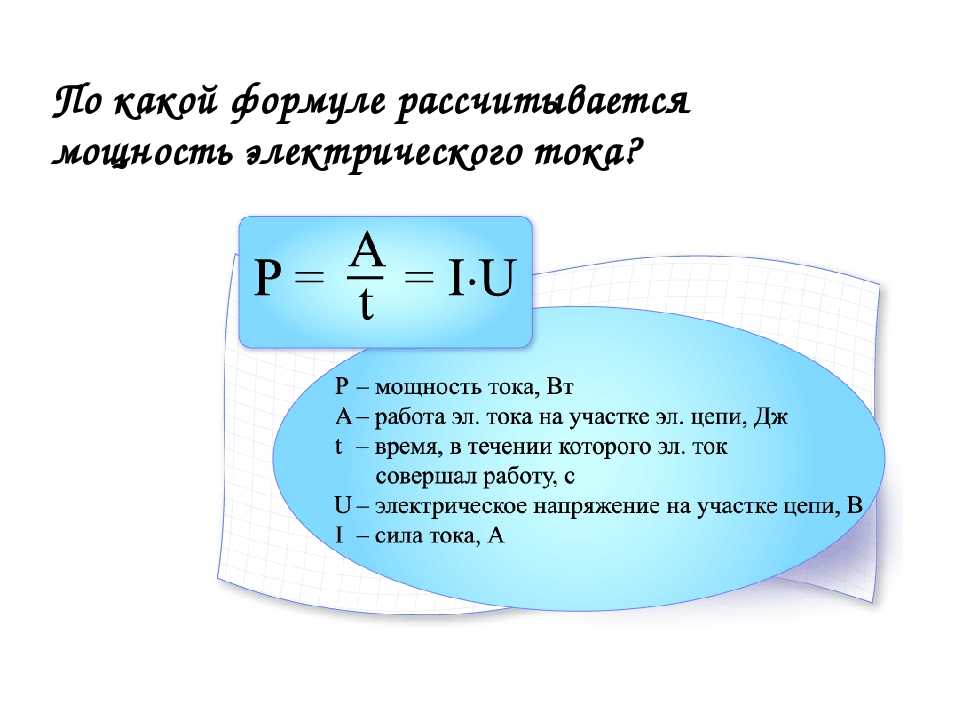 По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.

Рассмотрим груз с весом на наклонной плоскости длиной , высотой  (рис. 3.3). Здесь на тело действует сила трения , параллельная наклонной поверхности тянущая вверх сила , перпендикулярно направленная к наклонной плоскости и противоположно направленная перпендикулярно к поверхности сила (реактивная сила поверхности).
Если не учитывать силу трения, получим уравнение:

Однако с учетом силы трения,

Тогда пишется в следующем виде:

Коэффициент полезного действия:

Сила притяжения, действующая на груз, равна:
 

Работа

Работа

Работа, совершаемая постоянной силой

Предположим, вы поднимаете предмет массой 20 кг с земли на высоту. 1,5 м. Предположим, что вы прилагаете постоянную силу в восходящем направлении. направление и что вы перемещаете объект вверх с постоянной скоростью. результирующая сила, действующая на объект, равна нулю. Сила, которую вы прилагаете, равна по величине и противоположно по направлению силе тяжести. Пока вы поднимаетесь объект, над которым вы работаете.

Работа Вт, совершаемая над объектом постоянной силой, определяется как W = Ф · д . Он равен величине силы, умноженной на расстояние до объекта. движется в направлении действия силы.
В примере выше F = мг = (20 кг) (9,8 м/с ² ) = 196 Н, W = (196 Н)(1,5 м) = 294 Нм.

Работа — это скаляр, число с единицами измерения. Единица работы СИ Нм = Джоуль (Дж).

---

Работа ” скалярное произведение ” или “ скалярное произведение ” силы и вектора смещения. Скалярное произведение двух векторов A и B — скалярная величина (число с единицами), равная произведение величин двух векторов и косинуса наименьшего угол между ними.

А · В = ABcosθ.

В терминах декартовых компонент векторов А и Б скалярное произведение записывается как

А · В = А _х В _х + А _у В _у + А _z Б _z .

Работа, совершаемая силой, может быть положительной или отрицательной. Если составляющая силы в направление перемещения положительное, то работа положительна, а если составляющая силы в направлении перемещения отрицательна, то произведение отрицательное. В одном измерении скалярное произведение положительно, если два вектора параллельны друг другу, и отрицательно, если два вектора антипараллельны друг к другу, т. е. если они направлены в противоположные стороны.

Пример:

Предположим, вы забыли установить парковочный тормоз, и ваша машина начала катиться. вниз по холму. Вы тщетно пытаетесь остановить его, дергая изо всех сил. бампер, но машина продолжает двигаться вперед. Вы прилагаете силу к автомобиль против направления движения. Расстояние, пройденное в направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но автомобиль тянет вас по ходу движения с силой, равной величины (третий закон Ньютона). Машина производит на вас положительное впечатление.

---

Схема свободного тела объекта, поднимаемого с постоянная скорость на расстоянии d показано справа.
Суммарная сила, действующая на объект, равна нулю, F _a + F _г = 0.
Вектор смещения направлен вверх.
Работа, совершенная приложенной силой F _a , W = F _a · d = F _a д = мгд , положительный.
Работа силы тяжести F _g , W = F _г ·d = -F _г d = -mgd , отрицательно.
Чистая работа всех сил, действующих на объект, W _net = F _net ·d равна нулю.

Проблема:

Для А = 3 i + дж – к , Б = – я + 2 я + 5 к , и С = 2 j – 3 k , найти С ·( А – В ).

Решение:

• Обоснование:
  Оцените скалярное произведение двух векторов.
• Детали расчета:
  A = 3 i + j – k . B = – i + 2 j + 5 k . А – В = 4 я – к – 6 к . С = 2 j – 3 k . С ·( А – В ) = -2 + 18 = 16.

Проблема:

Объясните, почему работа силы трения скольжения отрицательна. когда объект испытывает смещение на шероховатой поверхности?

Решение:

• Обоснование:
  Сила трения скольжения всегда направлена ​​в сторону, противоположную скорости v = d r /dt. Поэтому он указывает в направлении, противоположном направлению рабочий объем d r . dW = F _f · d r = -F _f др.

Проблема:

При движении частицы по окружности на нее действует сила, направленная центр вращения. Почему эта сила не действует на частицу?

Решение:

• Обоснование:
  Так как в любой точке окружности центростремительная сила перпендикулярна скорости v и, следовательно, к смещению d r скалярное произведение dW = F· d r это ноль.

Проблема:

Во время стрижки газона мальчик толкает газонокосилку на расстояние 350 м. траву с силой 90 Н, направленной по горизонтали. Какую работу выполнил мальчик?

Решение:

• Обоснование:
  Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = Fdcosθ.
  Здесь F и d указывают в одном направлении, θ = 0, cosθ = 1,
• Детали расчета:
  Вт = F · d = 90 Н * 350 м = 31500 Дж.

Проблема:

Покупатель в супермаркете толкает тележку с силой 35 Н. направлена ​​под углом 25 ^o вниз от горизонтали. Найдите работу, выполненную покупателем, когда он проходит по проходу длиной 50 м. длина.

Решение:

• Обоснование:
  Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = F _x ∆x _{+ F y ∆y + F z ∆z.
  Тележка движется в направлении x, ∆y = ∆z = 0,
  X-компонента сила F x = Fcosθ = (35 Н)cos(25 ^o ).
  Работает только х-компонента силы, так как нет смещение тележки в направлении Y.}
• Детали расчета:
  Работа, совершаемая покупателем, равна W = F _x ∆x = (35 Н)cos(25 ^o )(50 м) = 1586 Дж.

---

Рампы

Предположим, вы хотите поднять свой мотоцикл на свой пикап. Вероятно, вы будете использовать рампу.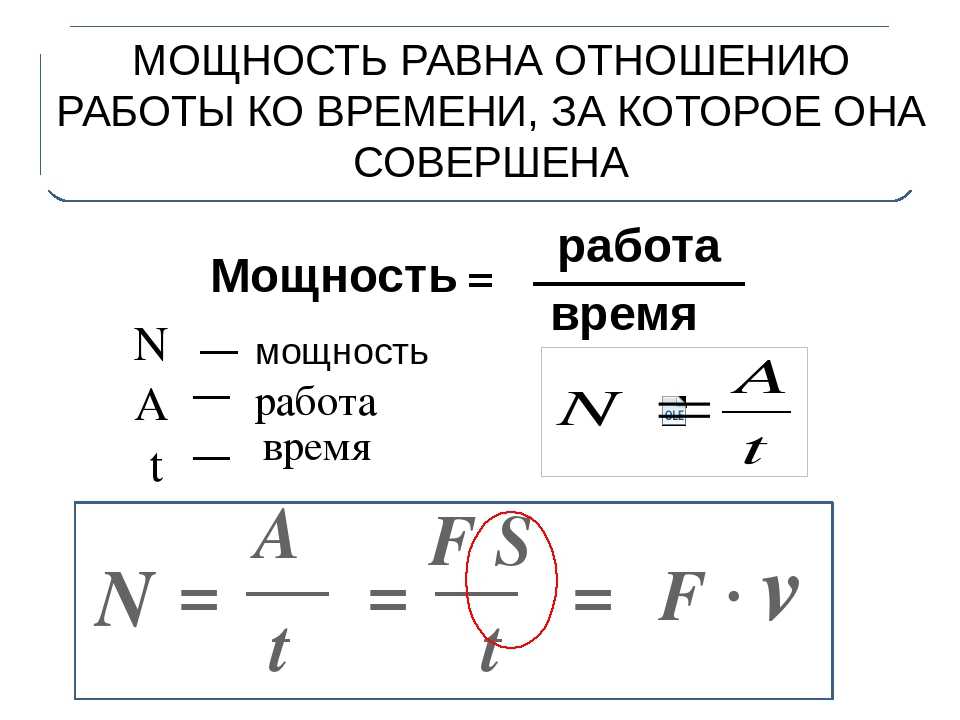 Вы выберете длинная доска. Один конец доски будет опираться на кузов грузовика, а другой конец будет лежать на земле. Вы закатите свой мотоцикл эта рампа.

Вы прикладываете силу F _a равную по величине и противоположное по направлению компоненту гравитационной силы параллельно рампе. Величина F _a равна mgsinθ. Ты переместите мотоцикл на расстояние h/sinθ в направлении действия силы. Работа, которую вы совершаете, равна W = F·d = mgh, где mg — вес вашего мотоцикл и h высота кровати. Если бы вы подняли мотоцикл прямо, вы бы приложили силу, равную его весу. через расстояние ч. Когда вы катите его по рампе, вы должны нажать на это через гораздо большее расстояние. Чтобы выполнить ту же работу, вы, следовательно, нужна гораздо меньшая сила. Рампа обеспечивает механическое преимущество .

Работа = большая сила × малое расстояние = малая сила × большое расстояние .

---

Работа переменной силы в одном измерении

Если вы не знакомы с интегралами, пожалуйста, перейдите по этой ссылке, прежде чем продолжить.

Краткий обзор определенных интегралов

Работа, совершаемая переменной силой F только с x-компонентой определяется как
W = ∫ _х ^хf F(x)dx = lim _∆x–>0 Σ _xi ^xf Ф(х)∆х.
(Символ Σ обозначает сумму. Σ _xi ^xf F∆x представляет собой сумму произведений F∆x из от начального до конечного положения с шагом ∆x.) 
Мы можем построить составляющую силы F воздействуя на объект в положении x по сравнению с положением x.
Работа силы равна площади под кривой.

График для постоянной силы, действующей от x _i до x _f показано справа.
Работа силы W = F(x _f – x _i ).

Работа, совершаемая переменной силой в трех измерениях

В трех измерениях работа, совершаемая переменной силой, равна W = ∫ _{r i} ^{r f} F ·dr = lim _{∆ r –>0} Σ _{r i} ^{r f} F ·∆ r .
Здесь d r — бесконечно малый отрезок пути от начального в конечное положение. По компонентам F и д р the integral can be written as
∫ _path ^{F ·d r = ∫ _path F _x dx + ∫ _path F _y dy + ∫ _путь F _z dz.}

---

Подъем объекта вблизи поверхности Земли

Чтобы поднять предмет массой m так, чтобы его высота увеличилась на расстояние h, вы должны приложить среднюю силу mg на расстоянии h.
Работа, которую нужно выполнить, чтобы поднять предмет, равна W = mgh.

Проблема:

Ящик на 100 Н стоит на земле и крепится к одному концу веревки. Человек на балконе тянет веревку с постоянной силой 100 Н, подъем ящика на расстояние 3 м.
а) Какой объем работы выполняет человек?
б) Какую работу совершает сила тяжести?

Решение:

• Обоснование:
  Человек подтягивается, и ящик движется вверх в направлении действия силы.
  Работа, совершаемая человеком, положительна, W = Fd = mgd = (100 Н)d.
  Сила тяжести 100 Н направлена ​​вниз, в то время как ящик движется вверх. Гравитация совершает отрицательную работу.
• Детали расчета:
  (a) Работа, выполненная человеком, равна W = (100 Н) * (3 м) = 300 Дж.
  (б) Гравитация совершает 300 Дж отрицательной работы.

Проблема:

(a) Рассчитайте работу, выполненную на кабине лифта массой 1500 кг его трос, чтобы поднять его на 40 м с постоянной скоростью, при условии, что сила трения усредняется 100 Н.
б) Какую работу совершает над кабиной лифта гравитационная сила в этом процессе?

Решение:

• Рассуждение:
  Кабина лифта весит 1500*9,8 Н = 14700 Н. Чтобы заставить кабину двигаться со постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Сила кабеля воздействующая на автомобиль должна иметь величину 14800 Н, чтобы компенсировать вес и сила трения 100 Н направлена ​​в противоположном направлении. тележка движется в направлении силы, действующей на трос, поэтому работа этой силой положительна.
• Детали расчета:
  (a) Работа, выполненная кабелем, равна W 9Кабель 0047 = (14800 Н)*(40 м) = 5,92*10 ⁵ Дж.
  (б) Работа, выполненная над кабиной лифта силой тяжести составляет Вт _г = -(14700 Н)*(40 м) = -5,88*10 ⁵ Дж.
  Эта работа отрицательна, так как точка смещения направлена ​​в сторону, противоположную действию силы.

Как рассчитать работу по его формуле?

Дата публикации: 24 декабря 2021 г. 🖩 Рабочий калькулятор

Прежде чем погрузиться в эту тему, важно, чтобы вы знали о скалярном произведении и силе.

Определение работы в науке отличается от определения, с которым знаком любой другой человек. Это означает гораздо больше, чем простая работа в офисе, учеба и домашние дела.

В этом посте мы узнаем «Что такое работа?» в науке. И мы также узнаем, как найти работу, используя ее формулу, которая является нашей основной темой.

Что такое работа?

Когда тело перемещается на некоторое расстояние под действием некоторой силы, совершается работа. В этом процессе энергия переходит из одной формы в другую.

Научное определение проделанной работы:

«Работа, совершаемая над системой постоянной силой, равна скалярному произведению силы и расстояния, на которое действует сила ».

Обратите внимание, что в физике используется термин «выполненная работа». Это потому, что оно относится к движению или движению, которое имело место или находится в процессе. Это отличается от работы, которая означает работу или работу по дому.

Основные компоненты работы:

Далее, есть три компонента, которые абсолютно необходимо держать в поле зрения при поиске выполненной работы. Эти три вещи: 

• Сила
• Причина
• Смещение

Это могло быть очевидным, но все же было необходимо упомянуть эти моменты. Почему это важно? Читайте дальше, чтобы знать.

Первый форс . Вы должны знать горизонтальную составляющую силы. Если нет, то важно, чтобы вы знали о массе и ускорении тела. Затем вы можете рассчитать силу с помощью калькулятора силы.

Далее эта сила должна быть Причина смещение мы находим работу. Если сила приложена перпендикулярно объекту, то по правилу скалярного произведения работа не должна совершаться.

Но если тело еще совершило какое-то перемещение, то перпендикулярная сила не является причиной . Должна быть какая-то другая сила. Следовательно, сила, которую мы используем, должна быть причиной смещения.

В: Почему мы используем скалярное произведение, чтобы найти проделанную работу? Скалярное произведение используется в произведенной работе, потому что нам нужна «та» составляющая силы, которая действует в направлении движения. (т.е. F cos θ ). Кросс-произведение в данном случае нам не поможет, так как оно использует вертикальную составляющую силы, перпендикулярную плоскости. Это не причина .

Формула проделанной работы

Согласно определению, работа есть точечный продукт силы и перемещения. Формула работы;

Работа выполнена = |F||d| cos θ

В то время как угол ???? имеет силу. Работа — это скалярная величина, которую всегда обеспечивает скалярный продукт. Его единица СИ – Джоуль (Дж), такая же, как энергия. Один джоуль определяется как:

«Когда сила в один ньютон заставляет тело двигаться на один метр , тогда совершенная работа составляет один джоуль ».

Джоуль в основных величинах представлен как ньютон-метр (Нм) и имеет размерность [ML ² T ^-2 ].

Прежде чем мы узнаем, как найти выполненную работу, давайте кратко рассмотрим типы выполненной работы.

Виды выполняемой работы

В зависимости от угла действия силы различают три типа выполняемой работы.

• Положительная работа

Если угол силы меньше 90 градусов, то работа положительна. Это связано с тем, что значение cos < 90 больше 0 и меньше 1,

• Выполнена отрицательная работа

Когда угол силы больше 90, в таких случаях работа считается отрицательной. Значение cos > 90 меньше 0 и больше -1.

• Нулевая проделанная работа

Наконец, когда значение угла силы равно точно 90, проделанная работа равна нулю. Его также называют минимальной выполненной работой . Потому что cos 90 = 0,

Существует также термин максимальная проделанная работа . Это когда сила и перемещение совершенно параллельны, а угол между ними равен нулю. Значение cos 0 = 1 и является максимальным значением cos.

Как найти проделанную работу?

Теперь к основной теме статьи. Вы будете учиться на разных примерах.

Пример 1:

Какова будет работа, выполненная при силе 80 Н под углом 45 градусов. Водоизмещение 20м.

Решение:

Шаг 1: Определите значение.

Сила = 80 Н

Угол = 45

Перемещение = 20 м

Шаг 2: Используйте значения в формуле.

Ф . D = |F||d| cos θ

= (80)(20) cos (45)

= 1,131,4 Дж

Пример 2:

По какой формуле найти работу, параллельную перемещению? Найдите его значение для следующих данных:

Сила = 10 Н

Перемещение = 5 м

Ответ:

Формулу для работы, совершаемой, когда сила и перемещение параллельны, можно вывести следующим образом.

Поскольку угол между обеими величинами равен 0, отсюда:

Работа = |F||d| cos θ

Работа = |F||d| cos (0)

Работа = |F||d| значение cos (0) = 1

Работа = F.d

Это максимальная выполненная работа. Вы можете использовать калькулятор работы, чтобы найти его значение.

Теперь о решении. Во-первых, определите значения.

Сила = 10 Н

Перемещение = 5 м

Теперь используйте эти значения в полученной формуле.

Работа = F.d

Работа = (10)(5)

Работа = 50 Дж

Пример 3:

Мешок массой 4 кг упал со стола высотой 30м. Вычислить выполненную работу.

Решение:

Данные:

Масса = 4 кг

Высота = Перемещение = 30 м

Гравитация = 9,8 мс ^-2

Кроме того, объект падает в направлении действия силы (гравитационной), что означает, что оба объекта параллельны.

Во-первых, нам нужно найти силу. В нашем случае сила – это вес. (пренебрегая сопротивлением воздуха)

F = мА

F = мг

F = (4)(9,8)

F = 39,2 Н

Теперь используйте это в формуле.

Работа = F.d

Работа = (39.2)(30)

Работа = 1176 Дж

Пример 4:

Объект массой 400 грамм начинает двигаться с постоянной скоростью из точки А. Когда он проходит 20 м (точка b), к нему приложена сила в направлении движение.

Ускоряется со скоростью 15 мс ^-2 и достигает на расстоянии 40 метров (точка с) от точки А. Найдите совершенную работу. Кроме того, сила трения составляет 1,1 Н.

Решение:

Шаг 1: Запишите указанные данные.

Масса = 400 г = 0,4 кг

Ускорение = 15 мс ^-2

Перемещение = От B до точки C = 40 – 20 = 20 м

Сила трения = 1,1 Н

5 9000. Вы можете либо рассчитать работу, проделанную для каждой силы отдельно, либо найти чистую силу и использовать ее в формуле проделанной работы.

Мы будем использовать первый метод.

Шаг 2: Найдите силу, приложенную к телу.

F = ma

F = (0,4)(15 мс ^-2 )

F = 6 Н

Шаг 3: Найдите работу, выполненную вычисленной силой.

РаботаF = |F||D| cos θ

WorkF = (6)(20) cos (0) (угол равен нулю, так как F и d параллельны)

WorkF = 120 Дж

Шаг 4: Найдите работу трения.

Рабочий = |F||D| cos θ

Workfri = (1.1)(20) cos 180 (угол равен 180, так как трение противодействует движению)

Workfri = -22 Дж

Шаг 5: Рассчитайте чистую выполненную работу.

Worknet = W _F + W _FRI

Worknet = (120 J) + (-22 J)

Worknet = 98 J

СПИСОК

• HTTPS:///////cth. brainkart.com/article/Solved-Example-Problems-for-Work-and-Work-done-by-a-force_34544/

• https://www. physicsclassroom.com/class/energy/Lesson-1/ Определение и математика работы

• https://courses.lumenlearning.com/physics/chapter/7-1-work-the-scientific-definition/

Работа и энергия – Уроки Византа

Написал преподаватель Тони С.

Работа

Работа — это физическая величина, определяемая через силу, вызывающую перемещение объекта. Например, если человек толкает коробку, и эта коробка перемещается на некоторое расстояние, человек выполнил работу над коробкой. Мы можем точно рассчитать, сколько работы было выполнено, используя следующую формулу:

W = Fd

, где W — работа, F — сила, d — перемещение. Стандартной единицей работы в СИ является джоулей (Дж) , что равно работе, совершаемой силой в один ньютон при перемещении объекта на один метр:

1 Дж = 1 Н · 1 м

Вернемся назад к предыдущему примеру. Если человек толкает с постоянной силой в десять ньютонов, а ящик перемещается на расстояние пяти метров в направлении, в котором его толкнул человек, то человек совершил над ящиком работу в пятьдесят джоулей:

10,0 Н · 5,00 м = 50,0 Дж

Но что произойдет, если направление, в котором толкает человек, не параллельно направлению движения ящика? Допустим, ящик не очень высокий, и человеку приходится наклоняться, чтобы его толкнуть, из-за чего направление его толчка направлено под углом двадцать градусов ниже горизонтали:

В данном случае не все силы способствует перемещению ящика. Только горизонтальная составляющая вектора силы F cos Θ отвечает за работу, совершаемую над ящиком. Мы можем включить это в наше предыдущее уравнение для работы, получив:

W = Fd cos Θ

Теперь, когда человек сгорбился и прилагает силу под углом к ​​смещению, он совершает меньшую работу над ящиком:

10,0 Н · 5,00 м · cos20. 0° = 47,0 Дж

(Для тех из вас, кто знаком с векторным исчислением, мы можем представить работу как скалярное произведение вектора силы F и вектора смещения d:

W = F · d = Fd cos Θ

где F и d — величины векторов силы и смещения соответственно, а Θ — угол между двумя векторами.)

Добавление cosΘ к нашей формуле проливает свет на некоторые интересные концепции:

• Когда Θ равно нулю, cosΘ равно единице. Это происходит, когда сила и перемещение направлены в одном направлении, и поэтому у нас есть исходная формула W=Fd .
• Когда Θ равно 90°, cosΘ равно нулю, что, в свою очередь, делает работу равной нулю. Это происходит, когда сила и перемещение перпендикулярны друг другу. Таким образом, , когда сила приложена к объекту в направлении, перпендикулярном смещению объекта, эта сила не действует.
• Когда Θ находится между 90° и 180°, cosΘ меньше нуля, что, в свою очередь, делает работу меньше нуля. Это дает нам концепцию отрицательной работы , которую можно проиллюстрировать, добавив трение к нашему предыдущему сценарию толкания коробки.

Предположим, что введенная кинетическая сила трения является постоянной силой в девять ньютонов. Мы уже рассчитали работу, совершенную человеком, в сорок семь джоулей. Теперь мы можем вычислить работу трения, зная, что угол между векторами смещения и трения равен 180°:

9,00 Н · 5,00 м · cos180° = -45,0 Дж

Мы можем добавить эту работу к работе, выполненной человеком, чтобы получить общую чистую работу, выполненную на ящике, которая составит два джоуля. Вместо того, чтобы находить работу, связанную с каждой силой в отдельности, а затем суммировать их, мы можем сначала вычислить результирующую силу и использовать ее для расчета чистой работы: где Σ W — чистая работа, а Σ F — величина чистой силы. Вы можете доказать это, рассчитав чистую силу для приведенного выше сценария, а затем рассчитав работу. (Вы должны обнаружить, что результирующая сила равна 3,44 Н при угле 83,4° ниже горизонтали.)

Энергия

Энергия — еще одна физическая величина, некоторые виды которой тесно связаны с работой. Первый тип, который мы обсудим, — это кинетическая энергия , то есть энергия, которой обладает объект, просто находясь в движении. Мы можем рассчитать кинетическую энергию объекта по следующей формуле:

К = ¹ / ₂ мв ²

, где К — кинетическая энергия, м — скорость 9048. (Вы можете использовать это уравнение, чтобы убедиться, что единицы энергии такие же, как и единицы работы: джоули. )

В нашем предыдущем примере с человеком, толкающим коробку, предположим, что коробка весит десять килограммов. Мы можем сделать некоторые вычисления, чтобы определить, какое ускорение ящика зависит от чистой силы, которую он испытывает (0,0395 ^м / _с² ), а затем еще несколько вычислений, чтобы узнать, какую скорость имеет ящик после того, как его толкнули на пять метров ( 0,629 ^м / _с ), чтобы, наконец, добраться до точки, где мы можем рассчитать окончательную кинетическую энергию коробки:

K = ¹ / ₂ ·10 кг·(0,629 ^м / _с ) ² = 1,98 Дж

Это очень много вычислений! К счастью, есть более простой способ расчета кинетической энергии на основе чистой работы, и он называется принципом работы-энергии :

Чистая работа, выполненная над объектом, равна изменению кинетической энергии объекта.
ΣW = ΔK = K _f – K _i = ¹ / ₂ m(v _f ² -v ​​ _i ² )

(нижние индексы f и i обозначают конечный и начальный соответственно). два джоуля. Вуаля! Двигаясь дальше с этого момента в своих исследованиях физики, вы должны обнаружить, что будете использовать принцип работы-энергии так же (если не больше), как и предыдущий набор уравнений кинематики для расчета скорости движения объекта.

Другим типом энергии является потенциальная энергия , которая определяется в контексте определенных типов сил, которые мы называем консервативными силами . Мы не будем вдаваться в то, почему одни силы консервативны, а другие нет. Просто знайте, что консервативные силы (например, гравитация и сила упругости) имеют связанную потенциальную энергию, а неконсервативные (например, трение, сопротивление воздуха и толчок или притяжение человека) — нет.

В общем случае изменение потенциальной энергии, связанное с консервативной силой, равно отрицательной работе, совершаемой этой силой. Мы можем использовать эту информацию, чтобы получить формулы для наших двух типов потенциальной энергии:

• Гравитационный : Представьте себе, что ящик весом в пять килограммов поднимают на десять метров вертикально вверх.