Физика l: Книга "Физика. 7-8 классы. Опорные конспекты и дифференцированные задачи" - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

3. Графики зависимости кинематических величин равноускоренного движения

Когда на тело действует постоянная сила \(\vec{F}\), скорость тела \(\vec{v}\) изменяется с течением времени \(t\).

Если скорость тела возрастает на одну и ту же величину Δυ за промежуток времени \(\Delta t\), то движение называют равноускоренным:
a→=υ2→−υ1→t2−t1.

Обозначение ускорения \(a\) — первая буква латинского слова \(acceleratio\).

Если скорость тела возрастает \(v_2>v_1\), то ускорение является положительным: a>0.

Если скорость тела убывает \(v_2<v_1\), то ускорение является отрицательным: a<0.

Обрати внимание!

При равномерном движении скорость тела не изменяется с течением времени \(v(t)=const\), ускорение тела равно нулю: a=0.

Рис. \(1\). Графики зависимости ускорения от времени при различных видах движения тела

Скорость при равноускоренном движении вычисляется по формуле:

\(\vec{\upsilon}(t)=\vec{\upsilon}_0+\vec{a}\cdot\Delta t\),

где \(\Delta\)\(t=t-t_0\) — время изменения скорости.

Графики зависимости скорости от времени при равноускоренном движении изображаются прямыми или отрезками прямых. Чем больше ускорение, тем больше угол наклона графика скорости относительно оси времени.

При положительном значении ускорения графики скорости направлены вверх.

Рис. \(2\). Графики зависимости скорости от времени при равноускоренном движении тела

При равнозамедленном движении графики скорости направлены вниз.

Рис. \(3\). Графики зависимости скорости от времени при равноускоренном движении тела с отрицательным ускорением

Уравнение координаты тела при равноускоренном движении:

x(t)=x0+υ0x⋅t+ax⋅t22,

где \(\vec{v}_0\)\(_x\) — проекция вектора начальной скорости \(\vec{v}_0\) на ось \(x\),

\(a_x\) — проекция вектора ускорения \(\vec{a}\) на ось \(x\).

Графиком зависимости координаты от времени при равноускоренном движении будет часть параболы.

При равноускоренном движении ветвь параболы направлена вверх.
a>0

Рис. \(4\). Графики зависимости координаты от времени при равноускоренном движении тела

При равнозамедленном движении ветвь параболы направлена вниз.
a<0

Рис. \(5\). Графики зависимости координаты от времени при равноускоренном движении тела с отрицательным ускорением

Физика БФУ им. И. Канта наградили за победу в конкурсе L’OREAL-UNESCO «Для женщин в науке»

26 ноября в Москве в Государственном музее изобразительных искусств имени А.С. Пушкина прошла XII церемония вручения национальных стипендий L’Oreal-UNESCO «Для женщин в науке». Одна из победительниц конкурса – исследователь нашего университета, заведующая лабораторией новых магнитных материалов БФУ им. И. Канта Валерия Родионова.

Отметим, проект L’Oreal-UNESCO реализуется при участии Российской академии наук и Комиссии Российской Федерации по делам ЮНЕСКО. В этом году в списке победителей ученые из Москвы, Санкт-Петербурга, Калининграда, Томска, Казани, Саратова и Нижнего Новгорода.

Десяти молодым российским женщинам-учёным вручены стипендии, призванные помочь талантливым и перспективным специалистам в различных областях знаний развивать научную карьеру в России.
Гостей вечера приветствовал генеральный директор L’Oreal в России

Клаудио Кавикьоли. Он рассказал о международном проекте For Women in Science, частью которого является российская премия «Для женщин в науке». В этом году зарубежная программа празднует 20-летие:

«Это самые долгие отношения ЮНЕСКО с частной организацией. Более 3000 женщин-ученых получили награды с момента запуска программы в 1998 году. В России мы уже наградили 115 женщин-ученых. Каждая из вас отмечена за ценный вклад в своей области исследования, начиная от регенеративной медицины и заканчивая лазерной физикой».

Торжественную церемонию награждения победителей провел Алексей Хохлов, академик, вице-президент РАН и председатель жюри конкурса «Для женщин в науке». Он представил членов жюри, среди которых профессор кафедры молекулярной биофизики физического факультете СпбГУ, главный научный сотрудник ИВС РАН

Татьяна Бирштейн, генеральный секретарь L’Oreal в России Жорж Шишманов, заведующая лабораторией транскрипционных факторов эукариот ИБГ РАН Софья Георгиева, академики РАН Ольга Донцова, Михаил Егоров, Сергей Недоспасов и профессор физического факультета МГУ Александр Образцов.

По словам Алексея Хохлова, в этом году было подано 287 заявок из 41 города России. Академик РАН рассказал о процедуре отбора победителей:

«Сначала мы отбираем 30 лучших кандидатов. Это делается путем сравнения наукометрических показателей. Мы смотрели на цитируемость статей наших коллег-молодых ученых в журналах из основной коллекции Web of Science. Затем эти заявки 30 лучших в наукометрии коллег мы рассылали рецензентам, и они давали экспертную оценку».

Второй этап — отбор из 30 кандидатов десяти победителей, имена которых назвали во время церемонии. Обладательницами премии L’Oreal-UNESCO «Для женщин в науке» стали:

1. Родионова Валерия, Балтийский федеральный университет им. И. Канта, Калининград.
2. Герасимова Татьяна, Институт органической и физической химии им. А.Е. Арбузова — ОСП ФИЦ КазНЦ РАН, Казань.

3. Ефименко Анастасия, Институт регенеративной медицины Медицинского научно-образовательного центра МГУ имени М.

В. Ломоносова, Москва .
4. Иванова Ольга, Институт общей и неорганической химии имени Н.С. Курнакова РАН, Москва.
5. Калугина Юлия, Томский государственный университет, Томск.
6. Мельникова Наталия, Институт молекулярной биологии им. В.А. Энгельгардта РАН, Москва.
7. Панфилова Елизавета, Институт биохимии и физиологии растений и микроорганизмов РАН, Саратов.
8. Пенькова Анастасия, Санкт-Петербургский государственный университет, Санкт-Петербург.
9. Анашкина Елена, Федеральный исследовательский центр Институт прикладной физики РАН, Нижний Новгород.
10. Скорб Екатерина, Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, Санкт Петербург.

Валерия Родионова — кандидат физико-математических наук, автор научных статей, опубликованных в престижных научных журналах, научный руководитель и организатор престижных международных научных конференций. Валерия Родионова – приехала в БФУ им. И. Канта из Москвы. За ее плечами активная научная деятельность в МГУ имени М.В. Ломоносова, получение там учёной степени кандидата физико-математических наук, после – PhD в университете Страны Басков в Испании. В 2018 году Валерия Родионова уже одержала победу в конкурсе на право получения грантов Президента РФ, а также получила грант РФФИ “стабильность”, направленный на поддержание сформированных на территории РФ молодых научных групп.

Конкурс «Для женщин в науке» проходит в России с 2007 года. Обладательницами стипендий могут стать кандидаты и доктора наук, работающие по дисциплинам «физика», «химия», «биология», «медицина» в вузах и научных институтах России. Возраст соискательниц должен быть не выше 35 лет.

Ссылка на оригинал статьи

“Стихотворство – моя утеха, физика – мои упражнения” М.В.Ломоносов

Вашему вниманию представляется образовательный квест “Стихотворство – моя утеха, физика – мои упражнения”.

Александр Пушкин о Ломоносове выразился так: ” Соединяя необыкновенную силу воли с необыкновенною силою понятия, Ломоносов обнял все отрасли просвещения. Жажда науки была сильнейшею страстию сей души, исполненной страстей. Историк, ритор, механик, химик, минералог, художник и стихотворец, он все испытал и все проник”. К этому трудно что добавить по существу – можно лишь рассказать подробнее.

Современники в большинстве своем не понимали Ломоносова, отмечая в основном его гордыню и грубость в общении с ближними. В “наше все” российской науки он начал превращаться лишь во второй половине XIX века. При этом общественное представление об ученом формировалось в основном на уроках литературы: Ломоносов представал в образе стихотворца средней руки, автором напыщенных од, чуждых читателем последующих эпох. Кроме того, всегда находились скептики, считавшие что “первым” и “единственным” Ломоносов выглядел лишь на фоне общего – крайне низкого – уровня общественной науки XVIII века: мол, на безрыбье и рак рыба.

Таким образом, слава Ломоносова – дутая, она создана из ничего квасными патриотами…

Такого рода критики, как правило, исходили из общих соображений, не делая попыток всерьез изучить историю естествознания – взглянуть на систему представлений, распространенную в XVIII веке, сравнить её с современной научной картиной мира и определить, какое место в ней занимают идеи М. В. Ломоносова.

Между тем, такая работа историками науки в ХХ веке была проведена, и вывод их однозначен: русский ученый действительно во многих отношениях опережал свою эпоху.

В данном квесте Вы можете познакомиться с научными трудами М.В. Ломоносова в области физики, языка и литературы, связанными с его пребыванием в Москве и Санкт-Петербурге. А также стать участником викторины и проверить свои знания, полученные на уроках литературы, языка и физики.

Внимание! По карте необходимо найти начало квеста, отмеченное цифрой 1 (переместиться по карте к поселку Ломоносово).

#openarctic

Архивы задач 2009-2018 – Всероссийская олимпиада по физике.

Олимпиада Максвелла.

Год

Муниципальный

этап

Региональный этап

Финал России

Азиатская

APhO

Международная

IPhO

Естественнонаучная

IJSO

2018

LIII

LII

Тюмень

7-8 класс, Сочи

Вьетнам

Португалия

Ботсвана

2017

LII

Казань

7-8 класс, Сочи

Россия, Якутск

Индонезия

Голландия

2016

Сочи

7-8 класс, Сочи

Гонконг

Швейцария

Индонезия

2015

XLIX

Екатеринбург

Китай

Индия

Южная Корея

2014

XLIX

XLVIII

Санкт-Петербург

Сингапур

Казахстан

Аргентина

2013

XLVIII

XLVII

Владивосток

Индонезия

Дания

Индия

2012

XLVI

Саранск

Индия

Эстония

Иран

2011

XLVI

XLV

Оренбург

Израиль

Таиланд

ЮАР

2010

XLV

XLIV

Белгород

Тайвань

Хорватия

Нигерия

2009

XLIV

XLIII

Жуковский

Таиланд

Мексика

Муниципальный этап 2010

Азербайджан

Скачать задания

Муниципальных этапов

2009-2016

одним архивом

Скачать задания

Региональных этапов

2009-2016

одним архивом

Скачать задания

Финалов России

2009-2016

одним архивом

Скачать задания

APhO

2009-2016

одним архивом

Скачать задания

IPhO

2009-2016

одним архивом

Скачать задания

IJSO

2009-2016

одним архивом

Архив за 2000-2008 годы

Математическая физика | Николай Филонов.

2. Увеличения степени гладкости до бесконечности здесь нет, как это происходит у эллиптического уравнения.
15:40 Сделаем замену функции u на u~=u−μ, после чего произойдут такие изменения в уравнении
f~=f−μ”, φ~=φ−μ, ψ~=ψ−μ’ и u~(0, t)=u~'(0, t)=0, в точке x=0 струна закреплена.
Применим метод отражений и распространим функции f~, φ~, ψ~ симметричным образом на всю вещественную прямую f~(t, −x)=−f~(t, x). Свели задачу к бесконечной в обе стороны струне.
u~(t, x)=1/2(φ~(x+ct)+φ~(x−ct))+1/2c [x−ct, x+ct]_∫ ψ~(y)dy+1/2c [0, t]_∫[x−c(t−τ), x+c(t−τ)]_∫ f~(τ, y)dydτ
Если x−ct ≥ 0, x≥ct, мы находимся далеко от начала и прошло мало времени, в этом случае всё происходит как на бесконечной прямой, две волны бегут в разные стороны.
u(t, x)=1/2(φ(x+ct)+φ(x−ct))+1/2c [x−ct, x+ct]_∫ ψ(y)−μ'(0)dy+1/2c [0, t]_∫[x−c(t−τ), x+c(t−τ)]_∫ f(τ, y)−
μ”(τ)dydτ+μ(t)−μ(0)
Так как [0, t]_∫(t−τ)
μ”(τ)dτ=t(μ'(t)−μ'(0))−[0, t]_∫τ
μ”(τ)dτ=по частям=t(μ'(t)−μ'(0))−tμ'(t)+μ(t)−μ(0)=μ(t)−μ(0)−tμ'(0)
, то u(t, x)=1/2(φ(x+ct)+φ(x−ct))+1/2c [x−ct, x+ct]_∫ ψ(y)dy+1/2c [0, t]_∫[x−c(t−τ), x+c(t−τ)]_∫ f(τ, y)dydτ
Двигающаяся из начала часть волны здесь отсутствует, она не успела ещё дойти.

В случае, если произошло наложение с отражённой волной, то есть когда x−ct < 0
u(t, x)=1/2(φ(x+ct)−φ(−x+ct))+1/2c [−x+ct, x+ct]_∫ ψ(y)−μ'(0)dy+
+1/2c [0, t−x/с]_∫[−x+c(t−τ), x+c(t−τ)]_∫ f(τ, y)−
μ”(τ)dydτ+1/2c [t−x/с, t]_∫[x−c(t−τ), x+c(t−τ)]_∫ f(t, y)−
μ”(τ)dydτ+μ(t)
Так как [0, t−x/с]_∫
μ”(τ)dτ=μ'(t−x/с)−μ'(0),
[t−x/с, t]_∫(t−τ)μ”(τ)dτ=t(μ'(t)−μ'(t−x/с))−[t−x/с, t]_∫τμ”(τ)dτ=по частям=
=t(μ'(t)−μ'(t−x/с))−tμ'(t)+(t−x/с)μ'(t−x/с)+μ(t)−μ(t−x/с)=μ(t)−μ(t−x/с)−x/сμ'(t−x/с)
,то u(t, x)=1/2(φ(x+ct)−φ(−x+ct))+1/2c [−x+ct, x+ct]_∫ ψ(y)dy+
+1/2c [0, t−x/с]_∫[−x+c(t−τ), x+c(t−τ)]_∫ f(τ, y)dydτ+1/2c [t−x/с, t]_∫[x−c(t−τ), x+c(t−τ)]_∫ f(t, y)dydτ+μ(t−x/с)
Начальное колебание μ(t) приходит в точку x с запаздыванием x/с, как раз столько времени нужно на распространение сигнала.
Пусть начальная точка неподвижна μ(t)=0 и f=0, тогда решение
u(t, x)=1/2(φ(x+ct)−φ(−x+ct))+1/2c [−x+ct, x+ct]_∫ ψ(y)dy.
Отражённая волна бежит вправо −φ(−x+ct)/2, а относящаяся к ψ часть интерферировала с отражением на отрезке [0, −x+ct] в ноль.

2=T/ρ, круговая частота ω=π/√ρ √T/L=π/√L √T/√m. Итак частота звуковой волны прямо пропорциональна квадратному корню из силы натяжения струны и обратно пропорциональна её длине, при фиксированной длине обратно пропорциональна корню из массы.

Открытая Физика. Электромагнитная индукция. Правило Ленца

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину Φ = B · S · cos α, где B – модуль вектора магнитной индукции, α – угол между вектором B→ и нормалью n→ к плоскости контура (рис. 1.20.1).

Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура.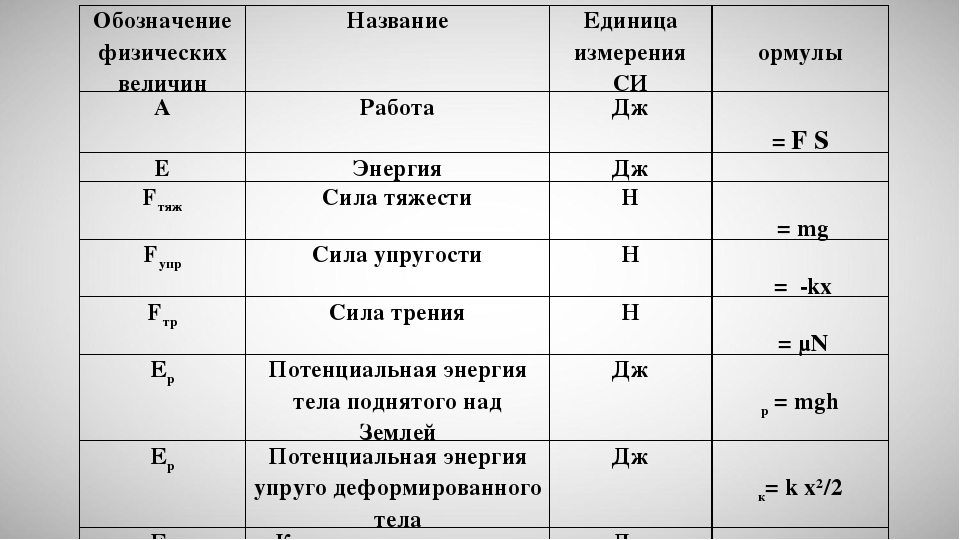 Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м²: 1 Вб = 1 Тл · 1 м².

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ℰ_инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус: ℰинд=-ΔΦΔt.

Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.

Иллюстрация правила Ленца. В этом примере ΔΦΔt>0, а ℰ_инд < 0. Индукционный ток I_инд течет навстречу выбранному положительному направлению l→ обхода контура

Правило Ленца отражает тот экспериментальный факт, что ℰ_инд и ΔΦΔt всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле B→, перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью υ→ по двум другим сторонам (рис. 1.20.3).

Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон

На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью υ→ зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен F_Л = eυB

Работа силы F_Л на пути l равна A = F_Л · l = eυBl.

По определению ЭДС ℰинд=Ae=υBl.

В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для ℰ_инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно, |ℰинд|=|ΔΦΔt|.

Для того, чтобы установить знак в формуле, связывающей ℰ_инд и ΔΦΔt, нужно выбрать согласованные между собой по правилу правого буравчика направление нормали n→ и положительное направление обхода контура l→, как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.

Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный I_инд = ℰ_инд/R. За время Δt на сопротивлении R выделится джоулево тепло ΔQ=RIинд2Δt=υ2B2l2RΔt.

Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера F→A. Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен F_A = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа A_мех равна Aмех=-FυΔt=-I B l υ Δt=-υ2B2l2RΔt.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.

Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Электромагнитная индукция Опыты Фарадея Генератор переменного тока

Высокочувствительный алмазный магнитометр с наноразмерным разрешением

Bending, S.J. Локальные магнитные зонды сверхпроводников. Adv. Phys. 48 , 449–535 (1999).

ADS Статья Google Scholar

Chang, A. M. et al. Сканирующая зондовая микроскопия Холла. заявл. Phys. Lett. 61 , 1974–1976 (1992).

ADS Статья Google Scholar

Будкер, Д.и другие. Резонансные нелинейные магнитооптические эффекты в атомах. Ред. Мод. Phys. 74 , 1153–1201 (2002).

ADS Статья Google Scholar

Auzinsh, M. et al. Может ли квантовое неразрушающее измерение улучшить чувствительность атомного магнитометра? Phys. Rev. Lett. 93 , 173002 (2004).

ADS Статья Google Scholar

Савуков, И.М., Зельцер, С. Дж., Ромалис, М. В. и Зауэр, К. Л. Настраиваемый атомный магнитометр для обнаружения радиочастотных магнитных полей. Phys. Rev. Lett. 95 , 063004 (2005).

ADS Статья Google Scholar

Коминис, К., Корнак, Т. У., Оллред, Дж. К. и Ромалис, М. В. Субфемтотесловый многоканальный атомный магнитометр. Nature 422 , 596–599 (2003).

ADS Статья Google Scholar

Vengalattore, M.и другие. Магнитометрия высокого разрешения со спинорным конденсатом Бозе – Эйнштейна. Phys. Rev. Lett. 98 , 200801 (2007).

ADS Статья Google Scholar

Чжао, К. Ф. и Ву, З. Магнитометр с исчезающей волной. заявл. Phys. Lett. 89 , 261113 (2006).

ADS Статья Google Scholar

Мамин, Х.Дж., Поджио, М., Деген, К. Л. и Ругар, Д. Ядерно-магнитно-резонансная томография с разрешением 90 нм. Nature Nanotech. 2 , 301–306 (2007).

ADS Статья Google Scholar

Сетон, Х., Хатчисон, Дж. И Басселл, Д. Настроенный усилитель СКВИДа для МРТ на основе контура синхронизации потока DOIT. IEEE Trans. Прил. Сверхсекунда. 7 , 3213–3216 (1997).

ADS Статья Google Scholar

Шленга, К.и другие. Магнитно-резонансная томография в слабом поле с помощью сверхпроводящего квантового интерференционного устройства с высоким постоянным током T c. заявл. Phys. Lett. 75 , 3695–3697 (1999).

ADS Статья Google Scholar

Jelezko, F. , Gaebel, T., Popa, I., Gruber, A. & Wrachtrup, J. Наблюдение когерентных колебаний в спине одного электрона. Phys. Rev. Lett. 92 , 076401 (2004).

ADS Статья Google Scholar

Jelezko, F. et al. Наблюдение когерентной осцилляции одиночного ядерного спина и реализация двухкубитового условного квантового вентиля. Phys. Rev. Lett. 93 , 130501 (2004).

ADS Статья Google Scholar

Хэнсон, Р., Мендоса, Ф. М., Эпштейн, Р. Дж. И Авшалом, Д. Д.Поляризация и считывание связанных одиночных спинов в алмазе. Phys. Rev. Lett. 97 , 087601 (2006).

ADS Статья Google Scholar

Чайлдресс, Л. и др. Когерентная динамика связанных электронных и ядерных спиновых кубитов в алмазе. Наука 314 , 281–285 (2006).

ADS Статья Google Scholar

Эпштейн, Р. Дж., Мендоса, Ф. М., Като, Ю. К. и Авшалом, Д. Д. Анизотропные взаимодействия одиночной спиновой и темноспиновой спектроскопии в алмазе. Nature Phys. 1 , 94–98 (2005).

ADS Статья Google Scholar

Gaebel, T. et al. Когерентная связь одиночных спинов в алмазе при комнатной температуре. Nature Phys. 2 , 408–413 (2006).

ADS Статья Google Scholar

Датт, М.V.G. et al. Квантовый регистр на основе отдельных электронных и ядерных спиновых кубитов в алмазе. Наука 316 , 1312–1316 (2007).

Артикул Google Scholar

Kühn, S., Hettich, C., Schmitt, C., Poizat, J.-Ph. & Сандогдар, В. Алмазные центры окраски как наноскопический источник света для сканирующей ближнепольной оптической микроскопии. J. Microsc. 202 , 2–6 (2001).

MathSciNet Статья Google Scholar

Чанг, Д.Э., Соренсен, А. С., Хеммер, П. Р., Лукин, М. Д. Квантовая оптика с поверхностными плазмонами. Phys. Rev. Lett. 97 , 053002 (2006).

ADS Статья Google Scholar

Meiboom, S. & Gill, D. Модифицированный метод спинового эха для измерения времен ядерной релаксации. Rev. Sci. Instrum. 29 , 688–691 (1958).

ADS Статья Google Scholar

Салихов, К.М., Цветков Ю. D. in Time Domain Electron Spin Resonance (ред. Кеван, Л. и Шварц, Р. Н.) (Wiley, New York, 1979).

Google Scholar

Мейз, Дж. Р., Тейлор, Дж. М. и Лукин, М. Д. Декогеренция электронного спина одиночных дефектов азот-вакансия в алмазе. Препринт на & lt; http: //arxiv. org/abs/0805.0327> (2008).

Будкер Д. и Ромалис М. Оптическая магнитометрия. Nature Phys. 3 , 227–234 (2007).

ADS Статья Google Scholar

Хуцишвили Г.Р. Спиновая диффузия. Сов. Phys. Усп. 8 , 743–769 (1966).

ADS Статья Google Scholar

Rabeau, J. R. et al. Имплантация меченых центров одиночных вакансий азота в алмаз с использованием ¹⁵ N. заявл. Phys. Lett. 88 , 023113 (2006).

ADS Статья Google Scholar

Meijer, J. et al. Генерация одиночных центров окраски с помощью сфокусированной азотной имплантации. заявл. Phys. Lett. 87 , 261909 (2005).

ADS Статья Google Scholar

Чарнок, Ф. Т. и Кеннеди, Т. А. Комбинированный оптический и микроволновый подход для выполнения операций квантового спина на азотно-вакансионном центре в алмазе. Phys. Ред. B 64 , 041201R (2001).

ADS Статья Google Scholar

Хансон Р., Добровицкий В. В., Фейгуин А. Э., Гиват О. и Авшалом Д. Д. Когерентная динамика одного спина, взаимодействующего с регулируемой спиновой ванной. Наука 320 , 352–355 (2008).

ADS Статья Google Scholar

Виола, Л.И Ллойд, С. Динамическое подавление декогеренции в квантовых системах с двумя состояниями. Phys. Ред. A 58 , 2733–2744 (1998).

ADS MathSciNet Статья Google Scholar

Принс, Дж. Ф. Активация атомов бора в ионно-имплантированных алмазах. Phys. Ред. B 38 , 5576–5584 (1988).

ADS Статья Google Scholar

Слихтер, К. P. Principles of Magnetic Resonance 3rd edn (Springer, Berlin, 1996).

Google Scholar

Меринг М. Принцип ЯМР высокого разрешения в твердых телах (Спрингер, Нью-Йорк, 1983).

Книга Google Scholar

Рей, А. М., Цзян, Л., Флейшхауэр, М., Демлер, Э. и Лукин, М. Д. Генерация многотельной защищенной запутанности во взаимодействующих спиновых системах. Phys. Ред. A 77 , 052305 (2008).

ADS Статья Google Scholar

Ходжастех К. и Лидар Д. А. Характеристики детерминированных схем динамической развязки: каскадные и периодические импульсные последовательности. Phys. Ред. A 75 , 062310 (2007).

ADS Статья Google Scholar

Мэнсфилд, П.Симметричные последовательности импульсов в ЯМР высокого разрешения в твердых телах. J. Phys. C 4 , 1444–1452 (1971).

ADS Статья Google Scholar

Секацкий С.К., Летохов В.С. Сканирующий оптический микроскоп с нанометровым разрешением и резонансным возбуждением флуоресценции образцов от одноатомного возбужденного центра. Письма в ЖЭТФ. 63 , 311–315 (1996).

ADS Статья Google Scholar

Черноброд, Б.М. и Берман, Г. П. Спиновый микроскоп на основе оптически детектируемого магнитного резонанса. J. Appl. Phys. 97 , 014903 (2005).

ADS Статья Google Scholar

Degen, C.L. Сканирующий магнитный полевой микроскоп с алмазным одинарным вращением. заявл. Phys. Lett. 92 , 243111 (2008).

ADS Статья Google Scholar

Мамин, Х. Дж., Будакян, Р., Чуй, Б. В. и Ругар, Д. Магнитно-резонансная силовая микроскопия ядерных спинов: обнаружение и управление статистической поляризацией. Phys. Ред. B 72 , 024413 (2005).

ADS Статья Google Scholar

Meriles, C. A. Оптически обнаруженный ядерный магнитный резонанс в субмикронном масштабе. J. Magn. Резон. 176 , 207–214 (2005).

ADS Статья Google Scholar

Вови, К., Hasselbach, K. & Mailly, D. Сканирующий силовой микроскоп с квантовым интерференционным устройством μ, сверхпроводимость и сверхпроводимость. Rev. Sci. Instrum. 73 , 3825–3830 (2002).

ADS Статья Google Scholar

43
Maze, J. R. et al. Наномасштабное магнитное зондирование с индивидуальным электронным спином в алмазе. Nature DOI: 10. 1038 / nature07279 (2008).

44
Баласубраманян, Г.и другие. Магнитометрия с наноразмерными изображениями с алмазными вращениями в условиях окружающей среды. Nature DOI: 10.1038 / nature07278 (2008).

45
Мэнсон, Н. Б., Харрисон, Дж. П. и Селларс, М. Дж. Азотно-вакансионный центр в алмазе: модель электронной структуры и связанной с ней динамики. Phys. Ред. B 74 , 104303 (2006).
ADS Статья Google Scholar

46
ван Оорт, Э., Мэнсон, Н. Б. и Гласбек, М. Оптически обнаруженная спиновая когерентность алмазного N-V центра в его триплетном основном состоянии. J. Phys. C: Физика твердого тела. 21 , 4385–4391 (1988).
ADS Статья Google Scholar

Учебник по физике: математика стоячих волн

Как обсуждалось в Уроке 4, модели стоячих волн – это волновые структуры, возникающие в среде, когда две волны одинаковой частоты интерферируют таким образом, чтобы образовать точки вдоль среды, которые всегда кажутся неподвижными.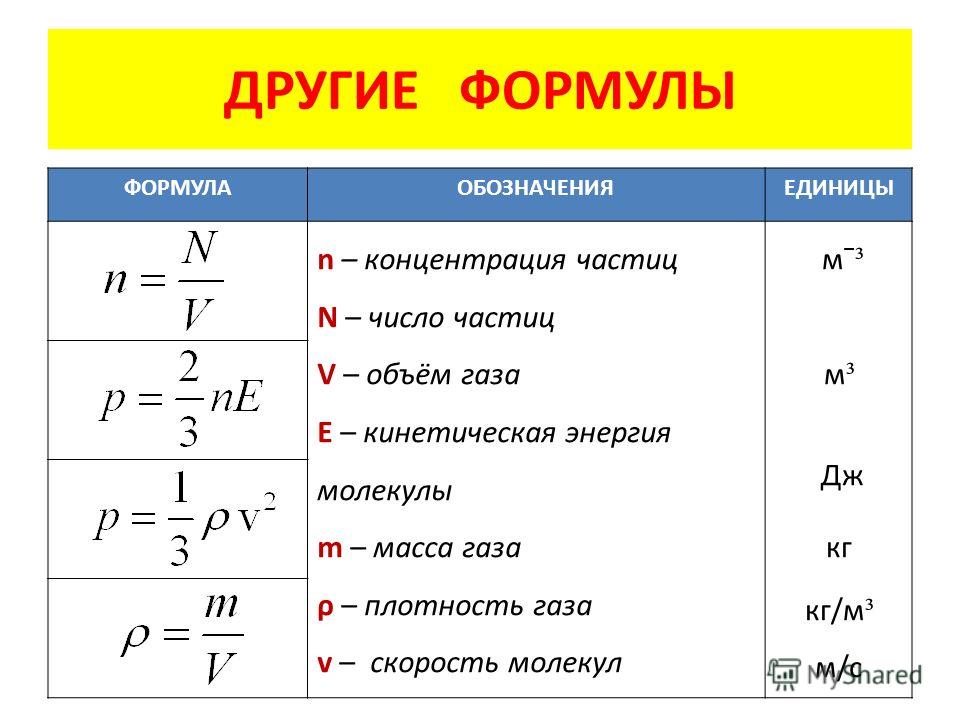 Такие модели стоячих волн образуются в среде, когда она колеблется на определенных частотах. Каждая частота связана с разным характером стоячей волны. Эти частоты и связанные с ними волновые структуры называются гармониками. Тщательное изучение паттернов стоячей волны выявляет четкую математическую связь между длиной волны, которая создает паттерн, и длиной среды, в которой этот паттерн отображается. Более того, это математическое соотношение предсказуемо, что позволяет обобщить и вывести утверждение, касающееся этого отношения.Чтобы проиллюстрировать это, рассмотрим картину стоячей волны первой гармоники для вибрирующего каната, как показано ниже.

Анализ первой гармонической картины
Паттерн первой гармоники показывает единственную пучность в середине веревки. Это положение пучности вдоль каната колеблется вверх и вниз от максимального смещения вверх из состояния покоя до максимального смещения вниз, как показано. Вибрация каната таким образом создает вид петли внутри струны. Полную волну в модели можно описать как начало в положении покоя, подъем вверх до пикового смещения, возврат обратно в положение покоя, затем спуск до пикового смещения вниз и, наконец, возвращение в положение покоя. На анимации ниже изображен этот знакомый паттерн. Как показано на анимации, одна полная волна в шаблоне стоячей волны состоит из двух петель . Таким образом, одна петля эквивалентна половине длины волны.
При сравнении картины стоячей волны для первой гармоники с ее одиночным контуром с диаграммой полной волны становится очевидным, что только половина волны растягивается по длине струны.То есть длина струны равна половине длины волны. Представьте в виде уравнения:
Анализ второй гармоники Теперь представьте, что струна вибрирует с частотой, которая задает картину стоячей волны для второй гармоники.
Диаграмма второй гармоники состоит из двух узлов. Таким образом, в длине струны есть две петли. Поскольку каждая петля эквивалентна половине длины волны, длина струны равна двум половинам длины волны. Представьте в виде уравнения:
Та же схема рассуждений может быть применена к случаю, когда струна вибрирует с частотой, которая задает картину стоячей волны для третьей гармоники.
Анализ третьей гармоники Третья гармоническая картина состоит из трех пучков узлов.Таким образом, в длине струны есть три петли. Поскольку каждая петля эквивалентна половине длины волны, длина струны равна трем половинам длины волны. Представьте в виде уравнения:
При исследовании диаграмм стоячих волн и соотношений длина-длина волны для первых трех гармоник выявляется четкая картина. Количество пучностей в паттерне равно гармоническому номеру этого паттерна.Первая гармоника имеет одну пучность; вторая гармоника имеет две пучности; а третья гармоника имеет три пучности. Таким образом, можно обобщить, что n -я гармоника имеет n пучностей, где n – целое число, представляющее номер гармоники. Кроме того, можно заметить, что в длине струны присутствует n половинных длин волн. Представьте в виде уравнения:

Обобщение математических соотношений
Эта информация обобщена в таблице ниже.
Для рисунков стоячей волны существует четкая математическая зависимость между длиной струны и длиной волны, которая создает рисунок. Математическая взаимосвязь просто возникает из рассмотрения шаблона и понимания того, что каждая петля в шаблоне эквивалентна половине длины волны. Общее уравнение, описывающее эту взаимосвязь длины волны для любой гармоники:
Проверьте свое понимание этой взаимосвязи, ответив на вопросы в разделе Проверьте свое понимание .
Мы хотели бы предложить . .. Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного шаблона стоячих волн. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Модели стоячей волны» предоставляет учащемуся среду для изучения формирования стоячих волн, моделей стоячих волн и математических соотношений для моделей стоячих волн.
Проверьте свое понимание
1. Предположим, что струна имеет длину 1,2 метра и колеблется в виде стоячей волны первой, второй и третьей гармоник. Определите длину волны для каждого из трех паттернов.
2. Струна справа имеет длину 1,5 метра и колеблется как первая гармоника.Струна совершает 33 полных колебательных цикла за 10 секунд. Определите частоту, период, длину волны и скорость этой волны.
3. Струна справа имеет длину 6,0 метра и колеблется как третья гармоника. Струна совершает 45 полных колебательных циклов за 10 секунд. Определите частоту, период, длину волны и скорость этой волны.
4.Струна справа имеет длину 5,0 метра и колеблется как четвертая гармоника. Струна совершает 48 полных колебаний за 20 секунд. Определите частоту, период, длину волны и скорость этой волны.
5. Струна справа имеет длину 8,2 метра и колеблется как пятая гармоника. Струна совершает 21 полный колебательный цикл за 5 секунд.Определите частоту, период, длину волны и скорость этой волны.
o :: Веб-страница Эдвина Л. (Теда) Вуллетта :: o:
: o :: Веб-страница Эдвина Л. (Теда) Вуллетта :: o:
Эдвин Л. (Тед) Вуллет
Почетный профессор физики и астронии., CSULB
к.э.н. – Университет штата Канзас, 1965,
Вычислительная физика
& nbsp
Тед Вуллетт активно преподавал и занимался исследованиями в течение 35 лет (начиная с 1966) в качестве преподавателя на факультете физики и астрономии в Калифорнии Государственный университет, Лонг-Бич.Его исследования включали рецензируемые работы по теоретической физике плазмы, неравновесная термодинамика, теоретические рентгеновские спектры, ядерная энергия высоких энергий физика, и вопросы физики и общества.
За время преподавательской деятельности Тед создал первокурсника. курс физики “Человек и энергия”, посвященный физическим аспектам социальных проблем. связанных с использованием энергии и окружающей средой. Этот популярный курс предлагался во время 1970-е годы использовали разные тексты в каждом семестре курса, и даже включали один семестр посвящен физике воздействия радиации на здоровье.
Включены курсы физики и астрономии для студентов и аспирантов Феноменология физики элементарных частиц, Специальная теория относительности, Общая теория относительности, Введение в астрофизику, вычислительную физику, физику плазмы, статистическую физику, Термодинамика, электричество и магнетизм, квантовая механика, классическая механика и Математические методы физики.
Тед и Кэтлин сейчас живут в Сан-Луис-Обиспо, на центральном побережье Калифорнии.Ежемесячные социальные “изюминки” – это группа ресторанов Morro Bay AAUW и унитаристско-универсалистская книжный клуб “Литвиты”.
Сейчас его контактный адрес электронной почты: Woollett@charter. net
ФИЗИЧЕСКИЙ ОТДЕЛ CSULB. ГЛАВНАЯ 11 октября 2021 г.
Тед, Кэтлин, Бев и Пол, до совершения преступления, плюс сумасшедший офис Теда.
1975 и 2009
Сан-Диего Лайтнинг 2021
Пересмотренный функционал M06-L для повышения точности определения высоты барьера химических реакций, нековалентных взаимодействий и физики твердого тела
Значение
Локальные обменно-корреляционные функционалы, которые зависят от локальных спиновых плотностей, их градиентов и локальных спиновых плотностей. удельные плотности кинетической энергии широко используются для расчетов электронной структуры как в химии, так и в физике благодаря их вычислительной эффективности в кодах плоских волн и для больших молекул, а также их относительно высокой точности для переходных металлов и других по своей природе многоконфигурационных систем. Локальный функционал Миннесоты 2006 (M06-L) оказался одним из наиболее точных локальных функционалов, доступных в настоящее время, но его можно улучшить в отношении числовой стабильности и общей точности. Здесь мы представляем обновленный функционал M06-L под названием revM06-L, который дает как более гладкие кривые потенциальной энергии, так и улучшенную общую точность, особенно для высоты барьера химических реакций, нековалентных взаимодействий и физики твердого тела.
Abstract
Мы представляем функционал revM06-L, который мы разработали путем оптимизации для большей базы данных, чем использовался для локального функционала Миннесоты 2006 (M06-L), и с использованием ограничений плавности.Стратегия оптимизации сократила количество параметров с 34 до 31, потому что мы удалили некоторые большие члены, которые увеличили требуемый размер квадратурной сетки и количество итераций самосогласованного поля. Средняя беззнаковая ошибка (MUE) revM06-L для 422 химических энергий составляет 3,07 ккал / моль, что лучше 3,57 ккал / моль, рассчитанных с помощью M06-L. MUE revM06-L для базы данных высоты барьера химической реакции (BH76) составляет 1,98 ккал / моль, что более чем в 2 раза выше по сравнению с функционалом M06-L.Функционал revM06-L дает лучший результат среди локальных функционалов, протестированных для базы данных нековалентных взаимодействий (NC51), с MUE всего 0,36 ккал / моль, и MUE revM06-L для базы данных постоянных решетки твердого тела (LC17) вдвое меньше, чем для M06-L. Функционал revM06-L также дает более гладкие кривые потенциала и предсказывает более точные результаты, чем M06-L, для семи из восьми разнообразных наборов тестов, не используемых для параметризации. Мы пришли к выводу, что функционал revM06-L хорошо подходит для широкого круга приложений в химии и физике конденсированного состояния.
За последние 30 лет теория функционала плотности Кона-Шэма (KS-DFT) стала наиболее надежным и популярным методом электронной структуры в химии и физике конденсированных сред. Однако точность KS-DFT зависит от качества обменно-корреляционного функционала, и точный функционал неизвестен (1). Много усилий было направлено на разработку лучших приближений к обменно-корреляционному функционалу. Полезные функционалы должны быть точными и экономичными в использовании, потому что высокое соотношение производительности и стоимости является ведущим фактором широкого использования KS-DFT.Особенно хорошо на шкале соотношения производительности и стоимости функционалы, которые зависят только от локальных свойств, называются локальными функционалами, особенно химиками (их также называют «полулокальными», особенно физиками; здесь мы используем «локальные»). Функционалы локальной плотности обычно зависят от локальных спиновых плотностей [ρσ (r), σ = α, β, где r – точка в реальном пространстве] и их градиентов (| ∇ρσ |), а иногда также от спин-специфической кинетической плотность энергии τσ (r), которая в атомных единицах определяется выражением (1/2) ∑i = 1nσ | ∇ψiσ (r) | 2, где ψiσ – пространственная часть занятой спиновой орбитали Кона-Шэма, и n _σ – количество занятых спиновых орбиталей спина σ . Локальные функционалы не включают нелокальную обменную энергию Хартри-Фока или нелокальную корреляционную энергию.
Точный функционал плотности не может быть явным и дифференцируемым функционалом плотности, локальной или нелокальной (2), но локальные приближения по-прежнему предпочтительны для широкого круга приложений (3⇓⇓ – 6), и они широко используются как в химии, так и в физике твердого тела. Основная причина заключается в том, что локальные функционалы требуют меньших вычислительных затрат, чем нелокальные функционалы (7⇓⇓⇓ – 11) в кодах плоских волн и для больших молекул, когда используются алгоритмы подгонки плотности (12⇓ – 14) в кодах базисных функций Гаусса; таким образом, они больше подходят для практических вычислений при моделировании сложных систем, макромолекул и систем конденсированной фазы с периодическими граничными условиями.Кроме того, локальные функционалы обычно более точны для систем, содержащих переходные металлы (ПМ), где обменные функционалы на основе плотности могут лучше описывать статическую корреляцию, чем обмен Хартри-Фока (15, 16). В-третьих, локальные функционалы часто обеспечивают более точные длины связей и частоты колебаний для молекул с равновесной геометрией, чем функционалы, содержащие обмен Хартри – Фока, которые называются гибридными функционалами (17, 18).
Локальный функционал Миннесоты 2006 (M06-L) (19), который был опубликован в 2006 году, представляет собой приближение локального метаобобщенного градиента (мета-GGA, где мета обозначает зависимость от τσ), параметризованное по нескольким молекулярным базам данных.M06-L имеет высокую точность для термохимии основной группы, термохимической кинетики, металлохимических и нековалентных взаимодействий, длин связей и частот колебаний; например, было обнаружено, что он хорошо работает в различных тестах на основе точных и экспериментальных данных. Тем не менее, M06-L все еще нуждается в улучшении с точки зрения общей точности, численной стабильности, требуемой точности интегрирующих сеток и сходимости самосогласованного поля (SCF). Например, средняя ошибка без знака (MUE) M06-L для базы данных высоты барьера химической реакции BH76 равна 4. 0 ккал / моль, что значительно больше, чем у более поздних локальных функционалов, таких как локальный функционал Миннесоты 2011 г. (M11-L) (20), несепарабельный локальный функционал Миннесоты 2012 г. (MN12-L) (21) и неразрывный локальный функционал Миннесоты 2015 г. функциональный (МН15-Л) (17). Кроме того, M06-L иногда не хватает вычислительной устойчивости и требует более мелкой сетки для сходимости (22, 23).
Как и другие функционалы, M06-L не всегда точен для различных типов взаимодействий. Особого внимания заслуживает тот факт, что постоянные решетки твердых тел, предсказанные M06-L, имеют большие ошибки, чем те, которые были получены с помощью нескольких других локальных функционалов, таких как приближение локальной плотности, пересмотренный функционал Тао – Пердью – Староверова – Скузериа (revTPSS) (24) и мета -GGA made simple 2 (MGGA_MS2) (25).
В этой работе, чтобы достичь более высокой универсальной точности и повысить точность определения высоты барьера химической реакции, нековалентных взаимодействий и постоянных решетки, мы повторно параметризовали функционал M06-L, подгоняя его под большую базу данных, включая как молекулярные, так и молекулярные. твердотельные данные. Результирующий функционал называется revM06-L. Кроме того, аналогично предыдущему приближению градиента для молекул (GAM) (26), MN15-L (17) и несепарабельному функционалу 2015 г. из Миннесоты (MN15) (18), во время процедуры подгонки использовались ограничения гладкости для параметров подгонки.Мы также удалили из функционала некоторые крупные электронные интегральные члены, которые требуют более мелкого квадратурного размера сетки для сведения энергии. Введя ограничения гладкости и удалив большие интегральные члены, мы смогли сделать функционал revM06-L менее чувствительным к размеру квадратурной сетки и потребовать меньшего количества итераций SCF.
Результаты и обсуждение
Все параметры были оптимизированы самосогласованным образом, а полная информация о функционалах и их оптимизации представлена в Приложении SI .Все расчеты проводились с использованием локально модифицированной версии (27) программы Gaussian 09 (28). База данных Миннесоты 2015A (17, 26) использовалась в качестве обучающего набора данных, как указано в Приложении SI, таблица S1. SI Приложение , Таблица S2 дает значения линейных параметров окончательного функционала revM06-L. Мы обнаружили, что в результате ограничений плавности, которые были добавлены при оптимизации, параметры в revM06-L намного меньше, чем в M06-L.Кроме того, как упоминалось во введении, мы также удалили некоторые крупные термины. В результате общее количество параметров в revM06-L сокращается до 31 по сравнению с 34 параметрами в исходном функционале M06-L. Окончательная функциональная форма насчитывает 32 члена.
В этой работе, помимо сравнения результатов revM06-L с результатами исходного функционала M06-L (19), мы также выбрали некоторые другие функционалы для сравнения. В предыдущей работе (17, 18, 26) мы рассчитали всю базу данных из 422 атомных и молекулярных энергий (AME422) с большим количеством функционалов плотности.Здесь, на основе этих оценок, мы выбрали для сравнения функционал каждого типа [приближение градиента (GA), мета-GA, гибридный GA и гибридный мета-GA], который дает самый низкий MUE для AME422. Функционалы, выбранные таким образом в каждой категории: GAM (26) в GA, MN15-L (17) в мета-GA, функционал Becke 1997 revision-1 (B97-1) (29) в гибридных GA и MN15 (18) в гибридные мета-ГА. (Обратите внимание, что ГА может быть либо GGA, либо несепарабельным ГА.) Мы также выбрали один из самых популярных функционалов в каждой из этих четырех категорий, а именно, функционал Пердью – Берка – Эрнцерхофа (PBE) (30) в GA, TPSS (31) в мета-ГА, 3-параметрический функционал Беке Ли – Янга – Парра (B3LYP) (32⇓ – 34) в гибридных ГА и Миннесота 2006 с функционалом двойного обмена Хартри – Фока (M06-2X) ( 14) в гибридных мета-ГА.Кроме того, в таблице 1 мы также сравниваем результаты с результатами некоторых других функционалов, выбранных как репрезентативные для других подходов, в частности, обменно-корреляционного функционала Ван Вурхиса – Скузериа (VSXC) (35) и мета-функционала Хампрехта – Коэна – Тозера – Хэнди. функционал (τ-HCTH) (36) в виде мета-GGA, функционал Becke 1997 с разделением по диапазонам с ненулевым обменом Хартри-Фока для всех межэлектронных расстояний и с молекулярно-механической дисперсией (ωB97X-D) (37) в виде гибридного GGA с разделением по диапазонам с молекулярно-механической затухающей дисперсией и функционалом Миннесоты 2006 г. (M06) (14) и функционалом высокого обмена Хартри – Фока Миннесоты 2008 г. (M08-HX) (38) в качестве гибридных мета-GGA.В некоторых сравнениях результатов для нетренировочных наборов тестов мы также сравниваем с результатами для нескольких других функционалов.
Таблица 1.
MUE (ккал / моль) для базы данных AME422 и ее дополнительных баз данных
Атомная и молекулярная энергия.
Таблица 1 показывает характеристики для полного набора атомных и молекулярных энергий в последнем столбце и для выбранных интересных подмножеств в предыдущих столбцах, в частности, для 137 энергий основных групп (MGBE137), 33 энергий TM-связей (TMBE33) , 76 высот реакционного барьера (BH76), 51 энергия нековалентного взаимодействия (NC51) и 18 энергий возбуждения p-блока и переходного металла (EE18).
Таблица 1 показывает, что функционал revM06-L дает лучшие результаты, чем M06-L для MGBE137, BH76, NC51, EE18 и AME422, и дает четвертый лучший результат в целом среди 16 локальных и нелокальных функционалов, перечисленных в таблице 1. с MUE 3,1 ккал / моль. Три наиболее эффективных функционала в таблице 1 для AME422 – это MN15, MN15-L и M06 с MUE от 2,2 до 2,8 ккал / моль.
Производительность revM06-L на высоте барьера (BH76) значительно улучшена по сравнению с M06-L, уменьшая MUE с 4.От 0 ккал / моль до 2,0 ккал / моль. Для высоты барьера revM06-L уступает только одному локальному функционалу, MN15-L, а также превосходит пять гибридных функционалов, показанных в таблице 1. Большинство функционалов плотности (за исключением MN15) не дают точных результатов как для высоты барьера, так и для Энергии связи TM. Например, два функционала в таблице 1 с лучшими результатами для BH76, M08-HX и M06-2X предсказывают худшие результаты для TMBE33. Только MN15-L, MN15 и revM06-L имеют MUE ниже 7,0 ккал / моль для TMBE33 и ниже 2.0 ккал / моль для BH76.
Трудно предсказать слабые нековалентные взаимодействия с помощью функционалов локальной плотности (39) без нелокальной электронной корреляции (40, 41) или эмпирических поправок Ван-дер-Ваальса (42). Тем не менее, функциональная форма, разработанная для функционалов типа M06, позволяет им описывать слабые нековалентные взаимодействия в геометриях Ван-дер-Ваальса, где электронные плотности взаимодействующих партнеров перекрываются. Таблица 1 показывает, что среди локальных функционалов revM06-L дает самый низкий MUE для нековалентных взаимодействий (NC51).
Кроме того, таблица 1 показывает, что revM06-L дает второй самый низкий MUE для MGBE137 среди локальных функционалов и дает лучшие результаты для EE18, чем M06-L.
Рис. 1 и приложение SI Приложение , таблица S5 показывают подробное сравнение MUE для всех 25 субданных по атомной и молекулярной энергии (AME) между M06-L и revM06-L. Функционал revM06-L дает более низкую MUE для 15 из 25 суббаз, и в 12 из этих 15 случаев разница составляет более 10%. В частности, характеристики в трех суббазах энергий связей основных групп (SR-MGM-BE9, SR-MGN-BE107 и MR-MGN-BE17) и двух суббазах энергий связей TM (SR-TM-BE17 и MR- TM-BE13) все улучшены. Однако точность MR-TMD-BE3 становится хуже. Примечательно, что MUE revM06-L для HTBh48 / 08, NHTBh48 / 08, NGDWI21, 4dAEE5, IsoL6 / 11, AE17 и DC9 / 12 все на 30–60% ниже, чем у M06-L.
Рис. 1.
Процентное изменение MUE revM06-L по сравнению с M06-L в базах данных по атомной и молекулярной энергии (суббазы данных AME22). По ординате [MUE (revM06-L) –MUE (M06-L)] / MUE (M06-L). Подбаза данных MR-TMD-BE3 на рисунке не показана.
База данных молекулярной структуры.
SI Приложение , таблица S6 показывает характеристики revM06-L в базе данных молекулярной структуры (MS10), включая шесть длин двухатомных связей молекул легких атомов (DGL6) и четыре длины двухатомных связей молекул с Zn, Br, или Ag (DGh5). Функционал revM06-L дает второй лучший результат (MUE = 0,009 Å) для DGh5, уступая только MN15, у которого MUE 0,008 Å по сравнению с 0,011 Å для M06-L. Функционал revM06-L дает четвертый самый низкий MUE 0,009 Å для полного MS10 среди 22 функционалов в Приложении SI, Таблица S6, при этом MN15, MN15-L и PBE0 входят в тройку лидеров с MUE равными 0. 006, 0,008 и 0,008 Å соответственно. Мы пришли к выводу, что функционал revM06-L может обеспечить хорошую длину связи для молекулярных структур.
Твердотельные базы данных.
Таблица 2 показывает MUE 16 функционалов [репрезентативные локальные функционалы и HSE06 (43), который представляет собой гибридный GGA с экранированным обменом] в двух твердотельных базах данных: 17 постоянных решетки (LC17, обучающий набор) и 31 полупроводник. запрещенные зоны (SBG31, нетренировочный набор). Эти расчеты проводились с периодическими граничными условиями, как обсуждалось в предыдущей работе (15, 17, 18, 44).Таблица 2 показывает, что MUE revM06-L для LC17 снижен до 0,041 Å с 0,080 Å для M06-L, а MUE для SBG31 снижен до 0,45 эВ с 0,73 эВ. Новый revM06-L дает лучшие результаты среди всех локальных функционалов в таблице 2 как для LC17, так и для SBG31. Таким образом, функционал revM06-L имеет общую точность как для химических, так и для физических баз данных, принятых в этой работе.
Таблица 2.
MUE для постоянных решетки (LC17: расстояния до ближайших соседей в ангстремах) и ширины запрещенной зоны полупроводников (SBG31 в электрон-вольтах)
Характеристики revM06-L на необучаемых испытательных наборах.
Функционал revM06-L был протестирован с использованием необучаемых баз данных (см. SI Приложение , таблица S3), включая запрещенные зоны полупроводников (SBG31), нековалентно связанные комплексы (S66 и S66x8), энергии вертикального возбуждения (EE69), координацию TM реакции (WCCR10), высоты барьера реакции TM (TMBh31), длины равновесных связей димера TM (TMDBL7), энергии диссоциации алкильных связей (ABDE13) и геометрии переходного состояния (TSG48). SBG31 уже обсуждался в Solid-State Databases ; здесь мы обсуждаем остальные семь.
База данных S66 (45) имеет эталонные энергии взаимодействия 66 нековалентных связывающих комплексов в равновесной ван-дер-ваальсовой геометрии, и ее можно разделить на три суббазы данных: комплексы с преобладанием затухающей дисперсии (DD23), комплексы с водородными связями (HB23 ), и комплексы, в которых преобладает смесь затухающей дисперсии и электростатических взаимодействий (Mix20). База данных S66x8 включает набор данных S66, а также точные энергии взаимодействия для этих 66 комплексов на семи других расстояниях взаимодействия; в результате база данных S66x8 имеет 528 энергий взаимодействия.Рис. 2 и приложение SI, приложение , таблица S8 показывают результаты для 13 функционалов для базы данных S66, ее под-баз данных и базы данных S66x8 (18, 46). Как показано на рис. 2, функционал revM06-L работает лучше, чем M06-L, M06 и MN15-L. RevM06-L дает лучшие результаты, чем другие четыре локальных функционала из SI Приложение , Таблица S8 для DD23, Mix20, S66 и S66x8, хотя M06-L лучше для HB23. Функционал revM06-L лучше, чем шесть из восьми нелокальных функционалов в таблице для DD23, лучше, чем четыре из них для S66 и S66x8, лучше, чем два для Mix20, и лучше, чем один для HB23.Обратите внимание, что SI Приложение , таблица S8 включает PW6B95-D3 (BJ) (47, 48), гибридный мета-GGA с поправками на молекулярную механику; этот функционал включен, потому что в другом месте (49) подчеркивалось, что PB6B95 с коррекцией дисперсии типа D3 имеет широкую точность, и SI Приложение , Таблица S8 подтверждает это.
Рис. 2.
MUE (килокалорий на моль) 10 выбранных функционалов плотности для баз данных и суббаз S66 и S66x8.
Рис. 3 и SI Приложение , Таблица S9 показывают результаты зависимого от времени расчета функционала плотности валентной энергии и энергии ридберговского возбуждения 11 органических молекул (EE69) с использованием различных функционалов.Данные для других функционалов были представлены в предыдущих исследованиях (50, 51). Как показано на рис. 3, гибридные функционалы обеспечивают лучшую производительность на EE69; лучше всего работает MN15 с MUE 0,26 эВ для всех состояний. Функционал revM06-L примерно одинаково хорошо работает для валентной энергии и энергии ридберговского возбуждения и снижает общую MUE с 0,73 эВ для M06-L до 0,51 эВ, так что он дает лучшую общую производительность для EE69 среди локальных функционалов; он даже превосходит некоторые гибридные функционалы, например.g., PBE0 (52), B3LYP и M06 с MUE соответственно 0,55, 0,67 и 0,88 эВ для всех состояний.
Рис. 3.
MUE (в электронвольтах) 15 выбранных методов для вертикальных энергий возбуждения 30 валентных состояний и 39 ридберговских состояний и для всех 69 переходов. Цифровые метки представляют собой процент обмена Хартри-Фока; когда указан диапазон, первое значение соответствует небольшому межэлектронному расстоянию, а второе соответствует большому межэлектронному расстоянию.WFT, теория волновых функций.
Таблица 3 и SI Приложение , Таблица S10 показывают характеристики нескольких репрезентативных функционалов для базы данных реакций координационного комплекса переходных металлов (WCCR10). Результаты revM06-L, M06-L, ωB97X (53) и ωB97X-D рассчитаны в настоящем исследовании. Результаты MN15, MN15-L и GAM взяты из исх. 18. Все остальные результаты взяты из исх. 54. Таблица 3 показывает, что функционал revM06-L дает лучшие результаты для WCCR10 среди функционалов, представленных в этой таблице.MUE revM06-L составляет 4,8 ккал / моль, что выше 5,2 ккал / моль, заданных M06-L.
Таблица 3.
MUE (килокалорий на моль) для энергий диссоциации лигандов больших катионных комплексов переходных металлов (WCCR10)
База данных высот реакционных барьеров переходных металлов (TMBh31) с участием Mo, W, Zr и Re (55 ⇓ – 57), и результаты приведены в SI Приложение , Таблица S11. Хотя функционал revM06-L хуже работает с высотой реакционного барьера молекул, содержащих W и Zr, чем M06-L, revM06-L по-прежнему дает более низкую среднюю MUE для TMBh31, чем M06-L, из-за пониженных MUE в реакциях с элементами Mo и Re. .Данные Re не участвуют в обучающем наборе, но revM06-L дает лучшие результаты для Re среди всех локальных функционалов и занимает пятое место среди 15 функционалов, представленных в приложении SI , таблица S11. Более того, только один локальный функционал, MN15-L, дает более низкое среднее значение MUE для TMBh31, чем revM06-L. Хорошая производительность revM06-L для TMBE33 в таблице 1 и TMBh31 в приложении SI, приложение , таблица S11 и отличная производительность для WCCR10 в таблице 3 делают revM06-L хорошим выбором функционала для химии TM.
SI Приложение , таблица S12 показывает результаты 13 функционалов (семь локальных функционалов и шесть гибридных функционалов) для базы данных длин гомоядерных димерных связей димеров переходных металлов (58) (TMDBL7). Функционал revM06-L работает несколько хуже, чем M06-L. Однако результаты для TMDBL7, представленные M06-L и revM06-L, очень близки с MUE 0,034 и 0,037 Å соответственно. SI Приложение , таблица S12 показывает, что локальные функционалы предсказывают более точные равновесные длины связи, чем гибридные функционалы для димеров TM.Пять наиболее эффективных функционалов для этой базы данных: MGGA_MS2 (22, 25), MN15-L, M06-L, revM06-L и LSDA, с MUE (2) между 0,028 и 0,043 Å, тогда как ωB97X-D имеет MUE 0,085 Å.
Тринадцать энергий диссоциации алкильных связей (ABDE13) в базе данных SR-MGN-BE Миннесотской базы данных 2015B (18) также используются в качестве тестового набора в этом исследовании. Результаты 21 функционала на ABDE13 показаны в приложении SI, таблица S13. Функционал revM06-L значительно улучшает результат для ABDE13 по сравнению с M06-L, снижая MUE с 5.От 4 ккал / моль до 2,4 ккал / моль. Кроме того, revM06-L дает лучший результат среди 11 локальных функционалов в SI Приложение , Таблица S13. MUE 2,4 ккал / моль близок к MUE 2,0 ккал / моль, который revM06-L дает для базы данных MGBE137 в обучающей выборке (Таблица 1 и SI Приложение , Таблица S4). Следовательно, точность функционала revM06-L хорошо переносится из обучающей базы данных в нетренировочный набор тестов.
Сложной задачей для локальных функционалов является предсказание геометрии структур переходного состояния, которые являются седловыми точками первого порядка для химических реакций.Чтобы изучить этот вопрос, в приложении SI, приложение , таблица S14 показаны результаты TSG в базе данных TSG48 (59), которая содержит 48 данных TSG (в частности, межъядерные расстояния в структурах переходного состояния) для 16 реакций основной группы. Как показано в Приложении SI, Таблица S14, гибридные функционалы обычно предсказывают более точные TSG, чем локальные функционалы. Функционал revM06-L дает лучшие результаты для TSG48, чем M06-L; соответствующие MUE равны 0,052 и 0,070 Å. Функционал revM06-L также дает более низкую MUE, чем 14 из других 17 локальных функционалов в Приложении SI, Таблица S14, при этом M11-L, MN15-L и MN12-L являются первыми тремя, с MUE равными 0. .От 035 до 0,047 Å. Функционал revM06-L также превосходит несколько гибридных функционалов, включая широко используемый B3LYP с MUE 0,065 Å. Обратите внимание, что геометрические данные переходного состояния не использовались для оптимизации каких-либо функционалов.
Кривые потенциальной энергии димеров редких газов и воды.
Потенциальные кривые, рассчитанные для димеров инертных газов Ar ₂ и Kr ₂ с использованием revM06-L и M06-L с базисом aug-cc-pVQZ и сеткой, имеющей 99 радиальных оболочек и 590 угловых точек на оболочку для каждый атом показан в приложении SI , рис.S2 и рис. 4. Расчетные кривые также сравниваются с экспериментальными результатами (60). Из рисунков видно, что функционал revM06-L обеспечивает гораздо более точные кривые связывания для Ar ₂ и Kr ₂, чем M06-L. Хотя энергии связи этих двух димеров вблизи равновесных геометрий находятся в базе данных NGDWI21 обучающей выборки, обнадеживает то, что потенциальные кривые как функции межъядерного расстояния являются разумными, хотя дальний хвост отсутствует, потому что KS-DFT с локальный функционал не предсказывает дисперсию на большие расстояния в области, где взаимодействующие зарядовые облака не перекрываются.Потенциальные кривые M06-L дают слишком пологие минимумы для этих двух систем. Более того, равновесные расстояния связывания, рассчитанные M06-L, на 0,3–0,5 Å больше экспериментальных. Напротив, функционал revM06-L не только дает точную энергию связи вблизи равновесия, но также предсказывает точные равновесные расстояния как для Ar ₂, так и для Kr ₂.
Рис. 4. Кривая потенциала
Kr – Kr, рассчитанная с помощью M06-L и revM06-L с сеткой (99, 590) и базисом aug-cc-pVQZ, по сравнению с экспериментальной кривой.
Расчетные потенциальные кривые для Ar ₂ и Kr ₂ с помощью revM06-L также намного более гладкие, чем кривые, полученные с помощью M06-L. Сообщалось, что ошибки сетки, демонстрируемые набором функционалов M06, возникают из-за ошибок интегрирования в обменно-корреляционной составляющей энергии (23). Для сглаживания потенциальных кривых димеров инертных газов с M06-L требуется не менее 250 радиальных оболочек (25). Как показано в приложении SI , рис. S2 и рис. 4, потенциальные кривые Ar ₂ и Kr ₂, вычисленные с помощью функционала revM06-L, уже являются гладкими с сеткой (99, 590), потому что мы использовали ограничения гладкости для подгоночных параметров, а также удалили некоторые крупные электронные интегральные члены в функциональной форме.Напротив, потенциальные кривые, рассчитанные M06-L, показывают некоторые колебания, которые могут вызвать вычислительную нестабильность при оценке небольших изменений энергии. Делаем вывод, что требования к сетке для функционала revM06-L значительно снижаются.
Кривые потенциала димера воды, рассчитанные с помощью M06-L, revM06-L, MP2 и CCSD (T) с базисным набором aug-cc-pVQZ, показаны в приложении SI , рис. S3. Кривая, рассчитанная с помощью revM06-L, ближе к результату CCSD (T), чем кривая M06-L, особенно в области, где расстояние больше, чем равновесное, даже если обучающая выборка имеет только одну энергию связи димер воды в базе данных NCCE30.Таким образом, мы делаем вывод, что функционал revM06-L больше подходит, чем M06-L, для моделирования молекулярной динамики с участием воды.
Выводы
В этой работе представлена исправленная версия, называемая revM06-L, функционала корреляции обмена M06-L для KS-DFT. Целью этого исследования было изменение параметров функциональной формы M06-L для повышения общей точности и большей вычислительной стабильности для задач как химии, так и физики конденсированного состояния. Мы удалили некоторые большие интегральные члены из функциональной формы, потому что они требуют более мелкого размера сетки и большего количества итераций SCF, а затем мы оптимизировали функционал revM06-L с ограничениями гладкости для базы данных Minnesota 2015A. В результате ограничений плавности параметры в revM06-L намного меньше, чем в M06-L, а количество параметров в revM06-L уменьшено с 34 до 31; кроме того, функционал revM06-L дает более гладкие кривые потенциала для димеров инертных газов, с уменьшенными ошибками сетки и улучшенной вычислительной стабильностью.
Общая производительность revM06-L на AME422 улучшена по сравнению с M06-L, при этом MUE снизился с 3,6 ккал / моль до 3,1 ккал / моль. Характеристики revM06-L для высоты барьера химической реакции (BH76), нековалентных взаимодействий (NC51) и постоянных решетки твердого тела (LC17) особенно значительно улучшены.
Поскольку revM06-L и MN15-L являются двумя наиболее эффективными локальными функционалами, если судить по общему MUE в таблице 1, полезно сравнить их более подробно. Для 25 суббаз AME в Приложении SI, Приложение , Таблица S5, MN15-L имеет MUE, который для 19 из них ниже более чем на 1%. Для энергий изомеризации больших молекул и энергий связи димеров мультиреференсных TM два функционала имеют MUE, которые совпадают в пределах 1%, но revM06-L имеет меньшую MUE для следующих четырех суббаз данных: абсолютные атомные энергии атомов, энергии связей одиночных эталонные металлы основной группы, энергии нековалентного комплексообразования и химический состав углеводородов (соответственно на 36%, 29%, 25% и 13%). Функционал revM06-L также имеет меньшую MUE для двухатомной геометрии молекул тяжелых атомов (на 36%), для постоянных решетки твердого тела (на 11%) и для запрещенной зоны полупроводников (на 44%). Обратите внимание, что запрещенные зоны полупроводников не были включены в обучающую выборку. Однако окончательная полезность различных функционалов, вероятно, проявится только после того, как они будут применены ко многим другим задачам, чтобы увидеть, насколько хорошо они выдерживают испытание временем.
Для нетренирующих тестовых наборов функционал revM06-L дает лучшие результаты среди всех локальных функционалов для баз данных о ширине запрещенной зоны полупроводников (SBG31), нековалентных взаимодействиях (S66), энергиях возбуждения (EE69), реакциях координации переходных металлов (WCCR10). ) и энергии диссоциации алкильной связи (ABDE13).Кроме того, revM06-L дает вторые лучшие результаты (после MN15-L) среди локальных функционалов для высоты барьера реакции ТМ (TMBh31). Для WCCR10 revM06-L работает даже лучше, чем все гибридные функционалы, протестированные в этой работе и предыдущих исследованиях, проведенных нами и другими исследователями.
Локальные функционалы вычислительно эффективны для твердотельных систем с базисными наборами плоских волн, и поэтому revM06-L особенно подходит для практических вычислений при моделировании систем с конденсированной фазой.
Мы пришли к выводу, что функционал revM06-L хорошо подходит для широкого круга приложений в химии и физике конденсированного состояния.
Благодарности
Мы благодарим Pragya Verma за полезную помощь. Эта работа была поддержана Национальным фондом естественных наук Китая (гранты 21303057 и 21673074), Министерством науки и технологий Китая (грант 2016YFA0501700), Специализированным исследовательским фондом для докторской программы высшего образования (грант 20130076120019), Молодежь высшего класса Программа поддержки талантов Шанхая, Центр вычислительной химии Нью-Йоркского университета – Восточно-Китайского педагогического университета (NYU – ECNU) при Нью-Йоркском университете в Шанхае и Министерство энергетики США, фундаментальные энергетические науки (награда DE-SC0012702 Центру проектирования неорганических металлов).
Сноски
Вклад авторов: H.S.Y., D.G.T. и X.H. спланированное исследование; Y.W., X.J. и X.H. проведенное исследование; Y.W., X.J., H.S.Y., D.G.T. и X.H. проанализированные данные; и Y.W., X.J., H.S.Y., D.G.T. и X.H. написал газету.
Рецензенты: G.A.V., Чикагский университет; и W.Y., Университет Дьюка.
Авторы заявляют об отсутствии конфликта интересов.
Эта статья содержит вспомогательную информацию на сайте www.pnas.org/lookup/suppl/doi:10.1073/pnas.1705670114/-/DCSupplemental.
Годунов Александр Леонидович, физический факультет, Университет Олд Доминион
Физический факультет
Университет Олд Доминион,
4600 Элкхорн Авеню
Норфолк, VA 23529
Рабочий телефон: (757) 683-5805
Почта: [email protected]
Отделение: океанография и физика 219
Текущий
Доцент кафедры физики
Университет Олд-Доминион, Норфолк, Вирджиния
Дополнительный
Директор программ бакалавриата
Другие места, где я работал
Образование
Научные интересы
Атомные столкновения
Динамическая корреляция электронов
Распыление
Ускоритель с физикой
Атомная спектроскопия
Вычислительная физика
Атомные данные
Преподавание (текущие и недавние курсы)
Физика 111: Введение в общую физику I
Физика 112: Введение в общую физику II
Физика 231: Университетская физика I
Физика 232: Университетская физика II
Physics 355: Математические методы в физике
Физика 420: Введение в вычислительную физику
Физика 695: Дополнительные темы чистой и прикладной физики
Физика 811: Вычислительная физика
Физика 831: Семинар для выпускников продвинутого уровня I и II
Math 206: Введение в исчисление II
Недавние переговоры
«Решение проблем: искусство, наука и ремесло» (2 октября 2015 г. )
Решение проблем – это один из самых практических навыков, который студент может освоить, если он собирается сделать карьеру в области науки, техники, бизнеса или политики.Что наиболее важно, это также важный навык, который можно использовать в повседневной жизни. К сожалению, хотя в большинстве учебных программ школ и колледжей значительный упор делается на обучение критическому мышлению, это лишь первый шаг в овладении искусством решения проблем. Но как можно взять этот невероятно мощный, но неуловимый навык, разбить его на несколько идентифицируемых шагов и научить других?
Опубликованные книги
10 Избранных публикаций (из 75)
Независимое приближение времени для динамически взаимодействующих многоэлектронных систем
А.Л. Годунов, Дж. Х. МакГуайр,
J.Phys.B: At.Mol.Opt.Phys., Т. 34, L223-L229 (2001) (IOP Publishing)
Взаимодействие атомных систем с рентгеновскими лазерами на свободных электронах
Корнберг М. А., Годунов А.Л., Ица-Ортис С. Эдерер, Дж. McGuire, L.Young,
, Журнал синхротронного излучения, вып. 9, 298-303 (2002)
Эволюция времени и многократное использование в задаче N тел
J. H. McGuire, A. L. Godunov
Phys. Ред.А, т. 67, выпуск 4, 042701 (6 стр.) (2003)
Упорядочение по времени в многоэлектронной динамике
Дж. Х. Макгуайр, А.Л. Годунов, Х. Х. Шаков, В. А. Щипаков, Х. Мерабет, Р. Брух, Дж. Ханни,
J. Phys. Летучая мышь. Мол. Опт. Phys. т. 36, 209-216 (2003) (IOP Publishing)
Полностью дифференциальные сечения для переносной ионизации – чувствительный зонд высокоуровневых корреляционных эффектов в атомах
Годунов А.Л., Колм Т.Уилан, Х. Р. Дж. Уолтерс,
J. Phys. Летучая мышь. Мол. Опт. Phys. т. 37, L201-8 (2004) (IOP Publishing)
Выявление эффекта угловой корреляции в волновой функции He в основном состоянии: исследование совпадений процесс ионизации переноса
М. Шёффлер, А. Л. Годунов, Колм Т. Велан, Х. Р. Дж. Вальтерс, В. С. Щипаков, В. Мергель, Р. Дёрнер, О. Ягуцки, L Ph H Schmidt, J Titze, E Weigold и H Schmidt-Böcking
J. Phys. Летучая мышь. Мол. Опт. Phys.т. 38, L123-8 (2005) (IOP Publishing)
Полные сечения переносной ионизации при столкновениях быстрых ионов с гелием
А. Л. Годунов, Дж. Х. Макгуайр, В. С. Щипаков, Х. Р. Дж. Уолтерс, Колм Т. Велан,
J. Phys. Летучая мышь. Мол. Опт. Phys. т. 39, 987-996 (2006) (IOP Publishing)
О распространении теории (e, 2e) на изучение совпадений в ион-атомных столкновениях
А. Л. Годунов, Марко Кампп, Б. Сулик, Х. Р. Дж. Уолтерс и Колм Т. Велан
Ядерные инструменты и методы в физических исследованиях B 261, 222-225 (2007)
Эффект угловой электронной корреляции в He: расчеты второго порядка для переносной ионизации
А. Л. Годунов, Г. Р. Дж. Уолтерс, Колм Т. Велан,
Phys.Ред. А, т. 78, 012714 (5 стр. ) (2008)
Двойные дифференциальные спектры рассеянных протонов, ионизирующих атомарный водород
М. Шульц, А.С. Лафорж, К. Эгодапития, Ю. Александр, А. Хасан, М.Ф. Чаппина, А.С. Рой, Р. Дей, А. Самолов и
Годунов А.Л.
Phys. Ред. А, т. 81, 052705 (11 стр.) (2010)
Карл Родригес – Физический факультет
Хэлстон Лим и Карл Л.Родригес, Релятивистские эффекты трех тел в иерархических тройках , arXiv: 2001.03654 (2020)
Клэр С. Е. и др. ., О скорости двойных слияний нейтронных звезд из шаровидных скоплений , Astrophys. J. Lett. 888, Л10 (2020)
Кейтлин Брейвик и др. ., КОСМИЧЕСКАЯ Дисперсия в двоичном синтезе популяций , arXiv: 1911.00903 (2019)
Карл Л. Родригес и др. ., Черные дыры: следующее поколение – повторяющиеся слияния в плотных звездных скоплениях и их гравитационно-волновые свойства , Phys. Ред. D 100, 043027 (2019)
Клэр С. Йе и др. ., Миллисекундные пульсары и черные дыры в шаровых скоплениях , Astrophys. J. 877, 122 (2019)
Карл Л. Родригес и др. ., Новый гибридный метод моделирования плотных звездных скоплений , Comput. Astrophys. 5, 5 (2018)
Карл Л.Родригес и Абрахам Леб, Эволюция красного смещения скорости слияния черных дыр из шаровидных скоплений , Astrophys. J. Lett. 866, Л5 (2018)
Карл Л. Родригес и Фабио Антонини, Тройное происхождение тяжелых и низкоспиновых двойных черных дыр, обнаруженных LIGO / VIRGO , Astrophys. J. 863, 7 (2018)
Carl L. Rodriguez et al ., Постньютоновская динамика в плотных звездных скоплениях: высокоэксцентричные, высокоспиновые и повторяющиеся слияния двойных черных дыр , Phys. Rev. Lett. 120, 151101 (2018)
Карл Л. Родригес и др. ., Двойные слияния черных дыр из шаровых скоплений: массы, скорость слияния и влияние звездной эволюции , Phys. Ред. D 93, 084029 (2016)
Carl L. Rodriguez et al ., Слияние двойных черных дыр из шаровидных скоплений: последствия для расширенного LIGO , Phys. Rev. Lett. 115, 051101 (2015)
Стюарт Л.Шапиро | Физика
Стюарт Л. Шапиро Основное направление исследований
Астрофизика / Относительность / Космология

Профессор
(217) 333-5427
237A Лаборатория Лумиса
Образование
Доктор астрофизических наук, Принстонский университет, 1973
А.Б. (Summa Cum Laude), Астрономия, Гарвардский университет, 1969 г.
Биография
Профессор Стюарт Шапиро получил степень А.Бакалавр астрономии из Гарварда в 1969 году, а также степень магистра и доктора философии. Степени астрофизики в Принстонском университете в 1971 и 1973 годах соответственно. Он прошел путь от младшего научного сотрудника до профессора астрономии и физики в Корнеллском университете (1973–1995), а в 1996 году переехал в Иллинойсский университет.
Профессор Шапиро имеет широкие исследовательские интересы, которые охватывают многие области теоретической астрофизики и общей теории относительности, включая физику черных дыр и нейтронных звезд, гравитационный коллапс, генерацию гравитационных волн и динамику больших динамических систем из N тел.Его исследования делают упор на использование суперкомпьютеров для решения давних фундаментальных проблем численной теории относительности и вычислительной астрофизики. Шапиро работал над теорией аккреции на компактные объекты, релятивистской звездной динамикой, гравитационным коллапсом, двойной черной дырой и нейтронной звездой по спирали и слиянием, генерацией гравитационных волн, образованием черных дыр, нуклеосинтезом Большого взрыва и нейтринной астрофизикой, чтобы назовите несколько тем. Некоторые из его наиболее важных симуляций включают спектр испускаемого излучения от аккреции газа на черные дыры и нейтронные звезды, разрушение и поглощение звезд в звездных скоплениях, содержащих сверхмассивную черную дыру в центре, образование сверхмассивной черной дыры в центре галактики. или квазар от коллапса релятивистского бесстолкновительного газа, спирали и слияния двух черных дыр и образования релятивистских струй остатками черных дыр сливающихся намагниченных двойных нейтронных звезд.Он объединил области звездной динамики и численной теории относительности, что привело к моделированию катастрофического коллапса нестабильного релятивистского скопления в черную дыру, численному исследованию космической цензуры и гипотезам “обруча”, а также к демонстрации того, что тороидальные черные дыры могут возникать как переходные процессы во время гравитационного коллапса. Он был первым, кто рассчитал спектр излучения от сферической аккреции на невращающуюся черную дыру в общей теории относительности. Он и его сотрудники придумали термины «супрамассивный» и «сверхмассивный» для описания двух важных классов быстро вращающихся нейтронных звезд, свойства которых они затем определили. Он помог разработать так называемый формализм BSSN (названный по имени Баумгарт-Шапиро-Шибата-Накамура), который теперь так широко используется в численной теории относительности. Давно заинтересовавшись будущим обнаружением гравитационных волн с помощью лазерных интерферометров, таких как LIGO и LISA, Шапиро и его группа работают над теорией генерации гравитационных волн и идентификацией многообещающих астрофизических источников.
Глубокий интерес профессора Шапиро к обучению молодых ученых дал ему репутацию вдохновляющего и эффективного классного руководителя и научного консультанта. Он создал и прочитал более десятка курсов физики и астрофизики. Учебник, соавтором которого он является, Черные дыры, белые карлики и нейтронные звезды: физика компактных объектов (Джон Вили, 1983) является стандартом в этой области. Его исследования привели его к созданию множества видеороликов с компьютерным моделированием, которые предлагают как отличные технические знания для экспертов, так и качественное понимание для неспециалистов.Он возглавляет активную группу аспирантов и докторов наук, работающих в области теоретической астрофизики и общей теории относительности. На протяжении более четырех десятилетий он обучал команду опытных студентов, занимающихся исследованиями в области теоретической астрофизики и общей теории относительности с помощью суперкомпьютерного моделирования и визуализации. Его исследовательская программа бакалавриата является одной из самых успешных в стране; члены его команды пользуются большим спросом среди наиболее избранных программ магистратуры в области физики, астрономии, информатики и смежных областей; многие теперь сами по себе являются выдающимися учеными и преподавателями.
Важные ссылки
Заявление об исследовании
Я вместе с моей группой занимаюсь исследованиями в области общей теории относительности и теоретической астрофизики, финансируемые моими грантами NSF и NASA. Наша сфера деятельности – решение проблем, связанных с общей теорией относительности, генерацией гравитационного излучения, релятивистской гидродинамикой и релятивистской магнитогидродинамикой. Общей нитью, объединяющей различные теоретические темы, является решающая роль гравитации, особенно релятивистской гравитации.Компактные объекты представляют собой главный форум, а динамика материи в сильном гравитационном поле – главная тема. Некоторые из тем для исследования включают в себя спиральное слияние и слияние компактных двойных систем (двойные черные дыры, двойные нейтронные звезды, двойные черные дыры – нейтронные звезды и двойные белые карликовые нейтронные звезды), генерацию гравитационных волн из двойных систем и другие многообещающие астрофизические аспекты. источники и сопутствующие электромагнитные сигналы, гравитационный коллапс, стабильность вращающихся, релятивистских звезд, эволюция и окончательная судьба нестабильных звезд, источники гамма-всплесков, окружные диски вокруг сливающихся сверхмассивных черных дыр в ядрах галактик и квазаров, распределение темной материи вокруг сверхмассивных черных, а также гравотермическое сжатие и коллапс скоплений темной материи в сверхмассивные черные дыры. Большинство этих тем представляют собой давние фундаментальные проблемы теоретической физики, для решения которых требуются крупномасштабные вычисления. Следовательно, подход включает в себя в значительной степени крупномасштабные вычисления на параллельных машинах, а также аналитическое моделирование. Во многих численных расчетах используются самые современные вычислительные ресурсы и средства визуализации. Они включают в себя вычисления как начальных значений, так и эволюции и рассматривают вакуумные пространства-времени, содержащие черные дыры, а также пространства-времени, содержащие реалистичные источники материи, магнитные поля, а также электромагнитное и нейтринное излучение.Результаты имеют важное значение для астрономических наблюдений, в том числе тех, которые измеряются нынешними и будущими интерферометрами гравитационных волн и детекторами гамма-всплесков.
Книги
Избранные статьи в журналах
M. Ruiz, S.L. Шапиро и А. Цокарос. GW170817, Общее релятивистское магнитогидродинамическое моделирование и максимальная масса нейтронной звезды. Ред. D: Rapid Commun. 97, 021501 (2018). Максимальная масса нейтронной звезды
М. Руис, Р. Ланг, В. Пасхалидис и С.Л. Шапиро. Слияние двойных нейтронных звезд: реактивный двигатель для коротких гамма-всплесков. Astrophys. J. Lett. 824, Л1 (2016). GRB форсунки
M.D. Duez, Y.T. Лю, С. Шапиро и Б. Стивенс. Релятивистская магнитогидродинамика в динамическом пространстве-времени: численные методы и тесты. Phys. Ред. D 72, 024029 (2005). «Кодекс GRMHD Иллинойса»
Т.W. Baumgarte, S.L. Шапиро и М. Шибата, «О максимальной массе дифференциально вращающихся нейтронных звезд», he Astrophysical Journal Letters 538, L29 (2000). «Гипермассивные нейтронные звезды»
T.W. Баумгарт и С. Шапиро, «Численное интегрирование уравнений поля Эйнштейна», Physical Review D 59, 024007 (1998). «БССН»
S.L. Шапиро, С.А. Теукольский, “Релятивистская динамика звезд на компьютере.I. Мотивация и численный метод ”, The Astrophysical Journal, bf 298, 34 (1986).
А.П. Лайтман, С.Л. Шапиро, «Динамическая эволюция шаровых скоплений», Review of Modern Physics 50, 437 (1978).
S.L. Шапиро, А.П. Лайтман, Д. Эрдли, «Двухтемпературная модель аккреционного диска для Лебедя X-1: структура и спектр», The Astrophysical Journal 204, 187 (1976).
S.L. Шапиро, «Аккреция на черные дыры: новый спектр излучения», The Astrophysical Journal 180, 531 (1973).
Награды за научные исследования
Премия Ханса А. Бете, Американское физическое общество (2017)
Зал почета средней школы Амити (2006)
Научный сотрудник, Институт физики, Великобритания (2004 г.)
Сотрудник Американского физического общества (1998)
Первая премия, IBM Supercomputing Competition (1991)
Премия за выдающиеся достижения в области крупномасштабных вычислений (1990)
Премия IBM Supercomputing Competition Award (1990)
Стипендия Мемориального фонда Джона Саймона Гуггенхайма (1989-90)
Премия Ассоциации американских издателей (1984)
Альфред П.

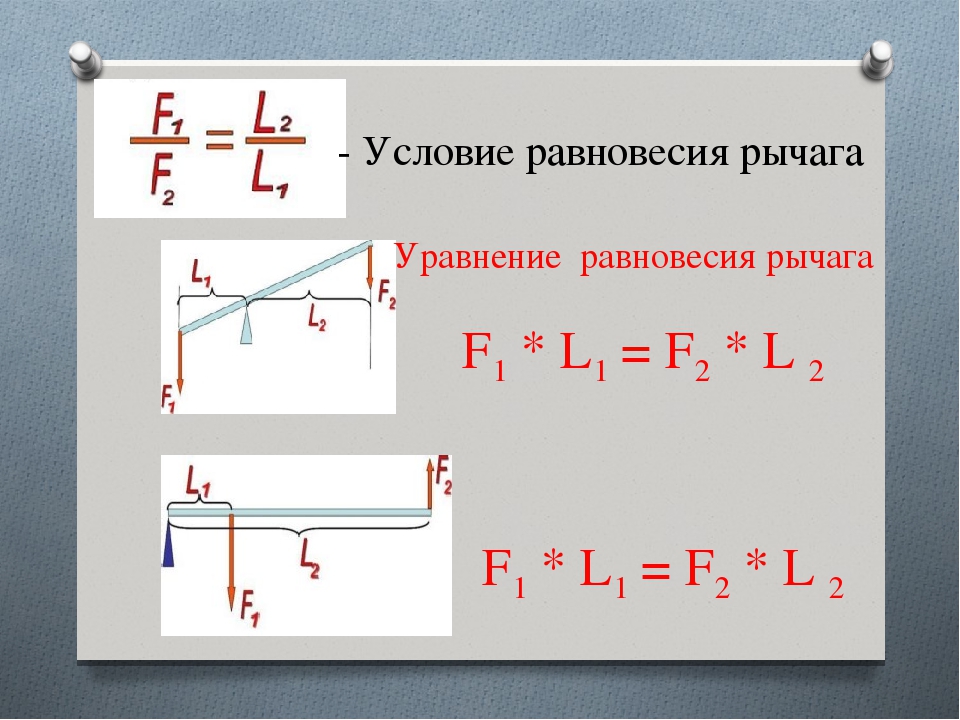Эдвин Л. (Тед) Вуллет Почетный профессор физики и астронии., CSULB к.э.н. – Университет штата Канзас, 1965, Вычислительная физика

3. Графики зависимости кинематических величин равноускоренного движения

Физика БФУ им. И. Канта наградили за победу в конкурсе L’OREAL-UNESCO «Для женщин в науке»

“Стихотворство – моя утеха, физика – мои упражнения” М.В.Ломоносов

Архивы задач 2009-2018 – Всероссийская олимпиада по физике.

Математическая физика | Николай Филонов.

Открытая Физика. Электромагнитная индукция. Правило Ленца

Высокочувствительный алмазный магнитометр с наноразмерным разрешением

Учебник по физике: математика стоячих волн

o :: Веб-страница Эдвина Л. (Теда) Вуллетта :: o:

Пересмотренный функционал M06-L для повышения точности определения высоты барьера химических реакций, нековалентных взаимодействий и физики твердого тела

Значение

Abstract

Результаты и обсуждение

Атомная и молекулярная энергия.

База данных молекулярной структуры.

Твердотельные базы данных.

Характеристики revM06-L на необучаемых испытательных наборах.

Кривые потенциальной энергии димеров редких газов и воды.

Выводы

Благодарности

Сноски

Годунов Александр Леонидович, физический факультет, Университет Олд Доминион

Текущий

Дополнительный

Другие места, где я работал

Образование

Научные интересы

Преподавание (текущие и недавние курсы)

Недавние переговоры

Опубликованные книги

10 Избранных публикаций (из 75)

Карл Родригес – Физический факультет

Стюарт Л.Шапиро | Физика

Основное направление исследований

Образование

Биография

Заявление об исследовании

Книги

Избранные статьи в журналах

Награды за научные исследования

Оставить комментарий Отменить ответ