Физика мгновенная скорость формула: Мгновенная скорость – формула определения, уравнение

Мгновенная скорость – формула определения, уравнение

4.3

Средняя оценка: 4.3

Всего получено оценок: 64.

4.3

Средняя оценка: 4.3

Всего получено оценок: 64.

Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.

Скорость при неравномерном движении

Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

$$v= {S\over t}$$

Рис. 1. Скорость равномерного прямолинейного движения.

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.

В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:

$$v={20\over 2.02}=9.9(м/с)$$

Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.

9м ниже.

Однако, проведя реальное измерение, можно убедиться, что это совсем не так. За первую секунду предмет пройдет только 4.9м. А за первые полсекунды – всего лишь 1.23м ! Если же высота падения будет больше, то за три секунды путь составит не 29.7м, как следует из формулы, а больше 40м !

Рис. 2. Стробоскопическое фото свободного падения.

Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.

Свести неравномерное движение к равномерному невозможно.

Мгновенная скорость

Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.

Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:

Время	Координата	Скорость
1.000	4.905	–
2.000	19.620	14.715
1.500	11.036	12.263
1.100	5.935	10.301
1.050	5.408	10.055
1.010	5.004	9.859
1.001	4.915	9.815

Можно видеть, что с уменьшением рассматриваемого отрезка времени, изменение вычисленной скорости между строками таблицы также становится меньше.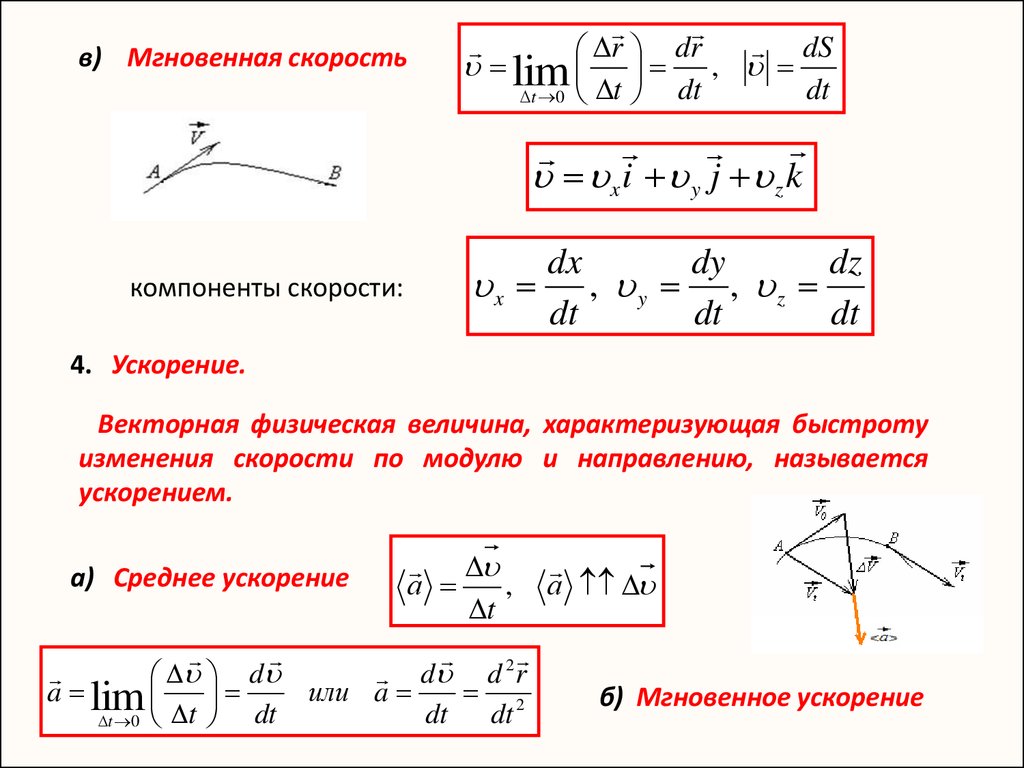

Приведенный пример показывает главный прием, который используется для изучения непрерывных величин – изучаемый диапазон разбивается на мелкие участки, на которых изменение скорости невелико, и движение мало отличается от непрерывного. В пределе время прохождения каждого такого участка стремится к нулю, а скорость на его протяжении постоянна.

Скорость материальной точки в данный момент времени при прохождении данного малого участка пути называется мгновенной скоростью.

Рис. 3. Мгновенная скорость.

Мгновенная скорость материальной точки равна отношению малого перемещения на пути движения к времени прохождению этого перемещения. Формула мгновенной скорости:

$$v={ΔS\over Δt}, при Δt \rightarrow 0$$

Если для моментов времени, приведенных выше, измерить точные значения мгновенной скорости падающего предмета, то получим следующую таблицу (с отличиями от предыдущей таблицы):

Время	Мгновенная скорость	Отличие,%
2. 000	19.620	25.00
1.500	14.715	16.67
1.100	10.791	4.55
1.050	10.301	2.38
1.010	9.908	0.5
1.001	9.820	0.05

Можно видеть, что по мере уменьшения рассматриваемых отрезков времени отличия между первой и второй таблицей уменьшаются.

Что мы узнали?

Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 64.

---

А какая ваша оценка?

Мгновенная скорость, теория и онлайн калькуляторы

Мгновенная скорость, теория и онлайн калькуляторы

Мгновенная скорость при прямолинейном движении материальной точки

При рассмотрении неравномерного движения часто интересует не средняя скорость движения тела, а скорость в определенный момент времени, или мгновенная скорость. Так, если тело стукнулось о препятствие, то сила воздействия тела на препятствие в момент удара, определено скоростью в момент соударения, а не средней скоростью движения тела. Форма траектории перемещения снаряда и его дальность полета зависит от скорости в момент запуска, а не от средней скорости.

Средняя скорость ($\left\langle v\right\rangle $) движения материальной точки по оси X равна:

\[\left\langle v\right\rangle =\frac{\Delta x}{\Delta t}\left(1\right),\]

$\Delta t$ – промежуток времени движения тела.

Определение

Мгновенную скорость определим как предел к которому стремится средняя скорость за бесконечно малый промежуток времени:

\[v={\mathop{\lim }_{\Delta t\to 0} \left\langle v\right\rangle \ }={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta x}{\Delta t}\left(2\right).\ }\]

Такой предел в математике называют производной:

\[v=\frac{dx}{dt}=\dot{x}\left(3\right).\]

Выражение (3) обозначает, что мгновенная скорость (скорость в определенный момент времени) – производная от координаты. При прямолинейном движении материальной точки Мгновенную скорость можно определить как производную от пути ($s$) по времени:

\[v=\frac{ds}{dt}=\dot{s}\left(4\right).\]

Мгновенная скорость равномерного движения материальной точки

Средняя скорость равномерно движущейся точки величина постоянная, значит, мгновенная скорость равномерно перемещающейся точки является неизменной величиной.

Скорость равномерного движения численно равна тангенсу угла наклона прямой к оси времени (рис.1):

\[v=k\ tg\ \alpha \ \left(4\right),\]

где $k$ – безразмерный коэффициент, определяющий отношение масштаба единиц перемещения (ось ординат) и единиц времени (ось абсцисс).

При графическом изображении переменного движения материальной точки мгновенная скорость численно равна тангенсу угла наклона касательной к графику и осью абсцисс.

Мгновенная скорость при криволинейном движении

Положение материальной точки на траектории зададим радиус-вектором $\overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:

\[\overline{v}=\frac{d\overline{r}}{dt}=\dot{\overline{r}}\left(5\right).\]

скорость – это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.

2\to 8t+4t=1+3\to 12t=4\to t=\frac{1}{3}\left(c\right).\]

Ответ. $t=\frac{1}{3}$ с

   

Пример 2

Задание. Материальная точка движется на плоскости XOY. Закон изменения координаты $x$ задан графиком рис.2 . Координата $y\ $задана аналитическим выражением: $y=At(1+Bt)$, где $A$ и $B$ постоянные величины. Запишите выражение, связывающее мгновенную скорость и время ($v(t)$).

       

Решение. Из рис. 2 мы можем записать уравнение, которое определяет изменение координаты $x$ от времени:

\[x\left(t\right)=At\ \left(2.1\right).\]

Получили, что движение материальной точки в плоскости XOY описывают при помощи системы уравнений:

\[\left\{ \begin{array}{c} x\left(t\right)=At;;\ \\ y=At\left(1+Bt\right) \end{array} \left(2.2\right). 2}$

   

Читать дальше: механические волны.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Мгновенная и средняя скорость | Физика

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).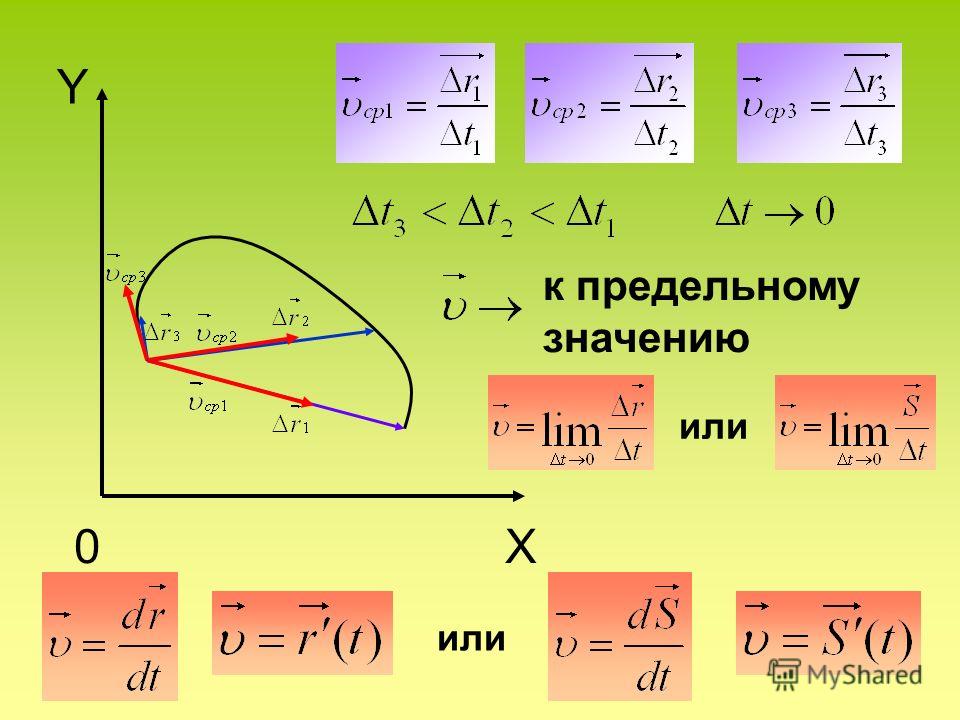

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t.     (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂),     (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

Формула мгновенной скорости – GeeksforGeeks

Скорость определяется как скорость изменения его положения относительно его системы отсчета. Это векторная величина, поскольку она имеет величину и направление. Единицей скорости в системе СИ является метр в секунду или м/с. В то время как скорость измеряет расстояние, пройденное объектом за изменение времени. У него есть величина, но нет направления, и, следовательно, это скалярная величина. Единицей скорости в системе СИ является метр в секунду или м/с.

Введение в мгновенную скорость

Мгновенная скорость определяется как скорость объекта в определенный момент времени. Это величина скорости. Это реальная скорость в конкретный момент. Когда время приближается к нулю, расстояние, пройденное объектом, также приближается к нулю. Это ненулевой предел отношения расстояния ко времени. С точки зрения графика мгновенная скорость — это наклон касательной в любой точке пути.

Формула мгновенной скорости:

Согласно формуле, мгновенная скорость представляет собой отношение расстояния ко времени.

Скорость (I) = LIM _{DT-> 0} DS/DT

Где,

Скорость (I) = Мгновенная скорость

DS = пройденная дистанция

DT = временный интервал

. Установленная скорость. можно рассчитать, разделив кратчайшее расстояние, пройденное объектом за короткий промежуток времени. мы также можем рассчитать его, определив наклон позиции в зависимости от графика времени.

Единица мгновенной скорости

Единицей мгновенной скорости в системе СИ является метр в секунду или м/с. Единицей мгновенной скорости в СГС является см/с. Это скалярная величина, потому что она имеет величину, но не имеет направления.

Разница между средней скоростью и мгновенной скоростью

Средняя скорость	Мгновенная скорость
Средняя скорость в общей сумме.	Мгновенная скорость определяется как скорость в конкретный момент времени.
Формула: Общее расстояние / Общее время	Формула: Расстояние в этот момент / Время в этот момент.
Измеряется путем расчета скорости на всем пути	Измеряется с помощью спидометра.
Всегда постоянна.	Это не константа.
Пример: Велосипед движется со скоростью 40 миль/час; таким образом, средняя скорость составляет 40 миль в час.	Пример: Велосипед, движущийся с определенной скоростью в момент времени, может быть определен спидометром.

Difference between Instantaneous Speed ​​and Instantaneous Velocity

4 Единица измерения: 9003 секунда (м/с)

Instantaneous Speed ​​	Instantaneous Velocity
Instantaneous speed is the magnitude of instant velocity at a given instant of time	Instantaneous velocity is изменение положения, происходящее за очень небольшой промежуток времени
Это скалярная величина.	Это векторная величина.
Формула: Скорость(I) = ds/dt	Формула: Vi = lim ∆t→0 ds/dt
Единица: Метры в секунду (м/с)

Примеры задач

Вопрос 1. Вычислите мгновенную скорость объекта, который проходит расстояние, заданное функцией x(t) = 5t ³ – 16t +100 м при t =8с.

Решение:

Дано:

x (t) = 5T ³ -16T +100 M

T = 8S

S _Inst = LIM _{T-> T} (DX/DT)

= LIM _t->8 d[x(t)]/dt

= lim _t->8 d[5t ³ – 16t + 100] / dt

= lim _t->8 [134t 900 2 – 16]

= 15(8) ² – 16

= 15(64) – 16

S _inst = 944 м/с

A делает снимок телескопа: метеор, преодолевший расстояние 100 км за 0,001 секунды.

Какова мгновенная скорость этого метеора в момент съемки?

Решение:

За очень короткое время мгновенная скорость метеора будет равна:

Скорость = Расстояние/Время

= 100 км/0,001 секунды .

Вопрос 3: Мяч подброшен в воздух. Он проходит весь путь вверх, а затем в момент времени t = a единиц прекращает движение вверх и начинает движение обратно вниз. Какова будет мгновенная скорость мяча в момент времени t = a единиц?

Ответ:

В момент времени t = a единиц мгновенная скорость мяча будет равна нулю, поскольку мяч останавливается, а затем начинает свое движение вниз под действием силы тяжести.

Вопрос 4: Когда объект падает под действием силы тяжести, его положение изменяется в соответствии с функцией x(t) = 4,9t ² , а x(t) выражается в метрах. Чему равна мгновенная скорость в момент времени t = 2,5 с?

Решение:

Дано:

x(t) = 4,9t ²

t = 2,5 с

Найдите мгновенную скорость по формуле: t->2,5 d[x(t)]/dt

= lim _t->2,5 d[4,9t ² ] / dt

= lim _t->2,5 [9,023] 90,8t = 9,8(2,5)

= 24,5 м/с

Вопрос 5: Рассчитайте мгновенную скорость объекта, который проходит расстояние, определяемое функцией x(t) = 2t ² + t + 10 см при t = 2с.

Ответ:

Дано:

x (t) = 2t ² + T + 10 см

T = 2S

S _Inst = LIM _{T-> T-} (DX/DT)

= lim _t->2 d[x(t)]/dt

= lim _t->2 d[2t ² + t + 10] / dt

= lim t-> ₂ [4t + 1]

= 4(2) + 1

S _inst = 9 см/с

Формула мгновенной скорости – определение и измерение

Существует два способа измерения скорости движения объекта или частицы в заданном положении и времени: Мгновенная скорость и Средняя скорость. На Vedantu вы можете узнать больше о значениях обоих типов скорости, о том, как различать мгновенную и среднюю скорость и как рассчитать мгновенную скорость с помощью формулы.

 

Мы знаем, что общее пройденное расстояние, деленное на общее время, равно средней скорости за данный интервал времени. Пройденное расстояние приближается к 0, когда временной интервал приближается к нулю. Мгновенная скорость, с другой стороны, является ненулевым пределом отношения расстояния ко времени. Мы также можем сказать, что Мгновенная Скорость в любой момент времени есть величина Мгновенной скорости в это время, другими словами.

Средняя скорость за данный промежуток времени равна пройденному расстоянию, деленному на общее необходимое время. Когда временное окно приближается к нулю, пройденное расстояние приближается к нулю. Мгновенная скорость, с другой стороны, является ненулевым пределом отношения расстояния ко времени. Иными словами, мгновенная скорость в любой момент времени — это величина мгновенной скорости в этот конкретный момент времени.

 

Формула мгновенной скорости

Формула мгновенной скорости выглядит следующим образом:

Скорость(i) =\[ \frac{ds}{dt}\]

• ds здесь обозначает расстояние

• Им обозначается интервал времени.

• Мгновенная скорость — это скорость(i).

 

Подробнее по теме

Когда мы рассматриваем, насколько быстро или медленно движется тело, мы сталкиваемся с понятием скорости. Мы как-то связываем перемещение тела со временем, проведенным в таком перемещении. Этот тип отношений проявляется как мгновенная скорость. В этой главе мы узнаем о мгновенной скорости и формуле мгновенной скорости.

 

Что такое скорость?

Давайте узнаем, что такое скорость! Скорость определяется как скорость, с которой положение объекта изменяется с течением времени. Скорость объекта может изменяться по мере его движения. Скорость объекта в данный момент времени называется его мгновенной скоростью. Если положение является функцией времени, скорость определяется изменением положения с течением времени.

 

Поскольку изменение во времени становится небольшим, можно найти мгновенную скорость. Нахождение предела функции положения, когда изменение во времени приближается к нулю, требуется для вычисления мгновенной скорости.

 

(Изображение будет загружено в ближайшее время)

 

Что такое мгновенная скорость?

Скорость изменения расстояния до объекта во времени. Единицей скорости является метр в секунду (м/с).

 

Мгновенная скорость никогда не меньше или равна нулю. Скалярная величина – это мгновенная скорость. Мгновенная скорость равномерного движения постоянна. Другими словами, величина мгновенной скорости может быть определена как величина мгновенной скорости в любой момент времени. Поскольку временной интервал становится очень маленьким, мгновенная скорость становится пределом средней скорости.

 

Как измерить мгновенную скорость?

Мгновенная скорость (v) =\[ \frac{\text{расстояние}}{\text{время}}\]

v = предел изменения в 90983 время приближается к нулю (изменение положения/изменение времени)

 

Мгновенное и среднее

Когда полицейский останавливает вас за превышение скорости, он измеряет мгновенную скорость вашего автомобиля или скорость в определенный момент времени, когда он ускоряется по дороге. «Мгновенный» происходит от слова «мгновенный», которое относится к одному моменту.

 

Это отличается от средней скорости вашего путешествия, которая учитывает, сколько времени ушло на прохождение всего пути, а также пройденное расстояние. Будьте осторожны: измерение средней скорости предполагает, что вы двигались примерно с одной и той же скоростью на протяжении всей поездки.

 

Чтобы вычислить мгновенную скорость, разделите часть общего пройденного расстояния на время.

 

Разница между мгновенной скоростью и мгновенной скоростью

Мгновенная скорость	Мгновенная скорость
	Изменение положения, происходящее при небольшом изменении времени, называется мгновенной скоростью.
Величина мгновенной скорости является скалярной величиной.	Векторная величина — это мгновенная скорость.

Калькулятор мгновенной скорости – формула и функция

Онлайн-калькулятор мгновенной скорости позволяет рассчитать мгновенную скорость, соответствующую мгновенной скорости изменения формулы скорости. Да, вычисление мгновенной скорости становится эффективным с помощью этого инструмента, поскольку он устраняет вероятность ошибки ручных вычислений.

Этот пост поможет вам понять, как найти мгновенную скорость и все факты, которые вам нужно знать об этом. Итак, начнем с его основного определения в физике! Кроме того, попробуйте этот калькулятор скорости для физики, с помощью которого вы можете легко рассчитать скорость движущегося объекта.

Что такое мгновенная скорость в физике?

В физике изменение расстояния во времени в определенной точке называется мгновенной скоростью и определяет скорость объекта, движущегося по дороге в любой конкретной точке его пути. Обычно мы называем это простой скоростью, а ее величину называют мгновенной скоростью. Кроме того, это векторная величина, и мы также можем сказать, что это средняя скорость, которая присутствует между любыми двумя точками на любом пути в конкретное ограниченное время или в любой конкретный момент. Для удобства калькулятор мгновенной скорости онлайн поможет вам рассчитать скорость объекта в определенный момент времени.

Математическое представление:

Для его математического представления предположим две точки на любой дороге. Очки будут представлены «x». Теперь предположим, что автомобиль движется между этими двумя точками в определенный промежуток времени «t». Простая средняя скорость движущегося автомобиля между этими двумя точками будет представлена ​​следующим образом:

«v=x(t2) −x(t1) t2−t1v—=x(t2) −x(t1) t2−t1», в частности время «t»

Мгновенная скорость в любой точке дороги будет следующей:

«t1=tt1=t и t2=t+Δtt2=t+Δt»

Теперь подставим эти значения в уравнение средней скорости и возьмем предел следующим образом:

«Δt→0Δt→0»

Наконец, мы получим окончательное физическое представление мгновенной скорости в численном виде следующим образом: (t)=limΔt→0x(t+Δt)−x(t)Δt=dx(t)dt»

На основании приведенного выше объяснения можно сказать, что мгновенная скорость любого движущегося объекта является пределом средняя скорость и скорость изменения положения любого объекта.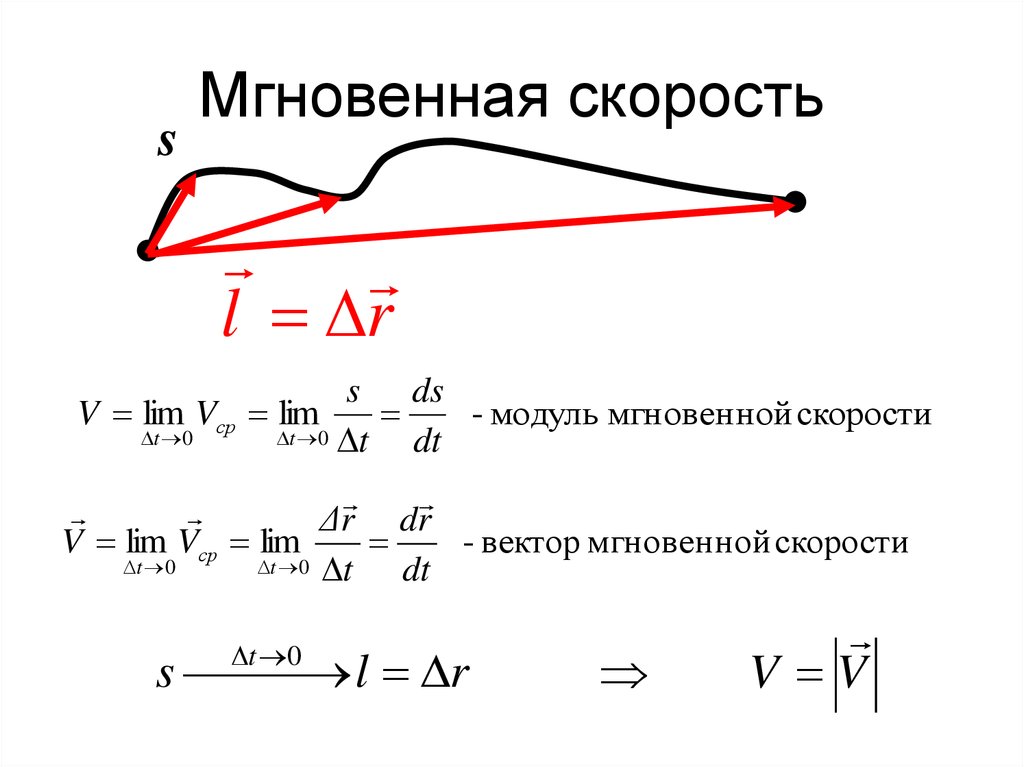 Его значение всегда будет небольшим.

Какова формула мгновенной скорости?

Иногда в случае движущегося автомобиля нас интересует вычисление мгновенной скорости, чтобы узнать его скорость в любой конкретный момент времени. Это можно определить простым способом, применяя следующую формулу:

Формула мгновенной скорости: Vint=limΔt→0Δx/Δt=dx/dt.

Объясненное выше уравнение мгновенной скорости можно упростить следующим образом:

Vi=limΔt→0ds/dt

Принимая во внимание:

• Δt = очень малая часть времени или интервала времени.
• Vi= мгновенная скорость любого движущегося объекта.
• с = водоизмещение.
• т = время.

Хотя мы можем найти это по формулам, использование калькулятора мгновенной скорости является еще одним вариантом проверки ответов.

Единица мгновенной скорости:

В соответствии с международной системой единиц его единицей является комбинация: единица расстояния / единица скорости. Следовательно:
Единица СИ: ds/dt = м/с = мс-1.

Мгновенная скорость Пример:

Если вы куда-то едете на автомобиле, то его измеритель скорости показывает вам мгновенную скорость. Поэтому можно сказать, что это текущая скорость любого движущегося объекта. Более того, если автомобиль имеет равномерную скорость, то его мгновенная скорость будет аналогична его стандартной скорости.

Возьмем еще один пример велосипедиста, который участвовал в гонке и двигался вперед. Во время езды на велосипеде его скорости постоянно меняются. В один конкретный момент, если вы хотите рассчитать его скорость, она будет известна как мгновенная скорость. Для вычисления мгновенной скорости велосипедиста можно использовать следующие два подхода:

1. Применение формулы мгновенной скорости =limΔt→0Δx/Δt=dx/dt.
2. Использование калькулятора мгновенной скорости, чтобы избежать ручных вычислений.

О калькуляторе мгновенной скорости:

Калькулятор мгновенной скорости поможет вам найти мгновенную скорость в соответствии с физической формулой мгновенной скорости. Этот калькулятор не только помогает рассчитать мгновенную скорость, но также начальное перемещение, конечное перемещение, начальное затраченное время и конечное затраченное время.

Как найти мгновенную скорость С помощью этого калькулятора мгновенной скорости:

Вы можете легко найти мгновенную скорость с помощью этого калькулятора, все, что вам нужно придерживаться указанных шагов:

Входные данные:

Эта мгновенная скорость Калькулятор предоставил вам пять полей ввода, а именно:

• Начальное смещение
• Окончательное смещение
• Начальное время взято
• Последнее время
• Мгновенная скорость

Вам просто нужно ввести значения в любые четыре поля выше, чтобы рассчитать пятое!

Выходы:

• После того, как вы введете значения в любые четыре поля, нажмите кнопку расчета, результаты могут быть либо мгновенной скоростью, начальным смещением, конечным смещением, начальным затраченным временем и конечным затраченным временем.

Разница между мгновенной скоростью и мгновенной скоростью:

Мгновенная скорость:

• Говорят, что мгновенная скорость равна величине мгновенной скорости
• Говорят, что это скалярная величина
• Формула мгновенной скорости: Скорость (i) = ds/dt

Мгновенная скорость:

• Мгновенная скорость определяется как изменение положения при небольшом изменении времени
• Говорят, что это векторная величина
• Формула мгновенной скорости: Vint=limΔt→0Δx/Δt=dx/dt

Как рассчитать мгновенную скорость (вручную)?

Предположим, что частица движется вперед по прямой линии в течение 3 секунд. Его положение x определяется как: 5² + 2t + 4? Какова будет его мгновенная скорость?

В предыдущем вопросе:

• x =5t² + 2t + 4.

Мы просто применим формулу мгновенной скорости: Vi=dx/dtVi=dx/dt

На следующем шаге мы подставим значение функции x в уравнение мгновенной скорости.

• Vi=ddt5t2+2t+4Vi=ddt5t2+2t+4
• Vi=10t+2Vi=10t+2

Теперь подставим значение t= 3

• Vi=10×3+2Vi=10×3+2
• Vi=32 мс-1Vint=32 мс-1
• Vi = 32 мс или 132 мс-1.

Примечание. Определение мгновенной скорости может быть очень сложным, поскольку это постоянная скорость любого движущегося объекта в любой конкретный период времени. Он существует в течение очень короткого периода времени, а затем меняется. С другой стороны, чтобы избежать риска ошибки при ее расчете, онлайн-калькулятор мгновенной скорости — лучший вариант.

Часто задаваемые вопросы (мгновенная скорость):

Можно ли непосредственно измерить мгновенную скорость?

Нет, помните, что мгновенную скорость никогда нельзя измерить, потому что нет единственного способа сделать что-либо мгновенно. Помните, что все измерения требуют некоторого времени для выполнения.

Как найти мгновенную скорость функции?

Исследование физики показывает, что мгновенная скорость указывается как непрерывная функция времени и даже дает скорость в любой момент времени во время движения частицы. Чтобы вычислить мгновенную скорость в определенное время, вам просто нужно взять производную функции положения, которая дает вам функциональную форму мгновенной скорости v(t).

В чем разница между мгновенной скоростью и средней скоростью?

С точки зрения физики мгновенная скорость обозначается как конкретная скорость изменения смещения (или положения), соответствующая времени в одной точке (x,t), а когда речь идет о средней скорости, говорят быть как средняя скорость изменения смещения (или положения) во времени за интервал.

Является ли мгновенная скорость такой же, как ускорение?

Нет, оба различны, так как когда расстояние (s) объекта изменяется со временем, его скорость называется скоростью, с которой расстояние изменяется в соответствии с t во времени, а его ускорение указывается как скорость, с которой скорость меняется соответственно времени.

Если объект имеет мгновенную скорость 40 миль в час, то какова его мгновенная скорость?

Просто говорят, что мгновенная скорость этого объекта составляет 40 миль в час.