Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси
- Подробности
- Просмотров: 662
«Физика – 10 класс»
Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?
Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.
Момент импульса.
Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис.
Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.
Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):
L = mvr.
Линейная и угловая скорости связаны соотношением v = ωr, тогда
L = mr2ω.
Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:
Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.
Основное уравнение динамики вращательного движения в импульсной форме.
Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: Подставим это выражение в основное уравнение динамики вращательного движения отсюда I(ω
Таким образом,
ΔL = MΔt. (6.4)
Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.
Закон сохранения момента импульса:
Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.
ΔL = 0, L = const
Изменение импульса системы равно суммарному импульсу сил, действующих на систему.
Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.
Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).
Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.
На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.
Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.
Кинетическая энергия вращающегося твёрдого тела.
Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:
Угловая скорость вращения всех точек тела одинакова, следовательно,
Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид
В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна
В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика
Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса.
“Момент инерции абсолютно твердого тела 10 класс”
План урока
Раздел : ДинамикаШкола:
Дата:
ФИО учителя:
Класс: 10
Количество присутствующих:
Отсутствующих:
Тема урока
Момент инерции абсолютно твердого тела
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
использовать теорему Штейнера для расчета момента инерции материальных точек
Цели урока
Научится рассчитывать энергию вращательного движения и применять теорему Штейнера для расчета момента инерции абсолютно твердых тел
Критерии оценивания
Учащийся достигли цели обучения если могут рассчитывать энергию вращательного движения и применять теорему Штейнера для расчета момента инерции абсолютно твердых тел
Языковые цели
Развитие навыков говорения и слушания при обсуждении материала.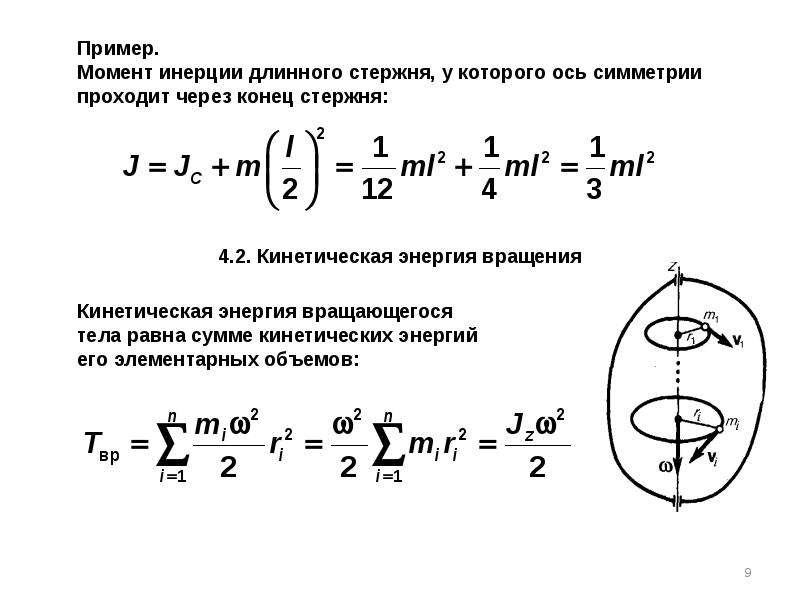
Лексика и терминология, специфичная для предмета:
энергия вращательного движения, момент инерции тела, теорема Штейнера, второй закон Ньютона для вращательного движения
Привитие ценностей
Коммуникативные навыки, ответственность, аккуратность, расширение кругозора, множественный интеллект, функциональная грамотность
Межпредметные связи
Математика, геометрия
Навыки использования ИКТ
Интерактивная доска, ноутбуки, PowerPoint
Предварительные знания
Кинетическая энергия поступательного движения, основные характеристики вращательного движения, второй закон Ньютона
Ход урока
Запланированные этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока 2 мин
5 мин
Вступительное слово учителя (Мобилизующее начало урока. Психологический настрой на урок.)
Психологический настрой на урок.)
Проверка выполнения домашнего задания (сочетания контроля, самоконтроля и взаимоконтроля)
Цель: Проверить уровень усвоения учебного материала, выявить пробелы и скорректировать их.
А)Актуализация опорных знаний
Форма: коллективная
Метод: индивидуальный
Прием: вопрос-ответ
Взаимопроверка
Вопросы:
сформулируйте три знаменитые законы движения.
I закон (закон инерции): Материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её (его) изменить это состояние.
II закон В ИСО ускорение тела пропорционально векторной сумме всех действующих на тело сил и обратно пропорционально массе тела:
III закон Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению:
В) Решения задач (Индивидуальная работа)
1. Человек везет двое связанных саней, прикладывая силу под углом 300 к горизонту. Найдите эту силу, если известно, что сани движутся равномерно. Массы саней по 40кг. Коэффициент трения 0,3.
Человек везет двое связанных саней, прикладывая силу под углом 300 к горизонту. Найдите эту силу, если известно, что сани движутся равномерно. Массы саней по 40кг. Коэффициент трения 0,3.
2.Шайба остановилась через 5с после удара клюшкой на расстоянии 20м от места удара. Масса шайбы 100г. Определить силу трения между шайбой и льдом.
3.Чему должен быть равен минимальный коэффициент трения и между шинами и поверхностью дороги с уклоном 300, чтобы автомобиль мог двигаться по ней вверх с ускорением 0,5м/с2?
Интерактивная доска
Карточки вопросники
Середина урока
15 мин
17 мин
18 мин
Подготовка к активному усвоению и осмысления учебного материала
Цель: Обеспечить мотивацию и принятия учащимися цели учебно-познавательной деятельности.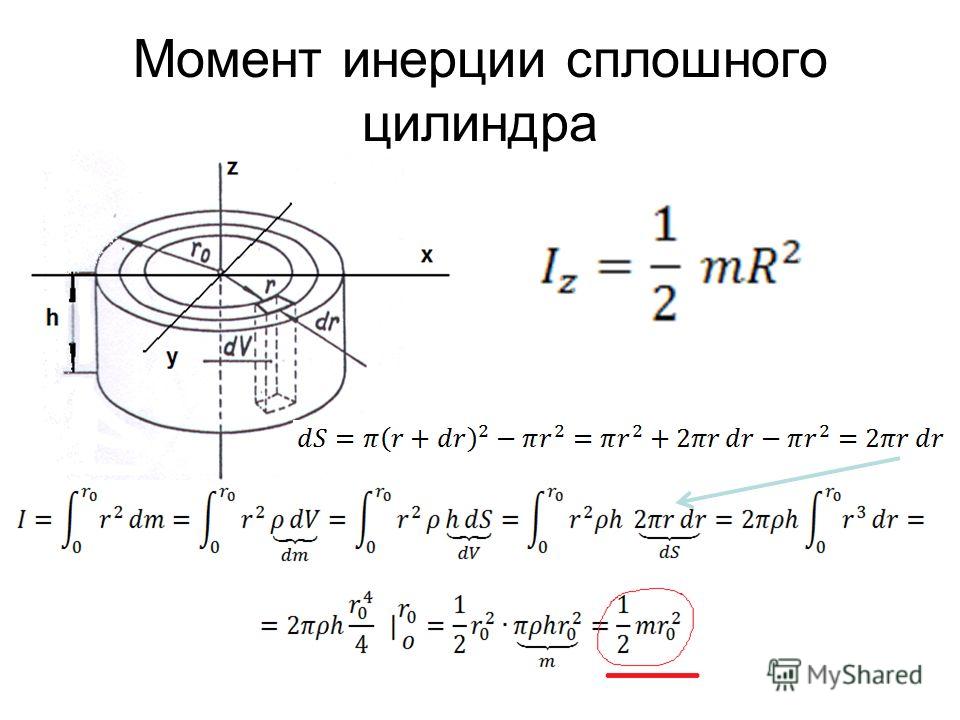
Форма: ППС и индивидуальная
Метод: поисково-эвристический
А) Рассмотрим вращающееся вокруг закрепленной оси OO′ твердое тело
Скажите пожалуйста обладает ли тело кинетической энергии?
Знакомое нам выражение для кинетической энергии поступательного движения Wк = mv2/2 неудобно для вычисления кинетической энергии вращательного движения.
Чтобы вычислить полную кинетическую энергию вращательного движения, необходимо просуммировать кинетические энергии поступательного движения по всем точкам, т.е.
(1)
Задача упрощается в связи с тем, что угловая скорость вращения ω = ∆ ф/∆t у всех точек одинакова, поэтому линейную скорость υ в выражении (1) заменим на угловую, так как υ = ωR.
Тогда выражения (1) запишем следующим образом
(2)
Сумма, находящаяся в скобках:
1. Эта сумма — скалярная величина.
2. Она зависит от распределения массы тела относительно оси вращения: чем дальше находится масса от оси вращения, тем больше эта сумма.
Вопрос ученикам : У какого тела — тонкого обруча или сплошного диска, одинаковых по радиусу и массе, эта сумма больше.
У обруча, так как все mi-е точки обруча находятся на самом максимальном расстоянии ri = R. Поэтому эта сумма — конкретная величина для данного тела. Она называется
момент инерции тела, обозначается символом J. Следовательно:
(3)
Выражение (3) похоже на уравнение для кинетической энергии поступательного движения, т. е. формула (3) позволяет рассчитать кинетическую энергию вращательного движения. Из нее следует, что обруч и диск, раскрученные до одинаковой угловой скорости, обладают разными кинетическими энергиями.
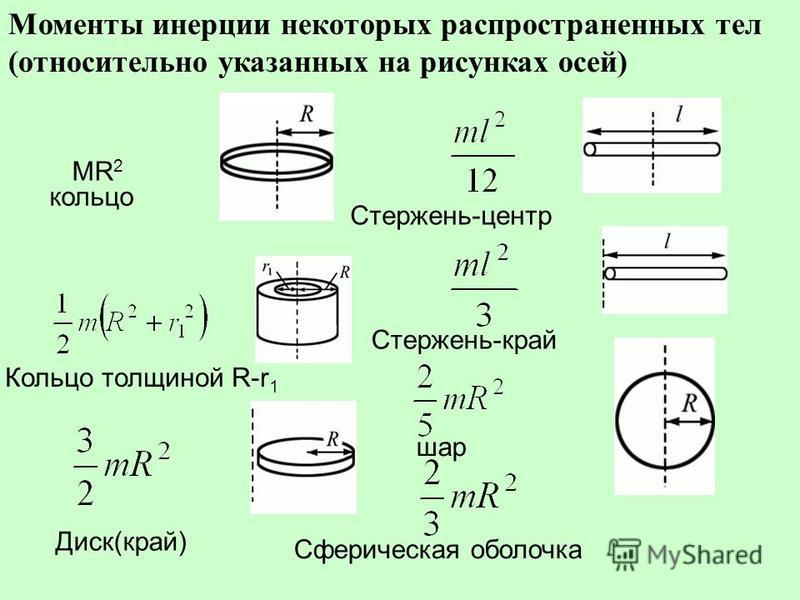
Моменты инерции некоторых тел, вычисленные относительно оси вращения, проходящей через центр масс
Моменты инерции различных тел правильной геометрической формы.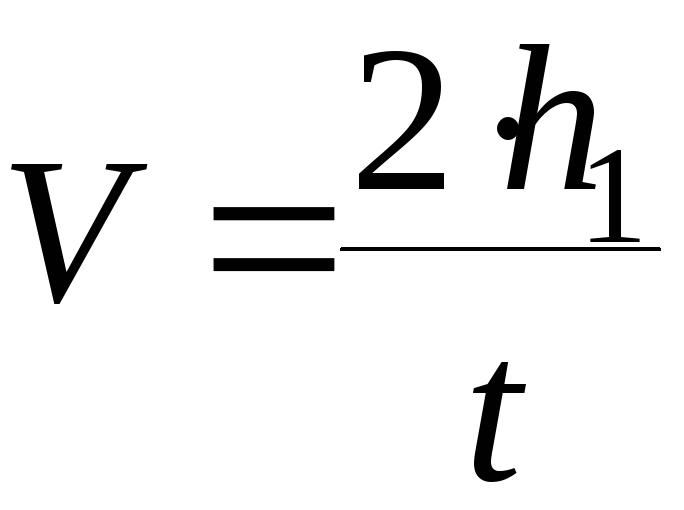
перпендикулярно к его концу
Обратите внимание, что в примере 6 по таблице дан случай, когда ось вращения не проходит через центр масс. В таких случаях для нахождения момента инерции можно воспользоваться теоремой Гюйгенса — Штейнера:
момент инерции тела относительно любой оси, не проходящей через центр тяжести, равен сумме момента инерции данного тела относительно оси, проходящей через центр тяжести, и произведению массы тела на расстояние между этими осями.
Практическая часть урока (применения теоретические данные в решении задач)
1.Определите момент инерции материальной точки массой 300 г относительно оси, отстоящей от нее на расстоянии 20 см.
(Ответ: 12 г · м2)
2. На концах тонкого однородного стержня длиной 90 см и массой 300 г прикреплены шарики массами 100 г и 200 г. Определите момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: а) первый шарик; б) точку, отстоящую от первого шарика на 30 см в) середину стержня.
Определите момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: а) первый шарик; б) точку, отстоящую от первого шарика на 30 см в) середину стержня.
(Ответ: а) 0,243 кг · м2; б) 108 г · м2; в) 81 г · м2)
3. Определите момент инерции плоской однородной прямоугольной пластинки массой 900 г относительно оси, совпадающей с одной из сторон, если длина другой стороны 20 см.
Конец урока
5 мин
1.Рефлексия
Цель: Мобилизация учащихся на рефлексию своего поведения (мотивации, способов деятельности, общения).
Рефлексия:
– что узнал, чему научился
– что осталось непонятным
– над чем необходимо работать
2. Домашнее задание.
Учебник Б.А.Кронгарт, стр. 73,
Упр.5
Итог урока
Цель: Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы.
Стикеры
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности
Все учащиеся:
знают момент инерции тела
Большинство учащихся будут:
Применять теоретические навыки полученные на уроке при решении задач на доске
Некоторые учащиеся смогут:
Применять самостоятельно теоретические навыки полученные на уроке при решении задач
Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
Здоровье сберегающие технологии.
Используемые физминутки и активные виды деятельности.
Пункты, применяемые из Правил техники безопасности на данном уроке.
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
1:
2:
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
3 Момент инерции тела относительно оси. Радиус инерции
Момент инерции тела относительно оси. Радиус инерции.
Радиус инерции.
Положение центра масс характеризует распределение масс системы не полностью. Например (рис.32), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).
Рис.32
Поэтому в механике вводится еще одна характеристика распределения масс – момент инерции. Моментом инерциитела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении.
Рекомендуемые файлы
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси, .
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством
,
где М – масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл. В результате, учитывая, что , где – плотность, а V-объем, получим
В результате, учитывая, что , где – плотность, а V-объем, получим
или
Интеграл здесь распространяется на весь объем V тела, а плотность и расстояние h зависят от координат точек тела.
Моменты инерции некоторых однородных тел:
1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси Аz, перпендикулярной к стержню и проходящей через его конец А (рис. 33).
Рис.33
Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса , где – масса единицы длины стержня. В результате
Заменяя здесь его значением, найдем окончательно:
2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис. 34,а).Так как все точки кольца находятся от оси Cz на расстоянии hk=R, то
34,а).Так как все точки кольца находятся от оси Cz на расстоянии hk=R, то
Следовательно, для кольца
Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.
3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси Сz, перпендикулярной к пластине и проходящей через ее центр (см. рис.34,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34,б).
Рис.34
Площадь этого кольца равна , а масса , где – масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
а для всей пластины . Заменяя здесь его значением, найдем окончательно
Такая же формула получится, очевидно, и для момента инерции однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc. 34,в).
34,в).
Обратите внимание на лекцию “Методы разрушения нефтяных эмульсий”.
4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:
а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у – вдоль BD):
б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):
г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра):
Массовый момент инерции и момент инерции площади – применения, различия и единицы измерения
Термин «момент инерции» очень часто используется в расчетах механического проектирования. Есть два различных типа момента инерции: момент инерции массы и момент инерции площади. Иногда это создает путаницу относительно того, какой момент инерции следует использовать в каком месте. Поймите концепцию момента инерции массы и момента инерции площади, и у вас не возникнет этой проблемы.
Поймите концепцию момента инерции массы и момента инерции площади, и у вас не возникнет этой проблемы.
Массовый момент инерции
Массовый момент инерции (иногда называемый просто «моментом инерции») отвечает за обеспечение сопротивления изменению скорости вращения вращающегося тела. Момент инерции массы представлен как « I » в механических и конструктивных расчетах.
Единицы измерения момента инерции массы: кг-м² , грамм-см **** ² , фунт-дюйм **** ² и т. Д.
Общая формула для расчета момента массы инерции можно представить как:
I = ∫ r **** ² дМ ………………….1.1
Где,
I – Момент инерции массы.
dM – Очень маленькая масса, параллельная желаемой оси.
r – Расстояние небольшого участка от оси.
Однако вам не нужно использовать это уравнение большую часть времени, поскольку значения момента инерции массы для стандартных геометрических форм легко доступны.
Момент инерции массы является вращательным аналогом массы. Это означает, что во всех уравнениях вращения для углового момента, угловой кинетической энергии, силы и т. Д.следует использовать момент инерции массы (I).
Момент инерции площади
Момент инерции площади или второй момент площади или второй момент инерции используется в уравнениях балки для расчета валов или аналогичных элементов. Момент инерции площади – это свойство сечения. Как и момент инерции массы, момент инерции площади также представлен как « I» , но единицы момента инерции площади отличаются от единиц момента инерции массы. Единицы измерения момента инерции площади: м4, мм 4 , дюйм5 и т. Д.
Общая формула для расчета момента инерции площади может быть представлена как:
Ixx = ∫ y **** ² dA ………………… .1.2
Где,
Ixx – Момент инерции площади относительно оси X.
dA – Очень маленькая область, параллельная оси X.
y – Расстояние небольшой области от оси X.
Однако вам не нужно использовать это уравнение большую часть времени, поскольку значения момента инерции площади для стандартных геометрических форм легко доступны.
Заключение
Момент инерции массы и момент инерции площади представлены как I . Иногда это может сбивать с толку, но вам нужно разобраться в этом с помощью приложения. Момент инерции массы используется как вращательный аналог массы, а момент инерции площади используется в основном для уравнений балки. Другое отличие состоит в единицах измерения обоих моментов инерции.
Момент инерции цилиндра (Деривация)
Определение момента инерции полого / сплошного цилиндра
Полый цилиндр имеет внутренний радиус R 1 , массу M, внешний радиус R 2 и длину L.{2} $$
Проверка работоспособности: ожидается, что I будет самым высоким для обруча или цилиндрической оболочки, так как вся масса находится дальше всего от оси вращения.
Назад к механике (UY1)
Расчет момента инерции общих форм:
Вращательная инерция – BCIT Physics 0312 Учебник
Сводка
- Поймите взаимосвязь между силой, массой и ускорением.
- Изучите вращающий эффект силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением.
Если вы когда-либо крутили колесо велосипеда или толкали карусель, вы знаете, что для изменения угловой скорости требуется сила, как показано на рисунке 1. На самом деле ваша интуиция надежна в предсказании многих факторов, которые участвуют в этом процессе. . Например, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается.Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе.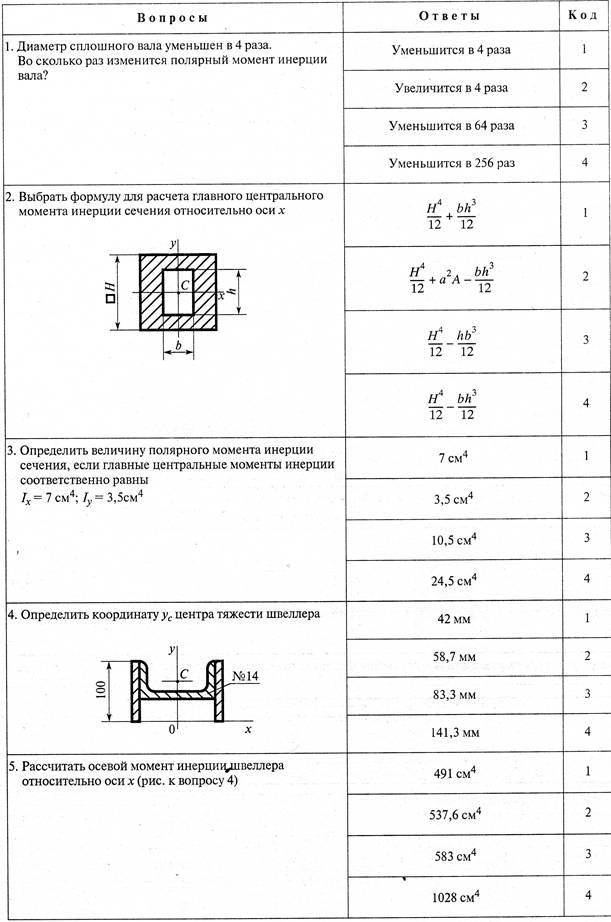 Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Чтобы определить точную взаимосвязь между силой, массой, радиусом и угловым ускорением, подумайте, что произойдет, если мы приложим силу [латекс] \ boldsymbol {F} [/ latex] к точечной массе [латекс] \ boldsymbol {m} [ / latex], который находится на расстоянии [latex] \ boldsymbol {r} [/ latex] от точки поворота, как показано на рисунке 2. Поскольку сила перпендикулярна [latex] \ boldsymbol {r}, [/ latex] ускорение [латекс] \ boldsymbol {a = \ frac {F} {m}} [/ latex] получается в направлении [латекс] \ boldsymbol {F}.[/ latex] Мы можем изменить это уравнение так, чтобы [latex] \ boldsymbol {F = ma} [/ latex], а затем искать способы связать это выражение с выражениями для вращательных величин.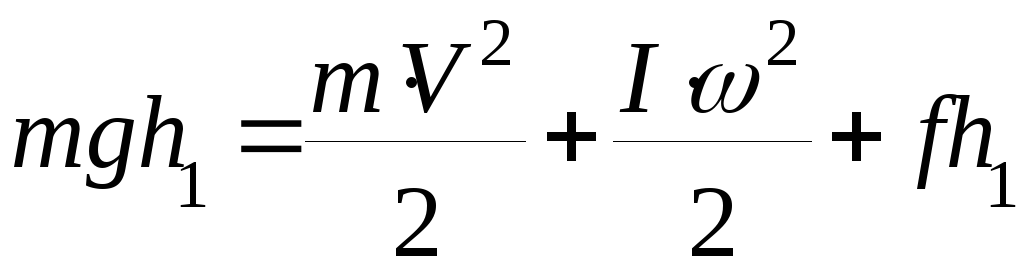 Мы отмечаем, что [latex] \ boldsymbol {a = r \ omega}, [/ latex], и подставляем это выражение в [latex] \ boldsymbol {F = ma}, [/ latex], получая
Мы отмечаем, что [latex] \ boldsymbol {a = r \ omega}, [/ latex], и подставляем это выражение в [latex] \ boldsymbol {F = ma}, [/ latex], получая
[латекс] \ boldsymbol {F = mr \ alpha}. [/ Latex]
Напомним, что крутящий момент – это эффективность поворота силы. В этом случае, поскольку [latex] \ textbf {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] равен просто [latex] \ boldsymbol {\ tau = Fr}.2} [/ latex] называется инерцией вращения или моментом инерции точечной массы [латекс] \ boldsymbol {m} [/ latex] на расстоянии [латекс] \ boldsymbol {r} [/ латекс] от центр вращения.
Рисунок 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, который создает центростремительную силу. Сила F применяется к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки поворота. Усилие сохраняется перпендикулярно к r .
Усилие сохраняется перпендикулярно к r .ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика связана с силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силе и массе, которые ведут себя так, как мы ожидали из нашего предыдущего опыта.
Прежде чем мы сможем рассматривать вращение чего-либо, кроме точечной массы, подобной показанной на рисунке 2, мы должны распространить идею инерции вращения на все типы объектов.2}, [/ latex], где [latex] \ boldsymbol {M} [/ latex] – его общая масса, а [latex] \ boldsymbol {R} [/ latex] – его радиус. (Мы используем [latex] \ boldsymbol {M} [/ latex] и [latex] \ boldsymbol {R} [/ latex] для всего объекта, чтобы отличать их от [latex] \ boldsymbol {m} [/ latex] и [ latex] \ boldsymbol {r} [/ latex] для точечных масс.) Во всех остальных случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица – это произведение искусства, которое имеет формы, а также формулы) для формул для [латекса] \ жирный символ {I} [/ latex], полученные в результате интегрирования непрерывного тела. 2} [/ latex]), как и следовало ожидать из его определения.
2} [/ latex]), как и следовало ожидать из его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением равно
.[латекс] \ boldsymbol {\ textbf {net} \ tau = I \ alpha} [/ latex]
или
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ textbf {net} \ tau} {I}}, [/ latex]
где net [latex] \ boldsymbol {\ tau} [/ latex] – это общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только моменты, действующие под действием сил в плоскости вращения.Такие моменты могут быть положительными или отрицательными и складываются как обычные числа. Отношение в [latex] \ boldsymbol {\ tau = I \ alpha}, \: \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}} [/ latex] является аналогом вращения Ньютона. второй закон и очень широко применяется. Это уравнение действительно справедливо для любого крутящего момента , приложенного к любому объекту , относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение.Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением состоит в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть еще один нюанс. Момент инерции зависит не только от массы объекта, но также от его распределения массы относительно оси, вокруг которой он вращается.Например, карусель, полную детей, будет намного легче разогнать, если они будут стоять близко к ее оси, чем если все они будут стоять у внешнего края. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на грани.
ЭКСПЕРИМЕНТ НА ДОМУ
Вырежьте из плотного картона круг радиусом около 10 см. На краю круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и с номером 12, расположенным вверху, прикрепите кусок синей замазки (липкий материал, используемый для крепления плакатов к стене) под номером 3. Насколько велик шишка должна быть просто кружить круг? Опишите, как можно изменить момент инерции круга. Как это изменение повлияет на количество синей замазки, необходимое для числа 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки.Повторите этот процесс несколько раз.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и с номером 12, расположенным вверху, прикрепите кусок синей замазки (липкий материал, используемый для крепления плакатов к стене) под номером 3. Насколько велик шишка должна быть просто кружить круг? Опишите, как можно изменить момент инерции круга. Как это изменение повлияет на количество синей замазки, необходимое для числа 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки.Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определите интересующую систему .
- Нарисуйте схему свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую систему.
- Применить [латекс] \ boldsymbol {\ textbf {net} \ tau = I \ alpha}, \: \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}}, [/ latex ] вращательный эквивалент второго закона Ньютона, чтобы решить задачу .
 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения. - Как всегда, проверьте правильность решения .
ПОДКЛЮЧЕНИЕ
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. Во вращательном движении чистый крутящий момент является причиной углового ускорения, как и во втором законе движения Ньютона для вращения.
Рисунок 3. Некоторые инерции вращения.Пример 1: Расчет влияния распределения массы на карусель
Представьте, что отец толкает карусель на детской площадке на рис. 4. Он прилагает силу 250 Н к краю 50,0 кг карусели, имеющей радиус 1,50 м. Вычислите угловое ускорение, возникающее (а), когда никого нет на карусели, и (б), когда ребенок весом 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с незначительным тормозящим трением.
Рис. 4. Отец толкает карусель на детской площадке за край и перпендикулярно ее радиусу, чтобы добиться максимального крутящего момента.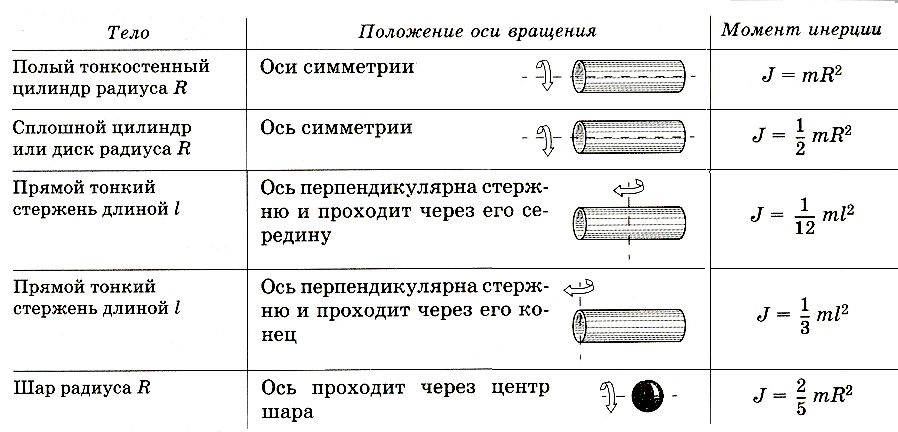
Стратегия
Угловое ускорение задается выражением [latex] \ boldsymbol {\ alpha = \ frac {\ textbf {net} \ tau} {I}}: [/ latex]
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ tau} {I}}. [/ Latex]
Чтобы найти [latex] \ boldsymbol {\ alpha}, [/ latex], мы должны сначала вычислить крутящий момент [latex] \ boldsymbol {\ tau} [/ latex] (который одинаков в обоих случаях) и момент инерции [latex] \ boldsymbol {I} [/ latex] (во втором случае больше).2}}. [/ Latex]
Решение для (b)
Мы ожидаем, что угловое ускорение для системы в этой части будет меньше, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти полный момент инерции [latex] \ boldsymbol {I}, [/ latex], мы сначала находим момент инерции ребенка [latex] \ boldsymbol {I _ {\ textbf {c}}} [/ latex], рассматривая ребенок должен быть эквивалентен точечной массе на расстоянии 1,25 м от оси. 2 = (18.2}}. [/ Latex]
2 = (18.2}}. [/ Latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось незначительным. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он дал бы карусели угловую скорость 13,3 рад / с, когда она пуста, и только 8,89 рад / с, когда на ней сидит ребенок.В оборотах в секунду эти угловые скорости составляют 2,12 об / с и 1,41 об / с соответственно. В первом случае отец разгонялся до 50 км / ч. Летние Олимпийские игры, вот он! Подтверждение этих чисел оставлено читателю в качестве упражнения.
Проверьте свое понимание
1: Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса – это физические величины, которые зависят только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Одинаково ли просты крутящий момент и момент инерции?
Одинаково ли просты крутящий момент и момент инерции?
- Чем дальше от оси приложена сила, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы приложим силу [латекс] \ boldsymbol {F} [/ latex] к точечной массе [латекс] \ boldsymbol {m} [/ latex], которая находится на расстоянии [латекс] \ boldsymbol {r} [/ latex ] от точки поворота, и поскольку сила перпендикулярна [латексу] \ boldsymbol {r}, [/ latex], ускорение [латекс] \ boldsymbol {a = F / m} [/ latex] достигается в направлении [ латекс] \ boldsymbol {F}.[/ latex] Мы можем переписать это уравнение так, чтобы
[латекс] \ boldsymbol {F = ma}, [/ latex]
, а затем поищите способы связать это выражение с выражениями для вращательных величин. Отметим, что [latex] \ boldsymbol {a = r \ alpha}, [/ latex], и мы подставляем это выражение в [latex] \ boldsymbol {F = ma}, [/ latex], получая
[латекс] \ boldsymbol {F = mr \ alpha} [/ латекс]
- Крутящий момент – это эффективность силы при повороте.
 В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] равен просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])
В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] равен просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])2: Почему момент инерции обруча имеет массу [латекс] \ boldsymbol {M} [/ latex] и радиус [латекс] \ boldsymbol {R} [/ latex] больше, чем момент инерция диска такой же массы и радиуса? Почему момент инерции сферической оболочки, имеющей массу [латекс] \ boldsymbol {M} [/ latex] и радиус [латекс] \ boldsymbol {R} [/ latex], больше, чем у твердой сферы, имеющей такая же масса и радиус?
3: Приведите пример, в котором малая сила вызывает большой крутящий момент.Приведите другой пример, в котором большая сила вызывает небольшой крутящий момент.
4: При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
Рис. 5. На изображении показан гоночный велосипед, вид сбоку. Можете ли вы увидеть в конструкции колес этого гоночного велосипеда свидетельство того, что их момент инерции был намеренно уменьшен? (Источник: Хесус Родригес)5: Мяч скользит по наклонной поверхности без трения.Затем его катят без проскальзывания и с той же начальной скоростью по другому пандусу без трения (с тем же углом наклона). В каком случае он достигает большей высоты и почему?
Задачи и упражнения
1: В этой задаче рассматриваются дополнительные аспекты примера 1. (a) Сколько времени требуется отцу, чтобы дать карусели угловую скорость 1,50 рад / с? б) Сколько оборотов он должен совершить, чтобы получить эту скорость? (c) Если он прикладывает замедляющую силу 300 Н на радиусе 1.35 м, сколько времени ему понадобится, чтобы их остановить?
2: Рассчитайте момент инерции фигуриста с учетом следующей информации. (а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой примерно цилиндр весом 52,5 кг, имеет радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.
3: Трехглавая мышца задней части плеча разгибает предплечье.2}. [/ Latex] Какова сила, действующая на мышцу, если ее эффективное перпендикулярное плечо рычага составляет 1,90 см?
5: Предположим, вы прилагаете усилие 180 Н по касательной к точильному камню массой 75,0 кг радиусом 0,280 м (твердый диск).
(а) Какой крутящий момент прилагается? (b) Какое угловое ускорение предполагает незначительное встречное трение? (c) Каково угловое ускорение, если существует противодействующая сила трения 20,0 Н, действующая на 1,50 см от оси?
6: Рассмотрим 12.Колесо мотоцикла весом 0 кг показано на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, чтобы достичь угловой скорости 80.7 \ textbf {N}} [/ latex] (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для динамики вращения.
8: Автомобильный двигатель может развивать крутящий момент 200 Н ∙ м. Рассчитайте угловое ускорение, возникающее, если 95,0% этого крутящего момента приложено к ведущему валу, оси и задним колесам автомобиля, учитывая следующую информацию. 2/12}.2}. [/ Latex] (a) Сколько времени ей нужно, чтобы полностью изменить вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?
11: Необоснованные результаты
В рекламе утверждается, что автомобилю массой 800 кг помогает его маховик массой 20,0 кг, который может разогнать автомобиль от состояния покоя до скорости 30,0 м / с. Маховик представляет собой диск радиусом 0,150 м. (a) Рассчитайте угловую скорость, которую должен иметь маховик, если 95,0% его энергии вращения используется для того, чтобы автомобиль набрал скорость.б) Что неразумного в результате? (c) Какая предпосылка является необоснованной, а какие несовместимы?
Глоссарий
- крутящий момент
- эффективность поворота силы
- инерция вращения
- сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его повернуть на
- момент инерции
- масса, умноженная на квадрат расстояния по перпендикуляру от оси вращения; для точечной массы это [латекс] \ boldsymbol {I = mr ^ 2} [/ latex], и, поскольку любой объект может быть создан из набора точечных масс, это соотношение является основой для всех других моментов инерции
Упражнения
Проверьте свое понимание
1: No.Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.
Задачи и упражнения
1:
(а) 0,338 с
(б) 0,0403 изм.
(в) 0,313 с
3:
[латекс] \ boldsymbol {0.2} \ end {array} [/ latex]
10:
(а) 2,0 мс
(b) Временной интервал слишком короткий.
(c) Момент инерции слишком мал, на один-два порядка величины. Крутящий момент [латекс] \ boldsymbol {500 \ textbf {N} \ cdotp \ textbf {m}} [/ latex] является разумным.
11:
(а) 17500 об / мин
(б) Эта угловая скорость очень велика для диска такого размера и массы. Радиальное ускорение на краю диска> 50 000 gs.
(c) Масса и радиус маховика должны быть намного больше, что позволяет снизить скорость вращения (угловую скорость).
Представьте себе объект неправильной массы. Его момент инерции измеряется относительно оси A (параллельно оси плоскости страницы), которая проходит через центр масс (см. вторая диаграмма), дается выражением. Оси B, C, D и E параллельны оси A; их расстояния от оси A показаны на схеме.MasteringPhysics 2.0: Проблемный вид для печати
Цель обучения: Понять теорему о параллельной оси и ее приложения
Чтобы решить многие проблемы, связанные с вращательным движением, это Важно знать момент инерции каждого задействованного объекта. Расчет моментов инерции различных объектов, даже очень высоких симметричные, могут оказаться длительным и утомительным процессом.Пока это важно уметь рассчитывать моменты инерции по определение (), в большинстве случаев полезно просто вспомнить момент инерции конкретный тип объекта. Моменты инерции часто встречающиеся формы (например, однородный стержень, однородный или полый цилиндр, форма или полая сфера) хорошо известны и легко доступно из любого учебника по механике, включая ваш учебник. Тем не мение, необходимо учитывать, что объект имеет не одну, а бесконечную количество моментов инерции.Одно из отличий момент инерции и масса (последняя является мерой трансляционная инерция) заключается в том, что момент инерции тела зависит от на оси вращения. Моменты инерции, которые можно найти в учебники обычно рассчитываются относительно прохождения оси через центр масс объекта. Однако во многих задачах ось вращения не проходит через центр масс. Это означают, что нужно пройти долгий процесс поиска момент инерции с нуля? Оказывается, во многих случаях вычислить момент инерции можно довольно легко, если использовать теорема о параллельной оси.Математически это может быть выражено как, где – момент инерции относительно оси, проходящей через центр масс, – это общая масса объекта, и – это момент инерции относительно другой оси, параллельной той, для которой рассчитывается и расположен на расстоянии от центра масс. В этой задаче вы покажете, что теорема действительно работает по крайней мере с одним предметом: гантель длиной, сделанная из двух маленьких сфер массы каждый соединен световым стержнем (см. рисунок).ПРИМЕЧАНИЕ: Если не указано иное Как отмечалось, все рассматриваемые оси перпендикулярны плоскости страницы.Часть A Используя определение момента инерции, вычислите момент инерции относительно центра масс этого объекта. Подсказка A.1 Подсказка не отображается
Подсказка A.2 В последующих вопросах нижний индекс указывает ось с относительно которого измеряется момент инерции: например, это момент инерции относительно оси C.
Часть F Какой момент инерции наименьший?
Один из важных результатов, полученных из теоремы о параллельности осей, заключается в том, что для любого объекта всегда наименьший из семейства моментов инерции по отношению к различным параллельным осям.Деталь G Какой момент инерции самый большой?
Часть H Какие моменты инерции равны?
Часть I Какому моменту инерции равен? Часть J Ось X, не показанная на схеме, параллельна показанным осям.Известно, что . Что из следующего является возможным местоположением оси X? Физический маятник: определение момента инерции
Введение в физический маятникУстановите любое твердое тело так, чтобы оно могло качаться в вертикальной плоскости вокруг оси, проходящей через тело. Вы построили так называемый физический маятник . На видео ниже показан пример такого маятника. На этом видео твердое круглое тело качается вокруг оси очень близко к краю круга.Круг был вырезан из куска картона. PocketLab Voyager опирается на нижнюю часть подставки для колец, прямо под точкой поворота маятника. К нижней части круга прикреплен крошечный магнит. Вы заметите, что дважды в течение каждого периода PocketLab регистрирует всплеск напряженности магнитного поля, когда магнит находится ближе всего к PocketLab. Анализ этих всплесков за несколько периодов дает точное определение периода колебаний физического маятника.
Теория физического маятникаНа рисунке 1 показан объект неправильной формы, который вращается вокруг оси без трения, перпендикулярной плоскости фигуры в точке P.Объект смещен из положения равновесия на угол θ . Положение равновесия – это когда центр масс C объекта находится непосредственно под точкой поворота. Расстояние между точкой поворота и центром масс составляет d . С учетом задействованной динамики на рисунке показан вывод уравнения для периода T физического маятника. Решая это уравнение для момента инерции I , получается уравнение в прямоугольнике внизу рисунка.Ускорение свободного падения g принимается как известная величина, а T , M и d все являются измеримыми. Это уравнение, таким образом, позволяет нам определить момент инерции любого объекта через любую конкретную точку поворота на этом объекте! Обратите внимание на предположение, что θ предполагается малым. Если угол поворота поддерживается не более чем примерно 30 °, тогда θ и sin θ будут отличаться не более чем примерно на 4%.Расчет I немного утомителен, когда его нужно повторять много раз. Следовательно, вам может быть удобно создать электронную таблицу для расчета I после ввода значений для T, g, M, и d.
Рисунок 1 – Теория физического маятника Роль PocketLab в этом урокеСуществует явное преимущество использования PocketLab, как описано выше в этом уроке. PocketLab позволяет рассчитать период физического маятника гораздо точнее, чем это возможно с помощью секундомера.Использование PocketLab для этой цели устраняет ошибки, связанные с временем реакции при запуске и остановке секундомера. PocketLab также следует установить на максимально возможную скорость передачи данных (50 точек в секунду). Успех этого урока зависит от точного измерения периода T физического маятника. Также рекомендуется измерять массу маятника с помощью весов с точностью до 0,1 г или даже 0,01, если это возможно.
Установка физического маятникаДля ясности на рисунке 2 показан вид устройства под углом.Физический маятник, картонный прямоугольник, подвешен к точке поворота очень близко к короткому краю прямоугольника. Ось представляет собой тонкий металлический стержень, прикрепленный к кольцевой стойке. Также используется деревянный стержень для дюбеля (или что-то подобное), поскольку винт зажима не завинчивается достаточно сильно, чтобы зажать металлический стержень в зажиме. Учащиеся должны носить защитные очки, чтобы не ткнуть их в глаз тонким металлическим стержнем. PocketLab опирается на нижнюю часть подставки для кольца.К центру короткого нижнего края прямоугольника приклеен крошечный магнит. Магнитометр PocketLab определяет магнитное поле каждый раз, когда магнит проходит мимо PocketLab.
Рисунок 2 – Угловой вид аппарата Определение момента инерцииМомент инерции объекта, вращающегося вокруг определенной оси, в некоторой степени аналогичен обычной массе объекта. Момент инерции можно определить по уравнению
Момент инерции представляет собой сумму масс частиц, составляющих объект, умноженных на их соответствующие расстояния, возведенные в квадрат от оси вращения .Для непрерывных твердых объектов уравнение будет аналогичным, но с использованием интегралов вместо суммы. Следует отметить, что по определению момент инерции тела зависит не только от конкретной оси, на которой оно вращается, но также от его формы и способа распределения его массы. Вычисление этих интегралов может быть очень утомительным. Поэтому в этом уроке мы будем использовать таблицу моментов инерции, чтобы мы могли сосредоточиться на физике и не беспокоиться о вычислении того, что часто является комплексными интегралами.
Цели урока по физическому маятнику- В этом уроке вы определите момент инерции для нескольких распространенных геометрических фигур из картона относительно определенной точки поворота в каждом объекте. Объекты будут физическими маятниками, которые вращаются вокруг указанной оси, перпендикулярной плоскости формы. PocketLab будет использоваться для измерения периода каждого маятника.
- Затем вы сравните свои экспериментальные моменты инерции с теоретическими моментами инерции, представленными в статье Википедии «Список моментов инерции».Сравнения будут выражены как процентная разница между вашим экспериментальным результатом и теоретическим моментом инерции, основанная на доле теоретического момента инерции. Разница в процентах будет отрицательной, если ваш экспериментальный результат меньше теоретического, и положительным, если экспериментальный результат больше теоретического. Формы будут исследованы в порядке сложности задействованных физико-математических наук. Эти формы, в том порядке, в котором они исследуются, следующие:
- Прямоугольник
- Круг
- Квадрат
- Равносторонний треугольник
- Наконец, вы определите момент инерции относительно конкретной оси обычного прямоугольника, неправильной изогнутой формы и объекта с «отрицательным пространством».Никаких теоретических формул для этих фигур в таблице Википедии не представлено. Тем не менее, вы все еще можете определить эти моменты инерции экспериментально . Основываясь на процентах ошибок, которые вы получили от известных форм в задаче 2, насколько вы уверены в моментах инерции общего прямоугольника, неправильной изогнутой формы и объекта с отрицательным пространством?
Вырежьте из картона прямоугольник, который по размеру и форме аналогичен изображенному на Рисунке 2.Экспериментально определите его момент инерции относительно оси, показанной на рисунке 2.
Прокрутите список моментов инерции Википедии вниз, пока не увидите запись, показанную на рисунке 3. Эта запись соответствует прямоугольнику, который вы в настоящее время исследуете. Используя формулу, показанную на рисунке 3, определите теоретический момент инерции вашего прямоугольника относительно оси вращения x . Вычислите разницу в процентах и запишите свои результаты в таблицу данных.
Рисунок 3 – Прямоугольная пластина (из списка моментов инерции Википедии) Circle InvestigationВырежьте из картона круг, который по размеру похож на тот, что показан во встроенном видео.Экспериментально определите его момент инерции относительно оси, показанной на видео.
Прокрутите вниз Список моментов инерции Википедии, пока не увидите запись, показанную на рисунке 4. Вас интересует момент инерции z . Это дает вам момент инерции круга, который на вращается вокруг своего центра масс . Но ваш круглый картон на вращается вокруг точки около края круга! Как упоминалось ранее, момент инерции зависит от конкретной оси вращения .Итак … как мы можем определить момент инерции, когда круг вращается вокруг точки возле своего края?
Рисунок 4 – Круглая пластина (из Списка моментов инерции Википедии)Как оказалось, существует простая и чрезвычайно полезная теорема, известная как Теорема о параллельных осях , которая выражает взаимосвязь между моментом инерции. I объекта относительно любой любой оси и его момент инерции относительно параллельной оси, проходящей через центр масс.Если Ic – это момент инерции относительно центра масс, m – масса объекта, а w – расстояние между двумя осями, эта теорема говорит нам, что момент инерции I определяется выражением уравнение
Используйте теорему о параллельности оси и запись z в таблице Википедии, чтобы определить уравнение для момента инерции относительно точки около края круглой пластины. Полученное уравнение должно соответствовать записи в Википедии, показанной на рисунке 5.
Рисунок 5 – Равномерный диск (из Списка моментов инерции Википедии)Рассчитайте теоретическое значение для этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите свои результаты в таблицу данных.
Square InvestigationВырежьте из картона квадрат, размер которого аналогичен показанному на рисунке 6. Экспериментально определите его момент инерции относительно оси, показанной на этом рисунке, т.е.е., ось, которая очень близка к одной из вершин квадрата.
Рисунок 6 – Квадратный физический маятникПрокрутите список моментов инерции Википедии до тех пор, пока не увидите запись, показанную на рисунке 7.
- Какое значение n в уравнении, показанном для вашего квадрата?
- Получите формулу для момента инерции относительно центра масс (центра масс) через м и R ?
- Перепишите уравнение в виде м и a , где a – длина каждой стороны квадрата.
- Используйте теорему о параллельных осях, чтобы определить уравнение для теоретического момента инерции относительно вершины квадрата в виде м и a .
- Рассчитайте теоретическое значение этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите свои результаты в таблицу данных.
Вырежьте из картона равносторонний треугольник, размер которого аналогичен изображенному на рисунке 8.Экспериментально определите его момент инерции относительно оси, показанной на этом рисунке, то есть оси, которая очень близка к одной из вершин равностороннего треугольника.
Рисунок 8 – Равносторонний треугольник Физический маятникТеоретическое уравнение для момента инерции равностороннего треугольника относительно его центра масс следует из рисунка 7 для правильного многоугольника.
- Какое значение n в уравнении, показанном для вашего равностороннего треугольника?
- Получите формулу для момента инерции относительно центра масс в виде м и R ?
- Перепишите уравнение в виде м и a , где a – длина каждой стороны равностороннего треугольника.
- Используйте теорему о параллельной оси, чтобы определить уравнение для теоретического момента инерции относительно вершины равностороннего треугольника в виде м и a .
- Рассчитайте теоретическое значение этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите свои результаты в таблицу данных.
В таблице моментов инерции Википедии нет записей для общего треугольника.Следовательно, вы будете определять момент инерции такого треугольника только экспериментально. Вырежьте из картона общий треугольник, который по форме и размеру аналогичен изображенному на рисунке 9. Точка поворота должна быть выбрана около одной из трех вершин.
Рисунок 9 – Общий треугольникКак обычно, чтобы использовать уравнение для момента инерции, показанное на рисунке 1, вам необходимо знать расстояние d между точкой поворота и центром масс. Это означает, что вам нужно знать расположение центра масс.Чтобы найти центр масс, вам нужно только вспомнить основную теорему из геометрии. Эта теорема утверждает, что три медианы треугольника пересекаются в его центроиде (центре масс). Каждая медиана проводится от вершины к центру противоположной стороны, как показано на рисунке 9. Вас не должно удивлять, что, когда треугольник подвешен к одной из его вершин, медиана лежит вертикально вверх и вниз. Это показано на Рисунке 9.
Запишите экспериментальный момент инерции в таблицу данных.
Исследование неправильной криволинейной формыВырежьте из картона изогнутую форму неправильной формы, аналогичную по размеру и форме изображенной на рисунке 10. Определите момент этой изогнутой формы. Он вращается вокруг внутренней оси, перпендикулярной форме. Запишите экспериментальный момент инерции в таблице данных.
Рисунок 10 – Неправильная кривая форма Объект с исследованием «отрицательного пространства»Вам может быть интересно, что подразумевается под термином отрицательное пространство ? Согласно определению художника, негативное пространство можно рассматривать как пространство между предметом и вокруг него.Вырежьте из картона предмет, который по размеру и форме аналогичен изображенному на рисунке 11. Определите момент инерции этой изогнутой формы. Он вращается вокруг оси около одной из вершин фигуры. Запишите экспериментальный момент инерции в таблице данных.
Рисунок 11 – Объект с «отрицательным пространством»На основе процента ошибок, полученных вами для известных форм, насколько вы уверены в моментах инерции обычного прямоугольника, неправильной изогнутой формы и объекта с отрицательным пространством?
Таблица данныхОсновы углового ускорения и вращательного момента инерции
Угловое ускорение и момент инерции в конструкции машинКак поставщик гибких приводных муфт и предохранительных муфт с шариковой фиксацией нас часто просят оказать небольшую помощь в расчете крутящих моментов, особенно для клиентов, желающих модернизировать существующее оборудование.Чтобы помочь в процессе оценки крутящих моментов, мы рассмотрим один из основных расчетов, используемых для оценки крутящего момента, необходимого для ускорения вращающейся массы до определенной скорости в течение заданного времени. 2).Уравнение ниже определяет скорость изменения угловой скорости.
ω = угловая скорость в стандартной системе СИ, радиан в секунду (рад / сек), 1 радиан = 57,3 градуса
t = время разгона в секундах
π = 3,1416
n = скорость привода в оборотах в минуту об / мин
В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об / мин за одну секунду. Обратите внимание, что 2π радиан в секунду = 60 об / мин.
Этот расчет очень полезен при проектировании машин, поскольку угловое ускорение, умноженное на крутящий момент инерции, равняется крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно вычислить на основе сложной геометрии реальных приводных линий, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении базовых минимальных значений для определения размеров компонентов.

 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения. В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] равен просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])
В этом случае, поскольку [latex] \ boldsymbol {F} [/ latex] перпендикулярно [latex] \ boldsymbol {r}, крутящий момент [/ latex] равен просто [latex] \ boldsymbol {\ tau = rF}.2/4}. [/ Латекс])