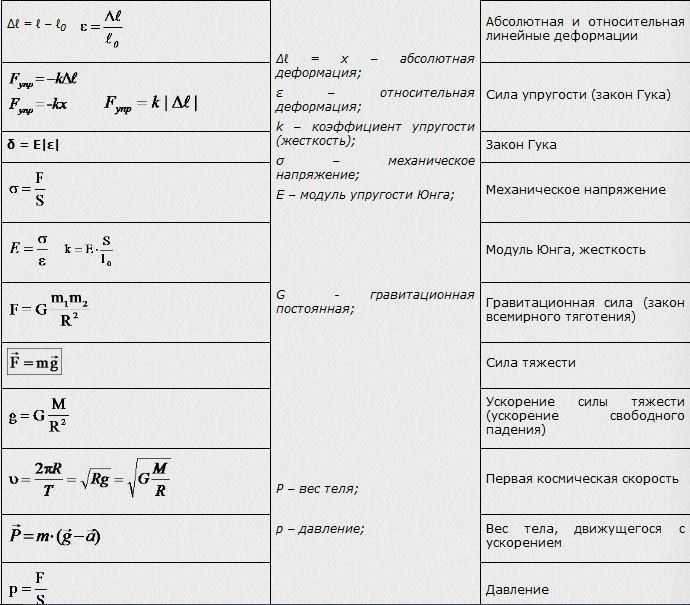
Физика основные формулы и понятия 10 класс: "Основные формулы за курс физики 10 класс. Основные положения МКТ.". Скачать бесплатно и без регистрации. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Физика. 10 класс – Конспекты

Подробности: Просмотров: 2481

«Физика – 10 класс»

По учебнику “Физика. 10 класс” – базовый и профил. уровни, авторы Мякишев, Буховцев, Сотский.

Введение

Физика и познание мира ………. смотреть
Механика ………. смотреть

КИНЕМАТИКА

Кинематика точки и твёрдого тела

§ 1. Механическое движение. Система отсчёта ………. смотреть
§ 2. Способы описания движения ………. смотреть
§ 3. Траектория. Путь. Перемещение ………. смотреть
§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения ………. смотреть
§ 5. Примеры решения задач по теме «Равномерное прямолинейное движение» ………. смотреть
§ 6. Сложение скоростей ………. смотреть
§ 7. Примеры решения задач по теме «Сложение скоростей» ….. ….. смотреть

§ 8. Мгновенная и средняя скорости ………. смотреть
§ 9. Ускорение ………. смотреть
§ 10. Движение с постоянным ускорением ………. смотреть
§ 11. Определение кинематических характеристик движения с помощью графиков ………. смотреть
§ 12. Примеры решения задач по теме «Движение с постоянным ускорением» ………. смотреть
§ 13. Движение с постоянным ускорением свободного падения ………. смотреть
§ 14. Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» ………. смотреть
§ 15. Равномерное движение точки по окружности ………. смотреть
§ 16. Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение ………. смотреть

§ 16. Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями ………. смотреть
§ 17. Примеры решения задач по теме «Кинематика твёрдого тела» .

……… смотреть

ДИНАМИКА

Законы механики Ньютона

§ 18. Основное утверждение механики ………. смотреть
§ 19. Сила ………. смотреть
§ 19. Инертность тела. Масса. Единица массы ………. смотреть
§ 20. Первый закон Ньютона ………. смотреть

§ 21. Второй закон Ньютона ………. смотреть
§ 22. Принцип суперпозиции сил ………. смотреть
§ 23. Примеры решения задач по теме «Второй закон Ньютона» ………. смотреть
§ 24. Третий закон Ньютона ………. смотреть
§ 25. Геоцентрическая система отсчёта ………. смотреть
§ 26. Принцип относительности Галилея. Инвариантные и относительные величины ………. смотреть

Силы в механике

§ 27. Силы в природе ………. смотреть
§ 28. Сила тяжести и сила всемирного тяготения ………. смотреть
§ 29. Сила тяжести на других планетах .

……… смотреть
§ 30. Примеры решения задач по теме «Закон всемирного тяготения» ………. смотреть
§ 31. Первая космическая скорость ………. смотреть
§ 32. Примеры решения задач по теме «Первая космическая скорость» ………. смотреть
§ 33. Вес. Невесомость ………. смотреть
§ 34. Деформация и силы упругости. Закон Гука ………. смотреть
§ 35. Примеры решения задач по теме «Силы упругости. Закон Гука» ………. смотреть
§ 36. Силы трения ………. смотреть
§ 37. Примеры решения задач по теме «Силы трения» ………. смотреть
§ 37. Примеры решения задач по теме «Силы трения» (продолжение) ………. смотреть

ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

Закон сохранения импульса

§ 38. Импульс материальной точки ………. смотреть
§ 38. Закон сохранения импульса ………. смотреть
§ 38. Реактивное движение. Успехи в освоении космоса . ……… смотреть
§ 39. Примеры решения задач по теме «Закон сохранения импульса» ………. смотреть

Закон сохранения энергии

§ 40. Механическая работа и мощность силы ………. смотреть
§ 41. Энергия. Кинетическая энергия ………. смотреть

§ 42. Примеры решения задач по теме «Кинетическая энергия и её изменение» ………. смотреть
§ 43. Работа силы тяжести. Консервативные силы ………. смотреть
§ 43. Работа силы упругости. Консервативные силы ………. смотреть
§ 44. Потенциальная энергия ………. смотреть
§ 45. Закон сохранения энергии в механике ………. смотреть
§ 46. Работа силы тяготения. Потенциальная энергия в поле тяготения ………. смотреть
§ 47. Примеры решения задач по теме «Закон сохранения механической энергии» ………. смотреть

Динамика вращательного движения абсолютно твёрдого тела

СТАТИКА

Равновесие абсолютно твёрдых тел

§ 51. Равновесие тел ………. смотреть
§ 52. Примеры решения задач по теме «Равновесие твёрдых тел» ………. смотреть

МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ

Основы молекулярно-кинетической теории

§ 53. Основные положения молекулярно-кинетической теории. Размеры молекул ………. смотреть
§ 54. Примеры решения задач по теме «Основные положения МКТ» . ……… смотреть
§ 55. Броуновское движение ………. смотреть
§ 56. Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел ………. смотреть

Молекулярно-кинетическая теория идеального газа

§ 57. Идеальный газ в МКТ. Среднее значение квадрата скорости молекул ………. смотреть
§ 57. Основное уравнение молекулярно-кинетической теории газов ………. смотреть
§ 58. Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» ………. смотреть
§ 59. Температура и тепловое равновесие ………. смотреть
§ 60. Определение температуры. Энергия теплового движения молекул ………. смотреть
§ 60. Абсолютная температура. Температура — мера средней кинетической энергии молекул ………. смотреть
§ 61. Измерение скоростей молекул газа ………. смотреть

Уравнение состояния идеального газа. Газовые законы

§ 63. Уравнение состояния идеального газа ………. смотреть
§ 64. Примеры решения задач по теме «Уравнение состояния идеального газа» ………. смотреть
§ 65. Газовые законы ………. смотреть
§ 66. Примеры решения задач по теме «Газовые законы» ………. смотреть
§ 67. Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов» ………. смотреть

Взаимные превращения жидкостей и газов

§ 68. Насыщенный пар ………. смотреть
§ 69. Давление насыщенного пара ………. смотреть
§ 70. Влажность воздуха ………. смотреть
§ 71. Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» ………. смотреть

Твёрдые тела

§ 72. Кристаллические тела … ……. смотреть
§ 72. Аморфные тела ………. смотреть

Основы термодинамики

§ 73. Внутренняя энергия ………. смотреть
§ 74. Работа в термодинамике ………. смотреть
§ 75. Примеры решения задач по теме «Внутренняя энергия. Работа» ………. смотреть
§ 76. Количество теплоты. Уравнение теплового баланса ………. смотреть
§ 77. Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» ………. смотреть
§ 78. Первый закон термодинамики ………. смотреть
§ 79. Применение первого закона термодинамики к различным процессам ………. смотреть
§ 80. Примеры решения задач по теме: «Первый закон термодинамики» ………. смотреть
§ 81. Второй закон термодинамики ………. смотреть

ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

Что такое электродинамика ………. смотреть

Электростатика

§ 84. Электрический заряд и элементарные частицы. Закон сохранения заряда ………. смотреть
§ 85. Закон Кулона. Единица электрического заряда ………. смотреть
§ 86. Примеры решения задач по теме «Закон Кулона» ………. смотреть
§ 87. Близкодействие и действие на расстоянии ………. смотреть
§ 88. Электрическое поле ………. смотреть
§ 89. Напряжённость электрического поля. Силовые линии ………. смотреть
§ 90. Поле точечного заряда и заряженного шара. Принцип суперпозиции полей ………. смотреть
§ 91. Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» ………. смотреть
§ 92. Проводники в электростатическом поле ………. смотреть
§ 92. Диэлектрики в электростатическом поле ………. смотреть
§ 93. Потенциальная энергия заряженного тела в однородном электростатическом поле ………. смотреть
§ 94. Потенциал электростатического поля и разность потенциалов ………. смотреть
§ 95. Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности ………. смотреть
§ 96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» ………. смотреть
§ 97. Электроёмкость. Единицы электроёмкости. Конденсатор ………. смотреть
§ 98. Энергия заряженного конденсатора. Применение конденсаторов ………. смотреть
§ 99. Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора» ………. смотреть

Законы постоянного тока

§ 100. Электрический ток. Сила тока ………. смотреть
§ 101. Закон Ома для участка цепи. Сопротивление ………. смотреть
§ 102. Электрические цепи. Последовательное и параллельное соединения проводников ………. смотреть
§ 103. Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» ………. смотреть
§ 104. Работа и мощность постоянного тока ………. смотреть
§ 105. Электродвижущая сила ………. смотреть
§ 106. Закон Ома для полной цепи ………. смотреть
§ 107. Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи» ………. смотреть

Электрический ток в различных средах

§ 108. Электрическая проводимость различных веществ. Электронная проводимость металлов ………. смотреть
§ 109. Зависимость сопротивления проводника от температуры. Сверхпроводимость …….. .. смотреть
§ 110. Электрический ток в полупроводниках. Собственная и примесная проводимости ………. смотреть
§ 111. Электрический ток через контакт полупроводников с разным типом проводимости. Транзисторы ………. смотреть
§ 112. Электрический ток в вакууме. Электронно-лучевая трубка ………. смотреть
§ 113. Электрический ток в жидкостях. Закон электролиза ………. смотреть
§ 114. Электрический ток в газах. Несамостоятельный и самостоятельный разряды ………. смотреть
§ 115. Плазма ………. смотреть
§ 116. Примеры решения задач по теме «Электрический ток в различных средах» ………. смотреть

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Назад в раздел «10-11 класс»

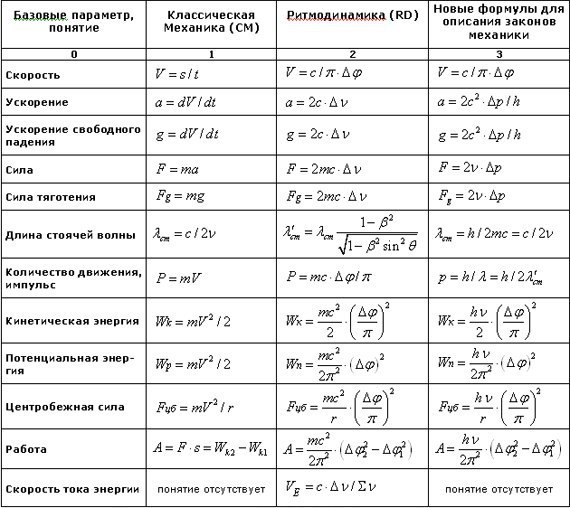
Физика – 10 класс. 1 – й пакет формул. Лекции 1, 2.

1.Средняя путевая скорость: ( ).

2. Мгновенная скорость:

3. Уравнение прямолинейного

равномерного движения: ; , при .

4. Путь в равномерном

прямолинейном движении: = , при , .

5. Ускорение в равнопеременном движении: .

6. Ускорение в равноускоренном движении : , при , =

7. Скорость в равноускоренном движении : , при .

8. Скорость в равнозамедленном движении: .

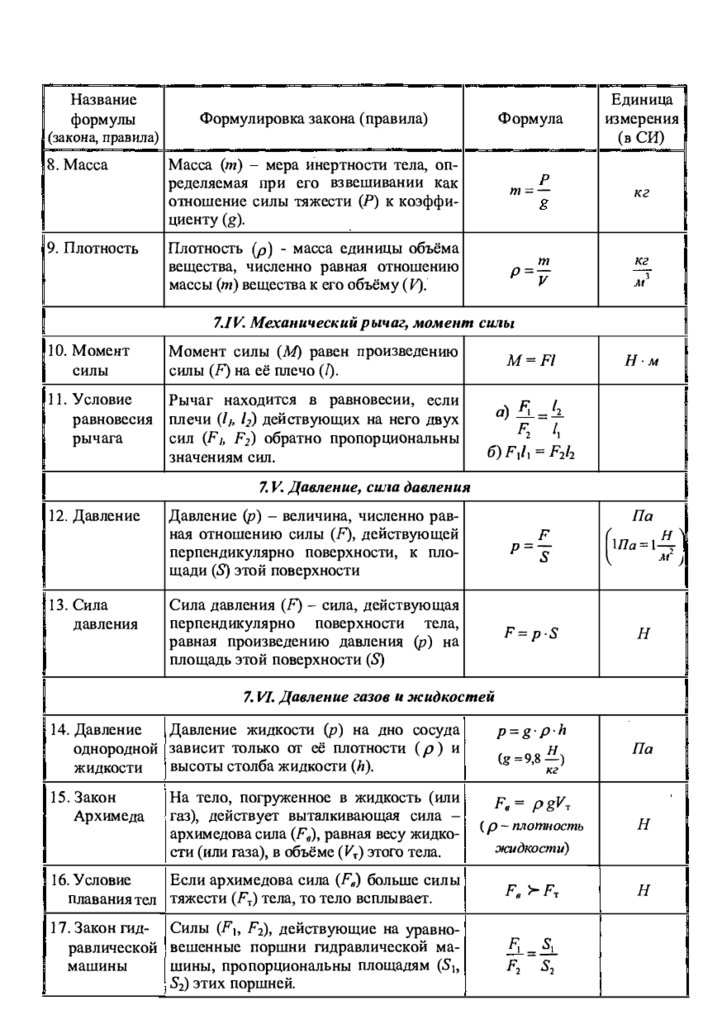
9. Перемещение в равноускоренном

прямолинейном движении : , при , .

10.Уравнение равноускоренного , при: , ,

прямолинейного движения: при , .

11. Перемещение в равнозамедленном

прямолинейном движении:

12. путь в равноускоренном движении: , ,

13. Средняя скорость равноускоренного

движения: . то .

14. Формулы связывающие ускорение,

скорость и путь: . то и .

15. Максимальная высота при движении тела,

брошенного вертикально вверх :

16. Максимальные высота и дальность полета , .

тела, брошенного под углом к горизонту:

1. Средняя путевая скорость:

2. Мгновенная скорость:

3. Уравнение прямолинейного

равномерного движения:

4. Путь в равномерном

прямолинейном движении:

5. Ускорение в равнопеременном движении:

6. Ускорение в равноускоренном движении :

7. Скорость в равноускоренном движении :

8. Скорость в равнозамедленном движении:

9. Перемещение в равноускоренном

прямолинейном движении :

10.Уравнение равноускоренного

прямолинейного движения:

11. Перемещение в равнозамедленном

прямолинейном движении:

12. путь в равноускоренном движении:

13. Средняя скорость равноускоренного

движения:

14. Формулы связывающие ускорение,

скорость и путь:

15. Максимальная высота при движении тела,

брошенного вертикально вверх :

16. Максимальные высота и дальность полета

тела, брошенного под углом к горизонту:

Физика – 10 класс. Коллоквиум – 2. Лекция – 3.

24. Записать определение равномерного движения по окружности, определения линейной и угловой скорости. Сделать рисунок. Единицы измерения линейной и угловой скоростей.

25. Записать определение периода и частоты равномерного движения по окружности. Связь частоты и периода, единицы их измерения. Выражение периода и частоты через число оборотов и время.

26. Записать вывод формулы связи угловой и линейной скорости, линейной скорости и частоты.

27. Записать вывод формулы центростремительного ускорения равномерного движения по окружности. Записать центростремительное ускорение в трёх вариантах

28. Равнопеременное движение по окружности. Формула углового ускорения и угловой скорости равнопеременного движения по окружности.

29.Тангенциальное ускорении и линейная скорость в равнопеременном движении по окружности.

30. Закон равнопеременного движения по окружности.

31. Полное ускорение в равнопеременном движении по окружности

32. Средняя угловая скорость равнопеременного движения по окружности (без вывода).

33. Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности ( без вывода).

Физика – 10 класс. 2 – й пакет формул. Лекция – 3.

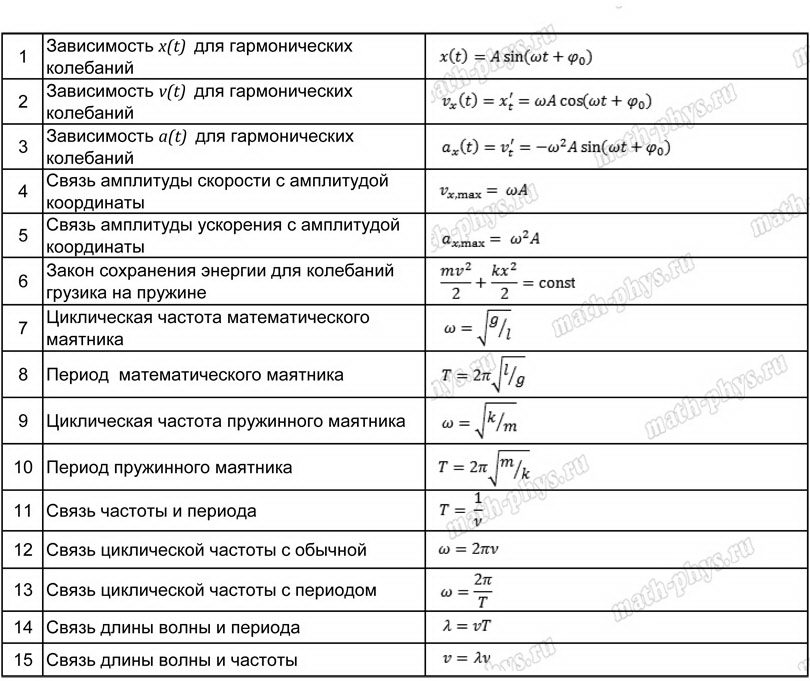
17. Линейная скорость равномерного

движения по окружности: ( .

18. Угловая скорость равномерного

по окружности: ( .

19. Связь периода и частоты

20. Выражение угловой скорости

через период и частоту: .

21. Центростремительное ускорение:

22. Угловое ускорение и угловая скорость

равноускоренного движения по окружности: , .

23. Закон равноускоренного движения

по окружности: , то .

Физика – 10 класс. 2 – й пакет формул. Лекция – 3.

17. Линейная скорость равномерного

движения по окружности:

18. Угловая скорость равномерного

по окружности:

19. Связь периода и частоты:

20. Выражение угловой скорости

через период и частоту:

21. Центростремительное ускорение:

22. Угловое ускорение и угловая скорость

равноускоренного движения по окружности:

23. Закон равноускоренного движения

по окружности:

Физика – 10 класс. Коллоквиум – 3. Лекция – 4.

34.Что изучает динамика.

35.Первый закон Ньютона.

36.Свободная материальная точка. Инерциальная система отсчёта (ИСО) 37.Формулировка первого закона Ньютона на основе определения (ИСО) 38.Неинерциальная система отсчёта. Привести примеры. 39.Принцип относительности Галилея. 40.Принцип относительности Галилея в трёх формулировках. Привести примеры проявления принципа относительности. 41.Определение силы. Как направлены сила, действующая на тело и ускорение вызванное действием этой силы.

42.Правило сложения сил. Правило параллелограмма.

43.Понятие массы в физике. Единица измерения массы в СИ.

44.Определение центра масс тела.

45.Определение плотности вещества, единица измерения плотности.

46.Записать словесную формулировку и математическую запись второго закона Ньютона.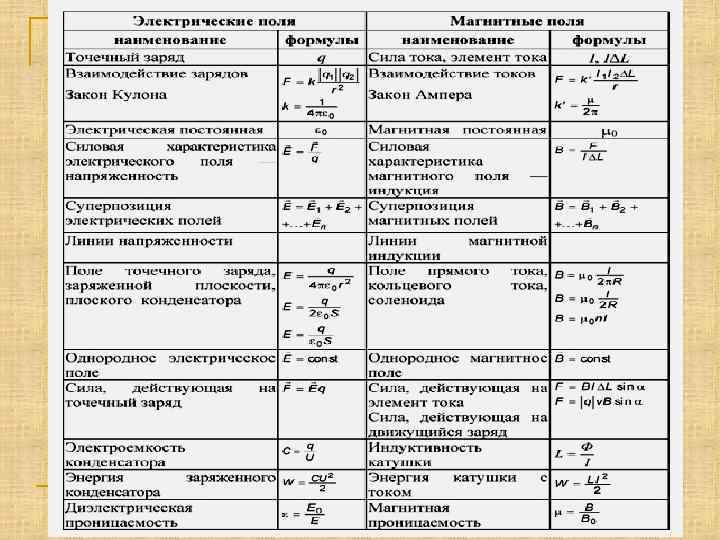

47.Определение силы. Словесная формулировка единица измерения силы в СИ.

48.Записать словесную формулировку и математическое выражение третьего закона Ньютона. Следствия из второго и третьего законов Ньютона.

Физика – 10 класс. 3 – й пакет формул. Лекция 4.

24. Второй закон Ньютона: , ,

25. Плотность вещества: , , .

26. Третий закон Ньютона: =

27. Следствия из второго и третьего

законов Ньютона: .

Физика – 10 класс. 3 – й пакет формул. Лекция -4.

24. Второй закон Ньютона:

25. Плотность вещества:

26. Третий закон Ньютона:

27. Следствия из второго и третьего

законов Ньютона:

Физика 10 – класс. Коллоквиум – 4. Лекция – 5.

49. Записать словесную формулировку и математическое выражение закона всемирного

тяготения. В чём заключается физический смысл гравитационной постоянной.

50. Записать определение силы тяжести и её математическое выражение на поверхности

планеты и на некоторой высоте над её поверхностью.

51. Записать математическое выражение ускорения свободного падания как следствие

второго закона Ньютона и закона всемирного тяготения.

52. Что называется весом тела. Как направлена реакция опоры по отношению к поверхности опоры.

53. Вывести формулу веса тела в системе отсчёта, движущейся ускоренно вверх. Сделать рисунок.

54. Вывести формулу веса тела в системе отсчёта, движущейся ускоренно вниз. Сделать рисунок.

55. Что называется перегрузкой. В каком случае наступает состояние невесомости показать математически.

Физика – 10 класс. 4-й пакет формул. Лекция – 5.

28. Закон всемирного тяготения: .

29. Сила тяжести: , , .

30. Ускорение свободного падения

на некоторой высоте:

31. Ускорение свободного падения на

поверхности Земли: .

32. Сила тяжести на поверхности Земли:

33. Перегрузка: .

Физика – 10 класс. 4-й пакет формул. Лекция – 5.

28. Закон всемирного тяготения:

29. Сила тяжести:

30. Ускорение свободного падения

на некоторой высоте:

31. Ускорение свободного падения на

поверхности Земли: .

32. Сила тяжести на поверхности Земли:

33. Перегрузка: .

Физика – 10 класс. Коллоквиум – 5. Лекция – 6.

56. Что называется деформацией тела? Какие деформации называются упругими, а какие пластическими?

57. Cуществуют ли абсолютно упругие и абсолютно пластические тела?

58. Что называется силой упругости и какова её природа?

59. Абсолютная и относительная деформации, механическое напряжение.

60. Закон Гука, модуль Юнга и его физический смысл. Коэффициент жесткости и его зависимость от размеров, формы и свойств материала.

61. Вывести формулу потенциальной энергии деформированного тела на основе графика зависимости упругой силы от удлинения.

62. Вывести формулу коэффициента жесткости системы последовательно соединённых пружин.

63. Вывести формулу коэффициента жесткости системы параллельно соединённых пружин.

64. Записать определение силы трения. Что называется силой трения покоя,- трения скольжения, – трения качения. Какая из них наибольшая, а какая наименьшая.

65. Какое трение называется сухим, а какое – вязким?

66. Какова природа силы трения? С помощью рисунка объяснить происхождение силы трения качения.

67. Закон трения: закон Амонтона – Кулона. Коэффициент трения, что он показывает.

68. Объяснить физику вязкого (жидкого) трения.

69. Объяснить электромагнитную природу силы трения.

Физика – 10 класс. 5-й пакет формул. Лекция – 6.

34. Относительная деформация (удлинение):

35.Напряжение ( механическое): .

36.Закон Гука: .

37. Коэффициент жёсткости:

38. Потенциальная энергия деформированного

тела:

39.Коэффициент жесткости

системы параллельных пружин: .

40. Коэффициент жесткости системы

последовательно соединенных пружин:

41. Коэффициент трения: .

42.Сила трения: .

Физика – 10 класс. 5-й пакет формул. Лекция – 6.

34. Относительная деформация (удлинение):

35.Напряжение ( механическое):

36.Закон Гука:

37. Коэффициент жёсткости:

38. Потенциальная энергия деформированного

тела:

39.Коэффициент жесткости

системы параллельных пружин:

40. Коэффициент жесткости системы

последовательно соединенных пружин:

41. Коэффициент трения:

42.Сила трения:

Физика – 10 класс. Коллоквиум – 6. Лекция – 7.

70.Как направлены силы, действующие на тело по отношению к ускорению при поступательном движении.

71.Как направлены сила тяги и сила трения при поступательном движении. Рассмотреть случаи и написать формулы.

72. Разложить силу тяжести на составляющие, действующие на тело при его положении на наклонной плоскости.

73. Вывести уравнение движения тела вверх по наклонной плоскости с учётом трения.

74. Вывести уравнение движения тела вниз по наклонной плоскости с учётом трения.

75. Вывести условие равновесия тела на наклонной плоскости.

76.Рассмотреть движение грузов, связанных нитью, перекинутой через неподвижный блок.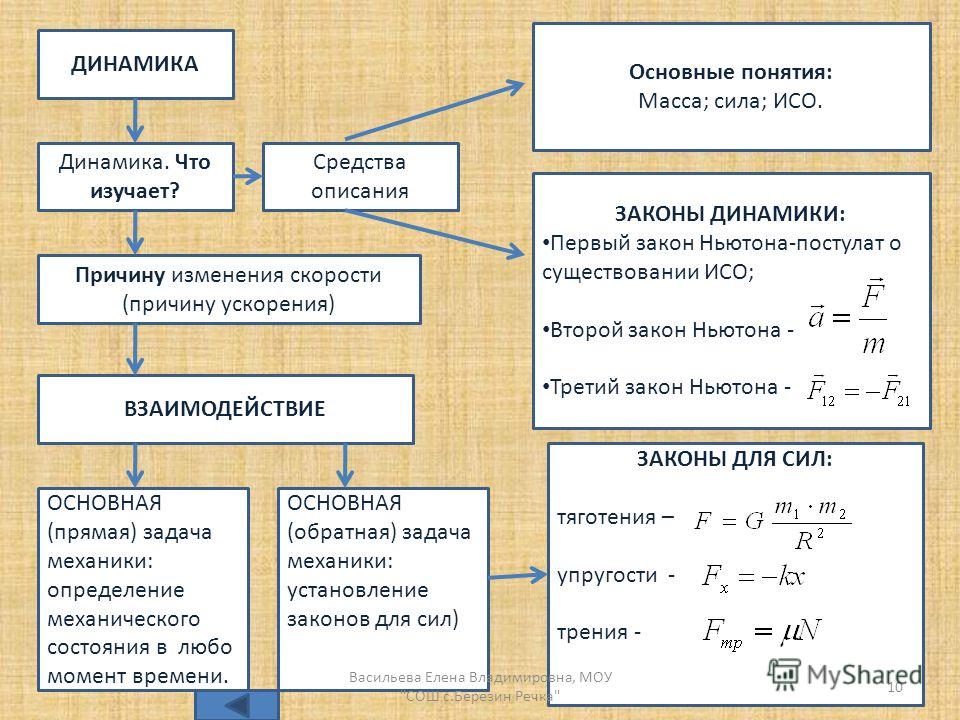

77. Рассмотреть движение тела по вогнутому мосту и вывести выражение для силы реакции опоры (веса тела).

78. Рассмотреть движение тела по выпуклому мосту и вывести выражение для силы реакции опоры (веса тела).

79. Вывести выражение скорости искусственного спутника планеты на некоторой высоте над её поверхностью и получить выражение первой космической скорости.

Физика – 10 класс. 6-й пакет формул. Лекция – 7.

43. Силы действующие на тело, , .

расположенное на наклонной

плоскости:

44. Сила трения на наклонной плоскости: .

45.Условие равновесия на накл. Плоскости: .

46. Уравнение ускоренного движения вверх

по наклонной плоскости:

47. Уравнение ускоренного движения вниз

по наклонной плоскости:

48. Уравнения движения грузов, связанных

нитью, перекинутой через неподвижный

блок:

49.Уравнение движения тела по

вогнутому мосту: .

50. Уравнение движения тела по

выпуклому мосту:

51.Вес тела при движении по вогнутому

мосту :

52. Вес тела при движении по выпуклому мосту:

53. Скорость искусственного спутника на

некоторой высоте над поверхностью планеты:

54. Первая космическая скорость:

4 полезных совета для запоминания физических формул и понятий

Если у вас проблемы с математикой и физикой, вам нечего стыдиться. Ты не один. Но не волнуйтесь, потому что, если вы ищете курсы по физике и хотите лучше запоминать различные формулы, есть способы сделать именно это.

Имейте в виду, однако, что для изучения формул не существует короткого пути за один день. Нельзя просто зубрить и рассчитывать на высокие оценки. Для всего, что связано с числами, например, с математикой и физикой, вам нужна постоянная практика и знакомство с формулами.

Ниже приведены несколько советов, которые помогут вам запомнить все эти надоедливые формулы:

Шаг 1. Избавьтесь от стресса

Чтобы научиться чему-либо, вам нужно сначала избавиться от стресса. В этом помогает медитация. Потратьте время, чтобы успокоить свои мысли на 5-10 минут перед началом. Позвольте себе почувствовать давление проблемы и одним махом позвольте ей раствориться. Когда вы закончите, потратьте еще несколько минут, чтобы увидеть, испытываете ли вы жажду, чувство голода или просто отвлеклись. Сделайте небольшой перерыв, чтобы позаботиться о том, что вас отвлекает, чтобы сразу перейти к делу.

Как только вы почувствуете себя хорошо и позитивно, прочитайте формулы снова и снова и бросьте себе вызов, чтобы освоить их одну за другой.

Шаг 2. Попытайтесь понять формулу

Концептуальное понимание, как его называют некоторые, представляет собой тип обучения, при котором вместо запоминания чего-либо вы пытаетесь понять его основную концепцию, применяя ее к чему-то реальному.

Например, если вы пытаетесь выучить формулу второго закона Ньютона, а именно: ускорение = сила/масса, попытайтесь концептуализировать сценарий, в котором вы можете ее применить. Например, вы толкаете тележку во время покупки продуктов. Чем больше вы кладете внутрь тележки, тем медленнее она становится, поскольку ее масса увеличивается, и она становится тяжелее. Знакомство с концепциями и их связь со знакомыми сценариями помогут вам быстрее изучить соответствующие формулы. Шаг 3. Постоянно работайте над этим. Если вы учитесь с друзьями, не бойтесь играть с ними в игры. Например, игра, в которой один описывает формулу, а другой пытается ее угадать, — хорошее начало. Но, даже если вы один, вы все равно можете сделать что-то похожее. Такие простые вещи, как создание таблиц формул и их запись, помогут вам лучше запомнить формулы. Чем больше листов вы сделаете, тем больше шансов, что вы их не забудете. Для большего эффекта сделайте большую схему и прикрепите ее к себе на стену. Затем напишите уменьшенные версии листа, которые можно положить в карман, чтобы просматривать их в течение дня.

Если вы достаточно изобретательны, сочинение фраз, рифм, песен или рассказов также может помочь вам запомнить формулы, которые иначе легко забыть.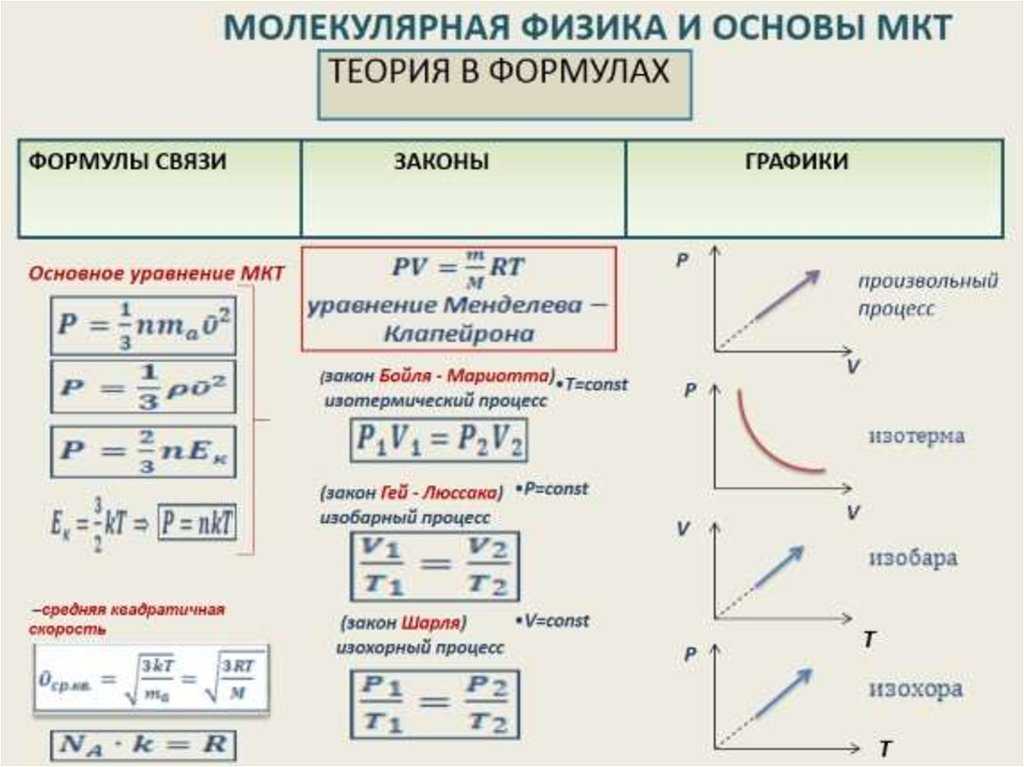

Шаг 3. Постоянно работайте над этим

Если вы учитесь с друзьями, не бойтесь играть с ними в игры. Например, игра, в которой один описывает формулу, а другой пытается ее угадать, — хорошее начало. Но, даже если вы один, вы все равно можете сделать что-то похожее. Такие простые вещи, как создание таблиц формул и их запись, помогут вам лучше запомнить формулы. Чем больше листов вы сделаете, тем больше шансов, что вы их не забудете. Для большего эффекта сделайте большую схему и прикрепите ее к себе на стену. Затем напишите уменьшенные версии листа, которые можно положить в карман, чтобы просматривать их в течение дня. Если вы достаточно изобретательны, сочинение фраз, рифм, песен или рассказов также может помочь вам запомнить формулы, которые в противном случае легко забыть.

Шаг 4. Перестаньте полагаться на формулу

Если вы действительно хотите, чтобы формула надолго осталась в вашей голове, простого запоминания будет недостаточно. Вместо этого вы захотите использовать их для решения задач по математике и физике снова и снова.

Чем больше задач вы решите, используя определенную формулу, тем лучше вы ее запомните.

Повторение является ключом к запоминанию формул. Решайте как можно чаще. А еще лучше, перестаньте полагаться на лист формул и попытайтесь решать проблемы, полагаясь исключительно на свой мозг. Конечно, не забудьте проверить, правильный ответ или нет.

Математика 10-го класса CBSE Важные формулы для пересмотра в последнюю минуту перед экзаменом 2 семестра 2022

Прочтите здесь важные формулы из всех глав 10-го класса CBSE по математике. Важные термины и свойства, полезные в математических расчетах для класса 10, также представлены в этой статье для быстрого ознакомления перед экзаменом по математике CBSE, семестр 2, 2022 г. вызывает кошмары у студентов. Хотя математика немного сложна, это не сложно. Это просто требует глубокого понимания концепций, регулярной практики и хорошего владения важными формулами, чтобы получить высокие оценки на экзамене по математике. Чтобы помочь учащимся получить все важные формулы, теоремы и свойства в одном месте, мы собрали формулы по главам вместе с важными терминами и свойствами, встречающимися в математике для 10 класса. Учащиеся должны усвоить все формулы и теоремы, чтобы быстро выполнять расчеты и получать высокие баллы по математике.

Важно* CBSE Класс 10 Математика 7 самых важных советов, как набрать более 90% баллов за экзамен 2 семестра 2022

если у нас есть два положительных целых числа a и b, то существуют уникальные целые числа q и r такие, что a = bq + r, где 0 ≤ r ≤ b. (Здесь a = делимое, b = делитель, q = частное и r = остаток.)

2. Многочлены:

(i) (a + b) ² = a ² + 2ab + b ²

(ii) (a – b) ² = a ^{2 9 9068 0 8 0}

(iii) а ² – б ² = (а + b) (а – b)

(iv) (а + b) ³ = а ³ + b ⁸

(a + b)

(v) (a – b) ³ = a ³ – b ³ – 3ab(a – b)

(vi) a ³ + 8 ^{(а + б) (а ² – ab + b ² )}

(vii) a ³ – b ³ = (a – b) (a ² + ab + b ² 9 а vi)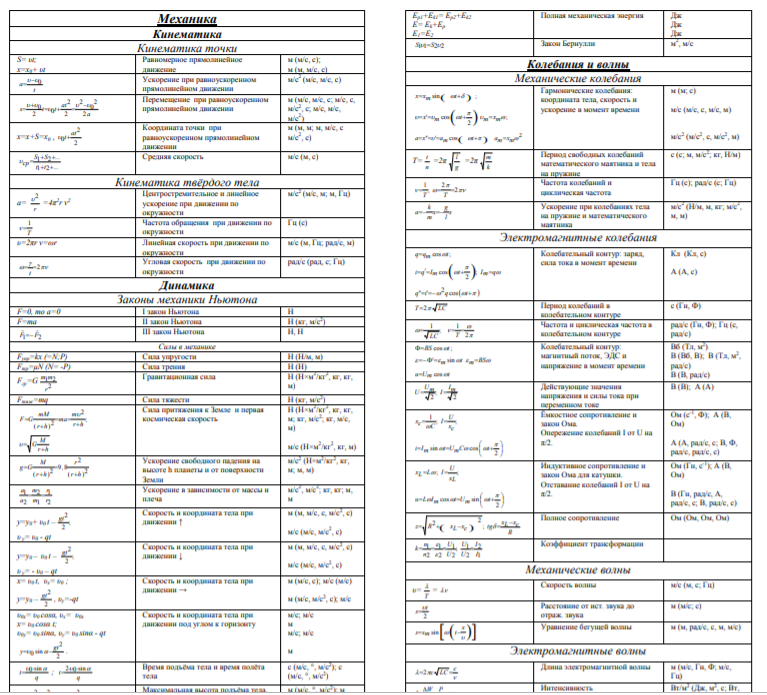

– B ⁴ = (A ²) ² – (B ²) ² = (A ²+ B ²) (A ² – B ^{2 9008) = = = = a ² – B ^{2 9008) = = = = = a ² – B ^{2 9008) = = a ². (a ² + b ² ) (a + b) (a – b)}}}

(ix) (a + b + c) ² = a ² + b ²

0 6 + c 9 + 2аб + 2бс + 2ас

(x) (a + b – c) ² = a ² + b ² + c ² + 2ab – 2bc – 2ca

(xi) (20 – b06 c 6 c) = A ²+ B ²+ C ² – 2AB – 2BC+ 2CA

(XII) (A – B – C) ² = A ²+ B ²+ C ² – 2ab + 2bc – 2ca

(xiii) a ³ + b ³ + c ³ – 3abc = (a + b + c)(a ^{2 9 6 b 8} 0 +0067 2 – AB – BC – CA)

CBSE класс 10 Вопросы по математическому изучению. Вопросы по тематическому исследованию для термина 2 экзамена 2022

3. Линейные уравнения в двух переменных:

Для пары линейных уравнений

A ₁ + b ₁ y + c ₁ = 0 и a ₂ + b ₂ y + c ₂ = 0,

характер корней (нулей) или решений определяется следующим образом:

(i) Если a ₁ /a ₂ ≠ b ₁ /b ₂, то мы получаем единственное решение и пара линейных уравнений с двумя переменными совместна.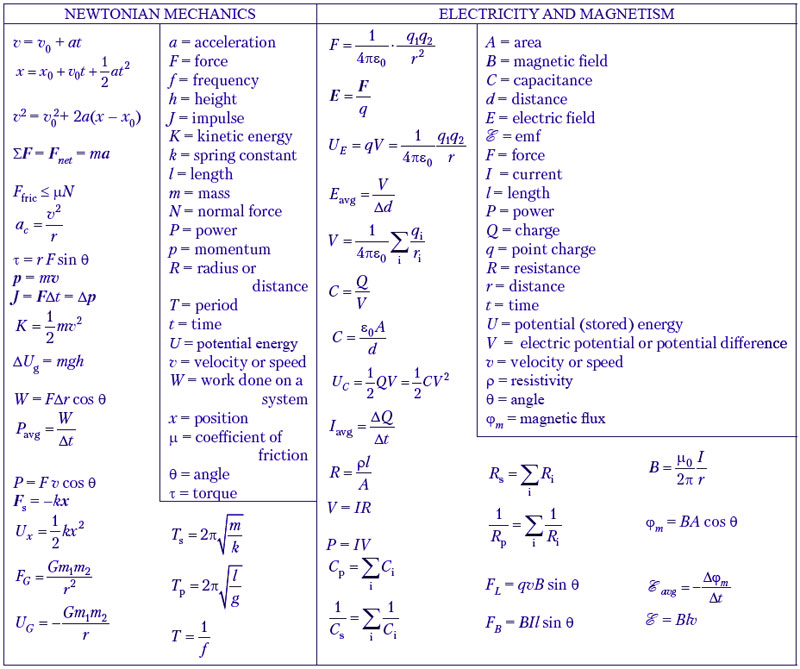 Здесь график состоит из двух пересекающихся линий.

(i) Если a ₁ /a ₂ ≠ b ₁ /b ₂ ≠ c ₁ /c ₂ , то решения двух линейных уравнений в системе не существует и пара линейных уравнений не существует и пара говорят, что они несовместимы. Здесь график состоит из параллельных линий.

(iii) Если a ₁ /a ₂ = b ₁ /b ₂ = c ₁ /c ₂ , то существует бесконечно много решений и пара прямых совпадает, а значит, зависима и непротиворечива. Здесь график состоит из совпадающих линий.

4. Квадратное уравнение:

Для квадратного уравнения: ax ² + bx + c = 0

• = Сумма корней = –0/a

3 9000

• Если даны корни квадратного уравнения, то квадратное уравнение можно представить в виде:

x ² – (сумма корней)x + произведение корней = 0

• Если Дискриминант > 0, то корни квадратного уравнения действительны и неравны/единственны.

• Если Дискриминант = 0, то корни квадратного уравнения действительны и равны.

• Если Дискриминант < 0, то корни квадратного уравнения мнимые (не вещественные).

• Важные формулы — лодки и течения

(i) Вниз по течению

В воде направление вдоль течения называется вниз по течению.

(ii) Вверх по течению

В воде направление против течения называется вверх по течению.

(iii) Пусть скорость лодки в стоячей воде u км/ч, а скорость течения v км/ч, тогда

Скорость по течению = (u + v) км/ч
Скорость против течения = (u – v) км/ч.

CBSE Класс 10 Математика Важные вопросы с решениями

5. Арифметическая прогрессия:

• n-й член арифметической прогрессии: Для данного AP, где a — первый член, d — общая разность, n — количество членов, его n-й член (a _n ) дается как

a _n = a + (n−1)×d

• Сумма первых n членов арифметической прогрессии, S _n дается как:

3 6. Подобие треугольников:

• Если два треугольника подобны, то отношения их сторон равны.

• Теорема о площади подобных треугольников: если два треугольника подобны, то отношение площадей обоих треугольников пропорционально квадрату отношения их соответствующих сторон.

7. Геометрия координат:

• Формулы расстояний: Рассмотрим прямую, имеющую две точки A(x ₁ , y ₁ ) и 21B(x 2 9 00216 , y ₂ ), то расстояние между этими точками определяется как:

• Формула сечения: Если точка p делит прямую AB с координатами A(x ₁ , y ₁ ) и B(x ₂ , y ₂ ) в соотношении m:n, то координаты точки p задаются как:

• Формула средней точки: линия AB с координатами A(x ₁ , y ₁ ) и B(x ₂ , y ₂ ), задаются как:

• Площадь треугольника: Рассмотрим треугольник, образованный точками A(x ₁ , y ₁ ) и 2B(152×290 ) , y ₂ ) и C(x ₃ , y ₃ ), то площадь треугольника определяется как-

, Тригонометрия:

В прямоугольном треугольнике теорема Пифагора утверждает

(перпендикуляр) ² + (основание) ² = (гипотенуза) ²

Важные тригонометрические свойства: (с P = перпендикуляр, B = основание и H = P в A)

3

/ H
• CosA = B / H
• TanA = P / B
• CotA = B / P
• CosecA = H / P
• SecA = H/B
Тригонометрические
• sin ² A + cos ² A=1
• TAN ² A +1 = SEC ² A
• COT ² A + 1 = COSEC ² A
Отношения между тригонометрическими идентификациями приведены ниже:
9000 2 9 Дополнительные углы задаются следующим образом:
• sin (90° – A) = cos A
• cos (90° – A) = sin A
• tan (90° – A) = cot A
• cot (90° – A) = tan A
• sec (90° – A) = cosec A
• cosec (90° – A) = sec A
Значения тригонометрических отношений 0° и 90° приведены в таблице ниже:

• Равные хорды окружности равноудалены от центра.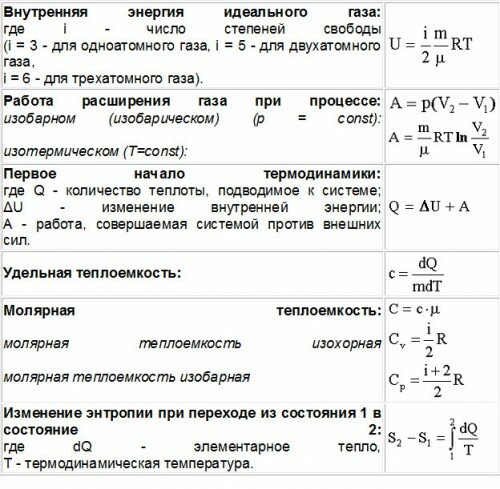
• Перпендикуляр, проведенный из центра окружности, делит хорду окружности пополам.
• Угол, образуемый дугой в центре, = удвоенный угол в любой части окружности окружности.
• Углы, опирающиеся на одну и ту же дугу в одном сегменте, равны.
• Для окружности, если провести касательную и хорду из точки касания, то угол между хордой и касательной равен углу, образуемому в альтернативном сегменте.
• Сумма противоположных углов вписанного четырехугольника всегда равна 180 ^o .
Важные формулы, связанные с кругами:

• Площадь сегмента круга: если AB — это хорда, которая делит круг на две части, то большая часть называется большим сегментом, а меньшая — второстепенным сегментом.
Здесь, Площадь сегмента APB = Площадь сектора OAPB – Площадь ∆ OAB
Решения NCERT для CBSE Класс 10 Математика: Все главы формулы площадей и объемов твердых тел:

11. Статистика:
Для несгруппированных данных:
Среднее значение: Среднее значение переменной определяется как сумма всех значений переменной, деленная на число.
Медиана: Медиана набора значений данных — это среднее значение набора данных, если он расположен в порядке возрастания. То есть от наименьшего значения к наибольшему.
Медиана рассчитывается как

, где n — количество значений в данных. Если количество значений в наборе данных четное, то медиана – это среднее значение двух средних значений.
Режим: Режим статистических данных — это значение той переменной, которая имеет максимальную частоту
Для сгруппированных данных:
Среднее значение: ,……x _n являются наблюдениями с соответствующими частотами f1, f2, f3,…..fn, тогда среднее значение определяется как:
Медиана: Для заданных данных нам нужно иметь интервал класса, частотное распределение и кумулятивное частотное распределение. Затем медиана рассчитывается как
Где
l = нижний предел медианного класса,
n = количество наблюдений,
cf = кумулятивная частота класса, предшествующего среднему классу,
f = частота медианного класса,
h = размер класса (при условии, что размеры классов равны)
Режим: Модальный класс : Интервал класса с наибольшей частотой называется модальным классом, а режим получается с использованием модального класса.
Где
l = нижний предел модального класса,
h = размер интервала класса (при условии, что все размеры классов равны),
f ₁ = частота модального класса,
f ₀ = частота класса, предшествующего модальному классу,
f ₂ = частота класса, следующего за модальным классом.
12. Вероятность:
Понимания основных понятий и изучения всех важных формул чрезвычайно достаточно, чтобы успешно сдать экзамен по математике.