Физика перемещение и путь: Перемещение, путь, траектория при равномерном прямолинейном движении

Отличия перемещения и пути

☰

На первый взгляд перемещение и путь — близкие по смыслу понятия. Однако в физике между перемещением и путем есть ключевые отличия, хотя оба понятия связаны с изменением положения тела в пространстве и нередко (обычно при прямолинейном движении) численно равны друг другу.

Чтобы понять отличия перемещения и пути, дадим сначала им определения, которыми их наделяет физика.

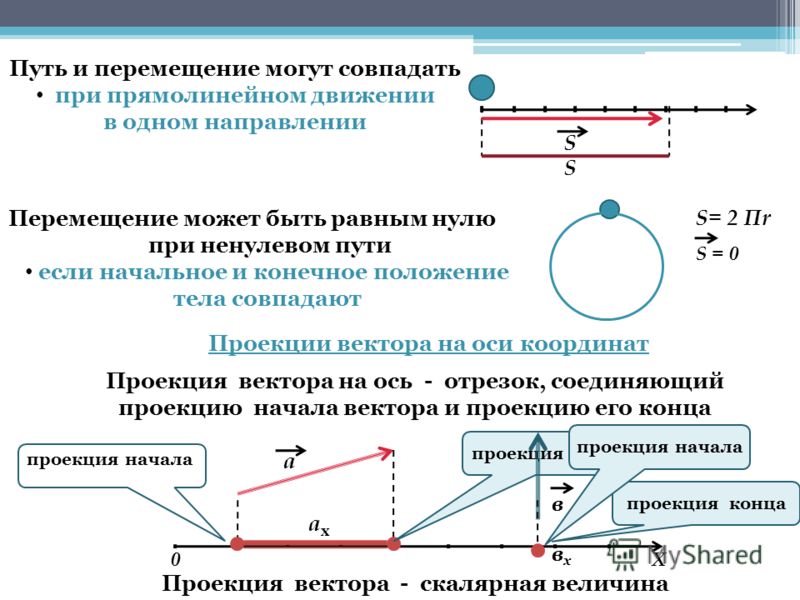
Перемещение тела — это направленный отрезок прямой (вектор), начало которого совпадает с начальным положением тела, а конец совпадает с конечным положением тела.

Путь тела — это расстояние, которое прошло тело за определенный промежуток времени.

Представим себе, что вы стали у своего подъезда в определенную точку. Обошли дом и вернулись в исходную точку. Так вот: ваше перемещение будет равно нулю, а путь — не будет. Путь будет равен длине кривой (например, 150 м), по которой вы шли вокруг дома.

Однако вернемся к системе координат. Пусть точечное тело двигается прямолинейно из точки A с координатой x₀ = 0 м в точку B с координатой x₁ = 10 м. Перемещение тела в данном случае составит 10 м. Так как движение было прямолинейным, то 10-ти метрам будет равен и проделанный телом путь.

Если же тело прямолинейно двигалось из начальной (A) точки с координатой x₀ = 5 м, в конечную (B) точку с координатой x₁ = 0, то его перемещение составит -5 м, а путь 5 м.

Перемещение находится как разность, где из конечной координаты вычитают начальную. Если конечная координата меньше начальной, т. е. тело двигалось в обратном направлении по отношению к положительному направлению оси X, то перемещение будет отрицательной величиной.

Так как перемещение может иметь как положительное, так и отрицательное значение, то перемещение является векторной величиной. В отличие от него, путь — всегда положительная или равная нулю величина (путь — скалярная величина), так как расстояние не может быть отрицательным в принципе.

Рассмотрим еще один пример. Тело прямолинейно двигалось из точки A (x₀ = 2 м) в точку B (x₁ = 8 м), далее также прямолинейно из B переместилось в точку C с координатой x₂ = 5 м. Чему равны и отличаются ли общий путь (A→B→C) проделанный данным телом и его суммарное перемещение?

Изначально тело было в точке с координатой 2 м, в конце своего движения оказалось в точке, имеющей координату 5 м. Таким образом, перемещение тела составило 5 – 2 = 3 (м). Также можно вычислить общее перемещение как сумму двух перемещений (векторов). Перемещение из A в B составило 8 – 2 = 6 (м). Перемещение из точки B в C составило 5 – 8 = -3 (м). Сложив оба перемещения получим 6 + (-3) = 3 (м).

Общий путь вычисляется путем сложения двух расстояний, прошедших телом. Расстояние от точки A до B составляет 6 м, а от B до C тело проделало путь в 3 м. Итого получаем 9 м.

Таким образом, в данной задаче путь и перемещение тела отличаются между собой.

Рассмотренная задача не совсем корректна, так как необходимо указывать моменты времени, в которые тело находится в определенных точках. Если x₀ соответствует момент времени t₀ = 0 (момент начала наблюдений), то пусть например x₁ соответствует t₁ = 3 c, а x₂ соответствует t₂ = 5 c. То есть промежуток времени между t₀ и t₁ составляет 3 с, а между t₀ и t₂ составляет 5 с. В этом случае получается, что путь тела за промежуток времени в 3 секунды составил 6 метров, а за промежуток в 5 секунд — 9 метров.

В определении пути фигурирует время. В отличие от него для перемещения время не имеет особого значения.

Путь и перемещение тела

С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.

Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.

Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.

Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.

Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления).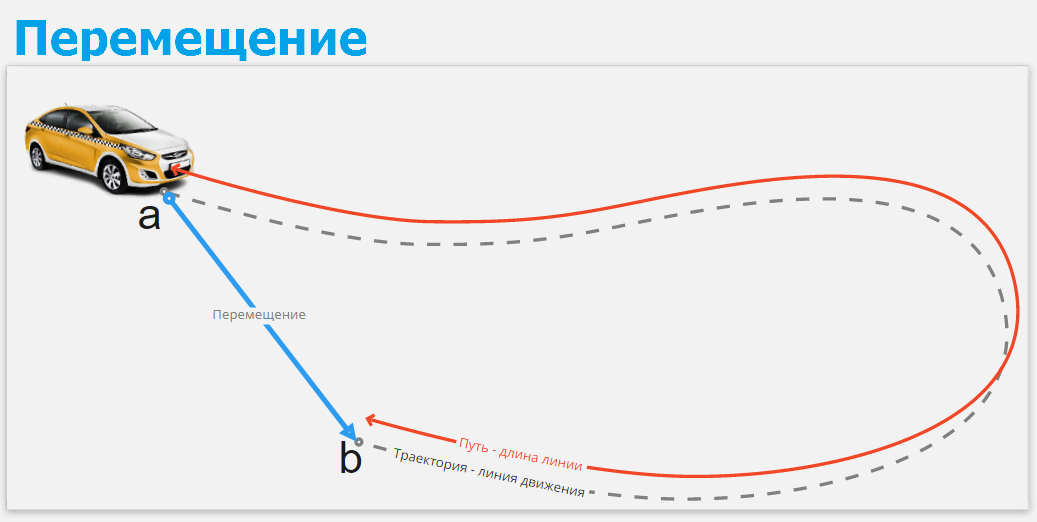 Путь обозначают символом l, перемещение обозначают символом (важно: со стрелочкой). Символом s без стрелочки обозначают модуль перемещения. Примечание: изображение любого вектора на чертеже (в виде стрелки) или упоминание его в тексте (в виде слова) делает необязательным наличие стрелочки над обозначением.

Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.

Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.

Решение 1 – с измерениями линейкой и транспортиром.

Перемещение – это вектор, соединяющий начальное и конечное положения тела.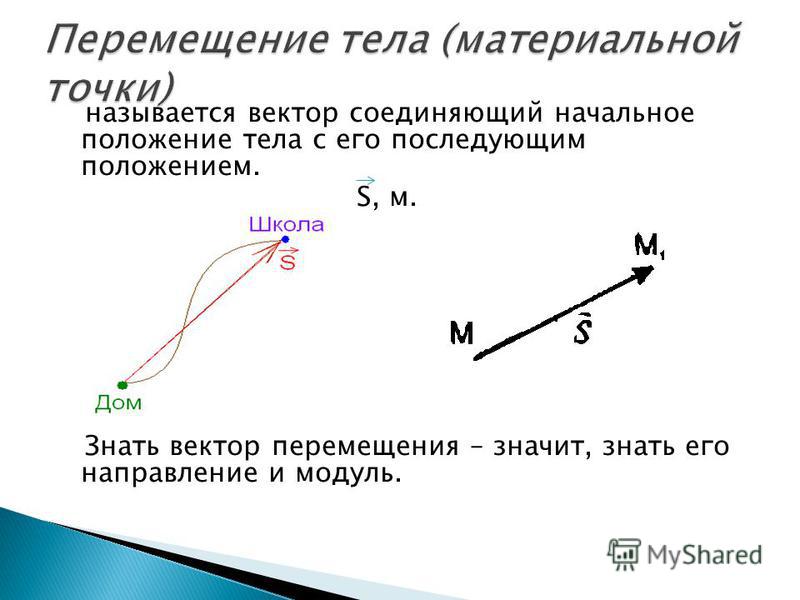 Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).

Решение 2 – без использования линейки и транспортира.

Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:

Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):

Итак, задача решена двумя способами с совпадающими ответами.

Опубликовано в разделах: 9 класс, Введение в кинематику

Объяснение урока: Расстояние и смещение

В этом объяснении мы научимся определять расстояние как длину пути между двумя положениями и смещение как расстояние по прямой линии между двумя положениями.

Давайте сначала обсудим расстояние.

Когда объект перемещается из одной точки в другую, он движется по траектории, соединяющей эти точки. Путь, по которому движется объект, имеет длину. Эта длина равна расстоянию, на которое перемещается объект.

Путь между двумя точками может быть прямой линией между ними. На следующем рисунке показан прямой путь, по которому движется объект.

Путь между двумя точками также может быть изогнутым, как показано на следующем рисунке.

Как для прямых, так и для кривых не имеет значения пройденное расстояние, из какой точки перемещается объект и в какую, поскольку длина линии одинакова в обоих направлениях. Расстояние не имеет направления, а только величину.

Величины, имеющие величину, но не направление, являются скалярными величинами; следовательно, расстояние является скалярной величиной.

Когда объект движется, движение может происходить между более чем двумя точками.

Предположим, что объект перемещается из точки A в точку B, а затем из точки B в точку C, как показано на следующем рисунке.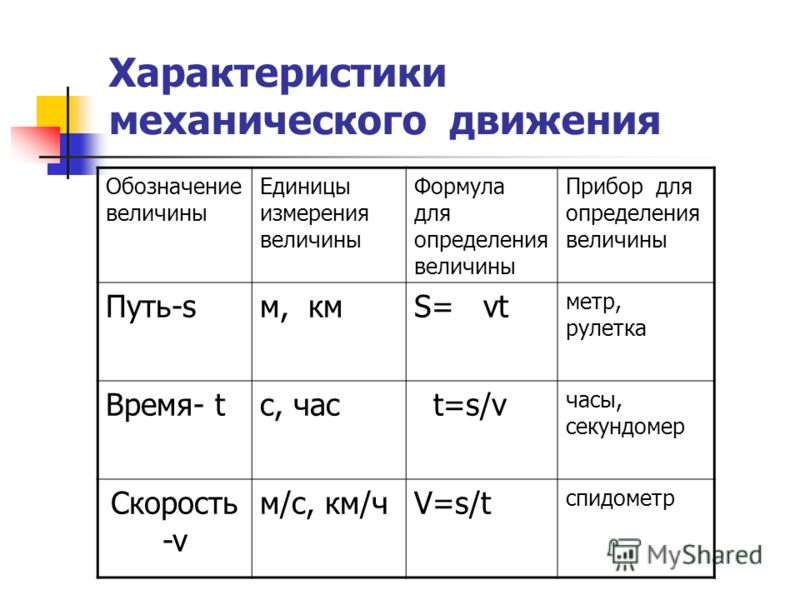

Движение объекта можно разделить на движение из А в В и движение из В в С.

Расстояние 𝑑, которое проходит объект, определяется выражением 𝑑=()+().0003

Рассмотрим пример, в котором определяется расстояние, пройденное по пути, меняющему направление.

Пример 1. Определение расстояния, пройденного по пути, меняющему направление

Каково общее расстояние, пройденное кем-то по линиям, показанным на диаграмме?

Ответ

Человек идет по трем прямым. Расстояние, на которое они перемещаются, равно сумме длин этих линий. Пройденное расстояние, 𝑑, определяется как 𝑑=15+10+20=45,м

Мы видим, что расстояние всегда увеличивается по мере движения объекта. Наименьшее расстояние, на которое может переместиться объект, равно нулю, когда он остается в покое.

Теперь рассмотрим другой пример, в котором определяется расстояние, пройденное по пути, меняющему направление.

Пример 2. Определение расстояния, пройденного по пути, который меняет направление

Какое общее расстояние пройдёт тот, кто идёт по линиям, показанным на диаграмме?

Ответ

Человек идет по трем прямым. Расстояние, на которое они перемещаются, равно сумме длин этих линий. Пройденное расстояние 𝑑 определяется выражением 𝑑=5+8+7=20 м

Предположим, что объект также перемещается из точки C обратно в точку A, как показано на следующем рисунке.

Расстояние 𝑑, которое проходит объект, теперь определяется выражением 𝑑=()+()+().расстояние отAдоBрасстояниеотBдоCрасстояниеотCдоA A, совершая путешествие несколько раз. Мы можем

назовите количество раз, которое объект повторяет это путешествие 𝑛.

Теперь мы можем назвать расстояние, которое проходит объект, 𝐷, которое определяется как 𝐷=𝑛𝑑.

Рассмотрим пример, в котором определяется пройденное расстояние по замкнутому пути.

Пример 3. Определение расстояния, пройденного по пути, меняющему направление

Какое общее расстояние пройдёт человек, который идёт по линиям, показанным на схеме, не проходя ни по одной линии более одного раза?

Ответ

Человек идет по трем прямым. Ни одна линия не проходится более одного раза и ни одна линия не проходится, поэтому каждая линия проходится один раз.

Расстояние, на которое перемещается человек, равно сумме длин этих линий. Пройденное расстояние 𝑑 определяется выражением 𝑑=6+6+6=18.м

То, что было показано в этих примерах для расстояний, пройденных по прямым линиям, также применимо к расстояниям, пройденным по кривым путям.

Предположим, что объект движется по круговой траектории, как показано на следующем рисунке.

Предположим также, что объект проходит один раз по круговой траектории, возвращаясь в исходную точку и не меняя направления. Расстояние, на которое перемещается объект, равно длине окружности.

Вместо этого предположим, что объект движется по пути, показанному на следующем рисунке, который ведет объект из A в B, затем из B в C и, наконец, из C в A.

Расстояние, на которое перемещается объект, равно сумме длины кривых путей между точками.

Расстояние объяснено.

Теперь поговорим о смещении.

Когда объект меняет положение, а также перемещается на расстояние, он также имеет смещение.

Смещение также является величиной, описывающей удаление точек друг от друга, но это не то же самое, что расстояние.

Причина того, что смещение отличается от расстояния, заключается в том, что смещение имеет направление. Величины, у которых есть направление, а также величина, являются векторными величинами, поэтому перемещение является векторной величиной. Смещение часто обозначается символом 𝑠.

Рассмотрим линию, соединяющую точки, показанные на следующем рисунке.

Объект может двигаться из A в B или из B в A. Перемещение объекта, движущегося из A в B, происходит в направлении, противоположном смещению объекта, движущегося из B в A.

Предположим, что расстояние от А до В 1 метр. Это то же самое, что и расстояние от B до A.

Смещение объекта, который движется из A в B, составляет 1 метр, но смещение объекта, который движется из B в A, составляет −1 метр, как показано на следующем рисунке. фигура.

Отсюда видно, что расстояние между А и В равно величине смещения объекта, движущегося из А в В, и равно величине смещения объекта, движущегося из В в А. Направление смещения показывается положительным или отрицательным знаком смещения.

В этом примере положительное направление — от A к B. Какое направление считается положительным, можно выбирать свободно. Какое бы направление ни считалось положительным, противоположное направление должно считаться отрицательным.

Смещение имеет направление, поэтому смещение между двумя точками должно представлять собой прямую линию между точками. Изогнутый путь меняет направление по всей своей длине, поэтому у него нет одного определенного направления.

Теперь рассмотрим пример, в котором определяются смещения точек относительно других точек.

Пример 4: Определение перемещений между позициями

Быстроходный катер проходит мимо маркеров в точках A, B и C, как показано на диаграмме. Положительное смещение считается направленным от А к С.

• Каково водоизмещение лодки из точки А, когда она находится в точке В?
• Каково водоизмещение лодки из точки С, когда она находится в точке В?
• Каково водоизмещение лодки из точки А, когда она находится в точке С?
• Каково водоизмещение лодки из точки С, когда она находится в точке А?

Ответ

В вопросе указано, что положительное направление смещения должно быть от А к С. Это верно для любой точки, из которой в вопросе требуется взять смещение.

Когда лодка находится в точке B, смещение от A к B происходит в том же направлении, что и от A к C, т. е. в положительном направлении, как показано на следующем рисунке.

Расстояние от А до В равно расстоянию от А до С минус расстояние от В до С, поэтому перемещение от А до В определяется как 𝑠=250−180=70,м

в B смещение от C к B происходит в направлении, противоположном направлению от A к C, поэтому оно имеет отрицательное направление, как показано на следующем рисунке.

Расстояние от С до В равно 180 м, поэтому перемещение от С до В определяется выражением 𝑠=−180,м показано на следующем рисунке.

Расстояние от А до С равно 250 м, поэтому перемещение от А до С определяется выражением 𝑠=250 м

Когда судно находится в А, перемещение от С до А происходит в отрицательном направлении, как показано на рисунке на следующем рисунке.

Расстояние от C до A равно 250 м, поэтому перемещение от C до B определяется выражением 𝑠=−250,м

Объект может вернуться в исходную точку, переместившись на некоторое расстояние вдоль линии, а затем вернувшись на такое же расстояние вдоль этой линии. На следующем рисунке показаны точки A и B, соединенные прямой линией.

Если объект перемещается из A в B и обратно в A, его перемещение равно нулю. Однако расстояние, пройденное объектом, не будет равно нулю, а будет в два раза больше расстояния от А до В. в сравнении.

Пример 5: Определение чистого смещения объекта, который меняет направление

Ветром дует лист. Лист перемещается на 5 м вперед, а затем на 3 м назад.

• Какое расстояние проходит лист?
• Каково чистое смещение створки вперед?

Ответ

Лист движется по прямой линии вперед на расстояние 5 м, а затем движется по прямой линии назад на расстояние 3 м. Расстояние, на которое перемещается лист, равно сумме длин этих путей. Пройденное расстояние, 𝑑, определяется как 𝑑=5+3=8.м

Вопрос касается чистого смещения листа вперед, поэтому мы должны считать движение листа вперед положительным, а движение листа назад — отрицательным. Чистое смещение листа вперед определяется как 𝑠=5+(−3)=5−3=2.m

Если движение объекта включает в себя изменение направления, которое не является полным изменением этого направления, то объект не перемещается по одной линии. Затем можно считать, что объект имеет смещение в 𝑥-направлении и в 𝑦-направлении, как показано на следующем рисунке.

Объект проходит одинаковое расстояние в 𝑥-направлении и в 𝑦-направлении. Объект имеет два смещения, каждое в другом направлении.

Теперь рассмотрим пример, в котором определяются смещения в направлениях 𝑥 и 𝑦 движущегося объекта.

Пример 6. Определение чистого смещения объекта в перпендикулярных направлениях

Человек идет из точки А в точку Б, как показано на диаграмме.

• Каково смещение точки B из точки A в 𝑥-направлении?
• Каково смещение точки B от точки A в 𝑦-направлении?

Ответ

Диаграмма показывает, что положительное 𝑥-направление вправо. Объект перемещается на 4 м вправо и также на 1 м влево. Смещение в 𝑥-направлении определяется как 𝑠=4+(−1)=4−1=3.m

Диаграмма показывает, что положительное 𝑦-направление направлено вверх. Объект перемещается на 3 м вверх и также на 5 м вниз. Перемещение в 𝑦-направлении определяется выражением 𝑠=3+(−5)=3−5=−2.m

Объект может вернуться в исходную точку, двигаясь по замкнутому пути, который меняет направление. Путь, по которому объект возвращается в исходное положение, может состоять из прямых линий, кривых или как прямых, так и кривых, как показано на следующем рисунке.

В замкнутых путях, показанных на предыдущем рисунке, только прямые линии могут представлять смещения. Только смещения являются векторами, поэтому только прямые линии имеют стрелки, указывающие направление.

Рассмотрим пример, связанный со смещением в 𝑥- и 𝑦-направлениях объектов, которые движутся по замкнутым траекториям.

Пример 7. Определение чистого смещения объекта по замкнутому пути

Два человека идут по треугольным линиям, соединяющим точки A, B и C, показанные на диаграмме. Первый человек идет из точки А по треугольному пути, который возвращает его в точку А. Когда первый человек возвращается в точку А, он останавливается. Второй человек идет из точки B по треугольному пути, который возвращает его в точку B. Когда второй человек возвращается в точку B, он останавливается.

• Каково смещение первого человека из точки А в 𝑥-направлении, когда он останавливается?
• Каково смещение первого человека из точки А в 𝑦-направлении, когда он остановится?
• Каково смещение второго человека из точки B в 𝑥-направлении, когда он останавливается?
• Каково смещение второго человека из точки B в 𝑦-направлении, когда он останавливается?

Ответ

Первый человек выходит из точки А и идет по треугольной траектории обратно в точку А, где останавливается. Точка А — это точка, в которой начинается движение первого лица, и точка, в которой оно заканчивается. Таким образом, перемещение человека равно нулю. Смещение нуля равно нулю в любом направлении, поэтому смещение в 𝑥-направлении равно нулю, а смещение в 𝑦-направлении равно нулю.

Движение второго человека почти точно такое же, как и у первого человека, с той лишь разницей, что второй человек начинает с точки B, а не с точки A.

Различное начальное положение двух людей не имеет значения к их смещениям, поскольку каждый человек возвращается в исходное положение, и поэтому оба имеют нулевое смещение.

Давайте теперь обобщим то, что мы узнали из этих примеров.

Ключевые точки

• Расстояние — это длина пути между двумя точками.
• Путь между точками может быть прямой или кривой.
• Направление перемещения объекта между двумя точками не влияет на расстояние, на которое перемещается объект. Расстояние имеет величину, но не имеет направления, так что это скалярная величина.
• Общее расстояние, пройденное объектом, который перемещается между несколькими точками, представляет собой сумму расстояний, которые он перемещает между этими точками.
• Смещение — это расстояние по прямой от одной точки до другой точки.
• Смещение имеет направление, а также величину, поэтому оно является векторной величиной.
• Для движения по линии необходимо выбрать направление от одного конца линии к другому, для которого перемещение считается положительным. Для противоположного направления смещение принимается отрицательным.
• Величина смещения по прямолинейному пути между двумя точками — это расстояние между этими точками на этом пути.
• Движение объекта из точки обратно в ту же точку приводит к нулевому смещению
• Для движения объекта, включая изменение направления, которое не является полным изменением направления, объект будет иметь смещения по более чем одной линии.

Прогнозирование моделей движения с использованием оптимальных путей

1 Введение

Представьте себе большую городскую площадь. На площади есть стационарные конструкции, такие как фонтаны и т. Д., Которые блокируют прямые проходы через нее. Это оживленное место, где многие проходят через него во всех направлениях. Установлены камеры, которые фиксируют движение людей по городской площади. Вопрос, который мы рассмотрим в этой статье, заключается в следующем: можно ли на основе записей предсказать движение одного человека из некоторой начальной точки 9?0241 A до конечной точки B через городскую площадь, даже если точки A и B не расположены вдоль обычных путей, которыми люди пользуются через площадь. Этот вопрос уже давно ставится в различных контекстах [1]. Примеры варьируются от поведения экосистем до роботизированных систем навигации и дорожного движения. Хищник должен учитывать будущее движение своей добычи, чтобы поймать ее, точно так же, как корабль должен учитывать будущее положение других кораблей, чтобы избежать столкновений [2].

На движущиеся объекты влияет как ландшафт, в котором они движутся, так и другие объекты, движущиеся или неподвижные, в пределах той же области [3–5]. Существует несколько различных подходов к прогнозированию движения. Наиболее прямолинейный подход состоит в том, чтобы предсказать движение каждого объекта в системе индивидуально, назначая каждому объекту положение как функцию времени [6]. Однако для больших систем этот метод привел бы к большому количеству связанных уравнений. Следовательно, в данном случае такой подход будет непродуктивным. Лучшим подходом является использование того факта, что объекты имеют тенденцию двигаться по шаблону [3, 7]. В зависимости от своей природы и окружения движущиеся объекты имеют тенденцию двигаться по регулярной схеме. Создав модель этих паттернов движения в данной области, можно использовать сам паттерн при прогнозировании будущего движения. Это основная идея нашего подхода.

При применении методов распознавания образов к прогнозированию движения процесс обычно выполняется в два этапа. Первый этап – это фактическое распознавание образов, при котором изучаются регулярные образцы движения с использованием набора обучающих данных. Следующий этап применяет изученный шаблон для предсказания будущего движения. Кроме того, этот двухэтапный процесс можно разделить на две основные группы методов; Методы на основе сетки и методы на основе кластера [3].

Методы на основе сетки основаны на концепции сетки занятости [8]. То есть ландшафт моделируется в виде сетки, а вероятности перехода между ячейками рассчитываются на основе обучающих данных. Затем сетка используется непосредственно для прогнозирования движения. Методы на основе сетки часто используются в системах навигации роботов [9].–11].

Методы на основе кластеров, с другой стороны, применяют инструменты статистического принятия решений для группировки схожих траекторий в репрезентативные кластеры. Существует несколько различных методов кластеризации, подход максимизации ожиданий [12] считается современным [3]. Будущее движение движущегося объекта затем оценивается как репрезентативный кластер, к которому данный маршрут, скорее всего, принадлежит.

В этой статье мы предлагаем основанный на динамической сетке метод изучения моделей движения путем сопоставления его с оптимальными путями в задаче о неупорядоченном ландшафте [13, 14]. Опишем эту проблему следующим образом. Представьте себе плоскость и x→ — точка на этой плоскости. Существует стохастическое поле e(x→), связанное с плоскостью. Мы выбираем путь P через плоскость, начинающийся в точке x→A и заканчивающийся в точке x→B. Проинтегрируем поле e(x→) по пути P,

EP=∫x→∈Pe(x→)dx→.(1)

Оптимальный путь находится путем минимизации

EO=minPEP=minP∫x→∈Pe(x→)dx→.(2 )

Эта проблема вызвала большой объем работы в сообществе статистической физики. Она также тесно связана с задачей оптимального пути, которая является центральной во многих приложениях и областях [15–18].

Центральная идея, которую мы представляем в этой статье, состоит в том, чтобы связать функцию e(x→) с обратной плотностью более ранних путей, возведенных в некоторую степень. Затем мы определяем оптимальный путь от x → A к x → B через этот ландшафт.

Мы применяем эту идею к движению судов, используя координаты морской системы автоматической идентификации. Преобразуем координаты в безразмерную область и введем сетку по площади. Мы связываем каждую точку сетки с локальной плотностью координат AIS. Мы реализуем оптимальные пути через область с помощью итерационного алгоритма Хансена и Кертеса [19, 21], но могут быть использованы любые другие алгоритмы, например, алгоритмы Беллмана-Форда или Дейкстры [22–24].

Подчеркнем, что мы не пытаемся представить здесь полностью реализуемый алгоритм, готовый к использованию на кораблях. Скорее, это технико-экономическое обоснование, проверяющее, могут ли основные идеи работать.

Отметим, что оптимальные траектории использовались ранее в связи с прогнозированием морского движения [20]. Однако пути в этом случае оптимизируются по длине. Это совсем другое понятие, чем то, что мы представляем здесь.

Мы организуем эту статью следующим образом. Раздел 2 описывает предлагаемый нами метод. В разделе 3 мы реализуем метод для морских данных АИС. Мы заканчиваем кратким подведением итогов и обсуждением.

2 Алгоритм

Теперь мы опишем, как мы преобразовываем координаты AIS, заданные в единицах долготы и широты, в точки сетки. Затем мы переходим к описанию концепции оптимальных путей в этом контексте и алгоритму, используемому для ее извлечения. Наконец, мы опишем, как мы превращаем это в предсказание пути.

2.1 От координат автоматической системы идентификации к координатной сетке

Система автоматического слежения AIS использует приемопередатчики, позволяющие судам видеть окружающий морской транспорт и быть видимыми сами. Он обеспечивает, среди прочих услуг, запись позиции в зависимости от времени для оборудованных судов, проходящих через этот район. Сюда входят большинство крупных судов.

Мы определяем интересующую нас область как прямоугольник, определяемый углами, заданными координатами долготы и широты longmin, longmax, laemin и laemax. Данный корабль в данное время находится в позиции (longk, laek), где нижний индекс относится к записи позиции (т. е. какой корабль и в какое время). Введем безразмерные декартовы координаты для описания его положения, xk∈{0,N−1} и yk∈{0,N−1}, где N — целое число, заданное как

xk=longk-longminlongmax-longmin(N−1), (3)

и

yk=laek-laeminlaemax-laemin(N-1).(4)

Положение данного корабля в данный момент времени k в (xk,yk) определяется в ячейке сетки, определяемой угловыми узлами ik1mod(xk), ik2mod(xk)+1, jk1mod(yk) и jk2mod(yk). )+1. Чтобы построить плотность пути, определенную в узлах (i,j), ρi,j, мы присваиваем вес положению корабля и времени k , (xk,yk) распределены между четырьмя угловатыми узлами (ik1,jk1), (ik2,jk1), (ik2,jk2) и (ik1,jk2). Если rik1,jk1 — расстояние между (xk,yk) и (ik1,jk1), а также для rik2,jk1, rik2,jk2 и rik1,jk2, мы определяем

Rxk,yk=rik1,jk1+rik2,jk1 +rik2,jk2+rik1,jk2.(5)

Определим веса

,jk1),Wik2,jk2=13Rxk,yk(Rxk,yk−rik2,jk2),Wik1,jk2=13Rxk,yk(Rxk,yk−rik1,jk2). (6)

Затем можно определить плотность пути как

ρi,j=∑k=1KWik,jk,(7)

, когда K — количество записей положения в ячейке сетки.

Теперь свяжем вес с узлом (i,j),

ei,j={ρi,j−α,if ρi,j>0,m,if ρi,j=0,M,if(i, j) находится на суше, (8)

, где α — регулируемый параметр, управляющий величиной флуктуаций ei,j: если α→0, флуктуации сглаживаются и исчезают при α=0, так как все узлы тогда присвоен одинаковый вес. Параметр м выбирается таким образом, чтобы существовал баланс между тенденцией прохождения пути по обычным судоходным путям (где ρi,j велико) и максимально коротким путем. Другое значение M≫m гарантирует, что никакие пути не пересекают сушу.

Последним шагом в настройке системы является присвоение весов ссылкам между соседними узлами. Пусть узел (inn,jnn) является одним из четырех ближайших соседей узла (i,j). Затем связи между ними присваивается вес

ei,j;inn,jnn=12(ei,j+einn,jnn).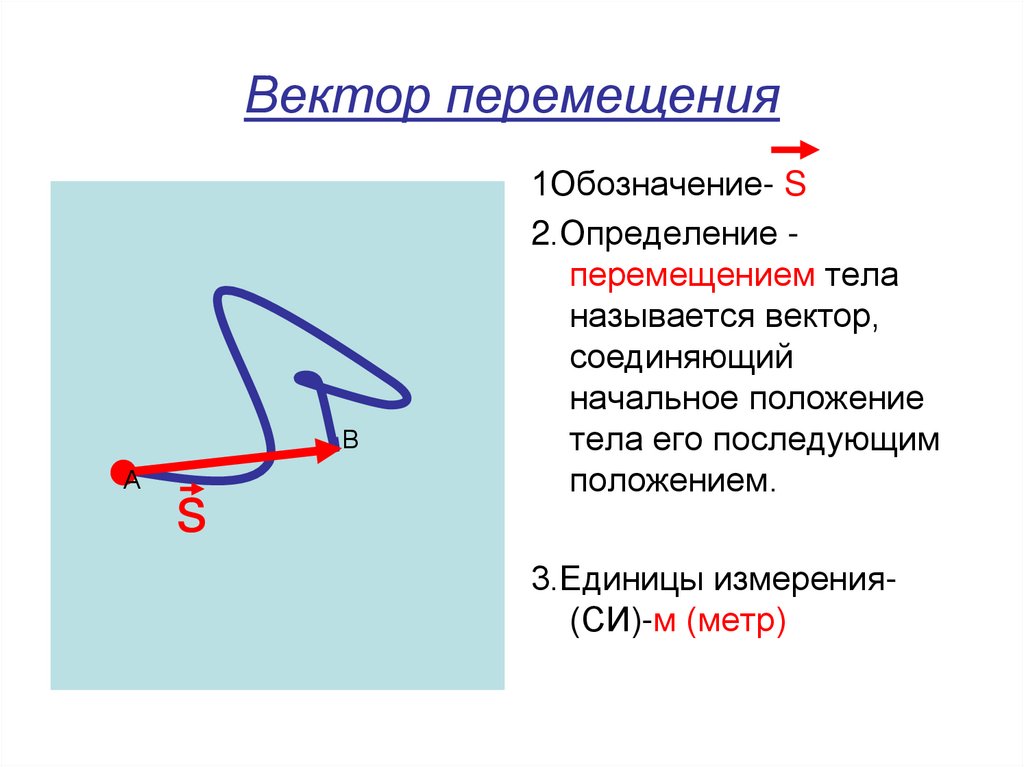 (9)

Мы также допускаем диагональные пути. Связь между узлом (i,j) и его диагональными соседями (inn,jnn) как

ei,j;inn,jnn=22(ei,j+einn,jnn),(10)

, где коэффициент 2 равен введен для учета дополнительной длины диагональных ребер.

2.2 Оптимальное построение пути

Определим путь P между двумя узлами A в точке (iA,jA) и B в точке (iB,jB) как непрерывную цепочку соседних звеньев, соединяющих два узла. Мы связываем вес пути так же, как в уравнении. 1,

EP=∑(i,j)∈Pei,j;inn,jnn.(11)

Оптимальный путь тогда

EO=minPEP=minP∑(i,j)∈Pei,j;inn,jnn .(12)

Далее мы будем предполагать, что оба узла A и B лежат на краях сетки. Для определения оптимального пути воспользуемся алгоритмом Хансена и Кертеса [19]. Он состоит из двух основных этапов; сначала инициализация, а затем процесс обновления. Каждому узлу присваивается переменная ei,j. Для узлов на краях сетки значения ei,j остаются фиксированными, в то время как для внутренних узлов они обновляются итеративно. Алгоритм итерации для внутренних узлов

ei,j→ei,j=mininn,jnn(ei,j;inn,jnn+einn,jnn).(13)

После M итераций переменная ei,j будет содержать сумму весов по оптимальному пути, начинающемуся в узле (i,j) длиной M. Конечная точка оптимального пути не указана. Кроме того, оптимальный путь может скручиваться сам по себе, создавая конфигурацию головастика.

Теперь рассмотрим узел (iA,jA) на границе сетки. Чтобы найти оптимальный путь от внутреннего узла (i,j) к (iA,jA), мы устанавливаем значение eiA,jA равным нулю, а для остальных граничных узлов значение eic,jc устанавливается очень большим. положительное значение. Процесс обновления для внутренних узлов выполняется в соответствии с формулой. 13, до тех пор, пока все значения ei,j не перестанут изменяться. В этот момент значение ei,j содержит значение EO=Ei,j;iA,jA вдоль оптимального пути между узлами (i,j) и (iA,jA).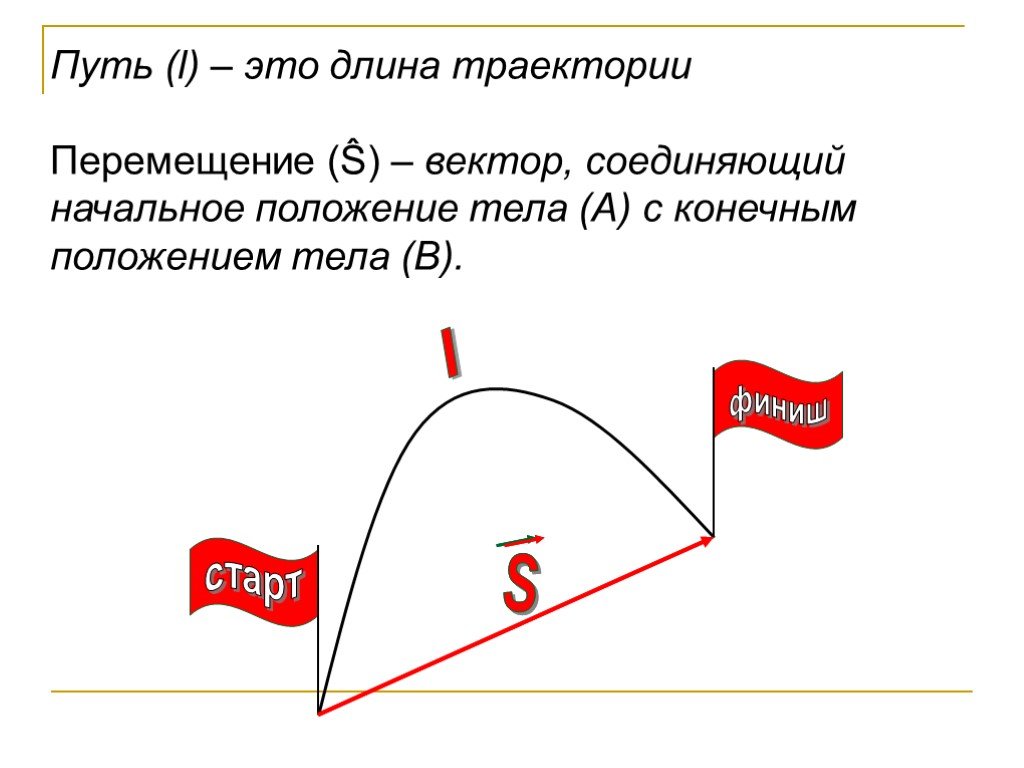

Теперь мы выбираем другой граничный узел (iB,jB) в качестве конечной точки для оптимальных путей. Следовательно, мы фиксируем eiB,jB=0 и фиксируем все остальные граничные узлы на большое положительное значение, включая граничный узел (iA,jA). Внутренние значения узлов изначально установлены равными нулю, ei,j=0. Затем мы повторяем в соответствии с уравнением. 13. Когда числа больше не меняются, ei,j будет содержать Ei,j;iB,jB=EO для оптимального пути между узлами (i,j) и (iB,jB).

Теперь мы можем объединить оптимальные пути, начинающиеся в граничном узле (iA,jA) и заканчивающиеся во внутреннем узле (i,j), с оптимальным путем, начинающимся во внутреннем узле (i,j) и заканчивающимся в граничном узле (iB,jB ). Оптимальный вес EO для этого комбинированного пути определяется как

EiA,jA;i,j;iB,jB=mininn,jnn(EiA,jA;i,j+ei,j;inn,jnn+Einn,jnn;iB,jB,EiA,jA;inn,jnn+ einn,jnn;i,j+Ei,j;iB,jB).(14)

Связывание каждого внутреннего узла (i,j) со значением ei,j=EiA,jA;i,j;iB,jB ведет построению траектории [21]. Оптимальный путь между краевыми узлами (iA,jA) и (iB,jB) — это последовательность узлов, связанных с наименьшими значениями ei,j. Затем будет последовательность узлов, имеющих вторые наименьшие значения ei,j. Эта последовательность ответвится от глобально оптимального пути как некоторый узел, чтобы воссоединиться с ним в другом узле пути. Затем будет последовательность с третьими наименьшими значениями ei,j, ответвляющимися и воссоединяющимися узлами, принадлежащими двум путям, содержащим два меньших ei,j, и так далее. Каждый внутренний узел будет принадлежать какому-то пути в этой иерархии.

2.3 Предсказание путей

Теперь сосредоточим наше внимание на путях, где граничные узлы (iA,jA) и (iB,jB) расположены вдоль разных ребер. Возможных комбинаций 6N2. Может оказаться удобным укрупнить конечные точки оптимальных путей. Следовательно, разобьем каждое ребро на отрезки длины LI. Это означает, что мы устанавливаем вес всех краевых узлов (i′A,j′A), принадлежащих интервалу, eiA’,jA’=0.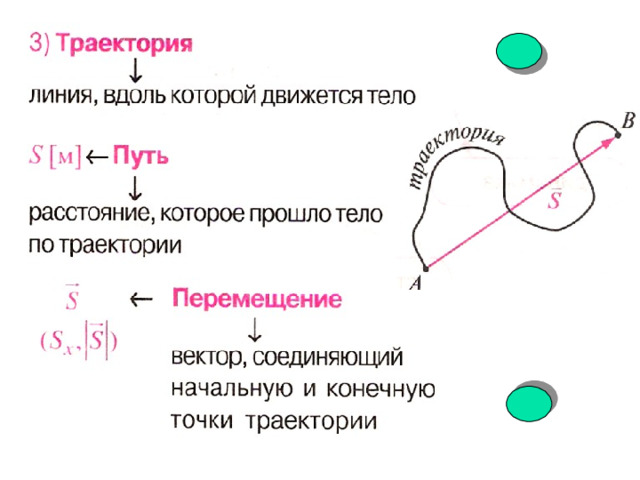 Путь тогда будет состоять из всех оптимальных путей, начинающихся где-то в первом интервале (i′A,j′A), проходящих через внутренний узел (i,j) и затем заканчивающихся в узле (iB’,jB’) где-то в конечный интервал. Следовательно, количество путей затем уменьшается с 6N2 до 6n2, где n=N/LI.

Предположим, что оптимальный путь (iA’,jA’;i,j;iB’,jB’) имеет длину LiA’,jA’;i,j;iB’,jB’ и вес EiA’,jA’; i,j;iB’,jB’. Использование одного только веса при прогнозировании путей неэффективно, поскольку короткий путь через область с большим весом может быть таким же оптимальным, как и более длинный путь через область с низким весом. Поэтому мы перенормируем веса EiA’,jA’;i,j;iB’,jB’→E’iA’,jA’;i,j;iB’,jB’, установив

E′iA’,jA’ ;i,j;iB’,jB’=CpEiA’,jA’;i,j;iB’,jB'(LiA’,jA’;i,j;iB’,jB’)β,(15)

где β — регулируемый параметр. Константа Cp введена для дальнейшего разделения между различными оптимальными путями. Мы отмечаем, что чем выше β , тем более благоприятны более длинные пути.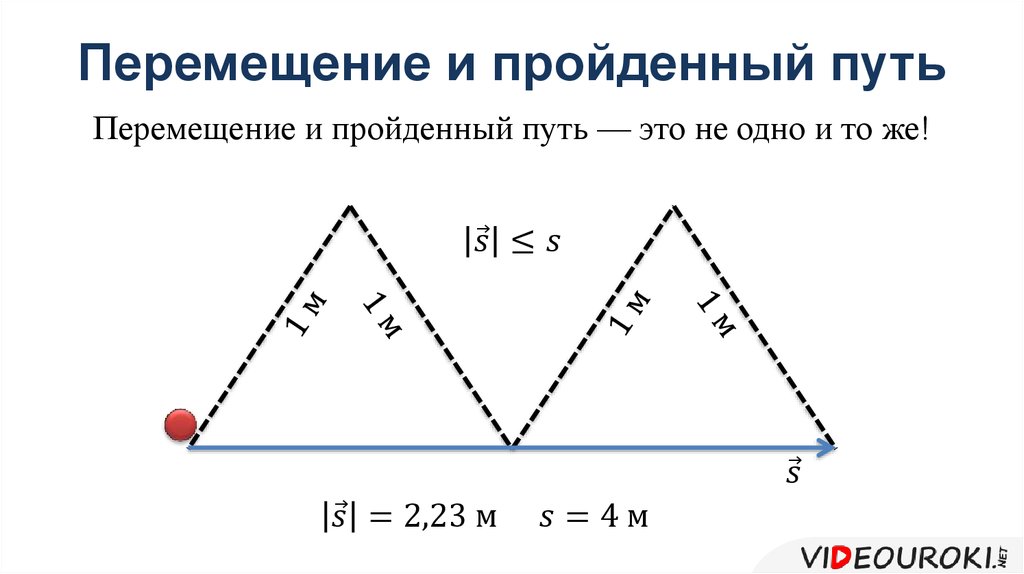

3 Анализ двух шаблонов системы автоматической идентификации

Мы обозначаем два рассматриваемых нами набора AIS A и B . На рисунках 1, 2 показаны две области и подмножества, которые мы используем в нашем анализе. Оба подмножества, показанные на рисунках 1B, 2B, имеют размер 100 × 100, и каждый блок сетки имеет размер 100 × 100 м 9 .0395 2 (район A ) и 1000 × 1000 м ² (район B ). Мы видим, что A имеет более простую структуру, чем B , состоящую из двух вертикальных кластеров, а B включает несколько кластеров с разной ориентацией. Под «кластером» мы подразумеваем область с высокой плотностью записей о местоположении.

РИСУНОК 1 . (A) Набор данных A , показывающий записи положения AIS с положениями в градусах относительно исходной точки. (B) Выбранное подмножество области A , охватывающее 0,3∘ как в долготе, так и в широтном направлении, преобразованное в сетку размерами 334 × 334 с размером сетки 100 × 100 м ² .

РИСУНОК 2 . (A) Набор данных B , показывающий записи положения AIS с положениями в градусах относительно исходной точки. (B) Выбранное подмножество области B , охватывающее 3∘ как в долготе, так и в широтном направлении, преобразованное в сетку размерами 334 × 334 с размером ячейки 1000 × 1000 м ² .

Теперь рассмотрим область A . Установка параметра β=0 в уравнении 15 мы показываем на рисунке 3 оптимальный путь между нижним левым и верхним правым углами сетки 1b для различных значений α .

РИСУНОК 3 . Оптимальные пути между нижним левым и верхним правым углами сетки на рисунке 1B для α = 0, 0,25, 0,50, 0,75 и 1. Параметр β , определенный в уравнении. 15 был установлен в ноль.

На рис. 4 показана длина оптимального пути между нижним левым и верхним правым углами на рис. 3 для различных значений α и при β=0, LO. Заметим, что LO примерно линейна по α для α<0,75, при котором наблюдается скачок.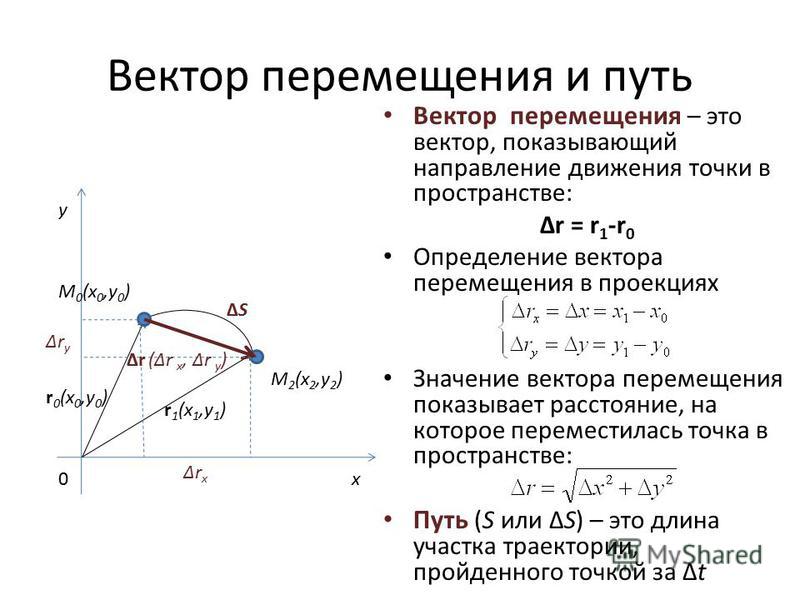

РИСУНОК 4 . Длина оптимальных путей LO между нижним левым и верхним правым углами III как функция α , при сохранении β=0.

Обращаясь к области B , мы показываем на рисунке 5 оптимальные пути, начинающиеся из нижнего левого угла и заканчивающиеся в верхнем правом углу сетки, показанной на рисунке 2B, как функцию α при сохранении β=0.

РИСУНОК 5 . Оптимальные пути между нижним левым и верхним правым углами сетки на рисунке 2B для α=0, 0,25, 0,50, 0,75 и 1. Параметр β , определенное в уравнении 15 был установлен в ноль.

На рис. 6 показана длина оптимального пути между нижним левым и верхним правым углами на рис. 5 для различных значений α и β=0. Как и на рис. 4, для области A находим скачок длины оптимальных путей при заданном значении α, здесь α≈0,4. Однако на оптимальной длине пути имеются четко выраженные плато, например, при 0,05<α<0,4.

РИСУНОК 6 . Длина оптимальных путей, LO между левым нижним и правым верхним углом V как функция α , сохраняя при этом β=0.

Теперь мы вводим интервалы LI, как описано в разделе C. Рассмотрим сначала более крупнозернистый участок площадью A , покрытый сеткой размером 148 × 148 с размером сетки 100 × 100 м ² . Каждое ребро делим на две части. На рис. 7А показаны два наиболее оптимальных пути в этой системе. На рисунке 7В показаны пять наиболее оптимальных путей. На рисунке 7В мы видим, что некоторые из пяти оптимальных путей значительно перекрываются, создавая впечатление, что на рисунке путей меньше, чем в действительности.

РИСУНОК 7 . Площадь A : (A) Два наиболее оптимальных пути между отрезками по разным ребрам. (B) Пять наиболее оптимальных путей между разными ребрами. Каждое ребро было разделено на два интервала с фиксированием α=0,8 и β=0,8.

На рис. 8 показана упорядоченная последовательность весов E’O для оптимальных путей на рис.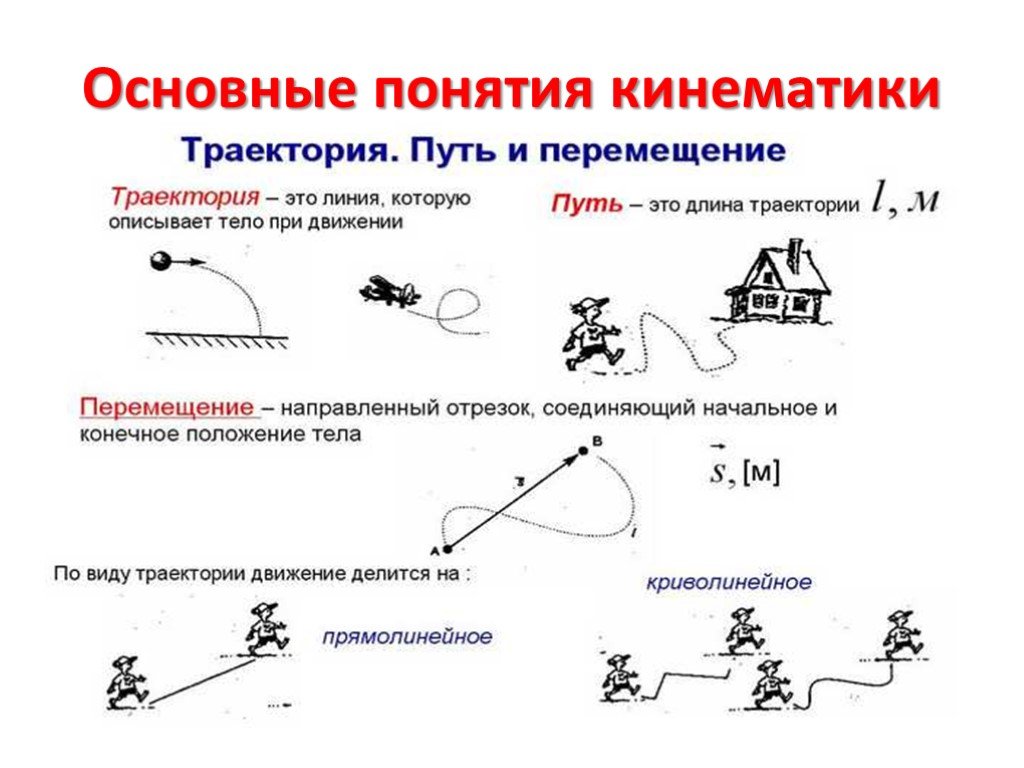 7. Мы видим, что веса первых пяти путей очень похожи, тогда как начиная с шестого и далее они существенно выше. Создание этой плоской области достигается путем настройки β и означает, что эти оптимальные пути одинаково хороши.

РИСУНОК 8 . Вес EO варьируется от наиболее оптимального (№ 0) до наименее оптимального (№ 20) для путей между интервалами на разных ребрах, как показано на рисунке 7.

Делаем то же построение, что и на рисунке 7, для области B на рис. 9. Мы делим ребра на три интервала и выбираем значения α=0,08 и β=0,8 для двух регулируемых параметров.

РИСУНОК 9 . Область B : здесь сетка разделена на три сегмента вдоль каждого края. В (A) мы показываем 24 наиболее оптимальных пути, а в (B) мы показываем 48 наиболее оптимальных путей. Мы зафиксировали значения параметров равными α=0,08 и β=0,8.

На рис. 10 показана возрастающая последовательность перенормированных весов E’O для двух случаев, показанных на рис.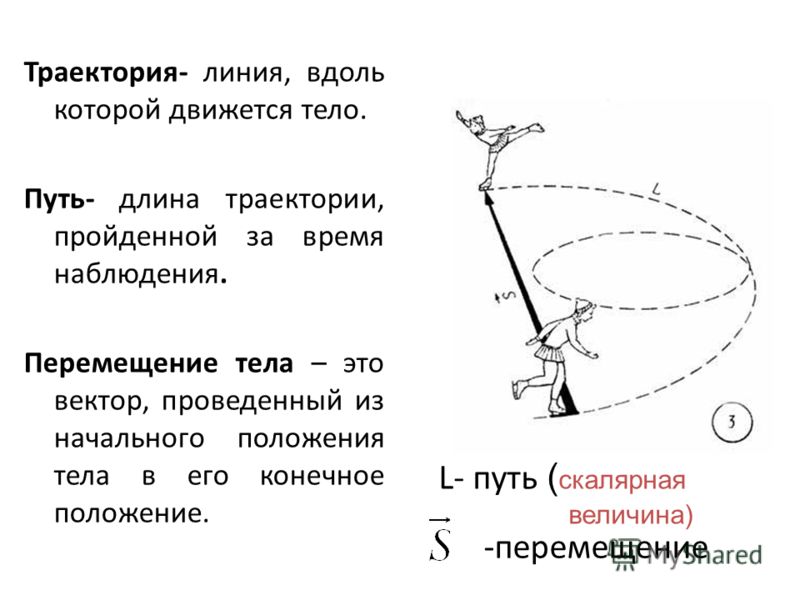 9A, B. Мы находим 48 оптимальных путей с медленно растущим весом, прежде чем он подскочит до гораздо более высокого значения.

РИСУНОК 10 . Вес EO варьируется от наиболее оптимального (№ 0) до наименее оптимального (№ 50) для путей между интервалами на разных ребрах, как показано на рисунке 9.

На рисунке 9 показана та же область, что и на рисунке 5. Имеем здесь разделил ребра на три промежутка. Вес 50 наиболее оптимальных путей показан на рисунке 10. Как и в гораздо более простой схеме на рисунке 7, в этом случае также имеется значительное перекрытие между оптимальными путями.

4 Обсуждение и заключение

В этой статье мы представили метод прогнозирования движения в области на основе более раннего движения в той же области. То есть, учитывая историю движения в этом районе, каким будет наиболее вероятный путь, по которому новый путешественник пойдет между позициями 9?0241 A и B , даже если эти позиции находятся за пределами обычных маршрутов передвижения в этом районе. Метод основан на понятии оптимальных путей через ландшафт, образованный ранее пройденными путями. Это динамический метод, так как каждая новая траектория, пройденная в этом районе, добавляется в историю.

Мы протестировали метод на данных морской автоматической идентификационной системы (АИС). С визуальной точки зрения, метод эффективно определяет характер движения как в изученном нами простом случае ( A ) и в более сложной дорожной картинке ( B ). Тем не менее, надлежащий тест производительности не был проведен. Кроме того, результаты показали, что разделения ребер всего на несколько интервалов было достаточно для получения хорошей оценки шаблона. Так как все узлы сетки вдоль ребер могут быть представлены всего несколькими интервалами, с коротким временем работы алгоритма. Размер сетки и размер ячеек, по-видимому, не влияют на полученные результаты.

Эта работа показывает, что предлагаемый нами метод позволяет определить разумные пути, которые оптимизируют между длиной пути и частотой использования — двумя, казалось бы, очень разными величинами. Чтобы превратить это в практический метод , требуется гораздо больше работы, т.е. в отношении идентификации кластера, построения сетки, типа судна (если оно будет реализовано как морской инструмент).

Заявление о доступности данных

Исходные материалы, представленные в исследовании, включены в статью/дополнительный материал. Дальнейшие запросы можно направлять соответствующему автору.

Авторские вклады

MF выполнила числовую работу, основанную на идее AH. М. Ф. написать первый черновик рукописи. АХ написал вторую версию.

Финансирование

Эта работа была частично поддержана Исследовательским советом Норвегии через схему финансирования Центров передового опыта, номер проекта 262644.

Конфликт интересов

финансовые отношения, которые могут быть истолкованы как потенциальный конфликт интересов.

Ссылки

1. Hirakawa T, Yamashita T, Tamaki T, Fujiyoshi H, Umezu Y, Takeuchi I, et al. Может ли ИИ предсказывать движения животных? Заполнение пробелов в траекториях животных с помощью обучения с обратным подкреплением.

Экосфера (2018) 9:e02447. doi:10.1002/ecs2.2447

Полный текст CrossRef | Google Scholar

2. Паллотта Г., Веспе М., Брайан К. Обнаружение знаний о схеме судна на основе данных АИС: основа для обнаружения аномалий и прогнозирования маршрута. Энтропия (2013) 15:2218–45. doi:10.3390/e15062218

Полный текст CrossRef | Google Scholar

3. Васкес Д., Фрайчард Т. Прогнозирование движения движущихся объектов: статистический подход. Proc ICRA’04, IEEE (2004) 4:3931–6. doi:10.1109/ROBOT.2004.1308883

Полный текст CrossRef | Google Scholar

4. Мартинес Дж., Блэк М.Дж., Ромеро Дж. О прогнозировании движения человека с использованием рекуррентных нейронных сетей. В: Материалы конференции IEEE по компьютерному зрению и распознаванию образов (2017 г.). п. 2891–900.

Google Scholar

5. Гонсалес Д., Перес Дж., Миланес В., Нашашиби Ф. Обзор методов планирования движения для автоматизированных транспортных средств. IEEE Trans Intell Transport Syst (2016) 17:1135–45. doi:10.1109/TITS.2015.2498841

CrossRef Полный текст | Google Scholar

6. Zhu Q. Стохастический алгоритм прогнозирования движения препятствий в визуальном управлении движением роботов. В: Международная конференция IEEE по системной инженерии IEEE (1990). дои: 10.1109/ICSYSE.1990.203136

Полнотекстовая перекрестная ссылка | Google Scholar

7. Weiming Hu W, Xuejuan Xiao X, Zhouyu Fu Z, Xie D, Tieniu Tan T, Maybank S. Система для изучения статистических моделей движения. IEEE Trans Pattern Anal Mach Intel (2006) 28: 1450–64. doi:10.1109/TPAMI.2006.176

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

8. Эльфес А. Использование сетки занятости для восприятия и навигации мобильных роботов. Компьютер (1989) 22:46–57. Дои: 10.1109/2.30720

CrossRef Полный текст | Google Scholar

9. Tadokoro S, Hayashi M, Manabe Y, Nakami Y, Takamori T.

Планировщик движения мобильных роботов, которые избегают движущихся человеческих препятствий на основе стохастического прогнозирования. Intel Syst 21st Century (1995) 4:3286–91. doi:10.1109/ICSMC.1995.538292

Полный текст CrossRef | Google Scholar

10. Kruse E, Gutsche R, Wahl FM. Оценка вероятности столкновения в динамических средах для планирования пути с минимальной вероятностью столкновения. В: Труды Международной конференции IEEE/RSJ по интеллектуальным роботам и системам. ИРОС’96, 3 (1996). п. 1288–95. doi:10.1109/IROS.1996.568983

Полный текст CrossRef | Google Scholar

11. Танака К. Обнаружение путей без столкновений путем наблюдения за идущими людьми. В: Международная конференция IEEE/RSJ по интеллектуальным роботам и системам, 1 (2002). п. 55–60. doi:10.1109/IRDS.2002.1041362

Полный текст CrossRef | Google Scholar

12. Бенневиц М., Бургард В., Трун С. Изучение моделей движения людей для мобильных сервисных роботов. В: Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02Ch4729).2), 4 (2002). п. 3601–6. doi:10.1109/ROBOT.2002.1014268

Полный текст CrossRef | Google Scholar

13. Halpin-Healy T, Zhang Y-C. Кинетические явления огрубления, стохастический рост, направленные полимеры и все такое. Аспекты междисциплинарной статистической механики. Phys Rep (1995) 254:215–414. doi:10.1016/0370-1573(94)00087-J

CrossRef Full Text | Google Scholar

14. Алава М., Даксбери П., Мукарзель С., Ригер Х. Комбинаторная оптимизация и неупорядоченные системы. В: C Domb и JL Lebowitz, редакторы. Фазовые переходы и критические явления , Vol. 18. Амстердам: Эльзевир (2000).

Google Scholar

15. Алур Р., Ла Торре С., Паппас Г.Дж. Оптимальные пути во взвешенных автоматах с временными параметрами. В: Международный семинар по гибридным системам: вычисления и управление , 49–62. Берлин: Спрингер (2001). п. 49–62. doi:10.1007/3-540-45351-2_8

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

16. Ся В. Оптимальные пути, связанные с транспортными задачами. Commun Contemp Math (2003) 05: 251–79. doi:10.1142/S021919970300094X

Полный текст CrossRef | Google Scholar

17. Gendreau M, Ghiani G, Guerriero E. Проблемы маршрутизации, зависящие от времени: обзор. Comput Operations Res (2015) 64:189–97. doi:10.1016/j.cor.2015.06.001

Полный текст CrossRef | Google Scholar

18. Ю Дж., ЛаВалль С.М. Планирование оптимальных путей для нескольких роботов на графиках. В: Международная конференция IEEE по робототехнике и автоматизации (2013). п. 3612–7. Дои: 10.1109/ICRA.2013.6631084

CrossRef Full Text | Google Scholar

19. Хансен А., Кертес Дж. Фазовая диаграмма оптимальных путей. Phys Rev Lett (2004) 93:040601. doi:10.1103/PhysRevLett.93.040601

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

20. Сулеймани Б.Х., Де Соуза Е.Н., Хиллиард С., Матвин С. Обнаружение аномалий в морских данных на основе геометрического анализа траекторий.