Читать онлайн «ФИЗИКА. Курс для начинающих», Антон Рихванов – Литрес
© Антон Рихванов, 2019
ISBN 978-5-4493-1538-0
Создано в интеллектуальной издательской системе Ridero
АННОТАЦИЯ
Привет, друзья. Перед Вами учебник по физике для начинающих. Если Вам надоели скучные и сухие учебники по физике, в которых невозможно разобрать ни слова, если Вы хотите научиться видеть законы физики вокруг себя и использовать их в своей практической жизни, то этот учебник для Вас. Уникальность его в том, что он позволяет объяснить сложные и громоздкие физические явления простым детским языком. Этот учебник не стремится охватить школьную или вузовскую программу по физике. Его задача заинтересовать читателя этой наукой. Цель автора не столько давать ответы на вопросы, сколько сделать так, чтобы эти вопросы возникали у читателя. Курс объясняется простым и понятным языком, поэтому даже представители гуманитарных наук с легкостью смогут понять, о чем здесь идет речь. Этот учебник является первым из серии учебников по физике (среди которых «Физика.
Курс для продолжающих» и «Физика. Глубокий курс»). Обязательным эта книга является для тех, кто хочет ознакомиться в дальнейшем с другими книгами автора («Биофизика», «Биология, физика и аюрведа» и др.)
ЧАСТЬ 1. ЗНАНИЯ ИЗ РАЗНЫХ НАУК, ПОДГОТАВЛИВАЮЩИЕ ПОЧВУ ДЛЯ ФИЗИКИ
Вы, наверное, спрашиваете себя, – «зачем мне знания из других наук, если я хочу изучать физику?». К сожалению, так уж получается, что многие физическая явления нельзя объяснить самой физикой. Лишь другие науки способны объяснить это. К примеру, физика не может объяснить, зачем в микрофоне звук превращают в электричество. Она может ответить, как это происходит, но не может сказать зачем это нужно. На этот вопрос может ответить наука о языках – лингвистика. Лингвисты знают, что слова это шифры, словами мы кодируем наши мысли. Так вот оказывается, когда мы в микрофоне превращаем звук в электричество, то мы как раз и пытаемся зашифровать звук в электрические сигналы. Без знания лингвистики на этот вопрос было бы невозможно ответить.
Другой пример. Вы, наверное, знаете, что физика полностью построена на математике. Так вот оказывается, что если Вы не понимаете, как работает математическое мышление, если Вы не понимаете, как это мышление у людей появилось и как его можно воспитать в себе, то Вы никогда не поймёте математику. Учёные-математики не могут ответить на этот вопрос, зато на него может ответить биология. Не зная биологии мышления, вы никогда не научитесь думать математически.
Запомните: что для того, чтобы понять физику, недостаточно знать только физику. На многие вопросы физика ответить не может, именно поэтому в этом учебнике активно привлекаются знания из других наук. Помните, что все самые известные учёные были энциклопедистами. Узкие специалисты практически ничего не открывали.
О том, как автор будет излагать мысли в этом учебнике
Перед тем как приступить к изучению физики. Автор расскажет Вам о том, как он излагать свои мысли в этом курсе
Много лет назад, работая с пятилетними малышами и пытаясь объяснить им такие вещи как сложение и вычитание чисел, я натолкнулся на любопытный, но довольно тяжелый для неопытного ума момент.
В то время я имел лишь небольшой опыт работы со столь юными и неимоверно непоседливыми существами. Темой для объяснения было вычитание чисел. Вы помните, как ВАМ объясняли это арифметическое действие? Если нет, то я Вам напомню.
Объяснение вычитания было несложным: на пальцах, а также в столбик учились вычитать из БОЛЬШЕГО числа МЕНЬШЕЕ, то есть 3 – 1 = 2 или 5 – 1 = 4. И вот тут-то шло самое интересное.
Оказывается, что в начальной школе, где это обычно и объясняли, говорили одну очень интересную вещь. Якобы, от большего числа меньшее отнять можно, а вот от меньшего числа большее нельзя, то есть три минус один – можно, а вот один минус три нельзя.
Почему практически все преподаватели начальных классов решились на такой, казалось бы, крайне неправильный подход? Ведь он противоречит пониманию математики. Не трудно ли будет детям потом перестроить свое мышление? Ведь такое объяснение по сути является ничем иным, как педагогическим обманом, недоговариванием.
Оказывается никаких трудностей не возникнет.
Наоборот, именно из-за этого подхода дети как раз и усваивают весь материал, научаясь и складывать, и вычитать, и умножать. Суть такого подхода проста. Не нужно объяснять всё и сразу чтобы не перегрузить ученика информацией.
Используя такой подход, педагоги начальных классов руководствуются мыслью, что в начале ребенок должен запомнить что-то одно. Пускай и с огрехами и недомолвками, пускай и не совсем правильно. Ничего страшного.
А вот, когда когда ребенок хорошо усвоит первую тему (например, 3—1=2) то вот тут-то и надо сказать ему о том, что оказывается можно не только из трех вычесть один, но также из одного вычесть три. И далее пошли отрицательные числа.
Если Вы попробуете объяснить ребенку всё и сразу, включая отрицательные числа, то Вы столкнетесь с тем, что дети не поймут и не запомнят тему просто из-за обилия информации.
Не надо объяснять всё и сразу. Объясните что-то одно. Любая новая тема будет корректировать и уточнять весь предыдущий материал. Соответственно, чем больше материала, тем более точный и более научным становится рассказ.
Такой метод подачи материала давайте назовем элементарной педагогикой. Именно на элементарной педагогике будет построен весь этот учебник
У элементарной педагогики есть еще одно прелестное свойство. С ее помощью одни и те же темы можно изучать по нескольку раз. И при этом каждый раз всё глубже и глубже.
К примеру, если мы хотим выучить какой-то иностранный язык, то вначале мы должны взять его целиком, но поверхностно. Во второй раз мы будем изучать этот язык уже глубже, разбирая каждую тему более подробно. На третий раз совсем глубоко, забираясь в дебри грамматики и семантики. И вот так с каждым разом мы будем все глубже и глубже
Приведем пример, как можно использовать элементарную педагогику. Допустим в медицине. Представим себе, что в медицине только пять заболеваний А, Б, В, Г, Д и мы хотим их изучить. Вначале мы поверхностно изучим все пять заболеваний.
Изучив их на первый раз, мы начнем их изучать по второму кругу. Но теперь будем изучать подвиды каждого из заболеваний, то есть А1 и А2, Б1 и Б2, В1 и В2, Г1 и Г2, Д1 и Д2.
Как вы видите мы тот же самый материал начали изучать на более глубоком уровне. Если мы пойдем по третьему кругу, то мы будем уже изучать, так сказать, подтипы у подтипов. То есть заболевание А мы разделим на А1 и А2 и каждый из этих подтипов еще на два. Получится А1.1, А1.2, А2.1, А2.2. В итоге выйдет что на каждое из пяти заболеваний приходится по четыре подтипа.
Так строится обучение через элементарную педагогику. Чтобы не перегрузиться информацией, мы разбираем одну и ту же науку несколько раз, сначала поверхностно, а потом все глубже и глубже. Так будет строится и наш курс.
Один печальный момент элементарной педагогики: есть опасность того, что просмотрев только одну лекцию, вы можете сделать неверное мнение. Ведь каждая лекция будет уточняться с помощью последующих лекций.
Слишком высокий риск того, что если Вы прочитаете лекцию о том, что 3—2 = 1 и при этом не прочитаете следующую лекцию (про 2—3), то всю оставшуюся жизнь вы будет в плену заблуждений, что кроме 3—2 больше ничего не существует.
ЧЕМ ЖЕ ЗАНИМАЕТСЯ ФИЗИКА?
Если говорить простым языком, то физика занимается изучением абстракций природы, а также материальными предметами, из которых состоят эти абстракции. Напрашивается вопрос, что же такое абстракции и что такое материальные предметы?
Мысленно представьте себе нашу вселенную. Условно мы можем разделить ее на материальные предметы и на абстракции. Грубо говоря,
материальные предметы это всё, что мы можем увидеть и потрогать. Это может быть стол, камень, цветок, человек, улитка и тд.
Распознать материальные предметы не сложно. У них есть три важных свойства: все они имеют массу, любой материальный предмет можно разделить на части и, кроме того, любой материальный предмет можно переместить из одного места в другое. Запомните это!
Материальные предметы по другому называют физическими телами либо конкретными предметами
Абстракции или абстрактные явления в отличие от физических тел не имеют массы, не делятся на части и при этом их нельзя переместить.
Абстракции нельзя потрогать или увидеть!
Примеры абстракций: холод, давление, прыжок, колебание. Прыжок не имеет массы, прыжок нельзя разделить на части и его нельзя переместить из одного места в другое.
Оказывается, что любая абстракция это взаимодействие нескольких материальных предметов. К примеру, давление. Когда шкаф давит на пол, то здесь происходит взаимодействие шкафа, пола и центра земли, к которому шкаф как раз и притягивается.
Еще один пример, растяжение. Когда мы рукой растягиваем пружину, то здесь происходит взаимодействие пружины, руки, а также стены, к которой пружина прикреплена.
Обратите внимание, что абстракции не могут существовать без материальных предметов, которые слагают эту абстракцию. Смотрите, абстракция «хлопок» это взаимодействие двух ладоней, звуковых волн, а также ушей человека, который всё это слышит.
Если мы мысленно уберем из этой абстракции ладони, которые взаимодействуют, то не появятся звуковые волны (то бишь звук),а значит не будет и самой абстракции.
Любое абстрактное явление мы можем разложить на сумму материальных предметов. Примеры: хождение это взаимодействие наших ног и земли. Стук это взаимодействие двух твердых материальных тел, звуковых волн и наших ушей. Выстрел это взаимодействие ружья, патрона, пороха в патроне и руки человека, которая нажимает на спусковой крючок.
Такой подход, когда мы раскладываем абстракцию на материальные предметы, давайте называть абстрактно-материальным анализом.
– – – – – – – – – – – – – – – – – – – – – – – —
Ваше задание: придумайте 10 абстракций и разложите их на материальные предметы. Особой точности пока не требуется.
– – – – – – – – – – – – – – – – – – – – – – – —
Итак теперь, когда мы знаем с Вами, что такое абстракции и материальные тела, мы можем четко сказать что физика это наука которая занимается изучением абстракций природы, а также материальными телами, из которых эти абстракции состоят.
АБСТРАГИРОВАНИЕ И АБСТРАКЦИИ
Когда мы говорим о какой-либо абстракции, то мы можем представить ее мысленно.
С точки зрения нейрофизиологии всё, что мы можем мысленно представить это наши фантазии. Из этого следует, что абстракции это фантазии.
Обратите внимание, когда мы мысленно представляем какую-либо абстракцию (к примеру, давление), то в этой картинке, которая возникает у нас в голове, мы игнорируем всё кроме нашей абстракции.
Когда вы мысленно видите «давление», (допустим как камень давит на песок), то весь окружающий фон Вы мысленно удаляете. Это можно сравнить с редактирование фотографий в графических редакторах (наподобие adobe photoshop или gimp).
К примеру, у вас есть фотография, где вы стоите на фоне леса. Этот фон вы хотите удалить. Вы вырезаете его из фотографии и оставляет на ней
только себя.
Так вот наш мозг работает подобным образом: он оставляет на фотографии, сохраненной в нашей голове, только самое главное и удаляет, игнорирует всё ненужное (любые другие предметы или абстракции). Такое явления называется абстрагирование.
Все абстракции это абстрагированные фантазии, то есть фантазии, где удалён фон, окружающий эту абстракцию.
Если абстрагирование это процесс происходящий внутри нас, значит и абстракции существуют тоже внутри нас. Снаружи нас существуют только сами материальные предметы.
Когда физики рассматривают какую либо абстракцию, то эта абстракция по умолчанию абстрагирована. Это очень удобно. Ведь рассматривать несколько абстракций тяжело.
Абстрагирование помогает нам рассмотреть природное явление так сказать без помех, без других абстракций или материальных предметов
ШИЗОФРЕННЫЕ НАКЛОННОСТИ И ФИЗИКО-МАТЕМАТИЧЕСКИЕ СПОСОБНОСТИ
Как ни странно, но есть прямая связь между «шизофренными» наклонностями и физико-математическими способностями. Давайте вначале разберемся, что же такое шизофрения и как она проявляется.
Генетическое происхождение шизофрении мы не берем, так как генетику сложно назвать точной наукой. Шизофрения как и многие другие психические расстройства зарождается в детстве, приблизительно до семи лет, то есть тогда, когда у ребенка еще нет логического мышления.
Логическое мышление появится лишь, когда ребенок пойдет в школу. Именно оно мешает возникновению любого психического расстройства. Итак, что же нужно для того, чтобы проявилась шизофрения? Если мы будем наблюдать за семьёй, где у ребенка потихоньку проявляется шизофрения, то мы заметим несколько интересных явлений.
Первое это эмоциональная холодность родителей у «шизофренного» ребенка. И она действительно поражает. В таких семьях родители никогда ни за что не извиняются, даже если они сами в чем-то виноваты. Им проще скинуть вину на ребенка. К примеру, родитель взял пульт от телевизора, куда-То его положил, забыл об этом и первой реакцией такого родителя, когда он не найдёт пульт, это обвинить во всём ребенка. Если же такому родителю докажут, что это он взял пульт, то родитель просто отшутится, но так и не извинится.
Такие родители редко обнимают и редко целуют своих детей либо вообще этого не делают. Частенько в таких семьях не принято говорить «привет» и «пока». Довольно распространено, когда ребенок в такой семье называет родителя по имени.
Второе, что характерно для семей, порождающих шизофрению, так это материальная необеспеченность и маленькая жилплощадь, которые усугубляют отношения в семье.
Представим себе семью из трех человек. Мать, отец и ребенок 5 лет. Из-за маленького дохода в семье постоянные скандалы. Маленькое жилье еще больше нагнетает обстановку. Почему, спросите вы? Потому что, если бы у них была большая жилплощадь, то после скандала каждый мог бы закрыться в своей комнате и просидеть там до тех пор, пока агрессия не утихнет. Однако когда жилплощадь мала, то воюющие стороны постоянно в течение дня наталкиваются другу на друга, подливая еще больше масла в огонь, что нередко может привести к рукоприкладству. К примеру, уставший от скандалов муж, от горя напьётся и, как результат, побьёт жену и ребенка. После баталий муж уйдет на работу и сможет выплеснуть свою агрессию там, а вот жена выплеснет агрессию на того, кто рядом, то есть на ребенка.
Очень часто шизофреники, описывая свое детство, говорят о постоянных ЕЖЕДНЕВНЫХ, а иногда ежечасных унижениях.
Нередко они слышат от родителей фразы наподобие «чтоб ты сдох! / зачем ты родился (лась)!… / Надо было тебя удавить еще в детстве!».
Надо сказать, что шизофреники воспринимают своих родителей как опасность, как хищника или врага и постоянно ждут от них подвоха.
Довольно часто родители шизофреников страдают алкоголизмом.
Какие «ингредиенты» необходимы для того, чтобы проявились признаки шизофрении? Во-первых, необходимо чтобы это моральное и физическое давление родителей на ребенка, было ежедневным (а точнее ежечасным), а во-вторых, необходимо, чтобы ребенок ощутил угрозу существования (то есть так много унижений и избиений, что у ребенка запустился инстинкт самосохранения. Инстинкт самосохранения запускается лишь при наличии реального хищника, реальной опасности).
Ребенку пять лет, а это значит, что он не сможет физически (на своих двоих) уйти от ежедневной опасности. Вариант самоубийства как способ уйти от опасности тоже исключен. Ребенок еще не знает, что он смертен.
Давление с каждым днем растет и маленький человечек чтобы защититься от этого давления, уходит в свои фантазии (то есть в себя, в свой внутренний мир). Представьте себе, что реальность это одно измерение, а фантазии (они же мечты, грезы, картинки в голове) это другое измерение (как в фантастическом фильме). В это «другое» измерение мы можем переместиться, чтобы укрыться от хищников нашего мира.
«Для чего ребенок уходит в мир фантазий?» – спросите вы. Я отвечу Вам: Фантазии служат ребенку ракушкой, «домиком», где можно спрятаться в любое время от любого врага. Там ему спокойно и безопасно, там он чувствует себя нужным. К сожалению, чем дольше там пребываешь, тем неохотнее возвращаешься. И вот однажды врата между измерениями захлопываются и ты остаешься там навсегда
Довольно часто дети-фантазёры играют сами с собой. В реальности такие дети не могут постоять за себя (их никто этому не научил), но в своих играх они видят себя всемогущими и способными дать отпор. В своих играх они генералы или могущественные волшебники, богатейшие люди или мастера кунг-фу, императоры или даже злодеи, которые могут сделать другому больно.
Давайте поглядим как работает механизм шизофрении. Рассмотрим два вида расстройства
КАТАТОНИЧЕСКАЯ ШИЗОФРЕНИЯ (F20.0)
Представьте себе курицу, которая ходит по улице и выклёвывает из земли насекомых. Если Вы погонитесь за этой курицей, то она отчаянно от Вас побежит, но если Вы её поймаете, то здесь Вы увидите своеобразные чудеса. Схватив курицу руками, вы заметите, что она замерла. Когда вы опустите курицу на землю, то увидите, что курица никуда не бежит. Она словно окаменела. Пройдёт еще несколько минут, курица придёт в себя и побежит прочь. Такое явление встречается только у травоядных. Оно называется катаплекси́я. Катаплексия это состояние это когда животное под влиянием испуга словно каменеет и не реагирует на внешние раздражители. Природа создала такое состояние, вероятно, потому, что хищникам довольно тяжело догнать травоядное. 10 раз гепард должен гнаться за антилопами, но только 1 раз будет успешным. Можно сказать, что катаплексия это некий подарок, которые сделала природа для хищников, некая уверенность в том, что жертва не убежит.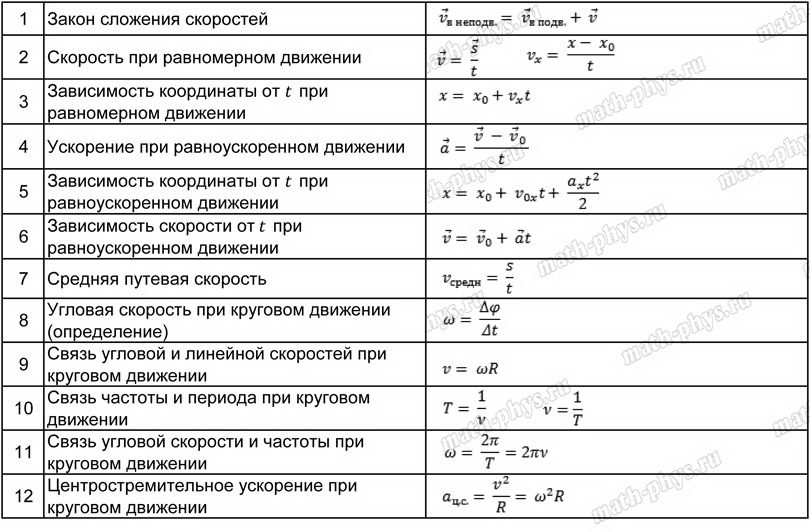
Кататоническая шизофрения, по сути, есть ничто иное, как человеческая катаплексия. Если родитель ведёт себя как хищник, если родитель считает, что может делать со своим ребенком всё, что вздумается (унизить, ударить, забрать личные вещи или прочитать дневник), то ребёнок от испуга замирает. Он не может пошевелиться, потому что не знает, как справиться с таким врагом. Ребенок просто сдаётся. И действительно, кататонию часто называют «восковой гибкостью», потому что человек в этом состоянии не управляет своим телом. Оно подобно воску или пластилину, из которого окружающие люди могут лепить, что угодно. Посадите кататоника в неудобное положение и он может просидеть так несколько недель.
ПАРАНОИДНАЯ ШИЗОФРЕНИЯ (F20.2) несколько «легче», чем кататоническая. Если при кататонической шизофрении пациент полностью уходит в мир фантазий, то при параноидной он уходит не полностью. Он и там и тут (так сказать «ворота между измерениями открыты»). Грубо говоря, пациент «два часа здесь, два часа там» либо «на границе двух измерений».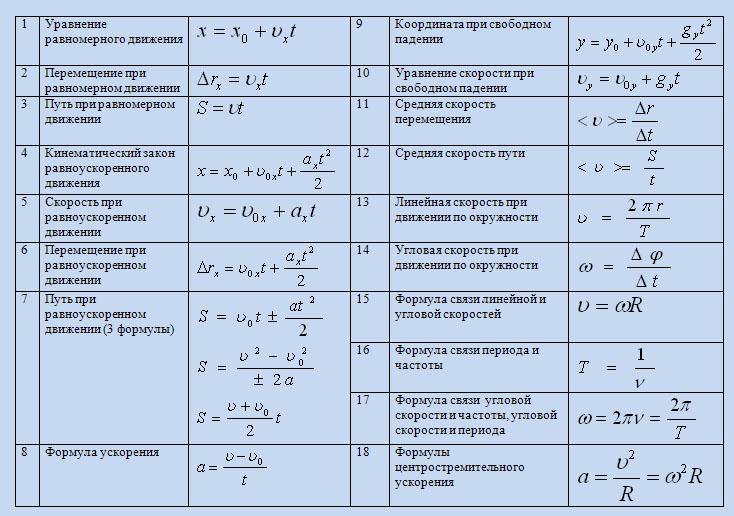
К примеру, пациент разговаривал с вами и неожиданно «провалился в другое измерение», то есть включились патологические фантазии. Он уже не будет ни видеть и ни слышать вас. К примеру, он видит как к нему подходят люди, которые много лет назад умерли. Он будет их слышать, он будет их видеть, будет чувствовать их запах, он даже будет ощущать их прикосновение. Если они сделают ему больно, то он ощутит это. Он даже попытается отбиваться от них. Но как всё это будет выглядеть со стороны? Человек смотрит в пустое пространство, затем с кем-то разговаривает и от кого-то отбивается. Со стороны, конечно, это будет выглядеть странно. Такие патологические фантазии называют галлюцинациями. А то, как пациент пытается словами объяснить реальность своих галлюцинаций, называют бред.
Боязнь людей у шизофреников
Из-за постоянного морального и физического давления, родители шизофреника становятся для него объектом страха. Одна их фигура или мысль о них, вызывает у него патологический ужас.
Они не приучили ребенка любить их. Они приучили бояться их, ненавидеть их. Ребенок, который будет бояться и ненавидеть родителей, тем паче будет бояться и ненавидеть других людей, ведь ему не объяснили «а что с ними делать?» и «как с ними общаться?». Такой ребенок будет испытывать либо страх либо агрессию – знакомые ему модели поведения. Взгляд обычно выдает шизофреников. Они боятся людей, поэтому избегают телесных контактов в том числе визуальных. Обратите внимание, шизофреники почти всегда отводят глаза, когда вы смотрите на них. Нередко они глядят как бы исподлобья, с наклоненной вперед головой как бы «из-под бровей». Разговаривая с кем-то, они упорно смотрят куда-то в сторону, как будто смотрят в «подмышку».
Итак, представьте себе человека, который боится людей. Как вы думаете сможет ли он заняться работой, которая связана с общением? Сможет ли такой человек к примеру, работать гидом или социологом? Интересно ли будет такому человеку заниматься деятельностью, в которой требуется общаться с людьми? Я думаю, ответ понятен.
Конечно же, нет. Шизофреники которые боятся людей не смогут заниматься вещами, при которых нужно контактировать с людьми.
Из всего вышесказанного можно сделать вывод, что именно хорошо развитые фантазии являются грунтом, на котором строится физика и математика, а сами эти фантазии являются частью шизофренных или шизоидных явлений. Вот поэтому шизоидам так легко дается математика или физика. Можно сказать, что они «видят математику в своей голове». Они превратили свои шизоидные черты в способности. Возьмите это на вооружение. Представляйте любую абстракцию в своей голове, фантазируйте и физика вам покажется не сложнее таблицы умножения.
– – – – – – – – – – – – – – – – – – – – – – – – —
Надо сказать, что боязнь людей характерна не только для шизофреников, но и для шизóидов. Можно привести такую аналогию: если шизофрения это концентрированный сок, то шизоидность это сок, разбавленный литром воды. Шизоидов всегда больше, чем шизофреников. В отличие от шизофрении шизоидность это не болезнь.
Это патология характера.
– – – – – – – – – – – – – – – – – – – – – – – – —
Однако у шизоидных наклонностей есть и свой минус. Шизоиды и шизофреники частенько не различают, где фантазии, а где реальность. Как результат, свои фантазии они считают чем-то реально существующим. По сути, явления ВНУТРИ СЕБЯ они считают чем-то ВНЕ СЕБЯ. Можно сказать, что они выносят внутренние явления наружу. Давайте назовем это психической трансгрессией (от латинского transgressio – пересечение, переход).
– – – – – – – – – – – – – – – – – – – – – – – – —
Приведем пример. Шизоид пришел устраиваться на работу. Поднимаясь по лестнице, он мысленно в своих фантазиях представил как его унижает начальник. Разумеется, когда наш герой пришёл к начальнику, то уже был к нему негативно настроен. Мало того, наш герой уже ненавидел этого начальника. В результате, даже не договорившись о работе, наш герой разворачивается и с недовольным видом идёт домой, на чём свет стоит проклиная этого начальника.
Обратите внимание, сам шизоид даже не замечает, что скандал с начальником произошел в его фантазиях и что в реальности начальник хороший человек.
– – – – – – – – – – – – – – – – – – – – – – – – —
К сожалению, в физике и математике довольно часто возникают явления подобной психической трансгрессии. Многие явления, которые существуют внутри человека, физики считают или считали чем-то вне человека. Например, цвета, звук, теплота, тень и тд. Эти явления можно понять только, если мы знаем биологию и психологию человека. В последующих лекциях мы будем использовать биологический подход к изучению физики, то есть будем выискивать психическую трансгрессию в физических явлениях. Ведь так много явлений нельзя объяснить физикой, однако можно объяснить биологией. Психическая трансгрессия, к сожалению, это одно из больных мест физики.
Читать онлайн «Физика для «чайников». Несерьезное пособие», Андрей «Dront» Ильин – Литрес
Дизайнер обложки Марта Миронова
Иллюстратор Екатерина Аникина
© Андрей «Dront» Ильин, 2018
© Марта Миронова, дизайн обложки, 2018
© Екатерина Аникина, иллюстрации, 2018
ISBN 978-5-4490-2051-2
Создано в интеллектуальной издательской системе Ridero
От автора
В школьные годы меня очень раздражало то, что учебники по всем предметам пишутся сухим академическим языком.
По мне, читать такие учебники, не имея представления о предмете, – адская мука из серии «без пол-литра не разберёшь». Иногда мне даже казалось, что именно по этой причине особо тянущиеся к знаниям ученики (равно как и те, кто школьные знания жёстче всего отторгают) могут быстро начать пить.
Ладно, глупые шутки в сторону. Поскольку школьная и студенческая жизнь у меня остались позади вместе со всеми наивными надеждами на тему «есть ещё такие учебники или неофициальные издания, в которых объясняются все те же вещи, что и в школе, но как можно более простым языком», я решил написать собственный опус на эту тему.
Почему именно физика? Полагаю, потому, что у меня техническое образование, и сей предмет впрессовывали в мою голову тысячами часов и сотнями страниц (я серьёзно), как в школе, так и в университете. Однако, смотря на то, как мучаются другие люди в попытке понять, как, зачем и почему происходят все те природные явления (не побоюсь этого заумного выражения), факты о которых так скрупулезно и точно разъясняются в учебниках (или читаются на лекциях), возникло желание помочь всем страждущим.
А поскольку вся техника держится на физике, то волей-неволей приходилось разбираться во всех свалившихся на голову умных изречениях.
А вот дальше нужно написать большими красными буквами:
ВНИМАНИЕ! Это «собрание сочинений» нельзя использовать как учебник!
Книгу вполне можно считать за шпаргалку, «объяснялку», или даже использовать не по назначению (мало ли будет плохое настроение, да ещё вдобавок не поймёте очередную порцию умных мыслей… всякое бывает). Но если будет соблазн прийти на экзамен, держа в зубах только эту книгу, – не надо. Не поймут. Или поймут, но неправильно. Система образования (и – уж тем более – науки) терпеть не может, когда научные вещи объясняют простыми словами. Именно поэтому в конце каждого раздела я буду подсказывать, как можно рассказывать объяснённые вещи более сухим, но и более правильным языком.
1 / 5: Механика
Кинематика
Что это вообще такое, и зачем это нужно?
Раздел школьной механики про движение состоит из трёх основных частей: кинематики, динамики и статики.
Проще всего это объяснить так. Например, ты идёшь по улице, и вдруг на пути появляется яма. Не заметив её, ты падаешь. Говоря умным словом – движешься.
И все эти три раздела смотрят на это движение каждый со своей стороны.
Так вот. Кинематика – это:
Как ты движешься? (Вниз, ускоряясь.) Когда остановишься? (Когда долетишь до дна.) Через какое расстояние остановишься? (Ровнёхонько глубина ямы, ну и углубление, оставленное туловищем, если хорошо упадёшь.)
Динамика – это: почему ты начал двигаться, почему продолжаешь это делать и почему закончил (если закончил). Например: начал потому, что это сила притяжения Земли к тебе такая вредная, и продолжаешь лететь, потому что она по-прежнему действует.
А статика – это что надо делать, чтобы ты оставался в равновесии. То есть когда занёс одну ногу над ямой, надо было успеть сообразить, что делаешь, и убрать её обратно, и в то же время податься туловищем немного назад.
Говоря чуть более умным языком: кинематика как бы отвечает на вопрос «как тело движется?», динамика – «почему тело движется?», а статика – «при каких условиях тело будет в равновесии?».
Кругом умное слово: движение. Оказывается, и это тоже понятие! Причём оно настолько заумное, что означает всего-навсего изменение. Просто изменение, и всё. В широком смысле – то есть в физике вообще. Если брать более узко, то механическое движение – это когда что-то меняет своё положение.
Но есть один подкол. Вспомним детство: едем на машине, автобусе, электричке… это не так важно, – и смотрим в окно. И кажется, будто дома или деревья едут мимо тебя, а ты стоишь на месте. А вот если на тебя посмотрит кот из окна первого этажа дома (мимо которого проезжаешь) – ему будет казаться, что ты движешься.
Короче, суть всей этой маленькой шизофрении – движением можно считать что-то, только если это движется относительно чего-то.
Нет, это ещё не страшная теория относительности Эйнштейна, не надо пугаться. Обзывается сие хозяйство «системой отсчёта». Вот поставил на себе жирную белую точку мелом – всё, теперь считаешь себя точкой с координатами (0;0;0). А тот момент, когда поставил точку – это считаешь, что пошло время (с 0 секунд и до бесконечности… плюс бесконечности – для особых умников).
Всё, теперь ты – система отсчёта! Относительно тебя, например, крутятся Земля и другие планеты. Ну прямо центр Вселенной!
Вкратце и поумнее: для положения тела необходимо определить систему отсчёта (это «отправная» точка с координатами (0;0;0) и начало отсчёта времени), относительно которой будет считаться всё, что связано с тем, как оно движется. Если относительно данной системы отсчёта тело меняет своё положение, то считаем, что оно двигается.
Материальная. И точка!
Вот не могут физики без упрощений, хоть убей. Что мешает взять, например, самолёт и посчитать, как он летит? Нет, это слишком сложно для умных мозгов местных учёных! Для этого, видите ли, надо считать, как движется чуть ли не каждая точка сего транспортного средства. А из скольких точек состоит самолёт? А пёс его знает. Даже что такое точка, те же умники учёные сказать не могут: это настолько простой термин, что его даже не определить. Поэтому тут в мозгах у них происходит что-то, похожее на деление на ноль в калькуляторе: точек настолько много, что их всех не посчитаешь.
А значит, не посчитаешь и весь самолёт! Ну и что тогда делать?
А вот что. Мы встанем далеко-далеко от самолёта – говоря проще, вернёмся с неба на землю. Нет, совсем на землю. А самолёт поднимем ещё выше. Настолько высоко, чтобы он казался точечкой. Во, теперь получилась материальная точка.
Самолёт кажется отсюда настолько малым, что его размерами можно пренебречь: сколько он там метров в длину, и какой у него размах крыльев, уже не интересует. Летит себе одной точкой, и всё: одну эту точку теперь можно посчитать. Материальную точку, выражаясь умным языком. Но главное – не отрываться при этом от земли! Ну и, чтобы всё совсем было хорошо, надо на земле поставить точечку (0;0;0) и включить секундомер. Всё, поехали… то есть полетели. Считать.
Вкратце и поумнее: материальная точка – это модель тела, размерами которого можно пренебречь в условиях данной задачи. Для простоты счёта все тела, которые можно рассматривать как материальные точки, рассматриваем именно так.
Траектория? Перемещение? Не, не слышал
Ну хорошо, выбираем самолёт. Посмотрим, как он летит весь свой путь. Вот он разгоняется на взлётно-посадочной полосе в аэропорту, отрывается от земли, взмывает ввысь, летит… Затем снова снижается, тормозит и останавливается уже на месте назначения. Если бы он чертил за собой линию, то получилась бы дуга. (Напоминаю, мы смотрим по-прежнему настолько издалека, что самолёт кажется точкой. Будь мы ближе – конечно, это была бы не дуга.) По-умному сия дуга называется траекторией. Если померить её длину, то получим путь. Тот самый, который в начальной школе считается, как скорость, умноженная на время. Но если бы всё было так просто… Помимо пути, есть ещё перемещение. Слово похожее, но значит другое. Перемещение – это если соединить начальную и конечную точки прямой линией. То есть, получается, самый короткий из всех возможных путей: обычный путь может быть изогнут хоть буквой Зю, а этот всегда только отрезок. Но здесь есть ещё один подвох.
Перемещение – это ещё и направленный отрезок. Зачем такое умное нагромождение? Потому, что физика тесно сплетена с математикой. Мы же не просто так поставили точку (0;0;0) и включили время – теперь в тех координатах, которые мы создали, можно считать всё, что требуют от бедных нас в тоннах задач. И считать нужно именно по перемещению, а не по пути. В конце концов, нам же выгоднее добираться до места назначения быстрее всего, то бишь кратчайшим путём? А стрелочка ставится затем, чтобы точно знать, откуда и куда держим наш путь… нет, наше перемещение.
Вкратце и поумнее: траектория – воображаемая линия, по которой движется материальная точка. Путь – длина траектории. Перемещение – направленный отрезок (или уж совсем по-умному – вектор), соединяющий точки, соответствующие начальному и конечному положению тела.
И всё-таки: ну зачем нужны все эти упрощения?!
Всё, наконец-то все приготовления закончили. Теперь, собственно, а зачем всё это было нужно. Считается, что полный венец любой решённой задачи механики, когда всё становится хорошо, – это когда мы можем знать:
а) в какой момент наше подопытное туловище где находится;
б) суметь предсказать его движение в дальнейшем,
или в) по нынешнему его движению показать, что было «до того».
(Ну прямо как детектив.)
Вроде бы кажется страшно сложным, но строгая математика тут грозит пальцем: для неё ничего сложного здесь нет. Почему? Потому, что можно выделить всего три основных вида движения: равномерное прямолинейное, неравномерное и равномерное движение по окружности.
Равномерное прямолинейное – это как на шоссе. Втопил газу до круиз-контроля на 120 – и езжай хоть целый день, если дорога достаточно длинная. Всё время едешь постоянно 120 км/ч – значит, движешься равномерно. И прямолинейно, если без крутых поворотов. Если 120 вдарить на кольцевой дороге, получится движение по окружности. А если нажать на тормоз и держать педаль в одном положении, пока не остановишься – получится неравномерное движение. Если совсем точно – равнозамедленное: тормозишь, едешь всё медленнее и медленнее, причём каждую секунду скорость понижается одинаково.
То есть, по-русски: равномерное – значит, за любой промежуток времени у тебя будет одно и то же перемещение. Если взять ту же машину, то за каждый час это будет 120 километров ровно, за каждую минуту – 20 км, ну и так далее. Неравномерное – это всё, что отличается от равномерного. За один час проехал 119 км, а за второй 120, – всё, если считать строго, это уже неравномерно. Движение по окружности стоит особняком: там перемещение получается всегда меньше, чем любой из путей (особенно если приезжаешь ровно в ту же точку, откуда уехал). Но если скорость по значению остаётся одна и та же, то оно будет равномерным.
Да. Скорость. К счастью, это та же самая скорость, с которой привыкли обычно иметь дело. Только в физике мерят её не в километрах в час, а в метрах в секунду. Это если говорить о её значении, или – по-умному – о модуле. Да-да, тот самый модуль с палочками из математики. К сожалению, он не полностью определяет скорость в физике. А полностью будем определять, если ещё и зададим ей направление. То есть – по-умному – получается вектор. Отрезок со стрелочкой: если знаешь, куда он направлен и сколько у него длина, только тогда всё хорошо. Тогда скорость известна.
А если рядом с нашей едущей машиной проедет другая? Тоже со скоростью 120 километров в час? Тогда получится, что относительно нас она стоит на месте.
Потому что скорости одинаковые. Если будет чуть быстрее (например, 121) – то очень медленно станет двигаться вперёд. Чуть медленнее (ну, скажем, 119) – так же медленно, но назад. То есть скорость нашей машины вычитается из той, второй. 121 минус 120 будет 1 – понятно, медленно ползёт вперёд. А 119 – 120 будет -1 (минус один). Что означает – она по-прежнему едет, но не вперёд, а в противоположную сторону, задом наперёд. Что нам и кажется – она как бы медленно даёт задний ход с той же скоростью 1 км/ч.
Вкратце и поумнее: при равномерном прямолинейном движении тело за один и тот же промежуток времени совершает одинаковые перемещения. Если хотя бы для одного промежутка времени это не соблюдается, движение не считается равномерным. Скорость при равномерном движении – это перемещение, которое совершили, делить на время, за которое оно было совершено, т.е. тоже вектор, причём постоянный по модулю. Единица измерения – метр в секунду (м/с). При движении двух тел в некоторой системе отсчёта, чтобы посчитать скорость движения второго тела относительно первого, достаточно из скорости второго тела вычесть скорость первого.
А в реальности всё по-другому…
Ну, это всё был идеал. Равномерное движение – это то, чего хотят составители расписания автобусов, поездов метро и прочего транспорта. Которое, как мы видим, толком и не соблюдается (а даже если и соблюдается, то не секунда в секунду, а всё равно с отклонениями). Потому что движение там хоть и прямолинейное, но никак не равномерное. Трудно очень удержать одну и ту же скорость в наше нелёгкое время. Для этого физика предусмотрела более широкий вариант под названием «переменное движение».
При переменном движении тоже есть скорость, только она имеет немного другой характер. Это всё то же «перемещение поделить на время», но есть одно «но». Скорость-то, зараза такая, всё время меняется… если смотреть от того момента, как начал двигаться, до того, как закончил. То есть за большое время. А если посмотреть время поменьше – скорость будет меняться не так резко. Ну и, наконец, если совсем-совсем сузить обзор, то будет казаться, что скорость вообще постоянная (но за очень маленький промежуток времени).
Вот за это и можно зацепиться!
Поэтому здесь получается так: очень маленькое перемещение делить на очень маленькое время. Они настолько маленькие, что первое стремится к точке, а второе – к мигу. То бишь, оба стремятся к нулю. В страшной математике (на которую, увы, физика опирается) такую дробь называют производной. Если совсем по-русски – то это скорость изменения по тому, по чему «производят». То есть получается, что наша многострадальная скорость – это скорость, с которой перемещение меняется во времени. Или, совсем по-простому, – как с течением времени меняется то самое разное расстояние, которое мы проезжаем на нашей машине.
И всё бы хорошо, да не помогает это избавиться от основной головной боли: скорость-то эта всё равно меняется всё время! И считать её получается совсем невыгодно: чтобы точно знать, как что движется, придётся считать эту скорость чёрт-те сколько раз. (Сколько? Ну, попробуйте посчитать, сколько бесконечно маленьких промежутков времени, например, в одной секунде.
) Поэтому придумали ещё одну фишку.
Называется она ускорением. Это как бы вторая производная – оно показывает, как меняется скорость. Если смотреть так же: при очень маленьком времени это будет изменение нашей «типа постоянной» скорости (тоже может быть близким к нулю, хотя по факту точно не ноль) делить на наше очень маленькое время. То есть получается, что ускорение – скорость изменения скорости. Тоже получается всё тот же несчастный вектор (из-за того, что скорость векторная, а время – число, на которое вектору по барабану, умножат его или разделят). А в чём мерят ускорение, можно даже догадаться. Если скорость (метр в секунду) разделить на время (секунду), получится метр на секунду в квадрате. Звучит странно, но именно в таких единицах и мерят. Хорошо ещё, что не обзывают никак дополнительно. А то в физике местами есть такие загоны – все величины называть именами кого-нибудь. (К счастью, в механике это ещё не так заметно.)
Ладно, отвлеклись. Зачем вообще нужны все эти заумные скорости, ускорения, скорости изменения скорости и ещё чёрт знает чего… А вот зачем.
Переменное движение, вообще говоря, может быть либо ускоренным, либо замедленным. Когда едем на той же машине, мы либо потихоньку ускоряемся, либо потихоньку тормозим. И в большинстве случаев это движение бывает равноускоренным или равнозамедленным. Это означает, что ускорение при нём постоянно!
То есть, если посчитать ускорение, то можно размотать клубок в обратном направлении: посчитать скорость в тот момент, который нам нужен, а из неё уже можно получить перемещение за общее время. Больше, как правило, не просят, так что дальше можно расслабиться. Более того, разница между ускоренным и замедленным движением состоит всего лишь в знаке ускорения. Когда ускоряемся – оно положительно (здравый смысл рулит), а когда замедляемся – оно отрицательно. Как это так? Отрицательное ускорение означает, что скорость со временем не увеличивается, а уменьшается. Чтобы узнать, насколько, надо то число, которое стоит после минуса, умножить на то время, за которое тормозим. Например, за две секунды машина равнозамедленно движется с ускорением -4 м/ (с2).
Это значит, что за каждые 2 секунды скорость машины снижается на 2.4 = 8 метров в секунду. То есть ехала сначала 30 метров в секунду, через 2 секунды – 22 м/с, ещё через 2 – 14, ещё через 2 – 6, а до следующих двух дойти не успеем – она остановится.
Расстояние тут посчитать посложнее, но всё-таки возможно. Если посчитать, а сколько она метров проехала за эти 6 секунд, получится следующее. Надо умножить начальную скорость на общее время и сложить с этим следующее: ускорение, умноженное на квадрат общего времени, и всё это делённое пополам. Не спрашивайте, почему именно пополам – тут по-простому, без математики, к сожалению, не объяснишь. (А вот почему именно квадрат времени, могу кинуть подсказку: нам надо «метры, делённые на секунду в квадрате» умножить на что-то, чтобы получить метры. Логично, хотя и непривычно, предположить, что это должны быть секунды в квадрате. Это одна из фишек всех формул физики: смотри, чтобы размерность того, что считаешь, сошлась! Потом это ещё увидим.)
В общем, получается такая штука:
30.
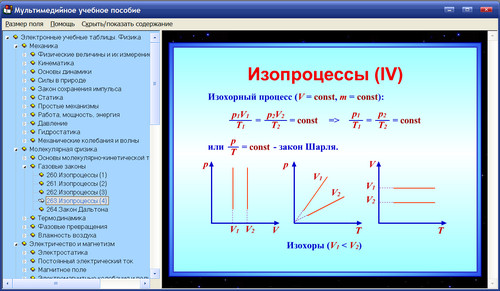6 = 180 метров.
К этому надо ещё прибавить ту страшную дробь, а она получится так:
– 4.62/2 = -2.36 = -72 метра. Именно с минусом, потому что ускорение отрицательное: не забываем, что мы тормозим!
И в итоге получим 180 + (-72) = 108 метров.
То есть, получается, если ты шпаришь на машине со скоростью 30 м/с (это 108 км/ч) и будешь плавно тормозить по 8 м/с (это почти 29 км/ч) в секунду, то значительно замедлишься только почти через 100 метров, а остановишься ещё дальше. (Для любознательных – вредное домашнее задание: посчитать, в какой момент времени наша машина остановится.)
Вкратце и поумнее: скорость переменного движения – это отношение перемещения тела к промежутку времени, за которое оно было совершено, при условии, что промежуток времени бесконечно мал (стремится к нулю). Ускорение – это скорость изменения скорости: отношение изменения скорости к промежутку времени, за которое это изменение произошло – опять-таки, при условии, что промежуток времени бесконечно мал (иначе говоря – стремится к нулю).
Это также векторная величина, в общем случае может меняться. Единица измерения – метр на секунду в квадрате (м/с2). Частные случаи переменного движения – равноускоренное и равнозамедленное движение, по характеру отличаются лишь знаком ускорения, по модулю же оно будет постоянно в обоих случаях. Подсчёт скорости (v) при равноускоренном или равнозамедленном движении такой: v = v0 + a.t, где v0 – начальная скорость (с которой двигались в начальный момент времени t = 0), a – ускорение, t – время. Перемещение считается следующим образом: s = v0.t + a.t2/2.
Пони бегает по кругу. Ай, то есть, по окружности
Это всё было прямолинейное движение. То есть: когда беззаботно летим по шоссе, траектория наша является прямой линией, и всё хорошо. Но вот теперь мы въехали в город и едем по круглой площади. Это уже криволинейное движение – траектория не прямая. Если начать умничать, то перемещение здесь получится меньше пути, скорость будет менять своё направление и, более того, направления скорости и ускорения не будут совпадать.
То есть если тут что-то надо будет считать – ребята, тушите свет. Если в общем случае…
Но здесь, опять-таки, есть случаи частные. Самый распространённый здесь – равномерное движение по окружности. При нём траектория – окружность, а скорость по модулю не меняется. Всего два уточнения, но от них становится легче. Почему?
Потому, что при этом гораздо проще посчитать путь (это просто длина окружности). Раз. Второе – гораздо проще посмотреть, куда направлено ускорение. Тут оно называется заумным словом «центростремительное» – типа, когда едешь по кругу, невольно стремишься к центру. Как следует из названия, его «стрелочка» направлена к центру окружности. Скорость же при этом направлена по касательной к окружности (едешь-то как будто прямо). Получается, что центростремительное ускорение всегда перпендикулярно скорости. Повёрнуто под 90 градусов по отношению к ней, то бишь.
То есть, по-русски. Когда ты едешь по кругу, то получается, что как будто всё время стремишься к центру: каждый момент поворачиваешь на какой-то маленький уголок, и эти повороты заставляет тебя ехать дальше не «абсолютно прямо», а «чуть криво», чтобы постоянно держать одно и то же расстояние от центра.
Тогда, собственно, и получается окружность. Это самое центростремительное ускорение и показывает, насколько сильно меняется направление твоего движения (по-умному – направление вектора скорости).
А считается оно как квадрат скорости, делённый на радиус окружности. Опять бредовая формула? А это потому, что скорость берём линейную (метры в секунду). Если же мысленно смотреть из центра и крутить головой, смотря на едущую по кругу машину, то за какое-то время голова повернётся на какой-то угол. Скорость, с которой она повернётся, будет угловой (радианы в секунду). Вот если через такую скорость считать, то будет… квадрат угловой скорости, умноженный на радиус. Опять не угодил?! Почему квадрат? Да пёс его знает, если честно. Одно из лучших оправданий физиков при вопросах «Почему формула такая бредовая?!» – размерность. Если посчитать размерность по формуле, и она получится равной размерности того, что хотим получить, то в 75% случаев формула правильная. (Число 75% беру с потолка. Кто уже точно рассчитал, что на самом деле не 75, а 76%, – смело кидайте тухлые помидоры.
)
Смеха ради проверим это предположение про размерность. Если для формулы ускорения взять обычную скорость, то получится: метры в квадрате, делённые на секунду в квадрате, делить на метры. Итого получится – метр на секунду в квадрате – размерность ускорения. Не придерёшься. Если брать угловую, то тут похитрее: радианы в подсчёте размерности считаются безразмерными. (Это одна из причин, почему радианы стали использовать как единицу измерения. Не просто так же брать какую-то непонятную цифирь в 57.3 градуса с потолка.) Поэтому здесь выходит так: метры умножить на обратную секунду в квадрате (1/c2). То есть – опять м/с2.
Достаточно всех этих прибамбасов для того, чтобы посчитать, как же наше несчастное тело движется по окружности? Ну, хоть в той же машине? Почти. Остаётся последнее «но». В какое-то время мы проедем один круг и вернёмся в точности в то же положение, с которого начинали. Через такое же время (так как движение равномерное, то оно будет точно таким же) – опять вернёмся, и так до бесконечности.
При таком раскладе путь считать становится накладным (может кто-нибудь навскидку сказать, как посчитать длину куска окружности?), а перемещение и вовсе теряет смысл. Чтобы внести ясность, через какое время мы будем в какой точке, придумали ещё одну величину: период. Это минимальное время, за которое мы вернёмся в первоначальное положение (которое было тогда, когда запустили тот самый воображаемый секундомер, и время побежало прочь от нуля). Измеряется в секундах, как обычное время. Но на случай, если период очень маленький, придумали вторую, родственную ему, штуку: частоту. Это число оборотов в единицу времени (читай: секунду). Соответственно, она обратна периоду и измеряется в обратных секундах (1/с). В простонародье… э-э, простите, в физике, это обозначается «Гц». По фамилии учёного Генриха Герца. У той же машины есть прибор под названием тахометр – он показывает количество оборотов в минуту или секунду, которые делает вал внутри двигателя. На них обычно пишут циферки от 1 до 10, но с припиской «умножить на тысячу».
То есть количество этих оборотов измеряется тысячами! А что будет, если вместо частоты станет период? Некрасивые цифры в виде 0.005 и тому подобные. Как-то проще, когда имеешь дело с тысячами, а не с тысячными.
Вкратце и поумнее: равномерное движение по окружности – это движение тела с постоянной по модулю скоростью, при этом траекторией движения является окружность. Центростремительное ускорение показывает, как меняется направление вектора скорости, оно всегда направлено к центру. Может быть посчитано как v2/R или ω2.R (v – линейная скорость, ω – угловая, R – радиус окружности). Угловая скорость – это отношение угла поворота радиуса, на котором находится наша движущаяся точка, ко времени, за которое произошёл этот поворот. Период обращения – минимальное время, за которое тело вернётся в первоначальное положение. Частота – величина, обратная периоду: количество оборотов, совершаемым телом, в единицу времени (секунду). Частота измеряется в герцах (Гц).
Игровая физика с нуля · код @liabru
Игровая физика с нуля · код @liabruФриланс – Подробности
Если вы разработчик игр, заинтересованный в изучении физических движков, эти ресурсы — хорошее место для начала.
Темы включают такие вещи, как интеграция , обнаружение столкновений , разрешение столкновений и трение .
- Продвинутая физика персонажей от Томаса Якобсена
- Rigid Body Dynamics Статьи Chris Hecker
- Примечания к курсу физического моделирования, авторы Эндрю Уиткин и Дэвид Барафф
- Документы и технические отчеты Baraff by David Baraff
- Итеративная динамика с временной согласованностью Эрин Катто
- Непрерывное столкновение Эрин Катто
- Презентации Эрин Катто на GDC от Эрин Катто
- Унифицированная структура для динамики твердого тела Гельмут Гарстенауэр
- Интеграция на примере – Эйлер против Верле против Рунге-Кутта по Флориан Беш
- Простой метод интеграции Verlet с поправкой на время, Джонатан Даммер
- Основы интеграции – Реализация Рунге-Кутта-4 (RK4) от Glenn Fiedler
- SAT (Теорема о разделяющей оси) Уильям Биттл
- GJK (Гилберт-Джонсон-Кирти)
- N Учебное пособие A — Обнаружение столкновений и реагирование на них, авторы Raigan Burns и Mare Sheppard
- Как создать собственный 2D-физический движок, Рэнди Гол
- Физические двигатели для чайников от Paul Firth
- Записи по физике от Florian Boesch
- Game Physics от Glenn Fiedler
- Реакция на столкновение и кулоновское трение Гленн Фидлер
- Методы обработки столкновений от Эрика Ноймана
- Расчет инерции полигона по
- Баязит Выпуклый многоугольник Разложение по Марк Баязит
Типографика Material Design в CSS
Фрактальные шестерни
Более надежная библиотека одинаковых высот
Эрудит для ленивых, используя OCR в реальном времени
Игровая физика с нуля
Более легкая тема для dat gui
Вот как научиться физике и математике
Футуризм
4.
22. 16 Джолин Крейтон
/ Hard Science
Познакомьтесь с удивительной физикой, которая управляет нашей вселенной… и математикой, стоящей за ней.
/ Твердые науки/ Математика/ Физика/ Квантовая физика
4. 22. 16 Джолин Крейтон
Изображение WallUp
Физика и математика являются чрезвычайно важными предметами. На самом деле, это немного преуменьшение.
Физика и математика позволяют нам заглянуть в космос и понять внутреннюю работу Вселенной. Они сразу показывают нам нашу ничтожность и наш замечательный потенциал; они намекают нам на огромные возможности, которые существуют — на то, что мы могли бы (и можем) однажды сделать. Они позволяют нам увидеть мир и увидеть себя заново.
Это начинает царапать поверхность этих предметов.
Никто не может отрицать их важность; однако фактом является и то, что многие люди не знают с чего начать изучение этих тем… какие книги изучать, с каких тем начинать. Вдобавок ко всему, многие боятся физики и математики — кажется, они думают, что это вещи, которые могут понять только самые умные люди.
Но нет ничего более далекого от истины.
Правда, эти предметные области могут быть не самыми простыми, с которыми вам когда-либо приходилось сталкиваться, но они далеко не невозможные. Так. Если вы хотите стать физиком или математиком или просто хотите разбираться в предметах, вот с чего начать.
Огромное спасибо замечательному Мойнаку Банерджи за его работу над этим.
Физика
- Вот совет профессора Джона Баэза о том, как изучать физику и математику. Он упоминает книги, которые вы должны прочитать, и они удобно перечислены в соответствии с возрастающими уровнями сложности.
- Это список книг, которые Беркли рекомендует людям, которые хотят изучать физику.
- И еще один неплохой список, составленный на Physics Stack Exchange.
- Лауреат Нобелевской премии профессор Джерард ‘т Хофт порекомендовал несколько бесплатных источников обучения, а также дал советы, как получить собственную Нобелевскую премию.
- Вот отличный совет от физика на форумах по физике относительно того, что вам следует делать, если вы хотите делать больше, чем просто изучать физику, — что делать, если вы действительно хотите построить карьеру в области физики.
