Физика внутренняя энергия формула: Формула внутренней энергии

Внутренняя энергия тела | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Любое макроскопическое тело имеет энер­гию, обусловленную его микросостоянием. Эта энергия называется внутренней (обо­значается U). Она равняется энергии дви­жения и взаимодействия микрочастиц, из которых состоит тело. Так, внутренняя энер­гия идеального газа состоит из кинетической энергии всех его молекул, поскольку их вза­имодействием в данном случае можно пре­небречь. Поэтому его внутренняя энергия за­висит лишь от температуры газа (U ~ T).

Модель идеального газа пре­дусматривает, что молекулы на­ходятся на расстоянии несколь­ких диаметров друг от друга. Поэтому энергия их взаимо­действия намного меньше энер­гии движения и ее можно не учитывать.

У реальных газов, жидкостей и твердых тел взаимодействием микрочастиц (атомов, молекул, ионов и т.

п.) пренебречь нельзя, поскольку оно существенно влияет на их свойства. Поэтому их внутренняя энергия состоит из кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия. Их внутренняя энергия, кроме температуры T, будет за­висеть также от объема V, поскольку изме­нение объема влияет на расстояние между атомами и молекулами, а, следовательно, и на потенциальную энергию их взаимодей­ствия между собой.

Внутренняя энергия — это функция состояния тела, которая опреде­ляется его температурой T и объемом V.

Внутренняя энергия однознач­но определяется температурой

T и объемом тела V, характе­ризующими его состояние: U = U(T, V)

Чтобы изменить внутреннюю энергию те­ла, нужно фактически изменить или кинетическую энергию теплового движения мик­рочастиц, или потенциальную энергию их взаимодействия (или и ту и другую вместе). Как известно, это можно сделать двумя способами — путем теплообмена или вслед­ствие выполнения работы. В первом случае это происходит за счет передачи опреде­ленного количества теплоты Q; во втором — вследствие выполнения работы A.

Таким образом, количество теплоты и выполненная работа являются мерой изме­нения внутренней энергии тела:

ΔU = Q + A.

Изменение внутренней энер­гии происходит за счет отдан­ного или полученного телом не­которого количества теплоты или вследствие выполнения ра­боты.

Если имеет место лишь теплообмен, то изменение внутренней энергии происходит путем получения или отдачи определенного количества теплоты: ΔU = Q. При нагрева­нии или охлаждении тела оно равно:

ΔU = Q = cm(T₂ — Т₁) = cmΔT.

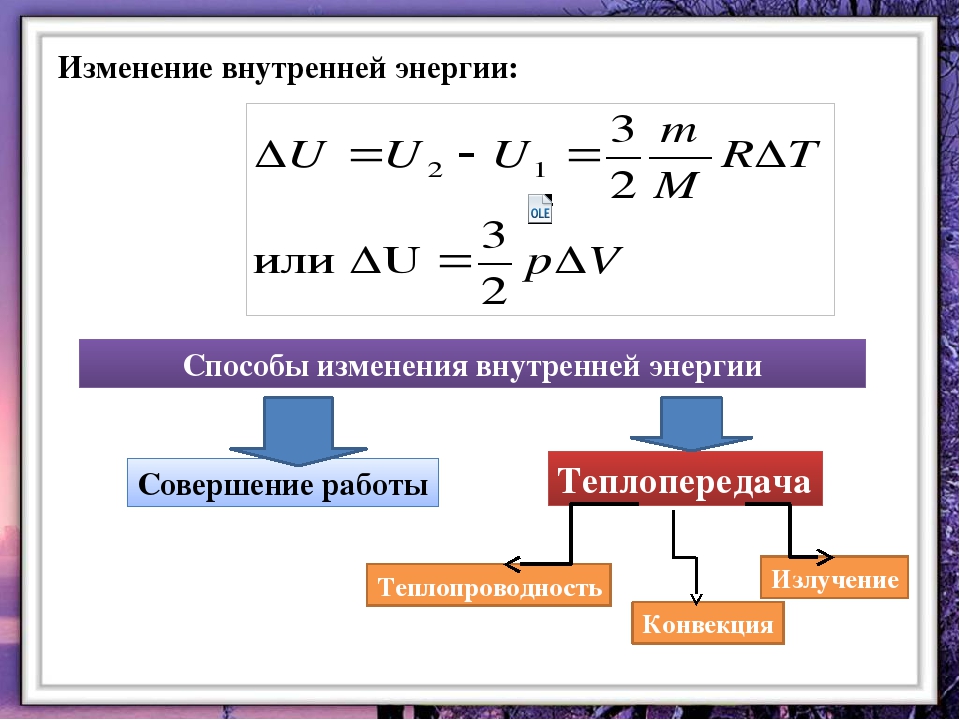
При плавлении или кристаллизации твер­дых тел внутренняя энергия изменяется за счет изменения потенциальной энергии вза­имодействия микрочастиц, ведь происходят структурные изменения строения вещества. В данном случае изменение внутренней энер­гии равняется теплоте плавления (кристал­лизации) тела: ΔU — Q_пл = λm, где λ — удель­ная теплота плавления (кристаллизации) твер­дого тела.

Испарение жидкостей или конденсация пара также вызывает изменение

внутренней энергии, которая равна теплоте парообра­зования: ΔU = Q_п = rm, где r — удельная теп­лота парообразования (конденсации) жидко­сти.

Изменение внутренней энергии тела вслед­ствие выполнения механической работы (без теплообмена) численно равно значению этой работы: ΔU = A.

Если изменение внутренней энергии происходит вследст­вие теплообмена, то ΔU = Q = cm(T₂ — T₁), или ΔU = Q_пл =

λm, или ΔU = Q_п = rm.

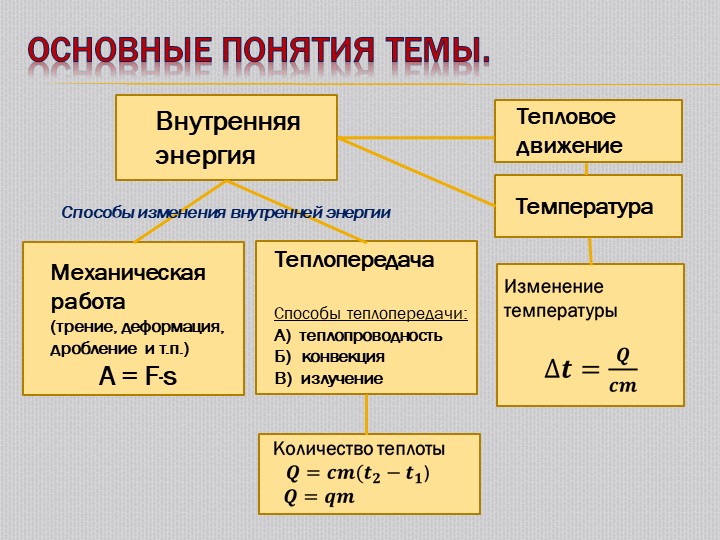
Следовательно, с точки зрения моле­кулярной физики: Материал с сайта http://worldofschool.ru

Внутренняя энергия тела является суммой кинетической энергии теп­лового движения атомов, молекул или других частиц, из которых оно состоит, и потен­циальной энергии взаимодействия между ни­ми; с термодинамической точки зрения она является функцией состояния тела (системы тел), которая однозначно определяется его макропараметрами — температурой T и объе­мом V.

Таким образом, внутренняя энергия — это энергия системы, которая зависит от ее внутреннего состояния. Она состоит из энергии теплового движения всех микро­частиц системы (молекул, атомов, ионов, электронов и т. п.) и энергии их взаи­модействия. Полное значение внутренней энергии определить практически невоз­можно, поэтому вычисляют изменение внут­ренней энергии ΔU, которое происходит вследствие теплопередачи и выполнения ра­боты.

Внутренняя энергия тела равна сумме кинетической энергии теплового движения и потен­циальной энергии взаимодей­ствия составляющих его мик­рочастиц.

На этой странице материал по темам:

• От каких макропараметров зависит внутренняя энергия тела

• Как обозначается измерение внутрений энергии

• Внутренняя энергия твёрдого тела

• Определения теплового движения и внутренней энергии

• Доклад по физике на тему внутренняя энергия

Вопросы по этому материалу:

• От каких макропараметров системы зависит внутренняя энер­гия идеального газа?

• Какие макропараметры вообще определяют внутреннюю энер­гию тела?

• Чему равно изменение внутренней энергии, если происходит лишь теплообмен?

• Каким образом выполненная механическая работа влияет на внутреннюю энергию тела?

• Какое толкование дают внутренней энергии молекулярно-ки­нетическая теория и термодинамика?

Внутренняя энергия.

Количество теплоты. Работа в термодинамике Определение 1

Термодинамика – раздел физики, изучающий превращения энергии в макроскопических системах и основные свойства этих систем.

Термодинамика опирается на общие закономерности тепловых процессов и свойств макроскопических систем. Выводы термодинамики эмпирические, то есть опираются на факты, проверенные опытным путем с использованием молекулярно-кинетической модели.

Для описания термодинамических процессов в системах, состоящих из большого числа частиц, используются величины, не применимые к отдельным молекулам и атомам: температура, давление, концентрация, объем, энтропия)

Определение 2

Термодинамическое равновесие – состояние макросопической системы, когда описывающие ее макроскопические величины остаются неизменными.

В термодинамике рассматриваются изолированные системы тел, находящиеся в термодинамическом равновесии.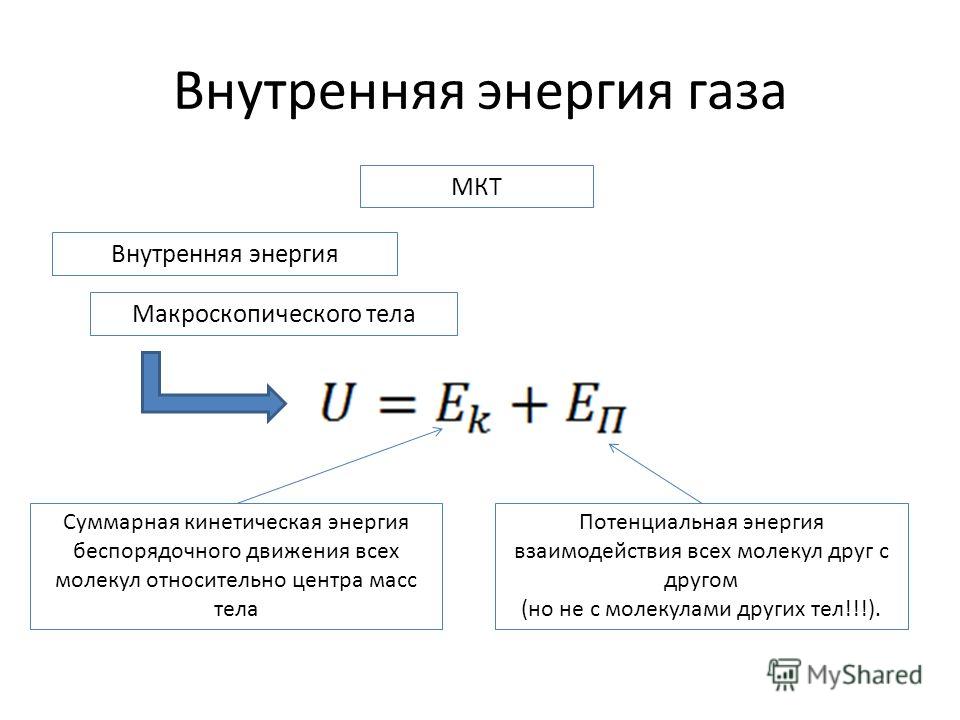

То есть в системах с прекращением всех наблюдаемых макроскопических процессов. Особую важность представляет свойство, которое получило название выравнивания температуры всех ее частей.

При внешнем воздействии на термодинамическую систему наблюдается переход в другое равновесное состояние. Он получил название термодинамического процесса. Когда время его протекания достаточно медленное, система приближена к состоянию равновесия. Процессы, состоящие из последовательности равновесных состояний, называют квазистатическими.

Внутренняя энергия. Формулы

Внутренняя энергия считается важнейшим понятием термодинамики. Макроскопические тела (системы) имеют внутреннюю энергию, состящую из энергии каждой молекулы. Исходя из молекулярно-кинетической теории, внутренняя энергия состоит из кинетической энергии атомов и молекул, а также потенциальной энергии их взаимодействия.

Например, внутренняя энергия идеального газа равняется сумме кинетических энергий частиц газа, которые находятся в непрерывном беспорядочном тепловом движении. После подтверждений большим количеством экспериментов, был получен закон Джоуля:

Определение 3

Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема.

Применение молекулярно-кинетической теории говорит о том, что выражение для определения внутренней энергии 1 моля одноатомного газа, с поступательными движениями молекул записывается как:

U=32NАkT=32RT.

Зависимость от расстояния между молекулами у потенциальной энергии очевидна, поэтому внутренняя U и температура Т обусловлены изменениями V:

U=U(T, V).

Определение 4

Определение внутренней энергии U производится с помощью наличия макроскопических параметров, характеризующих состояние тела. Изменение внутренней энергии происходит по причине действия на тело внешних сил, совершающих работу. Внутренняя энергия является функцией состояния системы.

 

Пример 1

Когда газ в цилиндре сжимается под поршнем, то внешние силы совершают положительную работу A’.

Силы давления газа на поршень также совершают работу, но равную A=-A’. При изменении объема газа на величину ∆V, говорят, что он совершает работу pS∆x=p∆V, где p – давление газа, S – площадь поршня, ∆x – его перемещение. Подробно показано в примере на рисунке 1.

Наличие знака перед работой говорит о работе газа в разных состояниях: положительная при расширении и отрицательная при сжатии. Переход из начального в конечное состояние работы газа может быть описан с помощью формулы:

A=∑pidVi или в пределе при ∆Vi→0:

A=∫V1V2pdV.

Рисунок 1. Работа газа при расширении.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Обратимые и необратимые процессы

Работа численно равняется площади процесса, изображенного на диаграмме p, V. Величина А зависит от метода перехода от начального состояния в конечное. Рисунок 2 показывает 3 процесса, которые переводят газ из состояние (1) в состояние (2). Во всех случаях газ совершает работу.

Рисунок 2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.

Процессы из рисунка 2 возможно провести в обратном направлении. Тогда произойдет изменение знака А на противоположный.

Определение 5

Процессы, которые возможно проводить в обоих направлениях, получили название обратимых.

Жидкости и твердые тела могут незначительно изменять свой объем, поэтому при совершении работы разрешено им пренебречь. Но их внутренняя энергия подвергается изменениям посредствам совершения работы.

Пример 2

Механическая обработка деталей нагревает их. Это способствует изменению внутренней энергии. Имеется еще один пример опыта Джоуля 1843 года, служащий для определения механического эквивалента теплоты, изображенного на рисунке 3. Во время вращения катушки, находящейся в воде, внешние силы совершают положительную работу A’>0, тогда жидкость повышает температуру из-за наличия силы трения, то есть происходит увеличение внутренней энергии.

Определение 6

Процессы примеров не могут проводиться в противоположных направлениях, поэтому они получили название необратимых.

Рисунок 3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты.

Изменение внутренней энергии возможно при наличии совершаемой работы и при теплообмене. Тепловой контакт тел позволяет увеличиваться энергии одного тела с уменьшением энергии другого. Иначе это называется тепловым потоком.

Количество теплоты

Определение 7

Количество теплоты Q, полученное телом, называется его внутренней энергией, получаемой в результате теплообмена.

Рисунок 4. Модель работы газа.

Процесс передачи тепла тел возможен только при разности их температур.

Направление теплового потока всегда идет к холодному телу.

Количество теплоты Q считается энергетической величиной и измеряется в джоулях (Дж).

4.

2 Внутренняя энергия

Внутренняя энергия есть сумма всех видов энергии движения и взаимодействия частиц, составляющих рассматриваемое тело, вычисленная в системе координат, в которой центр масс тела неподвижен. Поэтому внутренняя энергия не содержит кинетическую энергию движения тела как целого и ее потенциальную энергию во внешнем поле сил. Таким образом, внутренняя энергия складывается из кинетической энергии движения молекул, составляющих тело, кинетической энергии атомов внутри молекул, потенциальной энергии взаимодействия между молекулами, потенциальной энергии взаимодействия между атомами в молекуле, а также внутриатомной и внутриядерной энергии. (Последние две части внутренней энергии в курсах молекулярной физики не рассматриваются.)

Термодинамика не исследует внутреннее движение частиц и силы взаимодействия между ними, поэтому в рамках этой науки невозможно получить математическое выражение для вычисления внутренней энергии термодинамической системы. Это выражение находят из специальных опытов или из статистической теории.

Наиболее просто получить выражение для вычисления внутренней энергии идеального газа. Так как молекулы идеального газа не взаимодействуют между собой, то его внутренняя энергия U равна

(4.2.1)

где N – число молекул в газе, а средняя энергия , приходящаяся на одну молекулу, согласно теореме распределения, равна

(4.2.2)

где i – число степеней свободы молекулы. Подставляя последнее выражение в (4.2.1), получим

(4.2.3)

Умножив и разделив правую часть формулы (4.2.3) на число Авогадро , получим

(4. 2.4)

Учитывая, что , соотношение (4.2.4) можно представить в виде:

(4.2.5)

Как видно из формулы (4.2.4), внутренняя энергия идеального газа зависит от его температуры T, количества молей и от сложности строения молекулы, характеризуемой ее числом степеней свободы i.

Внутренняя энергия должна являться функцией равновесного состояния системы, т. е. функция U должна однозначно определяться термодинамическими параметрами, характеризующими это состояние. Если бы это было не так, и в некотором состоянии система частиц могла обладать разными значениями внутренней энергии, т. е. последняя не была бы однозначной функцией состояния, то разность этих значений внутренней энергии можно было бы превратить в работу, не изменяя состояния тела, что противоречит закону сохранения энергии. При отсутствии внешних воздействий на однокомпонентное (чистое) вещество, любая величина, являющаяся функцией его состояния, однозначно определяется, если заданы два других параметра вещества в этом состоянии. Так, молярный объем вещества однозначно определен, если заданы давление Р и температура Т. (К примеру, для идеального газа из уравнения Менделеева –Клапейрона молярный объем и таким образом, однозначно определяется значениями Т и Р.) Аналогично внутренняя энергия как функция состояния является функцией любых двух параметров состояния из трех возможных Р, V, T : с одинаковым основанием можно записать или Однако в приложениях, как правило, используют функцию , т.к. она позволяет в ряде случаев разделить внутреннюю энергию на кинетическую энергию движения молекул, зависящую от температуры, и потенциальную энергию взаимодействия молекул, зависящую от объема.

Выясним, каким математическим свойством должна обладать внутренняя энергия, если она действительно является функцией состояния системы.

Для этого переведем систему из состояния 1, характеризующегося объемом и температурой , в состояние 2 с объемом и температурой . Обозначим внутреннюю энергию в состоянии 1 через , а в состоянии 2 – . Так как внутренняя энергия – функция состояния, то ее изменение при этом переходе:

(4.2.6)

С другой стороны, это изменение внутренней энергии может быть найдено суммированием бесконечно-малых изменений dU, т.е.

(4.2.7)

Из выражений (4.2.6–4.2.7) заключаем, что

(4.2.8)

Последнее соотношение полностью совпадает с основной формулой, интегрального исчисления, выражающей обыкновенный определенный интеграл через первообразную. Откуда следует, что бесконечно-малая величина dU является точным (полным) дифференциалом:

(4. 2.9)

Если выражение (4.2.8) проинтегрировать по замкнутому контуру, то в результате получим нуль:

(4.2.10)

так как при круговом процессе система возвращается к исходному состоянию и внутренняя энергия как функция состояния принимает свое начальное значение.

Нетрудно показать, что равенство (4.2.10) эквивалентно утверждению: изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 не зависит от пути перехода, а определяется только коо-рдинатами T,V начальной 1 и конечной 2 точек. В самом деле (рис. 1),

Из последнего равенства находим

(4.2.11)

т. е. разность действительно не зависит от пути перехода из 1 в 2.

рис. 1

Таким образом, следствием того, что внутренняя энергия является однозначной функцией состояния системы, служат соотношения (4.2.10–4.2.11), в которых подинтегральная функция – полный дифференциал.

В общем случае, чтобы установить, является ли произвольная функция функцией состояния системы, используется следующая теорема из математического анализа: если значение криволинейного интеграла не зависит от пути интегрирования, а определяется только начальной и конечной точками интегрирования, то подинтегральное выражение представляет собой полный дифференциал некоторой функции, которую называют функцией состояния системы. Таким образом, функция состо-яния не зависит от того процесса (пути), который к этому состоянию привел систему, а определяется только параметрами, характеризующими это состояние.

Следует обратить внимание, что внутренняя энергия как функция параметров состояния системы имеет смысл только для равновесных состояний, когда эти параметры имеют постоянные значения по всему объему системы. При неравновесных состояниях постоянные параметры, характеризующие эти состояния системы, не существуют.

Работа, внутренняя энергия термодинамической системы, газа. Графическое определение

Тестирование онлайн

• Внутренняя энергия, работа. Основные понятия

• Работа, внутреннняя энергия

Работа

В термодинамике работа – это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы

Рассмотрим цилиндр с идеальным газом, который находится под подвижным поршнем. Пусть внешняя сила, действующая на поршень, перемещает его из состояния 1 в состояние 2

Работа силы равна . Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня . Подставив вторую формулу в первую, получим .

Знак “-” в формуле означает, что при уменьшении объема (как в нашем примере, ) работа внешних сил положительная. И наоборот, когда газ расширяется, работа внешней силы, удерживающей поршень, отрицательная.

Графическое определение работы

Строим график процесса p(V). Определяем на графике точки, которые соответствуют состоянию системы в 1 и 2 состояниях. Площадь фигуры под графиком – есть термодинамическая работа самой системы. Внешняя работа над системой равна работе системы, но с противоположным знаком

Работа термодинамической системы при изобарном процессе

Работа термодинамической системы при изотермическом процессе

При изохорном процессе объем не изменяется, работа равна нулю A=0.

Внутренняя энергия

Любое тело (газ, жидкость или твердое) обладает энергией, даже если кинетическая и потенциальные энергии самого тела нулевые. То есть тело не имеет скорости и находится на Земле. Эта энергия называется внутренней, обусловлена она движением и взаимодействием частиц, из которых состоит тело.

Внутренняя энергия состоит из кинетической и потенциальной энергии частиц поступательного и колебательного движений, из энергии электронных оболочек атомов, из внутриядерной энергии и энергии электромагнитного излучения.

Внутренняя энергия зависит от температуры. Если изменяется температура, значит изменяется внутренняя энергия.

При изотермическом процессе зависимость p(V) не является линейной, поэтому площадь фигуры под графиком определяется интегрированием

Внутренняя энергия. – Физика за 8 класс. Учебник.

Опре­де­ле­ние.Ки­не­ти­че­ская энер­гия – часть ме­ха­ни­че­ской энер­гии, ко­то­рая опре­де­ля­ет дви­же­ние тела.

Опре­де­ле­ние.По­тен­ци­аль­ная энер­гия – энер­гия, ко­то­рую имеют тела или части од­но­го тела из-за того, что вза­и­мо­дей­ству­ют с дру­ги­ми те­ла­ми (или ча­стя­ми тел).

Обо­зна­че­ния в при­ве­ден­ных фор­му­лах:

 – уско­ре­ние сво­бод­но­го па­де­ния, Н/кг (м/с2),

 – рас­тя­же­ние пру­жи­ны, м.

Вер­нем­ся к во­про­су о том, во что пре­вра­ща­ет­ся ки­не­ти­че­ская энер­гия тела сразу после па­де­ния на по­верх­ность. Она пре­вра­ща­ет­ся во внут­рен­нюю энер­гию, что и яв­ля­ет­ся ос­нов­ным объ­ек­том изу­че­ния дан­но­го урока.

Чтобы по­нять, что такое внут­рен­няя энер­гия, сле­ду­ет об­ра­тить вни­ма­ние на мик­ро­мир ча­стиц ве­ще­ства (атомы и мо­ле­ку­лы) и вспом­нить, что они на­хо­дят­ся в непре­рыв­ном дви­же­нии, это уже под­ска­зы­ва­ет о на­ли­чии у них ки­не­ти­че­ской энер­гии, кроме того, ча­сти­цы вза­и­мо­дей­ству­ют друг с дру­гом, что при­во­дит к воз­ник­но­ве­нию у них по­тен­ци­аль­ной энер­гии.

Опре­де­ле­ние.Ки­не­ти­че­ская энер­гия дви­же­ния ча­стиц и по­тен­ци­аль­ная энер­гия их вза­и­мо­дей­ствия со­став­ля­ют внут­рен­нюю энер­гию тела. Внут­рен­нюю энер­гию обо­зна­ча­ют  и из­ме­ря­ет­ся она, как и все дру­гие виды энер­гии, в Дж (джо­у­лях).

Сле­до­ва­тель­но, имеем фор­му­лу для внут­рен­ней энер­гии тела: . Где под  по­ни­ма­ет­ся ки­не­ти­че­ская энер­гия ча­стиц тела, а под  – их по­тен­ци­аль­ная энер­гия.

Вспом­ним преды­ду­щий урок, на нем мы го­во­ри­ли о том, что дви­же­ние ча­стиц тела ха­рак­те­ри­зу­ет его тем­пе­ра­ту­ра, с дру­гой сто­ро­ны, внут­рен­няя энер­гия тела свя­за­на с ха­рак­те­ром (ак­тив­но­стью) дви­же­ния ча­стиц. Сле­до­ва­тель­но, внут­рен­няя энер­гия и тем­пе­ра­ту­ра – вза­и­мо­свя­зан­ные по­ня­тия. При по­вы­ше­нии тем­пе­ра­ту­ры тела его внут­рен­няя энер­гия тоже по­вы­ша­ет­ся, при по­ни­же­нии – умень­ша­ет­ся.

Вза­и­мо­связь между внут­рен­ней энер­ги­ей и раз­лич­ны­ми ви­да­ми про­цес­сов можно изоб­ра­зить на схеме: 

Если срав­ни­вать внут­рен­нюю энер­гию с дру­ги­ми ви­да­ми энер­гий, то она как по­ня­тие су­ще­ству­ет от­дель­но и имеет осо­бое свой­ство: любое тело при любых усло­ви­ях все­гда имеет некий запас внут­рен­ней энер­гии.

На сле­ду­ю­щем уроке мы по­го­во­рим о том, какие су­ще­ству­ют спо­со­бы из­ме­не­ния внут­рен­ней энер­гии, и по­зна­ко­мим­ся с по­ня­ти­ем теплообмен. 

http://interneturok.ru/physics/8-klass/teplovye-yavleniya/vnutrennyaya-energiya?seconds=0

Вопросы: 

 1. Какие превращения энергии происходят при подъеме шара и при его падании?

2. Как изменяется состояние свинцового шара и свинцовой плиты в результате их соударения?

3. Какую энергию называют внутренней энергией тела?

 4. Зависит ли внутренняя энергия тела от его движения и положения относительно других тел?

Ответы:

1. При подъеме растет потенциальная энергия, при падении потенциальная падает, кинетическая растет
2. В результате удара шара о плиту происходит превращение механической энергии, которой обладал в начале опыта шар, во внутреннюю энергию тела
3. Внутренняя энергия – это которая содержится в атомах и молекулах в виде механической энергии движения и соударения молекул (зависит от температуры) , в виде химической энергии электронов в атомах и в виде ядерной энегии  протонов и нейтронов в ядрах атомов. 
4. Внутренняя энергия тела (обозначается как E или U) — это сумма энергетических  молекулярных взаимодействий и тепловых движений молекул. Внутренняя энергия является однозначной функцией состояния системы, поэтому она не зависит от движения и положения относительно других тел. Другими словами, внутренняя энергия раскалённого ядра не зависит от того летит ядро или уже упало.

http://znanija.com/task/19391260

Примеры решения задач по теме «Внутренняя энергия. Работа»

Примеры решения задач по теме «Внутренняя энергия. Работа»

Подробности

Просмотров: 803

«Физика – 10 класс»

Для решения задач нужно уметь вычислять внутреннюю энергию и работу, пользуясь формулами (13.1) и (13.4). Надо ещё иметь в виду, что величины A, Q, ΔU могут быть как положительными, так и отрицательными.

Задача 1.

Аэростат объёмом V = 500 м³ наполнен гелием под давлением р = 10⁵ Па. В результате солнечного нагрева температура газа в аэростате поднялась от t₁ = 10 °С до t₂ = 25 °С. На сколько увеличилась внутренняя энергия газа?

Р е ш е н и е.

Гелий является одноатомным газом, поэтому его внутренняя энергия определяется формулой (13.1). При температуре Т₁ эта энергия равна а при температуре Т₂ равна Изменение энергии равно:

Масса гелия неизвестна, но её можно выразить с помощью уравнения Менделеева—Клапейрона через начальную температуру, давление и объём газа: Подставляя значение в уравнение для изменения энергии, получаем

Задача 2.

В цилиндре под тяжёлым поршнем находится углекислый газ (М = 0,044 кг/моль) массой m = 0,20 кг. Газ нагревается на ΔТ = 88 К. Какую работу он при этом совершает?

Р е ш е н и е.

Газ расширяется при некотором постоянном давлении р, которое создаётся атмосферой и поршнем. В этом случае работа газа А’ = p(V₂ – V₁), где V₁ и V₂ — начальный и конечный объёмы газа. Используя уравнение Менделеева—Клапейрона, выразим произведения pV₂ и pV₁ через Тогда

Задача 3.

Чему равна работа, совершённая газом в количестве 3 моль при сжатии, если температура увеличилась на 100 К? Потери тепла не учитывайте.

Р е ш е н и е.

При сжатии внешняя сила совершает положительную работу, за счёт которой происходит изменение внутренней энергии и соответственно температуры газа, т. е. А = ΔU. Изменение внутренней энергии

Работа, совершённая силой давления газа:

Задача 4.

На рисунке 13.4 показана зависимость давления газа от объёма при его переходе из состояния 1 в состояние 4.

Определите работу газа.

Р е ш е н и е.

Работа газа численно равна площади заштрихованной фигуры. Процессы 1—2 и 3—4 изобарные, поэтому работа газа в этих процессах

А’_{1 – 2} = p₁(V₂ – V₁),     А’_3-4 = p₂(V₄ – V₃).

В процессе 2—3 изменяются все три параметра газа. Работа газа в этом процессе

Таким образом, учтя, что V₂ — V₁ = V₃ — V₂ = V₄ — V₃ = ΔV, получим

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основы термодинамики. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика

Насыщенный пар — Давление насыщенного пара — Влажность воздуха — Примеры решения задач по теме «Насыщенный пар. Влажность воздуха» — Кристаллические тела — Аморфные тела — Внутренняя энергия — Работа в термодинамике — Примеры решения задач по теме «Внутренняя энергия. Работа» — Количество теплоты. Уравнение теплового баланса — Примеры решения задач по теме: «Количество теплоты. Уравнение теплового баланса» — Первый закон термодинамики — Применение первого закона термодинамики к различным процессам — Примеры решения задач по теме: «Первый закон термодинамики» — Второй закон термодинамики — Статистический характер второго закона термодинамики — Принцип действия тепловых двигателей. Коэффициент полезного действия (КПД) тепловых двигателей — Примеры решения задач по теме: «КПД тепловых двигателей»

Богданов К.Ю. – учебник по физике для 10 класса

§ 28. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕЛА. ФОРМУЛА ДЛЯ ВНУТРЕННЕЙ ЭНЕРГИИ ИДЕАЛЬНОГО ГАЗА.

Внутренней энергией тела называют сумму кинетической энергии теплового движения его атомов и молекул и потенциальной энергии их взаимодействия между собой.

Во многих случаях механическая энергия тела, являющаяся суммой его кинетической и потенциальной энергии (см. §17), изменяется. Например, мяч, катящийся по полю, замедляется, а сосулька, упавшая с крыши, разбивается о землю и превращается в несколько неподвижных осколков. Когда мяч катится по полю, он преодолевает силу трения, совершая работу, в результате чего его кинетическая энергия уменьшается на величину совершённой работы, а вместе с ней – и скорость. Работа против силы трения приводит к различным деформациям вдоль траектории мяча, его нагреву, а также к нагреву всего того, чего он касался при движении. Механическая энергия ударившейся о землю сосульки частично расходуется на работу, необходимую для того, чтобы расколоть ее на куски,  а остальная часть энергии тратится на деформацию этих осколков и участка земли, на который они упали. Ну, а если эти осколки скользили по земле прежде, чем остановиться, то часть механической энергии превратилась и в тепло.

Так как энергия не может исчезать или возникать из неоткуда, то уменьшение механической энергии движущегося мяча и падающей сосульки означает, что механическая энергия переходит в какой-то другой вид энергии, зависящий от внутреннего состояния тела – его температуры, энергии связи между его частями и т.п. Этот вид энергии тела называют его внутренней энергией.

Внутренняя энергия тела увеличивается при нагреве, так как с ростом температуры кинетическая энергия молекул тоже растёт. Вторым слагаемым внутренней энергии является потенциальная энергия связей между частицами тела, т.к. эти частицы притягиваются друг к другу, чем и обеспечивается его целостность (рис. 28). Поэтому, внутреннюю энергию тела можно изменить, если сжать, растянуть или даже раздробить его, совершая, таким образом, работу над телом.

Однако внутренняя энергия тела зависит не только от его температуры, действующих на него сил и степени раздробленности. При плавлении, затвердевании, конденсации и испарении, т.е. при изменении агрегатного состояния тела, потенциальная энергия связи между его атомами и молекулами тоже изменяется, а значит, изменяется и его внутренняя энергия. Кроме того, внутренняя энергия может изменяться, когда вещество, из которого состоит тело, вступает в химическую (или ядерную) реакцию, в результате чего химическая структура вещества (или структура атомного ядра) изменяется и его внутренняя энергия – тоже.

Очевидно, что внутренняя энергия тела должна быть пропорциональна его объёму и равна сумме кинетической и потенциальной энергии всех молекул и атомов, из которых состоит это тело. К сожалению, для большинства веществ величины кинетической и потенциальной энергии молекул неизвестны, и поэтому вычислить значение внутренней энергии соответствующих тел не представляется возможным. В то же время, идеальный газ устроен очень просто и состоит из молекул, не взаимодействующих между собой, а значит, потенциальная энергия из взаимодействия равна нулю. Поэтому внутренняя энергия идеального газа равна кинетической энергии теплового движения его атомов или молекул и может быть вычислена довольно просто следующим образом.

Пусть газ одноатомный, т.е. состоит из отдельных атомов, а не молекул, например, любой из инертных газов. Тогда кинетическая энергия атомов этого газа равна кинетической энергии их поступательного движения, так как вращательное отсутствует. Поэтому для вычисления внутренней энергии, U одноатомного газа массы m необходимо умножить среднюю кинетическую энергию, Е_СР его атома (см. 23.6) на общее количество, N атомов в газе (см. 19.1 и 19.2):

Как следует из (28.1), внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре и не зависит от других макроскопических параметров газа – его давления и объёма. Таким образом, сжимая газ в изотермических условиях, мы не изменяем его внутренней энергии.       

Вопросы для повторения:

·        Дайте определение внутренней энергии тела?

·        Как внутренняя энергия зависит от агрегатного состояния и температуры?

·        Как зависит внутренняя энергия идеального газа от его температуры, давления и объёма.

Рис. 28. Схематическое изображение внутренней энергии воды в стакане, состоящей из кинетической энергии движения её молекул (верх) и потенциальной энергии из взаимодействия (низ).

Формула внутренней энергии и примеры

Внутренняя энергия – это сумма всех форм молекулярных энергий (кинетической и потенциальной) вещества. В исследовании термодинамики обычно идеальный газ рассматривается как рабочее вещество. молекулы идеального газа – это просто материальные точки, которые не действуют друг на друга. таким образом, внутренняя энергия идеальной газовой системы – это, как правило, поступательная кинетическая энергия ее молекул.
, поскольку температура системы определяется как средняя кинетическая энергия ее молекул, таким образом, для идеальной газовой системы внутренняя энергия прямо пропорциональна ее температуре .

, когда мы нагреваем вещество , энергия , связанная с его атомами, или молекул, увеличивается, т.е. тепла преобразуется в внутренней энергии .

См. Также: Разница между теплом и температурой

Важно отметить, что энергия может быть добавлена ​​к системе, даже если теплообмен не происходит. например, когда два предмета трутся друг о друга, их внутренняя энергия увеличивается из-за механической работы.Повышение температуры объекта является показателем увеличения внутренней энергии. аналогично, когда объект скользит по любой поверхности и останавливается из-за силы трения , механическая работа, выполняемая системой или системой, частично преобразуется во внутреннюю энергию .

В термодинамике внутренняя энергия является функцией состояния. следовательно, он не зависит от пути, а зависит от начального и конечного состояний системы.Рассмотрим систему, которая претерпевает изменение давления и объема с Па и Va на Pb и Vb соответственно, независимо от процесса, посредством которого система переходит из начального в конечное состояние. экспериментально было видно, что изменение внутренней энергии всегда одинаково и не зависит от путей C1 и C2.

Таким образом, внутренняя энергия подобна гравитационной потенциальной энергии. поэтому, как и потенциальная энергия, важно изменение внутренней энергии, а не ее абсолютное значение.

Изменение внутренней энергии

Внутренняя энергия систем частиц может изменяться независимо от их пространственного положения или приобретаемой формы (в случае жидкостей и газов). Например, при подаче тепла в замкнутую систему частиц добавляется тепловая энергия, которая влияет на внутреннюю энергию сборки.
Однако внутренняя энергия является функцией состояния , то есть она не учитывает вариацию, которая связывает два состояния материи, а ее начальное и конечное состояние.Вот почему расчет изменения внутренней энергии в данном цикле всегда будет нулевым. , поскольку начальное и конечное состояния – одно и то же.
Формулировки для расчета этого изменения:
ΔU = U _B – U _A , где система перешла из состояния A в состояние B.
ΔU = -W, в случаях, когда количество механической работы W равно осуществляется, что приводит к расширению системы и уменьшению ее внутренней энергии.
ΔU = Q, в случаях, когда мы добавляем калорийную энергию, которая увеличивает внутреннюю энергию.
ΔU = 0, в случае циклических изменений внутренней энергии.
Все эти и другие случаи можно суммировать в уравнении, описывающем принцип сохранения энергии в системе:
ΔU = Q + W

Примеры внутренней энергии в повседневной жизни?

Вот список некоторых примеров внутренней энергии:

• Аккумуляторы . В теле заряженных аккумуляторов используется внутренняя энергия благодаря химическим реакциям между кислотами и тяжелыми металлами внутри.Указанная внутренняя энергия будет больше, когда ее электрический заряд будет завершен, и меньше, когда она будет израсходована, хотя в случае перезаряжаемых батарей эта энергия может снова увеличиться за счет подачи электричества из розеток.
• Сжатые газы . Учитывая, что газы имеют тенденцию занимать весь объем контейнера, в котором они содержатся, поскольку их внутренняя энергия будет изменяться по мере увеличения этого объема и увеличиваться, когда оно меньше. Таким образом, газ, рассеянный в комнате, имеет меньшую внутреннюю энергию, чем если бы мы сжимали его в цилиндр, поскольку его частицы будут вынуждены более тесно взаимодействовать.
• Повышение температуры материи. Если мы увеличим температуру, например, одного грамма воды и одного грамма меди, при базовой температуре 0 ° C, мы заметим, что, несмотря на то же количество вещества, для льда потребуется большее количество общая энергия для достижения желаемой температуры. Это связано с тем, что его удельная теплоемкость больше, то есть его частицы менее восприимчивы к введенной энергии, чем частицы меди, и гораздо медленнее добавляют тепло к его внутренней энергии.
• Взбить жидкость . Когда мы растворяем сахар или соль в воде или продвигаем аналогичные смеси, мы обычно перемешиваем жидкость с помощью инструмента, чтобы способствовать дальнейшему растворению. Это происходит из-за увеличения внутренней энергии системы, производимой за счет того количества работы (W), которое обеспечивается нашим действием, что обеспечивает большую химическую реактивность между участвующими частицами.
• Вода пар . При кипячении воды мы заметим, что у пара более высокая внутренняя энергия, чем у жидкой воды в емкости.Это связано с тем, что, несмотря на то, что молекулы остаются теми же (состав не изменился), чтобы вызвать физическое преобразование, мы добавили в воду определенное количество калорийной энергии (Q), вызвав большее перемешивание ее частиц.

Предлагаемое видео:


Связанные темы:

12.2 Первый закон термодинамики: тепловая энергия и работа

Биология: биологическая термодинамика

Мы часто думаем о термодинамике, как о полезной для изобретения или тестирования оборудования, такого как двигатели или паровые турбины.Однако термодинамика также применима к живым системам, таким как наши собственные тела. Это составляет основу биологической термодинамики (рис. 12.7).

Рис. 12.7 (а) Первый закон термодинамики применим к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, тогда как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую организмом.) (Б) Растения преобразуют часть лучистой энергии солнечного света в запасенную химическую энергию, процесс, называемый фотосинтез .

Сама жизнь зависит от биологической передачи энергии. Посредством фотосинтеза растения поглощают солнечную энергию и используют эту энергию для преобразования углекислого газа и воды в глюкозу и кислород. Фотосинтез принимает одну форму энергии – свет – и преобразует ее в другую форму – химическую потенциальную энергию (глюкозу и другие углеводы).

Метаболизм человека – это преобразование пищи в энергию, выделяемую теплом, работой, выполняемой клетками тела, и накопленным жиром.Метаболизм – интересный пример действия первого закона термодинамики. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии; это неромантичный взгляд на хороший буррито.

Организм усваивает всю пищу, которую мы потребляем. По сути, метаболизм – это процесс окисления, в котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы. Упражнения помогают вам похудеть, поскольку они обеспечивают передачу энергии от вашего тела как за счет тепла, так и за счет работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.

Биологическая термодинамика также включает изучение трансдукции между клетками и живыми организмами. Трансдукция – это процесс, при котором генетический материал – ДНК – передается от одной клетки к другой. Это часто происходит во время вирусной инфекции (например, гриппа), и именно так вирус распространяется, а именно путем передачи своего генетического материала все большему количеству ранее здоровых клеток. Как только достаточное количество клеток заражается, вы начинаете ощущать воздействие вируса (симптомы гриппа – мышечная слабость, кашель и заложенность носа).

Энергия передается вместе с генетическим материалом и, таким образом, подчиняется первому закону термодинамики. Энергия передается – а не создается и не уничтожается – в процессе. Когда с элементом выполняется работа или тепло передает энергию ячейке, внутренняя энергия ячейки увеличивается. Когда клетка работает или теряет тепло, ее внутренняя энергия уменьшается. Если количество работы, выполняемой ячейкой, такое же, как количество энергии, передаваемой теплом, или количество работы, выполняемой ячейкой, совпадает с количеством энергии, передаваемой теплом, чистого изменения внутренней энергии не будет. .

Проверка захвата

Исходя из того, что вы знаете о теплопередаче и о первом законе термодинамики, нужно ли вам есть больше или меньше, чтобы поддерживать постоянный вес в холодную погоду? Объяснить, почему.

еще
1. ; поскольку в холодную погоду организм теряет больше энергии, потребность в еде увеличивается, чтобы поддерживать постоянный вес
Еще
2. ; употребление большего количества пищи означает накопление большего количества жира, что защитит организм от холодной погоды и уменьшит потерю энергии
На
3. меньше; поскольку в холодную погоду организм теряет меньше энергии, потребность в еде уменьшается, чтобы поддерживать постоянный вес
На
4. меньше; употребление меньшего количества пищи означает накопление меньшего количества жира, поэтому для сжигания жира потребуется меньше энергии, и в результате вес останется постоянным

Теплопередача: сохранение энергии

Поток жидкости, теплопередача и массоперенос Теплопередача: сохранение энергии

Уравнение энергии

Первый закон термодинамики определяет внутреннюю энергию, утверждая, что изменение внутренней энергии для замкнутой системы, Δ U , равно теплу, подводимому к системе, , за вычетом работы, выполненной системой, :

⁽¹⁾

Если системе разрешено движение, уравнение (1) может быть расширено, чтобы включить кинетическую энергию для системы:

⁽²⁾

Уравнение (2) может быть записано для бесконечно малого объема жидкости, и результат известен как уравнение сохранения полной внутренней энергии (см.1):

⁽³⁾

В этом уравнении:

Тензор полного напряжения обычно записывается как:

⁽⁴⁾

где – давление, а – тензор вязких напряжений.

Используя это определение , второй член в правой части уравнения (3), который представляет работу поверхностных сил, можно записать как

⁽⁵⁾

Первый член в правой части обычно обозначается как работа под давлением , а второй член известен как вязкая работа .Эти термины могут быть дополнительно разложены следующим образом:

⁽⁶⁾
Верхняя строка в уравнении (6) представляет обратимые эффекты; то есть они могут описывать работу, которая увеличивает внутреннюю энергию, и то, как внутренняя энергия может производить работу. В нижнем ряду описаны необратимые эффекты; то есть, как работа увеличивает внутреннюю энергию за счет так называемой вязкой диссипации и как вязкие эффекты уменьшают кинетическую энергию.

Уравнение (3) содержит уравнение сохранения кинетической энергии.Это уравнение можно получить, взяв скалярное произведение скорости на уравнение импульса. Некоторые алгебраические манипуляции дают: ⁽⁷⁾

Видно, что вся работа объемных сил в уравнении полной энергии (3) идет на изменение кинетической энергии. Остальная часть правой части уравнения (7) состоит из частей рабочего члена поверхностной силы, описанного в уравнении (6) как влияющего на кинетическую энергию. Вычитание уравнения (7) из уравнения (3) дает уравнение для внутренней энергии: ⁽⁸⁾

В случае наличия внутренних источников тепла, вызванных, например, реакциями или взаимодействием с излучением, добавляется дополнительный член внутреннего источника тепла,, и уравнение внутренней энергии принимает следующий вид:

⁽⁹⁾

Уравнение энтальпии

Внутренняя энергия – это термодинамическая переменная состояния, которая редко используется в практических приложениях.Более часто используемая величина – это энтальпия, , которая связана с внутренней энергией через:

⁽¹⁰⁾

Используя уравнение (10) в (9) и переставляя его, получаем уравнение энтальпии (ссылка 2):

⁽¹¹⁾

Уравнение (11) записано в так называемой консервативной форме. Это относится к тому, как левая часть записывается с плотностью и скоростью внутри оператора дивергенции. Так называемая неконсервативная форма уравнения энтальпии может быть получена с помощью уравнения неразрывности.Левая часть уравнения (11) может быть расширена следующим образом:

⁽¹²⁾

Первый член в правой части уравнения (12) – это уравнение неразрывности, умноженное на энтальпию, и поэтому оно тождественно равно нулю. Следовательно, уравнение (11) можно записать как:

⁽¹³⁾

Уравнение (13) по-прежнему описывает сохранение энтальпии, даже если форма уравнения обозначена как неконсервативная.

Уравнение температуры

Все инженеры знакомы с понятием температуры, поэтому сохранение энергии удобно выражать в терминах температуры.Энтальпия связана с температурой и давлением следующим дифференциальным соотношением:

⁽¹⁴⁾

где – теплоемкость при постоянном давлении, а β – коэффициент объемного расширения.

Уравнение (14) может использоваться для замены в уравнении (13). Повторное использование уравнения неразрывности дает уравнение температуры:

⁽¹⁵⁾

Последний шаг – определить вектор теплопроводности, используя закон теплопроводности Фурье, где – теплопроводность.Тогда уравнение температуры выглядит следующим образом:

⁽¹⁶⁾

Обратите внимание, что уравнение температуры нельзя преобразовать в консервативную форму без возврата к энтальпии или внутренней энергии.

Уравнение температуры – это еще один способ выразить сохранение энергии, которое математически эквивалентно уравнению (3). Однако различные уравнения сохранения не ведут себя эквивалентно при реализации с использованием численного метода. Многие коммерческие коды основаны на методе конечных объемов и решают уравнение переноса в консервативной форме для полной энтальпии.Таким образом, коммерческие коды достигают экономии общей энергии. Однако уравнение полной энтальпии подвержено числовым колебаниям, которые снижают числовую точность. Решение температурного уравнения намного надежнее и точнее. Метод конечных элементов позволяет решить температурное уравнение и при этом сохраняет полную энергию (ссылка 3).

Особые случаи энергосбережения

Для идеальных газов этот член равен единице, и (16) принимает следующий вид: ⁽¹⁷⁾

Если жидкость несжимаема, член работы под давлением исчезает и уравнение (16) сводится к:

⁽¹⁸⁾

Членом работы под давлением можно пренебречь для большинства инженерных приложений, если только система не подвергается значительному изменению давления или если число Маха близко к единице или выше.

Вязкий нагрев важен в некоторых особых случаях, связанных с очень высокими скоростями сдвига. Некоторые инженерные примеры – подшипники и гидравлические системы. Однако в большинстве других случаев вязким нагревом можно пренебречь, и уравнение (18) затем упрощается до:

⁽¹⁹⁾

Дата публикации: 29 июня 2018 г.
Последнее изменение: 29 июня 2018 г.

Список литературы

1. Panton, R.L., Incompressible Flow , ed.2, John Wiley & Sons Inc., 1996.
2. Берд Р. Б., Стюарт У. Э., Лайтфут Е. Н., Явления переноса , изд. 2, Нью-Йорк: John Wiley & Sons Inc., 2002.
3. Хьюз Т.Дж.Р., Энгель Г., Маццеи Л. и Ларсон М.Г., «Непрерывный метод Галеркина является локально консервативным», Journal of Computational Physics , vol. 163, pp. 467–488, 2000.

фазовых изменений

Как известно, материя может существовать в разных состояниях.Эти состояния включают твердые тела, жидкости, газы и плазму. Вы, вероятно, уже знакомы с твердыми телами, жидкостями и газами. Плазма – это энергетический газ, который был ионизирован, чтобы проводить электричество (например, звезды, молнии, неоновые вывески и т. Д.)

Когда материя меняет состояние, изменяется ее внутренняя энергия, поэтому изменяется кинетическая энергия составляющих ее частиц. Когда он переходит из одного состояния в другое, изменение энергии отражается на связях между частицами, и поэтому температура объекта не изменяется.Однако после того, как изменение состояния завершено, снова наблюдаются изменения энергии в виде изменений температуры.

Энергия, необходимая для изменения состояния конкретного материала, известна как скрытая теплота трансформации материала (L). Когда объект переходит из твердой фазы в жидкую, вы используете скрытую теплоту плавления (L _f ). Когда объект переходит из жидкой фазы в газообразную, вы используете скрытую теплоту парообразования (L _v ).Вы можете рассчитать энергию, необходимую материалу для изменения фаз, используя следующую формулу, где Q – добавленное тепло, m – масса объекта, а L – удельная скрытая теплота преобразования материала.

Вопрос: На приведенном ниже графике представлена ​​кривая охлаждения 10 кг вещества при его охлаждении от пара при 160 ° C до твердого вещества при 20 ° C. Энергия удаляется из образца с постоянной скоростью.

Пока вещество охлаждается в жидкой фазе, средняя кинетическая энергия молекул вещества

1. уменьшается
2. увеличивается
3. остается прежним

Ответ: (1) уменьшается с понижением температуры, а средняя кинетическая энергия связана с температурой.

Вопрос: На основании графика предыдущей задачи, какова температура плавления вещества?

Ответ: 70 ° C

Вопрос: Сколько тепла необходимо добавить к свинцовому стержню массой 10 кг, чтобы стержень превратился из твердого в жидкое при 327 ° C?

Ответ:

Вопрос: Сколько тепла нужно добавить к 1 кг воды, чтобы изменить температуру пара с 50 ° C на 100 ° C при стандартном давлении?

Ответ: Чтобы решить эту проблему, вы должны определить количество тепла, необходимое для изменения температуры воды, а также количество тепла, необходимое для изменения состояния воды.

Вопрос: График ниже показывает зависимость температуры от времени для одного килограмма неизвестного материала, поскольку тепло добавляется с постоянной скоростью.

В течение интервала xy материал испытывает

1. уменьшение внутренней энергии и фазовый переход
2. увеличение внутренней энергии и изменение фазы
3. без изменения внутренней энергии и смены фаз
4. без изменения внутренней энергии и без изменения фазы

Ответ: (2) увеличение внутренней энергии и изменение фазы.

Внутренняя энергия

1 Газы 2 Микроскопические энергии 3 Первый закон 4 Второй и третий закон 5 Фазовые переходы 6 Смеси 7 Фазовые диаграммы 8 Равновесие 9 Молекулярные взаимодействия

Внутренняя энергия | Энтальпия | Термохимия | Изменить функции Для изучения термодинамики нам нужно определить несколько основных идей.это важно понимать эти идеи точно или развивать термодинамические концепции. которые разработаны на их основе, скорее всего, не будут понятны. Система: Система – это часть вселенной, которая на самом деле учился. То, что мы называем системой, в значительной степени зависит от экспериментатор, чтобы определить. В некоторых случаях мы можем ограничиться к, например, только реагентам, в других случаях мы не можем правильно изолировать растворитель и, в других случаях, аппарат сам становится частью системы.Обычно мы определяем систему на основе удобного физического разделения. Окрестности: Окружающая среда – это остальная часть вселенной, после того, как мы извлек систему. В некоторых случаях можно говорить о небольшой детали Вселенной, как если бы это было все окружение. Энергия: энергии уходящей система (ящик) работает, w, или тепло, q, выходя из системы, отрицательный знак.Положительные значения для w или q означают энергию входит в систему. Мы только что обсудили энергию с точки зрения кинетической энергия и потенциальная энергия. на самом деле термодинамика изучение движения (динамики) энергии. Работа: ( w ) Это один из двух способов передачи энергии или вне системы. Работа предполагает упорядоченное движение системы (или часть их).Например, изменение объема связано с работой. У нас есть основное соглашение о знаках, которое гласит, что если энергия передается из система, т.е. , система работает с окружением , скажем, нажав на него при расширении системы, , затем знак срока работы отрицательный. И наоборот, если энергия передается в систему, то есть окружение работает на система, скажем, сжав ее в меньший объем, знак w положительный. Тепло: ( q ) Тепло – это передача тепловой энергии. Это своего рода энергии мы видели в предыдущем разделе этих заметок. Тепловой энергия включает поступательную кинетическую энергию молекул, колебательная энергия и вращательная энергия. Итак, если у нас есть процесс с положительным q означает найденную энергию в этих трех режимах формы увеличились. Если у процесса отрицательное q, то эти формы энергии имеют уменьшилось.Он использует то же соглашение о знаках в отношении энергии внутри и как работает. Открытая система: Рис. 2.1 (от Аткинса) (a) Открытая система может обмениваться материей и энергией с окружающей средой. (б) А замкнутая система может обмениваться энергией с окружающей средой, но он не может обмениваться материей. (c) Изолированная система может не обмениваются ни энергией, ни материей с окружающей средой. открытая система позволяет материи и энергии проходить между система и окружение. Мы могли бы рассмотреть открытый контейнер который не был изолирован как хороший пример Закрытая система: Системы, которые не позволяют материи обмениваться, но позволяют энергии для обмена между системой и окружением называются закрытыми системы.Хорошая аналогия – банка с попой до того, как ее открыли. в содержимое не может выйти из системы, но довольно быстро достигнет тепловое равновесие с окружающей средой. Изолированная система: любая система, препятствующая обмену материей и энергией. со вселенной изолирован. герметичный термос – хороший пример того, что можно назвать изолированной системой. На самом деле это физически невозможно построить по-настоящему изолированную систему, такую, которая вообще не будет обмениваться энергией.Но до тех пор, пока количество обмен энергии в течение эксперимента относительно small, мы можем использовать эту концепцию для наших экспериментальных установок. Внутренняя энергия В последнем разделе мы увидели, что можем вычислять энергию вклады поступательных, колебательных и вращательных мод движение отдельных молекул в образце. Мы также определили энергия системы согласно уравнению 2.21 и 2.22. Это важно помнить, что в этих уравнениях предположение, что мы всегда начинаем с нуля энергии внизу коллектора. Таким образом, как мы это делали в уравнение 2.33, нам нужен аддитивный коэффициент U 0 что сдвигает коллектор к истинному нулю энергии. Эта проблема в том, что нам не обязательно знать значение U 0 и, следовательно, мы можем никогда не узнать истинную внутреннюю энергию системы. Вместо этого мы полагаемся на тот факт, что U определен как состояние функции, и поэтому мы всегда можем измерить разницу в U при изменении системы с некоторое начальное состояние до конечного состояния. Напомним, функция состояния – это функция, которую можно вычислить из параметры состояния системы, такие как температура, объем, давление, количество молей, масса и т.д … Мы можем записать уравнение для внутренней энергии при начальная или конечная энергия как U = U (0) + E транс + E виб + E гниль 3.2 Вклад во внутреннюю энергию этих три формы кинетической энергии составляют примерно 1 / 2kT на градус Свобода. Когда мы подсчитываем степени свободы, мы ограничиваем себя тем, у кого есть доступные уровни энергии. Обычно это перевод (3 степени свободы) и вращение. (2 градуса, если линейный, и 3 градуса, если нелинейный). Таким образом, мы иметь следующие Для одноатомных (идеальных) газов внутренняя энергия равна просто Таким образом, мы видим, что внутренняя энергия линейно возрастает. с температурой с крутизной 3 / 2R . Для линейных молекул внутренняя энергия равна сумме поступательной кинетической энергии и вращательной энергии (два градуса свободы) U м = U м (0) + 3/2 РТ + РТ U м = U м (0) + 5/2 РТ 3,4 Таким образом, мы видим, что внутренняя энергия растет линейно с температурой с крутизной 5 / 2R . Для нелинейных молекул внутренняя энергия сумма поступательной кинетической энергии и вращательной энергии (три степеней свободы) U м = U м (0) + 3/2 РТ + 3/2 РТ U м = U м (0) + 3 РТ 3,5 Таким образом, мы видим, что внутренняя энергия растет линейно с температурой с крутизной 2R . Очевидно, количество тепла, необходимое для повышения температуры температура системы зависит от этих различных режимов и нелинейной молекулам потребуется больше тепла, чем линейным, которые, в свою очередь, потребовалось бы больше тепла, чем атомные частицы для заданного роста температура. Например, окна “low E” имеют газообразный аргон. впрыскивается между двумя (или даже тремя) стеклами (также покрытыми до уменьшить радиационную передачу ИК). У этого газа низкий способность поглощать тепло (без вибрации и вращения) и, следовательно, будет переносить небольшое количество тепла между холодным стеклом и теплым панель по отношению к воздуху, состоящая в основном из многоатомных молекулы типа O 2 или N 2 .Аргон также полезно, потому что это большой тяжелый атом, который легче содержать чем небольшие атомы, такие как гелий ( см. излияние ). Первый закон термодинамики Первый закон термодинамики формулируется обычно. во многих отношениях. «Энергия не может быть ни создана, ни уничтожена», «энергия Вселенной постоянна», и, возможно, самый полезный – «Энергия изолированной системы постоянна». По практическим соображениям лучше ограничить наши измерения небольшие системы. Измерения, которые мы можем провести, не включая U напрямую. Мы измеряем такие вещи, как температура, давление, объем и, следовательно, мы можем рассчитать изменения энергии в результате теплопередачи и работы. Таким образом, мы можем написать Это выражение инкапсулирует первый закон термодинамика в том, что единственные два средства обмена энергией между системой и Вселенной посредством теплопередачи, q , или работа, w .Таким образом, первый закон позволяет приравнять эти два системных процесса к изменению внутренняя энергия. Сумма q + Вт , очевидно, состояние функции, даже если отдельные системные процессы не работают. Например, изменение внутренней энергии пружину можно рассчитать, зная проделанную работу, когда она заведена, скажем, 100 Дж , и измерения тепло, потерянное в окружающую среду, 15 J как ΔU = 100 Дж – 15 Дж = 85 Дж Внимательно следя за условностями знаков, мы можем Теперь определите, что есть чистое изменение внутренней энергии пружина +85 Дж после он намотан, по сравнению с до намотки. Расширение При измерении работы у нас может быть несколько форм. Мы можем измерить механическую работу, | w | = f × d , исходя из простых физических понятий, мы могли бы также измерять работу от электричества как произведение переданного заряда и напряжение, при котором он перемещался, скажем, через электрический мотор. Вид работ, которыми чаще всего интересуются химики это работы по расширению. Когда система увеличивает свой объем на отталкивает окружающую среду или уменьшает ее громкость, когда окружение давит на него.тогда работа сделана. Это изменение в объем может произойти наиболее заметно, когда реакции производят газообразное продукты (расширение) или израсходовать газообразные реагенты (сжатие). давайте рассмотрим бесконечно малое изменение энергии для процесс выполняется очень маленькими шагами. Мы хотим ограничиться работой, выполняемой исключение теплопередачи (адиабатический процесс). Мы можем определить функцию по проделанной работе, начиная с с простыми понятиями физики.Считайте работу, проделанную путем перемещения объект на расстоянии dz против сила величиной F . dw = – Fdz Знак минус говорит нам в этом случае, что система, которая выполняла работу, теперь имеет меньше энергии в этом. p из = F / A или F = p ex × A Мы может связать силу с изменением положения поршня площади А.Поршень содержит нашу систему внутри стенок. цилиндра, и любое изменение объема связано с движением поршень. Из этого движения мы получаем изменение громкости . dV = Adz dw = – p ex dV Итак, теперь нам нужно интегрировать по общему давлению и изменение объема, чтобы определить общую выполненную работу. IIЕсли мы можем настроить условия так, чтобы внешнее давление постоянно, а изменение объема происходит за один «мгновенный» шаг, тогда интеграция становится легкой Инжир.2.7 (от Аткинса) Работа, выполняемая газом, когда он расширяется против постоянного внешнего давления, п из , есть равна заштрихованной области в этом примере индикатора диаграмма. Поскольку расширение было выполнено против постоянного давления, интеграл решается равным w = – p ex (V f – V и ) = – p ex ΔV 3.9 Поскольку PV для идеального газа постоянна, она невозможно изменить V, сохраняя P постоянным, если только T или n изменения. Таким образом, это уравнение полезно либо специально контролируемые эксперименты по изменению температуры или в случаях, когда изменение объема вызвано химической реакцией, которая либо создает или расходует чистое количество молекул газа. Как правило, если V изменяется, то же самое происходит и с P, поэтому простой функция не всегда работает.Мы можем изучить идею обратимая работа с учетом расширения и сжатия идеальный газ в баллоне с постоянной температурой (изотермический): Изначально мы находимся в состоянии А, удерживая газ в объем В А в баллоне с давлением п. А . Мы мгновенно сбросить давление стр. B .Затем газ расширяется до нового объема. В В . Модель pV проделанная работа (системой) легко измерима как площадь под кривой 1. Чтобы повернуть вспять процесс, мы увеличьте давление на поршень до п. A а затем газ снова сжимается до В А .Проделанная работа (в системе) – это область под кривая 2. Обратите внимание, что работа сделано для сжатия газа было больше, чем проделано газом по окрестностям. Таким образом, мы теряют энергию в этом циклическом процессе. Теперь рассмотрим тот же процесс снова, но где мы отпускаем давление бесконечно медленно, так что мы всегда следуем точному Изотерма ПВ .В этом случае мы идем по пути 3 в в любом направлении, и мы отмечаем, что проделанная работа по окружающей среде системой в фазе расширения точно так же, как и работа выполняется средой в системе на стадии сжатия. Этот обратимая работа. Обратите внимание, что во время этого процесса Система и Вселенная находятся в равновесии друг с другом. Уравнение этого очень медленного процесса немного отличается от уравнения 3.8 потому что под обратимые условия, которые мы описываем здесь, давление системы и давление окружающей среды всегда одинаково. Таким образом, мы можем написать Если наша система содержит идеальный газ, уравнение которого состояния p = nRT / V , мы получить: Логарифмические свойства журнал x <0, если x <1 журнал x> 0, если x> 1 Если конечный объем больше начального объем, то интеграл будет положительным и работа будет отрицательный.Другими словами, система работала (теряла энергию) на отталкивая окрестности. Если конечный объем меньше начального объем, то интеграл будет отрицательным и работа будет положительный. Окружающие сделали работу над системой (которая теперь имеет больше энергии). Пример: какова работа, когда 50 г железо реагирует с избытком соляной кислоты; а) в закрытом сосуде фиксированный объем и б) в открытом контейнере при 25ºC. В химической реакции между кислотой Бренстеда-Лоури и металл, металл окисляется и выделяется газообразный водород. Таким образом, уравновешенная реакция – Fe (т.) + 2 H + (водн.) → Fe 2+ (водн.) + H 2 (г) а) это просто, так как нет изменения громкости, нет никакой работы. Вт = 0 . б) при этом выделяется газ, который занимает значительно больший объем, чем твердое вещество и кислота. Таким образом, ΔV = V f – V i . где V f включает объем газа, а раствор и V i включает объем раствора и твердого вещества. Объемы раствора исключается из расчета (существенно не меняется) и объем твердого тела мал по сравнению с объемом газовый продукт, поэтому мы его проигнорируем.Таким образом, изменение громкости упрощается до объема выделяемого газа. Поскольку газ эволюционирует при постоянном давлении, мы можем приравнять давление газа к внешнее давление, р из . ΔV = V h3 = nRT / p из . Таким образом, проделанная работа, согласно уравнение 3.9 это w = –p ex (nRT / p ex ) = nRT Итак, все, что нам нужно сделать, это определить количество родинок выделившегося газа, n , и мы можете рассчитать проделанную работу. Процессы постоянного объема В общем, мы можем написать уравнение для изменения внутреннего энергия системы для любого процесса как dU = dq + dw ехр + dw e 3,12 , где два условия работы относятся к работам по расширению (опыт) и любым другим условиям форма работы (e для дополнительных), которая может быть задействована в процессе, например электромонтажные работы. Итак, если предположить, что в системе нет электрических или других компонентов, кроме pV работа и предполагая объем не меняется, мы можем переписать это уравнение как Интегрируя, мы получаем макроскопически измеримое Итак, мы можем написать (надеюсь) знакомое уравнение для изменения внутренней энергии системы, находящейся в процессе при постоянной громкости. Как мы намекали ранее, если в системе меняется энергия через изменение температуры у нас может возникнуть соблазн определить количество изменения энергии, связанного с изменением температуры, с помощью уравнения Обширная собственность: свойство, зависящее от количества материала. Примеры включают массу и объем. Обширные свойства являются действительными измеряемыми величинами. Интенсивная недвижимость: недвижимость, не зависящая от суммы материал. Например, плотность вещества равна то же самое для небольшой выборки, как и для большого количества это вещество. На самом деле мы не можем измерить интенсивный собственность напрямую. Обычно нам нужно измерить два обширные свойства, скажем, масса и объем и вычислить интенсивное свойство как соотношение двух экстенсивных характеристики. Преобразовать из интенсивной собственности в экстенсивную свойство, как правило, нам нужно умножать друг на друга обширная собственность. Например, чтобы преобразовать плотность к массе, нам нужно умножить на объем. где C теплоемкость. Теплоемкость – обширное свойство в том, что это зависит от количества материала. Тем не мение, теплоемкости часто указываются в таблицах как интенсивные свойства, исходя из либо по массе (удельная теплоемкость), либо по числу молей (молярная теплота емкость).Преобразовать в интенсивное свойство (из таблицы) до экстенсивного значения нам понадобится уравнение 3.15, нам нужно умножить на массу или моль соответственно, чтобы сократить единицы правильно. Некоторые люди на самом деле добавляют два дополнительных уравнения к списку вещей для запоминания; q = мКДТ и q = nCΔT . Эти последние два уравнения просто делают явным преобразование интенсивное свойство в экстенсивную (измеримую) ценность. Уравнение 3.15 представляет собой прямолинейное уравнение, в котором предполагается, что значение для теплоемкость (наклон) постоянна с температурой. Это не всегда правда. Лучшее определение теплоемкости учитывает это и допускает, что теплоемкость равна крутизна, взятая за бесконечно малый шаг по температуре. Пример, какова теплоемкость одноатомный идеальный газ? Уравнение энергии моля одноатомного идеальный газ – уравнение 3.3, U м = U м (0) + 3/2 RT . Если вставляем это в производную, получаем: Итак, ясно, что одноатомный идеальный газ имеет высокую температуру емкость, не зависящая от температуры. Жара емкость изменяется при изменении температуры для многоатомных газов поскольку статистические суммы зависят от температуры (уравнение 2.33), а значит, и само уравнение энергии для этих газы меняются с температурой. Рис. 2.11 Внутренняя энергия система зависит от объема и температуры, возможно, как показано здесь на поверхности. Вариация внутренней энергии с температурой при одном конкретном постоянном объеме проиллюстрирована кривой, параллельной T . В наклон этой кривой в любой точке является частной производной (∂ U / ∂T) V . В общем, определяющее уравнение для теплоемкости (уравнение 3.16 при постоянном объеме) должно быть используется, поскольку C v на самом деле является функцией T и должен быть рассматривается при интегрировании, а не как константа. Чтобы получить измеримые числа, нам нужно интегрировать. Если мы можем с уверенностью предположить, что теплоемкость постоянна в течение диапазон температур, который мы используем, тогда мы можем использовать упрощенный версия ΔU = C V ΔT или q V = C V ΔT 3.18 Нижний индекс V указывает, что эти уравнения применимы только в условиях постоянного объема. Дополнительный пример: Мы видели, что если мы подаем тепло в систему, она имеет разные способы справиться с этим. Иногда система температура изменяется по мере того, как тепло идет, чтобы увеличить кинетическую энергию но в других случаях кажется, что температура меняется незначительно или совсем не меняется (изменение фазы, например) Давайте посмотрим на наш статистический подход для некоторых ответы: Уравнение 2.27 дает нашу отправную точку. Мгновенный наклон относительно Температура дает нам Помните: ν гниль равно 0 для одноатомного, 2 для двухатомного (линейного) и 3 для нелинейного и нам нужно проверить колебательные режимы, чтобы увидеть, активны ли они на основе . Что такое C ν, м для воды при 100ºC ?. Три частоты колебаний воды равны . см -1 Из экспериментального данные λ (м) ν (с -1 ) ω = ν * 2π 1 3657.65 2,734E-06 1.0936E + 14 6.8715E + 14 .071 … неактивный 2 1594,59 6.2712E-06 4,7678E + 13 2.9957E + 14 .16 скажем неактивный 3 3755.79 2.66256E-06 1.1230E + 14 7.0559E + 14 .069 … неактивный , поэтому мы заключаем, что колебательные моды не способствуют теплоемкости воды при этой температуре. Таким образом, Помните, что, поскольку вода нелинейна, ν гниль = 3. Экспериментальное значение для C ν, м 26 лет.1 Дж / моль К. Учитывая, что мы игнорировали вибрации полностью, неплохо.

15.1 Первый закон термодинамики – Физика колледжа: OpenStax

Сводка

• Определите первый закон термодинамики.
• Опишите, как сохранение энергии соотносится с первым законом термодинамики.
• Укажите примеры первого закона термодинамики, работающие в повседневных ситуациях, включая биологический метаболизм.
• Рассчитать изменения внутренней энергии системы после учета теплопередачи и проделанной работы.

Рисунок 1. Этот кипящий чайник представляет энергию в движении. Вода в чайнике превращается в водяной пар, потому что тепло передается от плиты к чайнику. По мере того, как вся система нагревается, работа выполняется – от испарения воды до свиста чайника. (кредит: Джина Гамильтон)

Если нас интересует, как теплопередача преобразуется в работу, тогда важен принцип сохранения энергии.Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых передача тепла и выполнение работы являются методами передачи энергии в систему и из нее. Первый закон термодинамики гласит, что изменение внутренней энергии системы равно чистой теплопередаче в систему за вычетом чистой работы, проделанной системой . В форме уравнения первый закон термодинамики равен

.

[латекс] \ boldsymbol {\ Delta {U} = QW}.[/ латекс]

Здесь [latex] \ boldsymbol {\ Delta {U}} [/ latex] – это изменение внутренней энергии [latex] \ boldsymbol {U} [/ latex] системы. [Latex] \ boldsymbol {Q} [/ latex] – это чистое тепло, передаваемое в систему . – то есть [латекс] \ boldsymbol {Q} [/ latex] – это сумма всей теплопередачи в систему и из нее. [латекс] \ boldsymbol {W} [/ latex] – это работа сети , выполненная системой , то есть [latex] \ boldsymbol {W} [/ latex] – это сумма всей работы, проделанной в системе или ею.Мы используем следующие условные обозначения: если значение [latex] \ boldsymbol {Q} [/ latex] положительное, то в системе имеется чистый теплообмен; если значение [latex] \ boldsymbol {W} [/ latex] положительное, значит, система выполняет сетевую работу. Итак, положительный [латекс] \ boldsymbol {Q} [/ latex] добавляет энергии системе, а положительный [латекс] \ boldsymbol {W} [/ latex] забирает энергию из системы. Таким образом, [латекс] \ boldsymbol {\ Delta {U} = Q-W}. [/ Latex] Обратите внимание, что если в систему передается больше тепла, чем выполненная работа, разница сохраняется как внутренняя энергия.Тепловые двигатели – хороший тому пример – в них происходит передача тепла, чтобы они могли выполнять свою работу. (См. Рис. 2.) Теперь мы рассмотрим [latex] \ boldsymbol {Q}, \: \ boldsymbol {W}, [/ latex] и [latex] \ boldsymbol {\ Delta {U}} [/ latex] дальше.

Рисунок 2. Первый закон термодинамики – это принцип сохранения энергии, установленный для системы, в которой тепло и работа являются методами передачи энергии для системы, находящейся в тепловом равновесии. Q представляет собой чистую теплопередачу – это сумма всех теплопередач в систему и из нее. Q положительно для чистой передачи тепла в систему. W – это общий объем работы, выполненной в системе. W положительно, когда система выполняет больше работы, чем над ней. Изменение внутренней энергии системы, ΔU , связано с теплом и работой по первому закону термодинамики, ΔU = Q − W .

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ЗАКОН ТЕРМОДИНАМИКИ И ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

Первый закон термодинамики – это закон сохранения энергии, сформулированный в форме, наиболее полезной в термодинамике.Первый закон устанавливает связь между теплопередачей, проделанной работой и изменением внутренней энергии системы.

Теплопередача ([латекс] \ boldsymbol {Q} [/ latex]) и выполнение работы ([латекс] \ boldsymbol {W} [/ latex]) – два повседневных средства передачи энергии в систему или вывода энергии из системы. . Процессы совершенно разные. Теплопередача, менее организованный процесс, определяется разницей температур. Работа – это вполне организованный процесс, в котором действует макроскопическая сила, действующая на расстоянии.Тем не менее тепло и работа могут дать одинаковые результаты. Например, оба могут вызвать повышение температуры. Передача тепла в систему, например, когда Солнце нагревает воздух в шине велосипеда, может повысить ее температуру, и поэтому может работать над системой, например, когда велосипедист нагнетает воздух в шину. Как только произошло повышение температуры, невозможно сказать, было ли оно вызвано теплопередачей или работой. Эта неопределенность – важный момент. Теплообмен и работа – это энергия в пути, и ни одна из них не хранится как таковая в системе.Однако оба могут изменить внутреннюю энергию [латекс] \ boldsymbol {U} [/ латекс] системы. Внутренняя энергия – это форма энергии, полностью отличная от тепла или работы.

Мы можем думать о внутренней энергии системы двумя разными, но последовательными способами. Первый – это атомно-молекулярная точка зрения, которая исследует систему в атомном и молекулярном масштабе. внутренняя энергия [латекс] \ boldsymbol {U} [/ latex] системы – это сумма кинетической и потенциальной энергий ее атомов и молекул.Напомним, что кинетическая плюс потенциальная энергия называется механической энергией. Таким образом, внутренняя энергия – это сумма атомной и молекулярной механической энергии. Поскольку невозможно отследить все отдельные атомы и молекулы, мы должны иметь дело со средними значениями и распределениями. Второй способ взглянуть на внутреннюю энергию системы – с точки зрения ее макроскопических характеристик, которые очень похожи на средние атомные и молекулярные значения.

Макроскопически мы определяем изменение внутренней энергии [латекс] \ boldsymbol {\ Delta {U}} [/ latex] как то, что определяется первым законом термодинамики:

[латекс] \ boldsymbol {\ Delta {U} = QW}.[/ латекс]

Многие подробные эксперименты подтвердили, что [latex] \ boldsymbol {\ Delta {U} = QW}, [/ latex], где [latex] \ boldsymbol {\ Delta {U}} [/ latex] – это изменение общей кинетики и потенциальная энергия всех атомов и молекул в системе. Также экспериментально было определено, что внутренняя энергия [латекс] \ boldsymbol {U} [/ латекс] системы зависит только от состояния системы, а не от того, как она достигла этого состояния . Более конкретно, [латекс] \ boldsymbol {U} [/ latex] оказывается функцией нескольких макроскопических величин (например, давления, объема и температуры), независимо от прошлой истории, например, было ли тепло перевод или работа сделана.Эта независимость означает, что, зная состояние системы, мы можем вычислить изменения ее внутренней энергии [latex] \ boldsymbol {U} [/ latex] с помощью нескольких макроскопических переменных.

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: МАКРОСКОПИЧЕСКИЕ И МИКРОСКОПИЧЕСКИЕ

В термодинамике мы часто используем макроскопическую картину при расчетах поведения системы, в то время как атомная и молекулярная картина дает основные объяснения в терминах средних значений и распределений. Мы еще раз увидим это в следующих разделах этой главы.Например, в теме энтропии расчеты будут производиться с использованием атомно-молекулярного представления.

Чтобы лучше понять, как думать о внутренней энергии системы, давайте рассмотрим систему, переходящую из состояния 1 в состояние 2. Система имеет внутреннюю энергию [латекс] \ boldsymbol {U_1} [/ latex] в состоянии 1, и он имеет внутреннюю энергию [латекс] \ boldsymbol {U_2} [/ latex] в Состоянии 2, независимо от того, как он попал в любое из состояний. Таким образом, изменение внутренней энергии [латекс] \ boldsymbol {\ Delta {U} = U_2-U_1} [/ latex] не зависит от того, что вызвало изменение.Другими словами, [latex] \ boldsymbol {\ Delta {U}} [/ latex] не зависит от пути . Под путем мы подразумеваем способ добраться от начальной до конечной точки. Почему важна эта независимость? Обратите внимание, что [latex] \ boldsymbol {\ Delta {U} = QW}. [/ Latex] Оба [latex] \ boldsymbol {Q} [/ latex] и [latex] \ boldsymbol {W} [/ latex] зависят от путь , а у [latex] \ boldsymbol {\ Delta {U}} [/ latex] нет. Эта независимость от пути означает, что внутреннюю энергию [латекс] \ boldsymbol {U} [/ latex] легче учитывать, чем теплопередачу или проделанную работу.

Пример 1: Расчет изменения внутренней энергии: одно и то же изменение в

U производится двумя разными процессами

(a) Предположим, что теплопередача в систему составляет 40,00 Дж, в то время как система выполняет 10,00 Дж работы. Позже происходит передача тепла из системы на 25,00 Дж, в то время как в системе выполняется 4,00 Дж работы. Каково чистое изменение внутренней энергии системы?

(б) Каково изменение внутренней энергии системы, когда всего 150.00 Дж теплопередачи происходит из (от) системы и 159,00 Дж работы выполняется в системе? (См. Рисунок 3).

Стратегия

В части (а) мы должны сначала найти чистую теплопередачу и чистую работу, выполненную на основе данной информации. Тогда первый закон термодинамики [латекс] \ boldsymbol {(\ Delta {U} = Q-W)} [/ latex] может быть использован для определения изменения внутренней энергии. В части (b) приведены чистая теплопередача и проделанная работа, поэтому уравнение можно использовать напрямую.

Решение для (а)

Чистая теплопередача – это теплопередача в систему за вычетом теплопередачи из системы, или

[латекс] \ boldsymbol {Q = 40.00 \ textbf {J} -25.00 \ textbf {J} = 15.00 \ textbf {J}}. [/ Latex]

Аналогично, общая работа – это работа, выполненная системой за вычетом работы, выполненной в системе, или

[латекс] \ boldsymbol {W = 10.00 \ textbf {J} -4.00 \ textbf {J} = 6.00 \ textbf {J}}. [/ Latex]

Таким образом, изменение внутренней энергии определяется первым законом термодинамики:

[латекс] \ boldsymbol {\ Delta {U} = Q-W = 15.00 \ textbf {J} -6.00 \ textbf {J} = 9.00 \ textbf {J}}. [/ Latex]

Мы также можем найти изменение внутренней энергии для каждого из двух шагов.Во-первых, рассмотрим 40,00 Дж теплопередачи на входе и 10,00 Дж на тренировке, или

[латекс] \ boldsymbol {\ Delta {U} _1 = Q_1-W_1 = 40.00 \ textbf {J} -10.00 \ textbf {J} = 30.00 \ textbf {J}}. [/ Latex]

Теперь рассмотрим 25,00 Дж теплоотдачи и 4,00 Дж работы на входе, или

[латекс] \ boldsymbol {\ Delta {U} _2 = Q_2-W_2 = -25.00 \ textbf {J} – (- 4.00 \ textbf {J}) = – 21.00 \ textbf {J}}. [/ Latex]

Общее изменение – это сумма этих двух шагов, или

[латекс] \ boldsymbol {\ Delta {U} = \ Delta {U} _1 + \ Delta {U} _2 = 30.00 \ textbf {J} + (- 21,00 \ textbf {J}) = 9,00 \ textbf {J}}. [/ Latex]

Обсуждение на (а)

Неважно, смотрите ли вы на процесс в целом или разбиваете его на этапы, изменение внутренней энергии одинаково.

Решение для (b)

Здесь чистая теплопередача и общая работа даны как [латекс] \ boldsymbol {Q = -150.00 \ textbf {J}} [/ latex] и [латекс] \ boldsymbol {W = -159.00 \ textbf {J} }, [/ latex] так, чтобы

[латекс] \ boldsymbol {\ Delta {U} = QW = -150.00 \ textbf {J} – (- 159,00 \ textbf {J}) = 9,00 \ textbf {J}}. [/ Latex]

Обсуждение на (б)

Совершенно другой процесс в части (b) дает такое же изменение внутренней энергии на 9,00 Дж, что и в части (a). Обратите внимание, что изменение в системе в обеих частях связано с [латексом] \ boldsymbol {\ Delta {U}} [/ latex], а не с отдельным [латексом] \ boldsymbol {Q} \ text {s} [/ latex ] или [латекс] \ boldsymbol {W} \ text {s} [/ latex]. Система оказывается в том же состоянии и как в (a), так и (b).Части (а) и (b) представляют два разных пути, по которым система должна следовать между одними и теми же начальными и конечными точками, и изменение внутренней энергии для каждой из них одинаково – оно не зависит от пути.

Рисунок 3. Два разных процесса производят одно и то же изменение в системе. (a) Всего в системе происходит передача тепла 15,00 Дж, в то время как работа потребляет всего 6,00 Дж. Изменение внутренней энергии составляет Δ U = Q − W = 9,00 Дж . (б) Отвод тепла 150.00 Дж из системы во время работы дает ей 159,00 Дж, что приводит к увеличению внутренней энергии на 9,00 Дж. Если система начинает работу в одном и том же состоянии в пунктах (а) и (б), она окажется в одном и том же конечном состоянии в любом случае – ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была получена.

Метаболизм человека и первый закон термодинамики

Метаболизм человека – это преобразование пищи в теплообмен, работу и накопленный жир. Метаболизм – интересный пример действия первого закона термодинамики.Теперь мы еще раз посмотрим на эти темы с помощью первого закона термодинамики. Рассматривая тело как интересующую нас систему, мы можем использовать первый закон для изучения теплопередачи, выполнения работы и внутренней энергии в различных видах деятельности, от сна до тяжелых упражнений. Каковы некоторые из основных характеристик теплопередачи, выполнения работы и энергии в организме? Во-первых, температура тела обычно поддерживается постоянной за счет передачи тепла в окружающую среду. Это означает, что [latex] \ boldsymbol {Q} [/ latex] отрицательный. Другой факт: тело обычно работает с внешним миром.Это означает, что [latex] \ boldsymbol {W} [/ latex] положительный. В таких ситуациях тело теряет внутреннюю энергию, поскольку [latex] \ boldsymbol {\ Delta {U} = Q-W} [/ latex] отрицательно.

Теперь рассмотрим эффекты еды. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии (это неромантичный взгляд на хороший стейк). Тело метаболизирует всю пищу, которую мы потребляем. По сути, метаболизм – это процесс окисления, в котором высвобождается химическая потенциальная энергия пищи.Это означает, что питание осуществляется в форме работы. Энергия пищи указывается в специальной единице, известной как калория. Эта энергия измеряется сжиганием пищи в калориметре, как и определяются единицы.

В химии и биохимии одна калория (пишется со строчной буквы c) определяется как энергия (или передача тепла), необходимая для повышения температуры одного грамма чистой воды на один градус Цельсия. Диетологи и любители веса склонны использовать диетических калорий, которые часто называют калориями (пишется с заглавной буквы C).Одна еда Калория – это энергия, необходимая для повышения температуры одного килограмма воды на один градус Цельсия. Это означает, что одна диетическая калория для химика равна одной килокалории, и нужно быть осторожным, чтобы не путать их.

Опять же, рассмотрим внутреннюю энергию, потерянную телом. Эта внутренняя энергия может идти по трем направлениям – на теплопередачу, выполнение работы и накопленный жир (крошечная часть также идет на восстановление и рост клеток). Передача тепла и выполнение работы забирают внутреннюю энергию из тела, а пища возвращает ее.Если вы едите нужное количество пищи, ваша средняя внутренняя энергия остается постоянной. Все, что вы теряете на теплопередачу и выполнение работы, заменяется едой, так что в конечном итоге [латекс] \ boldsymbol {\ Delta {U} = 0}. [/ Latex] Если вы постоянно переедаете, то [латекс] \ boldsymbol {\ Delta {U}} [/ latex] всегда положительный, и ваше тело сохраняет эту дополнительную внутреннюю энергию в виде жира. Обратное верно, если вы едите слишком мало. Если значение [latex] \ boldsymbol {\ Delta {U}} [/ latex] отрицательное в течение нескольких дней, тогда организм метаболизирует собственный жир, чтобы поддерживать температуру тела и выполнять работу, которая забирает у тела энергию.Именно так соблюдение диеты способствует снижению веса.

Жизнь не всегда так проста, как знает любой человек, сидящий на диете. Тело накапливает жир или метаболизирует его только в том случае, если потребление энергии меняется в течение нескольких дней. После того, как вы сели на основную диету, следующая будет менее успешной, потому что ваше тело изменит способ реагирования на низкое потребление энергии. Ваша основная скорость метаболизма (BMR) – это скорость, с которой пища преобразуется в теплообмен и работу, выполняемую, когда организм находится в полном покое. Организм регулирует базальную скорость метаболизма, чтобы частично компенсировать переедание или недоедание.Организм будет снижать скорость метаболизма, а не устранять собственный жир, чтобы заменить потерянную еду. Вы легче простужаетесь и чувствуете себя менее энергичным из-за более низкой скорости метаболизма, и вы не будете терять вес так быстро, как раньше. Упражнения помогают похудеть, потому что они обеспечивают теплоотдачу от вашего тела и работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя. Снижению веса также способствует довольно низкая эффективность тела в преобразовании внутренней энергии в работу, так что потеря внутренней энергии в результате выполнения работы намного больше, чем проделанная работа. Следует, однако, отметить, что живые системы не находятся в тепловом равновесии ^.

Тело дает нам отличный показатель того, что многие термодинамические процессы необратимы . Необратимый процесс может идти в одном направлении, но не в обратном, при заданном наборе условий. Например, хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир.В противном случае мы могли бы пропустить обед, загорая или спустившись по лестнице. Другой пример необратимого термодинамического процесса – фотосинтез. Этот процесс представляет собой поглощение растениями одной формы энергии – света – и ее преобразование в химическую потенциальную энергию. Оба применения первого закона термодинамики показаны на рисунке 4. Одно большое преимущество законов сохранения, таких как первый закон термодинамики, состоит в том, что они точно описывают начальную и конечную точки сложных процессов, таких как метаболизм и фотосинтез, без учета осложнения между ними.В таблице 1 представлена ​​сводка терминов, относящихся к первому закону термодинамики.

Рис. 4. (а) Первый закон термодинамики применительно к метаболизму. Тепло, передаваемое из тела ( Q ), и работа, выполняемая телом ( W ), удаляют внутреннюю энергию, в то время как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую телом.) (Б) Растения преобразуют часть лучистой теплопередачи в солнечном свете в запасенную химическую энергию – процесс, называемый фотосинтезом.

Срок	Определение
[латекс] \ boldsymbol {U} [/ латекс]	Внутренняя энергия – сумма кинетической и потенциальной энергий атомов и молекул системы. Можно разделить на множество подкатегорий, таких как тепловая и химическая энергия. Зависит только от состояния системы (например, ее [латекс] \ boldsymbol {P}, \: \ boldsymbol {V}, [/ latex] и [латекс] \ boldsymbol {T} [/ latex]), а не от как энергия попала в систему. Изменение внутренней энергии не зависит от пути.
[латекс] \ boldsymbol {Q} [/ латекс]	Тепло – энергия, передаваемая из-за разницы температур. Характеризуется случайным движением молекул. Сильно зависит от пути. [Latex] \ boldsymbol {Q} [/ latex] вход в систему положительный.
[латекс] \ boldsymbol {W} [/ латекс]	Работа – энергия, передаваемая силой, перемещающейся на расстояние. Организованный, упорядоченный процесс. В зависимости от пути. [Latex] \ boldsymbol {W} [/ latex], выполненное системой (либо против внешней силы, либо для увеличения объема системы), является положительным.
Таблица 1. Сводка терминов для первого закона термодинамики, ΔU = Q − W

• Первый закон термодинамики задается как [latex] \ boldsymbol {\ Delta {U} = QW}, [/ latex], где [latex] \ boldsymbol {\ Delta {U}} [/ latex] – это изменение внутренняя энергия системы, [латекс] \ boldsymbol {Q} [/ latex] – это чистая теплопередача (сумма всей теплопередачи в систему и из нее), а [латекс] \ boldsymbol {W} [/ latex ] – это выполненная сетевая работа (сумма всей работы, выполненной в системе).
• И [латекс] \ boldsymbol {Q} [/ latex], и [латекс] \ boldsymbol {W} [/ latex] – это энергия в пути; только [latex] \ boldsymbol {\ Delta {U}} [/ latex] представляет собой независимую величину, которую можно хранить.
• Внутренняя энергия [латекс] \ boldsymbol {U} [/ latex] системы зависит только от состояния системы, а не от того, как она достигла этого состояния.
• Метаболизм живых организмов и фотосинтез растений – это специализированные виды передачи тепла, выполнения работы и внутренней энергии систем.

Концептуальные вопросы

1: Опишите фотографию чайника в начале этого раздела с точки зрения теплопередачи, выполненной работы и внутренней энергии. Как передается тепло? Какая работа и что делается? Как чайник поддерживает свою внутреннюю энергию?

2: Первый закон термодинамики и закон сохранения энергии, как обсуждалось в главе 7.6 «Сохранение энергии», явно связаны.Чем они различаются по рассматриваемым видам энергии?

3: Теплопередача [латекс] \ boldsymbol {Q} [/ latex] и проделанная работа [латекс] \ boldsymbol {W} [/ latex] всегда являются энергией в пути, тогда как внутренняя энергия [латекс] \ boldsymbol {U } [/ latex] – это энергия, запасенная в системе. Приведите пример каждого типа энергии и конкретно укажите, как он передается или находится в системе.

4: Чем отличаются теплопередача и внутренняя энергия? В частности, что можно сохранить как таковое в системе, а что нет?

5: Если вы сбежите по лестнице и остановитесь, что произойдет с вашей кинетической энергией и вашей начальной гравитационной потенциальной энергией?

6: Объясните, как энергия пищи (калории) может рассматриваться как молекулярная потенциальная энергия (в соответствии с атомарным и молекулярным определением внутренней энергии).6 \ textbf {J}} [/ latex] теплопередачи происходит в окружающую среду?

5: Предположим, что женщина выполняет 500 Дж работы, и 9500 Дж передается в окружающую среду в процессе. а) Как уменьшается ее внутренняя энергия, если не меняется температура или потребление пищи? (То есть другой передачи энергии нет.) Б) Какова ее эффективность?

6: (a) Сколько энергии пищи человек усвоит в процессе выполнения 35,0 кДж работы с эффективностью 5.00%? б) Сколько тепла передается в окружающую среду, чтобы поддерживать постоянную температуру? Ясно покажите, как вы следуете шагам стратегии решения проблем термодинамики, приведенной в главе 15.5 Стратегии решения проблем термодинамики.

7: (a) Какова средняя скорость метаболизма в ваттах у человека, который усваивает 10 500 кДж пищевой энергии за один день? (б) Какое максимальное количество работы в джоулях он может выполнить без расщепления жира, предполагая максимальную эффективность 20.0%? (c) Сравните его производительность с дневной мощностью двигателя 187 Вт (0,250 лошадиных сил).

8: (a) На сколько времени хватит энергии в чашке йогурта на 1470 кДж (350 ккал) у женщины, выполняющей работу мощностью 150 Вт с эффективностью 20,0% (например, при неторопливом лазании? лестница)? (б) Означает ли время, указанное в части (а), легко потребить больше пищевой энергии, чем вы можете разумно ожидать, работая с упражнениями?

9: (a) Женщина, поднимающаяся на памятник Вашингтону, усваивает [латекс] \ boldsymbol {6.2 \ textbf {kJ}} [/ latex] пищевой энергии. Если ее КПД составляет 18,0%, сколько тепла передается в окружающую среду, чтобы поддерживать ее температуру постоянной? (б) Обсудите величину теплопередачи, указанную в (а). Это согласуется с тем, что вы быстро разминаетесь во время тренировки?

Глоссарий

первый закон термодинамики

утверждает, что изменение внутренней энергии системы равно чистой теплопередаче в систему минус чистая работа, выполненная на система

внутренняя энергия

сумма кинетической и потенциальной энергий атомов и молекул системы

метаболизм человека

преобразование пищи в теплообмен, работу и накопленный жир

Решения

Задачи и упражнения

1:

[латекс] \ boldsymbol {1.7 \ textbf {J}} [/ latex]; таким образом, двигатель производит в 7,67 раза больше работы, чем человек

9:

(а) 492 кДж

(b) Такое количество тепла соответствует тому факту, что вы быстро согреваетесь во время тренировки. Поскольку организм неэффективен, выделяемое избыточное тепло должно рассеиваться через потоотделение, дыхание и т. Д.

Изменение внутренней энергии идеального газа – Сборник решенных задач

При расчете тепла необходимо иметь в виду, что во время изохорного процесса, когда давление увеличивается в четыре раза, работа не выполняется, а температура увеличивается до значения T ₂ = 4 T ₁ (что следует из того факта, что согласно закону идеального газа, в случае изохорного процесса V = const, соотношение \ (\ frac {p} {T} \) также постоянна).

В результате увеличивается внутренняя энергия газа, поэтому необходимо подводить тепло к системе. Для количества тепла, полученного системой Q ₁ (и увеличения внутренней энергии Δ U ₁ ), верно:

\ [Q_ {1} = \ mathrm {\ Delta} U_ {1} = C_ {V} n \ left (T_ {2} -T_ {1} \ right) = \ frac {3} {2} nR \ left (4 T_ {1} -T_ {1} \ right) = \ frac {9} {2} nRT_ {1}. \]

Для расчета Q ₁ мы также используем закон идеального газа в следующей форме:

\ [nRT_ {1} = p_ {1} V_ {1} \]

и получаем

\ [Q_ {1} = \ frac {9} {2} p_ {1} V_ {1}.\]

Значение C _V можно рассчитать с использованием постоянной Пуассона и следующей формулы

\ [\ kappa = \ frac {C_ {p}} {C_ {V}} \]

и отношение Мейера \ (C_ {p} = C_ {V} + R. \)

После подстановки получаем

\ [\ kappa = \ frac {C_ {p}} {C_ {V}} = \ frac {C_ {V} + R} {C_ {V}} = 1+ \ frac {R} {C_ {V}} \, \Правая стрелка\] \ [\ Rightarrow \, C_ {V} = \ frac {R} {\ kappa – 1} = \ frac {R} {\ frac {5} {3} – 1} = \ frac {3} {2} R \]

А для C _p применяется

\ [C_ {p} = \ kappa C_ {V} = \ frac {5} {3} \, \ cdot \, \ frac {3} {2} R = \ frac {5} {2} R.\]

При изобарическом охлаждении температура газа понижается, а это значит, что его внутренняя энергия также уменьшается, а именно на Δ U ₂ . Кроме того, внешние силы выполняют работу W . Следовательно, в соответствии с законом термодинамики 1 ^st , газ должен обеспечивать окружающую среду теплом Q ₂ (тепло Q ₂ будет отрицательным, потому что это тепло, поставляемое системой) :

\ [Q_ {2} = C_ {p} n \ left (T_ {3} -T_ {2} \ right) = \ frac {5} {2} Rn \ left (\ frac {1} {2} T_ { 2} – T_ {2} \ right) = – \ frac {5} {4} RnT_ {2} \] \ [Q_ {2} = – \ frac {5} {4} p_ {2} V_ {2} = -5 p_ {1} V_ {1} \]

При расчете мы учли тот факт, что при изобарическом сжатии, при котором объем уменьшается вдвое, термодинамическая температура также должна уменьшаться вдвое (что следует из того, что в случае процесса при постоянном давлении \ (\ frac {V} {T} = const \)).После этого мы снова использовали закон идеального газа, на этот раз в форме \ (nRT_ {2} = p_ {2} V_ {2} \).

Общее количество тепла, поставляемого газом в течение всего процесса, определяется суммой тепла Q ₁ , полученного в изохорном процессе, и тепла Q ₂ , поставляемого газом во время изобарного охлаждения.