Физика задачи по механике: Задачи по динамике с подробными решениями

Задачи по динамике с подробными решениями

Задачи по динамике с решениями

Сила, импульс, законы Ньютона

2.1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени
2.1.2 Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить
2.1.3 На тело массой 5 кг подействовали горизонтальной силой 4 Н. Какую скорость
2.1.4 Под действием какой силы прямолинейное движение частицы массой 100 г
2.1.5 Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной
2.1.6 Определить плотность тела массой 100 г и объемом
2.1.7 Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно
2.1.8 С какой силой давит человек массой 70 кг на вертикальную спинку сиденья
2.1.9 К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить
2.1.10 К нити подвешен груз массой 1 кг, который опускается с ускорением 5 м/с2
2.1.11 Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково
2.1.12 Поезд, подъезжая к станции со скоростью 60 км/ч, тормозит. За какое минимальное
2.1.13 При каком ускорении разорвется трос, прочность которого на разрыв равна
2.1.14 Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н
2.1.15 Автомобиль массой 1,2 т движется с места с ускорением 0,8 м/с2. Какую силу тяги
2.1.16 Под действием силы 30 Н тело поднимается вверх с ускорением 10 м/с2. Определить
2.1.17 Тело массой 3 кг падает в воздухе вертикально вниз с ускорением 8 м/с2
2.1.18 С какой силой давит тело массой 2 кг на пол лифта, поднимающегося с ускорением
2.1.19 Шар массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку шар стал
2.1.20 Автомобиль массой 2 т, двигаясь равноускоренно, через 4 с достиг скорости 2 м/с
2.1.21 На тело массой 15 кг, лежащее на земле, действует направленная вверх сила 45 Н
2.1.22 Автомобиль массой 2 т, трогаясь с места, прошел путь 100 м за 10 с. Найти
2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2. 1.24 Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч
2.1.31 Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины
2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
2.1.34 Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
2.1.40 Две стальные проволоки одинаковой длины, диаметр первой в 3 раза больше
2.1.41 Ракета на старте с поверхности Земли движется вертикально вверх с ускорением
2.1.42 С каким ускорением будет опускаться груз на нити, если сила натяжения нити в 1,25
2.1.43 С какой минимальной силой, направленной горизонтально, нужно прижать плоский
2.1.44 С какой силой давит человек массой 70 кг на пол лифта, движущегося вниз с ускорением
2.1.45 С какой силой следует придавить тело массой 4,5 кг к вертикальной стене, чтобы
2.1.46 Автомобиль идет по горизонтальной дороге со скоростью 72 км/ч. Найти тормозной
2. 1.47 Тело массой 5 кг покоится на горизонтальной поверхности. К телу приложена сила
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.49 Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.51 Тело массой 100 кг движется по горизонтальной поверхности под действием силы
2.1.52 Тело массой 200 кг упало на грунт со скоростью 100 м/с и погрузилось в него
2.1.53 Брусок массой 50 кг прижимается к вертикальной стенке с силой 100 Н. Какая сила
2.1.54 Троллейбус, масса которого 12 т, трогаясь с места, за 5 с проходит по горизонтальному
2.1.55 Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
2. 1.59 Тело массой 100 г движется вверх по вертикальной стенке под действием силы 2 Н
2.1.60 Груз массой 1 кг падает с высоты 240 м и углубляется в землю на 0,2 м. Определить
2.1.61 Дождевая капля массой 0,02 г под влиянием горизонтально дующего ветра падает
2.1.62 Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону
2.1.63 Канат лежит на плоской горизонтальной крыше так, что часть его свешивается
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с
2.1.65 Пуля массой 0,3 г, выпущенная из пневматической винтовки вертикально вверх, упала
2.1.66 Стержень длиной 0,9 м движется с ускорением под действием приложенной к его
2.1.67 Тело массой 2 кг начинает движение под действием постоянной по направлению
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки
2.1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.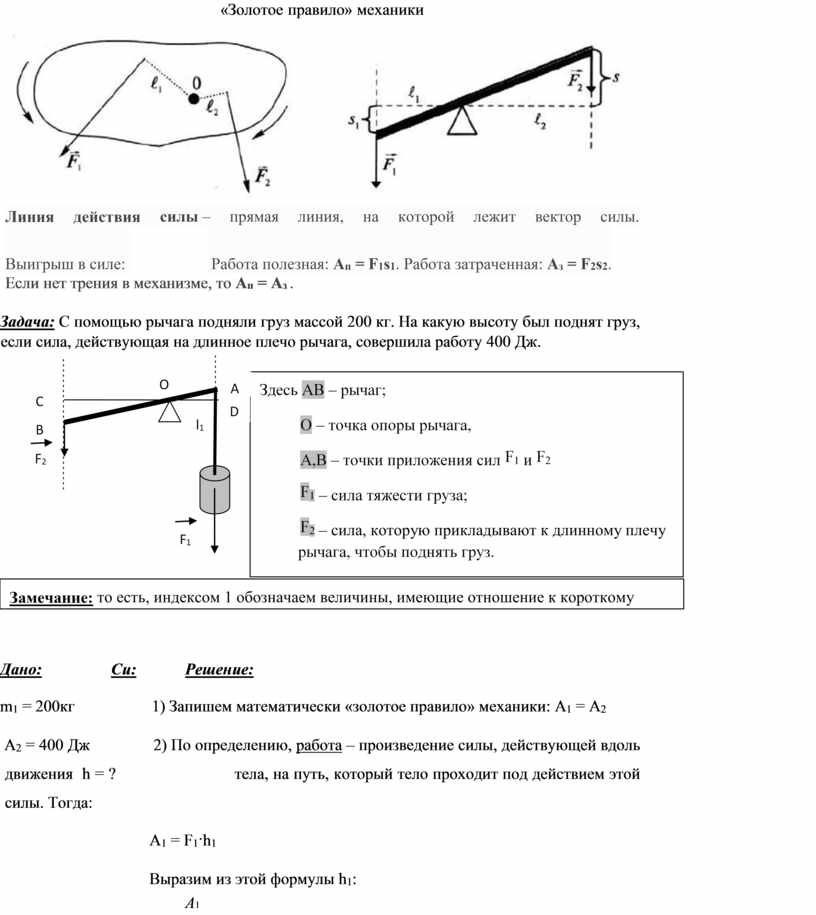 1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.74 Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60 градусов к нормали
2.1.75 На скользкой дороге коэффициент трения между дорогой и колесами мотоцикла
2.1.76 Груз массой 10 кг привязан к свободно свисающему концу веревки, намотанной
2.1.77 Координаты тела массы m=1 кг, движущегося прямолинейно вдоль оси x, меняются
2.1.78 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.1.79 Молекула массы m, летящая со скоростью v, ударяется о стенку сосуда под углом a
2.1.80 К невесомой нити подвешен груз массы 1 кг. Точка подвеса нити движется
2.1.81 Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому
2.1.82 Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной
2. 1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
2.1.84 Тело массы 10 кг движется по горизонтальной плоскости под действием силы
2.1.85 В кузове автомобиля лежит груз. При каком минимальном ускорении автомобиля груз
2.1.86 На шероховатой горизонтальной поверхности лежит тело массы 1 кг. Коэффициент
2.1.87 Тело массы m движется под действием силы F. Как изменится модуль ускорения тела
2.1.88 Тело массы m движется под действием двух равных по модулю взаимно
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные

Неподвижный блок

2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
2. 2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой
2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок

Наклонная плоскость

2.3.1 Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона
2.3.2 Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2. 3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.7 Тело скользит равномерно по наклонной плоскости, угол наклона которой 30 градусов
2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2. 3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском

Центростремительное ускорение

2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси
2. 4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.11 Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления
2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
2.4.18 Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности
2. 4.19 Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол
2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2. 4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
2.4.33 Спортивный молот – ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного
2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.42 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной
2. 4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна

Закон всемирного тяготения

2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его
2.5.2 Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.5 Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе
2.5.10 Сколько метров пройдет тело, свободно падая без начальной скорости в течение трех
2. 5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.12 Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус
2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2. 5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения

Упругая сила

2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой
2.6.2 Какую работу надо совершить, чтобы удлинить на 0,1 м резиновый шнур с коэффициентом
2.6.3 Под действием силы 4 Н пружина удлинилась на 2 см. Чему равна при этом
2.6.4 Какова начальная скорость шарика массой 1 г, которым выстрелили из пружинного
2.6.5 При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения
2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.7 Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2. 6.11 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную
2.6.14 Какую минимальную работу необходимо совершить, чтобы передвинуть по
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью

Работа, мощность, энергия

2.7.1 Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
2.7.4 Автомобиль поднимается в гору со скоростью 36 км/ч. Определить силу тяги мотора
2.7.5 Пуля массой 10 г вылетает из винтовки со скоростью 600 м/с. Определить работу
2.7.6 Автомобиль массой 1800 кг, двигаясь с ускорением 2 м/с2, прошел 100 м пути
2.7.7 Найти кинетическую энергию стрелы массой 0,5 кг, пущенную вертикально вверх
2. 7.8 Мальчик везет санки, прилагая к веревке силу 10 Н, которая образует угол 30 градусов
2.7.9 При подъеме тела массой 10 кг на высоту 2 м совершена работа 230 Дж
2.7.10 Санки тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30 градусов
2.7.11 Во сколько раз изменится запас потенциальной энергии упруго деформированного тела
2.7.12 При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной
2.7.15 Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см
2.7.16 Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести
2.7.18 Автомобиль массой 1,5 т едет со стоянки с постоянным ускорением 2 м/с2. Коэффициент
2.7.19 Автомобиль движется со скоростью 72 км/ч. Мощность двигателя 60 кВт, его КПД 30%
2.7.20 Вертолет весит 3 т. На его подъем тратится 30% мощности мотора. Определить
2.7.21 Двигатели электровоза при движении со скоростью 72 км/ч потребляют мощность
2.7.22 Какая работа совершается внешней силой при поднятии тела массой 5 кг на высоту
2.7.23 Какую работу должен совершить двигатель, чтобы разогнать по горизонтальной
2.7.24 Какую работу надо совершить, чтобы поднять груз массой 30 кг на высоту 10 м
2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м
2.7.26 Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой
2.7.27 Камень брошен под углом 30 градусов к горизонту. Кинетическая энергия камня в верхней
2.7.28 Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с
2.7.29 На тело массой 10 кг действует постоянная сила 5 Н. Определить кинетическую энергию
2.7.30 Подъемный кран поднимает груз массой 5 т на высоту 15 м. 3 (м). Определите
2.7.38 Футбольный мяч весом 8 Н летит со скоростью 15 м/с. Вратарь ловит мяч и за 0,1 с
2.7.39 Пуля летит со скоростью v0. Она пробивает доску толщиной 3,6 см и продолжает полет
2.7.40 Максимальная высота подъема тела массой 2 кг, брошенного с поверхности Земли
2.7.41 На рисунке приведена зависимость потенциальной энергии от времени движения
2.7.42 Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она
2.7.43 Самолет массой 2 т летит со скоростью 50 м/с. На высоте 420 м он переходит на снижение
2.7.44 Тело массой 3 кг падает вертикально вниз с начальной скоростью 2 м/с. Найти работу
2.7.45 Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может
2.7.46 Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с
2.7.47 Ядро массой 8 кг, выпущенное метателем под углом 45 градусов к горизонту с высоты
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2. 7.49 Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает
2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.51 Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась
2.7.52 На тело массы 5 кг действует постоянная сила 10 Н. Чему будет равна кинетическая
2.7.53 Какой кинетической энергией обладает свободно падающее тело массой 0,1 кг
2.7.54 Чему равна кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх
2.7.55 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения

Законы сохранения энергии и импульса

2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
2. 8.3 Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой
2.8.6 Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
2.8.8 Велосипедист движется со скоростью 8 м/с. Определить расстояние, пройденное
2.8.9 Мальчик, стреляя из рогатки, натянул резиновый шнур так, что шнур растянулся
2.8.10 Винтовка массой 2,8 кг подвешена горизонтально на двух параллельных нитях
2.8.11 Во сколько раз изменится потенциальная энергия пружины при увеличении
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
2. 8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный
2.8.17 Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории
2.8.18 При выстреле из орудия снаряд получил начальную скорость 300 м/с и летит
2.8.19 Телеграфный столб длиной 7 м и массой 140 кг при установке перемещается
2.8.20 Укажите график зависимости кинетической энергии свободно падающего тела
2.8.21 Чему равна работа по подъему лежащей цепи массой 50 кг и длиной 2 м, если
2.8.22 Подъемный кран поднимает груз массой 8 т на высоту 15 м. Определить время
2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.24 Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
2. 8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
2.8.33 Шарик массой m, подвешенный на нити, отклонен от положения равновесия на угол
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу
2.8.36 Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
2. 8.39 Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка
2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту
2.8.42 Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.44 В школьном опыте с “мертвой петлей” шарик массой 0,1 кг отпущен с высоты h=3R
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
2.8.47 Небольшое тело скользит с вершины полусферы вниз. На какой высоте h от вершины
2.8.48 Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется
2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной

Абсолютно упругий удар

2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно
2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой

Абсолютно неупругий удар

2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
2. 10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.3 Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
2.10.10 На вагонетку массой 800 кг, катящуюся по горизонтальным рельсам со скоростью
2.10.11 На тележку с песком массой 49 кг, движущуюся по прямой со скоростью 1 м/с, падает
2.10.12 Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30 градусов
2.10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2. 10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга
2.10.18 Вагон массой 50 т движется со скоростью 12 км/ч и встречает стоящую на пути
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
2.10.21 На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается
2.10.23 Пуля массой 10 г застревает в первоначально покоящемся бруске, масса которого 0,1 кг
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.25 В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой
2. 10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
2.10.28 В шар массой 1,5 кг, подвешенный на нерастяжимой нити длиной 55 см, попадает
2.10.29 Какая доля кинетической энергии перейдет в теплоту при неупругом столкновении
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно
2.10.32 Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.34 На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен
2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается
2.10.37 Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса

( 49 оценок, среднее 4.51 из 5 )

Вы можете поделиться с помощью этих кнопок:

Задачи для подготовки к ОГЭ по физике по теме: “Механика”

Задачи для подготовки к ОГЭ по физике по теме: «Механика»

Подборка расчетных задач из Открытого банка задач ФИПИ «Механические явления»

Кинематика

1. На соревнованиях по бегу спортсмен в течение первых двух секунд после старта двигался равноускоренно по прямой дорожке и разогнался из состояния покоя до скорости 10 м/с. Какой путь пробежал спортсмен за это время?

2. Водитель автобуса, ехавшего по прямой улице со скоростью 15 м/с, увидел красный сигнал светофора и нажал на педаль тормоза. После этого автобус начал двигаться равноускоренно и через 10 секунд после начала торможения остановился. Какой путь прошёл автобус за это время?

Динамика

3. При спуске с горы скорость лыжника увеличилась на 6 мс за 4 с. Масса лыжника 60 кг. Чему равна равнодействующая всех сил, действующих на лыжника?

4. Какой путь пройдёт машина на горизонтальном участке дороги после выключения двигателя, если коэффициент трения составляет 0,2, а скорость движения машины 72 кмч?

5. С помощью горизонтальной пружины по полу равномерно тянут коробку с книгами, преодолевая силу трения 5 Н. Длина пружины при этом увеличивается с 15 до 25 см. Чему равна жесткость этой пружины?

6. Деревянный брусок массой 2 кг тянут по горизонтальной деревянной доске с помощью пружины жёсткостью 100 Н/м. Коэффициент трения бруска по доске равен 0,2. Найти удлинение пружины, если брусок движется с ускорением 0,5 мс².

7. Мотоцикл массой 150 кг, движущийся со скоростью 10 мс, начинает тормозить и, проехав некоторый путь, останавливается. Если считать, что общая сила сопротивления движению мотоцикла составляет 300 Н, определите пройденный им путь в процессе торможения.

8. Автомобиль массой 1000 кг начал торможение и до полной остановки прошел путь 50 м. С какой скоростью двигался автомобиль в момент начала торможения, если суммарная сила, вызывающая его торможение, равна 4 кН?

9. Поезд массой 800 т движется со скоростью 36 км/ч и в результате торможения останавливается, пройдя расстояние 200 м. Чему равна сила трения и работа, совершённая этой силой?

10. Автомобиль массой 1 т трогается с места и движется с ускорением 1,2 м/с

2. На первых метрах пути сила тяги совершила работу 14000 Дж. Чему равен этот путь,  если коэффициент трения 0,02?

11. Автомобиль массой 1 т трогается с места и движется с ускорением 1,2 м/с². Определите работу силы тяги на первых 10 м пути, если коэффициент трения 0,02.

12. Чему равна сила натяжения троса, с помощью которого поднимают груз массой 500 кг с направленным вверх ускорением 2 мс2? Сопротивлением воздуха пренебречь.

13. Чему равна масса груза, который опускают с помощью троса с ускорением 2 мс2, направленным вниз, если сила натяжения троса 4000 Н? Сопротивлением воздуха пренебречь.

14. Мальчик стоит на напольных весах в лифте. Лифт начинает движение вверх с ускорением 1 мс2. Что покажут весы в этот момент времени, если в покоящемся лифте они показывали 40 кг?

15. Тело массой 5 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 3 с груз был поднят на высоту 12 м?

16. Бетонную плиту объёмом 0,25 м³ равномерно подняли на высоту 6 м. Чему равна совершённая при этом работа? Плотность бетона равна 2000 кгм3

17. Бетонную плиту подняли на высоту 6 м, совершив работу 3 • 10

4 Дж. Чему равен объём плиты? Плотность бетона равна 2000 кгм³

Законы сохранения в механике

18. Между двумя шарами массами 2 кг и 4 кг, движущимися вдоль одной прямой в одном направлении со скоростями 8 м/с и 2 м/с соответственно, происходит неупругое соударение. С какой скоростью шары будут продолжать совместное движение после соударения?

19. Тележка массой 20 кг, движущаяся со скоростью 0,5 м/с, сцепляется с другой тележкой массой 30 кг, движущейся навстречу со скоростью 0,2 м/с. Чему равна скорость движения тележек после сцепки, когда тележки будут двигаться вместе?

20. С какой скоростью следует бросить тело массой 200 г с поверхности земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.

21. Потенциальная энергия пули массой 50 г, выпущенной из ствола вертикально вверх, через 4 с после начала движения равна 40 Дж. Чему равна начальная скорость пули?

22. С высоты 2 м вертикально вниз бросают мяч. Абсолютно упруго отразившись от горизонтальной поверхности, мяч поднимается на высоту 4 м. С какой скоростью бросили мяч?

23. С некоторой высоты  вертикально вниз бросают мяч со скоростью 6,3 м/с. Абсолютно упруго отразившись от горизонтальной поверхности, мяч поднимается вверх на 4 м.

С какой высоты был брошен мяч?

Физика. Вопросы – ответы. Задачи

Представлены первые три части выпускаемой серии методических рекомендаций к решению задач по физике. Пособие призвано помочь усвоить основные законы механики. Контрольные вопросы в сочетании с приведенными ответами являются дополнением к основному учебнику физики. Приведены алгоритмы решения большого количества типовых задач. Кроме того, для самостоятельной работы подобраны задачи различной трудности, которые могут быть использованы учителем для работы с учениками. Пособие предназначено учащимся 9-го класса для самостоятельной работы, для подготовки к единому государственному экзамену, а также может быть использовано абитуриентами для подготовки к вступительным экзаменам.

Автор	Трубецкова Софья Васильевна
Издательство	ООО “Физматлит”
Дата издания	2003
Кол-во страниц	352
Номер тома	1
Название тома	Механика
ISBN	978-5-9221-0316-9
Тематика	Физика.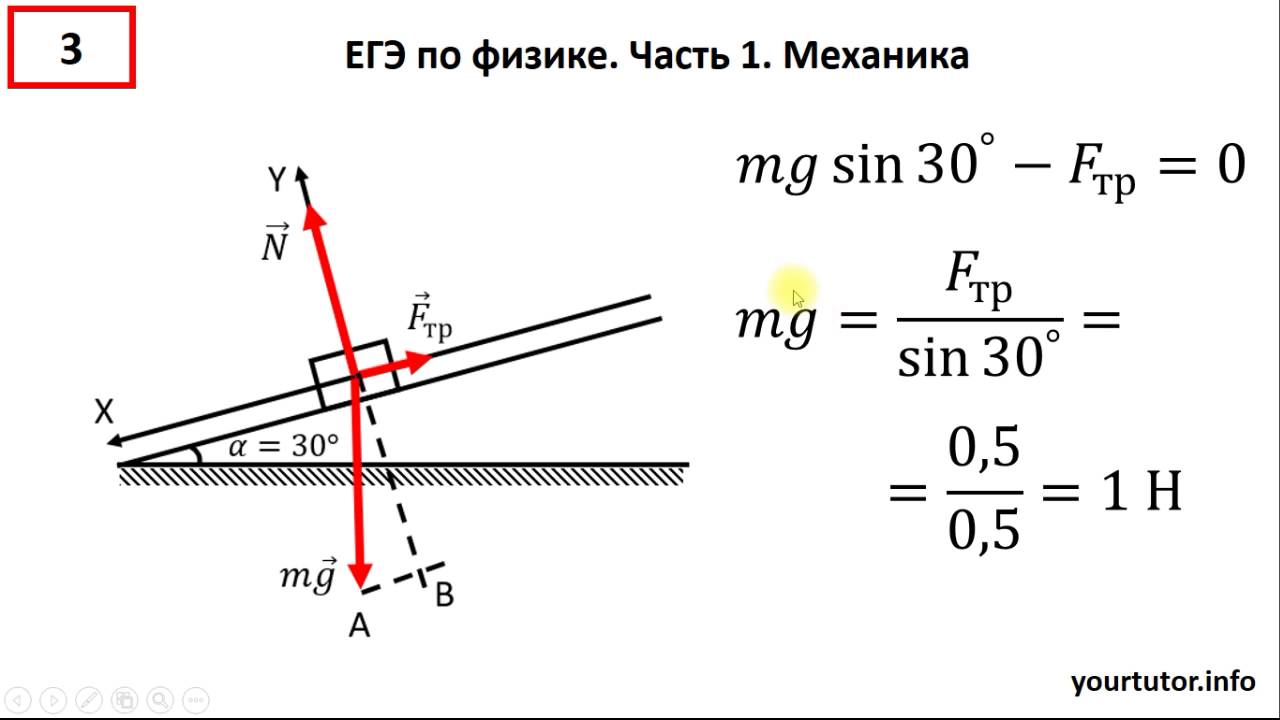 Химия. Биология (егэ,вуз)
Вес книги	360 г
№ в каталоге	316

Категории: Для подготовки к ЕГЭ и поступлению в ВУЗ

Решение задач по физике – Как решать задачи по физике?

 

Никогда нельзя решить задачу по физике, если не знать теорию, которая должна быть использована в её решении.

Поэтому начинать, конечно, надо с теории. Причём, несмотря на то, что теория по физике логически переходит от простых к более сложным понятиям, изучать можно начинать именно с того раздела, по которому необходимо в данное время решить задачу. Но в этом случае по условию задачи надо точно определить по какой она теме. Понятно, что на этом этапе к рекомендациям есть существенный вопрос: как же, не зная теорию, определить раздел физики, по которому дана задача. Но это как раз не сложно, сейчас постараемся в этом Вас убедить.

В школе все изучают физику. Но каждый усваивает предмет по разным причинам на своём уровне. Допустим, Вы не выучили определения, необходимые формулы и законы, но то, что законы движения и взаимодействия тел изучаются в «Механике», а свет в «Оптике» и т.д., – это усваивают все.

Теперь, к примеру, вспоминаем, что «Механика» состоит из нескольких разделов, в каждом из которых изучаются конкретные вопросы.

Кратко определим это так: в кинематике изучаются все формулы любых видов движения – прямолинейного равномерного и равноускоренного, криволинейного (на примере движения по окружности).

Поэтому, если в условии дано уравнение движения, скорости или ускорения поступательного или вращательного движения, а найти надо путь, перемещение, скорость, т.е. любую величину, характеризующую движение, открывайте раздел «Кинематика» в механике. Несколько формул по разделу находите в любом справочнике, но для правильного решения задачи надо всё- таки знать необходимую теорию по данной теме. Это не так много: прочитанных внимательно 4-5 страниц в любом учебнике внесёт ясность и понимание того, какие формулы надо использовать в данной задаче.

Дальше по механике: если в условии прочитали, что два тела, (это чаще всего, а может три или несколько), взаимодействуют друг с другом (упруго или неупруго), например, происходит столкновение, разрыв, выстрел и т.п., то здесь используем законы сохранения импульса и энергии ( это только при упругом взаимодействии).
Если в тексте задачи дано или найти энергию, работу, количество теплоты полученное или отданное газом, то это раздел «Молекулярная физика». Так же объём, давление, температура, молярная масса газа в условии задачи – это всё из того же раздела. Надо изучить теорию по газовым законам, первый закон термодинамики и несколько основных формул, чтобы решить задачу среднего уровня сложности по данной теме.

Точно также по тексту условия легко определить задачи по таким разделам, как «Оптика», «Электродинамика», «Законы постоянного тока», «Магнетизм», «Ядерная физика».

Несколько основных формул и законов, к этому добавим рассмотрение решения типовых задач в каждом разделе и Вы самостоятельно сможете решить большинство задач, необходимых для контрольной работы или зачёта.

Но если Вы всё-таки затрудняетесь в решении более сложных задач, для этого нужен определённый опыт и навык, то мы за небольшую оплату и в небольшой срок поможем Вам в решении задач по любым темам и любой сложности.

Умение решать задачи является искусством применять теоретические знания на практике.  Для этого требуется понимание, здравый смысл  и творчество. Решению задач легко научиться некоторым студентам, для которых процесс решения может показаться “очевидным” или “тривиальным”. Большинству студентов будет нужно совсем немного практики, прежде чем они достигнут уверенности в своих силах.

Студенту, который имеет мало практики в решении задач, следует начинать с систематических занятий для накопления опыта.

Многие люди говорят, если они оставят решение задачи на некоторое время и вернуться к нему позже, они ее решат, так как получат новый взгляд на задачу, увидят простой способ решения, тот что они не заметили раньше.

Говорят, что новый материал как пирамида: новая информация создается на основе старой. Попробуйте сначала понять задачу. Если задача является особенно трудной, попробуйте решить некоторые более простые по той же теме. Вы сможете найти способ сделать это. Сохраняйте позитивный настрой – это Вам поможет.

Если вы нервничаете, попробуйте жевательную резинку или есть попкорн, чтобы успокоить свои нервы. Вы “съедают” ваши нервные чувства.

Если у вас возникли проблемы решения задач, это никогда не помешает спросить! Попросите объяснить Вам решение друга или сокурсника,  они могут иметь другую точку зрения, которая переключит Вас на верный путь решения. Если вы можете, попробуйте понять их рассуждения и попытаться выяснить, чего вам не хватает для решения и почему. Тогда вы узнаете, что Вам делать.

Помните, физика не сложная наука, главное понимать задачи и вспоминать формулы. Остальное все просто: использование алгебры, тригонометрии и арифметики, в зависимости от темы вашего курса.

Задачи по теоретической физике. Ч.1: Механика

Search DSpace Advanced Search Subject Search Home   Browse Communities & Collections Issue Date Author Title Subject Submit Date   Sign on to: Receive email updates My DSpace authorized users Edit Profile   Help About DSpace

eScriptorium > 9. Рідкісні та цінні видання > 2. Видання ХХ ст. > Please use this identifier to cite or link to this item: http://escriptorium.univer.kharkov.ua/handle/1237075002/237 Название:  Задачи по теоретической физике. Ч.1: Механика Авторы:  Ландау, Л.Д. Лифшиц, Е.М. Розенкевич, Л. Ключевые слова:  теоретическая физика механика твердое тело канонические уравнения уравнения движения малые колебания интегрирование уравнений движения Issue Date:  1935 Издатель:  Х. : ОНТИ ДНТВУ НКТП Библиографическое описание:  Ландау Л.Д. Задачи по теоретической физике. Ч.1: Механика / Ландау, Лев Давидович, Лифшиц, Евгений Михайлович, Розенкевич Л. – Х. : ОНТИ ДНТВУ НКТП, 1935. – 119 с. URI:  http://escriptorium.univer.kharkov.ua/handle/1237075002/237 Appears in Collections: 2. Видання ХХ ст. 4. Рідкісні видання Харкова ХХ ст. Files in This Item: File Description Size Format zadachi po teor. pfizike.pdf 3,01 MB Adobe PDF View/Open View Statistics Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.

Качественные задачи по физике. Механика.

Качественные задачи по теме «Механика» Повернуть или остановиться? Порой от знания физики может зависеть ваша жизнь.  Представьте себе, что автомобиль, за рулем которого вы сидите, едет прямо на кирпичную стену, которая находится в конце  Т­ образного перекрестка. Что делать? Тормозить изо всех сил, не допуская заноса, стараясь рулить  прямо?  Поворачивать  на  полной  скорости  или   выруливать   вбок, тормозя по  мере возможности? Рассмотрим задачу последовательно. Для начала, предположим, что вы успеете вовремя, если будете тормозить, не сворачивая. Будет ли при этом поворот столь же безопасным?   Прежде   всего,   конечно,   следует   рассмотреть   идеальный   случай.   Затем   можно   учесть возможность заносов, различие в сцеплении с дорогой передних и задних колес, «усталость» тормозов. А что если торможение на прямой не спасет вас? Стоит ли тогда стараться повернуть или, может быть, смириться с трагической неизбежностью? Другой вариант    аналогичной ситуации: перед вами на дороге большой предмет. Что лучше сделать: остановиться или попытаться его объехать? Конечно, все зависит от размеров предмета. Не давайте поспешных ответов. Пусть вы и опытный водитель, но интуиция порой может   подвести, а ведь дело касается вашей жизни. Ответ:   Если   пренебречь   тем,   насколько   может   быть   опасен   для   пассажиров   удар автомобиля тем или другим бортом, и если стену объехать нельзя, то нужно двигаться прямо на   нее,   пытаясь   затормозить   как   можно   скорее.   Расчет   показывает,   что   при   идеальном состоянии тормозов и дорожного покрытия избежать столкновения со стеной, двигаясь по дуге окружности, можно только в том случае, если сила трения между колесами и дорогой будет вдвое больше, чем при торможении, когда автомобиль движется прямо. Если   шофер   затормозит,   автомобиль   остановится,   когда   его   кинетическая   энергия израсходуется на работу против силы трения. При повороте автомобиля та же сила трения будет играть роль центростремительной силы, Заставляющей автомобиль двигаться по дуге окружности. В случае торможения  где  F  − сила трения,  х  − путь, который пройдет автомобиль после включения тормоза. mv2/2 = Fx, Отсюда  Очевидно, чтобы автомобиль не врезался в стену, должно быть х = mv2/(2F). или В случае поворота  х = mv2/(2F) ≤ S, F ≥ mv2/(2S). F = mv2/R, и, чтобы автомобиль не разбился, должно быть или R = mv2/F ≤ S F ≥ mv2/S. Для того чтобы избежать   столкновения со стенкой, при торможении нужна сила трения, вдвое меньшая, чем при повороте. Очевидно, выгоднее тормозить, чем поворачивать!    Трение и автомобильные гонки Во   время   автомобильных   гонок   результаты   оцениваются   в   первую   очередь   по   двум главным   показателям:   максимальной   скорости   автомобиля   и   времени   прохождения   им дистанции в четверть мили. Чтобы увеличить сцепление колес с дорогой, перед стартом под задние   колеса   подливают   липкую   жидкость.   Однако  увеличение   трения,   как  оказывается, влияет на время, затрачиваемое на прохождение дистанции, но мало влияет на максимальную скорость. Почему? Ответ: Вначале скорость зависит от сцепления колес автомобиля с дорожным покрытием. Чем лучше сцепление, тем меньшее время затрачивается на прохождение начальной части дистанции,   однако в  дальнейшем   сцепление   влияет  на скорость  незначительно  (изменение скорости не превышает нескольких процентов). Максимальная скорость, которой автомобиль достигает на финише, определяется мощностью двигателя. Автомобильные шины без протектора Если бы вам представилась возможность выбирать между нормальными и широкими  шинами без протектора, то какие бы вы предпочли с точки зрения лучшего торможения? Во время гонок серийных автомобилей на их задние колеса часто надевают широкие шины без  протектора. Почему? Ответ:   Сила   трения   между   шиной   и   дорожным   покрытием   не   зависит   от   площади контакта,   так   что   широкие   шины   без   протектора   ничем   не   лучше   узких.   Если   колеса автомобиля   пробуксовывают,   когда   он  трогается   с   места   (так  во   время   гонок  бывает   на старте),   то   широкие   шины   имеют   определенное   преимущество,   потому   что   у   них   нагрев распределяется по большей площади и, следовательно, снижается вероятность того, что шина расплавится (при плавлении шины сильно уменьшается коэффициент трения). Блокирование колес Если вам нужно быстро остановить машину, следует ли резко нажать на педаль тормоза и заблокировать   колеса?   (Опытные   водители   рекомендуют   при   торможении   на   скользкой дороге   не   выключать   сцепления,   т.   е.   не   отсоединять   колеса   от   двигателя.   Попробуйте объяснить, почему такой способ торможения безопаснее.) Ответ: Коэффициент трения скольжения меньше коэффициента трения покоя. Поэтому, когда колеса крутятся, со стороны дороги на них действует большая сила трения, чем в том случае, когда они скользят. На сухом ровном асфальте коэффициент трения покоя (колеса не   проскальзывают)   достигает  0,8,   тогда   как   при   скольжении   он   не   превышает  0,6.   Когда начинается скольжение («блокирование» колес), асфальт и шины могут расплавиться, и тогда автомобиль будет двигаться по тонкому слою жидкости. Чтобы затормозить, автомобиль с «блокированными» колесами (при прочих равных условиях) должен пройти расстояние, на 20 %  большее, чем при вращающихся колесах. Поэтому автомобиль останавливается быстрее всего,   если   к   тормозам   прикладывать   усилие,   чуть   меньшее   того,   при   котором   колеса блокируются. При скольжении колес возникает опасность бокового «заноса» автомобиля, так как при этом движение вбок может быть вызвано даже очень малой силой. Ускорение и торможение автомобиля на повороте Почему   не   следует   резко   тормозить   на   повороте?   Предположим,   вы,   уже   совершая поворот, вдруг решили, что едете слишком быстро. Что произойдет, если вы резко нажмете на педаль тормоза? Гонщики нажимают на педаль газа, выходя из поворота, но не на повороте. Почему? Ответ: При резком торможении на повороте машина наклоняется вперед; давление на передние колеса увеличивается, а на задние − уменьшается. При этом на повороте зад машины может   занести   в   сторону.   При   ускорении   автомобиля   давление   на   его   задние   колеса возрастает, и их сцепление с дорогой улучшается. Автомобиль трогается с места Много   спорят   о   том,   как   следует   трогаться   с   места   на   скользкой   дороге.   Одни утверждают, что это нужно делать на низкой передаче, другие говорят, что на высокой. Имеет ли вообще значение, какая передача включена? Что требуется, чтобы автомобиль тронулся с места? Почему его начальная скорость должна быть малой?  Какое преимущество  имеет одна передача перед другой? Попробуйте объяснить, как зависит момент силы, действующей на колесо, от передачи, и установить, в каком случае этот момент должен быть больше, а в каком − меньше. Ответ:   Начальная   скорость   вращения   колес   должна   быть   мала,   и   момент   сил, действующих на колеса со стороны трансмиссии и двигателя, должен быть меньше момента сил   трения   покоя.   Иначе   колеса   будут   проворачиваться   −   буксовать.   Какую   передачу выбрать, зависит от опыта водителя и плавности работы сцепления. Если водитель привык «газовать», трогаясь с места, то момент сил можно уменьшить вдвое, начиная движение со второй В этом случае   передачи.  нагрузка передается от двигателя через шестерни с меньшим передаточным   числом и сила, действующая на колеса, уменьшается. Как объяснить шум, издаваемый колесами автомобилей? Ответ: Шум, издаваемый колесами автомобилей, − одна из основных проблем больших городов. Огромные средства тратятся ежегодно на борьбу с этим шумом, так как стоимость   одного   километра   звукопоглощающего   барьера,   устанавливаемого   вдоль   шоссе,   близка   к одному   миллиону   долларов.   Есть   несколько   теорий   возникновения   этого   шума. Одна   из   них   считает,   что   шум   возникает внешней     части   из­за   колебаний   деформированных   участков покрышки. Другая     теория   связывает   появление   шума   с   отлипанием   резины   от   дороги.    романтичная гипотеза объясняет шум тем, что воздух двигается по канавкам Ну, а самая автомобильных покрышек, как по трубам органа, и поэтому поет. Какие шины используют в гонках Формула­1? Ответ: Каждый пилот гоночного болида хочет иметь хорошее    сцепление с дорогой, чтобы обеспечить быстрый старт. Но это значит, что шины его автомобиля должны хорошо прилипать к дорожному покрытию. Но такая шина всегда будет оставлять на дороге след из частичек,   прилипших   навсегда   к   дорожному   покрытию.   Другими   словами,   износ   шин   с высоким  сцеплением тоже высок. Поэтому на гонках «Формулы 1» средний ресурс шины всего около 200 км, в то время как у обычных шин он может составлять несколько десятков тысяч километров. Известно,   что   автомобильные   гонки   проходят   на   «лысой»   резине   или   на   шинах   с несколькими очень неглубокими канавками. Канавки в шинах гоночных машин  не нужны, так как они увеличивают  сцепление  с дорогой   только   тогда,   когда   она   мокрая.   А   при   мокрой   дороге   гонки   отменяются.   Для производства  шин  гоночных автомобилей  используется  специальная  липкая  резина. Поэтому сила трения этих шин на сухой дороге растет с увеличением площади контакта,   вступая, таким образом, в противоречие с классическим законом, справедливым для трения твердых и неэластичных поверхностей. Чтобы обеспечить максимальную силу трения, шины колес гоночных автомобилей делают очень широкими (до 0,38 м), что также позволяет лучше рассеивать   тепло,   выделяющееся   при   трении   о   дорожное   покрытие. Чистая  резина    прилипает  к  дороге  лучше,  чем грязная. Поэтому  перед  самым   стартом покрышки с помощью специальных устройств и процедур нагревают до  80 °С, очищая ее поверхность   и   обеспечивая   хорошее   прилипание   к   дорожному   покрытию.   Кстати,   шины гоночных   автомобилей   иногда   надувают   чистым   азотом,   так   как   влага,   содержащаяся   в обычном воздухе, при нагревании шин испаряется и увеличивает  давление в колесах,  что создает дополнительные трудности в управлении.  Почему все шины черные? Ответ: Все изготовители шин используют один и тот же процесс − вулканизацию жидкой резины,   при   котором   одной   из   добавок   служит   угольная   пудра.   В   результате   длинные молекулы   жидкой   резины   смешиваются   между   собой,   что   превращает   ее   в   эластичный   и прочный материал. Так как частички угля черные и их относительно много (около 25 % по массе),   то   резина   становится   черной.   Чем   больше   добавлять   при   вулканизации   угольной пудры,   состоящей  практически  из  одного  углерода,  тем  более  жесткой,  прочной   и  менее прилипчивой будет резина. Брошенный на льду Допустим, ваши приятели  решили сыграть  с вами  злую шутку и бросили  вас посреди большого замерзшего пруда. Лед настолько скользкий, что вы не в состоянии ни пройти, ни даже   проползти   по   нему   к   берегу.   Как   же   вам   поступить? Теперь   предположим,   что   вас   положили   на   лед   на   спину.   Через   некоторое   время   вы почувствуете, что спина промерзла и вам нужно перевернуться. Как это сделать на таком скользком льду? Шутка   могла   бы   оказаться   еще   злее.   Например,   вас   стоя   привязали   бы   к   столбу, торчащему   где­то   посередине   льда.   Как   вам   повернуться   вокруг   столба,   если   ваши   руки   свободны? Столб слишком гладкий и скользкий, чтобы за него ухватиться, а лед еще более скользкий,   и   ногами   в  него   не  упереться.   Что   нужно   сделать,   чтобы   повернуться   вокруг столба лицом в другую сторону? Ответ:   Если   вас   не   связали,   попытайтесь   бросить   ботинок   или   что­нибудь   другое   в направлении, противоположном тому, в котором вы хотите передвинуться. Если трение о лед полностью   отсутствует,   то   полный   импульс   системы   должен   оставаться   равным   нулю,   и поэтому вы начнете скользить в нужную сторону. Автомобиль, велосипед, поезд на повороте Как вы поворачиваете на велосипеде, а точнее, как вы начинаете поворот? Мотоциклист поворачивает,   наклоняя   мотоцикл,   а   руль   при   этом   стоит   прямо.   Иначе   обстоит   дело   с велосипедом. С чем связано это различие? Для того чтобы поезд на повороте не сошел с рельсов под действием центробежной силы, полотно железной дороги делается наклонным и наружный рельс на повороте часто бывает приподнят.   Влияет   ли   этот   наклон   на   поворот   поезда   так   же,   как   наклон   при   повороте мотоцикла?   Попробуйте   сделать   хотя   бы   грубый   расчет,   чтобы   выяснить   это.  И наконец, что вы можете сказать о повороте гоночных автомобилей?   Ответ: Момент импульса колеса мотоцикла много больше, чем велосипедных колес, и играет существенную роль. Для того чтобы повернуть мотоцикл, вы наклоняете его. Момент силы   реакции   земли,   действующей   на   переднее   колесо   мотоцикла,   заставляет   колесо прецессировать, благодаря чему мотоцикл поворачивает. Моменты импульса велосипедных колес   много   меньше,   поэтому   здесь   полагаться   на   прецессию   нельзя.   Для   того   чтобы осуществить поворот на велосипеде, нужно наклонить его и одновременно повернуть руль. Кстати, в какую сторону вы сначала поворачиваете руль − влево или вправо, − если хотите повернуть, скажем, влево? Конструкция велосипеда Почему современный велосипед делается именно таким? В прошлом существовало много различных конструкций велосипедов (рис.). Одни   имели   колеса   разного   диаметра,   у   других   педали   соединялись   прямо   с   осью переднего колеса. Отличается   ли   современный   велосипед   большей   устойчивостью   и   большим  коэффициентом   полезного   действия   (КПД)   по   сравнению   со   своими   предшественниками? Почему   вилка   переднего   колеса у   современного   велосипеда   изогнута?   Сохранит   ли велосипед устойчивость, если этой вилке придать другие формы, скажем, такие, как показано   на рис.? Ответ: Устойчив такой велосипед, у которого точка пересечения оси вращения руля с горизонталью,   проходящей   через   центр   колеса,   при   повороте   его   опускается   в   сторону наклона велосипеда.  Из трех конструкций, изображенных на рис., последняя неустойчива, тогда как вторая − чрезмерно устойчива, и в этом случае велосипед плохо «слушается» на   оказывают   существенного   влияния   на поворотах.   Гироскопические   эффекты   не   устойчивость велосипеда, хотя вращение колес в течение некоторого времени обеспечивает устойчивость велосипеда, если его толкнуть без седока. Шины большого диаметра Будет   ли   автомобиль   двигаться   быстрее,   если   поставить   на   колеса   шины   большого диаметра? Ответ: Существует некое максимальное угловое ускорение, которое можно сообщить автомобильному  колесу.  Чем  больше диаметр  шины, тем большее  расстояние  автомобиль проходит при каждом обороте колеса и тем больше его линейное ускорение. Однако при   ограниченной мощности двигателя установка шин большего диаметра приведет к уменьшению углового ускорения, в результате линейное ускорение останется прежним. Автомобиль на льду Что нужно делать, чтобы выправить автомобиль, если его «заносит» в гололед: пытаться вырулить прямо или поворачивать руль в сторону заноса? Почему? Ответ:   Выбор   наилучшей   тактики   зависит   от   ряда   факторов,   в   первую очередь   от соотношения скорости заноса и линейной скорости центра масс автомобиля, а также от того, какие колеса сохранили сцепление с дорогой. Необходимо также четко уяснить, что важнее:   воспрепятствовать заносу или приостановить движение вперед. Допустим, к примеру, что заднюю часть автомобиля заносит вправо, что движением вдоль дороги можно пренебречь и что передние колеса сохранили сцепление с дорогой. Тогда, чтобы помешать заносу, следует поворачивать передние колеса в направлении вращения (то есть вправо) и потихоньку давать газ. По мере уменьшения заноса нужно выводить передние колеса влево, восстанавливая тем самым правильную ориентацию автомобиля на дорожном полотне. Балансировка колес Будет   ли   сбалансировано   вращающееся   колесо   автомобиля,   если   оно   балансировалось статически при помощи обычного пузырькового уровня? Можно ли добиться одновременно статического и динамического баланса колеса, прикрепляя к его ободу один балансировочный груз? А два груза? Ответ:   Статически   сбалансированное   с   помощью   одного   груза   колесо     может   при вращении оказаться несбалансированным динамически. С другой стороны, колесо можно сбалансировать динамически и оно не будет «бить»; однако   если   это   сделать   с   помощью   одного   груза,   то   статическая   балансировка   может оказаться   нарушенной.   При   обычной   балансировке   колес   удовлетворяются   каким­либо компромиссным   вариантом.   Если   же   использовать   два   груза,   то   можно   добиться   как статического, так и динамического баланса. При   статической   балансировке   колеса   его   центр   масс   лежит   на   оси   колеса,   однако распределение   массы   колеса   может   оказаться   несимметричным   относительно   плоскости, перпендикулярной оси. При вращении такое колесо будет вести себя как диск, плоскость которого не перпендикулярна оси вращения. Такое колесо не сбалансировано динамически. Дифференциал автомобиля Когда автомобиль совершает поворот, колеса, движущиеся  по наружной дуге, должны вращаться быстрее, чем те, что движутся по внутренней дуге. Как это может происходить, если «наружные» и «внутренние» колеса (попарно − передние и задние) установлены на одной оси? Ответ. Задние колеса соединены между собой не жестко, а через    дифференциал. На повороте   дифференциал,   который   состоит   из   четырех   конических   шестерен,   позволяет «внешнему» колесу вращаться быстрее «внутреннего». Вспучивание дороги На дороге, которая первоначально была ровной, возникает ухаб, а вслед  за ним через некоторое время еще один. Кажется, он сам собой вырастает поперек дороги. И дорога − будь то грунтовая, асфальтированная или даже бетонная − становится  похожей на стиральную доску,   особенно   после   дождя,   когда   в   складках   собирается   вода. Подобное явление наблюдается на    трамвайных и железнодорожных путях. Когда по такому деформированному участку проходит поезд, возникает страшный грохот. Недаром подобные участки называют «ревущими». Аналогичные «стиральные доски» встречаются лыжникам на лыжне. Почему возникает такая волнообразная («гофрированная») поверхность и чем определяется ее период? Можете ли  вы оценить этот период, моделируя  описанный эффект в ящике с песком  с помощью небольшого колесика? Ответ: Представьте, что на дороге имеется ухаб, при проезде через который у машин начинает колебаться «передок». В тех местах, где колебание направлено вниз, шины могут вдавливаться   в   дорогу.   Если   в   одном   и   том   же   месте   это   происходит   со   многими автомобилями, то может образоваться еще один ухаб и т. д. Трение. Как объяснить сущность трения моей бабушке, не прибегая к каким­то сложным научным построениям,   а   на   самой   простой   модели.   Обусловлено   ли   трение   неровностями сцепляющихся   поверхностей   или,   возможно,   действием   электростатических   сил?   Может быть, местное «прилипание» вызывают молекулярные силы, а может, твердая поверхность «проникает» в более мягкую и они сцепляются? Вопрос этот очень стар, незамысловат и наверняка должен иметь простой ответ. Ответ:   Прежде   трение   объясняли   неровностями   соприкасающихся     поверхностей. Современная   теория   трения   отвергает   эти   представления   и   рассматривает   адгезию («слипание»)   поверхностей   в   результате   межмолекулярных   взаимодействий   как   основную причину трения. Несмотря на это, во многих учебниках по­прежнему трение описывается как явление,   обусловленное   только   микроскопическими   «холмиками»   и   «впадинками»   на соприкасающихся поверхностях. Зависит   ли   трение   от   площади   контакта   соприкасающихся поверхностей?   Cила   трения   скольжения   прямо   пропорциональна   весу   трущегося   предмета. Парадоксальность  закона, что сила трения не зависит от площади контакта тел, стала на     долгие И   сейчас   не   на   все   вопросы   получены   ответы,   хотя   ряд   соображений   между   предметом   оживленных годы   споров учеными.   представляется     довольно убедительным. Дело в том, что касание твердых тел    происходит не по всей поверхности, а в отдельных пятнах, или «очагах», контакта. Суммарная (фактическая) площадь таких очагов Sф обычно очень мала и составляет весьма малую часть от номинальной площади  Sн. Однако если  Sн вceгдa задана, то Sф как показывает опыт, растет с увеличением веса груза Р. Стоит теперь предположить,   что   этот   рост   прямо   пропорционален  Р,   как   парадокс   закона   Амонтона разрешается − сила трения прямо пропорциональна фактической площади контакта, которая, в свою очередь, линейно растет с ростом груза. Ставя кирпич на различные грани, мы во всех случаях   сохраняем   постоянной  Sф  которая   зависит   только   от   веса   кирпича  Р.   Отсюда   и постоянство трения. Увы!   Легко   обнаруживается,   что    Sф  растет   пропорционально  P  далеко   не   всегда. Типичный пример стальной шарик, прижимаемый к жесткой плите. Площадь кругового пятна контакта увеличивается здесь, как показывают теория и эксперимент, заметно медленнее, чем прижимающая сила, а закон Амонтона по­прежнему соблюдается! Разумеется, если шарик не катится, плоскости. Только   в   нашем   веке   стало   ясно,   что   тупик,   В   который   Зашли   ученые,   объясняется скользит   по а         слишком упрощенным подходом к явлению трения. Накопилось много фактов в пользу того, что  трение   −  результат   тонких   микроскопических  процессов,   прямо  связанных   с  атомно­ молекулярным строением вещества. В  1929 г., английский физик Д. Томлинсон выказал смелую гипотезу о том, что атомы, расположенные   на   поверхности   твердого   тела   и   первыми   воспринимающие   нагрузку   при взаимодействии с такими же атомами дрyгого тела, работают по принципу «да − нет»: каждый из   них или  держит  гpуз  q, подобно древнегреческой  кариатиде,  или   не работает  вообще. Характерная   величина   q,   названная   постоянной   Томлинсона,   определяется   особенностями строения кристаллической решетки материала. С ростом нагрузки автоматически вступают в строй новые «кариатиды», число которых оказывается cтpoгo пропорциональным нaгpузке. Так исчезает старое представление о сплошном и огpомном, по сравнению с атомом, очaге контакта с максимальным давлением в центре. Вместо него возникает модель из множества сравнимых   с   атомом   «пятен»   контакта,   каждое   из   которых   воспринимает   одинаковую внешнюю силу. Из гипотезы Томлинсона сразу следует закон Амонтона. В итогe, парадокс этого закона разрешается   переосмыслением   на   основе   атомно­молекулярных   представлений   такого простогo и очевидноrо, казалось бы, понятия, как площадь фактического касания твердых тел. Сейчас   уже   не   существует   сомнений,   что   в   основе   трения   лежат     сложные микроскопические   явления.   Вполне   вероятно,   что   закон   Амонтона   служит   как   раз естественным пpoявлением этой тонкой природы трения. Следы на песке. Если вам приходилось, гулять по пляжу во время отлива, то, вероятно, вы заметили, что, как только нога ступает на мокрый твердый песок, он немедленно подсыхает и белеет вокруг вашего следа.  Обычно это объясняют  тем, что под тяжестью тела вода «выжимается»  из песка. Однако это не так, потому что песок не ведет себя подобно мочалке. Почему же белеет песок?   Будет   ли   песок   оставаться   белым   все   время,   пока   вы   стоите   на   месте? Мяч, наполненный песком и водой. Наполните камеру мяча песком и водой так, чтобы вода полностью   покрывала   песок,   но   не   заполняла   всю   камеру.   Теперь   завяжите   камеру   и попробуйте сжать ее. Вначале это получается легко, но, чем дальше вы сжимаете ее, тем сильнее она сопротивляется сжатию, с какой бы силой вы на нее ни давили. Чем это вызвано? Покупка мешка кукурузы. В те времена, когда кукурузное зерно продавалось не на вес, а на   объем,   некоторые   торговцы   всячески   старались   сделать   так,   чтобы   зерна   занимали возможно   больший   объем.   Мешки   кукурузы   у   таких   хитрецов   казались   полными,   хотя содержали меньше кукурузы, чем мешки такого же объема у более честных торговцев. Как вы думаете, следовало ли покупателю, столкнувшись с таким обманом, попытаться нажимать на мешок,   чтобы   уплотнить   в  нем   зерна?   Оказывается,   именно   нажимать   на   мешок  в   таком случае и не следует. Почему? Ответ: Все эти три явления в действительности одинаковы. Я рассмотрю первое из них, а остальные два предлагаю вам объяснить самостоятельно. Побеление песка на пляже впервые объяснил Рейнольде  в 1885 г. Он показал, что объем песка увеличивается,  когда на него наступают. До этого песчинки были «упакованы» самым плотным образом. Под действием деформации   сдвига,   которая   возникает   под   подошвой   ботинка,   объем,   занимаемый песчинками,   может  лишь  увеличиться.  В  то время  как  уровень  песка  поднимается  резко, уровень воды может подняться лишь в результате капиллярных явлений, а на это требуется время. Поэтому на дне следа ноги песок некоторое время оказывается выше уровня воды − он сухой и белый. Заполнение следа на песке водой. Многие из вас, по­видимому, замечали, что в тот момент, когда вы ступаете на мокрый песок, он светлеет. Это связано с тем, что песок становится суше. Но как только вы убираете ногу, след оставленный ногой, немедленно заполняется водой. Объясните это явление. Ответ: Чтобы объяснить, что происходит с песком на берегу реки, начнем с шариков. Одинаковые шарики можно уложить на плоскости так, чтобы каждый из них касался шести других шаров. В лунки между шарами первого стоя можно положить шары второго слоя. Каждый из них будет касаться трех шаров нижнего слоя и шести соседей своего слоя и т. д. Полученное таким образом расположение шаров называется плотной упаковкой шаров. Если нарушить плотную упаковку, выведя шары одного из слоев из лунок между шарами нижнего слоя, промежутки между шарами увеличатся. Возрастет и объем всей системы. Это означает, что если на систему из плотно упакованных шаров действуют силы, приводящие к нарушению плотной упаковки, объем  системы  увеличивается  за счет увеличения промежутков между шарами. Аналогично ведет себя и любая зернистая среда. Возьмите, например, пшено (или кофе), наполните им стакан, слегка встряхивая стакан, чтобы зерна располагались, образуя наиболее плотную из возможных упаковку. Затем надавите на пшено. Давление приведет к увеличению объема,   занимаемого   зернами,   то   есть   к   нарушению   плотной   упаковки.   Часть   зерен высыплется. Если теперь слегка постучать по стакану с тем, чтобы зерна вновь «упаковались» доверху. наиболее заполненным   окажется стакан плотно,         не   Теперь вернемся к песку на берегу. Он тоже плотно упакован. При давлении на песок плотная упаковка разрушается, и объем песка увеличивается за счет увеличения пространства между песчинками.   Вода   из   верхних   слоев   песка   уходит   вглубь,   заполняя   эти   увеличившиеся промежутки.   Песок   как   бы   «высыхает».   Когда   ногу   убирают,   плотная   упаковка восстанавливается, а вытесненная из уменьшившихся вновь промежутков вода заполняет след, оставленный ногой. Геофизическое «оружие». Китайская   Народная   Республика,   возможно,   обладает   новым   устрашающим   видом «оружия» − геофизическим. Некоторые специалисты считают, что если все население Китая (свыше 1 млрд. человек) одновременно спрыгнет с двухметровых платформ, то в земле начнет распространяться ударная волна. Прыгая снова всякий раз, как эта волна будет проходить через Китай, китайцы могут усилить ее до такой степени, что она может разрушить отдельные районы   Соединенных   Штатов,   особенно   в   Калифорнии,   нередко   и   сейчас   страдающие   от землетрясений. По какой траектории будет распространяться в земле такая волна? Как часто придется прыгать китайцам, чтобы усиливать эту волну, и насколько будет увеличиваться ее энергия при каждом таком прыжке? Сможет ли население другой страны каким­то образом защититься   от   воздействия   геофизического   «оружия»,   например   с   помощью   аналогичных прыжков (рис.). Будет ли зависеть амплитуда такой волны от того, как именно станут прыгать китайцы?   Кое­кто   утверждает,   что   прыгать   следует,   не   сгибая   ног,   так   как   прыжок   на полусогнутых   ногах   вызовет   гораздо   меньшую   волну.   Что   вы   можете   сказать   по   этому поводу? Ответ:   Первоначальные   (и   едва   ли   серьезные)   вычисления   Д.   Стоуна     показали,   что такой прыжок может привести к землетрясению мощностью  4,5 балла  по шкале Рихтера. Часть   Китая   при   этом   неминуемо   будет   разрушена.   Но   если   эту   сейсмическую   волну периодически «подкачивать», то она может произвести разрушения и в других местах. Для того чтобы попасть в резонанс, прыгать придется каждые  53 − 54 мин  − именно за такое время сейсмическая волна огибает Землю. «Обороняющейся» стране придется организовать свои   прыжки,   волны   от   которых   гасили   бы   волны,   создаваемые   прыжками   китайцев.   Но, поскольку жителей в этой стране меньше, им придется прыгать с соответственно большей высоты. Как утверждает Стоун, чтобы сообщить сейсмическим волнам наибольшую энергию, нужно прыгать, не сгибая ног в коленях. Мне это утверждение не вполне ясно, поскольку в любом   случае   энергия,   сообщаемая   волнам,   определяется   потенциальной   энергией   тела человека в поле силы тяжести. Стоит ли ехать на желтый свет? Каждый водитель порой оказывается перед необходимостью быстро решить, остановиться или   проехать   на   желтый   свет   светофора.   Это   подсказывает   ему   интуиция,   выработанная методом проб и ошибок; однако точный расчет позволяет проанализировать такие ситуации, где   интуиция   бессильна.   При   каких   значениях   начальной   скорости   и   расстояния   до перекрестка следует остановиться (или рискнуть проехать на красный свет), если заранее известны время, в течение которого горит желтый свет, и размеры перекрестка? (Согласно «Правилам   дорожного   движения»   ускорение   автомобиля   не   должно   превышать  5,8   м/с2) Определите интервал скоростей и расстояний, при которых вы успеваете проехать вовремя. Обратите   внимание,   что   при   некоторых   значениях   этих   параметров   вы   можете   решать, проезжать или  нет. Но, возможно, что скорость или расстояние будут таковы, что вы  не успеете ни проехать, ни остановиться вовремя ? и тогда вас ждут большие неприятности. Ответ: Подъезжая к перекрестку, на котором только что загорелся желтый свет, водитель может затормозить с максимальным отрицательным ускорением, проскочить перекресток с максимальным положительным ускорением или продолжать ехать с прежней скоростью. Для примера рассмотрим следующий набор параметров: автомобиль движется со скоростью  54 км/ч (15 м/с), ширина перекрестка  10 м, желтый свет горит 2 с, а максимальное ускорение равно  −3м/с2  при торможении и  +3 м/с2  при разгоне. Определим, на каком расстоянии от перекрестка нужно находиться, чтобы выбрать какой­либо из трех вариантов прохождения перекрестка   (при   условии,   что   двигатель   немедленно   реагирует   на   нажатие   педали акселератора). Для того чтобы успеть вовремя проскочить перекресток в тот момент, когда загорается желтый сигнал, вы должны находиться от него не дальше, чем в  26 м. Чтобы вовремя остановиться, нужно быть от перекрестка не ближе чем в 37,5 м. При расстоянии в пределах 26 − 37,5 м можно выбрать любую тактику. Встречные поезда. Скоростные   поезда   при   встрече   должны   замедлить   ход,   иначе   стекла   в   вагонах разобьются.   Почему?   В   какую   сторону   при   этом   выпадают   стекла:   внутрь   вагонов   или наружу? Может ли случиться подобное, если поезда движутся в одном направлении? Будет ли вас притягивать к поезду или отталкивать от него, если вы окажетесь слишком близко от быстро идущего поезда?  Ответ: Впереди быстро идущего поезда создается фронт высокого давления, а за ним − область низкого давления. Когда встречные поезда разъезжаются, стекла поезда могут быть выдавлены наружу, поскольку между поездами возникает область пониженного давления.

Помощь с решением задач по технической механике

Медиана Жириновского:

Техническая механика: решение задач по любому из предметов ЕГЭ.

Помощь с решением Вашей задачи по технической механике

Определить координаты центра тяжести сечения.

Примеры решения задач технической механике: на этой странице я собрал теорию и практику с примерами решения задач по предмету техническая механика с решением по каждой теме, чтобы вы смогли освежить знания!

Если что-то непонятно, вы всегда можете написать мне в мейл-агент, и я вам помогу!

Нажмите на интересующую вас тему, и она сразу откроется!

Это упрощение, принятое в технической механике, значительно облегчает решение задач о движении.

Лекции:

Понятие о силе и системе сил.

Уметь определять параметры движения с помощью теорем динамики.

Лекция репетитора Алекса Э. Султанова:

Общие теоремы динамики — смотрите решение задачи по технической механике

Примеры решения задач технической механики

Примеры решения задач по технической механике и выполнения заданий, расчетно-графических, контрольных и курсовых работ для студентов всех форм обучения.

Техническая механика, теормех, сопромат, ТММ, детали машин и строймех.

• Онлайн помощь.
• Заказать решение.
• Помощь на экзаменах.
• Техническая механика.
• Теормех.
• Сопромат.

Знаменитый американский физик предлагает

Подготовка к олимпиаде
Услуги репетиторов
Метод быстрого счёта в уме
Ментальная Арифметика – это вам не матан!
В данной группе вы можете заказать решение задач по Технической механике, контрольных работ, РГР (расчетно-графических работ), курсовых проектов по Технической механике (Техмех), Сопротивлению материалов (Сопромат), Теоретической механике (Термех, Теормех), Строительной механике (Строймех)

Вступайте в нашу группу и получите скидку

Всё сдал! Техническая механика – на пять!
Нужен специалист по дисциплине техническая механика?

Решение задач онлайн хотите заказать недорого и без посредников?
Не успеваете подготовить курсовую по электротехнике или диплом
Написание студенческих работ любой сложности.

Решатель

Решение задач по теоретической механике, сопромату и деталям машин.

1. Формулы.
2. Примеры.
3. Алгоритмы.
4. Советы.
5. Рекомендуемая литература.

Техническая механика – это наука, изучающая различные механизмы, их синтез и анализ.

На практике же это означает соединение трех дисциплин – сопротивления материалов, теоретической механики и деталей машин.

Она удобна тем, что каждое учебное заведение выбирает, в какой пропорции преподавать эти курсы.
Соответственно, в большинстве контрольных работ задачи разбиты на три блока, которые необходимо решать по отдельности или вместе.

Рассмотрим наиболее часто встречающиеся задачи.

Решение задач по ТММ.

Раздел первый.
Теоретическая механика.
Решение задач
Задачи и методы их решения
Задачи, предложенные для самостоятельного решения, и методы их решения охватывают все основные темы по разделам «Статика» и «Кинематика» данной дисциплины.
В приложениях изложены минимально необходимые сведения из тригонометрии, векторного и дифференциального исчисления.

А это – к первой задаче по статике.
Номера условий проставлены в столбце таблицы.
Задача относится к кинематике точки и решается с помощью формул методом Султанова, которым определяются скорость и ускорение точки в декартовых координатах – координатный способ задания движения точки.
Все искомые величины нужно определить только для данного момента времени.
Срочное решение задач по теории поля онлайн векторный способ

Механика и общая физика

• Механика и общая физика
• E&M and Optics
• Современная физика и квантовая механика

Законы Ньютона: движение точечной частицы

Формулы
Кинематика (1D) и описание траектории, трансформации кадров
Кинематика (движение снаряда)
Второй закон Ньютона (с заданной силой)
Второй закон Ньютона (с трением)
2-й закон Ньютона (с сопротивлением)
Равномерное круговое движение и центростремительное ускорение
Круговое движение (в постоянном гравитационном поле)
Законы сохранения (энергия и импульс)
Работа
Энергия
Движение в неинерциальной системе отсчета
Статическое и динамическое равновесие

Закон всемирного тяготения Ньютона

закон всемирного тяготения Ньютона, Закон Гаусса

Импульсные силы, столкновения, взаимодействующие объекты

Формулы
Взаимодействующие объекты, 2-я ньютоновская и 3-й закон, законы сохранения
Упругие столкновения
Неупругие столкновения
Ракеты
«Переменная масса» проблемы
Цепи и т. д.

Законы Ньютона: движение твердого тела

Формулы
Момент инерции и CM
Кинематика вращения
Законы движения Ньютона применяется к твердым телам
Сохранение углового момента
Работа и сохранение энергии
Импульсы (соединяющие линейные и вращательное движение)
Статическое равновесие
Упругие свойства твердые предметы

Уравнения Лагранжа и Гамильтона

Формулы
Стандартные лагранжевые задачи (связанные точечные массы)
Стандартные лагранжевые задачи (наклонные плоскости)
Стандартные лагранжевые задачи (колебания)
Стандартные лагранжевые задачи (другие проблемы)
Проблемы с гамильтонианом
Расширения лагранжиана и гамильтониана формализм
Множители Лагранжа

Колебания и волны

Формулы
Простые колебания
Управляемые и затухающие колебания
Связанные колебания (точечные массы и пружины)
Связанные колебания (маятник)
Связанные колебания (другие системы)
Механические волны

Движение в центральном потенциале

Формулы
Проблема Кеплера
Другие центральные потенциалы
Рассеяние (твердые сферы, центральные потенциалы)

Релятивистская кинематика и динамика

Формулы
Собственное время
Правильная длина
Преобразование Лоренца
Добавление скорости
Доплеровский сдвиг
Столкновения (с участием только массивных частиц)
Столкновения (включая безмассового партнера)
Распад (с участием только массивных партнеров)
Распад (включая безмассового партнера)
Релятивистская энергия и импульс
Сила

Общая физика

Формулы
Плавучесть (жидкости)
Плавучесть (газы)
Статические и текущие жидкости
Статистика Больцмана
Тепловое расширение и проводимость
Удельная и скрытая теплота
Законы излучения
Закон идеального газа
Поверхность напряжение
Кинетическая теория
Первое начало термодинамики и идеал газовый закон
Второй закон термодинамики
Энтропия
Энтропия с участием идеальных газов
Анализ ошибок и математика

% PDF-1.4 % 386 0 объект > эндобдж xref 386 231 0000000017 00000 н. 0000005093 00000 н. 0000007361 00000 н. 0000007718 00000 н. 0000007995 00000 н. 0000008204 00000 н. 0000008548 00000 н. 0000008854 00000 н. 0000009187 00000 н. 0000009375 00000 п. 0000009556 00000 п. 0000009724 00000 н. 0000009900 00000 н. 0000010254 00000 п. 0000010536 00000 п. 0000010883 00000 п. 0000011136 00000 п. 0000011441 00000 п. 0000011809 00000 п. 0000011952 00000 п. 0000012047 00000 п. 0000012323 00000 п. 0000012700 00000 п. 0000013004 00000 п. 0000013285 00000 п. 0000013583 00000 п. 0000013850 00000 п. 0000014039 00000 п. 0000014217 00000 п. 0000014384 00000 п. 0000014593 00000 п. 0000014926 00000 п. 0000015102 00000 п. 0000015422 00000 п. 0000015692 00000 п. 0000016008 00000 п. 0000016253 00000 п. 0000016537 00000 п. 0000016860 00000 п. 0000017038 00000 п. 0000017276 00000 п. 0000017581 00000 п. 0000017950 00000 п. 0000018241 00000 п. 0000018513 00000 п. 0000018765 00000 п. 0000018931 00000 п. 0000019141 00000 п. 0000019357 00000 п. 0000019542 00000 п. 0000019824 00000 п. 0000020229 00000 п. 0000020404 00000 п. 0000020561 00000 п. 0000020726 00000 п. 0000020989 00000 п. 0000021203 00000 п. 0000021483 00000 п. 0000021651 00000 п. 0000021918 00000 п. 0000022144 00000 п. 0000022368 00000 п. 0000022591 00000 п. 0000022818 00000 п. 0000023072 00000 п. 0000023239 00000 п. 0000023435 00000 п. 0000023597 00000 п. 0000023795 00000 п. 0000024018 00000 п. 0000024204 00000 п. 0000024443 00000 п. 0000024636 00000 п. 0000024831 00000 п. 0000025060 00000 п. 0000025297 00000 п. 0000025488 00000 н. 0000025743 00000 п. 0000025980 00000 п. 0000026236 00000 п. 0000026488 00000 п. 0000026672 00000 п. 0000027212 00000 н. 0000027339 00000 н. 0000027561 00000 п. 0000036258 00000 п. 0000036433 00000 н. 0000036763 00000 н. 0000036932 00000 п. 0000037148 00000 п. 0000037781 00000 п. 0000037966 00000 п. 0000038261 00000 п. 0000038487 00000 п. 0000045405 00000 п. 0000045589 00000 п. 0000045745 00000 п. 0000045968 00000 п. 0000049491 00000 п. 0000049763 00000 п. 0000050812 00000 п. 0000051073 00000 п. 0000051340 00000 п. 0000051512 00000 п. 0000051686 00000 п. 0000051858 00000 п. 0000052044 00000 п. 0000052236 00000 п. 0000052421 00000 п. 0000052579 00000 п. 0000052813 00000 п. 0000052981 00000 п. 0000053174 00000 п. 0000053360 00000 п. 0000053527 00000 п. 0000053690 00000 н. 0000053904 00000 п. 0000054157 00000 п. 0000054373 00000 п. 0000054622 00000 п. 0000054957 00000 п. 0000055251 00000 п. 0000055559 00000 п. 0000055843 00000 п. 0000056029 00000 п. 0000056212 00000 п. 0000056534 00000 п. 0000056714 00000 п. 0000056877 00000 п. 0000057227 00000 п. 0000057400 00000 п. 0000057730 00000 п. 0000057992 00000 н. 0000058332 00000 п. 0000058588 00000 п. 0000058886 00000 п. 0000059218 00000 п. 0000059398 00000 п. 0000059650 00000 п. 0000059976 00000 п. 0000060379 00000 п. 0000060644 00000 п. 0000060912 00000 п. 0000061178 00000 п. 0000061448 00000 п. 0000061729 00000 п. 0000061945 00000 п. 0000062275 00000 п. 0000062494 00000 п. 0000062662 00000 п. 0000062864 00000 н. 0000063149 00000 п. 0000063313 00000 п. 0000063559 00000 п. 0000063773 00000 п. 0000064048 00000 п. 0000064319 00000 п. 0000064599 00000 п. 0000064813 00000 п. 0000065085 00000 п. 0000065293 00000 п. 0000065499 00000 н. 0000065770 00000 п. 0000066095 00000 п. 0000066392 00000 п. 0000066697 00000 п. 0000066929 00000 п. 0000067132 00000 п. 0000067434 00000 п. 0000067756 00000 п. 0000068013 00000 п. 0000068301 00000 п. 0000068624 00000 п. 0000068870 00000 п. 0000069341 00000 п. 0000069785 00000 п. 0000070056 00000 п. 0000070503 00000 п. 0000070783 00000 п. 0000071044 00000 п. 0000071242 00000 п. 0000071412 00000 п. 0000071628 00000 п. 0000071799 00000 н. 0000072018 00000 п. 0000072371 00000 п. 0000072658 00000 п. 0000072955 00000 п. 0000073227 00000 н. 0000073524 00000 п. 0000073803 00000 п. 0000074061 00000 п. 0000074406 00000 п. 0000074672 00000 п. 0000074876 00000 п. 0000075185 00000 п. 0000075390 00000 п. 0000075672 00000 п. 0000075923 00000 п. 0000076217 00000 п. 0000076521 00000 п. 0000076758 00000 п. 0000077039 00000 п. 0000077277 00000 п. 0000077526 00000 п. 0000077788 00000 п. 0000078108 00000 п. 0000078419 00000 п. 0000078660 00000 п. 0000078990 00000 п. 0000079174 00000 п. 0000079560 00000 п. 0000079784 00000 п. 0000079999 00000 н. 0000082837 00000 п. 0000082990 00000 п. 0000083147 00000 п. 0000083356 00000 п. 0000084097 00000 п. 00000 00000 н. 0000092387 00000 п. 0000092440 00000 п. 0000092930 00000 н. 0000093186 00000 п. 0000094314 00000 п. 0000094426 00000 п. 0000095689 00000 п. 0000096063 00000 п. 0000096312 00000 п. 0000097279 00000 н. 0000005152 00000 н. трейлер ] >> startxref 0 %% EOF 387 0 объект > эндобдж 616 0 объект > транслировать xWiTi * V1 Ž.`YCMqaSpY \` C ڨ (Y5 Z = 93? F ~ gWw}

Давайте займемся классической сложной физической задачей. Будет весело – Обещание

Вот программа.

Если вы действительно хотите взглянуть на код, вот он. Честно говоря, я до сих пор не совсем понимаю кнопки или взаимодействие с мышью, но у меня все заработало.

Попробуйте разные пути. Посмотри, сможешь ли ты ускорить время. Да, если вы заставите трек идти выше начальной точки, это не сработает (надеюсь, вы это уже тестировали). Я попытался добавить комментарии к коду, чтобы вы могли поиграть с ним.Вы можете изменить две вещи. Сначала отрегулируйте количество подвижных точек на пути. Во-вторых, настройте расположение второй точки. Оба могут быть забавными.

Численное решение

Ключ к численному решению – взять сложную задачу и разбить ее на кучу более простых задач. Что, если бы между двумя фиксированными точками была только одна подвижная точка?

Здесь я могу перемещать среднюю позицию вверх и вниз (с переменной y ) и вычислять время, необходимое для перехода от позиции 1 к позиции 2.Позвольте мне сделать это немного иначе, чем исходная задача. В этом случае я позволю бусинке начинаться в позиции 1 с некоторой начальной скоростью. Бусинка будет ускоряться по мере продвижения к средней точке (при условии, что я перемещаю ее ниже начальной точки).

Подсчитать время достижения средней точки несложно, но немного утомительно. Сначала я рассчитаю скорость бусинки в средней точке. Здесь я могу использовать принцип работы-энергии. Используя гравитационную потенциальную энергию и изменение кинетической энергии, я получаю:

Для времени в пути мне нужна средняя скорость и расстояние.Средняя скорость – это сумма начальной и конечной скорости, разделенная на два (поскольку ускорение постоянно). Я назову расстояние для этого частичного пути переменной s . Он будет иметь следующее значение.

Возможно, вы заметили, что я называю «вниз» положительное направление y. Надеюсь, это вас не испортило. Теперь я могу сложить среднюю скорость с расстоянием, чтобы получить время скольжения. Помните, что бусинка должна оставаться на проволоке, так что это одномерная проблема.

Да, и v ₂ , и s зависят от вертикального положения — y . Но ждать! Мы еще не закончили. Теперь я должен сделать то же самое для пути от середины до точки 2. Запомните две важные вещи. Во-первых, конечная скорость для первой части является начальной скоростью для второй части. Во-вторых, очень возможно, что ускорение борта будет отрицательным (если провод идет вверх).

Кинематика и исчисление – Задачи – Гипертекст по физике

Кинематика и исчисление – Задачи – Гипертекст по физике

Проблемы

практика

1. Выведите уравнения движения для постоянного рывка.
2. Положение объекта описывается следующим полиномом от 0 до 10 с…

   с = т ³ -15 т ² + 54 т

   , где s, – в метрах, t, – в секундах, а положительное – вперед. Определить…

   1. зависимость скорости объекта от времени
   2. ускорение объекта как функция времени
   3. максимальная скорость объекта
   4. минимальная скорость объекта
   5. время, когда объект двигался назад
   6. раз, когда объект возвращался в исходное положение
   7. средняя скорость объекта
   8. средняя скорость объекта
3. На графике ниже показано ускорение гидравлического лифта в четырехэтажном школьном здании как функция времени.
   График начинается с t = 0 с, когда дверь лифта закрылась на втором этаже, и заканчивается на t = 20 с, когда дверь открылась на другом этаже. Предположим, что положительные направления смещения, скорости и ускорения направлены вверх. Определять…
   1. максимальная скорость лифта
   2. продолжительность кратковременного рывка лифта с центром 17,5 с
   Нарисуйте соответствующие графики…
   3. скорость-время
   4. время позиции
   Определять…
   5. наиболее вероятный этаж, на котором остановился лифт
4. youtu.be / R1g07RpTPFE В один прекрасный день на неиспользуемой взлетно-посадочной полосе в аэропорту спортивный автомобиль высокого класса провел тест производительности от 0 до 400 км / ч. Его скорость изменялась согласно следующей функции …

   v = a (1 – e ^{– t / b} )

   где…

   =	128,1 м / с
   б =	13,31 с

   Ответьте на эти три связанных вопроса.

   1. Сколько времени потребовалось автомобилю, чтобы разогнаться до 400 км / ч (111,111 м / с)?
   2. Какое было его среднее ускорение во время теста?
   3. Какова теоретическая максимальная скорость автомобиля?

   Ответьте на эти три связанных вопроса.

   4. Выведите выражение для ускорения как функции времени.
   5. Какое ускорение было у автомобиля в начале теста?
   6. С каким ускорением автомобиль разгонялся до 400 км / ч?

   Ответьте на эти два связанных вопроса.

   7. Выведите выражение для смещения как функции времени.
   8. Какое расстояние проехала машина при ускорении?

   После достижения целевой скорости 400 км / ч (111,111 м / с) водитель немедленно выключил двигатель и нажал на тормоза. Автомобиль полностью остановился через 9.451 с. Ответьте на эти три связанных вопроса.

   9. Какое было среднее ускорение автомобиля при остановке?
   10. Какое расстояние проехала машина при остановке?
   11. Какое общее расстояние проехала машина от старта до финиша.

алгебраический

1. Определите соотношение ускорения и скорости для постоянного рывка. (Ради аргументации назовем это пятым уравнением движения.)

исчисление

1. Скорость объекта v в метрах в секунду описывается следующей функцией времени, t , в секундах в течение значительного промежутка времени…

   v = 4 т (4- т ) + 8

   Предполагая, что объект расположен в начале координат ( с, = 0 м), когда t = 0 с, определяют…

   1. положение объекта, с , как функция времени
   2. ускорение объекта, a , как функция времени
   3. максимальная скорость объекта
   4. если и когда, когда объект останавливается
   5. , если и когда объект возвращается в исходную точку ( с, = 0 м)
2. Следующие уравнения описывают смещение как функцию времени.Выведите последующие уравнения для скорости и ускорения как функции времени. (Символы A , f , j , k , s ₀ , π и τ – все константы.)
   1. с = ⅙ jt ³
   2. с = A sin (2π футов )
   3. с = с ₀ e ^{– т / τ}
3. Грубая математическая модель проходки туннелей представлена ​​уравнением… где v – скорость туннелирования; с – длина тоннеля; а k – постоянная.
   1. Каким образом (увеличивается или уменьшается) изменяется скорость туннелирования при удлинении туннеля? Какой инженерный аспект туннелирования вызывает это изменение?
   2. Определите следующие величины как функцию времени…
      1. длина тоннеля
      2. скорость проходки
      3. туннельное ускорение
   (Это довольно сложная проблема для студентов, которые только начали изучать математику.)
4. Упрощенная модель автомобиля, ускоряющегося с места по прямой по прямой, задается следующим уравнением…

   v ( t ) = a (1- e ^{– bt} )

   Где v ( t ) – мгновенная скорость автомобиля в футах в секунду, t – время в секундах, а A и b – постоянные.
   1. скорость
      1. Какие единицы используются в коэффициентах a и b ?
      2. В чем физический смысл коэффициента а ?
      3. Какая скорость автомобиля при т = 0 с?
      4. Какова асимптота этой функции при t → ∞?
      5. Нарисуйте график зависимости скорости от времени. Включите значение v (0 с) и асимптоту v как t → ∞.
   2. позиция
      1. Выведите уравнение с ( t ) для мгновенного положения автомобиля как функции времени.(Убедитесь, что ваша функция имеет значение с = 0 м, когда t = 0 с.)
      2. Какова асимптота этой функции при t → ∞?
      3. Каков физический смысл наклона этой асимптоты?
      4. Нарисуйте график зависимости положения от времени. Включите значение с (0 с) и наклон асимптоты с как t → ∞.
   3. разгон
      1. Выведите уравнение a ( t ) для мгновенного ускорения автомобиля как функции времени.
      2. Какое ускорение автомобиля при т = 0 с?
      3. Какова асимптота этой функции при t → ∞?
      4. Нарисуйте график зависимости ускорения от времени. Включите значение a (0 с) и асимптоту a как t → ∞.
   4. youtu.be/9eH837Fh2Oo Примените эту модель к настоящему, но исключительному автомобилю – Red Victor 1. У этого автомобиля время разгона от нуля до шестидесяти составляет около одной секунды, а время четверти мили – около восьми секунд.Другими словами, пусть…

      v (1 сек) =	88 фут / сек
      с (8 с) =	1320 футов

      затем определите…
      1. значения коэффициентов a и b [я думаю, что это можно сделать только с помощью красивого калькулятора.]
      2. максимальная скорость, а
      3. максимальное ускорение.
5. Положение объекта описывается следующим полиномом за 10 с…

   с = т ³ -12 т ² + 24 т

   , где с, – в метрах, а т, – в секундах.

   Определить…

   1. зависимость скорости объекта от времени
   2. ускорение объекта как функция времени
   3. максимальная скорость объекта
   4. минимальная скорость объекта
   5. время, когда объект двигался назад
   6. время (с), когда объект находился в исходной точке ( с = 0 м)
   7. время (а), когда объект вернулся в исходное положение
   8. средняя скорость объекта
   9. средняя скорость объекта

статистический

1. лифт.txt
   Данные о времени ускорения в сопроводительном текстовом файле были записаны студентом, когда он ехал на лифте в офисном здании. Студент прошел из вестибюля на самый верхний этаж. Используйте эти данные и ваше любимое графическое приложение для решения следующих задач.
   1. Скорость
      1. Постройте график скорость-время.
      2. Определите крейсерскую скорость лифта.
   2. Рабочий объем
      1. Постройте график смещения-времени.
      2. Определите высоту здания.
      3. Оценить этажность дома.
2. table-splits.shtml
   Сплит – это время, когда бегун достигает контрольной дистанции в гонке. Например, в беге на 100 метров промежуточное время берется каждые 10 метров. Спуски для некоторых из самых быстрых спринтеров в мире указаны на прилагаемой веб-странице. Подгоните полином высокого порядка (четвертый, пятый, шестой или выше) к данным одного из этих спортсменов с помощью приложения для анализа данных.Определите скорость вашего спринтера как функцию времени, взяв производную от этого многочлена. Постройте график этой новой функции, а затем проанализируйте ее.
   1. Какова была начальная и конечная скорости бегуна?
   2. Какая была максимальная скорость бегуна и когда это произошло?
   3. Какая была средняя скорость бегуна?
   4. Скорость бегуна увеличилась, уменьшилась или осталась примерно такой же ближе к концу забега?
   5. Как вы думаете, насколько хорошо этот график описывает реальную производительность бегуна? Есть ли на графике проблемные участки? Как можно изменить функцию, чтобы улучшить посадку?
3. таблицы-табеля.shtml
   Любительский дрэг-рейсинг открыт для всех, у кого есть уличный транспорт (легковой автомобиль, легкий грузовик или мотоцикл), действующие водительские права, страховка, топливо и достаточно денег для покрытия регистрационного сбора. Он популярен в США, Великобритании и Австралии. Гонки проходят на прямой ровной трассе длиной четверть мили. В конце забега каждому участнику выдается небольшой бумажный «листок времени» с данными, собранными во время забега. Данные варьируются от места к месту, но почти всегда присутствуют следующие элементы.
   • Время реакции (R / T) – это время между сигналом о запуске и моментом, когда водитель фактически заставляет автомобиль двигаться вперед.
   • Истекшее время (ET) – это разбиения, записанные в нескольких позициях. Истекшее время начинается с момента пересечения автомобилем линии старта, а не с момента подачи сигнала о старте (как это делается в легкой атлетике).
   • Мгновенная скорость измеряется на мили (на полпути) и ¼ мили (на финише). Мы не будем использовать этот номер для этой деятельности.
   На веб-странице, которая сопровождает эту проблему, есть ссылки на изображения 50 различных временных бюллетеней – выборка из тысяч, собранных энтузиастами во время перетаскивания.com.
   1. Выберите разовый промах и перенесите информацию в таблицу, как показано ниже.
   2. Добавьте время реакции к истекшему времени, чтобы получить время гонки. (Я придумал этот термин. Я не знаю, как он на самом деле называется.)

      Необработанные данные об увольнении во времени для дрэг-рейсинга

      расстояние			осталось в машине время (с)		правый автомобиль время (с)
      (фут)	(миль)	(м)	истекло	гонка	истекло	гонка
      0000	0	000	0		0
      0060	–	018
      0330	–	101
      0660	⅛	201
      1000	–	305
      1320	¼	402

   3. Постройте график времени для каждой машины.(Сделайте два графика.)
   4. Выполните следующую аппроксимацию кривой на каждом графике…
      1. линейный
      2. квадратичный
      3. куб.
   5. Заполните следующую таблицу. Обязательно укажите в своих ответах правильные единицы. Поскольку вы сделали три разных подбора кривой, некоторые величины можно найти более чем одним методом. В разделе «методология» укажите, какая функция (линейная, квадратичная, кубическая), какой коэффициент ( t ⁰ , t ¹ , t ² , t ³ ), сколько масштабирования (× 2, × 3, × 4,…, ÷ 2, ÷ 3, ÷ 4,…) потребовалось, чтобы получить ответ.

      Промежуток времени Drag Racing – анализ

      количество	методология	левая машина	правый вагон
      средняя скорость
      начальная скорость
      среднее ускорение
      начальное ускорение
      средний рывок

4. мустанг.txt
   В 2016 году журнал Road & Track (платная ссылка) протестировал восемь очень дорогих и очень быстрых автомобилей, чтобы определить автомобиль года с высокими характеристиками. Данные испытания на ускорение для Ford Mustang Shelby GT350R 2016 года выпуска приведены в прилагаемом текстовом файле с разделителями-табуляторами. (Мустанг не получил награду в том году.) Поскольку данные были собраны в Соединенных Штатах, основные скорости были выбраны кратными 10 милям в час. Для вашего удобства эти скорости были преобразованы в единицы СИ.
   1. Используя ваше любимое приложение для анализа данных, создайте диаграмму разброса скорости (в метрах в секунду) в зависимости отвремя (в секундах) и добавьте подходящую кривую наилучшего соответствия.
   2. Используйте результаты аппроксимации кривой и свои знания в области вычислений, чтобы создать уравнения для…
      1. ускорение как функция времени
      2. смещение как функция времени
   3. Во время этого теста…
      1. Увеличилось ли расстояние, пройденное автомобилем, уменьшилось или осталось прежним?
      2. Скорость автомобиля увеличилась, уменьшилась или осталась прежней?
      3. Ускорение автомобиля увеличилось, уменьшилось или осталось прежним?
5. зарм-кинематика.txt
   Данные в сопровождающем текстовом файле с разделителями табуляции дают мгновенную скорость вертикально установленного поршня, используемого для запуска снарядов, как функцию времени. Используйте этот набор данных и ваше любимое приложение для анализа данных, чтобы решить следующие проблемы.
   1. Используя предоставленные данные, создайте график скорость-время и определите…
      1. максимальная скорость и
      2. средняя скорость поршня при его ускорении вверх
   2. Определите ускорение поршня как функцию времени, создайте график ускорения-времени и определите…
      1. максимальное ускорение и
      2. среднее ускорение поршня при его ускорении вверх
   3. Определите смещение поршня как функцию времени, создайте график смещения-времени и определите…
      1. окончательное перемещение поршня после его остановки

   Данные адаптированы из Кампена, Качмарчика и Рата; 2006 г.

Нет постоянных условий.

1. Механика
   1. Кинематика
      1. Движение
      2. Расстояние и перемещение
      3. Скорость и скорость
      4. Разгон
      5. Уравнения движения
      6. Свободное падение
      7. Графики движения
      8. Кинематика и расчет
      9. Кинематика в двух измерениях
      10. Снарядов
      11. Параметрические уравнения
   2. Динамика I: Сила
      1. Силы
      2. Сила и масса
      3. Действие-реакция
      4. Масса
      5. Динамика
      6. Статика
      7. Трение
      8. Силы в двух измерениях
      9. Центростремительная сила
      10. Кадры справки
   3. Энергия
      1. Работа
      2. Энергия
      3. Кинетическая энергия
      4. Потенциальная энергия
      5. Сохранение энергии
      6. Мощность
      7. Простые машины
   4. Dynamics II: Импульс
      1. Импульс и импульс
      2. Сохранение импульса
      3. Импульс и энергия
      4. Импульс в двух измерениях
   5. Вращательное движение
      1. Кинематика вращения
      2. Инерция вращения
      3. Вращательная динамика
      4. Статика вращения
      5. Угловой момент
      6. Энергия вращения
      7. Прокатный
      8. Вращение в двух измерениях
      9. Сила Кориолиса
   6. Планетарное движение
      1. Геоцентризм
      2. Гелиоцентризм
      3. Вселенская гравитация
      4. Орбитальная механика I
      5. Гравитационная потенциальная энергия
      6. Орбитальная механика II
      7. Плотность вытянутых тел
   7. Периодическое движение
      1. Пружины
      2. Простой генератор гармоник
      3. Маятники
      4. Резонанс
      5. Эластичность
   8. Жидкости
      1. Плотность
      2. Давление
      3. Плавучесть
      4. Расход жидкости
      5. Вязкость
      6. Аэродинамическое сопротивление
      7. Режимы потока
2. Теплофизика
   1. Тепло и температура
      1. Температура
      2. Тепловое расширение
      3. Атомная природа вещества
      4. Газовые законы
      5. Кинетико-молекулярная теория
      6. Фазы
   2. Калориметрия
      1. Явное тепло
      2. Скрытая теплота
      3. Химическая потенциальная энергия
   3. Теплопередача
      1. Проводимость
      2. Конвекция
      3. Радиация
   4. Термодинамика
      1. Тепло и работа
      2. Диаграммы давление-объем
      3. Двигатели
      4. Холодильники
      5. Энергия и энтропия
      6. Абсолютный ноль
3. Волны и оптика
   1. Волновые явления
      1. Природа волн
      2. Периодические волны
      3. Интерференция и суперпозиция
      4. Интерфейсы и барьеры
   2. Звук
      1. Природа звука
      2. Интенсивность
      3. Эффект Доплера (звук)
      4. Ударные волны
      5. Дифракция и интерференция (звук)
      6. Стоячие волны
      7. ударов
      8. Музыка и шум
   3. Физическая оптика
      1. Природа света
      2. Поляризация
      3. Эффект Доплера (световой)
      4. Черенковское излучение
      5. Дифракция и интерференция (свет)
      6. Тонкопленочная интерференция
      7. Цвет
   4. Геометрическая оптика
      1. Отражение
      2. Преломление
      3. Зеркала сферические
      4. Сферические линзы
      5. Аберрация
4. Электричество и магнетизм
   1. Электростатика
      1. Электрический заряд
      2. Закон Кулона
      3. Электрическое поле
      4. Электрический потенциал
      5. Закон Гаусса
      6. Проводников
   2. Электростатические приложения
      1. Конденсаторы
      2. Диэлектрики
      3. Батареи
   3. Электрический ток
      1. Электрический ток
      2. Электрическое сопротивление
      3. Электроэнергия
   4. цепей постоянного тока
      1. Резисторы в цепях
      2. Батареи в цепях
      3. Конденсаторы в цепях
      4. Правила Кирхгофа
   5. Магнитостатика
      1. Магнетизм
      2. Электромагнетизм
      3. Закон Ампера
      4. Электромагнитная сила
   6. Магнитодинамика
      1. Электромагнитная индукция
      2. Закон Фарадея
      3. Закон Ленца
      4. Индуктивность
   7. Цепи переменного тока
      1. Переменный ток
      2. RC цепи
      3. Цепи РЛ
      4. Цепи LC
   8. Электромагнитные волны
      1. Уравнения Максвелла
      2. Электромагнитные волны
      3. Электромагнитный спектр
5. Современная физика
   1. Теория относительности
      1. Пространство-время
      2. Масса-энергия
      3. Общая теория относительности
   2. Quanta
      1. Излучение черного тела
      2. Фотоэффект
      3. Рентгеновские снимки
      4. Антиматерия
   3. Волновая механика
      1. Волны материи
      2. Атомарные модели
      3. Полупроводники
      4. Конденсированные вещества
   4. Ядерная физика
      1. Изотопы
      2. Радиоактивный распад
      3. Период полураспада
      4. Энергия связи
      5. Деление
      6. Fusion
      7. Нуклеосинтез
      8. Ядерное оружие
      9. Радиобиология
   5. Физика элементарных частиц
      1. Квантовая электродинамика
      2. Квантовая хромодинамика
      3. Квантовая динамика вкусов
      4. Стандартная модель
      5. Помимо стандартной модели
6. Фонды
   1. шт.
      1. Международная система единиц
      2. Гауссова система единиц
      3. Британо-американская система единиц
      4. Разные единицы
      5. Время
      6. Преобразование единиц
   2. Измерение
      1. Значащие цифры
      2. По порядку величины
   3. Графики
      1. Графическое представление данных
      2. Линейная регрессия
      3. Подгонка кривой
      4. Исчисление
   4. Векторы
      1. Тригонометрия
      2. Сложение и вычитание векторов
      3. Векторное разрешение и компоненты
      4. Умножение векторов
   5. ссылку
      1. Специальные символы
      2. Часто используемые уравнения
      3. Физические константы
      4. Астрономические данные
      5. Периодическая таблица элементов
      6. Люди в физике
7. Назад дело
   1. Предисловие
      1. Об этой книге
   2. Связаться с автором
      1. гленнелерт.нас
      2. Behance
      3. Instagram
      4. Твиттер
      5. YouTube
   3. Аффилированные сайты
      1. hypertextbook.com
      2. midwoodscience.org

[PDF] Путеводитель по физическим проблемам, часть 1: механика, теория относительности и электродинамика

ПОКАЗЫВАЕТ 1-10 ИЗ 13 ССЫЛКИ

СОРТИРОВАТЬ ПО НАИБОЛЕЕ ЗНАМЕНИТОМУ Взаимодействие с ньютоновской теорией дрэг-рейсер – сила трения, спортивный парашютный спорт – стрельба из лука с использованием вязкой силы – методы решения силы пружины простой гармонический осциллятор затухает… Развернуть На материале для выпускников, эта книга представляет отработанные решения широкого круга информационных задач.Эти проблемы были… Развернуть

Статическое и динамическое электричество

Секционное игровое устройство, имеющее центральную часть и множество относительно длинных рычагов, прикрепленных с возможностью отсоединения к центральной части. Плечи имеют опорные поверхности, которые входят в контакт с опорными поверхностями на… Развернуть

Механика жидкости, Том 6 курса теоретической физики, 2-е изд., Элмсфорд

Механика, Том 1 курса теоретической физики, 3-е изд., Элмсфорд

• Классическая теория полей, Том 2 курса теоретической физики,
• 1976

Классическая электродинамика, Нью-Йорк: Джон

Введение в сверхпроводимость

Подходит для промежуточных или продвинутых курсов по сверхпроводимости, это издание было пересмотрено, чтобы включить много новых разработок в области сверхпроводимости.Расширенный охват темы включает… Развернуть

О динамике системы твердых тел

Существующие трактаты по рациональной механике не уделяют внимания динамике системы твердых тел, ограничивая свой интерес общими теоремами механики, теория вращения… Развернуть

Математические методы для физиков

Векторный анализ. Кривые координаты, тензоры. Детерминанты и матрицы. Теория групп. Бесконечная серия. Функции комплексной переменной I.Функции комплексного переменного II. Дифференциальные уравнения.… Развернуть

Институт проблем механики им. Ишлинского РАН (ИПМех РАН)

Текущие и предстоящие события

04-08 октября 2021, Цахкадзор, Армения

01-03 декабря 2021 г.

Прошедшие события

01-03 декабря 2020

24-26 августа 2020 г.

03-05 декабря 2019

01-06 октября 2019, Дилижан, Армения

05-07 декабря 2018

27-29 ноября 2018 г.

Сентябрь 3, 2018

Проф. Александр Манжиров скончался в своем доме 03 сентября 2018 г. в Москве, 61 год. Он был профессором, иностранным членом Национальной академии наук Республики Армения, заведующим лабораторией моделирования в твердом теле. Механика в ИПМех РАН (сайт Александра Манжирова).

20-25 августа 2018 г.

08-10 августа 2018 г., Владивосток

21-24 ноября 2017 г.

7-9 ноября 2017 г.

1-3 ноября 2017 г.

2-7 октября 2017 г., Цахкадзор, Армения

V Международная конференция «Актуальные проблемы механики сплошной среды» со специальным заседанием в честь 60-летия Александра Манжирова
Сайт и информация: www.mechins.sci.am/tpcm2017/

24 сентября 2017 г.

Проф. Роберт Гольдштейн скончался у себя дома 24 сентября 2017 года в Москве, в возрасте 77 лет. Член-корреспондент РАН, Заведующий лабораторией механики прочности и Разрушение материалов и конструкций в ИПМех РАН (о Роберте Гольдштейне).

5-9 декабря 2016 г.

30 ноября – 2 декабря 2016 г.

11-13 ноября 2015 г.

23-27 июня 2015 г.

25-28 июня 2015 г., Калининград

21-23 июня 2015 г., Калининград

2-3 декабря 2014 г.

25-28 ноября 2014 г.

26-29 ноября 2013 г.

25-28 июня 2013 г., г.-Петербург

24-28 сентября 2012 г., г. Севастополь

I Международная конференция « Актуальные проблемы прикладной физики (APAP’12) ».
Объявление

18-22 июня 2012 г.

28-30 мая 2012 г.

29-30 ноября 2011 г.

5-й Всероссийский семинар « Аэрофизика и физическая механика классической и квантовой физики АФМ-2011 ». >>> Программа

27-30 сентября 2011 г., Владивосток

26-29 сентября 2011 г.

24-30 августа 2011 г., г. Нижний Новгород

21-24 июня 2011 г.

8-9 декабря 2010 г.

4-й Всероссийский семинар « Аэрофизика и физическая механика классической и квантовой физики АФМ-2010 ».>>> Программа

2-3 декабря 2009 г.

3-й Всероссийский семинар « Аэрофизика и физическая механика классической и квантовой физики АФМ-2009 ». >>> Программа

24-27 июня 2009 г.

Международная конференция « Потоки и структуры в жидкостях: Физика геосфер ». >>>

26-30 января 2009 г.

Международная конференция « Управление динамическими системами ». >>>

Ньютоновская механика – AP Physics B

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.