II закон Ньютона. III закон Ньютона. Физика. 10 класс. – Объяснение нового материала.
Комментарии преподавателяВТОРОЙ ЗАКОН НЬЮТОНАВторой закон Ньютона определяет:
как движется тело, если на него действует сила?
– с ускорением!
Причиной возникновения ускорения является сила, действующая на тело.
Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу,
и обратно пропорционально его массе.
Расчетная формула:
Единица измерения силы в СИ: 1Н
Сила 1Н -это такая сила ,которая телу массой 1кг придает ускорение1м/c2.
Ускорение, приобретаемое телом в результатедействия силы, направлено также, как и сила.
2-ой закон Ньютона справедлив только в инерциальных системах отсчета.
Известно, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы.
Представьте, что вы и ваш друг катаетесь на скейте, причём друг катается на одном скейте с братом (см. Рис. 1).
Рис. 1. Приобретение ускорения при взаимодействии
Ваша масса – , масса друга с братом – . Если вы отталкиваетесь друг от друга, то приобретаете ускорения, которые направлены по одной прямой в противоположные стороны. Отношение масс участников этого процесса обратно пропорционально отношению модулю ускорений.
Следовательно:
Согласно второму закону Ньютона:
– сила, с которой на вас действует друг с братом
– сила, с которой вы действуете на друга с братом
Так как ускорения противонаправленные, то:
Данное равенство выражает 
Более простая формулировка третьего закона Ньютона звучит так: сила действия равна силе противодействия.
Каждая из сил взаимодействия приложена к разным телам. Следовательно, при рассмотрении второго закона Ньютона для каждого тела в отдельности, силы взаимодействия между телами не могут компенсировать друг друга, хотя формально:
Для иллюстрации этого закона возьмём два динамометра (см. Рис. 2). Один из них наденем колечком на что-то неподвижное, например на гвоздь в стене, а второй соединим с первым крючками. И потянем за колечко второго динамометра. Оба прибора покажут одинаковые по модулю силы натяжения.
Рис. 2. Опыт с динамометрами (Источник)
Сила действия и сила противодействия – это всегда силы одной природы. Например, в предыдущем опыте сила действия первого динамометра на второй и сила действия второго динамометра на первый – это силы упругости; силы действия одного заряженного тела на другое и наоборот – это силы электрической природы.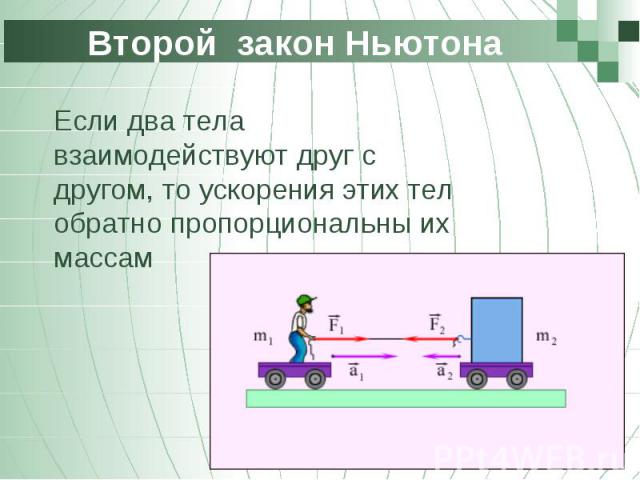
Таким образом, первый закон Ньютона утверждает: если на тело не действует посторонние тела, то оно находится в состоянии покоя или равномерного прямолинейного движения относительно инерциальных систем отсчёта. Из него следует, что причиной изменения скорости тела является сила. Второй закон Ньютона объясняет, как движется тело под действием силы. Он устанавливает количественное отношение между ускорением и силой.
В первом и во втором законах Ньютона рассматривается только одно тело. В третьем законе рассматривается взаимодействие двух тел с силами, одинаковыми по модулю и противоположными по направлению. Эти силы называют силами взаимодействия. Они направлены вдоль одной прямой и приложены к разным телам.
При выводе третьего закона Ньютона мы видели, что при взаимодействии двух тел отношение двух ускорений, которые приобретает первое и второе тело, является величиной постоянной. Причём отношение этих ускорений не зависит от характера взаимодействия, следовательно, оно определяется самими телами, какой-то его характеристикой. Такая характеристика называется
Причём отношение этих ускорений не зависит от характера взаимодействия, следовательно, оно определяется самими телами, какой-то его характеристикой. Такая характеристика называется
Рис. 3. Взаимодействие двух тел с разными массами
Закон, который описывает соотношение масс тел и ускорений, приобретённых в результате взаимодействия, называется 
Домашняя работа.
Задание 1. Ответь на вопросы.
- Причина возникновения ускорения – …
- Как движется тело, когда сумма действующих на него сил равна нулю?
- Какие из величин: сила, скорость, ускорение, перемещение – всегда совпадают по направлению?
- Формула II закона Ньютона.
- В чем суть III закона Ньютона?
- Формула III закона Ньютона?
- Где в повседневной жизни используется III закона Ньютона?
Задание 2. Найти графическим построением равнодействующую cилу.
Задание 3. Заполните пропуски:
1) Под действием силы тело движется _____________________________
2) Если при неизменной массе тела увеличить силу в 2 раза, то ускорение _____________ в ______раз(а).
3) Если массу тела уменьшить в 4 раза, а силу, действующую на тело, увеличить в 2 раза, то ускорение ____________________ в _______раз(а).
4) Если силу увеличить в 3 раза, а массу _______________________________, то ускорение останется неизменным.
После удара футболиста неподвижный мяч массой 500 г получает скорость 10 м/с. Определите среднюю силу удара, если он длился в течение 0,5 с.
К занятию прикреплены файлы ” Самостоятельная работа.”. Вы можете скачать файлы и решить задания самостоятельно в любое удобное для вас время.
Использованные источники:
- http://interneturok.ru/ru/school/physics/10-klass/
- http://znaika.ru/catalog/10-klass/physics/
- http://www.youtube.com/watch?v=f0i9ok3ajW0
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.
 2 Динамика
2 Динамика - 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.
 4 Электромагнитные колебания и волны
4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.
 2 Ядерная физика
2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Второй закон Ньютона | Частная школа. 8 класс
Конспект по физике для 8 класса «Второй закон Ньютона». Как связаны между собой сила и ускорение. Как формулируется второй закон Ньютона.
Конспекты по физике Учебник физики Тесты по физике
В случае, когда на тело не действуют силы или равнодействующая всех сил, действующих на тело, равна нулю, тело может двигаться только равномерно, т. е. без ускорения. Действие на тело других тел с некоторой силой приводит к изменению скорости тела. А если изменяется скорость, значит, возникает ускорение.
ВЗАИМОСВЯЗЬ СИЛЫ И УСКОРЕНИЯ
Как же связаны между собой сила, действующая на тело, и ускорение, которое при этом возникает?
Если тело движется, на него действуют, как правило, две силы: сила тяги и сила трения или сопротивления воздуха. Если направление равнодействующей силы совпадает с направлением силы тяги, то скорость тела увеличивается, а если с направлением силы трения, то скорость тела уменьшается.
Направление ускорения совпадает с направлением вызывающей его силы. При этом ускорение, сообщаемое данному телу, тем больше, чем больше действующая на него сила.
Изучение взаимосвязи силы и ускорения удобно проводить на дорожке с воздушной подушкой, обеспечивающей движение тележки с малым трением. Выходящий из маленьких отверстий сжатый воздух, нагнетаемый с помощью компрессора, обеспечивает положение тележки в приподнятом состоянии.
Выходящий из маленьких отверстий сжатый воздух, нагнетаемый с помощью компрессора, обеспечивает положение тележки в приподнятом состоянии.
При помощи пружинного динамометра соединим тележку с перекинутой через блок нитью, на которой закреплён груз. При движении тележки пружина будет растягиваться под действием силы натяжения нити, которая зависит от силы тяжести, действующей на груз: чем больше сила тяжести, тем сильнее натяжение нити и растяжение пружины.
Опыт показывает, что при движении тележки показания динамометра не меняются, т. е. сила F, действующая на тележку, постоянна. Измеряя путь s, пройденный тележкой за определённое время t, можно вычислить её ускорение.
Результаты измерений показывают, что путь, пройденный тележкой, пропорционален квадрату промежутка времени, прошедшего от начала движения: s ~ t2. Следовательно, тележка движется равноускоренно. Ускорение найдём из формулы а = 2s/t2.
Подвешивая грузы различной массы и определяя в каждом случае силы и ускорение, можно сделать вывод: ускорение, с которым движется тело, прямо пропорционально приложенной к этому телу силе: а ~ F.
Сила тяги приводит к ускорению тела, а сила трения — к торможению. Эти две силы противоположно направлены, поэтому направление их равнодействующей совпадает с направлением большей из сил. Если же эти две силы уравновешивают друг друга, тело движется равномерно или покоится.
Конечно, опыты, в которых используется простейшее оборудование, слишком грубы для точного установления закона пропорциональности между силами и ускорениями. Однако при помощи всё более и более точных методов измерений этот закон был подтверждён.
ВЗАИМОСВЯЗЬ МАССЫ И УСКОРЕНИЯ
Сила, действуя на разные тела, придает им различные ускорения. Почему?
Описанный выше опыт можно видоизменить, если сцепить вместе две одинаковые тележки. При этом оказывается, что сила F сообщает им ускорение, вдвое меньшее того, которое она сообщала одной тележке. Использование двух связанных тележек равносильно увеличению массы тележки вдвое. Измерения показывают, что ускорения, приобретаемые телами при взаимодействии, обратно пропорциональны их массам: а ~ 1/m.
Использование двух связанных тележек равносильно увеличению массы тележки вдвое. Измерения показывают, что ускорения, приобретаемые телами при взаимодействии, обратно пропорциональны их массам: а ~ 1/m.
ПОНЯТИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
При решении задач динамики часто не важно знание ни размеров тела, ни его геометрической формы. В этих случаях мы можем рассматривать тело как материальную точку, т. е. будем считать, что оно обладает массой, но не имеет геометрических размеров.
ВТОРОЙ ЗАКОН НЬЮТОНА
Обобщив выводы, получим, что ускорение тела прямо пропорционально действующей силе, приложенной к телу, и обратно пропорционально его массе: а ~ F/m
Закон, устанавливающий связь ускорения с массой тела и действующей на него силой, называют основным законом динамики или вторым законом Ньютона. Математически его записывают следующим образом:
Из этой формулы видно, что направление ускорения тела всегда совпадает с направлением вектора равнодействующей сил, действующих на тело.
Второй закон Ньютона справедлив только в инерциальных системах отсчёта.
Инертность — свойство, присущее всем телам. Из двух тел, изменяющих скорость на одно и то же значение, более инертно то, которому для этого изменения требуется большее время. Инертность характеризуется физической величиной, называемой массой тела. Более инертное тело имеет большую массу, менее инертное тело — меньшую массу.
Если на тело действует несколько сил, то под F следует понимать их равнодействующую. Важно понимать, что ускорение пропорционально действующей силе и обратно пропорционально массе тела и не зависит ни от каких других свойств тела.
Второй закон Ньютона имеет следующую формулировку: ускорение тела прямо пропорционально действующей силе, приложенной к телу, и обратно пропорционально его массе.
ЕДИНИЦЫ СИЛЫ
Из второго закона Ньютона можно найти равнодействующую сил, действующих на тело: F = ma.
За единицу силы в СИ принимают такую силу, которая сообщает телу массой 1 кг ускорение 1 м/с2.
1 Н = 1 кг • 1 м/с2.
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
Ускорение свободного падения является тем коэффициентом пропорциональности, который связывает силу тяжести и массу тела: g = Fтяж/m
Эта формула — запись второго закона Ньютона для случая, когда на тело действует только сила тяжести.
Вы смотрели Конспект по физике для 8 класса «Второй закон Ньютона».
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров: 3 447
Второй закон Ньютона – формула, запись и определение кратко
4.7
Средняя оценка: 4.7
Всего получено оценок: 165.
4.7
Средняя оценка: 4.7
Всего получено оценок: 165.
Второй закон Ньютона – фундамент классической механики, который дает понятие о причинах движения. На его основе строится решение многих прикладных задач и задач школьного курса физики. Поэтому важно понимать его суть и уметь применять на практике.
Формулировка второго закона Ньютона
В первоначальной формулировке закона было сказано, что изменение количества движения (то есть импульса) пропорционально силе, заставляющей тело двигаться, и направлено по направлению действия силы.
Математически это можно записать так:
$$\vec{F} = {d\vec{p} \over \vec{dt}}$$
Буква d от delta – изменение, разность. Называется дифференциалом, а частное двух дифференциалов, в котором одно значение – переменная (время t), другое – функция (импульс p) – производная. То есть, это скорость изменения функции.
Называется дифференциалом, а частное двух дифференциалов, в котором одно значение – переменная (время t), другое – функция (импульс p) – производная. То есть, это скорость изменения функции.
Но: $\vec{p} = {m\vec{v}}$
Тогда уравнение (2) можно переписать в следующем виде:
$$\vec{F} = m{d\vec{v} \over \vec{dt}}$$
Второй множитель – это определение ускорения. Ускорение есть быстрота изменения скорости движения.
Тогда запись второго закона Ньютона примет привычный вид:
$$\vec{F} = m\vec{а}$$
Или, разделив обе части на m:
$\vec{a} = {\vec{F} \over \ {m}}$ – ускорение, с которым движется тело, прямо пропорционально приложенной к нему силе и обратно пропорционально его массе. Чем больше масса, тем меньше ускорение, чем больше сила, тем больше ускорение. Данный закон также называют основным законом классической механики.
Под F здесь понимают геометрическую сумму всех действующих на тело (то есть внешних) сил. Иными словами, их равнодействующую.
Иными словами, их равнодействующую.
Геометрическая сумма – это сумма векторных величин. Сложение векторов выполняется по правилу треугольника или параллелограмма. Поэтому для расчета равнодействующей сил необходимы значение модулей сил и углы между силами.
Рис. 2. Нахождение равнодействующей сил.Второй закон справедлив для инерциальных и неинерциальных систем отсчета, для материальных точек и произвольных тел, так как любое тело можно представить множеством материальных точек (местом приложения силы будет центр масс тела.
Для расширения второго закона Ньютона на случай неинерциальных систем отсчета вводят понятие инерциальных сил, таких, например, как центробежная сила или сила Кориолиса. Математическая формулировка будет выглядеть так: $\ m\vec{а}={\vec{F} \ + \vec{F_и}}$. Индексом “и” обозначены инерциальные силы.
Применение основного закона классической динамики
Рассмотрим тело, на которое действует несколько сил. Допустим, это машина, застрявшая в грязи. Ее пытается вытянуть вторая машина, зацепив ее тросом. Таким образом, первая машина стремится изменить свое количество движения под действием силы натяжения троса, силы тяги и сил трения. Так будет выглядеть формула второго закона Ньютона для первой машины:
Ее пытается вытянуть вторая машина, зацепив ее тросом. Таким образом, первая машина стремится изменить свое количество движения под действием силы натяжения троса, силы тяги и сил трения. Так будет выглядеть формула второго закона Ньютона для первой машины:
$$m\vec{а}={\vec{T} \ + \vec{F_{тр}} + \vec{F_т}}$$
Или в скалярной форме:
$$mа={T – F_{тр} + F_т}$$
Теперь же предположим, что равнодействующая сил обращает в нуль (силы трения, силы тяги и силы натяжения нити). Тогда машина будет покоиться или двигаться равномерно и прямолинейно. Это утверждение можно расширить на случай системы тел: если при взаимодействии друг с другом частей системы внутренние силы суммарно равны нулю, а внешние силы скомпенсированы или не действуют, то система тел покоится или движется равномерно.
Рис. 3. Исаак Ньютон.Задачи
- На тело действуют две силы. Угол между ними – 60˚. Найти их равнодействующую.
Решение первой задачи
Так как равнодействующая сил равна их геометрической (векторной сумме), запишем:
$$\vec{F}={\vec{F_1} \ + \vec{F_2}}$$
Сложение будем выполнять по правилу треугольника. 2 – F_1F_2}$$ – окончательный ответ.
2 – F_1F_2}$$ – окончательный ответ.
- Через блок перекинута веревка. На одном ее конце закреплен груз. На другом конце висит альпинист той же массы, что и груз. Что будет с системой, если альпинист начнет карабкаться вверх? Массой веревки и трением в блоке пренебречь.
Решение второй задачи
Запишем второй закон Ньютона для альпиниста и для груза.
$$mа_1={T_1 – mg}$$
$$mа_2={T_2 – mg}$$
Но $T_1={T_2}$
Поэтому:
$${mа_1} = {mа_2}$$
Сократив массы, получим, что их ускорения одинаковы. Альпинист и груз будут подниматься с одинаковыми ускорениями и достигнут блока одновременно. Если бы масса альпиниста была меньше массы груза, то груз поднимался бы быстрее.
Что мы узнали?
В ходе урока был сформулирован второй закон Ньютона в его современной форме, выяснена его сущность и рассмотрены примеры его использования в реальных ситуациях. В завершение урока были кратко разобраны две простые задачи на нахождение равнодействующей сил и на применение второго закона Ньютона.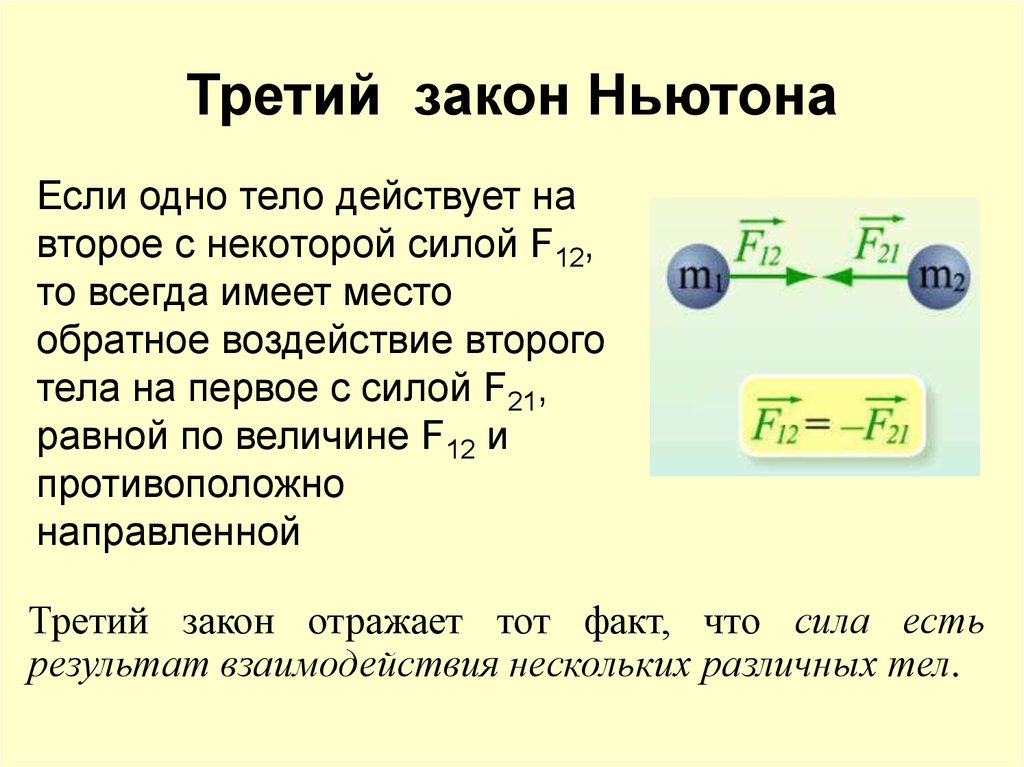
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 165.
А какая ваша оценка?
Законы Ньютона 9 класс. доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Законы Ньютона 9 класс. , предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 11 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 11 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Законы Ньютона
Задачи:
изучить 1 закон ньютона.
изучить 2 закон Ньютона.
изучить 3 закон ньютона.
ввести понятия масса, силы.
рассмотреть особенности 2 и 3 законов Ньютона.
раскрыть суть законов.
узнать границы применимости.
Первый закон Ньютона
Если на тело не действуют силы или их действие компенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.
Первый закон Ньютона
Первый закон Ньютона называют законом инерции.
Системы отсчета, относительно которых тела движутся с постоянной скоростью или покоятся при компенсации внешних воздействий на них, называются инерциальными. Причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами.
Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу.
Первый закон Ньютона
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
Сила – мера взаимодействия тел.
Второй закон Ньютона
Если два тела взаимодействуют друг с другом, то ускорения этих тел обратно пропорциональны их массам.
m
М
F1
a1
a2
F2
F1 = F2
Второй закон Ньютона
Сила, приложенная к телу, является
причиной его ускорения.
Одна и та же сила действует на тела
разной массы, сообщая им разные ускорения.
a
a/2
Второй закон Ньютона
Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
Другая формулировка второго закона Ньютона
Изменение импульса тела, равно
Произведению силы на промежуток
времени, в течении которого действовала
указанная сила.
Выводы по 2 закону:
Закон справедлив для любых сил.
Сила F является причиной и определяет ускорение а.
Вектор ускорения сонаправлен с вектором силы.
Если на тело действуют несколько сил, берется результирующая.
Если результирующая сила равна нулю, то ускорение равно нулю, т.е. получаем 1 закон Ньютона.
Третий закон Ньютона
Если нить нерастяжима, тогда показания
динамометров будут одинаковы. Мы будем
говорить – одинаковы по модулю.
Силы, возникающие при взаимодействии
тел, всегда имеют одинаковую природу.
Они приложены к разным телам и поэтому
не могут уравновешивать друг друга.
Третий закон Ньютона
Формулировка:
Силы, возникающие при взаимодействии двух тел, приложены к разным телам. Они равны по модулю, но противоположны по направлению.
Знак «минус» выражает здесь тот факт, что
ускорения взаимодействующих тел всегда
направлены в противоположные стороны
Особенности 3 закона Ньютона
Силы появляются только парами.
Всегда применяется при взаимодействии тел.
Обе силы – одной природы.
Силы не уравновешиваются, так как приложены к разным телам.
Закон верен для любых сил.
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Законы Ньютона – FIZI4KA
ОГЭ 2018 по физике ›
1. В основе классической механики лежат три закона Ньютона, которые были сформулированы им при обобщении результатов наблюдений и опытов в конце XVII в.
Первый закон, включённый Ньютоном в систему законов, был открыт Галилеем и назван им законом инерции. Закон инерции формулируется следующим образом: если на тело не действуют другие тела, то оно либо находится в покое, либо движется равномерно прямолинейно.
2. В природе не существует отдельных изолированных тел. Любое тело взаимодействует с окружающими телами. Несмотря на это, взаимодействующие тела могут находиться в покое или двигаться равномерно и прямолинейно.
Например, лежащая на столе книга взаимодействует с Землёй, и на неё действует сила тяжести \( (\vec{F}_т) \), направленная вниз (рис. 33). Книга также взаимодействует со столом, и со стороны стола на неё действует сила, направленная вертикально вверх \( (\vec{F}) \). При этом книга находится в покое, следовательно, \( |\vec{F}_т|=|\vec{F}| \), т.е. действия Земли и стола на книгу компенсируют друг друга.
3. При компенсации действия на тело других тел оно может двигаться равномерно прямолинейно.
Например, если по прямой горизонтальной дороге движется автомобиль, то при компенсации действия на него силы тяги двигателя и силы трения со стороны поверхности дороги движение автомобиля будет равномерным.
Можно утверждать, что тело сохраняет состояние покоя, если действие на него других тел скомпенсировано.
Явление сохранения скорости тела постоянной (в том числе и равной нулю) называют явлением инерции.
4. Тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел скомпенсировано не во всех системах отсчёта, а только в инерциальных системах отсчёта.
Инерциальными системами отсчёта называются такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Инерциальной можно считать систему отсчёта, связанную с Землёй. Системы отсчёта, движущиеся относительно Земли равномерно и прямолинейно, также являются инерциальными.
Системы отсчёта, движущиеся относительно Земли равномерно и прямолинейно, также являются инерциальными.
Системы отсчёта, движущиеся с ускорением относительно инерциальной системы отсчёта, например относительно Земли, называют неинерциальными.
5. Значение первого закона Ньютона состоит в том, что он устанавливает существование инерциальных систем отсчёта (таких систем отсчёта, относительно которых тела движутся с постоянной скоростью при компенсации внешних воздействий). Именно для таких систем отсчёта справедливы все другие законы Ньютона.
6. Второй закон Ньютона устанавливает зависимость ускорения одного из взаимодействующих тел от его массы и действующей на него силы. Наблюдения и опыты свидетельствуют о том, что чем больше сила, действующая на тело, тем больше ускорение, которое оно приобретает. Так, чем сильнее водитель нажимает на педаль тормоза, тем
больше сила и тем быстрее автомобиль остановится.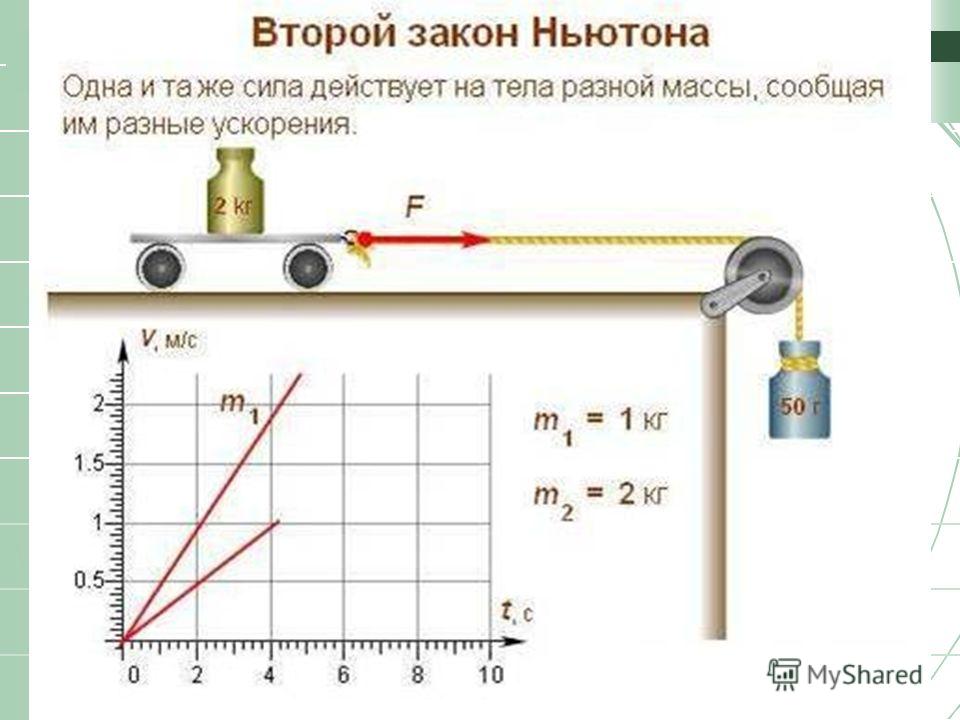 Значит, чем больше действующая на автомобиль сила сопротивления, тем больше его ускорение.
Значит, чем больше действующая на автомобиль сила сопротивления, тем больше его ускорение.
Ускорение, которое приобретают тела под действием одинаковой силы, зависит от массы тел. Например, грузовому автомобилю требуется большее время, чем легковому, для того, чтобы, имея некоторую одинаковую скорость, остановиться, выключив двигатель. Из этого примера следует, что чем больше масса тела, тем меньшее ускорение оно получает под действием некоторой постоянной силы.
7. Второй закон Ньютона формулируется следующим образом: ускорение, с которым движется тело прямо пропорционально действующей на тело силе и обратно пропорционально массе тела.
\[ \vec{a}=\frac{\vec{F}}{m} \]
Записанное равенство представляет собой второй закон Ньютона.
В механике Ньютона ускорение тел обусловлено только их взаимодействием. Следовательно, второй закон Ньютона справедлив в инерциальных системах отсчёта.
8. Действие тел друг на друга носит взаимный характер, т. е. в результате взаимодействия
е. в результате взаимодействия
каждое тело приобретает ускорение, и, следовательно, на каждое из взаимодействующих тел действует сила. Например, груз, висящий на нити, действует на нить с силой, направленной вертикально вниз \( (\vec{F}_1) \), и растягивает её (рис. 34). В свою очередь, нить действует на груз с силой, направленной вертикально вверх \( (\vec{F}_2) \).
9. Измерения показывают, что:
- при взаимодействии тел сила действует как на одно тело, так и на другое;
- модуль силы, действующей на одно тело, равен модулю силы, действующей на другое тело;
- силы, действующие на тела, направлены в противоположные стороны.
10. Из соотношения следует: \( m_1a_1=m_2a_2 \).
Поскольку ускорение — величина векторная и ускорения, которые получают тела, направлены в противоположные стороны, то \( m_1\vec{a}_1=-m_2\vec{a}_2 \).
Так как \( m_1\vec{a}_1=\vec{F}_1 \), а \( m_2\vec{a}_2=\vec{F}_2 \), то можно записать: \( \vec{F}_1=-\vec{F}_2 \).
Это равенство и выражает третий закон Ньютона.
Третий закон Ньютона формулируется следующим образом: тела действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны. Эти силы направлены вдоль прямой, соединяющей взаимодействующие тела (материальные точки).
Третий закон Ньютона говорит о том, что силы всегда проявляются парами.
Эти силы часто называют силами действия и противодействия. При этом безразлично, какую из двух сил назвать силой действия, а какую — силой противодействия.
Эти силы приложены к разным телам, и их нельзя складывать, т.е. нельзя сказать, что силы действия и противодействия уравновешивают друг друга.
Силы, с которыми взаимодействуют тела, всегда одной природы.
Третий закон Ньютона, так же как первый и второй законы, справедлив в инерциальных системах отсчёта.
10. При переходе от одной инерциальной системы отсчёта к другой не изменяются ни ускорение, ни масса тала, ни действующая на него сила. Следовательно, можно утверждать, что законы механики одинаковы для всех инерциальных систем отсчёта, или, что то же самое, все механические явления протекают одинаково во всех инерциальных системах отсчёта при одинаковых начальных условиях. Это утверждение называется принципом относительности Галилея.
Следовательно, можно утверждать, что законы механики одинаковы для всех инерциальных систем отсчёта, или, что то же самое, все механические явления протекают одинаково во всех инерциальных системах отсчёта при одинаковых начальных условиях. Это утверждение называется принципом относительности Галилея.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Утверждение, что материальная точка покоится или движется равномерно прямолинейно, если на неё не действуют другие тела или действие на неё других тел взаимно уравновешено,
1) неверно ни для каких систем отсчёта
2) верно для инерциальных систем отсчёта
3) верно для неинерциальных систем отсчёта
4) верно при любых условиях
2. Система отсчёта, связанная с Землёй, может считаться инерциальной. Система отсчёта, связанная с автобусом, тоже будет инерциальной, если он
1) движется равномерно по извилистой дороге
2) тормозит у остановки
3) отъезжает от светофора
4) движется равномерно по прямолинейному участку пути
3. В каком из приведённых примеров тело движется по инерции:
В каком из приведённых примеров тело движется по инерции:
1) равномерно движущийся по горизонтальной дороге автомобиль
2) автомобиль, движущийся по горизонтальной дороге с выключенным двигателем
3) автомобиль, поворачивающий направо
4) автомобиль, выезжающий со стоянки
4. Яблоко, лежащее неподвижно на столе вагона движущегося поезда покатился вправо, если смотреть по ходу поезда. Как изменилось движение поезда?
1) скорость поезда увеличилась
2) скорость поезда уменьшилась
3) поезд повернул влево
4) поезд повернул вправо
5. Можно ли считать инерциальной системой отсчёта движущийся автомобиль?
1) можно всегда
2) можно, только если он движется равномерно и прямолинейно
3) можно только во время разгона и торможения
4) нельзя ни при каких условиях
6. Массивный груз подвешен на тонкой нити 1. К грузу прикреплена такая же нить 2. Если
медленно тянуть за нить 2, то оборвётся
1) только нить 1
2) только нить 2
3) нить 1 и нить 2 одновременно
4) либо нить 1, либо нить 2, в зависимости от массы груза
7. Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?
Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?
1) 25 Н
2) 50 Н
3) 75 Н
4) 100 Н
8. Два ученика тянут динамометр в противоположные стороны с силой 60 Н каждый. Каково показание динамометра?
1) 0 Н
2) 30 Н
3) 60 Н
4) 120 Н
9. Земля притягивает яблоко с силой \( \vec{F}_1 \). Яблоко притягивает Землю с силой \( \vec{F}_2 \). При этом
1) \( F_2 = 0 \)
2) \( F_1=F_2 \)
3) \( F_1>F_2 \)
4) \( F_1<F_2 \)
10. Чему равна масса автомобиля, трогающегося с места с ускорением 0,6 м/с2, если развиваемая им сила тяги равна 15 000 Н? Сила сопротивления, действующая на автомобиль, равна 6000 Н.
1) 1,5 т
2) 7,5 т
3) 15 т
4) 75 т
11. Из приведенных утверждений выберите два правильных и запишите их номера в таблицу.
1) законы Ньютона справедливы во всех системах отсчета
2) первый закон Ньютона утверждает существование инерциальных систем отсчета
3) равнодействующая сил действия и противодействия равна нулю
4) силы действия и противодействия имеют одинаковую природу
5) второй закон Ньютона говорит о том, что масса тела прямо пропорциональна действующей на тело силе
12. Два тела движутся по оси \( Ox \). На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени \( t_3-t_5 \) на тело 2 действует постоянная сила.
2) В промежутке времени \( 0-t_3 \) сила сообщает телу 1 положительное ускорение
3) В промежутке времени \( t_4-t_5 \) на тело 1 сила не действует
4) Модуль силы, действующей на тело 1 в промежутки времени \( 0-t_1 \), \( t_1-t_2 \) различен.
5) В промежутке времени \( t_1-t_2 \) сила сообщает телу 1 отрицательное ускорение
Часть 2
13. Тело массой 7 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 4 с груз был поднят на высоту 16 м?
Ответы
Сила трения →
← Сила. Сложение сил
4.3 Второй закон движения Ньютона: концепция системы – College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить результирующую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона носит более количественный характер и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.
Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости означает, по определению, что есть ускорение. Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что суммарная внешняя сила вызывает ускорение .
Сразу возникает другой вопрос. Что мы понимаем под внешней силой? Интуитивное представление о внешнем верно — внешняя сила действует извне интересующей системы. Например, на рис. 4.5(а) интересующей нас системой является повозка плюс ребенок в ней. Две силы, действующие со стороны других детей, являются внешними силами. Между элементами системы действует внутренняя сила. Снова взглянув на рис. 4.5(а), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. К этой концепции мы будем возвращаться много раз в нашем путешествии по физике.
4.5(а), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. К этой концепции мы будем возвращаться много раз в нашем путешествии по физике.
Рисунок
4,5
Разные силы, действующие на одну и ту же массу, вызывают разное ускорение. а) Двое детей толкают тележку с ребенком. Показаны стрелки, представляющие все внешние силы. Система интереса — это повозка и ее всадник. Вес ww системы и опоры грунта NN также показаны для полноты и предполагаются сокращающимися. Вектор ff представляет трение, действующее на вагон, причем он действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу FnetFnet. Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая результирующая внешняя сила создает большее ускорение (a′>aa′>a), когда взрослый толкает ребенка.
Вектор ff представляет трение, действующее на вагон, причем он действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу FnetFnet. Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая результирующая внешняя сила создает большее ускорение (a′>aa′>a), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и направлено в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было проверено экспериментально и показано на рис. 4.5. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (в). Для полноты показаны также вертикальные силы; предполагается, что они компенсируются, поскольку ускорение в вертикальном направлении отсутствует. Вертикальные силы – это вес
вв
и поддержка земли
НН,
а горизонтальная сила ff представляет собой силу трения. Они будут обсуждаться более подробно в последующих разделах. Сейчас мы определим трение как силу, противодействующую движению соприкасающихся объектов относительно друг друга. На рис. 4.5(b) показано, как векторы, представляющие внешние силы, складываются вместе, образуя результирующую силу.
ФнетФнет.
Вертикальные силы – это вес
вв
и поддержка земли
НН,
а горизонтальная сила ff представляет собой силу трения. Они будут обсуждаться более подробно в последующих разделах. Сейчас мы определим трение как силу, противодействующую движению соприкасающихся объектов относительно друг друга. На рис. 4.5(b) показано, как векторы, представляющие внешние силы, складываются вместе, образуя результирующую силу.
ФнетФнет.
Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения и результирующей внешней силы в виде пропорциональности
∝∝
означает «пропорционально», а FnetFnet — чистая внешняя сила. (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически с использованием метода «голова к хвосту» или аналитически с использованием компонентов. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами — ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. И действительно, как показано на рис. 4.6, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
a∝1ma∝1m
4,2
, где mm — масса системы. Эксперименты показали, что ускорение точно обратно пропорционально массе, так же как оно точно линейно пропорционально суммарной внешней силе.
Рисунок 4.6 Одна и та же сила, действующая на системы с разной массой, дает разное ускорение. а) Баскетболист толкает мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (b) Тот же игрок прикладывает такую же силу к заглохшему внедорожнику и создает гораздо меньшее ускорение (даже если трением можно пренебречь). (c) Диаграммы свободного тела идентичны, что позволяет проводить прямое сравнение двух ситуаций. Ряд паттернов для диаграммы свободного тела появится по мере того, как вы будете решать больше задач.
Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Сочетание двух только что приведенных пропорций дает второй закон движения Ньютона.
Второй закон Ньютона
Ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе.
В форме уравнения второй закон Ньютона равен
a=Fnetm.a=Fnetm.
4.3
Это часто записывается в более знакомой форме
Fnet=ma.Fnet=ma.
4.4
Когда учитываются только величина силы и ускорения, это уравнение выглядит просто как
Fnet=ma.Fnet=ma.
4,5
Хотя последние два уравнения на самом деле одинаковы, первое дает более полное представление о том, что означает второй закон Ньютона. Закон представляет собой причинно-следственную связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
Единицы силы
Fnet=maFnet=ma используется для определения единиц силы с точки зрения трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м/с21 м/с2. То есть, поскольку Fnet=maFnet=ma,
То есть, поскольку Fnet=maFnet=ma,
1 N = 1 кг⋅м/с2,1 N = 1 кг⋅м/с2.
4,6
Хотя почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее распространенной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую его весом ww. Вес можно обозначить как вектор ww, потому что он имеет направление; вниз по определению является направлением силы тяжести, и, следовательно, вес есть направленная вниз сила. Величина веса обозначается как ww . Галилей доказал, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением gg. Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой мм, падающий вниз к Земле. Он испытывает только направленную вниз силу тяжести, которая имеет величину ww. Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна Fnet=maFnet=ma.
Поскольку на объект действует только направленная вниз сила тяжести, Fnet=wFnet=w. Мы знаем, что ускорение объекта под действием силы тяжести равно gg, или a=ga=g. Подстановка их во второй закон Ньютона дает
Масса
Это уравнение для веса —силы гравитации на массу mm:
w=mg.w=mg.
4,7
Поскольку на Земле g=9,80 м/с2g=9,80 м/с2, вес объекта массой 1,0 кг на Земле равен 9,8 Н, как мы видим:
w=mg=(1,0 кг)(9,80 м /с2)=9,8 Н.w=мг=(1,0 кг)(9,80 м/с2)=9,8 Н.
4.8
Напомним, что gg может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат.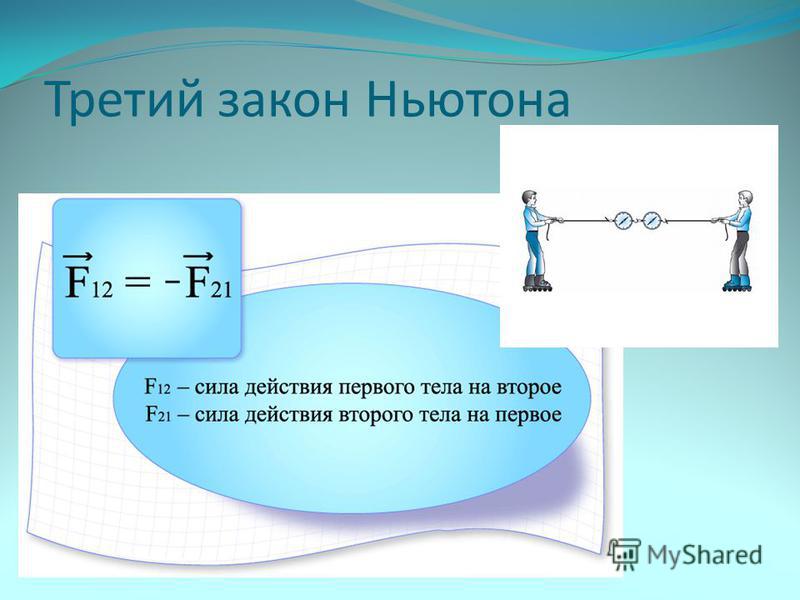 Обязательно учитывайте это при решении задач с весом.
Обязательно учитывайте это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении. То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует восходящая сила воздуха.
Ускорение свободного падения gg незначительно варьируется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является неотъемлемым свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения составляет всего 1,625 м/с21,625 м/с2. Таким образом, масса 1,0 кг имеет вес 90,8 с. ш. на Земле и всего около 1,7 с. ш. на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и т. д. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.
д. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно помнить, что вес и масса — очень разные физические величины, хотя и тесно связанные между собой. Масса — это количество материи (сколько «вещества») и не меняется в классической физике, тогда как вес — это гравитационная сила, которая зависит от гравитации. Заманчиво приравнять их, поскольку большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, термы масса и вес взаимозаменяемы в повседневном языке; например, наши медицинские записи часто показывают наш «вес» в килограммах, но никогда в правильных единицах измерения — ньютонах.
Распространенные заблуждения: масса против веса
Масса и вес часто используются как синонимы в повседневном языке. Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте. Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта (мм), умноженной на ускорение свободного падения (гг). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения).
Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от своего местоположения. Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться , когда объект входит в область с более сильным или более слабым гравитационным полем. Например, ускорение свободного падения на Луне составляет 1,625 м/с21,625 м/с2 (что намного меньше ускорения свободного падения на Земле 9,80 м/с29,80 м/с2). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Возьмите домой эксперимент: масса и вес
Что измеряют напольные весы? Когда вы встаете на напольные весы, что происходит с весами? Это слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9,80, чтобы получить показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?
Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?
Пример 4.1
Какое ускорение может создать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Каково его ускорение?
Рисунок 4.7 Чистая сила, действующая на газонокосилку, равна 51 Н вправо. С какой скоростью газонокосилка ускоряется вправо?
Стратегия
Поскольку FnetFnet и mm заданы, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в Fnet=maFnet=ma.
Решение
Величина ускорения aa равна a=Fnetma=Fnetm. Ввод известных значений дает
a=51 N24 кгa=51 N24 кг
4,9
Подстановка единиц кг⋅м/с2кг⋅м/с2 вместо N дает
a=51 кг⋅м/с224 кг=2,1 м/ s2. a=51 кг⋅м/с224 кг=2,1 м/с2.
a=51 кг⋅м/с224 кг=2,1 м/с2.
4.10
Обсуждение
Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны уравновешиваться, если не должно быть ускорения в вертикальном направлении (ускорение в вертикальном направлении). косилка движется только горизонтально). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример 4.2
Какая ракетная тяга разгоняет эти сани?
До космических полетов с астронавтами ракетные сани использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Рассчитайте величину силы, действующей на каждую ракету, называемую ее тягой ТТ, для четырехракетной двигательной установки, показанной на рис. 4.8. Начальное ускорение саней 49м/с2,49 м/с2, масса системы 2100 кг, сила трения, противодействующая движению, известна как 650 Н.
Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Рассчитайте величину силы, действующей на каждую ракету, называемую ее тягой ТТ, для четырехракетной двигательной установки, показанной на рис. 4.8. Начальное ускорение саней 49м/с2,49 м/с2, масса системы 2100 кг, сила трения, противодействующая движению, известна как 650 Н.
Рис. 4,8 Сани испытывают реактивную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу ТТ. Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы компенсируются. Земля воздействует на систему направленной вверх силой NN, равной по модулю и противоположной по направлению ее весу ww. Система здесь — сани, их ракеты и всадник, так что ни одна из сил между эти объекты считаются. Стрелка, обозначающая трение (ff), нарисована больше масштаба.
Стратегия
Хотя существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения.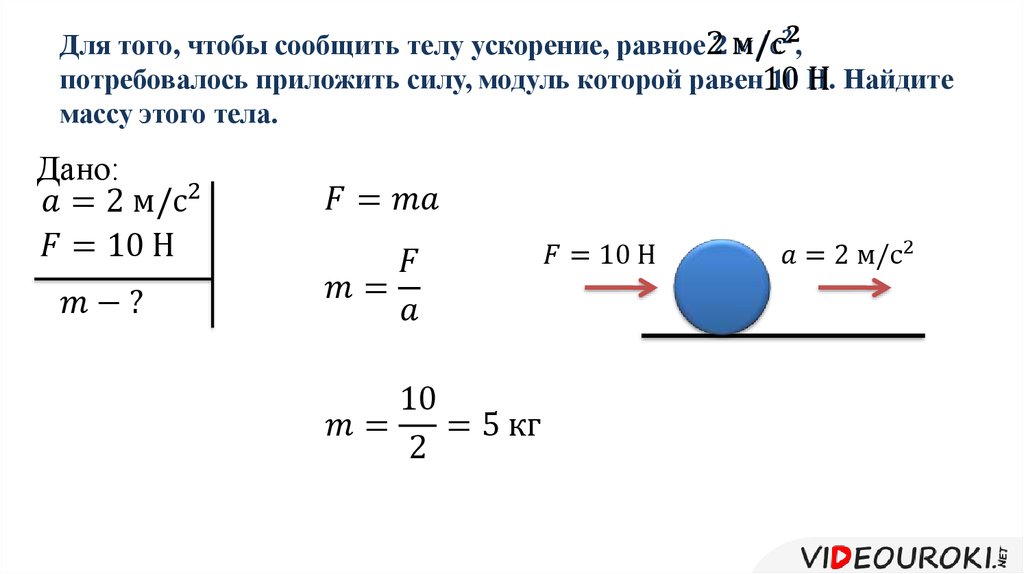 Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.
Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения известны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с
Fnet=ma,Fnet=ma,
4.11
, где FnetFnet — результирующая сила в горизонтальном направлении. Из рисунка 4.8 видно, что тяга двигателя добавляется, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна
Fnet=4T-f.Fnet=4T-f.
4.12
Подставляя это во второй закон Ньютона, получаем
Fnet=ma=4T−f. Fnet=ma=4T−f.
Fnet=ma=4T−f.
4.13
Используя немного алгебры, находим полную тягу 4 T :
4T=ma+f.4T=ma+f.
4.14
Подстановка известных значений дает
4T=ma+f=(2100 кг)(49 м/с2)+650 Н.4T=ma+f=(2100 кг)(49 м/с2)+650 Н
4,15
Таким образом, общая тяга равна
4T=1,0×105 Н,4T=1,0×105 Н,
4.16
и отдельные тяги равны
T=1.0×105 N4=2.6×104 N.T=1.0×105 N4=2.6×104 N.
4.17
Обсуждение
7 результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийном катапультировании реактивного истребителя. Были получены скорости 1000 км/ч, с ускорениями 45 гс. (Напомним, что gg, ускорение свободного падения, равно 90,80 м/с29,80 м/с2. Когда мы говорим, что ускорение равно 45 gg’s, это 45×9,80 м/с245×9,80 м/с2, что примерно равно 440 м/с2440 м/с2.) Пока живые предметы больше не используются, наземные скорости 10 000 км /ч были получены с ракетными салазками. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Когда мы говорим, что ускорение равно 45 gg’s, это 45×9,80 м/с245×9,80 м/с2, что примерно равно 440 м/с2440 м/с2.) Пока живые предметы больше не используются, наземные скорости 10 000 км /ч были получены с ракетными салазками. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Понимание второго закона Ньютона — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по физике для старших классов » Движение и механика » Законы Ньютона » Понимание второго закона Ньютона
Что из следующего не является частью второго закона Ньютона?
Возможные ответы:
Масса
Перемещение
Сила
Ускорение
Правильный ответ: 5
4 Перемещение
Объяснение:
Второй закон Ньютона гласит . Следовательно, все, что нам нужно, это сила, масса и ускорение!
Следовательно, все, что нам нужно, это сила, масса и ускорение!
Сообщить об ошибке
Блок толкается с силой в ньютонах. Какая еще информация нам нужна, чтобы найти ускорение бруска?
Возможные ответы:
Начальная скорость
Окончательная скорость
Работа, выполненная в блоке
Ускорение из -за гравита Пояснение:
Второй закон Ньютона утверждает, что .
Если мы знаем силу , то нам нужно знать только массу , чтобы найти ускорение.
Сообщить об ошибке
Апельсин падает с дерева. Какова сила тяжести апельсина?
Возможные ответы:
Правильный ответ:
Объяснение:
Второй закон Ньютона гласит:
Нам известны масса апельсина и ускорение; поскольку мы смотрим на силу гравитации, ускорение будет ускорением силы тяжести. Используйте эти заданные значения для расчета силы.
Используйте эти заданные значения для расчета силы.
Имейте в виду, что сила будет отрицательной, так как гравитация действует в направлении вниз.
Сообщить об ошибке
Мяч лежит на плоском столе. Какая нормальная сила действует на мяч со стороны стола?
Возможные ответы:
Правильный ответ:
Объяснение:
Второй закон Ньютона позволяет нам найти силу тяжести, действующую на мяч:
Третий закон Ньютона говорит нам, что сила притяжения мяча на столе под действием силы тяжести будет равна и противоположна силе притяжения мяча. нормальная сила стола на шаре.
Подставьте уравнение для силы тяжести.
Теперь мы можем использовать массу мяча и ускорение свободного падения, чтобы найти нормальную силу. Сначала переведите массу в килограммы. Затем используйте уравнение, чтобы найти нормальную силу.
Затем используйте уравнение, чтобы найти нормальную силу.
Сообщить об ошибке
Что из этого необходимо для того, чтобы результирующая сила была ненулевой?
Возможные ответы:
Ненулевая сила трения
Ненулевое чистое перемещение
Ненулевое чистое ускорение
Ненулевой полезный крутящий момент
Равная и противоположная реакция
Правильный ответ:
Ненулевое чистое ускорение
Пояснение:
Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение.
Чтобы сила существовала, к массе должно быть приложено ускорение. Сила не может существовать на безмассовом объекте и не может существовать без результирующего ускорения.
Третий закон Ньютона гласит, что для каждой силы, действующей на объект, существует равная и противоположная сила со стороны объекта. Однако эти силы часто уравновешиваются и дают результирующую силу, равную нулю.
Однако эти силы часто уравновешиваются и дают результирующую силу, равную нулю.
Сообщить об ошибке
Что из перечисленного не является примером ньютоновской механики?
Возможные ответы:
Правильный ответ:
Пояснение:
Ньютоновская механика применима ко всем объектам значительной массы, движущимся со скоростью, значительно меньшей скорости света.
Закон всемирного тяготения Ньютона, второй закон Ньютона, импульс и уравнение механической энергии — все они подпадают под действие ньютоновской механики.
Эквивалентность массы и энергии предполагает, что масса может изменяться по мере того, как скорость объекта (например, электрона) приближается к скорости света. Ньютоновская механика предполагает, что масса постоянна, и не применяется к объектам, приближающимся к скорости света.
Сообщить об ошибке
Пара пушистых игральных костей висит на шнурке у вас в зеркале заднего вида. Пока вы замедляетесь с постоянной скоростью от до состояния покоя, какой угол образует струна с вертикалью и в каком направлении (к лобовому стеклу или от него)?
Возможные ответы:
61 градусов к ветровому стеклу
29 градусов от ветрового стекла
45 градусов к ветровому стеклом
29 градусов от ветрового стекла
9000 40005 9000 61grees от ветрового стекла 9000 9000 9000 616 61 DEGREEEEES от ветрового стекла 9000 4000 7000 61GEEES. Правильный ответ:29 градусов по направлению к лобовому стеклу
Объяснение:
Когда вы замедляете машину, нечеткие кубики продолжают двигаться вперед. Следовательно, угол, который они образуют, будет направлен к лобовому стеклу. Сила натяжения нечетких игральных костей — это то, что удерживает их вместе с автомобилем, не позволяя им вылететь через лобовое стекло. Эта сила натяжения состоит из двух составляющих. Y-компонента натяжения равна силе тяжести, действующей на нечеткие игральные кости. Х-компонента натяжения равна силе торможения автомобиля.
Сила натяжения нечетких игральных костей — это то, что удерживает их вместе с автомобилем, не позволяя им вылететь через лобовое стекло. Эта сила натяжения состоит из двух составляющих. Y-компонента натяжения равна силе тяжести, действующей на нечеткие игральные кости. Х-компонента натяжения равна силе торможения автомобиля.
Угол нечеткой кости связан с этими двумя компонентами через тангенс тригонометрической функции.
Затем мы можем использовать функцию обратного загара, чтобы определить угол, действующий на нечеткие игральные кости.
Обратите внимание, как масса игральной кости выпадает из уравнения
Теперь мы можем подставить наши значения и решить.
Сообщить об ошибке
Две собаки тянут кость в противоположных направлениях. Если первая собака тянет с силой влево, а другая тянет с силой в противоположном направлении, каково будет ускорение кости?
Возможные ответы:
Нам нужно знать массы собак, чтобы решить
Правильный ответ:
Пояснение:
Сначала нам нужно найти результирующую силу, которая будет равна сумме сил, действующих на кость.
Поскольку силы действуют в противоположных направлениях, мы знаем, что одна сила будет отрицательной (поскольку сила является вектором). Обычно праву присваивается положительное значение направления. Сила слева будет отрицательной.
Отсюда мы можем использовать второй закон Ньютона, чтобы расширить силу и найти ускорение, используя массу кости.
Сообщение о ошибке
Дерек толкает ящик вдоль шероховатой поверхности. Он замечает, что он только ускоряется со скоростью . Чему должна быть равна сила трения?
(Предположим, что на объект действуют только две силы: трение и сила Дерека).
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что .
Если Дерек толкает с силой, то мы должны найти ускорение ящика.
Дерек замечает, что ящик ускоряется со скоростью , а не с ожидаемой. На него действует внешняя сила, замедляющая ускорение.
Уравнение для чистой силы, действующей на объект: . Мы также знаем из второго закона Ньютона, что F результирующая = ma результирующая, где результирующая сила и ускорение являются фактически наблюдаемыми значениями.
Подставьте полученную информацию, чтобы найти силу трения.
5 90 найти силу трения.
Трение будет отрицательным, поскольку оно действует в направлении, противоположном силе Дерека.
Сообщить об ошибке
Если вы толкаете груз с той же силой, с которой вы толкаете груз из состояния покоя.
Возможные ответы:
Масса ускоряется в 6 раз быстрее, чем масса
Ничего из вышеперечисленного неверно
Масса ускоряется в 6 раз быстрее, чем масса
Обе массы ускоряются с одинаковой скоростью
Правильный ответ:
Масса ускоряется в 6 раз быстрее массы
Пояснение:
Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение.
Поскольку на обе массы действует одинаковая сила, мы можем посмотреть на связь между массой и ускорением. Эти две вещи обратно пропорциональны друг другу. Когда одно увеличивается, другое уменьшается. Следовательно, большая масса будет иметь меньшее ускорение. Меньшая масса будет иметь большее ускорение.
Предположим, что сила, действующая на оба объекта, равна . Мы можем подтвердить это, найдя ускорение.
Мы можем подтвердить это, найдя ускорение.
4
4
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
Распространенные применения второго закона Ньютона
Нурхан Эссам 15 ноября 2021 г. Физика Комментарии отключены о наиболее распространенных применениях второго закона Ньютона 50 947 просмотров
Законы движения Ньютона — это три физических закона, на которых основывается наука о кинематике. Эти законы описывают связь между движением объекта и действующей на него силой. Они необходимы, поскольку лежат в основе классической механики, одного из основных разделов физики. Эти законы были установлены Исааком Ньютоном, и он использовал эти законы для объяснения многих физических систем и явлений.
Эти законы были установлены Исааком Ньютоном, и он использовал эти законы для объяснения многих физических систем и явлений.
В этой статье мы сосредоточимся на наиболее распространенных примерах и применениях второго закона Ньютона в повседневной жизни.
Второй закон Ньютона изучает движение объекта при воздействии на него внешних сил. Когда постоянная сила воздействует на огромный объект, она заставляет его ускоряться, то есть изменять свою скорость с постоянной скоростью.
Второй закон Ньютона — это количественное описание изменений, которые сила может произвести при движении тела. Он утверждает, что скорость изменения импульса тела во времени равна как по величине, так и по направлению приложенной к нему силе.
Откройте для себя праксилабс лучшее лабораторное моделирование
Содержание
Сэр Исаак Ньютон Если мы собираемся говорить о классической механике и применении второго закона Ньютона в повседневной жизни, мы должны сначала пролить свет об основателе этих законов и о том, кто донес их до нас, сэре Исааке Ньютоне. Вот несколько кратких фактов об Исааке Ньютоне.
Вот несколько кратких фактов об Исааке Ньютоне.
Законы движения Ньютона были впервые опубликованы Исааком Ньютоном в его «Philosophiæ Naturalis Principia Mathematica» в 1687 году, которая является основой классической механики. Ньютон использовал эти законы для объяснения и исследования многих физических явлений. Ньютон показал, что эти законы в дополнение к закону всемирного тяготения способны объяснить кеплеровские законы движения планет, и эти законы до сих пор остаются одними из самых важных физических законов.
Для получения дополнительной информации о сэре Исааке Ньютоне и других законах движения посетите нашу статью «Применение законов движения Ньютона в повседневной жизни».
Сформулируйте и докажите второй закон движения Ньютона«Если на объект действует сила, объект получает ускорение, пропорциональное его силе и обратно пропорциональное его массе».
Второй закон Ньютона Второй закон Ньютона гласит, что сила, приложенная к системе, равна скорости изменения импульса во времени.
Итак, F=dP/dt
Но P=mv
Итак, F=d(mv)/dt
Или F=m(dv/dvt)
900 F004 ⟨ Примечания- Ускорение a определяется как изменение скорости, означающее изменение ее величины или направления, или того и другого.
- Внешняя сила — это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона выглядит так: a=Fnetma=Fnetm.
- Это часто записывается в более привычной форме: Fnet = м а.
- Вес объекта w определяется как сила тяжести, действующая на объект массой м . Объект испытывает ускорение свободного падения g:
w = м g.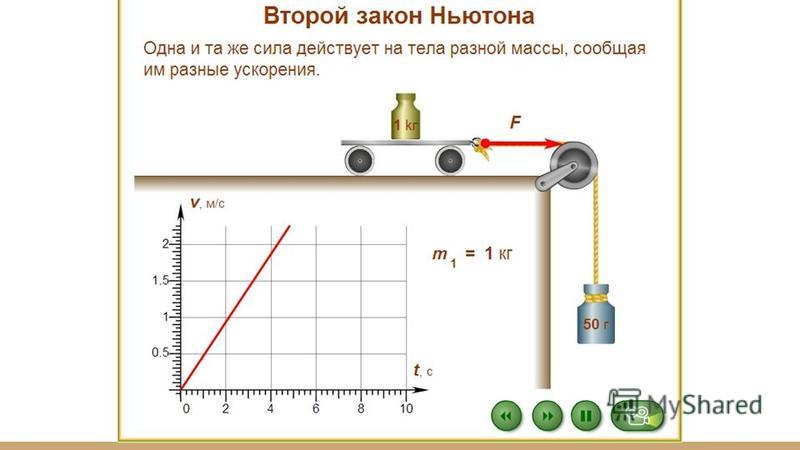
- Если на объект действует только сила тяжести, объект находится в свободном падении.
- Трение — это сила, препятствующая движению соприкасающихся объектов относительно друг друга.
Второй закон Ньютона изучает движение объекта под действием внешних сил. Когда постоянная сила воздействует на огромный объект, она заставляет его ускоряться, то есть изменять свою скорость с постоянной скоростью.
В простейшем случае сила, действующая на покоящийся объект, заставляет его ускоряться в направлении действия силы. Однако, если объект действительно находится в движении, может показаться, что объект ускоряется, замедляется или меняет свое направление в зависимости от направления силы, направления, принимаемого объектом, и системы отсчета, в которой он движется. друг другу.
Математически второй закон Ньютона можно выразить следующим уравнением:
где F — результирующая сила, m — масса объекта, a — ускорение тела.
В этом соотношении применяется принцип сохранения количества движения, заключающийся в том, что когда сумма результирующих сил, действующих на объект, равна нулю, количество движения объекта остается постоянным. Результирующая сила равна скорости изменения импульса.
Этот закон также означает, что когда две равные силы действуют на два разных тела, объект с большей массой будет иметь меньшее ускорение и более медленное движение, а объект с меньшей массой имеет большее ускорение. Например, для иллюстрации:
Если у нас есть два одинаковых двигателя, один для большой машины, а другой для маленькой машины, то маленький будет иметь большее ускорение, потому что его масса меньше, а большой будет иметь меньшее ускорение, потому что его масса больше.
Пояснительное видео о втором законе НьютонаВы можете попробовать виртуальную лабораторию PraxiLabs для экспериментов по физике … Подпишитесь сейчас и выберите свой план
Попробуйте виртуальную лабораторию PraxiLabs БЕСПЛАТНО
10 примеров нового закона движения Повседневная жизнь
Мы всегда наблюдаем применение второго закона Ньютона в повседневной жизни, когда:
1·
Пытаемся сдвинуть объект так же, как останавливаем движущийся мяч, катящийся по земле.
Второй закон Ньютона может быть соблюденным по сравнению с акцентированным, производимым в автомобиле, а также на грузовике. силы обоим. Нетрудно заметить, что после того, как автомобиль и грузовик толкнут с одинаковой интенсивностью, автомобиль разгоняется больше, чем грузовик. Это связано с тем, что масса автомобиля меньше массы грузовика.
3· Гоночные автомобилиСнижая вес гоночных автомобилей, чтобы увеличить их скорость, инженеры стараются максимально уменьшить массу автомобиля, так как меньшая масса означает большее ускорение, а чем выше ускорение, тем больше шансы на победу в гонке.
4·
Запуск ракеты Чтобы ракета покинула земную орбиту и вышла в открытый космос, необходима сила, называемая тягой. Согласно второму закону движения, данному сэром Исааком Ньютоном, сила пропорциональна ускорению; поэтому для запуска ракеты увеличивается величина тяги, что, в свою очередь, увеличивает ускорение. Скорость, достигнутая ракетой, наконец-то помогает ей вырваться из гравитационного поля Земли и выйти в космос.
Скорость, достигнутая ракетой, наконец-то помогает ей вырваться из гравитационного поля Земли и выйти в космос.
5·
Удар по мячуКогда мы ударяем по мячу, мы прикладываем силу в определенном направлении, которое является направлением движения мяча. Кроме того, чем сильнее удар по мячу, тем больше силы мы прикладываем к нему и тем дальше находится мяч.
6·
Автомобильная аварияВо время автомобильной аварии существует сила между препятствием и автомобилем, известная как ударная сила. Величина силы удара зависит от массы объектов, участвующих в столкновении, и скорости, с которой объекты движутся. Это означает, что чем больше масса объектов, участвующих в столкновении, тем больше будет интенсивность силы удара. Аналогично, чем больше ускорение, с которым движется автомобиль, тем больше будет величина силы удара.
7· Два человека, идущих Из двух идущих людей, если один тяжелее другого, тот, кто весит больше всех, идет медленнее, потому что ускорение того, кто весит меньше, больше.
Когда предмет брошен с определенной высоты, гравитационное притяжение Земли помогает ему развить ускорение. Ускорение увеличивается по мере продвижения объекта к земле. Согласно второму закону движения Ньютона ускорение, развиваемое телом, прямо пропорционально силе. Когда предмет ударяется о землю, в действие вступает сила удара. По этой причине хрупкий предмет, брошенный с высокого здания, деформируется сильнее, чем тот же предмет, брошенный со сравнительно более низкого здания.
9· Каратист разбивает плиту из кирпичей
Каратист использует второй закон движения, чтобы разбить плиту. Поскольку по закону сила пропорциональна ускорению, игрок стремится быстро провести руками по плите из кирпичей. Это помогает ему/ей получить ускорение и произвести пропорциональное количество силы. Усилия достаточно, чтобы разбить кирпичи.
10· Вождение автомобиля Проще говоря, второй закон Ньютона гласит, что если сила приложена к любому объекту, имеющему массу, это приведет к созданию эквивалентного ускорения в объект. Например, когда мы включаем систему зажигания автомобиля, двигатель автомобиля производит достаточную мощность, которая позволяет автомобилю двигаться с пропорциональным ускорением.
Например, когда мы включаем систему зажигания автомобиля, двигатель автомобиля производит достаточную мощность, которая позволяет автомобилю двигаться с пропорциональным ускорением.
Законы движения Ньютона составляют основу принципов, используемых в спортивных движениях. Методы обучения, отклоняющиеся от этих законов, механически не имеют смысла. Советы по эффективной спортивной деятельности строятся на этих законах и принципах.
- Бейсбольный мяч
В нормальных условиях бейсбольный мяч находится в состоянии покоя. Для его движения требуется внешняя сила: его бросают или ударяют. Расстояние, которое пройдет мяч, зависит от силы, действующей на него.
Если бейсболист ударит по мячу с удвоенной силой, то скорость, с которой мяч ускорится (ускорится), удвоится
- Теннис быть пораженным. Ускорение, с которым движется мяч, прямо пропорционально приложенной к нему силе.
 Это означает, что чем сильнее вы ударите по мячу, тем быстрее он будет двигаться, тем самым демонстрируя второй закон движения Ньютона в повседневной жизни.
Это означает, что чем сильнее вы ударите по мячу, тем быстрее он будет двигаться, тем самым демонстрируя второй закон движения Ньютона в повседневной жизни.- Каратист разбивает кирпичную плиту
Каратист использует второй закон движения, чтобы разбить кирпичную плиту. Поскольку по закону сила пропорциональна ускорению, игрок стремится быстро провести руками по плите из кирпичей. Это помогает ему/ей получить ускорение и произвести пропорциональное количество силы. Усилия достаточно, чтобы разбить кирпичи.
- Футбол
Футболисты могут замедлять, останавливать или изменять направление движения других игроков в зависимости от того, какую силу они могут генерировать и в каком направлении.
Когда мы пинаем мяч, мы прикладываем силу в определенном направлении, то есть в том направлении, в котором будет двигаться мяч. Кроме того, чем сильнее удар по мячу, тем больше силы мы прикладываем к нему и тем дальше находится мяч.

Начните работу с Praxilabs БЕСПЛАТНО
Примеры закона о ускорении в реальной жизни , потому что полная корзина имеет большую массу, чем пустая. Это означает, что для толкания тележки требуется больше силы.
- Закон ускорения можно наблюдать, сравнивая ускорение, производимое легковым и грузовым автомобилем после приложения одинаковой силы к обоим . Нетрудно заметить, что после того, как автомобиль и грузовик толкнут с одинаковой интенсивностью, автомобиль разгоняется больше, чем грузовик.
(Если вы используете одинаковую силу, чтобы толкнуть грузовик и автомобиль, автомобиль будет иметь большее ускорение, чем грузовик, потому что автомобиль имеет меньшую массу. )
)
- Если автомобиль поворачивает за угол с постоянной скоростью , оно ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
Примеры второго закона Ньютона из реальной жизни
- Хорошим примером действия этого закона движения является езда на велосипеде. Ваш велосипед – это масса. Мышцы ног, давящие на педали велосипеда, и есть сила. Когда вы нажимаете на педали, ваш велосипед ускоряется. Вы увеличиваете скорость велосипеда, прилагая усилие к педалям.
- Во время поездки в автомобиле, когда автомобиль ускоряется, мы чувствуем, как спинка сиденья толкает нас вперед. Спинка нашего сиденья воздействует на нашу спину силой, которая пропорциональна ускорению и нашему весу (массе).

- Когда объект падает при свободном падении на землю, он ускоряется, потому что его притягивает сила земного притяжения.
Вопросы и ответы о применении второго закона Ньютона
Какая технология использует второй закон Ньютона?
Существует множество технологий, основанных на законах движения Ньютона. Например, второй закон движения Ньютона обеспечивает основу для большей части математики инженерной механики.
При изучении динамики инженеры применяют второй закон Ньютона для предсказания движения объекта, на который действует результирующая сила. Используя уравнение F = ma, инженеры могут моделировать положение, скорость и ускорение объекта или измерять эти значения, чтобы узнать о силах, действующих на объект.
В области статики инженеры используют второй закон Ньютона для расчета сил, действующих на неподвижные объекты. Поскольку ускорение неподвижного объекта равно нулю, сумма сил, действующих на объект, должна быть равна нулю. Например, при проектировании конструкций инженеры применяют второй закон Ньютона при расчете сил, действующих на соединения каркасов зданий и мостов.
Например, при проектировании конструкций инженеры применяют второй закон Ньютона при расчете сил, действующих на соединения каркасов зданий и мостов.
Как можно получить первый закон движения Ньютона из второго закона движения?
Когда результирующая сила равна нулю и при движении с постоянной скоростью.
Первый закон движения Ньютона гласит, что покоящееся тело будет оставаться в покое, если на него не действует внешняя сила, а тело, движущееся с постоянной скоростью, будет продолжать двигаться прямолинейно, если на него не действует внешняя сила.
Если тело испытывает ускорение (или замедление) или изменение направления движения, на него должна действовать внешняя сила. Внешние силы иногда называют чистыми силами или неуравновешенными силами.
Второй закон движения гласит, что если на тело действует неуравновешенная сила, то это тело испытает ускорение (или замедление), то есть изменение скорости.
Итак, внешние силы иногда называют чистыми силами. Если результирующая сила, действующая на движущееся тело, равна нулю, то скорость тела будет постоянной. Таким образом, первый закон движения Ньютона можно получить из второго закона движения.
Если результирующая сила, действующая на движущееся тело, равна нулю, то скорость тела будет постоянной. Таким образом, первый закон движения Ньютона можно получить из второго закона движения.
Как первый закон движения лежит во втором законе движения?
Первый закон движения Ньютона гласит, что тело будет оставаться в состоянии покоя или продолжать свой путь с постоянной скоростью, если на него не действует внешняя сила.
Второй закон движения Ньютона гласит, что результирующая сила, действующая на тело, равна произведению массы тела на ускорение, вызванное результирующей силой. Другими словами, Fnet=ma.
Теперь можно утверждать, что второй закон движения Ньютона ведет к первому закону. Учтите это: поскольку Fnet=ma, с нулевой результирующей силой (без внешних сил), 0=ma.
Теперь m — некоторое конечное положительное значение. Другими словами, это означает, что а=0. Таким образом, по определению существует постоянная скорость (возможно, постоянная нулевая скорость). Таким образом, кажется, что второй закон движения Ньютона ведет к первому закону.
Таким образом, кажется, что второй закон движения Ньютона ведет к первому закону.
Почему второй закон движения является самым важным?
Второй закон движения Ньютона F=ma очень важен, потому что он показывает взаимосвязь между силами и движением. Он позволяет рассчитать ускорение (и, следовательно, скорость и положение) объекта с известными силами. Это невероятно ценно для ученых, инженеров, изобретателей и т. д.
Какие два фактора влияют на второй закон Ньютона?
Второй закон гласит, что ускорение объекта зависит от двух переменных – общей силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно пропорционально массе объекта.
Виртуальные лаборатории Praxilabs по механической физике
Виртуальные научные лаборатории PraxiLabs позволяют проводить различные лабораторные эксперименты по физике, химии и биологии онлайн в любое время и в любом месте.
Создайте бесплатную учетную запись и попробуйте виртуальные лаборатории механики, объясняющие законы движения Ньютона и применение законов движения Ньютона в повседневной жизни.
Начните прямо сейчас с виртуальными лабораториями Praxilabs 3D!
5.4: Второй закон Ньютона – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3994
- OpenStax
- OpenStax
Цели обучения
- Различать внешние и внутренние силы
- Опишите второй закон движения Ньютона
- Объясните зависимость ускорения от результирующей силы и массы
Второй закон Ньютона тесно связан с его первым законом. Он математически дает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые идеи, о которых мы упоминали ранее.
Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые идеи, о которых мы упоминали ранее.
Сила и ускорение
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения. Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что результирующая внешняя сила вызывает ненулевое ускорение .
Мы определили внешнюю силу в Силах как силу, действующую на объект или систему, которая возникает вне объекта или системы. Рассмотрим это понятие дальше. Интуитивное представление о внешнее верно — оно вне интересующей нас системы. Например, на рисунке \(\PageIndex{1a}\) система, представляющая интерес, представляет собой автомобиль и человека внутри него.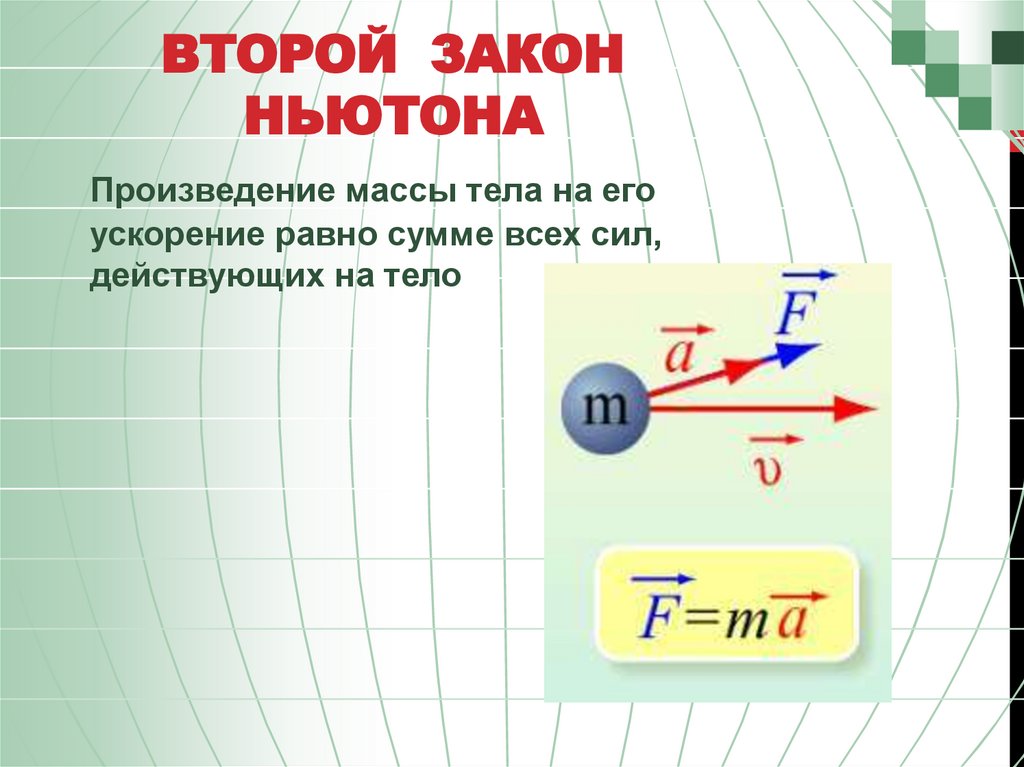 Две силы, приложенные двумя студентами, являются внешними силами. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в машине держится за руль, является внутренней силой между элементами рассматриваемой системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы уравновешивают друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними. Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. Эта концепция неоднократно пересматривалась при изучении физики.
Две силы, приложенные двумя студентами, являются внешними силами. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в машине держится за руль, является внутренней силой между элементами рассматриваемой системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы уравновешивают друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними. Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. Эта концепция неоднократно пересматривалась при изучении физики.
 (b) Силы, действующие на автомобиль, перенесены на координатную плоскость (диаграмма свободного тела) для упрощения анализа. (c) Эвакуатор может оказывать большую внешнюю силу на ту же массу и, следовательно, большее ускорение.
(b) Силы, действующие на автомобиль, перенесены на координатную плоскость (диаграмма свободного тела) для упрощения анализа. (c) Эвакуатор может оказывать большую внешнюю силу на ту же массу и, следовательно, большее ускорение. Из этого примера видно, что разные силы, действующие на одну и ту же массу, вызывают разные ускорения. На рисунке \(\PageIndex{1a}\) два студента толкают машину с водителем. Показаны стрелки, представляющие все внешние силы. Систему интереса представляет автомобиль и его водитель. Вес \(\vec{w}\) системы и опора на землю \(\vec{N}\) также показаны для полноты и предполагаются сокращающимися (поскольку не было вертикального движения и дисбаланса силы в вертикальном направлении, чтобы создать изменение в движении). Вектор \(\vec{f}\) представляет трение, действующее на автомобиль, и он действует слева, противодействуя движению автомобиля. (Более подробно мы обсудим трение в следующей главе.) На рисунке \(\PageIndex{1b}\) все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу \(\vec{F}_{net} \). Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на рисунке \(\PageIndex{1c}\) большая результирующая внешняя сила создает большее ускорение (\(\vec{a}’ > \vec{a}\)), когда эвакуатор тянет машину.
Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на рисунке \(\PageIndex{1c}\) большая результирующая внешняя сила создает большее ускорение (\(\vec{a}’ > \vec{a}\)), когда эвакуатор тянет машину.
Кажется разумным, что ускорение должно быть прямо пропорционально и направлено в том же направлении, что и общая внешняя сила, действующая на систему. Это предположение было проверено экспериментально и показано на рисунке \(\PageIndex{1}\). Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения \(\vec{a}\) и чистой внешней силы \(\vec{F}_{net}\) как пропорциональность
\[\ век{а}\; \пропто\; \vec{F}_{net}\]
, где символ \(\alpha\) означает «пропорционально». (Вспомним из «Сил», что чистая внешняя сила представляет собой векторную сумму всех внешних сил и иногда обозначается как \(\sum \vec{F}\). ) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистая внешняя сила. Как только интересующая система выбрана, определите внешние силы и проигнорируйте внутренние. Пренебрежение многочисленными внутренними силами, действующими между объектами внутри системы, такими как мышечные силы в телах учащихся, не говоря уже о бесчисленных силах между атомами в объектах, является огромным упрощением. Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.
) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистая внешняя сила. Как только интересующая система выбрана, определите внешние силы и проигнорируйте внутренние. Пренебрежение многочисленными внутренними силами, действующими между объектами внутри системы, такими как мышечные силы в телах учащихся, не говоря уже о бесчисленных силах между атомами в объектах, является огромным упрощением. Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.
Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. Как показано на рисунке \(\PageIndex{2}\), та же внешняя сила, приложенная к баскетбольному мячу, дает гораздо меньшее ускорение, когда она приложена к внедорожнику. Пропорциональность записывается как
\[a\; \пропто\; \frac{1}{m},\]
где m – масса системы, a – величина ускорения. Эксперименты показали, что ускорение точно обратно пропорционально массе, точно так же, как оно прямо пропорционально результирующей внешней силе.
Эксперименты показали, что ускорение точно обратно пропорционально массе, точно так же, как оно прямо пропорционально результирующей внешней силе.
Было обнаружено, что ускорение объекта зависит только от суммарной внешней силы и массы объекта. Объединение двух только что данных пропорциональностей дает второго закона Ньютона .
Второй закон движения Ньютона
Ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе. В форме уравнения второй закон Ньютона равен
В форме уравнения второй закон Ньютона равен
\[\vec{a} = \frac{\vec{F}_{net}}{m},\]
где \(\vec{a}\) — ускорение, \(\vec{F}_{net}\) — результирующая сила, а m — масса. Это часто записывается в более знакомой форме
\[\vec{F}_{net} = \sum \vec{F} = m \vec{a}, \label{5.3}\]
, но первый уравнение дает больше понимания того, что означает второй закон Ньютона. Когда учитываются только величина силы и ускорения, это уравнение можно записать в более простой скалярной форме:
\[\vec{F}_{net} = ma \ldotp \label{5.4}\]
Закон есть причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона основана на экспериментальной проверке. Диаграмма свободного тела, которую вы научитесь рисовать в разделе «Рисование диаграмм свободного тела», является основой для написания второго закона Ньютона.
Пример 5.2: Какое ускорение может создать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле (рис. \(\PageIndex{3}\)). Масса косилки 24 кг. Каково его ускорение?
\(\PageIndex{3}\)). Масса косилки 24 кг. Каково его ускорение?
Стратегия
Эта задача касается только движения в горизонтальном направлении; нам также дана результирующая сила, обозначенная единственным вектором, но мы можем подавить природу вектора и сконцентрироваться на применении второго закона Ньютона. Поскольку F net и m заданы, ускорение можно рассчитать непосредственно из второго закона Ньютона как F 9{2} \ldotp\]
Значение
Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. Это результат векторного соотношения, выраженного во втором законе Ньютона, то есть вектор, представляющий результирующую силу, является скалярным множителем вектора ускорения. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах.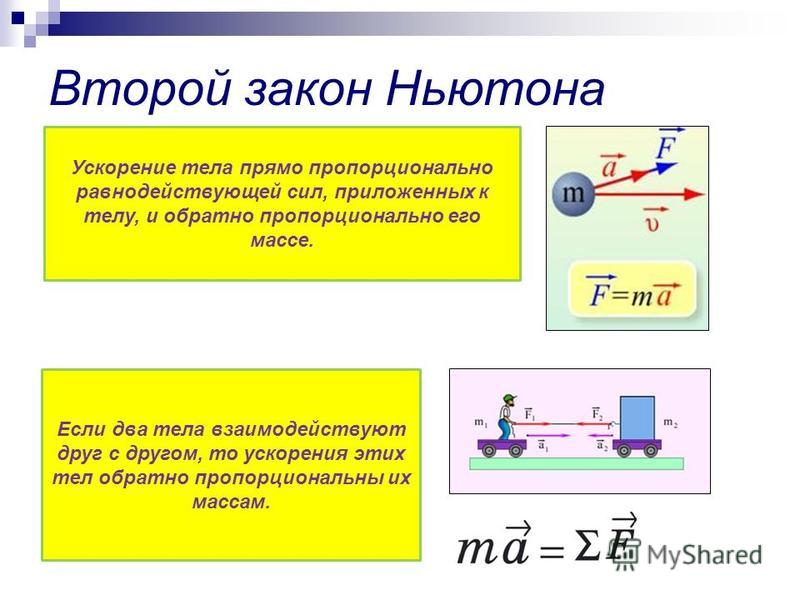 Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны компенсироваться, поскольку в вертикальном направлении не возникает никакого ускорения (косилка движется). только по горизонтали). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.
Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны компенсироваться, поскольку в вертикальном направлении не возникает никакого ускорения (косилка движется). только по горизонтали). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.
Упражнение 5.3
На момент спуска на воду HMS Titanic был самым массивным мобильным объектом из когда-либо построенных, его масса составляла 6,0 x 10 7 кг. Если к кораблю приложить силу 6 МН (6 х 10 6 Н), какое ускорение он испытает?
В предыдущем примере мы имели дело с чистой силой только для простоты. Однако на газонокосилку действует несколько сил. Вес \(\vec{w}\) (подробно обсуждаемый в разделе «Масса и вес») тянет косилку вниз к центру Земли; это создает контактную силу на земле.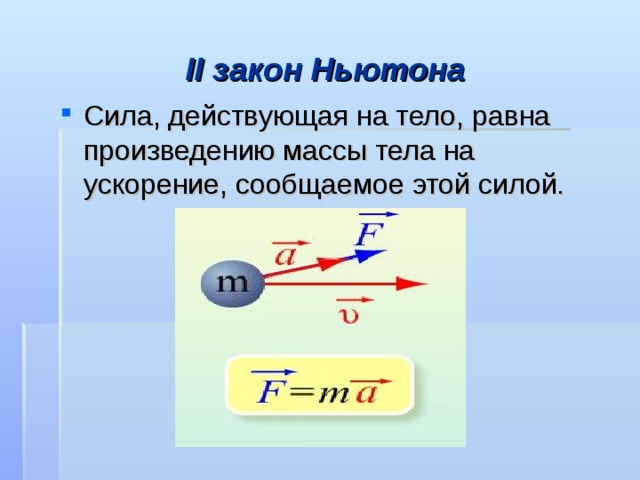 Земля должна воздействовать на газонокосилку направленной вверх силой, известной как нормальная сила \(\vec{N}\), которую мы определяем в Common Forces. Эти силы уравновешены и поэтому не создают вертикального ускорения. В следующем примере мы показываем обе эти силы. Продолжая решать задачи, используя второй закон Ньютона, не забудьте показать множественные силы.
Земля должна воздействовать на газонокосилку направленной вверх силой, известной как нормальная сила \(\vec{N}\), которую мы определяем в Common Forces. Эти силы уравновешены и поэтому не создают вертикального ускорения. В следующем примере мы показываем обе эти силы. Продолжая решать задачи, используя второй закон Ньютона, не забудьте показать множественные силы.
Пример 5.3. Какая сила больше?
- Автомобиль, показанный на рисунке \(\PageIndex{4}\), движется с постоянной скоростью. Какая сила больше, \(\vec{F}_{двигатель}\) или \(\vec{F}_{трение}\)? Объяснять.
- Та же машина ускоряется вправо. Какая сила больше, \(\vec{F}_{двигатель}\) или \(\vec{F}_{трение}\)? Объяснять.
Стратегия
Для анализа ситуации необходимо учитывать первый и второй законы Ньютона. Нам нужно решить, какой закон применим; это, в свою очередь, расскажет нам о соотношении между силами.
Нам нужно решить, какой закон применим; это, в свою очередь, расскажет нам о соотношении между силами.
Решение
- Силы равны. Согласно первому закону Ньютона, если результирующая сила равна нулю, скорость постоянна.
- В этом случае \(\vec{F}_{engine}\) должно быть больше, чем \(\vec{F}_{friction}\). Согласно второму закону Ньютона, чтобы вызвать ускорение, необходима результирующая сила.
Значение
Эти вопросы могут показаться тривиальными, но на них обычно отвечают неправильно. Чтобы автомобиль или любой другой объект двигался, его необходимо разогнать из состояния покоя до нужной скорости; для этого требуется, чтобы сила двигателя была больше силы трения. Когда автомобиль движется с постоянной скоростью, результирующая сила должна быть равна нулю; в противном случае автомобиль будет ускоряться (набирать скорость). Чтобы решать задачи, связанные с законами Ньютона, мы должны понимать, следует ли применять первый закон Ньютона (где \(\sum \vec{F}\) = \(\vec{0}\)) или второй закон Ньютона (где \(\sum \vec{F}\) не равен нулю). Это станет очевидным, когда вы увидите больше примеров и попытаетесь решить проблемы самостоятельно.
Это станет очевидным, когда вы увидите больше примеров и попытаетесь решить проблемы самостоятельно.
Пример 5.4. Какая ракетная тяга ускоряет эти сани?
До пилотируемых космических полетов ракетные салазки использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами.
Рассчитайте величину силы, действующей на каждую ракету, называемую ее тягой T, для четырехракетной силовой установки, показанной на рисунке \(\PageIndex{5}\). Начальное ускорение саней 49м/с 2 , масса системы 2100 кг, сила трения, противодействующая движению, 650 Н.
Рис. право. Каждая ракета создает одинаковую тягу T. Система здесь — это салазки, их ракеты и их наездник, поэтому никакие силы между этими объектами не учитываются. Стрелка, представляющая трение (\(\vec{f}\)) нарисована больше масштаба.Стратегия
Хотя силы действуют как по вертикали, так и по горизонтали, мы предполагаем, что вертикальные силы компенсируются, потому что нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке \(\PageIndex{5}\).
Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке \(\PageIndex{5}\).
Решение
Поскольку ускорение, масса и сила трения известны, начнем со второго закона Ньютона и будем искать способы найти тягу двигателей. Мы определили направление силы и ускорения как действующие «вправо», поэтому в расчетах нам нужно учитывать только величины этих величин. Следовательно, мы начинаем с
\[F_{net} = ma\]
, где F net – результирующая сила в горизонтальном направлении. Из рисунка видно, что тяги двигателя добавляются, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна 9{5}\; N \ldotp\]
Значимость
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости, а установка была разработана для защиты людей при аварийном катапультировании реактивного истребителя. Были получены скорости 1000 км/ч с ускорениями 45g. (Вспомним, что g, ускорение свободного падения, равно 9,80 м/с 2 . Когда мы говорим, что ускорение равно 45 g, это 45 x 90,8 м/с 2 , что примерно равно 440 м/с 2 .) Хотя живые объекты больше не используются, с ракетными салазками была получена наземная скорость 10000 км/ч.
Были получены скорости 1000 км/ч с ускорениями 45g. (Вспомним, что g, ускорение свободного падения, равно 9,80 м/с 2 . Когда мы говорим, что ускорение равно 45 g, это 45 x 90,8 м/с 2 , что примерно равно 440 м/с 2 .) Хотя живые объекты больше не используются, с ракетными салазками была получена наземная скорость 10000 км/ч.
В этом примере, как и в предыдущем, интересующая система очевидна. В более поздних примерах мы видим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе.
Упражнение 5.4
Спортивный автомобиль массой 550 кг сталкивается с грузовиком массой 2200 кг, и во время столкновения результирующая сила, действующая на каждую машину, равна силе, действующей на другую.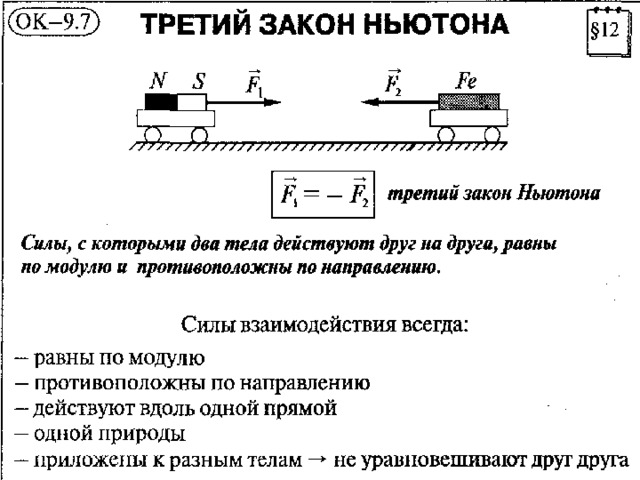 Если величина ускорения грузовика равна 10 м/с 2 , какова величина ускорения спортивного автомобиля?
Если величина ускорения грузовика равна 10 м/с 2 , какова величина ускорения спортивного автомобиля?
Компонентная форма второго закона Ньютона
Мы разработали второй закон Ньютона и представили его в виде векторного уравнения в уравнении \ref{5.3}. Это векторное уравнение можно записать в виде трех компонентных уравнений:
\[\sum \vec{F}_{x} = m \vec{a}_{x}, \sum \vec{F}_{y} = m \vec{a}_{y}, \sum \vec{F}_{z} = m \vec{a}_{z} \ldotp \label{5.5}\]
Второй закон описывает, как тело механически реагирует на окружающую среду. Влияние среды есть результирующая сила \(\vec{F}_{net}\), отклик тела есть ускорение \(\vec{a}\), а сила отклика обратно пропорциональна масса м. Чем больше масса объекта, тем меньше его реакция (ускорение) на воздействие окружающей среды (заданная результирующая сила). Следовательно, масса тела является мерой его инерции, как мы объяснили в Первом законе Ньютона.
Пример 5.5: Сила, действующая на футбольный мяч
Футбольный мяч массой 0,400 кг перебрасывается через поле игроком; он подвергается ускорению, определяемому формулой \(\vec{a}\) = 3,00 \(\hat{i}\) + 7,00 \(\hat{j}\) м/с 2 . Найдите: а) результирующую силу, действующую на мяч; б) модуль и направление результирующей силы.
Найдите: а) результирующую силу, действующую на мяч; б) модуль и направление результирующей силы.
Стратегия
Задействованы векторы в формате \(\hat{i}\) и \(\hat{j}\), которые указывают направление силы вдоль оси x и оси y соответственно. , поэтому мы применяем второй закон Ньютона в векторной форме. 9{o} \ldotp$$
Значение
Мы должны помнить, что второй закон Ньютона является векторным уравнением. В (а) мы умножаем вектор на скаляр, чтобы определить результирующую силу в векторной форме. В то время как векторная форма дает компактное представление вектора силы, она не говорит нам, насколько он «большой» или куда он движется, в интуитивно понятных терминах. В (b) мы определяем фактический размер (величину) этой силы и направление, в котором она движется.
Пример 5.6: Масса автомобиля
Найдите массу автомобиля, если результирующая сила −600,0 \(\hat{j}\) Н создает ускорение −0,2 \(\hat{j}\) м/с 2 .
Стратегия
Деление вектора не определено, поэтому \(m = \frac{\vec{F}_{net}}{\vec{a}}\) не может быть выполнено. Однако масса m является скаляром, поэтому мы можем использовать скалярную форму второго закона Ньютона, \(m = \frac{F_{net}}{a}\).
Решение
Мы используем m = \(\frac{F_{net}}{a}\) и подставляем величины двух векторов: F 9{2}} = 3000\; кг \ldotp \nonumber\]
Значение
Сила и ускорение даны в формате \(\hat{i}\) и \(\hat{j}\), но ответ, масса m, равен скаляр и, таким образом, не задается в форме \(\hat{i}\) и \(\hat{j}\).
Пример 5.7
Несколько сил, действующих на частицу На частицу массой m = 4,0 кг действуют силы четырех величин. F 1 = 10,0 Н, F 2 = 40,0 Н, F 3 = 5,0 Н и F 4 = 2,0 Н, с направлениями, как показано на диаграмме свободного тела на рисунке \(\PageIndex{6}\). Чему равно ускорение частицы?
Рисунок \(\PageIndex{6}\): Четыре силы в плоскости xy действуют на частицу массой 4,0 кг.
Стратегия
Поскольку это двумерная задача, мы должны использовать диаграмму свободного тела. Во-первых, \(\vec{F}_{1}\) необходимо разложить на x- и y-компоненты. Затем мы можем применить второй закон в каждом направлении.
Решение
Мы рисуем диаграмму свободного тела, как показано на рисунке \(\PageIndex{6}\). Теперь применим второй закон Ньютона. Мы рассматриваем все векторы, разложенные на x- и y-компоненты: 9{2},\]
, который представляет собой вектор величиной 8,4 м/с 2 , направленный под углом 276° к положительной оси x.
Значение
В повседневной жизни можно найти множество примеров, когда три или более сил действуют на один объект, например, тросы, идущие от моста «Золотые Ворота», или футболиста, которого трое защитников атакуют. Мы видим, что решение этого примера является просто расширением того, что мы уже сделали.
Упражнение 5.5
На автомобиль действуют силы, как показано ниже. Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трением можно пренебречь. а) Чему равна результирующая сила, действующая на автомобиль? б) Чему равно ускорение автомобиля?
Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трением можно пренебречь. а) Чему равна результирующая сила, действующая на автомобиль? б) Чему равно ускорение автомобиля?
Второй закон Ньютона и импульс
Ньютон фактически сформулировал свой второй закон в терминах импульса: «Мгновенная скорость изменения импульса тела равна суммарной силе, действующей на тело». («Мгновенная скорость» подразумевает, что задействована производная.) Это может быть задано векторным уравнением
\[\vec{F}_{net} = \frac{d \vec{p}}{dt} \ldotp \label{5.6}\]
Это означает, что второй закон Ньютона решает центральный вопрос движения : Что вызывает изменение движения объекта? Импульс был описан Ньютоном как «количество движения», способ сочетания скорости объекта и его массы. Мы посвящаем «Линейный импульс» и «Столкновения» изучению импульса.
Пока достаточно определить импульс \(\vec{p}\) как произведение массы объекта m на его скорость \(\vec{v}\):
\[\vec{p} = m \vec{v} \ldotp \label{5. 7}\]
7}\]
Так как скорость является вектором, то и импульс.
Легко визуализировать импульс. Поезд, движущийся со скоростью 10 м/с, имеет больший импульс, чем тот, который движется со скоростью 2 м/с. В повседневной жизни мы называем одну спортивную команду «имеющей импульс», когда она набирает очки против команды соперника.
Если мы подставим уравнение \ref{5.7} в уравнение \ref{5.6}, мы получим
\[\vec{F}_{net} = \frac{d \vec{p}}{dt} = \ frac{d (m \vec{v})}{dt} \ldotp\]
Когда m постоянно, мы имеем
\[\vec{F}_{net} = m \frac{d(\vec{v})}{dt} = m \vec{a} \ldotp\]
Таким образом, мы видим, что импульсная форма второго закона Ньютона сводится к форме, данной ранее в этом разделе.
Моделирование
Изучите силы, действующие при буксировке тележки или толкании холодильника, ящика или человека. Создайте приложенную силу и посмотрите, как она заставляет объекты двигаться. Поместите объект на рампу и посмотрите, как это повлияет на его движение.
Эта страница под названием 5.4: Второй закон Ньютона распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Второй закон Ньютона
- Второй закон движения Ньютона
- источник@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1
Сегмент C: Второй закон Ньютона, часть 1
Теги:
- Образование
- Физика в движении
- Модуль 3: Силы
Второй закон Ньютона объясняется, когда мы исследуем силы гравитации, натяжения, трения, пружины и нормали. Мы используем пример задачи для анализа сил, действующих на объект, покоящийся на поверхности.
Сегмент C: второй закон Ньютона, часть 1
Из журнала Physics in Motion, Unit 3
Сегмент C: Второй закон Ньютона, часть 1
Второй закон Ньютона объясняется по мере изучения сил гравитации, натяжения, трения, пружины и нормали. Мы используем пример задачи для анализа сил, действующих на объект, покоящийся на поверхности.
Дополнительный сегмент
Наука
Получайте, оценивайте и сообщайте информацию о том, как силы влияют на движение объектов.
Составьте объяснение, основанное на доказательствах, используя Законы Ньютона о том, как силы влияют на ускорение тела.
- Объясните и предскажите движение тела в отсутствие силы и при приложении сил, используя 1-й закон Ньютона (принцип инерции).
- Рассчитайте ускорение объекта, используя 2-й закон Ньютона, включая ситуации, когда несколько сил действуют вместе.
- Определите пару равных и противоположных сил между двумя взаимодействующими телами и свяжите их величины и направления, используя 3-й закон Ньютона.
Разработайте и используйте модель диаграммы свободного тела для представления сил, действующих на объект (как равновесных, так и неравновесных).
Используйте математические представления для расчета величин и компонентов вектора для типичных сил, включая гравитационную силу, нормальную силу, силы трения, силы натяжения и силы пружины.
Получайте, оценивайте и сообщайте информацию для объяснения отношений между силой, массой и движением.
SPS8.b
Придумайте объяснение, основанное на экспериментальных данных, в поддержку утверждений, представленных в трех законах движения Ньютона.
Получать, оценивать и передавать информацию о причинно-следственных связях между силой, массой и движением объектов.
S8P3.b
Постройте объяснение, используя законы движения Ньютона, чтобы описать влияние уравновешенных и неуравновешенных сил на движение объекта.
S8P3.c
Приведите аргумент на основе данных в поддержку утверждения о том, что сила, необходимая для ускорения объекта, пропорциональна его массе (инерции).
– Проведите различие между полевыми силами и контактными силами и приведите примеры каждой из них.
-Используйте второй закон Ньютона, чтобы вычислить результирующую силу, действующую на объект, и определить, ускоряется ли этот объект.
-Исследуйте различные типы сил, действующих на объекты, такие как гравитация, нормаль, приложенная сила, напряжение и трение.
– Нарисуйте диаграмму свободного тела для объекта, чтобы помочь в определении сил, действующих на него.
контактная сила – толчок или притяжение, передаваемые через соприкасающиеся друг с другом объекты; примерами являются приложенная сила, сила пружины и нормальная сила.
сила поля – толчки или притяжения, возникающие между двумя объектами без соприкосновения объектов друг с другом; примерами являются гравитация и электростатическая сила.
трение – сила, противодействующая движению.
гравитация (ФГ) — одна из четырех фундаментальных сил Вселенной; воздействует на все, что имеет массу, на все, что имеет массу.
закон обратных квадратов – любой закон, утверждающий, что величина убывает обратно пропорционально квадрату физического параметра, например расстояния.
чистая сила – сумма всех сил, действующих на объект.
ньютон (Н) – производная единица измерения силы; один ньютон равен одному килограмму, умноженному на метры, деленному на секунды в квадрате (кгм/с2).
Второй закон движения Ньютона – объект ускоряется в направлении чистой силы, действующей на него.
нормальная сила (FN) – опорная сила, действующая на объект со стороны поверхности; всегда перпендикулярна поверхности.
масса (w) – сила тяжести, действующая на объект; равна массе объекта, умноженной на ускорение свободного падения на Земле.
Набор инструментов для учителя Physics in Motion содержит инструкции и ключи к ответам на учебные вопросы, практические задачи, лабораторные работы по всем семи блокам обучения. GPB предлагает набор инструментов для учителей бесплатно для преподавателей Грузии. Чтобы заказать набор инструментов для учителей, заполните и отправьте эту форму, чтобы запросить набор инструментов для учителей. Вам нужно отправить эту форму только один раз, чтобы получить материалы для всех семи модулей.
Физика в движении Сегменты
Модуль 3: Силы
Модуль 1. Введение в физику. Модуль 2. Описание движения. Модуль 3. Силы. Модуль 4. Импульс и энергия. Модуль 5. Электричество и магнетизм. Модуль 6. Волны и оптика. Модуль 7. Ядерная физика.
Введение в физику. Модуль 2. Описание движения. Модуль 3. Силы. Модуль 4. Импульс и энергия. Модуль 5. Электричество и магнетизм. Модуль 6. Волны и оптика. Модуль 7. Ядерная физика.Модуль 03: Динамика >
2: Второй закон движения Ньютона.
Деятельность (лаборатория PhET): Силы и движение
- Виртуальная лаборатория (PhET): Силы и движение (JAVA для компьютеров)
- Виртуальная лаборатория (PhET): Силы и движение (для телефонов и планшетов)
- Раздаточный материал/Практические навыки: Лаборатория PhET – Силы и движение
В конце этого раздела учащиеся должны быть в состоянии объяснить, что подразумевается под
чистой силой (F чистой ) или неуравновешенной силой.Демонстрация: тема
Чистая сила это сумма всех сил, действующих на объект в любой момент времени. Для того, чтобы там
чтобы было какое-либо изменение в движении, должна быть результирующая сила, действующая на объект.
Если объект имеет результирующую силу, равную нулю (F нетто = 0), то есть
не изменится в движении, и объект останется в своем состоянии
движение (движение или неподвижное сидение). Чистая сила необходима для того, чтобы
объект для ускорения.
Для того, чтобы там
чтобы было какое-либо изменение в движении, должна быть результирующая сила, действующая на объект.
Если объект имеет результирующую силу, равную нулю (F нетто = 0), то есть
не изменится в движении, и объект останется в своем состоянии
движение (движение или неподвижное сидение). Чистая сила необходима для того, чтобы
объект для ускорения.
- Website (Hyperphysics): Force
- Tutorial (Khan Academy): Newton’s Laws – Playlist
- Virtual lab (PhET): Forces & motion basics
- Handout/Practice skills: тема
- Активность: Тема
- Лаборатория/Виртуальная лаборатория (PHET): Тема
2 -й закон Ньютона.
(a) укажите и объясните Второй закон Ньютона (закон ускорения) и
(b) применяются к
физические ситуации и,
(c) различать вес и массу.
:
«The
изменение движения всегда пропорционально движущей силе
впечатлен; и производится в направлении правой линии, в которой
Force Is Impress’d ”
- Учебник (Ханская академия): 2 -й Закон Ньютона
- Демонстрация: Тема
- Веб -сайт (гиперфизика): . тема
- Учебник (Академия Хана): topic
- Handout/Practice skills: topic
- Activity: topic
- Laboratory/Virtual lab (PhET): topic
Apparent weight
Demo: Spring scale lift and падение
- К концу этого раздела учащиеся должны быть в состоянии вычислить кажущийся вес объекта на основе его ускорения в вертикальном направлении.
Вес объекта зависит от его движения.
- Если объект движется с постоянной скоростью (0-∞)
- Нормальный = мг
- Если объект ускоряется вверх, то его предполагаемый вес:
- Больше нормального веса = (м + ma)
- Если объект движется с ускорением вниз, то его предполагаемый вес:
- Меньший, чем нормальный вес = (мг – ma)
Vomit Comet
youtube.com/embed/2V9h52yspbo?rel=0&wmode=opaque” frameborder=”0″ allowfullscreen=”true”>- (TED): STEPHEN DAWKENG ON THE VOMIT (TED): . Тема
- Раздача/тренировочный навыки: Тема
- Активность: Тема
- Лаборатория/Виртуальная лаборатория (PHET): Тема
#: #: #: #: #: №
0 #: #: #: #: #: № #: #: №
9 ученики должны уметь
Текст
Картинка
Демо: Тема
Веб -сайт (Гиперфизика): Тема
Видео (веб -сайт): Тема
Учебник (KHAN Academy): Тема
. : тема
Занятие: тема
Лаборатория/Виртуальная лаборатория (PhET): тема
День №: Тема
К концу этого раздела учащиеся должны уметь
Текст
Картинка
Демо: Тема
Веб -сайт (Гиперфизика): Тема
Видео (веб -сайт): Тема
Учебник (KHAN Academy): Тема
.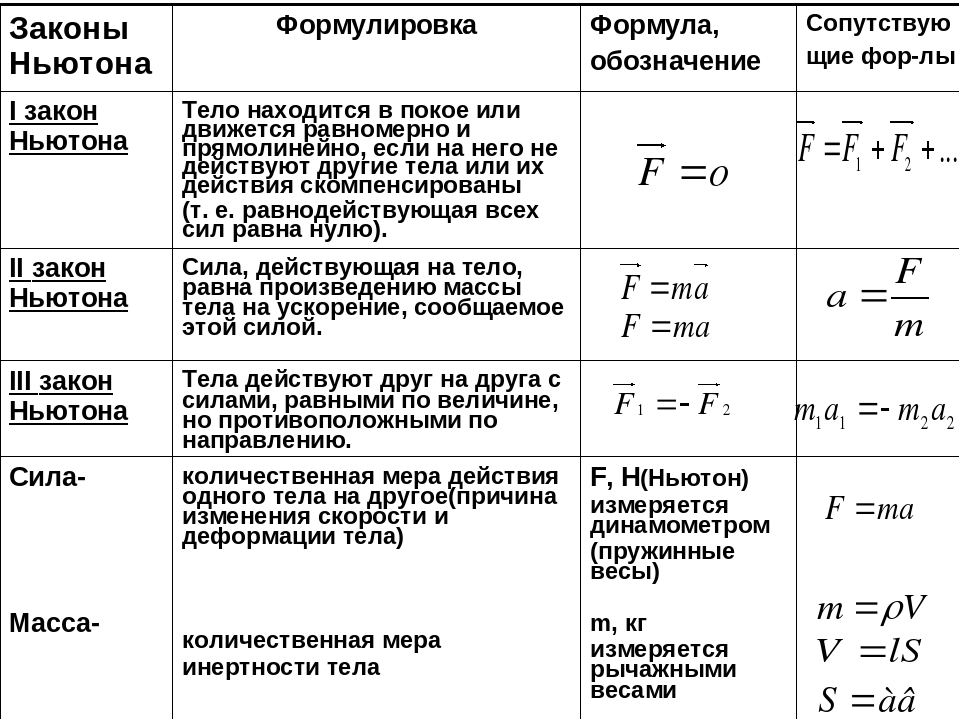

 2 Динамика
2 Динамика 4 Электромагнитные колебания и волны
4 Электромагнитные колебания и волны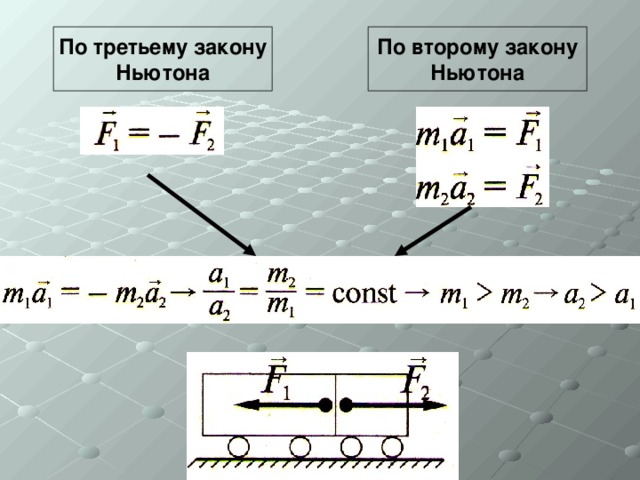 2 Ядерная физика
2 Ядерная физика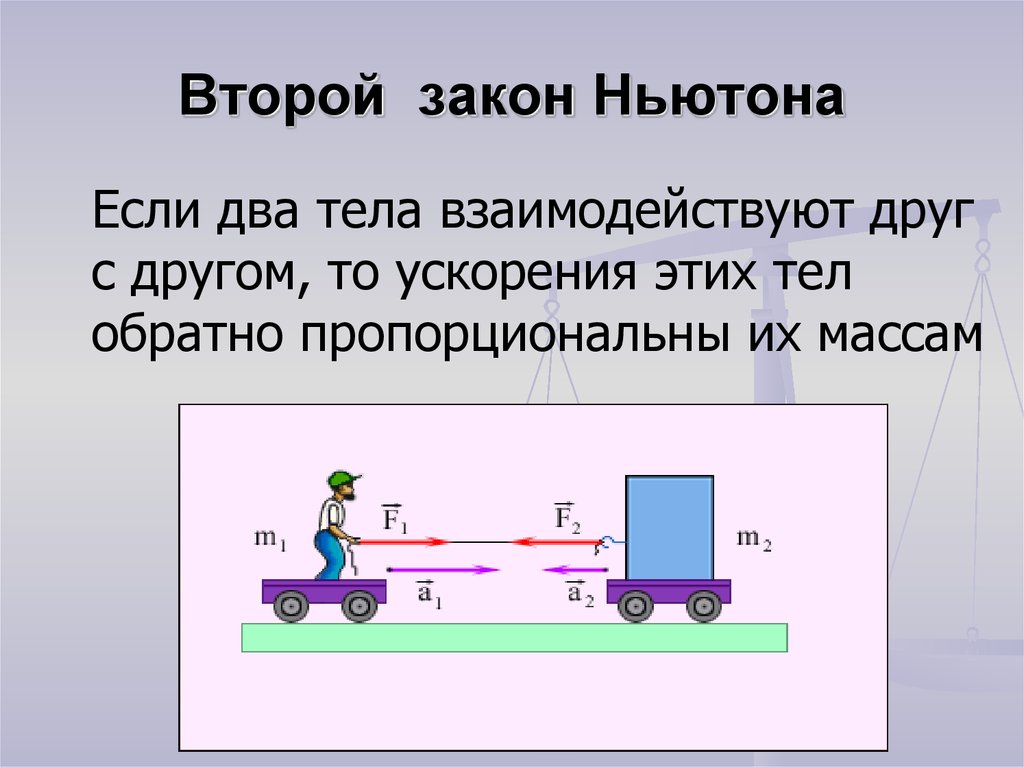 Это означает, что чем сильнее вы ударите по мячу, тем быстрее он будет двигаться, тем самым демонстрируя второй закон движения Ньютона в повседневной жизни.
Это означает, что чем сильнее вы ударите по мячу, тем быстрее он будет двигаться, тем самым демонстрируя второй закон движения Ньютона в повседневной жизни.

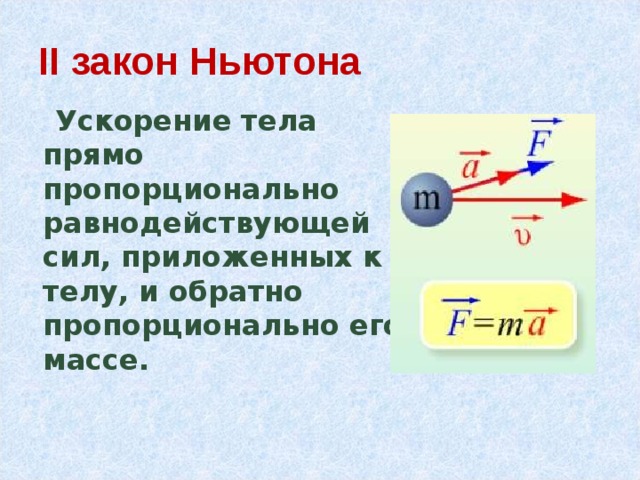 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1