Физики-теоретики доказали устойчивость черных дыр
Группа гравитационистов изучила устойчивость черной дыры Керра с малым угловым моментом. В работе на 912 страниц физики доказали целый ряд теорем, связанных с постановкой задачи Коши для вакуумных уравнений Эйнштейна, и разработали для этого новый формализм. Препринт статьи доступен на сайте arxiv.org.
В математике и физике задача о начальных данных (задача Коши) в общих чертах может быть сформулирована следующим образом: зная состояние системы в некоторый момент времени, можно ли предсказать ее дальнейшее развитие и если да, то как это развитие зависит от начального состояния? Конкретный путь развития системы для определенных начальных данных принято называть решением задачи Коши. Задача Коши поставлена корректным образом, когда у нее существует решение, которое единственно и устойчиво. Устойчивость решения задачи Коши подразумевает, что «малые» изменения начальных данных порождают «малые» изменения самого решения.
Последние несколько десятков лет теоретики пытались математическим образом доказать устойчивость черных дыр — решений вакуумных уравнений Эйнштейна.
В Эйнштейновской гравитации взаимодействие между объектами материи происходит за счет искривления пространства. Само пространство-время может быть описано с помощью пары (M, g), где M — некоторое 4-мерное многообразие , которое имеет одну временную координату t и три пространственных координат xi (i=1, 2, 3), а g — метрика на этом многообразии. Найти метрику g можно из уравнений Эйнштейна, которые в случае отсутствия материи (в вакууме) имеют вид (подробнее о гравитации Эйнштейна): Rab=0, где Rab — тензор Риччи, который зависит от первых и вторых производных метрики по координатам многообразия M (a, b = 0, 1, 2, 3).
Для задания начальных условий можно зафиксировать метрику g’ на некоторой пространственноподобной гиперповерхности S0 (то есть, на 3-х мерной поверхности в M, любые две точки которой соединены пространственноподобным интервалом) в начальный момент времени t0.
Тогда уравнения Эйнштейна можно воспринимать как уравнения, описывающие дальнейшую эволюцию этой гиперповерхности в различные моменты времени. Решением такой задачи Коши является метрика g(t, xi), заданная на M , которая в момент t0 совпадает с g’ на гиперповерхности S0, называемой гиперповерхностью Коши. Устойчивость решения приобретает следующий смысл: если мы возьмем две достаточно близких метрики на гиперповерхности Коши S0, то решения гравитационных задач (каждая со своим начальным условием) должны быть также близки.
В одной из первых работ физиков Ивонны Шоке-Брюа (Yvonne Choquet-Bruhat) и Роберта Героха (Robert Geroch) 1969 года была доказана теорема о существовании, единственности и устойчивости решения гравитационной задачи в случае, когда 4-мерное пространство-время (M, g) является глобально гиперболическим пространством или, другими словами, когда любая времени- или светоподобная кривая, проходящая через любую точку 4-мерного пространства, пересекает S0.
Однако приведенное ими доказательство не работает в случае решений уравнений Эйнштейна в виде черных дыр, так как последние имеют более сложную причинную структуру.
Спустя 53 года, Элена Джорджи (Elena Giorgi), Серджиу Клейнерман (Sergiu Klainerman) и Джереми Шефтель (Jeremie Szeftel) смогли обобщить теорему на случай асимптотически плоских пространств (которым является черная дыра Керра). В своей работе теоретики показали, что для начальных данных близких к решению в виде вращающейся черной дыры Керра решения асимптотически ведут себя как пространство-время Керра. По-другому, если малым образом возмутить решение Керра, то бесконечно-удаленный наблюдатель, спустя достаточное время, увидит то же решение в виде черной дыры с возможно немного измененными угловым моментом J и массой m. Приведенное физиками доказательство работает в случае вращающихся черных дыр с малым угловым моментом: J/m<<1.
Важным «ингредиентом» для доказательства главной теоремы стал механизм фиксирования калибровочных условий (ОТО является калибровочной теорией относительно диффеоморфизмов пространства-времени), основанный на обще-ковариантно модулированных (GCM, generally covariant modulated) сферах и гиперповерхностях.
GCM сферы — это компактные поверхности с коразмерностью 2, не связанные с начальными условиями, на которых определенные геометрические величины принимают Шварцшильдовские значения. В свою очередь, GCM гиперповерхности являются пространственноподобными гиперповерхностями с коразмерностью 1, которые покрыты GCM сферами и на которых проверяются дополнительные условия.
Полученные результаты дополняют знания о гравитации Эйнштейна, и, в частности, показывают, что медленно вращающиеся черные дыры не «разрушаются» в результате малого воздействия гравитационными волнами. Теоретики надеются, что в ближайшие несколько лет они смогут обобщить полученные результаты на случай произвольного углового момента и, таким образом, окончательно доказать теорему об устойчивости решения гравитационной задачи о начальных данных.
Узнать больше про черные дыры и проверить свои знания можно в нашем тесте «Рыбалка на горизонте событий», а чтобы лучше понять причинную структуру пространства-времени рекомендуем прочесть лонгрид про путешествие во времени «Убить дедушку и выжить».
Стефан Курлянд
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Физики доказали применимость теоремы квантовой физики при «неквантовых» температурах – Газета.Ru
Физики доказали применимость теоремы квантовой физики при «неквантовых» температурах – Газета.Ru | Новости
close
100%
Отечественные физики показали применимость одной из центральных теорем квантовой физики при «неквантовых» температурах. При абсолютном нуле (-273,15 по Цельсию) могут реализоваться далекие от классических законов эффекты, а их описание заметно упрощается. В жизни столь низких температур достичь невозможно, а потому требуется расширять имеющиеся фундаментальные подходы — что и сделали авторы статьи. Результаты работы, поддержанной грантом Российского научного фонда (РНФ), опубликованы в Physical Review A.
Квантовая физика в некоторой степени находится за гранью классических законов, с которыми мы сталкиваемся в повседневной жизни.
«Однако в силу третьего начала термодинамики абсолютный нуль недостижим — он является лишь полезной абстракцией. В реальной жизни температуры всегда конечны, и они могут полностью разрушить деликатные квантовые суперпозиции, лежащие в основе работы квантовых устройств. Поэтому контроль тонких процессов при конечной температуре является центральной задачей квантовых технологий», — рассказывает Олег Лычковский, кандидат физико-математических наук, старший научный сотрудник Сколковского института науки и технологий, Московского физико-технического института и Математического института имени В.
Если изменятся внешние параметры, изменится и состояние системы. Его описывают при помощи оператора плотности, который в такой ситуации эволюционирует. Даже системы из относительно небольшого количества простейших квантовых элементов чрезвычайно сложны, равно как и описание их развития. Чтобы создавать устройства будущего важно эту «сложность» приручить, например, с помощью адиабатической эволюции: плавное изменение внешних параметров делает развитие квантового состояния более предсказуемым. Макс Борн и В. А. Фок сформулировали адиабатическую теорему, которая гарантирует, что на всех этапах своей эволюции квантовое состояние может оставаться близким к так называемому мгновенному собственному состоянию.
Проблема теоремы заключается в ее применимости к системам только в чистом состоянии, что предполагает и наличие абсолютного нуля, но не реальные конечные температуры. Сотрудники Сколтеха (Москва), Математического института имени В. А. Стеклова (Москва) и Московского физико-технического института (Долгопрудный) показали, как можно использовать адиабатическую теорему в случае систем с конечной температурой.
«Адиабатические протоколы приготовления квантовых состояний с заданными свойствами весьма разнообразны. Пожалуй, самый известный пример — адиабатический квантовый компьютер, работа которого целиком основана на адиабатической теореме. Устройство такого вида пытаются сконструировать в канадской компании D-Wave Systems Inc. Кроме того, адиабатическое приготовление состояний используется в качестве предварительного или вспомогательного шага и в других схемах квантовых вычислений, а также симуляций и измерений. Наши результаты помогут выбирать оптимальные режимы работы адиабатических протоколов с учетом конечности рабочей температуры квантовых устройств», — подводит итог Олег Лычковский.
Подписывайтесь на «Газету.Ru» в Новостях, Дзен и Telegram.
Чтобы сообщить об ошибке, выделите текст и нажмите Ctrl+Enter
Новости
Дзен
Telegram
Марина Ярдаева
Какая серость!
О перспективах выхода России из тени
Мария Дегтерева
Песни о далекой родине
О том, можно ли запрещать культуру, если она антипатриотична
Анастасия Миронова
Зарплата 30 тысяч в день – не миф
О том, как аппетиты отделочников дестабилизируют обстановку в стране
Георгий Бовт
Дедушка старый, ему все равно
О том, почему публикацию Сеймура Херша многие предпочли «не заметить»
Алена Солнцева
По законам сказки
О разнице между законами жанра и авторским искусством
Найдена ошибка?
Закрыть
Спасибо за ваше сообщение, мы скоро все поправим.
Продолжить чтение
Теорема статистической физики также действительна в квантовом мире, исследование показало
Йоханнес Зайлер, Rheinische Friedrich-Wilhelms-Universität Bonn
Экспериментальная схема для измерения числовых флуктуаций и функции отклика фотонного конденсата Бозе-Эйнштейна, связанного с резервуаром внутри микрополости красителя. Часть излучения резонатора, регистрируемая фотоумножителем (ФЭУ), дает среднюю населенность конденсата ⟨n⟩; другая часть диспергируется на решетке, а спектрально-фильтрованное выделение конденсата регистрируется электронно-оптической камерой, что дает g (2) (τ) и расстройке резонатора красителя Δ.
Физики Боннского университета экспериментально доказали, что важная теорема статистической физики применима к так называемым «конденсатам Бозе-Эйнштейна». Их результаты теперь позволяют измерить определенные свойства квантовых «суперчастиц» и вывести характеристики системы, которые в противном случае было бы трудно наблюдать. Исследование было опубликовано в Письма о физическом обзоре .
Предположим, перед вами стоит сосуд, наполненный неизвестной жидкостью. Ваша цель — узнать, насколько частицы в нем (атомы или молекулы) беспорядочно перемещаются вперед и назад за счет своей тепловой энергии. Однако у вас нет микроскопа, с помощью которого вы могли бы визуализировать эти колебания положения, известные как «броуновское движение».
Оказывается, это совсем не нужно: можно просто привязать предмет к нитке и протянуть его через жидкость. Чем больше силы вы должны приложить, тем более вязкой будет ваша жидкость.
И чем она более вязкая, тем меньше частицы в жидкости в среднем меняют свое положение. Таким образом, вязкость при данной температуре можно использовать для прогнозирования степени колебаний.
Физический закон, описывающий это фундаментальное соотношение, — теорема флуктуации-диссипации. Проще говоря, он гласит: чем большую силу вам нужно приложить, чтобы возмущать систему извне, тем меньше она будет колебаться случайным образом (т. е. статистически) сама по себе, если вы оставите ее в покое.
«Теперь мы впервые подтвердили справедливость теоремы для специальной группы квантовых систем: конденсатов Бозе-Эйнштейна», — объясняет доктор Джулиан Шмитт из Института прикладной физики Боннского университета.
«Суперфотоны», состоящие из тысяч частиц света
Бозе-эйнштейновские конденсаты — это экзотические формы материи, которые могут возникать благодаря квантово-механическому эффекту: при определенных условиях частицы, будь то атомы, молекулы или даже фотоны (частицы составляющие свет), становятся неразличимыми.
В жидкости при конечной температуре молекулы беспорядочно движутся вперед и назад. Чем теплее жидкость, тем сильнее выражены эти тепловые колебания. Конденсаты Бозе-Эйнштейна также могут флуктуировать: меняется количество сконденсированных частиц. И это колебание также увеличивается с повышением температуры.
«Если теорема флуктуации-диссипации применима к БЭК, то чем больше флуктуация числа их частиц, тем чувствительнее они должны реагировать на внешнее возмущение», — говорит Шмитт. «К сожалению, число флуктуаций обычно изучаемых БЭК в ультрахолодных атомарных газах слишком мало, чтобы проверить эту взаимосвязь».
Однако исследовательская группа профессора доктора Мартина Вайца, в которой Шмитт является младшим руководителем исследовательской группы, работает с конденсатом Бозе-Эйнштейна, состоящим из фотонов. И для этой системы ограничение не действует. «Мы заставляем фотоны в наших БЭК взаимодействовать с молекулами красителя», — объясняет физик.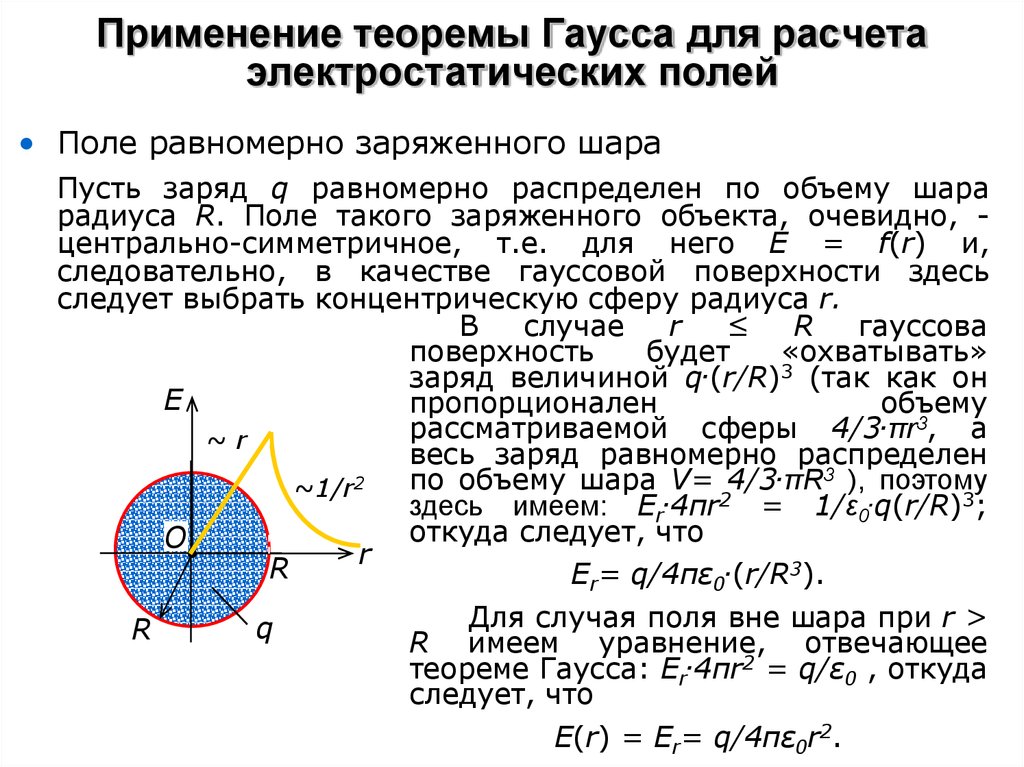
При взаимодействии фотонов с молекулами красителя часто бывает так, что молекула «проглатывает» фотон. Таким образом, краситель становится энергетически возбужденным. Позже он может высвободить эту энергию возбуждения, «выплевывая» фотон.
Фотоны низкой энергии проглатываются реже
«Из-за контакта с молекулами красителя количество фотонов в наших БЭК показывает большие статистические колебания», — говорит физик. Кроме того, исследователи могут точно контролировать силу этого изменения: в эксперименте фотоны захватываются между двумя зеркалами, где они отражаются туда и обратно, как в игре в пинг-понг.
Расстояние между зеркалами можно варьировать. Чем он больше, тем ниже энергия фотонов. Поскольку низкоэнергетические фотоны с меньшей вероятностью возбуждают молекулу красителя (поэтому они реже проглатываются), количество сконденсированных световых частиц теперь колеблется гораздо меньше.
Физики из Бонна теперь исследовали, как степень флуктуации связана с «откликом» БЭК.
Если верна теорема о флуктуации-диссипации, эта чувствительность должна уменьшаться по мере уменьшения флуктуации.
«На самом деле, мы смогли подтвердить этот эффект в наших экспериментах», — подчеркивает Шмитт, который также является членом Трансдисциплинарной исследовательской области (TRA) «Материя» Боннского университета и Кластера передового опыта «ML4Q— Материя и свет для квантовых вычислений».
Как и в случае с жидкостями, теперь можно вывести микроскопические свойства конденсатов Бозе-Эйнштейна из макроскопических параметров отклика, которые легче измерить. «Это открывает путь к новым приложениям, таким как точное определение температуры в сложных фотонных системах», — говорит Шмитт.
Дополнительная информация: Фахри Эмре Озтюрк и др., Соотношение флуктуации-диссипации для фотонного конденсата Бозе-Эйнштейна, Письма о физическом обзоре (2023). DOI: 10.1103/PhysRevLett.130.033602
Предоставлено Рейнский университет Фридриха-Вильгельма в Бонне
Цитата :
Исследование показало, что теорема статистической физики также действительна в квантовом мире (20 января 2023 г.
)
получено 16 февраля 2023 г.
из https://phys.org/news/2023-01-statistical-physics-theorem-valid-quantum.html
Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.
Как теорема математика Эмми Нётер изменила физику
В 1915 году два ведущих математика мира, Дэвид Гильберт и Феликс Кляйн, пригласили Эмми Нётер в Геттингенский университет для решения головоломки. Проблема возникла в новой теории гравитации Альберта Эйнштейна, общей теории относительности, которая была представлена ранее в этом году. Казалось, что теория не придерживается хорошо известного физического принципа, известного как сохранение энергии, который утверждает, что энергия может изменять форму, но никогда не может быть уничтожена. Предполагается, что полная энергия остается постоянной. Нётер, молодой математик, не имевший официальной академической должности, с радостью принял вызов.
Она решила вопрос в лоб, показав, что энергия не может сохраняться «локально» — то есть в сколь угодно маленьком участке пространства — но все получается, когда пространство достаточно велико. Это была одна из двух теорем, которые она доказала в том же году в Геттингене, Германия. Другая теорема, которая, в конечном счете, имела гораздо большее влияние, раскрыла тесную связь между законами сохранения (такими, как сохранение энергии) и симметриями природы, связь, которую с тех пор используют физики. Сегодня наше представление о физическом мире, от субатомных частиц до черных дыр, в значительной степени опирается на эту теорему, теперь известную просто как теорема Нётер.
«Трудно переоценить важность работы Нётер в современной физике», — сказала столетие спустя физик Даремского университета Рут Грегори. «Ее основные взгляды на симметрию лежат в основе наших методов, наших теорий и нашей интуиции. Связь между симметрией и сохранением — это то, как мы описываем наш мир».
Трудовая жизнь
Кем была эта женщина, которую два известных математика призвали помочь спасти шедевр Эйнштейна? На первый взгляд, Noether (произносится как NUR-tuh) кажется любопытным выбором.
У нее не было реальной работы в области математики, и она едва могла получить образование в этой области. Тем не менее она опубликовала несколько важных статей, и Гильберт чувствовал, что ее опыт может помочь прояснить проблему с общей теорией относительности.
Родившаяся в Эрлангене, Германия, в 1882 году, Нётер надеялась пойти по стопам своего отца-математика Макса. Но немецкие университеты не принимали женщин, когда они достигали студенческого возраста, поэтому Нётер вместо этого приходилось проверять классы. В конце концов она так хорошо сдала выпускные экзамены, что получила степень бакалавра.
В свои 53 года, многие из которых боролись с системой, препятствовавшей ее занятиям математикой, Нётер оказала огромное влияние как на алгебру, так и на физику. Трудно сказать, чего еще она могла бы добиться, если бы общество и судьба были более добры. (Источник: Эмилиана и Моника Нётер через Mathematical Association of America/Flickr)
В 1904 году ей разрешили поступить в докторантуру Эрлангенского университета.
Она получила докторскую степень. в 1907 году и провела там почти восемь лет, работая без заработной платы или официального положения, полагаясь на финансовую поддержку своей семьи, время от времени заменяя своего отца учителем. После поездки в Геттинген в 1915 году она осталась преподавать, снова не получая зарплаты.
После нескольких лет работы в основном в качестве волонтера, Нётер, наконец, стал внештатным адъюнкт-профессором математики в 1922 года в Геттингене, где ей выплачивалась скромная зарплата. Но 11 лет спустя она потеряла работу, когда она и другие евреи были изгнаны из научных кругов в нацистской Германии. Вскоре после этого она уехала из страны и с помощью Эйнштейна устроилась на работу в колледж Брин-Мор в Пенсильвании. Она умерла всего через 18 месяцев из-за осложнений после операции по удалению кисты яичника.
В свои 53 года, которые многие потратили на борьбу с системой, препятствовавшей ее занятиям математикой, Нётер оказала огромное влияние как на алгебру (ее основное направление), так и на физику.
Трудно сказать, чего еще она могла бы добиться, если бы общество и судьба были более добры. Тем не менее, ее работы было более чем достаточно, чтобы обеспечить ей место в пантеоне великих ученых, а ее одноименная теорема, возможно, является ее самым прочным вкладом.
Суть теоремы
Теорема Нётер — это простая и элегантная связь между, казалось бы, несвязанными понятиями, которая сегодня почти очевидна для физиков. Но и нефизики могут понять ее суть.
По сути, он утверждает, что каждой «непрерывной» симметрии в природе соответствует закон сохранения, и наоборот. Давайте разберем некоторые из этих терминов.
Симметрия в этом контексте относится к операции, которая может быть выполнена с объектом или системой, которая оставляет их неизменными. Поворот квадрата на 90 градусов — это пример «дискретной» симметрии. Квадрат по-прежнему выглядит так же, тогда как поворот на 45 градусов дает что-то другое (обычно называемое ромбом). С другой стороны, круг обладает непрерывной симметрией, поскольку его вращение на любой градус или его долю не меняет его внешний вид.
Это тот вид симметрии, к которому применима теорема Нётер.
Симметрия (Фото: Джей Смит)
Между тем закон сохранения относится к физической величине, которая остается фиксированной и, следовательно, не колеблется во времени. Энергия, например, не может быть создана или уничтожена; как только вы вычислите его значение, нет необходимости повторять вычисление.
Закон сохранения (Фото: Джей Смит)
Теорема Нётер раскрыла скрытую связь между двумя основными понятиями — симметриями и сохраняющимися величинами — которые до этого рассматривались отдельно. Теорема дает явную математическую формулу для нахождения симметрии, лежащей в основе данного закона сохранения, и, наоборот, нахождения закона сохранения, соответствующего данной симметрии.
Вот пример теоремы в действии. Представьте себе хоккейную шайбу, скользящую по идеально гладкому, бесконечному и не имеющему трения льду. Далее предположим, что на шайбу не действуют никакие внешние силы. В этих идеализированных условиях шайба будет продолжать скользить по прямой линии, никогда не замедляясь.
Его импульс, произведение его массы и скорости, сохранится или сохранится. Единственное, что может заставить шайбу изменить свой курс, увеличить или уменьшить скорость, — это изменение самого пространства — в данном случае поверхности льда. Однако ничего не изменится, если лед останется гладким, а пространство — неизменным.
Теорема Нётер показывает, что сохранение импульса шайбы связано с ее «симметрией перемещения в пространстве», что является еще одним способом сказать, что на физику не влияют линейные движения (или перемещения) в однородном пространстве. Шайба движется одинаково на одном участке гладкого льда, как и на другом.
Сохранение импульса (Фото: Джей Смит)
Точно так же теорема Нётер показывает, что симметрия относительно вращения или вращательная инвариантность приводит к сохранению углового момента, который измеряет, насколько сильно объект вращается. Иными словами, в физике нет предпочтительного направления. Если вы проведете эксперимент на столе, а затем повернете этот стол на 45 градусов или на любую другую величину, результаты эксперимента не будут отличаться.
Теорема также связывает симметрию «перевода времени» с сохранением энергии, поэтому физике также все равно, проводите ли вы эксперимент сегодня, в следующий вторник или в третье воскресенье октября.
Сохранение углового момента (Фото: Джей Смит)
Физики знали о сохранении импульса, углового момента и энергии задолго до появления теоремы Нётер. Они являются основополагающими положениями классической механики. Но не было известно, что эти священные законы имеют общее происхождение, каждый связан с определенной симметрией. Это новое понимание, появившееся в результате работы Нётер, является руководящим принципом, который пронизывает исследования физики, а также формирует наши взгляды на Вселенную в целом.
Сохранение энергии (Фото: Джей Смит)
Собираем все вместе
Теорема Нётер применима не только к этим интуитивным симметриям — вращениям и сдвигам во времени или пространстве — но также и к более абстрактным, «внутренним» симметриям, лежащим в основе силы природы.
Например, сохранение электрического заряда, центральный принцип теории электромагнетизма, проистекает из симметрии, связанной с деталями вращения частицы. Другой пример: симметрия, называемая изоспином, которая позволяет электронам заменять нейтрино, а нейтрино вместо электронов, помогла физикам разработать теорию в XIX веке.60-х годов, которые объединили электромагнитное взаимодействие и слабое взаимодействие (объясняющее распад частиц и радиоактивные процессы) в единое электрослабое взаимодействие. Сохраняющейся величиной здесь является «гиперзаряд» — своего рода заряд, аналогичный электрическому заряду, который связан с этой электрослабой силой.
Сохранение электрического заряда (Фото: Джей Смит)
Десять лет спустя физики разработали теорию сильного ядерного взаимодействия, связывающего протоны и нейтроны в атомном ядре. В основе этой силы лежит то, что называется цветовой симметрией. (Цвет — это свойство кварков, из которых состоят протоны и нейтроны, которые физики рассматривают как еще один вид заряда.
)
Цветовая симметрия (Фото: Джей Смит)
В 1970-х годах физики определили все известные частицы (в том числе и некоторые, существование которых еще не было подтверждено, например, бозон Хиггса) и силы, управляющие их взаимодействием, — электромагнитное, слабые и сильные — в единую теоретическую основу, известную как Стандартная модель.
Стандартная модель (Источник: Джей Смит)
По словам физика из Стэнфордского университета Майкла Пескина, теорема Нётер была основным инструментом в построении этой удивительно успешной модели. «В квантовой механике вы идентифицируете две или три частицы, которые должны быть связаны симметрией, а затем проверяете, верен ли выведенный закон сохранения. Вот как вы узнаете, является ли это реальной симметрией природы, и именно так была построена Стандартная модель» — посредством кумулятивного пошагового процесса, подобного этому. Это также то, как исследователи сейчас пытаются двигаться вперед.
Супернаследие
Ведется охота за новыми частицами и более глубокими и широкими симметриями, из которых они происходят, — процесс, в котором теорема Нётер продолжает играть ключевую роль.
Большая часть текущих усилий сосредоточена на поиске признаков суперсимметрии – теории, которая постулирует симметрию между частицами, составляющими материю (фермионами), и частицами, передающими силы, такими как электромагнетизм (бозоны). Если суперсимметрия верна, у каждого известного фермиона есть еще не наблюдаемый бозонный «суперпартнер», и точно так же у каждого известного бозона есть еще невидимый фермионный суперпартнер.
Суперсимметрия (Источник: Джей Смит)
Гипотетические суперсимметричные частицы, которые физики надеются обнаружить на гигантских ускорителях частиц, таких как Большой адронный коллайдер, будут «отражением всех частиц Стандартной модели с использованием слегка искаженного зеркала». », — объясняет Джозеф Инкандела, физик из Калифорнийского университета в Санта-Барбаре. «Частицы по другую сторону зеркала выглядят точно так же, как частицы Стандартной модели, за исключением того, что их спины немного смещены».
Одной из возможностей, связанных с этой предполагаемой симметрией, говорит Инкандела, является сохранение чего-то, называемого r-четностью, что означает, что легчайшая суперсимметричная частица должна быть стабильной и никогда не распадаться.
Если четность r действительно сохраняется, невидимый суперсимметричный партнер каждой обычной частицы в конце концов распадется на легчайшую суперсимметричную частицу, которая останется с нами навсегда. Эта частица, чем бы она ни была, будет доступна в изобилии и, таким образом, может быть хорошим кандидатом на роль загадочной темной материи, которая, как считается, составляет более четверти вещества во Вселенной.
Освещение черных дыр
Теорема Нётер, однако, важна не только для поиска новых частиц; она распространяется на все разделы физики. Гарвардский физик Эндрю Строминджер, например, определил бесконечное количество симметрий, связанных с мягкими частицами, то есть частицами, не имеющими энергии. Эти частицы бывают двух видов: мягкие фотоны (частицы, передающие электромагнитные силы) и мягкие гравитоны (частицы, передающие гравитационные силы).
Мягкие частицы (Фото: Джей Смит)
В недавних работах Строминджера и его коллег Стивена Хокинга и Малкольма Перри из Кембриджского университета предполагается, что вещество, падающее в черную дыру, добавляет мягкие частицы к границе черной дыры или горизонту событий.
Эти частицы, по сути, будут служить записывающими устройствами, которые хранят информацию, предоставляя подсказки об исходном материале, который попал в черную дыру.
Информационный парадокс черной дыры (Источник: Джей Смит)
Идея, предложенная тремя физиками, предлагает новую стратегию для решения давней загадки в физике, известной как информационный парадокс черной дыры. Хокинг показал в 1970-х годах, что каждая черная дыра в конечном итоге испарится и исчезнет, потенциально уничтожая всю информацию, которую когда-то содержал объект о том, как он формировался и развивался с течением времени. Постоянная потеря информации в сценарии Хокинга беспокоила теоретиков, включая Хокинга, поскольку это нарушило бы заветный закон квантовой физики, согласно которому информация, как и энергия, всегда сохраняется.
Присутствие мягких частиц вдоль горизонта событий и сопутствующие им симметрии могут указать на выход из этой дилеммы. «С помощью теоремы Нётер мы быстро поняли, что существуют законы сохранения, соответствующие новым симметриям, которые накладывают очень строгие ограничения на образование и испарение черных дыр», — говорит Строминджер, хотя и признает, что эта работа все еще находится на ранней стадии.