“Числовые фокусы” | Образовательная социальная сеть
МБОУ «Средняя школа№1»
Проектно-исследовательская работа
по математике
Тема: «Числовые фокусы»
ученицы 6 класса
МБОУ «Средняя школа№1»
Столяровой Анастасии
Руководитель: Виноградова Г.В.
План проектно-исследовательской работы
Введение
- Числовые фокусы
- Классификация числовых фокусов
- Числовые задачки
- Магические квадраты
- Числовые ребусы
Заключение
Список литературы
«Числа — это строительный материал
божественного творения»
Введение
Мир математики многообразен и не так скучен, как может показаться на первый взгляд. Числовые забавы могут завлечь и развлечь, ничуть не меньше, чем компьютерные игры. Умное обращение с цифрами дает возможность каждому попасть в удивительный мир математики.
Замечательные числа очень просты. А фокусы с ними! Не нужно проводить долгих тренировок, дополнительного реквизита не требуется, но эффектность проведения их вам гарантированна.
Головоломки, числовые фокусы, ребусы отлично подходят для учащихся, желающих удивлять своих сверстников и не только! Смысл любого фокуса в угадывании чисел. Главный секрет – отсутствие секрета! Все чудеса основаны на реальных математических закономерностях. Существует достаточно много числовых свойств, о которых простому ученику не известно и даже неинтересно, но нам в своей работе хочется приоткрыть занавес для тех, кто стоит только в начале своих математических открытий. Провести всех в загадочный мир «числовой иллюзии».
Цель работы: исследование числовых фокусов.
Задачи:
- Дать определение термину «числовой фокус»;
- Классифицировать числовые фокусы.
- Привести примеры различных числовых фокусов.
- Показать в классе самые интересные числовые фокусы.
Методы исследования:
Поиск, изучение, систематизация, применение
Новизна проекта:
К числовым играм можно относиться по-разному, неоспоримым является тот факт, что любой способ, позволяющий, заинтересоваться и увлечься предметом, уже хорош сам по себе, потому что позволяет развивать устный счет, логику, мышление.
Толковый словарь Ожегова дает нам такое обозначение слова «фокус» – искусный трюк, развлечение, игра, основанная на обмане зрения, внимания при помощи ловкого и быстрого приёма или движения. Мы уверены, что немногие свяжут слово игра и математика в одно единое, оттого наше исследование становится ещё интереснее. Что же такое числовой фокус в нашем понимании? Головоломки, иллюзии, забавы или всё это вместе взятое?
Числовой фокус – это математическая закономерность, позволяющая изучать мир точных наук с помощью игры, в основе которой лежит не иллюзия, как может показаться на первый взгляд, а конкретное правило действий с числами.
Классификация числовых фокусов
Проведя наше исследование можно выделить несколько видов числовых фокусов:
- Числовые задачки
- Магические квадраты
- Числовые ребусы
Числовые задачки
В каждом уголке нашей большой планеты можно найти человека, увлекающимся числовыми задачками. И это закономерно.
«Гимнастика ума» полезна для каждого. Разгадывание таких задачек тренируют память, развивают смекалку, вырабатывают упорство, учат мыслить логически, анализировать, систематизировать и сопоставлять.
Приведем пример числовой задачки.
Задание:
Угадать день рождения постороннего человека. Необходимо:
- Увеличить в два раза число, являющееся днем рождения.
- Прибавить пятерку, к получившемуся результату.
- Полученную сумму умножить на 50.
- К этому произведению необходимо прибавить номер месяца рождения
- Произнести получившееся число.
Через некоторое время можно назвать день рождения этого постороннего человека.
Секрет фокуса:
От произнесенного в результате вычислений числа надо отнять 250. Получается трехзначное или четырехзначное число. Дата рождения это первая и вторая цифры. Месяц рождения – две последние.
Магические квадраты
Арифметические действия с числами известны человеку с древних времен.
Постепенно развивая математическую науку, люди обнаружили самостоятельную жизнь чисел, удивительную, таинственную.
Магические квадраты можно найти в математических работах арабов, индусов, после чего они стали известны и получили свою популярность в Римской империи, после чего появились и в Западной Европе. Им приписывали волшебные свойства, поэтому методы их получения заинтересовали ума многих ученых. В мистическую силу люди верили, поэтому магические квадраты использовали для изготовления всевозможных амулетов и оберегов.
Магический квадрат – это таблица, которая составлена из целых чисел. В ней сумма чисел в каждых строках и столбцах, а так же в любой из двух диагоналей должна равняться одному и тому же числу.
Приведем пример.
Задание:
Клеточки квадрата нужно заполнить числами от 1 до 9. Сумма чисел во всех столбцах и строках, а так же по диагоналям квадрата должна равняться числу 15.
1. Прибавим средний столбец и в среднюю строку к исходному квадратику дополнительные окошки.
2. Выделим диагональные клетки, их мы будем заполнять числами в первую очередь.
3. В выделенные клетки записываем числа от 1 до 9.
4. Передвинем числа из дополнительных окошек внутрь квадрата, пример показан в таблице.
Числовые ребусы – это математические примеры на сложение, вычитание, умножение и деление, часть цифр, в которых заменена на различные символы. Это могут быть и буквы, и значки, и какие-то объекты. Задача состоит в том, чтобы расшифровать эти выражения.
Для разгадывания таких ребусов необходимо подставить нужную цифру так, чтобы это выражение стало верным.
Можно выделить три вида числовых ребусов:
- Буквенный
- Такие ребусы называются криптарифмами. В них разгадываемые цифры заменены буквами.
Приведем пример буквено-числового ребуса.
Задание:
- Символьно-численный
В нем присутствуют и числа, и символы.
Приведем пример символьно-числового ребуса.
Задание: Ответ:
- Символьный
В нем, все разгадываемые цифры, спрятаны только за всевозможные символы.
Задание:
Одинаковые фигуры это одинаковые цифры. Необходимо найти эти цифры.
Ответ: Квадратом является 2
кругом – 8
за обычным треугольником спряталась -6
за перевернутым треугольником – 9
пятиугольник – 3
шестиугольник – 4.
Заключение
В математике много различных числовых фокусов, если хорошо пофантазировать, можно придумать их самому. Математика – это не только утомительная учёба. Фокусы, ребусы, магические квадраты можно использовать в качестве игры, используя числа и фантазию. Задачи, представленные в увлекательной форме, очень занимательны. Трудный путь поиска ответов развивает желание невозможное сделать реальным, а именно использовать математику для забавы, игры.
Список литературы:
Интернет ресурсы:
- http://kvant.
mccme.ru/1991/02/chislovye_fokusy.htm - http://www.kakprosto.ru/kak-105258-kak-reshat-matematicheskie-rebusy
- http://infourok.ru/proekt_po_matematike_matematicheskie_fokusy-118665.htm
mccme.ru/1991/02/chislovye_fokusy.htmПечатные издания:
- «Занимательная арифметика» Я.И. Перельман 1976 год издания
- «Живая математика» Я.И. Перельман 1994 год издания
Числовые фокусы | Методическая разработка по алгебре (7 класс) по теме:
О сколько нам открытий чудных
Готовит просвещенья дух
И опыт, сын ошибок трудных
И гений парадоксов друг
И случай, бог изобретатель
А.С. Пушкин
Фокусы? – Да, если хотите, а лучше сказать – эксперименты основанные на математике, на свойствах фигур и чисел и лишь обличенные в несколько экстравагантную форму. Понять суть того или иного эксперимента это значит понять пусть небольшую, но точную математическую закономерность.
Математические фокусы – очень своеобразная форма демонстрации математической закономерности.
Фокусы развивают творческие начала личности, артистические способности, стимулируют потребность в творческом самовыражении. Математические фокусы способствуют концентрации внимания и активизации учащихся на уроках математики. Магия фокуса способна разбудить сонных, растормошить ленивых, заставить думать тугодумов. Ведь не разгадав секрета фокуса, невозможно понять и оценить всей его прелести. А секрет фокуса чаще всего имеет математическую природу.
Математические игры и фокусы появились вместе с возникновением математики, как науки. Первое упоминание о математических фокусах мы встречаем в книге русского математика Леонтия Филипповича Магницкого, опубликованной в 1703 году и содержащей начала математических знаний того времени. Одна глава книги была названа автором “Об утешных некиих действах, через арифметику употребляемых”. Эта глава содержала математические игры и фокусы. Сам Магницкий пишет, что поместил эту главу в книгу для “утехи и особенно для изощрения ума учащихся”.
Все мы знаем великого русского поэта М.Ю. Лермонтова, но не каждому известно, что он был большим любителем и математики, особенно его привлекали математические фокусы, которых он знал великое множество, причем некоторые из них он придумывал сам.
Математические фокусы интересны именно тем, что каждый фокус основан на свойствах чисел, действий, математических законах.
Фокусами с числами можно удивлять друзей за столом, в долгой поездке или летним днем в тени ветвистой яблони. Смысл этих фокусов состоит в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними.
Главное — это то, что фокусник знает секрет: особые свойства чисел. Все эти чудеса основаны на математических закономерностях, свойствах фигур и чисел.
И хотя вместо цифр, геометрических фигур в некоторых фокусах используются различные предметы, все они связаны с числами. Только надо помнить: фокусы с цифрами будут получаться только тогда, когда мы научимся быстро считать в уме.
Слово illusio переводится с латинского как “заблуждение” или “обман”. А вот откуда взялось слово “фокус” никто не знает. Есть несколько версий. Наиболее популярная из них – все началось с латинской фразы “хок эст корпус меум”. Эта фраза переводится как “сие есть тело моё”. Она произносилась священниками при вечерней трапезе и символизировала религиозный обряд превращение хлеба в тело бога. Позднее словосечетание превратилось в “хокус-покус” и стало употребляться для обозначения всех видов превращений.
Искусство фокусов зародилось очень давно, предположительно несколько тысяч лет до нашей эры. Считается, что родиной фокусов является Древний Египет.
Миллионы людей во всех частях света увлекаются математическими фокусами, которые являются очень своеобразной формой демонстрации математических закономерностей. И это не удивительно. “Гимнастика ума” полезна в любом возрасте, она тренируют память, обостряют сообразительность, вырабатывают настойчивость, способность логически мыслить, анализировать и сопоставлять.
Еще в Древней Элладе без игр не мыслилось гармоническое развитие личности. И игры древних не были только спортивными. Наши предки знали шахматы и шашки, не чужды им были ребусы и загадки. Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они и создавали их. С древних времен известны головоломки Пифагора и Архимеда, русского флотоводца С.О. Макарова и американца С. Лойда.
На огромную познавательную и воспитательную ценность интеллектуальных игр неоднократно указывали К.Д. Ушинский, А.С. Макаренко, А.В. Луначарский. Среди тех, кто увлекался ими, были К.Э. Циолковский, К.С. Станиславский, И.Г. Эренбург и многие другие выдающиеся люди.
Отдельно хочется отметить американского математика, фокусника, журналиста, писателя и популяризатора науки Мартина Гарднера (Gardner).
Он родился 21 октября 1914 г. Окончил математический факультет Чикагского университета. Основатель (середина 50-х гг.), автор и ведущий (до 1983) рубрики “Математические игры” журнала «Scientific American» (“В мире науки”).
Особую популярность снискали статьи и книги Гарднера по занимательной математике. В нашей стране было издано семь книг Мартина Гарднера, которые увлекают читателя и подталкивают к самостоятельным исследованиям «Гарднеровский» стиль характеризуют доходчивость, яркость и убедительность изложения, блеск и парадоксальность мысли, новизна и глубина научных идей.
Фокус 1. Телепатия.
Понадобятся: карандаш, лист бумаги, калькулятор (необязательно)
1) Попроси друга записать любое трехзначное чисто, какое ему вздумается, но цифры должны идти по убыванию, например 9, 7 и 2.Он не должен показывать тебе, что написал.
2) После попроси друга записать под ним то же чисто, но задом наперёд.
В нашем примере-2, 7 и 9.
3) Теперь он должен вычесть второе число из первого и назвать тебе только последнюю цифру, у нас это 3.
4) Ты сразу же сможешь сказать ему, что остальные цифры 6 и 9, потому что вычтя 3 из 9,ты узнаешь первую цифру-6. Средняя цифра всегда будет девять, какое бы число твой друг не выбрал.
Девятка – хитрое число.
Фокус 2. Телепатия.
Всегда 1089.
Понадобятся: два листа бумаги, конверт, карандаш, стол, калькулятор (необязательно).
1) Положив свой реквизит на стол, встань перед зрителями. Поговори о силе разума-телепатии и чтении мыслей. Произнеси что-нибудь вроде: «В зале всегда найдется человек, чьи мысли для меня – открытая книга. «Затем замри и скажи, что в зале сидит человек, чьи мысли ты ловишь прямо сейчас. Укажи на кого-то из зрителей.
2) Притворись, что напряженно думаешь и попроси «медиума» сосредоточится на передаче мыслей тебе. Скажи, что, кажется, принимаешь число. Быстро запиши на листе бумаги число 1089, положи лист в конверт и запечатай его.
3) Дав другой лист и карандаш «медиуму», попроси его записать любое трехзначное число, цифры в котором не совпадают (в примере мы взяли 341). Теперь попроси его записать число задом наперёд и вычесть меньшее из большего. Попроси его записать трехзначный ответ, даже если первая цифра ноль.
4) Теперь ему надо записать полученное число задом наперёд и сложить два последних числа. Попроси его вслух зачитать ответ зрителям. А теперь попроси открыть конверт и прочесть число, которое записал ты. Оба числа равны 1089.
5) Результат всегда будет равен 1089, так что перед одной и той же аудиторией этот фокус можно показывать лишь раз.
Фокус 3.
Плюс и минус
Понадобятся: листок бумаги, карандаш.
1) Попроси кого-нибудь из зрителей записать на листке пятизначное число. Число должно состоять из пяти разных цифр, использовать одну и ту же цифру дважды нельзя. Показывать этот листок и свои расчеты тебе доброволец не должен ни в коем случае. К примеру, взято число 36412.
2) Теперь попроси его записать под первым числом его же, но задом наперёд, и вычесть второе число из первого.
3) Пусть теперь твой доброволец запишет под результатом его же но задом наперёд, и сложит эти два числа.
4).Когда доброволец решит пример – не теряй ни секунды.
Скажи, что начал видеть число, как только оно появилось у добровольца перед глазами. Почти всегда это будет 109890, хотя иногда получается 99099. Если твоя первая догадка-109890-окажется неправильной, спиши вину на шум мыслей, доходящих от зрителей и скажи: «Ого, теперь прояснилось -это 99099!»
Фокус 4. 10 чисел Фибоначчи
Раскрою Вам секрет интересного, вычислительного фокуса с числами Фибоначчи.
Этот фокус демонстри руют так: показывающий просит кого-нибудь записать друг под другом два любых числа, какие он пожела ет. Допустим для примера, что были выбраны 2 и 7. Затем зритель должен сложить эти числа. Найденное таким образом третье число складывается со вторым (стоящим над ним), и получается четвертое число. Этот процесс повторяют до тех пор, пока в вертикаль ном столбце не окажется десять чисел:
2
7
9
16
25
41
66
107
173
280
Во время записывания чисел фокусник стоит, повернувшись спиной к зрителям. Когда все числа будут записаны, он поворачивается, проводит под колонкой цифр черту и, не задумываясь, подписывает сумму этих чисел.
Чтобы получить эту сумму, ему просто нужно взять четвертое число снизу и умно жить его на 11 -операция, которую легко можно проделать в уме. В нашем случае четвертым чис лом будет 66, поэтому в ответе получится число 66, взятое 11 раз, т.е. 726.
Фокусы с предсказанием результатов действий над числами и фокусы с отгадыванием чисел легко обратимы; под этим подразумевается, что фокус с предсказанием числа можно показывать как фокус с отгадыванием этого числа, и наоборот. Допустим, например, что показывающий знает наперед резуль тат вычисления, который, как предполагает зритель ему не может быть известен. Тогда показывающий может оформить фокус в виде предсказания, записав известный ему результат будущего вычисления на листке бумаги; в этом случае фокус следует рассмат ривать как фокус с предсказанием. Но этот же фокус он может оформить как «чтение мыслей» зрителя – после того как зритель закончит свои вычисления,- в этом случае фокус нужно отнести к категории фоку сов с отгадыванием числа.
(Третьим вариантом может быть оформление фокуса в виде молниеносного вы числения.) Удивляйте и удивляйтесь!
Фокус 5: “Волшебная таблица”.
На доске или экране таблица, в которой известным образом в пяти столбцах записаны числа от 1 до 31. Фокусник предлагает присутствующим задумать любое число из этой таблицы и указать, в каких столбиках таблицы находится это число. После этого он называет задуманное вами число.
Разгадка фокуса: Например вы задумали число 27. Это число находится в 1-ом, 2-ом, 4-ом и 5-ом столбиках. Достаточно сложить числа, расположенные в последней строке таблицы в соответствующих столбиках, и получим задуманное число. (1+2+8+16=27).
Проект по математике: “Математические фокусы”
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа №1
Камышловского городского округа
Направление: ЕСТЕСТВЕННЫЕ НАУКИ (математика)
МАТЕМАТИЧЕСКИЕ ФОКУСЫ
Петрушко Артем
МАОУ СОШ №1 КГО, 6 класс
Школьный учитель:
Устьянцева Надежда Владимировна,
учитель математики
г.
Камышлов, 2013 г.
Содержание
Введение……………………………………………………………………….3
Глава 1. История возникновения математических фокусов.
1.1 Что такое фокус……………………………………………………………5
1.2 Когда появились фокусы…………………………………………………5
1.3 История возникновения математических фокусов……………………7
Глава 2. Математические фокусы и их виды
2.1 Числовые фокусы……………………………………………………………8
2.2 Фокус с предопределенным выбором……………………………………..10
2.3 Фокусы с уравнениями……………………………………………………..11
Глава 3. Секреты математических фокусов………………………………….13
Заключение……………………………………………………………………..17
Литература ……………………………………………………………………..18
Введение
“Предмет
математики настолько серьезен,
что полезно не упускать случаев
делать его немного занимательным»
Б. Паскаль
Математические фокусы не пользуются особым вниманием ни у математиков, ни у
фокусников.
Математикам они сложны, рассматривать их как забаву, фокусники
пренебрегают ими как слишком скучным делом. И все-таки математические фокусы
имеют свою особую прелесть.
Математические фокусы – очень своеобразная форма демонстраций математических закономерностей. В математических фокусах изящество математики соединяется с занимательностью.
Математические фокусы – это эксперименты, основанные на математике, на свойствах фигур и чисел, и лишь обличенные в экстравагантную форму. И понять суть того или иного эксперимента – это значит понять пусть небольшую, но математическую закономерность.
Каждый из нас, несомненно, встречался с «фокусами» по отгадыванию чисел.
Удивительной для непосвященных кажется, способность человека отгадывать
задуманные другими числа. Но если вы узнаете секрет математических фокусов, то
сможете не только их показывать, но и придумывать свои новые фокусы. Секрет
фокуса становится понятен, если записать предложенные действия в виде
алгебраического выражения, где выполнены действия, получаем секрет отгадывания
чисел.
Цель работы: исследование математических фокусов.
Задачи:
1. Изучить литературу по данному вопросу и интернет ресурсы;
2. Выбрать и обобщить наиболее интересные, увлекательные математические фокусы;
3. Провести выбранные математические фокусы в классе.
4. Выяснить в чем секрет математических фокусов.
Объект исследования: математические фокусы, основанные на свойствах чисел, действий, математических законах, уравнениях.
Методы исследования
Изучение, анализ, практическое применение полученных знаний.
Новизна проекта
Новизна данного проекта заключается в следующем: математические фокусы редко рассматриваются и применяются в обучении математики.
Данный проект призван привлечь внимание обучающихся к изучению математики.
Практическая значимость: 1. Математические фокусы помогают развивать память, устный счет, сообразительность, способность мыслить логически;
2.
В результате привлечения внимания обучающих к математике должна повысится их
заинтересованность в данном предмете, что несомненно должно повысить
успеваемость.
Существуют также фокусы с магическими таблицами для угадывания чисел, фокусы с настенным календарем, фокусы с прикосновениями, фокусы на нахождение числа, фокусы с мелкими предметами (домино и игральные кости), фокусы с уравнениями и фокусы с предопределенным выбором. В своей работе я более подробно рассмотрел числовые фокусы, фокусы с уравнениями, с предопределенным выбором.
Глава 1. История возникновения математических фокусов.
1.1 Что такое фокус?
Фокус или иллюзионное искусство – один из видов деятельности человека. В основном – это выступления артистов в виде концертных номеров, аттракционов, спектаклей и шоу.
Фокус – искусный трюк, основанный на обмане зрения, внимания при помощи ловкого и быстрого приема, движения (словарь Ожегова)
Иллюзионное искусство привлекает зрителей своей фантастичностью происходящего
на сцене.
Зритель сам может убедиться в том, что на сцене происходит
невероятное, невозможное действие. Показывая и наблюдая фокусы, люди
развлекаются. Но не только. Один человек создал фокус, другие удивляются ему,
пытаются разобраться в фокусе, понять его и добраться до истины. Действия
фокусника, на самом деле, не представляют собой чего-то необыкновенного,
сверхъестественного. Они просты, естественны и логичны, но зрителю они
представляются невероятными потому, что фокусник применил приём, в результате
чего зритель сам сделал ошибочный вывод и поверил в него. Не всё, что
летает — самолёт. Так и в фокусах. Не всё, что непонятно —
обязательно фокус.
1.2 Когда появились фокусы?
С глубокой древности людей интересовали мистические и загадочные вещи, иллюзионизм и магические искусства. Великие Тайны этих искусств известны лишь избранным. Иллюзионисты и фокусники ревниво охраняют их, хорошо зная, что, чем не доступнее ключ к их таинствам, тем эти таинства более ценны.
Первый документ, в котором упоминается об иллюзионном искусстве, –
древнеегипетский папирус.
В нём содержатся предания относящиеся к 2900 году до
н.э., эпохе царствования фараона Хуфу (Хеопса). В одном из преданий упоминается
о выступлении фокусника и дрессировщика ДЖЕДИ, который умеет приставить на место
и прирастить отрезанную голову гуся и может заставить льва следовать за собой
без пут.
Изначально фокусы использовали колдуны и знахари. Жрецы Вавилона и Египта создавали огромное количество уникальных трюков с помощью прекрасных знаний математики, физики, астрономии и химии. В перечень чудес исполняемых жрецами можно включить, например такие: раскаты грома, сверкание молний, сами собой раскрывающиеся двери храмов, появляющиеся вдруг из-под земли статуи богов, сами звучащие музыкальные инструменты, голос, раздававшийся ниоткуда, предвещающий будущее и т. д.
Фокусники того времени заставляли исчезать и появляться драгоценности, в толпе у народа пропадало множество вещей и оказывалось в наличии у фокусника, при этом он все время был на виду.
Но ремесло фокусника могло караться
смертью – в средневековой Европе фокусы считались колдовством и за это
фокусники расплачивались своей жизнью.
В Россию иллюзионное искусство пришло из Византии. При пышном византийском дворе оно было одним из любимых развлечений. После окончания придворной службы русские певцы и музыканты возвращались в родные места и там показывали, чему научились. Они называли себя скоморохами (от греческого слова «скоммархос» — потешники). Это название надолго закрепилось за народными артистами Древней Руси. Скоморохи исполняли былины и песни, акробатические номера, демонстрировали фокусы, которые в древних русских документах назывались «шутками», а скоморохи-фокусники — «шуткарями» и «морочниками». О них чаще говорится как о колдунах: «…скоморошничают и совершают разные чары». Царская грамота 1648 г. запретила скоморохам проводить «чародеяния, гадания, а также всякие игры, музыку, песни, пляски, переряживание, игры…». «Чародеяниями» именовались фокусы и непонятные явления.
1.3 История возникновения математических фокусов.
Математические игры и фокусы появились
вместе с возникновением математики, как науки.
Математические фокусы
интересны именно тем, что каждый фокус основан на математических законах. Смысл
их состоит в отгадывании чисел, задуманных зрителями, или в каких-нибудь
операциях над ними. Главное — это то, что фокусник знает секрет: особые
свойства чисел. Миллионы людей во всех частях света увлекаются математическими
фокусами. И это не удивительно. “Гимнастика ума” полезна в любом возрасте. А
фокусы тренируют память, обостряют сообразительность, вырабатывают
настойчивость, способность логически мыслить, анализировать и сопоставлять.
Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они и создавали их.
Глава 2. Математические фокусы и их виды
2.1 Числовые фокусы
Угаданный день рождения Содержание этого математического фокуса.Объявите зрителям, что вы сможете угадать день рождения любого незнакомого человека, сидящего в зале.
- Вызовите любого желающего и предложите ему умножить на 2 число дня своего рождения
- Затем пусть зритель сложит получившееся произведение и число 5,
- теперь пусть умножит на 50 полученную сумму.
- К этому результату необходимо прибавить номер месяца рождения (июль — 7, январь — 1)
- вслух назвать полученное число.
Через секунду вы называете день и
месяц рождения зрителя.
Фокус «Угадай возраст».
1.Возраст умножить на 10.
2.Взять любое число от 1 до 9 и умножить на 9.
3.Из первого результата вычесть второй.
Фокус с Отгадыванием числа Вариант 1: Содержание фокуса.Предложите зрителям задумать трехзначное число и записать его на бумаге. При загадывании числа должно быть выполнено одно условие: цифра сотен не должна быть равна цифре единиц и не должна быть на единицу меньше или больше ее. Если вы еще путаетесь в сотнях и единицах, то на первом месте в трехзначных числах стоят сотни, на втором десятки, на третьем единицы (например, подойдет число 531).
Теперь зрители должны перевернуть задуманное число, т.е. написать цифры в обратном порядке (135).
Затем зрители должны взять эти два числа и из большего вычесть меньшее (531 – 135).
Получившуюся разницу снова нужно перевернуть (396; 693) и сложить эти два числа (396 + 693).
Потом
один из зрителей должен прибавить к полученной сумме 100, второй — 200, третий
— 300 и т.
д.
Теперь вы можете отгадать, что получилось у каждого зрителя, но при том условии, что они к своему последнему числу прибавят цифру 1 089. У первого зрителя, прибавлявшего 100, получится 1 189, у второго — 1 289, у третьего — 1 389.
Фокус «Сколько братьев и сестер…»
Содержание фокуса:
Вы сможете угадать, сколько братьев, сестер, дедушек и бабушек у вашего приятеля, после того как он выполнит несколько арифметических действий на калькуляторе!
1. Пример:
Допустим, у вашего приятеля: братьев — 4; сестер — 3; бабушек и дедушек —
Предложите приятелю:
Набрать на калькуляторе цифру, соответствующую количеству братьев– 4
1. Умножить это число на 2: 4.х2=8
2. Прибавить к произведению 3: 8 + 3=11
3. Умножить полученную сумму на 5: 11 х5=55
4.Прибавить к результату сестер. 55 + 3 = 58
5. Умножить полученную сумму на 10: 58 х10=580
6. Прибавить бабушек и дедушек. 580 + 2 = 582
7.
И, наконец, прибавить 125. 582 + 125 = 707
Затем возьмите калькулятор произведите некоторые действия и на табло появиться количество братьев, сестер и бабушек с дедушками!
Фокус « Зачеркнутая цифра»
Содержание фокуса:
Ведущий предлагает на листе бумаги записать какое-то 4-значное число. Затем предлагается поменять местами цифры в этом числе в любом порядке. Далее от большего числа отнять меньшее. В полученном результате зачеркнуть любую цифру, кроме нуля. Оставшиеся цифры необходимо озвучить ведущему. После чего ведущий отгадывает, какая цифра была зачеркнута.
2.2 Фокус с предопределенным выбором.
Содержание фокуса:
Записывается число 159654.
Предлагается под этим числом записать любое 6-значное число, при чем
желательно, чтобы числа в нем были различными. Под этим числом ведущий
записывает другое 6-значное число. Затем под ним предлагается записать еще одно
6-значное число. Затем ведущий записывает другое 6-значное число.
Предлагается
сложить данных 5 чисел, получается какой, то 7-значный ответ, но ведущий
предугадал его и записал на бумаге, которую предварительно отдал.
Фокусы с часами
Содержание фокуса:
Вариант 1
Задумайте какой-нибудь час (от 1 до 12). Задуманный вами час запомните. Теперь я буду указкой постукивать по часам. Каждый раз, когда постучу, прибавляйте к задуманному вами числу по одному. Когда вы досчитаете до двадцати, остановите меня. Получившееся число озвучивается ведущему, а в ответ он называет задуманное число.
Вариант 2
Также начнется с того, что зритель задумывает какое-нибудь число от 1
до 12. Фокусник берет указку и начинает притрагиваться ее кончиком к числам
на циферблате часов, причем делает это, по-видиму, в совершенно произвольном
порядке. Зритель считает про себя прикосновения фокусника к часам и, дойдя до
20, произносит слово «стоп». И странное совпадение: в этот момент указка
оказывается как раз на задуманном числе.
2.3 Фокусы с уравнениями
В книге Я.И. Перельмана в главе «язык алгебры» есть глава «искусство отгадывать числа». Здесь автор раскрывает секрет фокуса, который очень прост, и в основе его лежат все те же уравнения. Пусть фокусник предлагает вам выполнить программу действий. Затем он просит вас сообщить оконча- тельный результат и, получив его, моментально называет задуманное число. Как он это делает? Чтобы понять это, достаточно все команды перевести на язык алгебры.
Фокусник мысленно решает простое уравнение, поэтому заранее знает, что надо сделать с результатом, чтобы получить задуманное число. В работе рассмотрены несколько вариантов этих фокусов.
Фокус «Задуманное число»
Задумайте число. Прибавьте 1.
Умножьте на 3. Прибавьте снова 1.Прибавьте задуманное число. Скажите, что у вас
получилось. Когда вы называете фокуснику конечный результат всех этих выкладок,
он отнимает 4, остаток делит на 4 и получает то, что было задумано. Например,
вы задумали число 12.
Прибавили 1 -получили 13. Умножили на 3 -получи ли 39.Прибавили
1 – у вас 40. Прибавили задуманное число: 40 + 12 = 52. Когда вы называете
число 52, он отнимает от него 4, а оставшееся 48 делит на 4. Получает 12
-число, которое было вами задумано.
Фокус «Числа Фибоначчи»
Числа Фибоначчи — элементы числовой последовательности
в которой каждое последующее число равно сумме двух предыдущих чисел.
Содержание фокуса:
Ведущий предлагает записать цифры в столбик: меньшую вверху, а большую внизу. Далее необходимо записать результат сложение этих чисел ниже (под ними). Далее складываются два последних числа (2 и 3 числа), а результат записывается ниже. И так далее пока не будет записано 10 чисел. Далее записи показываются ведущему, а он тут же пишет результат сложения этих 10 чисел.
Глава 3.
Секреты математических
фокусов
Числовые фокусы
Угаданный день рожденияСекрет фокуса:
Например, мой день рожденья 8 января.
8 * 2 = 16
16 + 5= 21
21 * 50 = 1050
1050 + 1 = 1051
А теперь надо вычесть 250:
1051 – 250 = 801
8 – это число, а 01- месяц рождения.
Фокус «Угадай возраст».
Секрет фокуса:
Например, мне 12 лет.
12 * 10 = 120
Я возьму число 7:
7 * 9 = 63
120 – 63 = 57
А теперь надо сложить 5 и 7:
5 + 7 = 12
Фокус с Отгадыванием числа Вариант 1:
Секрет фокуса:
Например, я загадал 321:
321 в перевёрнутом виде выглядит, как 123:
321 – 123 = 198
198 в перевёрнутом виде выглядит, как 891:
891 + 198 = 1089
А фокусник давно знает, что при правильных вычислениях получится 1089.
А потом сколько бы
меня не попросили прибавить, 100, 200 или 300, фокусник смело назовёт ответ.
Секрет фокуса:
Например, загадал 85
8 * 2 = 16
16 + 5 = 21
21 * 5 = 105
105 + 10 + 5 = 120
А теперь надо вычесть 35:
120 – 35 = 85
Фокус «Сколько братьев и сестер…»
Секрет фокуса:
Закончив вычисления, попросите у приятеля калькулятор с результатом на табло. Вычтите из него 275, и на табло чудесным образом появится количество братьев, сестер и бабушек с дедушками!
Исключения:
1. Если после вычитания числа 275 на табло появится двузначное число, значит, у вашего приятеля нет братьев.
Пример 12 = 012; следовательно, число братьев равно 0.
2.Если после вычитания числа 275 на табло явится, лишь одна цифра, значит, у вашего приятеля нет ни братьев, ни сестер.
Пример 2 = 002;
Следовательно, число братьев равно нулю и число сестер также равно нулю.
Фокус « Зачеркнутая цифра»
Секрет фокуса:
Известно, что сумма цифр числа при
делении на 9 имеет тот же остаток, что и само это число при делении на 9.
Соответственно, если поменять в числе цифры местами то сумма их цифр останется
прежней и при делении на 9 это число будет давать тот же остаток, что и
исходное число. Поэтому, если мы производим вычитание одного числа от другого,
то остатки от деления числа сократятся и в ответе получится число, которое при
делении на 9 не дает остатка. То есть если в ответе зачеркнуть какое-то число,
то сумма оставшихся цифр делиться на 9 без остатка не будет (если не зачеркнута
цифра 9). Поэтому к сумме цифр необходимо добавить такое число, чтобы сумма
делилась на 9 без остатка. Это число и будет искомой – зачеркнутой цифрой.
Фокус с предопределенным выбором.
Секрет фокуса:
Ведущий заранее определяет число, которое получится в итоге, и из него вычитает 1999998, результат разности ведущий записывает первым числом фокуса. Далее третье число записывается так, чтобы сумма второго и третьего чисел давало 999999
Фокусы с часами
Секрет фокуса:
Вначале нужно ударять указкой по
циферблату по любым делениям до семи ударов.
Восьмым ударом показывается число
12, а потом с каждым ударом перемещаемся влево (11, 10, 9 и т.д.) Когда вы
скажете: “Довольно”, — указка будет стоять на том часе, который вы
задумали. Расчет очень простой. Всего будет ударов (20-х). Когда будет сделано
восемь ударов, указка покажет число 12. С этого момента мы делаем еще столько
ударов, сколько не достает вам до двадцати, так как, двигаясь влево, будут
показываться числа, последовательно уменьшенные на единицу.
Фокус «Задуманное число»
Секрет фокуса:
Почему же всегда так получается? Фокусник заранее знает, что после всех выкладок получается уравнение 4 х + 4.
Необходимо заранее составить уравнение:
(Х+1) · 3 + 1+ Х = 4х + 4
Фокус «Числа Фибоначчи»
Весь секрет заключается в этом уравнении:
а1 + а2 + а3 + а4 + а5 + а6 + а7 + а8 + а9 + а10 = 88а2 + 55а1 = 11 ( 8а2 + 5а1 ) = 11а7
Другими словами, чтобы быстро узнать сумму, нужно найти седьмое число и умножить его на 11
Заключение
Математические фокусы разнообразны.
Во многих математических
фо- кусах числа завуалированы предметами, имеющими отношение к числам. Они
развивают навыки в быстром устном счете, навыки вычислений т.к. можно
загадывать малые и большие числа.
Наука и развлечения неотделимы от математики. Она нашла самое раз- ное применение в различных областях науки: Физике, Химии, Биологии, Экономике, в искусстве, так же математика нашла огромное практическое применение в медицине, инженерии, судостроении, информационных технологиях и даже в проектах освоения Солнечной системы. В информацион-ных технологий так же невозможно представить без математики и индуст- рию развлечений: кинотеатры с трехмерным изображением и новые возможности для сети-Интернет, а так же многое другое.
Математика плотно связана со всей нашей жизнью. Математика везде окружает нас: на улице, дома, на работе, в гостях.
Литература
1.
М.Б. Бланк, Г.
Д.Бланк « Математика после уроков»
2. М. Гарднер «Математические чудеса и тайны»
3. М.Гарднер «Математические головоломки и развлечения»
4. М.Гарднер «Математические досуги»
5. М.Гарднер «А ну-ка догадайся Б.А.
6. Е.И.Игнатьев « В царстве смекалки»
7. Б.А.Кордемский « Математическая смекалка»
8. Б.А.Кордемсий «Удивитеьный мир чисел»
9. Б.А.Кордемсий «Увлечь школьников математикой»
10. Е.М. Минскин «От игры к знаниям»
11. Я.И.Перельман «Арифметические фокусы»
12. Я.И.Перельман «Фокусы и развлечения»
13. М. Гарднер «Математические чудеса и тайны» Москва «Наука» 1970
14. Б. А. Кордемский «Удивительный мир чисел» Москва Просвещение 1986
15. Я. И Перельман «Занимательная алгебра» Москва «Наука» 1970
16. Я. И. Перельман «Занимательные задачи и опыты» Минск «Беларусь»1994
17. В.В. Трошин «Магия чисел и фигур» Москва «Глобус» 2007
18. 365 веселых игр и фокусов. Москва АСТ – пресс 2005
19.
moikompas.ru/compas/focus_pocus
20. deltadim.narod.ru/matfocus.htm
21. nauka.relis.ru/52/0002/52002048.htm
22. http://www.youtube.com/watch?v=gZdmFmjOTPI
Фокусы
- Мастер-класс
- Фокусы
- Юмор
- Книги
- Вы здесь:
- Главная
- 6-11 лет
- Фокусы
Подписаться на этот канал RSS
Вам понадобится: пластмассовая бутылка, деревянная палочка или леска, яблоко, маркер, ножовка по металлу, ножницы.
Подробнее …
Вам понадобится: мандарины и мягкий стаканчик.
На перевернутый вверх дном стаканчики фокусник помещает мандарины, произносит заклинание и без особого труда, на глазах у зрителей, заставляет мандарин переместиться в соседний стаканчик.
Подробнее …
Вам понадобится: платок, кофта с длинным рукавом.
Секрет фокуса: Платок за уголок пришит к тонкой прочной нити или (булавкой), которая протягивается через рукав и другим концом крепится сзади к ремню брюк. Пока рука находится в согнутом положении, платок торчит из рукава. Но стоит поднять руку вверх, нить натянется, и платок просто-напросто «уйдет» вовнутрь.
Подробнее …
Вам понадобится: пакет и карандаши
Показ фокуса: в полиэтиленовый пакет набрать воды. Карандашом проткнуть пакет. Вааля, из пакета вода не вытекает.
Подробнее .
..
Источник фото: https://cdn.pixabay.comВам понадобится: монеты и платок.
Показ фокуса:
Берём пятирублевую монету и кладём её в середину платка. Затем держим монету через платок и соединяем оба конца платка.
Фокусник показывает монету двухрублевую, которая должна будет оказаться в платке. Большим пальцем он прижимает к ладони и ударяет посередине натянутого платка. Когда фокусник разворачивает платок, там находятся пятирублевая и двухрублевая монета.
Подробнее …
Источник фото: https://script-money.ruТы будешь настоящим телепатом! Ты сможешь отгадать предметы в конверте, которые положили участники.
Вот секрет: Конверты надо заранее пометить. Например, поставить маленькие точки в разных углах. Главное запомнить кому какой конверт даёте. Тогда вы без труда узнаете «хозяина» каждой вещи. Однако не забывайте про актерскую игру: хмурьте брови, изображайте, как вам сложно «отгадать».
Подробнее .
..
Фокус с шоколадомВам понадобится: плиточный шоколад.
Секрет фокуса: возьмите плиточный шоколад и разрежьте его (так как показано на рисунке).
Желтую часть мы меняем с оранжевой частью, и у нас получается лишняя плиточка, которую можно съесть.
Секрет в том, что после каждой перестановки кусочков длина шоколада немного уменьшается. Поначалу это не бросается в глаза. Но если повторить еще раз-другой, вы заметите, насколько меньше стала плитка. Главное – правильно предварительно её разрезать.
Подробнее …
Источник: pixabay.comВам понадобится: газета, ножницы, резиновый клей, белую пудру, лента.
Секрет фокуса: ленту надо подготовить заранее. Возьмите газету, отрежьте белое поле по всей длине. Затем резиновым клеем тонко смажьте с одной стороны ленту в середине во всю её ширину и длиной 8-10 см. (Этот клей не засыхает долго). Его надо посыпать белой пудрой, чтобы не было заметно клея и чтобы бумага не склеилась раньше времени при складывании.
Сложите пополам ленту, чтобы клеевой слой оказался внутри, отрежьте 1 см со стороны сгиба. Возьмите ленту за любой конец и встряхните. Лента цела! Это клей при отрезании склеил её концы. Соединение непрочно, но достаточно, чтобы показать целую ленту зрителям. Важно только не давать её любопытным в руки.
Подробнее …
Волшебный стаканВам понадобится: прозрачный стакан, бумажный круг (для верхнего края стакана), клей или силикон.
Секрет фокуса: к фокусу надо подготовиться заранее. А именно – наклеить бумажный кружок на верхний край стакана. Вырежьте кружок точно по контуру окружности стакана и приклейте к краям, смазав их силиконовым клеем.
Накройте стаканом монетку на листе бумаги. Она исчезнет! Главное – после демонстрации переключить внимание зрителя на что-то другое, не менее интересное.
Подробнее …
Сила взглядаВам понадобится: бумажная полоска примерно 2*6 см.
, теплая ладонь.
Скажите: «Я сейчас силой взгляда заставлю согнуться бумажную полоску…»
Секрет фокуса: Перед демонстрацией фокуса подержите руки под струёй теплой, почти горячей воды, а затем слегка вытрите, чтобы ладони остались влажными и тёплыми. Теперь главное, чтобы они не высохли и не успели остыть!
Положите бумажную полоску на ладонь и остатки воды начнут испаряться, повышая влажность бумаги. Та сторона полоски, что лежит на ладони, набухнет, бумага расширится и заставит изгибаться всю полоску.
Подробнее …
Рождественская звездаТебе понадобится: вода, спички и пипетка.
- Берем 5 спичек, надламываем посередине.
- Надломанные спички (получились как галочки) выкладываем на тарелку так, чтобы углы были параллельно друг к другу.
- Набираем в пипетку воды и капаем на изгиб спичек.
- Получилась звезда.
Подробнее …
Волшебные веревочкиВам понадобится: длинный кусок веревки, ножницы.
1. Поверните ладонь тыльной стороной к зрителям, возьмите три куска веревки, расположите их рядом в левой руке. Вы должны зажимать веревки между большим и указательным пальцами, причем верхние концы веревок должны выступать над ладонью приблизительно на 4 см.
2. По-прежнему, повернув ладонь тыльной стороной к зрителям, возьмите нижний конец короткой веревки и поместите его рядом с верхним концом длинной веревки.
Подробнее …
Девочка с кувшином водыВам понадобится: пластиковый стакан, скрепка, два куска плотной бумаги (приблизительно 25 см в ширину и 30 см в длину), липкая лента, пищевой краситель, стакан или другая прозрачная емкость, кувшин, кружка или чашка (она не должна быть прозрачной).
Подробнее …
https://mirkuponov.kz
Вам понадобится: большая вместительная чаша непрозрачная, два одинаковых пластиковых стаканчика, картон, ножницы, клей канцелярский, несколько упаковок разноцветных конфетти, платок, скотч, кусочек лески, карамельки в цветных бумажных упаковках.
- Демонстрируем публике большую чашу, наполненную разноцветными кружочками конфетти.
- Берем пластиковый стаканчик и показываем, что он совершенно пуст.
Подробнее …
http://imperiya.byВам понадобится: два воздушных шарика одного цвета, вода, бумага и стакан.
1. Возьмите два воздушных шарика одного цвета.
2. В один налейте воды, опустите в него второй шарик, а потом надуйте его. Вода равномерно распределиться между стенками шариков, и зрители ее не увидят.
3. Когда вы прокалываете шарик, вода вытекает в кулек.
Подробнее …
http://ondesktop.comЭтот фокус про волшебный глаз-алмаз, который видит сквозь любые препятствия, потребует от вас, ребята, актерского таланта, и сработает, если только вы не будете грызть ногти!
Собрав зрителей, скажите всем, что обладаете редким даром видеть сквозь предметы. И прямо сейчас докажете, что вы говорите чистую правду. Например, вы можете «увидеть» цвет воскового карандаша, зажатого в вашей же руке, не глядя на него.
Подробнее …
Фото ШколаЖизни.ру1. Положи одну книгу на лист белой бумаги формата А4 и предложи зрителям вытянуть этот лист, не сдвинув книгу с места. Это не получиться ни у кого.
2. Скажи, что ты можешь загипнотизировать книгу, да не одну, а хоть целый десяток. И они будут «спать» так крепко, что не заметят исчезновения бумаги.
3. Положи на лист бумаги стопку из нескольких книг. Разводя над ними руками, приговаривай заклинание: «Вам хочется спать… очень хочется спать. На раз-два-три вы уснете крепким и беспробудным сном! Раз, два, три!». И резко потяни бумагу.
Подробнее …
Фото vreticule.com1. В блокноте 3 участника по очереди по одному четырехзначному числу – одно под другим.
2. Пишем на чистом листе бумаги заранее известное число, но зрителям пока не показываем.
3. Потом просим пятого зрителя сложить все четыре числа и громко назвать полученную сумму.
4. Когда пятый зритель огласит результат, ты показываешь лист бумаги, на котором написано именно это число.
Подробнее …
Фото www.fotovarka.ruФокусы – это всегда хорошо. Особенно числовые. Математическими фокусами с числами можно удивлять друзей за столом, в долгой поездке или на каникулах. Смысл этих фокусов состоит в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними.
1. Задумайте любую цифру от 0 до 9. Задумали?
2. Умножьте ее на 5. Только не ошибитесь, иначе у вас не получится фокус.
Подробнее …
Фото http://beyondmediaonline.com1. Перед представлением намажьте немного клея на тыльную сторону левой руки;
2. Теперь показываем монету зрителям правой рукой, а левую сжимаем в кулак и поднимаем его вверх тыльной стороной к себе;
3. Говорим зрителям, что сейчас вы спрячете монету в кулак. И делаем вид, что на самом деле засовываем монетку в кулак левой руки;
4. В это же время незаметно для зрителей приклеиваем монетку к тыльной стороне кулака, где она прилепиться к клею;
Подробнее .
..
Числовые фокусы «Аргументов и фактов»
Числовые фокусы “Аргументов и фактов”
Выступление П.А. Тревогина
по СПб радио 30 ноября 2000 г.
Расшифровка магнитофонной записи с прямого
эфира
Ф — Александр Федоров, ведущий
РМ — радиослушатель-мужчина
РЖ — радиослушательница-женщина
Т — П. Тревогин
Прямой шрифт — заранее заготовленный текст
Ф. Итак, вновь в нашей студии Петр Александрович Тревогин, кандидат технических наук и публицист. Итак, начинаем.
Здравствуйте, дорогие радиослушатели!
Поговорим сегодня об очередной
антинаучной сенсации, на которые так щедр
еженедельник “Аргументы и факты”.
В прошлом
году (и, кажется, в позапрошлом тоже) он печатал
большую серию статей и интервью профессора
Эрнста Рифгатовича Мулдашева, талантливого
глазного хирурга. Но материалы эти были
посвящены не хирургии глаза, а совсем другим
темам: происхождению человека от
перепончатолапых атлантов, тысячелетним
оживающим мумиям и прочей восточной мистике,
почерпнутой профессором из своей тибетской
экспедиции. Если верить Эрнсту Рифгатовичу,
Тибет — это такая особая область Вселенной, где
обычные законы физики отменяются, а действуют
совсем другие — законы кармы, колдовских сил,
магической энергии из Космоса и прочего в таком
же духе. От всего этого просто руки опускаются и
становится обидно за талантливого человека,
ударившегося в суеверия. Но вот в № 45 “АиФ”а
появилось очередное откровение неутомимого
оккультиста. Беседа с журналистом Николаем
Зятьковым называется “Загадка числа 108”.
Как
математик по образованию и просто
цивилизованный человек я никак не мог пройти
мимо этой поразительной статьи.
Ф. Уважаемые наши слушатели, вы можете принять участие в нашем разговоре. Телефоны контактные включены: 315 04 87 и второй телефон 315 78 23. Вот мы о загадочных числах… цифрах… и числах мы сейчас и поговорим. Кстати, в студии уже есть телефонный звонок. Здравствуйте. Пожалуйста, ваш вопрос.
РЖ. Здравствуйте. Вы знаете, я вот хочу сказать. Дело в том, что вот то, что пытаются распространить лжеучения, они используют такие приемы обаятельные, что, знаете, … душу… (нрзбр) человека. А у вас, когда вы излагаете, ваше против мнение, вы как-то несколько суховато и по-научному, и очень как-то так быстро, понимаете. Поэтому…
Ф. Петр
Александрович.
..
Т. Критика принята.
Ф. Критика принята, и камешки и в ваш огород…
Т. Постараюсь…
Ф. …и в наш тоже, потому что быстро, быстро, понимаете…
Т. Постараюсь не так быстро.
Ф. У нас время эфирное, оно, к сожалению, очень быстро пролетает, а сказать хочется много. Поэтому, может, так это всё быстро. Ну, а что касается “не так сухо”, то это к вам.
Беседа начинается с того,
что тибетские ламы придают этому натуральному
числу магическое значение: они очень любят, чтобы
число молитвенных четок, ниш с божествами, число
ритуальных обходов вокруг того или иного
священного места и так далее — было равно 108. Ну
что ж, религия есть религия, и бесполезно искать в
ней рациональные мотивы.
Но дальше идет развитие
этой темы, совершенно удивительное по уровню
невежества.
Мулдашев говорит о трех вогнутых
каменных зеркалах по сторонам священной горы
Кайлас. Если я правильно понял, они предназначены
для улавливания тантрической энергии из Космоса,
то есть это что-то вроде древних радиотелескопов.
Так вот, дуги этих зеркал 108, 78 и 30° . Сумма двух
последних чисел тоже равна 108, подчеркивает
профессор. Право, не знаешь, смеяться или плакать.
Это все равно как если бы кто-то стал складывать
килограммы с амперами. Или гвозди с панихидами.
Дуга, угол, доля окружности — это не есть целое
число в привычном понимании, такое, скажем, как
количество зубов во рту или овец в стаде. Дуга —
непрерывная величина, а не дискретная. Для ее
измерения люди используют условную единицу —
градус, 360-ю долю полного угла, окружности.
Необходимо отдавать себе отчет в том, что эта
единица именно условная, произвольно
придуманная человеком. Научно говоря —
антропоцентрическая. Когда-то древним
вавилонянам показалось, что окружность удобно
делить на 360 равных частей. Но это дело вкуса,
можно было бы выбрать любое другое число. В
артиллерии, например, принято делить окружность
на 6000 частей, в некоторых других областях
человеческой деятельности — на 400 и так далее.
Ф. Извините, Петр Александрович, я прерву вас. Телефонный вопрос. Давайте на них отвечать тоже будем
.РМ. Алё,
здравствуйте. Вот восточные единоборства,
значит, движения, построены на числах, на
движениях … (нрзбр) триграмм и гексограмм.
Всё это построено на числах. Соотношения неба и
земли, как биоэнергетика в восточных
единоборствах, строится тоже на числах.
Всё это
пришло из степи (? — нрзбр). Как к этому
относится… э-э…
Т. Участник.
Ф. Участник нашей передачи.
Т. Вы знаете, отрицательно отношусь. Конкретно, о каких числовых соотношениях там или свойствах тех или иных чисел, я не знаю, о чем идет речь, но я представляю себе, что это тоже какая-то мистика — в том духе, о котором я сейчас говорю. В духе статьи в “Аргументах и фактах”.
Но это еще цветочки. Дальше Мулдашев
заявляет: “Видимо, это число является
своеобразной константой для Вселенной”. И
приводит в качестве аргумента изыскания другого
ученого-оккультиста Сергея Проскурякова,
цитирую: “Длина сторон основания пирамиды
Хеопса составляет 108 ? 1,0810 м, пирамиды
Хефрена — 108 ? 1,089 м, пирамиды Миккерина — 108
м, скорость света в вакууме составляет 108 ? 1010 м/ч”
— ну и так далее, там еще масса Солнца и другие
астрономические величины, и даже длина молекулы
ДНК.
Здесь нагорожено столько невежественной
чепухи, что просто не знаешь, с какого конца ее
разгребать.
Прежде всего числовые фокусы с
египетскими пирамидами, вошедшие в моду очень
давно, убедительно высмеял — лет 60 или 70 назад —
замечательный ленинградский популяризатор
науки Яков Исидорович Перельман. Он справедливо
заметил, что говорить о точной длине стороны
пирамиды, скажем, Хеопса бессмысленно — по той
простой причине, что за тысячелетия своего
существования ее размеры хоть и незначительно,
но изменились благодаря выветриванию и
частичному разрушению. Далее, совершенно
бессмысленно и абсурдно выражать эти длины в
метрах. Что такое метр? Эта — опять же
антропоцентрическая — единица длины была
введена в 1791 году, во время Великой Французской
революции — как одна десятимиллионная доля
четверти парижского меридиана.
Древним
египтянам эта мера длины не была и не могла быть
известна.
Теперь о жонглировании степенями
дроби 1,08 в обоснование какой-то таинственной
космической сущности числа 108. Здесь тоже
заключается двойная нелепость. Во-первых, это
совершенно разные числа. Они отличаются одно от
другого множителем 100 — это опять-таки
антропоцентрическая величина. 100 — это десять в
квадрате, а 10 — основание системы счисления,
которой мы пользуемся. В одной из прежних передач
я уже говорил о том, что наша десятичная система
счисления — условна, в основе ее лежит тот
случайный биологический факт, что у человека на
двух руках 10 пальцев. Абсолютизировать
десятичную систему, не понимать ее
антропоцентризма — не пристало человеку,
претендующему на звание цивилизованного.
Во-вторых, число 1,08 очень мало отличается от
единицы, а это значит, что степени этого числа,
которыми пользуется Проскуряков, образуют
весьма медленную прогрессию.
А отсюда в свою
очередь следует, что манипулируя этими степенями
на манер Проскурякова, можно “доказать” — в
кавычках — что угодно. И я действительно берусь
это сделать. Дайте мне размеры и массу любого
предмета — Александровской колонны, тросточки
Чарли Чаплина, Эйфелевой башни, трубки Иосифа
Сталина, — выраженные в любых единицах — в
аршинах, пудах, дюймах, в китайских ли — и я вам на
блюдечке с голубой каемочкой преподнесу цифры
единица, нуль и восемь. Или любой другой набор
цифр по желанию заказчика. Просто уму
непостижимо, как взрослые и образованные люди не
понимают простой вещи: что число 10, градус, метр,
час, секунда — так же условны, так же не заданы
природой, как День студента, День торгового
работника или день рождения моей бабушки.
Ф. У нас есть
телефонные звонки. Давайте ответим на вопросы.
Слушаем вас. Здравствуйте.
РМ. День добрый, здравствуйте. Здесь очень много рассуждается о науке. У меня один только вопрос. Будь добр, ученый, ответь: был на Тибете хоть один раз или нет?
Т. Нет.
Ф. Мы продолжаем свою статью… в “Аргументах” … ээ… в газете “Аргументы и факты”.
А дальше идет, так сказать, десерт, сладкое. Послушайте теперь пространную цитату, она заслуживает вашего терпеливого внимания:
“В эзотерической литературе можно встретить упоминания о том, что кроме числа p , равного 3,14 и отражающего основные геометрические закономерности, существовало еще и древнее значение p . Если 360° (круг) разделить на 108, то мы получим число 3,33.
Уж не является ли число 3,33 древним
значением p , характерным для того периода жизни
Земли, когда Северный полюс располагался в
районе горы Кайлас и планета имела иную
магнитную структуру?”.
Конец цитаты.
Что по этому поводу можно сказать?
Случай, как говорится, тяжелый. Налицо дремучее
непонимание разницы между физикой и математикой.
Число p — это не физическая константа наподобие
скорости звука или массы Венеры, а математическая.
Число p не может меняться в зависимости от
каких-то физических (астрономических)
обстоятельств вроде дрейфа магнитных полюсов
Земли (или любого другого тела). Допускать
подобную мысль так же абсурдно, как предполагать,
что на Тибете или на горе Кайлас иная таблица
умножения. Что трижды девять в этом загадочном
месте — не 27, как у нас, грешных, а 31 или 19. А насчет
того, что раньше, дескать, число p было иным — так
то не само число, а его приближенное значение у
древних наших предков. Египтяне, например,
полагали отношение длины окружности к ее
диаметру равным дроби 22/7.
Ну так ведь на то они и
древние — они об иррациональных числах ни сном,
ни духом не помышляли, да и с простыми-то дробями
управлялись с большим трудом. И не будем их за это
корить: научные знания добывались веками и
тысячелетиями, стараниями многих поколений
мыслителей. Сегодня число p известно с
несколькими тысячами знаков (это своего рода
спорт — так порой испытывают компьютеры новых
поколений, хотя практически такая точность
никому не нужна).
Ф. В нашей студии вновь телефонные звонки. Слушаем вас. Здравствуйте.
РЖ. Здравствуйте; Людмила Анатольевна. Я бы хотела задать вопрос выступающему.
Ф. Да. Петр Александрович Тревогин. Слушаем вас.
РЖ. Да. Вот я хочу
сказать: я читаю все эти в “Аргументах и фактах”
статьи.
И там же написано, что это всего лишь
гипотеза — то, что говорится. Я думаю, что к
вашему коллеге вы не очень-то корректно к нему, к
его высказываниям относитесь. Это раз. Второй
вопрос. Если вы не были там, на Памире, как вы
можете с такой уверенностью опровергать то, что
вы не видели?
Т. Спасибо за вопрос. Отвечаю. Для того, чтобы опровергать математические, извините за резкость, глупости, не надо бывать ни на Памире, ни в Австралии, ни в Аргентине, ни в Гренландии, ни где-либо еще. Математика есть математика. Она всюду одинакова. Как сказал бы преферансист, она и в Африке математика. Говорят: туз — он и в Африке туз. То же самое о математике. Таблица умножения.
Но сегодня не знать самых
элементарных вещей, не понимать, чтo идет от
природы, а чтo от человека — просто позор. Это не
изъян в конкретных познаниях, это не то что
забыть, когда была семилетняя война, или как
выглядит структурная формула бензола.
Это уже
серьезный изъян в мировоззрении.
Подобными изъянами как раз и подпитывается вера
в сверхъестественное.
Помнится, несколько лет назад “Аргументы и факты”, напечатав очередную свою откровенно мракобесную статью, дали потом откат, заявив, что они якобы всего лишь пошутили. Хотя публикация эта была отнюдь не в апрельском номере. А впрочем, судя по очень многим (слишком многим) “АиФ”овским публикациям, первое апреля для этого еженедельника царит круглый год.
Дорогие радиослушатели! Очень советую
вам четко различать то, что идет от человека и то,
что идет от природы (или, если угодно, если вы
верующий человек, — от Бога). Иногда такое
различие очевидно, а иногда для этого требуется
некоторое умственное усилие. Тренируйтесь,
обсуждайте эту тему друг с другом! Поверьте,
умение отличать эти две вещи чрезвычайно важно
для цивилизованного мировоззрения.
И еще. Пожалуйста, вырабатывайте в себе здоровый скептицизм, критическое мышление. Не принимайте слепо на веру всё, что напечатано типографским способом — это отнюдь не гарантия истины. Научные “погоны и лампасы” тоже истину не гарантируют. И когда вы прочтете в “АиФ”е (или где-нибудь еще) очередную сногсшибательную сенсацию, не спешите, захлебываясь, делиться ею с друзьями. Подумайте сначала, как она согласуется с тем, что вам хорошо известно из школьного курса физики, биологии, математики, астрономии. Наконец, просто со здравым смыслом. Всего хорошего.
Ф. Но все-таки, прежде чем попрощаться, еще один телефонный звонок. Видно, кого-то он сильно задел за живое — наш разговор. Слушаем вас. Здравствуйте.
РЖ. Здравствуйте.
Я бы хотела выступить вот на сегодняшнюю тему.
Я
считаю, что каждое мнение, вот, имеет свое право
на жизнь, и как бы верить или не верить — это
решает человек сам, это его личное дело. А вот то,
что вы рассуждаете, мне кажется, это … (? нрзбр)
Т. Спасибо. Конечно, верить или не верить — это дело каждого, но каждый имеет право и на заблуждения, в том числе — считать, например, что дважды девять — семнадцать или тридцать один, это право каждого. Но право каждого также и указывать другим людям на эту ошибку. Именно ошибку, а не какое-то мнение.
Ф. Цикл “Наука и
лженаука”. Ученые, публицисты и писатели
выступают в этом цикле. Они борются с различными
формами мистики. И вот, на примере сегодняшней
статьи, которую прокомментировал Петр
Александрович Тревогин, вы могли возможность
убедиться в каких-то несоответствиях того, что
напечатано, и здравого смысла.
“Наука и
лженаука” — пишите нам.
Петр Тревогин
Презентация проектной -исследовательской работы по теме математические фокусы доклад, проект
Проектная работа
Предмет: Математика
Тема: «Математические фокусы»
Выполнил: Глотов Данил, ученик 6 класса
МКОУ «Ушакинская СОШ №1»
Научный руководитель: Кудринская И.Ю., учитель математики МКОУ «Ушакинская СОШ №1»
«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным»
Б. Паскаль
Актуальность
Существует необходимость в повышении внимания учащихся к изучению математики через её занимательные стороны, что, несомненно:
должно повысить успеваемость обучающихся
должно решить проблему быстрого устного счета
должно помочь успешно сдать ОГЭ и ЕГЭ
Цель
Повысить у школьников интерес к математике и убедить их в том, что вычисления на калькуляторе и телефоне пагубно влияют на их способности быстрого устного счета.
Гипотеза
Если знать математические свойства чисел, то можно разгадать тайну любого фокуса, а демонстрация и выполнение математических фокусов способствует развитию навыков устного счета.
Объект исследования: математические фокусы, основанные на свойствах чисел, действий, математических законах, уравнениях.
Предмет исследования: природа математические фокусов.
Задачи
1.Изучить литературу по данному вопросу и интернет-ресурсы;
2.Выбрать и обобщить наиболее интересные, увлекательные математические фокусы;
3.Выяснить в чем секрет математических фокусов;
4.Провести мастер-класс в 5-6 классах по теме;
5.Пользуясь освоенными «секретами» готовых фокусов, придумать свои фокусы и проверить их в действии;
6.Создать копилку своих математических фокусов.
Теоретическая часть
Миллионы людей во всех частях света увлекаются математическими фокусами.
И это не удивительно.
“Гимнастика ума” полезна в любом возрасте:
она тренирует память
обостряет сообразительность
вырабатывает настойчивость
способность логически мыслить, анализировать и сопоставлять.
Все вы знакомы с творчеством великого русского поэта М.Ю. Лермонтова, но не каждому известно, что он был большим любителем и математики, особенно его привлекали математические фокусы, которых он знал великое множество, причем некоторые из них он придумывал сам.
Вот один из фокусов М.Ю. Лермонтова:
Задумать любое число, прибавить к нему 25, прибавить еще 125, отнять 36,
вычесть задуманное число, остаток умножить на 5, полученное число разделить на 2.
!!! Получится 285!!!
Секрет фокуса :
(а + 25 + 125 – 36 – а) · 5 : 2 = 114 · 5 : 2 =
285.
Классификация математических фокусов
1.
Числовые фокусы
Задуманное число;
предсказывание результата;
угадывание даты, номера;
мгновенный устный счет.
2.Фокусы с настенным календарем
3.Фокусы с мелкими предметами
Категория : числовые фокусы
Тип: задуманное число
Первый человек записывает на листочке бумаги любое трехзначное число. Второй приписывает к этому числу справа такое же число. Третий делит получившееся шестизначное число на 7. Четвертый делит этот результат на 11 . Пятый делит результат на 13, записывает его на отдельном листе и передает отгадывающему.
Если все вычисления были выполнены правильно, то отгадывающий получит трехзначное число, которое первоначально написал на бумаге.
Весь секрет фокуса состоит в том, что 7∙11∙13=1001!!! И данное число называют числом Шахеризады! При умножении его на трехзначное число мы получаем его же, но записанное дважды!!!
Очень занимательны и интересны математические фокусы, в основе которых лежат уравнения.
В эту группу входят фокусы, где фокусник
предлагает вам выполнить
программу действий, затем
он просит вас сообщить
окончательный результат и,
получив его, моментально
называет задуманное число.
Фокус: Задумайте число, умножьте его на 4 и к произведению прибавьте 1. Результатом всех действий будет число 49. Каково задуманное число?
Разгадка: Фокусник мысленно решает простое уравнение: 4 х+1=49; от результата вычитает 1 и делит полученное число на 4. После сообщает вам, что вы задумали 12.
Можно придумать сколько угодно таких фокусов, достаточно быстро считать в уме и уметь решать уравнения.
Мгновенный устный счет
А как быстро умножить любое число на11?
Складываем две цифры двузначного числа, затем помещаем сумму между двумя цифрами двузначного числа.
53∙11=5(5+3)3=583
93∙11 = 9 (9+3) 3 = 1023
По сути техника умножения на 11 любого числа сводится к сложению соседних чисел!!!
5 1 726 ∙ 11 = 5 (5+1) (1+7)(7+2)(2+6) 6 =
568 986
А сейчас я вас удивлю !!! Быстро и без калькулятора и столбиков возведу в квадрат число 145!!!
Чтобы возвысить в квадрат число, оканчивающееся цифрой 5 (например 85), умножают число десятков (8) на него же плюс единица (8∙9) и приписывают 25 (в нашем примере получается 7225).
1452; 14∙15 = 210; 21025
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25
Этапы практической части
1. Анкетирование
2. Проведение мастер-класса
3. Создание копилки математических фокусов
Знаете ли вы, что такое математические фокусы?
Какие фокусы вы знаете?
После этого был проведен мастер-класс по теме: «Математические фокусы».
Структура мастер-класса:
1.Ребят познакомили с темой исследования.
2. Показали ряд математических фокусов.
3. Часть секретов фокусов была раскрыта, а другую часть было предложено раскрыть самостоятельно.
4. В конце занятия было продолжено анкетирование.
Заинтересовала ли вас тема математических фокусов?
Будете ли Вы знакомить с фокусами своих друзей, родственников?
Домашнее задание
придумать свои математические фокусы;
проверить и показать, как работают фокусы;
оформить работы;
защитить их.
В результате мы создали
копилку своих математических
фокусов, которая будет
пополняться с каждым годом.
Наши фокусы
1.Загадайте любое трехзначное число
2.Увеличьте его в 7 раз.
3. Результат умножьте на 143.
4. Назовите, что получилось у вас, и я отгадаю число, которое вы задумали.
Секрет фокуса: 7∙143=1001
!!! Число Шахеризады !!!
Умножая его на трехзначное число, мы получаем задуманное число, но записанное дважды!!!
Выполнил ученик 5 класса Петросян Эдуард
Наши фокусы
Задумайте число (от 1 до 9), запишите в тетрадку и никому не показывайте.
К 888 прибавьте (- 444)
Получившееся число умножьте на (-3)
Получившийся результат разделите на
(-2)
От получившегося числа отнимите (-334)
Результат умножьте на задуманное число
Секрет моего фокуса в том, что при помощи математических действий:
888+(-444)=444; 444∙(-3)=-1332 ;
-1332:(-2)=666 ; 666-(-334)=1000
мы получаем 1000 и умножаем на задуманное число (например 7).
Так по первой цифре ответа (например 7000) я узнаю загаданную цифру.
Выполнил ученик 6 касса Кокорин Дмитрий
Наши фокусы
Загадываем число от 1-10
Умножаем это число на 9
Складываем получившиеся две цифры
Прибавляем к получившемуся числу число 491
Это число делим на 100
Вычитаем 5
В результате должен получиться 0
Секрет фокуса – признак делимости на 9. Если любое число умножить на 9, то результат обязательно будет делиться на 9 без остатка. Любое число делится на 9 тогда и только тогда, если сумма цифр делится на 9. Так как мы берем числа от 1 до 10, то сумма цифр всегда будет 9.
Например: загадываем число 2, 2∙9=18 ,
1+8=9, 9+491=500, 500:100=5, 5-5=0
Выполнил ученик 5 класса Анхимков Роман
Наши фокусы
Задумать любое положительное однозначное число, к нему прибавить 6, полученную сумму умножить на 4, к результату прибавить 8, все разделить на 4, вычесть 2 и вычесть число, которое было задумано.
В результате смело говорите 6!!!
Секрет фокуса:
((х+6)∙4+8):4-2-х=х+8-2-х=6
Выполнил ученик 6 класса Глотов Данил
Репортаж с мастер – класса
Заключение
В исследовательской работе мы выполнили поставленные перед собой цели и задачи.
Математический интерес каждого фокуса заключается в разоблачении его теоретических основ, которые в большинстве случаев довольно просты, но иногда бывают хитро замаскированы.
В дальнейшем мы хотели бы продолжить работу над этой интересной и увлекательной темой.
Спасибо за внимание!
10 советов по тесту на численное мышление: узнайте, как пройти
Тесты на численное мышление используются работодателями на этапах отбора при приеме на работу для выявления кандидатов с наивысшим уровнем математических способностей.
Хотя типы и структура вопросов различаются в разных издательствах тестов, их суть одинакова в том, что они имеют дело с данными в виде графиков, таблиц и диаграмм, которые требуют интерпретации и анализа для формирования обоснованных выводов.
Предназначенные для измерения врожденных способностей, они не требуют предварительных знаний. Тем не менее, числовые тесты рассуждений непросты.
Сложность представленных данных, нехватка времени и необходимость соответствовать конкурентоспособным стандартам делают их сложными, часто нервными.
Приведенные ниже 10 советов дают советы о том, как лучше всего подходить к этому типу оценки как до, так и во время теста на числовое мышление.
1. Уточните, кто будет поставщиком тестов
Перед днем экзамена рекомендуется связаться с рекрутером для получения информации о том, какое тестовое издательство они используют, так как это будет определять характер вашей оценки.
Например, числовые тесты на рассуждение Cappfinity являются адаптивными, не имеют ограничения по времени и содержат несколько типов вопросов.
Напротив, тесты способностей Saville имеют фиксированную продолжительность, и все вопросы имеют одинаковую структуру.
Знание стиля оценивания, с которым вы столкнетесь, позволит вам потренироваться специально для этого типа теста.
2. Освежить в памяти основы арифметики
Способность быстро и точно работать с процентами, отношениями, дробями и десятичными дробями дает вам огромное преимущество в тесте на логическое мышление.
В рамках подготовки освежите сложение, вычитание, умножение, деление и преобразование этих числовых представлений. Другими словами, учебник по основам счета.
В большинстве случаев вы будете работать с несколькими вариантами ответов, поэтому не обязательно каждый раз получать точный ответ. Это больше касается знания того, как применять правильные методы в любом заданном уравнении, чтобы дать себе ответ, который точно соответствует одному из доступных вариантов.
3. Возьмите с собой калькулятор (и знайте, как им пользоваться)
Если при оценке разрешены калькуляторы, обязательно используйте тот, с которым вы знакомы (а не калькулятор вашего мобильного телефона).
Борьба с оборудованием приведет к разочарованию, добавляя стресс к и без того напряженному событию.
Используйте свой калькулятор во всех пробных тестах и ознакомьтесь со всеми полезными функциями, такими как память.
Следует отметить, что вам может быть разрешено использование только простого калькулятора, поэтому научитесь не полагаться на расширенную функциональность научного.
4. Используйте практические вопросы
В самом начале теста на числовое мышление вам будут предложены один или два практических вопроса. Используйте их с умом.
Спешить некуда, так как практические вопросы не будут включены в отведенное вам время. Поэтому внимательно прочитайте их и изучите содержание и структуру вопросов.
Это заставит ваш мозг работать так, как ему нужно, до конца экзамена, сосредоточит ваше внимание на поставленной задаче и успокоит ваши нервы, мягко расслабив вас.
5. Уделяйте пристальное внимание деталям
При работе в условиях ограниченного времени может возникнуть соблазн применить быстрый подход, просматривая вопросы в гонке, чтобы ответить на как можно больше.
Это верный способ упустить важную информацию, будь то в теле самого вопроса или в числовых данных, сопровождающих его.
Убедитесь, что вы точно понимаете, о чем вас спрашивают, и никогда не делайте предположений. Вся необходимая вам информация будет содержаться в вопросе, поэтому определите более мелкие детали, прежде чем пытаться ответить.
6. Перепроверьте единицы измерения, единицы измерения, валюты
Вопросы в тестах на числовое мышление часто включают различные наборы данных, будь то несколько валют, комбинация числовых представлений или различные единицы измерения.
Поскольку вам будут предложены три из четырех вопросов, касающихся одной и той же числовой информации, всегда перепроверяйте, правильно ли вы работаете с данными, отвечая на поставленный вопрос.
Это может показаться очевидным советом, но на нем легко споткнуться, работая в условиях дефицита времени.
7. Остерегайтесь отвлекающих факторов
Отвлекающие факторы часто встречаются в числовых тестах на рассуждение.
Это фрагменты информации, предназначенные для того, чтобы ввести вас в заблуждение или сделать вопрос более сложным, чем он есть на самом деле.
Приступая к вопросу, обработайте всю информацию логически, затем сосредоточьтесь на том, что относится к делу, и отбросьте все отвлекающие факторы.
Как правило, чем сложнее вопрос, тем больше в нем отвлекающих факторов, поэтому ключевой навык — умение их быстро обнаружить.
8. Если проблема слишком сложна, продолжайте
Когда вы сталкиваетесь с вопросом, который изо всех сил пытаетесь понять, обычно лучше двигаться дальше, чем тратить много времени на разгадку его сложности.
Сосредоточение всей вашей энергии на сложном вопросе съест ваше время и, вероятно, вызовет разочарование, что повлияет на остальную часть вашей работы.
В большинстве случаев, если у вас останется время, вы сможете вернуться и ответить на вопросы, оставшиеся без ответа.
9. Сделайте наилучший вывод
В большинстве тестов на числовое мышление не используется отрицательная маркировка.
То есть за неправильный ответ вы получите ноль очков, как и за вопрос, оставшийся незаполненным.
Имея это в виду, если вы не уверены, разумно сделать обоснованное предположение.
Помните, что обычно перед вами будет несколько вариантов ответа, поэтому всегда есть шанс выбрать правильный, даже если вы не уверены в своем ответе.
10. Сохраняйте постоянный темп
Возможно, самым сложным аспектом теста на числовое мышление является темп. Точность является ключевым фактором, но скорость также играет роль в вашем счете, поэтому вам нужно работать быстро.
Если вы заранее узнали, какой тест будете проходить, сравните количество содержащихся в нем вопросов с его продолжительностью, чтобы получить контрольное время на каждый вопрос.
Хорошие темпы приходят с практикой, так что сделайте это основной частью вашего теста на числовое мышление и подготовки.
Руководство по тестированию численного мышления (включая наши 12 лучших советов)
Oliver Savill Обновлено:
Это руководство поможет вам развить свои навыки, знания и стратегии при выполнении тестов на числовое мышление.
Содержание страницы:
Перейти к:
- Как работает тест на числовое мышление
- Какую математику мне нужно знать?
- Критическое мышление высокого уровня в числовых тестах
- Станьте черным поясом по результатам тестирования
- Фокус, нервы и концентрация
- Наши последние лучшие советы по тестированию числового мышления
- Теперь пришло время практиковать
Как работает тест на числовое мышление
Самое замечательное в числовых тестах то, что они не такие, как тесты по математике. Конечно, они включают в себя числа и расчеты, но они не пытаются измерить ваши математические способности так же, как школьный экзамен. Это отличная новость для тех из нас, у кого мрачные воспоминания о неразрешимых математических вопросах, требующих таких навыков, как алгебра, тригонометрия и вероятности.
Численные тесты не требуют написания ответов от руки и знания необычных формул и теорий.
Так что же такое «численные тесты»?
Численные тесты коренным образом отличаются от математических из-за того, для чего они предназначены. Вместо того, чтобы оценивать ваше понимание и применение программы по математике (например, GCSE или A-Level), они предназначены для измерения вашей способности правильно интерпретировать числовую информацию и использовать ее для решения проблем и принятия решений. Современные тесты основывают информацию на реальных числовых данных, которые вы можете найти на рабочем месте. Таким образом, числовые тесты действительно требуют от вас выполнения только тех видов анализа с числами, которые вы должны выполнять на работе.
Эта разница между экзаменами по математике и числовыми тестами означает, что иногда результаты людей по обоим тестам различаются. Работодатели часто видят кандидатов с отличной математической квалификацией, которые демонстрируют плохие результаты числовых тестов.
Как правило, это результат того, что квалификация по математике подталкивается хорошей техникой экзамена, большим количеством повторений и эффективной памятью. Числовой балл теста ниже, потому что он не зависит от техники экзамена, повторения и памяти; численный тест основан на эффективном анализе, решении проблем и хорошей технике прохождения теста, о чем вы узнаете больше в этом руководстве.
Это отличная новость для тех, кто традиционно с трудом сдавал экзамены по математике. Численные тесты разные – они измеряют разные навыки по-разному. Работодатели часто видят кандидатов с низкой или средней квалификацией по математике, которые очень хорошо справляются с числовым тестом, гораздо более важным для работы.
Численные тесты не только отличаются от экзаменов по математике, но и имеют ряд общих характеристик, поэтому вы всегда будете знать, чего ожидать.
Общие характеристики численных тестов включают:
- Ответы с несколькими вариантами ответов – никаких ответов от руки или показа вашей тренировки.
- Разрешено использование калькуляторов – арифметика в уме не требуется
- Строгие временные ограничения – некоторые из них щедрые, а некоторые очень короткие (мы рассмотрим это позже)
- Примеры вопросов перед началом теста – они не рассчитаны по времени и не подсчитаны 90 111
- Предварительные знания не требуются – не нужно запоминать уравнения (или тайком писать на руке)
- Относится к рабочему месту — современные тесты основаны на числовой информации, с которой вы будете иметь дело на работе
Понимание того, как работают числовые тесты, чем они отличаются от экзаменов по математике и их общих характеристик, должно начать рассеивать страх перед неизвестным. Любые оставшиеся беспокойству по поводу вашей работы можно противопоставить развитие более глубокого понимания внутренней работы тестов и, в разделе 2 этого руководства, наиболее эффективных методов сдачи тестов, которые следует разработать на основе этого понимания.
Какую математику мне нужно знать
Численные тесты — это не то же самое, что экзамены по математике, но вам все равно понадобятся некоторые математические навыки — в конце концов, вам придется решать задачи, основанные на числах. К счастью, вам нужны навыки намного проще, чем ожидается по математике GCSE.
Математика для числовых тестов
Вот список наиболее часто используемых математических вычислений в числовых тестах:
- Дополнение
- Вычитание
- Умножение
- Подразделение
- Средние значения
- Проценты
- Передаточные числа
Если вы не знакомы или не уверены в каком-либо из этих математических навыков, вам следует сосредоточьтесь на своем времени на вопросах тестовой практики, которые требуют форм расчета, которые вас беспокоят. Вы также можете использовать базовые пособия по математике, чтобы дополнить свое развитие с помощью практических вопросов.
Помните, что вам будет разрешено использовать калькулятор во время числового теста для выполнения этих расчетов.
Высокоуровневое критическое мышление в числовых тестах
Тесты для выпускников и профессиональные тесты находятся на вершине дерева числовых тестов с точки зрения сложности. Эти тесты высшего уровня измеряют продвинутый навык числового критического мышления, чтобы отразить требования рабочих мест, для которых они используются, чтобы помочь в наборе, и уровень кандидатов, которые подают заявку.
Сложность этих тестов заключается не в типах вычислений, которые вам необходимо выполнить; численные тесты критического мышления по-прежнему основаны на семи основных математических навыках, описанных выше. Их сложность является результатом сложности числовых данных, на которых основаны вопросы, и характера проблем, которые вам необходимо решить.
Что такое критическое мышление?
Численное критическое мышление — это способность анализировать числовую информацию и манипулировать ею, чтобы делать выводы, определять лежащие в основе отношения и принимать решения.
Эти высокоуровневые тесты отличаются от тех, которые вы, возможно, должны пройти для ролей начального или среднего уровня, потому что вы должны продемонстрировать способности, которые выходят за рамки простого понимания числовых данных и ответов на вопросы о них. Вместо этого вам нужно будет работать более сложным способом, чтобы получить правильные ответы.
На самом деле это означает, что для ответа на числовой тест на критическое мышление вам часто требуется выполнить несколько вычислений. Другими словами, может быть несколько этапов вычислений, которые вам нужно выполнить, чтобы получить ответ. Иногда это даже требует некоторой оценки или устранения неясностей, как это иногда бывает на работе.
Если это звучит немного пугающе, не волнуйтесь. Расчеты по-прежнему основаны на базовых математических навыках. Вы можете максимизировать свой результат, разработав эффективную технику прохождения теста. Вы можете заполните несколько практических вопросов , чтобы получить представление о требованиях, предъявляемых вопросами критического рассуждения; они могут быть не так плохи, как вы думаете!
Получите черный пояс по результатам тестирования
Как стратегии влияют на ваш счет
Различия, которые мы видим в результатах тестов людей, часто сводятся к факторам, не связанным с их числовыми способностями, например:
- Отсутствие знаний о сдаче теста
- Плохое время
- Глупые ошибки
- Нервы и тревога
Кандидаты с высокими баллами, как правило, обладают высокими способностями к вычислениям в сочетании с эффективными стратегиями прохождения теста.
Эти черные пояса, сдающие тесты, знают, что когда вы проходите числовой тест, дело не только в максимальных усилиях; речь идет о правильных усилиях в нужных местах.
Этот раздел знакомит вас с расширенными стратегиями сдачи теста , который вы разработаете, чтобы убедиться, что ваш результат теста не снижается из-за ошибок, промахов и плохой техники. Обладатели черного пояса, сдающие тесты, достигают своих высоких результатов, применяя числовые способности, которые они развили на практике, используя самые острые стратегии. Вы можете изучить выигрышные стратегии, которые могут существенно повлиять на результаты ваших числовых тестов.
Фокус, нервы и концентрация
Для многих из нас худшая часть числового теста — это ожидание заранее. Нервозность и тревога, которые мы можем испытать перед тестовой сессией, могут распространиться на ранние стадии самого теста, влияя на ваше внимание и концентрацию. Вам нужно сохраняйте максимальную концентрацию во время тестовой сессии, чтобы показать себя с лучшей стороны.
Нервы и беспокойство должны быть сведены к минимуму, прежде чем они приведут к ошибкам и падению производительности.
Концентрационные насадки
Вот несколько советов по борьбе с нервозностью и концентрации перед тестовой сессией:
1. И дышать…
Если вы нервничаете, переключите внимание на свое дыхание. Убедитесь, что вы делаете длинные, медленные вдохи и сосредоточьтесь на медленном счете от 10 с каждым вдохом. Каждый раз, когда ваш разум отвлекается от дыхания во время этого обратного отсчета, вы должны осторожно отодвигать отвлекающую мысль в сторону и снова начинать счет с 10. Это упражнение на концентрацию снижает уровень стресса и позволяет частям вашего разума, занятым концентрацией и рассуждениями, направить свою энергию в нужное русло. готов к самому испытанию.
2. Почувствуйте страх и все равно сделайте это
Иногда наши нервы и беспокойство могут вызывать отвлекающие физические и психические симптомы стресса.
Учащенное сердцебиение, потные ладони и мысли, полные болтающих обезьян, — обычные ощущения, связанные со стрессом, которые значительно усложняют достижение концентрации и максимальной производительности. Вместо того, чтобы пытаться бороться с этими чувствами, вы должны использовать «технику принятия и приверженности», чтобы преодолеть их. Успокойте свой разум, двигаясь вокруг своего тела, чтобы заметить, обозначить и принять каждое ощущение, связанное со стрессом, которое вы идентифицируете. Не пытайтесь противодействовать им; просто признать, что они есть. Затем вы должны работать над своим обязательством; напомните себе о своих целях, а затем отрепетируйте, что именно вы собираетесь делать, когда начнется тестовая сессия. Техника принятия и приверженности помогает вам почувствовать страх и все равно сделать это.
Убедившись, что вы сосредоточены и спокойны, вы сможете использовать эффективные стратегии сдачи теста во время самой тестовой сессии, которые дадут вам преимущество.
Наши последние лучшие советы по тестированию числового мышления
Теперь, когда вы лучше разобрались с числовыми тестами на мышление и ключевыми моментами, которые следует учитывать, пришло время перейти к нашим последним советам.
Посмотрите следующее видео или прочитайте приведенный ниже список и усвойте наши последние советы по тестам на числовое мышление. После того, как вы усвоили все наши советы, пора приступать к практике!
Совет 1 по числовому тесту: разберитесь в вопросах
Если вы попрактикуетесь в некоторых психометрических тестах на способности, вы сами увидите, как легко быть уличенным в неправильном прочтении вопроса. Это включает в себя нераспознавание единиц, невидение применимости графика или таблицы (например, дат) и предположения о подразумеваемом значении. Стоит перечитать вопрос после того, как вы ответили на него, чтобы убедиться, что вы его поняли, так как это займет долю секунды, но не позволит вам выбросить время, потраченное на этот вопрос.
Числовой тест Совет 2. Возьмите с собой собственный калькулятор
Если вы проходите тест на числовое мышление в оценочном центре, скорее всего, вам скажут, что вы должны использовать калькулятор, который они вам предоставили. Но на всякий случай возьми свой. Вы будете знакомы со своими функциями, а расположение кнопок будет интуитивно понятным, что позволит вам сэкономить несколько жизненно важных секунд по сравнению с другими кандидатами. Если ваш психометрический тест находится в сети, очевидно, вы можете использовать свой собственный калькулятор.
Числовой тест Совет 3. Знайте свой калькулятор
Если вам разрешено пользоваться собственным калькулятором (часто это не так в центрах оценивания) или вы проходите онлайн-тесты на численное мышление, убедитесь, что ваш калькулятор знаком вам, имеет большие кнопки и четкий экран. Например, не используйте калькулятор на своем мобильном телефоне! Все это поможет сэкономить время и уменьшит вероятность ошибок при вводе калькулятора.
Также убедитесь, что вы знакомы со всеми полезными функциями калькулятора. Численные тесты на рассуждение, с которыми вам придется столкнуться, вероятно, не будут включать длительный статистический анализ и сложные функции. Но как минимум убедитесь, что вы знаете:
- Как использовать скобочную функцию для расчетов, включающих несколько этапов
- Как ввести значения в несколько ячеек памяти и вызвать их
- Пауэрс. Это полезно, например, при расчете сложных процентов за несколько лет.
Численный тест Совет 4. Используйте грубую бумагу
В большинстве психометрических тестов вам будет разрешено использовать грубую бумагу для работы. Разумное использование этого сократит количество ошибок и сэкономит ваше время, если вам придется вернуться к середине расчета. Степень, в которой вы записываете свою работу, очевидно, должна быть сбалансирована с тем, что вы слишком долго отвечаете на каждый вопрос; вы почувствуете, сколько вам нужно записать, когда будете практиковать некоторые тесты на способности для себя.
Записывание вещей также помогает вам обнаружить ошибки с единицами измерения, которые слишком распространены, если вы выполняете всю работу на своем калькуляторе. Иногда работа над одним вопросом потребуется при работе над следующим вопросом, поэтому, если вы уже записали его, вам не нужно повторять эту часть расчета.
Численный тест Совет 5. Учитывайте только доступные варианты
Это относится только к числовым тестам на мышление, поскольку наиболее распространенная форма тестов на вербальное мышление имеет только три варианта; Правда, Ложь и Не могу сказать. В некоторых числовых вопросах вы можете сразу отказаться от некоторых доступных вариантов, используя дедукцию или здравый смысл. В частности, в вопросах соотношения (например, каково соотношение A:B:C:D) вам может не понадобиться вычислять все A, B, C и D. Если вы вычислили A и B и видите, что только один из доступных вариантов – ваш ответ для A: B, затем нажмите на него и двигайтесь дальше! Это хорошая техника экономии времени.
Совет по числовому тесту 6. Распределение времени для решения числового вопроса
Для вопросов на числовые рассуждения бегло просмотрите следующие несколько вопросов, чтобы увидеть, к скольким вопросам относится цифра. Обычно одна цифра применяется к трем или четырем вопросам, и в этом случае стоит потратить время на то, чтобы понять, что говорят вам данные, прежде чем переходить к первому вопросу. Затем по каждому вопросу вы можете вернуться к данным, но, по крайней мере, вы знаете, где искать и на что вы смотрите. Типичным примером распределения времени для набора из трех вопросов может быть:
- 3 секунды сканирования вперед, чтобы увидеть, к скольким вопросам относится цифра;
- 15 секунд на изучение и усвоение графика/таблицы/данных;
- 10 секунд на чтение и понимание первого вопроса;
- 60 секунд, отвечая на вопрос и быстро возвращаясь к данным;
- 10 секунд на чтение и понимание второго вопроса;
- 60 секунд, отвечая на вопрос и быстро возвращаясь к данным;
- 10 секунд на чтение и понимание третьего вопроса;
- 60 секунд, отвечая на вопрос и быстро возвращаясь к данным.
Это примерно три с половиной минуты на ответ на три вопроса, что примерно соответствует типичному набору из трех вопросов на числовое мышление.
Совет 7 по числовому тестированию: графики Financial Times
Важно уметь быстро усваивать и интерпретировать представленные данные, такие как графики, гистограммы и таблицы. Один из способов улучшить свою скорость в тесте на способности — это сократить время, необходимое для усвоения информации, представленной в вопросах числового рассуждения. Вскоре вы обнаружите, что это вторая натура, чтобы проверить, какие оси и в каком масштабе, проверить, был ли перебазирован график или нет, проверить, даны ли числа в других единицах, и проверить, что является оценочной проекцией по сравнению с записанными значениями. .
Все эти вещи помогают вам быстро отвечать на вопросы, связанные с числовыми рассуждениями, и вы можете улучшить свои навыки интерпретации данных, читая новости, основанные на цифрах , например, в The Economist или Financial Times.
Вы также можете использовать данные на страницах этих публикаций, чтобы попрактиковаться в конвертации из одной валюты в другую, что обычно встречается.
Численный тест Совет 8: человеческий фактор
При выполнении вычислений на калькуляторе, например, при суммировании длинного списка чисел, считывайте числа непосредственно с экрана монитора/тестовой бумаги, а не грубую работу. Легко неправильно прочитать ваши каракули. Также он исключает одну возможность человеческой ошибки (неправильное написание чисел на бумаге).
Численный тест Совет 9: проверьте единицы измерения и основания
Широко используемый метод проверки кандидатов — представить, например, таблицу чисел в тысячах. Небрежный тестируемый пропустит это и даст неверный ответ. Неправильный ответ обычно является одним из вариантов, поэтому обязательно регистрируйте всю информацию, представленную в таблицах и графиках. Практика поможет вам научиться искать эти детали.
Числовой тест Совет 10: Процентное увеличение и уменьшение
Одной из наиболее распространенных областей путаницы и источников ошибок в вопросах числового рассуждения является понимание того, как применять процентные вычисления к информации, указанной в вопросе.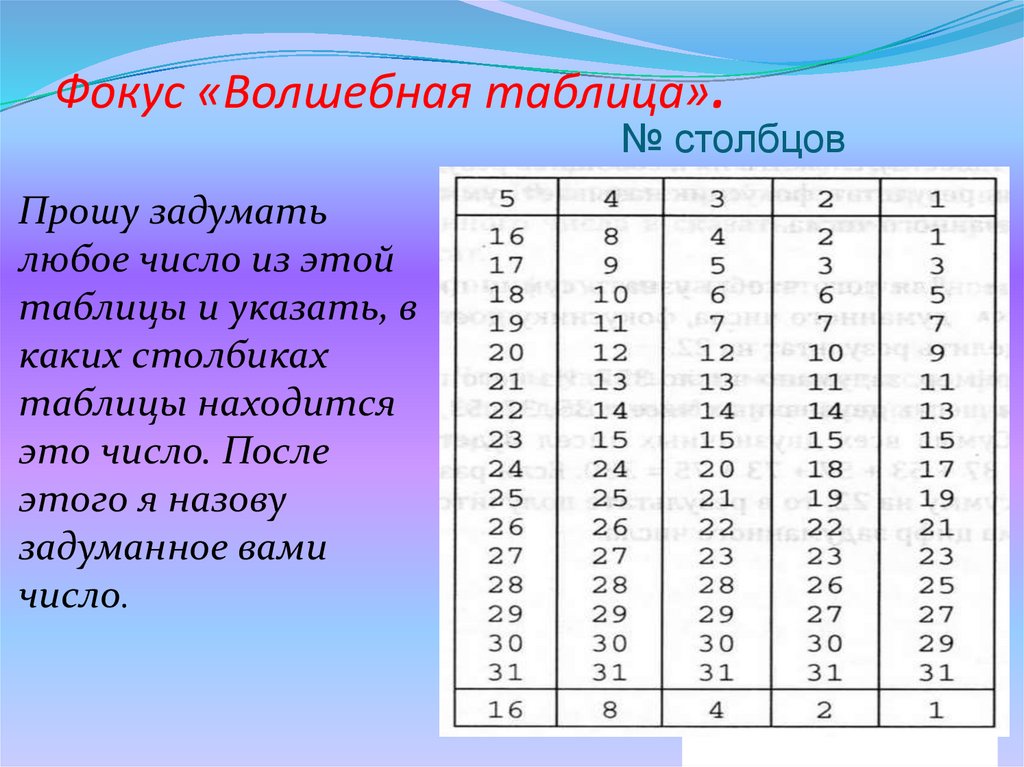
Важно понимать, просят ли вас рассчитать процентное изменение от A до B или от B до A. Это определит, является ли правильным расчет A ÷ B или A x (1-B).
Рассмотрим два примера:
“В 2009 г.объем продаж составил 1000 фунтов стерлингов, что на 10% больше, чем в предыдущем году. Каковы были продажи в 2008 году?”
По существу нам нужно решить следующую задачу: ? х 110% = 1000 фунтов стерлингов. Итак, расчет ? = (1000 фунтов стерлингов ÷ 1,1). Итак, ? = 909,091. Почему не 1000 фунтов стерлингов x 0,9? Потому что это будет уменьшение на 10%, применяемое к 1000 фунтов стерлингов, а не увеличение на 10%, применяемое к неизвестному числу.
Рассмотрим второй подобный вопрос:
“В 2009 году продажи составили 1000 фунтов стерлингов. Если в 2010 году продажи упадут на 10%, каковы будут продажи в 2010 году?”
Так как это уменьшение на 10% от одного числа к другому, мы начинаем со ссылочного числа и умножаем на (100 – 10)%.
Таким образом, во втором примере правильное вычисление равно 1000 фунтов стерлингов x 0,9 = 900 фунтов стерлингов.
Помните: все дело в формулировке вопроса. Понять, что такое начальный номер и понять, что такое конечный номер.
ПРИМЕЧАНИЕ: В наших решениях вы увидите сокращенный способ расчета процентных изменений. Допустим, мы хотим найти процентное изменение от 500 до 600. Длинный способ состоит в том, чтобы найти абсолютную разницу (600 – 500 = 100), а затем разделить на начальное число. Таким образом, у нас будет (100 ÷ 500) х 100 = 20%. Этот расчет на самом деле упрощается до 600 ÷ 500 = 1,2, что, как мы знаем, является увеличением на 20%.
Ознакомьтесь с нашим листом формул теста численного мышления для получения дополнительной информации о формулах, которые вам необходимо знать.
Совет 11 по числовому тестированию. Проведите проверку работоспособности
Потратив драгоценные минуты на понимание графика или таблицы, было бы глупо не потратить пару секунд на проверку своего ответа.
Это не означает повторного выполнения всей работы (это было бы пустой тратой времени), но вам следует потратить несколько секунд на перечитывание вопроса, чтобы убедиться, что вы действительно рассчитали, о чем вас спрашивают, и попытаться оценить диапазон, в котором должен лежать разумный ответ. Это служит быстрой проверкой, чтобы убедиться, что вы не сделали ничего глупого или не ошиблись в своих единицах измерения. И, надеюсь, вы уверенно перейдете к следующему вопросу.
Все равно проверьте смысл, если ваш ответ соответствует одному из вариантов множественного выбора. Дистракторы часто возникают из-за распространенных ошибок.
Числовой тест Совет 12. Используйте калькулятор, который отображает последнюю запись
В вопросах интерпретации данных вам неизбежно придется в какой-то момент сложить (или вычесть, или что-то подобное) большой список записей из таблицы или графика. В этом типе работы с калькулятором очень легко пропустить запись или случайно взять запись из соседнего столбца.
Если вы используете калькулятор, который отображает ваш последний расчет или ввод (все научные калькуляторы делают это), вы можете использовать эту функцию, чтобы проверить, до чего вы дошли, а также проверить, что ваш последний ввод был правильным. Базовые калькуляторы этого не делают.
Этот совет действительно относится только к онлайн-психометрическим тестам, потому что для тех, которые проводятся в центре оценки, вам обычно говорят, что вы должны использовать предоставленный калькулятор.
Теперь пришло время попрактиковаться
Бесплатный тест на числовое мышление 1
БесплатноЭтот бесплатный тест на числовое мышление содержит 12 вопросов и имеет ограничение по времени 12 минут .
Начать тест 1 вопросов PDF Решения PDF
Бесплатный тест на числовое мышление 2
Бесплатно Этот бесплатный тест на числовое мышление содержит 10 вопросов и имеет ограничение по времени 12 минут .
Начать тест 2 вопросов PDF Решения PDF
Дальнейшая практика числовых логических тестов
- 33 реалистичных теста на логическое мышление
- Онлайн и оффлайн практика
- Отслеживайте свой прогресс
Тесты численного мышления
Советы и подсказки по численному мышлению
В GradTests у нас есть куча советов и подсказок, которые помогут вам пройти следующий тест по численному мышлению. Помните, что лучший способ улучшить свой тест на числовое мышление — это практика.
Прямо сейчас вы можете пройти бесплатный тест на числовое мышление здесь. Вы также можете получить немедленный доступ к 150 вопросам численного рассуждения прямо сейчас. Вы можете ознакомиться с нашими общими советами по использованию всех психометрических тестов здесь
Настройте технологию
Для тестов на числовое мышление мы рекомендуем использовать настольный компьютер или ноутбук с клавиатурой, мышью и, в идеале, с дополнительным монитором.
Мышь позволит вам эффективно выбирать ответы. Вместо карманного калькулятора все необходимые расчеты лучше всего делать в Excel. Ввод данных в Excel с помощью клавиатуры будет намного эффективнее и менее рискованно (опечатки легко исправить), чем с помощью калькулятора, и многие вычисления будут более эффективно выполняться в Excel, потому что вы можете копировать формулы вместо повторить тот же расчет. Наконец, использование Excel позволит вам сохранить данные для использования в более позднем вопросе, который иногда необходим.
Выберите наиболее правильный ответ
В числовых тестах на рассуждение может быть несколько вариантов ответа, которые хотя бы частично верны в каком-то смысле. Вы должны выбрать наиболее правильный ответ на каждый вопрос. Мы рассмотрим пример этого ниже в разделе «Остерегайтесь вариантов ответа с подвохом».
Guestimate
Для многих вопросов лучше приблизительно вычислить ответ с помощью вычислений в уме, чем мучиться с поиском точного ответа.
Это будет особенно актуально, когда все варианты ответов сильно отличаются друг от друга. Если они все близки друг к другу, вы действительно не сможете оценить.
Знайте, когда двигаться дальше
Некоторые вопросы предназначены для того, чтобы тратить ваше время. Это обычная ловушка, которую расставляют поставщики тестов. Они дают вам столько расчетов, что на их выполнение уходят минуты. С практикой вы заметите эти вопросы и узнаете, как прагматично с ними справляться. Имейте в виду, что почти все тесты присваивают каждому вопросу одинаковое значение, поэтому тратить слишком много времени на один вопрос неразумно. Если вы заметили вопрос, который, как вы понимаете, потребует много вычислений, постарайтесь исключить все возможные варианты ответа, а затем просто сделайте предположение.
Будьте осторожны с единицами измерения
Часто единицы измерения по осям на графиках отличаются от единиц измерения в вопросе или вариантах ответа. Например, график может быть в милях в час, но ответ должен быть в километрах в час, или таблица может быть в евро, но ответы в фунтах. Этот трюк делается, чтобы проверить ваше внимание к деталям. Вам нужно знать об этом трюке и выполнять любые необходимые преобразования. Следите за правилами конвертации, которые часто напечатаны мелким шрифтом внизу таблицы или даны в вопросе. Например, они могут предложить обменный курс для конвертации между евро и фунтами стерлингов — вы бы не предположили его.
Следите за вариантами ответов с подвохами
Обычно поставщики тестов предлагают как минимум один или два варианта ответов с подвохами. Когда мы говорим о вариантах ответа с подвохом, это ответы, к которым, как они знают, люди придут, когда допустят определенную ошибку. Они стремятся еще раз проверить ваше внимание к деталям, внушая вам ложное чувство безопасности. Вы закончите расчет и найдете значение как один из вариантов ответа, поэтому, естественно, вы думаете, что это правильно. Но это неправильно. Например, предположим, что в вопросе вас просили найти валовую прибыль из таблицы, которая показана в долларах США. Вы вычисляете его правильно и находите, что он равен 500 000 долларов. Вы замечаете это как вариант ответа и выбираете его. Однако один из других вариантов составляет 420 000 евро, и с учетом обменного курса этот ответ имеет то же значение. Вы можете заметить, если внимательно посмотрите, что ответ был запрошен в евро, так что это действительно правильный ответ; если бы вы выбрали ответ в долларах США, вы были бы неправы. Помните, что в тестах на числовое мышление вам необходимо выбрать «самый правильный» ответ.
Сократите варианты ответов
Даже если вам нужно угадать из-за нехватки времени или просто из-за того, что вы не знаете ответа, стоит попытаться сузить варианты. Это значительно повысит ваши шансы угадать правильный ответ. Вы сможете исключить некоторые ответы как явно неправильные, предварительно оценив правильный ответ, или внимательно прочитав вопрос, чтобы увидеть, не соответствует ли какой-либо из вариантов ответа тому, что требуется. Например, как указано выше, если на вопрос требуется ответ в евро, вы можете исключить любые варианты, отличные от евро.
Разберитесь с основами
Фактические математические расчеты, необходимые для хороших результатов в этих тестах, довольно минимальны. Вам не нужно знать продвинутую математику, статистику или что-то в этом роде. Но для математики, которая тестируется, вам нужно понять от и до. Вы должны быть очень эффективными в этом. Единственные настоящие математические навыки, которые вам нужны, это базовая арифметика (сложение, вычитание, умножение и деление), основные показатели степени, процентные изменения, отношения, средние значения и скорости изменения. Убедитесь, что вы на 100 % разбираетесь в этих темах, в том числе в том, как использовать Excel или калькулятор для их расчета. Вы можете пройти бесплатный тест на числовое мышление прямо сейчас, чтобы получить представление о типах вычислений, которые вам нужно будет выполнять, и вы можете отточить любые области, в которых вы слабы.
Следите за сносками таблицы
Иногда в таблице или диаграмме могут быть сноски с важной информацией. Некоторые кандидаты, как правило, пропускают их, потому что они часто набраны мелким шрифтом и немного затемнены. Следите за ними.
Это конец наших советов по тесту на числовое мышление. Теперь пришло время вам заняться своей практикой!
Прямо сейчас вы начнете с бесплатного теста на числовое мышление. После этого вы можете двигаться дальше и разблокировать 150 числовых вопросов с подпиской.
5 проверенных советов для достижения успеха
Готовы пройти тест на числовое мышление? Просто следуйте советам и рекомендациям в этом руководстве. У нас есть все, что вам нужно знать!
В этом бесплатном руководстве по тесту на числовое мышление мы покажем вам:
- 5 обязательных советов о том, как пройти тест на числовое мышление
- 2 ключевых практических примера вопросов
- 12 числовых понятий, рассматриваемых в тесте
Вы Здесь вы можете найти некоторые из лучших адаптированных числовых тестов для практики.
Что такое тест на числовое мышление?
Начнем с основ.
Тест на числовое мышление измеряет вашу способность использовать числа.
Можете ли вы понять числовую информацию, применить правильные математические операции и прийти к правильному ответу?
Хотя это может звучать как тест по математике, числовой тест на рассуждение , а не , используется для оценки ваших математических способностей.
Вместо этого он предназначен для того, чтобы выяснить, можете ли вы интерпретировать и анализировать числовые данные для принятия логических решений.
Работодатели обычно используют тесты на численное мышление как часть процесса отбора на руководящие должности и должности в сфере продаж, а также в отраслях, которые требуют от вас регулярного использования чисел, таких как финансы, банковское дело и бухгалтерский учет.
Эти тесты могут многое рассказать работодателям о том, насколько комфортно вы работаете с числами и данными, как вы понимаете основные математические функции и насколько точны вы в условиях дефицита времени.
Чего ожидать от теста на числовое мышление
Численные тесты на рассуждение предполагают множественный выбор и строго рассчитаны по времени.
Обычно вы можете рассчитывать на то, что у вас будет от 45 секунд до 2 минут на вопрос.
Большинство из этих тестов позволят вам пользоваться калькулятором, ручкой и бумагой.
Вам не придется запоминать какие-либо математические формулы или уравнения или показывать результаты своей работы.
Но вам нужно быть быстрым и точным в определении , какие операции использовать и в каком порядке.
Вопросы могут быть представлены в различных формах, включая диаграммы, таблицы, графики, числовые последовательности и текстовые задачи.
Вам нужно будет уметь интерпретировать числовую информацию в вопросе и выяснить, какую операцию использовать, чтобы найти правильный ответ.
Численные понятия, рассматриваемые в тесте
Сколько математических знаний вам нужно знать, чтобы пройти тест на числовое мышление?
Математика соответствует уровню GCSE и не сложнее, чем в старшей школе.
Так что не беспокойтесь — не будет ни алгебры, ни вычислений.
Тем не менее, многие люди находят эти тесты довольно сложными, особенно если математика не является вашей сильной стороной.
Основные математические концепции, которые вы можете ожидать в тестах на числовые рассуждения, включают в себя:
- Дополнение
- Вычитание
- Умножение
- Дивизион
- Фракции
- Процент
- Ratios9999999999999999999999999999999999999999999999999999999999999999999999999999991111111111111111111111111111111111111111111.0111
- Графики и таблицы
- Преобразование валюты и единиц измерения
- Инфляция
Примеры вопросов теста на числовое мышление
Взгляните на некоторые примеры вопросов числового мышления из JobTestPrep и посмотрите, сможете ли вы выбрать правильный ответ:
Пример вопроса 8 1 Джанет купила пачку Smarties в супермаркете за 2 фунта стерлингов. Люси купила в киоске такую же пачку умников за 2,40 фунта стерлингов. Люси заплатила ____ больше, чем Джанет.
A. 25%
B. 20%
C. 15%
D. 10%
Как решить вопрос 1…
В этом вопросе нужно перевести дроби в проценты.
40p ÷ 200p = 0,2
0,2 x 100 = 20
Попробуем еще.
Пример вопроса 2Вот числовая последовательность, в которой вам нужно выбрать следующее число:
1 | 4 | 4 | 7 | 10 | 16 | ?
Как решить вопрос 2…
Эта числовая последовательность является разновидностью последовательности Фибоначчи, где каждое число равно сумме двух предыдущих чисел минус 1. это видеоруководство «Как пройти тесты на численное мышление» от GradTests. Не забудьте взять ручку и сделать несколько заметок.
Как пройти тест на логическое мышление: 5 советов от профессионалов0479
Как видите, вопросы теста на числовое мышление требуют от вас хорошего понимания основных математических операций и способов их применения.
Итак, лучшее, что вы можете сделать для подготовки к тесту, — убедиться, что вы знакомы и уверены во всех числовых понятиях, перечисленных выше.
Лучше всего начать с освежения знаний по математике на уровне GCSE.
Посетите BBC Skillswise, чтобы получить практические уроки математики, рабочие листы и викторины для всех уровней.
Затем попробуйте свои силы в этих математических тестах GCSE от Maths Quiz, чтобы попрактиковаться в применении основных понятий к тестовым вопросам.
#2: Практикуйтесь как можно больше
Мы имеем в виду не только тренировку ваших общих математических навыков.
Чтобы по-настоящему подготовиться, вы также должны пройти большое количество тренировочных тестов на числовое мышление, которые предназначены для имитации реального опыта тестирования.
Это поможет вам узнать, чего ожидать в плане форматов вопросов и временных ограничений, а также поможет вам лучше управлять своим временем.
Чем больше вы практикуетесь, тем быстрее и точнее вы будете получать результаты!
Здесь вы можете найти рекомендуемые практические тесты.
#3: Не стоит недооценивать ценность ручки и бумаги
Большинство этих тестов позволит вам взять с собой ручку и бумагу, а также калькулятор.
Мы не можем не подчеркнуть:
Держите бумагу рядом с собой во время теста и используйте ее.
Если вы пытаетесь запомнить большое количество цифр и информации в своей голове, это может очень быстро утомить вас.
Вместо этого запишите все важные моменты, когда будете работать над каждым вопросом.
Это поможет вам ничего не пропустить и облегчит поиск информации, если она вам понадобится.
#4: Внимательно прочитайте вопросы
Хотя вы можете чувствовать давление из-за ограничения по времени, важно, чтобы это не мешало вам внимательно читать каждый вопрос.
Ошибки часто делаются из-за неправильного понимания вопроса или спешки и забывания шага вычислений.
Кроме того, многие тесты с множественным выбором будут включать намеренно каверзные вопросы, которые призваны сбить вас с толку, если вы не будете осторожны.
Например, в вопросе может быть предложено найти ответ с точностью до целого числа, но некоторые из возможных ответов будут включать десятичные дроби.
Такого рода вопросы предназначены для проверки того, правильно ли вы читаете информацию и склонны ли вы к обычным ошибкам.
Лучший совет:
Дважды читайте каждый вопрос, делайте пометки о том, что важно, и внимательно изучайте инструкции, чтобы полностью понять, о чем вас спрашивают.
#5: Выспитесь
Это может показаться простым, но правильный ночной сон может означать разницу между сдачей и провалом.
Когда вы работаете в условиях цейтнота, важно иметь ясную голову и сосредоточиться, чтобы получить как можно больше отметок.
Выспитесь 8-10 часов в ночь перед тестом на числовое мышление, убедитесь, что вы хорошо питаетесь и пьете много воды.
Если вы чувствуете себя не лучшим образом, вы не сможете показать себя наилучшим образом. Это действительно так просто.
И наконец: УДАЧИ!
Еще несколько руководств, которые помогут вам добиться успеха…
- Вербальное мышление: тест на вербальное мышление: что нужно знать для прохождения
- Логическое мышление: тест на логическое мышление: полное руководство по прохождению Руководство: 4 секрета успеха UKCAT 2020
- Watson-Glaser: Тест Watson-Glaser: все, что вам нужно знать, чтобы пройти
- Понимание механики: Руководство по тестированию на понимание механики 2020
12 математических приемов, которые помогут вам решать задачи без калькулятора | by Andrew Jamieson
Разработайте это в уме
Photo by Crissy Jarvis на Unsplash1. Дополнение
Первый прием — упростить задачу, разбив ее на более мелкие части. Например, мы можем переписать
567 + 432
= 567 + (400 + 30 + 2)
= 967 + 30 + 2
= 997 + 2
= 999
Переключить
Часто проще работать с добавлением меньшего числа, поэтому вместо 131 + 858 поменяйте местами числа
858 + 131
= 858 + 100
= 989
2. Вычитание
Использование дополнения числа может облегчить вычитание. Дополнение — это разница между исходным числом и круглым числом, скажем, 100, 1000.
Вот несколько примеров с числом и его дополнением по сравнению со 100:
67:33, 45:55, 89:11, 3:97
Обратите внимание, что вторые цифры в сумме составляют 10, а первая цифра в сумме составляет 9.
Вот как это может быть полезно
721– 387
# дополнение 87 равно 13, поэтому мы можем поменять местами 387 с 400 – 13
-> 721 – (400 – 13)
= 321 – -13
= 321 + 13
= 334
Другой метод: чтобы записать большее число, чтобы оно заканчивалось на 99. Тот же пример:
721 -> (699 + 22)Photo by Chris Liverani on Unsplash
= 699 – 387 + 22
= 312 + 22
= 334
умножение:
35 x 11
-> 3 _ 5
-> 3+5 = 8
-> 3 8 5
Если сумма больше 10, добавьте разряд десятков в следующий столбец влево и впишите в ответ цифру единиц. Например, 4+8 = 12, запишите 2 и перенесите 1 в следующий столбец.
48 x 11
-> 4_8
-> 4+8 = 12
-> 4,12,8
-> 528
Процесс немного сложнее для трехзначных и более чисел, но он работает аналогичным образом. На этот раз сохраните первую и последнюю цифру и суммируйте цифры попарно
725 X 11
-> 7__5
-> 7_, (7+2=9), (2+5=7), _5
-> 7975 51973 x 11
-> 5__3
-> 5_,(5+1=6),(1+9=10), (9+7=16), (7+3=10), _3
# где сумма больше десяти, мы перемещаем цифру десятков в следующий столбец
-> 5,(6+1),(0+1),(6+1),(0),3
-> 571703
4.
ДевяткиУмножение на девятки можно упростить, умножив на 10 и вычитание исходного числа
799 x 9
= 799 x (10 -1)
= 7990 – 799
= 7191
. (90–1)
= (70 х 90) + (2 х 90) — 72
= 6300 + 180–72
= 6408
5. Как решать квадраты 92
= 4200 + 25
= 4225
6. Метод сближения
Аналогичный метод работает для умножения близких чисел. Формула работает для всех чисел, но она не упрощается, если числа не похожи.
Вот формула. n — «базовое» число
(n+a)(n+b) = n(n + a + b) + ab
Пример:
47 x 43
= (40 + 7)(40 + 3)
= 40 х (40 + 3 + 7) + (7 х 3)
= (40 х 50) + (7 х 3)
= 2000 + 21
= 2021
В этом примере сумма единиц составляет десять, поэтому наше «базовое» число и множитель — круглые числа (40 и 50).
Вот еще один пример. Уменьшите меньшее число, чтобы получить ближайшее круглое число — наше базовое число, в данном случае 40. Добавьте разницу к большему числу. Умножьте основание и большее число. Наконец, добавьте произведение разницы между исходными числами и базовым числом.
47 х 42
= (40 + 7) х (40 + 2)
= (40 + 7 + 2) х 40 + (7 х 2)
= (49 х 40) + (7 х 2)
= (40 х 40) + (40 х 9) + (7 х 2)
= 1600 + 360 + 14
= 1974
Вы также можете округлить до основного числа. Поскольку исходные числа меньше основания, мы добавляем произведение двух отрицательных чисел.
47 х 42
= (50 х 39) + (-3 х -8)
= (50 х 30) + (50 х 9) + (-3 х -8)
= 1500 + 450 + 24
= 1974
Это работает и для трехзначных чисел. В этом случае основное число находится между нашими числами, поэтому произведение является отрицательным числом.
497 х 504Photo by Sandro Schuh на Unsplash
= (500 - 3) х (500 + 4)
= (500) х (500 + 4 - 3) + (-3 х 4)
= 500 х 501 - 12
= 250 000 + 500 – 12
= 250 488
7.
Упрощение вычисленийВы можете упростить некоторые уравнения еще до того, как начнете. Например, разделить и делитель, и делимое на два.
898 / 4
= 449 / 2
= 224 и ½
Обратите внимание, что при использовании этого метода остаток нужно записать в виде дроби:
898/4 имеет остаток 2 при делении на 4
449/2 имеет остаток 1 при делении на 2
Дробь та же, но абсолютное число другое.
При делении на 5 измените уравнение, умножив на 2. Гораздо проще делить на 10. Например:
1753/5
= 3506 / 10
= 350,6
8. Признак делимости 900
Есть много способов быстро определить, является ли число фактором.
2 : Число четное.
Пример: 28790 четное число, поэтому оно делится на 2.
3 : Сумма цифр делится на 3.
Пример: 1281 -> 1+2+8+1 = 12
-> 12 кратно 3, поэтому 1281 делится на 3
4 : Последние две цифры делятся на 4. Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.
Пример: 1472, 72 делится на 4, поэтому 1472 делится на 4.
5 : Число оканчивается на 5 или 0.
Пример: 575 оканчивается на 5, поэтому оно делится на ноль
6 : Число четное, сумма цифр делится на 3 6 — это 3 x 2, поэтому применяются правила 2 и 3.
Пример: 774 четно и 7+7+4 = 18
-> 18 делится на 3, поэтому 774 делится на 6. заканчивается нулем. Отбросьте последнюю цифру с нулем и повторите процесс. Продолжайте, пока не сможете определить, делится ли результат на 7.Пример: 2702 добавить 98 (7 x 14) -> 2800, отбросить нули
-> 28 кратно 7, поэтому 2702 делится на 7.8 : Последние три цифры делятся на 8
Пример: 79256, 256 делится на 8, поэтому 79256 делится на 8. (Альтернативное правило: если цифра сотен четная , последние 2 цифры делятся на 8, если цифра сотен нечетная , последний 2 цифр + 4 делится на 8)9 : То же правило, что и для 3, но с 9.
Пример: 13671 -> 1+3+6+7+1 = 18
-> 18 делится на 9, поэтому 13671 делится на 910 : Число оканчивается на 0.
Пример: 280 оканчивается на 0, 280 делится на 109 100907 Аналогичное правило до 3 и 9, начните с правой цифры и попеременно вычитайте и добавляйте оставшиеся цифры. Если ответ равен нулю или кратен 11, то число делится на 11.
Пример: 12727 -> 1 - 2 + 7 - 2 + 7 = 11, поэтому 12727 делится на 11.Вы можете ознакомиться с некоторыми дополнительными методами здесь.
9. Деление больших чисел на 9
Пример:
-> 10520/9Напишите первую цифру над уравнением и напишите «R» (для остатка) над последней цифрой. Добавьте число, которое вы только что написали, и число по диагонали ниже и справа от него. Запишите это новое число во втором месте. Добавьте это число к числу по диагонали ниже и справа. Продолжайте этот процесс, пока не дойдете до R.
Суммируйте числа одного цвета, чтобы получить следующую цифру.Наконец, добавьте последнюю цифру к числу под буквой R, чтобы получить остаток.
10520/9
= 1168 R8
или 1168,889Вот еще пример:
-> 57423/9внизу и справа больше десяти (5+7=12). Ставим единицу над первой цифрой и вычитаем девять из него. (Мы делим по основанию девять, поэтому мы вычитаем девять, а не десять). Поместите полученное число на вторую позицию (12–9 = 3). Продолжайте тот же процесс.
В этом примере остаток больше 9 (9+3 = 12). Снова переносим единицу выше предыдущей цифры и вычитаем девять из остатка, оставляя три. Теперь добавьте результат и цифры переноса.
57423 / 9Фото Элисон Панг на Unsplash
= 6380 R3
или 6380,33310. Переверните вопрос
Проценты являются ассоциативными, поэтому иногда изменение порядка вопросов облегчает вычисления.
Пример:
Что составляет 36% от 25
-> равно 25% от 36
-> 25% равно ¼
-> 36/4 = 9
36% от 25 равно 911.
Как вы можете видеть, использование ¼ в последнем примере помогает узнать дроби и то, как они связаны с процентами.
1/2 = 50 %1/3 = 33,33 %, 2/3 = 66,67 %, 1/4 = 25 %, 3/4 = 75 %1/5 = 20 %, 2/5 = 40 % …1 /6 = 16,67%, 5/6 = 83,33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3) 1/7 = 14,2857%, 2/7 = 28,5714% , 3/7 = 42,8571 %, 4/7 = 57,1428 % (обратите внимание на повторяющийся шаблон 0,142857) 1/8 = 12,5 %, 3/8 = 37,5 %, 5/8 = 62,5 %, 7/8 = 87,5 %1 /9= 11,11 %, 2/9 = 22,22 %, 3/9 = 33,33 % … 1/10 = 10 %, 2/10 = 20 % … 1/11 = 9,09 %, 2/11 = 18,18 %, 3/11 = 27,27% …1/12 = 8,33%, 5/12 = 41,67%, 7/12 = 58,33%, 11/12 = 91,67%12. Правило 72
Правило 72 позволяет оценить, сколько лет потребуются инвестиции, чтобы удвоить стоимость при заданном процентном доходе. Он работает путем деления 72 на процент, а ответом является количество лет, которое потребуется, чтобы удвоиться.
2% -> 72/2 = 36, примерно 36 лет, чтобы удвоить
8% -> 72/8 = 9, примерно 9 лет, чтобы удвоитьОбратите внимание, что правило 72 является ориентиром, основанным на натуральном логарифме 2, что дает 0,693.
Существует также правило 114 для утроения инвестиций и правило 144 для учетверения ваших денег.
Я нашел две книги Артура Бенджамина, которые могут быть полезными по этой теме. Многие примеры в этом блоге были вдохновлены этими книгами. Вы можете проверить их здесь.
Магия математики: нахождение x и выяснение почему
Купить Магия математики: нахождение x и выяснение почему на Amazon.com ✓ БЕСПЛАТНАЯ ДОСТАВКА для квалифицированных заказов
www.amazon.com
Пожалуйста, оставьте комментарий, если вы нашли это полезным, или поделитесь другими полезными приемами, с которыми вы столкнулись.
Советы по обучению математике - Восходящие звезды
Что может быть более захватывающим, чем сочетание математики и магии? Они естественные партнеры и идут вместе, как Муравей и Дек, копируют и вставляют, яйца и бекон, клубнику и сливки.
Математические фокусы — малоиспользуемая часть математической жизни, но они представляют собой изобретательный, приятный и увлекательный способ воплотить числа в жизнь. Они способны мотивировать, вдохновлять и удивлять детей, помогать детям понимать математические концепции и развивать свои математические навыки. Дети с удовольствием их исполняют.
Исследование Ричарда Уайзмана показало, что обучение детей магии может повысить их самодисциплину и социальные навыки, а также развить их чувство собственного достоинства, уверенность в себе, эмпатию и взаимодействие. Хотя таланты большинства учителей могут подтолкнуть к преподаванию уроков в стиле Гарри Поттера, они могут научить некоторым простым трюкам, вызывающим вау-фактор.
Исследование профессора Уайзмана показало, что часовой урок изучения магии принес группе от 10 до 12 лет больше пользы, чем их обычные уроки PSHE. Это также повышает их статус игровой площадки!
Вот классический фокус с использованием двоичной арифметики, основы всей компьютерной логики.
Что делать:
Выберите номер, не сообщая мне, но укажите на карту или карты, на которых он появляется.
Я скажу вам номер, который у вас в голове!
Например, если кто-то выбирает цифру 5 и указывает на две карты, на которых она изображена, просто посмотрите в верхний левый угол карт и добавьте цифры (4 +1).
Математические фокусы могут зарядить энергией любой урок математики и вызвать чувство удивления и любопытства к математике. Вы можете представить их как задачи по решению проблем и предложить детям демистифицировать их, чтобы они стали ценными занятиями для развития навыков критического мышления. THOAN, вероятно, проще всего начать с ( TH чернила O f AN умбра).
Поделитесь с детьми следующими 10 трюками и объясните, как они выполняются.
Поощряйте их заниматься с семьей и друзьями, но не забудьте сказать им, что фокусник никогда не раскрывает их секреты!
Уловка 1.
- Выберите целое число от 1 до 10.
- Добавить 2.
- Умножить на 2.
- Вычесть 2.
- Разделить на 2.
- Вычтите исходное число.
- Окончательный ответ каждого будет 1
Уловка 2. Задумайте число
- Выберите число от 1 до 8.
- Умножьте на 2.
- Теперь умножьте на 5.
- Вычесть 5.
- Наконец добавьте 7.
- Первая цифра — это номер, который вы выбрали, а вторая цифра — это число 2.
Уловка 3: Задумайте число
- Задумайте любое число.
- Удвойте число.
- Добавьте 9 к результату.
- Вычесть 3 из результата.
- Разделить результат на 2.
- Вычтите число, с которого начинается первое число.
- Ответ всегда будет 3.
Уловка 4. Задумайте число
- Попросите кого-нибудь выбрать число.
- Добавьте к нему следующее большее число.
- Прибавьте 9 и разделите на 2, а затем вычтите исходное число.
- Ответ будет 5.
Уловка 5. Задумайте число
- Запишите число.
- Добавить 5.
- Умножить на 3.
- Минус 15.
- Разделите на исходное число.
- Добавить 7.
- Ваш ответ 10.
Уловка 6. Задумайте число от 20 до 100
- Выберите число от 20 до 100.
- Теперь сложите свои цифры.
- Теперь вычтите сумму из исходного числа.
- Наконец, сложите цифры нового числа вместе.
- Ваш ответ всегда будет 9
Уловка 7. Задумайте трехзначное число
- Выберите трехзначное число, состоящее из трех разных цифр.
- Теперь поменяйте местами цифры, чтобы получить новое число.
- Теперь у вас есть два числа. Вычесть меньшее число из большего числа.
- Теперь сложите цифры результата.
- Ответ всегда будет 18
Уловка 8: придумайте трехзначное число
- Выберите трехзначное число, все три цифры которого различны.
- Переверните цифры и вычтите, чтобы получить еще одно трехзначное число.
- Переверните цифры разницы и добавьте их к разнице.
- Ваша сумма будет 1089.
Например, начните с 845. Тогда 845 – 548 = 29.7 и 297 + 792 = 1089.
Уловка 9: Выберите число от 1 до 14
- Попросите кого-нибудь придумать число от 1 до 14.
- Посмотрите на 5 карточек ниже и попросите их указать на карточку, на которой изображен их секретный номер.
- Чтобы выяснить, какой у них секретный номер, посмотрите на центральный номер на выбранной(ых) карте(ах) и сложите их вместе.
- Например, если они выберут 10, то укажут на карточки 2, 3 и 5. Если посмотреть на центральные числа на этих карточках, получится 2 + 3 + 5 = 10
| 12 | 6 | 11 |
| 1 | ||
| 13 | 7 | 8 |
| 11 | 9 | 10 |
| 2 | ||
| 12 | 7 | 14 |
| 13 | 9 | 10 |
| 3 | ||
| 11 | 8 | 14 |
| 13 | 9 | 12 |
| 4 | ||
| 14 | 7 | 8 |
| 12 | 6 | 11 |
| 5 | ||
| 14 | 10 | 13 |
Уловка 10: Dicey
- Попросите кого-нибудь бросить два кубика, не сообщая вам выпавшие числа, например. 4 и 6.
- Попросите их умножить число на первом кубике на 2 (4 x 2 = 8).
- Прибавьте 5 (8 + 5 = 13).
- Умножить на 5 (13 х 5 = 65).
- Добавьте число на втором кубике (65 + 6 = 71).
- Теперь вы можете предсказать числа на двух кубиках, вычитая 25 (71 - 25 = 46).
- 4 = первая матрица и 6 = вторая матрица.
Так же, как у каждого учителя должна быть наготове коллекция анекдотов, у каждого учителя должна быть в рукаве коллекция математических фокусов, чтобы показать их детям.
Поощряйте детей практиковать и персонализировать пару трюков с партнером по математике, превращая их в представление перед небольшой группой; добавьте к этому немного театрализованного представления по мере роста уверенности.
В рамках общего занятия попросите детей взять на себя роль математика-волшебника, готового поразить всех чудесной памятью и завораживающим математическим волшебством!
Джон Дабелл — учитель с более чем 20-летним опытом преподавания на всех ключевых этапах.