Архимед. Архимед кучу
И.Арабаев атындагы Кыргыз мамлекеттик университети.
Жаңы Маалыматтык Технологиялар Иниститутту:
План конспект
Класс 7-класс.
Тема:Архимед күчү, Архимед күчүн эсептөө жолу.
Мугалим: Күлчоро кызы Света
Бишкек 2015.
Сабактын темасы:Архимед күчү, Архимед күчүн эсептөө жолу.
Өтүү мөөнөтү: 45-мүнөт.
Класс : 7-класс
Сабактын максаты: Билим берүүчүлүк.
А) Окуучуларга Архимед күчү боюнча кеңири маалымат берүү жана жеткиликтүү түшүндүрүү.
Б) Архимед күчү боюнча турмуштан мисал келтирүү.
В) Окуучуларды терең ой жүгүртүүгө тарбиялоо.
Сабактын тиби: Жаңы материялды түшүндүрүү.
Сабактын ыкмасы:Стандарттык сабак.
Сабактын формасы: Көрсөтмөлүү.
Сабактын жабдылышы: Доска, маркер, батманга тартылган сүрөт.
Сабактын жүрүшү: Жагымдуу жагдай 2 мин Кайталоо 7-8 мин
Жаңы теманы түшүндүрүү 20-25 мин
Бышыктоо 5 мин
Окуучулардын билимин баалоо. 2-3 мин
Үйгө тапшырма. 1 мин
Жоктоо үйгө берилген тапшырманы текшерүү,
Жаңы теманы өтүү.
Алардын сабака болгон кызыгуусун арттыруу.
Үй тапшырманы текшерүү: Ийри сызыктуу кыймыл деп кандай кыймылды айтат экенбиз? Айлануу мезгили деген эмне экен? Айлануу жыштыгы деген эмне? Бир калптпгы кыймыл деп кандай кыймылды айтабыз?
Архимед күчү: Биздин заманга чейин 260-жылы Сиракуз (байыркы Грециядагы шаар мамлекет) падышасы Гиерон өзүнө алтын таажы жасаган устанын ак ниет иштегенин текшерүү максатында Архимедге тапшырма берет.
Демек суютука матырылган нерсеге төмөнтөн жогору карай түртүү күчү аракет этсе бул күч Архимед күчү деп аталат. Архимед күчү төмөндөн жогору карай багытталган. Башка күчтөрдө күч нерсенин салмагына жогорудан төмөн карай аракет этсе. Архимед күчү нерсенин салмагына төмөндөн жогору карай аракет эткен күч болуп саналат экен. Биз Архимед күчүн -тамгасы менен белгилейт экенбиз.
Архимед күчүн эсептөө жолу: Архимед күчүнүн формуласы . Мында: g- эркин түшүүнүш ылдамдануусу.
– болсо суюктуктун тыгыздыгы ал эми
– болсо суюктукка матырылган нерсенин көлөмү.
Ошентип суюктукка матырылган нерсеге карама-каршы багытталган эки күч таасир этет. 1) Төмөн карай багытталган оордук күчү.
1) Төмөн карай багытталган оордук күчү.
2)Жогору карай багытталган Архимед күчү.
№1 Эсеп Көлөмү 0,28 болгон кирпичти сууга салышты. Ага карата аткарган күчеүн чоңдугун тапкыла?
Берилди: формула Чыгаруу
V 1000 кг/ * =2470Н
ρ =1000кг/ Жообу: 2470Н
-?
№2 Жыгачтан жасалган оюнчук кайыкты суунун үстүнө койгондо ал калкып калды. Эгерде кеменин жалпы көлөмү болжол менен 0,15 болсо анда ага суу тарабынан аракет эткен Архимед күчүн тапкыла?
Берилди Формула Чыгаруу
v=0,15 1000 кг/ *0,15 =1470Н ρ=1000кг/
-? Жообу: 1470Н
1)Архимед кайсыл өлкөнүн окмуштуусу болгон?
2)Архимед законунун аныктамасын айтып бергиле?
3)Архимед күчүнүн башка күчтөрдөн айырмысы?
4)Архимед б. з.ч канчанчы жылдары жашаган?
з.ч канчанчы жылдары жашаган?
5)Архимед күчүнүн формуласын жазып бергиле?
6)Арчимед күчүнө турмуштан мисал келтиргиле?
7)Архимеддин ачылыш жасоосуна түрткү берген окуя?
Архимедова сила сообщение. Закон Архимеда: определение и формула
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды.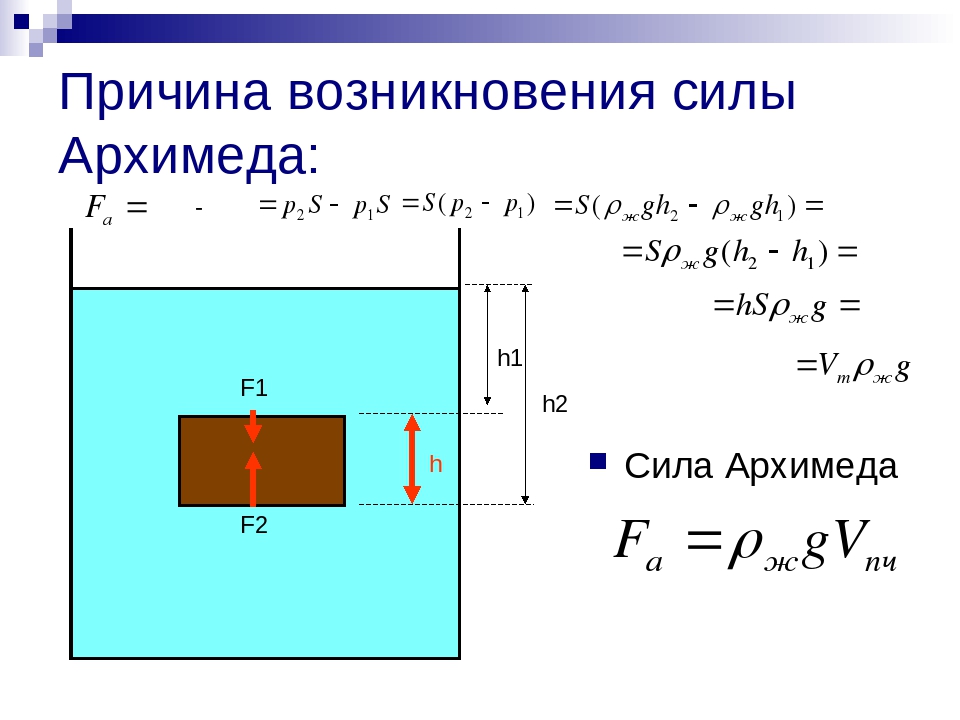
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам – очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.
В интегральной форме
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами
В формуле мы использовали.
ЗАКОН АРХИМЕДА –закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну.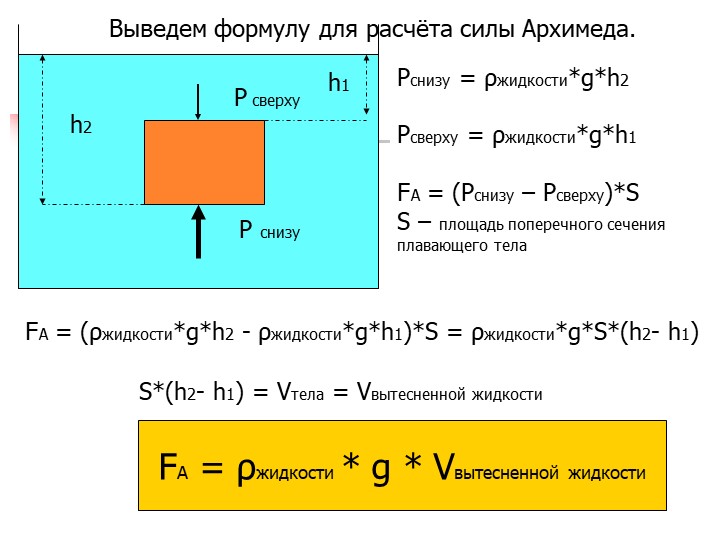 Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
1).
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.
Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, r – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно
r · g · h = p 1
а на нижнюю
r · g (h+a ) = p 2
Сила давления равна давлению, умноженному на площадь, т. е.
е.
F 1 = p 1 · a \up122, F 2 = p 2 · a \up122 , где a – ребро кубика,
причем сила F 1 направлена вниз, а сила F 2 – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F 1 и F 2 и определяется их разностью, которая и является выталкивающей силой:
F 2 – F 1 =r · g · (h+a ) a \up122 – r gha ·a 2 = pga 2
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F 2 – F 1 = pga 3 равна объему тела (кубика) a 3 , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед , один из величайших ученых Земли.
Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V , то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V . Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V , т.е. pgV .
Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g , т.е. веса единицы объема вещества: g = pg ; если принять, что для воды g = 1 , то сплошное тело из вещества, у которого g > 1 утонет, а при g g = 1 тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Владимир Кузнецов
Цели урока: убедиться в существовании
выталкивающей силы, осознать причины её
возникновения и вывести правила для её
вычисления, содействовать формированию
мировоззренческой идеи познаваемости явлений и
свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н.э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал
закон, впоследствии названный законом Архимеда.
Существует предание, что идея этого закона
посетила Архимеда, когда он принимал ванну, с
возгласом “Эврика!” он выскочил из ванны и нагим
побежал записывать пришедшую к нему научную
истину. Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса
жидкости или газа.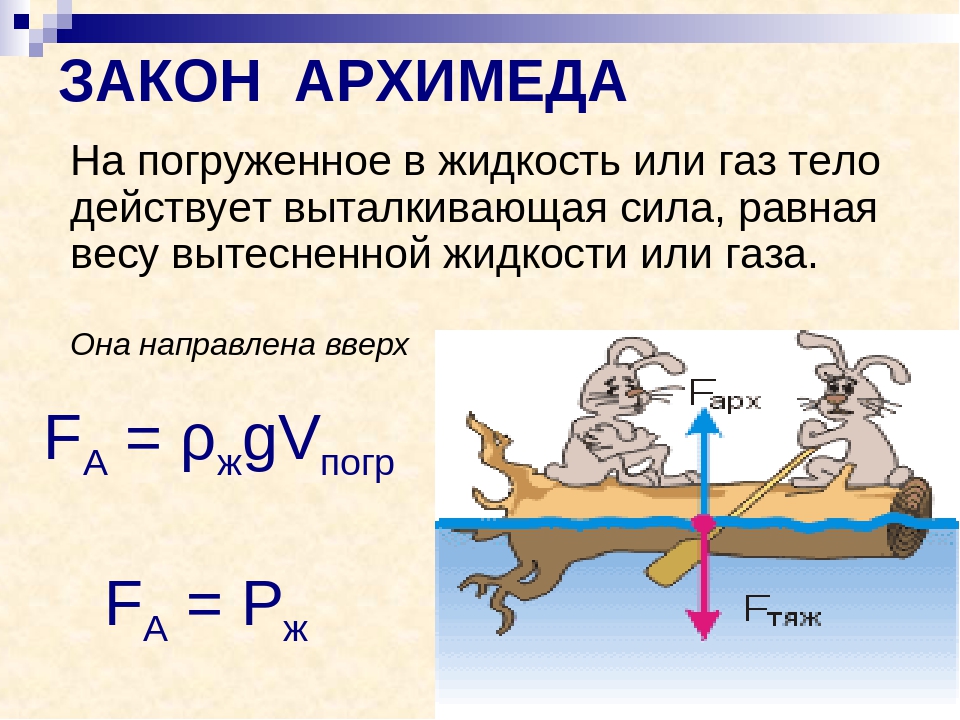 Следовательно, разность сил
равна весу вытесненной телом жидкости:
Следовательно, разность сил
равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны жидкости, направлена по вертикали вверх, приложена к центру тяжести вытесненного объема жидкости. Тело движется в направлении, перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не
отличается от плотности воды, поэтому прочные
скелеты им не нужны! Рыбы регулируют глубину
погружения, меняя среднюю плотность своего тела.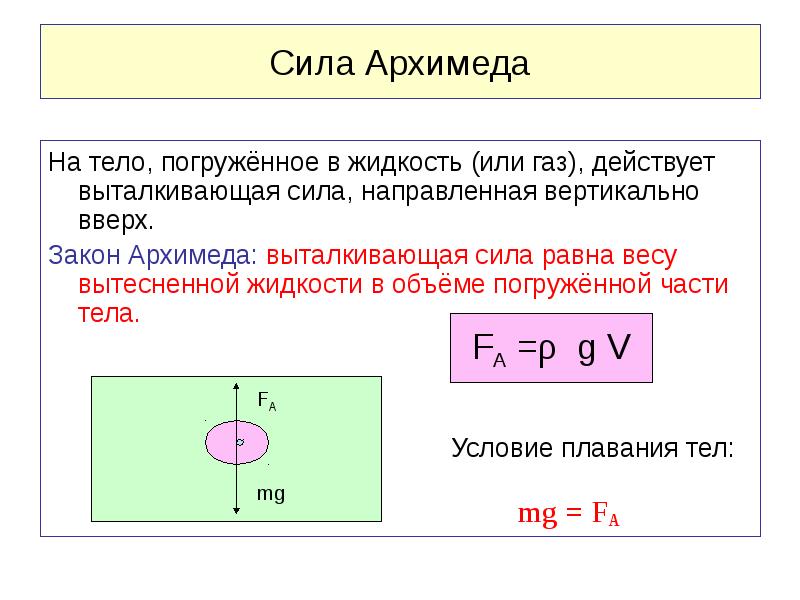 Для этого им необходимо лишь изменить объем
плавательного пузыря, сокращая или расслабляя
мышцы.
Для этого им необходимо лишь изменить объем
плавательного пузыря, сокращая или расслабляя
мышцы.
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает
статической устойчивостью, во втором случае
устойчивость отсутствует. Устойчивость тела
зависит от взаимного расположения центра
тяжести тела Т и метацентра М (точки
пересечения линии действия архимедовой силы при
крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.
Выталкивающая сила
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н. э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в
Сиракузах, осажденных римским флотом и войском.
Шла 2-я Пуническая война. И великий ученый, не
жалея сил, организовывает инженерную оборону
родного города. Он построил множество
удивительных боевых машин, топивших вражеские
корабли, разносивших их в щепы, уничтожавших
солдат. Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины
погружения тела и приводит к появлению
выталкивающей силы, действующей на тело и
направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
р1 = ж*g*h2,
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
р2= ж*g*h3,
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом
в трактате “О плавающих телах”. Архимед
писал: “тела более тяжелые, чем жидкость,
опущенные в эту жидкость, будут опускаться пока
не дойдут до самого низа, и в жидкости станут
легче на величину веса жидкости в объеме, равном
объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
PА= mтg – mж g = g (mт – mж )
Таким образам, если тело погружено в жидкость
(или газ), то оно теряет в своём весе столько,
сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
| № | Сила тяжести в воздухе F1 | Сила тяжести в чистой воде F2 | Сила тяжести в соленой воде F3 | Сила Архимеда FА1 = F1 – F2 FА2 = F1 – F3 |
Сделать вывод как зависит сила Архимеда от
плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны жидкости, направлена по вертикали вверх, приложена к центру тяжести вытесненного объема жидкости. Тело движется в направлении, перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и силы Архимеда FA, которые действуют на это тело. Возможны следующие три случая:
- Fт > FA — тело тонет;
- Fт = FA — тело плавает в жидкости или газе;
- Fт < FA — тело всплывает до тех
пор, пока не начнет плавать.

Другая формулировка (где Pt — плотность тела, Ps — плотность среды, в которую оно погружено):
- Pt > Ps — тело тонет;
- Pt = Ps — тело плавает в жидкости или газе;
- Pt < Ps — тело всплывает до тех пор, пока не начнет плавать.
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести
тела G проходит через центр
тяжести K (центр водоизмещения)
вытесненного объема жидкости. В нормальном
положении плавающего тела центр тяжести
тела Т и центр
водоизмещения K размещены по одной
вертикали, называемой осью плаванья.
В нормальном
положении плавающего тела центр тяжести
тела Т и центр
водоизмещения K размещены по одной
вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.
Дирижабль является летательным
аппаратом легче воздуха и “плавает” в воздухе
за счет архимедовых
сил, если его средняя плотность меньше или равна
плотности атмосферы. Обычно оболочка
классического дирижабля наполняется газом легче
воздуха (водородом, гелием или метаном), при этом
грузоподъёмность дирижабля пропорциональна
внутреннему объёму оболочки с учётом массы
конструкции. Дирижабль – управляемый
летательный аппарат. Перемещение его по
горизонтали осуществляется с помощью
двигателей.
Обычно оболочка
классического дирижабля наполняется газом легче
воздуха (водородом, гелием или метаном), при этом
грузоподъёмность дирижабля пропорциональна
внутреннему объёму оболочки с учётом массы
конструкции. Дирижабль – управляемый
летательный аппарат. Перемещение его по
горизонтали осуществляется с помощью
двигателей.
Ареометры служат для определения плотности жидкости по глубине погружения поплавка. Градуировка производится эмпирически в зависимости от области применения. Измерители кислотности дают процент кислоты, лактометры – процент содержания жира.
Закрепление, тест и домашнее задание
Презентация
Закон Архимеда: вытеснение жидкости погруженным телом
Закон Архимеда — один из первых физических законов, изучаемых учениками средней школы.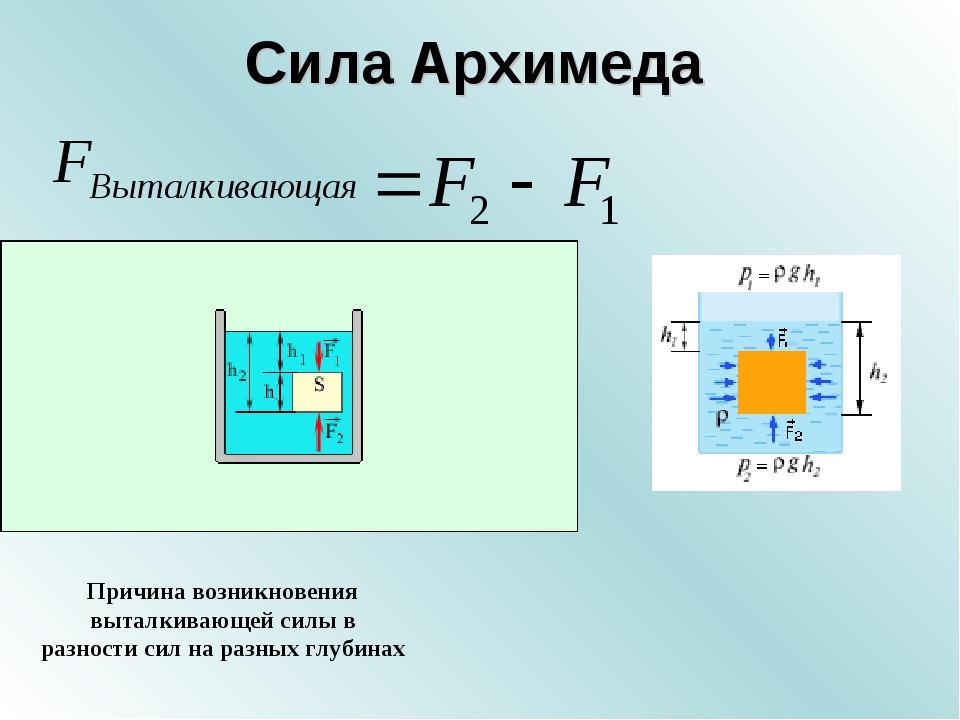 Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, которые могли позабыться.
Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу — и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов — только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще — сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него — они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства — они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него — они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства — они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Похожие статьи
Открытая Математика. Алгебра. Архимед
Архимед (Aρξιμηδηζ; около 287–212 до н. э.), древнегреческий учёный, математик и механик. Развил методы нахождения площадей поверхностей и объёмов различных фигур и тел. Его математические работы намного опередили своё время и были правильно оценены только в эпоху создания дифференциального и интегрального исчислений. Архимед – пионер математической физики. Математика в его работах систематически применяется к исследованию задач естествознания и техники. Архимед – один из создателей механики как науки. Ему принадлежат различные технические изобретения.
Архимед – один из создателей механики как науки. Ему принадлежат различные технические изобретения.
Архимед родился в Сиракузах (Сицилия) и жил в этом городе в эпоху первой и второй Пунических войн. Предполагают, что он был сыном астронома Фидия. Научную деятельность начал как механик и техник. Архимед совершил поездку в Египет и сблизился с александрийскими учёными, в том числе с Кононом и Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. Архимед был близок к сиракузскому царю Гиерону II.
Его работы показывают, что он был прекрасно знаком с математикой и астрономией своего времени, и поражают глубиной проникновения в сущность рассматриваемых задач. Ряд работ имеет вид посланий к друзьям и коллегам. Иногда Архимед предварительно сообщал им без доказательств свои открытия, с тонкой иронией добавляя несколько неверных предложений.
В IX–XI веках работы Архимеда переводились на арабский язык, в XIII веке они появляются в Западной Европе в латинском переводе.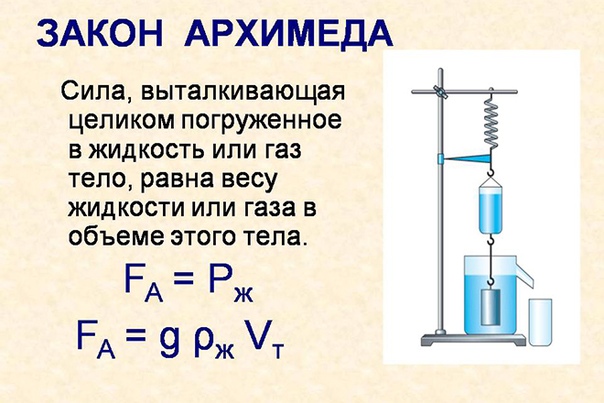 Первое издание отдельных трудов Архимеда на русском языке относится к 1823 году. Некоторые работы до нас не дошли.
Первое издание отдельных трудов Архимеда на русском языке относится к 1823 году. Некоторые работы до нас не дошли.
Центральной темой математических работ Архимеда являются задачи на нахождение площадей поверхностей и объёмов. Рассмотрение Архимедом двусторонних оценок погрешности при проведении интеграционных процессов позволяет считать его предшественником не только И. Ньютона и Г. Лейбница, но и Г. Римана. Архимед вычислил площадь эллипса, параболического сегмента, нашёл площадь поверхности конуса и шара, объём шара и сферического сегмента, а также различных тел вращения и их сегментов.
Архимед исследовал свойства т. н. архимедовой спирали. Дал построение касательной к этой спирали, нашёл площадь её витка. В ходе своих исследований он нашёл сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым примером появления в математике бесконечного ряда. При исследовании одной задачи, сводящейся к кубическому уравнению, Архимед выяснил роль характеристики, которая позже получила название дискриминанта. Ученому принадлежит формула для определения площади треугольника через 3 его стороны (традиционно именуемая формулой Герона). Архимед дал (не вполне исчерпывающую) теорию полуправильных выпуклых многогранников (архимедовы тела). Особое значение имеет аксиома Архимеда: из неравных отрезков меньший, будучи повторен достаточное число раз, превзойдёт больший. Эта аксиома определяет т. н. архимедовскую упорядоченность, которая играет важную роль в современной математике. Архимед построил счисление, позволяющее записывать и называть весьма большие числа. Он с большой точностью вычислил значение числа π и указал пределы погрешности:
Ученому принадлежит формула для определения площади треугольника через 3 его стороны (традиционно именуемая формулой Герона). Архимед дал (не вполне исчерпывающую) теорию полуправильных выпуклых многогранников (архимедовы тела). Особое значение имеет аксиома Архимеда: из неравных отрезков меньший, будучи повторен достаточное число раз, превзойдёт больший. Эта аксиома определяет т. н. архимедовскую упорядоченность, которая играет важную роль в современной математике. Архимед построил счисление, позволяющее записывать и называть весьма большие числа. Он с большой точностью вычислил значение числа π и указал пределы погрешности:
Из работ по физике учёному принадлежат определение понятия центра тяжести тела, математический вывод законов рычага (ему приписывают гордую фразу: «Дай мне, где стать, и я сдвину Землю(в т.ч. знаменитый»), вывод основ гидростатики (в т.ч. знаменитый закон Архимеда), исследование равновесия плавающих тел. При этом он выделяет устойчивые положения равновесия.
Архимед изобрёл водоподъёмный механизм (т. н. архимедов винт), который явился прообразом корабельных, а также воздушных винтов. Рассказывают, что Архимед нашёл решение задачи об определении количества золота и серебра в жертвенной короне Гиерона, когда садился в ванну, и нагим побежал домой с криком «эврика!» («нашёл!»).
Архимед занимался также астрономией. Он сконструировал прибор для определения видимого (углового) диаметра Солнца и нашёл значение этого угла с поразительной точностью. При этом он вводил поправку на размер зрачка. Ученый также построил небесную сферу – механический прибор, на котором можно было наблюдать движения планет, фазы Луны, солнечные и лунные затмения.
Во время 2-й Пунической войны ученый организовал инженерную оборону Сиракуз от римских войск. Его военные машины заставили римлян отказаться от попыток взять город штурмом и вынудили их перейти к длительной осаде. При взятии города войсками Марцелла Архимед был убит римским солдатом, которого, по преданию, встретил словами «не трогай моих чертежей». На могиле ученого был поставлен памятник с изображением шара и описанного около него цилиндра. Эпитафия указывала, что объёмы этих тел относятся, как 2:3 – открытие Архимеда, которое он особенно ценил.
На могиле ученого был поставлен памятник с изображением шара и описанного около него цилиндра. Эпитафия указывала, что объёмы этих тел относятся, как 2:3 – открытие Архимеда, которое он особенно ценил.
Сила Архимеда | Компьютерная графика
Закон Архимеда — это закон статики жидкостей и газов, согласно которому на тело, погруженное в жидкость (или газ), действует выталкивающая сила (сила Архимеда), равная весу вытесненной этим телом жидкости (или газа).
Fа = ρgV,
где ρ — плотность жидкости (газа),
g — ускорение свободного падения,
V — объем погруженного тела (или объем той части тела, которую погрузили в жидкость (или газ)).
Архимедова сила направлена всегда противоположно силе тяжести. Она равна нулю, если погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Следует помнить, что в состоянии невесомости закон Архимеда не работает.
Условия плавания тел в жидкостях и газах.
Fт — сила тяжести, Fа — сила Архимеда.
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы (или иначе силы Архимеда), действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме. Величина Архимедовой силы определяется по закону Архимеда.
Fa=pжgVT
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит …. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
FA=mжg=Pж
ИНТЕРЕСНО, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
определение и формула. Применение закона Архимеда
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела.
Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытесняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к нашим специалистам . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе.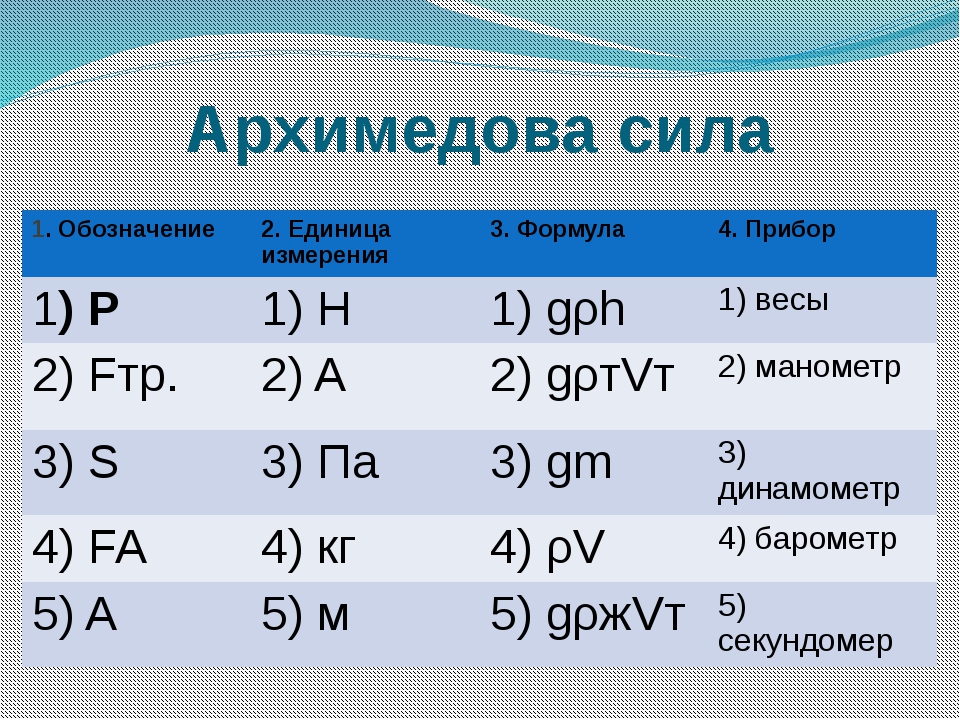 Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Задачи:
Изучить историю открытия архимедовой силы;
Изучить учебную литературу по вопросу действия архимедовой силы;
Выработать навыки проведения самостоятельного эксперимента;
Доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
Исследовательские;
Расчетные;
Информационного поиска;
Наблюдений
1.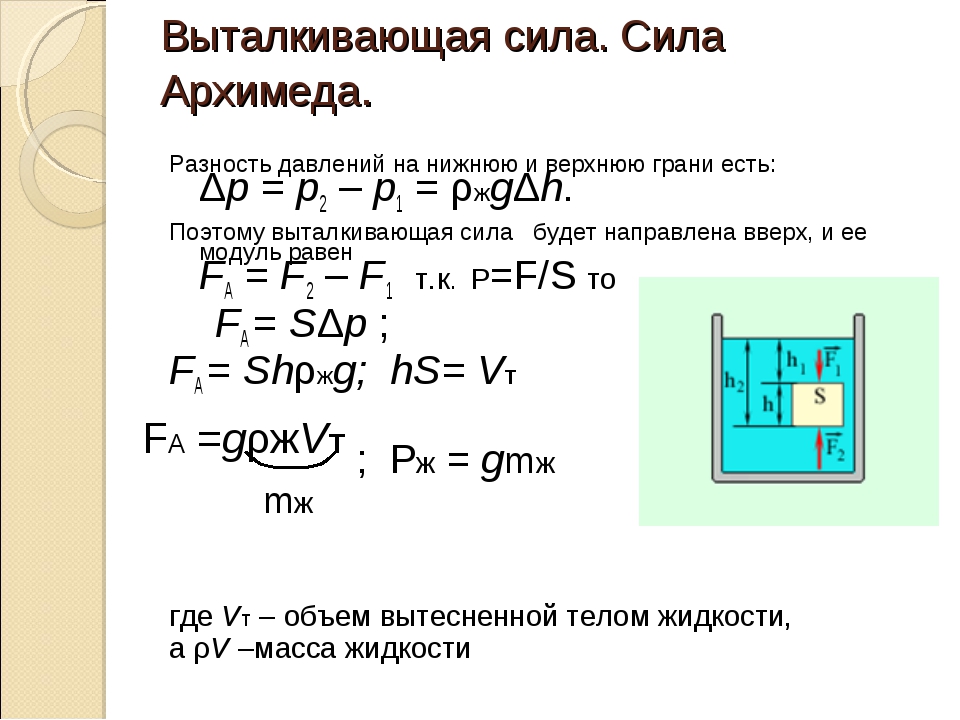 Открытие силы Архимеда
Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон – царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда :
,
где – плотность жидкости (газа), – ускорение свободного падения, – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3)
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
Вода чистая;
Вода, насыщенная солью;
Подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло – «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом – яйцо опустилось на дно (приложение 4).
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
Вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ 1 , а затем – при погружении в воду ℓ 2 . После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ 1 до уровня ℓ 2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. – книга 1. – Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. – книга 2.- Екатеринбург.: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. – 16-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы / или иначе силы Архимеда /, действующей на любое тело, погруженное в жидкость или газ.
Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Величина Архимедовой силы определяется по закону Архимеда.
Закон назван в честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки. Скорее всего вы уже знаете легенду о том, как Архимед открыл свой закон: “Вызвал его однажды сиракузский царь Гиерон и говорит…. А что было дальше? …
Закон Архимеда, впервые был упомянут им в трактате ” О плавающих телах”. Архимед писал: ” тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Еще одна формула для определения Архимедовой силы:
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
ВЕС ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ (ИЛИ ГАЗ)
Вес тела в вакууме Pо=mg .
Если тело погружено в жидкость или газ,
то P = Pо – Fа = Ро – Pж
Вес тела, погруженного в жидкость или газ, уменьшается на величину выталкивающей силы, действующей на тело.
Или иначе:
Тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость.
КНИЖНАЯ ПОЛКА
ОКАЗЫВАЕТСЯ
Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.
ЗАКОН АРХИМЕДА –закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.
Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, r – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно
r · g · h = p 1
а на нижнюю
r · g (h+a ) = p 2
Сила давления равна давлению, умноженному на площадь, т.е.
F 1 = p 1 · a \up122, F 2 = p 2 · a \up122 , где a – ребро кубика,
причем сила F 1 направлена вниз, а сила F 2 – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F 1 и F 2 и определяется их разностью, которая и является выталкивающей силой:
F 2 – F 1 =r · g · (h+a ) a \up122 – r gha ·a 2 = pga 2
Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F 2 – F 1 = pga 3 равна объему тела (кубика) a 3 , умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед , один из величайших ученых Земли.
Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V , то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V . Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V , т.е. pgV .
Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V , можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.
Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g , т.е. веса единицы объема вещества: g = pg ; если принять, что для воды g = 1 , то сплошное тело из вещества, у которого g > 1 утонет, а при g g = 1 тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).
Владимир Кузнецов
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
11.7: Принцип Архимеда – Physics LibreTexts
Цели обучения
К концу этого раздела вы сможете:
- Определите выталкивающую силу.
- Государственный принцип Архимеда.
- Понять, почему предметы плавают или тонут.
- Поймите взаимосвязь между плотностью и принципом Архимеда.
Когда вы встаете из теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки со стороны воды.Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары (Рисунок \ (\ PageIndex {1} \))?
Рисунок \ (\ PageIndex {1} \): (a) Даже тонущие объекты, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (Фото: ВМС союзников) (c) Воздушные шары, наполненные гелием, тянут вверх свои струны, демонстрируя плавучесть воздуха.(кредит: Crystl)Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта. На любой объект в любой жидкости действует направленная вверх или выталкивающая сила (Рисунок \ (\ PageIndex {2} \)). Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет.Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.
Определение: плавучесть
Выталкивающая сила – это чистая направленная вверх сила на любой объект в любой жидкости.
Рисунок \ (\ PageIndex {2} \): Давление из-за веса жидкости увеличивается с глубиной, поскольку \ (P = h \ rho g \). Это давление и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра.Их отличие – подъемная сила \ (F_B \). (Горизонтальные силы отменяются.)Насколько велика эта подъемная сила? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на рисунке \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \): (a) Объект, погруженный в жидкость, испытывает выталкивающую силу \ (F_B \). Если \ (F_B \) больше веса объекта, объект поднимется. Если \ (F_B \) меньше веса объекта, объект утонет.(b) Если объект удален, он заменяется жидкостью, имеющей вес \ (w_ {fl} \). Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости. То есть \ (F_B = w_ {fl} \), утверждение принципа Архимеда.Пространство, которое он занимало, заполнено жидкостью, имеющей вес \ (w_ {fl} \). Этот вес поддерживается окружающей жидкостью, поэтому подъемная сила должна равняться \ (w_ {fl} \), весу жидкости, вытесняемой объектом. Это дань гению греческого математика и изобретателя Архимеда (ок.287–212 до н. Э.), Что он сформулировал этот принцип задолго до того, как концепции силы утвердились. Проще говоря, принцип Архимеда заключается в следующем: подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет. В форме уравнения принцип Архимеда –
.\ [F_B = w_ {fl}, \]
где \ (F_B \) – подъемная сила, а \ (w_ {fl} \) – вес жидкости, вытесняемой объектом. Принцип Архимеда справедлив в целом для любого объекта в любой жидкости, частично или полностью погруженной в воду.
Принцип Архимеда
Согласно этому принципу выталкивающая сила, действующая на объект, равна весу жидкости, которую он вытесняет. В форме уравнения принцип Архимеда выглядит так: \ [F_B = w_ {fl}, \], где \ (F_B \) – подъемная сила, а \ (w_ {fl} \) – вес жидкости, вытесняемой объектом.
Humm… Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны обеспечивать преимущества плавучести.Как вы думаете, можно ли проверить это правило?
Установление связей: расследование на вынос
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и опустите в воду. Тонет? Почему или почему нет? Вы можете заставить его утонуть?
Плавучие и тонущие
Бросьте кусок глины в воду. Он утонет. Затем вылепите из глины форму лодки, и она будет плавать. Благодаря своей форме лодка вытесняет больше воды, чем комок, и испытывает большую выталкивающую силу.3 \) воды?
Стратегия для (а)
Чтобы найти подъемную силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, указанные в [ссылка]. Отметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Как только мы узнаем объем воды, мы сможем найти ее массу и вес.
Решение для (а)
Сначала мы используем определение плотности \ (\ rho = \ frac {m} {V} \), чтобы найти объем стали, а затем подставляем значения массы и плотности.7 \, Н \),
, что намного превышает выталкивающую силу, поэтому сталь останется под водой. Обратите внимание, что подъемная сила округляется до двух цифр, потому что плотность стали дается только до двух цифр.
Стратегия для (б)
Здесь указан максимальный объем воды, который может вытеснить стальная лодка. Подъемная сила – это вес этого объема воды.
Решение для (b)
Масса вытесненной воды находится из ее отношения к плотности и объему, оба из которых известны.8 \, N. \]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, что означает, что судно может нести груз, в девять раз превышающий его собственный вес, без утопления.
Установление связей: расследование на вынос
- Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Используйте кусок фольги размером 10 на 15 см. а) Какова масса этого количества фольги? (b) Если фольга сложена с четырех сторон, и к этой «лодке» добавлены скрепки или шайбы, то какая форма лодки позволит ей удерживать больше «груза» при погружении в воду? Проверьте свое предсказание.
Плотность и принцип Архимеда
Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта – это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше, чем у окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, выталкивающая сила, равная весу вытесняемой жидкости, превышает вес объекта.Точно так же утонет предмет, более плотный, чем жидкость.
Степень погружения плавающего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке \ (\ PageIndex {4} \), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же самым загруженным кораблем. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или
.\ [фракция \, погруженная = \ dfrac {V_ {sub}} {V_ {obj}} = \ dfrac {V_ {fl}} {V_ {obj}}.\]
Погруженный объем равен объему вытесненной жидкости, который мы называем \ (V_ {fl} \). Теперь мы можем получить соотношение между плотностями, подставив \ (\ rho = \ frac {m} {V} \) в выражение. Это дает
\ [\ dfrac {V_ {fl}} {V_ {obj}} = \ dfrac {m_ {fl} / \ rho_ {fl}} {m_ {obj} / \ overline {\ rho} _ {obj}}, \]
где \ (\ overline {\ rho} _ {obj} \) – средняя плотность объекта, а \ (\ rho_ {fl} \) – плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя
\ [дробь \, погруженное = \ dfrac {\ overline {\ rho} _ {obj}} {\ rho_ {fl}}.\]
Рисунок \ (\ PageIndex {4} \): Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли плавучего объекта, находящегося под водой, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес:
.\ [удельная \, гравитация = \ dfrac {\ overline {\ rho}} {\ rho_W}, \] где \ (\ overline {\ rho} \) – средняя плотность объекта или вещества, а \ (\ rho_W \) – плотность воды при 4.00 ° C. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для \ (\ rho \). Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта равен 1, то он будет оставаться во взвешенном состоянии в жидкости, ни тонуть, ни плавать. Аквалангисты пытаются достичь этого состояния, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, жидкость для радиаторов и моча, как индикатор их состояния.Одно устройство для измерения удельного веса показано на рисунке \ (\ PageIndex {5} \).
Определение: Удельный вес
Удельный вес – это отношение плотности объекта к плотности жидкости (обычно воды).
Рисунок \ (\ PageIndex {5} \): Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр заполнен воздухом и утяжелен свинцом внизу. Он плавает выше всего в самых плотных жидкостях и был откалиброван и промаркирован так, что удельный вес может быть считан непосредственно с него.Пример \ (\ PageIndex {2} \): Расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде с погружением \ (97,0 \% \) ее объема, когда ее легкие полны воздуха. Какая у нее средняя плотность?
Стратегия
Плотность женщины можно найти, решив уравнение
\ [фракция \, погруженная = \ dfrac {\ overline {\ rho} _ {obj}} {\ rho_ {fl}} \]
для плотности объекта. Это дает
\ [\ overline {\ rho} _ {obj} = \ overline {\ rho} _ {person} = (дробь \, погружено) \ cdot \ rho_ {fl}.3}. \]
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела – это один из показателей процента жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. Рисунок \ (\ PageIndex {7} \))
Рисунок \ (\ PageIndex {6} \): Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, как часть определения плотности тела. Субъект должен полностью опорожнить свои легкие и удерживать металлический груз, чтобы утонуть.Внесены поправки на остаточный воздух в легких (измеряется отдельно) и вес металла. Его скорректированный подводный вес, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процента жира в организме.Существует множество очевидных примеров объектов или веществ с меньшей плотностью, плавающих в жидкостях с более высокой плотностью – масло на воде, воздушный шар, пробка в вине, айсберг и горячий воск в «лавовой лампе», назвать несколько. Менее очевидные примеры включают подъем лавы в вулкане и горные цепи, плавающие на более плотной коре и мантии под ними.Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Другие измерения плотности
Один из наиболее распространенных методов определения плотности показан на рисунке \ (\ PageIndex {7} \). Объект, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается, будучи погруженным в жидкость. Плотность монеты, показатель ее подлинности, может быть вычислена, если плотность жидкости известна. Этот же метод можно использовать для определения плотности жидкости, если плотность монеты известна.Все эти расчеты основаны на принципе Архимеда.
Рисунок \ (\ PageIndex {7} \): (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что объект , кажется, весит меньше при погружении; мы называем это измерение видимым весом объекта .Объект испытывает видимую потерю веса , равную массе вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. То есть
\ [кажущаяся \, масса \, потеря = масса \, из \, жидкость \, смещенная \] или
\ [кажущаяся \, масса \, потеря = масса \, из \, жидкость \, вытесненная \]
Следующий пример иллюстрирует использование этой техники.
Пример \ (\ PageIndex {3} \): Расчет плотности: подлинность монеты?
Масса древнегреческой монеты в воздухе определена равной 8.3 \)
, и что эффекты, вызванные проволокой, на которой подвешена монета, незначительны.
Стратегия
Чтобы рассчитать плотность монеты, нам нужны ее масса (указанная) и ее объем. Объем монеты равен объему вытесненной воды. Объем вытесненной воды \ (\ rho = \ frac {m} {V} \) для \ (V \).
Решение
Объем воды равен \ (V_W = \ frac {m_W} {\ rho_W} \), где \ (m_W \) – масса вытесненной воды.3. \]
Обсуждение
Из [ссылка] видно, что эта плотность очень близка к плотности чистого серебра, подходящей для этого типа древних монет. Большинство современных подделок – это не чистое серебро.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, король Сиракуз дал Архимеду задание определить, поставлял ли изготовитель королевской короны корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и при этом выглядит желтым, как чистое золото), а другие аналитические методы еще не были придуманы.Однако даже древние народы понимали, что плотность золота выше, чем у любого другого известного в то время вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение, когда находился в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой теперь знаменитый принцип, увидел, как применить его для определения плотности, и побежал голый по улицам Сиракуз с криком «Эврика!» (Греческое означает «Я нашел это»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Исследования PhET: плавучесть
Когда объекты всплывут, а когда утонут? Узнайте, как плавучесть работает с блоками.Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Сводка
- Подъемная сила – это чистая направленная вверх сила на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.
- Принцип Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет.
- Удельный вес – это отношение плотности объекта к плотности жидкости (обычно воды).
Глоссарий
- Принцип Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- подъемная сила
- чистая направленная вверх сила на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Архимед делает свое величайшее открытие
Архимед был очарован изгибами. Его мощный ум овладел формами прямых линий как в 2D, так и в 3D.
Ему нужно было что-то более интеллектуальное, чтобы проверить его. Это были круги, эллипсы, параболы, гиперболы, сферы и конусы.
Расчет объема сферы
Он мастерски принял вызов, став первым человеком, который вычислил и доказал формулы для объема и площади поверхности сферы. Метод, который он использовал, получил название метод истощения , тщательно разработанный около века назад одним из героев Архимеда, Евдоксом Книдским.
То, как Архимед находил свои формулы, удивительно умен и показывает, что он является первоклассным математиком, намного опережающим других своего времени, занимаясь математикой в пределах досягаемости от интегрального исчисления за 1800 лет до его изобретения.
Кривые приручения в трех измерениях – не для робких
Поверхность шара невероятно трудна для восприятия по сравнению с формой, подобной кубу. Кубики меняются только по углам и краям. Поверхность сферы меняет направление в каждой точке. Как вы могли с этим работать?
Сфера, разрезанная на полусферы.
Изображение Jhbdel
Сначала Архимед представил себе, как разрезать сферу на две половины – полушария.
Взяв одно полушарие, он получил форму с плоской поверхностью, с которой можно было работать – легче, чем сфера, и если бы он смог найти объем полусферы, удвоение его дало бы ему объем сферы.
Затем он представил, как кладет полушарие лицевой стороной вниз на плоскую поверхность.
Затем он мысленно обернул цилиндр вокруг своего полушария.
Круг на каждом конце цилиндра был того же размера, что и круг в нижней части полусферы, а высота цилиндра была равна высоте полусферы, как показано на изображении ниже:
Архимед представил полусферу внутри цилиндра
Тактика салями
Затем Архимед сделал нечто невероятно умное.Любой, кто изучал математику в университете, узнает нечто похожее на интегральное исчисление.
Архимед вообразил разрезание цилиндра горизонтальными срезами.
Он взял свой первый кусок математической салями на самом верху цилиндра. Здесь полушарие самое маленькое. Если смотреть на этот первый срез сверху, радиус круга от самого верха полушария бесконечно мал.
Затем мысленным взором он переместил свое внимание немного ниже по цилиндру и взял еще один ломтик салями через цилиндр и полусферу.На этом срезе круг полусферы немного увеличился.
Затем он снова переместил свое внимание немного ниже, разрезая еще один ломтик салями. Круг цилиндра остался того же размера, в то время как круг полусферы снова был немного больше, чем предыдущий срез.
Затем он двинулся вниз по цилиндру, снимая срезы до самого дна. В каждом срезе размер внутреннего круга увеличивался, а размер внешнего круга оставался прежним, как показано на этих изображениях.
Архимед представил поперечные сечения полусферы и цилиндра.
Собираем все вместе
Архимед рассмотрел каждый ломтик салями. В частности, его интересовал зазор между двумя кружками в каждом срезе, показанный синим цветом на изображениях выше.
Он взял все эти синие области – их было столько, сколько он хотел представить, причем глубина каждого среза была настолько близка к бесконечно малой, насколько ему хотелось. Затем он умножил площади синих колец на их глубину, чтобы найти объем, представленный всеми синими кольцами салями, сложенными друг на друга.(Он не рассматривал бесконечное количество бесконечно тонких срезов, потому что в противном случае он изобрел бы интегральное исчисление за 1800 лет до Исаака Ньютона.)
Архимед обнаружил, что объемы синих колец складываются в объем конуса, радиус основания и высота которого такие же, как у цилиндра.
Это означало, что объем полусферы должен быть равен объему цилиндра за вычетом объема конуса.
Формула для объема цилиндра была известна как πr 2 ч, а формула для объема конуса была известна как 1 ⁄ 3 πr 2 ч.В этом примере r и h идентичны, поэтому объемы равны πr 3 и 1 ⁄ 3 π r 3 .
Вычитание одного из другого означало, что объем полусферы должен составлять 2 ⁄ 3 πr 3 , а поскольку объем сферы в два раза больше объема полусферы, объем сферы составляет:
V = 4 ⁄ 3 πr 3
Архимед также доказал, что площадь поверхности сферы равна 4πr 2 .
Архимед считал это доказательство своим величайшим математическим достижением и приказал запомнить его на его надгробии как сферу в цилиндре.
Подробнее об Архимеде
Сфера внутри цилиндра. Изображение Андре Карвата.
Объявления
Архимед и интегральное исчисление | Марко Тавора, доктор философии.
Архимед Сиракузский был величайшим ученым и математиком классической античности.Он был эрудитом, внесшим вклад в широкий круг тем, включая математику, физику, астрономию и инженерию. Архимед был также блестящим изобретателем и конструктором оружия.
Вот некоторые из его многочисленных достижений:
Рисунок 1: Согласно принципу Архимеда восходящая выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, вытесняемой телом (источник).- Он доказал формулы для объема и площади поверхности сферы и других геометрических объектов (подробнее см. По этой ссылке).
- Он был пионером в применении физики для решения математических задач (а не только наоборот). В статье ниже приведен пример такого приложения.
- Он предвосхитил методы интегрального исчисления, которые будут полностью разработаны только две тысячи лет спустя.
По словам математика Стивена Строгаца, «мягко говоря, [Архимед] опередил свое время».
Рисунок 3: Картина с изображением Архимеда (Джузеппе Ногари) середины 18 века (источник).- Изобрел несколько боевых машин. Он даже применил свойства зеркал в качестве параболических отражателей для сжигания кораблей, атакующих Сиракузы (хотя правдивость этой истории долгое время обсуждалась).
В этой статье я объясню, основываясь на Симмонсе, как он рассчитал площадь внутри сегмента параболы (см. Рис. 6 ниже). Доказательство Архимеда содержится в его трактате «Квадратура параболы», написанном в 3 веке до нашей эры (за две тысячи лет до того, как современное исчисление было разработано несколькими великими математиками, включая Барроу, Декарта, Ферма, Паскаля, Уоллиса, Кавальери, Грегори, Ньютона. , и Лейбниц).
Рисунок 5: Смерть Архимеда Томасом Деджорджем. Согласно мифу (достоверных свидетельств нет), он сказал римскому солдату: «Не тревожь мои круги», прежде чем солдат убил его своим мечом (источник).На рис. 6 и 7 конструкция, использованная Архимедом для вычисления площади S , ограниченной хордой AB , показана . Он строит три треугольника, а именно ΔABC, ΔADC и ΔCEB, следующим образом:
- Сначала он находит точку C , где касательная параллельна граничной хорде AB.
- Аналогично, D выбирается как точка, в которой касательная параллельна AC .
- Выбор точки E и хорды BC осуществляется по тому же правилу.
- Затем он делает те же шаги с областями, которые еще не содержат вписанных треугольников. Затем он повторяет процесс до бесконечности (это называется методом исчерпания). Подробнее об этом будет рассказано в последнем разделе статьи.
Целью Архимеда было показать, что площадь S внутри параболического сегмента равна 4/3 площади треугольника ΔABC:
Уравнение 1: Равенство, доказанное Архимедом в его трактате «Квадратура параболы».Доказательство будет описано в этой статье.Как мы увидим в последнем разделе, это может быть сделано, сначала показав, что
Уравнение 2: Если это соотношение соблюдается, это простая задача доказать наш окончательный результат, данный уравнением. 1., а затем применяя метод исчерпания, упомянутый выше, к треугольникам под ΔACD и ΔBCE и так далее.
В этом разделе я покажу, как доказать уравнение. 2 (доказательство следует Симмонсу). В следующем я докажу, используя простое применение метода истощения, что площадь параболического сегмента равна 4/3 площади треугольника ΔABC.
Уравнение, представляющее параболу, может быть записано как (с удобным выбором осей):
Уравнение 3: Уравнение, представляющее параболу. Рисунок 7: Три точки A, B и C определены в параболическом сегменте рис. 1.Затем мы определяем три точки A, , B, и C и строим конструкцию, показанную на рис. 7, где:
Уравнение 4: определение трех точек, A, B и C, показанных на рис. 7Из рис. 7 мы находим следующее соотношение:
Уравнение 5: Из производной y в точке x₁ находим, что вертикальная линия, проходящая через C , является биссектрисой хорды AB.Согласно формуле. 5 вертикальная линия, проходящая через C , является биссектрисой хорды AB. Точка, в которой они пересекаются, обозначена как P. Достаточно доказать, что
Уравнение 6: Если это равенство доказано, Уравнение. 2 соблюдается.мы автоматически доказываем уравнение. 2 (подробнее по этой ссылке). Из рис.7 видно, что вертикаль через E делит пополам отрезок BC в точке G и отрезок BP в точке H. Если мы теперь докажем, что:
, мы получим:
Уравнение 7: Эти равенства являются следствием приведенного выше.Теперь, начиная с:
, мы напрямую получаем уравнение. 6. Теперь последний шаг, чтобы доказать уравнение. 2 заключается в проверке того, что:
или эквивалентно, из рис. 7:
Чтобы доказать это, мы применим аналитическую геометрию к рис. 7. Естественно, доказательство Архимеда было основано только на геометрии, поскольку аналитическая геометрия была разработана только в 17 веке. века (французского философа, математика и ученого Рене Декарта).
После некоторой простой алгебры получаем:
Ур. 8: Доказательство того, что FE = (1/4) QB с использованием конструкции на рис. 3.Теперь, используя метод исчерпания и , повторно применяем ту же процедуру, что и хорду ABC, к меньшим треугольникам (ниже ΔACD и ΔBCE), мы получаем геометрический ряд, сумма которого дает нам результат, который мы искали:
Архимедовское вычисление пи «Math Scholar
MathJax TeX Test PageКредит: Ancient Origins
Введение
Архимед считается величайшим математиком древности.Он был пионером прикладной математики, например, с его открытием принципа плавучести, и мастером инженерных разработок, например, со своим «винтом» для подъема воды с одного уровня на другой. Но его самым далеко идущим открытием был «метод истощения», который он использовал для определения площади круга, площади поверхности и объема сферы и площади под параболой. Действительно, с помощью этого метода Архимед почти на 2000 лет предвосхитил современное развитие исчисления, которое началось в 17 веке с Лейбница и Ньютона.Дополнительные сведения см. В статье в Википедии.
В этой статье мы представляем изобретательный метод Архимеда для вычисления периметра и площади круга, используя при этом гораздо более простую систему обозначений (алгебру), гораздо более простую систему вычислений (десятичная арифметика и компьютерные технологии). , и гораздо лучше разработанная структура для строгого математического доказательства. Пошаговое представление фактических вычислений Архимеда можно найти в этой статье Чака Линдси.
Пи-отказ
Одной из причин написания этой статьи является ответ некоторых недавних авторов, которые отвергают основную математическую теорию и принятое значение $ \ pi $, утверждая, вместо этого, что они обнаружили, что $ \ pi $ представляет собой другое значение. Например, один автор утверждает, что $ \ pi = 17-8 \ sqrt {3} = 3.1435935394 \ ldots $. Другой автор утверждает, что $ \ pi = (14 – \ sqrt {2}) / 4 = 3.1464466094 \ ldots $. Третий автор обещает раскрыть «точное» значение $ \ pi $, значительно отличающееся от принятого значения.Другие примеры см. В блоге Math Scholar. Конечно, $ \ pi $ не может быть задано каким-либо алгебраическим выражением вроде этого, поскольку $ \ pi $ был доказан Линдеманом в 1882 году как трансцендентный, и с тех пор его доказательство было тщательно проверено многими тысячами математиков.
Эта статья демонстрирует, как можно проще и лаконичнее, почему $ \ pi = 3.1415926535 \ ldots $ и, конечно же, не любое из этих значений вариантов. С этой целью этот материал не требует математической подготовки, кроме самой базовой алгебры, тригонометрии и теоремы Пифагора, и скрупулезно избегает исчислений, расширенного анализа или любых рассуждений, которые зависят от предварительных знаний о $ \ pi $.Вдоль этой линии для углов используется традиционная градусная нотация, а не радианная мера, обычная в профессиональной исследовательской работе, чтобы упростить представление, а также избежать любых концепций или методов, которые могут рассматриваться как зависящие от $ \ pi $.
Начнем с установления некоторых основных идентичностей. Эти доказательства предполагают только определения тригонометрических функций, а именно $ \ sin (\ alpha) $ (= противоположная сторона / гипотенуза в прямоугольном треугольнике), $ \ cos (\ alpha) $ (= смежная сторона / гипотенуза) и $ \ tan (\ alpha) $ (= напротив / рядом) вместе с теоремой Пифагора.\ circ $ из-за неоднозначности знака при извлечении квадратного корня.
Кредит: ВикимедиаДоказательство : Сначала мы установим некоторые более общие результаты: $$ \ sin (\ alpha + \ beta) = \ sin (\ alpha) \ cos (\ beta) + \ cos (\ alpha) \ sin (\ beta) , $$ $$ \ cos (\ alpha + \ beta) = \ cos (\ alpha) \ cos (\ beta) – \ sin (\ alpha) \ sin (\ beta), $$ $$ \ tan (\ alpha + \ beta) = \ frac {\ tan (\ alpha) + \ tan (\ beta)} {1 – \ tan (\ alpha) \ tan (\ beta)}. $$ Формула для $ \ sin (\ alpha + \ beta) $ имеет простое геометрическое доказательство, основанное только на формуле Пифагора и простых правилах прямоугольных треугольников, которое показано справа (здесь $ OP = 1 $).Сначала обратите внимание, что $ RPQ = \ alpha, \, PQ = \ sin (\ beta) $ и $ OQ = \ cos (\ beta) $. Кроме того, $ AQ / OQ = \ sin (\ alpha) $, поэтому $ AQ = \ sin (\ alpha) \ cos (\ beta) $ и $ PR / PQ = \ cos (\ alpha) $, поэтому $ PR = \ соз (\ альфа) \ грех (\ бета) $. Объединяя эти результаты, $$ \ sin (\ alpha + \ beta) = PB = RB + PR = AQ + PR = \ sin (\ alpha) \ cos (\ beta) + \ cos (\ alpha) \ sin (\ beta ) $$ Доказательство формулы для косинуса суммы двух углов полностью аналогично, а формула для $ \ tan (\ alpha + \ beta) $ получается делением формулы для $ \ sin (\ alpha + \ beta) $ по формуле для $ \ cos (\ alpha + \ beta) $, за которой следует некоторая простая алгебра.\ circ $ из-за неоднозначности знака при извлечении квадратного корня). Формулу для $ \ tan (\ alpha / 2) $ можно найти, разделив формулы для $ \ sin (\ alpha / 2) $ и $ \ cos (\ alpha / 2) $, плюс немного алгебры, но следующее еще проще и позволяет избежать квадратных корней: $$ \ tan (\ alpha / 2) = \ frac {\ sin (\ alpha / 2)} {\ cos (\ alpha / 2)} = \ frac {\ sin (\ альфа / 2) \ cos (\ alpha / 2)} {\ cos (\ alpha / 2) \ cos (\ alpha / 2)} = \ frac {1/2 \ cdot \ sin (\ alpha)} {1 / 2 \ cdot (1 + \ cos (\ alpha))} = \ frac {\ sin (\ alpha)} {1 + \ cos (\ alpha)}. $$
Алгоритм Архимеда для аппроксимации Пи
Авторы и права: Микеле Валлиснери, НАСА JPL
На этом фоне мы теперь можем представить алгоритм Архимеда для аппроксимации $ \ pi $.к \ грех (\ theta_k), \; c_k = a_k, \; d_k = b_ {k-1}. $$ Эти формулы полностью подходят для расчета полупериметров и площадей вписанных и описанных кругов, при условии, что у человека есть калькулятор или компьютерная программа для вычисления касательных и синусов. Но, учитывая наше намерение в этой статье работать, исходя из первых принципов, мы также можем использовать следующую итерацию, которая позволяет вычислять эти значения по простым формулам, включающим только арифметические операции и квадратные корни:
ТЕОРЕМА 2 (итерация Архимеда для Pi) : Определите последовательности действительных чисел $ A_k, \, B_k $ следующим образом: $ A_1 = 2 \ sqrt {3}, \, B_1 = 3 $.Затем для $ k \ ge 1 $ установите $$ A_ {k + 1} = \ frac {2 A_k B_k} {A_k + B_k}, \ quad B_ {k + 1} = \ sqrt {A_ {k + 1 } B_k}. {k + 1} \ tan (\ theta_ {k + 1}) = a_ {k + 1}.{k + 1} \ sin (\ theta_ {k + 1}) = b_ {k + 1}. $$
В качестве исторического комментария отметим, что Архимед определенно не использовал эту нотацию и не выводил явно формулы Архимеда или итерацию. Но его конструкция эквивалентна этим результатам.
Вычисления с использованием архимедовой итерации
Теперь мы можем напрямую вычислять некоторые приближения к $ \ pi $, используя только формулы теоремы 1 или теоремы 2. Эти результаты показаны в таблице до 16 знаков после запятой, но были выполнены с точностью до 50 знаков. арифметика, чтобы исключить любую возможность ошибки численного округления, искажающей результаты таблицы.Имейте в виду, что полупериметры и площади для описанных многоугольников являются завышенными для $ \ pi $, а для вписанных многоугольников – заниженными для $ \ pi $.
| Полупериметр | Площадь | ||||
| Итерация | Стороны | Описанный многоугольник | Вписанный многоугольник | Описанный многоугольник | Вписанный многоугольник |
| тыс. k $ | $ a_k $ | $ b_k $ | $ c_k $ | $ d_k $ | |
| 1 | 6 | 3.4641016151377545 | 3.0000000000000000 | 3.4641016151377545 | 2,5980762113533159 |
| 2 | 12 | 3,21531734724 | 3.1058285412302491 | 3,21531734724 | 3.0000000000000000 |
| 3 | 24 | 3,1596599420975004 | 3,1326286132812381 | 3,1596599420975004 | 3.1058285412302491 |
| 4 | 48 | 3.1460862151314349 | 3,1393502030468672 | 3,1460862151314349 | 3,1326286132812381 |
| 5 | 96 | 3,1427145996453682 | 3,14103195086 | 3,1427145996453682 | 3,1393502030468672 |
| 6 | 192 | 3,1418730499798238 | 3,1414524722854620 | 3,1418730499798238 | 3,14103195086 |
| 7 | 384 | 3.1416627470568485 | 3,14155760776 | 3,1416627470568485 | 3,1414524722854620 |
| 8 | 768 | 3,1416101766046895 | 3,1415838921483184 | 3,1416101766046895 | 3,14155760776 |
| 9 | 1536 | 3,1415970343215261 | 3,14152280500 | 3,1415970343215261 | 3,1415838921483184 |
| 10 | 3072 | 3.1415937487713520 | 3,1415921059992715 | 3,1415937487713520 | 3,14152280500 |
| 11 | 6144 | 3,1415929273850970 | 3,1415925166921574 | 3,1415929273850970 | 3,1415921059992715 |
| 12 | 12288 | 3,1415927220386138 | 3,1415926193653839 | 3,1415927220386138 | 3,1415925166921574 |
| 13 | 24576 | 3.1415926707019980 | 3,1415926450336908 | 3,1415926707019980 | 3,1415926193653839 |
| 14 | 49152 | 3,1415926578678444 | 3,1415926514507676 | 3,1415926578678444 | 3,1415926450336908 |
| 15 | 98304 | 3,1415926546593060 | 3,1415926530550368 | 3,1415926546593060 | 3,1415926514507676 |
| 16 | 196608 | 3.1415926538571714 | 3,1415926534561041 | 3,1415926538571714 | 3,1415926530550368 |
| 17 | 393216 | 3,1415926536566377 | 3,1415926535563709 | 3,1415926536566377 | 3,1415926534561041 |
| 18 | 786432 | 3,1415926536065043 | 3,1415926535814376 | 3,1415926536065043 | 3,1415926535563709 |
| 19 | 1572864 | 3.1415926535939710 | 3,1415926535877043 | 3,1415926535939710 | 3,1415926535814376 |
| 20 | 3145728 | 3,1415926535 | 63,1415926535892710 | 3,1415926535 | 63,1415926535877043 |
Как легко видеть, каждый из этих столбцов быстро сходится к хорошо известному значению $ \ pi $. В последней строке таблицы, в которой представлены результаты для описанных и вписанных многоугольников с 3 145 728 сторонами, все четыре записи соответствуют десяти цифрам после десятичной точки: $ 3.1415926535 \ ldots $. Обратите внимание, кстати, что оба из двух вариантов значения $ \ pi $, упомянутые в разделе запрета Pi выше, исключаются на четвертой итерации . От этих вычислений никуда не деться – значения вариантов для $ \ pi $ просто неверны.
Теперь мы строго докажем, что формулы Архимеда (или, что то же самое, архимедова итерация) сходятся к $ \ pi $ как в смысле окружности, так и в смысле площади, снова полагаясь только на рассуждения из первых принципов.
АКСИОМА 1 (аксиома полноты): Каждый ограниченный сверху набор вещественных чисел имеет наименьшую верхнюю границу; каждый ограниченный снизу набор вещественных чисел имеет точную нижнюю границу.
Комментарий : Эта фундаментальная аксиома действительных чисел просто утверждает свойство, что набор действительных чисел, в отличие от, скажем, набора рациональных чисел, не имеет «дыр». Эквивалентное утверждение аксиомы полноты: «Каждая последовательность Коши действительных чисел имеет предел в действительных числах». k $.В духе соблюдения современного соглашения мы представляем в отдельном блоге полное доказательство того, что $ \ pi $ по определению Архимеда совпадает с $ \ pi $ на основе обычных $ n $ -сторонних правильных многоугольников для круга из радиус один, и в качестве бонуса доказательство того, что пределы площадей этих многоугольников также равны $ \ pi $. Подробности смотрите в отдельном блоге.
Стратегия доказательства : Мы покажем, что (а) последовательность описанных полупериметров $ (a_k) $ строго убывает; (б) последовательность вписанных полупериметров $ (b_k) $ строго возрастает; (c) все $ (a_k) $ строго больше всех $ (b_k) $; и (г) расстояние между $ a_k $ и $ b_k $ становится сколь угодно малым при больших $ k $.k}, $$, так что разница между описанным и вписанным полупериметром уменьшается примерно в четыре раза с каждой итерацией (как также видно в таблице выше).
Напомним из вышесказанного, что все $ a_k \ gt 3 $, так что последовательность $ (a_k) $ описанных полупериметров ограничена снизу. Таким образом, по аксиоме 1 последовательность $ (a_k) $ имеет точную нижнюю грань $ L_1 $. Фактически, поскольку все $ a_k $ больше, чем все $ b_k $, любой $ b_k $ является нижней границей последовательности $ (a_k) $, так что мы можем написать для любого $ k $, $ a_k \ geq L_1 \ geq b_k $.Кроме того, все $ b_k \ lt 4 $, так что последовательность $ (b_k) $ вписанных полупериметров ограничена сверху и, следовательно, имеет точную верхнюю границу $ L_2 $. И, как и раньше, поскольку любой $ a_k $ является верхней границей для последовательности $ (b_k) $, для каждого $ k $ также следует, что $ a_k \ geq L_2 \ geq b_k $. Таким образом, $ L_1 $ и $ L_2 $ «зажаты» между $ a_k $ и $ b_k $, которые для достаточно больших $ k $ произвольно близки друг к другу (в соответствии с последним отображаемым уравнением выше), так что $ L_1 $ должно равняться $ L_2 $. Это завершает доказательство теоремы 3а.k}, $$, поскольку окончательное неравенство установлено несколькими строчками выше. Как и прежде, отсюда следует, что точная нижняя граница описанных областей $ c_k $ в точности равна наименьшей верхней границе вписанных областей $ d_k $. Кроме того, поскольку последовательность $ (a_k) $ полупериметров описанных многоугольников на совпадает с последовательностью , что и последовательность $ (c_k) $ площадей описанных многоугольников, мы заключаем, что общий предел площадей равен идентичен общему пределу полупериметров, а именно $ \ pi $.2). $$ Тогда $ 1 / a_k $ квартично сходится к $ \ pi $: каждая итерация примерно учетверяет количество правильных цифр. Всего за три итерации получается 171 правильная цифра, которые выглядят следующим образом: $$ 3,14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482 $$ 53421170679821480865132823066470938344828620899862803482
Другие записи из серии «Простые доказательства»
Остальные посты из серии «Простые доказательства великих теорем» доступны здесь.
Формула повторения Архимеда
Позвольте и быть периметрами описанного и
Выписанные -угольник и периметры
Описанный и вписанный -gon. потом
| (1) | |||
| (2) |
Первое следует из того факта, что длины сторон Многоугольников на Круг радиуса
| (3) | |||
| (4) |
так
| (5) | |||
| (6) |
Но
| (7) |
Использование идентичности
| (8) |
затем дает
| (9) |
Второе следует из
| (10) |
Использование идентичности
| (11) |
дает
| (12) |
Стенограмма видео
для этой проблемы. Мы сравниваем два тома. Мы хотим посмотреть объем конуса и объем соответствующего параболического тела. Я просто сокращу. Это P s. Мы хотим сравнить эти конусы и посмотреть, как соотносятся объемы. В частности, нам говорят, что объем твердого тела um, параболического твердого тела должен составлять три половины объема соответствующего конуса, как показано на нашем рисунке.Итак, давайте сделаем шаг назад, посмотрим, как найти объем каждого из них, и они сравнят их, чтобы убедиться, действительно ли они связаны так, как они говорят в нашей проблеме. Итак, начнем с объема конуса. Это объем, который мы ограничили без исчисления. Объем конуса равен одной трети площади основания, умноженной на высоту. Таким образом, объем конуса, который я буду сокращать, равен V, что составляет одну треть. Теперь область основания – круг. Итак, это пи r в квадрате, а радиус этой базы превышает.Итак, у меня есть pi r в квадрате, и им сказали, что высота равна H. Это означает, что объем моего конуса является числителем. У меня есть круговая диаграмма B, возведенная в квадрат в h, а знаменатель будет 12. Итак, вот объем моего кода. Теперь давайте посмотрим на объем нашего параметрического тела. Да, это самый простой способ найти это. Гм, для меня это дисковый метод, и у вас могут быть другие способы сделать это. Но для меня это имеет смысл. Итак, я собираюсь использовать дисковый метод. Итак, я собираюсь сложить все эти круглые диски по оси Y, и я буду исходить от y, равного нулю схождения, y равняется h.Площадь каждого из этих кругов будет пропорциональна квадрату пи r. И в этом случае R будет моим бывшим значением. Так что на самом деле я могу изменить это, чтобы сказать, что это pi X в квадрате de y de y – это тестируемое изменение роста младенца для каждого из этих кругов. Теперь, чтобы получить этот интеграл, я хочу, чтобы все было в терминах одной и той же переменной. Итак, мне нужно изменить X в квадрате и выразить это с точки зрения Почему? Хорошо, что Нам сказали, что мы просто отошли в сторону здесь. Нам говорят, что для нашей параболической кривой, почему равно четырем часам в квадрате B, умноженном на X в квадрате.Итак, если я хочу решить для X в квадрате, это дает мне b в квадрате. Почему более четырех часов, чтобы я мог сделать эту замену в моем интеграле, у меня есть круг, умноженный на b в квадрате. Почему более четырех h, заменяя это, сделайте вывод, что x возведено в квадрат, умноженное на d y. Хорошо, хорошая новость в том, что большинство из них – константы. Pi B в квадрате для h. Все это константы. Единственная переменная, которая у меня есть, – это почему. Итак, когда я собираюсь интегрировать это, интеграл того, почему это будет y в квадрате над двумя. И я собираюсь интегрировать от нуля до H, хорошо.И чтобы облегчить жизнь, я мог бы вытащить эти два, так что у меня действительно есть pi b в квадрате более восьми часов раз. Y в квадрате, когда я оценил. Итак, в H это H в квадрате. Когда y равно нулю, это просто ноль. Это дает мне квадрат пи b. Почему не возведены в квадрат h и знаменатель в H? Так что один из этих возрастов будет отменен, так что у меня pi b в квадрате h больше восьми. Итак, это два моих тома. Теперь давайте сравним их с тем, что нам говорят в нашей задаче, мы хотим показать, что объем параметрического тела в три раза меньше объема соответствующего конуса.Что ж, объем параметрического твердого тела Pi B в квадрате H больше восьми. Объем конуса пи B в квадрате H больше 12. И если я отменю, тройка войдет туда. 13 идет сюда. Четыре. Да, они будут равны. У меня pi b в квадрате h больше восьми, и как только я отменю, у меня pi b в квадрате h больше восьми. Таким образом, они связаны именно так, как указано в проблеме.
Архимеда и площадь параболического отрезка
Архимед был греческим математиком, жившим 2300 лет назад.
Многие из его изобретений и математических открытий опередили свое время на годы. Удивительно, насколько изобретательным ты становишься, когда тебя постоянно атакуют враги.
Найти площадь под кривой уже много лет было проблемой. Справедливая торговля зависела (частично) от способности определять объемы цилиндров и сфер. Архимед разработал хорошие приближения для площади круга и значения π (пи).
Самым замечательным в следующем примере мышления Архимеда является то, что он предшествует работе Исаака Ньютона и Готфрида Лейбница (математиков 17 века, которые разработали дифференциальное исчисление) примерно на 2000 лет.
У меня есть особый интерес к такого рода вещам, потому что название этого блога, squareCircleZ, происходит от исторической попытки построить квадрат с такой же площадью, что и данный круг (называемый «возведение круга в квадрат»).
Следующее обсуждение следует технике, изложенной Архимедом в его Квадратуре параболы , с использованием «метода исчерпания», предшественника исчисления бесконечно малых. Идея пришла от Антифона (V век до н.э.) и Евдокса Книдского (IV век до н.э.).
Площадь параболического сегмента
Параболический сегмент – это область, ограниченная параболой и линией, как показано голубой областью ниже:
[См. Справочную информацию об этой интересной форме в параболе.]
Я использовал простую параболу y = x 2 и выбрал конечные точки линии как A (-1, 1) и B (2, 4). Теорема будет работать для любой параболы и любой прямой, проходящей через эту параболу и пересекающейся в 2 точках.[Конечно, Архимед не использовал систему координат x-y , поскольку она не была изобретена Декартом до 17 века.]
Архимед затем расположил точку C так, что значение x для C находится посередине между значениями x точек A и B . Затем он построил треугольник ABC следующим образом:
В моем примере C имеет значение x 0,5, то есть 1.5 единиц от x = −1 и x = 2.
Архимед показал, что площадь (голубого) параболического сегмента составляет 4/3 площади треугольника ABC .
Способ, которым Архимед достиг этого результата, заключался в использовании метода исчерпания, который включает в себя нахождение области изогнутой формы путем вписывания последовательно уменьшающихся многоугольников, пока форма не будет заполнена. Мы можем найти площадь этих многоугольников и, следовательно, площадь изогнутой формы.
Теперь мы построим еще один треугольник, выбрав точку D на параболе так, чтобы его значение x находилось посередине между значениями x A и C , аналогично тому, что мы делали раньше.
Давайте увеличим масштаб и посмотрим на результат.
Мы делаем то же самое в строке BC , помещая точку E так, чтобы ее значение x находилось на полпути между C и B .
Мы уже видим, что если мы сложим площади треугольников ABC, ACD и BCE , мы получим разумное приближение для площади параболического сегмента, но мы можем добиться большего.
Если продолжить процесс, мы сформируем еще 4 треугольника следующим образом:
Осталось очень мало «белого пространства», и если бы мы добавили площади семи треугольников, у нас было бы даже лучшее приближение для площади параболического сегмента.
Если мы продолжим и добавим площади из бесконечного числа таких треугольников, мы получим точных площадей для параболического сегмента.
Итак, площадь каждого светло-зеленого треугольника составляет 1/8 площади розового треугольника. Это потому, что зеленый треугольник имеет 1/2 ширины розового треугольника (мы так сделали) и 1/4 высоты (что можно показать с помощью параметрических уравнений).
Тогда, учитывая красные треугольники, они будут 1/8 площади светло-зеленых треугольников.
Итак, если мы назовем площадь большого розового треугольника X , тогда площадь всех треугольников будет равна:
X + 2 ( X /8) + 4 ( X /64) + 8 ( X /512) + …
= X + X /4 + X /16 + X /64 + …
= X (1 + 1/4 + 1/16 + 1/64 + …)
Мы признаем, что выражение в скобках является геометрическим рядом с общим отношением r = 1/4 и первым членом a = 1.Сумма этого ряда определяется выражением:
Сумма = a / (1 – r ) = 1 / (1 – 1/4) = 1 / (3/4) = 4/3
[Архимед использовал геометрическое доказательство для этой части.]
Итак, общая площадь треугольников (которая дает нам площадь нашего голубого параболического сегмента) составляет 4 X /3, что, как утверждал Архимед, составляет 4/3 площади розового треугольника.
Идеи, лежащие в основе этого решения, очень похожи на идеи, лежащие в основе развития математического анализа.
Использование исчисления
Давайте воспользуемся интегральным исчислением, чтобы проверить ответ, который мы получили с помощью подхода Архимеда.
В моем конкретном примере с y = x 2 и прямой y = x + 2, пересекающей параболу в точках (−1, 1) и (2, 4), розовый треугольник имеет ширину AC = 1,68. единиц и перпендикулярной высоты 4,02 единицы, поэтому площадь составляет:
Площадь ΔABC = 0,5 × 1,68 × 4,02 = 3,38 ед. 2
Итак, согласно Архимеду, площадь (голубого) параболического сегмента будет:
Сегмент площади = 4/3 × 3.38 = 4,5 шт. 2
А теперь сравним этот результат с помощью вычислений. Требуемая область – это область между двумя кривыми. Верхняя кривая – это линия y 2 = x + 2, а нижняя кривая – это y 1 = x 2 . Пределы интеграции: x = −1 и x = 2.
Итак, мы получаем тот же ответ, 4.


