Формула давление газа через температуру и объем: Недопустимое название | Stationeers вики

Уравнение состояния идеального газа. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей

Связь трех параметров состояния идеального газа. Уравнение Менделеева – Клапейрона

 

Состояние газа однозначно задается тремя макроскопическими параметрами: давлением, объемом и температурой. Мы знаем, что горячий воздух поднимается вверх. С увеличением температуры он становится легче – уменьшается плотность, увеличивается расстояние между молекулами. То есть происходит расширение – увеличение объема. Можно сделать вывод, что объем и температура газа связаны. Если сдавить воздушный шарик, то внутри него увеличится давление. То есть объем газа также связан с давлением. Получается, что давление, объем и температура газа связаны между собой. Попробуем понять, как именно.

 

Мы работаем с моделью идеального газа, которая описывает реальный газ достаточно точно для решения многих задач. Мы уже получили для идеального газа основное уравнение МКТ, с помощью которого связали давление с микропараметрами – массой и средней скоростью одной молекулы:

Это уравнение – решение задачи в модели механики. Мы приняли, что газ состоит из хаотично движущихся молекул – и вычислили, как они действуют на стенку, какое давление создают, когда с ней сталкиваются. Но мы не измеряем скорости и массы отдельных молекул. На макроуровне мы умеем измерять температуру, которую мы связали со средней кинетической энергией молекул, а значит, и с микропараметрами: массой и средней скоростью одной молекулы:

Подставив кинетическую энергию из одного уравнения в другое, получили:

В таком виде применять уравнение для решения задач все еще не удобно. Для измерения давления газа существуют различные приборы (манометры, барометры), для измерения температуры – термометры. Но мы не можем напрямую измерять концентрацию – количество частиц в единице объема. Преобразуем уравнение до удобного вида. Концентрация – это, по определению, :

А количество молекул удобнее представить через количество вещества. Мы помним, что в одном моле вещества  молекул. Значит, :

Договоримся: чтобы каждый раз не перемножать постоянные величины  на , сделаем это один раз, а произведение обозначим :

Это значение назвали универсальной газовой постоянной, почему – станет понятно чуть позже. Умножим обе части уравнения на объем и перепишем:

Получили уравнение, которое связывает три макропараметра идеального газа, которые легко измерить: объем, температуру и давление. И если взять какое-то определенное количество газа , эти три параметра однозначно зададут его состояние, неизвестных в уравнении не останется. Поэтому это уравнение назвали уравнением состояния идеального газа, или иначе уравнением Менделеева – Клапейрона. А на случай, если нам неудобно пользоваться количеством вещества в молях, можно его выразить через массу вещества:

Именно в этом виде его чаще всего и записывают. Мы начали с движения молекул, придумали инструменты для его описания, а в итоге получили уравнение, которое связывает поддающиеся непосредственному измерению макропараметры.

Решим задачу.

Задача 1. Какое давление должен выдерживать газовый баллон объемом 50 л, чтобы при температуре 25 ˚С в нем можно было хранить 2 кг метана ()?

Анализ условия. В задаче сказано о метане – это газ, в баллоне не создается экстремальных условий, температура комнатная, так что будем описывать его с помощью модели идеального газа. Речь идет о связи трех макропараметров газа, поэтому будем применять уравнение состояния идеального газа.

Физическая часть решения. В условии задана масса газа, поэтому запишем уравнение состояния идеального газа в том виде, в котором есть масса:

Все величины известны, осталось только найти молярную массу метана (ее можно найти, зная состав его молекулы, см. рис. 1), перевести значения величин в СИ и получить ответ. На выборе уравнения физика закончилась, осталось решить простое уравнение. Выразим давление:

Рис. 1. Углерод и водород в таблице Менделеева

Молекула метана состоит из одного атома углерода с относительной атомной массой 12 (смотрим в таблице Менделеева) и четырех атомов водорода с относительной атомной массой 1. Тогда:

Будем использовать в СИ:

1 л – это 1  или в СИ . Значит, объем баллона в СИ будет равен .

Температуру выразим в кельвинах:

Вычислим давление:

Получили ответ: давление около 6,2 МПа, что в 62 раза больше атмосферного. Задача решена.

Во многих задачах берется некоторое фиксированное количество газа и рассматривается изменение его состояния. Это значит, что в рамках таких задач количество вещества постоянно (как и масса, смотря в чем выразим). Можно все постоянные перенести в одну часть уравнения, а три изменяющихся параметра состояния – в другую:

 или

Если взять 1 моль любого газа (одноатомного аргона, углекислого газа, водяного пара – лишь бы к нему была применима модель идеального газа), выражение  будет равно постоянной . Поэтому эта постоянная и названа универсальной. Но даже если мы возьмем произвольную, но – что важно – фиксированную массу газа, выражение  для этой массы газа будет постоянным:

Или, по-другому, если газ переходит из одного состояния с параметрами , ,  в состояние с параметрами , , , то можем записать:

В таком виде или в виде  это уравнение называют уравнением Клапейрона, хотя это то же уравнение состояния, записанное немного иначе.

 

Газовые законы

 

 

Рассматривать изменение переменной от двух других не очень удобно. У нас есть подходящий математический инструмент для описания одной переменной от другой – функция. В рассмотренных в начале урока примерах мы фиксировали один из трех параметров газа (например, температуру) и рассматривали зависимость двух других. Подробно рассмотрим все три случая.

 

Начнем с фиксированной температуры и рассмотрим связь давления и объема в этом случае. Процессы, в которых мы считаем неизменным один из параметров состояния газа, назвали изопроцессами, от древнегреческого ἴσος, что означает «одинаковый, равный». А процесс, в котором сохраняется температура (const), называется изотермическим (несложно запомнить: термос – то, что сохраняет температуру).

Умножим обе части уравнения Клапейрона на температуру:

Если умножить постоянную температуру на константу, то получим тоже константу, только другую:

Нам даже не нужно знать ее значение, главное, что произведение p на V каким было в начале процесса, таким и осталось в конце:

Из уравнения видно: при уменьшении объема (сжатии) при постоянной температуре увеличивается давление, и наоборот (на математике мы говорили, что такая зависимость называется обратной пропорциональностью).

Мы получили это уравнение, воспользовавшись математической моделью, но еще в XVII веке эту закономерность экспериментально выявили англичанин Бойль и француз Мариотт, поэтому ее назвали в их честь законом Бойля – Мариотта:

Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.

Как это выглядит на практике? Представьте шар с мягкой резиновой оболочкой или цилиндр со скользящим поршнем, в которых находится определенная масса газа. Как добиться того, чтобы при сжатии газа его температура оставалась постоянной? Газ должен обмениваться теплотой с большим телом с неизменной температурой – термостатом (см. рис. 2).

Рис. 2. Сжатие газа, отвод теплоты для постоянной температуры

Реально ли поддерживать таким способом постоянную температуру? Нет, для этого газ нужно сжимать очень медленно, чтобы он успевал остывать, едва начиная нагреваться. Но если не будет разности температур, то и теплообмена не будет: тепло передается от теплого холодному. Поэтому процесс сможет протекать так: небольшими шагами сжимаем газ, чтобы на каждом таком шаге он немного нагревался и это тепло тут же забирал термостат. Постоянная температура – это приближение, тем не менее достаточно точно описывающее реальный процесс и позволяющее решать задачи.

Зафиксируем второй параметр – давление, при этом меняться будут температура и объем. Давление мы ассоциируем с древнегреческим βαρύς – «тяжелый», вы знаете, что атмосферное давление измеряют барометром, поэтому процесс с постоянным давлением (onst) назвали изобарным.

Разделим обе части уравнения Клапейрона на давление:

Если разделить константу на постоянное давление, то получим тоже константу:

А если рассмотреть объем и температуру в начале и в конце изобарного процесса, можно записать:

Из уравнения видно: при увеличении температуры (нагревании) при постоянном давлении увеличивается объем (газ расширяется), и наоборот, при охлаждении – сжимается. Это пример прямой пропорциональности. До того как вывели этот закон математически, его экспериментально получил Гей-Люссак (это двойная фамилия одного человека, французского ученого), поэтому его назвали законом Гей-Люссака:

Для данной массы газа при постоянном давлении отношение объема к температуре постоянно.

Пример реального процесса, который можно описывать как изобарный: газ, который находится в цилиндре под поршнем, который свободно перемещается и на который снаружи действует постоянное давление, например атмосферное. Тогда, если нагреть этот газ, он будет расширяться, но давление как было равным атмосферному (плюс давление самого поршня), так и останется.

На самом деле, если давление газа совсем не будет увеличиваться, у поршня не будет причин двигаться, давления будут все время уравновешены. Так что давление немного увеличивается, но под его действием поршень сдвигается вверх, и оно тут же понижается до прежнего значения. Эти изменения небольшие, так что для решения многих задач давление можно действительно считать постоянным.

И остался третий параметр, который мы еще не фиксировали, – объем, при этом изменяются температура и давление. Называется такой процесс, при котором (onst), изохорным, от древнегреческого χῶρος – «место, пространство». Разделим обе части уравнения Клапейрона на объем:

Справа получилась константа:

Теперь можно связать давление и температуру в начале и в конце изохорного процесса:

Из уравнения видно: при увеличении температуры (нагревании) при постоянном объеме увеличивается давление газа, и наоборот. Это тоже прямая пропорциональность. И этот закон тоже сначала был получен экспериментально, французским ученым Шарлем, поэтому и назван его именем – закон Шарля:

Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.

Для этого процесса модель точнее описывает реальный процесс: в закрытом жестком сосуде объем действительно можно считать постоянным с хорошей точностью. Пример – металлический баллон. Если газ в нем нагреть, давление увеличится, но при большой жесткости баллона он практически не деформируется (по крайне мере настолько, чтобы внести заметную погрешность в расчеты).

 

Решение задач. Графики для описания газовых законов. Границы применимости модели

 

 

Итак, какие инструменты мы получили? Основной инструмент один – уравнение состояния идеального газа. А все остальное – это запись этого же уравнения в более удобных формах для решения той или иной задачи. Если мы имеем дело с неизменной массой газа (то есть нет утечек), то три параметра состояния связаны уравнением Клапейрона. А если при этом еще и остается неизменным один из параметров состояния, применяем уравнение для изотермического, изобарного или изохорного процесса, их еще называют газовыми законами. Применим наши инструменты, решив несколько задач.

 

Задача 2. При сжатии воздуха в цилиндре дизельного двигателя объем воздуха уменьшается в 15 раз, а температура повышается от 47 до 620 ˚С. Каково давление воздуха в конце сжатия, если в начале сжатия давление воздуха было равно атмосферному (100 кПа)?

Анализ условия.

В задаче описано изменение состояния воздуха, будем его описывать с помощью модели идеального газа – температура сотни градусов по Цельсию это позволяет. Состояние газа описано тремя макропараметрами (давлением, температурой и объемом), причем изменяются все три макропараметра, это не изопроцесс. При этом ничего об утечках воздуха из цилиндра ничего не сказано, значит, количество воздуха не изменяется. Будем применять уравнение Клапейрона.

Физическая часть решения. Запишем уравнение в виде, удобном для описания перехода из состояния 1 в состояние 2:

Температуры заданы (нужно только перевести их в кельвины), давление тоже. Что сказано об объеме – перепишем условие в математическом виде. Объем уменьшился в 15 раз, это значит, что в состоянии 2 объем в 15 раз меньше, чем в состоянии 1:

Получили простую систему уравнений, решим ее – это будет математическая часть решения. Подставим второе давление:

Выразим давление во втором состоянии:

Получили ответ: 4,2 МПа (или 42 атмосферы).

Задача 3. После повышения температуры на 15 К давление газа в закрытом баллоне увеличилось на 3 %. Какой была начальная температура?

Анализ условия. В задаче описано изменение состояния газа. За неимением другой информации будем применять модель идеального газа. Речь идет о закрытом баллоне. Это значит, во-первых, что масса газа постоянна, а, во-вторых, баллоны обычно жесткие, значит, и объем не изменяется. Поэтому можем описать процесс как изохорный.

Физическая часть решения. Запишем уравнение для изохорного процесса:

Перепишем условие в математическом виде, чтобы можно было подставлять в уравнение. Температура увеличилась на 15 К, значит,.

А давление увеличилось на 3 %, это по-другому можно записать:

Физика здесь закончилась на выборе закона, которым описывать процесс, осталось подставить переписанные величины и решить уравнение:

Нашли начальную температуру, она равна 500 К.

Или, в более привычных для нас градусах Цельсия, 227 ˚С.

Часто бывает удобно выразить зависимость одного параметра от другого в виде графиков. Это наглядно, помогает лучше представить себе процесс, а иногда по графикам можно оценить численные значения. Начертим графики зависимостей параметров газа и разберемся, какую информацию можно из них получить. Начнем с изотермического процесса, .

Чтобы начертить график зависимости давления от объема, нужно переписать уравнение в виде :

Это обратно пропорциональная зависимость типа , и ее график имеет вид гиперболы (см. рис. 3).

Рис. 3. Изотермический процесс на графике зависимости давления от температуры

От константы зависит расположение кривой: чем больше константа, тем выше располагается график. А вы помните, что константа содержит температуру, в промежуточном варианте уравнение выглядело так:

Так что если у нас есть две изотермы для одной и той же массы газа, значит, каждая изотерма описывает процесс, при котором температура постоянна. Но в первом случае эта постоянная температура равна , которая меньше, чем постоянная температура во втором случае (см. рис. 3).

Графики двух остальных изопроцессов мы будем рассматривать в координатах  и , поэтому сразу рассмотрим и изотермический процесс в этих координатах. Начертим график (см. рис. 4) изотермы в координатах .

Рис. 4. Изотермический процесс на графике зависимости

Температура не меняется, значит, графики будут перпендикулярны оси Т, а объем при этой температуре приобретает разные значения. И легко определить по оси Т, какая изотерма соответствует большей температуре. На этом графике не видно, как изменяется давление, но мы понимаем, что давление увеличивается при уменьшении объема, что соответствует движению точки на графике вниз.

Аналогично выглядят графики изотермического процесса в координатах : температура постоянна, температура для второго процесса больше, чем для первого. А давление изменяется при изменении объема, которого на графике явно не видно, но можно понять по изменению давления (см.

рис. 5).

Рис. 5. Изотермический процесс на графике зависимости

Теперь рассмотрим изобарный процесс.

Представим в виде зависимости :

Это прямо пропорциональная зависимость вида , ее график – прямая, которая начинается в точке начала координат (см. рис. 6).

Рис. 6. График зависимости  для изобарного процесса

Коэффициентом перед  определяется крутизна графика. Там у нас стоит константа, которая содержит давление, вспомните промежуточное уравнение, полученное из уравнения Клапейрона:

Там давление в числителе, поэтому чем больше давление, тем меньше коэффициент пропорциональности на графике и тем ниже располагается график. Поэтому у двух процессов, происходящих с одной и той же массой газа при разных давлениях: .

Рис. 7. График зависимости  для двух изобарных процессов при разных давлениях

Начертим графики изобары в двух других системах координат. В координатах  найдем на оси  нужное нам давление и горизонтальной прямой покажем, что при любом изменении объема  оно не изменяется.

При другом давлении это будет такая же прямая, только выше или ниже (см. рис. 8).

Рис. 8. Графики зависимости  и для изобарного процесса

Аналогично выглядят графики изобар в координатах : при любом значении температуры давление остается постоянным.

И последним рассмотрим изохорный процесс:

Представим в виде зависимости :

Это тоже прямо пропорциональная зависимость вида , с графиком – прямой, крутизна которой определяется коэффициентом перед переменной , а в нашем случае – .

Рис. 9. График зависимости  для изохорного процесса

Этот коэффициент определяется объемом, при котором протекает изохорный процесс, и чем объем меньше, тем коэффициент больше и график круче:

Графики, описывающие изохорные процессы при разных объемах, в координатах  и , начертите самостоятельно. И напоследок поговорим о границах применимости моделей.

Мы подробно обсудили, что в реальности нельзя абсолютно точно сохранять неизменными температуру, давление или объем при изопроцессах. Но даже в этом приближении модель работает с ограничениями. В уравнение, например , мы можем подставить любое значение температуры и получить соответствующее значение объема. Но вспомните: мы изначально всю эту модель строили на модели идеального газа. Это работает при привычных нам температурах, близких к комнатной, и более высоких, используемых в технике, и при давлениях, близких к атмосферному.

Но реальный газ нельзя, например, охлаждать до сколь угодно малых температур, чтобы он сжимался до сколь угодно малого объема. В какой-то момент размеры молекул не будут уже пренебрежимо малыми по сравнению с расстояниями между ними, а это уже не описывается моделью идеального газа. Усилится взаимодействие между молекулами, которым мы изначально пренебрегли, и газ перейдет в состояние жидкости (см. рис. 9).

Рис. 9. Границы применимости модели идеального газа

Конечно, это не значит, что физика здесь больше не работает. Если нужно рассмотреть состояние жидкости, это тоже можно сделать: у нее тоже можно измерить температуру, рассмотреть изменение объеме при сжатии – оно будет небольшим. Только это будет другая модель с другими инструментами ее описания.

 

Список литературы

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. Касьянов В.А. Физика 10. – М.: Дрофа, 2000.
3. М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Физика: Механика 10. – М.: Дрофа, 2004.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Класс!ная физика
2. Интернет-портал Класс!ная физика 

 

Домашнее задание

1. Начертите по памяти и объясните графики, описывающие изохорные процессы при разных объемах, в координатах  и .
2. До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой 40 ˚С, чтобы объем газа уменьшился при этом на одну четверть?

 

 

Открытая Физика. Основное уравнение МКТ газов. Температура

Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).

В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ_y скорости, параллельная стенке, остается неизменной (рис. 3.2.1).

Упругое столкновение молекулы со стенкой

Поэтому изменение импульса молекулы будет равно 2m₀υ_x, где m₀ – масса молекулы.

Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υ_x, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υ_xΔt.

Определение числа столкновений молекул с площадкой S

Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυ_xΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно 12nSυxΔt. Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m₀υ_x, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно nm0υx2SΔt. По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать: FΔt=nm0υx2SΔt.

Разделив обе части на SΔt, получим: p=FS=nm0υx2, где p – давление газа на стенку сосуда.

При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.

В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Дж. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.

Распределение молекул по скоростям. T₂ > T₁

Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υ_в, соответствующая максимуму кривой распределения, и среднеквадратичная скорость υкв=υ2¯, где υ2¯ – среднее значение квадрата скорости.

С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υ_в и υ_кв увеличиваются.

Распределение Максвелла

Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n₁, n₂, n₃ и т. д. молекул с проекциями скоростей υ_x1, υ_x2, υ_x3 и т. д. соответственно. При этом ∑ini=n. Каждая группа молекул вносит свой вклад nim0υxi2 в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υ_xi скоростей возникает суммарное давление p=m0∑iniυxi2.

Входящая в это выражение сумма – это сумма квадратов проекций υ_x всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение υx2¯ квадрата проекции υx скорости молекул: 1n∑iniυxi2=υx2¯.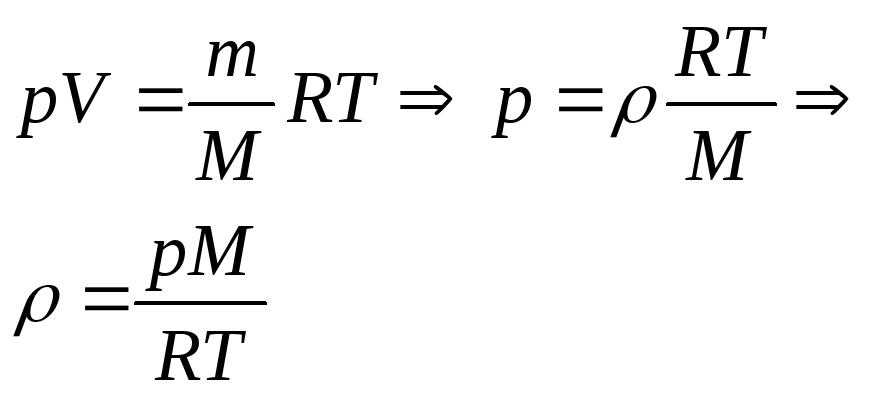

Теперь формулу для давления газа можно записать в виде p=nm0υx2¯.

Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой: υx2¯=υy2¯=υz2¯=13υ2¯.

Последнее равенство вытекает из формулы: υx2+υy2+υz2=υ2.

Формула для среднего давления газа на стенку сосуда запишется в виде p=p¯=13nm0υ2¯=23nm0υ2¯2=23nEk¯.

Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m₀, концентрацией молекул n, средним значением квадрата скорости υ2¯ и средней кинетической энергией Ek¯ поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.

Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию Ek¯ поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то n=NV=const (N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению ΔEk¯ средней кинетической энергии.

Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия Ek¯? Опыт показывает, что такой величиной является температура.

Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.

Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.

Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).

Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (T_F), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно, TF=95TC+32ˆ  или  TC=59(TF-32ˆ).

Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.

Газовый термометр с постоянным объемом

Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p₀ и p₁₀₀ на график, а затем провести между ними прямую линию (рис.  3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.

Зависимость давления газа от температуры при V = const

Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута: T_К = T_С + 273,15.

В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура T_С = 20 °С по шкале Кельвина равна T_К = 293,15 К.

Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.

Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.

Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.

Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.

Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда p~νV=NNAV=nNA~n, где N – число молекул в сосуде, N_А – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать: p = nkT, где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Л. Больцмана, одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно: k = 1,38ċ10^–23 Дж/К.

Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить: Ek¯=32kT.

Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.

Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.

Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа: p = p₁ + p₂ + p₃ + … = (n₁ + n₂ + n₃ + …)kT.

В этом соотношении n₁, n₂, n₃, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.

Полупроницаемая мембрана

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ “Облако знаний”.

Уравнение состояния

Газы имеют различные свойства, которые мы можем наблюдать с помощью чувства, в том числе газ давление р , температура Т , масса м , и объем В в котором содержится газ. Внимательное научное наблюдение определило, что эти переменные связаны друг с другом, и значения этих свойства определяют состояние газ. Если мы зафиксируем любые два свойства, мы сможем определить природу отношения между двумя другими. Вы можете изучить отношения между переменными в анимированный газ лаборатория Если давление и температура поддерживаются постоянными, объем газа напрямую зависит от массы или количества газа. Это позволяет нам определить одно дополнительное свойство, называемое газом. плотность r , что является отношением массы к объем. Если масса и температура остаются постоянными, произведение давление и объем практически неизменны для реального газ. Произведение давления на объем есть в точности постоянная величина. идеальный газ . Эта зависимость между давлением и объемом назван законом Бойля в честь Роберта Бойля который впервые наблюдал его в 1660 году. Наконец, если масса и давление равны при постоянном объеме объем прямо пропорционален температуре для идеального газа. Эти отношения называются Чарльз и закон Гей-Люссака в честь двух французских ученых, обнаружил отношения. Газовые законы Бойля и Шарля и Гей-Люссака можно комбинировать в единое уравнение состояния, выделенное красным цветом в центре горка: p * V / T = n * Rбар где * обозначает умножение, а / обозначает деление. Чтобы учесть влияние массы, мы определили константа, состоящая из двух частей: универсальная константа Rbar (на рисунке буква R с чертой наверху) и масса газа, выраженного в молях n . Проделав небольшую алгебру, мы получить более знакомую форму: р * V = n * Rбар * T Трехмерный график этого уравнения показан внизу слева. Перекресток точка любых двух линий на графике дает уникальное состояние для газ. Инженеры используют несколько иную форму уравнения состояние, специализированное для конкретного газа. Если разделить обе части общее уравнение на массу газа, объем становится удельный объем, который является обратным плотность газа. Определим также новую газовую постоянную Р , т.е. равна универсальной газовой постоянной, деленной на массу на моль газ. Значение новой константы зависит от типа газа, как в отличие от универсальной газовой постоянной, которая одинакова для всех газы. Значение уравнения состояния воздуха приведено на слайд как 0,286 кДж на килограмм на кельвин. Уравнение состояния можно записать в терминах конкретного объем или плотность воздуха как р * v = р * т р = г * р * т Обратите внимание, что уравнение данное здесь состояние относится только к идеальному газу или к реальному газу, который ведет себя как идеальный газ. На самом деле существует множество различных форм уравнение состояния для различных газов. Также имейте в виду, что температура, заданная в уравнении состояния, должна быть абсолютная температура который начинается с абсолютного нуля. В метрической системе единиц, мы должны указать температуру в Кельвинах (не в градусах Цельсия). В имперской системе абсолютная температура находится в Ренкина (не градусов по Фаренгейту). Виды деятельности: Экскурсии с гидом Газовая статика: Навигация .. Домашняя страница руководства для начинающих

Объем газа: уравнения, законы и единицы измерения

Газ — единственное состояние вещества, не имеющее определенной формы и объема. Молекулы газа могут расширяться, чтобы заполнить любой контейнер, в котором они находятся. Как же тогда рассчитать объем газа, если его нельзя зафиксировать? В этой статье рассматривается объем газа и его свойства. Мы также обсудим другие свойства, на которые влияет изменение объема газа. Наконец, мы рассмотрим примеры, где мы будем вычислять объем газа. Приятного обучения!

Определение объема газа

Рис. 1: Объем газа принимает форму сосуда, в котором хранится газ.

Газы не имеют четкой формы или объема , пока они контейнер. Их молекулы рассредоточены и движутся беспорядочно , и это свойство позволяет газам расширяться и сжиматься, когда газ выталкивается в контейнеры различных размеров и форм.

Объем газа можно определить как объем контейнера, в котором он содержится. 93\).

Приведенное выше уравнение справедливо только при комнатной температуре и атмосферном давлении. Но что, если давление и температура также меняются? На объем газа влияют изменения давления и температуры . Давайте посмотрим на их отношения.

Теперь давайте изучим влияние изменения давления на объем газа.

Зависимость между давлением и объемом газа

Рис. 3: По мере уменьшения объема газа давление увеличивается. Это связано с тем, что увеличивается частота и влияние столкновений между молекулами газа и стенками сосуда.

Теперь рассмотрим фиксированное количество газа, поддерживаемого при постоянной температуре. Уменьшение объема газа заставит молекулы газа двигаться ближе друг к другу. Это увеличит столкновения между молекулами и стенками контейнера. Это приводит к увеличению давления газа. Давайте посмотрим на математическое уравнение для этого отношения, называемое законом Бойля.

Формула, описывающая объем газа

Закон Бойля дает соотношение между давлением и объемом газа при постоянной температуре. 93\) . Проще говоря, закон Бойля звучит так:

\[\text{давление}\times \text{объем}=\text{константа}.\]

Приведенное выше уравнение верно, только если температура и количество газа постоянны. Его также можно использовать при сравнении одного и того же газа в разных условиях, 1 и 2:

\[p_1v_1=p_2V_2,\]

или прописью:

\[\text{начальное давление}\times \text{начальное volume}=\text{конечное давление}\times \text{конечный объем}. \]

Подводя итог, можно сказать, что для фиксированного количества газа (в молях) при постоянной температуре произведение давления на объем постоянно.

Чтобы дать вам более полное представление о факторах, влияющих на объем газов, мы рассмотрим изменение температуры газа в этом глубоком погружении. Мы говорили о том, как молекулы газа хаотично движутся в сосуде, в котором они находятся: эти молекулы сталкиваются друг с другом и со стенками сосуда.

Рис. 4: При нагревании газа при постоянном давлении его объем увеличивается. Это связано с тем, что средняя скорость частиц газа увеличивается и заставляет газ расширяться.

Теперь рассмотрим фиксированное количество газа, находящегося в закрытом контейнере при постоянном давлении . По мере повышения температуры газа средняя энергия молекул увеличивается, увеличивая их среднюю скорость. Это приводит к расширению газа. Жак Шарль сформулировал закон, связывающий объем и температуру газа следующим образом.