Формула дифракция света: Дифракция света – материалы для подготовки к ЕГЭ по Физике

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Определение 1

Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Рисунок 3.8.1 Принцип Гюйгенса-Френеля. ∆S1 и ∆S2_{– элементы волнового фронта, n1→ и n2→ – заданные нормали.}

Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

Для определения колебания в заданной точке P, которое вызвано волной, используя принцип Френеля, находят колебания, которые вызваны в этой точке с помощью отдельных вторичных волн, которые приходят от элементов поверхности S (∆S1, ∆S2 и так далее). Далее следует произвести сложение колебаний, учитывая амплитуды и фазы. Элементы, загороженные препятствиями, не учитываются при решении.

Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

Рисунок 3.8.2 Дифракция плоской волны на экране, содержащем круглое отверстие.

Р – точка наблюдения, находящаяся на оси симметрии, располагаемого на L расстоянии относительно экрана. По принципу Гюйгенса-Френеля распределить на волновой поверхности вторичные источники, совпадающие с плоскостью отверстия, где волны достигают точки Р. Интерференция волн в этой точке является причиной возникновения результирующего колебания, квадрат амплитуды которого определяется при наличии значений длин волн λ, амплитуды A0_{падающей волны и расположением элементов.}

Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Иначе говоря, r1=L+λ2, r2=L+2λ2, r3=L+3λ2…

При рассмотрении волновой поверхности исходя из точки Р, тогда получим, что границы зон Френеля будут иметь вид концентрических окружностей. Наглядно это изображено на рисунке.

Рисунок 3.8.3 Границы зон Френеля в плоскости отверстия.

По рисунку 3.8.2 определяем радиусы ρmзон по формуле: ρm=ρm2-L2=mλL+m2λ24≈mλL.

Зоны Френеля. Интерференционный максимум

Из определений раздела оптики имеем, что λ<<L, тогда при решении можно пренебречь вторым подкоренным выражением. Для определения количества зон Френеля, которые укладываются на отверстии, используется формула, включающая в себя значение радиуса R: m=R2λL.

Значение m может быть любым числом. От него зависит результат интерференции вторичных волн, проходящих точку Р. Такие открытые зоны Френеля обладают одинаковым значением площади:

Sm=πρm2-πρm-21=πλL=S1.

По теории равные площади возбуждают колебания с одинаковой амплитудой в точке наблюдения. Но каждая последующая зона угла α, располагаемая между лучом, проводимым к точке наблюдения, и нормалью относительно волновой поверхности, возрастает. Предположения Френеля говорит о том, что при увеличении угла α происходит незначительное уменьшение колебаний, то есть:

A1>A2>A3>…>A1, где Amобозначает амплитуду колебаний, которые были вызваны при помощи m-ой зоны.

Используя приближение, видно, что амплитуда колебаний, которая вызвана определенной зоной, равняется среднему арифметическому соседних зон. Иначе это запишем как Am=Am-1+Am+12.

Отличие от двух соседних точек расстоянием λ2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

A=A1–A2+A3–A4+…=A1–(A2–A3)–(A4–A5)–…<A1.

Отсюда делаем вывод, что суммарная амплитуда в точке меньше колебаний, вызванных только при помощи одной зоны Френеля. Если все имеющиеся зоны Френеля являлись открытыми, тогда к точке наблюдения двигалась волна с амплитудой A0, невозмущенная препятствием. Тогда запись принимает вид:

A=A0+A12-A2+A32+A32-A4+A52+…=A12.

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Когда отверстие непрозрачного экрана дает возможность только одной зоне Френеля быть открытой, тогда наблюдается возрастание амплитуды колебаний в количестве 3 раз, а интенсивности – 4 раз. При открытии двух зон действие становится равным нулю. При наличии непрозрачного экрана с несколькими нечетными открытыми зонами, очевидно, что произойдет резкое возрастание амплитуды. При открытии 1, 3, 5 зон получим, что A=6·A0, I=36·I0.

Определение 2

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

A=Am+1-Am+2+Am+3-…=Am+12+Am+12-Am+2-Am+32+…

Иначе можно записать как A=Am+1 2, ибо выражения в скобках будут равняться нулю.

Определение 3

Когда диск может закрыть небольшие зоны, тогда Am + 1≈2A0 и A≈A0, можно наблюдать интерференционный максимум. Иначе его называют пятном Пуассона, которое окружается дифракционными кольцами светлого и темного цвета.

Пример 1

Чтобы углубиться в понятие, необходимо оценить зоны Френеля. Имеется дифракционная картина на экране с расстоянием равным L=1м, а значение длины волны света λ=600нм (красный).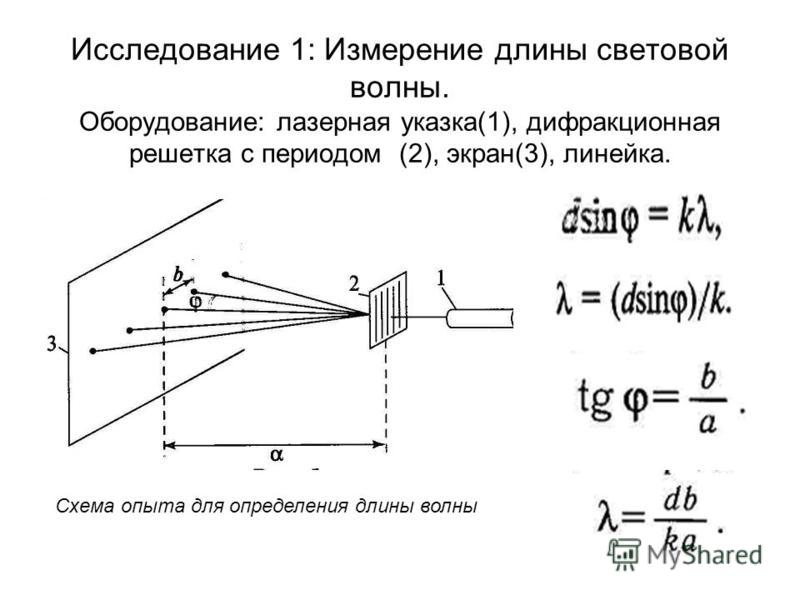 Отсюда получим, что радиусом первой зоны является ρ1=Lλ≈0,77мм.

Определение 4

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

m=R2Lλ≥1 или R2≥Lλ.

Название данного соотношения – критерий наблюдения дифракции.

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

m=R2Lλ>>1 или R2>>Lλ.

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Определение 5

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

Выше рассмотренный случай относится к дифракции света с удаленным источником, располагаемом на препятствиях округлой формы. При расположении точечного источника света на конечном расстоянии сферически расходящаяся волна должна падать на препятствие.

Данный случай усложняет задачу. Тогда построение зон Френеля необходимо выполнять на поверхности сферической формы, показанное на рисунке 3.8.4.

 Рисунок 3.8.4Зоны Френеля на сферическом фронте волны. 

При расчете видно, что радиусы ρmзон Френеля на волне сферического фронта запишется, как

ρm=aba+bλ.

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Рисунок 3.8.5 Модель дифракции света.

Рисунок 3.8.6 Модель зоны Френеля.

§20. Дифракция света Основные формулы

Угол отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия

,

где а – ширина щели; k – порядковый номер максимума (k = 1,2,3,…).

Угол отклонения лучей, соответствующий минимуму (темная полоса) при дифракции на одной щели, определяется из условия

.

Угол отклонения лучей, соответствующий максимуму при дифракции света на дифракционной решетке, определяется из условия

,

где k = 0,1,2,3,…; d – период дифракционной решетки.

Разрешающая способность дифракционной решетки равна

где – наименьшая разность длин волн двух соседних спектральных линий ( и ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решет­ки;

N – полное число щелей решетки; k – порядковый номер дифракционного максимума.

Формула Вульфа – Брэггов имеет вид

,

где – угол скольжения, то есть угол между направлением пучка парал­лельных рентгеновских лучей, падающих на кристалл, и гранью кристалла; d – расстояние между атомными плоскостями кри­сталла. Формула Вульфа – Брэггов определяет направление лучей, при которых возникает дифракционный максимум.

Задачи

20.1. На щель шириной а = 0,05 мм падает нормально монохро­матический свет (λ= 0,6 мкм). Определить угол φ между первоначаль­ным направлением пучка света и направлением на четвертую тем­ную дифракционную полосу.

20.2 Точечный источник света с длиной волны λ =0,5мкм расположен на расстоянии а = 100 см перед диафрагмой с круглым отверстием радиуса r = 1,0 мм. Найти расстояние b от диафрагмы до точки наблюдения, для которой число зон Френеля в отверстии составляет к = 3.

20.3. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояние от диафрагмы до источника и экрана равны

а = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r₁ = 1,00 мм и следующий максимум — при r₂ = 1,29 мм.

20.4. На узкую щель падает нормально монохроматический свет. Угол φ отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 1⁰. Скольким длинам волн падающего света равна ширина щели?

20.5. На щель шириной а = 0,1 мм падает нормально монохрома­тический свет (λ= 0,5 мкм). За щелью помещена собирающая лин­за, в фокальной плоскости которой находится экран. Что будет на­блюдаться на экране, если угол φ дифракции равен: 1) 17

/; 2) 43^/?

20.6. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (λ= 0,6 мкм) максимум пятого порядка отклонен на угол φ = 18⁰?

20.7. На дифракционную решетку, содержащую n = 100 штри­хов на 1 мм, падает нормально монохроматический свет. Зритель­ная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол = 20°. Определить длину волны света.

20.8. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ₁ = 14⁰. На какой угол φ₂ откло­нен максимум третьего порядка?

20.9. Дифракционная решетка содержит n = 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ= 0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

20.10. На дифракционную решетку, содержащую n = 400 штри­хов на 1 мм, падает нормально монохроматический свет (λ= 0,6мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол φ дифракции, соответствующий послед­нему максимуму.

20.11. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (λ= 0,4 мкм) спектра третьего порядка?

20. 12. На дифракционную решетку, содержащую n = 500 штри­хов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра = 780 нм, = 400 нм.

20.13. Дифракционная картина получена с помощью дифракционной решетки длиной l = 1,5 см и периодом d = 5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн = 0,1 нм, если линии лежат в крайней красной части спектра ( ≈ 760 нм).

20.14. Какой наименьшей разрешающей силой R должна обла­дать дифракционная решетка, чтобы с ее помощью можно было раз­решить две спектральные линии калия ( = 578 нм и = 580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

20. 15. С помощью дифракционной решетки с периодом d = 20 мкм требуется разрешить дублет натрия ( = 589,0 нм и = 589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно?

20.16. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ= 147 пм). Определить расстоя­ние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение надает под углом θ = 31⁰30^/ к поверхности кристалла.

20.17. Какова длина волны λ монохроматического рентгеновского излучения, падающего на кристалл кальцита, если дифракционный максимум первого порядка наблюдается, когда угол θ между на­правлением падающего излучения и гранью кристалла равен 3⁰? Расстояние d между атомными плоскостями кристалла принять рав­ным 0,3 нм.

20.18. Параллельный пучок рентгеновского излучения падает на грань кристалла. Под углом θ = 65⁰ к плоскости грани наблю­дается максимум первого порядка. Расстояние d между атомными плоскостями кристалла 280 пм. Определить длину волны рентге­новского излучения.

4.3 Двухщелевая дифракция — University Physics Volume 3

Цели обучения

К концу этого раздела вы сможете:

• Описать комбинированный эффект интерференции и дифракции с двумя щелями, каждая из которых имеет конечную ширину
• Определение относительной интенсивности интерференционных полос на дифракционной картине
• Определите пропущенные порядки, если таковые имеются

Когда мы изучали интерференцию в эксперименте Юнга с двумя щелями, мы игнорировали эффект дифракции в каждой щели. Мы предполагали, что щели настолько узкие, что на экране вы видите только интерференцию света всего от двух точечных источников. Если щель меньше длины волны, то на рис. 4.10 (а) видно, что на экране наблюдается только распространение света, а не пики и провалы. Поэтому было разумно исключить в этой главе эффект дифракции. Однако, если вы сделаете щель шире, рис. 4.10 (b) и (c) показывают, что вы не можете игнорировать дифракцию. В этом разделе мы изучаем сложности эксперимента с двумя щелями, которые возникают, когда вам также необходимо учитывать дифракционный эффект каждой щели.

Чтобы рассчитать дифракционную картину для двух (или любого количества) щелей, нам нужно обобщить метод, который мы только что использовали, для одной щели. То есть поперек каждой щели мы размещаем равномерное распределение точечных источников, излучающих вейвлеты Гюйгенса, а затем суммируем вейвлеты от всех щелей. Это дает интенсивность в любой точке экрана. Хотя детали этого вычисления могут быть сложными, окончательный результат довольно прост:

. Двухщелевая дифракционная картина

Дифракционная картина двух щелей шириной a , разделенных расстоянием d , представляет собой интерференционную картину двух точечных источников, разделенных d , умноженную на дифракционную картину щели шириной a .

Другими словами, местоположений интерференционных полос задаются уравнением дифракционные эффекты согласно уравнению 4.4. [Обратите внимание, что в главе об интерференции мы написали dsinθ=mλdsinθ=mλ и использовали целое число m для обозначения интерференционных полос. В уравнении 4.1 также используется м , но на этот раз для обозначения дифракционных минимумов. Если оба уравнения используются одновременно, рекомендуется использовать другую переменную (например, n ) для одного из этих целых чисел, чтобы они были различны.]

Эффекты интерференции и дифракции действуют одновременно и обычно дают минимумы при разных углы. Это приводит к сложной картине на экране, в которой отсутствуют некоторые максимумы интерференции от двух щелей, если максимум интерференции находится в том же направлении, что и минимум дифракции. Такой отсутствующий пик мы называем отсутствующим порядком. Один из примеров дифракционной картины на экране показан на рис. 4.11. Сплошная линия с несколькими пиками разной высоты — интенсивность, наблюдаемая на экране. Это результат интерференции волн от отдельных щелей и дифракции волн внутри одной щели.

Рисунок 4.11 Дифракция от двойной щели. Фиолетовая линия с пиками одинаковой высоты — результат интерференции волн от двух щелей; синяя линия с одним большим горбом посередине — дифракция волн внутри одной щели; а толстая красная линия — это произведение двух, то есть картина, наблюдаемая на экране. График показывает ожидаемый результат для ширины щели a=2λa=2λ и расстояния между щелями d=6λd=6λ. Максимум порядка m=±3m=±3 для интерференции отсутствует, поскольку минимум дифракции происходит в том же направлении.

Пример 4.3

Интенсивность полос

На рис. 4.11 показано, что интенсивность полос при m=3m=3 равна нулю, но как насчет других полос? Рассчитайте интенсивность полосы при m=1m=1 относительно I0,I0, интенсивности центрального пика.

Стратегия

Определите угол интерференционной полосы с двумя щелями, используя уравнение из Interference, затем определите относительную интенсивность в этом направлении из-за дифракции, используя уравнение 4.4.

Решение

Из главы об интерференции мы знаем, что яркие интерференционные полосы возникают при dsinθ=mλdsinθ=mλ, или

sinθ=mλd.sinθ=mλd.

Из уравнения 4.4,

I=I0(sinββ)2, где β=ϕ2=πasinθλ.I=I0(sinββ)2, гдеβ=ϕ2=πasinθλ.

Подстановка сверху,

β=πasinθλ=πaλ·mλd=mπad.β=πasinθλ=πaλ·mλd=mπad.

Для a=2λa=2λ, d=6λd=6λ и m=1m=1,

β=(1)π(2λ)(6λ)=π3.β=(1)π(2λ)(6λ )=π3.

Тогда интенсивность равна

I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684I0.I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684 I0.

Значение

Обратите внимание, что этот подход относительно прост и дает результат, почти такой же, как и более сложный анализ с использованием векторов для определения значений интенсивности двухщелевой интерференции (тонкая линия на рис. 4.11). Метод фазора учитывает нисходящий наклон интенсивности дифракции (синяя линия), так что пик около м=1м=1 возникает при значении θθ немного меньшем, чем мы показали здесь.

Пример 4.4

Двухщелевая дифракция

Предположим, что в эксперименте Юнга щели шириной 0,020 мм разнесены на 0,20 мм. Если щели освещаются монохроматическим светом с длиной волны 500 нм, сколько ярких полос наблюдается в центральном пике дифракционной картины?

Раствор

Из уравнения 4.1 угловое положение первого дифракционного минимума равно ×10−5м=2,5×10−2рад.

Используя dsinθ=mλdsinθ=mλ для θ=2,5×10−2радθ=2,5×10−2рад, находим

m=dsinθλ=(0,20 мм)(2,5×10−2рад)(5,0×10−7м)= 10,m=dsinθλ=(0,20 мм)(2,5×10-2рад)(5,0×10-7м)=10,

, что является максимальным порядком интерференции, который находится внутри центрального пика. Заметим, что m=±10m=±10 — недостающие порядки, так как θθ точно совпадает. Соответственно, мы наблюдаем яркие полосы для

m=−9,−8,−7,−6,−5,−4,−3,−2,−1,0,+1,+2,+3,+ 4,+5,+6,+7,+8 и+9m=-9,-8,-7,-6,-5,-4,-3,-2,-1,0,+1, +2,+3,+4,+5,+6,+7,+8 и+9

всего 19 ярких полос.

Проверьте свое понимание 4.3

Для эксперимента в примере 4.4 покажите, что m=20m=20 также является отсутствующим порядком.

Интерактивный

Исследуйте эффекты двухщелевой дифракции. В этой симуляции, написанной Фу-Квун Хвангом, выберите N=2N=2 с помощью ползунка и посмотрите, что произойдет, если вы зададите ширину щели, расстояние между щелями и длину волны. Можете ли вы сделать заказ «пропавшим без вести»?

27,5 Дифракция на одной щели – College Physics

Глава 27 Волновая оптика

Резюме

• Обсудите дифракционную картину с одной щелью.

Свет, проходящий через одиночную щель, образует дифракционную картину, несколько отличающуюся от той, что образуется от двойных щелей или дифракционных решеток. На рис. 1 показана картина дифракции от одной щели. Обратите внимание, что центральный максимум больше, чем с обеих сторон, и что интенсивность быстро уменьшается с обеих сторон. Напротив, дифракционная решетка создает равномерно расположенные линии, которые медленно тускнеют по обе стороны от центра.

Рис. 1. (а) Дифракционная картина с одной щелью. Монохроматический свет, проходящий через одну щель, имеет центральный максимум и множество меньших и более тусклых максимумов по обеим сторонам. Центральный максимум в шесть раз выше показанного. (b) На рисунке показан яркий центральный максимум и более тусклые и тонкие максимумы по бокам.

Анализ дифракции на одной щели показан на рис. 2. Здесь мы рассматриваем свет, исходящий из разных частей одной и той же щели . Согласно принципу Гюйгенса, каждая часть волнового фронта в щели излучает волны. Это как лучи, которые начинаются в фазе и расходятся во всех направлениях. (Каждый луч перпендикулярен волновому фронту вейвлета. ) Предполагая, что экран находится очень далеко по сравнению с размером щели, лучи, направляющиеся к общему месту назначения, почти параллельны. Когда они движутся прямо вперед, как на рис. 2(а), они остаются в фазе, и получается центральный максимум. Однако, когда лучи проходят под углом [латекс] {\ тета} [/латекс] относительно исходного направления луча, каждый из них проходит разное расстояние до общего места, и они могут приходить в фазе или не в фазе. На рисунке 2(b) луч снизу проходит расстояние на одну длину волны [латекс] {\ lambda} [/латекс] дальше, чем луч сверху. Таким образом, луч из центра проходит расстояние [латекс] {\ лямбда / 2} [/ латекс] дальше, чем луч слева, приходит в противофазе и деструктивно интерферирует. Луч, идущий немного выше центра, и луч, идущий чуть выше дна, также компенсируют друг друга. На самом деле каждый луч из щели будет деструктивно интерферировать с другим, и под этим углом будет иметь место минимум интенсивности. Будет еще один минимум под тем же углом справа от направления падения света.

Рис. 2. Свет, проходящий через одну щель, дифрагирует во всех направлениях и может интерферировать конструктивно или деструктивно, в зависимости от угла. Видно, что разница в длине пути для лучей с обеих сторон щели составляет D sin θ .

При большем угле, показанном на рис. 2(с), длины пути различаются на [латекс]{3 \лямбда/2}[/латекс] для лучей, исходящих сверху и снизу щели. Один луч проходит расстояние [латекс] {\ лямбда} [/латекс], отличное от луча снизу, и приходит в фазе, конструктивно интерферируя. Два луча, каждый немного выше этих двух, также конструктивно добавят. Большинство лучей от щели будут конструктивно интерферировать с другим, и максимум интенсивности будет иметь место под этим углом. Однако в этой ситуации не все лучи конструктивно интерферируют, поэтому максимум не такой интенсивный, как центральный максимум. Наконец, на рис. 2(d) показанный угол достаточно велик, чтобы получить второй минимум. Как видно из рисунка, разница в длине пути для лучей с обеих сторон щели составляет [латекс]{D \;\text{sin} \;\theta}[/latex], и мы видим, что деструктивный минимум равен получается, когда это расстояние является целым кратным длины волны.

Рис. 3. График интенсивности дифракции от одной щели, показывающий, что центральный максимум шире и намного интенсивнее, чем по бокам. На самом деле центральный максимум в шесть раз выше, чем показано здесь.

Таким образом, для получения деструктивной интерференции для одной щели ,

[латекс] {D \;\text{sin} = m \lambda , \;\text{for} \; м = \; 1, \; -1, \; 2, \; -2, \; 3, \; \точки\;\;\; \text{(разрушающий)}},[/latex]

, где [латекс]{D}[/латекс] — ширина щели, [латекс] {\ лямбда} [/латекс] — длина волны света, [латекс] {\ тета} [/латекс] — угол относительно исходное направление света, а размер мм 12{м} {} является порядком минимума. На рис. 3 показан график интенсивности однощелевой интерференции, и видно, что максимумы по обе стороны от центрального максимума гораздо менее интенсивны и не такие широкие. Это согласуется с иллюстрацией на рисунке 1(b). 9{\circ}}[/latex] относительно направления падения света. а) Какова ширина щели? б) Под каким углом образуется первый минимум?

Рис. 4. В этом примере анализируется график однощелевой дифракционной картины.

Стратегия

Исходя из данной информации и предполагая, что экран находится далеко от щели, мы можем использовать уравнение [латекс]{D \;\text{sin} \;\theta = m \lambda}[/ латекс] сначала найти [латекс]{D}[/латекс], а затем снова найти угол для первого минимума [латекс]{\тета _1}[/латекс]. 9{\ circ})} [/латекс]. Таким образом, второй максимум примерно вдвое меньше центрального максимума.

• Одна щель дает интерференционную картину, характеризующуюся широким центральным максимумом и более узкими и тусклыми максимумами по бокам.
• Имеется деструктивная интерференция для одиночной щели, когда
  [латекс]{D \;\text{sin} \;\theta = m \lambda , \; (\text{for} \; m = \; 1, \; -1, \; 2, \; -2, \; 3, \; \dots)}[/latex], где [латекс]{D} [/latex] — ширина щели, [latex] {\ lambda} [/latex] — длина волны света, [latex] {\ theta} [/latex] — угол относительно исходного направления света, а [ латекс]{м}[/латекс] — порядок минимума. {\circ}}[/латекс]? Подробно покажите, как вы следуете шагам, описанным в главе 27.7 «Стратегии решения проблем для волновой оптики» 9.0005

  9: а) Найдите угол между первыми минимумами двух линий паров натрия с длинами волн 589,1 и 589,6 нм, когда они падают на одну щель шириной [латекс] {2,00 мкм; \text{м}}[/латекс]. б) Каково расстояние между этими минимумами, если дифракционная картина падает на экран на расстоянии 1,00 м от щели? в) Обсудите легкость или трудность измерения такого расстояния.

  10: (a) Какова минимальная ширина одиночной щели (кратная [латекс] {\ лямбда} [/латекс]), которая дает первый минимум для длины волны [латекс] {\ лямбда} [/латекс]? б) Какова его минимальная ширина, если он дает 50 минимумов? с) 1000 минимумов? 9{\circ}}[/latex], при каком угле находится минимум второго порядка? б) Каков угол минимума третьего порядка? в) Существует ли минимум четвертого порядка? (d) Используйте свои ответы, чтобы проиллюстрировать, как угловая ширина центрального максимума примерно в два раза превышает угловую ширину следующего максимума (который представляет собой угол между первым и вторым минимумами).