Длина волны – формула расчета, значение
4.1
Средняя оценка: 4.1
Всего получено оценок: 178.
4.1
Средняя оценка: 4.1
Всего получено оценок: 178.
Для описания волновых процессов в Природе используется ряд специальных величин, специфичных для распространения волн. Важнейшим среди них является длина волны. Рассмотрим это понятие, а также его связь с другими понятиями волновых процессов.
Волна и ее распространение
Движение – форма существования материи. Одним из широко распространенных в природе движений является колебательное движение, при котором измеряемая величина изменяется не монотонно, а циклически увеличивая и уменьшая свое значение.
Рис. 1. Колебания в природе и технике.В протяженных объектах любые изменения (и в том числе колебательные процессы), как правило, происходят не сразу во всем объекте, а сперва начинаются в одной его части, а потом распространяются на остальной объект.
Для наблюдения распространения колебательных движений удобно использовать поверхность воды.
Волна – это колебания среды, распространяющиеся в ней с течением времени.
Параметры волны
Фаза, период и частота
Для распространяющейся волны можно ввести параметр, который называется фазой. Фаза – это одинаковое состояние среды распространения. Для поверхности воды фаза – это величина отклонения от спокойного состояния (от нулевого уровня). Точки волны, находящиеся в одинаковом состоянии, будут находиться в одинаковых фазах. Если записывать в таблицу время, проходящее между одинаковыми фазами какой-то точки, то можно заметить, что это время будет кратно некоторому минимальному значению. Это значение, минимальное время, за которое волна оказывается в одной и той же фазе, называется периодом колебаний $T$ волны.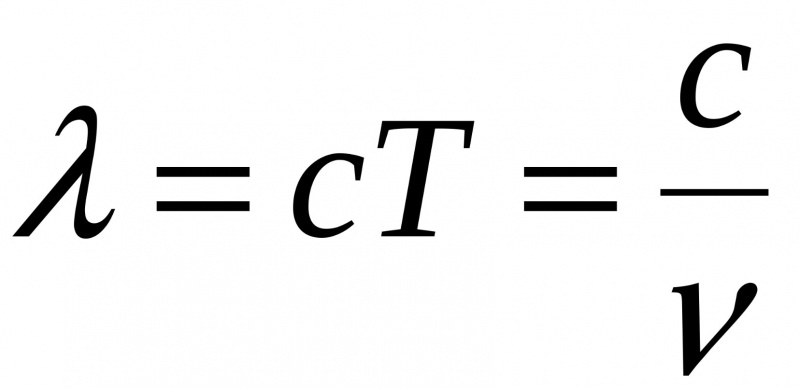
$$\nu={1\over T}$$
Фазу можно сопоставить с углом на координатной плоскости. Полная волна соответствует углу $2\pi$, все фазы повторяются с этим периодом точно так же, как повторяется значение круговых функций (синуса, косинуса и других).
Одному значению отклонения от нулевого значения соответствуют две фазы – одна в момент возрастания, другая – в момент спадания волны (исключение – самый «пик» или самое «дно» волны). Это разные фазы, путать их не следует.
Скорость распространения и длина волны
Поскольку волна распространяется не мгновенно, то, отметив одинаковую фазу волны (движущийся гребень), можно определить скорость этого распространения $v$ относительно неподвижных предметов (например, относительно берега, в случае, когда волна распространяется вдоль него). Для вычисления используется обычная формула скорости – отношение пройденного расстояния к прошедшему времени.
Расстояние, которое проходит волна за один период колебания, называется длиной волны, для обозначения используется греческая буква $\lambda$ (лямбда). Формула длины волны:
$$\lambda=vT$$
Рис. 3. Длина волны.Если известна частота колебаний, для расчета удобнее пользоваться другой формулой (она вытекает из определения частоты):
$$\lambda={v\over \nu}$$
Слышимый звук представляет из себя колебания плотности воздуха. Распространяется он в нормальных условиях со скоростью, имеющей значения порядка 300-350м/с, и имеет длину волны от ~15мм (самые высокие частоты) до ~15м (самые низкие частоты)
Что мы узнали?
Волна – это колебания среды, распространяющиеся в ней с течением времени. Волна характеризуется рядом параметров, среди которых фаза, период, скорость распространения, длина.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Егор Князев
7/10
Оценка доклада
4.
1
Средняя оценка: 4.1
Всего получено оценок: 178.
А какая ваша оценка?
| Волны де Бройляde Broglie waves Волны де Бройля – волны, связанные с любой движущейся материальной частицей. где E0 = mc2 − энергия покоя частицы массы m, λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ). Существование волн де Бройля доказано многочисленными
экспериментами, в которых частицы ведут себя как волны. Так при рассеянии
пучка электронов с энергией 100 эВ на упорядоченной системе атомов кристалла,
играющего роль дифракционной решётки, наблюдается отчётливая дифракционная
картина. Существование волн де Бройля лежит в основе работы электронного
микроскопа, разрешающая способность которого намного порядков выше, чем
у любого оптического микроскопа, что позволяет наблюдать молекулы и атомы,
а также в основе методов исследования таких сверхмалых объектов, как атомные
ядра и элементарные частицы, бомбардировкой их частицами высоких энергий.
|
Боттомоний
Чармоний
Любая движущаяся
частица (например, электрон) ведёт себя не только как локализованный в пространстве
перемещающийся объект – корпускула, но и как волна, причём длина этой волны
даётся формулой λ = h/р, где h = 6.6·10-34 Дж.сек
– постоянная Планка, а р – импульс частицы. Эта волна и получила название
волны де Бройля (в честь французского физика-теоретика
Луи де Бройля,
впервые высказавшего гипотезу о таких волнах в 1923 г.). Если частица имеет
массу m и скорость v << с (с – скорость света), то импульс частицы р = mv
и дебройлевская длина волны связаны соотношением λ = h/mv.
Метод дифракции частиц в настоящее время широко используется при изучении
строения и свойств вещества.Замедление времени/сокращение длины
Замедление времени/сокращение длины
| Индекс Концепции относительности | ||||
| 7
Для малых скоростей, при которых коэффициент относительности очень близок к 1, замедление времени можно разложить в биномиальное разложение, чтобы получить приблизительное выражение: См. также Гравитационное замедление времени
| Индекс Концепции относительности | |||||
| Назад |
Время всегда будет самым коротким, если измерять его в системе покоя. Время, измеряемое в системе отсчета, в которой часы покоятся, называется «собственным временем».| Увеличение «эффективной массы» со скоростью определяется выражением Оно следует из преобразования Лоренца при описании столкновений из неподвижной и подвижной системы отсчета, где оно возникает в результате сохранения импульса.  Вы также можете подойти к нему из релятивистского выражения энергии, где эффективная масса определяется как энергия, деленная на c 2 . Это говорит о том, что это «m» действительно относится к энергии, и что реальная масса — это масса покоя m 0 . Увеличение релятивистской «эффективной массы» связано со скоростью света c пределом скорости Вселенной. Эта увеличенная эффективная масса очевидна в циклотронах и других ускорители, где скорость приближается c. Изучение приведенного выше расчета покажет, что вы должны достичь 14% скорости света, или около 42 миллионов м/с, прежде чем вы измените эффективную массу на 1%. Этот термин об «эффективной массе» включен сюда, потому что он уже давно используется в элементарных учебниках для описания увеличения энергии со скоростью, и он имеет определенную привлекательность для описания релятивистских эффектов, таких как Кембриджский пример. “Ой! Понятие “релятивистская масса” может быть неправильно истолковано. Вот почему мы его не используем. Во-первых, оно применяет название массы – относящееся к величине 4-вектора – к совершенно другому понятию, временная составляющая 4-вектора. Во-вторых, это делает увеличение энергии объекта со скоростью или импульсом связанным с некоторым изменением внутренней структуры объекта. В действительности увеличение энергии со скоростью происходит не в объекта, а в геометрических свойствах самого пространства-времени». (Тейлор и Уилер в физике пространства-времени)
| Индекс Концепции относительности | |||
| 7
Но вы не найдете его в современных учебниках по физике. Один комментарий из классической работы по теории относительности:На ускорителе электронов в Кембридже, штат Массачусетс, последний этап ускорения имеет следующие характеристики:
Это увеличение скорости требует 186-кратного увеличения энергии, но экономит всего одну секунду на двухчасовом пути. Проблемы с концепцией переменной массы | Индекс Концепции относительности Справочник Zukav | ||||||||||||
| Вернуться назад |
99986 c
Точка зрения Эйнштейна описана в следующей цитате:Сокращение длины: определение, формула и примеры
Представьте, что вы путешествуете с другом.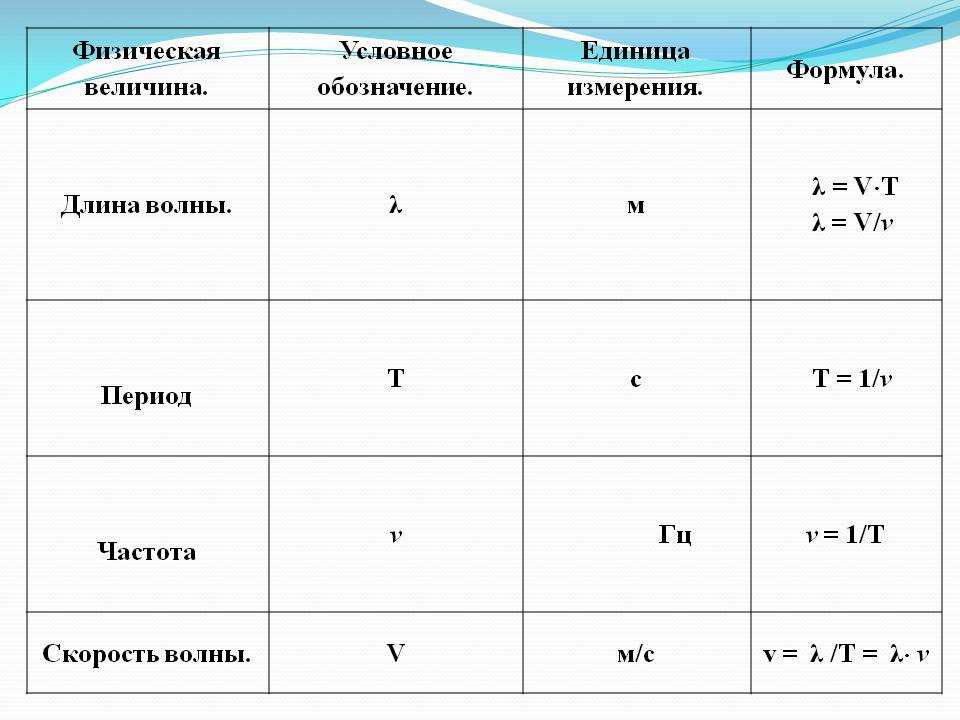
Вы говорите, что вам осталось пройти 20 км, а ваш друг говорит, что у вас осталось 30 км. Вы можете не соглашаться, но разногласие можно разрешить, измерив расстояние впереди. По крайней мере, так обстоит дело, когда вы путешествуете с обычной скоростью.
Однако при движении с релятивистскими скоростями , , близкими к скорости света , расхождение между двумя наблюдателями в разных системах отсчета может быть значительным.
Рисунок 1. Расстояния могут описываться разными людьми по-разному, но при релятивистских скоростях расстояния действительно разные.
Что такое сокращение длины?
Мы говорим о сокращении длины, когда длина объекта, движущегося с определенной скоростью относительно системы отсчета, оказывается меньше его собственной длины. Собственная длина (L 0 ) — это расстояние между двумя точками, наблюдаемыми наблюдателем, который находится в состоянии покоя в относительно обеих точек .
Несмотря на то, что часы измеряют разные истекшие периоды для одной и той же процедуры, относительная скорость , то есть расстояние, деленное на прошедшее время, одинакова. Это означает, что на расстояние также влияет относительное движение наблюдателя . Эти две затронутые величины компенсируют друг друга, оставляя скорость постоянной. Чтобы относительная скорость была одинаковой для двух наблюдателей, видящих разное время, они также должны измерить разные расстояния .
Сокращение длины — это явление, заключающееся в том, что когда наблюдатель движется со скоростью, близкой к скорости света, расстояния, полученные разными наблюдателями, неодинаковы.
Как рассчитать сокращение длины?
Обсудив, что мы подразумеваем под сокращением длины и правильной длиной, давайте рассмотрим пример, чтобы понять, как рассчитать сокращение длины.
Допустим, космический корабль движется со скоростью v, близкой к скорости света.
Наблюдатель A на Земле и наблюдатель B на космическом корабле будут наблюдать разные длины для расстояния, пройденного космическим кораблем.
Рис. 2. Уменьшение длины. Источник: Мануэль Р. Камачо, StudySmarter.
Мы знаем, что скорость космического корабля одинакова для всех наблюдателей. Если вычислить скорость v относительно земного наблюдателя A, то получим:
-связанный наблюдатель A.
Скорость относительно движущегося наблюдателя B равна:
Здесь Δt 0 — собственное время, наблюдаемое движущимся наблюдателем B, а L — расстояние, наблюдаемое движущимся наблюдателем B.
Две скорости одинаковы:
Мы знаем из замедления времени, что t = t 0 . Подставив это в предыдущее уравнение, мы получим:
Мы также знаем, что:
Вставив y, мы получим уравнение сокращения длины, как показано ниже:
Уменьшение длины объекта
Одним из последствий сокращения длины является то, что если объект движется со скоростью, близкой к скорости света, наблюдатель может заметить, что его длина меньше его собственной длины.
который покоится относительно движения. Рассмотрим следующий пример.
Рис. 3. Уменьшение длины. Источник: Огулкан Тезкан, StudySmarter.
Возьмите палку 10см. Его длина уже не будет казаться равной 10 см, если он пролетит мимо вас со скоростью, близкой к скорости света.
Длина стержня в состоянии покоя называется его собственной длиной . Когда палка движется со скоростью, близкой к скорости света, измеренная длина всегда будет на меньше, чем надлежащая длина. Когда скорость палки равна скорости света, палка теоретически не должна иметь длины .
Что является примером сокращения длины?
Отличным примером сокращения длины является перемещение объекта в пространстве, как в следующем примере.
Представим, что наблюдатель движется от синей планеты к красной со скоростью y=30.00. Расстояние между двумя планетами составляет 4000 световых лет, измеренное земным наблюдателем.