Размерности 10 класс онлайн-подготовка на Ростелеком Лицей
Как запомнить формулы? Как не ошибиться? Постарайтесь разобраться в концепции. Спросите себя, какие величины в принципе должны входить в эту формулу?
Для проверки и написания формулы используйте понятие размерности: Чтобы определить длину чего-то, необходимо сравнить ее с некоторой эталонной длинной. Если “веревка имеет длину 5 метров”, то имеется в виду, что ее длина в 5 раз больше эталонного объекта длиной 1 метр. Так же с любой другой величиной.
Некоторые единицы: Расстояние [м] Время [с] Масса [кг]
Операции с единицами измерения
Над размерностями можно проводить некоторые арифметические операции: их можно умножать и делить. Складывать и вычитать можно только величины одинаковых размерностей. (рис. 3.1)
Безразмерные величины, например, отношение двух сторон треугольника. Брать функции вроде синуса, косинуса или экспоненты можно только от безразмерных величин.
Размерности величин образуют системы. Одной из наиболее распространенных является система единиц СИ. В этой системе базовыми единицами измерения являются метр, килограмм и секунда, а также ампер, кельвин, моль, канделла. Все остальные величины могут быть из них получены, а потому называются производными. ■(Расстояние[м]@Время[с]@Масса[кг]@Ампер[А]@Кельвин[К]@Моль[моль]@Кандела[кд]) производные величины
Проверка формул Физика принципиально имеет дело с размерными величинами. И это накладывает существенные ограничения на структуру всех формул. Старайтесь проверять полученные вами формулы на размерности. Это позволит избежать ошибок.
Такая формула не верна, т.к. в ней складываются величины разных размерностей
А эта формула может быть правильной
Не всегда обязательно выписывать все единицы измерения. Например, такая формула, очевидно, подходит по размерности, так как m и m_0 имеют одинаковую размерность, а выделенное синим отношение безразмерно. Например, пусть m и m_0 – некоторые массы, т.е. измеряются в кг, а R – некоторые расстояния, т.е. измеряются в метрах. Тогда в синем выражении метры сокращаются. Такая формула подходит по размерности :
Например, пусть m и m_0 – некоторые массы, т.е. измеряются в кг, а R – некоторые расстояния, т.е. измеряются в метрах. Тогда в синем выражении метры сокращаются. Такая формула подходит по размерности :
А эти формулы неверные :
Получение формул
Для написания формулы спросите себя: какие величины в принципе должны входить в нее? Затем попробуйте составить формулу из интуитивных соображений. Воспользуйтесь размерным анализом. Например, надо получить формулу для длины окружности. На помощь приходят соображения размерности:
1) Длина окружности должна быть пропорциональна радиусу: l= r
2) Площадь окружности должна быть пропорциональна радиусу в квадрате: ■(l= r@S= r2 )
3) Плюс, числовой коэффициент Pi
Представим, что Вам на ЕГЭ попалась вот такая задача: Сепулятор модели ЗЛ-25 с длиной канала L=1м, вокатостью
и скоростью сепуляции V=23 м/с обеспечивает поток сепуляции
Какой будет обеспечен поток сепуляции J_1, если длина канала увеличится втрое, вокатость – в 4 раза, а скорость сепуляции V останется неизменной?
Решение: Может помочь метод размерностей. Нам известны 3 размерные величины; одну надо найти
Нам известны 3 размерные величины; одну надо найти
Начинаем подбирать
Таким образом, получаем формулу
Размерный анализ – мощный инструмент, который позволяет многое, но не все. Он не заменит понимания концепции, но может дополнить его.
Как обозначается длина окружности в физике. Как найти длину окружности: через диаметр и радиус
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее – и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус – 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14.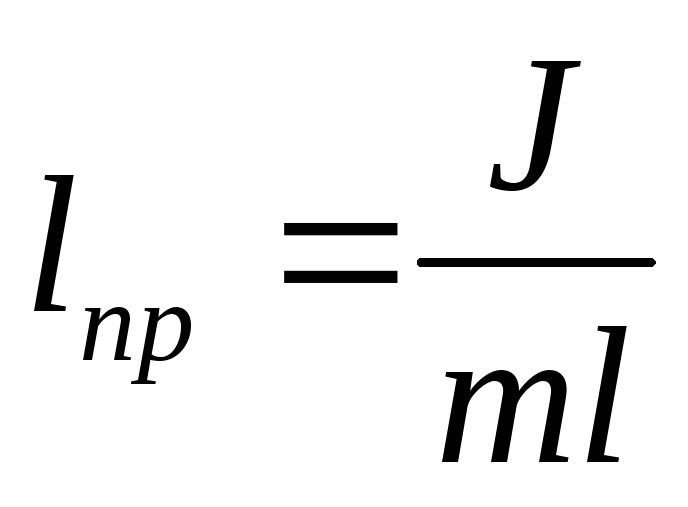 А так как известно, что R = D * 2, то формулу можно представить и другим способом
А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S – в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
- (·)O
— называется центром окружности.

- Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности . Радиус окружности обозначается буквой «R ». На рисунке выше — это отрезок «OA ».
- Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
Диаметр окружности обозначается буквой «D ». На рисунке выше — это отрезок «BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R , так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две – А и В – можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры – это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр – расстояние между точками , проходящее через центр фигуры.
Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр – расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С – это искомая величина, D – диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере – длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С – длина, r – радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.

- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек – это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве – рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.
Круг и окружность
Окружностью является множество точек, которые размещены на равном расстоянии от основной точки – центра. Это расстояние называется радиусом.
Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.
Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр – d. Поскольку соотношение длины очертания и диаметра – постоянное число, то его можно определить.
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π . Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π .
Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π – это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).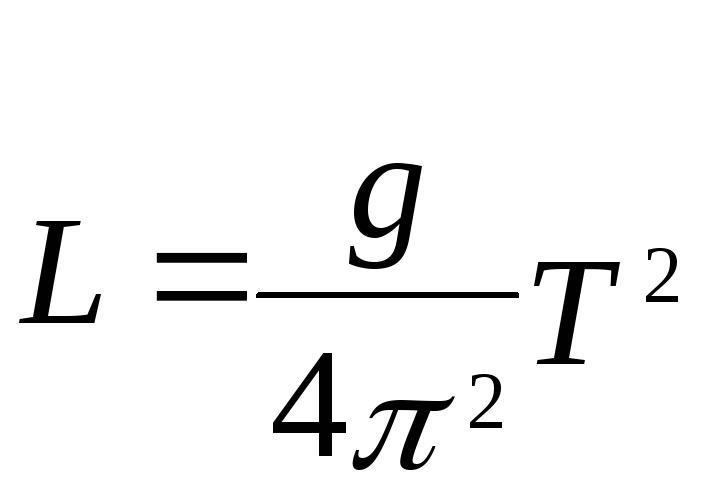
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π . Это будет выглядеть так d = C / π .
Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас – изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца – к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Калькулятор круга – это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Физика. Справочная информация Это краткий конспект основных понятий, законов и формул по механике, гидравлике, классической термодинамике, электромагнетизму и частично фотометрии, которые мне требуются наиболее часто. Он не претендует на исчерпывающую полноту, хотя и является достаточно полным для того, чтобы я обращался к другим справочникам лишь в довольно редких и частных случаях. Несколько общих замечанийРазмерности физических величин Все представленные ниже формулы и значения физических величин приведены в международной системе единиц измерения СИ (метр — килограмм — секунда — кельвин — ампер — кандела). При расчётах по собственным формулам необходимо проверять размерности (т.е. единицы измерения) левой и правой частей — они должны быть одинаковы (стерадианы, радианы, угловые градусы и синусы-косинусы-тангенсы от них, а также проценты, штуки и разы являются безразмерными величинами). В случае возникновения недоразумений (скажем, слева паскали, а справа ньютоны на квадратный метр) проверку размерностей следует выполнять, предварительно приведя все единицы измерения компонентов формулы к основным единицам измерения (указаны мелким шрифтом для тех величин, единицы измерения которых не являются основными). Несовпадение размерностей однозначно говорит о том, что формула ошибочна. И ещё одно важное замечание. Совпадение размерности (единиц измерения) результата той или иной формулы с размерностью одной из физических величин ещё не означает идентичности их физического смысла! Пример: произведение силы на механическую скорость F · v по своей размерности совпадает с мощностью, но физического смысла мощности как скорости совершения работы или скорости изменения энергии это произведение не имеет (вернее имеет, но в очень узких условиях — когда тело под действием силы набирает или теряет свою механическую скорость полностью, с нуля, причём строго за одну единицу времени, выбранную для расчёта). Скалярные и векторные величиныФизические величины могут быть скалярными и векторными. К скалярным величинам относятся те, к которым нельзя приложить понятие «направление». К векторным величинам относятся те, которые имеют определённое направление в пространстве. В механике это перемещение и все производные от него — скорость, ускорение, импульс, сила, давление. При их сложении обязательно нужно учитывать их взаимную ориентацию. Однородные величины, направленные в одну сторону, суммируются, в противоположные — вычитаются, а в общем случае их влияние определяется проекцией на нужное направление. Векторные величины выделены надчёркиванием над названием и обозначением. Как правило, величины, зависящие как от векторных, так и от скалярных величин, сами являются векторными и вычисляются как произведение трёхмерного вектора на число. Например, сила зависит от скалярной массы и векторного ускорения и является векторной величиной. Наоборот, если оба сомножителя являются векторами или оба — скалярами, результат обычно скалярный. Так, мощность определяется двумя скалярными величинами — работой (энергией) и временем — и является скалярной величиной. Скорости и градиентыМногие физические величины могут не только изменяться с течением времени, но и быть различными в разных точках пространства в один и тот же момент времени. Прежде всего это относится к потенциалам полей разного рода. В связи с этим можно говорить о временнóй и пространственной скоростях изменения таких физических величин. В первом случае речь идёт об изменении характеристик одного и того же объекта или точки пространства в разные моменты времени (время меняется, объект или координаты неизменны), во втором случае имеется в виду пространственное изменение характеристик в один и тот же момент времени либо тогда, когда течение времени не имеет значения, то есть поле стационарно (время одно, объекты или координаты разные). Следует заметить, что скорость, как и градиент, имеет смысл лишь при плавном изменении физической величины. Если изменение происходит резко, скачком, то в этот момент скорость становится бесконечно большой, а градиент терпит разрыв. На самом деле в классической физике неизвестны мгновенные процессы. Там даже самый быстрый процесс имеет конечную длительность, а значит конечную (хотя иногда и очень большую) скорость и неразрывный (хотя иногда очень крутой) временнóй градиент. МеханикаПомимо собственно механики (механического взаимодействия твёрдых тел), здесь приводятся некоторые сведения по аэро- и гидростатике, а также аэро- и гидродинамике. Механические величины
Основные законы механикиЗакон относительности движения: при равномерном прямолинейном движении тел, на которые нет внешних воздействий, невозможно выбрать абсолютную точку отсчёта и неоспоримо определить, какое тело движется, а какое стоит на месте. Система отсчёта, начало которой движется равномерно и прямолинейно, называется инерциальной системой отсчёта. Все инерциальные системы отсчёта равнозначны между собой. Внимание! Это верно лишь пока движущиеся тела не взаимодействуют ни с чем. Закон сохранения энергии в полной мере выполняется лишь в тех инерциальных системах отсчёта, которые неподвижны относительно центра масс всей системы взаимодействующих тел! Первый закон Ньютона: тело, двигающееся равномерно и прямолинейно, в отсутствие внешних воздействий сохраняет это движение неограничено долго. Второй закон Ньютона в современной формулировке: скорость изменения импульса тела равна действующей на него силе. Отсюда прямо вытекает формула, связывающая силу и ускорение: F = Δp / t = m · Δv / t = m · a, или в дифференциальной форме: F = dp / dt = m · dv / dt = m · a. Оригинальная (ньютоновская) формулировка этого закона: «изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует» (в те времена векторные величины не применялись, а абсолютное значение величины и её направление действия считались отдельными категориями). Таким образом, изменение импульса происходит только под действием приложенной силы и требует энергетических затрат (статическая сила, не изменяющая перемещения объекта приложения, на тело действует, но не меняет ни его импульс, ни энергию). Важное следствие: если объект не меняет скорость, т | ||
Формула расчета длины окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Физические величины. Измерение физических величин. Точность и погрешность измерений
Цели урока:
1) Обучающая: обеспечить формирование у учащихся представлений о физической величине, обеспечит усвоение учащимися теоретических знаний об основных характеристиках физической величины, познакомить учащихся с простейшими измерительными приборами, научить определять цену деления и точность отсчета при использовании различных шкал.
2) Развивающая: способствовать расширению кругозора учащихся о физике; умение находить некоторые закономерности; развитие памяти, самостоятельного суждения.
3) Воспитывающая: интерес, любознательность, наблюдательность, аккуратность в записях.
Ход урока:
1. Организационный этап.
Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний
Прежде чем начинать наш с вами уже второй урок в курсе Физики, хотелось бы вспомнить то, о чем мы говорили на предыдущем занятии.
Мы ввели понятие «Физическое тело». Что же это? Это любой предмет, окружающего нас мира.
Физическое явление — все изменения, которые происходят с физическими полями и телами.
Для описания физических тел и физических явлений используют физические величины.
Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.
Откройте тетради и запишите число и тему нашего урока.
3. Этап получения новых знаний.
Скачать видеоурок Физические величины. Измерение физических величин.
Точность и погрешность измерений
Для описания физических тел и физических явлений используют физические величины.
Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.
То есть физическая величина это то, что мы можем измерить. Измеряемое свойство тела или явления.
Каждая физическая величина имеет название, например масса; Буквенное обозначение (массу обозначают латинской буквой эм), способ измерения (с помощью весов), числовое значение (например, масса человека равна 45), и единицы измерения (кг). Получаем, масса тела равна 45 кг.
Получаем, масса тела равна 45 кг.
Для каждой физической величины приняты свои единицы измерения. Для удобства все страны мира стремятся пользоваться одинаковыми единицами измерения физических величин. С 1963 года во многих странах мира используется Международная система единиц — СИ (система интернациональная). В этой системе основной единицей длины является метр, времени — секунда, массы — килограмм.
Существует единицы, которые в 10, 100, 1000 раз больше принятых. Такие единицы называет кратными, и именуются с соответствующими греческими приставками. Например, десяти соответствует приставка «дека», стам — «гекто», тысячи — «кило».
Если используют единицы, которые в 10, 100, 1000 раз меньше принятых единиц (это дольные единицы), то используют приставки, взятые из латинского языка. «Деци» — ноль целых одна десятая, «санти» — ноль целых одна сотая, «милли» — ноль целых одна тысячная.
Измерения очень важны в нашей жизни, для их проведения необходимы измерительные приборы. Самые простые приборы для измерения длины линейка, рулетка, мерная лента.
Самые простые приборы для измерения длины линейка, рулетка, мерная лента.
Для измерения объема жидкости мензурка, мерный цилиндр, мерная колба.
Для измерения температуры используют комнатный, водный, медицинский термометры. Медицинский, в свою очередь, бывает электронный и ртутный.
Существуют и другие измерительные приборы. Например, времени секундомер, часы. Силы — динамометр. Давления, атмосферного — барометр, газов в сосуде — манометр.
Приборы делят на шкальные и цифровые. Каждый шкальный прибор имеет шкалу и цену деления.
Шкала измерительного прибора называют совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины
Цена деления — значение наименьшего деления шкалы прибора.
Для определения цены деления шкалы нужно от большего числа, соответствующего какому — либо делению шкалы, вычесть меньшее и полученную разность поделить на число делений между цифрами. Получаем 0,1 сантиметра на деление.
Получаем 0,1 сантиметра на деление.
Какой же прибор точнее, цена деления которого меньше или больше?
Рассмотрим мерную ленту А) и линейку б). У обоих приборов единицы измерения совпадают!
Для нахождения цены деления мерной ленты возьмем два рядом стоящих значения на шкале, от большего вычтем меньшее и разделим на количество делений между данными цифрами. Получим, 1 сантиметр на деление.
Также определим цену деления для линейки. Количество делений в данном случае 10. Получим, ноль целых одна десятая сантиметра на деление.
Сравним результат!
Точнее тот прибор у которого цена деления меньше. Значит данная линейка точнее мерной ленты.
То есть, имея меньшую цену деления, мы меньше ошиблись.
Чему же равна погрешность измерительных приборов?
Погрешность равна половине цены деления.
Например, погрешность при измерении температуры равна половине цены деления данного термометра.
Найдем ее: для этого определим цену деления термометра.
Берем два любых значения, например 20 и 10, от большего вычтем меньшее значение и разделим на количество делений между ними, их пять. Получили, что она равна 2 градуса на деление.
Значит погрешность равна 1 градус.
Как же это записать?
T = 20±1 C, где 20 — показания термометра, 1 — погрешность, знак полюс минус использует потому, что ошибиться можно как в большую так и в меньшую сторону.
При записи величин с учетом погрешности следует пользоваться формулой, где
А — измеряемая величина,
а — результат измерений,
а — погрешность измерений, – греческая буква «дельта»
Так что же значит измерить физическую величину?
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Например, чтобы измерить длину отрезка прямой между точками, А и В, надо приложить линейку и по шкале определить сколько сантиметров укладывается между данными точками.
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямыми. Например, измерение длины бруска, ширины или высоты бруска.
А как же определить объем этого самого бруска. Конечно же, используя формулу. Объем есть произведение длины, ширины и высоты.
В этом случае, когда физическую величину (объем), определили по формуле, говорят, что измерения провели косвенно.
3. Этап обобщения и закрепления нового материала.
Итак, сделаем основные выводы:
– Физическая величина — измеряемое свойство тела или явления
– Каждый шкальный прибор имеет шкалу и цену деления
– Шкала измерительного прибора — это совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины
– Цена деления (С) — значение наименьшего деления шкалы прибора
– Для определения цены деления шкалы нужно от большего числа, соответствующего какому- либо делению шкалы, вычесть меньшее и, разность поделить на число делений между цифрами
– Погрешность измерительных приборов равна половине цены деления
Для закрепления, изученного материала, ответим на ряд вопросов.
Что такое физическая величина? Какие основные физические величины входят в систему СИ? Какие шкальные измерительные приборы вам известны? Какие цифровые измерительные приборы вам известны? Перечислите приборы для измерения длины, времени, температуры. Что такое цена деления? Как определить цену деления прибора? От чего зависит точность измерения? Что необходимо учитывать при выборе измерительного прибора? Чем отличаются кратные и дольные единицы? Что значит измерить косвенно или прямым способом?
4. Рефлексия.
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
5. Домашнее задание: § 4- 5.
Дополнительное задание
Упражнение 2
1. Из перечисленных приборов выбрать а) шкальные, б) цифровые.
Линейка, весы электронные, напольные (не электронные весы), секундомер, часы наручные механические, часы электронные настенные, динамометр, мензурка, мерный стаканчик, барометр, манометр.
2. Определить цену деления данного прибора.
3. Определить цену деления данного термометра.
4. Определить цену деления и погрешность данной линейки.
5. Какая из данных мерных лент более точная? Почему? Чем точнее можно измерить длину стола линейкой или мерной лентой? Почему?
Волновая и квантовая оптика в физике: основные формулы
Световые волны — это электромагнитные волны с длиной волны от нескольких десятков микрон у инфракрасного света до сотых долей микрона у ультрафиолетового. На шкале электромагнитных волн световые волны располагаются между сверхвысокочастотными радиоволнами и рентгеновскими лучами. Свет обладает дуализмом, т.е двойственностью свойств, — он одновременно и волна, и поток частиц. Когда свет распространяется в пространстве, то обнаруживает свои волновые свойства: интерференцию, дифракцию, дисперсию и поляризацию. Когда он взаимодействует с веществом, то обнаруживает свои квантовые свойства — свойства частиц.
Условие максимума на дифракционной решетке
Здесь d — период решетки (м), — угол дифракции (рад), k — порядок максимума (безразмерный), — длина световой волны (м).
Формула Планка
Здесь — энергия порции излучения или энергия фотона (Дж), Дж • с — постоянная Планка, v — частота световой волны (Гц), Дж ■ с — постоянная Планка (с черточкой), —циклическая частота (рад/с).
Формула Эйнштейна для фотоэффекта
Здесь Е — энергия фотона (Дж), — работа выхода электрона из металла (Дж), — кинетическая энергия электрона (Дж), h — постоянная Планка (Дж ■ с), v — частота световой волны (Гц), — масса электрона (кг), v — скорость электрона (м/с).
Формула для расчета красной границы фотоэффекта
Здесь — работа выхода электрона из металла (Дж), h — постоянная Планка (Дж • с), с — скорость света в вакууме (м/с), — красная граница фотоэффекта по частоте (Гц), — красная граница фотоэффекта по длине волны.
Масса и импульс фотона
Здесь m — масса фотона (кг), р — импульс фотона (кг • м/с), — длина волны (м), с — скорость света в вакууме (м/с). Остальные величины названы в предыдущей формуле.
Длина волны де Бройля
Здесь — длина волны де Бройля (м), h — постоянная Планка (Дж • с), т — масса частицы (кг), v — скорость частицы (м/с), р — импульс частицы (кг • м/с).
Чтобы наблюдать интерференцию света, нужны когерентные источники. Два независимых источника света не могут быть когерентными, поэтому в опытах с интерференцией света световые пучки от одного источника разделяли на два пучка и заставляли их проходить разные расстояния, создавая тем самым разность хода, а затем соединяли. При этом, если разность их хода содержала четное число полуволн, то наблюдали усиление света, а если — нечетное, то ослабление, т.е. свет плюс свет давал темноту. Так было доказано, что свет есть волна.
Интерференцию с дифракцией света можно наблюдать с помощью дифракционной решетки — пластинки с нанесенными на нее чередующимися прозрачными и непрозрачными полосами — до нескольких тысяч на миллиметре ее длины. При этом ширина прозрачной полосы такова, что в ней укладывается несколько световых длин волн, вследствие чего световые волны, упав на решетку, дифрагируют под разными углами и на экране наблюдается интерференционная картина: чередование темных и светлых полос. Полоса под центром решетки всегда светлая, т.к. световые волны приходят сюда от симметричных прозрачных полос в одной фазе, — это нулевой максимум (порядок максимума k = 0). Слева и справа от нулевого максимума через темные полосы располагаются симметричные максимумы первого порядка, затем второго, третьего и т.д. (рис. 346).
При этом ширина прозрачной полосы такова, что в ней укладывается несколько световых длин волн, вследствие чего световые волны, упав на решетку, дифрагируют под разными углами и на экране наблюдается интерференционная картина: чередование темных и светлых полос. Полоса под центром решетки всегда светлая, т.к. световые волны приходят сюда от симметричных прозрачных полос в одной фазе, — это нулевой максимум (порядок максимума k = 0). Слева и справа от нулевого максимума через темные полосы располагаются симметричные максимумы первого порядка, затем второго, третьего и т.д. (рис. 346).
Сумма ширины прозрачной и непрозрачной полос решетки называется ее периодом d. Его можно определить, разделив длину решетки I на общее число полос на ней N:
С помощью дифракционной решетки по формуле можно экспериментально определить неизвестную длину световой волны.
Дисперсией света называется зависимость показателя преломления вещества от длины световой волны.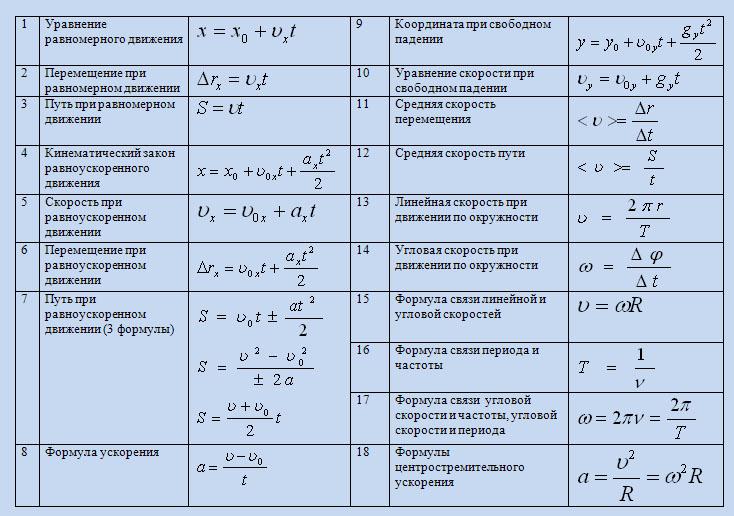 Из-за дисперсии световые волны с разной длиной волны по-разному преломляются веществом, что приводит к разложению белого света на цветные монохроматические (т.е. одного цвета) лучи (рис. 347).
Из-за дисперсии световые волны с разной длиной волны по-разному преломляются веществом, что приводит к разложению белого света на цветные монохроматические (т.е. одного цвета) лучи (рис. 347).
Слабее других световых лучей преломляются инфракрасные лучи. У них наибольшая из световых волн длина волны и наименьшая частота, в соответствии с формулой
У инфракрасных лучей наименьший показатель преломления n и поэтому, в соответствии с формулой
наибольшая скорость света в веществе. Инфракрасные лучи являются тепловыми лучами. Именно они переносят световую энергию Солнца через холод космического пространства на Землю, где, взаимодействуя с земной атмосферой, эта энергия превращается в тепло.
Спектр лучей видимого света очень узок — он лежит в диапазоне длин волн от м у красных лучей до м у фиолетовых. В спектре видимых лучей наблюдается следующий порядок по мере уменьшения длины волны и скорости света в веществе и увеличения частоты: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый (легко запомнить их порядок по фразе: Каждый Охотник Желает Знать, Где Сидит Фазан). Если с помощью линзы собрать лучи всех цветов видимого спектра, то вновь получим белый свет.
Если с помощью линзы собрать лучи всех цветов видимого спектра, то вновь получим белый свет.
За видимой фиолетовой границей света лежит область ультрафиолетовых лучей с еще меньшей, чем у фиолетовых длиной волны и еще большей частотой. Ультрафиолетовые лучи обладают проникающей способностью сквозь непрозрачные для видимого света тела, но стекло их полностью поглощает. У металлов ультрафиолетовый свет вызывает явление фотоэффекта. В малых дозах ультрафиолетовые лучи способствуют выработке у человека витамина Д, а в больших они опасны, т.к. приводят к болезням крови и опухолям.
Вид спектра зависит от агрегатного состояния светящегося вещества, его химического состава и температуры и не зависит от способа возбуждения свечения. В зависимости от агрегатного состояния вещества спектры бывают сплошные, полосатые и линейчатые.
Сплошной спектр излучают светящиеся твердые и жидкие вещества и высокотемпературная плазма.
Полосатый спектр излучают газы в молекулярном состоянии.
Линейчатый спектр излучают газы в атомарном состоянии. Каждая линия линейчатого спектра соответствует излучению одного атома данного вещества, поэтому по ней можно судить о наличии данного химического элемента. Метод изучения химического состава веществ по их спектрам называется спектральным анализом. Спектральный анализ — наиболее точный метод исследования состава веществ, с его помощью можно обнаружить вещество, даже если его масса составляет г. Каждое вещество испускает линии того цвета, которые само поглощает.
Атом вещества в возбужденном состоянии испускает электромагнитную волну, в которой вектор электрической напряженности — световой вектор — колеблется только в одной плоскости. Такая волна называется плоскополяризованной. Атомы светящегося вещества испускают световые волны, в которых световой вектор колеблется в разнообразных плоскостях. Такой свет называется естественным. Существуют вещества, например, кристаллы турмалина, после прохождения сквозь которые световая волна становится плоскополяризованной. Это явление называется поляризацией света, а сами вещества — поляризаторами. Поляризация света подтверждает поперечность световых волн.
Атом вещества, переходя из более возбужденного в менее возбужденное состояние, испускает световую волну, обладающую определенной порцией энергии .
Эта порция энергии называется фотон или квант и определяется формулой Планка
Когда световая волна падает на вещество, ее энергия(квант или фотон) передается атомам вещества и их валентные электроны переходят на более удаленные от ядра орбиты. Это явление называется внутренним фотоэффектом. При достаточно большой порции энергии фотона электроны могут быть выбитыми из вещества — произойдет внешний фотоэффект.
Для наблюдения внешнего фотоэффекта в вакуумную трубку помещают катод и анод, на которые подают высокое напряжение, и освещают катод К ультрафиолетовым светом сквозь кварцевое стекло, поскольку обычное стекло ультрафиолетовые лучи не пропускает (рис. 348). Выбитые светом электроны (фотоэлектроны) устремляются к положительному аноду А, и в цепи возникает фототок. На рис. 349 показана вольтамперная характеристика фотоэффекта, т.е. зависимость силы фототока I от приложенного к электродам напряжения U.
В отсутствие напряжения между катодом и анодом можно обнаружить в трубке слабый ток , образованный немногими выбитыми светом фотоэлектронами, импульс которых позволил им достичь анода. Чтобы и этот ток прекратить, надо подать на анод отрицательный относительно катода потенциал. Такое напряжение, при которых фототок прекращается, называется запирающим напряжением .
При небольших напряжениях на электродах, когда на аноде плюс, а на катоде минус, сила тока растет прямо пропорционально приложенному напряжению (участок 1-2 графика), т.к. все большее число выбитых светом из металла электронов достигает анода. При этом выполняется закон Ома для участка цепи.
При некотором достаточно большом напряжении, называемом напряжением насыщения все выбитые светом электроны достигают анода. Дальнейшее увеличение напряжения уже не приводит к росту силы тока (участок 2-3). При этом закон Ома уже не выполняется. Такой ток называется током насыщения . Теперь, чтобы увеличить силу тока, надо увеличить световой поток, т.е. энергию света, падающего на катод в единицу времени. Тогда свет выбьет из катода больше электронов, и сила тока возрастет.
Законы внешнего фотоэффектаРусский ученый А. Столетов установил законы внешнего фотоэффекта:
1 закон: сила фототока насыщения прямо пропорциональна падающему на катод световому потоку Ф, т.е. световой энергии, падающей в единицу времени:
Коэффициент пропорциональности k называется светочувствительностью трубки.
2 закон: кинетическая энергия летящих к аноду фотоэлектронов не зависит от падающего на катод светового потока, а зависит только от частоты световой волны. С увеличением частоты световой волны, падающей на катод, кинетическая энергия фотоэлектронов увеличивается.
3 закон: каждому металлу свойственна частота или длина световой волны, при которой у данного металла наступает фотоэффект. Такая частота v0 или длина волны называется красной границей фотоэффекта (порогом фотоэффекта, или длинноволновой границей, или коротковолновой границей фотоэффекта). Если металл освещать светом с большей, чем , длиной волны (или с меньшей, чем , частотой), то фотоэффект не наступит при любой световой энергии, а если длина волны будет меньше или частота v будет больше . то фотоэффект наступит при даже небольшой энергии света.
Фотоэффект практически безинерционен — он наступает через с от момента освещения катода.
Законы фотоэффекта обосновал А. Эйнштейн, исходя из закона сохранения энергии. Он записал формулу
которую называют уравнением Эйнштейна для фотоэффекта. Согласно этой формуле большей частоте v соответствует и большая кинетическая энергия фотоэлектронов, выбитых светом из данного металла, поскольку остальные величины в этих формулах постоянны.
Если частота световой волны, падающей на металл, меньше красной границы фотоэффекта (или длина волны больше ), то фотону не хватит энергии даже на то, чтобы вырвать электрон из металла, т. е. его энергия , и фотоэффекта не будет. Если частота , то энергии фотону хватит только на то, чтобы вырвать электрон из металла, а на сообщение ему кинетической энергии ее уже не хватит. В этом случае
С помощью этих формул можно рассчитать красную границу фотоэффекта .
Если же , и энергии фотону хватит и на вырывание электрона из металла, и на сообщение ему кинетической энергии. В этом случае фотоэффект будет наблюдаться.
Если в условии задачи идет речь о запирающем напряжении, то работу запирающего электрического поля надо приравнять кинетической энергии выбитых электронов:
Энергию любого светового источника Е можно представить как произведение целого числа фотонов N в нем и энергии одного фотона :
Энергию света, падающую на единицу площади освещаемой поверхности в единицу времени, называют интенсивностью света I. Интенсивность, как и энергия света, прямо пропорциональна числу фотонов, излучаемых источником света.
Массу и импульс фотона определяют формулы
Доказательством наличия у фотона импульса, а следовательно, и массы, послужили опыты П. Лебедева, в которых свет оказывал давление на легкую вертушку, расположенную в вакууме, — при ее освещении она вращалась. Световое давление играет большую роль в космических явлениях.
Поскольку фотоны, представляющие собой электромагнитные волны, обладают свойствами, присущими частицам вещества, то французский физик де Бройль выдвинул гипотезу, согласно которой и частицы вещества обладают волновыми свойствами. Он записал формулу длины волны, присущей частицам вещества, которая получила название длины волны де Бройля:
Гипотеза де Бройля легла в основу квантовой механики — науки о свойствах и поведении элементарных частиц и состоящих из них атомов и молекул.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Механические колебания и волны. Примеры решения задач по физике. 9-10 класс
Механические колебания и волны. Примеры решения задач по физике. 9-10 класс
- Подробности
- Просмотров: 1151
Задачи по физике – это просто!
Вспомним
Формула длины волны:
Период колебаний:
А теперь к задачам!
Элементарные задачи из курса школьной физики на механические колебания и волны.
Задача 1
Определить длину волны с частотой 300 Гц, которая распространяется в воздухе со скоростью 340 м/с.
Задача 2
Найти период колебания плота на волнах озера, если длина волны составляет 4 метра, а скорость распространения волн равна 2,5 м/с.
Задача 3
Определить сколько колебаний за 1 минуту совершает буек на воде, если скорость распространения волн составляет 3 м/с, а длина волны равна 5 метрам.
Задача 4
По поверхности воды идут волны. Определить параметры волны (период колебания, длину волны, скорость распространения), если расстояния между 1 и 4 гребнями волн составляет 9 метров, а мимо наблюдателя за 10 секунд проходят 5 гребней волн.
Задача 5
Поплавок удочки рыбака за 40 секунд сделал 20 колебаний, а расстояние между соседними гребнями волн составило 2 метра. Какова была скорость распространения волны?
Задача 6
С лодки в воду бросили камень. По воде пошли круги-волны. Расстояние между соседними гребнями волн составило 1 метр, а время за которое волна дошла до берега – 1 минута. Причем волны накатывались на берег с интервалом в 2 секунды. На каком расстоянии от берега бросили камень?
Задача 7
За время полета 30 секунд муха делает 15000 взмахов крыльями, а период колебания крыла комара составляет 1,6 миллисекунд. Во сколько раз отличаются частоты колебаний крыльев мухи и комара?
22.1: Масса, длина и время
- Последнее обновление
- Сохранить как PDF
- Участник
Любую механическую величину можно выразить тремя основными величинами: массой , длиной и временем . Например, скорость – это длина, разделенная на время. Сила – это масса, умноженная на ускорение, и, следовательно, масса, умноженная на расстояние, деленная на квадрат времени.
Поэтому мы говорим, что [Сила] = MLT −2 . Квадратные скобки означают: «Размеры количества внутри». Уравнения показывают, как сила зависит от массы, длины и времени. Мы используем символы MLT (не выделены курсивом ) для обозначения основных измерений массы, длины и времени. В приведенном выше уравнении MLT -2 – это , а не , заключенные в квадратные скобки; в этом нет смысла.
Мы различаем размеры , физической величины и единицы, в которых она выражается. В случае единиц MKS (которые являются подмножеством единиц СИ), единицами массы, длины и времени являются кг, м и с. Таким образом, можно сказать, что единиц , в которых выражена сила, – это кг · м · с -2 , а его размеры равны MLT -2 .
Для электромагнитных величин нам нужна четвертая фундаментальная величина. Мы могли бы выбрать, например, количество электричества Q, и в этом случае размерность тока будет QT -1 .Мы не касаемся здесь размеров электромагнитных величин. Более подробную информацию можно найти в моих заметках об электричестве и магнетизме, http://orca.phys.uvic.ca/~tatum/elmag.html
.Чтобы определить размерность физической величины, обычно проще всего взглянуть на определение этой величины. Большинству читателей не составит труда понять, что, поскольку работа – это сила, умноженная на расстояние, размеры работы (и, следовательно, также энергии) равны ML 2 T −2 .{-1}. \)
Объяснение сокращения длины: формула и пример – видео и стенограмма урока
Подготовка к сокращению длины
Чтобы глубже понять, как работает сокращение длины, вам необходимо знать три очень важных концепции. Во-первых, это опорная рамка или система отсчета, которую можно рассматривать как точку зрения наблюдателя. Представьте себе человека, сидящего в поезде, когда он проезжает мимо другого человека, стоящего у рельсов.Для человека, стоящего вне поезда, в их системе координат поезд движется мимо них с некоторой скоростью. Для человека в поезде, с их точки зрения, поезд стоит на месте, а человек за окном проходит мимо.
Следующая концепция – второй постулат специальной теории относительности . В нем говорится, что скорость света в вакууме постоянна для всех инерциальных систем отсчета. Инерциальная система отсчета – это система отсчета, в которой объект остается в покое или движется по прямой линии, если на него не действует другая сила.8 м / с в любой инерциальной системе отсчета.
Наконец, есть замедление времени . Замедление времени означает, что время для движущегося объекта идет медленнее, чем для неподвижного объекта. Это явление идет рука об руку с сокращением длины, поскольку оба они всегда влияют на любой движущийся объект, и оба заметны только на скоростях, приближающихся к скорости света.
Как и в предыдущем поезде, представьте себе человека на космическом корабле, движущемся с постоянной скоростью, близкой к скорости света, и стоящего за пределами корабля человека.На нашем корабле есть два зеркала, которые отражают световой луч вперед и назад в вакууме. С точки зрения наблюдателя внутри корабля, луч света отражается вверх и вниз, как показано на этом изображении:
С точки зрения наблюдателя вне корабля световой луч действует совершенно иначе. Поскольку корабль движется, луч света также должен двигаться в том же направлении, отражаясь взад и вперед, как показано на изображении здесь:
Для наблюдателя вне корабля световой луч движется на гораздо большее расстояние, чем видит наблюдатель внутри. 2).Гамма – это просто уравнение, которое так часто встречается в теории относительности, что ему был присвоен собственный символ.
- v = скорость объекта
- c = скорость света в вакууме
Сокращение длины
Чтобы понять сокращение длины, представьте, что наши два наблюдателя пытаются измерить длину корабля. Наблюдатель вне корабля не сможет взять линейку и измерить корабль, когда он проносится мимо. Если наблюдатель знает, с какой скоростью движется корабль, он или она может использовать немного физики, чтобы вычислить длину.
Мы знаем, что скорость = расстояние / время . Расстояние, которое мы пытаемся найти, – это длина корабля или расстояние между передней и задней частью корабля. Мы можем изменить формулу следующим образом.
l = v * t
l = длина корабля
Для определения длины корабля наблюдатель использует секундомер. Он или она начинает отсчет времени в тот момент, когда проходит передняя часть корабля, и останавливает часы в момент, когда проходит хвост.Точно так же наблюдатель внутри корабля может запустить свой секундомер в тот момент, когда наблюдатель снаружи проходит перед кораблем, и закончить его в тот момент, когда он или она пройдет мимо хвоста. В итоге мы получаем два разных наблюдения за длиной.
l = v * t
l {0} = v * t {0}
Первая формула находит длину, которую вычисляет наблюдатель, стоящий неподвижно вне корабля, и второй находит длину, которую вычисляет наблюдатель внутри.Мы знаем из замедления времени, что эти два времени не одно и то же. Следовательно, измеренная длина тоже должна быть разной. В формуле для сокращения длины, приведенной ниже, мы обнаруживаем, что они различаются в гамма-коэффициенте.
l = l {0} / gamma
Таким образом, сокращенная длина во время движения всегда должна быть меньше, чем длина судна в состоянии покоя.
Пример сокращающегося корабля
Давайте посмотрим, насколько сокращается длина судна, летящего на 150 метров со скоростью 50% от скорости света.2)
л = 150 * корень квадратный (0,75)
л = 130 метров
Корабль сжался в направлении движения на 20 метров. Он только сжимается больше по мере того, как корабль движется быстрее. При 75% скорости света l = 99 м , при 90% l = 65 м и 99% l = 21 м . Это означает, что 150-метровый корабль уменьшится в направлении движения на 129 метров.
Резюме урока
Сокращение длины утверждает, что когда объект движется, его длина сокращается в том же направлении, что и его скорость.Это происходит постоянно со всеми движущимися объектами, но заметно только на скоростях, приближающихся к скорости света. Чтобы понять, как работает сокращение длины, вам также необходимо понять систему отсчета , второй постулат специальной теории относительности и замедление времени . Используя эти три концепции, мы можем понять, почему математика для сокращения длины работает именно так. Наконец, формула для сокращения длины:
l = l {0} / гамма, где гамма = 1 / квадратный корень (1 – ( v / c ) ^ 2)
Веб-сайт класса физики
Релятивистское сокращение длины
Одним из характерных аспектов специальной теории относительности Эйнштейна является то, что длина объектов, движущихся с релятивистскими скоростями, сокращается по мере движения.Наблюдатель в состоянии покоя (относительно движущегося объекта) заметил бы, что движущийся объект короче по длине. Другими словами, покоящийся объект может иметь длину 200 футов; тем не менее, тот же объект при движении с релятивистскими скоростями относительно наблюдателя / измерителя будет иметь измеренную длину менее 200 футов. Это явление не связано с фактическими ошибками в измерениях или ошибочными наблюдениями. Объект фактически сокращен по длине, как видно из неподвижной опорной системы .Степень сжатия объекта зависит от его скорости относительно наблюдателя.
Анимация ниже изображает это явление сокращения длины. В каждой анимации космический корабль движется мимо Земли с большой скоростью. Космический корабль будет иметь длину 200 футов в состоянии покоя относительно наблюдателя.
Космический корабль движется со скоростью 10% скорости света
Космический корабль движется со скоростью 86,5% от скорости света
Космический корабль движется со скоростью 99% скорости света
Космический корабль движется на 99.99% Скорость света
Обратите внимание, что сокращение длины имеет значение только тогда, когда объект движется с релятивистскими скоростями, то есть скоростями, которые составляют значительную часть скорости света. Кроме того, обратите внимание, что сжатие происходит только в измерении движения объекта. Если объект движется по горизонтали, то сужается именно горизонтальный размер; не было бы сокращения высоты объекта. Эта информация обобщена в таблице ниже.
| Скорость космического корабля | Наблюдаемая длина | Наблюдаемая высота |
|---|---|---|
| В состоянии покоя | 200 футов | 40 футов |
| 10% скорости света | 199 футов | 40 футов |
| 86,5% скорости света | 100 футов | 40 футов |
| 99% скорость света | 28 футов | 40 футов |
| 99.99% скорость света | 3 фута | 40 футов |
Сокращение длины – предметный тест GRE: Физика
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Сокращение длины – Специальная теория относительности – Редакция высшей физики
Еще одним следствием фиксированной скорости света является то, что длина также должна измениться. На очень высоких скоростях, опять же в пределах 10% от скорости света, длина движущегося объекта, видимого неподвижным наблюдателем, сокращается.{-9}} \]
\ [l \ textquotesingle = 4 \ times 0.99999999834 \]
\ [l \ textquotesingle = 3.9999999933798m \]
Таким образом, четырехметровый корабль укоротился всего на 7 морских миль. как наивысшая скорость, которую удалось человечеству.
Чтобы дать представление о размере, самая маленькая частица дыма составляет 10 нм. По нашему опыту, релятивистские эффекты обычно не заметны.
- Вопрос
Заметят ли астронавты на борту космического корабля, близкого к скорости света, друг друга, что они стали тоньше?
- Показать ответ
No.Поскольку наблюдатель и его товарищ-космонавт движутся с одинаковой скоростью, они оба будут казаться нормальными.
Physical Review Journal – Руководство по расчету длины
Процедура подсчета слов
Следующие ниже рекомендации можно использовать для определения объема рукописи, отправляемой в журнал Physical Review . Общая формула для расчета объема рукописи:
Общее количество слов = текст + отображаемая математика + цифры + таблицы
| Рекомендации для писем и коротких статей, включая комментарии | |
|---|---|
| Текст | Включить
|
| Отображаемая математика | Словарный эквивалент отображаемой математики – 16 слов в строке для уравнений с одним столбцом.Уравнения с двумя столбцами считаются как 32 слова в строке. |
| Фигуры | Чтобы оценить эквивалент слова для цифр, используйте соотношение сторон фигуры (ширина / высота). Оценка составляет [(150 / соотношение сторон) + 20 слов] для фигур в один столбец и [300 / (0,5 * соотношение сторон)] + 40 слов для фигур в два столбца. |
| Таблицы | Словарный эквивалент для таблиц – 13 слов плюс 6,5 слов в строке для одностолбцовых таблиц.Таблицы с двумя столбцами считаются как 26 слов плюс 13 слов в строке. |
| Рекомендации для PRX и обзорных статей в PRApplied, PRMaterials, PRResearch и RMP | |
|---|---|
| Text | Включить
|
| Отображаемая математика | Словарный эквивалент отображаемой математики – 16 слов в строке для уравнений с одним столбцом.Уравнения с двумя столбцами считаются как 32 слова в строке. |
| Фигуры | Словарный эквивалент цифр – 170 слов на цифру для цифр в одну колонку. Цифры в двух столбцах считаются как 340 слов на рисунок. |
| Таблицы | Словарный эквивалент для таблиц – 13 слов плюс 6,5 слов в строке для одностолбцовых таблиц. Таблицы с двумя столбцами считаются как 26 слов плюс 13 слов в строке. |
Подсчет слов в файле TeX
Авторам рекомендуется использовать REVTeX 4.2 для подготовки рукописи, используя соответствующую опцию журнала (например, «prl» для Physical Review Letters ). Рукописи, которые умещаются в следующих пределах страниц, скорее всего, будут соответствовать руководящим принципам длины: Письма и PRPER Короткие статьи: 4 страницы, Письма: 4 страницы для PRB; 5 страниц для Physical Review A, C, D, E, Fluids, Materials, and Research. Кроме того, вы можете определить количество слов в файле REVTeX 4.2 с помощью:
- Комментарий к команде \ maketitle
- Использование опции ‘nofootinbib’
- Вставка \ end {document} перед библиографией
- Закомментировать любые отображаемые уравнения
- Комментирование строк (но не заголовков) любых таблиц
- Комментарий к сообщению
Бумага должна работать под LaTeX.Чтобы получить точное количество слов, вы можете затем использовать файл wordcount.tex, который находится по адресу https://ctan.org/tex-archive/macros/latex/contrib/wordcount.
Подсчет слов в файле Word
Чтобы подсчитать количество слов в документе Word, сделайте копию своей рукописи и удалите весь текст и другие элементы, которые не учитываются в соответствии с рекомендациями. Затем воспользуйтесь встроенной функцией подсчета слов Word.
Определение размера фигур
GhostScript можно использовать для определения ограничивающей рамки фигур в формате Encapsulated PostScript (EPS) и PDF:
| фигурка кота.eps | gs -q -dSAFER -dBATCH -sDEVICE = bbox – |
Затем вы можете использовать размер ограничивающей рамки, чтобы определить точную ширину и высоту фигуры. Различные программы обработки изображений будут отображать размеры файлов изображений JPEG, GIF, PNG и других типов. В качестве альтернативы вы можете использовать программу просмотра PDF-файлов с возможностью обрезки, чтобы нарисовать рамку обрезки вокруг фигуры и считать размеры. Наконец, вы можете просто распечатать фигуру и измерить ее размеры.Единицы измерения являются произвольными, потому что в рекомендациях используется соотношение сторон, то есть ширина / высота.
Предел количества слов
Ограничения по длине для разных типов статей в журналах Physical Review различаются. Пределы длины приведены в следующей таблице:
| Пределы длины изделия | ||
|---|---|---|
| PRL | Письмо Комментарий / ответ | 3750 слов 750 слов |
| PRX | Комментарий / ответ | 3500 слов |
| PRX Energy | Комментарий / ответ Перспектива Учебное пособие | 3500 слов 3000 слов 37500 слов |
| Ограничения по длине для статей о перспективах и учебных пособиях являются рекомендациями.При необходимости авторам следует проконсультироваться с редакторами PRX Energy . | ||
| PRX Quantum | Комментарий / ответ Перспектива Учебное пособие | 3500 слов 7500 слов 37 500 слов |
| Ограничения по длине для статей о перспективах и учебных пособиях являются лишь ориентировочными. При необходимости авторам следует проконсультироваться с редакторами PRX Quantum . | ||
| RMP | Артикул Коллоквиум | . 50 000 слов 20 000 слов |
| PRA | Письмо Комментарий / ответ | 4500 слов 3500 слов |
| ПРБ | Письмо Комментарий / ответ | 4500 слов 3500 слов |
| КНР | Письмо Комментарий / ответ | 4500 слов 1500 слов |
| PRD | Письмо Комментарий / ответ | 4500 слов 3500 слов |
| PRE | Письмо Комментарий / ответ | 4500 слов 3500 слов |
| PR Исследования | Обзор статьи Письмо Комментарий / ответ | 30 000 слов 4500 слов 3500 слов |
| PRAB | Без ограничений | |
| PR Заявлено | Обзор статьи Комментарий / ответ Письмо | 30 000 слов 3500 слов 3500 слов |
| PR Жидкости | Письмо Комментарий / ответ | 4500 слов 3500 слов |
| ПРМатериалы | Обзорная статья Обновление исследования Письмо Комментарий / ответ | 30 000 слов 10 000 слов 4500 слов 3500 слов |
| PRPER | Обзор статьи Краткая статья Комментарий / ответ | Без ограничений 3500 слов 3500 слов |
Клемсон У.Учебник по физике: стандартное отклонение
В любом эксперименте важно правильно отображать точность с которой производится каждое измерение. Ни одно измерение не является абсолютно точным. Например, невозможно измерить точную длину объекта. Мы длина может быть 1,23 см, но это не означает, что фактический размер 1,23000000 … см! Мы должны тщательно описать, как точное наше измерение.Экспериментальное значение 1,23 на 0,10 см меньше точнее, чем измерение 1,23 0,01 см. Срок дает меру точности измерения. Приведена точность значения либо по ошибке в процентах, либо по разнице в процентах.Чтобы найти погрешность в наших измерениях, мы часто рассчитываем стандартное отклонение , или , измеренного значения. Стандартное отклонение – это мера вариации из N точек данных ( x 1 …x N ) примерно в среднем ценить, , и обычно называется неопределенностью результата измерения.
Чтобы вычислить среднее значение или среднее значение , , комплекта N измерений есть
| (1) |
После определения среднего значения измерений полезно определить, насколько отдельные измерения разбросаны по иметь в виду.Отклонение , , любого измерения, , от среднего дается
| (2) |
Поскольку отклонение может быть как положительным, так и отрицательным, оно часто бывает более полезно использовать среднее отклонение , или , для определения неопределенности измерения. Это найдено усредняя абсолютные отклонения, ; то есть,
| (3) |
Обычно указывается экспериментальное значение, , измерения как
| (4) |
куда , дает меру точности измерения.
Чтобы избежать использования абсолютных значений, мы можем использовать квадрат отклонения, , для более точного определения неопределенности наших измерений. Стандартное отклонение, , (иногда называемый среднеквадратичным ) определяется как
| (5) |
(Можно показать, что для небольшого числа измерений уравнение 5 принимает вид
| (6) |
где N заменено на N – 1 .Ваш инструктор может попросить вас используйте эту формулу вместо уравнения 5.)
Наконец, экспериментальный результат, , тогда можно записать как
| (7) |
куда , дает меру точности измерения. Часто ученые использовать значение стандартного отклонения, чтобы служить их данными Планки погрешностей .
Обратите внимание на стандартное отклонение всегда положительно и имеет те же единицы, что и среднее значение.



 По возможности, большинство формул представлены в интегральном виде (так сказать, «школьном», в отличии от «институтского» дифференциального представления). Во-первых, часто этого вполне достаточно для практического использования. Во-вторых, в Интернете и солидных справочниках обычно всё приводится именно в дифференциальном виде, так что найти такой вид для той или иной формулы не проблема. Зато проблемой часто является правильно взять интеграл этой формулы при конкретных вычислениях, особенно для тех, кто изучал матанализ очень давно или не изучал высшую математику вообще и слабо разбирается в дивергенциях, роторах и градиентах. В-третьих, те, кто «чувствует» физику, знают и пределы использования интегральной формы — для установившихся процессов в относительно неизменных условиях, — и обычно им не составляет большого труда в нужный момент перейти к дифференциальной форме для учёта нестационарности того или иного параметра. Тех же, кто физики «не чувствует», в этих случаях не спасёт и дифференциальная запись формул.
По возможности, большинство формул представлены в интегральном виде (так сказать, «школьном», в отличии от «институтского» дифференциального представления). Во-первых, часто этого вполне достаточно для практического использования. Во-вторых, в Интернете и солидных справочниках обычно всё приводится именно в дифференциальном виде, так что найти такой вид для той или иной формулы не проблема. Зато проблемой часто является правильно взять интеграл этой формулы при конкретных вычислениях, особенно для тех, кто изучал матанализ очень давно или не изучал высшую математику вообще и слабо разбирается в дивергенциях, роторах и градиентах. В-третьих, те, кто «чувствует» физику, знают и пределы использования интегральной формы — для установившихся процессов в относительно неизменных условиях, — и обычно им не составляет большого труда в нужный момент перейти к дифференциальной форме для учёта нестационарности того или иного параметра. Тех же, кто физики «не чувствует», в этих случаях не спасёт и дифференциальная запись формул.
 Внимание! При расчётах, прежде чем подставить в формулы численные значения, необходимо убедиться, что все они преобразованы именно к СИ. Перевод в систему СИ национальных и неметрических единиц измерения представлен на отдельной странице.
Внимание! При расчётах, прежде чем подставить в формулы численные значения, необходимо убедиться, что все они преобразованы именно к СИ. Перевод в систему СИ национальных и неметрических единиц измерения представлен на отдельной странице.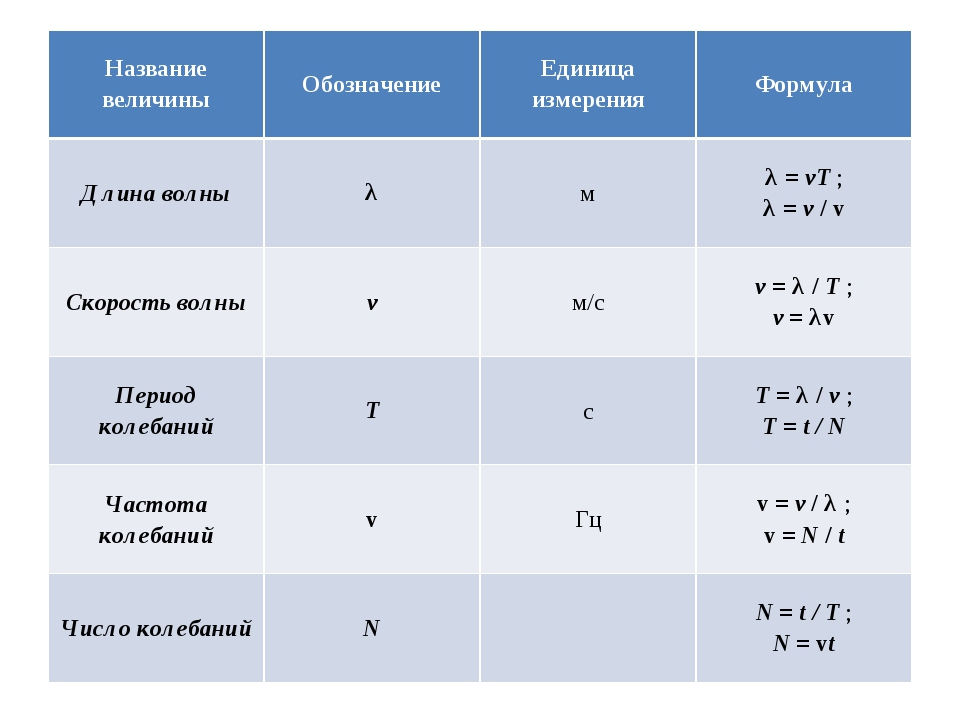 Другой пример — размерность момента силы, выраженная в основных единицах измерения, совпадает с размерностью работы и энергии, но это совершенно разные физические величины. Наконец, и сами работа и энергия измеряются в одних и тех же единицах — джоулях, — но имеют разные физические смыслы, хотя и тесно связанные между собой, — первое является мерой совершённого воздействия, а второе — мерой возможности совершить такое воздействие. Отождествление физических величин лишь на основе совпадения их размерностей иногда может привести к весьма нетривиальным «открытиям», но эти бумажные «открытия» не будут иметь отношения к реальному миру! Поэтому у названия каждой величины в скобках я специально указал её физический смысл. Каждый термин классической физики неслучаен и отражает своё особое понятие — здесь терминология отточена поколениями учёных отнюдь не последнего разряда…
Другой пример — размерность момента силы, выраженная в основных единицах измерения, совпадает с размерностью работы и энергии, но это совершенно разные физические величины. Наконец, и сами работа и энергия измеряются в одних и тех же единицах — джоулях, — но имеют разные физические смыслы, хотя и тесно связанные между собой, — первое является мерой совершённого воздействия, а второе — мерой возможности совершить такое воздействие. Отождествление физических величин лишь на основе совпадения их размерностей иногда может привести к весьма нетривиальным «открытиям», но эти бумажные «открытия» не будут иметь отношения к реальному миру! Поэтому у названия каждой величины в скобках я специально указал её физический смысл. Каждый термин классической физики неслучаен и отражает своё особое понятие — здесь терминология отточена поколениями учёных отнюдь не последнего разряда… В механике это длина, площадь, объём, масса, а также работа, энергия, мощность и время. При объединении однородных скалярных величин обычно просто складываются их значения. Однако многие скалярные величины могут иметь знак, который необходимо учитывать. Так, для работы знак означает направление передачи энергии. Иногда работа, совершаемая самим телом (тело отдаёт энергию) указывается со знаком «минус», а работа, совершаемая над телом (тело получает энергию из среды или от других тел) — со знаком «плюс», но может быть и наоборот. Ещё чаще знак вообще не ставится, а направление передачи указывается словами, например «тело совершило работу» или «тело приобрело энергию», но для расчёта баланса энергии всё равно надо правильно учитывать знаки, — иначе, рассматривая вращение обыкновенного колеса, на бумаге можно легко получить огромный выход «лишней» энергии, хотя в реальности ничего подобного нет! Строго говоря, работу, мощность и энергию (а в некоторых случаях и время) следует рассматривать как вектора в особых одномерных пространствах, представленные «скалярными величинами со знаком», однако обычно в физике «векторными» называют лишь величины, имеющие направление именно в обычном трёхмерном пространстве.
В механике это длина, площадь, объём, масса, а также работа, энергия, мощность и время. При объединении однородных скалярных величин обычно просто складываются их значения. Однако многие скалярные величины могут иметь знак, который необходимо учитывать. Так, для работы знак означает направление передачи энергии. Иногда работа, совершаемая самим телом (тело отдаёт энергию) указывается со знаком «минус», а работа, совершаемая над телом (тело получает энергию из среды или от других тел) — со знаком «плюс», но может быть и наоборот. Ещё чаще знак вообще не ставится, а направление передачи указывается словами, например «тело совершило работу» или «тело приобрело энергию», но для расчёта баланса энергии всё равно надо правильно учитывать знаки, — иначе, рассматривая вращение обыкновенного колеса, на бумаге можно легко получить огромный выход «лишней» энергии, хотя в реальности ничего подобного нет! Строго говоря, работу, мощность и энергию (а в некоторых случаях и время) следует рассматривать как вектора в особых одномерных пространствах, представленные «скалярными величинами со знаком», однако обычно в физике «векторными» называют лишь величины, имеющие направление именно в обычном трёхмерном пространстве.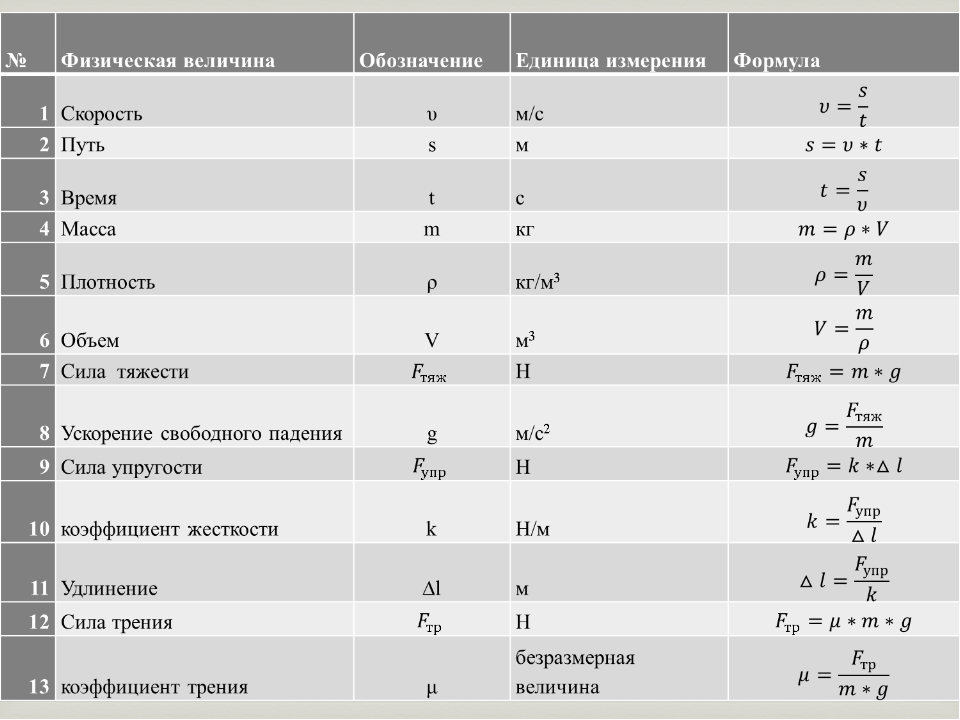
 В то же время работа, определяемая двумя векторными величинами — силой и перемещением — считается скалярной величиной и вычисляется как скалярное произведение трёхмерных векторов силы и перемещения. Но есть и исключения — скажем, сила Лоренца или скорость прецессии являются векторными величинами, вычисляемыми как векторное произведение других векторных величин.
В то же время работа, определяемая двумя векторными величинами — силой и перемещением — считается скалярной величиной и вычисляется как скалярное произведение трёхмерных векторов силы и перемещения. Но есть и исключения — скажем, сила Лоренца или скорость прецессии являются векторными величинами, вычисляемыми как векторное произведение других векторных величин. В «институтском» курсе физики в этих случаях часто говорят о «временнóм и пространственном градиентах» соответствующей физической величины. Для краткости и однозначности я постараюсь придерживаться следующей системы понятий: «скоростью» я буду называть темп изменения физической величины во времени, а «градиентом» — степень её изменения в пространстве. Таким образом, «скорость изменения высоты» подразумевает механическую скорость взлёта или падения, а «градиент высоты» соответствует уклону, то есть степени изменения высоты некоторой поверхности в пространстве.
В «институтском» курсе физики в этих случаях часто говорят о «временнóм и пространственном градиентах» соответствующей физической величины. Для краткости и однозначности я постараюсь придерживаться следующей системы понятий: «скоростью» я буду называть темп изменения физической величины во времени, а «градиентом» — степень её изменения в пространстве. Таким образом, «скорость изменения высоты» подразумевает механическую скорость взлёта или падения, а «градиент высоты» соответствует уклону, то есть степени изменения высоты некоторой поверхности в пространстве. Зато легко привести пример разрыва пространственного градиента, каковым является, скажем, любая кромка поверхности.
Зато легко привести пример разрыва пространственного градиента, каковым является, скажем, любая кромка поверхности. е. инерционности; мера взаимодействия тел с гравитационным полем)
е. инерционности; мера взаимодействия тел с гравитационным полем) е. по поверхности или по сечению тела)
е. по поверхности или по сечению тела)
 Это проявление инертности тел.
Это проявление инертности тел.