Формула для расчета внутренней энергии одноатомного идеального газа: Внутренняя энергия идеального газа. Расчет онлайн и формулы

Внутренняя энергия, теплопередача, работа – презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

Внутренняя
энергия
Теплопередача
Работа
Вопросы
1) Определение внутренней энергии
2) От чего зависит внутренняя энергия?
3) Внутренняя энергия одноатомного идеального газа
4) Способы изменения внутренней энергии.
5) Виды теплопередачи
6) Формула работы газа, работы внешних сил.
1. Внутренняя энергия тела равна сумме
кинетической энергии движения молекул и
потенциальной энергии взаимодействия молекул.

U Ek Е p
2. Внутренняя энергия зависит от температуры и от
количества частиц. Обозначается U, измеряется в
Дж.
3. Т.к. потенциальная энергия идеального газа равна 0,
то U Ek
Выведем формулу для расчета внутренней энергии
одноатомного идеального газа:
m
3
Ek E N ; N
N A ; E kT
M
2
3
m
3 m
3 m
E k kT
NA
kN A T
RT
2
M
2M
2M
3 m
U
RT – внутренняя энергия
2M
одноатомного идеального газа.
5 m
U
RT – внутренняя энергия
2M
двуатомного идеального газа.
Изменение внутренней энергии:
3 m
U U 2 U1
R T
2M
3
или U p V
2

Способы изменения внутренней энергии
Совершение работы
Теплопередача
Излучение
Теплопроводность
Конвекция
Количество теплоты, Q – это энергия, переданная
системе или полученная системой при теплообмене.
Процесс
Нагревание или
охлаждение
Формула
Q cm T
c- удельная теплоемкость, Дж/(кг*К)
m – масса, кг; T – изменение температуры, К
Кипение или
конденсация
Q=Lm
L – удельная теплота парообразования, Дж/кг
Плавление или
кристаллизация
Q=rm
r – удельная теплота плавления, Дж/кг
Сгорание
топлива
Q=qm
q – удельная теплота сгорания, Дж/кг
Уравнение теплового баланса:
Q1 Q2 Qn const
Работа в термодинамике – работа сил, приложенных к
внешним телам со стороны системы при её деформации.
Работа газа численно равна площади фигуры под графиком
зависимости давления от объёма в координатах p, V
Расширение газа
p
p
2
2
1
Сжатие газа
p
A>0
V1
1
A<0
V2
V
V1
V2
V
AГ p (V2 V1 ) p V – работа газа
Aвн AГ p V – работа внешних сил
Задача №1. В стальном баллоне находится гелий массой 0,5 кг при
температуре 10°С. Как изменится внутренняя энергия гелия, если его
температура повысится до 30°С?
Дано:
Решение:
m 0,5кг
3 m
U
R T
2M
t1 10 C
0
t 2 30 0 C
кг
M 4 10
моль
Дж
R 8,31
кг моль
U ?
3
Ответ. 31,2 кДж
T1 t1 273 283K ; T2 t2 273 303K ;
T T2 T1 20 K
3 0,5
3
U
8
,
31
20
31
,
2
10
Дж
3
2 4 10
Задача 2. Газ находится под давлением 3 10 5 Па и занимает объем 0,6 м 3 .
Какая работа будет совершена при уменьшении его объема до 0,2 м 3 .
Дано :
Решение :
p 3 10 5 Па
Aвн p (V2 V1 )
V1 0,6 м 3
Aвн 3 10 5 (0,2 0,6) 1,2 10 5 Дж
V2 0,2 м 3
Aвн ?
Ответ. 1,2 10 5 Дж
Домашнее задание.
§ 77-79.
Задачи:
1.
Определите изменение внутренней энергии кислорода ( O 2) массой
3 кг при изменении его температуры от 17ºС до 27ºС.
2. Газ. расширяясь изобарно, совершает работу 0,2 кДж при давлении
200 кПа. Определите первоначальный объём газа, если конечный
объём стал равен 2,5 л.

English     Русский Правила

Задачи на внутреннюю энергию с решениями

Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.

Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!

Решение задач: внутренняя энергия

Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.

Задача №1.

Изменение внутренней энергии

Условие

Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?

Решение

Для решения будем использовать формулу внутренней энергии идеального газа:

Массу гелия выразим из уравнения Клапейрона-Менделеева:

Тогда можно записать:

Ответ: 4 МДж.

Задача №2. Внутренняя энергия и работа

Условие

Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:

1. Изменение ∆U внутренней энергии газа.
2. Совершенную при расширении газа работу А.
3. Количество теплоты Q, полученное газом.

Решение

Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:

Ответ: 0; 11,6 кДж; 11,6 кДж.

Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе

Условие 

Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа. 

Решение

Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:

В изохорном и изобарном процессе соответственно:

Изохорное нагревание:

Изменение внутренней энергии при изохорном процессе:

Изменение внутренней энергии при изобарном процессе:

Общее изменение внутренней энергии:

Ответ: 4,75 кДж.

Задача №4. Изменение внутренней энергии двухатомного газа

Условие

Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.

Решение

Изменение внутренней энергии находим по формуле:

Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:

Ответ: 75,7 МДж.

Задача №5. Внутренняя энергия смеси газов

Условие

В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К. 

Решение

Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно: 
 

 
Изменение внутренней энергии:

Знак «минус» означает, что внутренняя энергия уменьшается.

Ответ: -539 Дж.

Вопросы на тему «Внутренняя энергия тела»

Вопрос 1. Что такое внутренняя энергия?

Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.

По определению:

Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.

Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:

Вопрос 2. От чего зависит внутренняя энергия идеального газа?

Ответ. Эта величина не зависит от объёма и определяется только температурой.

Вопрос 3. Как изменяется внутренняя энергия тела?

Ответ. Если тело совершает работу, его внутренняя энергия уменьшается.

Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.

Вопрос 4. Что такое функция состояния?

Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма. 

Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?

Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.

Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.

термодинамика – Всегда ли внутренняя энергия идеального газа $\frac{3}{2}nRT$?

спросил 6 лет, 9 месяцев назад

Изменено 6 лет, 9 месяцев назад

Просмотрено 1к раз

$\begingroup$

Всегда ли внутренняя энергия идеального газа равна $\frac{3}{2}nRT\,?$ Я видел в Википедии, что она равна $\alpha nRT\;.$ Всегда ли $\alpha$ равна $\ frac{3}{2}$ для идеального газа?

• термодинамика
• кинетическая теория

$\endgroup$

$\begingroup$

Ответ на ваш вопрос: Равнораспределение энергии .

При температуре $T\,_,$ средняя энергия любой квадратичной степени свободы равна $\frac{1}{2} kT\;.

$

Для каждой степени свободы молекула идеального газа может запасать $\frac12 kT$ энергии в среднем .

Для одноатомной молекулы идеального газа существует только три степени свободы: поступательные кинетические энергии для движения вдоль трех перпендикулярных осей. Следовательно, молярная теплоемкость при постоянном объеме $C_V$ для одноатомного газа равна $$C_V= \frac32 R \;.$$

Аналогично, для двухатомной молекулы имеется пять степеней свободы: три поступательных кинетической энергии; две вращательные кинетические энергии. Он может вращаться вокруг двух разных осей (не вдоль межъядерной оси). Следовательно, $$C_V= \frac52 R\;.$$

Внутренняя энергия идеального газа определяется выражением $$E_\textrm{int} = nC_VT\;.$$

Для одноатомного идеального газа $$E_ \textrm{int} = n \frac32 R T\,.$$

Для двухатомного идеального газа $$E_\textrm{int} = n \frac52 R T\,.$$

Итак, вообще говоря, $$E_\textrm{int} = n \alpha RT\,. $$

$\endgroup$

$\begingroup$

От газа зависит, будет ли его одноатомный двухатомный нежесткий ,жесткий как $\alpha$ степень свободы, которая зависит от газа для моно это $3/2$

$\endgroup$

$\begingroup$

Это зависит от того, что человек определяет как идеальный газ. В литературе по физике идеальный газ определяется как газ, который имеет постоянную теплоемкость от абсолютного нуля до температуры T. В технической литературе мы считаем, что идеальный газ имеет зависящую от температуры теплоемкость, как и реальный газ. газы делают при низких давлениях. В обоих случаях считается, что теплоемкость не зависит от давления. Поскольку это обмен физикой, инженерная трактовка может не вызывать большого интереса, но все же важно понимать различие, если обращаться к литературе.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

2.3 Теплоемкость и равнораспределение энергии – общая физика с использованием исчисления I

Глава 2 Кинетическая теория газов

OpenStax и Паула Эррера-Сиклоди

К концу этого раздела вы сможете:

• Решать задачи, связанные с передачей тепла к идеальным одноатомным газам и от них, объем которых поддерживается постоянным
• Решите аналогичные задачи для неодноатомных идеальных газов на основе числа степеней свободы молекулы
• Оценка теплоемкости металлов с использованием модели, основанной на степенях свободы

В главе о температуре и теплоемкости мы определили удельную теплоемкость с помощью уравнения [латекс]Q = mc\Delta T[/латекс], или [латекс]c = (1/m)Q/\Delta T[/ латекс]. Однако свойства идеального газа напрямую зависят от количества молей в образце, поэтому здесь мы определяем удельную теплоемкость с точки зрения количества молей, а не массы. Кроме того, говоря о твердых телах и жидкостях, мы игнорировали любые изменения объема и давления при изменении температуры — хорошее приближение для твердых и жидких тел, но для газов мы должны сделать некоторые условия для изменения объема или давления. Здесь мы сосредоточимся на теплоемкости при постоянном объеме. Мы можем вычислить его для идеального газа.

Мы определяем молярную теплоемкость при постоянном объеме [латекс]C_V[/латекс] как

[латекс]C_V = \frac{1}{n}\frac{Q}{\Delta T},\text{с постоянным V.}[/latex]

Это часто выражается в форме

[латекс]\begin{уравнение} \tag{2.13} Q = nC_V\Delta T. \end{уравнение}[/latex]

Если объем не изменяется, общего смещения нет, поэтому работа не совершается, и единственное изменение внутренней энергии происходит за счет теплового потока [латекс]\Delta E_\text{int} = Q[/latex] . (Это утверждение обсуждается далее в следующей главе.) Мы используем уравнение [латекс]E_\text{int} = 3nRT/2[/latex] для записи [латекс]\Delta E_\text{int} = 3nR\Delta T/2[/latex] и замените [latex]\Delta E[/latex] на Q , чтобы найти [латекс]Q = 3nR\Delta T/2[/латекс], что дает следующий простой результат для идеального одноатомного газа:

[латекс]C_V = \frac{3}{2}R. [/latex]

Она не зависит от температуры, что оправдывает использование конечных разностей вместо производной. Эта формула хорошо согласуется с экспериментальными результатами.

В следующей главе мы обсудим молярную удельную теплоемкость при постоянном давлении [латекс]C_p[/латекс], которая всегда больше, чем [латекс]C_V[/латекс]. 9\circ \text{C}[/latex], тепловыделение Q составляет 180 Дж, а масса m ксенона составляет 0,125 кг.

Определить неизвестное. Нам нужна конечная температура, поэтому нам понадобится [латекс]\Delta T[/латекс].

Определите, какие уравнения необходимы. Поскольку ксенон является одноатомным, мы можем использовать [латекс]Q = 3nR\Delta T/2[/латекс]. Затем нам нужно количество молей, [латекс]n = m/M[/латекс].

Подставьте известные значения в уравнения и найдите неизвестные.
Молярная масса ксенона 131,3 г, поэтому получаем

[латекс]n = \frac{125\text{g}}{131,3\text{г/моль}} = 0,952\text{моль},[/latex]

[латекс]\Delta T = \frac {2Q}{3nR} = \frac{2(180\text{J})}{3(0,952\text{моль})(8,31\text{Дж/моль}\cdot°\text{C})} = 15,2°\text{C}. [/latex]

Следовательно, конечная температура 35,2°C. С таким же успехом эту задачу можно было бы решить и в градусах Кельвина; так как кельвин имеет тот же размер, что и градус Цельсия изменения температуры, вы получите [латекс]\Delta T=15,2 \text{K}[/latex].

Значение
Нагрев идеального или почти идеального газа при постоянном объеме играет важную роль в автомобильных двигателях и многих других практических системах.

Предположим, 2 моля газообразного гелия при 200 К смешаны с 2 молями газообразного криптона при 400 К в калориметре. Какая конечная температура?

Мы хотели бы обобщить наши результаты на идеальные газы с более чем одним атомом на молекулу. В таких системах молекулы могут иметь другие формы энергии, помимо кинетической энергии поступательного движения, такие как кинетическая энергия вращения и кинетическая и потенциальная энергии колебаний. Мы увидим, что простое правило позволяет нам определять средние энергии, присутствующие в этих формах, и решать задачи почти так же, как мы это делали для одноатомных газов. 92_z}[/латекс]. Таким образом, мы можем рассматривать нашу энергию [latex]\frac{3}{2}k_\text{B}T[/latex] как сумму вкладов [latex]\frac{1}{2}k_\ text{B}T[/latex] из каждого из трех измерений поступательного движения. Переходя к газу в целом, мы видим, что число 3 в формуле [латекс]C_V = \frac{3}{2}R[/латекс] также отражает эти три измерения. Мы определяем степень свободы как независимое возможное движение молекулы, такое как каждое из трех измерений перемещения. Тогда, если d представляет число степеней свободы, молярная теплоемкость при постоянном объеме одноатомного идеального газа равна [латекс]C_V = \frac{d}{2}R[/латекс], где [латекс]d = 3[/латекс].

Раздел физики, называемый статистической механикой, говорит нам, и эксперимент подтверждает, что [латекс]C_V[/латекс] любого идеального газа задается этим уравнением, независимо от числа степеней свободы. Этот факт следует из более общего результата, теоремы о равнораспределении , которая справедлива в классической (неквантовой) термодинамике для систем, находящихся в тепловом равновесии при технических условиях, выходящих за рамки нашего рассмотрения. Здесь мы упомянем только, что в системе энергия распределяется между степенями свободы в результате столкновений.

Энергия термодинамической системы, находящейся в равновесии, распределяется поровну между ее степенями свободы. Соответственно, молярная теплоемкость идеального газа пропорциональна количеству его степеней свободы, d:

[латекс]\begin{equation} \tag{2.14} C_V = \frac{d}{2}R. \end{уравнение}[/латекс]

Этот результат принадлежит шотландскому физику Джеймсу Клерку Максвеллу (1831–1871 гг.), чье имя будет упоминаться в этой книге еще несколько раз.

Например, рассмотрим двухатомный идеальный газ (хорошая модель для азота, [латекс]N_2[/латекс], и кислорода, [латекс]О_2[/латекс]). Такой газ имеет больше степеней свободы, чем одноатомный газ. В дополнение к трем степеням свободы для перемещения он имеет две степени свободы для вращения перпендикулярно своей оси. Кроме того, молекула может колебаться вдоль своей оси. Это движение часто моделируют, представляя пружину, соединяющую два атома, и мы знаем из простого гармонического движения, что такое движение обладает как кинетической, так и потенциальной энергией. Каждой из этих форм энергии соответствует степень свободы, дающая еще две.

Мы могли бы ожидать, что для двухатомного газа мы должны использовать 7 как число степеней свободы; классически, если бы молекулы газа обладали только поступательной кинетической энергией, столкновения между молекулами вскоре заставили бы их вращаться и вибрировать. Однако, как объяснялось в предыдущем модуле, квантовая механика определяет, какие степени свободы активны. Результат показан на рисунке 2.13. И вращательная, и колебательная энергии ограничены дискретными значениями. При температурах ниже примерно 60 К энергия молекул водорода слишком мала для того, чтобы столкновение могло перевести вращательное или колебательное состояние молекулы с самой низкой энергии на вторую по величине, поэтому единственной формой энергии является поступательная кинетическая энергия, и [латекс]d = 3[/латекс] или [латекс]C_V = 3R/2[/латекс], как в одноатомном газе. Выше этой температуры начинают давать вклад две вращательные степени свободы, то есть некоторые молекулы возбуждаются до вращательного состояния со второй по величине энергией. (Эта температура намного ниже, чем при вращении одноатомных газов, потому что двухатомные молекулы имеют гораздо большую инерцию вращения и, следовательно, гораздо меньшую энергию вращения.) Приблизительно от комнатной температуры (чуть меньше 300 К) до примерно 600 К степени свободы полностью активны, а колебательные нет, и [латекс]d = 5[/латекс]. Затем, наконец, выше примерно 3000 К колебательные степени свободы полностью активны, и [латекс]d = 7[/латекс], как и предсказывала классическая теория.

Рисунок 2.13 Молярная теплоемкость водорода как функция температуры (в логарифмическом масштабе). Три «ступени» или «плато» показывают разное количество степеней свободы, которых должны достичь типичные энергии молекул для активации. Поступательная кинетическая энергия соответствует трем степеням свободы, вращательная — еще двум, а колебательная — еще двум.

Многоатомные молекулы обычно имеют одну дополнительную вращательную степень свободы при комнатной температуре, поскольку они имеют сравнимые моменты инерции вокруг любой оси. Так, при комнатной температуре они имеют [латекс]d = 6[/латекс], а при высокой температуре [латекс]d = 8[/латекс]. Обычно мы предполагаем, что газы имеют теоретические значения при комнатной температуре 9\circ \text{C}[/latex] и 1 атм Ар 1,50 Он 1,50 Не 1,50 СО 2,50 [латекс]\текст{H}_2[/латекс] 2,47 [латекс]\текст{N}_2[/латекс] 2,50 [латекс]\текст{О}_2[/латекс] 2,53 [латекс]\текст{F}_2[/латекс] 2,8 [латекс]\текст{CO}_2[/латекс] 3,48 [латекс]\текст{H}_2\текст{S}[/латекс] 3,13 [латекс]\текст{N}_2\текст{О}[/латекс] 3,66

Что можно сказать о внутренней энергии двухатомных и многоатомных газов? Для таких газов [латекс]C_V[/латекс] является функцией температуры (рис. 2.13), поэтому у нас нет такого простого результата, как для одноатомных идеальных газов.

Идея равнораспределения приводит к оценке молярной теплоемкости твердых элементов при обычных температурах. Мы можем смоделировать атомы твердого тела как прикрепленные к соседним атомам пружинами (рис. 2.14).

Рисунок 2.14 В простой модели твердого тела каждый атом прикреплен к другому шестью пружинами, по две на каждое возможное движение: x , y и z . Каждое из трех движений соответствует двум степеням свободы, одной для кинетической энергии и одной для потенциальной энергии. Таким образом, d=6.

Аналогично обсуждению вибрации в предыдущем модуле, каждый атом имеет шесть степеней свободы: одну кинетическую и одну потенциальную для каждого из направлений x , y и z . Соответственно, молярная удельная теплоёмкость металла должна быть 3 Р . Этот результат, известный как закон Дюлонга и Пти, довольно хорошо работает экспериментально при комнатной температуре.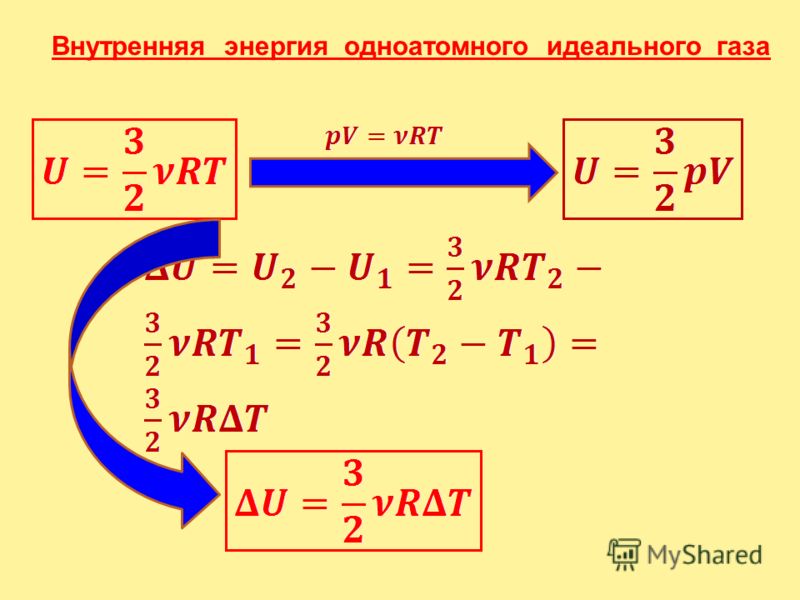 (Для каждого элемента он не работает при низких температурах по квантово-механическим причинам. Поскольку квантовые эффекты особенно важны для частиц с малой массой, закон Дюлонга и Пти уже не работает при комнатной температуре для некоторых легких элементов, таких как бериллий и углерод. Это также не работает для некоторых более тяжелых элементов по разным причинам, которые мы не можем охватить.)

Стратегия решения этих проблем такая же, как и в фазовых переходах для эффектов теплопередачи. Единственная новая особенность заключается в том, что вы должны определить, применим ли только что представленный случай — идеальные газы при постоянном объеме — к задаче. (Для твердых элементов поиск удельной теплоемкости, как правило, лучше, чем оценка ее по закону Дюлонга и Пти.) В случае идеального газа определите число d степеней свободы по числу атомов в молекулу газа и использовать ее для расчета [латекс]C_V[/латекс] (или использовать [латекс]C_V[/латекс] для решения 9\circ \text{C}[/latex] в изолированном контейнере.