Два источника ЭДС часто встречаются в электротехнических схемах.
Рассмотрим электрическую цепь, в которой включены два источника ЭДС, например, два аккумулятора.
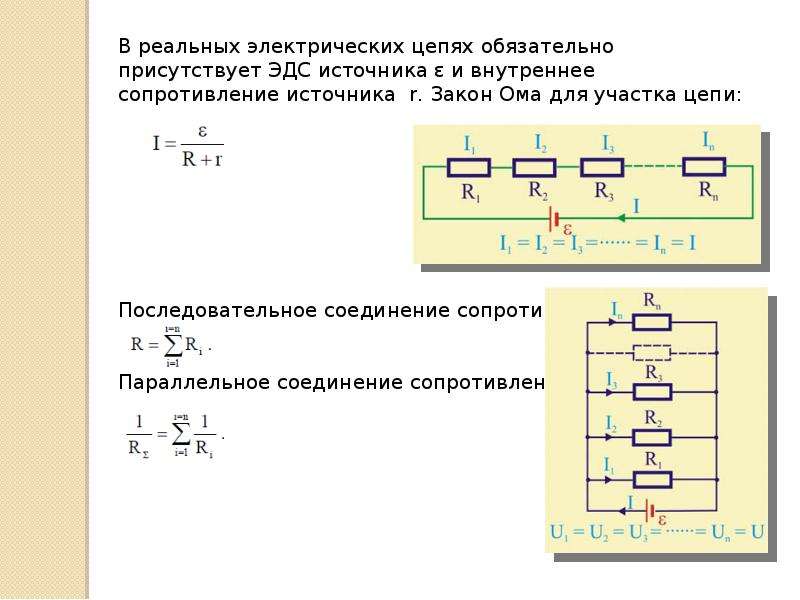
На рисунке изображена электрическая цепь с двумя источниками ЭДС.
По общефизическому принципу наложения ток в такой цепи равен алгебраической сумме токов, создаваемых в ней каждой из ЭДС, действующих отдельно друг от друга при неизменных сопротивлениях всех участков цепи.
Рассмотрим случай, когда имеем два источника эдс с внутренним сопротивлением r01 + r02. Положим сначала, что в цепи действует только источник с ЭДС E1. В этом случае получается простейшая цепь, и ток
I1 = E1 / r01 + r02 + r
будет направлен ту же сторону, что и ЭДС Е1. Затем находим ток, который возникнет, если будет действовать ЭДС Е2;
I2 = E2 / r01 + r02 + r
Этот ток будет совпадать по направлению с Е
Результирующий ток в цепи при совместном действии E1 и E2 при одинаковом их направлении равен сумме токов I1 и I2,
I = I1 + I2 = E1 + E2 / r01 + r02 + r
При встречном направлении E1 и E2 общий ток будет равен разности токов I1 и I2, т. е.
I = I1 — I2 = E1 — E2 / r01 + r02 + r
В последнем случае электрический ток возникает при условии, если E1 не равен E2 И будет направлен в сторону действия большей э. д. с. Пусть E
Электродвижущая сила, направленная противоположно току, называется встречной или противоэлектродвижущей силой.
Преобразуя формулу I = I1 — I2 = E1 — E2 / r01 + r02 + r, находим:
E1 — E2 = Ir01
откуда следует, что
E1 = E2 + Ir01 + Ir02 + Ir
Источник с ЭДС E1 развивает полную мощность
Р’ = E1I
и отдает во внешний для него участок цепи мощность
P1 = P’ — P01 = E1I — I2r01
так как работает в режиме генератора.
Напряжение на зажимах (БА) источника, работающего в генераторном режиме,
U БА = E1 — Ir01 = E2 + Ir02 + Ir
Произведение Ir есть напряжение U БВ
Мощность этого участка
Р = I2r.

Сумма E2 + Ir02 выражает напряжение U БА между точками В и А, т. е. на зажимах источника со встречной ЭДС. Таким образом,
U БА = E2 + Ir02,
а мощность
Р2 = E2I + I2r02 = Р» + Р02
где
Р» = E2I.
По закону сохранения энергии
P1 = P + Р
В участке ВА, где действует встречная э. д. с. E2, электрические силы преодолевают химические или механические силы, и происходит преобразование электрической энергии не только в тепловую, но также в химическую или механическую в зависимости от устройства источника с э. д. с. E2 (аккумулятор, который в этом случае заряжается, или машина постоянного тока, которая в этом случае работает в режиме электродвигателя).
Таким образом, источник с э. д. с. E2 является потребителем электрической энергии.
Итак, в общем случае источник э. д. с. может работать генератором или потребителем электрической энергии, а напряжение на его зажимах соответственно будет:
Электрические цепи с одним источником тока или эдс
Рассмотрим электрическую цепь, схема которой изображена на рис. 1, Пусть известны значения сопротивления резисторов R1, R2, R3, R4, R5, R6, эдс E и ее внутреннее сопротивление R0. Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками схемы а и d.
Рисунок 1
Такие задачи решаются методом свертывания схемы, по которому отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению относительно зажимов источников питания. Схема упрощается с помощью замены группы последовательно или параллельно соединенных резисторов одним эквивалентным по сопротивлению.
После произведенных преобразований схема принимает вид, показанный на рис. 2, а эквивалентное сопротивление всей цепи найдем из уравнения
Рисунок 2
Ток I1 в неразветвленной части схемы определим по закону Ома:
Воспользовавшись схемой (рис. 2), найдем токи I2 и I3:
Переходя к рис. 1, определим токи I4, I5, I6 по аналогичным уравнениям:
Зная ток I1, можно найти ток I2 по-другому. Согласно второму закону Кирхгофа,
Показания вольтметра можно определить, составив уравнение по второму закону Кирхгофа, например, для контура acda:
Для проверки решения можно воспользоваться первым законом Кирхгофа и уравнением баланса мощностей, которые для схемы, изображенной на рис. 1, примут вид
Электрические цепи с одним источником можно рассчитывать методом подобия (метод пропорциональных величин), который применим только для расчета линейных цепей, т.
Далее определяем
Рис. 3
Наконец, находим значение э.д.с. Е’:
Однако найденное значение E/ в общем случае отличается от заданной величины э.д. с. E. Поэтому для определения действительных и
вычисляем так называемый коэффициент подобия К=Е/Е’. Умножив на него полученные при расчете значения токов и напряжений, находим действительные значения токов цепи. Метод пропорциональных величин особенно эффективен при расчете разветвленных электрических цепей с одним источником.
Рассмотрим электрическую цепь, схема которой изображена на рис.
 3. К источнику тока J=0,1 А подключены резисторы с сопротивлениями R1 = 12 Ом; R2=10 Ом; R3 = 16 Ом; R4 Ом; R5=60 Ом. Определить напряжение Uab источника тока и все токи. Составить баланс мощностей. Задача решается
3. К источнику тока J=0,1 А подключены резисторы с сопротивлениями R1 = 12 Ом; R2=10 Ом; R3 = 16 Ом; R4 Ом; R5=60 Ом. Определить напряжение Uab источника тока и все токи. Составить баланс мощностей. Задача решается Находим входное сопротивление Rab схемы относительно зажимов источника тока:
Находим напряжение на зажимах источника тока Uab
По закону Ома находим ток I2
Ток I3 определяем из уравнения закона Кирхгофа:
Этот ток распределяется обратно пропорционально сопротивлениям R4 и R5:
Уравнение баланса мощностей отражает равенство мощностей, отдаваемой источником н расходуемой приемниками, т, е.
ЭДС и напряжение источника электрической энергии
Для того чтобы разобраться что такое электродвижущая сила источника электрической энергии, необходимо вспомнить, что представляет собой электрический ток и за счёт чего происходит его движение в электрической цепи.
Известно, электрический ток движется в цепи за счёт разницы потенциалов. Для того чтобы движение тока не прекращалось, нужно непрерывно обеспечивать эту разницу потенциалов между полюсами источника напряжения, к которому подключена цепь.
Подобное явление можно сравнить с трубкой, которая соединена с двумя резервуарами с водой. Если в этих резервуарах будет разный уровень воды, то она непременно начнёт перетекать через трубку из одного сосуда в другой и наоборот; так если разница в уровне воды между сосудами будет постоянной, то и движение воды не прекратиться.
Данный пример помогает понять, что происходит в электрической цепи. Электрическая энергия, действующая внутри источника, постоянно поддерживает электрический ток. Таким образом, обеспечивается непрерывная работа.
Понятие «Электродвижущая сила»
В данном случае, электродвижущая сила (ЭДС) – это сила, которая поддерживает разницу потенциалов на разных полюсах источника энергии, она вызывает и поддерживает движение тока, а также преодолевает внутренне сопротивление проводника и т. д.
д.
Ток может протекать по проводнику столь же долго, сколь существует разница потенциалов. Свободные электроны приходят в постоянное движение между телами, которые соединены в электрическую цепь.
Электродвижущая сила – величина физическая, т. е., её можно измерить и использовать как одну из характеристик электрической цепи. В источниках постоянного, либо переменного тока ЭДС характеризует работу непотенциальных сил. Это работа сторонних или непотенциальных сил в замкнутом контуре, когда они перемещают одиночный электрический заряд вдоль всего контура.
Возникновение электродвижущей силы
Существует различные виды источников электрической энергии. Каждый из них можно охарактеризовать по-разному, у каждого вида свои принципиальные особенности. Эти особенности влияют на возникновение электродвижущей силы, причины данного явления весьма специфичны, т. е. зависят от вида источника.
В чём же главная суть различий? К примеру, если мы берём химические источники электрической энергии, такие как аккумуляторы, другие гальванические элементы, то электродвижущая сила становится результатом химической реакции. Если рассмотреть генераторы, то здесь причиной является электромагнитная индукция, а в различных термических элементах основой является тепловая энергия. От этого возникает электрический ток.
Если рассмотреть генераторы, то здесь причиной является электромагнитная индукция, а в различных термических элементах основой является тепловая энергия. От этого возникает электрический ток.
Измерение электродвижущей силы
Электродвижущая сила измеряется в вольтах, также как и напряжение. Эти величины связаны между собой. Однако ЭДС можно измерять на отдельном участке электрической цепи, тогда будут измеряться работы не всех сил, действующих на этом контуре, а только те, которые есть на отдельно взятом участке цепи.
Разность потенциалов, являющуюся причиной возникновения и прохождения тока по цепи, также можно назвать напряжением. Однако, если ЭДС – работа сторонних сил, которая совершается при перемещении единичного заряда, то она не может быть охарактеризована с помощью разницы потенциалов, т. е., напряжения, так как работа зависит от траектории движения заряда, эти силы непотенциальны. В этом различие таких понятий как напряжение и электродвижущая сила.
Данная особенность учитывается при измерении ЭДС и напряжения. В обоих случаях используют вольтметры. Для того чтобы измерить ЭДС нужно при разомкнутой внешней цепи подключить вольтметр к концам источника энергии. Если требуется измерить напряжение на выбранном участке электрической цепи, то вольтметр должен быть подключён параллельно к концам конкретного участка.
ЭДС и напряжение источника электрической энергии могут быть независимо от величины электрического тока в цепи; в разомкнутой цепи ток равен нулю. Однако если генератор или аккумулятор будут работать, то они возбуждают ЭДС, а значит, между концами возникает напряжение.
Внутреннее сопротивление формула эдс. Краткие теоретические сведения. Закон Ома для полной цепи
Мы пришли к выводу, что для поддержания постоянного тока в замкнутой цепи, в нее необходимо включить источник тока. Подчеркнем, что задача источника заключается не в том, чтобы поставлять заряды в электрическую цепь (в проводниках этих зарядов достаточно), а в том, чтобы заставлять их двигаться, совершать работу по перемещению зарядов против сил электрического поля. Основной характеристики источника является электродвижущая сила 1 (ЭДС) − работа, совершаемая сторонними силами по перемещению единичного положительного заряда
Основной характеристики источника является электродвижущая сила 1 (ЭДС) − работа, совершаемая сторонними силами по перемещению единичного положительного заряда
Единицей измерения ЭДС в системе единиц СИ является Вольт. ЭДС источника равна 1 вольт, если он совершает работу 1 Джоуль при перемещении заряда 1 Кулон
Для обозначения источников тока на электрических схемах используется специальное обозначение (рис. 397).
рис. 397
Электростатическое поле совершает положительную работу по перемещению положительного заряда в направлении уменьшения потенциала поля. Источник тока проводит разделение электрических зарядов − на одном полюсе накапливаются положительные заряды, на другом отрицательный. Напряженность электрического поля в источнике направлена от положительного полюса к отрицательному, поэтому работа электрического поля по перемещению положительного заряда будет положительной при его движения от «плюса» к «минусу». Работа сторонних сил, наоборот, положительна в том случае, если положительные заряды перемещаются от отрицательного полюса к положительному, то есть от «минуса» к «плюсу».
В этом принципиальное отличие понятий разности потенциалов и ЭДС, о котором всегда необходимо помнить.
Таким образом, электродвижущую силу источника можно считать алгебраической величиной, знак которой («плюс» или «минус») зависит от направления тока. В схеме, показанной на рис. 398,
рис. 398
вне источника (во внешней цепи) ток течет 2 от «плюса» источника к «минусу», в внутри источника от «минуса» к «плюсу». В этом случае, как сторонние силы источника, так и электростатические силы во внешней цепи совершают положительную работу.
Если на некотором участке электрической цепи помимо электростатических действуют и сторонние силы, то над перемещением зарядов «работают» как электростатические, так и сторонние силы. Суммарная работа электростатических и сторонних сил по перемещению единичного положительного заряда называется электрическим напряжением на участке цепи
В том случае, когда сторонние силы отсутствуют, электрическое напряжение совпадает с разностью потенциалов электрического поля.
Поясним определение напряжения и знака ЭДС на простом примере. Пусть на участке цепи, по которому протекает электрический ток, имеются источник сторонних сил и резистор (рис. 399).
рис. 399
Для определенности будем считать, что φ o > φ 1 , то есть электрический ток направлен от точки 0 к точке 1 . При подключении источника, как показано на рис. 399 а, Сторонние силы источника совершают положительную работу, поэтому соотношение (2) в этом случае может быть записано в виде
При обратном включении источника (рис. 399 б) внутри него заряды движутся против сторонних сил, поэтому работа последних отрицательна. Фактически силы внешнего электрического поля преодолевают сторонние силы. Следовательно, в этом случае рассматриваемое соотношение (2) имеет вид
Для протекания электрического тока по участку цепи, обладающему электрическим сопротивлением, необходимо совершать работу, по преодолению сил сопротивления. Для единичного положительного заряда эта работа, согласно закону Ома, равна произведению IR = U которое, естественно совпадает с напряжением на данном участке.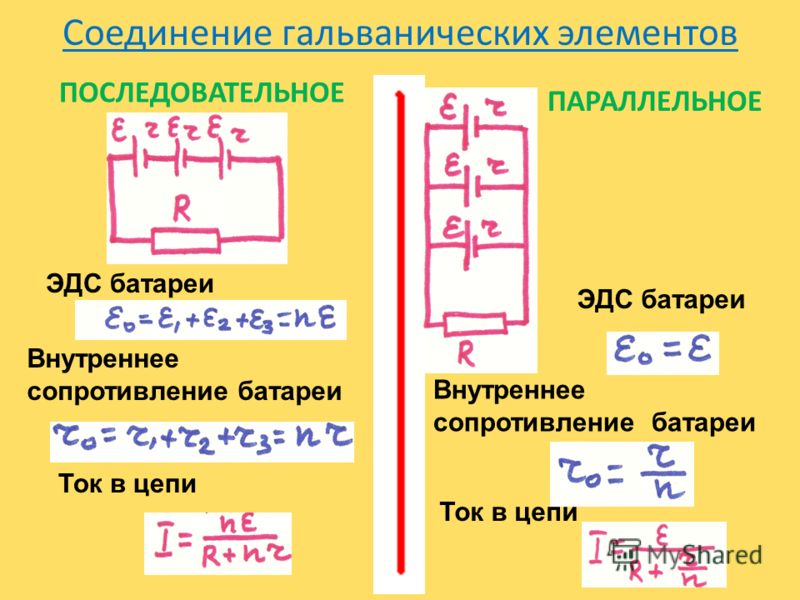
Заряженные частицы (как электроны, так и ионы) внутри источника движутся в некоторой окружающей среде, поэтому со стороны среду на них также действуют тормозящие силы, которые также необходимо преодолевать. Заряженные частицы преодолевают силы сопротивления благодаря действию сторонних сил (если ток в источнике направлен от «плюса» к «минусу») либо благодаря электростатическим силам (если ток направлен от «минуса» к «плюсу»). Очевидно, что работа по преодолению этих сил не зависит от направления движения, так как силы сопротивления всегда направлены в сторону, противоположную скорости движения частиц. Так как силы сопротивления пропорциональны средней скорости движения частиц, то работа по их преодолению пропорциональна скорости движения, следовательно, силе тока силе. Таким образом, мы можем ввести еще характеристику источника − его внутренне сопротивление r , аналогично обычному электрическому сопротивлению. Работа по преодолению сил сопротивления при перемещении единичного положительного заряда между полюсами источника равна A/q = Ir .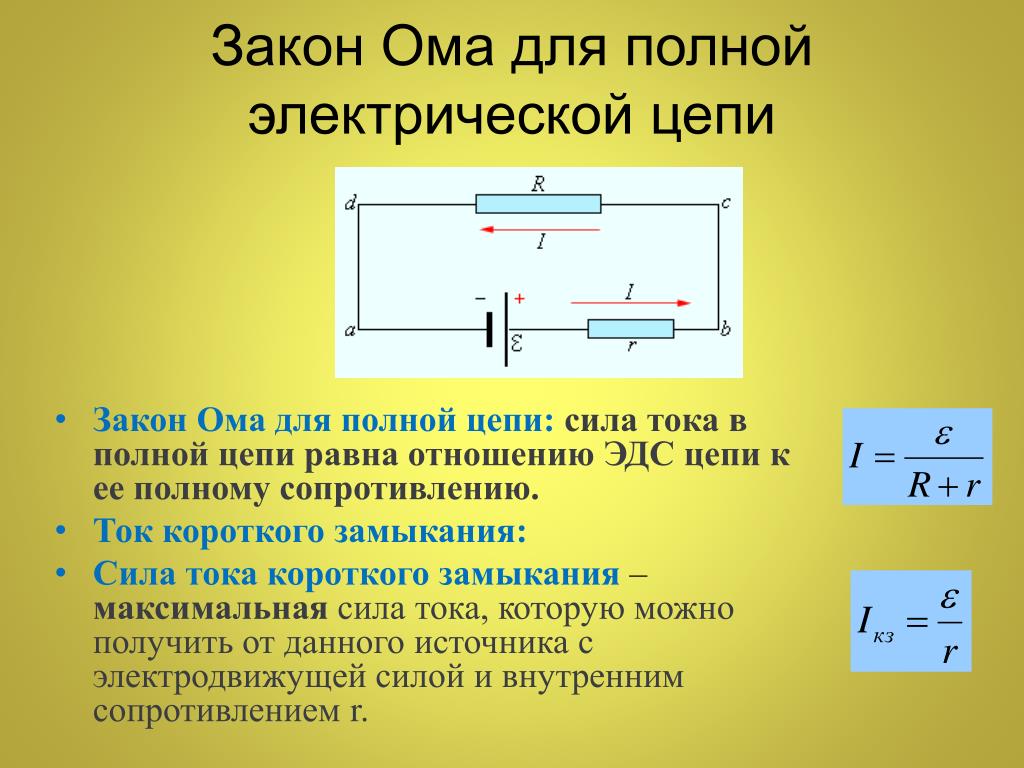 Еще раз подчеркнем, эта работа не зависит от направления тока в источнике.
Еще раз подчеркнем, эта работа не зависит от направления тока в источнике.
1 Название этой физической величины неудачно − так электродвижущая сила является работой, а не силой в обычном механическом понимании. Но этот термин настолько устоялся, что изменять его не «в наших силах». К слову, сила тока то же не является механической силой! Не говоря уж о таких понятиях «сила духа», «сила воли», «божественная сила» и т.д.
2 Напомним, за направление движения электрического тока принято направление движения положительных зарядов.
Закон Ома для полной цепи, определение которого касается значения электрического тока в реальных цепях, находится в зависимости от источника тока и от сопротивления нагрузки. Этот закон носит и другое название – закон Ома для замкнутых цепей. Принцип действия данного закона заключается в следующем.
В качестве самого простого примера, электрическая лампа, являющаяся потребителем электрического тока, совместно с источником тока есть не что иное, как замкнутая . Данная электрическая цепь наглядно показана на рисунке.
Данная электрическая цепь наглядно показана на рисунке.
Электроток, проходя через лампочку, также проходит и через сам источник тока. Таким образом, во время прохождения по цепи, ток испытает сопротивление не только проводника, но и сопротивление, непосредственно, самого источника тока. В источнике сопротивление создается электролитом, находящимся между пластинами и пограничными слоями пластин и электролита. Отсюда следует, что в замкнутой цепи, ее общее сопротивление будет состоять из суммы сопротивлений лампочки и источника тока.
Внешнее и внутреннее сопротивление
Сопротивление нагрузки, в данном случае лампочки, соединенной с источником тока, носит название внешнего сопротивления. Непосредственное сопротивление источника тока называется внутренним сопротивлением. Для более наглядного изображения процесса, все значения необходимо условно обозначить. I – , R – внешнее сопротивление, r – внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR. Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.
Однако, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.
Электродвижущая сила аккумулятора
Аккумулятор должен иметь следующее значение электродвижущей силы, способной поддерживать необходимый ток в цепи: Е=IхR+Iхr . Из формулы видно, что электродвижущая сила аккумулятора составляет сумму внешнего и внутреннего . Значение тока нужно вынести за скобки: Е=I(r+R) . Иначе можно представить: I=Е/(r+R) . Двумя последними формулами выражается закон Ома для полной цепи, определение которого звучит следующим образом: в замкнутой цепи сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений этой цепи.
На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .
Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).
Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.
При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).
В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:
– электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;
– термоэлектрическая – в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;
– фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;
– химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.
Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:
ɛ = A ст /q ,
где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.
Электродвижущую силу выражают в вольтах.
Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.
Внутреннее сопротивление источника тока.
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше).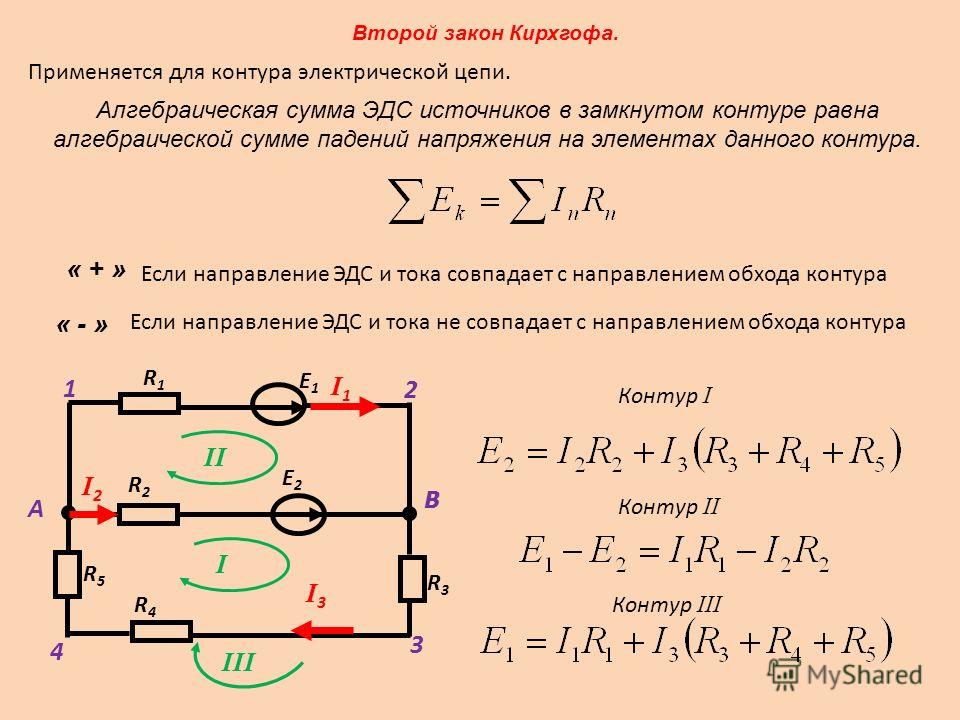 Это позволяет с их помощью получать токи, измеряемые амперами.
Это позволяет с их помощью получать токи, измеряемые амперами.
Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.
Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.
Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.
К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредственно к выходным гнездам источника подключают еще и вольтметр.
ЭДС
измеряют по показанию вольтметра при
разомкнутом ключе. Этот прием определения
ЭДС основан на следствии из закона
Ома для полной цепи, согласно которому
при бесконечно большом сопротивлении
внешней цепи напряжение на зажимах
источника равно его ЭДС. (См. параграф
“Закон Ома для полной цепи” учебника
“Физика 10”).
Для определения внутреннего сопротивления источника замыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока). Поскольку ЭДС источника равна сумме падения напряжений на внутреннем и внешнем участках цепи:
ε = U r +U R , то U r = ε -U R (1)
По закону Ома для участка цепи U r = I· r (2). Подставив равенство (2) в (1) получают:
I · r = ε – U r , откуда r = (ε – U R )/ J
Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо предварительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внешнем сопротивлении, а также силу тока в нем.
Ход работы
1. Подготовьте таблицу для записи результатов
измерений и вычислений:
Подготовьте таблицу для записи результатов
измерений и вычислений:
ε ,в | U r , B | i,a | r , Ом |
Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.
После проверки схемы соберите электрическую цепь. Ключ разомкните.
Измерьте величину ЭДС источника.
Замкните ключ и определите показания амперметра и вольтметра.
Вычислите внутреннее сопротивление источника.
Определение эдс и внутреннего сопротивления источника тока графическим методом
Цель
работы: изучить
измерения ЭДС, внутреннего сопротивления
и тока короткого замыкания источника
тока, основанный на анализе графика
зависимости напряжения на выходе
источника от силы тока в цепи.
Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.
Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:
так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).
Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. – силу тока короткого замыкания (ток, который потечет в цепи источника, когда внешнее сопротивление R станет равным нулю).
ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика соответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.
Силу
тока короткого замыкания определяют
по точке пересечения графика с осью
токов. В этом случае внешнее сопротивление
R
= 0 и, следовательно, напряжение на выходе
источника U
= 0.
Внутреннее сопротивление источника находят по тангенсу угла наклона графика относительно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомните смысл коэффициента при X).
Ход работы
- После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источнику тока, будет максимальным.
Для записи результатов измерений подготовьте таблицу:
Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.
Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.
Нанесите
полученные в эксперименте точки на
график. Напряжение откладывайте по
вертикальной оси, а силу тока – по
горизонтальной. Проведите по точкам
прямую линию.
Напряжение откладывайте по
вертикальной оси, а силу тока – по
горизонтальной. Проведите по точкам
прямую линию.
Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.
Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней цепи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.
Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла наклона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I К.З
Лабораторная работа № 8
Тема: « Определение электродвижущей силы и внутреннего сопротивления источника тока ».
Цель: научиться определять электродвижущую силу и внутреннее сопротивление источника электрической энергии.
Оборудование: 1. Амперметр лабораторный;
2. Источник электрической энергии;
3. Соединительные провода,
4. Набор сопротивлений 2 Ом и 4 Ом;
5. Переключатель однополюсный; ключ.
Теория.
Возникновение разности потенциалов на полюсах любого источника является результатом разделения в нем положительных и отрицательных зарядов. Это разделение происходит благодаря работе, совершаемой сторонними силами.
Силы неэлектрического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы A ст сторонних сил при перемещении заряда q внутри источника тока к величине этого заряда, называется электродвижущей силой источника (ЭДС):
ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда.
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах [В].
Чтобы измерить ЭДС источника, надо присоединить к нему вольтметр при разомкнутой цепи .
Источник тока является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Это сопротивление называют внутренним сопротивлением источника и обозначают r .
Если цепь разомкнута, то работа сторонних сил превращается в потенциальную энергию источника тока. При замкнутой цепи эта потенциальная энергия расходуется на работу по перемещению зарядов во внешней цепи с сопротивлением R и во внутренней части цепи с сопротивлением r , т.е. ε = IR + Ir .
Если цепь состоит из внешней части сопротивлением R и внутренней сопротивлением r, то, согласно закону сохранения энергии, ЭДС источника будет равна сумме напряжений на внешнем и внутреннем участках цепи, т.к. при перемещении по замкнутой цепи заряд возвращается в исходное положение , где IR – напряжение на внешнем участке цепи, а Ir – напряжение на внутреннем участке цепи.
Таким образом, для участка цепи, содержащего ЭДС:
Эта формула выражает закон Ома для полной цепи : сила тока в полной цепи прямо пропорциональна электродвижущей силе источника и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи.
ε и r можно определить опытным путем.
Часто источники электрической энергии соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3
2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1
3.
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС . Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3
2. Сопротивление батареи меньше, чем сопротивление одного источника r батареи = r 1 /n
3. Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы – параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Ход работы.
1. Начертите таблицу:
2. Рассмотрите шкалу амперметра и определите цену одного деления.
3. Составьте электрическую цепь по схеме, изображенной на рисунке 1. Переключатель поставить в среднее положение.
Рисунок 1.
4. Замкнуть цепь, введя меньшее сопротивление R 1 1 . Разомкнуть цепь.
5. Замкнуть цепь, введя большее сопротивление R 2 . Записать величину силы тока I 2 . Разомкнуть цепь.
6. Вычислить значение ЭДС и внутреннего сопротивления источника электрической энергии.
Закон Ома для полной цепи для каждого случая: и
Отсюда получим формулы для вычисления ε и r:
7. Результаты всех измерений и вычислений запишите в таблицу.
8. Сделайте вывод.
9. Ответьте на контрольные вопросы.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Раскройте физический смысл понятия «электродвижущая сила источника тока».
2. Определить сопротивление внешнего участка цепи, пользуясь результатами полученных измерений и законом Ома для полной цепи.
3. Объяснить, почему внутреннее сопротивление возрастает при последовательном соединении аккумуляторов и уменьшается при параллельном в сравнении с сопротивлением r 0 одного аккумулятора.
4. В каком случае вольтметр, включенный на зажимы генератора, показывает ЭДС генератора и в каком случае напряжение на концах внешнего участка цепи? Можно ли это напряжение считать также и напряжением на концах внутреннего участка цепи?
Вариант выполнения измерений.
Опыт 1. Сопротивление R 1 =2 Ом, сила тока I 1 =1,3 А.
Сопротивление R 2 =4 Ом, сила тока I 2 =0,7 А.
САМОИНДУКЦИЯ Каждый проводник, по которому протекает эл. ток, находится в собственном магнитном поле. При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл. поля и в цепи появляется ЭДС индукции. Это явление называется самоиндукцией. Замыкание цепи При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение
магнитного потока, возникает вихревое эл. поле, направленное против тока, т. Размыкание цепи При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке,
возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю
силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в
цепи. Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу). От чего зависит ЭДС самоиндукции? Эл. ток создает собственное магнитное поле. Магнитный поток через контур
пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе
тока в проводнике Индуктивность
– физ. величина,
численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока
на 1Ампер за 1 секунду. где Ф – магнитный поток через контур, I – сила тока в контуре. Единицы измерения индуктивности в системе СИ: Индуктивность катушки зависит от: ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию
силы тока при размыкании цепи. Вокруг проводника с током существует магнитное поле, которое обладает энергией. Энергия магнитного поля равнасобственной
энергии тока. Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы
тока. ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
|
Уравнение ЭДС генератора переменного тока и синхронного генератора
Уравнение ЭДС генератора переменного токаГенератор переменного тока или генератор переменного тока (также известный как синхронный генератор или динамо-машина) – это устройство, преобразующее механическую энергию в электрическую.
Когда мы подаем ток намагничивания от шунтирующего генератора постоянного тока через два контактных кольца (в последних генераторах переменного тока они используют электронную систему запуска вместо контактных колец и коммутаторов), потому что магниты поля вращаются.имейте в виду, что в большинстве генераторов переменного тока используется вращающееся магнитное поле со стационарным якорем.
Когда ротор вращается, проводники статора, которые остаются статичными в случае отключения генератора из-за магнитного потока, они индуцируют ЭДС, создаваемую в них (согласно закону Фарадея об электромагнитной индукции , который гласит, что если проводник или катушка соединяются с любым изменяющимся элементом). потока, в нем должна быть наведенная ЭДС.
потока, в нем должна быть наведенная ЭДС.
Примечание: мы подробно обсудим конструкцию, работу и работу, типы генераторов переменного тока в наших следующих публикациях.
Эту наведенную ЭДС можно найти с помощью уравнения ЭДС генератора переменного тока , которое выглядит следующим образом:
Лец,
P = количество полюсов
Z = количество проводников или сторон катушки в серии / фазе, т. Е. Z = 2T … где T – количество катушек или витков на фазу (обратите внимание, что один виток или катушка имеет два конца или стороны)
f = частота наведенной ЭДС в Гц
Φ = поток на полюс (Weber)
Н = частота вращения ротора (об / мин)
K d = Коэффициент распределения =
Где коэффициент распределения = K d =
K c или K P = Cos α / 2
Если наведенная ЭДС предполагается синусоидальной, то
K f = форм-фактор = 1. 11
11
За один оборот ротора, то есть за 60 / N секунд, каждый проводник перерезается магнитным потоком ΦP Webers.
d Φ = Φ P , а также d Φ = 60 / N секунд
, затем наведенная ЭДС на проводник (в среднем) =… .. (i)
Но мы знаем, что:
f = PN / 120 или N = 120 f / P
Подставляя значение N в Уравнение (i) , получаем
Среднее значение ЭДС на проводник = (N = 120 f / P)
Если имеется последовательно соединенных проводников на фазу,
затем синхронный генератор средний E.М.Ф на фазу = 2 f Φ Z Вольт = 4 f Φ T Вольт … . . (Z = 2T)
. (Z = 2T)
И мы это знаем;
Форм-фактор = среднеквадратичное значение / среднее значение
= среднеквадратичное значение = форм-фактор x среднее значение,
В AV = 1,11 x 4 f ΦT = 4,44 f ΦT Вольт.
А фактическое доступное напряжение генератора по фазе
В PH = 4.44 K C K D f ΦT PH
В = 4,44 К f K C K D f ΦT Вольт.
Где:
- В = Фактическое генерируемое напряжение на фазу
- K C = Коэффициент диапазона катушки или коэффициент шага
- K D = коэффициент распределения
- K f = Форм-фактор
- f = частота
- T = Количество катушек или количество витков на фазу
Примечание. Если генератор переменного тока или генератор переменного тока соединены звездой, как обычно, то линейное напряжение в √3 раз больше фазного напряжения, как вычислено из приведенного выше уравнения.
Если генератор переменного тока или генератор переменного тока соединены звездой, как обычно, то линейное напряжение в √3 раз больше фазного напряжения, как вычислено из приведенного выше уравнения.
Похожие сообщения:
ЭДС движущаяся
ЭДС движущаясяДвигательная ЭДС
Нейтральный прямой проводящий провод содержит равное количество положительных и отрицательных полюсов. отрицательные заряды. Однако электроны могут свободно перемещаться внутри проволоки, а положительные ядра – нет.
Если прямой токопроводящий провод размещен в плоскости, перпендикулярной однородной
магнитное поле и движется в направлении, перпендикулярном полю, то
каждый заряд q в проводе испытывает магнитную силу величиной F = qvB.Отрицательно заряженные электроны
будет ускоряться в ответ на эту силу. Поскольку они не могут покинуть
провод, отрицательный заряд будет накапливаться на одном конце провода, а положительный
заряд останется на другом конце. Разделенные заряды производят
электрическое поле, которое оказывает силу на другие заряды в проводе. Эта электрическая сила противостоит магнитной силе. Как только электрическая сила
достаточно сильные, чтобы нейтрализовать магнитную силу, электроны больше не будут ускоряться,
и их чистое движение остановится из-за сопротивления проволоки.Мы тогда
имеем qvB = qE. В
электрическое поле в проводе равно E = vB.
Эта электрическая сила противостоит магнитной силе. Как только электрическая сила
достаточно сильные, чтобы нейтрализовать магнитную силу, электроны больше не будут ускоряться,
и их чистое движение остановится из-за сопротивления проволоки.Мы тогда
имеем qvB = qE. В
электрическое поле в проводе равно E = vB.
Если мы поместим провод на токопроводящую шину, ток начнет течь в схема, образованная рельсом и проводом.
ЭДС, управляющая током, равна vB, умноженной на длину d участка. провода, соединяющего рельсы. (Работа, совершаемая на единицу заряда, равна vBd, когда заряд перемещается от одного конца движущегося провода к другому.) Ток, протекающий в цепи, будет I = vBd / R, где R – сопротивление цепи.
В приведенной выше «нити» цепи (состоящей только из проволоки или стержней)
двигательная ЭДС = B * d * v.
Магнитный поток через цепь в момент времени t равен Φ B = B * A = B * L * d,
где L – длина цепи в момент времени t.
Штанга движется со скоростью v.
Скорость изменения потока ΔΦ B / Δt = B * d * ΔL / Δt =
B * d * v, поскольку меняется только длина цепи, и ΔL / Δt = v.
Поэтому мы можем написать
ΔΦ B / Δt (нитевидный цепь с движущимися частями, постоянная B) = двигательная ЭДС.
Движущаяся ЭДС не индуцированная ЭДС. Поток магнитного поле, хотя фиксированная область не меняется. Вместо этого внешняя сила работать, перемещая провода, которые являются частью цепи, в постоянном магнитном поле. Но для нитевидных цепей мы можем записать одно математическое уравнение который выражает как закон Фарадея, так и ЭДС движения.
ΔΦ B / Δt (любой поток изменяется по нитевому контуру) = ЭДС.
В этом уравнении ЭДС означает двигательную и индуцированную ЭДС.
проблема:
На рисунке справа предположим, что R = 6 Ом, d = 1,2 м и a однородное магнитное поле 2,5 Тл направлено внутрь страницы. С какой скоростью нужно ли переместить полоску, чтобы на резисторе получилось 0,5 А?
Решение:
- Рассуждение:
Скорость изменения потока равна dΦ B / dt = B * d * dL / dt = B * d * v, поскольку меняется только длина цепи, и ΔL / Δt = v.
Ток, протекающий в цепи, будет I = vBd / R. - Детали расчета:
Я = vBd / R. Следовательно, v = IR / (Bd) = 0,5 А * 6 Ом / (2,5 Тл * 1,2 м) = 1 м / с.
Проблема:
Проводящий стержень длины L, лежащий в плоскости xy. поворачивается с постоянной угловой скоростью ω против часовой стрелки вокруг источник. Постоянное магнитное поле величина B 0 ориентирована в направлении оси z. Будет ли двигательная ЭДС индуцируется в стержне? Если да, то какой конец стержня будет положительное напряжение?
Решение:
- Рассуждение:
Проводящий стержень движется в плоскости, перпендикулярной к В .Возникает двигательная ЭДС. Правило правой руки говорит нам что магнитная сила на положительных зарядах будет указывать в сторону от от начала координат магнитная сила на отрицательных зарядах будет указывать в сторону от происхождения. Свободные электроны будут двигаться и накапливаться на источник, в то время как положительный заряд останется на другом конце. Разделенные заряды создают электрическое поле. Конец стержня
не в начале координат будет иметь положительное напряжение по отношению к началу координат.
Разделенные заряды создают электрическое поле. Конец стержня
не в начале координат будет иметь положительное напряжение по отношению к началу координат.
дюйм это видеоклип тонкий стержень быстро перемещается в магнитном поле, создаваемом набором магнитов. Северный полюс магнитов направлен вверх. Если ток через стержень от слева направо, затем он течет от красного провода через счетчик к черному ведение, то отклонение стрелки счетчика вправо.
Вы можете проверить направленные аспекты двигательной ЭДС.
Если вы пропускаете регулярные лекции, обратите внимание на эту видеолекцию.
Лекция 17: Двигательная ЭДС и ДинамоЭлектрические свойства цепей RC:
В простейшем виде цепь R-C содержит сопротивление R, конденсатор C и электродвижущую силу ЭДС (обычно аккумулятор). Принципиальная схема цепи R-C выглядит так: Когда тумблер находится в разомкнутом положении, показанном на схеме, к конденсатору не подключена электродвижущая сила, ЭДС, и, если конденсатор не был ранее заряжен, в конденсаторе не будет храниться зарядов (т. е.е., q = 0) и разность потенциалов между обкладками конденсатора, соответственно, также будет равна нулю.
е.е., q = 0) и разность потенциалов между обкладками конденсатора, соответственно, также будет равна нулю.
Если переключатель переключен так, что он соединяет конденсатор с электродвижущей силой, заряды будут накапливаться на пластинах конденсатора, + на одной пластине, _ на другой. Это будет продолжаться до тех пор, пока накопленный заряд не создаст разность потенциалов (V c ) между двумя пластинами, которая численно равна электродвижущей силе.То есть, когда:
ток через соединительные провода прекратится (т. Е. I = 0).
Когда переключатель переведен в свое альтернативное положение, (i) ЭДС обходится, (ii) две пластины конденсатора соединены, и (iii) заряды, накопленные на конденсаторе, будут стремиться пройти через соединительный провод к конденсатору. противоположная пластина. Другими словами, заряженный конденсатор разрядится.
Об электрических свойствах цепей R-C следует помнить две важные вещи:
1.Когда конденсатор (C) полностью заряжен, сохраняется следующее соотношение:
q = Ce Уравнение 1a где q – общее количество заряда, накопленного конденсатором, C – емкость конденсатора, а e – электродвижущая сила, которая фактически заряжает конденсатор.Обратите внимание, что q = 0, когда конденсатор разряжен. Также обратите внимание, что уравнение можно переставить так:
q / C = e = V c Уравнение 1b Это означает, что размещение избытка + на одной пластине конденсатора и избытка на другой пластине создаст разность потенциалов между пластинами.
2. Из-за наличия сопротивления (R) в цепи ток через цепь замедляется. В результате для изменения количества заряда, хранящегося на пластинах конденсатора, требуется время.
Например, если бы вы начали с полностью разряженного конденсатора (т.е. q = 0 и V c = 0) и подключили его к батарее, зарядка конденсатора описывалась бы экспоненциальным уравнением ,
q t = Ce (1 e -t / RC ) Уравнение 2a и если C = 1, e = 10 и R = 1 график зависимости q t отвремя будет выглядеть так:
Аналогичным образом, если бы вы начали с того же конденсатора в полностью заряженном состоянии (т.е. q = Ce и V c = e ) и соедините две его пластины друг с другом, разряд конденсатора будет описан экспоненциальным уравнением:
q t = Ce e -t / RC Уравнение 2b и график q t vs.
время будет выглядеть так:
Задания:
1. Имея в виду уравнения 1b, 2a и 2b и определение тока, можете ли вы предсказать внешний вид графиков V c и тока (I) в зависимости от времени для той же цепи R-C?
2. Запустите моделирование электрических свойств RC-цепи и получите качественное представление о влиянии изменения e на электрическое поведение RC-цепи.
3. Величина RC называется постоянной времени цепи R-C и иногда обозначается как t (= RC).Изучите влияние изменения t на электрическое «поведение» RC-цепи, повторив упражнение 2, на этот раз меняя R и / или C. плазматическая мембрана возбудимых клеток (подсказка: вспомните модель эквивалентного контура)?
Определение ЭДС и внутреннего сопротивления ячейки – Электрические источники и внутреннее сопротивление – Высшая физическая версия
Вольтметр и переменный резистор
1.0.$0.$1.$2″> Посмотрите это видео, чтобы узнать, как можно измерить ЭДС и внутреннее сопротивление ячейки.Как показано на видео, чтобы найти ЭДС и внутреннее сопротивление ячейки, создается следующая схема.
Изменяется переменный резистор и снимаются показания разности потенциалов на выводах элемента и тока через элемент. Затем строится график этих результатов, как показано ниже.
В точке, в которой линия пересекает ось конечной разности потенциалов, нет тока , протекающего из ячейки. Это называется потенциалом разомкнутой цепи цепи.
Поскольку нет тока, не будет потерь напряжения, поэтому это значение является ЭДС ячейки. Таким образом, точка, где линия пересекает ось конечной разности потенциалов (точка пересечения оси Y), является ЭДС ячейки.
Таким образом, точка, где линия пересекает ось конечной разности потенциалов (точка пересечения оси Y), является ЭДС ячейки.
В точке, где линия пересекает текущую ось (точка пересечения оси x), из ячейки берется максимальный ток. Это происходит, когда сопротивление нагрузки \ (R = 0 \ Omega. \)
. Это может быть достигнуто путем короткого замыкания ячейки (этого следует избегать, поскольку ячейка может перегреться и это потенциально опасно).Максимальный ток называется током короткого замыкания , \ (I_ {SC} \).
Чтобы найти внутреннее сопротивление ячейки, вычисляется градиент линии. Это отрицательное значение. Внутреннее сопротивление ячейки такое же, но без знака минус. Например, если наклон линии равен \ (- 4 \), то внутреннее сопротивление равно \ (4 \ Omega \).
Например, если наклон линии равен \ (- 4 \), то внутреннее сопротивление равно \ (4 \ Omega \).
Внутреннее сопротивление также можно найти, разделив ЭДС \ (E \) на ток короткого замыкания \ (I_ {SC} \).
Электричество – подробное содержание
Одноэлементный
E.M.F. (E) – это п.о. через ячейку, когда она не подает ток.
Его также можно рассматривать как энергию, преобразованную в электрическую, когда через нее проходит 1 кулон заряда.
Внутреннее сопротивление (r) ячейки – очень маленькое сопротивление.Для «свинцово-кислотного» элемента он составляет порядка 0,01 Ом, а для «сухого» элемента – около 1 Ом.
Это означает, что свинцово-кислотный элемент будет обеспечивать более высокий ток, чем сухой элемент.
Мы можем получить важные уравнения для E и r, рассматривая ячейку с сопротивлением в цепи.
Общее сопротивление R всего – это сумма последовательного резистора и внутреннего сопротивления ячейки.
путем суммирования п.о. по кольцевой,
вместо R итого
по закону Ома, заменяя IR = V R
Примечание, V R называется клеммой p.d. . Это p.d. через ячейку, когда она доставляет ток.
к началу
Измерение E&R
После снятия показаний клеммных п.о. (В R ) и тока ( I ) строится график.
Информацию можно получить из графика, управляя уравнением, полученным для E и r:
меняя местами I и r, меняя уравнение,
сравнивая с уравнением прямой,
Следовательно, градиент равен « – r », а точка пересечения вертикальной оси – « E ».
к началу
Ячейки в серии
но
и
где r – внутреннее сопротивление комбинации
следовательно,
Итак, два последовательно соединенных элемента эквивалентны одной ячейке с ЭДС, равной сумме двух ячеек.
Внутреннее сопротивление комбинации – это сумма внутренних сопротивлений двух ячеек.
к началу
Ячейки параллельно
Рассмотренное здесь расположение относится только к ячейкам, аналогичным . Для непохожих ячеек взаимосвязь сложна, но может быть разрешена с помощью законов Кирхгофа.
Для аналогичных ячеек ЭДС равны, и внутренние сопротивления также равны.
Следовательно, комбинированная ЭДС, E равна,
, а внутреннее сопротивление комбинации рассчитывается из двух параллельных внутренних сопротивлений:
к началу
Обратная ЭДС и ее значение в двигателе постоянного тока
Поскольку V и Ra обычно фиксированы, значение Eb будет определять ток, потребляемый двигателем.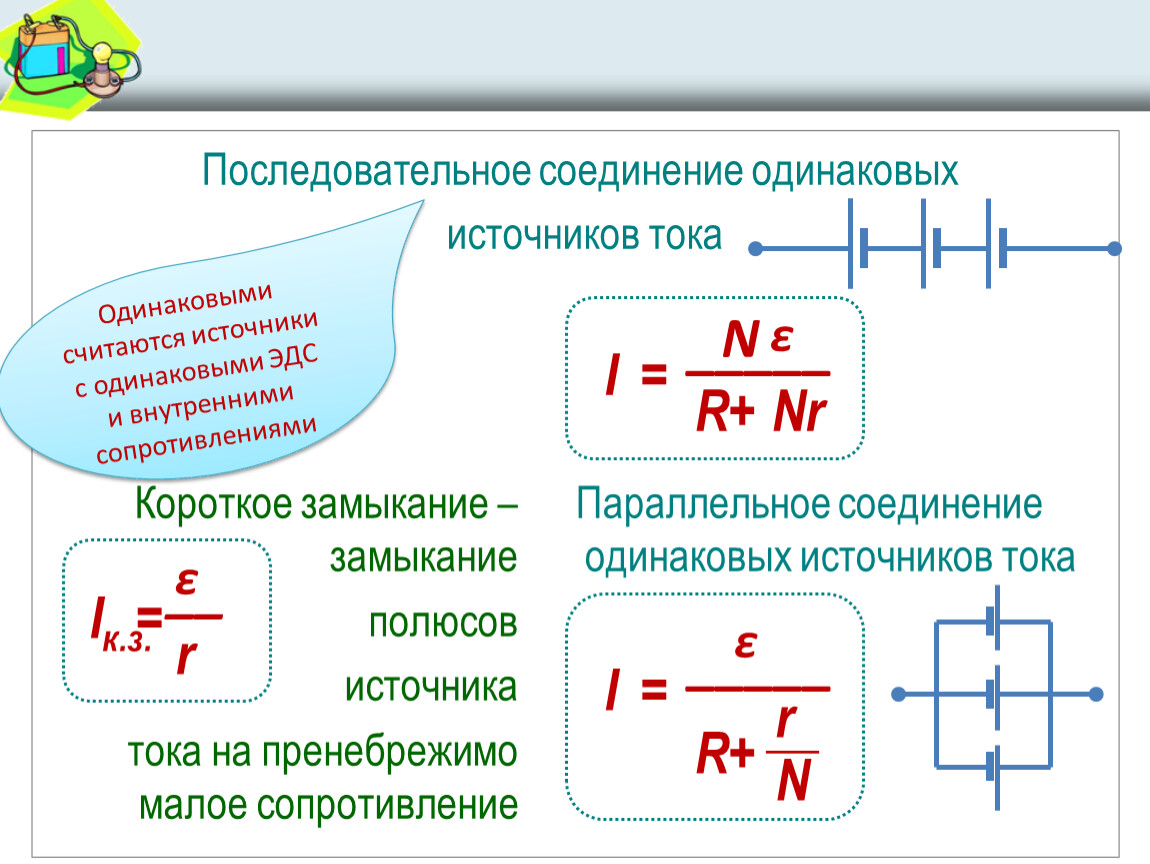
Если скорость двигателя высокая, то обратная э.д.с. Eb (= P φ ZN / 60 A) большой, поэтому двигатель потребляет меньше тока якоря и наоборот.
Обратная ЭДС очень важна для работы двигателя постоянного тока.
Наличие обратной ЭДС делает постоянный ток. двигатель саморегулирующаяся машина то есть заставляет двигатель потреблять столько тока якоря, сколько достаточно для развития крутящего момента, требуемого нагрузкой.
Ток якоря (Ia),
Когда двигатель работает без нагрузки , требуется небольшой крутящий момент для преодоления потерь на трение и сопротивление воздуха. Следовательно, ток якоря Ia невелик, и обратная ЭДС почти равна приложенному напряжению.
Если двигатель внезапно нагружается , первым следствием является замедление якоря. Следовательно, скорость, с которой проводники якоря движутся через поле, уменьшается, и, следовательно, падает обратная ЭДС Eb.
Уменьшенная противоэдс позволяет большему току проходить через якорь, а больший ток означает увеличенный крутящий момент.
Таким образом, крутящий момент увеличивается по мере замедления двигателя. Двигатель перестанет замедляться, когда ток якоря станет достаточным для создания увеличенного крутящего момента, необходимого для нагрузки.
Если нагрузка на двигатель уменьшена , крутящий момент на мгновение превышает требуемый, так что якорь ускоряется.
По мере увеличения скорости якоря обратная ЭДС Eb также увеличивается и вызывает уменьшение тока якоря Ia. Двигатель перестанет ускоряться, когда ток якоря станет достаточным для создания пониженного крутящего момента, необходимого для нагрузки.
Следовательно, обратная ЭДС в двигателе постоянного тока регулирует поток тока якоря, то есть автоматически изменяет ток якоря в соответствии с требованиями нагрузки.
Mr Toogood Physics – ЭДС и внутреннее сопротивление
Внутреннее сопротивление
Элементы и батареи преобразуют химическую энергию в электрический потенциал, который затем используется в цепи. Однако ни одна ячейка не эффективна на 100% при таком переносе. Никакая передача энергии не является эффективной на 100%, и электрические элементы и источники питания не исключение. Электрический элемент состоит из трех частей: анода, катода и электролита. Анод и катод изготовлены из двух разных металлов или из одного металла и углеродной пленки, а электролит представляет собой ионную жидкость, такую как гидроксид калия. Когда ячейка включается в цепь, химическая реакция начинается на аноде и катоде.На аноде реакция окисления удаляет электроны из металла, и они начинают течь в цепь. Это оставляет анод положительно заряженным, что притягивает больше электронов из электролита. Анод в отрицательной клемме ячейки. Возвращающиеся электроны собираются на катоде, и он восстанавливается. Катод – это положительный вывод. Через некоторое время анод потеряет почти все свои электроны, и электролит не сможет подавать больше, поэтому реакция замедляется, и ЭДС ячейки падает.
Однако ни одна ячейка не эффективна на 100% при таком переносе. Никакая передача энергии не является эффективной на 100%, и электрические элементы и источники питания не исключение. Электрический элемент состоит из трех частей: анода, катода и электролита. Анод и катод изготовлены из двух разных металлов или из одного металла и углеродной пленки, а электролит представляет собой ионную жидкость, такую как гидроксид калия. Когда ячейка включается в цепь, химическая реакция начинается на аноде и катоде.На аноде реакция окисления удаляет электроны из металла, и они начинают течь в цепь. Это оставляет анод положительно заряженным, что притягивает больше электронов из электролита. Анод в отрицательной клемме ячейки. Возвращающиеся электроны собираются на катоде, и он восстанавливается. Катод – это положительный вывод. Через некоторое время анод потеряет почти все свои электроны, и электролит не сможет подавать больше, поэтому реакция замедляется, и ЭДС ячейки падает.

Когда происходят химические реакции, а также вырабатывается электричество, элемент выделяет небольшое количество тепла, которое излучается от системы и теряется. Поскольку энергия, теряемая элементом, представляет собой тепло, его можно смоделировать, как если бы он был резистором, выделяющим тепло, и называется внутренним сопротивлением ( – ) элемента. Скорость потери энергии ячейкой, конечно, измеряется в $ \ units {ваттах} $, и для ее описания можно использовать уравнения мощности для резистора.
Рисунок 2: Когда элемент генерирует ток, он также выделяет тепло. Иногда на принципиальных схемах резистор соединен последовательно с ячейкой для обозначения внутреннего сопротивления; конечно, на самом деле внутри ячейки нет резистора, это просто полезный способ описания энергии, потерянной в цепи. Внутреннее сопротивление – это аналог эффективности ячейки. Чем больше внутреннее сопротивление, тем больше тепла он выделяет, производя электричество, и тем менее эффективен. Внутреннее сопротивление также будет иметь разность потенциалов на нем, что означает, что напряжение, измеренное на клеммах при протекании тока, ниже фактического истинного значения ЭДС ячейки. Истинная ЭДС ячейки – это «потерянных вольт» плюс напряжение на клеммах .
Внутреннее сопротивление также будет иметь разность потенциалов на нем, что означает, что напряжение, измеренное на клеммах при протекании тока, ниже фактического истинного значения ЭДС ячейки. Истинная ЭДС ячейки – это «потерянных вольт» плюс напряжение на клеммах .
ЭДС = клемма p.d. + потеряно вольт
Рисунок 3: ЭДС равна конечному п.о. плюс «потерянные вольт».Мы можем сформулировать это математически как:
$$ ε = IR + Ir $$Где:
- ε – ЭДС в $ \ units {V} $
- I – ток в $ \ units {A} $
- R – полное сопротивление цепи в $ \ units {Ω} $
- r – внутреннее сопротивление ячейки в $ \ units {Ω} $
Термин $ IR $ представляет собой терминал p.d. а член $ Ir $ – это потерянные вольты. Приведенное выше уравнение можно упростить до:
$$ \ large ε = I \ left (R + r \ right) $$ Часто в примерах схем внутренним сопротивлением пренебрегают и предполагается идеальный элемент без внутреннего сопротивления. Однако на уровне A вы должны будете выполнять вычисления в цепях, которые имеют значительное внутреннее сопротивление. Типичное внутреннее сопротивление для современных ячеек находится в диапазоне от $ \ amount {100} {mΩ} $ до $ \ amount {900} {mΩ} $.
Однако на уровне A вы должны будете выполнять вычисления в цепях, которые имеют значительное внутреннее сопротивление. Типичное внутреннее сопротивление для современных ячеек находится в диапазоне от $ \ amount {100} {mΩ} $ до $ \ amount {900} {mΩ} $.
Наверх
Рабочий пример
Батарея подключена последовательно к резистору $ \ amount {10} {Ω} $ и переключателю.К аккумулятору подключен вольтметр. Когда переключатель разомкнут (выключен), вольтметр показывает $ \ amount {1.45} {V} $. Когда переключатель замкнут, отображается значение $ \ amount {1.26} {V} $.
Какое внутреннее сопротивление аккумулятора?
- $ \ amount {0.66} {Ω} $
- $ \ amount {0.76} {Ω} $
- $ \ amount {1.3} {Ω} $
- $ \ amount {1.5} {Ω} $
Этот вопрос с несколькими вариантами ответов включает относительно простые вычисления, но важно, чтобы эти вопросы с несколькими вариантами ответов работали эффективно, чтобы вы не теряли время зря.
Мы знаем, что ЭДС ячейки равна $ \ amount {1.45} {V} $, а конечная p.d. падает до $ \ amount {1.26} {V} $, когда через резистор $ \ amount {10} {Ω} $ протекает ток, поэтому ток через резистор можно рассчитать как:
\ begin {align} I & = \ frac {V} {R} \\ I & = \ frac {\ amount {1.26} {V}} {\ amount {10} {Ω}} \\ \\ I & = \ количество {0.126} {A} \ end {align}Разность потенциалов на внутреннем сопротивлении равна $ \ amount {1.45} {V} – \ amount {1.45} {V} = \ amount {0.19} {V}
долл. СШАТеперь мы можем использовать это значение тока и значение потерянных вольт, чтобы найти значение внутреннего сопротивления:
$$ R = \ frac {V} {I} = {\ amount {0.19} {V}} {\ amount {0.126} {A}} = \ amount {1.5} {Ω} $$Наверх
Внутреннее сопротивление и протекание тока
Чем больше тока течет из элемента, тем выше скорость реакции в элементе и выделяется больше тепла, и, соответственно, чем выше потеря напряжения .Между током и энергией, теряемой внутренним сопротивлением, существует прямо пропорциональная зависимость.
Когда ток не течет, внутреннее сопротивление и вывод p.d. не теряют энергию. будет равняться ЭДС. На практике ЭДС ячейки можно определить с помощью мультиметра, который обычно имеет очень высокое сопротивление, и измерения на клемме p.d., которая и будет эдс, поскольку через измеритель не будет протекать ток.
Чем больше ток, протекающий через ячейку, тем больше разница между ЭДС и выводом p.д .. Если график терминальных п.д. и ток нанесен на график, ЭДС может быть найдена из точки пересечения оси y, а градиент будет представлять внутреннее сопротивление.
Рисунок 4: График терминального п.о. против тока для клетки. Внутреннее сопротивление можно найти по градиенту.Вы выполните это практическое упражнение для вашего CAP, но вам нужно будет разработать схему и предложить подходящий диапазон сопротивлений для проверки.
Наверх
Рабочий пример
Студент исследует, как мощность, рассеиваемая на переменном резисторе Y, изменяется при изменении сопротивления.
На схеме ниже показана схема, которую использует ученик. Y подключен к батарее с ЭДС ε и внутренним сопротивлением r .
Рисунок 5: Простая схема с ячейкой и переменным резистором.На графике показаны результаты, полученные учеником при изменении сопротивления Y от $ \ amount {0.5} {Ω} $ до $ \ amount {6.5} {Ω} $.
Рисунок 6: График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления.- Опишите, как мощность, рассеиваемая в Y, изменяется при увеличении его сопротивления с $ \ amount {0.5} {Ω} $ до $ \ amount {6.5} {Ω} $.
- ЭДС батареи равна $ \ amount {6.0} {V} $, а сопротивление Y установлено равным $ \ amount {0.80} {Ω} $.
- Используйте данные из графика , чтобы вычислить ток через батарею.
- Рассчитайте напряжение на Y.
- Рассчитайте внутреннее сопротивление аккумулятора.
- Студент повторяет эксперимент с батареей с такой же ЭДС, но с незначительным внутренним сопротивлением.Сформулируйте и объясните, как вы теперь ожидаете, что мощность, рассеиваемая в Y, будет изменяться при увеличении сопротивления Y с $ \ amount {0.5} {Ω} $ до $ \ amount {6.5} {Ω} $.
Ключевым словом в этом вопросе является описать , поэтому нам просто нужно сказать, что мы видим, но чтобы получить полную оценку, мы должны использовать данные из графика. Как мы видим, мощность увеличивается до тех пор, пока сопротивление не станет равным $ \ amount {3} {Ω} $ и $ \ amount {3} {W} $, а затем начинает уменьшаться по мере того, как сопротивление продолжает увеличиваться. {2}} {R} $.Когда внешнее сопротивление меньше внутреннего сопротивления, он будет иметь меньший p.d. поперек него, поэтому он будет иметь меньшую мощность, чем внутреннее сопротивление. Когда внешнее сопротивление равно внутреннему, они оба будут иметь одинаковую разность потенциалов и, следовательно, будут иметь одинаковую мощность. По мере увеличения переменного резистора, превышающего внутреннее сопротивление, мощность снова уменьшается, поскольку мощность обратно пропорциональна сопротивлению.
{2}} {R} $.Когда внешнее сопротивление меньше внутреннего сопротивления, он будет иметь меньший p.d. поперек него, поэтому он будет иметь меньшую мощность, чем внутреннее сопротивление. Когда внешнее сопротивление равно внутреннему, они оба будут иметь одинаковую разность потенциалов и, следовательно, будут иметь одинаковую мощность. По мере увеличения переменного резистора, превышающего внутреннее сопротивление, мощность снова уменьшается, поскольку мощность обратно пропорциональна сопротивлению.
Это известно как теорема максимальной мощности, т.е.е. максимальная мощность от источника (в данном случае ячейки) получается при нагрузке, либо внешнее сопротивление равно внутреннему сопротивлению источника питания.
При чтении данных с графика рекомендуется тщательно аннотировать диаграмму карандашом и линейкой, чтобы гарантировать точность считываемых значений. {2} R $ на поиск текущих:
{2} R $ на поиск текущих:
В подобном вопросе легко забыть найти квадратный корень из $ \ frac {P} {R} $, поэтому будьте особенно осторожны при использовании калькулятора.
Поскольку мы теперь знаем ток и сопротивление, мы можем использовать закон Ома, $ V = IR $, чтобы найти напряжение или p.d. по Ю.
$$ V = \ amount {1.56} {A} \ times \ amount {0.80} {Ω} = \ amount {1.2} {V} $$Это можно либо вычислить по уравнению $ ε = V + Ir $, либо считать по графику, используя теорему о максимальной мощности, как описано выше. Мы уже вычислили значения $ V $ и $ I $, поэтому, используя уравнение, сделав $ r $ объектом:
\ begin {align} r & = \ frac {\ left (ε-V \ right)} {I} \\ r & = \ frac {\ left (\ amount {6.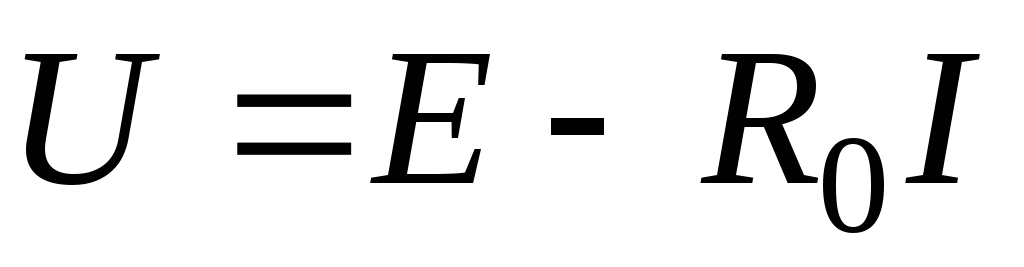 0} {V} – \ amount {1.2} {V} \ right)} {\ amount {1.56} {A}} \\ \\ г & = \ количество {3.1} {Ω} \ end {align}
0} {V} – \ amount {1.2} {V} \ right)} {\ amount {1.56} {A}} \\ \\ г & = \ количество {3.1} {Ω} \ end {align}Даже если вы не смогли рассчитать предыдущие значения для тока и разности потенциалов, вы можете прочитать значение сопротивления на пике графика, если вы укажете, что максимальная мощность будет рассеиваться, когда $ Y = r $ и четко аннотируйте график.
При незначительном внутреннем сопротивлении p.d. по оси Y будет равна ЭДС ячейки. Как p.d. теперь постоянна, и соотношение между мощностью и сопротивлением, для постоянного напряжения обратное, мощность будет уменьшаться с увеличением значения Y.
Это вопрос, на который студенты, как правило, очень плохо отвечают, и легко предположить, что форма графика будет аналогичной, но будет иметь более низкое или более высокое значение пиковой мощности.

 д. с. самоиндукции (рис. 60). Эта э. д. с. возникает при всяком изменении тока, например при замыкании и размыкании электрических цепей, при изменении нагрузки электродвигателей и пр. Чем быстрее изменяется ток в проводнике или катушке, тем больше скорость изменения пронизывающего их магнитного потока и тем большая э. д. с. самоиндукции в них индуцируется. Например, э. д. с. самоиндукции e L возникает в проводнике АБ (см. рис. 54) при изменении протекающего по нему тока i 1 . Следовательно, изменяющееся магнитное поле индуцирует э. д. с. в том же самом проводнике, в котором изменяется ток, создающий это поле.
д. с. самоиндукции (рис. 60). Эта э. д. с. возникает при всяком изменении тока, например при замыкании и размыкании электрических цепей, при изменении нагрузки электродвигателей и пр. Чем быстрее изменяется ток в проводнике или катушке, тем больше скорость изменения пронизывающего их магнитного потока и тем большая э. д. с. самоиндукции в них индуцируется. Например, э. д. с. самоиндукции e L возникает в проводнике АБ (см. рис. 54) при изменении протекающего по нему тока i 1 . Следовательно, изменяющееся магнитное поле индуцирует э. д. с. в том же самом проводнике, в котором изменяется ток, создающий это поле. д. с. самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 61, б). Если же ток в катушке не изменяется, то э. д. с. самоиндукции не возникает.
д. с. самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 61, б). Если же ток в катушке не изменяется, то э. д. с. самоиндукции не возникает. Точно
Точно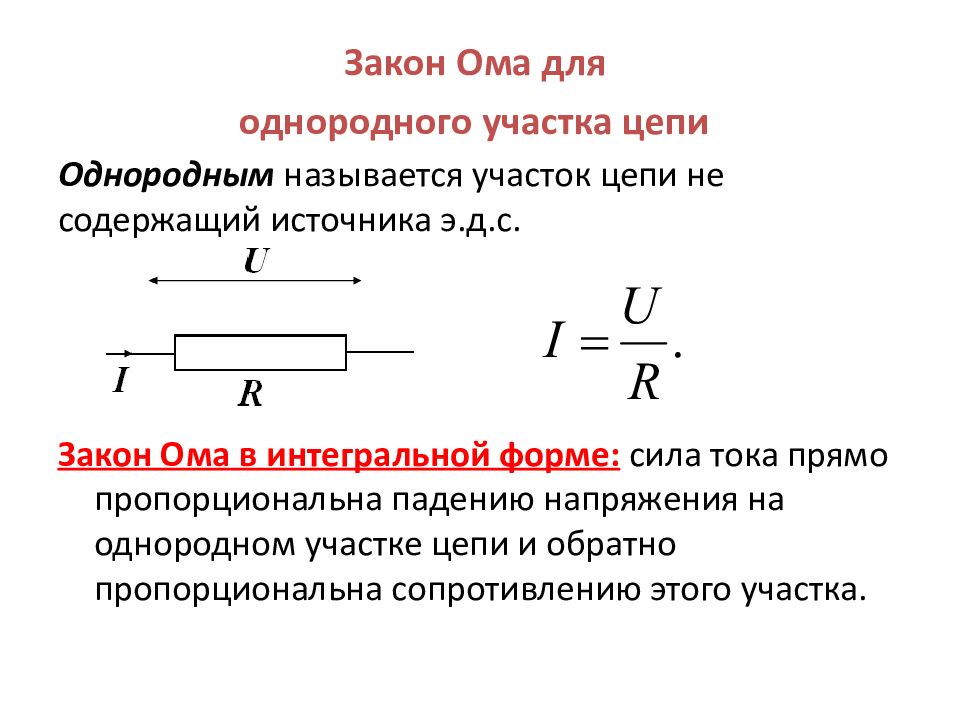
 Эта длительность теоретически бесконечно велика. Практически же обычно считают, что она составляет (3-4) Т. За это время ток в цепи достигает 95-98 % установившегося значения. Следовательно, чем больше сопротивление и чем меньше индуктивность L, тем быстрее протекает процесс изменения тока в электрических цепях с индуктивностью. Постоянную времени Т при апериодическом процессе можно определить как отрезок АВ, отсекаемый касательной, проведенной из начала координат к рассматриваемой кривой (например, тока i) на линии, соответствующей установившемуся значению данной величины.
Эта длительность теоретически бесконечно велика. Практически же обычно считают, что она составляет (3-4) Т. За это время ток в цепи достигает 95-98 % установившегося значения. Следовательно, чем больше сопротивление и чем меньше индуктивность L, тем быстрее протекает процесс изменения тока в электрических цепях с индуктивностью. Постоянную времени Т при апериодическом процессе можно определить как отрезок АВ, отсекаемый касательной, проведенной из начала координат к рассматриваемой кривой (например, тока i) на линии, соответствующей установившемуся значению данной величины.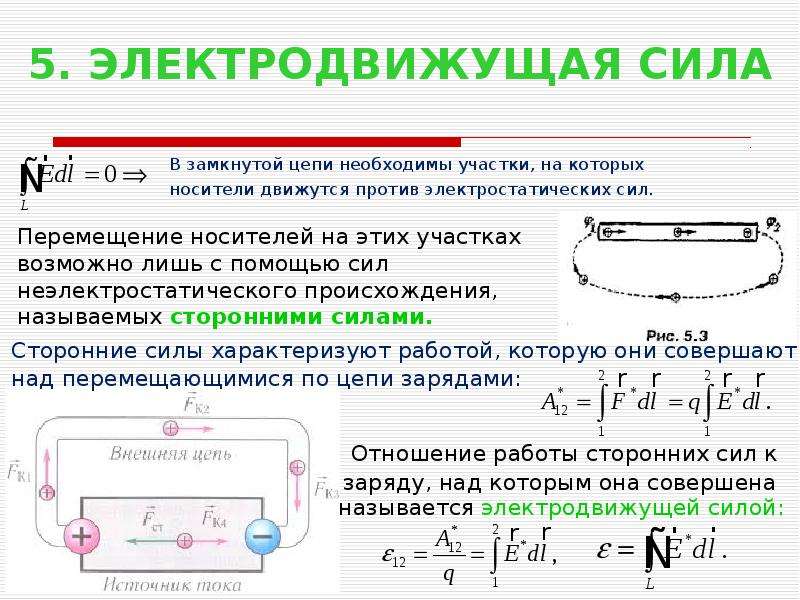 д. с. самоиндукции при размыкании цепей, содержащих катушки с большим числом витков и со стальными сердечниками (например, обмотки генераторов, электродвигателей, трансформаторов и пр.), т. е. цепей, обладающих большой индуктивностью. В этом случае возникающая э. д. с. самоиндукции e L может во много раз превысить напряжение U источника и, суммируясь с ним, послужить причиной возникновения перенапряжений в электрических цепях (рис. 64, а), называемых коммутационными (возникающими при коммутации – переключениях электрических цепей). Они являются опасными для обмоток электродвигателей, генераторов и трансформаторов, так как могут вызвать пробой их изоляции.
д. с. самоиндукции при размыкании цепей, содержащих катушки с большим числом витков и со стальными сердечниками (например, обмотки генераторов, электродвигателей, трансформаторов и пр.), т. е. цепей, обладающих большой индуктивностью. В этом случае возникающая э. д. с. самоиндукции e L может во много раз превысить напряжение U источника и, суммируясь с ним, послужить причиной возникновения перенапряжений в электрических цепях (рис. 64, а), называемых коммутационными (возникающими при коммутации – переключениях электрических цепей). Они являются опасными для обмоток электродвигателей, генераторов и трансформаторов, так как могут вызвать пробой их изоляции. Возникающая при этом электрическая дуга поддерживается в, течение некоторого времени э. д. с. самоиндукции, которая, таким образом, затягивает процесс отключения тока в цепи. Это явление весьма нежелательно, так как дуга оплавляет контакты отключающих аппаратов, что приводит к быстрому выходу их из строя. Поэтому во всех аппаратах, служащих для размыкания электрических цепей, предусматриваются специальные дугогасительные устройства, обеспечивающие ускорение гашения дуги.
Возникающая при этом электрическая дуга поддерживается в, течение некоторого времени э. д. с. самоиндукции, которая, таким образом, затягивает процесс отключения тока в цепи. Это явление весьма нежелательно, так как дуга оплавляет контакты отключающих аппаратов, что приводит к быстрому выходу их из строя. Поэтому во всех аппаратах, служащих для размыкания электрических цепей, предусматриваются специальные дугогасительные устройства, обеспечивающие ускорение гашения дуги. Оно равно напряжению, приложенному к цепи R-L, т. е. к зажимам соответ-
Оно равно напряжению, приложенному к цепи R-L, т. е. к зажимам соответ- Однако в некоторых элементах электрооборудования, в частности в устройствах промышленной электроники, переходные процессы являются рабочими режимами.
Однако в некоторых элементах электрооборудования, в частности в устройствах промышленной электроники, переходные процессы являются рабочими режимами.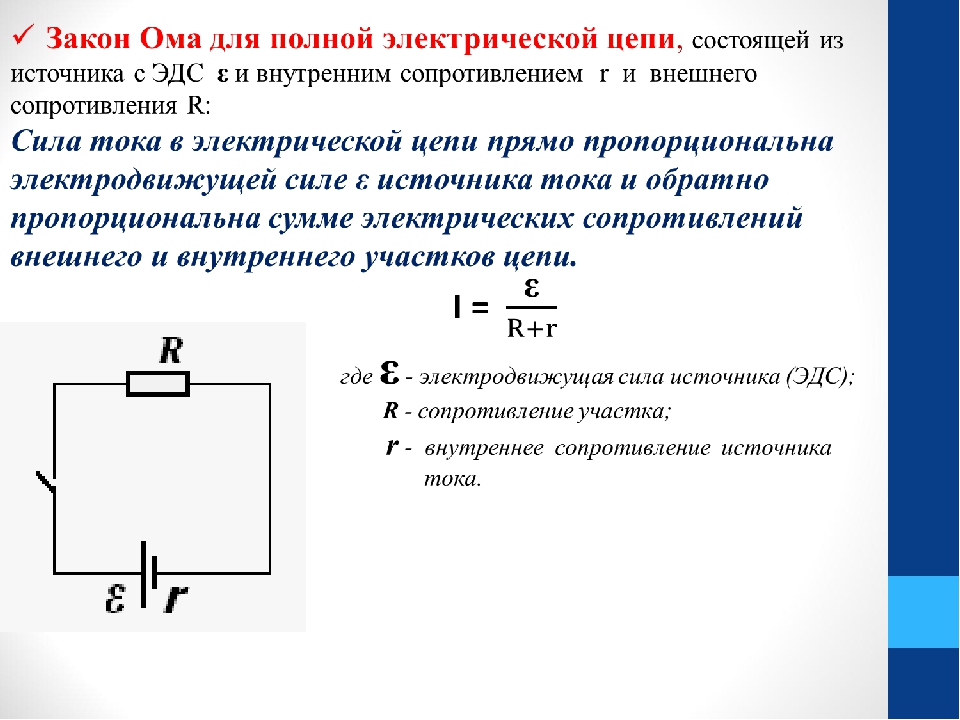

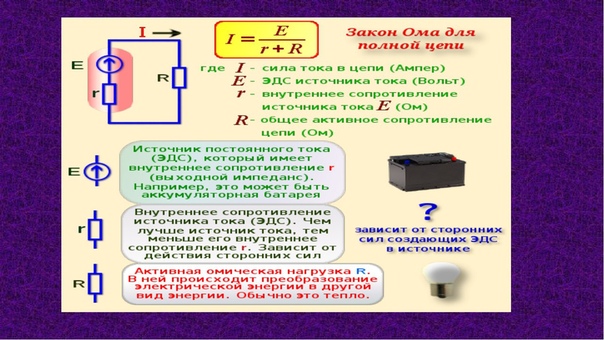 (11)
(11) 6.
6. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.
Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.



 jpg 680w”>
jpg 680w”> Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.
Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот. е. в
катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
е. в
катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).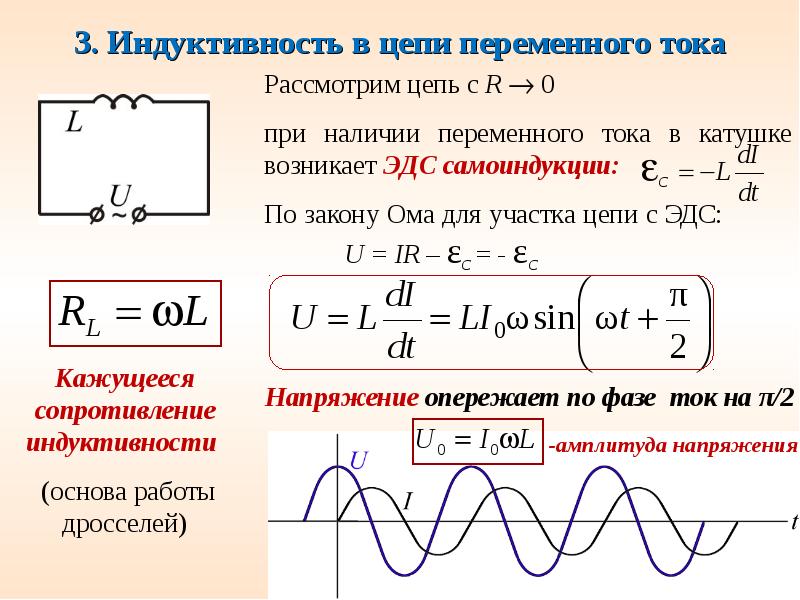 цепи, от свойств
проводника
цепи, от свойств
проводника


 При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия
При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
 Разделенные заряды создают электрическое поле. Конец стержня
не в начале координат будет иметь положительное напряжение по отношению к началу координат.
Разделенные заряды создают электрическое поле. Конец стержня
не в начале координат будет иметь положительное напряжение по отношению к началу координат. Когда конденсатор (C) полностью заряжен, сохраняется следующее соотношение:
Когда конденсатор (C) полностью заряжен, сохраняется следующее соотношение: Например, если бы вы начали с полностью разряженного конденсатора (т.е. q = 0 и V c = 0) и подключили его к батарее, зарядка конденсатора описывалась бы экспоненциальным уравнением ,
Например, если бы вы начали с полностью разряженного конденсатора (т.е. q = 0 и V c = 0) и подключили его к батарее, зарядка конденсатора описывалась бы экспоненциальным уравнением , время будет выглядеть так:
время будет выглядеть так: