Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)
ОглавлениеТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКАГлава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.  2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17.  КОЛИЧЕСТВО ТЕПЛОТЫ18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34.  ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ.  ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67.  ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД.  90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ |
38. Вывод эдс индукции из закона сохранения энергии. Механизм возникновения эдс индукции. Вихревые токи (Токи Фуко)
Обобщая
результаты своих многочисленных опытов,
Фарадей пришел к количественному закону
электромагнитной индукции. Он показал,
что всякий раз, когда происходит изменение
сцепленного с контуром потока магнитной
индукции, в контуре возникает индукционный
ток; возникновение индукционного тока
указывает на наличие в цепи электродвижущей
силы, называемой электродвижущей
силой электромагнитной индукции.
Значение
индукционного тока, а следовательно, и
э.д.с. электромагнитной
индукции определяются
только скоростью изменения магнитного
потока, т. е.
Теперь необходимо выяснить знак . В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.
(123.2)
Знак
минус показывает, что увеличение
потока вызывает
э. д. с. т.
е. поле индукционного тока направлено
навстречу потоку; уменьшение
потока вызывает т.е.
направления потока и поля индукционного
тока совпадают.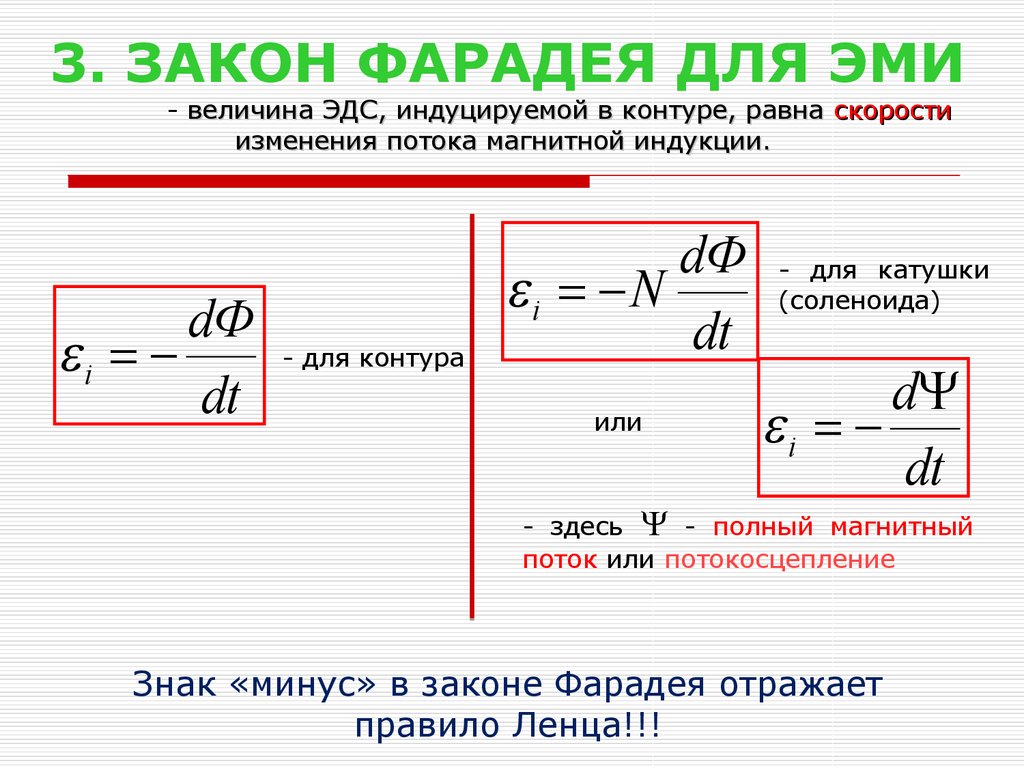
Знак минус в формуле
(123.2) определяется правилом Ленца —
общим правилом для нахождения направления
индукционного тока, выведенного в 1833
г.
Механизм возникновения э.д.с. индукции можно пояснить на простом примере. Пусть изменение магнитного потока, пронизывающего контур, проис-ходит за счет изменения площади контура вследствие движения одного из проводников, составляющих контур. Пусть, например, контур образован п-образным проводником 1 и скользящей перемычкой 2 (рис. 3.12), и пусть линии индукции магнитного поля В перпендикулярны плоскости контура и направлены от нас (показаны крестиками).
При
скольжении перемычки вниз площадь
контура S будет возрастать, что приведет
к возрастанию магнитного потока, равного
ВS. При этом, со-гласно закону Фарадея
должна возникнуть э.д.с. индукции.
Непосредственной физической причиной
возникновения индукционного тока в
контуре в данном случае является сила
Лоренца. Действительно, при движении
перемычки вниз со скоростью v, с той же
скоростью будут перемещаться находящиеся
в ней электроны.
Сила Лоренца, действующая
на каждый электрон, будет равна evB (где
е – заряд электрона) и направлена влево.
Формально эту силу можно рассматривать
как проявление поля сторонних сил,
имеющего напряженность Ес.
Из формулы (2.22) вытекает, что Ес =
vB. Электродвижущая сила индукции Еi,
создаваемая полем Есво
всей движущейся перемычке длиной l будет
согласно (2.24) равна
Еi = òЕсldl = Есl = vBl (3.25)
Скорость v движения перемычки представим как производную dx/dt. Тогда
Еi = В= В(3.26)
В (3.26) учтено, что произведение ldx представляет со-бой приращение dS площади контура. В свою очередь произведение BdS равно приращению dФ магнитного потока. В итоге мы получаем, что э.д.с. индукции равна производной dФ/dt от магнитного потока
Еi = dФ/dt,(3.27)
то
есть мы пришли к закону Фарадея. В
проведенных рассуждениях мы для простоты
оперировали модулями векторов Ес,
v и В, поэтому ве-личину э.
д.с.
индукции в формуле (3.27) определили
также лишь по модулю.
Рассмотренное объяснение механизма возникновения э.д.с. индукции относится к случаю, когда изменение магнитного потока происходит за счет подвижных проводников. Но магнитный поток может меняться также и путем изменения величины В при неизменной геометрии контура. Тогда сила Лоренца не возникает, а ин-дукционный ток возбуждается в этом случае вихревым электрическим полем, порождае-мым меняющимся во времени магнитным полем. Этот более общий случай возникновения э.д.с. индукции будет рассмотрен в следующем разделе (тема 4).
Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.
Впервые
вихревые токи были обнаружены французским
учёным Д.Ф
Араго (1786—1853)
в 1824 г. в медном диске, расположенном
на оси под вращающейся магнитной
стрелкой. За счёт вихревых токов диск
приходил во вращение.
Это явление,
названное явлением Араго, было объяснено
несколько лет спустя M.
Фарадеем с
позиций открытого им закона электромагнитной
индукции: вращаемое магнитное поле
наводит в медном диске токи (вихревые),
которые взаимодействуют с магнитной
стрелкой. Вихревые токи были подробно
исследованы французским
физиком Фуко (1819—1868)
и названы его именем. Он открыл явление
нагревания металлических тел, вращаемых
в магнитном поле, вихревыми токами.
Токи
Фуко возникают под воздействием
переменного электромагнитного
поля и
по физической природе ничем не отличаются
от индукционных токов, возникающих в
линейных проводах. Они вихревые, то есть
замкнуты в кольца. Электрическое
сопротивление массивного проводника
мало, поэтому токи Фуко достигают очень
большой силы. В соответствии с правилом
Ленца они
выбирают внутри проводника такое
направление и путь, чтобы противиться
причине, вызывающей их. Поэтому движущиеся
в сильном магнитном поле хорошие
проводники испытывают сильное торможение,
обусловленное взаимодействием токов
Фуко с магнитным полем.
Это свойство
используется для демпфирования подвижных
частей гальванометров, сейсмографов и
др.
Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.
С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.
Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.
13.4: ЭДС движения – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4430
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять величину ЭДС индукции в проводе, движущемся с постоянной скоростью через магнитное поле
- Обсудите примеры, использующие ЭДС движения, такие как рельсовая пушка и привязанный спутник
Магнитный поток зависит от трех факторов: силы магнитного поля, площади, через которую проходят силовые линии, и ориентации поля с площадью поверхности.
Если какая-либо из этих величин изменяется, происходит соответствующее изменение магнитного потока. До сих пор мы рассматривали только изменения потока из-за изменяющегося поля. Теперь мы рассмотрим другую возможность: изменение области, через которую проходят силовые линии, включая изменение ориентации области.
Два примера такого изменения потока представлены на рисунке \(\PageIndex{1}\). В части (а) поток через прямоугольную петлю увеличивается по мере ее перемещения в магнитное поле, а в части (б) поток через вращающуюся катушку изменяется в зависимости от угла \(\theta\).
Рисунок \(\PageIndex{1}\): (a) изменение магнитного потока по мере того, как петля перемещается в магнитное поле; б) изменение магнитного потока при вращении петли в магнитном поле. Интересно отметить, что то, что мы воспринимаем как причину конкретного изменения потока, на самом деле зависит от выбранной нами системы отсчета. Например, если вы находитесь в состоянии покоя относительно движущихся катушек на рисунке \(\PageIndex{1b}\), вы увидите, что поток меняется из-за изменяющегося магнитного поля — в части (а) поле перемещается слева направо.
прямо в вашей системе отсчета, а в части (b) поле вращается. Часто можно описать изменение потока через катушку, которая движется в одной конкретной системе отсчета, с точки зрения изменения магнитного поля во второй системе отсчета, где катушка неподвижна. Однако вопросы системы отсчета, связанные с магнитным потоком, выходят за рамки этого учебника. Мы избежим таких сложностей, всегда работая в системе отсчета, покоящейся относительно лаборатории, и объясняя изменения потока либо из-за изменяющегося поля, либо из-за изменяющейся площади.
Теперь давайте посмотрим на токопроводящий стержень, втянутый в цепь, изменяющую магнитный поток. Площадь, ограниченная схемой MNOP на рисунке \(\PageIndex{2}\), составляет лк x и перпендикулярна магнитному полю, поэтому мы можем упростить интегрирование \(\Phi _{\mathrm{m}} =\int_{S} \overrightarrow{\mathbf{B}} \cdot \hat{\mathbf{n}} d A\) в произведение магнитного поля и площади. Таким образом, магнитный поток через открытую поверхность равен
\[\Phi_m = Blx.
\]
С B и l постоянны, а скорость стержня равна \(v = dx/dt\), теперь мы можем переформулировать закон Фарадея, уравнение 13.2.2, для величины ЭДС в терминах движущейся проводящей стержень как
\[\epsilon = \frac{d\Phi_m}{dt} = Bl \frac{dx}{dt} = Blv.\]
Ток, индуцированный в цепи, равен ЭДС, деленной на сопротивление или
\[I = \frac{Blv}{R}.\]
Кроме того, направление ЭДС индукции удовлетворяет закону Ленца, в чем можно убедиться, рассмотрев рисунок.
Этот расчет ЭДС, вызванной движением, не ограничивается стержнем, движущимся по токопроводящим рельсам. Используя \(\vec{F} = q\vec{v} \times \vec{B}\) в качестве отправной точки, можно показать, что \(\epsilon = – d\Phi_m/dt\) выполняется для любого изменение потока, вызванное движением проводника. Мы видели в законе Фарадея, что ЭДС, индуцированная изменяющимся во времени магнитным полем, подчиняется тому же соотношению, которое является законом Фарадея.
Таким образом, закон Фарадея справедлив для всех изменений потока , независимо от того, вызваны ли они изменяющимся магнитным полем, движением или их комбинацией. 92}{R}.\]
При соблюдении принципа сохранения энергии производимая и рассеиваемая мощности равны.
Этот принцип можно увидеть в работе рельсовой пушки. Рельсовая пушка — это электромагнитная пусковая установка, в которой используется устройство, подобное показанному на рисунке \(\PageIndex{2}\), схематично показанное на рисунке \(\PageIndex{3}\). Проводящий стержень заменяется снарядом или оружием для стрельбы. До сих пор мы слышали только о том, как движение вызывает ЭДС. В рельсовой пушке оптимальное отключение/уменьшение магнитного поля уменьшает поток между рельсами, вызывая протекание тока в стержне (якоре), который удерживает снаряд. Этот ток через якорь испытывает магнитную силу и движется вперед. Рельсовые пушки, однако, не используются широко в вооруженных силах из-за высокой стоимости производства и больших токов: требуется почти один миллион ампер для производства энергии, достаточной для того, чтобы рельсовая пушка была эффективным оружием.
Мы можем рассчитать ЭДС, вызванную движением, с помощью закона Фарадея , даже если фактическая замкнутая цепь отсутствует . Мы просто представляем замкнутую область, граница которой включает в себя движущийся проводник, вычисляем \(\Phi_m\), а затем находим ЭДС по закону Фарадея. Например, мы можем позволить движущемуся стержню на рисунке \(\PageIndex{4}\) быть одной стороной воображаемой прямоугольной области, представленной пунктирными линиями. Площадь прямоугольника лк , поэтому магнитный поток через него равен \(\Phi_m = Blx\). Дифференцируя это уравнение, получаем
\[\frac{d\Phi_m}{dt} = Bl\frac{dx}{dt} = Blv,\]
, что идентично разности потенциалов между концами стержня, которую мы определили ранее.
Рисунок \(\PageIndex{4}\): С показанным воображаемым прямоугольником мы можем использовать закон Фарадея для расчета ЭДС индукции в движущемся стержне.
ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, при обычных движениях. Например, простой расчет ЭДС движения стержня длиной 1,0 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает 9{-5} Т)(1,0 л, м)(3,0 л, м/с) = 150 л, мкВ.\]
Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля “Шаттл” были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рисунке \(\PageIndex{5}\), чтобы создать ЭДС 5 кВ, двигаясь с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь, по которому мог течь ток.
(Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и стационарные рельсы и соединительный резистор на рисунке \(\PageIndex{3}\), без которых не было бы не может быть полной цепью.) Ток в кабеле за счет магнитной силы \(F = IlBsin \, \theta\) выполняет работу, которая уменьшает кинетическую и потенциальную энергию челнока и позволяет преобразовать ее в электрическую энергия. Оба теста оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Пример \(\PageIndex{1}\) указывает на принципиальную возможность.
{-5} Тл\) магнитного поля. 9о\) и, следовательно, \(sin\, \theta = 1\).Пример \(\PageIndex{2}\): металлический стержень, вращающийся в магнитном поле
Часть (a) рисунка \(\PageIndex{6}\) показывает металлический стержень OS , горизонтальная плоскость вокруг точки O . Стержень скользит по проволоке, образующей дугу окружности PST радиусом r . Система находится в постоянном магнитном поле \(\vec{B}\), которое направлено за пределы страницы. (a) Если вы вращаете стержень с постоянной угловой скоростью \(\omega\), какова сила тока I в замкнутом контуре ОПСО ? Предположим, что резистор R обеспечивает все сопротивление в замкнутом контуре. б) Вычислите работу, совершаемую вами при вращении стержня в единицу времени, и покажите, что она равна мощности, рассеиваемой на резисторе.
Рисунок \(\PageIndex{6}\): (a) Конец вращающегося металлического стержня скользит по круглой проволоке в горизонтальной плоскости.
(б) Индуцированный ток в стержне. (c) Магнитная сила на бесконечно малом отрезке тока. 92\omega}{2R}.\] По мере увеличения \(\theta\) увеличивается и поток через петлю из-за \(\vec{B}\). Чтобы противодействовать этому увеличению, магнитное поле из-за индуцированного тока должно быть направлено в страницу в области, ограниченной петлей. Следовательно, как показано в части (b) рисунка \(\PageIndex{6}\), ток циркулирует по часовой стрелке.Значение
Альтернативный способ рассмотрения ЭДС индукции из закона Фарадея состоит в интегрировании в пространстве, а не во времени.
Однако решение будет таким же. ЭДС движения равна
\[|\epsilon| = \int Bvdl.\]
Скорость может быть записана как произведение угловой скорости на радиус, а дифференциальная длина записана как 92,\], что является тем же решением, что и раньше.
Пример \(\PageIndex{3}\): прямоугольная катушка, вращающаяся в магнитном поле = B\hat{j}\), как показано на рисунке \(\PageIndex{7}\). Катушка вращается вокруг оси
z через ее центр с постоянной угловой скоростью \(\omega\). Получите выражение для ЭДС индукции в катушке. Рисунок \(\PageIndex{7}\): прямоугольная катушка, вращающаяся в однородном магнитном поле.Стратегия
Согласно диаграмме угол между перпендикуляром к поверхности ((\hat{n}\)) и магнитным полем \((\vec{B})\) равен \(\theta\ ). Скалярное произведение \(B \cdot \hat{n}\) упрощается только до \(cos \, \theta\) компонента магнитного поля, а именно там, где магнитное поле проецируется на единичный вектор площади \(\hat {н}\).
Величина магнитного поля и площадь петли фиксируются во времени, что упрощает интегрирование. ЭДС индукции записывается по закону Фарадея.
Решение
Когда катушка находится в таком положении, что ее вектор нормали \(\hat{n}\) образует угол \(\theta\) с магнитным полем \(\vec{B}\) магнитный поток через один виток катушки равен
\[\Phi_m = \int_S \vec{B} \cdot \hat{n} dA = BA \, cos \, \theta.\]
Из закона Фарадея , ЭДС в катушке равна
\[\epsilon = – N\frac{d\Phi_m}{dt} = NB A \, sin \, \theta \frac{d\theta}{dt}.\]
Постоянная угловая скорость равна \(\omega = d\theta /dt\). Угол \(\theta\) представляет изменение во времени угловой скорости или \(\omega t\). Это изменяет функцию на временное пространство, а не на \(\theta\). Следовательно, ЭДС индукции изменяется синусоидально со временем по закону 9.0034
\[\epsilon = \epsilon_0 \, sin \, \omega t,\], где \(\epsilon_0 = NBA \omega\).
Значимость
Если бы напряженность магнитного поля или площадь петли также изменялись во времени, эти переменные нельзя было бы вывести из производной по времени для простого решения, как показано.
Этот пример является основой для электрического генератора, поскольку мы дадим полное обсуждение в разделе «Приложения закона Ньютона».
Упражнение \(\PageIndex{1}\)
92 \omega/2\), с O при более высоком потенциале, чем SУпражнение \(\PageIndex{2}\)
Стержень длиной 10 см движется со скоростью 10 м/с перпендикулярно через магнитное поле силой 1,5 Тл. Чему равна разность потенциалов между концами стержня?
- Ответить
1,5 В
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс и многие другие авторы. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 13.4: Motional Emf распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- ЭДС движения
- источник@https://openstax.
org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2Вопрос Видео: Решение средней скорости катушки на основе ЭДС наведенной
Стенограмма видео
Проводящая катушка имеет радиус 𝑟, равный 18 сантиметрам и 25 виткам. Катушку перемещают так, чтобы половина ее площади находилась в пределах однородного магнитного поля напряженностью 0,12 тесла, направленного из плоскости диаграммы, изображенной вдоль оси катушки. При движении катушки индуцируется электродвижущая сила 0,33 В. С какой средней скоростью движется катушка?
В этой ситуации у нас есть круглая проводящая катушка, которая раньше находилась полностью вне этого однородного магнитного поля. Но затем, через какое-то время, катушка сдвинулась так, что теперь половина ее площади находится в пределах этого поля. Это означает, что магнитный поток через катушку менялся во времени. Закон физики, известный как закон Фарадея, говорит нам, что при изменении магнитного потока через площадь проводника возникает ЭДС, обозначаемая греческой буквой 𝜀.
Поскольку происходит изменение магнитного потока через эту проводящую катушку, когда она проходит половину пути в магнитном поле, она также будет испытывать ЭДС индукции. Закон Фарадея говорит нам, что ЭДС, индуцированная в катушке, связана с тем, насколько быстро изменяется магнитный поток через эту катушку. Чем больше △𝜙 sub 𝐵, изменение магнитного потока, более △𝑡, изменение во времени, тем больше ЭДС 𝜀 будет индуцироваться в катушке. Это означает, что чем быстрее эта катушка будет двигаться в поле, тем больше в ней будет индуцироваться ЭДС.
Нам сказали, что электродвижущая сила 0,33 вольта. И мы хотим использовать эту информацию для определения средней скорости, с которой эта катушка движется в поле. Чтобы начать делать это, давайте запишем некоторую информацию, которую нам дали. Радиус нашей проводящей катушки 𝑟 равен 18 сантиметрам. В катушке 25 витков. Мы назовем этот номер 𝑁. Напряженность однородного магнитного поля составляет 0,12 тесла. Это 𝐵. И, наконец, ЭДС индукции в катушке 𝜀 равна 0,33 вольта.
Зная все это, давайте освободим место и начнем думать о том, как мы хотим использовать закон Фарадея для определения средней скорости нашей проводящей катушки. Напомним, что за некоторый интервал времени, который мы назвали △𝑡, наша проводящая катушка перемещается на линейное расстояние 𝑟, равное радиусу катушки. Если мы вспомним, что в общем случае средняя скорость объекта равна расстоянию, которое проходит объект, деленному на время, необходимое для прохождения этого расстояния, то мы можем сказать, что средняя скорость 𝑣 нашей катушки равна радиусу катушки разделить на △𝑡. Эта средняя скорость нашей катушки соответствует ЭДС индукции 0,33 вольта в катушке. Если бы средняя скорость была больше, мы бы получили большую ЭДС индукции, а если бы она была меньше, ЭДС индукции была бы меньше.
Теперь у нас есть выражение для средней скорости 𝑣 нашей катушки. Но мы нигде не видим этого выражения в законе Фарадея. Однако напомним, что магнитный поток 𝜙 sub 𝐵 через некоторую площадь равен напряженности магнитного поля 𝐵 через эту площадь, умноженной на площадь 𝐴.
Это означает, что мы можем заменить 𝜙 sub 𝐵 на 𝐵 раз 𝐴 в этом выражении. В нашем конкретном сценарии мы знаем, что напряженность магнитного поля 𝐵 постоянна. Он не меняется со временем. Но площадь нашей проводящей катушки, подвергаемая воздействию этого постоянного магнитного поля, изменяется со временем. Это означает, что мы можем переписать это значение △𝐵 раз 𝐴 как напряженность магнитного поля 𝐵 раз △𝐴, изменение площади, подвергаемой воздействию этого поля. И что это за изменение в области △𝐴?
Мы видим, что изначально площадь нашей катушки, подвергаемой воздействию поля, равна нулю. Ни одна катушка не находится в поле. Однако после того, как катушка переместилась, половина этой площади поперечного сечения петли подвергается воздействию однородного магнитного поля. Поскольку площадь всего круга в 𝜋 умножается на квадрат радиуса круга, мы можем заменить △𝐴 на половину площади нашего круга, половину 𝜋𝑟 в квадрате минус ноль, потому что это начальная площадь нашей катушки. подвергается воздействию магнитного поля.
Вычитание нуля из нашего числителя не меняет его. Так что мы можем оставить эту часть.
А теперь, если мы запишем половину 𝜋𝑟 в квадрате как половину умножить на 𝜋 умножить на 𝑟 умножить на 𝑟, обратите внимание, что если мы возьмем одно из этих 𝑟 и разделим на △𝑡, то мы действительно нашли место, где средняя скорость 𝑣 нашей катушки появляется в этом уравнении. В этом уравнении мы учитываем, что индуцированная ЭДС может быть положительной или отрицательной. То есть можно было указать его направление. Допустим, однако, что мы рассматриваем только величину этой ЭДС, и в этом случае отрицательный знак в правой части нашего уравнения можно убрать.
Теперь мы можем работать с этим уравнением, чтобы найти среднюю скорость 𝑣 нашей катушки. Если мы умножим обе части нашего уравнения на два, сократив этот множитель справа, а затем разделим обе части на 𝑁 умножить на 𝐵 умножить на 𝜋 умножить на 𝑟, сократив все эти множители справа, мы найдем, поменяв местами стороны наше уравнение, что 𝑣 в два раза превышает величину 𝜀, это ЭДС, индуцированная в нашей катушке, деленная на количество витков в катушке, умноженное на напряженность магнитного поля, умноженная на 𝜋, умноженная на радиус катушки.