Формула эдс в замкнутом контуре: ЭДС индукции в контуре определяется…

Зависимость эдс от магнитного потока. Разработка урока”Опыты Фарадея. Электромагнитная индукция”. Лабораторная работа «Исследование явления электромагнитной индукции»

Индукционный ток это такой ток, который возникает в замкнутом проводящем контуре, находящемся в переменном магнитном поле. Этот ток может возникать в двух случаях. Если имеется неподвижный контур, пронизываемый изменяющимся потоком магнитной индукции. Либо когда в неизменном магнитном поле движется проводящий контур, что также вызывает изменение магнитного потока пронизывающего контур.

Рисунок 1 — Проводник перемещается в неизменном магнитном поле

Причиной возникновения индукционного тока является вихревое электрическое поле, которое порождается магнитным полем. Это электрическое поле действует на свободные заряды, находящиеся в проводнике, помещенном в это вихревое электрическое поле.

Рисунок 2 — вихревое электрическое поле

Также можно встретить и такое определение. Индукционный ток это электрический ток, который возникает вследствие действия электромагнитной индукции. Если не углубляется в тонкости закона электромагнитной индукции, то в двух словах ее можно описать так. Электромагнитная индукция это явление возникновение тока в проводящем контуре под действие переменного магнитного поля.

С помощью этого закона можно определить и величину индукционного тока. Так как он нам дает значение ЭДС, которая возникает в контуре под действие переменного магнитного поля.

Формула 1 — ЭДС индукции магнитного поля .

Как видно из формулы 1 величина ЭДС индукции, а значит и индукционного тока зависит от скорости изменения магнитного потока пронизывающего контур. То есть чем быстрее будет меняться магнитный поток, тем больший индукционный ток можно получить. В случае, когда мы имеем постоянное магнитное поле, в котором движется проводящий контур, то величина ЭДС будет зависеть от скорости движения контура.

Чтобы определить направление индукционного тока используют правило Ленца. Которое гласит что, индукционный ток направлен навстречу тому току, который его вызвал. Отсюда и знак минус в формуле для определения ЭДС индукции.

Индукционный ток играет важную роль в современной электротехнике. Например, индукционный ток, возникающий в роторе асинхронного двигателя, взаимодействует с током, подводимым от источника питания в его статоре, вследствие чего ротор вращается. На этом принципе построены современные электродвигатели.

Рисунок 3 — асинхронный двигатель.

В трансформаторе же индукционный ток, возникающий во вторичной обмотке, используется для питания различных электротехнических приборов. Величина этого тока может быть задана параметрами трансформатора.

Рисунок 4 — электрический трансформатор.

И наконец, индукционные токи могут возникать и в массивных проводниках. Это так называемые токи Фуко. Благодаря им можно производить индукционную плавку металлов. То есть вихревые токи, текущие в проводнике вызывают его разогрев.

В зависимости от величины этих токов проводник может разогреваться выше точки плавления.

Рисунок 5 — индукционная плавка металлов.

Итак, мы выяснили, что индукционный ток может оказывать механическое, электрическое и тепловое действие. Все эти эффекты повсеместно используются в современном мире, как в промышленных масштабах, так и на бытовом уровне.

ИНДУКЦИОННЫЙ ТОК — это электрический ток, возникающий при изменении потока магнитной индукции в замкнутом проводящем контуре. Это явление носит название электромагнитной индукции. Хотите узнать какое направление индукционного тока? Росиндуктор — это торговый информационный портал, где вы найдете информацию про ток.

Определяющее направление индукционного тока правило звучит следующим образом: «Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван». Правая рука развернута ладонью навстречу магнит¬ным силовым линиям, при этом большой палец направлен в сторону движения проводника, а четыре пальца по-казывают, в каком направлении будет течь индукционный ток. Перемещая проводник, мы перемещаем вместе с проводчиком все электроны, заключенные в нем, а при перемещении в магнитном поле электрических зарядов на них будет действовать сила по правилу левой руки.

Направление индукционного тока, как и его величина, определяется правилом Ленца, в котором говорится, что направление индукционного тока всегда ослабляет действие фактора, возбудившего ток. При изменении потока магнитного поля через контур направление индукционного тока будет таким, чтобы скомпенсировать эти изменения. Когда магнитное поле возбуждающее ток в контуре создается в другом контуре, направление индукционного тока зависит от характера изменений: при увеличении внешнего тока индукционный ток имеет противоположное направление, при уменьшении — направлен в ту же сторону и стремиться усилить поток.

Катушка с индукционным током имеет два полюса (северный и южный), которые определяются в зависимости от направления тока: индукционные линии выходят из северного полюса.

Приближение магнита к катушке вызывает появление тока с направлением, отталкивающим магнит. При удалении магнита ток в катушке имеет направление, способствующее притягиванию магнита.

Индукционный ток возникает в замкнутом контуре, находящемся в переменном магнитном поле. Контур может быть как неподвижным (помещенным в изменяющийся поток магнитной индукции), так и движущимся (движение контура вызывает изменение магнитного потока). Возникновение индукционного тока обуславливает вихревое электрическое поле, которое возбуждается под воздействием магнитного поля.

О том, как создать кратковременный индукционный ток можно узнать из школьного курса физики.

Для этого есть несколько способов:

• – перемещение постоянного магнита или электромагнита относительно катушки,
• – перемещение сердечника относительно вставленного в катушку электромагнита,
• – замыкание и размыкание цепи,
• – регулирование тока в цепи.

Основной закон электродинамики (закон Фарадея) гласит, что сила индукционного тока для любого контура равна скорости изменения магнитного потока, проходящего через контур, взятой со знаком минус.

Сила индукционного тока носит название электродвижущей силы.

9.5. Индукционный ток

9.5.1. Тепловое действие индукционного тока

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

I i = | ℰ i | R ,

где ℰ i – ЭДС индукции, возникающая в контуре; R – сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; t – время; ℰ i – ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; ℰ i – ЭДС индукции, возникающая в контуре.

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

q i = I i ∆t ,

где I i – сила индукционного тока в контуре; Δt – интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S  cos α,

где B 1 – первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S – площадь кольца; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S  cos α = 0,

где B 2 – значение модуля индукции после выключения магнитного поля, B 2 = 0.

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = −B 1 S  cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆t – интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R – сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца – площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr ,

где l – длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r = l 2 π ,

а его площадь –

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

R = ρ l S 0 ,

где ρ – удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 – площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

Вычислим:

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.

Решение . Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = ∆BS  cos α,

где ∆B – изменение модуля индукции магнитного поля за выбранный интервал времени; S – площадь, ограниченная контуром, S = 2,0 м 2 ; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

| ℰ i | = | Δ Ф Δ t | = | Δ B S cos α Δ t | = Δ B S | cos α | Δ t ,

где ∆B /∆t – скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B /∆t = 0,30 мТл/с.

Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = Δ B S | cos α | R Δ t ,

где R – сопротивление контура.

Мощность индукционного тока

P i = I i 2 R = (Δ B Δ t) 2 S 2 R cos 2 α R 2 = (Δ B Δ t) 2 S 2 cos 2 α R .

Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):

P i max = (Δ B Δ t) 2 S 2 R .

Вычислим:

P i max = (0,30 ⋅ 10 − 3) 2 (2,0) 2 15 ⋅ 10 − 3 = 24 ⋅ 10 − 6 Вт = 24 мкВт.

Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.

МАГНИТНОЕ ПОЛЕ

Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.

В – физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).

Магнитная индукция – векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:

Единица магнитной индукции . В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:

СИЛА ЛОРЕНЦА

Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F А = IBlsin a , а сила Лоренца действует на движущийся заряд:

где a – угол между векторами B и v .

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила м, постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:

В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,

Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.

Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.

Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м:

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.

МАГНИТНЫЙ ПОТОК

Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S – величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:

Ф=BScos

В СИ единица магнитного потока 1 Вебер (Вб) – магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:

Электромагнитная индукция -явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.

Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.

Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε i .

По закону Ома для замкнутой цепи

Так как R не зависит от , то

ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:

САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ

Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:

Ф = L*I .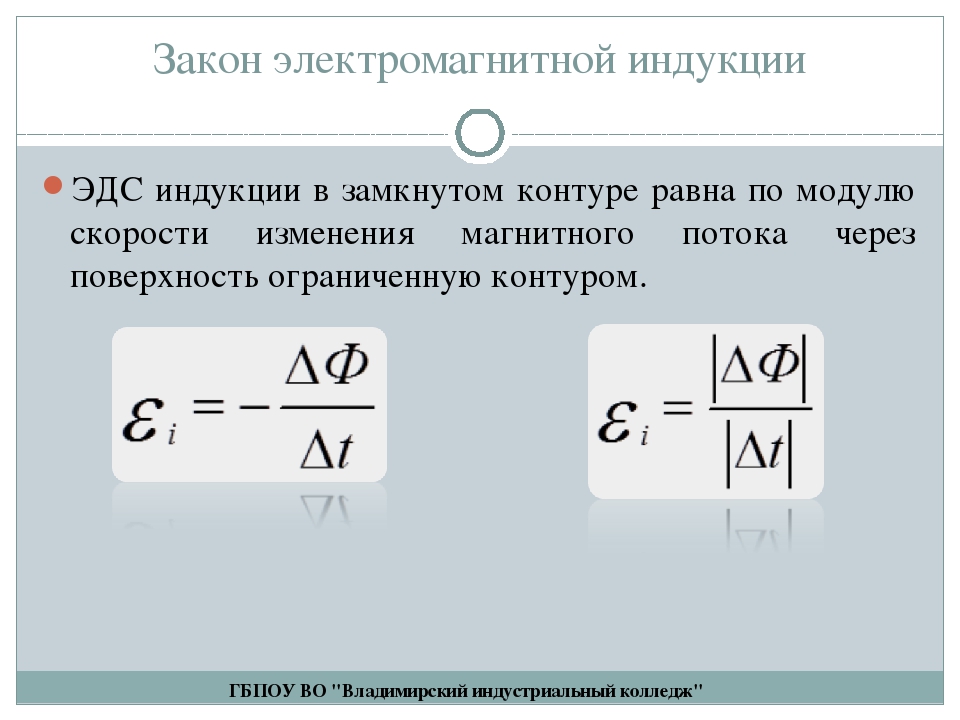

Индуктивность контура L – коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.

Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.

Самоиндукция – явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.

Самоиндукция – частный случай электромагнитной индукции.

Индуктивность – величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.

Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :

Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.

ЭДС самоиндукции имеет в этом случае постоянное значение:

где I – начальное значение тока, t – промежуток времени, за который сила тока убывает от I до 0.

За время t в цепи проходит электрический заряд q = I cp t . Так как I cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:

Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:

Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?

Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1 . Следовательно,

Темы кодификатора ЕГЭ : явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.

Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.

Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?

Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки – к гальванометру (гальванометр – чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока – первая катушка» и «вторая катушка – гальванометр».

Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.

При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.

Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.

При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.

Вывод .

Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует ) электрический ток во второй катушке. Этот ток называется индукционным током .

Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.

Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.

Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.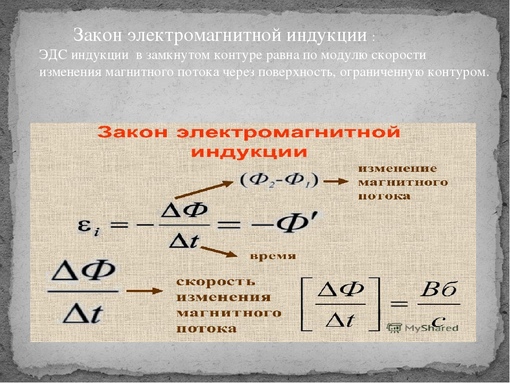

Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).

2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.

Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое – при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки .

3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.

Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим – при их уменьшении.

Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет – меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1 ).

Рис. 1.

В этом случае магнитный поток определяется очень просто – как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2 ).

Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2) , а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер (Вб). Как видим,

Вб = Тл · м = В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной – ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция – это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур .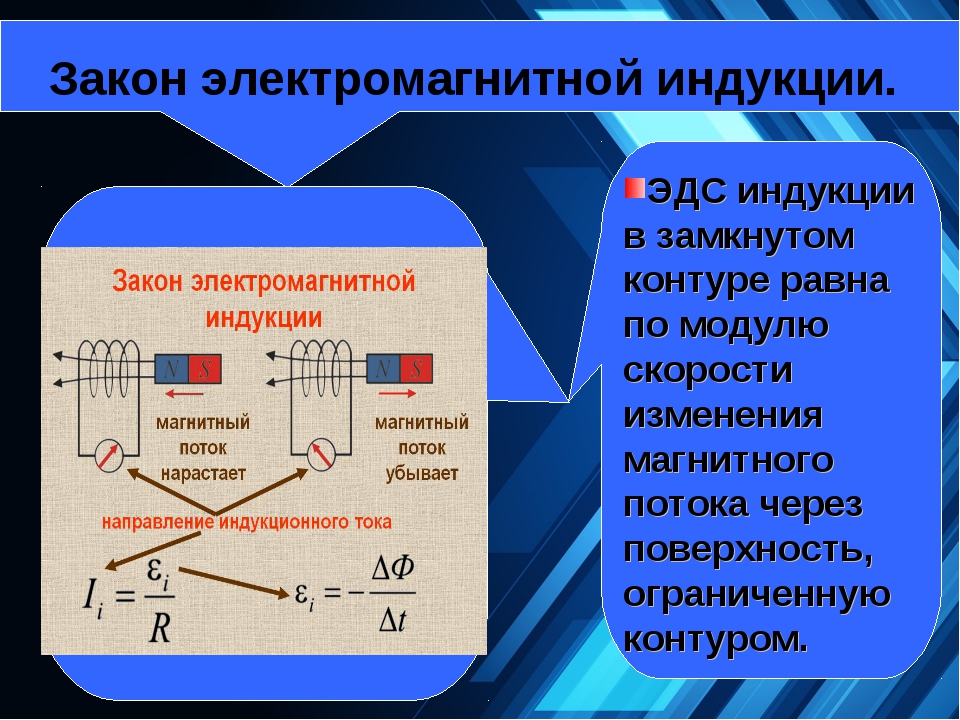

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы – сторонние силы , вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается .

Итак, ЭДС индукции – это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура .

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

Закон электромагнитной индукции Фарадея

Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.

Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока – это дробь (или, что тоже самое, производная магнитного потока по времени).

Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:

Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.

Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:

(4)

ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности – величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:

(5)

Это и есть закон электромагнитной индукции или закон Фарадея . Дадим его словесную формулировку.

Закон электромагнитной индукции Фарадея . При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока .

Правило Ленца

Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком . А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем .

Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.

Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.

Оказывается, эти два магнитных потока – собственный и внешний – связаны между собой строго определённым образом.

Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .

Правило Ленца позволяет находить направление индукционного тока в любой ситуации.

Рассмотрим некоторые примеры применения правила Ленца.

Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3) ). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.

Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.

Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3) ).

Рис. 3. Магнитный поток возрастает

Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4 ). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает

Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.

В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .

Уж во всяком случае вы должны запомнить этот факт – вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений – при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте – мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

Закон Фарадея + Правило Ленца = Снятие модуля

Выше мы обещали снять модуль в законе Фарадея (5) . Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции – ведь без модуля, стоящего в правой части (5) , величина ЭДС может получаться как положительной, так и отрицательной.

Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет – важно лишь сделать этот выбор.

Магнитный поток через контур считается положительным alt=”(\Phi > 0)”> , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .

ЭДС индукции считается положительной alt=”(\mathcal E_i > 0)”> , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.

Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.

Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: alt=”\Phi > 0″> .

Рис. 5. Магнитный поток возрастает

Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.

А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, alt=”\mathcal E_i > 0″> (рис. 6 ).

Рис. 6. Магнитный поток возрастает alt=”\Rightarrow \mathcal E_i > 0″>

Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :

(6)

Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.

Вихревое электрическое поле

Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?

Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое .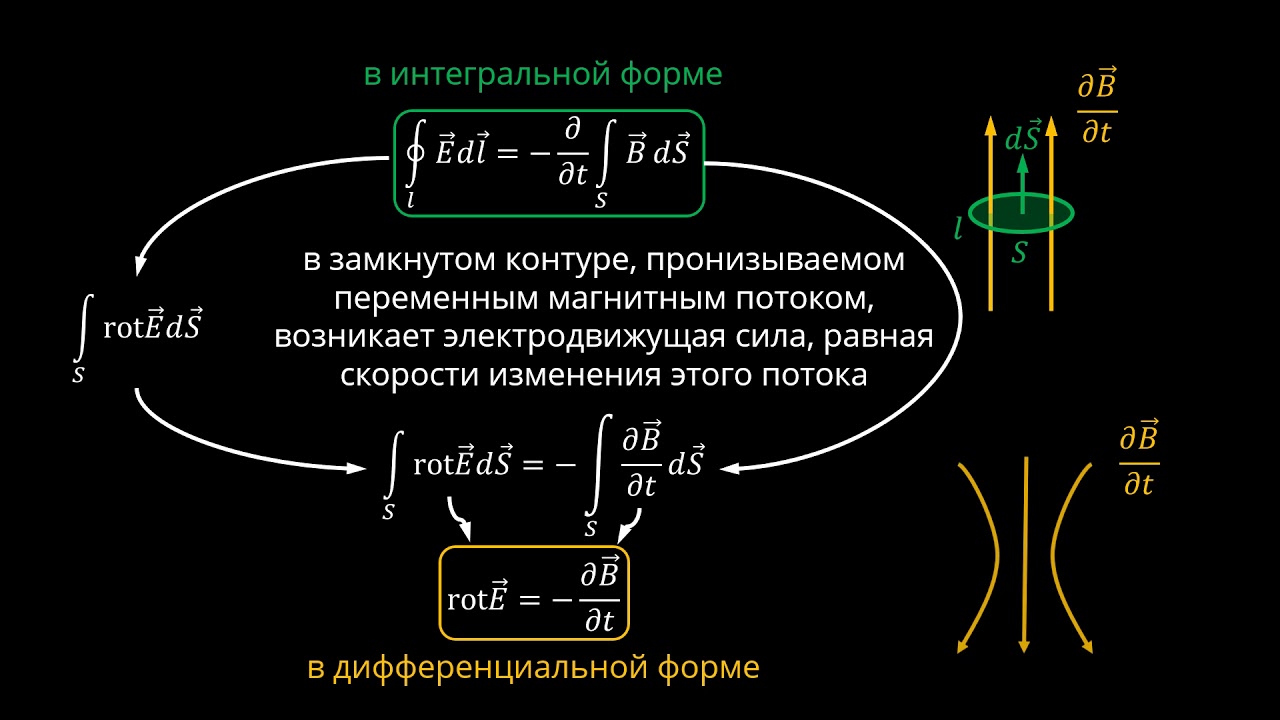 Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.

Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.

Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца – по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.

Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7 ).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля

Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8 ).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля

Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.

Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.

1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.

Итак, ЭДС индукции в неподвижном контуре – это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .

Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:

Следовательно, для ЭДС индукции получаем:

ЭДС индукции в движущемся проводнике

Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает – ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.

Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле . По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9 ).

Рис. 9. Движение проводника в магнитном поле

Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:

Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами – не забывайте правило часовой стрелки или левой руки!).

Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:

(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:

(7)

Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные – к точке .

Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к – и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7) .

Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N ). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:

Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9 ). Площадь контура возрастает на величину площади прямоугольника :

Магнитный поток через контур увеличивается. Приращение магнитного потока равно:

Скорость изменения магнитного потока положительна и равна ЭДС индукции:

Мы получили тот же самый результат, что и в (7) . Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.

На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.

Электромагнитной индукции -> Теория

Электромагнитной индукции -> Теория

Явление электромагнитной индукции.

   Открытое в 1831 году Фарадеем явление электромагнитной индукции состоит в  том, что в любом замкнутом контуре при изменении магнитного потока через поверхность, ограниченную этим контуром, возникает электродвижущая сила, величина которой пропорциональна скорости изменения магнитного потока:

 Eинд=-DФ/Dt

  Магнитный поток – это  физическая  величина, численно равная  количеству  ЛМИ, пронизывающих контур.

Ф=ВScosa

[Ф]=Вебер=Тл.м2

   В проводящем контуре существование ЭДС индукции приводит   к  появлению  индукционного  тока.  Знак минус   в   формуле   соответствует   правилу    Ленца, согласно    которому    направление    индукционного тока  всегда  таково,  что  создаваемое  им магнитное поле   препятствует   изменению  магнитного  потока, вызывающего индукционный ток. 

ЭДС индукции в движущихся проводниках.

  Изменение магнитного потока через контур, вызывающее появление ЭДС индукции, может происходить как за счет изменения магнитного поля, так и за счет изменения ориентации и формы контура.

   В  тех случаях, когда магнитное поле не изменяется во времени, а магнитный поток через контур изменяется из-за движения проводников контура в магнитном поле (изменения площади контура S), причиной возникновения ЭДС индукции является сила Лоренца.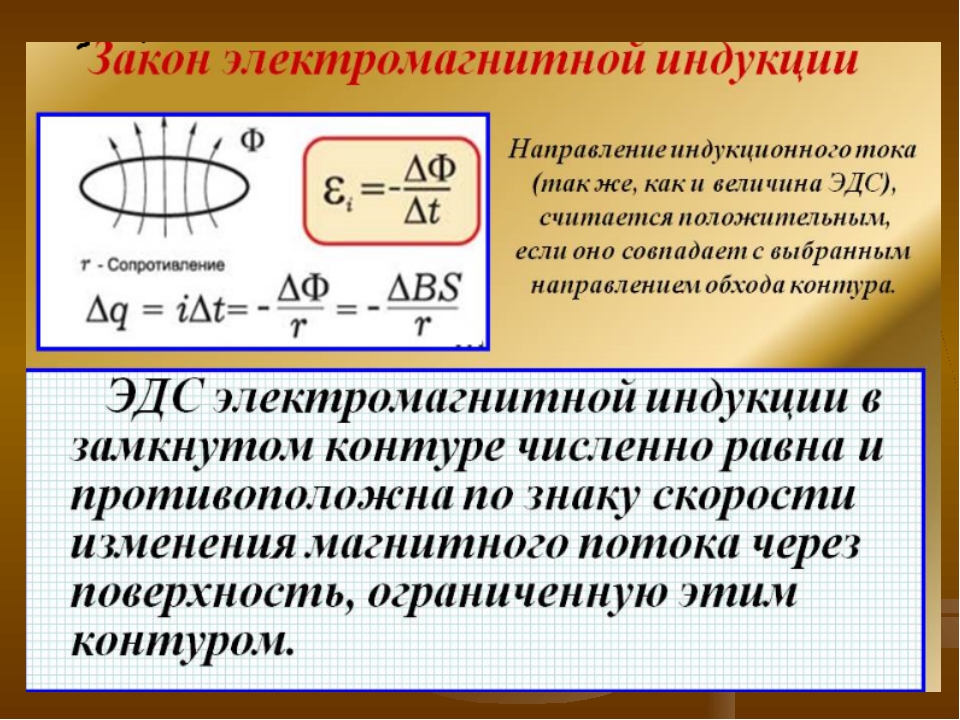

  Рассмотрим прямоугольный контур в однородном магнитном поле,  вектор индукции В  которого составляет угол a с плоскостью контура. Если провод скользит с постоянной скоростью v , то с такой же скоростью двигаются и заряды в нем. Следовательно, на них будет действовать сила Лоренца, равная  Fл=qvBsina,   и направленная вдоль проводника. Работа этой силы по переносу заряда по проводнику равна A=Fl, и ЭДС индукции по модулю равна  E=A/q.

   С другой стороны, за время Dt площадь контура изменяется на величину DS=lVDt, а магнитный поток: DФ=BVlsinaDt.

Итак, ЭДС индукции будет равна: E=BVlsina

 

ЭДС индукции в неподвижных проводниках.

  Если изменение магнитного потока через контур связано с изменением магнитного поля, то причина возникновения ЭДС индукции иная.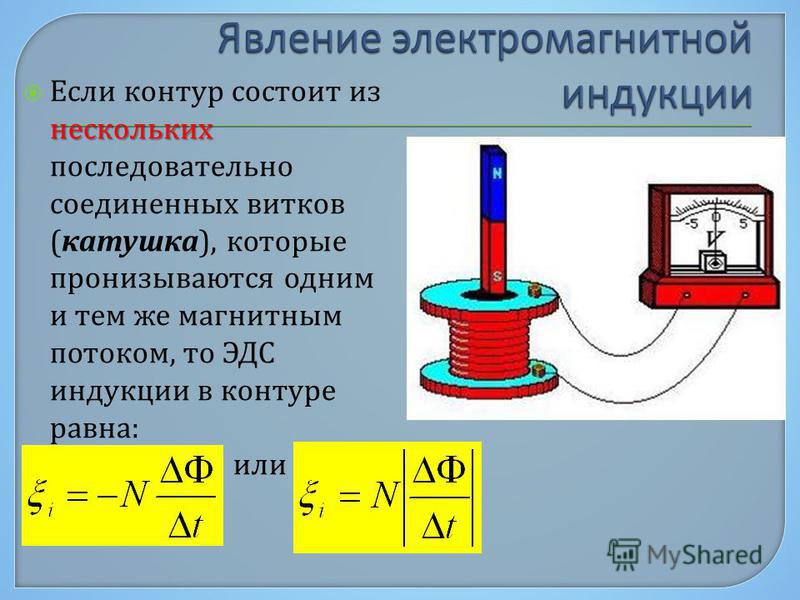 В общем случае, сила, действующая на электрический заряд q, складывается из силы   qE и силы Лоренца qVBsina. Т.к. движущихся проводников в данном случае нет, то сила Лоренца уже не может быть ответственной за возникновение ЭДС индукции.

  Остаётся допустить, что в области, где существует переменное магнитное поле, возникает электрическое поле, которое и обусловливает возникновение индукционного тока  в замкнутом контуре, т.е.  работа сил  этого  электрического  поля поля по замкнутому контуру уже не равна нулю. Поэтому, в отличие от потенциального электростатического поля, это электрическое поле называют вихревым.

   Итак,  переменное  магнитное   поле     создает    в   каждой   точке   пространства

вихревое электрическое поле. Чем быстрее меняется магнитное поле В, тем больше величина вихревого электрического E.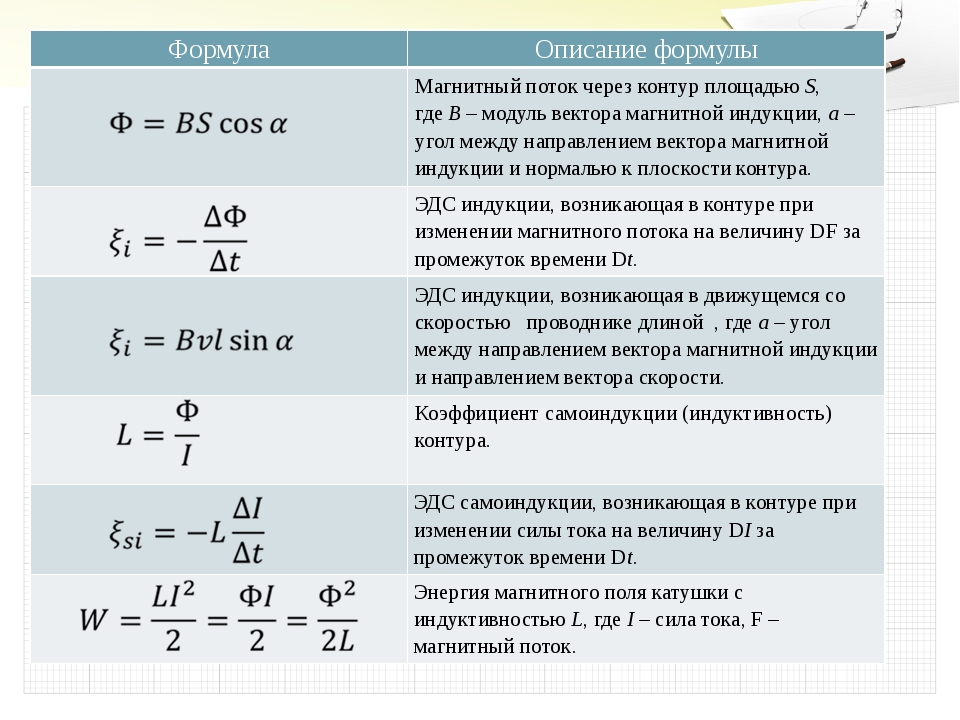

Самоиндукция. Индуктивность.

Если по катушке идет пepeмeнный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по  которому идет ток. Это явление называют самоиндукцией. При самоиндукции проводящий контур играет двоякую роль: по нему протекает ток, создающий переменное магнитное поле, и в нем же возникает ЭДС индукции. 

  Явление самоиндукции подобно явлению инерции в механике. За счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы прекращаем ток  сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.

Модуль B вектора индукции магнитного поля, создаваемого током, пропорционален  силе тока. Так как магнитный поток Ф пропорционален В, то Ф~В~I, следовательно:  

Ф=LI

 где  L- индуктивность контура. Это физическая величина, числено равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с. Зависит от числа витков, размеров, формы и сердечника катушки. Измеряется в генри (Гн).

Используя закон электромагнитной индукции и формулу для индуктивности контура, получаем равенство:

 Eинд=-L(DI/Dt)

Тест по физике на тему “Электромагнитная индукция”

Тест 11-1(электромагнитная индукция)

Вариант 1

1. Кто открыл явление электромагнитной индукции?

А. X. Эрстед. Б. Ш. Кулон. В. А. Вольта. Г. А. Ампер. Д. М. Фарадей. Е. Д. Максвелл.

2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечисленных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?

1. В катушку вставляется постоянный магнит.

2. Из катушки вынимается постоянный магнит.

3. Постоянный магнит вращается вокруг своей продоль­ной оси внутри катушки.

А. Только в случае 1. Б. Только в случае 2. В. Только в случае 3. Г. В случаях 1 и 2. Д. В случаях 1, 2 и 3.

3.Как называется физическая величина, равная произве­дению модуля В индукции магнитного поля на площадь S поверхности, пронизываемой магнитным полем, и косинус
угла а между вектором В индукции и нормалью п к этой поверхности?

А. Индуктивность. Б. Магнитный поток. В. Магнитная индукция. Г. Са­моиндукция. Д. Энергия магнитного поля.

4. Каким из приведенных ниже выражений определяется ЭДС индукции в замкнутом контуре?

A. Б. В. Г. Д.

5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индук­ционный ток. Этот ток создает магнитное поле. Каким по­люсом обращено магнитное поле тока в кольце к: 1) вдвигаемому северному полюсу магнита и 2) выдвигаемому се­верному полюсу магнита.

A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.

B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.

6. Как называется единица измерения магнитного потока?

А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.

7. Единицей измерения какой физической величины является 1 Генри?

А. Индукции магнитного ноля. Б. Электроемкости. В. Самоиндук­ции. Г. Магнитного потока. Д. Индуктивности.

8. Каким выражением определяется связь магнитного по­ тока через контур с индуктивностью L контура и силой тока I в контуре?

A. LI. Б. . В. LI ^‘ . Г. LI². Д. .

9. Каким выражением определяется связь ЭДС самоин­дукции с силой тока в катушке?

А. Б. В. LI. Г. . Д. LI ^‘.

10. Ниже перечислены свойства различных полей. Какими из них обладает электростатическое поле?

1. Линии напряженности обязательно связаны с электри­ческими зарядами.

2. Линии напрялсенности не связаны с электрическими зарядами.

3. Поле обладает энергией.

4. Поле не обладает энергией.

5. Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.

6. Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.

А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, 6. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.

11. Контур площадью 1000 см² находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Ка­ков магнитный поток через контур?

А. 250 Вб. Б. 1000 Вб. В. 0,1 Вб. Г. 2,5 · 10^-2 Вб. Д. 2,5 Вб.

12. Какая сила тока в контуре индуктивностью 5 мГн создает магнитный поток 2 · 10^-2 Вб?

А. 4 мА. Б. 4 А. В. 250 А. Г. 250 мА. Д. 0,1 А. Е. 0,1 мА.

13. Магнитный поток через контур за 5 · 10^-2 с равномер­но уменьшился от 10 мВб до 0 мВб. Каково значение ЭДС в контуре в это время?

А. 5 · 10^-4 В. Б. 0,1 В. В. 0,2 В. Г. 0,4 В. Д. 1 В. Е. 2 В.

14. Каково значение энергии магнитного поля катушки индуктивностью 5 Гн при силе тока в ней 400 мА?

А. 2 Дж. Б. 1 Дж. В. 0,8 Дж. Г. 0,4 Дж. Д. 1000 Дж. Е. 4·10⁵ Дж.

15. Катушка, содержащая n витков провода, подключена к источнику постоянного тока с напряжением U на выходе. Каково максимальное значение ЭДС самоиндукции в катушке при увеличении напряжения на ее концах от 0 В до U В?

A, U В, Б. nU В. В. U/п В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.

16. Две одинаковые лампы включены в цепь источника постоянного тока, первая последовательно с резистором, вторая последовательно с катушкой. В какой из ламп (рис. 1) сила тока при замыкании ключа К достигнет мак­симального значения позже другой?

А. В первой. Б. Во второй. В. В первой и второй одновременно. Г. В пер­вой, если сопротивление резистора больше сопротивления катушки. Д. Во второй, если сопротивление катушки больше сопротивления резистора.

17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 900 Ом, сила тока в катушке 0,5 А, электрическое сопротивление ка­тушки 100 Ом. Какой электрический заряд протечет в цепи катушки и резистора при отключении их от источника тока (рис. 2)?

А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10 ^-2 Кл. Д. 1,1 • 10^-3 Кл. Е. 1 • 10^-3 Кл.

18. Самолет летит со скоростью 900 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 10⁵ Тл. Какова разность потенциалов между концами крыльев самолета, если размах крыльев равен 50 м?

А. 1,8 В. Б. 0,9 В. В. 0,5 В. Г. 0,25 В.

19. Какой должна быть сила тока в обмотке якоря электромотора для того, чтобы на участок обмотки из 20 витков длиной 10 см, расположенный перпендикулярно век­тору индукции в магнитном поле с индукцией 1,5 Тл, действовала сила 120 Н?

А. 90 А. Б. 40 А. В. 0,9 А. Г. 0,4 А.

20. Какую силу нужно приложить к металлической пере­мычке для равномерного ее перемещения со скоростью 8 м/с по двум параллельным проводникам, располо­женным на расстоянии 25 см друг от друга в однородном магнитном поле с индукцией 2 Тл? Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Проводники замкнуты резистором с электрическим сопротивлением 2 Ом.

А. 10000 Н. Б. 400 Н. В. 200 Н. Г. 4 Н. Д. 2 Н. Е. 1 Н.

Вариант 2

1. Как называется явление возникновения электрического тока в замкнутом контуре при изменении магнитного по­тока через контур?

А. Электростатическая индукция. Б. Явление намагничивания. В. Сила Ампера. Г. Сила Лоренца. Д. Электролиз. Е. Электромагнитная индукция.

2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечислен­ных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?

1. В катушку вставляется постоянный магнит.

2. Катушка надевается на магнит.

3)Катушка вращается вокруг магнита, находящегося
внутри нее.

А.В случаях 1, 2 и 3. Б. В случаях 1 и 2. В. Только в случае 1. Г. Только в случае 2. Д. Только в случае 3.

3. Каким из приведенных ниже выражений определяется магнитный поток?

A. BScosα. Б. . В. qvBsinα. Г. qvBI. Д. IBlsina.

4. Что выражает следующее утверждение: ЭДС индукции в замкнутом контуре пропорциональна скорости измене­ния магнитного потока через поверхность, ограниченную контуром?

А. Закон электромагнитной индукции. Б. Правило Ленца. В. Закон Ома для полной цепи. Г. Явление самоиндукции. Д. Закон электролиза.

5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индук­ционный ток. Этот ток создает магнитное поле. Каким полюсом обращено магнитное поле тока в кольце к: 1) вдви­гаемому южному полюсу магнита и 2) выдвигаемому южному полюсу магнита.

A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.

B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.

6. Единицей измерения какой физической величины является 1 Вебер?

А. Индукции магнитного поля. Б. Электроемкости. В. Самоиндукции. Г. Магнитного потока. Д. Индуктивности.

7. Как называется единица измерения индуктивности?

А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.

8. Каким выражением определяется связь энергии маг­нитного потока в контуре с индуктивностью L контура и силой тока I в контуре?

А. . Б. . В. LI², Г. LI ^‘ . Д. LI.

9.Какая физическая величина х определяется выражением х= для катушки из п витков.

А. ЭДС индукции. Б. Магнитный поток. В. Индуктивность. Г. ЭДС само­индукции. Д. Энергия магнитного поля. Е. Магнитная индукция.

10. Ниже перечислены свойства различных полей. Какими из них обладает вихревое индукционное электрическое поле?

1. Линии напряженности обязательно связаны с электри­ческими зарядами.

2. Линии напряженности не связаны с электрическими зарядами.

3. Поле обладает энергией.

4. Поле не обладает энергией.

5. Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.

6. Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.

А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, в. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.

11. Контур площадью 200 см² находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Ка­ков магнитный поток через контур?

А. 50 Вб. Б. 2 · 10^-2 Вб. В. 5 · 10^-3 Вб. Г. 200 Вб. Д. 5 Вб.

12. Ток 4 А создает в контуре магнитный поток 20 мВб. Какова индуктивность контура?

А. 5 Гн. Б. 5 мГн. В. 80 Гн. Г. 80 мГн. Д. 0,2 Гн. Е. 200 Гн.

13. Магнитный поток через контур за 0,5 с равномерно уменьшился от 10 мВб до 0 мВб.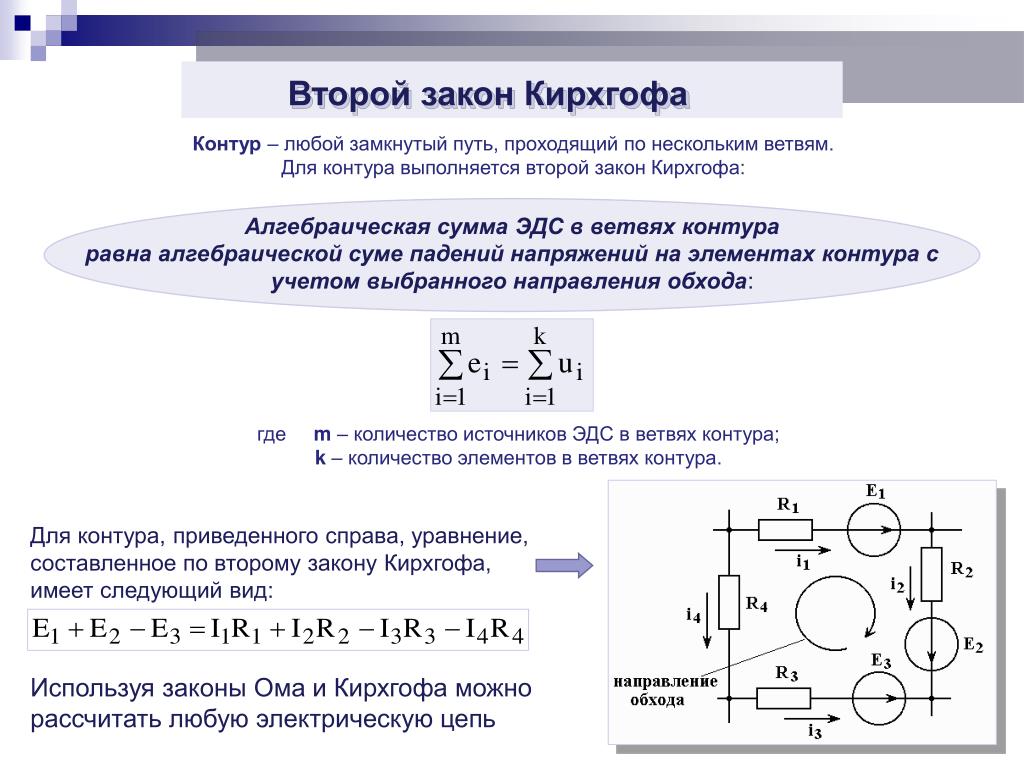 Каково значение ЭДС в контуре в это время?

А. 5 · 10^-3 В. Б. 5 В. В. 10 В. Г. 20 В. Д. 0,02 В. Е. 0,01 В.

14. Каково значение энергии магнитного поля катушки индуктивностью 500 мГн при силе тока в ней 4 А?

А. 2 Дж. Б. 1 Дж. В. 8 Дж. Г. 4 Дж. Д. 1000 Дж. Е. 4000 Дж.

15. Катушка, содержащая п витков провода, подключена к источнику постоянного тока с напряжением U на выхо­де. Каково максимальное значение ЭДС самоиндукции в катушке при уменьшении напряжения на ее концах от U В до 0 В?

A. U В. Б. nU В. В. U/n В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.

16. В электрической цепи, представленной на рисунке 1, четыре ключа 1, 2, 3 и 4 замкнуты. Размыкание какого из четырех даст лучшую возможность обнаружить явление самоиндукции?

А. 1. Б. 2. В. 3. Г. 4. Д. Любого из четырех.

17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 100 Ом, сила тока в катушке 0,5 А, электрическое сопротивление ка­тушки 900 Ом. Какой электрический заряд протечет в це­пи катушки и резистора при отключении их от источника тока (рис. 2)?

А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10^-2 Кл. Д. 1,1 • 10^-3 Кл. Е. 1 • 10^-3 Кл.

18. Самолет летит со скоростью 1800 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 10^-5 Тл. Какова разность потенциалов между кон­цами крыльев самолета, если размах крыльев равен 25 м?

А. 1,8 В. В. 0,5 В. В. 0,9 В. Г. 0,25 В.

19. Прямоугольная рамка площадью S с током I помеще­на в магнитном поле с индукцией В . Чему равен момент силы, действующей на рамку, если угол между вектором В и нормалью к рамке равен а?

A. IBS sin а. Б. IBS. В. IBS cos а. Г. I²BS sin а. Д. I²BS cos а.

20. По двум вертикальным рельсам, верхние концы кото­рых замкнуты резистором электрическим сопротивлением R, начинает скользить проводящая перемычка массой т и длиной I. Система находится в магнитном поле. Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Найдите установившуюся скорость и движения перемычки. Сила трения пренебрежимо мала.

А. . В. В. . Г. . Д. .

Ответы:

Номер вопроса и ответ

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

Вариант 1

Д

Г

Б

Б

Г

Б

Д

А

Д

В

Г

Б

В

Г

А

Б

Е

В

Б

Е

Вариант 2

Е

Б

А

А

В

Г

Д

Б

А

Г

В

Б

Д

Г

Г

А

Е

Б

В

А

Первый и второй законы Кирхгофа

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

 

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I₁– ток, втекающий в узел , а токи I₂ и I₃ — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:

I₁ = I₂ + I₃  (1)

Что бы подтвердить справедливость формулировки №2, перенесем токи I₂ и I₃ в левую часть выражения (1), тем самым получим:

I₁ – I₂ – I₃ = 0   (2)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

E₁– Е₂ = -UR₁ – UR₂ или E₁ = Е₂ – UR₁ – UR₂   (3)

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E₁ = Ur₁ + UR или E₁ = I₁*r₁ + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I₁ + I₂;

E₁-E₂ = I₁*r₁ – I₂*r₂;

E₁ = I₁*r₁ + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I₁ + I₂;

7 = 0,1I₁ – 0,1I₂;

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

I₂=I – I₁;

I₂ = I₁ – 70;

12 = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I – I₁= I₁ – 70;

12 = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

12 = 0,1I₁ + 2(2I₁ – 70).

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

I₁=152/4,1

I₁=37,073 (А)

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I – I₁

I₂=4,146 – 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I₂ вытекает из узла А.

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

Лекция 15, 11 октября 2000 г.

Лекция 15, 11 октября 2000 г.

индекс курса

Вспомнить с последней лекции:

• Создание магнитных полей:
• Длинный прямой провод: B = m ₀ I / 2p r
• Соленоид: B = m ₀ n I
• Сила магнитного поля:
• Движущийся заряд: F = q v B sinq
• Провод: F = B I l sinq
• Крутящий момент в токовой петле: t = B I A sinq
• Усилие между двумя проводами: F / l = m ₀ I ₁ I ₂ / 2p d
• привлекательный, когда токи одного направления
• отталкивающий, когда токи противоположны по направлению

Гл.20: Наведенные напряжения и индуктивность

Мы видели, что магнитное поле воздействует на провод, по которому течет ток, и что провод, по которому течет ток, создает магнитное поле. Токи создаются электрическими полями, так что, похоже, между электричеством и магнетизмом существует какая-то связь. В этой главе мы установим эту связь, увидев, как магнитное поле может создавать разность потенциалов. Магнитный поток будет играть важную роль на протяжении всей этой главы.

20.1 ЭДС индукции и магнитный поток

Эксперименты 19 века показали, что изменяющееся магнитное поле может создавать ЭДС. Мы количественно определяем изменение с точки зрения магнитного потока. Магнитный поток определяется аналогично электрическому потоку. Для проволочной петли площадью A в магнитном поле B магнитный поток F определяется выражением:

F = B _perp A = B A cosq

где q — угол между перпендикуляром к плоскости петли и магнитным полем B.Единицы магнитного потока в системе СИ — Тм².

Другой способ взглянуть на поток — представить его как количество силовых линий магнитного поля, проходящих через петлю. Если петля ориентирована перпендикулярно полю (q=0), то поток будет большим. Если петля ориентирована параллельно полю (q = 90°), силовые линии магнитного поля не проходят через петлю, и поток равен нулю.

Пример: P20.2

Квадратная петля со стороной 2,00 м помещена в магнитное поле с напряженностью 0.300т. Если поле образует угол 50,0° с нормалью к плоскости петли, как на рис. 20.2, определите магнитный поток через петлю.

Из того, что нам дано, мы используем
F = B A cosq = (0,300T)(2,00m)²cos50,0° = 0,386 Tm²

20.2 Закон индукции Фарадея

Закон индукции Фарадея связывает изменение магнитного потока с ЭДС индукции:

ЭДС = -N (DF / Dt)

где N — число витков в катушке, в которых индуцируется ЭДС, а DF — изменение потока, происходящее за время Dt.Это один из случаев, когда термин ЭДС несколько отличается от напряжения, и поэтому я буду использовать его.

ЭДС индукции пропорциональна изменению магнитного потока, F = BAcosq. Существует три способа изменения потока:

1. изменение величины магнитного поля, В,
2. изменение угла между контуром и магнитным полем, q, или
3. изменение площади петли, А.

Знак минус напоминает вам, что полярность ЭДС индукции препятствует изменению потока.Это точно указано в законе Ленца:

Полярность ЭДС индукции такова, что она создает ток, магнитное поле которого противодействует изменению магнитного потока через контур. То есть индуцированный ток имеет тенденцию поддерживать первоначальный поток через цепь.

Пример: P20.13

Проволочная петля радиусом 0,30 м расположена так, что внешнее магнитное поле с напряженностью +0,30 Тл перпендикулярно петле. Поле меняется на -0,20 Тл за 1,5 с. (Здесь знаки плюс и минус относятся к противоположным направлениям цикла.) Найти величину средней ЭДС индукции в контуре за это время.

Петля всегда перпендикулярна полю, поэтому нормаль к петле параллельна полю, поэтому q = 0, а cosq = 1. Таким образом, поток через контур равен F = BA = Bpr². Первоначально поток равен
F _i = (0,30T)p(0,30м) ² = 0,085Tm²
, а после изменения поля поток равен
F _f = (-0,20T)p(0,30м) ² = -0,057Tm²
Величина средней ЭДС индукции:
ЭДС = DF/Dt = (F _i – F _f )/Dt = (0. 085T – (-0,057T))/1,5 с = 0,095 В = 95 мВ.

Пример: P20.10

Гибкая петля на рис. P20.10 имеет радиус 12 см и находится в магнитном поле силой 0,15 Тл. Петлю захватывают в точках А и В и растягивают до закрытия. Если для замыкания контура требуется 0,20 с, найти величину средней ЭДС индукции в нем за это время.

Это тот случай, когда изменение потока вызвано изменением площади контура. И магнитное поле, и угол q остаются постоянными.Когда петля растянута так, что ее площадь равна нулю, поток через петлю равен нулю. Таким образом, изменение потока равно его первоначальному значению:
F _i = BA cosq = (0,15T)p(0,12m)² = 6,8×10 ^-3 Tm²
. Таким образом, средняя ЭДС индукции равна:
ЭДС = N (DF / Dt) = (6,8×10 ^-3 Тм²)/(0,20 с) = 3,4×10 ^-2 В = 34 мВ.

20.3 ЭДС движения

Интересным применением закона Фарадея является создание ЭДС посредством движения проводника. В качестве простого примера рассмотрим проводящий стержень, движущийся перпендикулярно однородному магнитному полю с постоянной скоростью v. На первый взгляд у нас есть просто стержень, а не полная проводящая петля, и мы рассмотрим, что происходит, используя только силу, действующую на движущийся заряд, F = qvBsinq. Эта сила будет действовать на свободные заряды в проводнике. Он будет иметь тенденцию перемещать отрицательный заряд к одному концу и оставлять другой конец стержня с чистым положительным зарядом.

Разделенные заряды создадут электрическое поле, которое будет стремиться сблизить заряды.Когда существует равновесие, магнитная сила F=qvB будет уравновешивать электрическую силу F=qE, так что свободный заряд в стержне не будет ощущать результирующей силы. Таким образом, в равновесии E = vB. Разность потенциалов на концах стержня определяется как DV = E l, или

DV = E л = B л v

Эта разность потенциалов существует из-за избытка заряда на концах проводника, создаваемого движением через магнитное поле. Если направление движения меняется на противоположное, меняется и полярность разности потенциалов.

Теперь давайте посмотрим, что произойдет, если мы добавим токопроводящие шины для верхней и нижней части стержня, чтобы они соприкасались, и резистор между ними, чтобы замкнуть контур. Мы можем применить закон Фарадея к полной петле. Изменение потока через петлю пропорционально изменению площади от движения стержня:

DF = B DA = B 1 Dx.

Используя закон Фарадея, мы находим величину ЭДС равной (N = 1):

ЭДС = DF/Dt = B l Dx/Dt = B l v

где я использовал соотношение v = Dx/Dt.Это тот же результат, который мы получили, рассматривая проводящий стержень сам по себе.

Если проводящая цепь имеет полное сопротивление, R, то ток равен

I = ЭДС / R = B l v / R

Пример: P20.18

Над областью, где вертикальная составляющая магнитного поля Земли 40,0 мкТл направлена ​​вниз, провод длиной 5,00 м удерживается в направлении восток-запад и перемещается горизонтально на север со скоростью 10,0 м/с. Рассчитайте разность потенциалов между концами провода и определите, какой конец положительный.

Вертикальная составляющая магнитного поля перпендикулярна проводу и его движению, так что это то, что нам нужно. Использование выражения, полученного для DV, дает:

DV = B l v = (40,0 мкТл)(5,00 м)(10,0 м/с) = 2,00 мВ

Чтобы определить, какой конец положительный, рассмотрим положительный заряд, движущийся на север через нисходящее магнитное поле. Правило правой руки дает силу, направленную на запад. Таким образом, западный конец провода будет иметь чистый положительный заряд и более положительный потенциал.

© Роберт Харр, 2000 г.

Магнитная индукция

Магнитная индукция
Следующая: ЭДС движения Вверх: Магнитная индукция Предыдущий: Закон Ленца

Магнитная индукция Рассмотрим одновитковую петлю проводника, помещенную в магнитное поле. поле . Петлю связи магнитного потока можно записать

(197)

где любая поверхность, присоединенная к петле.

Предположим, что магнитное поле изменяется во времени, вызывая цепь связи магнитного потока для изменения. Пусть поток изменяется на величину в интервале времени . По закону Фарадея ЭДС индуцированная петля определяется выражением

(198)

Если есть положительный тогда ЭДС действует вокруг контура в том же смысле, что и указал пальцами правой руки, когда большой палец указывает в направлении среднего магнитного поля, проходящего через контур.Так же, Если есть минус то ЭДС действует вокруг контура в напротив толку от этого указал пальцами правой руки, когда большой палец указывает в направлении среднего магнитного поля, проходящего через контур. в В первом случае мы говорим, что ЭДС действует в положительном направлении, тогда как в последнем случае мы говорим, что он действует в отрицательном направлении.

Предположим, что , так что ЭДС действует в положительном направлении.Как именно возникает эта ЭДС? Чтобы ответить на этот вопрос, нам нужно напомнить себе, что такое ЭДС на самом деле. Когда мы говорим, что вокруг контура действует ЭДС в положительном направлении, что мы на самом деле имеем в виду, так это то, что заряд, который циркулирует один раз вокруг петля в положительном направлении приобретает энергию . Как заряд приобретает эту энергию? Ясно, что либо электрический поле или магнитное поле, или их комбинация, должны выполнять работать над зарядом, когда он циркулирует по контуру.Однако, как мы уже видели, из разд. 8.4, что магнитный поле не может совершить работу над заряженной частицей. Таким образом, заряд должен получить энергию от электрического поля , поскольку это циркулирует один раз по контуру в положительном направлении.

Согласно разд. 5, работа, которую электрическое поле совершает над зарядом по мере его обращения. петля

(199)

где – линейный элемент цикла.Следовательно, по закону сохранения энергии мы можем написать , или

(200)

Срок в правой части приведенного выше выражения можно узнать как линейный интеграл электрического поля вокруг контура в положительное направление. Таким образом, ЭДС, возникающая вокруг цепь в положительном направлении равна линейному интегралу электрического поля вокруг цепи в том же направлении.

Уравнения (198) и (200) можно объединить, чтобы получить

(201)

Таким образом, из закона Фарадея следует, что линейный интеграл электрического поля вокруг цепи (в положительном направлении) равна минус скорости изменения магнитный поток, связывающий эту цепь. Распространяется ли этот закон только на проведение цепей, или мы можем применить его к произвольному замкнутому контуру в пространстве? Что ж, разница между проводящей цепью и произвольным замкнутым контуром заключается в том, что электрический ток может течь по цепи, тогда как ток не может, вообще говоря, обтекать произвольный цикл. В самом деле, ЭДС индуцированный вокруг проводящей цепи вызывает ток вокруг этой цепи, где сопротивление цепи. Тем не мение, мы можем сделать это сопротивление сколь угодно большим, не делая недействительным уравнение(201). В пределе, при котором стремится к бесконечности, ток по цепи не течет, поэтому схема становится неотличимой от произвольной петли. Поскольку мы можем разместить такая схема в любом месте в пространстве, и уравнение. (201) остается в силе, мы вынуждены вывод, что уравнение (201) справедливо для любого замкнутого контура в пространстве, а не только для проведения цепей.

Уравнение (201) описывает, как изменяющееся во времени магнитное поле генерирует электрическое поле, заполняющее пространство.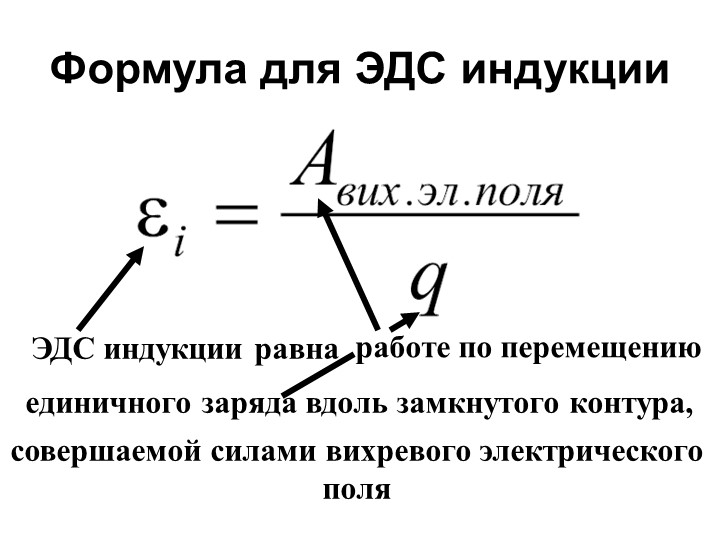 Напряженность электрического поля прямо пропорциональна скорости изменения магнитного поля. То силовые линии, связанные с этим электрическим поля образуют петли в плоскости, перпендикулярной магнитному полю. Если магнитное поле увеличивается, то силовые линии электрического поля циркулируют в в противоположном смысле к пальцам правой руки, когда большой палец указывает в направлении поля. Если магнитное поле уменьшается, то силовые линии электрического поля циркулируют в то же чувство, что и пальцы правой руки, когда большой палец указывает в направлении поля.Это показано на рис. 35.

Рис. 35: Индуктивно генерируемые электрические поля

Теперь мы можем понять, что когда проводящая цепь помещается в переменное во времени магнитное поле, это электрическое поле, индуцированное изменяющимся магнитное поле, которое создает ЭДС вокруг цепи. Если петля имеет конечное сопротивление, то это электрическое поле также вызывает ток в цепи.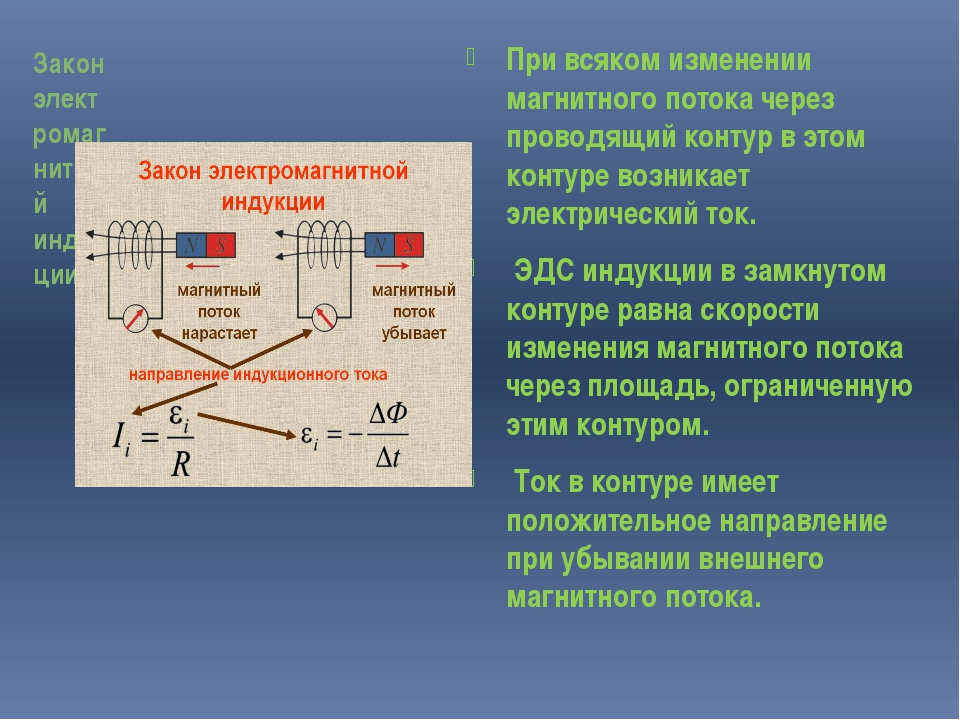 Обратите внимание, однако, что электрическое поле генерируется независимо от наличие токопроводящей цепи. Электрическое поле, создаваемое изменяющимся во времени магнитное поле по своей природе сильно отличается от поля, создаваемого набором стационарных электрические заряды. В последнем случае линии электрического поля начинаются на положительные заряды, заканчиваются на отрицательных зарядах, и никогда не образуют замкнутые петли в свободном пространстве. В первом случае силовые линии электрического поля никогда не начинаются или end, а всегда образуют замкнутые петли в свободном пространстве.На самом деле электрическая силовые линии, создаваемые магнитной индукцией, ведут себя почти так же, как силовые линии магнитного поля. Напомним, из разд. 5.1, что электрический поле, создаваемое фиксированными зарядами, не может совершать чистую работу над зарядом который циркулирует по замкнутому кругу. С другой стороны, электрический поле, создаваемое магнитной индукцией, безусловно, может совершать работу над зарядом который циркулирует по замкнутому кругу. Это в основном, как ток индуцируется в проводящая петля, помещенная в переменное во времени магнитное поле.Одно последствие этого факт состоит в том, что работа, совершаемая при медленном движении заряда между двумя точками в индуктивном электрическом поле зависит ли от путь, пройденный между двумя точками. Отсюда следует, что мы не можем рассчитать уникальную разность потенциалов между двумя точками индуктивного электрическое поле. На самом деле вся идея электрического потенциала рушится. в таком поле (к счастью, есть способ спасения идеи электрического потенциала в индуктивном поле, но эта тема выходит за рамки данного курса).Заметим, однако, что до сих пор можно рассчитать уникальное значение для ЭДС, генерируемой вокруг проводящего цепь индуктивным электрическим полем, потому что в этом случае путь, пройденный электрические заряды однозначно указаны: т.е. , заряды имеют следить за схема.

---

Следующая: ЭДС движения Вверх: Магнитная индукция Предыдущий: Закон Ленца

Ричард Фицпатрик 2007-07-14

10.

3 ЭДС движения – Введение в электричество, магнетизм и электрические цепи

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Определить величину ЭДС индукции в проводе, движущемся с постоянной скоростью через магнитное поле
• Обсудите примеры, использующие ЭДС движения, такие как рельсовая пушка и привязанный спутник

Магнитный поток зависит от трех факторов: силы магнитного поля, площади, через которую проходят силовые линии, и ориентации поля с площадью поверхности.Если какая-либо из этих величин изменяется, происходит соответствующее изменение магнитного потока. До сих пор мы рассматривали только изменения потока из-за изменяющегося поля. Теперь мы рассмотрим другую возможность: изменение области, через которую проходят силовые линии, включая изменение ориентации области.

Два примера этого типа изменения потока представлены на рисунке 10.3.1. В части (а) поток через прямоугольную петлю увеличивается по мере ее перемещения в магнитное поле, а в части (б) поток через вращающуюся катушку изменяется с углом .

(рис. 10.3.1)  

Рисунок 10.3.1  (a) Магнитный поток изменяется по мере того, как петля перемещается в магнитное поле; б) изменение магнитного потока при вращении петли в магнитном поле.

Интересно отметить, что то, что мы воспринимаем как причину конкретного изменения потока, на самом деле зависит от выбранной нами системы отсчета. Например, если вы находитесь в состоянии покоя относительно движущихся катушек на рисунке 10.3.1, вы увидите, что поток меняется из-за изменяющегося магнитного поля — в части (а) поле перемещается слева направо в вашей системе отсчета, а в части (б) поле вращается.Часто можно описать изменение потока через катушку, которая движется в одной конкретной системе отсчета, с точки зрения изменения магнитного поля во второй системе отсчета, где катушка неподвижна. Однако вопросы системы отсчета, связанные с магнитным потоком, выходят за рамки этого учебника. Мы избежим таких сложностей, всегда работая в системе отсчета, покоящейся относительно лаборатории, и объясняя изменения потока либо из-за изменяющегося поля, либо из-за изменяющейся площади.

Теперь давайте посмотрим на токопроводящий стержень, втянутый в цепь, меняющую магнитный поток.Площадь, ограниченная контуром на рис. 10.3.2, равна и перпендикулярна магнитному полю, поэтому мы можем упростить интеграцию уравнения 10.1.1 в произведение магнитного поля и площади. Таким образом, магнитный поток через открытую поверхность равен

.

(10.3.1)  

Поскольку  и  постоянны, а скорость стержня равна  , теперь мы можем переформулировать закон Фарадея, уравнение 10.1.2, для величины ЭДС с точки зрения движущегося проводящего стержня как

(10.3.2)  

Ток, индуцированный в цепи, равен ЭДС, деленной на сопротивление, или

   

Кроме того, направление ЭДС индукции удовлетворяет закону Ленца, в чем можно убедиться, рассмотрев рисунок.

Этот расчет ЭДС, вызванной движением, не ограничивается стержнем, движущимся по токопроводящим рельсам. Используя  в качестве отправной точки, можно показать, что выполняется для любого изменения потока, вызванного движением проводника.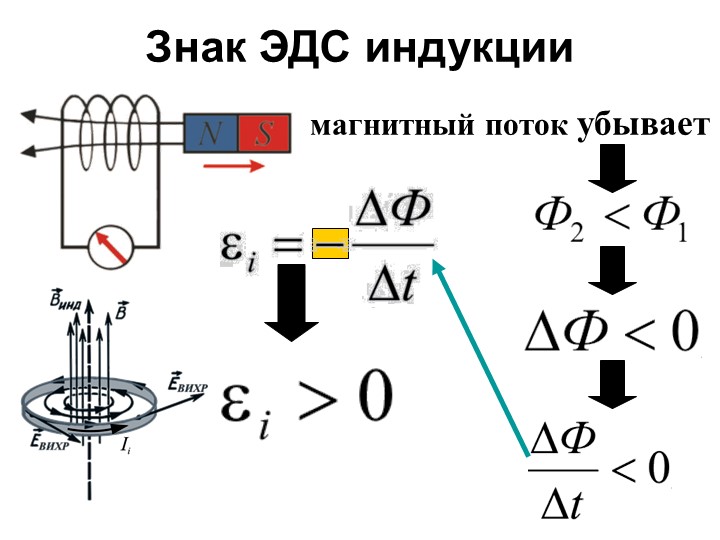 Мы видели в Законе Фарадея , что ЭДС, индуцированная изменяющимся во времени магнитным полем, подчиняется тому же соотношению, которое является законом Фарадея.Таким образом, закон Фарадея выполняется для всех изменений потока , независимо от того, вызваны ли они изменяющимся магнитным полем, движением или их комбинацией.

(рис. 10.3.2)  

Рисунок 10.3.2  Проводящий стержень толкают вправо с постоянной скоростью. Результирующее изменение магнитного потока индуцирует ток в цепи.

С энергетической точки зрения  вырабатывает мощность , а резистор рассеивает мощность . Поскольку стержень движется с постоянной скоростью, приложенная сила должна уравновешивать магнитную силу, действующую на стержень, когда он несет индуцированный ток.Таким образом, произведенная мощность равна

.

(10.3.3)  

Рассеиваемая мощность

(10.3.4)  

При соблюдении принципа сохранения энергии производимая и рассеиваемая мощности равны.

Этот принцип можно увидеть в работе рельсовой пушки . Рельсовая пушка — это электромагнитная пусковая установка, в которой используется устройство, аналогичное рисунку 10.3.2, схематично показанное на рис. 10.3.3. Проводящий стержень заменяется снарядом или оружием для стрельбы.До сих пор мы слышали только о том, как движение вызывает ЭДС. В рельсовой пушке оптимальное отключение/уменьшение магнитного поля уменьшает поток между рельсами, вызывая протекание тока в стержне (якоре), который удерживает снаряд. Этот ток через якорь испытывает магнитную силу и движется вперед. Рельсовые пушки, однако, не используются широко в вооруженных силах из-за высокой стоимости производства и больших токов: требуется почти один миллион ампер для производства энергии, достаточной для того, чтобы рельсовая пушка была эффективным оружием.

(рис. 10.3.3)  

Рисунок 10.3.3  Ток через два рельса толкает токопроводящий снаряд вперед за счет создаваемой магнитной силы.

Мы можем рассчитать ЭДС, индуцированную движением  с помощью закона Фарадея , даже если фактическая замкнутая цепь отсутствует . Мы просто представляем замкнутую область, граница которой включает в себя движущийся проводник, вычисляем , а затем находим ЭДС по закону Фарадея. Например, мы можем позволить движущемуся стержню на рисунке 10.3.5 быть одной стороной воображаемой прямоугольной области, представленной пунктирными линиями. Площадь прямоугольника равна , значит магнитный поток через него равен . Дифференцируя это уравнение, получаем

(10.3.5)  

, что идентично разности потенциалов между концами стержня, которую мы определили ранее.

(рис. 10.3.4)  

Рисунок 10.3.4  С показанным воображаемым прямоугольником мы можем использовать закон Фарадея для расчета ЭДС индукции в движущемся стержне.

ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, при обычных движениях.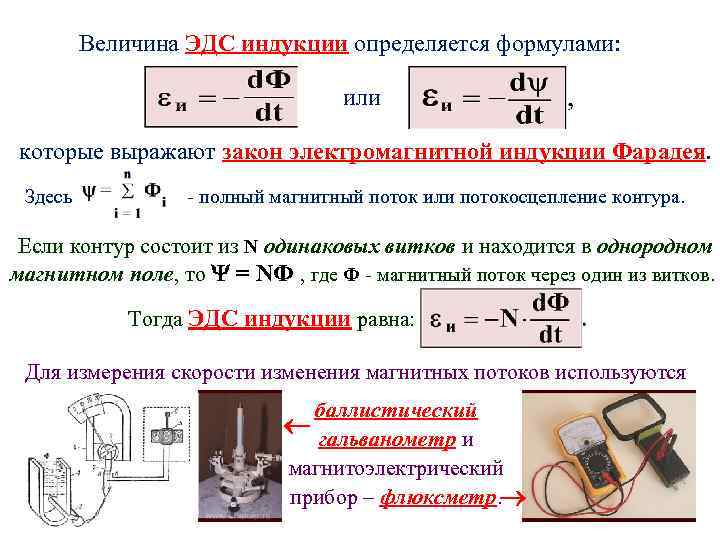 Например, простой расчет ЭДС движения стержня, движущегося перпендикулярно полю Земли, дает

   

Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля “Шаттл” были предприняты попытки создать большие ЭДС движения.Привязанный спутник должен был быть выпущен на отрезке провода, как показано на рисунке 10.3.5, чтобы создать ЭДС, двигаясь с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь, по которому мог течь ток. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах.Он проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и стационарные рельсы и соединительный резистор на рисунке 10.3.3, без которых не было бы полной цепи. ) Сопротивление току в кабеле из-за магнитной силы выполняет работу, уменьшающую кинетическую энергию шаттла. и потенциальной энергии, и позволяет преобразовать ее в электрическую энергию. Оба теста оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании.Пример 10.3.1 указывает на принципиальную осуществимость.

(рис. 10.3.5)  

Рисунок 10.3.5  ЭДС движения как преобразование электроэнергии для космического челнока послужила мотивом для эксперимента с привязанным спутником. Было предсказано, что ЭДС будет индуцироваться в тросе при движении с орбитальной скоростью в магнитном поле Земли. Цепь завершается обратным путем через стационарную ионосферу.

ПРИМЕР 10.3.2

---

Металлический стержень, вращающийся в магнитном поле

Часть (а) рисунка 10.3.6 показан металлический стержень, вращающийся в горизонтальной плоскости вокруг точки .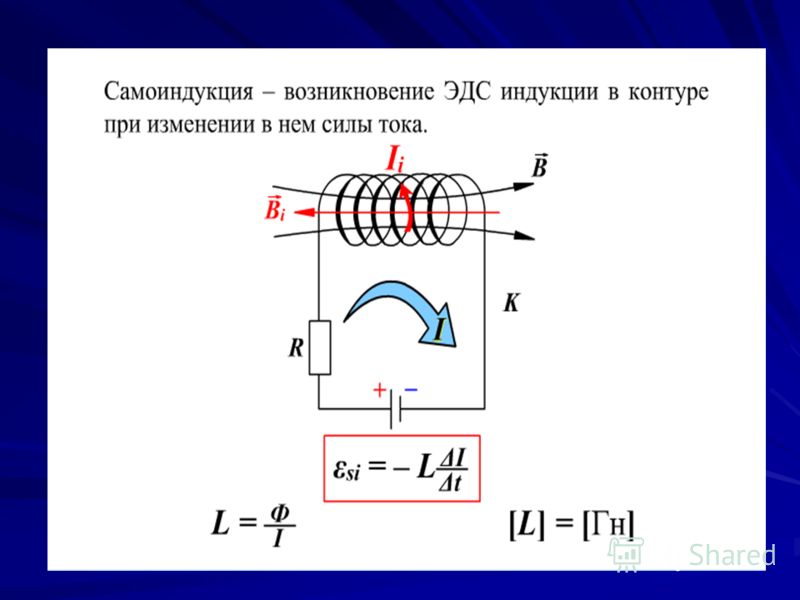 Стержень скользит по проволоке, образующей дугу окружности радиусом . Система находится в постоянном магнитном поле, которое направлено за пределы страницы. (а) Если вы вращаете стержень с постоянной угловой скоростью, какова сила тока в замкнутом контуре? Предположим, что резистор обеспечивает все сопротивление в замкнутом контуре. б) Вычислите работу, совершаемую вами при вращении стержня в единицу времени, и покажите, что она равна мощности, рассеиваемой на резисторе.

(рис. 10.3.6)  

Рисунок 10.3.6  (a) Конец вращающегося металлического стержня скользит по круглой проволоке в горизонтальной плоскости. (б) Индуцированный ток в стержне. (c) Магнитная сила на бесконечно малом отрезке тока.

Стратегия

Магнитный поток равен произведению магнитного поля на площадь четверти круга или . При нахождении ЭДС по закону Фарадея все переменные постоянны во времени, но , при . Чтобы рассчитать работу в единицу времени, мы знаем, что это связано с произведением крутящего момента на угловую скорость. Крутящий момент рассчитывается путем знания силы, действующей на стержень, и интегрирования ее по длине стержня.

Решение

а. Исходя из геометрии, площадь петли равна . Следовательно, магнитный поток через петлю равен

   

Дифференцируя по времени и используя , мы имеем

   

При делении на сопротивление контура это дает величину индуцированного тока

   

По мере увеличения  увеличивается и поток через контур из-за .Чтобы противодействовать этому увеличению, магнитное поле из-за индуцированного тока должно быть направлено в страницу в области, ограниченной петлей. Следовательно, как показано в части (b) рисунка 10.3.6, ток циркулирует по часовой стрелке.

б. Вы вращаете стержень, прикладывая к нему крутящий момент. Поскольку стержень вращается с постоянной угловой скоростью, этот крутящий момент равен и противоположен крутящему моменту, действующему на ток в стержне исходным магнитным полем. Магнитная сила на бесконечно малом отрезке длины, показанном в части (c) рисунка 10. 3.6 равно , поэтому магнитный момент на этом сегменте равен

   

Тогда чистый магнитный момент на стержне равен

.

   

Крутящий момент  , который вы прилагаете к стержню, равен и противоположен , а работа, которую вы совершаете, когда стержень поворачивается на угол, равна . Следовательно, работа в единицу времени, которую вы совершаете над стержнем, равна

.

   

, где мы заменили . Мощность, рассеиваемая на резисторе, равна , что можно записать как

.

   

Следовательно, мы видим, что

   

Следовательно, мощность, рассеиваемая на резисторе, равна работе, совершаемой в единицу времени при вращении стержня.

Значение

Альтернативный способ рассмотрения ЭДС индукции из закона Фарадея состоит в том, чтобы интегрировать его в пространстве, а не во времени. Однако решение будет таким же. ЭДС движения равна

.

   

Скорость может быть записана как произведение угловой скорости на радиус, а дифференциальная длина записана как dr .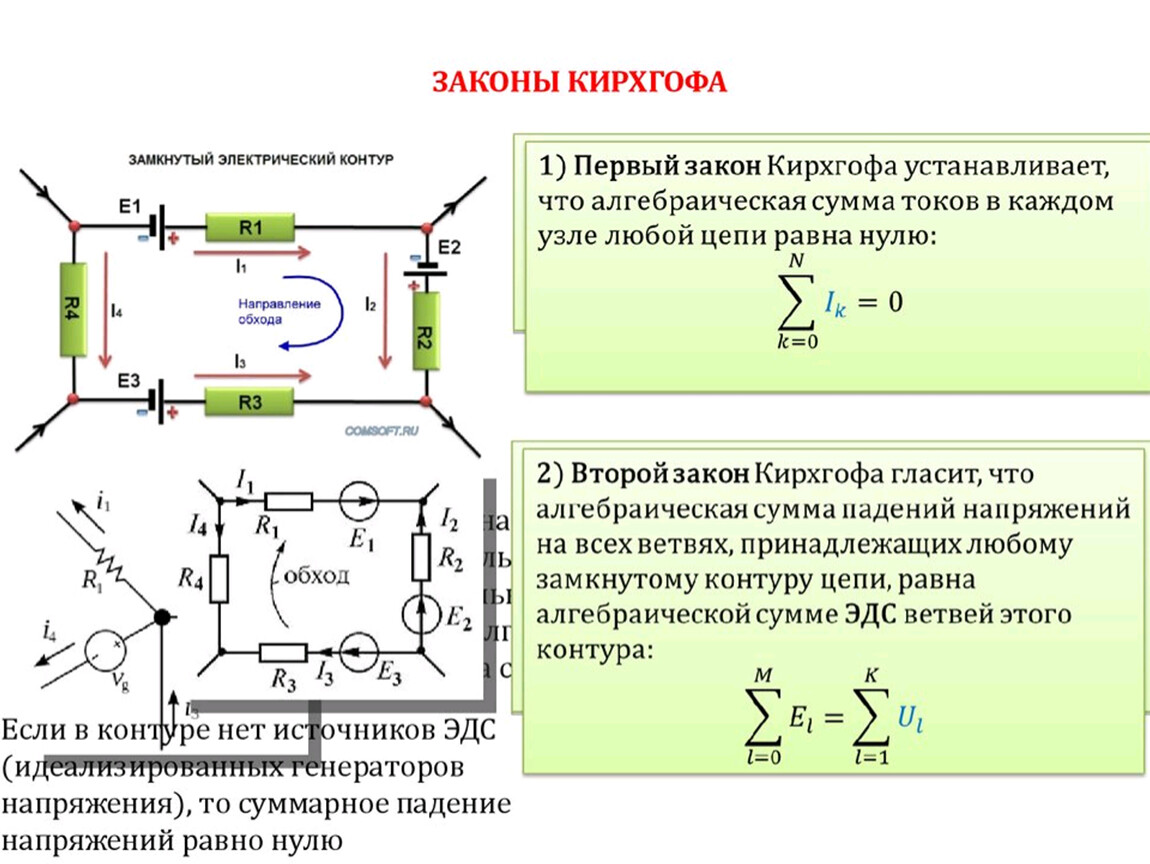 Следовательно,

   

, который является тем же решением, что и раньше.

ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 10.4

---

ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 10.5

---

Стержень длиной движется со скоростью перпендикулярно магнитному полю. Чему равна разность потенциалов между концами стержня?

Цитаты Кандела

Контент под лицензией CC, конкретное указание авторства

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

В замкнутой цепи ЭДС всегда А Меньше, чем ЧР класс 12 физика JEE_Main

Подсказка: Электродвижущая сила (ЭДС) — это сила, которая приводит в движение электрон в цепи, однако разность потенциалов в цепи возникает из-за батарея, и поэтому внутри батареи есть какая-то работа.

Полное пошаговое решение:
Что такое ЭДС?
В электромагнетизме и электронике электродвижущая сила (ЭДС) — это электрическое воздействие, создаваемое неэлектрическим источником.Устройства обеспечивают ЭДС путем преобразования других форм энергии в электрическую энергию, таких как батареи или генераторы. Иногда для описания электродвижущей силы используется аналогия с давлением воды.

В электромагнитной индукции ЭДС можно определить вокруг замкнутого контура проводника как электромагнитную работу, которая будет совершена электрическим зарядом (в данном случае электроном), если он пройдет один раз по контуру. Для изменяющегося во времени магнитного потока, соединяющего петлю, скалярное поле электрического потенциала не определяется из-за циркулирующего электрического векторного поля, но, тем не менее, действует ЭДС, которую можно измерить как виртуальный электрический потенциал вокруг петли.

Источник ЭДС можно рассматривать как своего рода зарядовый насос, который действует для перемещения положительных зарядов из точки с низким потенциалом через его внутреннюю часть в точку с высоким потенциалом.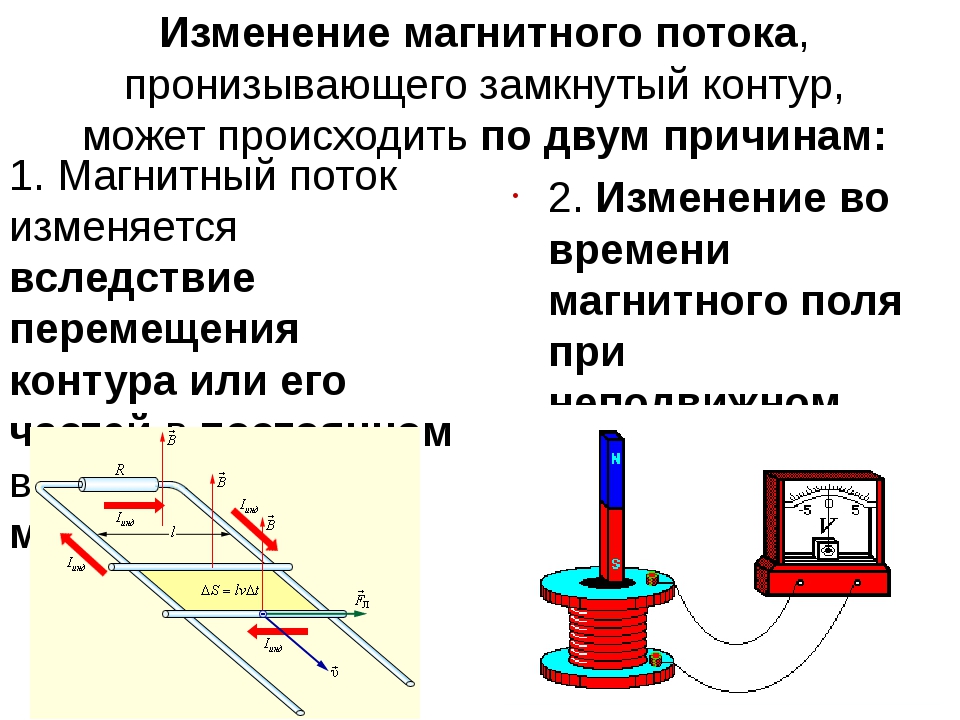 Химическим, механическим или другим способом источник ЭДС совершает работу $dW$ над этим зарядом, чтобы переместить его к высокопотенциальному выводу.

ЭДС $\varepsilon$ источника определяется как работа $dW$, совершаемая за один заряд $dq$.
Следовательно, $\varepsilon$ = $\dfrac{{dW}}{{dq}}$.

Какова разница «потенциалов» в замкнутом контуре?
Напряжение, разность электрических потенциалов, электрическое давление или электрическое напряжение — это разность электрических потенциалов между двумя точками, которая определяется как работа, необходимая на единицу заряда для перемещения пробного заряда между двумя точками.Разность электрических потенциалов между точками может быть вызвана электрическим зарядом, электрическим током через магнитное поле, изменяющимися во времени магнитными полями или комбинацией этих трех факторов. Вольтметр можно использовать для измерения напряжения (разности потенциалов) между двумя точками в системе; часто в качестве одной из точек используется общий опорный потенциал, такой как земля системы. Напряжение может представлять собой либо источник энергии (электродвижущая сила), либо потерянную, использованную или накопленную энергию (падение потенциала).у {Эдл} $.
ЭДС всегда больше напряжения. Когда ячейка находится в замкнутой цепи, т. е. когда от нее отводится ток, разность потенциалов между ее электродами называется терминальным напряжением. Она всегда меньше э.д.с. потому что, когда заряд течет в цепи, часть энергии тратится на поток заряда через электролит элемента.

Следовательно, вариант (Б) правильный.

Примечание:
1. Напряжение возникает только в электрическом поле.
2. ЭДС возникает в гравитационном поле, магнитном поле и электрическом поле.

Уравнение закона Фарадея с простыми примерами решения

Опыты показали, что при изменении магнитного потока через поверхность, ограниченную проводом, в проводе возникает ЭДС (напряжение), равная скорости изменения магнитного потока.

С помощью простой настройки мы можем продемонстрировать формулу закона Фарадея: 

1) Возьмите магнит и поднесите его к неподвижному проводящему кольцу, соединенному с амперметром. Амперметр показывает отклонение.

2) Теперь отодвиньте магнит от кольца. Опять же, амперметр показывает отклонение, но в обратном направлении.

3) В третьем случае и магнит, и кольцо неподвижны. Амперметр не показывает отклонения.

4) Теперь предположим, что магнит зафиксирован, а петля движется к магниту или от него. Результат: амперметр показывает ток!

Это простое наблюдение показывает, что ток индуцируется в проволочной петле, когда магнит или петля движутся друг к другу или удаляются друг от друга.

Другими словами, ток индуцируется (вырабатывается) в замкнутом проводящем пути, когда существует относительное движение между магнитом и замкнутым путем. Этот ток создается ЭДС индукции.

Все приведенные выше слова можно обобщить следующим образом:

Если магнитный поток через петлю изменяется со временем, то вокруг петли индуцируется ЭДС (напряжение). Средняя ЭДС индукции равна \[\mathcal{E}=-\frac{\Delta \Phi_m}{\Delta t}\] Это закон индукции Фарадея.

Знак минус в уравнении закона Фарадея связан с направлением ЭДС индукции.

Основные замечания об уравнении закона Фарадея:

(1) ЭДС индуцируется в замкнутом контуре или любой другой замкнутой проводящей цепи до тех пор, пока существует изменяющийся магнитный поток.

(2) магнитный поток в приведенном выше уравнении представляет собой полный поток через замкнутый контур. Если катушка имеет $N$ плотно намотанных витков, то $\Phi_m=N\phi_m$, где $\phi_m$ — поток через каждый виток катушки.2}$ расположен перпендикулярно однородному магнитному полю. Без изменения направления магнитного поля его величина уменьшается на $0,08\,{\rm T}$ в интервале времени $0,02\,{\rm с}$. Найдите среднюю ЭДС индукции в контуре?

Решение : согласно закону индукции Фарадея, изменяющийся магнитный поток через замкнутую поверхность, ограниченную проводом, создает ЭДС величиной $\mathcal{E}=|\frac{\Delta \Phi_m}{ \Дельта t}|$.

Напомним, что поток через поверхность площадью $A$ определяется как $\Phi_m=\vec{B}\cdot\hat{n}A$, где $\hat{n}$ — единичный вектор (a вектор, величина которого равна единице) нормали (перпендикулярны) к этой поверхности. 2}$ помещен в однородное магнитное поле напряженностью $B=0,2\,{\rm T}$ так, что плоскость петли перпендикулярна полю. После $2\,{\rm s}$ магнитное поле меняет направление на противоположное. Найти величину средней ЭДС, индуцируемой в контуре за это время.  

Решение : Согласно закону Фарадея, изменяющийся магнитный поток создает ЭДС в замкнутом пути или цепи.

С другой стороны, магнитный поток также является произведением магнитного поля , площади и косинуса угла между $\vec{B}$ и единичным вектором, перпендикулярным плоскости.\circ$ с однородным магнитным полем. Величина магнитного поля изменяется со временем как $8\,{\rm \frac{T}{s}}$, в то время как его направление остается фиксированным. Какова величина ЭДС индукции в катушке?

Решение : Величина ЭДС (напряжения) индукции определяется уравнением закона Фарадея как \[\mathcal{E}=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\] Здесь из трех факторов, входящих в формулу магнитного потока ($\Phi_m=BA\cos\theta$), со временем меняется только величина магнитного поля $B$, поэтому, подставив ее в приведенную выше формулу, мы получим \begin{align *} \mathcal{E}&=\left|\frac{\Delta \Phi_m}{\Delta t}\right|\\ \\&=\left|\frac{\Delta (BA\cos\theta)} {\Delta t}\right|\\\\&=\left|\left(\frac{\Delta B}{\Delta t}\right)A\cos\theta\right|\\\\&=( 8)(0. \circ\\ \\&=0,64\quad {\rm V}\end{align*} ЭДС индукции в одном витке катушки с $N$-витком.

Суммарная ЭДС равна числу витков, умноженному на $N$, на ЭДС, индуцированную в каждом витке, как $\mathcal{E}_t=N\mathcal{E}$, таким образом, мы получаем \[\mathcal{E}_t= 400 \times 0.64=256\quad {\rm V}\]

---

Пример (4): Круглая катушка со 100 витками радиуса $r=10\,{\rm см}$ и сопротивлением $10\,{\rm \Omega}$ помещена в однородное магнитное поле так, что перпендикулярно плоскости катушки.{-5}\quad {\rm Wb}\end{align*} Изменение полного потока через катушку равно \[\Delta \Phi_m=N\phi_1=0,02\]Величина ЭДС индукции определяется с помощью закона Фарадея. формула выглядит следующим образом: =-0,1\quad {\rm V}\end{align*} Знак минус показывает направление ЭДС, индуцируемой в соленоиде.

Для получения дополнительных решенных примеров перейдите сюда .

Дата публикации: 19.02.2021

Автор : Др. Али Немати
 

Мягкий зеленый дизайн

     История и качественный отчет:

Выработка электроэнергии в том виде, в каком мы ее знаем сегодня, основана на электромагнитная индукция. Джозеф Генри был первым физиком, открывшим электромагнитное индукция в 1831 году     однако открытие часто приписывают Майклу Фарадею, поскольку он был первым опубликовать статью и провел свой первый эксперимент по электромагнитной индукции на 29 августа 1831 года.

   Силовые линии и уравнения Максвелла:

Фарадей объяснил электромагнитную индукцию, используя концепцию, называемую силовые линии, которые были отвергнуты ведущими учеными из-за отсутствия математических доказательств до 1861 г. , когда Джеймс Клерк Максвелл опубликовал набор из 20 дифференциальных уравнения.
    Генрих Ленц в 1834 успешно описал «поток через цепь (замкнутый контур)», а также направление индуцированного Электродвижущая сила и ток, вызванные Электромагнитная индукция.

Самый широко используемая версия, как указано ниже:

«Индуцированный электродвижущая сила в любой замкнутой цепи равна отрицательная скорость изменения магнитного потока во времени через цепь».

ля мажор недостатком этой версии закона Фарадея является то, что она верна только для бесконечно длинной петли замкнутого провода.То Уравнение Максвелла-Фарадея более применимо на практике. Вариант закона Фарадея.

Количественный Анализ закона Фарадея:

Фарадея Закон индукции объясняет ток, индуцируемый в петле провод из-за изменения магнитного потока через поверхность на используя математическую сферическую поверхность, границей которой является проволочная петля (гарантия спермицида по Гауссу). При условии, что изменение магнитного потока вызвано движением поверхность, Магнитный поток через поверхность определяется выражением поверхностный интеграл.

d A : Бесконечно малый участок поверхности. подвижной поверхности

Б : Магнитное поле как функция расстояния и времени.

При изменении потока В контуре создается электродвижущая сила.

dl: бесконечно малая длина дуги вдоль провода
E: электрическое поле

B: магнитный поле

ЭДС также представляется как скорость изменения магнитного потока:

Для туго намотанной проволоки составлен из одинаковых витков

N: количество витков

Хотя уравнение Фарадея легко вычислим, практически бесполезен из-за ограничение в том, что оно применимо только для бесконечно замкнутый цикл. Уравнение Максвелла-Фарадея представляет собой обобщение закона Фарадея, которое преодолевает это ограничение.

Уравнение Максвелла-Фарадея:

Уравнение Максвелла-Фарадея утверждает, что «изменяющееся во времени магнитное поле всегда сопровождается пространственно изменяющимся, неконсервативным электрическое поле и наоборот».

математически,

Где:

E это электрическое поле

B — магнитное поле.

дℓ является бесконечно малый векторный элемент контура

d А является бесконечно малый векторный элемент поверхности

Используется правило правой руки чтобы получить направление и, следовательно, знак индуцированного текущий

Снаряд

Основные законы электродинамики

Законы Фарадея говорят нам что если магнитный поток, связанный с замкнутым контуром, изменяется, то ЭДС обязательно индуцированный. Кстати, вы знаете, что ЭДС не является физическим количество, представляющее силу. Это работа, совершаемая при перемещении единичного заряда. и его единицей измерения является вольт, а не ньютон!. Концепция состоит в том, что изменение магнитного потока индуцирует электрическое поле.

---

---

но Сэр, как мы можем иметь электрическое поле без зарядов.

 

Это хороший вопрос ! .электрическое поле из-за стационарных зарядов имеет некоторые дополнительные функции. Как линейный интеграл по замкнутому пути всегда ноль. Пока не будем обращать внимания на разницу.

OK, изменение потока индуцирует ток через петлю, но в каком направлении. Я имею в виду, как можно мы прогнозируем направление.

 

 

Для что у нас есть умный закон, который действительно очень удобен для электромагнитных Индукция. Этот закон основан на сохранении энергии и указывает направление тока в петле. Сформулируем прямо закон.

«ЭДС наведенная в электрической цепи всегда действует в таком направлении, что ток, который он пропускает по цепи, противодействует изменение магнитного потока, вызывающее ЭДС. ”

Этот результат известен как закон Ленца, после девятнадцатого века русский ученый Генрих Ленц, впервые сформулировавший ее.

 

Есть что причина, по которой мы поставили знак минус в формуле ЭДС = -(dFlux/dTime).d(Flux указывает на обычное бесконечно малое изменение потока).

 

точно. Итак, теперь пришло время закончить. Просмотрите свои заметки дома.

 

 

.