Формула физика момент силы: Момент силы — урок. Физика, 7 класс.

Нахождение момента силы. Момент силы, формулы

Почти две тысячи лет просуществовало правило рычага, открытое Архимедом еще в третьем веке до нашей эры, пока в семнадцатом веке с легкой руки французского ученого Вариньона не получило более общую форму.

Правило момента сил

Было введено понятие момента сил. Момент силы – это физическая величина, равная произведению силы на ее плечо:

где M – момент силы,
F – сила,
l – плечо силы.

Из правила равновесия рычага напрямую вытекает правило моментов сил:

F1 / F2 = l2 / l1 или, по свойству пропорции F1 * l1= F2 * l2, то есть M1 = M2

В словесном выражении правило моментов сил звучит следующим образом: рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки. Правило моментов сил справедливо для любого тела, закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы. Потом из точки, в которой находится ось вращения, проводят перпендикуляр до линии действия силы. Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо, получаем значение момента силы относительно оси вращения. То есть, мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.

Применение правила моментов сил в различных ситуациях

Отсюда вытекает применение правила моментов сил в различных ситуациях. Например, если мы открываем дверь, то толкать ее мы будем в районе ручки, то есть, подальше от петель. Можно проделать элементарный опыт и убедиться, что толкать дверь тем легче, чем дальше мы прилагаем силу от оси вращения. Практический эксперимент в данном случае прямо подтверждается формулой. Так как, дабы моменты сил при разных плечах были равны, надо, чтобы большему плечу соответствовала меньшая сила и наоборот, меньшему плечу соответствовала большая. Чем ближе к оси вращения мы прилагаем силу, тем она должна быть больше.

Чем дальше от оси мы воздействуем рычагом, вращая тело, тем меньшую силу нам необходимо будет приложить. Числовые значения легко находятся из формулы для правила моментов.

Именно исходя из правила моментов сил мы берем лом или длинную палку, если нам надо приподнять что-то тяжелое, и, подсунув под груз один конец, тянем лом возле другого конца. По этой же причине шурупы мы вворачиваем отверткой с длинной ручкой, а гайки закручиваем длинным гаечным ключом.

Момент силы относительно оси или просто момент силы называется проекция силы на прямую, которая перпендикулярна радиусу и проведена в точке приложения силы умноженная на расстояние от этой точки до оси. Либо произведение силы на плечо ее приложения. Плечо в данном случае это расстояние от оси до точки приложения силы. Момент силы характеризует вращательное действие силы на тело. Ось в данном случае это место крепления тела, относительно которого оно может совершать вращение. Если тело не закреплено, то осью вращения можно считать центр масс.

Формула 1 – Момент силы.

F – Сила действующая на тело.

r – Плечо силы.

Рисунок 1 – Момент силы.

Как видно из рисунка, плечо силы это расстояние от оси до точки приложения силы. Но это в случае если угол между ними равен 90 градусов. Если это не так, то необходимо вдоль действия силы провести линию и из оси опустить на нее перпендикуляр. Длинна этого перпендикуляра и будет равна плечу силы. А перемещение точки приложения силы вдоль направления силы не меняет ее момента.

Принято считать положительным такой момент силы, который вызывает поворот тела по часовой стрелки относительно точки наблюдения. А отрицательным соответственно вызывающий вращение против нее. Измеряется момент силы в Ньютонах на метр. Один Ньютонометр это сила в 1 Ньютон действующая на плечо в 1 метр.

Если сила, действующая на тело, проходит вдоль лини идущей через ось вращения тела, или центр масс, если тело не имеет оси вращения. То момент силы в этом случае будет равен нулю. Так как эта сила не будет вызывать вращения тела, а попросту будет перемещать его поступательно вдоль лини приложения.

Рисунок 2 – Момент силы равен нулю.

В случае если на тело действует несколько сил, то момент силы будет определять их равнодействующая. К примеру, на тело могут действовать две силы равные по модулю и направленные противоположно. При этом суммарный момент силы будет равен нулю. Так как эти силы будут компенсировать друг друга. Если по простому, то представьте себе детскую карусель. Если один мальчик ее толкает по часовой стрелке, а другой с той же силой против, то карусель останется неподвижной.

Определение 1

Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.

Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.

Момент силы выступает характеристикой вращательного воздействия силы на твердое тело.

Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.

В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).

Понятие момента силы

Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.

Замечание 1

В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.

К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:

$\vec {M}=\vec{r}\vec{F}$, где:

• $\vec {F}$ представляет силу, воздействующая на частицу,
• $\vec {r}$ является радиусом вектора частицы.

В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:

$E = M\theta $, где:

• $E$ представляет энергию;
• $M$ считается вращающимся моментом;
• $\theta $ будет углом в радианах.

Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.

Формулы расчета момента силы

Интересным в физике является вычисление момента силы в поле, производимого по формуле:

$\vec{M} = \vec{M_1}\vec{F}$, где:

• $\vec{M_1}$ считается моментом рычага;
• $\vec{F}$ представляет величину действующей силы.

Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину. При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:

$\vec{T}=\vec{r}\vec{F}$

При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.

$P = \vec {M}\omega $

В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы- в ньютон-метрах. При этом угловая скорость определяется в радианах в секунду.

Момент нескольких сил

Замечание 2

При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия.

Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).

В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.

Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.

$M={FL_1+FL-2} = F{L_1+L_2}=FL$

В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.

Враща́тельное движе́ние – вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Кинетические характеристики:

Вращение твердого тела, как целого характеризуется углом , измеряющегося в угловых градусах или радианах, угловой скоростью (измеряется в рад/с)и угловым ускорением(единица измерения – рад/с²).

При равномерном вращении (T оборотов в секунду):

Частота вращения – число оборотов тела в единицу времени.-

Период вращения – время одного полного оборота.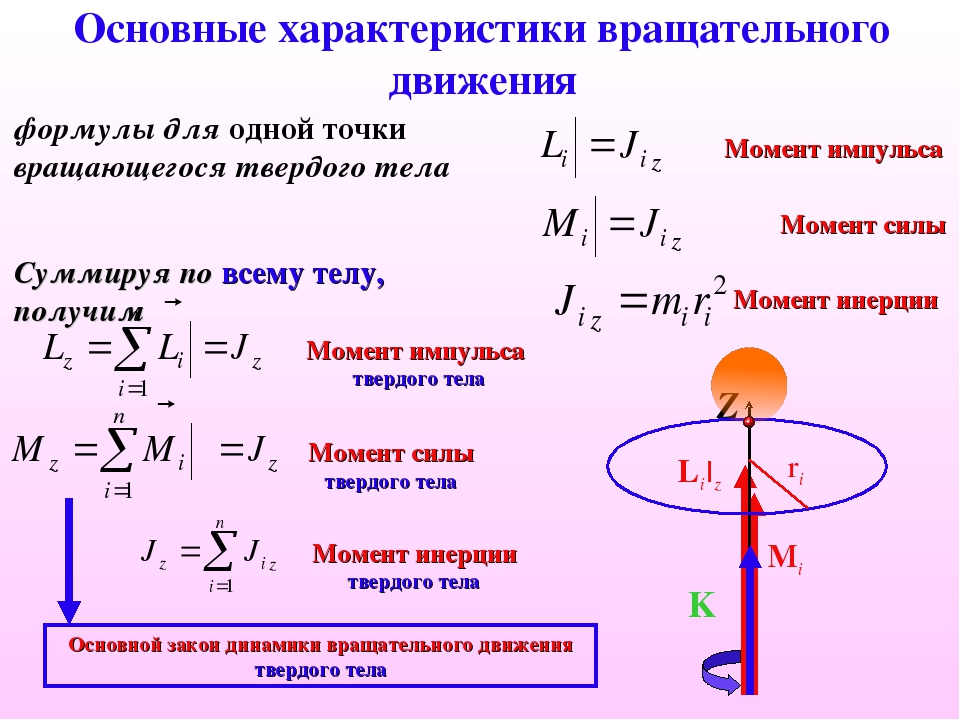 Период вращения T и его частота связаны соотношением.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

Угловая скорость вращения тела

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) – векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы – по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Момент силы измеряется в ньютон-метрах. 1 Н·м – момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.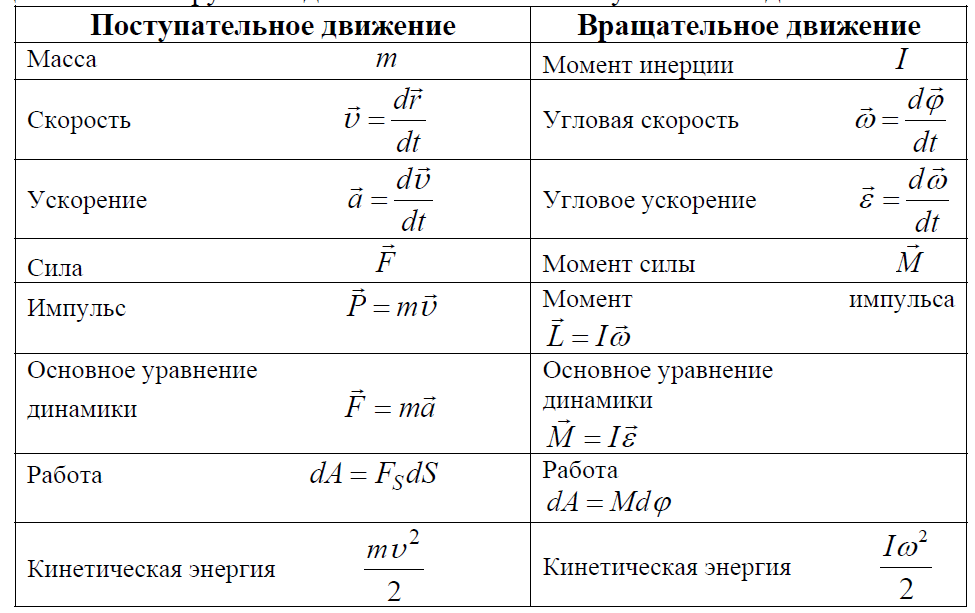 Момент импульса замкнутой системы сохраняется

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) – один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

16.Уравнение динамики вращательного движения. Момент инерции.

Основное уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

М = E*J или E = M/J

Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.

Момент инерции – скалярная (в общем случае – тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².Обозначение: I или J.

Различают несколько моментов инерции – в зависимости от многообразия, от которого отсчитывается расстояние точек.

Свойства момента инерции:

1.Момент инерции системы равен сумме момента инерции её частей.

2.Момент инерции тела является величиной, иманентно присущей этому телу.

Момент инерции твердого тела – это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.

Формула момента инерции:

Теорема Штейнера:

Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R – расстояние между осями.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

Центральный момент инерции (или момент инерции относительно точки O) – это величина

.

Определение

Векторное произведение радиус – вектора (), который проведен из точки О (рис.1) в точку к которой приложена сила на сам вектор называют моментом силы ()по отношению к точке O:

На рис.1 точка О и вектор силы ()и радиус – вектор находятся в плоскости рисунка. В таком случае вектор момента силы () перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.

Величина вектора равна:

где – угол между направлениями радиус – вектора и вектора силы, – плечо силы относительно точки О.

Момент силы относительно оси

Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.

Главный момент сил

Главным моментом совокупности сил относительно точки О называется вектор (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:

При этом точку О называют центром приведения системы сил.

Если имеются два главных моменты ( и )для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:

где – радиус-вектор, который проведен из точки О к точке О’, – главный вектор системы сил.

В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).

Основной закон динамики вращательного движения

где – момент импульса тела находящегося во вращении.

Для твердого тела этот закон можно представить как:

где I – момент инерции тела, – угловое ускорение.

Единицы измерения момента силы

Основной единицей измерения момента силы в системе СИ является: [M]=Н м

В СГС: [M]=дин см

Примеры решения задач

Пример

Задание. На рис.1 показано тело, которое имеет ось вращения OO”. Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.

Решение. За основу решения задачи примем формулу, определяющую момент силы:

В векторном произведении (видно из рисунка) . Угол между вектором силы и радиус – вектором также будет отличен от нуля (или ), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.

Ответ.

Пример

Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?

Момент силы, формулы 📙 – Физика

1. Основные понятия
2. Формулы для нахождения момента силы
3. Момент нескольких сил

Момент силы – это характеристика вращательного воздействия силы на объект. Момент силы рассчитывают, как векторное произведение вектора силы и радиус-вектора, опущенного от центра вращения до точки, к которой приложена сила.

Момент силы есть вращательным или крутящим моментом, представляющим собой векторную величину.

При этом понятия «крутящий» и «вращающий» нельзя отождествлять, потому что технически вращающим моментом принято считать внешнее усилие, которое прикладывается к телу, а крутящий момент обозначает внутреннее усилие, появляющееся в теле при нагрузке. Данное понятие применимо при расчете сопротивления материалов.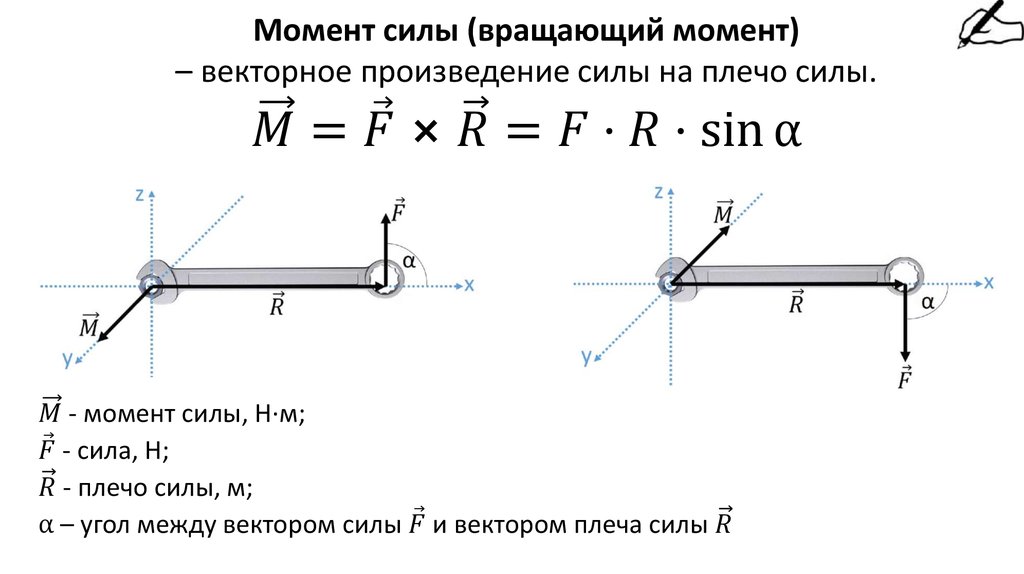

Момент силы – это вращающая сила. По международной системе СИ единицей измерения момента вращающей силы есть ньютон-метр. Архимед при работе с рычагами отмечал, что моментом силы также считается момент пары сил.

При перпендикулярном прикладывании силы к рычагу, момент данной силы прямо пропорционален ее величине и расстоянию до оси вращения этого рычага.

Таким образом, сила в \(3 Н\), что действует на рычаг в точке, отдаленной на 2 м от оси вращения, формирует момент, что равняется силе в \(1 Н\), что действует в точке, отдаленной на 6 м. Наиболее точным определением момента силы есть следующее выражение:
\(\vec {M}=\vec{r}\vec{F}\),
где \(\vec {F}\)– сила, что действует на объект;
       \(\vec {r}\)– радиус-вектор объекта.

С точки зрения физики момент силы есть псевдо векторной величиной, в отличие от энергии, которая есть величиной скалярной. Но совпадение их размерности не случайно. Момент силы величиной \(1 Н∙м\), что приложена через целый оборот при совершении механической работы, передает энергию в \(2π\) Джоуля:
\(E=Mθ\),
где \(E\) – энергия;
      \(θ\) – угол;
     \(M\) – вращающий момент.      

На сегодняшний день момент силы измеряют при помощи оптических, индуктивных и тензометрических приборов нагрузки.

Момент силы рассчитывают таким образом:
\(\vec{M} = \vec{M_1}\vec{F}\),
где \(\vec{M_1}\) – момент рычага;
       \(\vec{F}\)– сила действия.

Данная формула позволяет определить только значение момента силы, но не его направление. Когда сила перпендикулярна вектору \(r ⃗,\) то момент рычага равняется расстоянию от центра вращения до точки действия силы, а момент силы имеет наибольшее значение:
\(\vec{T}=\vec{r}\vec{F}\)

Если сила воздействует на определённом расстоянии, это значит, что она делает механическую работу. Момент силы тоже делает работу, выполняя действие через угловое расстояние.
\(P = \vec {M}\omega\)
где \(P\) – мощность, Ватт;
     \(\vec{M}\)– момент силы, ньютон-метр;
      \(ω\) – угловая скорость, радиан/секунда.

Если на тело воздействуют две равных силы, что направлены противоположно и не лежат на одной прямой, тело пребывает в неравновесном состоянии. Это происходит по причине того, что результирующий момент данных сил по отношению к любой оси не равен нулю, поскольку они представлены моментами с одинаковым направлением. То есть, это пара сил.

Если тело закрепить на оси, то под воздействием пары сил оно будет вращаться вокруг этой оси. Если же пару сил приложить к свободному телу, то его вращение будет вокруг оси, проходящей через его центр тяжести.

Момент пары сил одинаков по отношению к любой оси, перпендикулярной плоскости пары. Суммарный момент M пары равняется произведению одной силы \(F\) на отдаленность этих сил \(L\), то есть плечо пары, в независимости от длины отрезков, на которые плечо делит ось.

\(M=FL_1+FL_2=F(L_1+L_2 )=FL\)

Если равнодействующая момента нескольких сил равняется нулю, то он будет одинаковым по отношению ко всем параллельным между собой осям. Поэтому действие на объект данных сил можно заменить воздействием одной пары сил с таким же моментом.
 

 

Формула момента

– GeeksforGeeks

Момент – это в основном сила, которая определяется как движение, направленное на вращение тела вокруг определенного положения. Давайте разберемся в этом моменте на примерах. Если кто-то хочет закрыть окно, он просто отталкивает ручку пальцем, и окно плавно закрывается. Теперь попробуйте снова закрыть окно, но на этот раз поднесите палец слишком близко к петле и посмотрите, не слишком ли тяжело. Силы используются для того, чтобы заставить любое тело или объект вращаться. Следовательно, поворотное действие силы известно как момент силы. Есть еще много примеров моментов в нашей повседневной жизни, и это

• Осмотр достопримечательностей в парке
• Открытие консервной банки
• Использование рычага для подъема большого груза
• Молоток используется для удаления гвоздей и т. д.

Момент силы   

Момент силы – это движение который заставляет тело или объект вращаться и также известен как крутящий момент. Он также определяется как произведение силы и перпендикулярного расстояния. Момент имеет как величину, так и направление.

Формула момента

Рассчитывается по формуле

M = F × d

Где M — момент силы,

F — приложенная сила

d — расстояние от фиксированного положения.

Эта формула применима как для уравновешенных, так и для неуравновешенных сил. Единицей измерения момента в системе СИ является ньютон-метр (Нм). Его размеры составляют [ML ² T ^-2 ], а его направление задается правилом большого пальца правой руки.

Принцип момента

Он утверждает, что если система находится в равновесии, то сумма ее моментов по часовой стрелке будет равна сумме ее моментов против часовой стрелки.

Момент по часовой стрелке = момент против часовой стрелки.

F ₁ × d ₁ = F ₂ × d _2.

• Момент по часовой стрелке- Сила заставляет объект или тело вращаться по часовой стрелке. Это воспринимается как положительное.
• Момент против часовой стрелки – Сила заставляет объект или тело поворачиваться против часовой стрелки. Он воспринимается как отрицательный.

Термин Равновесие определяется как «это происходит, когда все силы, действующие на тело, уравновешены».

Применение принципа моментов

• Мы можем найти массу объекта.
• В простых машинах.
• Помогает объяснить, как расположены и организованы физические величины.

Пара 

Пара определяется как пара двух сил, которые равны по величине, но их направления противоположны друг другу, а движения линий не совпадают.

Формула пары:

τ = F × d.

СИ единица пары = ньютон-метр (Нм) и размеры [ML ² T ² ].

Здесь силы равны и противоположны, поэтому мы получаем, что сила равна нулю, а линейное ускорение отсутствует.

Несколько применений пары

• Открытие и закрытие крышки бутылки.
• С помощью ключа откройте шкафчик.
• Вращение отвертки.
• Рулевое колесо установлено водителем автобуса.

Импульс 

Называется свойством движения объекта. Импульс определяется как произведение массы и скорости объекта. Обозначается символом «р».

Формула импульса,

p = m × v

Где p = импульс тела или объекта

m = масса объекта

v = скорость объекта.

Единица количества движения в системе СИ – кг м/с.

Вот несколько задач на данный момент.

Примеры задач

Вопрос 1. Мальчик сидит на одной стороне качелей в 3 м от точки. Найдите момент, если вес мальчика 20 Н.

Решение: 

Учитывая, что вес мальчика создавал момент, направленный против часовой стрелки.

Момент = Сила × расстояние0003

М = 20 × 3

М = 60 Нм.

Вопрос 2: Момент силы 20 Н относительно неподвижной точки равен 2 Нм. Вычислите расстояние от точки до линии действия силы.

Решение :

Дано, Сила = 20 Н и Момент = 2 Нм.

Используя формулу момента M = F × d

2 = 20 × d 

d = 2/20

d = 0,1 м.

Вопрос 3: Найдите силу, приложенную к двери, вызывающую момент 10 Нм, если расстояние от оси петли до точки на двери, где была приложена сила, составляет 2 м.

 Решение:

Дано, момент (М) = 10 Нм 

Расстояние (d) = 2 м.

Как известно, M = F × d

10 = F × 2

F = 10/2

F = 5N.

Вопрос 4: Балочные весы имеют длину плеч 100см и 80см. Какой вес, помещенный на сковороду с более длинным плечом, уравновесит предмет весом 200 г, находящийся на других кастрюлях?

Решение:

По принципу моментов

Момент по часовой стрелке = Момент против часовой стрелки

Вт × 100 = 200 × 80

Вт = (200 × 80)/100

Вт = 160 г.

Вопрос 5: Два человека сидят на качелях противоположными сторонами, один человек весит 100 Н и находится на расстоянии 2 м от оси вращения, а вес другого человека составляет 200 Н. найти, где человек сидит, чтобы сбалансировать качели.

Решение:

Согласно принципу моментов,

Момент по часовой стрелке = Момент против часовой стрелки

100 × 2 = 200 × d

d = (100 × 2)/200

d = 1 м.

Вопрос 6: Является ли момент скалярной или векторной величиной? Объясните

Решение:

По формуле момента это произведение силы и расстояния от фиксированной точки или M = F × d.

Как мы знаем, сила является векторной величиной. Итак, Момент также является векторной величиной.

Вопрос 7: Найдите импульс тела массой 4 кг, движущегося со скоростью 2 м/с.

Решение: 

Учитывая, что масса (m) = 4 кг, а скорость (v) = 2 м/с. Согласно формуле количества движения,

p = m × v

p = 4 × 2

p = 8 кг м/с.

Определение, Первая и Вторая, Сила, Уравнение

Почему дверные ручки всегда находятся на противоположной стороне дверных петель? Если вы попытаетесь толкнуть дверь рядом с петлей, а затем с противоположного конца, вы заметите большую разницу. Находясь рядом с петлей, трудно закрыть дверь; на дверной ручке, это довольно легко. Причина этого в том, что чем дальше от шарнира, тем сильнее эффект поворота.

Что вызывает эффект поворота?

Если объект неподвижен или находится в статическом равновесии, все силы, действующие на этот объект, уравновешивают друг друга. Но если они уравновешивают друг друга и общей силы нет, означает ли это, что объект находится в статическом равновесии?

Взгляните на следующую схему:

Рис. 1 – Две силы, действующие на объект в разных точках

В первом примере обе силы имеют одинаковую величину и действуют в одной и той же точке, но в противоположном направлении, что заставляет бар оставаться неподвижным.

Во втором примере, поскольку силы не действуют в одной и той же точке, они создают эффект вращения, известный как крутящий момент . В этом случае стержень начнет вращаться против часовой стрелки и, следовательно, не будет находиться в статическом равновесии.

Моменты

Величина поворотного эффекта, создаваемого силой, называется моментом силы . Это происходит, когда силы заставляют объект вращаться вокруг некоторой оси .

Момент силы рассчитывается следующим образом:

Моменты измеряются в ньютон-метрах, записывается Нм. Сила в ньютонах, расстояние в метрах.

То, что мы исследовали до сих пор, объясняет, почему дверные ручки расположены по другую сторону дверных петель, которые действуют как стержень. Максимальное расстояние между силой, которую мы прикладываем к дверной ручке, и шарниром, приводит к большему моменту. Это облегчает открытие или закрытие двери. Тот же принцип применим к гаечным ключам с длинными рукоятками для увеличения величины момента, что облегчает затяжку болтов.

Груз массой 100 кг подвешен на расстоянии 30 м от оси, на которую опирается стальной стержень. Предполагая, что вес стержня пренебрежимо мал, каков крутящий момент относительно оси вращения?

Рис.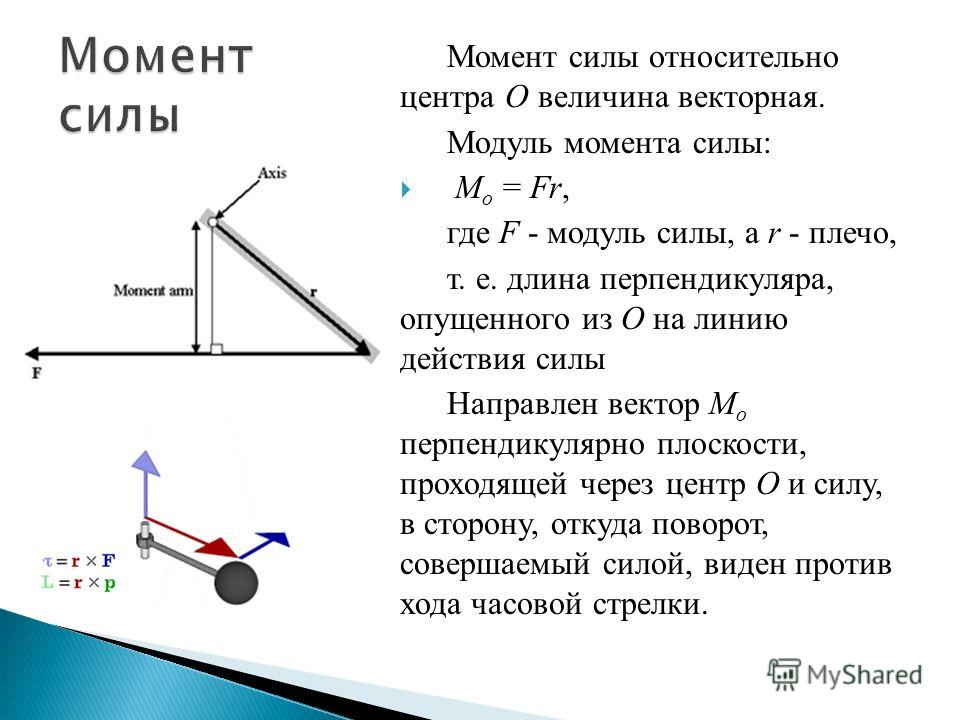 2. Масса 100 кг создает момент

Во-первых, нам нужно определить силу, создаваемую массой. Это его вес или его масса, умноженная на константу гравитационного ускорения. Это дает нам:

Теперь у нас есть сила, приложенная к стержню, в то время как перпендикулярное расстояние от силы до оси вращения было указано выше. Все, что нам тогда нужно сделать, это использовать момент силового уравнения следующим образом:

Пары

Уникальный случай моментов — это когда две параллельные силы, равные по величине, но противоположные по направлению, а также разделенные расстоянием d, заставляют объект вращаться. Это известно как пара .

Пара не имеет равнодействующей силы; он производит только поворотный эффект.

Например, ваши руки производят пару на руле автомобиля, чтобы повернуть руль.

Рис. 3 – Поворот руля на примере пары

Момент пары рассчитывается по следующему уравнению:

Давайте рассчитаем пару, создаваемую силами, действующими на этот стальной стержень длиной 1 м.

Рис. 4. Две силы, действующие на стальной стержень и создающие пару

Все, что нам нужно сделать, это применить уравнение, используя приведенные выше значения: против часовой стрелки.

Представьте себе двух детей, играющих на качелях, причем мальчик сидит слева, а девочка справа.

Вес мальчика слева создает момент, направленный против часовой стрелки, а вес девочки справа создает момент, который поворачивает качели по часовой стрелке.

Что означали бы два момента, созданные детьми, если бы качели были сбалансированы? Чтобы объект находился в равновесии — чтобы качели были сбалансированы — ни в одной точке не должно быть общего эффекта поворота. Таким образом, моменты по часовой стрелке и против часовой стрелки должны уравновешивать друг друга.

Это суммируется принцип моментов . Объект находится в статическом равновесии, когда:

Качели на следующей диаграмме сбалансированы. Рассчитайте W, вес блока слева от оси, используя принцип моментов.