Главная
Формула физика q: Как найти q нагревания в физике – Telegraph

Формула физика q: Как найти q нагревания в физике – Telegraph

формула, определение простыми словами, задачи, где применяется

Знание законов и способов использования электричества — необходимый элемент школьного образования. Вместе с экспертом разберем задачи на закон Джоуля-Ленца и узнаем, где он применяется в жизни

Закон Джоуля-Ленца. Фото: shutterstock.com

Борис Михеев Автор КП Николай Герасимов Старший преподаватель физики

Содержание

  1. Определение закона
  2. Формула
  3. Задачи с решениями
  4. Вопросы и ответы

Физики всегда искали способы практического применения электричества, чувствуя его гигантский потенциал.

Первой ступенькой на этом пути стал закон Ома, связавший в один узел основные понятия новой науки. Эксперименты показали, что электричество можно преобразовать в теплоту. Это стало научным прорывом, нужен был только математический аппарат для инженерных расчетов. И вот от он найден.

Определение закона Джоуля-Ленца простыми словами

Джеймс Джоуль и Эмилий Ленц независимо установили опытным путем, что проводник, по которому течет электрический ток, выделяет тепло. И его количество прямо пропорционально квадрату силы тока, его сопротивлению и времени протекания тока. Это, собственно говоря, и есть самое простое определение закона Джоуля-Ленца

Формула закона Джоуля-Ленца

Определить количество теплоты, выделяемой проводником при прохождении через него электричества, можно по следующей формуле:

Q=I2⋅R⋅t

Где:

Q — количество теплоты в джоулях;
I — сила тока в амперах;
R — сопротивление проводника в омах;
t — время в секундах.

Задачи на закон Джоуля-Ленца

Наиболее ярко этот закон проявляется при расчетах тепловых приборов.

Задача 1

25 минут через спираль электроплитки сопротивлением 30 Ом протекает электрический ток силой 1,3 А. Какое количество теплоты выделится за это время?

Подставляем данные в формулу:

Q=1,32*30*25*60=76 050 дж

Ответ: 76,05 килоджоулей.

это интересно

Закон Ома

Разбираем формулировку, формулу и задачи на закон Ома с решением

подробнее

Задача 2

Сколько времени нагревался проводник сопротивлением 25 Ом, если на нем выделилось 8 кДж теплоты при силе тока 2 А?

Преобразуем формулу закона Джоуля-Ленца к удобному для нас виду:

Q=I2⋅R⋅t → t=Q/(I2⋅R)

Подставляем исходные данные:

t=8000/(22*25)=80

Ответ: 80 секунд.

Популярные вопросы и ответы

Отвечает Николай Герасимов, старший преподаватель физики проекта «ИнтернетУрок».

Как открыли закон Джоуля-Ленца?

В первой половине (в 30-х – 40-х годах) XIX века русский учёный Эмилий Христианович Ленц и английский физик Джеймс Прескотт Джоуль независимо друг от друга провели опыты, которые позволили выяснить зависимость выделяющегося в проводнике тепла от его сопротивления и силы тока, протекающей через этот проводник. В научном сообществе подобные зависимости принято называть именами первооткрывателей. Так и появился закон Джоуля-Ленца.

Где применяется закон Джоуля-Ленца?

Электрический ток при протекании через проводник или любой электрический прибор совершает работу. Эта работа может быть полезной. Например, нагревание утюга, свечение электрической лампы и так далее. А может быть и вредной: нагревание подводящих проводов, которое как минимум ведет к потерям в электрических цепях или может привести к пожару. Данный закон позволяет рассчитать, какими, например, должны быть провода, а какими спирали нагревательных приборов, чтобы потери были минимальны, а энергия выделялась там, где нам нужно.

Где и как применяется закон Джоуля-Ленца в жизни?

Нельзя сказать, что каждый человек применяет в жизни этот закон, но его знание позволяет понять, почему, например, соединение проводов электрической цепи в доме должно быть очень надежным. Если контакт плохой, то в этом месте сопротивление будет большим, и место контакта станет нагреваться, что может спровоцировать пожар. Конструкторы используют этот закон для расчета спиралей электронагревательных приборов или элементов предохранителей, которые отключают электричество в случае опасности.

Формула полезной работы в физике

Вычисление полезной работы через КПД

Определение

Коэффициентом полезного действия (при сокращённом написании КПД) именуют безразмерную физическую величину, характеризующую отношение энергии, которую система потратила с пользой для нас, к полному количеству полученной энергии.

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся.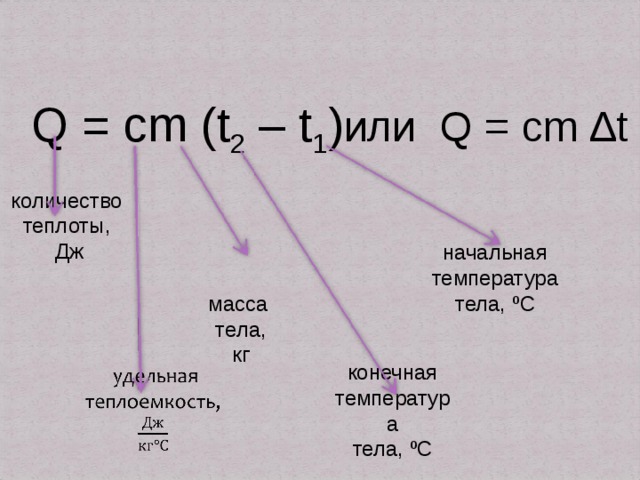 Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Формула

Общая формула КПД:

\[η = (Aполез/Aзатр) * 100%\].

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула

\[Aполез = (η*F*S)/100\]

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

\[\eta=(\text { Qнагревателя }-\text { Qхолодильника })^{*} 100 / \text { Qнагревателя }\]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы. 2)/R *t = UIt

  • A — работа электрического тока [Дж]
  • I — сила тока [А]
  • U — напряжение [В]
  • R — сопротивление [Ом]
  • t — время [c]

    • В нашем примере она примет вид

    η = Q/A *100% = Q/UIt *100%

    Переводим минуты в секунды и, подставляя численные значения, получаем

    η = 22176/220*1,4*120 *100% = 60%

    Формула полезной работы электродинамической системы будет:

    Формула

    \[Aполез = (η*U*I*t)/100%\]

    Схема – Схемы – Физика 106

    Схема — схемы

    1. Электрические цепи. Определение терминов
      1. Электрический ток I равен скорости протекания тока.
        Для постоянного тока I = q/t. Для переменного тока I = dq/dt.

      2. На рис. 1 выше электрон движется в проводнике с эквивалент постоянной скорости дрейфа v d в постоянное электрическое поле E. В действительности электрон испытывает серия ускорений в электрическом поле после столкновений с ядрами и внутренними электронами атомов, составляющих материал. Пусть n = число электронов/объем, e заряд электрона, A площадь поперечного сечения проводника, а L его длина = v
        д         т, где t — время, за которое электрон проходит длину проводника. Тогда суммарный заряд в движении равен q = neAv d t а ток I = q/t = neAv d .
      3. Пример проблемы в 106 Набор задач для цепей : 1.
    2. Сопротивления
      1. Сопротивление R проводника прямо пропорционально к его длине L, обратно пропорционально его поперечному сечению области A и зависит от сопротивления материала r.
        R = rL/А.
      2. Закон Ома. Разность потенциалов V ab через сопротивление R от a до b с током I от a до b определяется законом Ома, эмпирическим законом,
        В аб = ИК.

      3. Комбинации резисторов
        1. Резисторы в серии
          1. Ток I одинаков в каждом резисторе
          2. Разность потенциалов на всех резисторах равна сумме индивидуальных разностей потенциалов:
            В аб = В ac + В кд + В дБ

          3. R eq = В аб /I = В ac /I + V cd /I + V db /I = R 1 + R 2 + R 3
            (рис. 2а ниже)

        2. Резисторы параллельно
          1. Разность потенциалов В ab Поперек все резисторы одинаковые.
          2. Суммарный ток I равен сумме токов в каждом из резисторов:   I = I 1 + Я 2 + Я 3
          3. I/V ab = I 1 /V ab + I 2 /V ab + I 3 /V ab
          4. 1/R экв. = 1/R 1 + 1/R 2
            + 1/R 3  (рис. 2b ниже)

      4. Примеры проблем в 106 Набор задач для цепей : 2, 3, 7.
    3. Мощность
      1. Мощность = P = (U a – U b )/t = q(V a – V b )/t = (q/t)(V a – V b ) = IV ab
        Приведенное выше утверждение всегда верно.
      2. Если элемент цепи между a и b является омическим резистор, для которого
        В аб = IR, тогда P = I(V аб ) может можно записать как P = I(IR) = I 2 R   или
        P = (I)V ab  можно записать как P = (V ab /R)V ab = (V аб ) 2 /R.
      3. Пример проблемы в 106 Набор задач для схем : 4.
    4. Электродвижущая сила e
      1. Электродвижущая сила e = энергия/заряд = U/q  
        или
        qe = U и мощность = P = U/t = (q/t)e = Ie.

      2. Для схемы, показанной на рис. 3 выше, r — внутреннее сопротивление. аккумулятора. Для этой цепи:
        Входная мощность = Выходная мощность
        Химическая энергия в электрическую = электрическая мощность в тепло
        Тэ = Я 2 Р + I 2 r         (уравнение 1)

        1. Из уравнения. 1,
          1. I = e/(R + r)
          2. е – Ир = ИК = В аб
          3. Напряжение на клеммах батареи В ab = е-Ир
        2. Примеры проблем в 106 Проблема Набор для цепей : 5, 8.
    5. Правила Кирхгофа
      1. Правило соединения. Сумма токов, входящих в любой переход равна сумме токов, выходящих из этого соединения. Этот это просто утверждение о сохранении заряда.
      2. Правило цикла. Сумма разностей потенциалов по каждому элемент вокруг любой замкнутой цепи равен нулю. Это просто заявление о сохранении энергии.
        1. Если перейти от минуса к плюсу батареи, химическая энергия превращается в электрическую и вы собираете энергию, поэтому знак плюс. Если перейти от плюса батареи к минусу знак, знак отрицательный.
        2. Если обойти петлю в том же направлении, что и ток, электрическая энергия превращается в тепло, и вы теряете энергию поэтому этот IR отрицателен. Если пройти по петле напротив к направлению течения, вы идете от более низкий потенциал к более высокому потенциалу, поэтому этот IR положительный.
        3. Общий комментарий. Как только вы выбираете направления токов, и обходя петлю по часовой стрелке или против часовой стрелки, оставайтесь с ним. Вы можете изменить направление движения вокруг петли для второй петли, но не меняйте направления течений.
      3. Пример проблемы в 106 Набор задач для схем: 9.
    6. RC-цепи

      1. Разность потенциалов на омическом резисторе = IR
        и на конденсаторе = q/C
      2. Когда переключатель S переведен в положение зарядки
        1. Используя правило цикла, находим
          е = ИК + к/с.
          Поскольку I = dq/dt, мы можем записать это как
          е = dq/dt R + q/C             (Уравнение 2)
          Арифметика дает нам
          (dq/dt)RC = -(q – eC)          (Уравнение 3)
          Разделение переменных:
          dq/(q – EC) = -1/RC dt              (уравнение 4)
          Интеграция с обеих сторон:

          или
          ln [(q-eC)/-eC} = -t/RC              (Уравнение 5)
          Взяв антилогарифм обеих частей уравнения. 5:
          (q-eC)/-eC = e -t/RC
          q – eC = -eC(e -т/RC ) или наконец,
          q(t) = eC(1 – e -t/RC ) (Уравнение 6)
        2. Разность потенциалов на конденсаторе для зарядки конденсатор V cb иногда называют
          В С = q/C = e(1 – e -t/RC  ). (Уравнение 7)
        3. Текущий I = dq/dt = e/R( е -т/RC  ) (Уравнение 8)
        4. Разность потенциалов на резисторе для зарядки конденсатор В ac  иногда называется
          В Р = ИК = е( e -t/RC  )               (Уравнение 9)
        5. Для рисунков 4 (вверху) и 5 ​​(внизу) я выбрал e = 1,0 В,
          R = 10 6 Вт = 10 6 В/А, и C = 5 x 10 -6 F = 5 х 10 -6 К/В. Постоянная времени = RC =10 6 В/А x 5 x 10 -6 В/В = 5 В/А = 5 Кл/(Кл/с) = 5 с.

          Для накопления заряда,  В C (t) = e(1 – e -t/RC ). Когда t = RC = 5 с,
          В C (RC) = 1,0 В (1 – e -RC/RC ) = 1,0 V(1 – e -1 ) = 1,0 В(0,632) = 0,632 В, как показано ниже.

          Для накопления заряда  V R (t) = ee -t/RC . Когда t = RC = 5 с,
          В C (RC) = 1,0 В ( e -RC/RC ) = 1,0 V(e -1 ) = 1,0 В (0,368) = 0,368 В, как показано выше.

      3. Когда переключатель опущен, аккумулятор больше не в цепи и конденсатор разряжается.
        1. В аб = 0 = IR + q/C = dq/dt R + q/C              (уравнение 10)

          Преобразование уравнения: dq/q = -dt/RC

          Пределы теперь от максимального заряда Q = eC к q, когда t изменяется от 0 до t. Конденсатор разряжается а я в противоположном направлении.

          ln q/eC = – t/RC или
          q(t) = Qe -t/RC = eCe -t/RC                   (уравнение 11)

        2. I(t) = dq/dt = -(eC/RC)e -t/RC = – (e/R)e -t/RC
        3. V cb = V C = q/C = ee -t/RC и    V ac = ИК = -ee -т/RC
        4. Ссылаясь на рис. 5b ниже,

          Для распада заряда, В C (t) = e е -т/RC . Когда t = RC = 5 с,
          В C (RC) = 1,0 В (e -RC/RC ) = 1,0 В ( e -1 ) = 1,0 В (0,368) = 0,368 В.

          Для распада заряда V R (t) = -ee -t/RC . Когда t = RC = 5 с,
          В R (RC) = -1,0 В (e -RC/RC ) = -1,0 V(e -1 ) = -1,0 В(0,368) = -0,368 В.

      4. Пример проблемы в 106 Набор задач для цепей : 10.

    сил – Формула электрического поля $E=F/q$

    спросил

    Изменено 1 год, 3 месяца назад

    Просмотрено 466 раз

    $\begingroup$

    Если следовать формуле $E=F/q$, то получается, что чем больше сила, тем больше и электрическое поле, но если заряд, на который действует сила, больше, электрическое поле как-то уменьшается? Как это понять?

    • силы
    • электростатика
    • электрические поля
    • заряд

    $\endgroup$

    $\begingroup$

    Я бы сказал, что вы смотрите на это задом наперед; лучше представить себе, что электрические поля создают силы на зарядах. Для данного электрического поля чем больше заряд, тем больше сила; чтобы увеличить силу, действующую на заряд, необходимо также увеличить электрическое поле; таким образом, для данной силы, чем больше заряд, тем меньше электрическое поле. Это аналогично массе в том смысле, что разные массы (скажем, A больше, чем B), подверженные действию одной и той же силы, будут иметь разные ускорения (B больше, чем A).

    $\endgroup$

    $\begingroup$

    Это отличный пример того, как каузальное понимание физики не является явно очевидным, если вы наивно смотрите на математическое выражение.

    То, что вы говорите , является верным, но правильно сформулировано следующим образом: для заданной силы $F$ на заряде $q$ электрическое поле $E$ (в месте расположения заряда) будет увеличиваться по мере уменьшения заряда $q$. Другими словами, это говорит о том, что для создания той же силы при меньшем заряде вам нужно более сильное электрическое поле. Как видите, никакой тайны здесь нет, если понимать так.

    Конечно, как вы уже понимаете (как следует из вашего вопроса), электрическое поле, действующее на заряд, не меняется, если вы меняете только пробный заряд, потому что оно определяется внешней конфигурацией зарядов. С физической точки зрения, когда вы меняете только пробный заряд, изменяется только сила, действующая на него. Однако $E\propto 1/q$ говорит вам, что если вы хотите поддерживать постоянную силу на изменяющемся пробном заряде, вам нужно изменить электрическое поле обратно пропорционально значению пробного заряда (через изменение внешней конфигурации зарядов, создающих электрическое поле).

    $\endgroup$

    $\begingroup$

    Если вы, скажем, удвоите заряд $q$, то вы, естественно, также увидите удвоенную силу $F$. Потому что для поля $E$ теперь будет «вдвое больше» заряда для «втягивания».

    Но если вы хотите, чтобы сила была одинаковой, вам придется каким-то образом уменьшить напряженность поля. Например, изменив источник, который вызывает поле. Иначе поменять зарядку и 9 невозможно0551 поддерживать постоянную силу.

    Возможно, ваше замешательство произошло из-за ошибочного предположения, что сила может поддерживаться постоянной при нормальных, неограниченных обстоятельствах. И, таким образом, изменение заряда, казалось бы, меняет поле. Конечно, это математически возможно, но не физически возможно . Не без того, чтобы вы каким-то образом активно меняли поле. Скорее, это было бы поле, постоянное при таких обстоятельствах, и сила изменялась бы при изменении заряда.

    $\endgroup$

    $\begingroup$

    Определение электрического поля использует E = F/q, как вы показываете, но вы упускаете из виду остальную часть определения, а именно то, что это отношение F/q в пределе, когда q -> 0. Это сделано для того, чтобы пробный заряд не нарушает распределения заряда, создающего электрическое поле.

    Оставить комментарий