Урок физики “Закон Архимеда”. 7-й класс
Тип урока: изучение нового материала.
Основные термины: Сила Архимеда, масса, объем, плотность.
Оборудование: интерактивная доска, документ-камера, физическое оборудование по теме «Гидромеханика», портреты ученых.
Формы работы: беседа-диспут, проблемно-поисковая, исследовательская, групповая, индивидуальная.
Методические приемы: Поощрение, создание ситуации успеха, проблемно-поисковая учебная деятельность, игра.
Межпредметные связи: физика – математика (использование математических расчётов), физика – история (исторические сведения).
Цель урока:
- Образовательная: сформировать знания учащихся при изучении закона Архимеда, умение добывать и применять знания, формирование навыков самообразования при решении проблемных и экспериментальных задач;
- Развивающая: формирование кругозора учащихся, умение аргументированно объяснять, делать выводы из экспериментов, работать с таблицами, приводить примеры, развитие познавательного интереса активности, памяти, воли и выражение своих мыслей и эмоций;
- Воспитательная: воспитание культуры речи,
формирование коммуникативной культуры учащихся,
взаимопомощи.

ХОД УРОКА
1. Организация начала урока (1 мин.)
– Здравствуйте ребята! Давайте познакомимся, я
учитель физики гимназии №11 города Ельца, меня
зовут Наталья Михайловна. А вы, ученики 7 класса,
мне хотелось бы узнать с каким настроением вы
пришли ко мне на урок.
Приветствие, акцентирование внимания учащихся
на раздаточный материал и лабораторное
оборудование, находящийся на партах. (Три
карточки с изображением смайлика: весёлый,
недовольный и равнодушный).
Содержание деятельности: организация
подготовленности учащихся к уроку. (Учащиеся
показывают, с каким настроением они пришли на
урок, учитель показывает своё).
2. Сообщение темы и цели урока (1 мин.)
– Сегодня я проведу у вас урок физики по теме
«Закон Архимеда». А знаете ли, вы, что с действием
этого закона вы встречаетесь ежедневно,
наверное, нет. Мая задача познакомить вас с этим
законом и его применением.
А знаете ли, вы, что с действием
этого закона вы встречаетесь ежедневно,
наверное, нет. Мая задача познакомить вас с этим
законом и его применением.
– Ребята на ваших столах находится необходимое
оборудование: динамометры, различные тела
определенной формы и мерные стаканы, все это нам
будет нужно для проведения эксперимента, который
вы будите сегодня проводить. (Учитель сообщает
тему и цели урока, создает ситуацию успеха,
акцентирует внимание на физическое оборудование
для проведения эксперимента)
Содержание деятельности: Определение уровня владения знаниями. Коррекция знаний, умений и навыков.
3. Повторение, обобщение понятий и усвоение соответствующей им системы знаний (7 мин.)
– Ребята, мы продолжаем с вами знакомиться, я буду вам задавать вопросы, а вы постарайтесь на них правильно ответить.
1) Разминка
Весь класс в быстром темпе заканчивает фразу
учителя или отвечает на поставленный вопрос.
– Какое давление называется гидростатическим? (Давление,
оказываемое покоящейся жидкостью, называется
гидростатическим) (Слайд 2)
– Как определить давление жидкости на дно
сосуда? (Слайд 3) (Давление жидкости на дно и
стенки сосуда прямо пропорционально высоте
столба жидкости и зависит от рода жидкости, в
которое помещено тело). (На слайде показан график
зависимости давления жидкости от высоты столба и
плотности жидкости).
– По какой формуле рассчитывается давление
жидкости на дно сосуда? (Формула, треугольник
для запоминания) (слайд 4)
– Для того, чтобы вам легче было вспомнить
формулу, я предлагаю вам следующий прием для
запоминания: в вершине треугольника находится
давление, а в основании плотность, ускорение
свободного падения и высота.
– Как читается закон Паскаля? (Давление,
производимое на жидкость или газ, передается в
любую точку одинаково во всех направлениях. )
(Слайд 5)
)
(Слайд 5)
– Я вам напоминаю практическое применение
закона Паскаля (лейка, душ), с которыми вы
ежедневно встречаетесь.
– А знаете ли вы, что для того чтобы изучить закон
Архимеда нам понадобятся физические приборы.
– В физике много приборов. Знаете ли вы, как они
выглядят и где они применяются?
Для задания разрезают картинки динамометра и
измерительного цилиндра. Участники получают
пазлы с фрагментами приборов, которые они должны
собрать и пояснить название получившегося
прибора, область применения. Двое учащиеся
работают за учительским столом, затем показывают
свою картинку через документ-камеру. Пока
учащиеся собирают пазлы, остальные отвечают
на вопросы учителя.
– Какая сила называется выталкивающей? (Сила,
выталкивающая тело из жидкости или газа,
называется выталкивающей или архимедовой).
(Слайд 7) (Переход на другую программу «документ –
камера».
Учитель проводит эксперимент, учащиеся делают
выводы, основываясь на изученном материале
предыдущих уроков. (Демонстрация проводится
через документ – камеру)
Погружается мяч в воду и быстро убирается рука.
Мяч «выпрыгивает» из воды.
– Почему мяч всплыл? (На мяч подействовала
сила со стороны воды).
– Теперь поместим металлический цилиндр в
жидкость (можно монету). Тело утонуло. Действует
ли выталкивающая сила в этом случае? (Возможный
ответ ученика: «Так как тело утонуло, то
выталкивающая сила на него не действует»)
Камень или цилиндр, подвешенный на резиновой
нити, опускаем в воду, замечаем, длина резиновой
нити стала короче. Ребята анализируют опыт и
делают вывод: «На любое тело, погруженное в
жидкость, действует сила, выталкивающая тело из
жидкости». Сообщение учителя: из нашего
жизненного опыта мы знаем, что в воде тяжелый
камень поднять гораздо легче, чем в воздухе. Это
может означать, что жидкость выталкивает не
только легкие, но и тяжелые предметы.
Это
может означать, что жидкость выталкивает не
только легкие, но и тяжелые предметы.
Проверка учащихся, которые собирали пазлы. (Переход на программу с презентацией урока)
– Куда направлена выталкивающая сила? (Слайд 8 с рисунком, идет пояснение).
Если привязать короткой ниткой к пробке такой
груз, чтобы она погрузилась в воду. Отвесно
натянутая нить показывает, что выталкивающая
сила, которая действует на пробку, направлена
вертикально вверх, а сила тяжести вниз.
По какой формуле рассчитывается выталкивающая
сила? (Формула, треугольник, вывод)
(Слайд 9)
На тело, полностью погруженное в жидкость, действует вертикально вверх выталкивающая сила, равная весу жидкости вытесняемой телом.
4. Изучение нового материала (15 мин.)
1) Составление опорного конспекта, используется
проблемно -поисковый метод и выводы записываются
в таблицу.
– Итак, мы с вами подошли к изучению нового
закона. Запишите тему в тетради.
Мы с вами отправляемся в Древнюю Грецию в 3 век до
нашей эры. Именно в это время в Сиракузах, на
острове Сицилия проживал величайший математик и
физик древности – Архимед. Он прославился
многочисленными научными трудами, главным
образом в области геометрии и механики. В это
время Сиракузами правил царь Герон. Он поручил
Архимеду проверить честность мастера,
изготовившего золотую корону. Хотя корона весила
столько, сколько было отпущено на нее золота,
царь заподозрил, что она изготовлена из сплава
золота с другими, более дешевыми металлами.
Архимеду было поручено узнать, не ломая короны,
есть ли в ней примесь. Идея решения пришла к
ученому однажды, когда он решил принять ванну.
Ликующий и возбуждённый своим открытием, Архимед
воскликнул: «Эврика!», что значит: «Нашел». (Слайд
10)
Однако в дальнейшем на протяжении нескольких
столетий в развитии человечества наступила
эпоха всеобщего застоя.
– Для того чтобы сформулировать закон Архимеда нам необходимо провести эксперимент.
2) Экспериментальная проверка закона Архимеда. (Слайд 12)
– Проделаем следующий опыт: пустое ведерко и
сплошной цилиндр, имеющий объем, равный
вместимости ведерка, подвесим к пружине
динамометра. Показания динамометра зафиксируем.
Затем опустим цилиндр в отливной сосуд,
наполненной водой до уровня отливной трубки.
Когда цилиндр полностью погрузится в воду,
растяжение пружины уменьшится, а часть воды,
объем которой равен объему цилиндра, выльется из
отливного сосуда в стакан. Если теперь перелить
воду из стакана в ведерко, то пружина динамометра
снова растянется до прежней длины. Это означает,
что потеря в весе цилиндра в точности равна весу
воды в объеме цилиндра.
Если теперь перелить
воду из стакана в ведерко, то пружина динамометра
снова растянется до прежней длины. Это означает,
что потеря в весе цилиндра в точности равна весу
воды в объеме цилиндра.
Итак, опыт подтвердил, что архимедова сила
равна весу жидкости в объеме этого тела, т.е.
Fa = Pж = mg = жgVт.
Из описанного опыта видно, что вес тела,
погруженного в жидкость, уменьшается на
значение, равное архимедовой силе: Р1 =
Р – Fa = mg – m1g, где m – масса тела, а m1
– масса жидкости в объеме, равном объему
погруженного тела.
Если подобный опыт провести с газом, то он
показал бы, что сила, выталкивающая тело из
газа, также равна весу газа, взятого в объеме
тела. (Слайд 13)
Закон Архимеда формулируется таким образом:
Тело, находящееся в жидкости (или газе),
теряет в своем весе столько, сколько весит
жидкость (или газ) в объеме, вытесненном телом. (Учащиеся
работают с учебником) (Слайд 14)
(Учащиеся
работают с учебником) (Слайд 14)
3) Итак, первая цель достигнута, далее
начинается работа в шести группах. (Слайд 15)
От чего зависит, архимедова сила? А сейчас вы –
исследователи, вы выясните, от чего зависит,
архимедова сила. У каждой группы своя задача.
Приступаем к работе, соблюдая технику
безопасности, так как вы работаете со стеклом.
(Слайд 16)
Задание первой группе.
Оборудование: сосуд с водой, динамометр, алюминиевый и медный цилиндры одинакового объема, нить.
- Определить архимедову силу, действующие на первое и вторе тела.
- Сравнить плотность тел и архимедовы силы, действующие на тела.
- Сделайте вывод зависимости (независимости) архимедовой силы от плотности тела.
Вывод: архимедова сила не зависит от
плотности вещества, из которого изготовлено
тело.
Задание второй группе.
Оборудование: сосуд с водой, тела разного объема из пластилина, динамометр, нить.
- Определить архимедову силу, действующую на каждое из тел.
- Сравните эти силы.
- Сделайте вывод о зависимости (независимости) архимедовой силы от объема тела.
Вывод: архимедова сила зависит от объема тела, чем больше объем тела, погруженного в жидкость, тем больше архимедова сила.
Задание третьей группе.
Оборудование: динамометр, нить, сосуды с водой, с соленой водой и маслом, алюминиевый цилиндр.
- Определить архимедову силу, действующую на тело в воде, соленой воде и масле.
- Чем отличаются эти жидкости?
- Что можно сказать об архимедовых силах, действующих на тело в различных жидкостях?
- Установите зависимости архимедовой силы от
плотности жидкости.

Вывод: архимедова сила зависит от плотности жидкости, чем больше плотность жидкости, тем больше архимедова сила.
Задание четвертой группе.
Оборудование: тела разной формы, сосуд с водой, нить, динамометр,
- Поочередно опуская каждое тело в воду (кусок пластилина в форме шара, куба и цилиндра), с помощью динамометра определить архимедову силу.
- Сравним эти силы и сделаем вывод о зависимости и независимости архимедовой силы от формы тела.
Вывод: архимедова сила не зависит от формы тела, погруженного в жидкость или газ.
Задание пятой группе.
Оборудование: мензурка с водой, алюминиевый цилиндр, нить динамометра.
- Определю архимедову силу, действующую на тело, погруженное на 1/4 объема, 1/2 объема, 3/4 объема.
- Сделаем вывод зависимости архимедовой силы от
объёма погруженной части тела.

Вывод: архимедова сила зависит от объема погруженной части, чем больше объем погруженной части тела, тем больше архимедова сила.
Задание шестой группе.
Оборудование: мензурка с водой, алюминиевый цилиндр, нить динамометра.
1. Определю силу Архимеда на различной глубине h1
= , h2 =
2. Сделаем вывод о зависимости Архимедовой силы
от глубины погружения данного тела.
Вывод: Архимедова сила не зависит от глубины
погружения тела.
Поле получения результатов каждая группа отчитывается устно о своей проделанной работе. Затем учащиеся записывают выводы в виде таблицы, а учитель на доске. (Слайд 17 на презентации).
Архимедова сила |
|
Не зависит |
Зависит |
| От формы тела | От объема тела |
| От плотности тела | От плотности жидкости |
| От глубины погружения | От объема погруженной части |
5. Закрепление полученных знаний (16
мин.)
Закрепление полученных знаний (16
мин.)
– Ребята, для решения задач на закон Архимеда нам понадобится знание формул, которые вы соберёте с острова «Величин» на остров «Формул» в процессе эстафеты.
Эстафета «Кто быстрее?» (2 мин.)
(Слайд 18). Учащимся раздаются листы с островом
«Величин» и островом «Формул». Чей ряд больше и
быстрее соберет формулы с острова «Величин», тот
и выигрывает. (Проверка на слайде)
Пришла пора отдохнуть.
Физкультминутка «Ванька-встань-ка» (2 мин.) (Слайд 19)
Исходное положение:
Все сидят, учитель, закрыв глаза (лучше
отвернувшись), задает число – и выбрасывает над
головой соответствующее количество пальцев на
одной или обеих руках. Затем он произносит: «Раз-два-три!
Замри!» – открывает глаза, в классе должно стоять
ровно столько учеников, сколько пальцев им было
предъявлено при выполнении игрового занятия. Каждому из учеников приходится быстро
сориентироваться в упражнении, сесть или встать
в нужный момент.
Каждому из учеников приходится быстро
сориентироваться в упражнении, сесть или встать
в нужный момент.
– Итак, вы отдохнули, а теперь узнаем, как вы усвоили закон Архимеда.
Переход к другой программе для выполнения тестов. (Электронное приложение)
Тест. (4 мин.) Один из учащихся вызывается к доске, остальные на месте решают
– А теперь мы переходим с вами к решению расчетных задач.
Решение расчетных задач. (4 мин.) (Вернутся к презентации слайд 20, 21)
6. Приведение единых знаний в систему (2 мин.)
7. Подведение итогов урока. Рефлексия. (1 мин.)
Работа с ассоциативной схемой. (Слайд 22)
– Что Вы узнали сегодня на уроке? (А как
читается закон Архимеда?)
– Чему научились?
– Что для Вас было наиболее сложным?
Ответы учащихся в устной форме.
8. Информация о домашнем задании (1 мин.) (Слайд 23)
Уделить внимание, на решение сложных заданий,
подготовиться к лабораторной работе, решить
проблемную задачу.
Если на дно стеклянного сосуда, покрытого тонким
слоем парафина, положить кусочек парафина с
гладким основанием и аккуратно налить воды, то
парафин не всплывает. Чем это объясняется? Если
наклонить кусок парафина так, чтобы вода
проникла под его нижнюю поверхность, то он сразу
всплывет. Найдите ответ на эту задачу, почему так
происходит.
Можно предложить другую проблемную задачу:
Если налить воды в книгу и перевернуть, то вода не
выливается. Почему? (Фокус с сообщающимися
сосудами). Учитель обращается к классу с
вопросом: «С каким настроением Вы уходите с
урока?» (Работа с карточками)
Д/З: § 48, 49, упражнение 24
– Желаю всем успеха!
Академия занимательных наук.
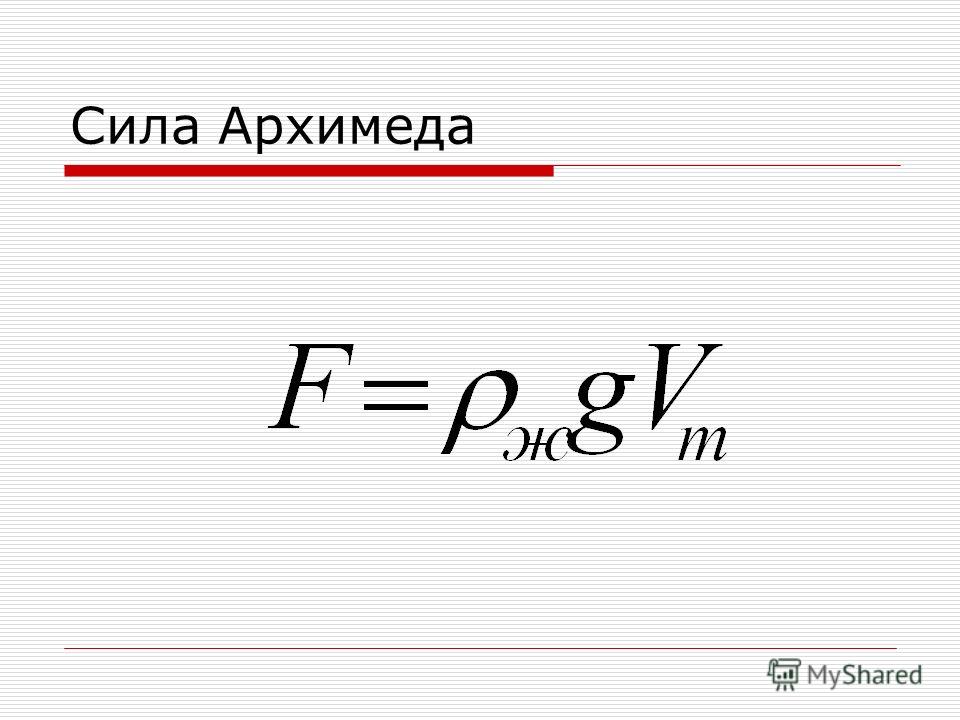 Физика – Архимедова сила. Закон Архимеда. Видеоуроки физики
Физика – Архимедова сила. Закон Архимеда. Видеоуроки физикиАрхимедова сила. Закон Архимеда. Видеоуроки физики
Выпуск 8В видеоуроке физики от Академии занимательных наук профессор Даниил Эдисонович расскажет о древнегреческом учёном Архимеде и некоторых из его удивительных открытий. Как узнать, является ли золото чистым? Каким образом многотонные корабли умудряются плавать по океанским волнам? Наша жизнь полна загадочных явлений и хитрых головоломок. Физика способна подобрать ключи к некоторым из них. Посмотрев восьмой видеоурок физики вы познакомитесь с законом Архимеда и Архимедовой силой, а также историей их открытия.
Закон Архимеда
Почему в воде предметы весят меньше, чем на суше? Для человека пребывание в воде сравнимо с пребыванием в состоянии невесомости. Это используют в своих тренировках космонавты. Но из-за чего же так происходит? Дело в том, что на тела, погружённые в воду действует выталкивающая сила, открытая древнегреческим философом Архимедом. Закон Архимеда звучит так — погружённое в жидкость тело теряет в весе столько, сколько весит объём вытесненной им воды. Выталкивающую силу назвали Архимедовой, в честь первооткрывателя. Архимед, был одним из величайших ученых Древней Греции. Этот гениальный математик и механик, жил в Сиракузах в III веке до н. э. Вэто время в Сиракузах правил царь Гиерон. Однажды Гиерон, получив от мастеров заказанную им золотую корону, усомнился в их честности. Ему показалось, что они утаили часть золота, выданного на ее изготовление, и заменили его серебром. Но как уличить ювелиров в подделке? Гиерон поручил Архимеду определить, есть ли в золотой короне примесь серебра. Архимед искал решение задачи постоянно, не переставая думать об этом, когда занимался другими делами. А решение нашлось… в бане. Архимед, намылился золой и полез в ванну.И произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну — вода в ней поднимается. Но то, на что обычно Архимед не обращал никакого внимания, вдруг заинтересовало его.
Закон Архимеда звучит так — погружённое в жидкость тело теряет в весе столько, сколько весит объём вытесненной им воды. Выталкивающую силу назвали Архимедовой, в честь первооткрывателя. Архимед, был одним из величайших ученых Древней Греции. Этот гениальный математик и механик, жил в Сиракузах в III веке до н. э. Вэто время в Сиракузах правил царь Гиерон. Однажды Гиерон, получив от мастеров заказанную им золотую корону, усомнился в их честности. Ему показалось, что они утаили часть золота, выданного на ее изготовление, и заменили его серебром. Но как уличить ювелиров в подделке? Гиерон поручил Архимеду определить, есть ли в золотой короне примесь серебра. Архимед искал решение задачи постоянно, не переставая думать об этом, когда занимался другими делами. А решение нашлось… в бане. Архимед, намылился золой и полез в ванну.И произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну — вода в ней поднимается. Но то, на что обычно Архимед не обращал никакого внимания, вдруг заинтересовало его. Он привстал – уровень воды опустился, он снова сел — вода поднялась; причем поднималась она по мере погружения тела. И вот в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача царя Гиерона разрешима. И так обрадовался своей случайной находке, что как был – голый, с остатками золы на теле – побежал домой через город, оглашая улицу криками: «Эврика! Эврика!». Вот так Архимед, если верить легенде, нашел решение задачи Гиерона. Архимед попросил у царя два слитка — серебряный и золотой. Вес каждого слитка был равен весу короны. Положив в сосуд до краёв наполненный водой сначала серебряный, а затем золотой слиток, учёный измерил объём вытесненной каждым из слитков воды. Золото вытеснило меньше воды, чем серебро. А всё потому, что объём куска золота был меньше куска серебра такого же веса. Ведь золото тяжелее серебра. Затем Архимед погрузил в сосуд корону и измерил объём вытесненной ею воды. Корона вытеснила меньше воды, чем слиток серебра.
Он привстал – уровень воды опустился, он снова сел — вода поднялась; причем поднималась она по мере погружения тела. И вот в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача царя Гиерона разрешима. И так обрадовался своей случайной находке, что как был – голый, с остатками золы на теле – побежал домой через город, оглашая улицу криками: «Эврика! Эврика!». Вот так Архимед, если верить легенде, нашел решение задачи Гиерона. Архимед попросил у царя два слитка — серебряный и золотой. Вес каждого слитка был равен весу короны. Положив в сосуд до краёв наполненный водой сначала серебряный, а затем золотой слиток, учёный измерил объём вытесненной каждым из слитков воды. Золото вытеснило меньше воды, чем серебро. А всё потому, что объём куска золота был меньше куска серебра такого же веса. Ведь золото тяжелее серебра. Затем Архимед погрузил в сосуд корону и измерил объём вытесненной ею воды. Корона вытеснила меньше воды, чем слиток серебра. но больше чем слиток золота. Так мошенничество ювелира было разоблачено. Благодаря Архимедовой силе способны плавать гигантские корабли, весящие сотни тысяч тонн. Это происходит благодаря тому, что они обладают большим водоизмещением. То есть, их объём таков, что вытесняет огромное количество воды. А как вы помните, чем больше объём тела, тем сильнее действует на него Архимедова сила.
но больше чем слиток золота. Так мошенничество ювелира было разоблачено. Благодаря Архимедовой силе способны плавать гигантские корабли, весящие сотни тысяч тонн. Это происходит благодаря тому, что они обладают большим водоизмещением. То есть, их объём таков, что вытесняет огромное количество воды. А как вы помните, чем больше объём тела, тем сильнее действует на него Архимедова сила.
Урок 15. основы гидромеханики – Физика – 10 класс
Физика, 10 класс
Урок 15. Основы гидромеханики
Перечень вопросов, рассматриваемых на уроке:
1.Сила давления
2.Давление
3.Закон Паскаля
4.Гидростатическое давление
5.Атмосферное давление
6.Закон Архимеда
Глоссарий по теме
Гидростатика – раздел механики, в котором изучается равновесие покоящихся жидкостей и их давление на погруженные в них тела.
Давление – это величина равная отношению силы давления к площади поверхности, на которую эта сила действует.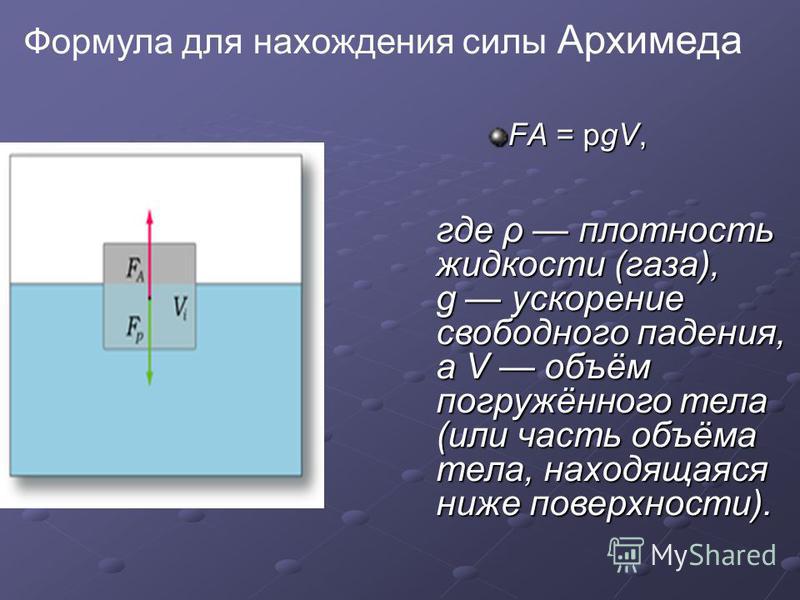
Нормальное атмосферное давление – это величина давления, равная 760 мм рт. ст. или 101325 Па.
Сила Архимеда –выталкивающая сила, действующая на тело, погруженное в жидкость или газ
Основная и дополнительная литература по теме урока:
Грачев А.В., Погожев В.А., Салецкий А.М., Боков П.Ю. Физика.10 класс. М.: Вентана-Граф, 2017. – С. 222 – 229.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006, С.36-50.
Основное содержание урока
Силой давления называется сила, действующая перпендикулярно некоторой поверхности.
Результатом действия силы давления является давление.
Отношение модуля силы давления F к площади поверхности S, на которую эта сила действует, называется давлением
Закон Паскаля.
Силы давления в данной точке покоящейся жидкости (газа) действуют во всех направлениях одинаково. При ведём простое доказательство закона.
Выделим в какой-нибудь точке покоящейся жидкости её малый объём в форме прямоугольного параллелепипеда или куба.
Если кубик покоится, значит сумма сил, действующих на его 6 граней равна нулю. Это означает, что силы, действующие попарно на противоположные грани куба, равны по модулю, а, следовательно, и давления будут равны по всем направлениям.
Ввиду произвольности ориентации выбранного нами малого объёма жидкости, очевидно, что давление по всем направлениям должно быть одинаково.
Гидростатическое давление. Атмосферное давление.
Это давление, оказываемое «столбом» жидкости на уровне плоскости своего нижнего основания.
Выделим в покоящейся жидкости «столб» – цилиндр высотой h и площадью основания S, верхнее основание которого совпадает со свободной поверхностью жидкости.
По первому закону Ньютона сумма проекций трех сил, действующих на столб жидкости: силы атмосферного давления, силы тяжести и силы давления жидкости- равна нулю
Fp– mg – Fатм = 0;
Но так как mg=ρ·V·g=ρ·S·h·g; Fp = p·S; Fатм = pатм ·S,
Получим p = pатм+ ρ·g·h;
где pатм – атмосферное давление; ρ – плотность жидкости; g – ускорение свободного падения; h – глубина.
Величина ρ·g·h называется гидростатическим давлением.
Атмосферное давление – это давление в какой-нибудь точке атмосферы.
Нормальное или среднее значение атмосферного давления равно 760 мм ртутного столба, что соответствует 101325 Па. Т.е. 1 мм рт. ст. = 133,322 Па.
Зависимость атмосферного давления от высоты имеет сложный вид из-за сжимаемости воздуха (в отличие от жидкостей).
Закон Архимеда. Сила Архимеда.
Выделим в жидкости объем прямоугольного параллелепипеда, ориентированного для удобства анализа так, чтобы нижняя и верхняя грани были параллельны поверхности жидкости
На тело в жидкости действуют сила тяжести и силы давления со стороны жидкости. Давление на боковые стенки равны. Сила давления снизу больше, чем сила давления сверху. Разность этих двух сил и есть выталкивающая сила – сила Архимеда.
FA=p2 S – p1 S =S( p2 – p1) = ρ g S(h2 – h1) = ρ gV
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
где – плотность жидкости; g – ускорение свободного падения; Vm – объём погруженной в жидкость части тела
Разбор тренировочных заданий
1. Найдите силу нормального атмосферного давления на грань куба с ребром 1 м. Округлите до целых кПа.
Варианты ответов:
1) 100;
2) 125;
3) 101;
4) 110
Решение. По определению сила давления равна F = p x S;
Нормальное атмосферное давление p = 101325 Па; площадь грани куба (1м)2 = 1м2;
Получим значение силы давления F = (101325 Н/м2 ) х (1 м2) = 101325 Н =101,325 кН.
Ответ: 3) 101
2. В первой строке таблицы приведены значения атмосферного давления на разных высотах. Занесите во вторую строку соответствующие значения высот из перечня: h1, h2, h3, h4, если известно, что h3 > h4 > h1 > h2
P (мм рт. | 738 | 750 | 550 | 525 |
h(м) |
Решение. Как известно, давление атмосферы падает с высотой. Выпишем в порядке убывания давления: 750,738,550,525. Из приведённого неравенства имеем, что наименьшая высота h2, затем h1, h4 и h3. Наименьшей высоте соответствует наибольшее давление и т.д. Высота растёт, давление падает. Или наоборот. В таблицу теперь под каждым давлением впишем соответствующее значение высоты.
Ответ:
P (мм рт. ст.) | 738 | 750 | 550 | 525 |
h(м) | h1 | h2 | h4 | h3 |
ФИЗИКА
ФИЗИКАВзаимодействие тел
Сила тяжести
Теоритические
сведения Сила тяжести, действующая на тело, находящееся на поверхности Земли равна массе тела, умноженной на постоянную Сила тяжести – сила (Fт), с которой Земля притягивает к себе тело, равная произведению массы (m) тела на коэффициент пропорциональности (g) – постоянную величину для Земли.
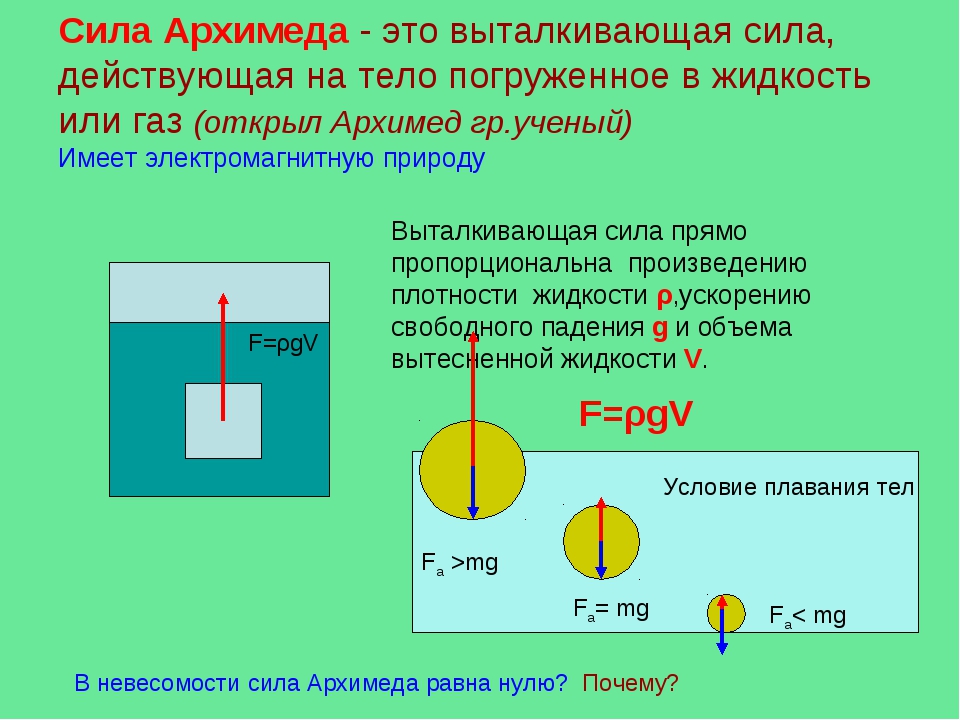
Здесь F – сила тяжести, m – масса, g — ускорение свободного падения.
Единица измерения силы – Н (ньютон).
Из-за того, что Земля имеет сплюснутую форму, то есть её радиус не везде одинаков, ускорение свободного падения меняется в зависимости от географической широты, от 9,832 на экваторе до 9,78 на полюсах. 9,8 – его среднее значение.
Сила тяжести действует на тело, имеющее опору или подвес. Если тело их не имеет, то есть находится в состоянии свободного падения, то говорят, что тело находится в невесомости. Сила тяжести всегда направлена к центру Земли.
Сила трения
Теоритические
сведения
Трение — процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. По-другому называется фрикционным взаимодействием. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии.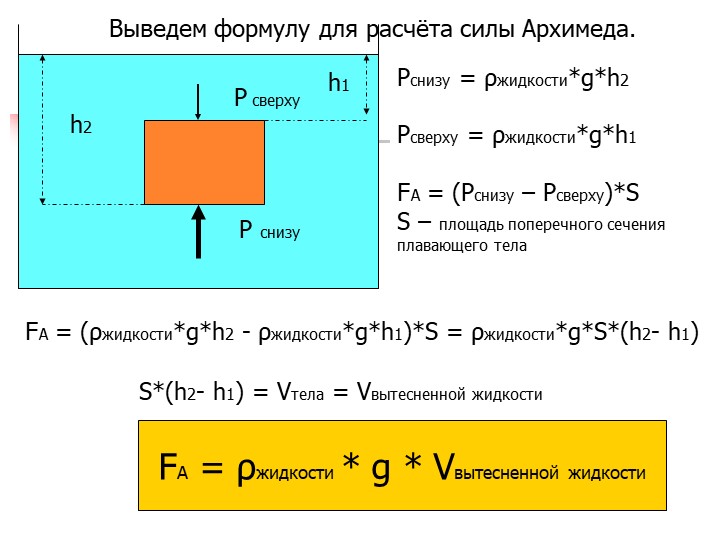 В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз
В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз
При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:
Трение скольжения
— сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
Трение качения
— момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
Трение покоя
— сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел.
 Она действует в направлении, противоположном направлению возможного относительного движения.
Она действует в направлении, противоположном направлению возможного относительного движения. Сила Архимеда
Теоритические
сведения
Закон Архимеда формулируется следующим образом:
на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела. Сила называется силой Архимеда:
F=qgV
q— плотность жидкости (газа), g — ускорение свободного падения, а V — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.ся в невесомости. Сила тяжести всегда направлена к центру Земли.
Brovko.A
380970538370
[email protected]
2016
Читай, познавай, исследуй! Мир физики интересен и увлекателен, он приглашает всех любознательных в путешествие по страницам сайта «Физика в картинках».
определение и формула. Какое значение имеет закон Архимеда
Проделаем простой эксперимент: возьмем слабо надутый резиновый мяч и «притопим» его в воде. Если глубина погружения будет даже 1-2 метра, то нетрудно видеть, что его объем уменьшится, т. е. со всех сторон мяч обжала некая сила. Обычно говорят, что здесь «виновато» гидростатическое давление – физический аналог силы, действующей в неподвижных жидкостях на погруженное тело. Гидростатические силы действуют на тело со всех сторон, а их результирующая, известная как архимедова сила, еще называется выталкивающей, что соответствует ее направлению действия на погруженное в жидкость тело.
е. со всех сторон мяч обжала некая сила. Обычно говорят, что здесь «виновато» гидростатическое давление – физический аналог силы, действующей в неподвижных жидкостях на погруженное тело. Гидростатические силы действуют на тело со всех сторон, а их результирующая, известная как архимедова сила, еще называется выталкивающей, что соответствует ее направлению действия на погруженное в жидкость тело.
Архимед открыл свой закон чисто экспериментально, а его теоретическое обоснование ждало еще почти 2000 лет до того, как Паскаль открыл для неподвижной жидкости. Согласно этому закону давление передается через жидкость по всем направлениям независимо от площади, на которую оно действует, на все плоскости, ограничивающие жидкость, а его величина P пропорциональна поверхности S и направлена по нормали к ней. Паскаль открыл и проверил этот закон на опыте в 1653 г. В соответствии с ним, на поверхность погруженного в жидкость тела со всех сторон действует гидростатическое давление.
Допустим, что в сосуд с водой погружено тело в форме куба с ребром L на глубину H – расстояние от поверхности воды до верхней грани. При этом нижняя грань находится на глубине H+L. Вектор силы F1, действующей на верхнюю грань, направлен вниз и F1 = r * g * H * S, где r – плотность жидкости, g – ускорение
При этом нижняя грань находится на глубине H+L. Вектор силы F1, действующей на верхнюю грань, направлен вниз и F1 = r * g * H * S, где r – плотность жидкости, g – ускорение
Вектор силы F2, действующей на нижнюю плоскость, направлен вверх, а ее величина определяется выражением F2 = r * g * (H+L) * S .
Векторы сил, действующих на боковые поверхности, взаимно уравновешиваются, поэтому в дальнейшем из рассмотрения исключаются. Архимедова сила F2 > F1 и направлена снизу вверх, и приложена к нижней грани куба. Определим ее величину F:
F = F2 – F1 = r * g * (H+L) * S – r * g * H * S = r * g * L * S
Заметим, что L * S – это объем куба V, а т. к. r * g = p представляет собой вес единицы жидкости, то формула архимедовой силы определяет вес объема жидкости, равный объему куба, т.е. это как раз и есть вес вытесненной телом жидкости. Интересно, что говорить о возможно только для среды, где присутствует сила тяжести – в условиях невесомости закон не работает. Окончательно формула закона Архимеда имеет следующий вид:
F = p * V, где p – удельный вес жидкости.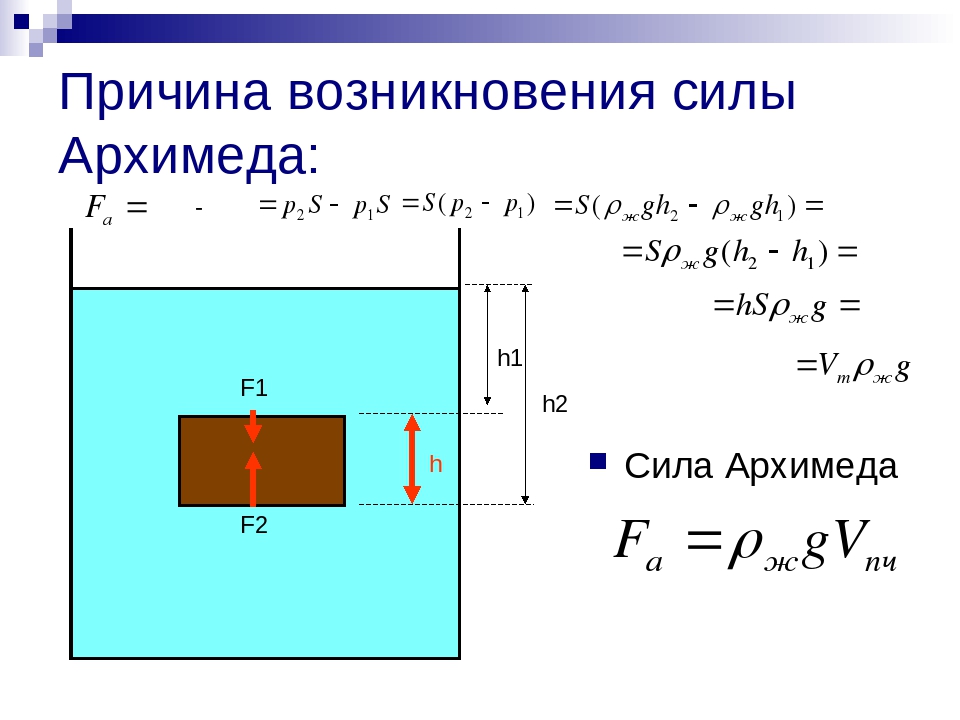
Архимедова сила может служить основанием для анализа плавучести тел. Условием для анализа служит соотношение веса погруженного тела Рт и веса жидкости Рж с объемом, равным объему погруженной в жидкость части тела. Если Рт = Рж, то тело плавает в жидкости, а если Рт > Рж, то тело тонет. В противном случае тело всплывает, пока выталкивающая сила не сравняется с весом вытолкнутой утопленной частью тела воды.
Закон Архимеда и его использование имеют длинную историю в технике, начиная с классического примера применения во всех известных плавсредствах и до воздушных шаров и дирижаблей. Здесь сыграло роль то, что газ относится к такому состоянию вещества, которое вполне моделирует жидкость. При этом, в воздушной среде на любые предметы действует архимедова сила, сродни такой же, как в жидкости. Первые попытки осуществить воздушный полет на воздушном шаре предприняли братья Монгольфьер – они наполняли воздушный шар теплым дымом, благодаря чему вес заключенного в шаре воздуха был меньше, чем вес такого же объема холодного воздуха. Это и было причиной появления а ее величина определялась как разность веса этих двух объемов. Дальнейшим усовершенствованием воздушных шаров была горелка, которая непрерывно подогревала воздух внутри шара. Понятно, что дальность полета зависела от длительности работы горелки. Позже на дирижаблях применялся для наполнения газ с удельным весом меньше, чем у воздуха.
Это и было причиной появления а ее величина определялась как разность веса этих двух объемов. Дальнейшим усовершенствованием воздушных шаров была горелка, которая непрерывно подогревала воздух внутри шара. Понятно, что дальность полета зависела от длительности работы горелки. Позже на дирижаблях применялся для наполнения газ с удельным весом меньше, чем у воздуха.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет).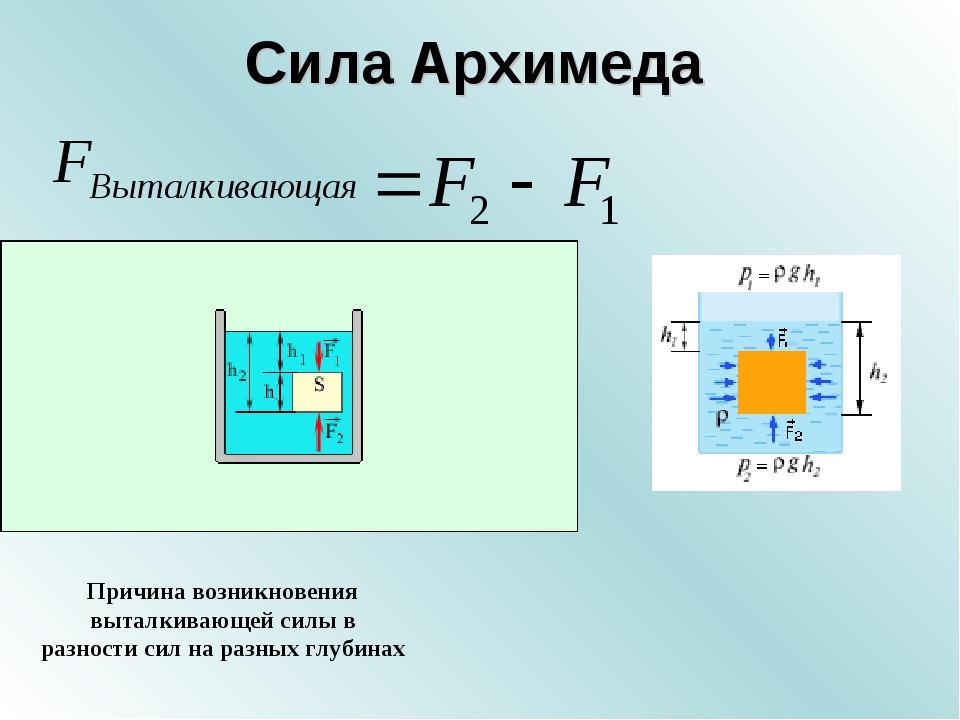 Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н. э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в
Сиракузах, осажденных римским флотом и войском.
Шла 2-я Пуническая война. И великий ученый, не
жалея сил, организовывает инженерную оборону
родного города. Он построил множество
удивительных боевых машин, топивших вражеские
корабли, разносивших их в щепы, уничтожавших
солдат. Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском. И в 212 г. до н.э. Сиракузы были
взяты.
И в 212 г. до н.э. Сиракузы были
взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под
действием выталкивающей силы оно будет
всплывать из более глубоких слоев в менее
глубокие. Выведем формулу для определения силы
Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые
грани равна нулю, поэтому в расчетах не
участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость
(или газ), то оно теряет в своём весе столько,
сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости. Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то
сила Архимеда равна нулю.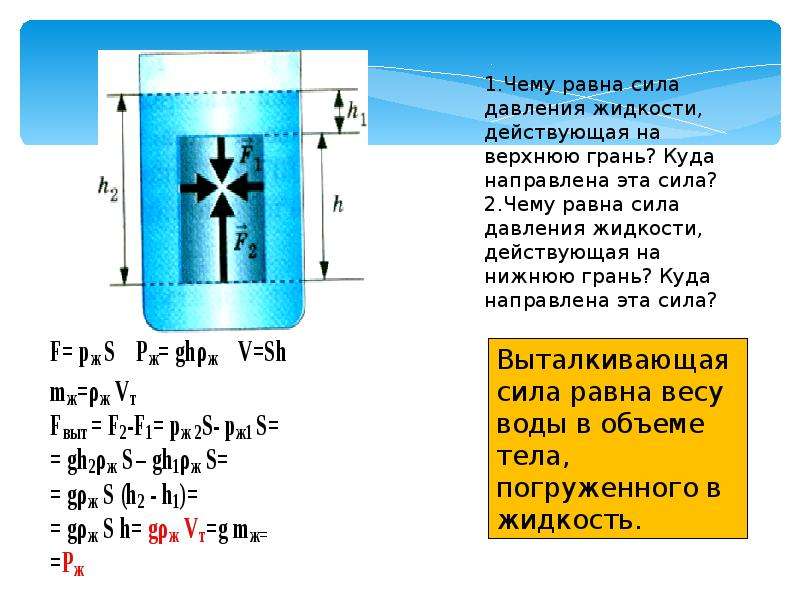
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили
огромный бумажный шар, под которым поместили
чашку с горящим спиртом. Шар наполнился горячим
воздухом и начал подниматься, достигнув высоты
2000 метров.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Если принять вес тела в вакууме за Р о, то его вес в воздушной среде может быть описан такой формулой: Р в =Р о – F а;
здесь Р о – вес в вакууме;
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
Это и есть закон Архимеда.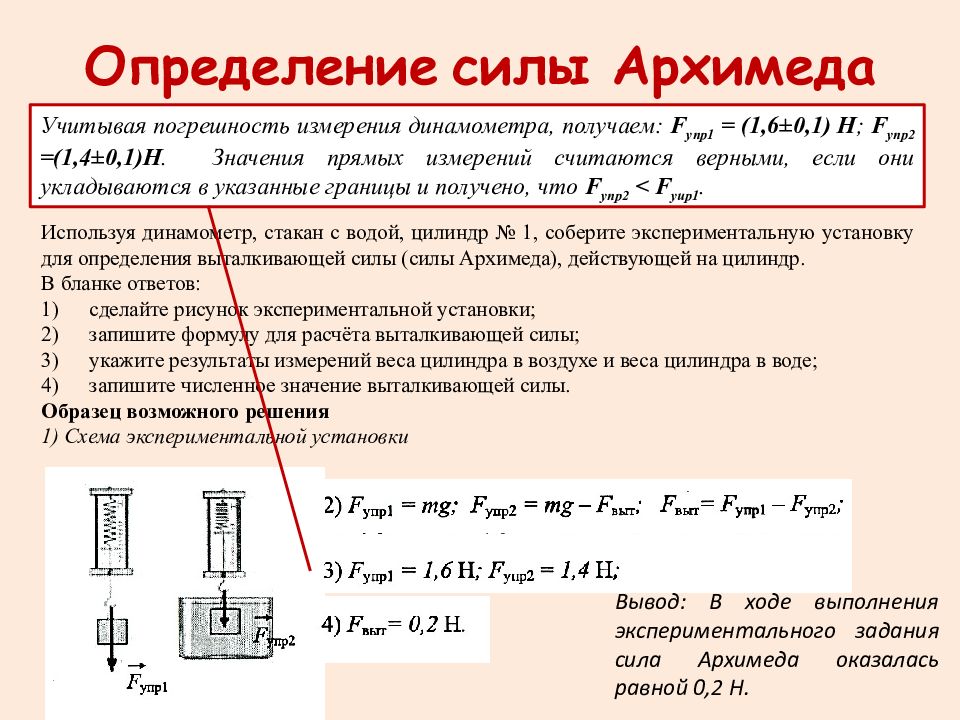
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.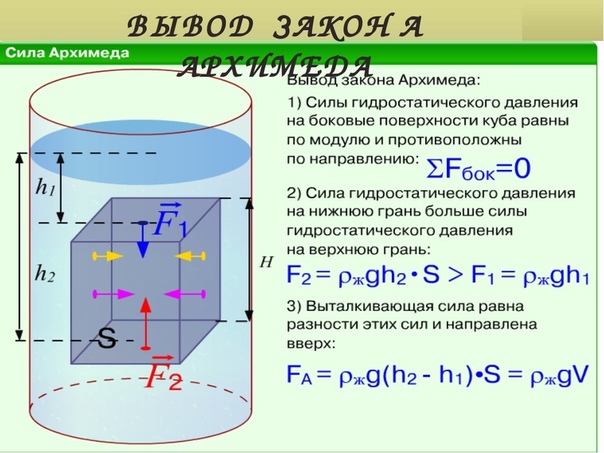
Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
«Сила Архимеда» – Международная Ассоциация Развития Образования
Галиева Винера Зиятдиновна,
Пермский край, г.Чернушка,
учитель математики и физики
МОУ «Кадетская школа имени
Героя Советского Союза Е.И. Францева»
Сила Архимеда
“Кто овладел творениями Архимеда, будет
меньше удивляться открытиям самых
великих людей нашего времени”
Лейбниц
Тип урока: урок – обобщение изученного материала
Цели урока:
1. Образовательные:
Образовательные:
v Повторение и обобщение изученного материала.
v Развитие навыков решения экспериментальных, качественных и количественных задач.
v Обеспечение единства теории и практики.
2. Развивающие:
v развитие познавательной мотивации;
v применять знания в знакомых и незнакомых ситуациях;
v развитие коммуникативных навыков;
v формирование навыков самостоятельной работы.
3. Воспитательные:
v воспитание убежденности в возможности познания природы;
v воспитание самостоятельности.
Ход урока:
1. Устная работа
Учитель: Мы в нашей жизни часто сталкиваемся с законом Архимеда: наблюдаем, как плавают рыбки, видим передвижение по реке лодок, пароходов, любим сами плавать, наблюдаем, как в воздухе летают воздушные шары. Сегодня мы с вами еще раз поговорим о законе Архимеда, о том, как он был открыт и как проявляется.
Сегодня мы с вами еще раз поговорим о законе Архимеда, о том, как он был открыт и как проявляется.
Начнём мы с вами наш урок с исторического экскурса:
1ученик рассказывает биографию Архимеда.
2 ученик рассказывает легенду о короне царя Гиерона (используется интерактивное сопровождение из электронного приложения к УМК «Сферы»)
Учитель: Теперь нам стало понятно, почему выталкивающую силу назвали силой Архимеда. Давайте посмотрим, а что мы знаем по нашей теме урока.
Ребята, в ваших тетрадях-тренажёрах есть задание, где необходимо дописать недостающие слова. Наше первое задание именно такого типа. Я предлагаю вам вставить пропущенные слова. (Текст)
«Сила, выталкивающая тело из жидкости или газа, называется… .
Она получила название в честь древнегреческого ученого … ,который впервые указал на ее существование и рассчитал ее значение. Сила Архимеда рассчитывается по формуле: … .
Она зависит от … и не зависит от плотности … . По закону Архимеда: на тело,
погруженное в жидкость, действует выталкивающая сила, равная по
величине … ,вытесненной телом.»
(Архимедовой силой, Архимеда, плотности жидкости и объема
тела, вещества, из которого сделано тело, весу жидкости).
Давайте обратим внимание на экран и вспомним основные моменты прошлых уроков. В презентации рассматриваются формула силы Архимеда, в динамике рассматриваются условия плавания тел. Далее учащимся предлагается выполнить тестовые задания по данной теме.
По окончании повторения на экран выводится итоговая схема по данной теме.
2. Физические опыты.
Опыт 1. “Удивительный картофель”.
Возьмем стеклянную банку с чистой водой. Опустим в нее сырую картофелину. Картофель сразу тонет. Возьмем вторую банку с насыщенным раствором соли и начнем подливать соленую воду в первую банку. В какой-то момент картофелина начнет всплывать вверх.
Вывод: соленая вода имеет большую плотность, чем картошка, поэтому она плавает в ней, а чистая вода имеет меньшую плотность, поэтому картошка тонет.
Опыт 2. «Плавание судов».
Берем пластинку из металлической фольги опускаем в воду. Она тонет. Сгибаем пластинку в виде коробки, она плавает на поверхности воды, даже если поставить груз. Вывод: вес воды, вытесненной подводной частью судна равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Опыт 3. «Бермудский треугольник»
Тайна исчезновения кораблей в Бермудском треугольнике уже давно привлекает ученых. За время исследования этого феномена было предложено большое число теорий как научно обоснованных, так и совершенно фантастических.
Одной из самых правдоподобных считается «пузырьковая» гипотеза, согласно которой корабли в Бермудском архипелаге могут тонуть из-за попадания в области, где идет активное выделение метана из подводных газовых месторождений. Ввиду огромного давления на больших глубинах метан находится в твердом состоянии, в виде так называемых гидратов. В случае землетрясений, подводных извержений и т.д. гидраты могут резко переходить в газообразную форму, порождая гигантские «облака» пузырей, поднимающихся к поверхности океана.
Ввиду огромного давления на больших глубинах метан находится в твердом состоянии, в виде так называемых гидратов. В случае землетрясений, подводных извержений и т.д. гидраты могут резко переходить в газообразную форму, порождая гигантские «облака» пузырей, поднимающихся к поверхности океана.
Насколько обоснована эта гипотеза? Каким образом выделение метана может приводить к гибели кораблей? Мы поставили опыт, чтобы экспериментально исследовать ситуацию, моделирующую условия гибели судов и проверить «пузырьковую» гипотезу.
Для этого в 3-х литровой банке с водой растворяем соду. Опускаем туда яйцо из «киндерсюрприза», наполненное песком так, чтобы оно держалось на воде. Это – корабль. Добавляем в воду лимонную или уксусную кислоту. Начинается бурная химическая реакция с выделением пузырьков углекислого газа по всему объему банки. Плотность жидкости уменьшается, что приводит к уменьшению силы Архимеда. Мы заметили, что яйцо немедленно тонет. Когда интенсивность выделения пузырьков заметно ослабевает, яйцо вновь всплывает на поверхность. Корабль при погружении, в отличие от яйца, заполняется водой. Поэтому после прекращения выделения пузырьков метана он не всплывет.
Корабль при погружении, в отличие от яйца, заполняется водой. Поэтому после прекращения выделения пузырьков метана он не всплывет.
Опыт 4. Сделаем бумажный цилиндр, подвесим вверх дном на рычаг и уравновесим. Поднесем спиртовку под цилиндр. Под действием тепла равновесие нарушается, сосуд поднимается вверх.
Вывод: оболочки, наполненные теплым газом или горячим воздухом называют воздушными шарами и применяют для воздухоплавания.
3.Решение задач
1 задача. Железобетонная плита имеет длину 3,5 м, ширину 1,5 м,
толщину 0,2 м. Вычислите архимедову силу, действующую в воде. (10,5 кН)
2 задача. Какую силу необходимо приложить, чтобы поднять в
воде камень массой 20 кг, объем которого 0,01 кубического метра? (100Н).
3 задача. Используя таблицу плотностей, найдите ответы на вопросы.
а) В какой воде легче плавать: морской или речной? Почему?
б) Почему горящий керосин нельзя тушить водой?
в) Из какого материала можно взять тело, чтобы оно плавало на
поверхности воды, внутри этой жидкости, тонуло?
4. Самостоятельная работа. Учащиеся заполняют таблицы, предложенные им на листах.(Решают тест на выбор учителя)
Самостоятельная работа. Учащиеся заполняют таблицы, предложенные им на листах.(Решают тест на выбор учителя)
5. Подведение итогов урока. подведение итогов, оглашение результатов
Домашнее задание: закончить работу в тетрадях-тренажёрах по теме, по желанию выполнить индивидуальную практическую работу, сделать отсчёт.
Литература:
- Белага В.В., Ломаченков И.А., Панебратцев Ю.А. Физика. 7 кл. [Просвещение], 2009
- Панебратцев Ю.А., Ломаченков И.А., Белага В.В. Под редакцией Панебратцева Ю.А. Физика. Тетрадь-практикум. 7 класс. [Просвещение],2009
- Физика. 7 класс. Электронное приложение к учебнику
- Панебратцев Ю.А., Ломаченков И.А., Белага В.В. Под редакцией Панебратцева Ю.А. Физика. Тетрадь-тренажёр. 7 класс. [Просвещение],2009
- http://ru.wikipedia.org/wiki/архимед
- http://www.claw.ru
- http://www.popmech.ru
Скачать презентацию
Скачать приложения
14.
 4 Принцип Архимеда и плавучесть – общая физика с использованием исчисления I
4 Принцип Архимеда и плавучесть – общая физика с использованием исчисления IЦели обучения
К концу этого раздела вы сможете:
- Определение выталкивающей силы
- Государственный закон Архимеда
- Опишите связь между плотностью и принципом Архимеда
При помещении в жидкость некоторые объекты всплывают благодаря выталкивающей силе. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Поддерживает ли ваше тело атмосфера или только воздушные шары с гелием (рисунок)?
Рис. 14.19 (a) Даже предметы, которые тонут, как этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (c) Воздушные шары, наполненные гелием, тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит b: модификация работы Allied Navy; кредит c: модификация работы «Crystl»/Flickr) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. На любой объект в любой жидкости действует направленная вверх сила или выталкивающая сила (рисунок). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. На любой объект в любой жидкости действует направленная вверх сила или выталкивающая сила (рисунок). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила
Выталкивающая сила — это направленная вверх сила, действующая на любой объект в любой жидкости.
Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что [латекс]p=hpg[/латекс]. Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра.
 Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс].(Горизонтальные силы компенсируются.)
Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс].(Горизонтальные силы компенсируются.)Закон Архимеда
Насколько велика выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке. Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [латексу] {w} _ {\ text {фл}}, [/ латексу] весу жидкости, вытесненной объектом.
Принцип АрхимедаВыталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равно
[латекс] {F} _ {\ text {B}} = {w} _ {\ text {fl}}, [/ латекс]
, где [латекс]{F}_{\text{B}}[/латекс] — выталкивающая сила, а [латекс]{w}_{\текст{fl}}[/латекс] — вес вытесненной жидкости. по объекту.
по объекту.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок.287–212 гг. до н. э.), который сформулировал этот принцип задолго до того, как утвердились концепции силы.
Рисунок 14.21 (a) На объект, погруженный в жидкость, действует выталкивающая сила [латекс] {F} _ {\ text {B}}. [/latex] Если [латекс] {F} _ {\ text {B} }[/latex] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости. Принцип Архимеда относится к силе плавучести, которая возникает, когда тело полностью или частично погружено в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила давления внизу направлена вверх, а сила давления вверху направлена вниз; силы из-за давлений по бокам направлены внутрь тела.
Поскольку нижняя часть тела находится на большей глубине, чем верхняя часть тела, давление в нижней части тела выше, чем давление в верхней части, как показано на рисунке.Следовательно, на тело действует направленная вверх сила. Эта направленная вверх сила есть сила плавучести, или просто плавучесть .
Плотность и закон Архимеда
Если бросить в воду кусок глины, он утонет. Но если вы слепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу, хотя ее масса одинакова. То же самое и со стальными кораблями.
Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он.Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта.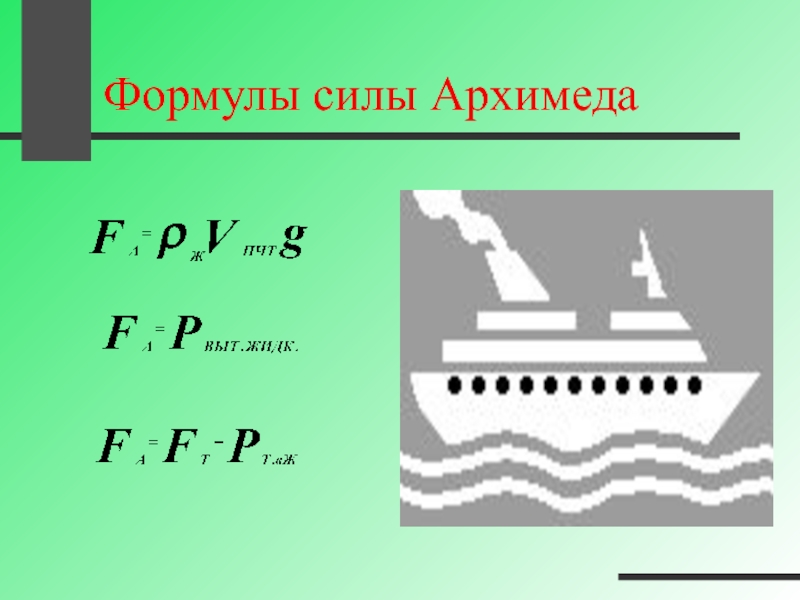 Точно так же объект, более плотный, чем жидкость, утонет.
Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавающего объекта зависит от того, как плотность объекта соотносится с плотностью жидкости.На рисунке, например, незагруженный корабль имеет меньшую плотность и меньше его погружено в воду по сравнению с тем же кораблем, когда он загружен. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \ text {фракция погружена} = \ frac {{V} _ {\ text {sub}}} {{V} _ {\ text {obj}}} = \ frac {{V} _ {\ text {fl}}}{{V}_{\text{obj}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]{V}_{фл}[/латекс].Теперь мы можем получить связь между плотностями, подставив в выражение [латекс]\ро =\фрак{м}{В}[/латекс]. Это дает
[латекс] \ frac {{V} _ {\ text {fl}}} {{V} _ {\ text {obj}}} = \ frac {{m} _ {\ text {fl}} \ text { /}{\rho}_{\text{fl}}}{{m}_{\text{obj}}\text{/}{\rho}_{\text{obj}}},[/latex]
, где [latex]{\rho }_{\text{obj}}[/latex] — средняя плотность объекта, а [latex]{\rho }_{\text{fl}}[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\текст{фракция погружена}=\фракция{{\rho}_{\text{obj}}}{{\rho}_{\text{fl}}}.[/латекс]
Мы можем использовать это соотношение для измерения плотности.
Рисунок 14.22 Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).Пример
Расчет средней плотности
Предположим, что женщина весом 60,0 кг плавает в пресной воде, при этом 97,0% ее объема погружено под воду, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение
[латекс]\текст{фракция погружена}=\фракция{{\rho}_{\text{obj}}}{{\rho}_{\text{fl}}}[/latex]
для плотности объекта.{3}}.[/латекс]
Значение
Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.
Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе», ” назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на рисунке.
Рис. 14.23 (a) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты. Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости.Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Все эти расчеты основаны на принципе Архимеда, согласно которому выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что погруженный в воду объект кажется менее весящим; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости.То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Резюме
- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине.
 Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Концептуальные вопросы
Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Показать РешениеВовсе нет. Принцип Паскаля гласит, что изменение давления осуществляется через жидкость.Причина, по которой полная ванна требует большего усилия, чтобы вытащить пробку, заключается в весе воды над пробкой.
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом корабле? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
Показать решение Выталкивающая сила равна весу вытесненной жидкости. Чем больше плотность жидкости, тем меньше жидкости необходимо вытеснить, чтобы удерживать вес объекта и плавать. {3}[/латекс]?
{3}[/латекс]?
а.погружено на 99,5 %; б. 96,9 % под водой
Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350.{3}[/латекс]; этиловый спирт
Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Объемом резины пренебречь.
Какова плотность женщины, плавающей в пресной воде с [латексом]4,00\текст{%}[/латекс] ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой.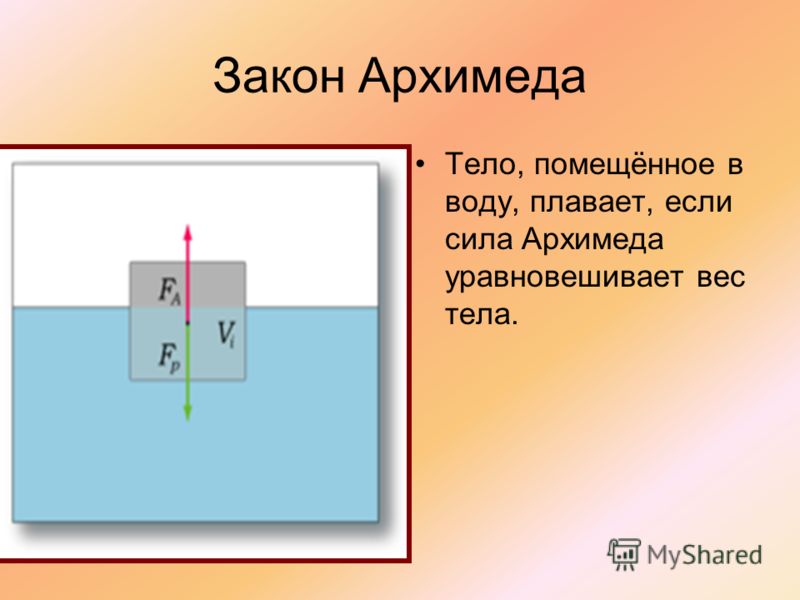 {3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
{3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
Показать решениеа.0,24; б. 0,68; в. Да, пробка будет плавать в этиловом спирте.
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
С помощью рисунка докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна [латекс]{F}_{2}-{F}_{1}[/латекс] и что концы цилиндра имеют равные площади [латекс]А[/латекс]. Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]({ч}_{2}-{ч}_{1})А[/латекс].
Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]({ч}_{2}-{ч}_{1})А[/латекс].
[латекс]\begin{array}{ccc}\text{net}\,F\hfill & =\hfill & {F}_{2}-{F}_{1}={p}_{ 2}A-{p}_{1}A=({p}_{2}-{p}_{1})A=({h}_{2}{\rho}_{\text{fl }}g-{h}_{1}{\rho}_{\text{fl}}g)A\hfill \\ & =\hfill & ({h}_{2}-{h}_{1 }){\rho}_{\text{fl}}gA,\,\text{где}\,{\rho}_{\text{fl}}=\text{плотность жидкости}\text{.} \hfill \\ \text{net}\,F\hfill & =\hfill & ({h}_{2}-{h}_{1})A{\rho}_{\text{fl}}g = {V} _ {\ text {fl}} {\ rho} _ {\ text {fl}} g = {m} _ {\ text {fl}} g = {w} _ {\ text {fl}} \hfill \end{массив}[/латекс]
А 75.Человек массой 0 кг плавает в пресной воде так, что 3,00% его объема над водой, когда его легкие пусты, и 5,00% его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости из-за разницы давлений на разных глубинах
Qalaxia — это бесплатный сайт вопросов и ответов для классных комнат. На Калаксии:
На Калаксии:
- Учащиеся обращаются за помощью к домашним заданиям на онлайн-форумах по домашним заданиям и получают помощь от экспертов и студентов-добровольцев
- Учащиеся задают вопросы и получают ответы от экспертов отрасли
- Студенты получают вознаграждение за вопросы и ответы на них
- Учащиеся зарабатывают волонтерские часы, помогая другим учащимся, не выходя из дома
- Учащихся поощряют публиковать вопросы и отвечать на вопросы, опубликованные экспертами
- Учителя имеют доступ к библиотеке вопросов, составленной учителями и отраслевыми экспертами
- Учащимся нравится индивидуальное обучение с механизмом рекомендаций, который адаптируется к успеваемости учащихся, и индивидуальной помощью от экспертов
Qalaxia будет готова к использованию в апреле 2017 года. Пожалуйста, подпишитесь здесь на обновления
Пожалуйста, подпишитесь здесь на обновления
Лучшие вопросы и ответы. От экспертов для классных комнат.
Qalaxia — это сайт вопросов и ответов для учителей, студентов и экспертов, где эксперты делятся своими мыслями и знаниями с классами.
Эксперты любят Qalaxia, поскольку они могут помогать учащимся в удобное для них время, отвечая и задавая вопросы.
Студенты любят Qalaxia, поскольку они получают вознаграждение за правильные ответы на вопросы викторины и за размещение хороших вопросов для экспертов. Qalaxia стимулирует и предоставляет учащимся необходимую помощь для своевременного выполнения домашних заданий и удовлетворения их любопытства.
Учителя любят Qalaxia, поскольку она не только помогает учащимся выполнять домашние задания и удовлетворяет их любопытство, но и дает учителям полную информацию о том, сколько усилий и помощи специалистов было потрачено учащимися на решение каждого домашнего задания.
Мир, в котором ни один студенческий вопрос не остается без ответа или без ответа
Мы пробуждаем и укрепляем пытливого человека в каждом ребенке и наставника в каждом человеке
Qalaxia — это платформа вопросов и ответов, созданная для того, чтобы воспитать в каждом ученике пытливого, искателя и исследователя.Qalaxia поощряет студентов получать знания не только от учителей, но и от удаленных отраслевых экспертов-добровольцев.
ИИ и помощник учителя в каждом классе
Актуальная помощь студентам
Удивительный учитель рядом с каждым учеником, когда это необходимо
- Увлеченный образованием
- Эксперты по искусственному интеллекту и программному обеспечению
- Иметь послужной список академического и профессионального мастерства
Принцип Архимеда – Учебники по основам физики
Корабль с огромной массой не тонет, а камень небольшого размера может утонуть. Это почему? Ответ прост, если вы понимаете концепцию плавучести и принцип Архимеда.
Это почему? Ответ прост, если вы понимаете концепцию плавучести и принцип Архимеда.
В повседневной жизни мы обнаружим, что предметы, погруженные в жидкость, например камень, имеют меньший вес, чем предметы, не находящиеся в жидкости. Вам может быть трудно поднять камень с земли, но тот же камень легко поднимается со дна морской воды. Это происходит из-за выталкивающей силы. Плавучесть возникает из-за различий в давлении жидкости на разных глубинах.Давление жидкости увеличивается с глубиной, чем гуще жидкость, тем больше давление жидкости. Когда объект помещается в жидкость, возникает разница в давлении между жидкостью в верхней части объекта и жидкостью в нижней части объекта. Жидкость, находящаяся в нижней части объекта, имеет большее давление, чем жидкость в верхней части объекта.
На рисунке вы видите объект, плавающий в воде. Жидкость в нижней части объекта имеет более высокое давление, чем жидкость, расположенная в верхней части объекта. Это связано с тем, что жидкость под объектом имеет большую глубину, чем жидкость над объектом (h 2 > h 1 ).
Это связано с тем, что жидкость под объектом имеет большую глубину, чем жидкость над объектом (h 2 > h 1 ).
Величина давления жидкости на глубине h 2 составляет:
Величина давления жидкости на глубине h 1 составляет:
F 2 = сила, приложенная жидкостью к нижней части объекта, F 1 = сила, приложенная жидкостью к верхней части объекта, A = площадь поверхности объекта
Разница между F 2 и F 1 представляет собой общую силу, действующую на объект со стороны жидкости, которую мы знаем как выталкивающую силу.Величина плавучести составляет:
F плавучесть = F 2 − F 1
F плавучесть = (ρ g h 2 A ) − (ρ g h 1 A)
F плавучесть = ρ g A ( h 2 − h 1 )
F плавучесть = ρ F g A ч
F плавучесть = ρ F g V
ρ F = плотность жидкости, g = ускорение свободного падения, V = объем объектов в жидкости
Итак, мы можем написать уравнение, определяющее величину плавучести (плавучесть F) выше:
F плавучесть = ρ F g V → m = ρ V
F Плавучесть = м F г
F Плавучесть = w F
m F g = w F = вес жидкости, объем которой равен объему погруженного объекта.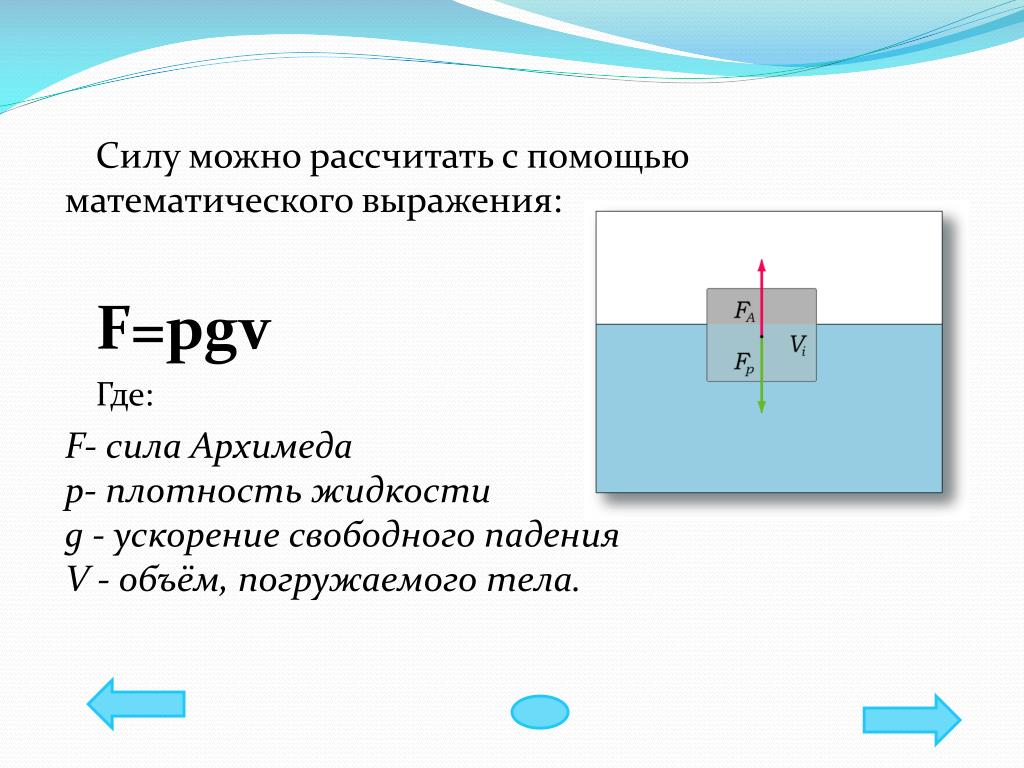
На основании вышеприведенного уравнения можно сказать, что выталкивающая сила равна весу вытесняемой жидкости, объем вытесненной жидкости подобен объему предмета, погруженного в жидкость.
Если объект погружен в жидкость, плавающий, где погруженная часть объекта является лишь частью, то объем вытесненной жидкости = объему части объекта, погруженной в жидкость. Независимо от того, что это за объект и какова его форма, все будут испытывать одно и то же.Это результат работы Архимеда (287-212 до н.э.), известный как принцип Архимеда.
Закон Архимеда утверждает, что:
Когда объект полностью или частично погружают в жидкость, жидкость будет создавать направленную вверх силу (выталкивающую силу) на объект, причем величина направленной вверх силы (выталкивающая сила) равна весу вытесняемой жидкости.
История Архимеда
Архимеду, жившему между 287-212 гг. до н.э., царь Гиерон II поручил выяснить, была ли корона, сделанная для царя, сделана из чистого золота или нет.Чтобы узнать, сделана ли корона из чистого золота или корона содержит другие металлы, Архимед сначала запутался. Проблема в том, что форма короны неправильная, и ее нельзя сначала разрушить, чтобы можно было определить, сделана корона из чистого золота или нет.
до н.э., царь Гиерон II поручил выяснить, была ли корона, сделанная для царя, сделана из чистого золота или нет.Чтобы узнать, сделана ли корона из чистого золота или корона содержит другие металлы, Архимед сначала запутался. Проблема в том, что форма короны неправильная, и ее нельзя сначала разрушить, чтобы можно было определить, сделана корона из чистого золота или нет.
Идея определения того, изготовлена корона из чистого золота или нет, состоит в том, чтобы сначала определить вес короны, а затем сравнить его с удельным весом золота. Если корона сделана из чистого золота, то удельный вес короны = удельный вес золота.
Удельный вес объекта – это отношение веса объекта в воздухе к весу воды, объем которой равен объему объектов. Математически записано:
Как определить вес воды, объем которой равен объему предметов?
Согласно Архимеду, вес воды, имеющей тот же объем, что и объем предмета, равен величине выталкивающей силы, когда предмет тонет (целая часть предмета погружается в воду). Это то же самое, что вес предметов, потерянных при взвешивании в воде. Следовательно:
Это то же самое, что вес предметов, потерянных при взвешивании в воде. Следовательно:
Для определения удельного веса коронки сначала взвешивают коронку в воздухе (вес коронки в воздухе). Затем корону опускают в воду и снова взвешивают, чтобы получить потерянный вес короны. Итак:
После получения удельного веса короны его сравнивают с удельным весом золота. Удельный вес золота = 19.3. Если удельный вес короны = удельный вес золота, то корона изготовлена из чистого золота. Но если корона не из чистого золота, то удельный вес короны не такой, как удельный вес золота.
Почему корабль не тонет?
Если плотность объекта меньше плотности воды, то объект будет плавать. И наоборот, если плотность объекта больше плотности воды, то объект утонет. Большинство кораблей сделаны из железа и стали.Плотность железа и стали = 7,8 x 10 3 кг/м 3 , а плотность воды = 1,00 x 10 3 кг/м 3 . Оказывается, плотность железа и стали больше плотности воды. В этом случае удельный вес железа и стали = 7,8. Корабль должен быть раковиной. Почему корабль не тонет? Общая плотность корабля меньше плотности воды или морской воды.
Оказывается, плотность железа и стали больше плотности воды. В этом случае удельный вес железа и стали = 7,8. Корабль должен быть раковиной. Почему корабль не тонет? Общая плотность корабля меньше плотности воды или морской воды.
Пример проблемы 1:
Камень массой 40 кг лежит на дне пруда.Если объем камня = 0,2 м3, какая минимальная сила необходима, чтобы поднять камень?
Известен:
Масса камня (м) = 40 кг
Объем камня (V) = 0,02 м 3
Плотность воды = 1000 кг/м 3
Ускорение свободного падения (g) = 10 м/с 2
Разыскивается: F минимум
Решение:
F Плавучесть = w F
F плавучесть = m F g → m = pV
F плавучесть = ρ F g V
F плавучесть = (1000 кг/м 3 )(10 м/с 2 )(0. 02 м 3 )
02 м 3 )
F плавучесть = 200 кг м/с 2
F плавучесть = 200 Н
вес камня (w) = м г
вес камня = (40 кг)(10 м/с 2 )
вес камня = 400 кг м/с 2
вес камня = 400 Н
Минимальная сила, необходимая для подъема камня:
вес камня – выталкивающая сила = 400 Н – 200 Н = 200 Н
Пример проблемы 2:
Вес объекта в воздухе = 5000 кг м/с 2 и вес объекта в воде = 4000 кг м/с 2 .Если плотность объекта = 2000 кг/м 3 , какова масса и объем объекта? g = 10 м/с 2
Решение
Ускорение свободного падения (g) = 10 м/с 2
Плотность объекта = 2000 кг/м 3
Плотность воды = 1000 кг/м 3
Вес объекта в воздухе = 5000 кг м/с 2
Вес объекта в воде = 4000 кг м/с 2
Выталкивающая сила (плавучесть F) = вес объекта в воздухе – вес объекта в воде
F плавучесть = 5000 кг м/с 2 – 4000 кг м/с 2
F плавучесть = 1000 кг м/с 2
F плавучесть = вес вытесненной воды
F плавучесть = (масса воды)(г)
F плавучесть = (объем вытесненной воды)(плотность воды)(г)
Объем вытесненной воды = объем объекта в воде
Объем объекта = 0.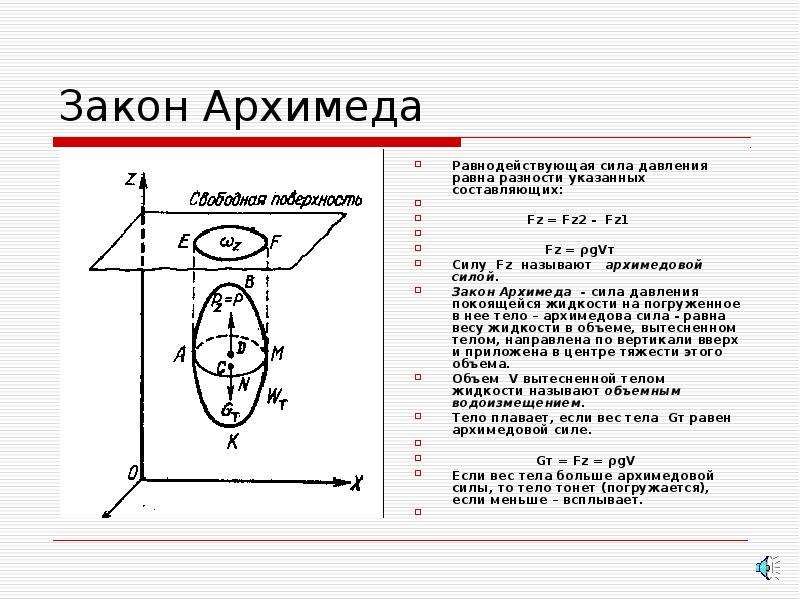 1 м 3
1 м 3
Масса объекта = ?
ρ = м/В
м = ρ В
м = (2000 кг/м 3 )(0,1 м 3 )
м = 200 кг
Масса объекта = 200 кг
Пример проблемы 3:
Какой объем гелия потребуется, если шар должен поднять груз массой 500 кг?
Решение:
Плотность гелия = 0,1786 кг/м 3
Плотность воздуха = 1,293 кг/м 3
Выталкивающая сила = вес вытесненного воздуха = вес предмета + вес гелия
Выталкивающая сила = вес объекта + вес гелия
Выталкивающая сила = (масса груза)(г) + (масса гелия)(г)
Выталкивающая сила = (масса груза + масса гелия) г — уравнение 1
Выталкивающая сила = вес воздуха, вытеснившего
Выталкивающая сила = (масса вытесненного воздуха)(г) — уравнение 2
Объединяем уравнение 1 и уравнение 2:
(масса груза + масса гелия)(г) = (масса вытесненного воздуха)(г)
масса груза + масса гелия = масса воздуха, вытеснившего
500 кг + ( ρ гелия)( V гелия) = ( ρ воздуха)( V воздуха)
500 кг = ( ρ воздуха)( V воздуха) – ( ρ гелия)( V гелия)
Объем вытесненного воздуха (V воздуха) = Объем гелия в баллоне (V гелия)
500 кг = ( ρ воздуха – ρ гелия)(V)
Это минимальный объем гелия, необходимый для подъема тяжестей на земную поверхность. Чтобы воздушный шар поднялся выше, необходимо добавить объем гелия. Объем гелия необходимо увеличить, потому что плотность воздуха уменьшается с высотой.
Чтобы воздушный шар поднялся выше, необходимо добавить объем гелия. Объем гелия необходимо увеличить, потому что плотность воздуха уменьшается с высотой.
жидкостей – принцип Архимеда | Шмуп
Принцип Архимеда
Архимед и золотая корона
Вы когда-нибудь слышали выражение Эврика ? Согласно словарю Merriam-Webster, мы используем слово «эврика», чтобы «выразить триумф открытия». Оно образовано от греческого слова эврика ( εὕρηκα), что означает «Я нашел это!»
В 3 rd веке до нашей эры жил великий изобретатель, математик и ученый по имени Архимед.Ему было поручено проверить, не смешал ли Голдсмит Крук (предок Механика Крука) серебро при изготовлении золотой короны короля Иеро II. Люди знали Архимеда за его гениальность (он был сообразительным парнем), и, видимо, люди знали Голдсмита Крука за его беспринципные методы. Это означает, что король Иеро, должно быть, был великолепен в том, чтобы улавливать нечестность или просто жить с крайним чувством паранойи.
Так или иначе, у золота очень высокая плотность, плотность золота .Неважно, в какой форме находится золото, его плотность всегда будет .
Архимед решил, что для того, чтобы определить, сделана ли корона короля из чистого золота, он должен определить плотность короны.
*Пауза*
Как нам снова измерить плотность? О, да, мы это помним. Плотность равна массе, деленной на объем, или . Легко определить массу объекта. Проблема Архимеда заключалась в том, чтобы определить объем короны. Это не было похоже на куб, цилиндр или любое другое правильное твердое тело.
*А теперь вернемся к истории*
Архимед крепко задумался. Переплавление короны в золотую сферу для расчета ее объема могло бы сработать, но в конечном итоге корона разрушилась бы. Царь Гиерон убеждал Архимеда найти другой путь. Ювелир Крук уверял короля, что корона сделана из чистого золота. Так что же сделал Архимед? Подобно Джону Уэйну несколько столетий спустя, Архимед принял ванну.
Архимед заметил, что уровень воды поднялся, когда он вошел в ванну.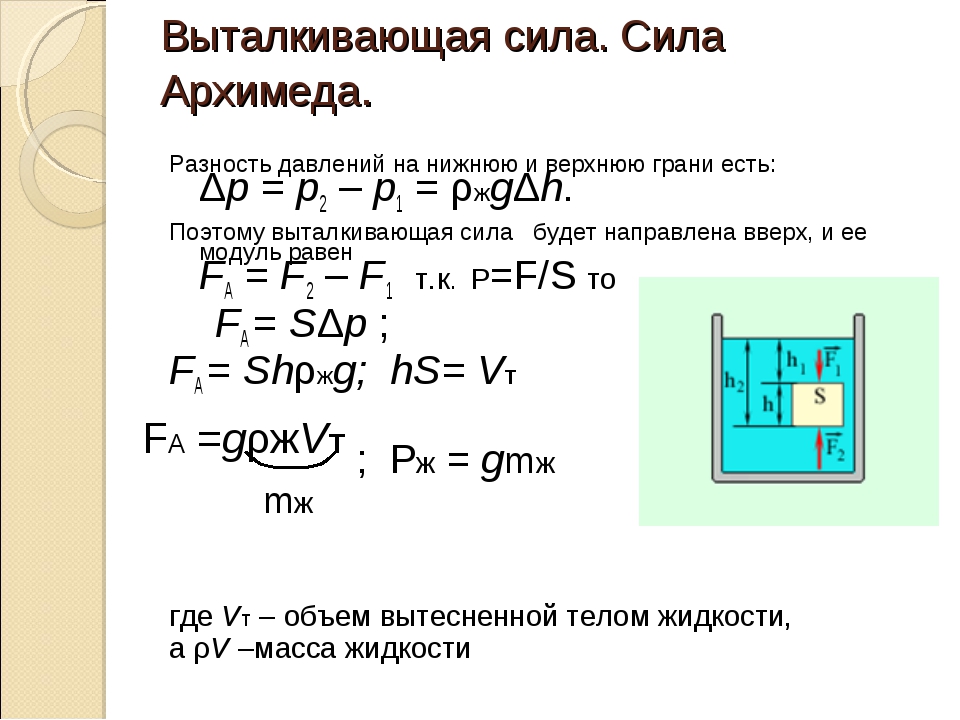 Именно в этот момент на него нашло озарение.Уровень воды был ключом.
Именно в этот момент на него нашло озарение.Уровень воды был ключом.
Уровень воды поднялся на определенную величину: на величину, основанную на объеме его тела. Логично предположить, что корона, погруженная в воду, вытеснит воду на количество, равное объему короны. В сущности, он мог найти V .
Архимед так разволновался, что побежал голышом по улицам, крича: “Эврика! Эврика!” Похоже, тогда все решалось по-другому, потому что его не арестовали.
А что случилось с Голдсмитом Круком? Мы не знаем.Однако мы знаем, что он оправдал свое имя Крук. Корона короля была не из чистого золота, а из смеси золота и серебра.
Плавучесть и выталкивающая сила
История Архимеда иллюстрирует явление, известное как плавучесть . Плавучесть – это способность плавать.
Если мы бросим мячик для пинг-понга в ведро с водой, он всплывет. Если мы бросим мячик для гольфа в ведро, он утонет. Какая разница?
Плотность мячика для пинг-понга меньше плотности воды, а плотность мяча для гольфа больше плотности воды, однако оба испытывают выталкивающую силу . Эта сила присутствовала, когда Архимед вошел в свою ванну, прежде чем бежать голышом по улицам. Объект, погруженный в жидкость, вытесняет количество жидкости, равное объему объекта, и вытесненная жидкость давит на объект вверх. Это выталкивающая сила. Толчок жидкости вверх равен весу самой вытесненной жидкости. Если вес вытесненной жидкости больше веса предмета, то предмет всплывает. Если нет, то тонет.
Эта сила присутствовала, когда Архимед вошел в свою ванну, прежде чем бежать голышом по улицам. Объект, погруженный в жидкость, вытесняет количество жидкости, равное объему объекта, и вытесненная жидкость давит на объект вверх. Это выталкивающая сила. Толчок жидкости вверх равен весу самой вытесненной жидкости. Если вес вытесненной жидкости больше веса предмета, то предмет всплывает. Если нет, то тонет.
Вес – это сила. Вес вытесненной воды, выталкиваемой вверх, известен как Закон Архимеда , который проиллюстрирован на следующей диаграмме.Это само определение выталкивающей силы.
Не забывайте, что выталкивающей силе соответствует вес жидкости, вытесненной объектом, а не вес объекта.
Кажется, что объекты имеют разный вес в различных жидкостях из-за чистой разницы между силой гравитации, притягивающей вниз, и выталкивающей силой, толкающей вверх. Вот почему мы чувствуем, что весим меньше в бассейне: нормальная сила, которую наши ноги ощущают на дне бассейна, меньше, чем нормальная сила, которую они ощущают на суше.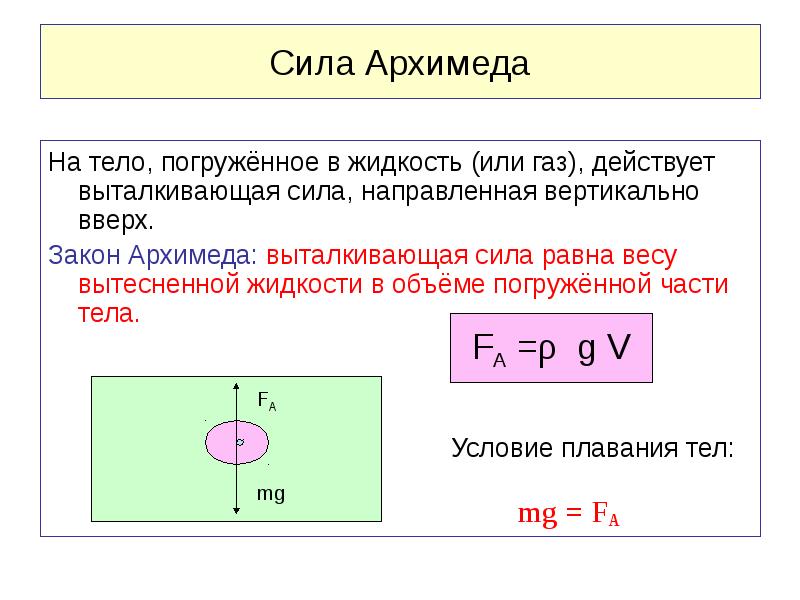
Диаграмма силы для этой системы представляет собой силу тяжести, направленную вниз, как обычно, и того же размера, что и обычно ( мг ), но вместо одной нормальной силы, направленной вверх, есть выталкивающая сила, направленная вверх, и меньшая нормальная сила, обе которые в сумме уравновешивают силу тяжести.
Чтобы перефразировать ту же мысль, обратите внимание, что выталкивающая сила одинакова для любых двух объектов одинакового размера. Плотность влияет на силу тяжести самого объекта, но не на вес вытесненной воды.Таким образом, плотность также определяет, плавает объект или тонет, а не выталкивающая сила.
Гидростатическое равновесие
Все объекты должны плавать или тонуть? Неа. Они могут просто… повиснуть. В прямом смысле.
Объект в жидкости, который не тонет полностью и не всплывает на поверхность, считается находящимся в равновесии. Если объект находится в равновесии, то силы, действующие на него, уравновешиваются: сила тяжести равна (и противоположна по направлению) выталкивающей силе, действующей на него.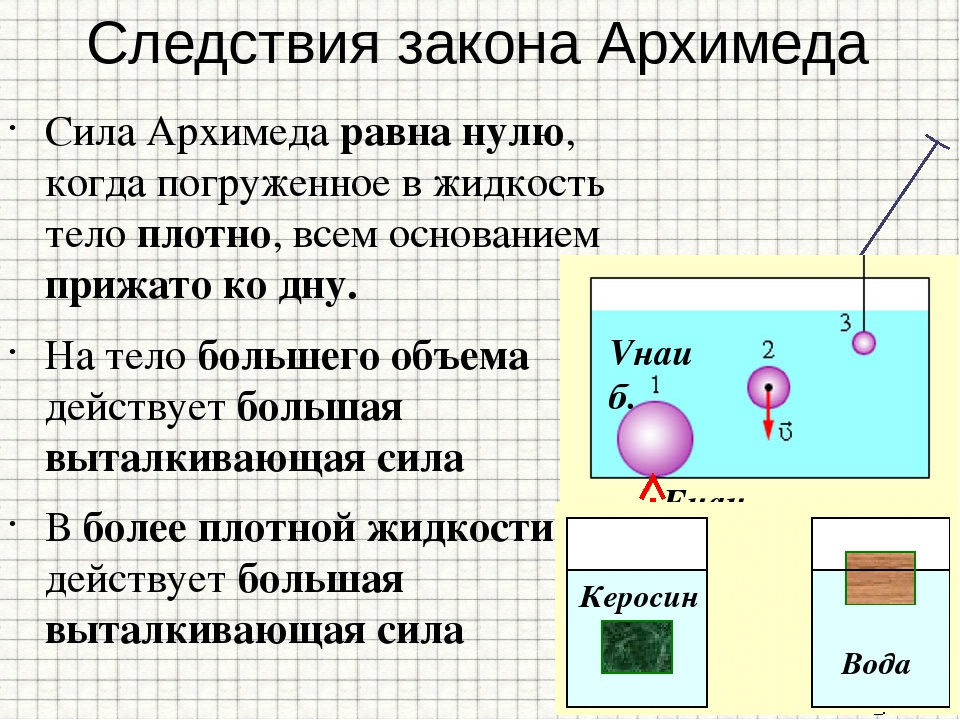
Гидростатическое равновесие относится к состоянию объекта, который не движется, будучи погруженным в другую жидкость.В этом случае выталкивающая сила F b жидкости равна ее весу F g при погружении в другую жидкость. Например, подумайте о нефти и воде. Нефть имеет меньшую плотность, чем вода, поэтому она плавает. На следующей диаграмме показаны три случая гидростатического равновесия с тремя шарами разной плотности.
Помните, что в конечном счете плавучесть объекта определяется его плотностью. Эта диаграмма использует ρ для описания плотности.Плотность объекта ρ 1 , а плотность жидкости ρ 2 .
Мы все знакомы с ситуациями, когда ρ 1 > ρ 2 , как если бы вы уронили iPhone в унитаз. Также распространены ситуации, когда ρ 1 < ρ 2 , например, пляжный мяч, плавающий на воде. Когда ρ 1 = ρ 2 , объект или другая жидкость имеет ту же плотность, что и окружающая ее жидкость.Это известно как нейтральная плавучесть .
Когда ρ 1 = ρ 2 , объект или другая жидкость имеет ту же плотность, что и окружающая ее жидкость.Это известно как нейтральная плавучесть .
Вот силовая диаграмма плавающего объекта, находящегося в равновесии. Обратите внимание, что выталкивающая сила (зеленая стрелка) того же размера, что и сила тяжести (красная стрелка), что указывает на то, что вес вытесненной воды равен силе тяжести, действующей на объект. Если бы объект держали под водой, а затем отпустили, то выталкивающая сила была бы больше, чем сила тяжести, и вытолкнула бы объект на поверхность, чтобы найти равновесие.
Позже мы научимся рассчитывать объем вытесненной воды для плавучего объекта (используя диаграммы сил и формулы плотности). Терпение, терпение.
Да ладно. Мы сделаем это сейчас.
Шарик для пинг-понга весом 2,7 г плавает в миске с водой. Сколько воды он вытесняет?
Первый шаг, давайте соберем информацию, чтобы посмотреть, достаточно ли у нас для работы.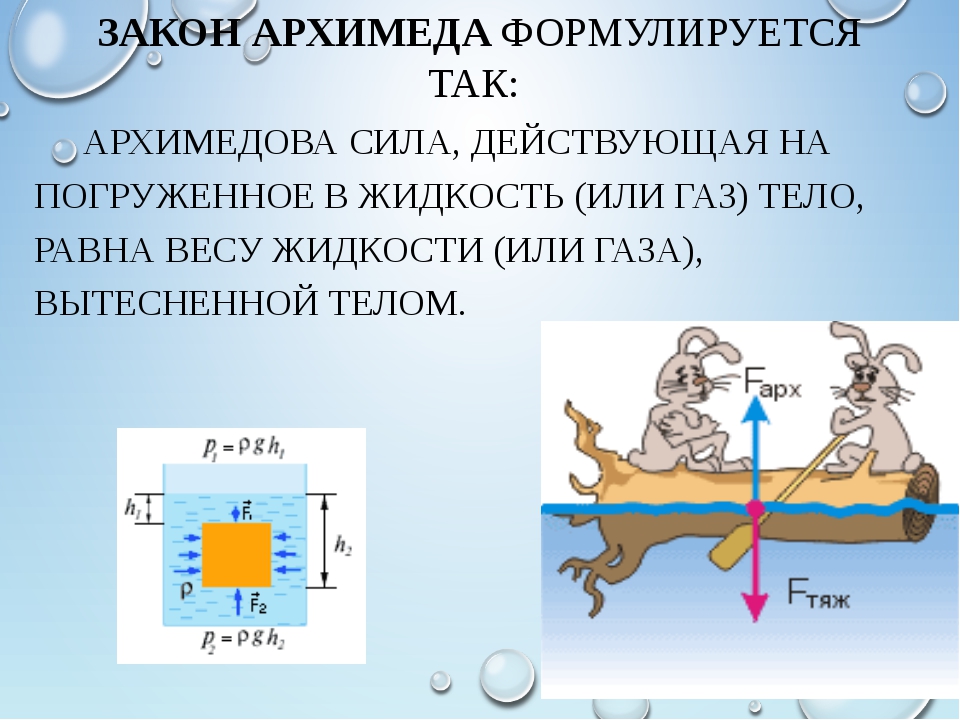 Поскольку шарик для пинг-понга не ускоряется, мы знаем, что F g = F b , и мы знаем, как рассчитать величину этой силы с помощью .Довольно маленький.
Поскольку шарик для пинг-понга не ускоряется, мы знаем, что F g = F b , и мы знаем, как рассчитать величину этой силы с помощью .Довольно маленький.
Выталкивающая сила также равна 0,026 Н, поскольку эти две силы уравновешены. Что теперь? Мы знаем плотность воды. Выталкивающая сила равна весу вытесненной воды, или м w г , поэтому вытесненная вода также равна 0,027 г. Теперь мы можем использовать плотность воды, чтобы найти вытесненный объем: V = = 2,7 × 10 6 м 3 или 2,7 см 3 . Та-да.
Если бы объем шарика для пинг-понга был равен 33.5 см 3 (или радиус, с помощью которого мы могли бы рассчитать объем), тогда мы могли бы сравнить отношение out to in и сказать, что шарик для пинг-понга только погружен, или 8,1%.
Поверхностное натяжение
Любой, кто раньше наблюдал водяных жуков в пруду, имеет представление о том, что такое поверхностное натяжение .
Эти насекомые на самом деле называются водомерками. Поскольку их плотность больше плотности воды, страйдер должен утонуть. Как объяснить это не совсем волшебное явление?
Представьте себе каплю воды со всеми ее 10 21 молекулами.Эти молекулы притягиваются друг к другу, иначе не было бы капли воды. Говоря языком физики, мы скажем, что эти молекулы действуют друг на друга с силой, которая «стягивает» их вместе в сферическую форму.
Однако, помня третий закон Ньютона, мы знаем, что для каждой силы существует равная и противоположная сила. Капля воды не исключение. Каждая сила, действующая на молекулу в капле воды, в конечном итоге нейтрализует другую силу, действующую на другую молекулу в капле, так что эти молекулы воды просто плавают вокруг… ла-ди-да… ни к чему не привязаны.За исключением молекул на краях: поверхность.
Эти поверхностные молекулы имеют несбалансированные силы. Поверхностные молекулы имеют тонны молекул с одной стороны, но не с другой, тонны молекул с одной стороны втягивают поверхностные молекулы в каплю воды и крепко удерживают их. Это создает своего рода напряжение, подобное мембране. Вот как мы можем «плавать» иглой или чем-то подобным на поверхности воды, несмотря на разницу в плотности, игла просто опирается на это напряжение.
Это создает своего рода напряжение, подобное мембране. Вот как мы можем «плавать» иглой или чем-то подобным на поверхности воды, несмотря на разницу в плотности, игла просто опирается на это напряжение.
Водомерка делает то же самое:
Диаграмма силы для каждой ноги водомерки будет включать гравитацию вниз и поверхностное натяжение вверх. Эти двое уравновешивают друг друга. Выталкивающей силы нет, потому что вода не вытесняется, ни одна часть водомерки не находится ниже поверхности воды.
Если бы насекомое было больше и имело более толстую ногу, то F ST должно было бы быть больше, чтобы компенсировать дополнительную массу, добавленную к весу.Это объясняет размер водомерок и то, почему мы сами не можем ходить по воде. Жалость.
По определению, поверхностное натяжение — это сила, деленная на единицу длины, поэтому единицей СИ является ньютон на метр. Чтобы найти силу, мы умножаем на длину, находящуюся в контакте с поверхностью, на часть ноги, касающуюся воды в случае страйдера.
Распространенные ошибки
Каждый раз, когда есть вытесненный объем жидкости, присутствует выталкивающая сила. И каждый раз, когда объект поддерживается поверхностным натяжением жидкости (на поверхности или площади поверхности ), сила поверхностного натяжения присутствует.
Объем — это все пространство, занимаемое трехмерным объектом, а площадь поверхности — граница, определяющая пространство объекта. Визуализируйте площадь поверхности одной капли жидкости, представляя объект, завернутый в тонкий слой пластика. Если мы отклеим пластик и растянем его, у нас останется двухмерная поверхность.
Закуска для мозгов
Водяные жуки. У некоторых ступни имеют чашеобразную форму, что объясняет их кажущуюся неестественной плавучесть. Может быть, если бы у нас были ноги-лодочки, мы бы тоже могли ходить или «шагать» по воде.Разве они не милые?
Примечания к определению коэффициента формулы плавучести
Примечания к коэффициенту определения формулы плавучести
Следующий текст используется только для обучения, исследований, научных исследований, использования в образовательных и информационных целях в соответствии с принципами добросовестного использования.
Мы благодарим авторов текстов и исходный веб-сайт, которые дают нам возможность поделиться своими знаниями
Физика
Почему ваши основные огромные огромные корабли плавают? Авианосец весит почти сотни тысяч тонн .Так почему же он не тонет, как камень?
Аристотель считал, что это связано с формой тела. Если бы у тела были острые края, оно бы утонуло. Если бы тело было гладким и округлым, как корпус корабля, оно бы плавало. (Так зачем тебе все эти круглые камни на дне реки?)
Как и большинство учений Аристотеля, это чистый вздор. Парнем, который на самом деле понял, почему вещи плавают, был другой греческий гений, Архимед ( ок.287 – 212 до н.э.). Он обнаружил, как работает плавучесть . Плавучесть – это направленная вверх сила, с которой жидкость действует на погруженный в нее объект. Это заставляет вещи плавать или приводит к очевидной потере веса тела, когда оно тонет в жидкости. Это называется выталкивающей силой .
Это заставляет вещи плавать или приводит к очевидной потере веса тела, когда оно тонет в жидкости. Это называется выталкивающей силой .
Важный закон физики, касающийся плавучести, называется принципом Архимеда.
Закон Архимеда º Объект поднимается вверх под действием силы, равной весу вытесняемой им жидкости.
Это правило справедливо как для газов, так и для жидкостей, поскольку они оба являются жидкостями.
Потерянный принцип Архимеда º Когда тело погружается в воду, звонит телефон.
Плавающий и тонущий: У вас есть 2 тонны стали. Сталь в 9 раз плотнее воды, поэтому 2 тонны стали вытеснят примерно 2/9 или 0.22 тонны воды. Выталкивающей силы недостаточно, чтобы плавать блок, поэтому он утонет.
Берем теперь те же 2 тонны стали и делаем из нее ящик. Этот полый ящик имеет гораздо больший объем, чем куб. Когда вы ставите ящик в воду, он вытесняет больший объем воды, чем куб, именно вытесненный объем жидкости создает выталкивающую силу. По мере того, как ящик погружается глубже в воду, он вытесняет все больше и больше воды, что приводит к увеличению выталкивающей силы.Когда выталкивающая сила равна весу ящика, он перестает тонуть и всплывает. Вес ящика равен выталкивающей силе, поэтому результирующая сила, действующая на систему, равна нулю.
Итак, если ящик достаточно большой, он будет плавать.
По мере того, как грузовые суда загружаются грузом, они все глубже погружаются в воду. Погружаясь глубже, они вытесняют больше воды. Это увеличивает выталкивающую силу. Вес лодки и выталкивающая сила или в состоянии равновесия. Выталкивающая сила равна весу корабля.Пока общий вес корабля не превышает веса вытесненной воды, корабль будет плавать.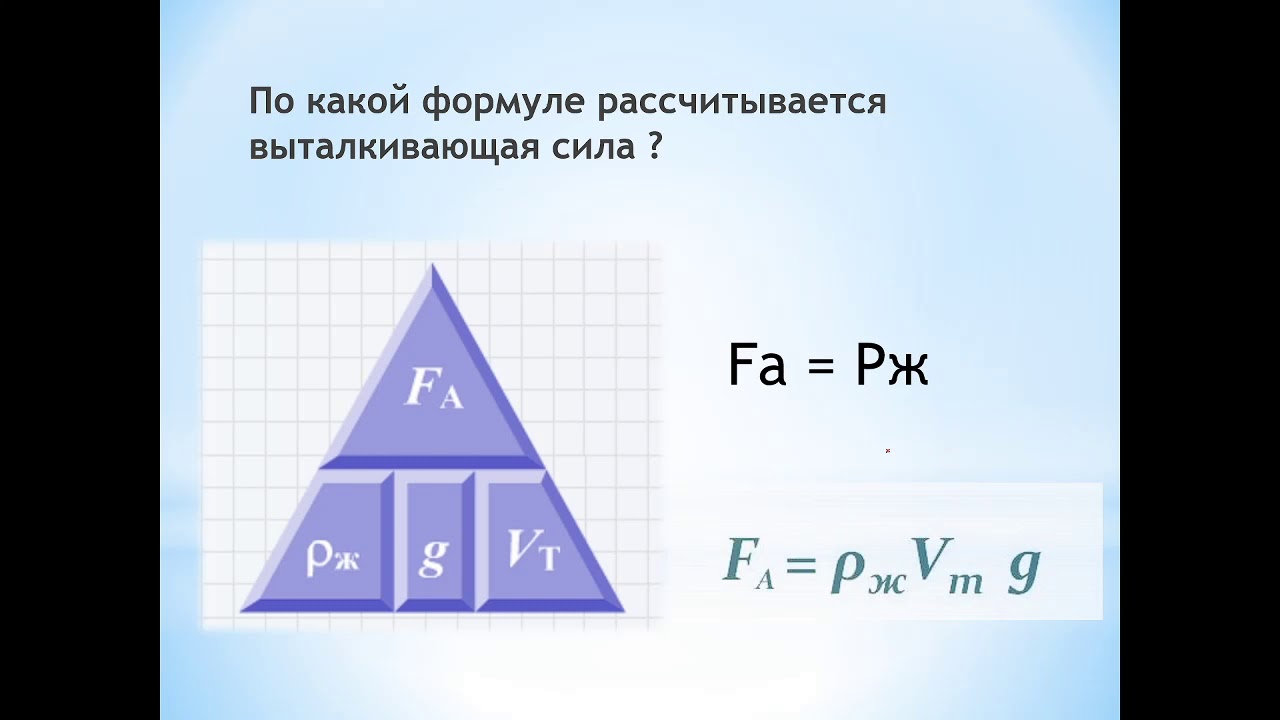
| |
Пустой корабль Корабль с грузом
Плавучесть в воздухе: Воздух — это жидкость, и принцип Архимеда применим к нему так же, как и к жидкостям.
Предмет, окруженный воздухом, поднимается вверх с силой, равной весу вытесненного воздуха.
Воздушные шары и дирижабли парят в воздухе так же, как лодки плавают на воде. Кубический метр воздуха имеет массу около 1,2 кг, поэтому его вес составляет около 12 Н. Таким образом, любой объект объемом один кубический метр и весом менее 12 Н будет плавать, т. е. подниматься. Если бы он весил больше 12 Н, он бы утонул, т. е. упал.
Когда вы построили воздушный шар в химии, вы воспользовались принципом Архимеда, даже если вы думали с точки зрения объемов и количества молей и всех других столь захватывающих химических вещей.
Представьте, что дирижабль фотографирует Суперкубок в виде большой рыбы, плавающей в воде. Они оба поддерживают свою «высоту», контролируя свою плотность и пользуясь принципом Архимеда.
Причина выталкивающей силы: Вы бросаете камень в воду, и он тонет. Силы давления воды действуют перпендикулярно внешним поверхностям камня (принцип Паскаля).
Посмотрим на силы.
Горизонтальные силы, воздействующие на стороны, уравновешивают друг друга.
Этого не происходит с вертикальными силами. С увеличением глубины давление увеличивается. Это означает, что силы, толкающие вверх основание скалы, больше, чем силы, толкающие вниз верхнюю часть скалы. Это связано с тем, что нижняя часть скалы находится на большей глубине, чем верхняя часть скалы, поэтому давление больше. Напомним, что чем больше глубина, тем больше давление.
Напомним, что чем больше глубина, тем больше давление.
Разность сил сверху и снизу отвечает за выталкивающую силу.
Определение выталкивающей силы: Куб площадью A со всех сторон погружен в жидкость.
Мы можем найти силу, давящую на вершину. Мы также можем найти силу, действующую на нижнюю поверхность куба:
так что
Мы также знаем, что
Мы можем включить это в уравнение силы, которое мы только что разработали:
Сила сверху:
Сила снизу:
g ускорение свободного падения. l — длина каждой стороны куба. h — глубина вершины куба.
Сила на дне больше силы наверху, разница и есть выталкивающая сила. Мы можем найти эту разницу:
Площадь куба A умножить на длину стороны куба l это объем куба, значит:
Но разница сил сверху и снизу, DF , является выталкивающей силой. Назовем его FB .
Назовем его FB .
B уравнение плавучей силы
FBuoy — выталкивающая сила, r — плотность жидкости, g — ускорение свободного падения, V — ускорение свободного падения
Это точно такое же уравнение, которое мы разработали для определения веса объекта, используя плотность и объем.Все, что мы на самом деле делаем, — это находим вес вытесненной жидкости.
Кажущийся вес: Если вес объекта меньше выталкивающей силы, объект будет плавать. Если вес объекта больше выталкивающей силы, то объект утонет, но весит меньше. Мы называем это кажущимся весом, FA . Кажущийся вес — это просто разница между его фактическим весом и выталкивающей силой.
Практические задачи:
- Стальной куб со стороной 5,0 см погружен в воду. Плотность стали 9,0 х 103 кг/м3. Плотность воды 1,0 х 103 кг/м3. Какова а) выталкивающая сила, действующая на куб, и б) его кажущийся вес?
(а) Найдите выталкивающую силу.
Объем куба:
(b) Найдите кажущийся вес.
Вес куба:
Теперь мы можем подключить и пыхтеть:
Чтобы найти кажущийся вес, мы используем это уравнение:
- Пробка имеет объем 4,25 см3. Плотность пробки 207 кг/м3. [a] Какой объем пробки находится под поверхностью, когда пробка плавает в воде? [b] Какая направленная вниз сила необходима, чтобы пробка полностью погрузилась в воду?
[а].Плавающая пробка вытеснит объем воды, равный ее собственному весу. Мы можем использовать плотность пробки, чтобы найти ее вес. По весу мы можем рассчитать объем вытесненной воды.
По весу мы можем рассчитать объем вытесненной воды.
Сначала переведем объем пробки в кубические метры:
Теперь находим вес пробки:
Теперь мы можем найти объем воды, который это представляет. Устанавливаем выталкивающую силу равной этому значению:
Или
(b) Чтобы найти силу, необходимую для погружения пробки, мы должны проанализировать силы.Сначала нарисуем FBD:
Силы следующие: FB выталкивающая сила, направленная вверх, w вес пробки, направленный вниз, и F сила, с которой мы должны толкнуть пробку вниз, чтобы заставить ее утонуть.
Сумма сил должна быть равна нулю:
Мы уже вычислили вес пробки, w .
Все, что нам нужно сделать, это рассчитать выталкивающую силу, это отличается от случая, когда пробка плавала, потому что вся пробка находится под водой. Таким образом, мы используем весь объем пробки, чтобы найти FB .
Таким образом, мы используем весь объем пробки, чтобы найти FB .
Теперь мы можем найти силу
- Большой сферический шар радиусом 9,0 м наполнен гелием. Масса баллонного мешка и маленькой корзинки, которая висит под ним, составляет 168 кг. Какой дополнительный вес может нести воздушный шар (предположим, что он находится на уровне моря)?
Вытесняемая жидкость — это воздух, поэтому мы можем легко найти выталкивающую силу.
Давайте посмотрим на FBD:
Сумма сил должна быть равна нулю, это точка, в которой восходящая сила (выталкивающая сила) равна сумме нисходящей силы – веса мешка, корзины и гелия:
Силы: FB (выталкивающая сила), w (вес сумки и корзины), FHe (вес гелия) и подъемная сила (подъемная сила) (вес, который нужно поднять).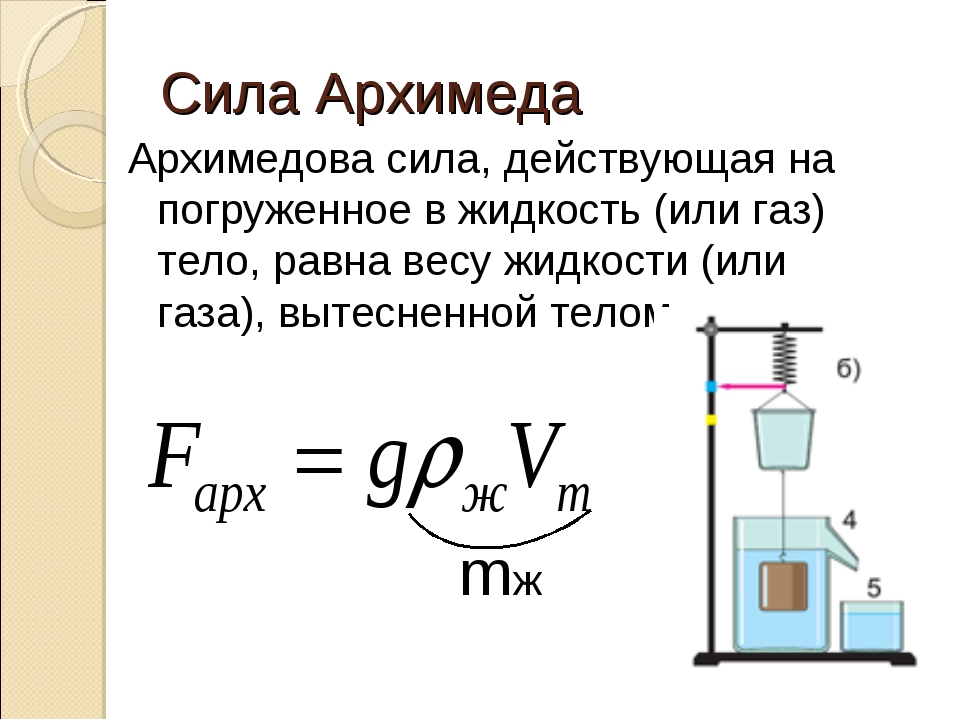
Объем баллона:
Мы уже знаем w (вес мешка и корзины). Теперь мы можем вычислить выталкивающую силу.
Нам нужно посмотреть плотность воздуха и использовать ее, чтобы найти выталкивающую силу.
Далее нам нужно найти вес гелия. Мы также должны проверить его плотность.
Теперь мы можем найти дополнительный вес, который может поднять воздушный шар.
Знаменитая история Архимеда: Архимед довольно известный человек. Ему приписывают множество изобретений. О нем рассказывают замечательную историю, связанную с идеей плавучести и тем, как он открыл свой принцип. Архимед жил в Сиракузах, греческом городе-государстве в третьем веке до нашей эры. Он был естествоиспытателем и работал своего рода специалистом по устранению технических неполадок у короля Гиеро.Говорят, что Архимед построил своего рода линзу, которая позволила ему поджечь флот вторгшихся кораблей от стен города. Также предполагается, что он построил какое-то рычажное устройство, которое могло протягиваться через стены города, хватать, поднимать корабли, встряхивать их, а затем бросать обратно в воду, чтобы они тонули. Неплохая сделка. Он также изобрел винт Архимеда — полую трубку с длинным винтом внутри. Один конец можно было поместить в воду, вращать винт, и воду можно было закачивать в трубку.Винт до сих пор используется на Ближнем Востоке.
Также предполагается, что он построил какое-то рычажное устройство, которое могло протягиваться через стены города, хватать, поднимать корабли, встряхивать их, а затем бросать обратно в воду, чтобы они тонули. Неплохая сделка. Он также изобрел винт Архимеда — полую трубку с длинным винтом внутри. Один конец можно было поместить в воду, вращать винт, и воду можно было закачивать в трубку.Винт до сих пор используется на Ближнем Востоке.
Итак, вот история. Однажды царь Гиерон попросил Архимеда определить, содержит ли его новая золотая корона действительное количество золота, данное мастеру короны. Король подозревал, что он мог быть подмешан с каким-то другим менее дорогим металлом (например, латунью или серебром). Однако на тот случай, если ювелир не обманул короля, короне не могло быть нанесено никакого вреда (поэтому никаких образцов керна).
Архимед обеспокоен этой проблемой.Ему пришлось придумать форму того, что сегодня мы называем «неразрушающим» контролем. Царь не отличался терпеливостью, поэтому Архимед находился под большим давлением. Плохие вещи могли случиться с людьми, которые не справились с его величеством. Наконец, не в силах решить проблему, Архимед решил сделать перерыв и освежиться в приятной ванне. Что ж, ванна стала его спасением, потому что именно в ванне к нему наконец пришло решение. Когда он окунул свое тело, он заметил, что уровень воды поднялся, когда он залез в ванну.Он также, казалось, весил меньше. Решение было под рукой! Он понял, что может измерить объем короны, погрузив ее в воду, а затем определить, золото ли это, найдя ее плотность. Предположительно, он был так взволнован, что голым выпрыгнул из ванны и побежал по улицам Сиракуз с криком: «Эврика! Эврика!!» (Я нашел это).
Плохие вещи могли случиться с людьми, которые не справились с его величеством. Наконец, не в силах решить проблему, Архимед решил сделать перерыв и освежиться в приятной ванне. Что ж, ванна стала его спасением, потому что именно в ванне к нему наконец пришло решение. Когда он окунул свое тело, он заметил, что уровень воды поднялся, когда он залез в ванну.Он также, казалось, весил меньше. Решение было под рукой! Он понял, что может измерить объем короны, погрузив ее в воду, а затем определить, золото ли это, найдя ее плотность. Предположительно, он был так взволнован, что голым выпрыгнул из ванны и побежал по улицам Сиракуз с криком: «Эврика! Эврика!!» (Я нашел это).
Девиз штата Калифорния — «Эврика».
Источник: http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Fluids/2%20-%20buoyancy%20info.doc
Ссылка на веб-сайт: http://teachers2.wcs.edu
Автор: не указан в исходном документе вышеуказанного текста
Если вы являетесь автором приведенного выше текста и не согласны делиться своими знаниями для обучения, исследований, стипендий (для добросовестного использования, как указано в законе об авторских правах США), отправьте нам электронное письмо, и мы удалим ваши текст быстро.
Примечания к определению коэффициента формулы плавучести
Примечания к коэффициенту определения формулы плавучести
Главная страница
Определение плавучести
Это правильное место, где можно найти ответы на ваши вопросы, такие как:
Кто? Какие ? Когда ? Где ? Почему ? Который ? Как ? Что означает плавучесть? В чем смысл заметок о плавучести?
Заметки по физике плавучести
Аланпедия. com с 1998 года новые сайты и инновации
com с 1998 года новые сайты и инновации
Главная страница – Отказ от ответственности – Свяжитесь с нами
Расчет максимальной загрузки корабля
Резюме
Учащиеся предсказывают максимальную массу, которую может выдержать корабль, не затонув. Затем учащиеся проверят свое предсказание, управляя своим загруженным кораблем.
Цели обучения
Это задание предназначено для того, чтобы учащиеся продемонстрировали свою способность применять навыки расчета плавучести к действиям по точному прогнозированию выталкивающей силы на загруженном судне.Учащиеся будут использовать навыки критического мышления для расчета объема корабля неправильной формы и успешно продемонстрируют свои знания о силах, включив в решение все части плавучей системы.
Ключевые термины: выталкивающая сила, принцип Архимеда
Контекст для использования
Это лабораторное задание, предназначенное для учащихся девятого класса по физике. Студенты будут ознакомлены с принципом Архимеда и должны знать, как рассчитать выталкивающую силу.
Студенты будут ознакомлены с принципом Архимеда и должны знать, как рассчитать выталкивающую силу.
Модификация 1: Это можно использовать как введение в плавучесть, позволяя учащимся обнаружить, что масса груза, помещенного в корабль, всегда равна массе воды, вытесненной плавучим кораблем.
Модификация 2: Эту операцию можно усложнить, заменив воду другой вытесняющей жидкостью.
Время: Два урока по 45 минут.
Материалы: Формы для хлеба (корабль), песок, линейка, весы, большой прозрачный пластиковый контейнер (для управления кораблями) и доступ к воде.
Предмет : Физика: механика жидкости
Тип ресурса : Виды деятельности: Лабораторная деятельность
Уровень класса : Средний (6-8), Старшая школа (9-12)
Описание и учебные материалы
1. Учащимся командам из 3-4 человек будет выдана форма для хлеба (корабль), и их попросят предсказать максимальное количество песка (в граммах), которое может вместить их корабль.
2. В качестве стимула для расширения возможностей корабля по перевозке грузов команды будут соревноваться, кто сможет загрузить свой корабль с наибольшим количеством песка и при этом остаться на плаву.
3. Команды должны измерить объем своего корабля и преобразовать эти данные в массу в граммах песка, который может вместить их корабль. (Выталкивающая сила равна массе воды, вытесненной кораблем.)
4. Командам не разрешается испытывать свои корабли на воде до начала соревнований.
5. Каждая команда загрузит свой корабль, как только он окажется в воде, песком, который был собран командой и помещен в контейнер, готовый к загрузке.
Учебные заметки и советы
Важно, чтобы командам не разрешалось спускать корабли на воду до теста.Наиболее упускаемой из виду частью проблемы является то, что масса корабля не учитывается как часть нагрузки. Команды, которые успешно учитывают массу корабля, демонстрируют хороший синтез мыслей в том, как они подходят к решению проблем.




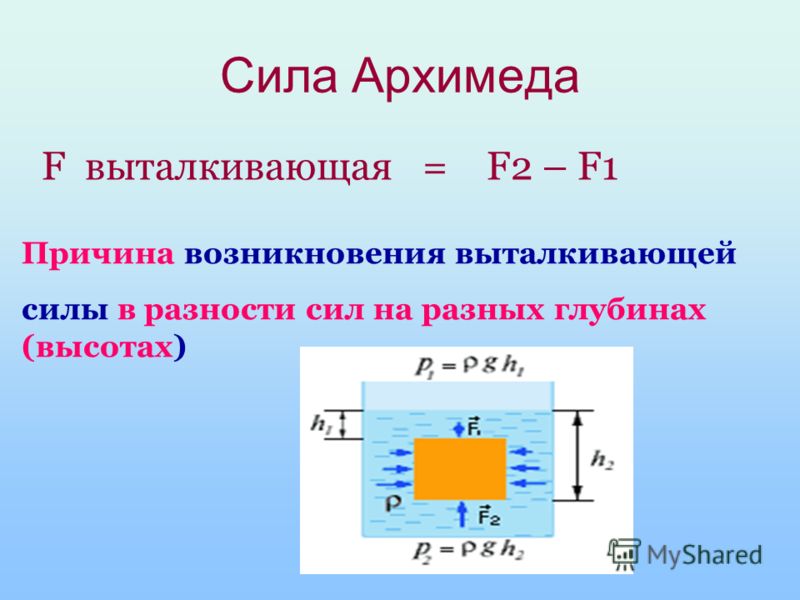 ст.)
ст.)
 Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.