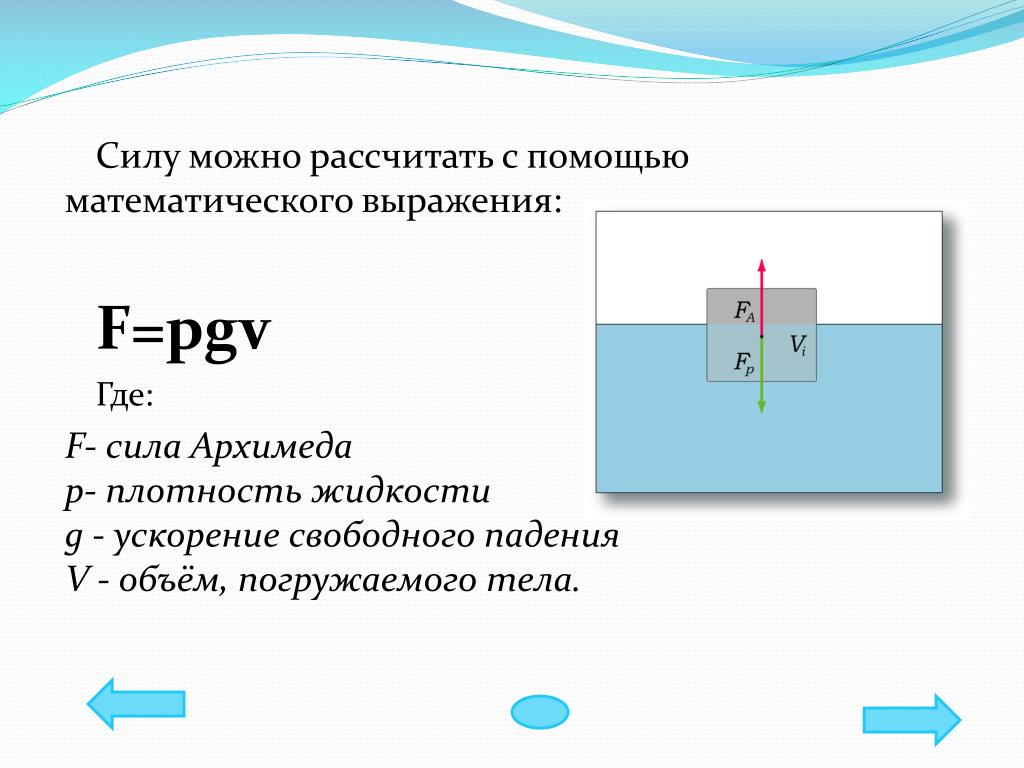
Архимедова сила – формула закона Архимеда, как найти (физика, 7 класс)
4.4
Средняя оценка: 4.4
Всего получено оценок: 353.
4.4
Средняя оценка: 4.4
Всего получено оценок: 353.
Наблюдения и опыты показывают, что на тела, помещенные в жидкость и газ оказывается давление. Давление жидкости и газа на одной высоте одинаково во всех направлениях. С изменением высоты происходит изменение давления. По этой причине возникает выталкивающая сила, которую называют архимедовой силой. Узнаем чему равна архимедова сила в жидкости и газе.
Чему равно давление в газах и жидкостях
Напомним определение давления. Давлением p называют физическую величину, равную отношению силы F, направленной перпендикулярно поверхности с площадью S:
$p={F\over S}$ (1)
Французский исследователь Блез Паскаль открыл закон, названный в последствии его именем, который звучит так: жидкости и газы передают производимое на них давление во все стороны одинаково. 2]}$$
2]}$$
Часто используются кратные единицы давления: килопаскаль (кПа) и мегапаскаль (МПа).
Закон Архимеда
Тяжелый предмет, который мы с огромным трудом отрываем от земли, удается довольно легко поднять, когда он находится в воде. Если взять пустую пластиковую бутылку с закрытой пробкой, погрузить ее полностью в воду и отпустить, то бутылка всплывет. Почему это происходит?
Для объяснения этих явлений достаточно взглянуть на последнюю формулу (4). Зависимость давления p в жидкости или газе от глубины h (высоты), приводит к появлению выталкивающей силы, действующей на любое тело, погруженное в жидкость или газ. Эта сила называется архимедовой силой.
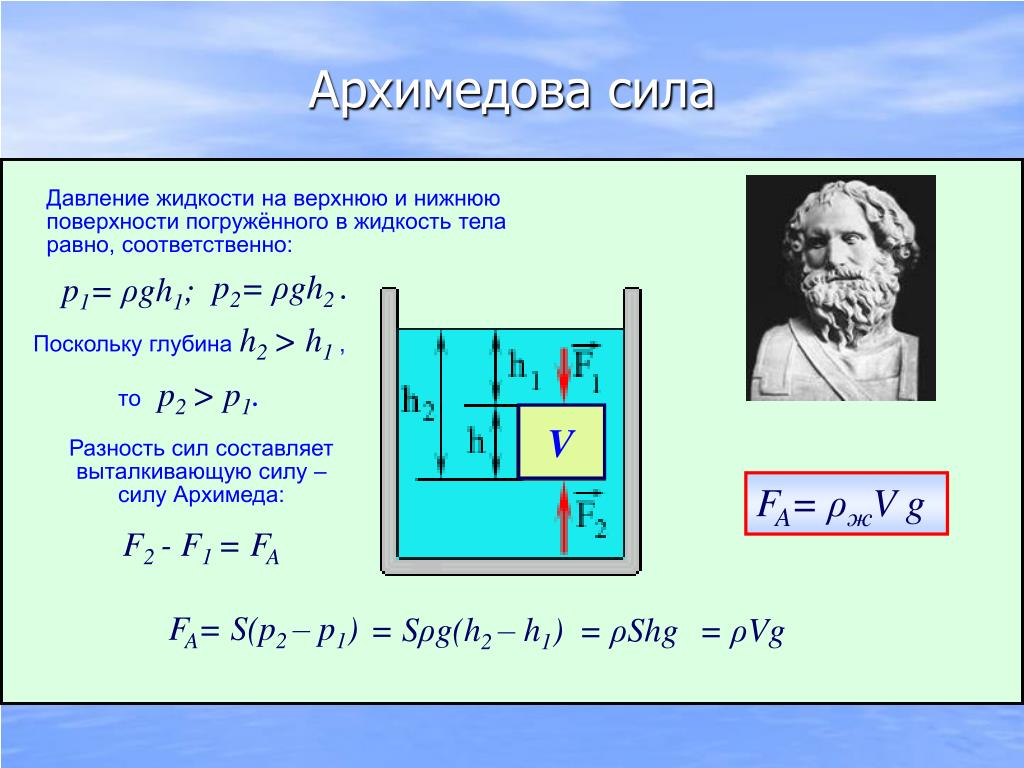
Рис. 1. Портрет, изображение АрхимедаДревнегреческий математик, инженер и физик Архимед (287-212 г.г. до н.э.) не только обнаружил это явление, но смог найти ему объяснение и вывел формулу для расчета выталкивающей силы. Кроме закона Архимеда он открыл знаменитое правило рычага, первым вывел математические формулы для вычисления площадей и объемов сложных геометрических поверхностей, открыл первый планетарий, изобрел много полезных приспособлений.
Рисунок, на котором изображен прямоугольный параллелепипед (высотой h и площадью основания S), помещенный в жидкость, поможет ответить на вопрос: как найти архимедову силу. Силы давления на боковые грани уравновешивают друг друга, а силы
Получим формулу для результирующей силы FA , равную разности F2 и F1:
$F_А=F_2−F_1=p_2*S−p_1*S=ρ*g*h_2*S−ρ*g*h_1*S=$
$ρ*g*S*{(h_2− h_1)}=ρ*g*S*h$ (5)
где: $S*h=V$ — объем, а $ρ*V=m$ — масса жидкости, которую вытеснило тело. Тогда, поскольку
$F_A =m*g=ρ*V*g$ (6)
Полученная формула позволяет сформулировать закон Архимеда:
Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.
Погружение, равновесие, всплытие
Теперь становится понятно почему в воде мы запросто поднимаем тяжелые камни: нам “помогает” архимедова сила, т.к. она направлена противоположно силе тяжести. По этой же причине вес тела при взвешивании в жидкости будет всегда меньше веса, измеренного в воздухе.
Из формулы (6) следует, что величина архимедовой силы зависит прямо пропорционально от плотности жидкости ρ и от объема погруженного тела V. Плотность вещества, из которого изготовлено тело, может быть любой — на величину выталкивающей силы она не влияет. В зависимости от соотношения архимедовой силы FA и силы тяжести Fg возможно три положения тела в жидкости:
- Если FA > Fg, то тело будет выталкиваться наверх — “всплывать”;
- Если FA
- Если FA = Fg, то тело может находиться в жидкости на любой глубине в состоянии равновесия.
Закон Архимеда положен в основу ареометра — прибора для измерения плотности жидкости.
Что мы узнали?
Итак, мы узнали, почему возникает архимедова сила в газах и жидкостях, и от каких величин зависит ее значение. На тело, погруженное в жидкость (или газ) действует выталкивающая сила. Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Для более подробного доклада об архимедовой силе можно подготовить интересные примеры с разными жидкостями, отличными от воды, например с керосином или ртутью. Тема этой статьи тесно связана с особенностями плавания и воздухоплавания тел, которые мы рассмотрим в следующих главах курса физики за 7 класс.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Ирина Кудинова
8/10
Кирилл Тугаринов
10/10
Елена Ратных
10/10
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 353.
А какая ваша оценка?
Архимедова сила, формулы 📙 – Физика
- Закон Архимеда
- Появление Архимедовой силы
Всем известно, что свойства газов и жидкостей резко отличаются, но не взирая на это, часто можно наблюдать, что они ведут себя одинаково, и их действия можно описать одинаковыми законами. Это дает возможность изучать их свойства в едином русле.
В разделе физики под названием механика газообразное или жидкое вещество считается сплошной средой. Принято считать, что оно располагается однородно в том объеме пространства, который занимает.
В законе Паскаля говорится о том, что величина давления внешних сил на поверхность жидкой среды одинакова по всем направлениям. Этим законом описываются равновесные состояния газообразных и жидких веществ.
При состоянии механического равновесия горизонтальное давление жидкости будет везде одинаковым, а это значит, что свободная поверхность неподвижной жидкости всегда будет горизонтальной, помимо мест прикосновения к сосуду. Принимая условие, что жидкость несжимаема, можно утверждать, что плотность среды не зависима от давления.
Рассмотрим определенный объем жидкости в виде вертикального цилиндра. Поперечным сечением цилиндра, и соответственно столба жидкости, будет \(S\), высотой – \(h\), плотностью – \(ρ\), тогда вес будет определяться по формуле: \(P=ρgSh.\) Принимая во внимание все вышесказанное, можно записать формулу давления на дно сосуда:
\(p= {P \over S}= {ρgSh \over S}=ρgh\)
Это значит, что величина давления на дно сосуда для одной и той же жидкости будет линейно изменяться только при изменении ее высоты столба.
В законе Архимеда говорится о том, что на тело, которое погружено в жидкую или газообразную среду, действует выталкивающая его сила, которая равняется весу объема жидкой или газообразной части, занятой этим телом. Этот закон является одним из главных законов, которые применяются в гидро- и аэростатике.
Явление силы Архимеда вызвано тем, что вытесненная телом среда стремится заполнить объем, который у нее отобрали, поэтому и появляется сила, выталкивающая тело наружу. Потому и называется она выталкивающая или подъемная гидростатическая сила. Величина этой силы не зависима от структуры и текстуры погруженного тела, его химического состава или иных характеристик.
Архимедова сила возникает из-за того, что на разной глубине давление жидкости отличается. К примеру, давление в нижнем слое воды всегда будет больше, чем в верхнем, так как оно зависит от высоты столба.
Явление силы Архимеда возможно только с наличием силы тяжести. К примеру, для одного и того же тела на Земле и на Луне сила тяжести отличается в шесть раз.
К примеру, для одного и того же тела на Земле и на Луне сила тяжести отличается в шесть раз.
Рассмотрим такой пример: представим, что в некотором объеме воды мы выделили произвольный объем, окруженный поверхностью \(S\). Так как условно по всей поверхности воды сохраняется равновесие, то и наш объем, выделенный поверхностью \(S\), тоже равновесен. Это значит, что сила равнодействия и сумма внешних сил для нашего объема жидкости равняются нулю. Внешними силами в нашем случае выступают давление жидкости, окружающей наш объем с поверхностью \(S\) и вес нашего объема воды. В это же время сила равнодействия F гидростатического давления, которое испытывает поверхность \(S\), будет равняться весу нашего объема воды, ограниченного поверхностью \(S\). При этом, чтобы сумма всех внешних сил была равна нулю, сила равнодействия F должна пересекать центр масс нашего объема воды и направляться снизу в верх.
Представим, что на место нашего условного выделенного объема воды поместили твердое тело того же объема. При условии сохранения механического равновесия, среда не изменится, то есть останется тем же давление, воздействующее на поверхность S. Теперь закон Архимеда можно сформулировать более точно: при условии, что погруженное в жидкость тело находится в состоянии механического равновесия, на него будет действовать выталкивающая сила гидростатического давления, равняющаяся весу объема жидкости, который вытеснило тело. Эта сила направляется снизу в верх и обязательно пересекает центр массы погруженного тела. Закон Архимеда будет выглядеть так:
При условии сохранения механического равновесия, среда не изменится, то есть останется тем же давление, воздействующее на поверхность S. Теперь закон Архимеда можно сформулировать более точно: при условии, что погруженное в жидкость тело находится в состоянии механического равновесия, на него будет действовать выталкивающая сила гидростатического давления, равняющаяся весу объема жидкости, который вытеснило тело. Эта сила направляется снизу в верх и обязательно пересекает центр массы погруженного тела. Закон Архимеда будет выглядеть так:
\(F_A=ρgV,\)
где \(F_A\) – Архимедова сила, Н;
\(ρ\) – плотность среды, кг/м3;
\(V\) – объем погруженного тела, м3;
\(g\) – ускорение свободного падения, м/с2.
Направление действия вытесняющей силы, действующей на погруженное в среду тело, противоположно направлению действия силы тяжести, из-за этого состояние погруженного тела будет зависеть от соотношения размеров этих сил. Бывает три различных варианта их соотношений. Рассмотрим варианты реакции тела при всех вариантах подробнее:
Рассмотрим варианты реакции тела при всех вариантах подробнее:
- если сила тяжести больше, чем Архимедова сила, тело, погруженное в среду, будет тонуть;
- если сила тяжести равняется Архимедовой силе – зависнет в среде погружения;
- сли сила тяжести будет меньше Архимедовой силы – будет плавать по верху.
Сила Архимеда | 7 класс
Содержание
На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже.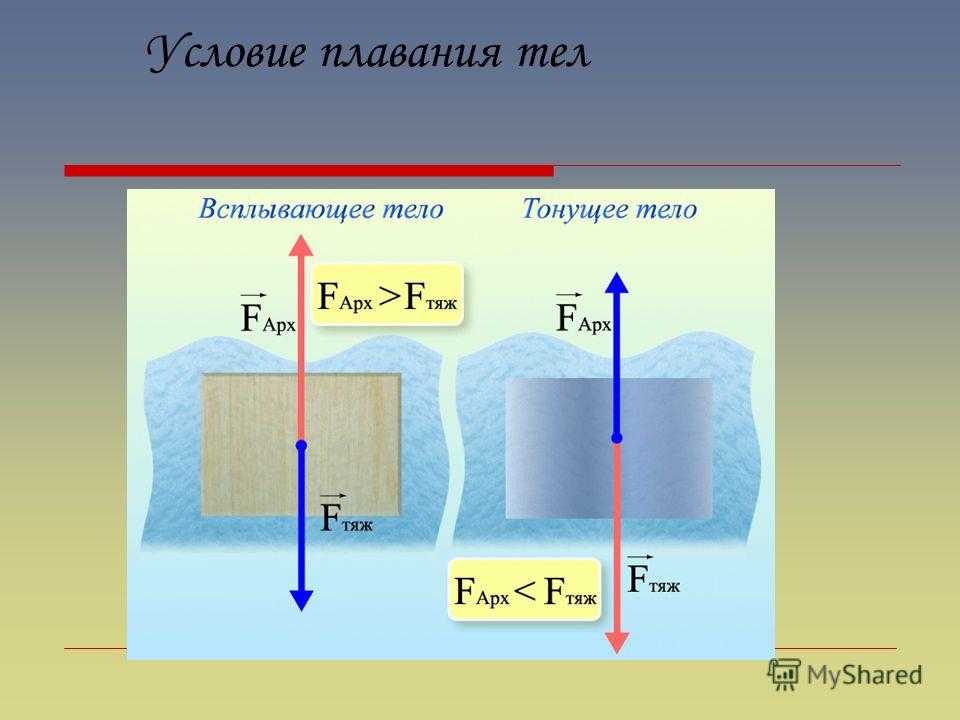 На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
{"questions":[{"content":"Чему равна сила, выталкивающая погруженное в газ тело?[[choice-99]]","widgets":{"choice-99":{"type":"choice","options":["весу газа в объеме этого тела","весу тела","силе тяжести, действующей на тело","силе тяжести, действующей на газ"],"answer":[0]}}}]}Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = \rho_ж \cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g \rho_ж V_т$.
{"questions":[{"content":"По какой формуле рассчитывается сила Архимеда?[[choice-104]]","widgets":{"choice-104":{"type":"choice","options":["$F_A = g \\rho_ж V_т$","$F_A = g \\rho_т V_ж$","$F_А = \\rho gh$","$F_А = g \\rho_т V_т$"],"answer":[0]}}}]}От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g \rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
{"questions":[{"content":"Архимедова сила зависит от[[choice-111]]","widgets":{"choice-111":{"type":"choice","options":["плотности жидкости","объема тела","плотности тела","формы тела","объема жидкости"],"answer":[0,1]}}}]}Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P \space − \space F_A = gm \space − \space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
{"questions":[{"content":"Чему равен вес тела в жидкости?[[choice-116]]","widgets":{"choice-116":{"type":"choice","options":["Разности веса тела в вакууме и архимедовой силы","весу тела в вакууме","разности веса жидкости и архимедовой силы"],"answer":[0]}}}]}Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2. 3 \approx 26 244 \space Н \approx 26.2 \space кН$.
3 \approx 26 244 \space Н \approx 26.2 \space кН$.
Ответ: $F_A \approx 26,2 \space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Рисунок 4. Цилиндры одинаковой массы, но изготовленные из разных материаловПосмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g \rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g \rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = \frac{m}{\rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
Рисунок 5. Погружение цилиндров из разных материалов в жидкостиПри этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. 3}$
3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} \space − \space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = \rho_б V$,
$F_{тяж} = g \rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g \rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} \space − \space F_{А1} = g \rho_б V \space − \space g \rho_1 V = gV \cdot (\rho_б \space − \space \rho_1)$,
$F_1 = 9.8 \frac {Н}{кг} \cdot 2 \space м^3 \cdot (2300 \frac{кг}{м^3} \space − \space 1000 \frac{кг}{м^3}) = 25 \space 480 \space Н \approx 25 \space кН$. 3}$
3}$
$\rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P \space − \space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 \space + \space F_{А1}$,
$gm = P_1 \space + \space g \rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 \space + \space g \rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 \space + \space g \rho_1 V = P_2 \space + \space g \rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 \space − \space P_2 = g \rho_2 V \space − \space g \rho_1 V$,
$P_1 \space − \space P_2 = gV (\rho_2 \space − \space \rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = \frac{P_1 \space − \space P_2}{g (\rho_2 \space − \space \rho_1)}$,
$V = \frac{20 \space Н \space − \space 18. 3}$.
3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с \space + \space V_з$.
То же самое с общей массой короны:
$m = m_с \space + \space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = \frac{m_с}{\rho_с}$,
$V_з = \frac{m_з}{\rho_з} = \frac{m \space − \space m_с}{\rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = \frac{m_с}{\rho_с} \space + \space \frac{m \space − \space m_с}{\rho_з} = \frac{m_с (\rho_з \space − \space \rho_с) \space + \space \rho_с m}{\rho_с \rho_з} = m_с \cdot \frac{\rho_з \space − \space \rho_с}{\rho_с \rho_з} \space + \space \frac{m}{\rho_з}$,
$m_с = \frac{V \space − \space \frac{m}{\rho_з}}{\frac{\rho_з \space − \space \rho_с}{\rho_с \rho_з}} = \frac{\rho_с (V \rho_з \space − \space m)}{\rho_з \space − \space \rho_с}$. 3$.
3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = \frac{F}{S} = \frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
определение и формула :: SYL.ru
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Если принять вес тела в вакууме за Ро, то его вес в воздушной среде может быть описан такой формулой: Рв=Ро – Fа;
здесь Ро – вес в вакууме;
Fа – сила Архимеда.
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
F = ρV * g.
Это и есть закон Архимеда.
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.
Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
Сила Архимеда | ЕГЭ по физике
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt, где x0 — начальная координата тела, Vx — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением
где r — радиус окружности.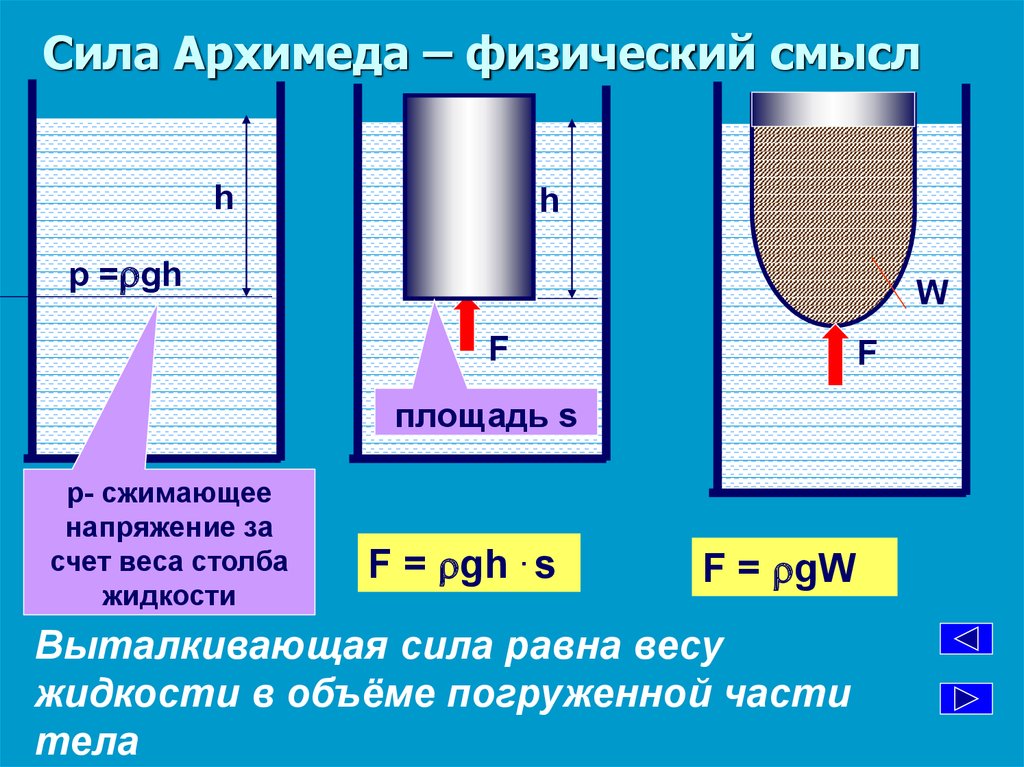
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией.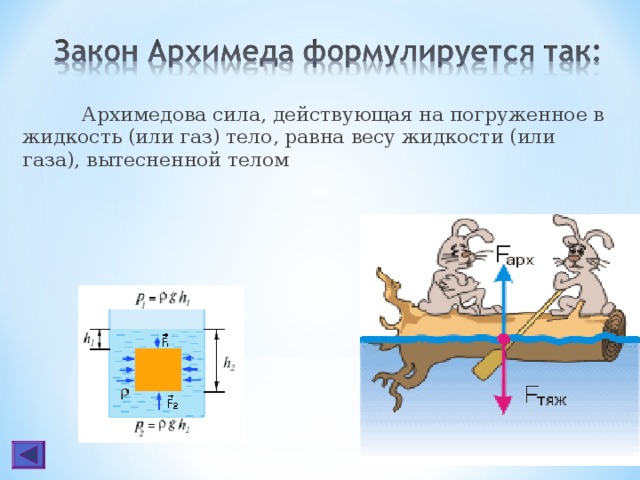 Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести — это сила, с которой все тела притягиваются к Земле:
При неподвижной опоре вес тела равен по модулю силе тяжести:
Если тело движется по вертикали с ускорением, то его вес будет изменяться.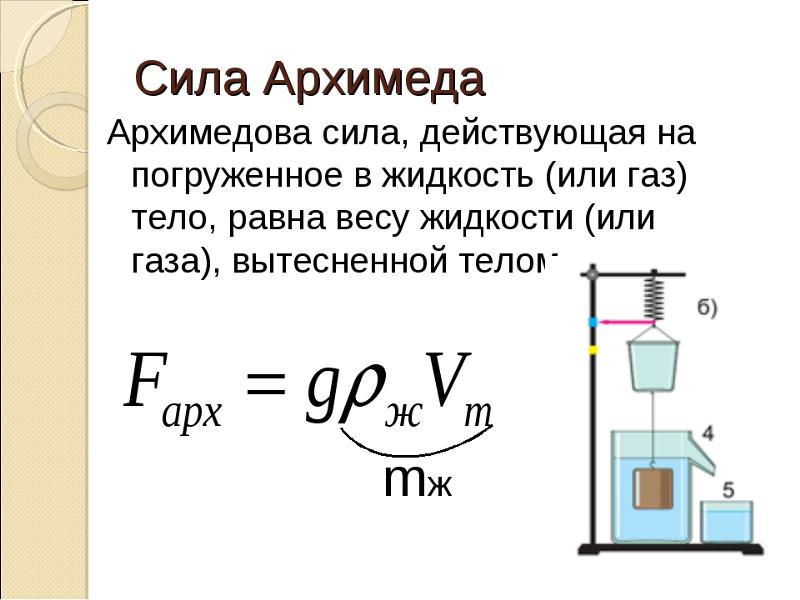
При движении тела с ускорением, направленным вверх, его вес
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.
где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).
Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).
Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.
Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей
где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.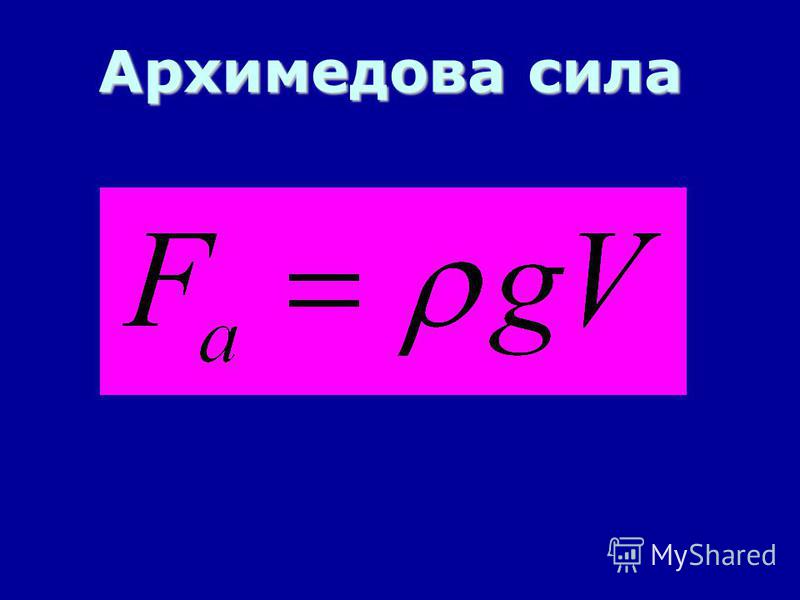
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:
где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохраненияИмпульсом тела называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность — это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волныКолебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины
x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое
колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:
Частота измеряется в с-1. Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле
где l — длина маятника.
Период колебаний груза на пружине определяется по формуле
где k — жёсткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
где v — скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.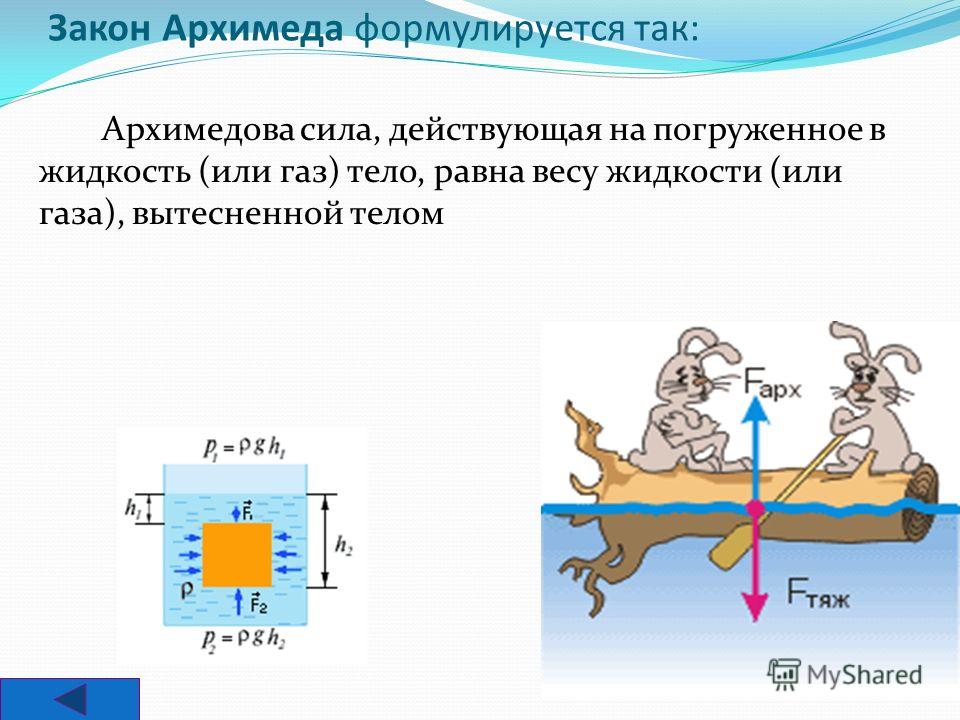
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
СИЛА АРХИМЕДА (ВЫТАЛКИВАЮЩАЯ СИЛА)
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Газдиев О.М. 1
1МО Г.о. Подольск МОУ СОШ пос. МИС
Яшина В.В. 1
1МО, Г.о. Подольск, МОУ СОШ пос. МИС
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Цель: Рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело.
Задачи:
– изучить историю открытия архимедовой силы;
– изучить учебную литературу по вопросу действия архимедовой силы;
– выработать навыки проведения самостоятельного эксперимента;
– доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
– исследовательские;
– расчетные;
– информационного поиска;
– наблюдений
1. Открытие силы Архимеда
Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон – царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда:
,
где – плотность жидкости (газа), – ускорение свободного падения, – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3) < — тело всплывает до тех пор, пока не начнет плавать.
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью.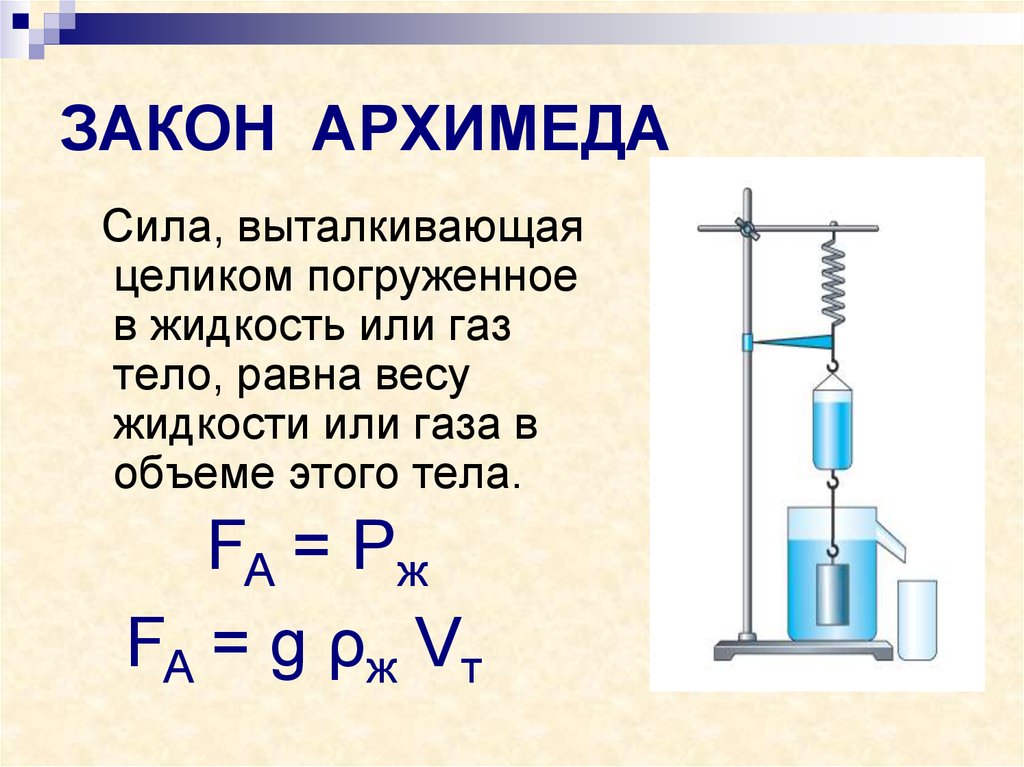 Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
-
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
– вода чистая;
– вода, насыщенная солью;
– подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло – «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом – яйцо опустилось на дно (приложение 4).
|
Название жидкости |
Плотность жидкости, |
Поведение тела в жидкости |
|
Чистая вода |
1000 |
Тело утонуло |
|
Соленая вода |
1030 |
Тело плавает |
|
Подсолнечное масло |
930 |
Тело утонуло |
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Задачи:
– определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
– вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ1, а затем – при погружении в воду ℓ2. После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ1 до уровня ℓ2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ1, а затем – при погружении в воду ℓ2. После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ1 до уровня ℓ2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
.
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
|
Масса испытуемого (без учета массы головы), кг |
53 |
|
Объем тела человека (без объема головы), м3 |
0,052 |
|
Плотность тела человека (без учета головы), |
1019 |
|
Плотность пресной воды, |
1000 |
|
Плотность морской воды, |
1030 |
|
Сила тяжести, действующая на тело в воздухе, Н |
530 |
|
Значение выталкивающей силы в пресной воде, Н |
520 |
|
Значение выталкивающей силы в морской воде, Н |
536 |
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. – книга 1. – Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. – книга 2.- Екатеринбург. : Тезис, 1994.
: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. – 16-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Просмотров работы: 17156
14.4 Принцип Архимеда и плавучесть. Общая физика с использованием исчисления I
14 Гидромеханика
Цели обучения
К концу этого раздела вы сможете:
- Определить выталкивающую силу
- Государственный закон Архимеда
- Опишите связь между плотностью и законом Архимеда
При помещении в жидкость некоторые объекты всплывают благодаря выталкивающей силе. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Поддерживает ли ваше тело атмосфера или только воздушные шары с гелием (рисунок)?
Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Поддерживает ли ваше тело атмосфера или только воздушные шары с гелием (рисунок)?
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Существует восходящая сила, или выталкивающая сила , действующая на любой объект в любой жидкости (рисунок). Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила
Выталкивающая сила — это направленная вверх сила, действующая на любой объект в любой жидкости.
Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что [латекс]p=hpg[/латекс]. Это изменение давления и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Различия в силе приводят к выталкивающей силе [латекс] {F} _ {\ текст {B}} [/латекс]. (Горизонтальные силы компенсируются.)
Принцип Архимеда
Насколько велика выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке.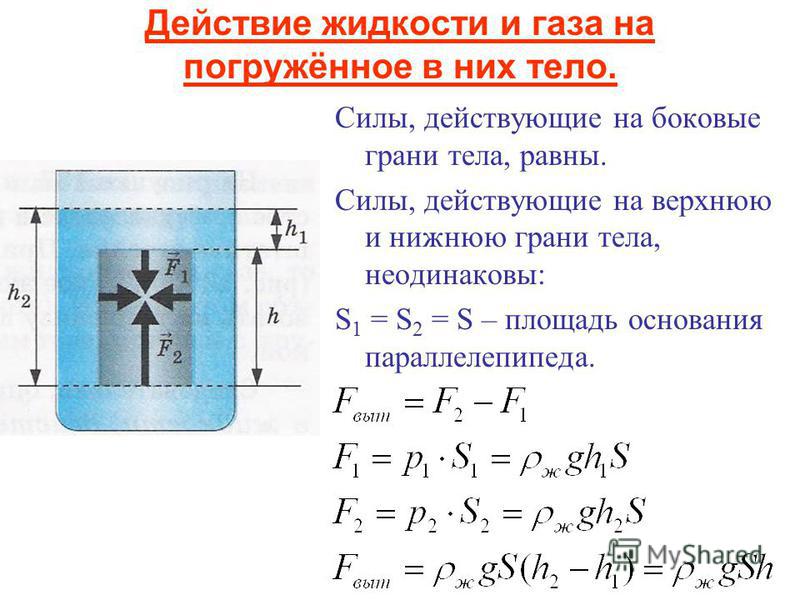 Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [латексу] {w} _ {\ text {фл}}, [/ латексу] весу жидкости, вытесненной объектом.
Если бы объект не находился в жидкости, пространство, занимаемое объектом, было бы заполнено жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex] Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться [латексу] {w} _ {\ text {фл}}, [/ латексу] весу жидкости, вытесненной объектом.
Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс] {F} _ {\ text {B}} = {w} _ {\ text {fl}}, [/latex]
, где [латекс] { F}_{\text{B}}[/latex] — выталкивающая сила, а [latex]{w}_{\text{fl}}[/latex] — вес жидкости, вытесненной объектом.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. до н. э.), который сформулировал этот принцип задолго до того, как понятие силы стало общепризнанным.
Рис. 14.21 (a) На объект, погруженный в жидкость, действует выталкивающая сила [латекс] {F} _ {\ text {B}}. }}[/latex] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости.
}}[/latex] больше веса объекта, объект поднимается. Если [латекс]{F}_{\text{B}}[/латекс] меньше веса объекта, объект тонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес [латекс] {w} _ {\ text {fl}}. [/latex]. Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться вес вытесненной жидкости.Принцип Архимеда относится к силе плавучести, которая возникает, когда тело полностью или частично погружено в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила давления внизу направлена вверх, а сила давления вверху направлена вниз; силы из-за давлений по бокам направлены внутрь тела.
Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на рисунке. Следовательно, на тело действует направленная вверх сила. Эта направленная вверх сила есть сила плавучести, или просто плавучесть .
Восклицание «Эврика» (означающее «Я нашел это») часто приписывают Архимеду, когда он сделал открытие, которое привело к принципу Архимеда. Некоторые говорят, что все началось в ванной. Чтобы прочитать историю, посетите NASA или откройте журнал Scientific American, чтобы узнать больше.
Плотность и закон Архимеда
Если вы бросите кусок глины в воду, он утонет. Но если вы слепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу, хотя ее масса одинакова. То же самое и со стальными кораблями.
Средняя плотность объекта определяет, будет ли он плавать. Если средняя плотность объекта меньше плотности окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта соотносится с плотностью жидкости. На рисунке, например, незагруженный корабль имеет меньшую плотность и меньше его погружено в воду по сравнению с тем же кораблем, когда он загружен. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс] \ text {фракция погружена} = \ frac {{V} _ {\ text {sub}}} {{V} _ {\ text {obj}}} = \ frac {{V} _ {\ text{fl}}}{{V}_{\text{obj}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, которую мы называем [латекс]{V}_{fl}[ /латекс]. Теперь мы можем получить связь между плотностями, подставив в выражение [латекс]\ро =\фрак{м}{В}[/латекс]. Это дает
[латекс]\frac{{V}_{\text{fl}}}{{V}_{\text{obj}}}=\frac{{m}_{\text{fl}} \text{/}{\rho} _{\text{fl}}}{{m}_{\text{obj}}\text{/}{\rho}_{\text{obj}}},[ /латекс]
, где [latex]{\rho }_{\text{obj}}[/latex] — средняя плотность объекта, а [latex]{\rho }_{\text{fl}}[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\текст{фракция под водой}=\фракция{{\rho} _{\текст{объект} }}{{\rho }_{\text{fl}}}.[/latex]
Мы можем использовать это соотношение для измерения плотности.
Рисунок 14.22 Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б).Пример
Расчет средней плотности
Предположим, что женщина массой 60,0 кг плавает в пресной воде, при этом 97,0% ее объема погружено в воду, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение \text{fl}}}[/latex]
для плотности объекта. Это дает
[латекс] {\ rho} _ {\ text {obj}} = {\ rho } _ {\ text {person}} = \ text {(фракция погружена)} \ cdot {\ rho} _ {\ текст{фл}}.[/латекс] 9{3}}.[/latex]
Значение
Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.
Мы ожидаем этого, потому что она плавает.
Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе». ,” назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на рисунке.
Рис. 14.23 (a) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты. Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Все эти расчеты основаны на принципе Архимеда, согласно которому выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что погруженный в воду объект кажется менее весящим; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Резюме
- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет.
 Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
Концептуальные вопросы
Чтобы вытащить пробку из полной ванны, требуется больше усилий, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Показать решениеСовсем нет. Принцип Паскаля гласит, что изменение давления осуществляется через жидкость. Причина, по которой полная ванна требует большего усилия, чтобы вытащить пробку, заключается в весе воды над пробкой.
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
Выталкивающая сила равна весу вытесненной жидкости. Чем больше плотность жидкости, тем меньше жидкости необходимо вытеснить, чтобы удерживать вес объекта и плавать. Поскольку плотность соленой воды выше, чем плотность пресной воды, меньше соленой воды будет вытеснено, и корабль будет плавать выше. 9{3}[/латекс]?
Показать раствора. погружено на 99,5 %; б. 96,9 % под водой
Установлено, что камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела. Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? б) Чему равен объем железа, если использовать его плотность, как показано на рисунке? в) Рассчитайте плотность жидкости и определите ее. 9{3}[/латекс]; этиловый спирт
9{3}[/латекс]; этиловый спирт
Рассчитайте выталкивающую силу 2-литрового гелиевого баллона. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Объемом резины пренебречь.
Какова плотность женщины, плавающей в пресной воде с [латексом]4,00\текст{%}[/латекс] ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой.) (b) Какой процент ее объема находится над поверхностью, когда она плавает в морской воде? 9{3}[/latex] (за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
Показать раствор а. 0,24; б. 0,68; в. Да, пробка будет плавать в этиловом спирте.
0,24; б. 0,68; в. Да, пробка будет плавать в этиловом спирте.
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
По рисунку докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна [латекс]{F}_{2}-{F}_{1}[/латекс] и что концы цилиндра имеют равные площади [латекс]А[/латекс]. Обратите внимание, что объем цилиндра (и объем вытесняемой им жидкости) равен [латекс]({ч}_{2}-{ч}_{1})А[/латекс].
Показать решение[латекс]\begin{array}{ccc}\text{net}\,F\hfill & =\hfill & {F}_{2}-{F}_{1}={p}_ {2}A-{p}_{1}A=({p}_{2}-{p}_{1})A=({h}_{2}{\rho}_{\text{ fl}}g-{h}_{1}{\rho}_{\text{fl}}g)A\hfill \\ & =\hfill & ({h}_{2}-{h}_{ 1}){\rho}_{\text{fl}}gA,\,\text{где}\,{\rho}_{\text{fl}}=\text{плотность жидкости}\text{. }\hfill \\ \text{net}\,F\hfill & =\hfill & ({h}_{2}-{h}_{1})A{\rho}_{\text{fl}} g = {V} _ {\ text {fl}} {\ rho} _ {\ text {fl}} g = {m} _ {\ text {fl}} g = {w} _ {\ text {fl} }\hfill \end{массив}[/latex]
Мужчина массой 75,0 кг плавает в пресной воде, при этом 3,00% его объема над водой, когда его легкие пусты, и 5,00% его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, воздействующая на любой объект в любой жидкости из-за разницы давлений на разных глубинах
Давление
ДавлениеПлавучесть возникает из-за того, что давление жидкости увеличивается с глубиной, и из-за того, что повышенное давление действует во всех направлениях (принцип Паскаля), так что на дно водоема действует неуравновешенная восходящая сила. затопленный объект.
Объекты одинакового объема испытывают одинаковые выталкивающие силы.Применение плавучести. | Индекс Концепции плавучести | ||||||||||||||||||||||||||||||||
|


 Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
 Но выталкивающая сила на каждом из них одинакова из-за одинакового давления окружающей среды и одинакового смещения воды. Разница в поведении происходит от сравнения этой выталкивающей силы с весом объекта.
Но выталкивающая сила на каждом из них одинакова из-за одинакового давления окружающей среды и одинакового смещения воды. Разница в поведении происходит от сравнения этой выталкивающей силы с весом объекта.
 Этот принцип полезен для определения объема и, следовательно, плотности объекта неправильной формы путем измерения его массы в воздухе и эффективной массы при погружении в воду (плотность = 1 грамм на кубический сантиметр). Эта эффективная масса под водой будет ее фактической массой за вычетом массы вытесненной жидкости. Таким образом, разница между реальной и эффективной массой дает массу вытесненной воды и позволяет вычислить объем объекта неправильной формы (например, царской короны в истории Архимеда). Масса, деленная на определенный таким образом объем, дает меру средней плотности объекта. Архимед обнаружил, что плотность предположительно золотой короны царя на самом деле была намного меньше плотности золота, что означает, что она была либо полой, либо заполнена менее плотным веществом.
Этот принцип полезен для определения объема и, следовательно, плотности объекта неправильной формы путем измерения его массы в воздухе и эффективной массы при погружении в воду (плотность = 1 грамм на кубический сантиметр). Эта эффективная масса под водой будет ее фактической массой за вычетом массы вытесненной жидкости. Таким образом, разница между реальной и эффективной массой дает массу вытесненной воды и позволяет вычислить объем объекта неправильной формы (например, царской короны в истории Архимеда). Масса, деленная на определенный таким образом объем, дает меру средней плотности объекта. Архимед обнаружил, что плотность предположительно золотой короны царя на самом деле была намного меньше плотности золота, что означает, что она была либо полой, либо заполнена менее плотным веществом. В этом суть закона Архимеда.
В этом суть закона Архимеда.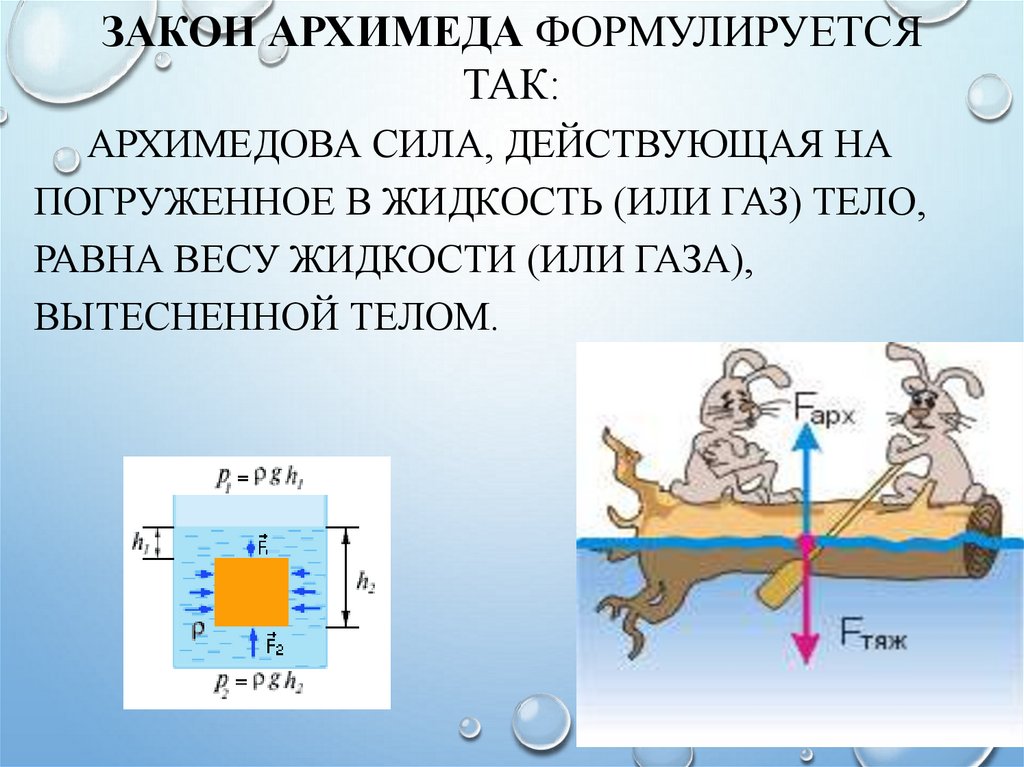
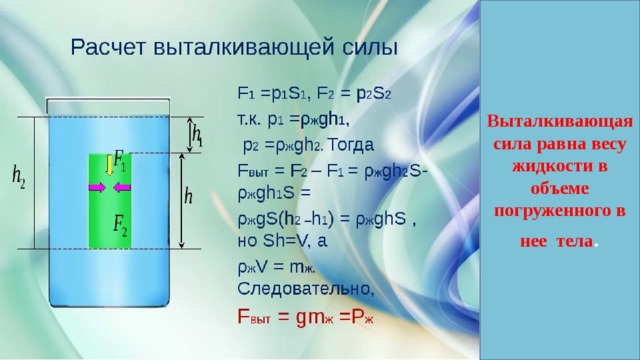 Эта сила называется выталкивающей силой, а это явление известно как выталкивающая сила.
Эта сила называется выталкивающей силой, а это явление известно как выталкивающая сила.  (2)
(2) Сначала предположим, что длина стороны кубического блока равна L .
Сначала предположим, что длина стороны кубического блока равна L .
 Эта направленная вверх сила, называемая выталкивающей силой, была объяснена на решенных примерах в другом руководстве.
Эта направленная вверх сила, называемая выталкивающей силой, была объяснена на решенных примерах в другом руководстве.
 92}$ или \[F_b=\rho_{fluid}\times V_{dis}\times g\]
92}$ или \[F_b=\rho_{fluid}\times V_{dis}\times g\]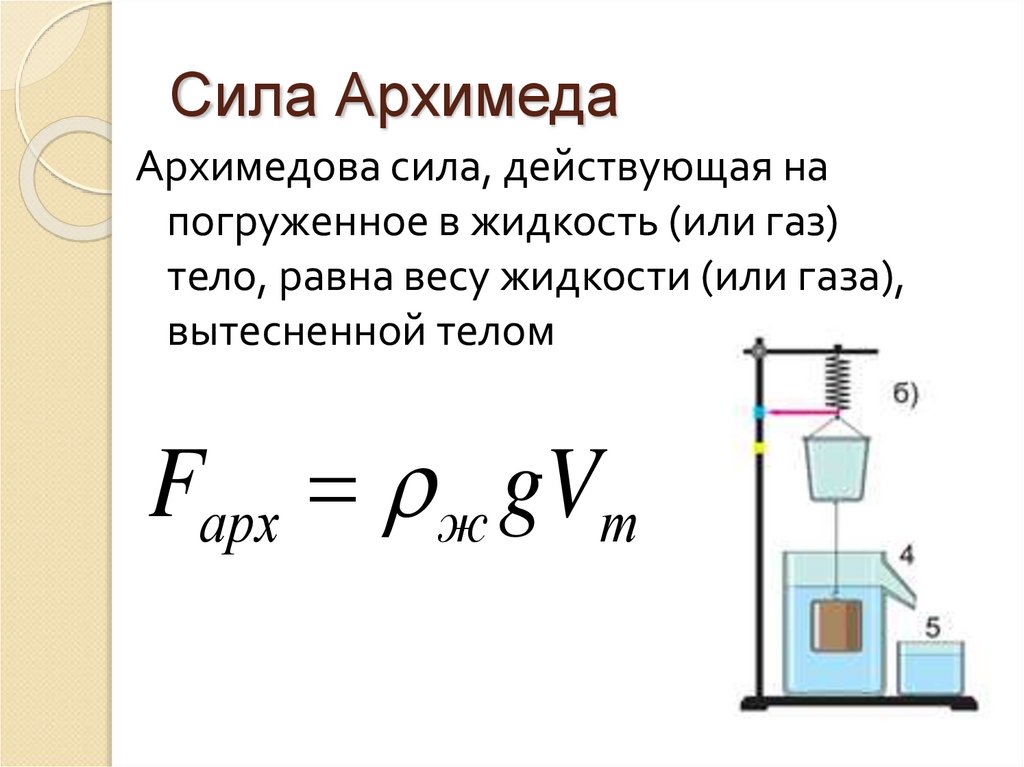 3}\end{выравнивание*} 93}$ медленно помещается в пресную воду. На какую глубину $h$ погружена плита?
3}\end{выравнивание*} 93}$ медленно помещается в пресную воду. На какую глубину $h$ погружена плита?  Согласно этому принципу, если записать все силы, приложенные неподвижной жидкостью к погруженному в нее телу, в виде направленной вверх выталкивающей силы $F_b$ и направленной вниз силы веса $W$, то в зависимости от знака результирующей силы возможны три ситуации $F_{net}=F_b \стрелка вверх-W\стрелка вниз$:
Согласно этому принципу, если записать все силы, приложенные неподвижной жидкостью к погруженному в нее телу, в виде направленной вверх выталкивающей силы $F_b$ и направленной вниз силы веса $W$, то в зависимости от знака результирующей силы возможны три ситуации $F_{net}=F_b \стрелка вверх-W\стрелка вниз$:
 93} \\ \\ &=0.9\end{align*} Где выше $\rho_{IB}$ и $\rho_{SW}$ — плотности айсберга и морской воды соответственно. Как видите, около 90% объема айсберга находится под водой.
93} \\ \\ &=0.9\end{align*} Где выше $\rho_{IB}$ и $\rho_{SW}$ — плотности айсберга и морской воды соответственно. Как видите, около 90% объема айсберга находится под водой.

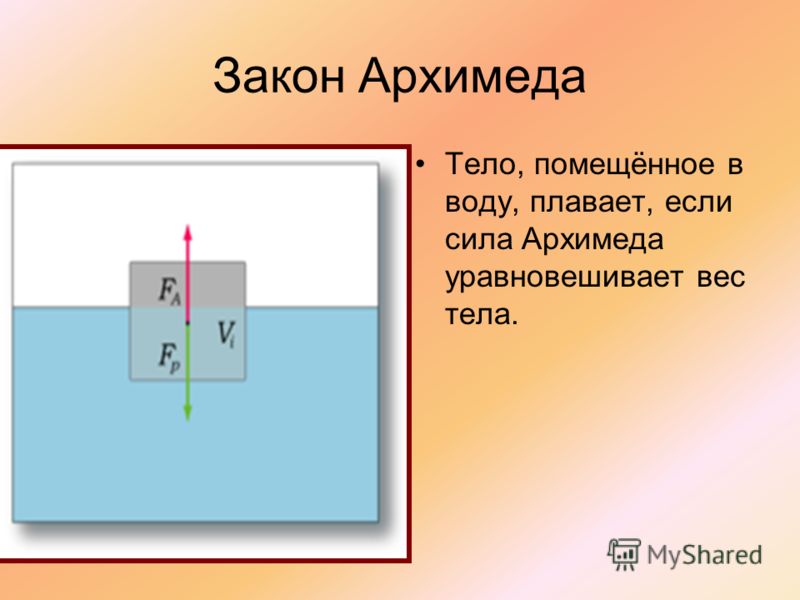 Рассчитать его довольно просто, но как рассчитать выталкивающую силу плавучего объекта?
Рассчитать его довольно просто, но как рассчитать выталкивающую силу плавучего объекта?


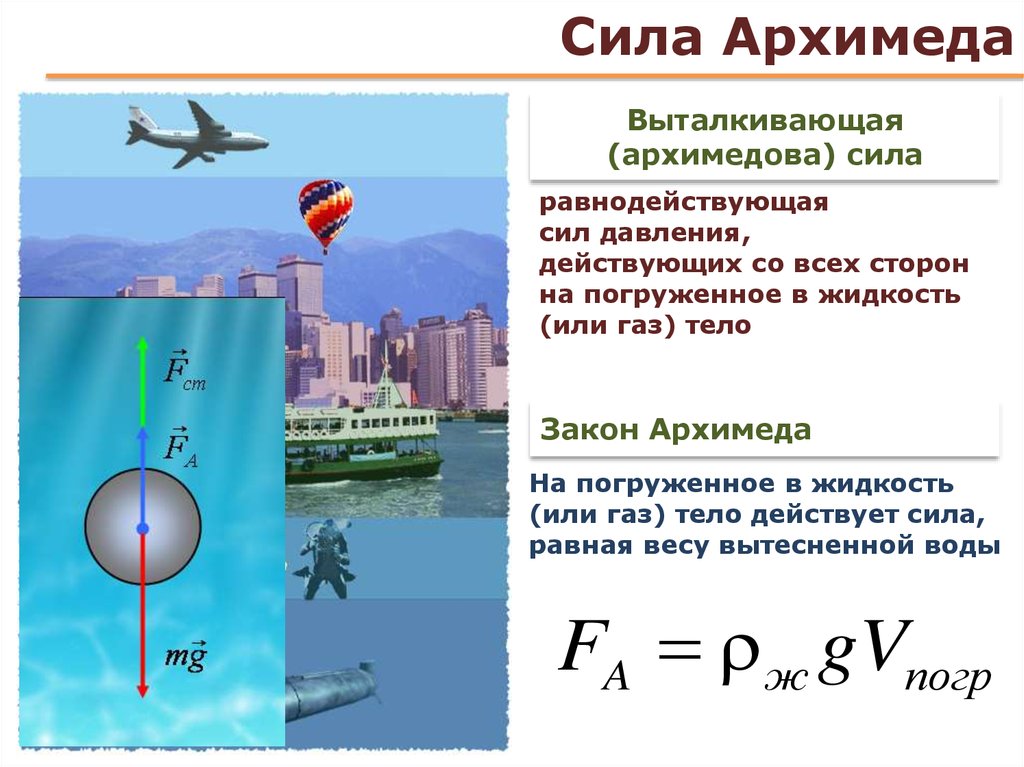


 w
w 
 Рассчитайте выталкивающую силу, действующую на объект, и, следовательно, рассчитайте вес объекта, который будет плавать в жидкости. (Примем ускорение свободного падения g=10м/с 2 )
Рассчитайте выталкивающую силу, действующую на объект, и, следовательно, рассчитайте вес объекта, который будет плавать в жидкости. (Примем ускорение свободного падения g=10м/с 2 )