Формула газ: Природный газ — что это такое кратко простыми словами

1. Смесь этанола и метанола сгорает в кислороде с образованием 35 см ³ CO ₂ и 55 см ³ H 1 H 1 происходит, и объемы обоих продуктов измеряются при 101 кПа и 120 градусах Цельсия. Каково молярное соотношение этанола к метанолу в смеси?
   

   
   
   

   
   

      

   
   
   
   

   а) Пусть соотношение этанол:метанол составляет 1:3. Тогда реакция метанола будет происходить в 3 раза чаще, чем реакция этанола. Таким образом, продуктов метанола будет в 3 раза больше, чем продуктов этанола.
   

      

   б) Пусть отношение будет 2:3.
   

      

   c) Пусть отношение будет 3:2.
   

      

   г) Пусть отношение будет 3:1
   

      

   Из этих значений видно, что вариант (d) имеет такое же молярное соотношение, как мы рассчитали ранее, и поэтому вариант (d) является правильным ответом.

6.3: Сочетание газовых законов: уравнение идеального газа и общее уравнение газа

1. Последнее обновление

2. Сохранить как PDF

Цели обучения

• Использовать закон идеального газа для описания поведения газа.

В этом модуле описывается взаимосвязь между давлением, температурой, объемом и количеством газа, а также способы объединения этих взаимосвязей для получения общего выражения, описывающего поведение газа.

Вывод закона идеального газа

Любой набор взаимосвязей между одной величиной (например, V) и несколькими другими переменными (\(P\), \(T\) и \(n\)) можно объединить в одно выражение, описывающее все отношения одновременно. Три отдельных выражения выглядят следующим образом:

• Закон Бойля

\[V \propto \dfrac{1}{P} \;\; \text{@ константы n и T}\]

• Закон Шарля

\[V \propto T \;\; \text{@ константа n и P}\]

• Закон Авогадро

\[V \propto n \;\; \text{@ константы T и P}\]

Объединение этих трех выражений дает

\[V \propto \dfrac{nT}{P} \tag{6.3.1}\]

, что показывает, что объем газ пропорционален числу молей и температуре и обратно пропорционален давлению.

\[V= {\rm Cons.} \left( \dfrac{nT}{P} \right) \tag{6.3.2}\]

По соглашению константа пропорциональности в уравнении 6.3.1 называется газовой постоянной, которая обозначается буквой \(R\). Подстановка R в уравнение 6.3.2 дает

\[ V = \dfrac{Rnt}{P} = \dfrac{nRT}{P} \tag{6.3.3}\]

Очистка дробей путем умножения обеих частей уравнения 6.3.4 на \(P \) дает

\[PV = nRT \tag{6.3.4}\]

Это уравнение известно как закон идеального газа .

Идеальный газ определяется как гипотетическое газообразное вещество, поведение которого не зависит от сил притяжения и отталкивания и может быть полностью описано законом идеального газа. На самом деле идеального газа не существует, но идеальный газ — это полезная концептуальная модель, которая позволяет нам понять, как газы реагируют на изменяющиеся условия. Как мы увидим, при многих условиях поведение большинства реальных газов очень близко к поведению идеального газа. Таким образом, закон идеального газа можно использовать для предсказания поведения реальных газов в большинстве условий. Закон идеального газа плохо работает при очень низких температурах или очень высоких давлениях, когда чаще всего наблюдаются отклонения от идеального поведения.

Примечание

Значительные отклонения от поведения идеального газа обычно возникают при низких температурах и очень высоких давлениях.

Прежде чем мы сможем использовать закон идеального газа, нам нужно знать значение газовой постоянной R. Его форма зависит от единиц, используемых для других величин в выражении. Если V выражено в литрах (л), P в атмосферах (атм), T в кельвинах (К) и n в молях (моль), то

\[R = 0,08206 \dfrac{\rm L\cdot атм} {\rm K\cdot моль} \tag{6.3.5}\] 95\;Pa\]

Обратите внимание, что в этой части STP определяется иначе. Старое определение основывалось на стандартном давлении 1 атм.

Мы можем рассчитать объем 1000 моль идеального газа при стандартных условиях, используя вариант закона идеального газа, приведенный в уравнении 6. 3.4:

\[V=\dfrac{nRT}{P}\tag{6.3 .7}\]

Таким образом, объем 1 моля идеального газа равен 22,71 л при СТП и 22,41 л при 0°C и 1 атм , что примерно эквивалентно объему трех баскетбольных мячей. Молярные объемы нескольких реальных газов при 0°C и 1 атм приведены в таблице 10.3, из которой видно, что отклонения от поведения идеального газа довольно малы. Таким образом, закон идеального газа хорошо аппроксимирует поведение реальных газов при 0°C и 1 атм. Соотношения, описанные в разделе 10.3 как законы Бойля, Шарля и Авогадро, являются просто частными случаями закона идеального газа, в котором два из четырех параметров (P, V, T и n) остаются фиксированными.

Таблица \(\PageIndex{1}\): Молярные объемы выбранных газов при 0°C и 1 атм

Газ	Молярный объем (л)
Он	22. 434
Ар	22.397
В 2	22.433
Н 2	22.402
О 2	22.397
СО 2	22.260
НХ 3	22.079

Применение закона идеального газа

Закон идеального газа позволяет нам вычислить значение четвертой переменной для газовой пробы, если мы знаем значения любых трех из четырех переменных ( P , V , T и n ). Это также позволяет нам предсказать конечное состояние образца газа (т. е. его конечную температуру, давление, объем и количество) после любых изменений условий, если параметры ( P , V , T и n ) указаны для начального состояния . Некоторые приложения проиллюстрированы в следующих примерах. Подход, используемый повсюду, заключается в том, чтобы всегда начинать с одного и того же уравнения — закона идеального газа — и затем определять, какие величины даны, а какие необходимо рассчитать. Начнем с простых случаев, когда нам даны три из четырех параметров, необходимых для полного физического описания газообразного образца.

Пример \(\PageIndex{1}\)

Воздушный шар, который Чарльз использовал для своего первого полета в 1783 году, был уничтожен, но мы можем оценить его объем в 31 150 л (1100 футов ³ ), учитывая записанные размеры в это время. Если температура на уровне земли была 86°F (30°C) и атмосферное давление 745 мм ртутного столба, сколько молей газообразного водорода потребовалось, чтобы заполнить воздушный шар?

Дано: объем, температура и давление

Запрошено: количество газа

Стратегия:

1. Решите закон идеального газа для неизвестного количества, в данном случае n .
2. Убедитесь, что все величины даны в единицах, совместимых с единицами газовой постоянной. При необходимости переведите их в соответствующие единицы, вставьте в полученное уравнение, а затем рассчитайте необходимое количество молей газообразного водорода.

Решение:

A Нам дают значения для P , T и V и просят вычислить n . Если мы решим закон идеального газа (уравнение 6.3.4) для n , получим \]

B P и T даны в единицах, несовместимых с единицами газовой постоянной [ R = 0,08206 (л•атм)/(К•моль)]. Поэтому мы должны перевести температуру в кельвины, а давление в атмосферы: 93\;mol\]

Упражнение \(\PageIndex{1}\)

Предположим, что «пустой» аэрозольный баллончик из-под краски имеет объем 0,406 л и содержит 0,025 моль газа-вытеснителя, такого как CO ₂ . Каково давление газа при 25°С?

Ответ: 1,5 атм

В примере \(\PageIndex{1}\) нам были даны три из четырех параметров, необходимых для описания газа при определенном наборе условий, и нас попросили рассчитать четвертый . Мы также можем использовать закон идеального газа, чтобы вычислить эффект заменяет в любом из указанных условий на любой из других параметров, как показано в примере \(\PageIndex{5}\).

Закон идеального газа: https://youtu.be/rHGs23368mE

Общее уравнение газа

Когда газ описывается при двух различных условиях, уравнение идеального газа должно применяться дважды — к конечное условие. Это:

\[\begin{array}{cc}\text{Исходное состояние}(i) & \text{Окончательное условие} (f)\\P_iV_i=n_iRT_i & P_fV_f=n_fRT_f\end{массив}\]

Оба уравнения можно преобразовать, чтобы получить:

\[R=\dfrac{P_iV_i}{n_iT_i} \hspace{1cm} R=\dfrac{P_fV_f}{n_fT_f}\]

Два уравнения равны друг другу другой, поскольку каждый из них равен одной и той же константе \(R\). Таким образом, мы имеем:

\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\tag{6. 3.8}\]

Уравнение называется общим уравнением газа . Уравнение особенно полезно, когда одно или два свойства газа остаются постоянными между двумя условиями. В таких случаях уравнение можно упростить, исключив эти постоянные свойства газа.

Пример \(\PageIndex{2}\)

Предположим, что Чарльз изменил свои планы и совершил свой первый полет не в августе, а в холодный январский день, когда температура у земли была -10°C ( 14°F). Насколько большой воздушный шар ему понадобился бы, чтобы содержать то же количество газообразного водорода при том же давлении, что и в примере \(\PageIndex{1}\)?

Дано: температура, давление, количество и объем в августе; температура в январе

Просили: объем в январе

Стратегия:

1. Используйте результаты примера \(\PageIndex{1}\) для августа в качестве начальных условий, а затем рассчитайте изменение объема из-за изменения температуры от 30 °С до -10°С. Начните с построения таблицы, показывающей начальные и конечные условия.
2. Упростите общее уравнение газа, исключив величины, которые остаются постоянными между начальным и конечным условиями, в данном случае \(P\) и \(n\).
3. Найдите неизвестный параметр.

Решение:

A Чтобы точно увидеть, какие параметры изменились, а какие остались постоянными, подготовьте таблицу начальных и конечных условий:

B И \(n\), и \(P\) в обоих случаях одинаковы (\(n_i=n_f,P_i=P_f\)). Следовательно, уравнение можно упростить до:

\[\dfrac{V_i}{T_i}=\dfrac{V_f}{T_f}\]

Это соотношение впервые было отмечено Чарльзом. 94\;L\]

Важно проверить свой ответ, чтобы убедиться, что он имеет смысл, на тот случай, если вы случайно инвертировали величину или умножили, а не разделили. При этом температура газа снижается. Поскольку мы знаем, что объем газа уменьшается с понижением температуры, конечный объем должен быть меньше начального объема, поэтому ответ имеет смысл. Мы могли бы рассчитать новый объем, подставив все заданные числа в закон идеального газа, но, как правило, гораздо проще и быстрее сосредоточиться только на изменяющихся величинах.

Упражнение \(\PageIndex{2}\)

На вечеринке в лаборатории наполненный гелием воздушный шар объемом 2,00 л при температуре 22°C опускают в большой контейнер с жидким азотом (T = −196°C). ). Каков конечный объем газа в баллоне?

Ответ : 0,52 л

Пример \(\PageIndex{1}\) иллюстрирует взаимосвязь, первоначально обнаруженную Чарльзом. Мы могли бы проработать аналогичные примеры, иллюстрирующие обратную зависимость между давлением и объемом, отмеченную Бойлем (9).0369 PV = константа) и соотношение между объемом и количеством, наблюдаемое Авогадро ( V / n = константа). Мы, однако, не будем этого делать, потому что важнее отметить, что исторически важные газовые законы являются лишь частными случаями идеального газового закона, в котором две величины изменяются, а две другие остаются постоянными. Метод, используемый в примере \(\PageIndex{1}\), может быть применен в 90 369 любых 90 370 таких случаях, как мы демонстрируем в примере \(\PageIndex{2}\) (который также показывает, почему нагрев закрытого контейнера с газом (например, картридж с бутановой зажигалкой или аэрозольный баллончик) может привести к взрыву).

Пример \(\PageIndex{3}\)

На аэрозольных баллончиках имеется четкая маркировка с предупреждением, например: «Не сжигайте пустой контейнер». Предположим, что вы не заметили этого предупреждения и бросили «пустой» аэрозольный баллончик в упражнении 5 (0,025 моль в 0,406 л, первоначально при 25°C и внутреннем давлении 1,5 атм) в огонь при 750°C. Какое давление было бы внутри банки (если бы она не взорвалась)?

Дано: начальный объем, количество, температура и давление; конечная температура

Запрос: конечное давление

Стратегия:

Следуйте стратегии, описанной в примере \(\PageIndex{5}\).

Решение:

Подготовьте таблицу, чтобы определить, какие параметры изменяются, а какие остаются постоянными:

И \(V\), и \(n\) в обоих случаях одинаковы (\(V_i=V_f,n_i=n_f\)). Следовательно, уравнение можно упростить до:

\[P_iT_i=P_fT_f\]

Решив уравнение для \(P_f\), мы получим:

\[P_f=P_i\times\dfrac{T_i}{T_f} =\rm1. 5\;atm\times\dfrac{1023\;K}{298\;K}=5.1\;atm\]

Этого давления более чем достаточно, чтобы разорвать контейнер из тонкого листового металла и вызвать взрыв !

Упражнение \(\PageIndex{3}\)

Предположим, что огнетушитель, заполненный CO ₂ до давления 20,0 атм при 21°C на заводе, случайно оставлен на солнце в закрытом автомобиле. в Тусоне, штат Аризона, в июле. Температура внутри автомобиля поднимается до 160°F (71,1°C). Какое внутреннее давление в огнетушителе?

Ответ : 23,4 атм

В примере \(\PageIndex{1}\) и примере \(\PageIndex{2}\) два из четырех параметров ( P , V , T и n ) были фиксированными, в то время как один из них можно было изменять, и нас интересовало влияние на значение четвертого. В самом деле, мы часто сталкиваемся со случаями, когда две переменные P , V и T могут изменяться для данной пробы газа (следовательно, n постоянно), и нас интересует изменение в значении третьего в новых условиях.

Пример \(\PageIndex{4}\)

В примере \(\PageIndex{1}\) мы видели, что Чарльз использовал воздушный шар объемом 31 150 л для своего начального подъема и что воздушный шар содержал 1,23 × 10 ³ моль газа H ₂ первоначально при 30°С и 745 мм рт.ст. Предположим, что Гей-Люссак также использовал этот воздушный шар для своего рекордного подъема на высоту 23 000 футов и что давление и температура на этой высоте составляли 312 мм ртутного столба и -30°C соответственно. До какого объема должен был бы расшириться воздушный шар, чтобы удержать такое же количество газообразного водорода на большей высоте?

Дано: начальное давление, температура, количество и объем; конечное давление и температура

Требуемый запрос: конечный объем

Стратегия:

Следуйте стратегии, описанной в примере \(\PageIndex{5}\).

Решение:

Начните с создания таблицы двух наборов условий:

Имеет ли этот ответ смысл? В этой задаче действуют два противоположных фактора: уменьшение давления имеет тенденцию к увеличению объема газа, а понижение температуры имеет тенденцию к уменьшению объема газа. Что мы ожидаем преобладать? Давление падает более чем в два раза, а абсолютная температура падает всего примерно на 20%. Поскольку объем пробы газа прямо пропорционален как T , так и 1/P , переменная , которая больше всего изменится , окажет наибольшее влияние на V . В этом случае преобладает эффект уменьшения давления, и мы ожидаем, что объем газа увеличится, как мы и обнаружили в нашем расчете.

Мы также могли бы решить эту задачу, решив закон идеального газа для V , а затем подставив соответствующие параметры для высоты 23 000 футов:

За исключением разницы, вызванной округлением до последней значащей цифры, это тот же результат, который мы получили ранее. Часто существует более одного «правильного» способа решения химических задач.

Упражнение \(\PageIndex{4}\)

Стальной баллон со сжатым аргоном объемом 0,400 л наполняли до давления 145 атм при 10°C. При давлении 1,00 атм и температуре 25 °C сколько лампочек накаливания объемом 15,0 мл можно наполнить из этого цилиндра? (Подсказка: найдите количество молей аргона в каждом сосуде. )

Ответ: 4,07 × 10 ³

Второй тип задач закона идеального газа: https://youtu.be/WQDJOqddPI0

Использование закона идеального газа для расчета плотности и молярной массы газа

Закон идеального газа также можно использовать для расчета молярной массы газа на основе экспериментально измеренных плотностей газа. Чтобы увидеть, как это возможно, мы сначала преобразуем закон идеального газа, чтобы получить

\[\dfrac{n}{V}=\dfrac{P}{RT}\tag{6.3.9}\]

сторона имеет единицы моли на единицу объема (моль/л). Количество молей вещества равно его массе (\(m\), в граммах), деленной на его молярную массу (\(M\), в граммах на моль):

\[n=\dfrac{m}{M}\tag{6.3.10}\]

Подстановка этого выражения для \(n\) в уравнение 6.3.9 дает

\[\dfrac{m}{ MV}=\dfrac{P}{RT}\tag{6.3.11}\]

Поскольку \(m/V\) — это плотность \(d\) вещества, мы можем заменить \(m/V \) на \(d\) и переставить, чтобы получить

\[\rho=\dfrac{m}{V}=\dfrac{MP}{RT}\tag{6. 3.12}\]

Расстояние между частиц в газах велик по сравнению с размером частиц, поэтому их плотности значительно ниже, чем плотности жидкостей и твердых тел. Следовательно, плотность газа обычно измеряется в граммах на литр (г/л), а не в граммах на миллилитр (г/мл).

Пример \(\PageIndex{5}\)

Рассчитайте плотность бутана при 25°C и давлении 750 мм рт.ст.

Дано: состав, температура и давление

Запрошено: плотность

Стратегия:

1. Рассчитайте молярную массу бутана и переведите все величины в соответствующие газовые константы для значения газовой константы.
2. Подставьте эти значения в уравнение 6.3.12, чтобы получить плотность.

Решение:

A Молярная масса бутана (C ₄ H ₁₀ ) равна

\[M=(4)(12,011) + (108)1. г/моль\]

Использование 0,08206 (л•атм)/(К•моль) для R означает, что нам нужно преобразовать температуру из градусов Цельсия в кельвины ( T = 25 + 273 = 298 K) и давление от миллиметров ртутного столба до атмосфер:

\[P=\rm750\;мм рт. ст.\times\dfrac{1\;атм}{760\;мм рт.ст.}=0,987\;атм\]

B Подстановка этих значений в уравнение 6.3.12 дает

\[\rho=\rm\dfrac{58,123\;г/моль\times0,987\;atm}{0,08206\dfrac{L\cdot atm} {K\cdot mol}\times298\;K}=2,35\;г/л\]

Упражнение \(\PageIndex{5}\)

Радон (Rn) представляет собой радиоактивный газ, образующийся при распаде встречающихся в природе уран в горных породах, таких как гранит. Он имеет тенденцию накапливаться в подвалах домов и представляет значительный риск для здоровья, если присутствует в воздухе помещений. Многие штаты теперь требуют, чтобы дома перед продажей проверялись на наличие радона. Рассчитайте плотность радона при давлении 1,00 атм и температуре 20°C и сравните ее с плотностью газообразного азота, составляющего 80% атмосферы, в тех же условиях, чтобы понять, почему радон находится в подвалах, а не на чердаках.

Ответ: радон, 9,23 г/л; N ₂ , 1,17 г/л

Уравнение 6.3.12 обычно используется для определения молярной массы неизвестного газа путем измерения его плотности при известной температуре и давлении. Этот метод особенно удобен для идентификации газа, образовавшегося в результате реакции, и его несложно осуществить. Колбу или стеклянную колбу известного объема тщательно высушивают, вакуумируют, запечатывают и взвешивают пустыми. Затем он заполняется образцом газа при известной температуре и давлении и повторно взвешивается. Разница в массе между двумя показаниями и есть масса газа. Объем колбы обычно определяют путем взвешивания пустой колбы и наполненной жидкостью известной плотности, например водой. Использование измерений плотности для расчета молярных масс показано в примере \(\PageIndex{6}\).

Пример \(\PageIndex{6}\)

Реакция медной монеты с азотной кислотой приводит к образованию красно-коричневого газообразного соединения, содержащего азот и кислород. Проба газа при давлении 727 мм рт.ст. и температуре 18°С весит 0,289 г в колбе объемом 157,0 мл. Рассчитайте молярную массу газа и предложите разумную химическую формулу соединения.

Дано: давление, температура, масса и объем

Запрошено: молярная масса и химическая формула

Стратегия:

1. Решите уравнение 6. 3.12 для определения молярной массы газа, а затем рассчитайте плотность газа на основе предоставленной информации.
2. Преобразуйте все известные величины в соответствующие единицы для используемой газовой постоянной. Подставьте известные значения в ваше уравнение и найдите молярную массу.
3. Предложите разумную эмпирическую формулу, используя атомные массы азота и кислорода и расчетную молярную массу газа.

Решение:

A Решение уравнения 6.3.12 для молекулярной массы дает

\[M=\dfrac{mRT}{PV}=\dfrac{dRT}{P}\]

Плотность масса газа, деленная на его объем:

\[\rho=\dfrac{m}{V}=\dfrac{0,289\rm g}{0,17\rm L}=1,84 \rm g/L\]

B Мы должны преобразовать другие величины в соответствующие единицы, прежде чем вставлять их в уравнение: 1\rm атм}{760\rm мм рт.ст.}=0,957\rm atm\]

Таким образом, молярная масса неизвестного газа равна

\[\rho=\rm\dfrac{1,84\;g/L\times0,08206\dfrac{L\cdot atm}{K\ cdot mol}\times291\;K}{0,957\;atm}=45,9 г/моль\]

C Атомные массы N и O примерно равны 14 и 16 соответственно, поэтому мы можем составить список, показывающий массы возможных комбинаций:

\[M({\rm NO})=14 + 16=30 \rm\; г/моль\]

\[M({\rm N_2O})=(2)(14)+16=44 \rm\;г/моль\]

\[M({\rm NO_2})= 14+(2)(16)=46 \rm\;г/моль\]

Наиболее вероятный выбор – NO ₂ , что согласуется с данными. Красно-коричневый цвет смога также является результатом присутствия газа NO ₂ .

Упражнение \(\PageIndex{6}\)

Вы отвечаете за интерпретацию данных беспилотного космического зонда, который только что приземлился на Венере и отправил отчет о ее атмосфере. Данные следующие: давление 90 атм; температура 557°С; плотность 58 г/л. Основная составляющая атмосферы (>95%) — углерод. Рассчитайте молярную массу основного присутствующего газа и определите ее.

Ответ : 44 г/моль; \(CO_2\)

Плотность и молярная масса газов: https://youtu.be/gnkGBsvUFVk

Резюме

Закон идеального газа выводится из эмпирических соотношений между давлением, объемом, температурой, и количество молей газа; его можно использовать для вычисления любого из четырех свойств, если известны остальные три.

Уравнение идеального газа : \(PV = nRT\),

где \(R = 0,08206 \dfrac{\rm L\cdot atm}{\rm K\cdot mol}=8,3145 \dfrac{\rm J}{ \rm K\cdot моль}\)

Общее уравнение газа : \(\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\)

Плотность газа: \(\ rho=\dfrac{MP}{RT}\)

Эмпирические отношения между объемом, температурой, давлением и количеством газа могут быть объединены в закон идеального газа , PV = нРТ . Константа пропорциональности, R , называется газовой постоянной и имеет значение 0,08206 (л•атм)/(К•моль), 8,3145 Дж/(К•моль) или 1,9872 кал/(К•моль) , в зависимости от используемых единиц измерения. Закон идеального газа описывает поведение идеального газа , гипотетического вещества, поведение которого можно количественно объяснить законом идеального газа и кинетической молекулярной теорией газов. Стандартная температура и давление (STP) : 0°C и 1 атм. Объем 1 моль идеального газа при СТП равен 22,41 л, стандартный молярный объем . Все эмпирические газовые соотношения являются частными случаями закона идеального газа, в котором два из четырех параметров остаются постоянными. Закон идеального газа позволяет вычислить значение четвертой величины ( P , V , T или n ), необходимой для описания газовой пробы, когда известны остальные, а также предсказать значение этих величин. количества после изменения условий, если исходные условия (значения P , V , T и n ). Закон идеального газа можно использовать и для вычисления плотности газа, если известна его молярная масса, или, наоборот, молярной массы неизвестной пробы газа, если измерена его плотность.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Показать страницу TOC

   нет на странице

2. Теги

   На этой странице нет тегов.

Свойства, формулы, законы, вывод, графики

Что такое газы?

Газы — это состояние вещества, в котором молекулы находятся далеко друг от друга и характеризуются отсутствием определенного объема и плотности. Закон Бойля, закон Шарля, закон Авогадро, закон Гей-Люссака, закон идеального газа и закон Грэма определяют соотношение между массой, давлением, объемом, температурой и плотностью молекул идеального газа.

Тщательные эксперименты показывают, что законы идеального газа лишь приблизительно соблюдаются различными газами. Газы, не подчиняющиеся этим законам, называются реальными газами.

Уравнение идеального газа можно использовать, чтобы отличить идеальный газ от реального газа. Газ, который подчиняется этому уравнению, называется идеальным газом, а не подчиняющийся этому уравнению – реальным газом. Уравнение Ван-дер-Ваальса используется для получения свойств реальных газов.

Свойства газов

• В газообразном состоянии вещество имеет свойство полностью заполнять любое доступное пространство с одинаковой плотностью.
• Низкая плотность, высокая сжимаемость также являются важными свойствами газов.
• Газы образуются, когда тепловая энергия намного превышает силу притяжения.
• Среди кристаллических твердых, жидких и газообразных агрегатных состояний газы допускаются для сравнительного изучения массы, давления, объема и температуры, плотности, теплоемкости и т. д.

Формула газов

Физические свойства газов очень просты и одинаковы для всех газов. Эти свойства различных газов очевидны из того факта, что все газы обычно подчиняются какой-либо простой или общей газовой формуле или соотношению. Это так называемые газовые законы.

При изучении химии или физики законы Бойля, Шарля, Авогадро, Гей-Люссака и Грэма являются общими законами, из которых выводятся формулы идеальных газов. После знания этих экспериментальных законов идеального газа была разработана теоретическая структура газов, основанная на модели, с помощью уравнения кинетической теории газа.

Что такое закон Бойля?

Закон Бойля гласит, что при постоянной температуре объем определенной массы газа обратно пропорционален его давлению. Следовательно, объем данного количества газов при постоянной температуре находится в равновесии с давлением газов.

При постоянной температуре и давлении 1 атм баллон содержит 10 мл метана или газообразного водорода. Если давление возрастет до 2 атм, то по закону Бойля объем уменьшится до 5 мл.

Формула закона Бойля

Согласно определению закона Бойля
V ∝ 1/P, когда температура (T) постоянна
или PV = K = постоянная для газа.

Значение газовой постоянной зависит от природы и массы молекул газа. Для данной массы газа, если объем V ₁ при давлении P ₁ и объеме V ₂ при давлении P ₂ . Следовательно, по закону Бойля
P ₁ V ₁ = P ₂ V ₂ .

Графическое представление закона Бойля

Связь между давлением и объемом газа может быть представлена ​​плечом прямоугольной гиперболы, приведенной ниже рисунка,

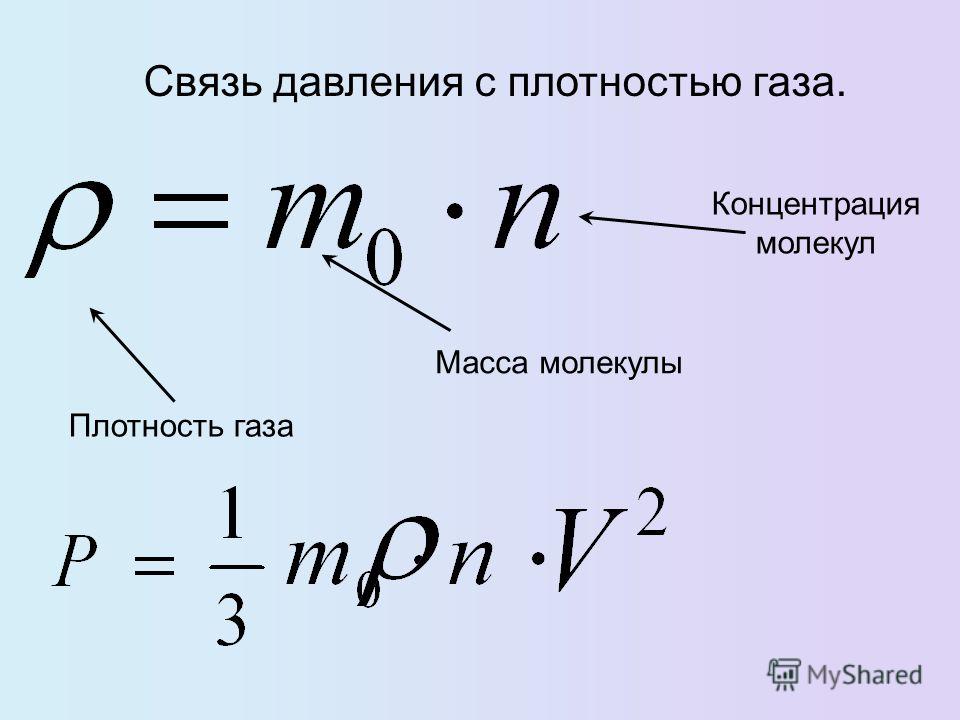• Значение газовой постоянной изменяется с температурой. Для каждой фиксированной температуры будет отдельная двухмерная кривая. Когда эти кривые строятся при различных фиксированных температурах, называемых изотермами.
• При постоянной температуре данная масса газа является произведением давления на объем. Если произведение давления и объема газа отложено по оси у, а давление отложено по оси абсцисс, то получается прямолинейный график, параллельный оси абсцисс.

Зависимость давления от плотности

Пусть при постоянной температуре M масса газа имеет давление P ₁ при объеме V ₂ и давление P ₂ при объеме V ₂ .

Согласно закону Бойля,
P ₁ V ₁ = P ₂ V ₂
или, P ₁ /P ₂ = V _{2 /V 1901.}

Пусть плотность газа D ₁ при давлении P ₁ и D ₂ при давлении P ₂ .

Следовательно, D ₁ = M/V ₁
OR, V ₁ = M/D ₁

D ₂ = M/V ₂

масса газа пропорциональна его давлению.

Что такое Чарльз Лоу?

Закон Шарля сделал измерение объема фиксированной массы газа при различных температурах в условиях постоянного давления. Закон Шарля гласит, что при постоянном давлении объем данной массы газа является линейной функцией температуры.

Математическая формула закона Чарльза

При постоянном давлении каждый градус повышения температуры определенной массы газа расширяет 1/273,5 своего объема при 0⁰C. Пусть V ₀ = объем при 0⁰C. Повышение температуры на 1⁰C увеличивает объем газа V ₀ /273,5 мл.

Удобно использовать абсолютную шкалу температур, по которой температура измеряется в Кельвинах. Следовательно, показание по этой шкале было получено путем прибавления 273 к значению по Цельсию. Следовательно, ТК = 273 + t°С.

Закон Шарля представлен как
V _t = (V ₀ × T)/273 = (V ₀ /273) × T.

заданное давление. Следовательно, приведенное выше соотношение выражается как
V _t = K ₂ T, где K ₂ = константа

Согласно этой газовой формуле закон Чарльза утверждает, что при постоянном давлении объем данной массы газа прямо пропорциональна его температуре по шкале Кельвина.

Графическое представление Чарльза Лоу

Типичным свойством объема газа при изменении его температуры по шкале Кельвина является полученная прямолинейная изобарограмма. Отсюда общий термин изобара, означающий постоянное давление, присвоенное этим участкам.

Что такое абсолютный нуль температуры?

Поскольку объем прямо пропорционален температуре по Кельвинам. Таким образом, объем теоретически равен нулю при нуле Кельвина или -273 ° C. Это гипотетически, потому что молекула нашей окружающей среды имеет физические свойства превращаться в жидкость, а затем в твердое состояние, прежде чем будет достигнута эта низкая температура газа.

На самом деле в газах при температуре около нуля градусов Кельвина нет вещества. Для сжижения реальных газов необходимо поддерживать критическую температуру.

Зависимость плотности от температуры

Пусть при постоянном давлении, для M масса газа имеет объем V ₁ при температуре T ₁ и объем V ₂ при температуре T ₂ . Согласно закону Шарля,
V ₁ /V ₂ = T ₁ /T ₂

Снова пусть плотности D ₁ и D ₂ при V ₂ и V ₁ соответственно.
Следовательно, T ₁ /T ₂ = V ₁ /V ₂ = D ₂ /D ₁
или, D ∝ выше 1/T

3, по формуле давление, плотность данной массы газа обратно пропорциональна его температуре.

Что такое закон Авогадро?

Объем газа зависит не только от количества газа, но также от его давления и температуры.