Формула глубины в физике: Как измерить глубину? Вопросы и ответы по физике :: Класс!ная физика - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Вы делаете это неправильно: расчет глубины / Хабр

Приветствую вас, глубокоуважаемые!

Что если я скажу, что глубина, что бы вы под ней не подразумевали, является одной из самых сложных для точного измерения величин? На какой глубине плывет подводная лодка? Какая глубина марианской впадины? На какой глубине лежит Титаник? Если вам не повезет с параметрами, то на первом километре глубины, вы можете ошибиться примерно на 30-40 метров и на 200-300 метров на 6-ом километре, используя датчик давления. Если вы предпочитаете эхолот, то при неудачном стечении обстоятельств, которые вы не учли, ошибка на первом километре составит метров 100, а на 6-ом — целый километр. Конечно, можно еще использовать длинную веревку… Но там, как известно, свои подводные камни.

Как такое могло случиться и как делать правильно я расскажу под катом. В довесок к статье есть Open-source библиотека на C#/C/Rust/Matlab/Octave/JavaScript и пара онлайн-калькуляторов для демонстрации.

Статья будет полезна разработчикам подводной техники, число которых за последние лет пять выросло в разы.

Итак, для начала сразу оговоримся, что глубиной часто называют две разных величины:

и расстояние по вертикали от поверхности воды до точки, где эту глубину измеряют,
и расстояние по вертикали от поверхности воды до дна.

В первом случае — это глубина погружения, а во втором — глубина места.

Есть ровно два с половиной фундаментальных способа изменения этих величин, как я уже упомянул:

по гидростатическому давлению столба жидкости, т.е. при помощи датчика давления;
по времени распространения звука — эхолотом
по длине выпущенной за борт веревки =)

С веревкой все понятно, а с остальными двумя давайте разберемся. Сегодня разберем:

Способ 1 — По давлению столба жидкости

Все мы знаем из школьного курса физики формулу гидростатического давления столба жидкости:

Из нее легко посчитать высоту столба жидкости (т.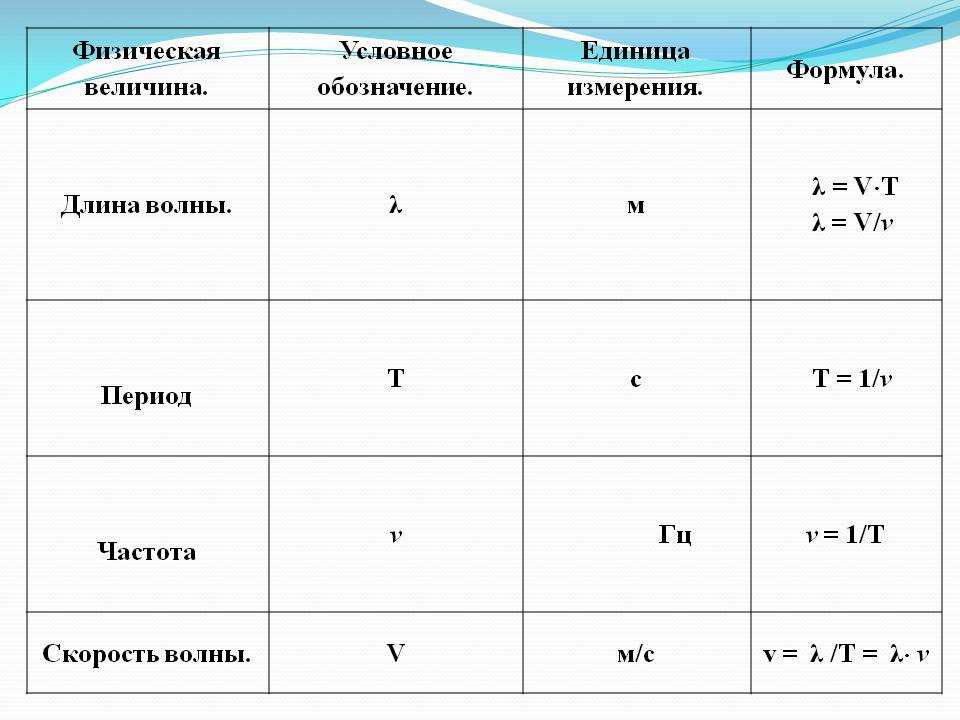 2.

Давайте абстрагируемся от точности конкретных приборов, пусть даже они у нас суперточные.
Проблема в том, что никакой член формулы не является константой. Даже атмосферное давление может меняться в течение часа.

Как влияет атмосферное давление?

Давление у поверхности моря может варьироваться в пределах 641-816 мм. рт. ст., или, тоже самое в миллибарах: от 855 до 1087. Если просто взять за стандартное значение в 1013.25 мБар, то в зависимости от погоды уже можно получить ошибку в 40-50 сантиметров, причем, как в «плюс», так и в «минус».

Что с ускорением свободного падения?

Боюсь показаться Кэпом, но все же напомню, что земля у нас

~~плоская~~

вращается, и за счет центробежной силы притягивает на экваторе слабее, чем на полюсах.

Если не крохоборничать и не учитывать гравитационные аномалии из-за разной плотности земных пород, гор, впадин, изменения скорости вращения земли от сброшенной земными деревьями листвы и перемещениями соков по их стволам, то нас вполне устроит стандартная зависимость ускорения свободного падения от георафической широты.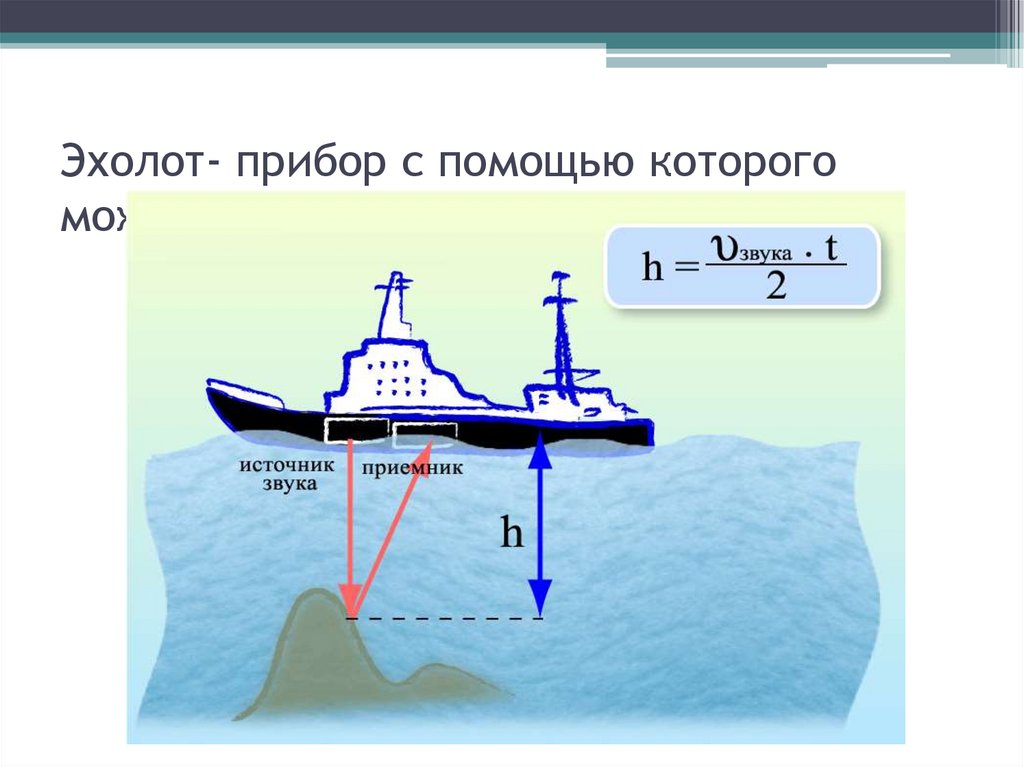

Т.н WGS-84 Gravity formula.

Согласно этой формуле, ускорение свободного падения меняется от 9.7803 м/с2 на экваторе (0° градусов широты) до 9.8322 м/с2 на полюсах (90/-90° широты).

Допустим, мы возьмем стандартное значение ускорения свободного падения 9.80665 м/с2, на сколько мы ошибемся в худшем случае?

Это иллюстрируетя картинкой ниже. На ней синий график показывает ошибку определения глубины на экваторе, если мы будем использовать стандартное значение , а оранжевый график — такую же ошибку на полюсах.

То есть, если мы подставим в формулу стандартное значение и пойдем погружаться где-то ближе к экватору, то на 100 метрах ошибемся всего на 20-30 сантиметров, на километре — на 2,5-3 метра, а на 9-10 километрах (Бездна Челленжера, кстати, находится на 11° северной широты) ошибка будет уже 25-30 метров. Т.е. реальная глубина будет больше, чем та, которую мы измерим.

А как влияет плотность воды?

Самым нехорошим образом.

Если два первых компонента погрешности учесть достаточно просто, да и вклад их весьма скромен, то с плотностью воды история более замысловатая.

Дело в том, что плотность воды в упрощенном случае есть функция температуры, давления и солености.

То есть мало измерять давление, атмосферное давление, учитывать географическую широту места. Нужно еще знать температуру и соленость воды.

Для определения плотности морской воды в (разумном) диапазоне условий на практике наиболее широко применяется формула из работы Чена и Миллеро (Да, ЮНЕСКО занимается еще и этим!)

Допустим, мы измерили и температуру и соленость, но остается сжимаемость воды — изменение плотности с давлением (т.е. с глубиной), и чтобы определить высоту столба жидкости нужно просуммировать высоты элементарных столбиков, на которых давление изменяется на какую-то малую величину . В целом это конечно интеграл, но чтобы сразу привнести некое практическое значение, запишем его так:

N — это число интервалов разбиения давления от до измеренного .

Плотность зависит от давления практически линейно, и считать такую сумму из-за учета одной лишь сжимаемости смысла нет, но я привел здесь эту формулу не просто так.

Сам факт, что плотность зависит от трех параметров — это еще пол беды. Сложность кроется в том, что все эти параметры могут сильно меняться с глубиной. В этом случае принято говорить о профиле температуры и солености. Вот так, к примеру, выглядит профиль из Арктики:

Вот так с северной части тихого океана:

А вот так, для сравнения — с юга атлантики:

Например, если представить, что мы погружается в северной части тихого океана (39°СШ,152°ВД) учитываем атмосферное давление и географическую широту места и сжимаемость воды, а наш датчик давления показывает 100 Бар (~1000 м), а температуру и соленость мы берем в точке измерения, но не учитываем профиль, мы ошибемся с глубиной на 2 метра.

Я специально запилил онлайн-калькулятор и добавил три тестовых профиля (их можно переключать кнопками), чтобы каждый мог сам попробовать.

Если теперь просто переключить профиль на «южноатлантический» и попробовать пересчитать, то мы увидим, что разница выросла до 6-и метров. Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.

Естественно, все меняется и со сменой времен года и со сменой времени суток. Летом (в северном полушарии, зимой — в южном) верхний слой прогревается, а зимой — остывает. Шторма перемешивают воду, дожди смывают грязь с суши и реками уносят в моря, таят снега и ледники.

Это я к тому, что нельзя один раз перемерить и выбить в граните все профили температуры и солености для всех морей и океанов — все течет, все меняется. И если вдруг вы собрались погружаться на ощутимые глубины и у вас нет температурного профиля — я не поверю в ваш рекорд )

Матчасть

Как я упомянул в начале статьи, все необходимое для расчета глубины я собрал в библиотеку и положил на GitHub.

Она в том числе переведена на JavaScript, а в качестве интерактивного примера ее использования привожу онлайн-калькулятор.

P.S.

Благодарю за внимание, буду искренне благодарен за конструктивную критику, сообщения об ошибках, пожелания и предложения.

В следующей статье разберу второй способ определения глубины — по эхолокации.

Как измерить глубину бездны? • Айк Акопян • Научно-популярные задачи на «Элементах» • Физика, Океанология

Задача

С необходимостью измерения морских глубин человечество столкнулось тысячелетия назад. Правильное определение расстояния до дна водоема и его состава требовалось по многим причинам: нужно было понимать, безопасен ли фарватер, где можно бросать якорь, как обустраивать укрепления и т. д. К XVIII–XIX векам к числу причин добавился и научный интерес, а вот способы измерения глубины за прошедшее время изменились не сильно.

Еще в XIX веке во многих странах (прежде всего — англоязычных) глубину было принято измерять в морских саженях (фатом, англ.

fathom) — единицах длины, равных 6 футам (примерно 182 см). Основным способом измерения с древних времен оставался длинный канат с закрепленным на конце грузом. Вместе с грузом иногда крепили термометры и барометры для измерения температуры и давления на дне, а также специальное устройство для захвата грунта (чтобы изучить состав дна).

Проблем с измерением больших глубин (англ. sounding) было несколько. Процесс представлял собой медленное опускание каната (лота), — а они иногда достигали километровой длины, — и подсчета количества узлов, завязанных на канате на расстоянии сажени друг от друга. Точность измерений во многом зависела от мастерства и терпения лотовых, которые должны были и узлы считать, и определять момент, когда груз достигал дна. Ясно, что сбиться со счета довольно легко, да и проворонить нужный момент — тоже.

Ко второй половине XIX века с развитием экспедиционного мореплавания (в особенности — в Британской Империи) появилось множество различных конструкций лотов, решавших проблему точности измерений, минимизируя человеческий фактор.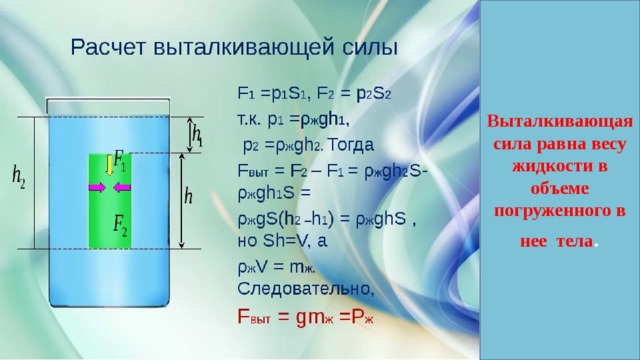 Несмотря на различия, однако, эти конструкции во многом были схожи между собой. Подумайте, как нужно изменить классический лот (то есть простой длинный канат с закрепленным на конце грузом), чтобы избежать описанных выше проблем.

В 1872 году британский корабль «Челленджер» (HMS Challenger) начал первую в историю океанографическую экспедицию (фактически, заложив основы океанографии). Одной из основных задач экспедиции было исследование глубин и состава дна Тихого океана. Плавание длилось три с половиной года, за это время удалось собрать большую коллекцию образцов морских животных и выполнить сотни промеров глубины. Короткая сводка результатов есть в открытом доступе, а более детальные статьи и научные труды публиковались еще десятилетия после завершения самой экспедиции.

Нас интересует следующий отрывок из экспедиционного дневника «Челленджера» — запись от 23 марта 1875 года (остановка №225, оригинал записи на английском можно посмотреть здесь):

<. ..> В 6 утра шли на пару, замерили глубину в 4576 фатомов [~8,3 км]. <…> Чтобы не сомневаться в верности измерений, в 12:30 лот был опущен вновь — на этот раз с грузом 4 хандредвейта [hundredweight — мера веса, равная 112 английским фунтам, то есть ~50,1 кг] (вместо обычных трех) и глубина составила 4475 саженей, что лишь на 100 саженей меньше чем в первый раз. <…> Во второй раз с лотом также были спущены два термометра и барометр. Оба термометра вернулись сломанными, а барометр не смог измерить давление на такой большой глубине — самой большой за всю экспедицию «Челленджера». <…>

Какой должна была быть шкала барометра, чтобы измерение давления на такой глубине было возможным?

Как выяснилось впоследствии, эти замеры проводились на южном конце Марианского желоба — самой глубокой впадины в Мировом океане. Глубочайшая часть желоба получила название Бездна «Челленджера» — в честь корабля.

В 2020 году в Марианском желобе была проведена серия погружений. В ходе одного из них проводились измерения давления, результат показан на рис. 2. На какую глубину опускался глубоководный аппарат? Какие основные факторы влияют на точность измерений с помощью барометра на такой большой глубине?

Подсказка 1

Общей чертой всех лотов второй половины XIX века был механизм, позволяющий избавиться от присоединенного веса при достижении дна. Подумайте, как это реализовать самым простым способом?

Подсказка 2

Давление на малой глубине можно оценить по формуле \(\rho g h\), где \(\rho\) — плотность воды, а \(h\) — глубина. Почему эта формула может плохо работать при большой глубине. Насколько важно значение \(g\)?

Решение

Давайте сперва посмотрим, как изменились классические лоты к XIX веку. Проблема с определением касания дна решается относительно просто: нужен механизм, который сбрасывает тяжелый груз при достижении дна, то есть в тот момент, когда груз перестает тянуть лот вниз. Конструкций таких механизмов было очень много. На рис. 3 приведены лишь три примера, но основной принцип их работы одинаков: когда груз отцепляется, лотовый чувствует, что натяжение троса ослабевает, и таким образом определяет глубину.

Но остается большая проблема с надежностью измерений. Первые попытки справиться с ней были предприняты в начале 1810-х годов, когда британский флот принял на «вооружение» лоты, изобретенные в 1802 году часовщиком из Стэффордшира Эдвардом Мэсси (Edward Massey). Этот лот представлял собой железную рамку обтекаемой формы, к которой можно было прицепить с разных сторон груз и канат. Принципиальным отличием этого лота являлось то, что измерение глубины проводилось специальным вращающимся ротором, который с помощью системы шестерней фиксировал пройденный путь на шкале. В лот также был встроен специальный рычаг, который блокировал ротор при достижении дна, фиксируя значение шкалы до тех пор, пока прибор не вытянут обратно на корабль (рис. 4).

Важнейшим качеством лота Мэсси была, как ни странно, не точность: на самом деле, возможно, он был даже менее точным, чем классический лот, так как ротор мог делать лишние обороты из-за подводных течений. Конструкция Мэсси прежде всего важна своим дисциплинарным эффектом. Точность измерений теперь не зависела от опыта и внимательности лотовых, а стала ответственностью соответствующих офицеров, которые могли снимать показания с прибора сами. Введение в эксплуатацию лотов Мэсси, как отмечает историк Джеймс Поскетт, было символическим началом реформ в военно-морском и экспедиционном флоте.

Лоты второй половины XIX века стали еще более механизированными и точными. Ярким примером является лот, изобретенный лордом Кельвином (рис. 5). Классический канат в его конструкции был заменен на длинную металлическую струну, что значительно уменьшало площадь сечения лота и, следовательно, морские течения меньше влияли на показания. Тонкую струну с тяжелым грузом вручную опускать и поднимать невозможно, поэтому она наматывалась на вспомогательную лебедку. К ней же крепился замкнутый канат, зафиксированный подвижным блоком на другом конце, что помогало достаточно точно определить момент касания дна. Вторичный канат также позволял на месте измерить глубину погружения лота с помощью еще одной лебедки с закрепленной на ней шкалой.

Позже, конечно же, появилось множество других конструкций. А с развитием технологий от классических лотов (канатов с грузом) постепенно отказались. Сейчас в основном используются эхолоты — приборы, испускающие звуковую (или ультразвуковую) волну и регистрирующие момент прихода ее отражения (зная скорость звука в воде — примерно 1500 м/с, — легко определить расстояние до дна). Но это не единственный способ использовать звук для измерения глубины: волну можно запустить со дна, чтобы «поймать» ее на корабле. Сделать это можно, например, при помощи глубинных бомб. Именно таким способом измеряли глубину Бездны «Челленджера» в 1951 году: в точке измерений глубина составила 10 800 метров.

Измерение давления все еще остается одним из наиболее точных способов нахождения глубины, при условии, что барометр может быть доставлен на такую глубину. Давление на глубине \(h\) можно оценить по формуле \(\rho g h\), где \(\rho\) — примерно постоянная плотность воды. График изменения плотности в зависимости от времени погружения показан на рис. 7: как видно, плотность растет по мере погружения лишь на 45%.

Приняв \(\rho \approx 1{,}05\) г/см³ и \(g\approx 9{,}8\) м/с², найдем, что 11249,48 дбар (1 дбар = 10⁴ Па) соответствует глубине примерно 10 930 м.

Теперь оценим, насколько мы могли ошибиться, и обсудим, чем может быть вызвана ошибка. Самая большая погрешность возникает из-за изменения плотности воды (которая зависит как от давления, так и от температуры, и от содержания соли): разница в 4–5% дает погрешность примерно 400–500 м на глубине ~11 км. Еще один источник ошибки — значение ускорения свободного падения, которое зависит от широты, так как земной шар немного сплюснут: на экваторе \(g\) меньше примерно на 0,5%, чем общепринятое значение 9,8 м/с². На глубине 11 км это даст погрешность в 50 м. Остальные факторы, такие как зависимость \(g\) от глубины, уровень воды и локальное атмосферное давление вносят поправки порядка 10 м и ниже.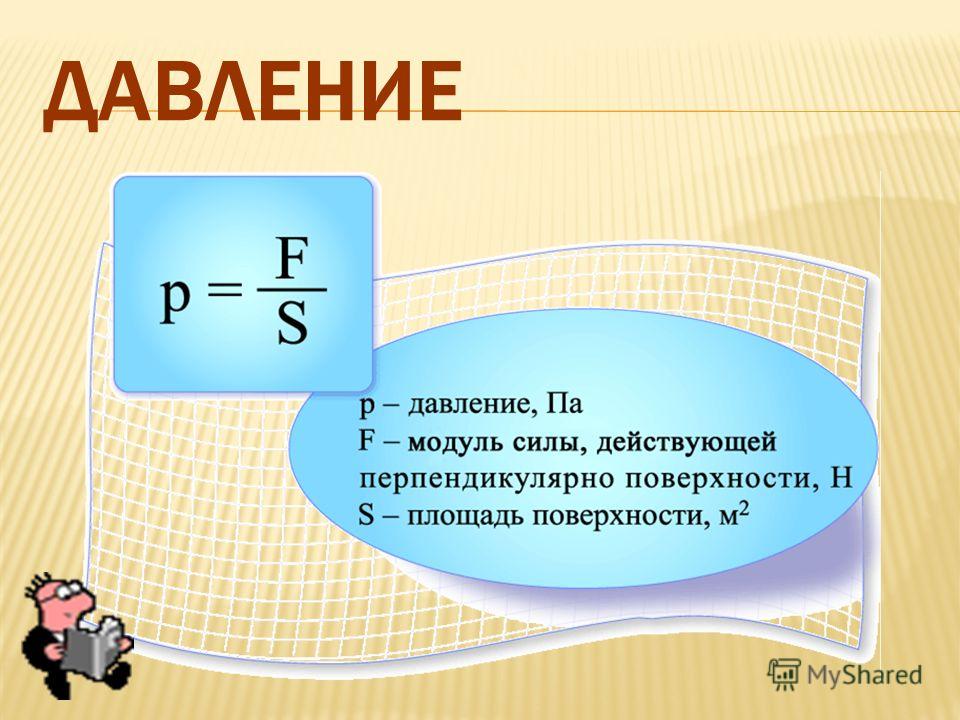 Данные для этой задачи были взяты из отчета о недавнем (июнь 2020) погружении (S. F. Greenaway et al., 2021. Revised depth of the Challenger Deep from submersible transects; including a general method for precise, pressure-derived depths in the ocean), во время которого глубина Марианской впадины была измерена с рекордной точностью: 10935±6 м.

Послесловие

В тех же данных, собранных во время погружения, можно увидеть еще один очень интересный эффект. Подводная лодка при погружении может напрямую измерять скорость звука в воде на данной глубине. Если построить график зависимости скорости звука от глубины, то мы увидим кривую, показанную на левом графике на рис. 8.

Где-то до километровой глубины скорость звука вместо того, чтобы расти, снижается. Минимальное значение равно примерно 1486 м/с. После достижения минимума скорость звука растет с глубиной по мере увеличения давления. Эта зависимость характерна для всех морей и океанов и связана с резким падением температуры в термоклине (верхнем теплом слое) и содержания соли в воде. Ниже термоклина температура воды примерно постоянна, и скорость звука возрастает с увеличением давления воды, как и должно быть.

Слой воды на глубине 700–1000 м (на которой достигается минимум скорости звука) иногда также называют подводным звуковым каналом. Эта область может работать в роли волновода, отражая звуковой сигнал как зеркало отражает свет (как это показано на рис. 9).

Интересно, что отражающие свойства подводного звукового канала широко использовались в 1960–1990-х годах в военных целях: например, для поиска подводных лодок, а также регистрации подводных ядерных испытаний с большого расстояния.

Предполагается, что усатые киты могут использовать звуковой канал для коммуникации на многие сотни километров с помощью низкочастотных (до десятков Гц) звуковых сигналов, запертых в этом «волноводе» (R. Payne, D. Webb, 1971. Orientation by means of long range acoustic signaling in baleen whales).

Показать комментарии (6)

Свернуть комментарии (6)

Иван_ 15. 11.2021 10:25 Ответить

Перед рис. 7 “…как видно, плотность растет по мере погружения лишь на 45%.” Пропущена запятая, т.е. 4,5% ?

Ответить

Юрий Фёдоров 21.11.2021 04:32 Ответить

Два соображения:
1) Как вообще можно ощутить на глубине 11 км , ткнулся в дно груз или нет??
Ведь по отношению к весу 11км верёвки или 11км стальной струны он – груз этот – малозаметная часть, как муха на тарелке…
2) что значит график зависимости давления от времени? Имеется ввиду время суток? Тогда почему до 15ти?
А если речь о продолжительномти погружения, так это “ниачём”, если скорость погружения (и, значит, глубину) не знать! Можно же на полуметровую глубину 15 часов погружать…
И что за 45 проц при этом??
Что за чушь?
Или я как-то необычайно круто туплю?

Ответить

Написать комментарий

Формула давления — примеры и условия расчетов » Kupuk.

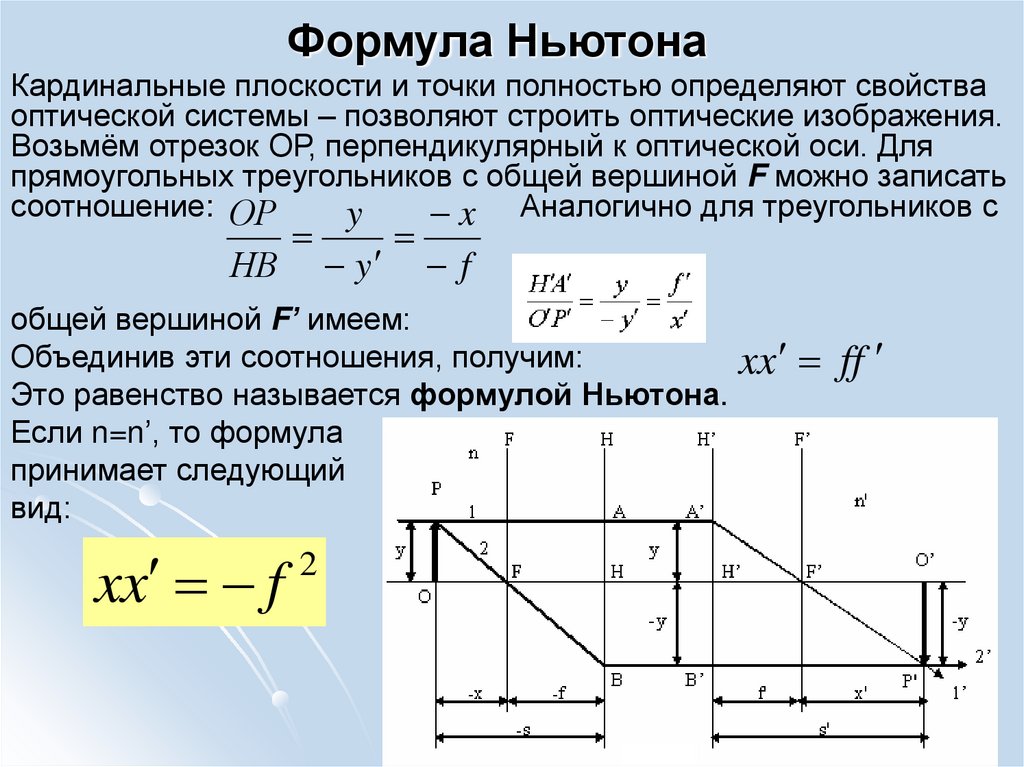
net

Термодинамическая величина зависит от силы, воздействующей на площадь поверхности. Для расчёта применяется формула давления газа, воды, твёрдого тела (Р = mg / S, где р — давление, m — масса, g — ускоренное падение, S — площадь). Явление не зависит от ёмкости сосуда, поэтому считается интенсивным показателем. В условиях равновесия Р одинаково для каждой точки системы. На основе закона работают приборы, по которым определяется р.

Точные науки

Единица измерения давления в физике и химии — буква «Р» (перевод на латинский — «pressūra). Если наблюдается равновесие внутри и снаружи стенок цилиндра, показатель обозначается «П». По международной системе используются Паскали. Используя формулу давления жидкости и силу, можно прийти к выводу, что 1 Па=1 Н/ 1 кв. м. Так как единица мала, применять её в расчётах сложно.

Из таблицы стандартных конвертеров в физике чаще используются обозначения:

Бары. 1 Бар=105 Па.

Торры либо мм ртутного столба (1 торр равен 133 Па).

Мм вод. столба.

Для определения давления используется сила и площадь: Р = mg / S. Существует зависимость величины от объёма и массы. Для показателя характерно следующее свойство: чем меньше площадь, тем большая сила оказывается на тело. Если давление не изменяется, но увеличивается S, тогда искомый показатель уменьшается.

Главные формулы

При изменении условия агрегатного состояния вещества наблюдаются отличные друг от друга свойства. С учётом этого принципа определяется способ вычисления Р. Для гидростатического состояния используется формула: Р = pgh, где:

р — плотность;
g — ускорение;
h — высота.

Гидростатика применяется к газам. Исключение — вычисление АД. Это объясняется разностью высот и плотностей воздушных масс.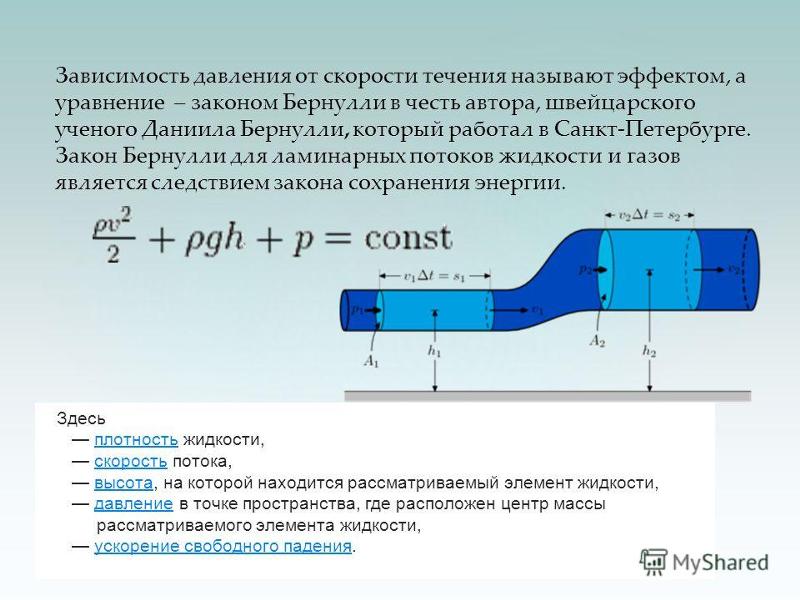 От глубины погружения предмета либо объекта зависит значение Р вещества. Так как сила F вычисляется путём умножения m на g, а масса воды — p на V, идеальным вариантом для расчёта давления считается выражение: P = pVg / S. Формула применяется на онлайн-ресурсах, где можно решать задачи по физике и химии.

Если площадь записать в виде S= V/h, тогда Р= pgh. Давление в воде либо иной жидкости вычисляется с учётом изменения верхнего слоя. Это приводит к образованию другого Р. Чтобы найти абсолютную силу, используется формула:

Р = Р0 + 2QH, где:

Р0 — давление неизменяемого слоя;
Q — поверхность натяжения жидкого вещества;
H — среднее значение.

Последний показатель должен сообщаться между первыми двумя, поэтому он считается усреднённым. Для определения значения используются радиусы кривизны: ½ (1/R1+ 1/R2). Каждый вид газа оказывает особенное парциальное давление. Для идеального состояния характерна сумма Р каждого отдельного компонента смеси. Частая ошибка, которую допускают школьники при вычислении давления воздуха — применение только кислорода. Но воздух представлен в виде различных газов:

аргон;
азот.

Для нахождения давления воздушных масс используется формула P=P1+P2+P3…

Виды величины

Давление может быть различным (избыточным, барометрическим). Абсолютное понятие характерно для вещества либо объекта, на которое не оказывают влияния иные газы. Показатель измеряется в Паскалях. Он вычисляется по следующему калькулятору: нормальное Р = Р2 + Р3 или Р = Р2 — Р4.

Начало отсчёта идёт от планеты Земля, силы внутри сосуда, из которого удалён воздух. Величина используется во многих термодинамических формулах. Для определения гравитации используется понятие барометрическое либо атмосферное давление. Оно изменяется с учётом температуры атмосферы, времени, высоты.

В норме показатель равняется 760 мм рт. ст., при этом температура должна соответствовать нулю по Цельсию.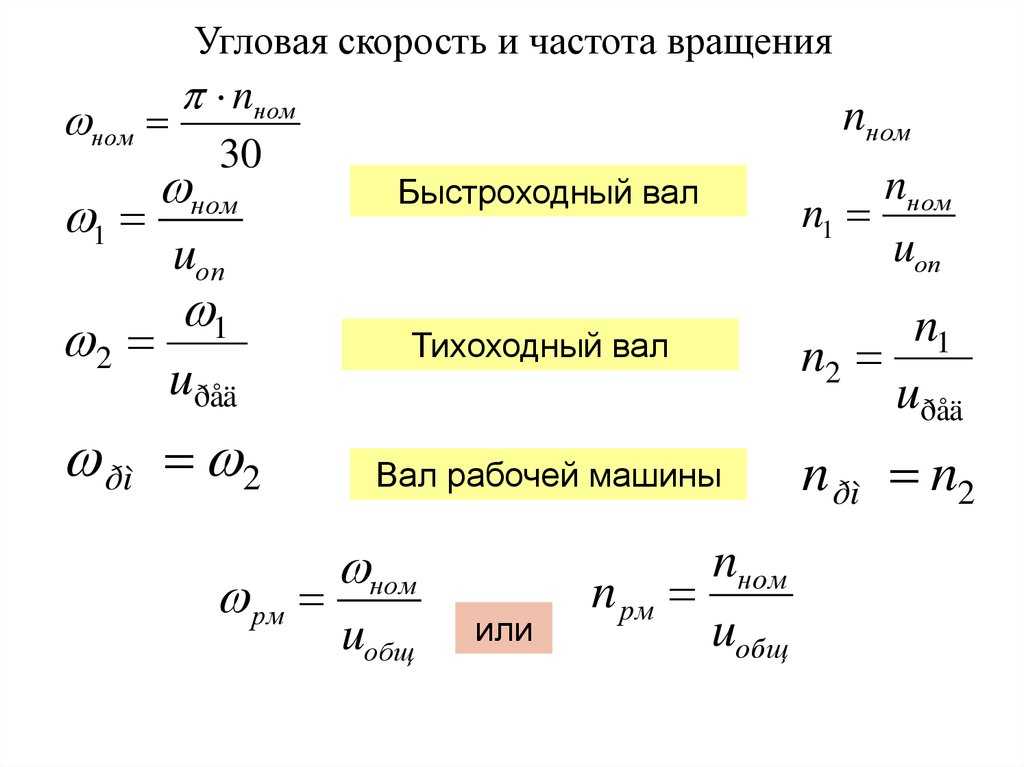 Чем выше находится объект от Земли, тем ниже оказывается на него давление. Значение уменьшается на 100 Па через каждый восьмой километр.

В горах вода закипает быстрее, чем в домашних условиях: давление воздействует на температуру кипения. Если оно снижается, уменьшается t. Зависимость сохраняется и в обратном порядке. На подобном свойстве функционируют некоторые кухонные приборы: скороварка, автоклав. При повышении номинального Р внутри поднимается температура.

Для расчётов применяется стандартная формула, где используются переменные:

плотность воздушных масс вблизи уровня Земли;
высота;
ускорение;
температура;
молярная масса.

Если количество частиц задано в молях, используется формула с постоянной величиной К. При проведении расчётов учитывается вероятность изменения температуры, что связано со сменой погоды, набором высоты, географической широтой. Если из атмосферного Р вычесть измеренное, получится избыточная сила. С учётом результата изменяется название показателя:

положительный — манометрический;
отрицательный — вакуумметрический.

Последнее значение не может превышать барометрический уровень. Разница давлений в разных точках называется дифференциальным явлением. Его используют, чтобы определить Р на определённом оборудовании. Такое понятие используется в нефтедобывающей отрасли.

Решение задач

В задачах по физике формулы давления могут выглядеть по-разному. Задача первая: нужно найти Р, оказываемое телом на судно и грунт под водой, когда водолаз находится в движении. Человек весит со снаряжением на суше 180 кг. Площадь стопы равняется 360 кв. см. Сила, с которой человек воздействует на судно равно 180/360 = 0. 5 (кгс/см). Используя таблицу, величину можно перевести в Па. Получится 49 кПа. На грунт под водой оказывается сила в 2,46 кПа.

Пример 2: нужно вычислить абсолютное Р воды, если глубина равна 150 м, сила — 765, а масса тела — 1,024 кгс/л. Решение: P = 765/735,6+1,024×150/10=16.4.

Пример 3: ёмкость баллона равна 40 л, давление в нём 150 кгс/см2. Нужно найти V свободных воздушных масс. Решение: начальное Р вычисляется следующим образом: 150+1 = 151 кгс/кв.см. Начальное V равно 40 литров. Свободное V вычисляется p1xнач V/p2=6.04 куб. м. Аналогичным способом решаются задачи, где нужно найти Р любой жидкости, твёрдого объекта, газового вещества.

Измерительные приборы

Можно сэкономить время на расчётах, воспользовавшись специальными приборами, функционирующими путём определения давления в соответствующей среде, что схоже с манометром. Их отличия между собой заключаются в инструкции по эксплуатации, сфере использования, точности, области применения.

Чтобы определить АД, понадобится манометр типа барометра. Для определения разряжения (Па меньше атмосферного) понадобится иная разновидность аппарата — вакуумметр. У человека показатель определяется с помощью сфигмоманометра. Большинство пациентов называют такое оборудование неинвазивным тонометром.

Подобные приборы классифицируются на следующие подвиды:

ртутные механические;
полуавтоматические;
автоматические цифровые.

Их погрешность зависит от материалов, используемых в процессе производства и области измерения. Некоторые устройства одновременно измеряют давление и пульс. Они работают автоматически от батареек. За счёт наличия цифрового табло легко узнать результат. Более точными считаются механические.

Чтобы определить Р, понадобится надеть манжет на правую руку больного. Зажав механизм, производится накачка груши. Максимальный и минимальный пределы начинаются с появления, а затем с исчезновения характерного стука. Постепенно механизм ослабляется. Для получения точных данных потребуется опыт работы с механическим тонометром и внимательность. Если наблюдаются колебания давления в воздухе, понадобится дифнамометр либо манометр.

Глубина резкости (DOF) – Русские Блоги

Сегодня я тайно отнес своего босса на курс компьютерного зрения для студентов, и тогда все, о чем я говорил, это физика камеры. Как любитель физики, я, естественно, очень интересовался этим, поэтому я также познакомился с концепцией глубины поле DOF Полное английское название – Depth of Field.

Эта статья посвящена представлению нескольких концептуальных вещей.

Когда свет, параллельный оптической оси, попадает в выпуклую линзу, идеальная линза должна фокусировать весь свет в точке, а затем распределять его по конусу.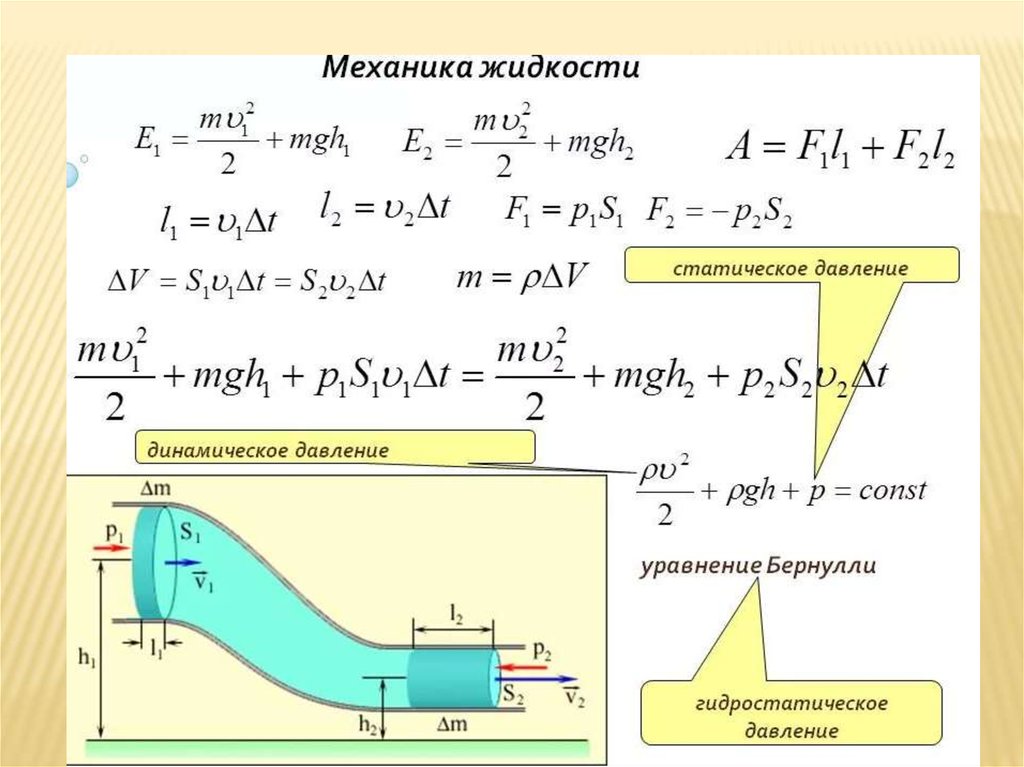 Эта точка, в которой собирается весь свет, называется точкой фокусировки. Чтобы

: Круг замешательства

До и после точки фокусировки свет начинает собираться и рассеиваться, и изображение точки становится размытым, образуя увеличенный круг, который называется кругом нерезкости. Чтобы
На самом деле захваченное изображение просматривается определенным образом (например, проекция, увеличение на фото и т. д.). Изображение и увеличение, воспринимаемое человеческим глазом, расстояние проецирования и Расстояние просмотра имеет большое значение.Если диаметр кружка нерезкости меньше, чем способность различения человеческого глаза, размытость, создаваемая фактическим изображением в определенном диапазоне, не может быть распознана. Этот неузнаваемый круг замешательства называется допустимым кругом замешательства. Чтобы

Глубина резкости

Существует допустимый кружок нерезкости до и после точки фокусировки.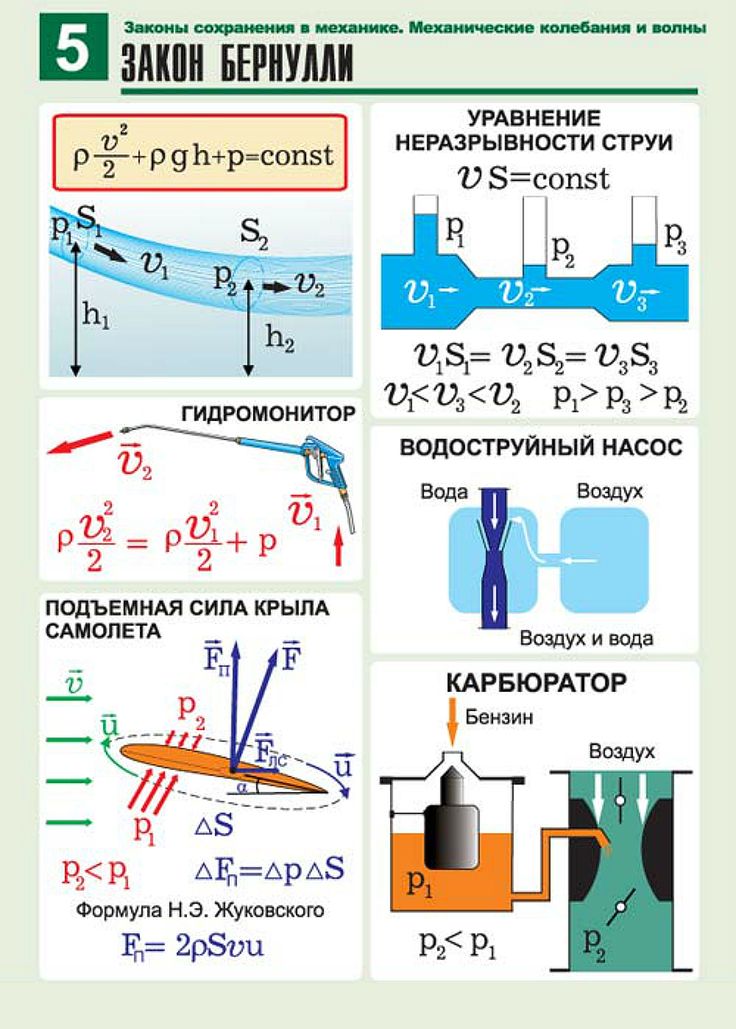 Расстояние между этими двумя кружками нерезкости называется глубиной резкости, то есть изображение, которое все еще имеет четкий диапазон до и после объекта (точки фокусировки), становится глубина резкости. Другими словами, передняя и задняя глубина объекта и размытие изображения на негативной поверхности находятся в пределах допустимого круга нерезкости. Чтобы

Глубина резкости зависит от фокусного расстояния объектива, значения диафрагмы и расстояния съемки. При фиксированном фокусном расстоянии и расстоянии съемки чем меньше диафрагма, тем больше глубина резкости.。

Расчет глубины резкости

Ниже приводится формула расчета глубины резкости. из их:

δ: допустимый круг диаметра рассеивания
f: фокусное расстояние объектива.
F: значение диафрагмы объектива.
L: фокусное расстояние
ΔL1: передний план глубокий
ΔL2: глубина резкости сзади
ΔL: глубина резкости

Глубокие перспективы
ΔL1=FδL2f2+FδLΔL1=FδL2f2+FδL
Глубина резкости сзади:

ΔL2=FδL2f2−FδLΔL2=FδL2f2−FδL

Глубина резкости:

ΔL=ΔL1+ΔL2ΔL=ΔL1+ΔL2

Из формулы видно, что глубина резкости сзади> глубина переднего плана.

Из формулы расчета глубины резкости видно, что глубина резкости связана с диафрагмой, фокусным расстоянием объектива, расстоянием съемки и требованиями к качеству изображения (выраженными как размер допустимого круга спутанность сознания). Эти основные факторы влияют на глубину резкости следующим образом (при условии, что другие условия остаются неизменными):

(1) Диафрагма объектива:

Чем больше диафрагма, тем меньше глубина резкости, чем меньше диафрагма, тем больше глубина резкости;

(2), фокусное расстояние объектива

Чем больше фокусное расстояние объектива, тем меньше глубина резкости; чем короче фокусное расстояние, тем больше глубина резкости;

(3), дистанция стрельбы

Чем дальше расстояние, тем больше глубина резкости; чем ближе расстояние, тем меньше глубина резкости.

Актуальные фото:

Ссылка URL:
http://www3.xitek.com/xuetang/optics/depthoffield.htm
Заявление: если есть какое-либо нарушение, его необходимо удалить!

Интеллектуальная рекомендация

Caused by: org.

springframework.beans.factory.BeanCreationException: Could not autowire field

1 Описание ошибки повествование 2 Причина ошибки Анализ информации, напечатанной консоли. Юнит Единый Тест. Существует только интерфейс DAO, который не записывает его; метод вызова интерфейса DAO при …

Запрос на расширение метода аннотации Mybatis

Расширяйте сложные методы запросов на основе кода, автоматически сгенерированного генератором Во-первых, используйте аннотацию @SelectProvider Аннотация @SelectProvider используется для генерации опер…

Linux использует функцию разбиения awk для удаления части поля в файле

Вот файл следующим образом: Мне нужно удалить предыдущую полосу, поэтому давайте проанализируем идею использования оболочки для решения проблемы. Команды grep и sed извлекаются для всей строки содержи…

Научите, как использовать расширенный текстовый редактор Baidu Ueditor и загружать изображения / файлы вне проекта (пользовательский путь загрузки ueditor)

очертание UEditor – это веб-редактор WYSIWYG с расширенным набором текстовых файлов, разработанный веб-интерфейсом отдела исследований и разработок Baidu. Он легкий, настраиваемый и ориентирован на ра…

Исследование схемы CDN на ресурсах Magento

Благодаря пониманию Magento было обнаружено, что файлы ресурсов Magento в основном распространяются в трех папках: media, js и skin. В папку media в основном входят ресурсы, относящиеся ко всем редакт…

Используйте LocalCheckPoint, чтобы ускорить итеративную расчет искры (линия разрыва)

Расчет искры и итерации Spark -это вычислительная структура на основе линии. Он записывает все операции с момента загрузки через линию, чтобы Spark мог легко реализовать ленивое выполнение. С другой с…

Установите двойные версии JDK1.8 и JDK11 в Mac и переключайтесь произвольно

Сначала загрузите установочные пакеты JDK8 и JDK11 с официального сайта и откройте bash после установки. Вы можете видеть, что две версии успешно установлены Затем отредактируйте переменную среды Тепе…

Класс упаковки MySQLDB от Python (Transfer)

От: http://blog. csdn.net/serverxp/article/details/6958459 …

Python поднимается в логотип и вправо от информации домашней страницы Baidu

Следующий код реализован в ноутбуке Jupyter Результат:…

uva12325 сундук с сокровищами

Классификационные методы перечисления, мы можем использовать различные методы перечисления в зависимости от размера диапазона S1 и S2. 1. Если значение N / s2 (N / s1) небольшое, укажите количество s2…

Расчёт давления жидкости на дно и стенки сосуда – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)

Разработки уроков (конспекты уроков)

Линия УМК А.В. Перышкина. Физика (7-9)

Физика

Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.

Тип урока: Урок открытия и первичного закрепления знаний.

Цель урока: получить выражение для расчёта давления жидкости на дно и стенки сосуда; проверка качества знаний учащихся при решении задач.

Задачи урока:

Предметные: углубить и закрепить знания о давлении жидкости.
Метапредметные: продолжить развивать внимание, память, логическое мышление, умение делать выводы.
Личностные: способствовать формированию научного мировоззрения, активизировать учебно-познавательную деятельность учащихся, содействовать формированию самостоятельности, воспитанию интереса к предмету.

Оборудование к уроку: компьютер, видеопроектор, интерактивная доска, два стакана с водой, цилиндрические сосуды с основаниями различной площади, деревянный брусок, камень, два одинаковые пластмассовые груза, широкий сосуд, аквариум, удочка, каточки с заданиями, учебник по физике.

1.Организационный момент.

2. Актуализация имеющихся знаний.

Взаимопроверка в парах по вопросам. Слайд 1

Чем отличается процесс передачи давления в жидкости и газе от передачи давления твёрдыми телами? (давление твёрдыми телами передаётся в направлении действия силы, в жидкости и газе по всем направлениям одинаково)
Сформулируйте закон Паскаля. (давление, производимое на жидкость или газ, передаётся в любую точку без изменений во всех направлениях)
Мальчик выдувает мыльные пузыри. Почему они принимают форму шара? (они приобретают форму шара, так как давление в газе, согласно закону Паскаля передаётся одинаково по всем направлениям)
От чего зависит давление газа? (от объёма, массы и температуры газа)
Для космонавтов пищу изготавливают в полужидком виде и помещают в тюбики с эластичными стенками. Что помогает космонавтам выдавливать пищу из тюбиков? (Закон Паскаля)
Почему взрыв снаряда под водой губителен для живущих в воде организмов? (давление взрыва в жидкости, согласно закону Паскаля, передаётся одинаково по всем направлениям, и от этого животные могут погибнуть)
Почему пловец, нырнувший на большую глубину, испытывает боль в ушах? (с глубиной давление увеличивается; пловец испытывает боль в ушах, так как вода с большой силой давит на барабанные перепонки)

3.

Открытие нового знания. Слайд 2

В три сосуда с одинаковой площадью дна, стоящие на столе, налили воды до одного уровня

1) В каком сосуде масса воды больше? Меньше?

2) Одинаковым ли будет давление воды на дно сосудов?

Вы уверены? Как рассчитать давление жидкости на дно сосуда? (Затруднение).

Какая цель нашего урока? (Узнать, как рассчитать давление жидкости на дно сосуда)
Какая тема урока? (Расчёт давления жидкости на дно и стенки сосуда) Слайд 3

Учащиеся записывают тему к себе в тетрадь.

Попытаемся вывести формулу для расчёта этого давления. Но какую же форму сосуда нам надо выбрать для расчёта нашей формулы? Я предлагаю взять форму прямоугольного параллелепипеда.

Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис.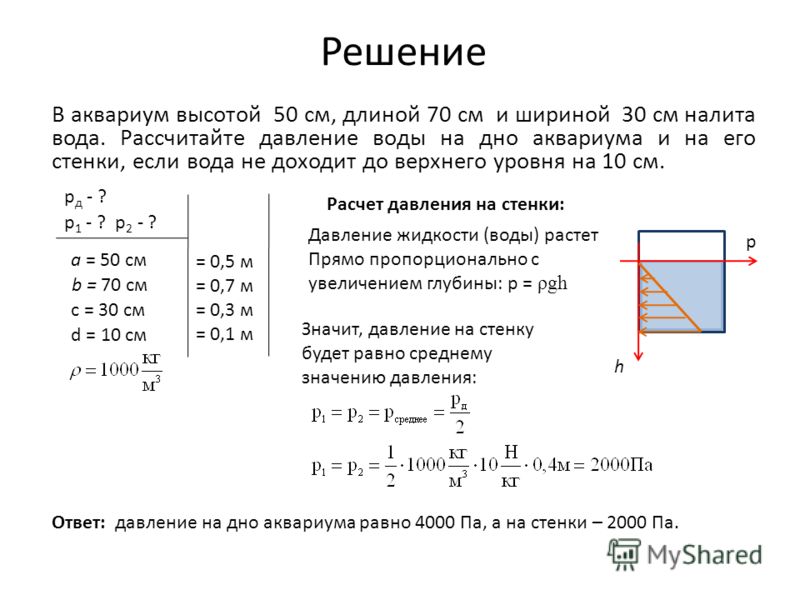 2).

Рис. 2. Сосуд для расчета давления жидкости

Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен

жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу,

действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде

p =	P
	S

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m.

P = mg

Напомним, что символом g обозначено ускорение свободного падения.

Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V

m = ρV

Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда

V = Sh

Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:

p =	ρShg
	S

В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:

p = ρgh

Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.

Полученная выше формула называется формулой гидростатического давления. Согласно этой формуле гидростатическое давление не зависит от формы сосуда, в котором находится жидкость и от площади его сечения. Оно зависит от высоты столба жидкости и от плотности жидкости.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов? (одинаковым)

Данная формула позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов?

4. Физминутка

(под медленную, спокойную мелодию)

– Я предлагаю вам, ребята, выполнить дыхательную гимнастику:

1-е упр. Набрать воздух в лёгкие (вдыхаем медленно, но как можно больше воздуха),

Медленно выдохнуть

2-е упр.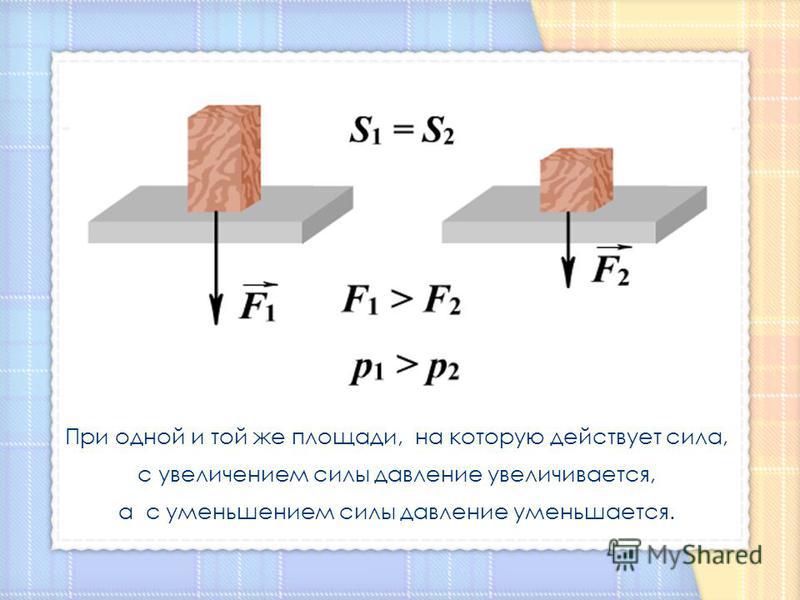 Руки медленно поднимаем вверх и делаем (одновременно) глубокий вдох.

Руки опускаем – выдох.

3-е упр. Глубоко вдохнуть, садясь за парту, медленно выдыхаем (гимнастика проводится под спокойную музыку).

– Сейчас вы выполнили дыхательную гимнастику, которую врачи рекомендуют проводить 3-4 раза в день.

– А какой физический закон лежит в основе дыхательной гимнастики, как он называется? (в основе дыхательной гимнастики лежит закон Паскаля)

5. Закрепление материала.

Решение задач.

а) Проведение игры «рыбалка»

Качественные задачи:

Куда бы вы перелили сок из литровой банки, чтобы его давление на дно сосуда стало больше: в пятилитровую кастрюлю или в литровую бутылку? (в литровую бутылку)
Какие из жидкостей: вода или керосин оказывает меньшее давление на дно сосудов одной формы, если объёмы жидкостей одинаковы? (керосин)
Как изменится давление воды на дно доверху наполненного стакана, если в воду опустить камень? (не изменится)
В цилиндрический сосуд, частично наполненный водой, опустили деревянный брусок. Как изменится давление воды на дно сосуда? (увечится)
Два одинаковых предмета были опущены в цилиндрические сосуды с основаниями различной площади. В цилиндрических сосудах уровень воды до погружения предмета одинаков. В каком сосуде гидростатическое давление больше? (в сосуде меньшей площади)

Ответы на задачи подтверждаются опытами.

б) Расчётные задачи:

упр. 17(2)
Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8 кПа. Слайд 4

Самостоятельная работа по решению задачи упр.17(1) по рядам?

6. Подведение итогов урока. Рефлексия.

Подведём итоги.

Давайте вспомним, что сегодня делали на уроке, что узнали?

Мне очень важно, с каким настроением вы уходите с урока. Поэтому я прошу вас заполнить лист самоанализа, который находится столах у каждого из вас.

Лист самоанализа (нужное подчеркнуть)

Чувствую вдохновение, подавленность .

Интересно, неинтересно.

Не устал(ла), устал(ла).

Доволен(довольна), недоволен(недовольна).

Вызвало затруднения(перечислить)…

7. Домашнее задание. Слайд 5

п. 40, упр.17(3), задания на с.118

“Давление жидкости на дно и стенки сосуда. Формулы и не только…”

Ключевые слова: физика, опытно-экспериментальная деятельность, закон Паскаля

Цели урока:

Дидактическая цель:
закрепить знания учащихся по давлению жидкостей на дно и стенки сосуда и проверить умение применять их при решении задач.

Воспитательная цель:
на примере обобщения материала по теме: «Давление жидкостей на дно и стенки сосуда, сообщающиеся сосуды», показать учащимся приемы и методы самоконтроля, которыми они должны владеть, чтобы хорошо усваивать программный материал по физике.

Основные знания и умения
1. Знать и уметь раскрывать физический смысл закона Паскаля и закона сообщающихся сосудов с точки зрения строения вещества.
2. Уметь применять эти законы при решении задач.

Мотивация познавательной деятельности учащихся
Перед повторением материала следует сообщить учащимся, что знания материала данного занятия необходимы для усвоения закона Паскаля и закона сообщающихся сосудов, которые будут применяться на последующих занятиях, а поэтому требуется хорошо осмыслить данные законы и их применение.

План занятия
I. Проверка знаний, умений и навыков учащихся.
К доске вызываются учащиеся, которые должны решить следующие задачи:
1. Манометр, установленный на подводной лодке, показывает давление воды 2500 КПА. Какова глубина погружения лодки? С какой силой давит вода на крышку люка площадью 0,45 м²? Ответ: 250 м; 1125 кн.
2. Какая жидкость налита в цилиндрический сосуд, если она производит давление 2840 Па, а высота ее столба 40 см? Ответ: бензин
3. Манометр, установленный на высоте 1,2 м от дна резервуара с нефтью показывает давление 2 н/см2. Какова высота нефти в резервуаре? Ответ: 3,7 м.
В то время, когда ребята решают задачи у доски, с остальными учащимися проводится фронтальный опрос по пройденной теме.
1. Что называется давлением газа?
2. От чего зависит давление газа?
3. Как читается закон Паскаля?
4. В каких единицах измеряется давление?
5. Какие опыты доказывают, что внутри жидкости существует давление?
6. Назовите формулу для расчета давления на дно и стенки сосуда.
7. Что называется сообщающимися сосудами?
8. Приведите примеры сообщающихся сосудов?
9. Заслушиваются сообщения учащихся (Газета «Физика» № 2, 8-15 января 2004 г.)
• Первые водопроводы. Первые простейшие водопроводы были сооружены несколько тысяч лет назад. В Древнем Египте подземная вода из глубоких колодцев поднималась водоподъемниками и по керамическим или деревянным трубам подавалась потребителям. В Древнем Риме система была более сложная – с акведуками (мостовыми сооружениями). В Вильнюсе строительство водопровода было начато в 1501 г., в Париже в конце XVIII в. был сооружен первый водопровод с деревянными трубами, в Англии – в XVIII в., в Москве - в 1804 г.
• Чего не знали древние! Древнеримские инженеры имели весьма смутное представление о законах сообщающихся сосудов. Трубы они прокладывали сверху, а не под землей, т.к. считали, что, следуя уклонам почвы, вода на некоторых участках будет течь вверх. Трубы устанавливались под одним уклоном, обходя все возвышенности.
10. Как располагается поверхность однородной жидкости, разнородных жидкостей в сообщающихся сосудах? Доказать формулу:
11. Какое явление используется в работе шлюзов? Принцип действия шлюзов.
12. Заслушиваются сообщения учащихся из «Книги рекордов Гиннеса» (Газета «Физика» № 2 8-15 января 2004 г.)
Шлюзы
Самый большой шлюз – в Бельгии, в г. Зеебрюгге. Его объем 655 300 м3, размеры 500 х 57 х 23 м. Шлюз Берендрехт в Антверпене такой же длины, но шириной 68 м, глубиной 13,5 м и объемом 459 000 м3.
– Самый глубокий шлюз – Карапатело – в Португалии, на реке Дару. Он способен принимать суда с осадкой 35 м.
– Самый большой перепад уровней (~ 68,58 м) – в шлюзовой камере на канале Шарлеруа в г. Брюгге (Бельгия). Два 236-колесных кессона грузоподъемностью 1350 т каждый, по наклонной плоскости перемещают судно на 1432 м в течение 22 мин.
– Во время проверки решенных задач на доске, классу дается задание на определение глубины воды с использованием художественной литературы.
Начало XIII века. Татаро-монгольское иго. Нашествие татар на Русь.
Ю.П. Кузнецов. Стальной Егорий.
Сквозь пустые тростинки дыша,
Притаились в реке наши деды.
Хан велел наломать камыша
На неровное ложе победы
И осталась тростинка одна.
Сквозь одну по цепочки дышали.
Не до всех доходила она.
По неполному кругу печали.
Избыточное давление, при котором человек может безопасно дышать, обычно не превышает 0,3 * 105 Па. Исходя из этого, определите максимальную глубину, на которой человек может дышать через трубку. Какая сила давит на человека, если площадь тела человека примерно 1,5 м2.
Ответ: = 3 м; 45000 н (эту силу перевели в кг, а затем в тонны: = 4,5 т, что очень впечатляет учащихся).
II. Решение задач:
Пусть в сосуде находится жидкость плотность р. Требуется найти разность давлений между двумя точками А и В, находящимися на одной вертикали, если расстояние между этими точками равно h.
Мысленно выделим в жидкости тонкий вертикальный цилиндр, такой, что ось цилиндра проходит через точки А и В, и пусть точка А лежит на нижнем основании, а точка В – на верхнем основании цилиндра. Пусть площадь основания цилиндра равна S.
Рассмотрим все силы, действующие на наш воображаемый цилиндр в вертикальном направлении. На верхнее основание со стороны жидкости действует сила давления F_B = p_ВS, а на нижнее основание – сила давления F_A = p_AS. Кроме того, на цилиндр действует еще одна сила - сила тяжести цилиндра вверх. Так как вся жидкость, а значит, и наш цилиндр неподвижны, то равнодействующая сил, действующих на цилиндр в вертикальном направлении, равна нулю. Следовательно, сумма величин сил, направленных вниз, FB + mg равна величине силы, направленной вверх F_A:
FA = FB + mg. (1)
Масса цилиндра равна: m = pV, где V – объем цилиндра, а объем цилиндра, V = Sh. Отсюда: m = pSh. Подставляя значения FA, FB и m в равенство (1), получим:
РAS = РBS +pShg.
Вынесем в правой части S за скобки:
pAS = S (рB +phg)
и разделим обе части последнего равенства на S, получим:
РА = pB + phg
отсюда:
РА – РB = phg
Задача решена. Заметим, что если точку В взять на поверхности жидкости, то давление жидкости в этой точке будет равно нулю: рB = 0, а величина рА будет равна величине давления жидкости на глубине h:
Р = pgh.
Формула позволяет рассчитывать гидростатическое давление в жидкости на глубине h. Заметим, что это давление зависит только от плотности жидкости р, напряженности гравитационного поля g и глубины h. От формы сосуда, в который налита жидкость, гидростатическое давление никак не зависит.
2. Определите давление жидкости на дно сосуда, показанного на рисунке. Плотность жидкости равна р. Все размеры указаны на рисунке.
Решение

Проведем вертикальные отрезки АВ и CD и горизонтальный отрезок СВ. Наша задача – найти давление на дне, то есть в точке D. Сначала найдем давление в точке D:
РB = pgb
Так как точки С и Б находятся на одной горизонтали, то давления в этих точках равны:

РB= РC = pgb.
Теперь рассмотрим вертикальный отрезок CD.
PD – Рс = pgc
Отсюда
pD = pgc + рC.
Подставим в последнюю формулу значение рC, получим:
pD=pgc + pgb = pg(b+c)
Следовательно, в качестве глубины h действительно надо брать величину:
h = c+b.
Индивидуальные задания (задания по рядам класса)
1.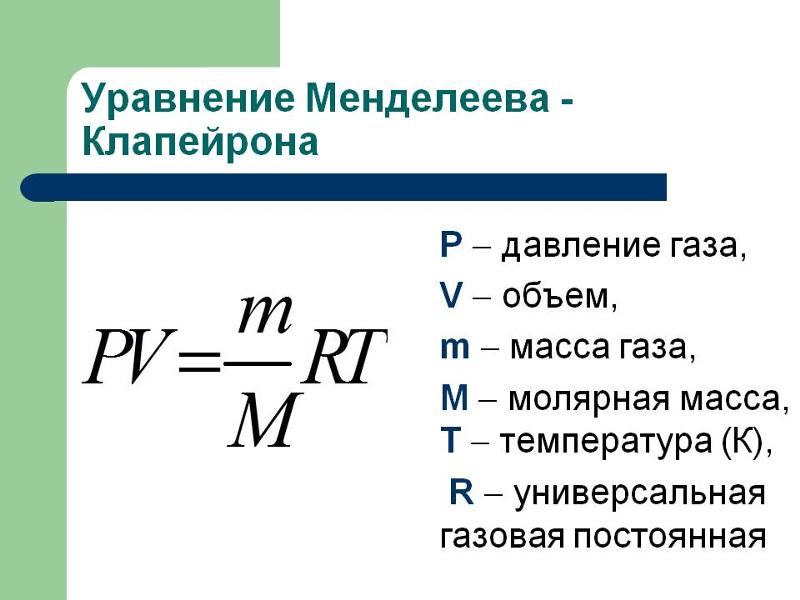 Задание на перевод единиц.
Переведите единицы давления и запишите в пустые кружки ответы.
2. Экспериментальное задание
Определите давление на дно стакана. Для этого измерьте высоту столба жидкости линейкой. Переведите сантиметры в метры.
3. Оставшиеся учащиеся решают задачи, предложенные учителем
1. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте
2. Прямоугольный сосуд вместимостью 2 л наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда?
б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата со стороной 10 см.
III. Проверка заданий и подведение итогов урока. Учащимся выставляются оценки за работу на уроке.
IV. Домашнее задание.§ 36-40 задачи № 519, 522, 523 (сборник задач В.И. Лукашик, Е.В. Иванова).
Литература
1. Газета «Физика» № 2 8-15 января 2004 г. стр. 10-11.
2. Е.Н. Филатов. Физика-7. Экспериментальный учебник, часть 2. Давление. Работа. Энергия. М.: ВШМФ Авангард 2000 г.
3. С.А. Тихомирова. Дидактический материал по физике 7-11. М.: «Просвещение» 1996 г.
4. А.В. Перышкин Физика – 7 Издательский дом «Дрофа». 1999 г.
5. В.И. Лукашик, Е.В. Иванова Сборник задач по физике 7-9. М.: «Просвещение» 2002 г.
11.4 Изменение давления в зависимости от глубины в жидкости – Колледж физики, главы 1-17
11 Статистика жидкости
Резюме
Определить давление по весу.
Объясните изменение давления в жидкости с глубиной.
Расчет плотности по давлению и высоте.
Если у вас когда-либо лопало ухо во время полета на самолете или болело во время глубокого погружения в бассейн, вы испытали влияние глубины на давление в жидкости. На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами. Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается. Под водой давление, оказываемое на вас, увеличивается с увеличением глубины. В этом случае давление, оказываемое на вас, является результатом веса воды над вами и — это атмосфера над вами. Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас во многие истории, но вам нужно всего лишь нырнуть на метр или около того под поверхность бассейна, чтобы почувствовать увеличение давления. Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Рассмотрим контейнер на рис. 1. Его дно поддерживает вес жидкости в нем. Рассчитаем давление, оказываемое на дно весом жидкости. Это давление – это вес жидкости[латекс]\boldsymbol{мг}[/латекс], деленный на площадь[латекс]\жирныйсимвол{А}[/латекс], поддерживающую его (площадь дна сосуда):
[латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{mg}{A}}. [/latex]
Мы можем найти массу жидкости по ее объему и плотности:
[латекс]\boldsymbol{m\:=\rho{V}}.[/латекс]
Объем жидкости[латекс]\boldsymbol{V}[/латекс]относится к размерам контейнера. это
[латекс]\boldsymbol{V=Ah},[/латекс]
, где [латекс]\boldsymbol{A}[/латекс]– площадь поперечного сечения, а [латекс]\boldsymbol{h}[/латекс]– глубина. Объединение последних двух уравнений дает
[латекс]\boldsymbol{m=\rho{Ah}}.[/latex]
Если мы подставим это в выражение для давления, то получим
[латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{(\rho{Ah})g}{A}}.[/latex]
Область отменяется, и перестановка переменных дает
[латекс]\boldsymbol{P=h\rho{g}.}[/латекс]
Это значение представляет собой давление из-за веса жидкости . Уравнение имеет общую справедливость вне особых условий, при которых оно здесь выведено. Даже если бы контейнера не было, окружающая жидкость все равно оказывала бы это давление, удерживая жидкость в статике. Таким образом, уравнение[латекс]\boldsymbol{P=h\rho{g}}[/latex] представляет собой давление, обусловленное весом любой жидкости со средней плотностью [латекс]\boldsymbol{\rho}[/latex] на любой глубине[латекс]\boldsymbol{h}[/латекс]ниже его поверхности. Для жидкостей, почти несжимаемых, это уравнение выполняется до больших глубин. Для газов, которые достаточно сжимаемы, это уравнение можно применять, пока изменения плотности малы на рассматриваемой глубине. Пример 2 иллюстрирует эту ситуацию.
Рисунок 1. Дно этого контейнера выдерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.
Пример 1: Расчет среднего давления и приложенной силы: какую силу должна выдерживать плотина?
В главе 11.2 Пример 1 мы рассчитали массу воды в большом резервуаре. Теперь рассмотрим давление и силу, действующие на удерживающую воду плотину. (См. рис. 2.) Плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину, и сравните ее с весом воды в плотине (ранее было установлено, что это [латекс]\boldsymbol{1.9{13}\textbf{ N}}[/latex]).
Стратегия для (a)
Среднее давление[латекс]\boldsymbol{\bar{P}}[/latex]из-за веса воды – это давление на средней глубине[латекс]\boldsymbol{ \bar{h}}[/latex] 40,0 м, так как давление увеличивается линейно с глубиной.
Решение для (a)
Среднее давление из-за веса жидкости равно
[латекс]\boldsymbol{\bar{P}=\bar{h}\rho{g}}.[/ латекс]
Вводя плотность воды из таблицы 1 и принимая [латекс]\жирныйсимвол{\бар{ч}}[/латекс]в качестве средней глубины 40,0 м, получаем 9{13}\textbf{ N}}[/latex]масса воды в резервуаре — на самом деле это всего лишь[latex]\boldsymbol{0,0800\%}[/latex]веса. Обратите внимание, что давление, найденное в части (а), совершенно не зависит от ширины и длины озера — оно зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, , а не от горизонтальной протяженности водохранилища. На диаграмме толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.
Рис. 2. Плотина должна выдерживать силу, действующую на нее удерживаемой ею воды. Эта сила мала по сравнению с весом воды за плотиной.
Атмосферное давление — еще один пример давления из-за веса жидкости, в данном случае из-за веса воздуха над заданной высотой. Атмосферное давление у поверхности Земли меняется незначительно из-за масштабного течения атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «понижения»). Однако среднее давление на уровне моря дается 95\textbf{N}},[/latex]эквивалентно[latex]\boldsymbol{1\textbf{atm}}.[/latex](см. рис. 3.)
Рисунок 3. Атмосферное давление на уровне моря в среднем 1,01×10 ⁵ Па (эквивалентно 1 атм), так как столб воздуха над этим 1 м ² , простирающийся до верхних слоев атмосферы, весит 1,01×10 ⁵ N .
Пример 2. Расчет средней плотности: насколько плотен воздух?
Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км. Сравните эту плотность с плотностью воздуха, указанной в таблице 1.
Стратегия
Если мы решим [латекс]\boldsymbol{P=h\rho{g}}[/latex]для плотности, мы увидим, что
[латекс]\boldsymbol{\bar{\rho}\ :=}[/latex][latex]\boldsymbol{\frac{P}{hg}}.[/latex]
Затем мы принимаем [latex]\boldsymbol{P}[/latex] за атмосферное давление,[ латекс]\boldsymbol{h}[/latex]дан, а [латекс]\boldsymbol{g}[/латекс]известен, поэтому мы можем использовать это для вычисления[латекс]\boldsymbol{\bar{\rho} }.[/latex]
Solution
Ввод известных значений в выражение для [latex]\boldsymbol{\bar{\rho}}[/latex] дает 93}[/latex] — примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Пример 3: расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?
Рассчитайте глубину под поверхностью воды, на которой давление от веса воды равно 1,00 атм.
Стратегия
Начнем с решения уравнения [латекс]\boldsymbol{P=h\rho{g}}[/latex]для глубины[латекс]\boldsymbol{h}:[/latex] 92)}}[/latex][latex]\boldsymbol{=\:10.3\textbf{ м.}}[/latex]
Обсуждение
Всего 10,3 м воды создают такое же давление, как 120 км воздуха . Поскольку вода почти несжимаема, мы можем пренебречь изменением ее плотности на этой глубине.
Как вы думаете, какое общее давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный. Это кажется вполне логичным, поскольку необходимо поддерживать как вес воды, так и вес атмосферы. Итак, общее давление на глубине 10,3 м составляет 2 атм — половина из воды наверху и половина из воздуха наверху. В главе 11.5 «Принцип Паскаля» мы увидим, что давления жидкости всегда складываются таким образом.
Давление – это вес жидкости[латекс]\boldsymbol{мг}[/латекс], деленный на площадь[латекс]\boldsymbol{A}[/латекс], поддерживающую ее (площадь дна сосуда):
[латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{mg}{A}}.[/latex]
Давление от веса жидкости определяется выражением
[латекс]\boldsymbol{P=h\rho{g}},[/латекс]
где[латекс]\жирныйсимвол{Р}[/латекс]это давление,[латекс]\жирныйсимвол{ч}[/латекс]это высота жидкости,[латекс]\жирныйсимвол{\ро}[/латекс] — плотность жидкости, а[latex]\boldsymbol{g}[/latex] — ускорение свободного падения.
давление
вес жидкости, деленный на площадь, поддерживающую его
1.4: Реальная и кажущаяся глубина
Последнее обновление
Сохранить как PDF
Идентификатор страницы
7069
Джереми Татум
Университет Виктории
Когда мы смотрим сверху вниз на бассейн с водой, он кажется менее глубоким, чем он есть на самом деле. На рисунке I.6 показано формирование виртуального изображения точки на дне бассейна за счет преломления на поверхности.

Диаметр зрачка человеческого глаза находится в диапазоне от 4 до 7 мм, поэтому, когда мы смотрим в бассейн (или вообще смотрим на что-то, что не очень близко к нашим глазам), вовлеченные углы малы . Так, на рис. I.6 вас просят представить, что все углы малы; на самом деле рисовать их маленькими было бы очень тесно. Поскольку углы малы, я могу аппроксимировать закон Снеллиуса:
\[\begin{align} n &= \frac{\sin \theta ‘}{\sin \theta} \label{eq2} \\[4pt] & \ приблизительно \dfrac{ \tan \theta ‘}{\ загар \theta } \label{eq:1.4.1} \end{align} \]
и, следовательно,
\[ \frac{\text{реальная глубина}}{\text{кажущаяся глубина}}=\frac{h}{h’}=\frac{\tan \theta’}{\tan \theta} = n. \label{eq:1.4.2} \]
Для воды \(n\) примерно равно \(\frac{4}{3}\), так что кажущаяся глубина примерно равна \(\frac{3}{4}\) реальной глубины. 2 \theta}} \] 92 \тета}} \метка{eq:1.4.3} \]
Упражнение \(\PageIndex{2}\)
Покажите, что в первом порядке по \( \theta \) уравнение \ref{eq:1.4.3} становится \(h/h’ = n\).
Уравнение \(\ref{eq:1.4.3}\) показывает \(h’\) как функцию \( \theta \) – и что не все преломленные лучи, проецируемые назад, исходят из единственная точка. Другими словами, точечный объект не дает точечного изображения. На рис. I.7 показаны (для \(n = 1,5\) – т.е. стекло, а не вода) проекции назад преломленных лучей для \(\theta ‘\)=15, 30, 45, 60 и 75 градусов вместе с их огибающая или «каустическая кривая». «Объект» находится в нижнем левом углу кадра, а поверхность — в верхней части кадра. 93 \theta = 0. \nonumber \]
Здесь \(y = 0\) принимается за преломляющую поверхность, а \( \theta\) и \( \theta ‘ \) связаны законом Снеллиуса.
Таким образом, преломление на плоской границе раздела создает аберрацию в том смысле, что свет от точечного объекта не расходится с точечным изображением. Этот тип аберрации несколько похож на тип аберрации, возникающей при отражении от сферического зеркала, и в этом отношении аберрацию можно назвать «сферической аберрацией». Если смотреть на точку на дне пруда под углом к поверхности, а не перпендикулярно ей, возникает дополнительная аберрация, называемая «астигматизмом». Это будет обсуждаться в главе 4.
Эта страница под названием 1.4: Real and Apparent Depth распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом с помощью исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
Джереми Татум
Лицензия
СС BY-NC
Версия лицензии
4,0
Показать оглавление
нет
Теги
аберрация
Закон преломления Снеллиуса
источник@http://orca. phys.uvic.ca/~tatum/goptics.html
11.4 Изменение давления в зависимости от глубины в жидкости – College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
Определить давление по весу.
Объясните изменение давления в жидкости с глубиной.
Расчет плотности по давлению и высоте.
Если у вас когда-либо закладывало уши во время полета на самолете или болело во время глубокого погружения в бассейн, вы испытали влияние глубины на давление в жидкости. На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами. Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается. Под водой давление, оказываемое на вас, увеличивается с увеличением глубины. В этом случае давление, оказываемое на вас, является результатом веса воды над вами и атмосферы над вами. Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас во многие истории, но вам нужно всего лишь нырнуть на метр или около того под поверхность бассейна, чтобы почувствовать увеличение давления. Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Рассмотрим контейнер на рис. 11.8. Его дно поддерживает вес жидкости в нем. Рассчитаем давление, оказываемое на дно весом жидкости. Это давление равно весу жидкости mgmg, деленному на площадь AA, поддерживающую его (площадь дна сосуда):
P=мгА.Р=мгА.
11,12
Массу жидкости можно найти по ее объему и плотности:
m=ρV.m=ρV.
11.13
Объем жидкости VV зависит от размеров контейнера. Это
V=Ah,V=Ah,
11,14
, где AA — площадь поперечного сечения, а hh — высота. Объединение двух последних уравнений дает
m=ρAh.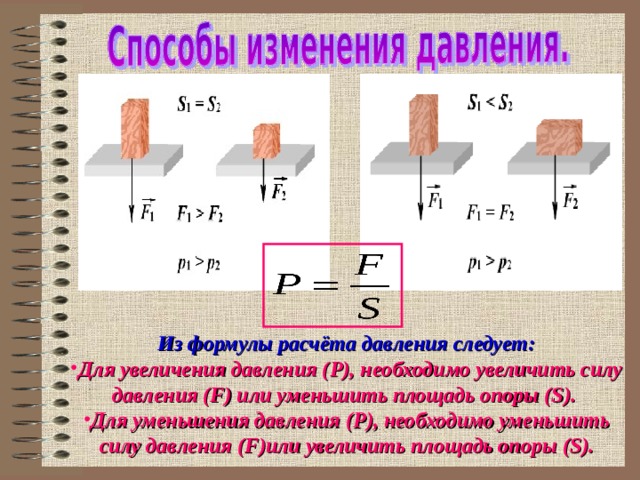 m=ρAh.
11,15
Если мы подставим это в выражение для давления, то получим
P=ρAhgA.P=ρAhgA.
11,16
Площадь сокращается, и перестановка переменных дает
P=hρg.P=hρg.
11.17
Это значение представляет собой давление из-за веса жидкости . Уравнение имеет общую справедливость вне особых условий, при которых оно здесь выведено. Даже если бы контейнера не было, окружающая жидкость все равно оказывала бы это давление, удерживая жидкость в статике. Таким образом, уравнение P=hρgP=hρg представляет давление из-за веса любой жидкости средняя плотность ρρ на любой глубине hh ниже его поверхности. Для жидкостей, почти несжимаемых, это уравнение выполняется до больших глубин. Для газов, которые достаточно сжимаемы, это уравнение можно применять, пока изменения плотности малы на рассматриваемой глубине. Пример 11. 4 иллюстрирует эту ситуацию.
Рисунок 11,8 Дно этого контейнера поддерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.
Пример 11.3
Расчет среднего давления и приложенной силы: какую силу должна выдерживать плотина?
В примере 11.1 мы рассчитали массу воды в большом резервуаре. Теперь рассмотрим давление и силу, действующие на удерживающую воду плотину. (См. рис. 11.9.) Плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину, и сравните ее с весом воды в плотине (ранее найденным равным 1,9).6×1013Н1,96×1013Н).
Стратегия для (a)
Среднее давление P¯P¯ за счет веса воды давление на средней глубине h¯h¯ 40,0 м, так как давление линейно возрастает с глубиной.
Решение для (a)
Среднее давление из-за веса жидкости равно
P¯=h¯ρg.P¯=h¯ρg.
11,18
Введя плотность воды из табл. 11.1 и приняв h¯h¯ за среднюю глубину 40,0 м, получим
P¯=(40,0 м)103кгм390,80 мс2=3,92×105 Нм2=392 кПа.P¯=(40,0 м)103 кгм39,80 мс2=3,92×105 Нм2=392 кПа.
11.19
Стратегия для (b)
Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта:
F=P¯A.F=P¯A.
11,20
Решение для (b)
Мы уже нашли значение P¯P¯. Площадь плотины A=80,0 м×500 м=4,00×104 м2, A=80,0 м×500 м=4,00×104 м2, так что
F=(3,92×105 Н/м2)(4,00×104 м2)=1,57×1010 Н .F=(3,92×105 Н/м2)(4,00×104м2)=1,57×1010 Н.
11.21
Обсуждение
Хотя эта сила кажется большой, она мала по сравнению с 1,96×1013Н1,96×1013Н веса воды в резервуаре — на самом деле, это только 0,0800%0,0800% вес. Обратите внимание, что давление, найденное в части (а), совершенно не зависит от ширины и длины озера — оно зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, , а не по горизонтальной протяженности резервуара. На диаграмме толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличения давления. epth, чтобы уравновесить возрастающую силу из-за увеличения давления.
Рисунок 11,9 Плотина должна выдерживать силу, действующую на нее удерживаемой ею воды. Эта сила мала по сравнению с весом воды за плотиной.
Атмосферное давление — еще один пример давления, обусловленного весом жидкости, в данном случае — весом воздух выше заданной высоты. Атмосферное давление у поверхности Земли меняется незначительно из-за масштабного течения атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «понижения»). Однако среднее давление на уровне моря определяется стандартным атмосферным давлением PatmPatm, измеренным как
1 атмосфера (атм)=Patm=1,01×105 Н/м2=101 кПа.1 атмосфера (атм)=Patm=1,01 ×105 Н/м2=101 кПа.
11,22
Это соотношение означает, что в среднем на уровне моря столб воздуха над земной поверхностью площадью 1,00м21,00м2 имеет вес 1,01×105Н1,01×105Н, что эквивалентно 1 атм1 атм. (См. рис. 11.10.)
Рисунок 11.10 Атмосферное давление на уровне моря составляет в среднем 1,01×105Па1,01×105Па (эквивалентно 1 атм), так как столб воздуха над этим 1м21м2, простирающийся до верхней границы атмосферы, весит 1,01×105 Н1,01×105 Н.
Пример 11,4
Расчет средней плотности: насколько плотен воздух?
Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км. Сравните эту плотность с плотностью воздуха, указанной в таблице 11. 1.
Стратегия
Если мы решим P=hρgP=hρg для плотности, мы увидим, что
ρ¯=Phg.ρ¯=Phg.
11,23
Затем мы принимаем PP за атмосферное давление, задано hh и известно gg, поэтому мы можем использовать это для вычисления ρ¯ρ¯.
Решение
Ввод известных значений в выражение для ρ¯ρ¯ дает
ρ¯=1,01×105 Н/м2(120×103 м)(9,80 м/с2)=8,59×10−2 кг/м3.ρ¯= 1,01×105 Н/м2(120×103м)(9,80м/с2)=8,59×10-2кг/м3.
11,24
Обсуждение
Этот результат представляет собой среднюю плотность воздуха между поверхностью Земли и верхней частью земной атмосферы, которая по существу заканчивается на отметке 120 км. Плотность воздуха на уровне моря дана в таблице 11.1 как 1,29 кг/м31,29 кг/м3 — примерно в 15 раз больше ее среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Пример 11,5
Расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?
Рассчитайте глубину под поверхностью воды, на которой давление от веса воды равно 1,00 атм.
Стратегия
Начнем с решения уравнения P=hρgP=hρg для глубины hh:
h=Pρg.h=Pρg.
11,25
Тогда мы принимаем PP равным 1,00 атм и ρρ плотностью воды, создающей давление.
Решение
Ввод известных значений в выражение для hh дает
h=1,01×105 Н/м2(1,00×103 кг/м3)(90,80 м/с2)=10,3 м·ч=1,01×105 Н/м2(1,00×103 кг/м3)(9,80 м/с2)=10,3 м.
11.26
Обсуждение
Всего 10,3 м воды создают такое же давление, как 120 км воздуха. Поскольку вода почти несжимаема, мы можем пренебречь изменением ее плотности на этой глубине.
Как вы думаете, какое полное давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный. Это кажется вполне логичным, поскольку необходимо поддерживать как вес воды, так и вес атмосферы. Итак, общее давление на глубине 10,3 м составляет 2 атм — половина из воды наверху и половина из воздуха наверху. Мы увидим в принципе Паскаля, что давления жидкости всегда складываются таким образом.
Как вычислить глубину в физике?
Ответ: Используйте следующую формулу для измерения глубины океана. D = V раз 1/2 T D = глубина (в метрах) T = время (в секундах) V = 1507 м/с (скорость звука в воде) Рассчитайте глубину для каждого из приведенных ниже моментов времени, используя приведенную выше формулу. 10 августа 2019 г.
Как измерить глубину воды?
Самый распространенный и быстрый способ измерения глубины океана — это звук. Корабли, использующие технологию, называемую гидролокатором, которая означает звуковую навигацию и измерение дальности, могут отображать топографию дна океана. Устройство посылает звуковые волны на дно океана и измеряет, сколько времени требуется для возвращения эха. 17 марта 2021 г.
Как вы измеряете глубину?
Глубина, обычно обозначаемая аббревиатурой D, представляет собой измерение того, насколько далеко назад находится трехмерный объект. Например, размеры объекта, такого как монитор компьютера, обычно измеряются как (Г х Ш х В), сокращение от «Глубина по ширине по высоте». На иллюстрации ось Z — это глубина. 30 апреля 2020 г.
Как рассчитать глубину физики воды?
Начнем с решения уравнения P = hρg для глубины h: h=Pρg h = P ρ g . Тогда мы принимаем P равным 1,00 атм, а ρ – плотностью воды, создающей давление.
Глубина и ширина одинаковы?
В качестве существительных разница между шириной и глубиной заключается в том, что ширина – это состояние ширины, а глубина – это вертикальное расстояние под поверхностью; степень глубины чего-либо.
Как найти плотность по давлению и глубине?
Давление на глубине для жидкости с постоянной плотностью p=p0+ρhg, где p — давление на определенной глубине, p0 — атмосферное давление, ρ — плотность жидкости, g — ускорение к силе тяжести, а h — глубина.
Что используется для измерения глубины океана?
Одним из таких инструментов, используемых для измерения глубины океана, является эхолот.
Как измерить длину, ширину и глубину?
– Длина: Самая длинная сторона, если смотреть на верхнюю часть коробки.
– Ширина: более короткая сторона, если смотреть на верхнюю часть коробки.
— Глубина (Высота): сторона, перпендикулярная длине и ширине.
Что на первом месте: длина, ширина или высота?
Что на первом месте? Отраслевой стандарт графики — ширина на высоту (ширина х высота). Это означает, что когда вы записываете свои измерения, вы пишете их со своей точки зрения, начиная с ширины. 29 марта., 2010
Как измерить глубину океана?
Самый распространенный и быстрый способ измерения глубины океана — это звук. Корабли, использующие технологию, называемую гидролокатором, которая означает звуковую навигацию и измерение дальности, могут отображать топографию дна океана. Устройство посылает звуковые волны на дно океана и измеряет, сколько времени требуется для возвращения эха. 17 марта 2021 г.
Как мы сегодня измеряем глубину?
Глубина воды обычно измеряется эхолотами, передающими звук на частоте 12 килогерц (кГц). Более низкие частоты (3,5 кГц) можно использовать для изучения слоев отложений под морским дном (см. Как звук используется для изучения истории Земли?). 3 января 2019 г.
Что на первом месте: ширина или глубина?
Более длинный размер соответствует длине и идет первым по порядку. Другой размер – ширина. Теперь измерьте расстояние от одного из внутренних углов до вершины. Это глубина.
В каком порядке указаны размеры?
Указанные размеры всегда являются внутренними размерами. Первое измерение, которое нужно измерить, это длина. Длина — это всегда самая длинная сторона коробки с клапаном. Следующее измерение – ширина.
Какова формула давления на глубине?
Таким образом, уравнение P = hρg представляет давление, обусловленное весом любой жидкости со средней плотностью ρ на любой глубине h ниже ее поверхности. Для жидкостей, почти несжимаемых, это уравнение выполняется до больших глубин.
Как указаны размеры?
Коробки: Длина x Ширина x Высота (см. ниже) Сумки: Ширина x Длина (Ширина всегда равна размеру отверстия сумки.) Этикетки: Длина x Ширина.
Что идет первым длина или ширина?
Обычно длина больше ширины. Итак, сначала вы пишете «длина», а затем «ширина».
В каком порядке длина и ширина?
Форма быстрого заказа Порядок отображения размеров зависит от категории продукта. Вот несколько популярных примеров: Коробки: Длина х Ширина х Высота (см. ниже) Мешки: Ширина х Длина (Ширина всегда равна размеру отверстия мешка.)
Как найти плотность?
Формула плотности представляет собой массу объекта, деленную на его объем. В форме уравнения это d = m/v, где d — плотность, m — масса, а v — объем объекта.
Как корабли измеряли глубину?
Моряки восемнадцатого века использовали свинцовые линии для измерения глубины воды, когда они были в море.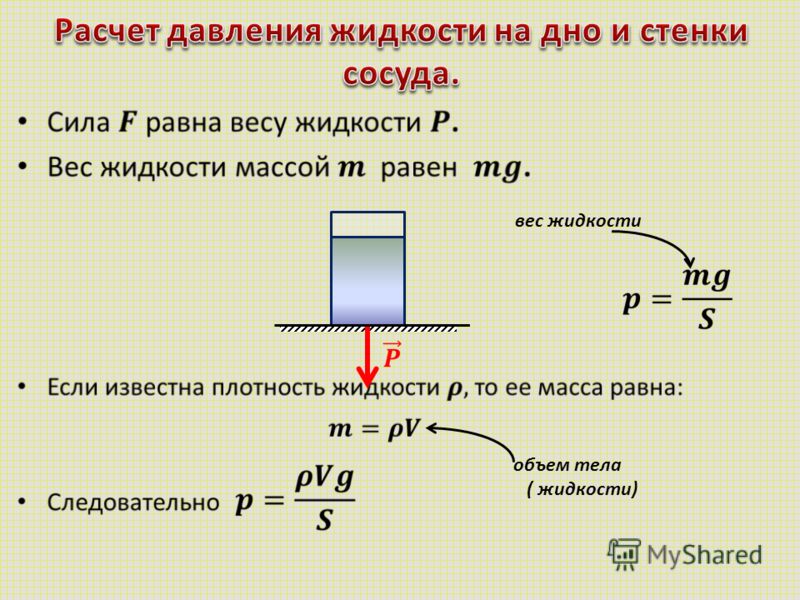 Линия представляла собой простое устройство, состоящее из длинной веревки, привязанной к свинцовому грузу на одном конце. … Как только груз достиг дна моря, глубина была рассчитана и записана в судовом журнале в морских саженях.
Как давление влияет на плотность объекта?
Давление воздуха или давление из контейнера может изменить объем и, следовательно, плотность объекта. … При заданной температуре и атмосферном давлении твердые и жидкие тела будут иметь определенный объем. Увеличивая давление на материал, вы часто можете немного уменьшить его объем и, таким образом, увеличить его плотность. 5 апреля 2014 г.
Теги: Как вы измеряете глубину воды?
Как кажущаяся глубина и реальная глубина связаны с показателем преломления?
18 декабря 2020 г. by Veerendra
Как кажущаяся глубина и реальная глубина связаны с показателем преломления?
На рисунке показаны две непрозрачные чашки, A и B. Чашка A частично заполнена водой, а чашка B полностью заполнена водой. Аналогичная монета кладется на дно каждой чашки.
При наблюдении с того же места монета в стакане А не видна, но монета в стакане В видна.
При большем количестве воды в чашке изображение монеты в чашке B на самом деле находится выше, чем в чашке A. Это сделало монету, которую нельзя увидеть в чашке A, видимой в чашке B без регулировки положения глаза.
Это показывает, что положение изображения зависит от глубины воды.
На рисунке показано, как наблюдатель видит монету в воде. Этот эффект вызван преломлением на поверхности воды.
Лучи света, исходящие от монеты, отклоняются от нормали, выходя из воды.
Когда они достигают глаза, кажется, что они сделаны из виртуальной монеты, которая находится над настоящей монетой.
Видимая глубина расстояние виртуального изображения, I от поверхности воды .
реальная глубина – это расстояние до реального объекта, O от поверхности воды .
Отношение показателя преломления n к реальной глубине и кажущейся глубине определяется формулой:
Люди также спрашивают
Что такое преломление света?
Примеры преломления света
Что такое показатель преломления?
Что такое атмосферная рефракция?
Преломление света через стеклянную пластину
Эксперимент с реальной и кажущейся глубиной
Цель: Найти взаимосвязь между реальной глубиной и кажущейся глубиной объекта, помещенного в воду.
Задача: Как кажущаяся глубина объекта в воде зависит от его реальной глубины?
Гипотеза: Когда реальная глубина объекта в воде увеличивается, его видимая глубина также увеличивается. Переменные:
(a) Управляемая переменная: Реальная глубина, d ₁
(b) Отвечающая переменная: Кажущаяся глубина, d ₂
(c) Фиксированная переменная: Плотность воды
Материалы: 2 стальных штифта, 1 пробка , кувшин с водой
Прибор: Высокий стакан, измерительная линейка, подставка для реторты
Метод:
Прибор устроен, как показано на рисунке.
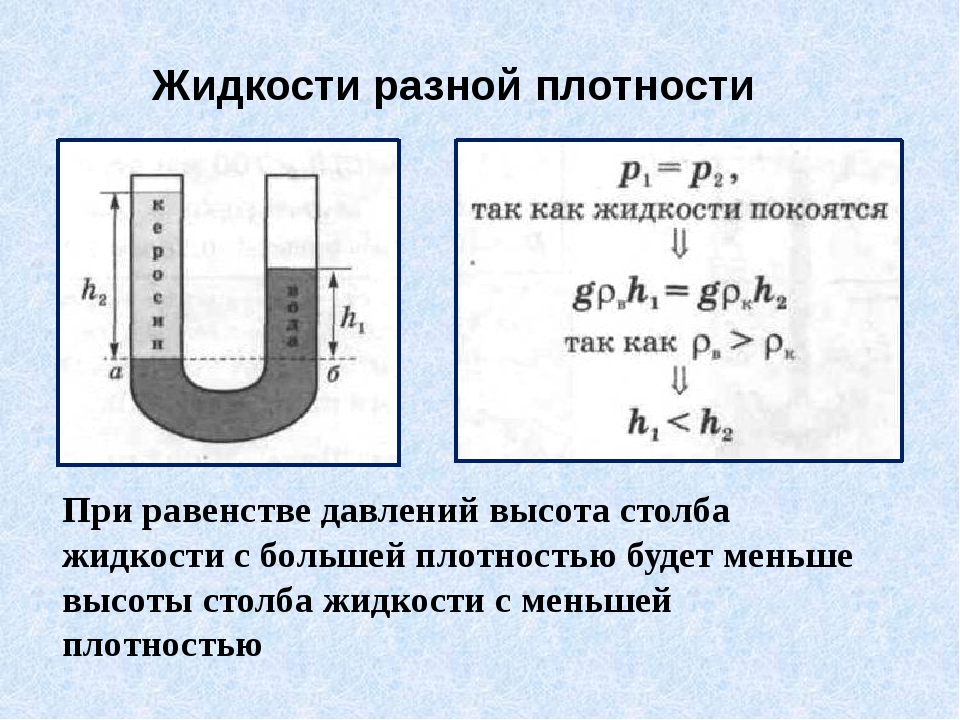
Стальной штифт (штифт O) помещается на дно высокого стакана.
Другой стальной штифт закреплен на пробке, удерживаемой зажимом ретортной стойки. Используется как поисковый штифт (Pin l).
Высокий стакан наполнен водой до высоты d ₁ = 20 см (реальная глубина).
Изображение стального штифта видно вертикально над краем стакана.
Поисковый штифт, примыкающий к мензурке, затем перемещают вверх или вниз, пока он не сравняется с изображением стального штифта, видимым сквозь воду.
Положение изображения, д ₂ (видимая глубина) измеряется по правилу метра.
Шаги с 4 по 7 повторяются с d ₁ = 30 см, 40 см, 50 см и 60 см. Результаты занесены в табл.
Строится график зависимости реальной глубины (d ₁) от кажущейся глубины (d ₂).
Результаты:
1. Таблица результатов.
2. График реальной глубины (d ₁ ) в зависимости от кажущейся глубины (d ₂ ).
Обсуждение:
Видимая глубина всегда меньше реальной глубины.
Когда реальная глубина увеличивается, кажущаяся глубина также увеличивается.
График зависимости реальной глубины d ₁ от кажущейся глубины d ₂ является прямым графиком, проходящим через начало координат. Это показывает, что кажущаяся глубина прямо пропорциональна реальной глубине.
Градиент графика реальной глубины d ₁ от кажущейся глубины d ₂ – показатель преломления воды.
Выводы:
Результаты эксперимента подтверждают гипотезу.
Отношение реальной глубины к кажущейся глубине является показателем преломления воды.
Проблемы с реальной и кажущейся глубиной
Рыба на дне пруда находится на расстоянии 1,2 м от поверхности воды. Какова глубина пруда?
[Показатель преломления воды = 1,33]
Решение:

На рисунке изображен мальчик, стоящий в бассейне. 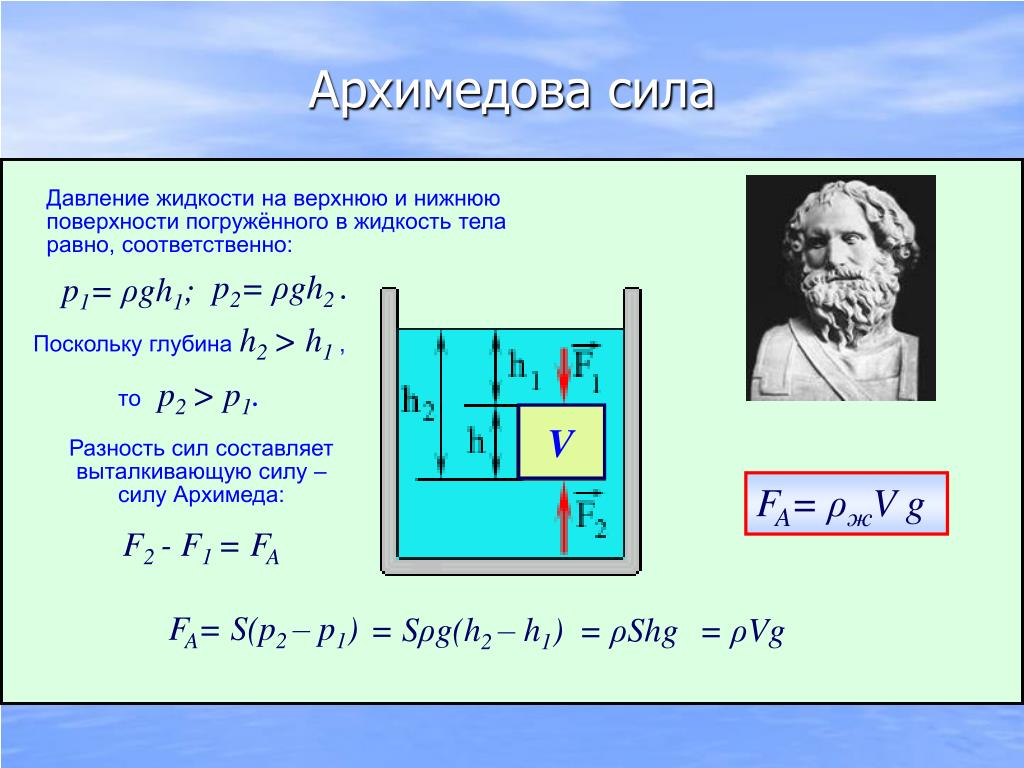Его ноги кажутся короче, когда его друг наблюдает за ним со стороны бассейна.

(а) Объясните, как происходит это явление.
(b) Нарисуйте лучевую диаграмму, чтобы показать, что его ноги кажутся короче.
(c) Если глубина бассейна составляет 0,8 м, рассчитайте расстояние от изображения его ног, если смотреть с поверхности воды.
[Показатель преломления воды = 1,33]
Решение:

В рубрике: Физика С тегами: кажущаяся глубина, вывод формулы кажущейся глубины, реальная и кажущаяся глубина, вывод реальной и кажущейся глубины, эксперимент с реальной и кажущейся глубиной, проблемы реальной и кажущейся глубины, реальная глубина, реальная глубина и кажущаяся глубина, реальная глубина и кажущаяся глубина могут быть объяснены с точки зрения этого явления, метод кажущейся глубины показателя преломления, что вызывает кажущуюся глубину, каково определение реальной глубины и кажущейся глубины в рефракции
Что такое гидростатическое давление — Давление жидкости и глубина
Что такое гидростатическое давление — Давление жидкости и глубина
Воздух вокруг нас на уровне моря давит на нас со скоростью ~ 14,7 фунтов на квадратный дюйм.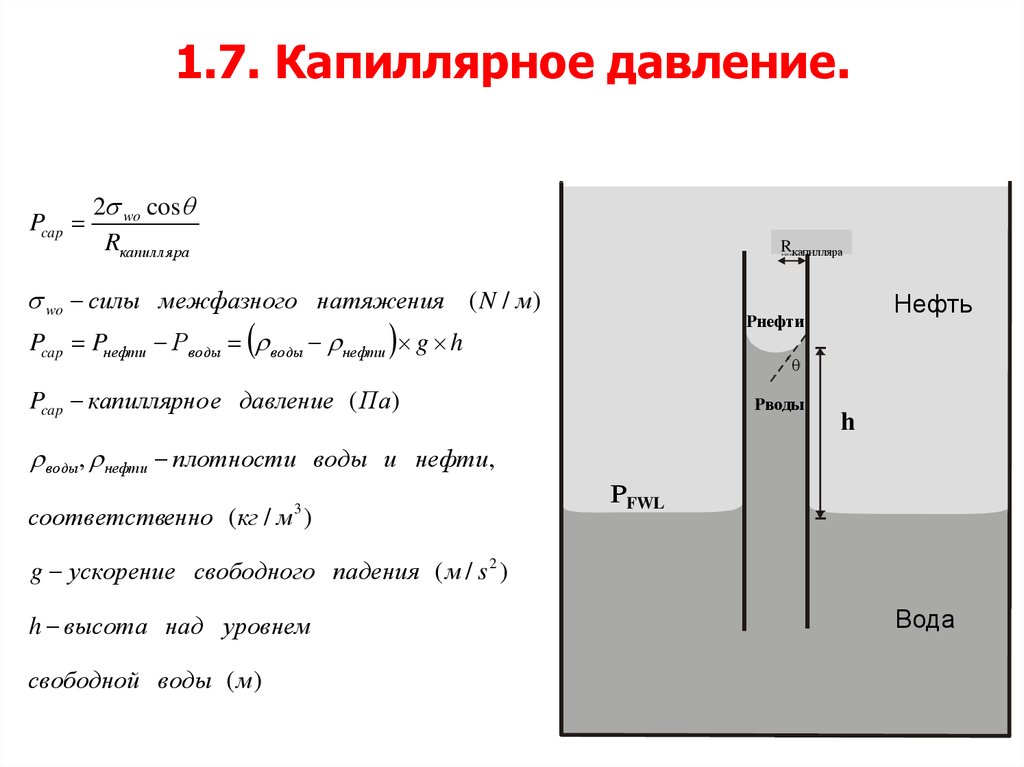 Мы не чувствуем этого давления, поскольку жидкости в нашем теле выталкиваются наружу с той же силой. Но если вы нырнете в океан всего на несколько футов, вы начнете замечать изменения. Вы почувствуете увеличение давления на барабанные перепонки. Это происходит из-за увеличения гидростатического давления, которое представляет собой силу, прикладываемую жидкостью к объекту на единицу площади. Чем глубже вы погружаетесь под воду, тем сильнее будет давление на вас. На каждые 33 фута (10,06 метра) спуска давление увеличивается на 14,5 фунтов на квадратный дюйм (1 бар).
Гидростатическое давление — это давление, оказываемое жидкостью, находящейся в равновесии в данной точке внутри жидкости, под действием силы тяжести. Гидростатическое давление увеличивается пропорционально глубине, измеренной от поверхности, из-за увеличения веса жидкости, оказывающей нисходящее давление сверху.
Если внутри контейнера находится жидкость, можно измерить глубину объекта, помещенного в эту жидкость. Чем глубже объект находится в жидкости, тем большее давление он испытывает. Это потому, что вес жидкости выше его. Чем плотнее жидкость над ним, тем большее давление оказывается на погруженный объект из-за веса жидкости.
Выведем формулу Давление на объект, погруженный в жидкость:
Откуда, что такое давление: Давление = Сила/Площадь
Из, что такое Сила: Сила = масса x ускорение = m x g (ускорение в гравитация)
Итак: Давление = F/A = мг/A
Из Что такое Плотность: Плотность = Масса/Объем ; Масса = Плотность x Объем
Теперь у нас есть Давление = (плотность x объем x ускорение)/площадь.
Таким образом, формула, которая дает давление P на объект, погруженный в жидкость, выглядит следующим образом:
P = r * g * h
r (rho) — плотность жидкости,
g — ускорение свободного падения
h — высота жидкости над объектом
Давление только за счет жидкости (т.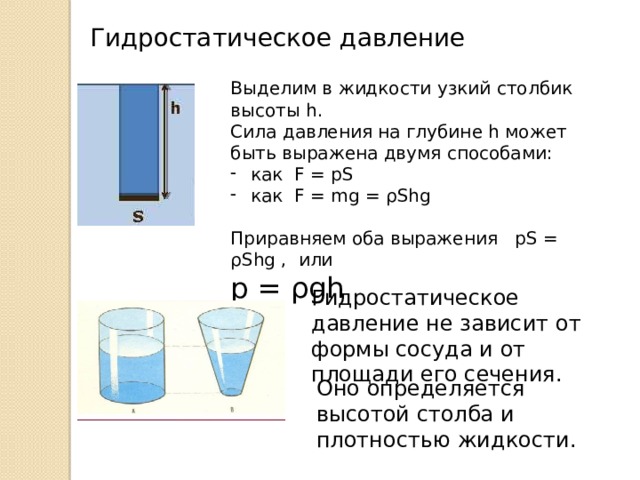 е. манометрическое давление) на данной глубине зависит только от плотности жидкости, ускорения свободного падения и расстояния под поверхностью жидкости.
.
Статическое давление жидкости на заданной глубине не зависит от общей массы, площади поверхности или геометрии контейнера.
Р = г * г * ч
Давление = (плотность жидкости) x (ускорение силы тяжести) x (высота)
См. дополнительные сведения о статическом давлении жидкости на физическом факультете Университета штата Джорджия
Если контейнер открыт для атмосферы сверху, необходимо добавить добавленное атмосферное давление, если нужно найти полное давление на объект. Давление на заданной глубине в неподвижной жидкости является результатом веса жидкости, действующего на единицу площади на этой глубине плюс любое давление, действующее на поверхность жидкости.
Ptotal = Патмосфера + Pфлюид
Ptotal = Патмосфера + ( r * g * h )
Пример :
Найдите давление на аквалангиста, который находится на глубине 10 метров от поверхности океана. Предположим стандартные атмосферные условия. Используйте плотность морской воды = 1,03 x 103 кг/м3 и атмосферное давление 1,01 x 105 Н/м2.0,8 м/с2) (10 м) = 1,09 x 105 Н/м 2.
Pобщ. = атмосферная среда + Pфлюид = (1,01 x 105) + (1,09 x 105) Па = 2,10 x 105 Па (Па)
Литература и ссылки
Статическое давление жидкости
Давление жидкости и глубина K-12 Урок от НАСА
Проверьте свои Понимание:
1. Какое из следующих уравнений не верно:
а) Сила = масса х ускорение
б) Плотность = Объем/Масса
c) Давление = плотность x ускорение x высота
г) Давление = Сила/Площадь
2. Атмосферное давление на уровне моря составляет 14,5 фунта/кв. дюйм. Почему мы не чувствуем это давление давит на нас?
а) сумма пренебрежимо мала по отношению к чувству тяжести
б) мы к этому привыкли с рождения
в) жидкости в нашем теле выталкиваются наружу с той же силой
г) сила тяжести сводит на нет ощущение давления
3. Статическое давление жидкости на любой заданной глубине зависит от:
а) общая масса
б) площадь поверхности
c) расстояние ниже поверхности
г) все вышеперечисленное
4. В уравнении для давления — P = rho x g x h единицы измерения g (система СИ):
а) кг/м ³
б) м/сек
в) кг-м/сек
г) м/сек ²
5.