Как измерить глубину? Вопросы и ответы по физике :: Класс!ная физика
ИЗМЕРЯЕМ ГЛУБИНУ !
Эхолот – технический прибор, в основе которого лежит использование часов для измерения глубины океана. Это принцип гидролокации.
До изобретения эхолота малые глубины до 4 м измеряли футштоком, т.е. шестом, размеченным в футах, а большие до 500 м – лотом, т.е. гирей, укрепленной на длинном тросе.
С поверхности океана в глубину посылается звуковой импульс и принимается эхо, отраженное от дна океана. Часы измеряют интервал времени от отправления импульса до возвращения эха. Глубина определяется по запаздыванию эха:
h = vt / 2,
где v – скорость звука в морской воде, t – время запаздывания, а двойка в знаменателе учитывает путь туда и обратно, пройденный сигналом.
Точность измерений зависит от того, насколько точно известна скорость звуковых волн в воде и с какой точностью измеряется запаздывание сигнала.
Обычный секундомер позволяет измерять время с точностью до десятых долей секунды (т.е. глубину с точностью до сотни метров). Для большей точности используются электронные секундомеры.
Источник: по материалам книги П.Маковецкого “Смотри в корень”
Есть еще вопросы по физике? – Отвечаем!
Вернуться к списку вопросов
Кто? Что? Где? Как? Куда? Когда? Какой?
Почему? Каково? Сколько? “Да” или “нет”?
ВЕНЕРА НА ЛИКЕ СОЛНЦА
Физику на заметку.
«Я говорю: увидел Венеру, как родинку на лике Солнца».
Эти строки написаны на пергаменте, возраст которого более тысячи лет! Автор — ученый-энциклопедист Древнего Востока аль-Фараби.
Не ошибался ли средневековый астроном? Ведь чтобы увидеть прохождение Венеры по диску Солнца, ему нужно было сначала с высокой точностью рассчитать движение планет, определить день и час затмения.
Вычисления современных специалистов показали, что в 910 году нашей эры с территории современного Казахстана действительно можно было наблюдать «родинку на лике Солнца».
НЕБО В АЛМАЗАХ
Это выражение приходит на ум, когда знакомишься с сообщением о том, что недавно налажен выпуск интегральных микросхем, в которых вместо полупроводниковой подложки используются кристаллы сапфира.
Такие микросхемы по стоимости во много раз выше традиционных.
Устали? – Отдыхаем!
Вы делаете это неправильно: расчет глубины / Хабр
Приветствую вас, глубокоуважаемые!
Что если я скажу, что глубина, что бы вы под ней не подразумевали, является одной из самых сложных для точного измерения величин? На какой глубине плывет подводная лодка? Какая глубина марианской впадины? На какой глубине лежит Титаник? Если вам не повезет с параметрами, то на первом километре глубины, вы можете ошибиться примерно на 30-40 метров и на 200-300 метров на 6-ом километре, используя датчик давления.
Как такое могло случиться и как делать правильно я расскажу под катом. В довесок к статье есть Open-source библиотека на C#/C/Rust/Matlab/Octave/JavaScript и пара онлайн-калькуляторов для демонстрации.
Статья будет полезна разработчикам подводной техники, число которых за последние лет пять выросло в разы.
Итак, для начала сразу оговоримся, что глубиной часто называют две разных величины:
- и расстояние по вертикали от поверхности воды до точки, где эту глубину измеряют,
- и расстояние по вертикали от поверхности воды до дна.
В первом случае — это
глубина погружения, а во втором —
глубина места.
Есть ровно два с половиной фундаментальных способа изменения этих величин, как я уже упомянул:
- по гидростатическому давлению столба жидкости, т.

Давайте абстрагируемся от точности конкретных приборов, пусть даже они у нас суперточные.
Проблема в том, что никакой член формулы не является константой. Даже атмосферное давление может меняться в течение часа.Как влияет атмосферное давление?
Давление у поверхности моря может
варьироваться в пределах 641-816 мм. рт. ст., или, тоже самое в миллибарах: от 855 до 1087. Если просто взять за
стандартное значение в 1013.25 мБар, то в зависимости от погоды уже можно получить ошибку в 40-50 сантиметров, причем, как в «плюс», так и в «минус».
Что с ускорением свободного падения?
Боюсь показаться Кэпом, но все же напомню, что земля у нас
вращается, и за счет центробежной силы притягивает на экваторе слабее, чем на полюсах.
Если не крохоборничать и не учитывать гравитационные аномалии из-за разной плотности земных пород, гор, впадин, изменения скорости вращения земли от сброшенной земными деревьями листвы и перемещениями соков по их стволам, то нас вполне устроит стандартная зависимость ускорения свободного падения от георафической широты.
 Т.н WGS-84 Gravity formula.
Т.н WGS-84 Gravity formula.Согласно этой формуле, ускорение свободного падения меняется от 9.7803 м/с2 на экваторе (0° градусов широты) до 9.8322 м/с2 на полюсах (90/-90° широты).
Допустим, мы возьмем стандартное значение ускорения свободного падения 9.80665 м/с2, на сколько мы ошибемся в худшем случае?
Это иллюстрируетя картинкой ниже. На ней синий график показывает ошибку определения глубины на экваторе, если мы будем использовать стандартное значение , а оранжевый график — такую же ошибку на полюсах.
То есть, если мы подставим в формулу стандартное значение и пойдем погружаться где-то ближе к экватору, то на 100 метрах ошибемся всего на 20-30 сантиметров, на километре — на 2,5-3 метра, а на 9-10 километрах (Бездна Челленжера, кстати, находится на 11° северной широты) ошибка будет уже 25-30 метров. Т.е. реальная глубина будет больше, чем та, которую мы измерим.
А как влияет плотность воды?
Самым нехорошим образом. Если два первых компонента погрешности учесть достаточно просто, да и вклад их весьма скромен, то с плотностью воды история более замысловатая.

Дело в том, что плотность воды в упрощенном случае есть функция температуры, давления и солености.
То есть мало измерять давление, атмосферное давление, учитывать географическую широту места. Нужно еще знать температуру и соленость воды.
Для определения плотности морской воды в (разумном) диапазоне условий на практике наиболее широко применяется формула из работы Чена и Миллеро (Да, ЮНЕСКО занимается еще и этим!)
Допустим, мы измерили и температуру и соленость, но остается сжимаемость воды — изменение плотности с давлением (т.е. с глубиной), и чтобы определить высоту столба жидкости нужно просуммировать высоты элементарных столбиков, на которых давление изменяется на какую-то малую величину . В целом это конечно интеграл, но чтобы сразу привнести некое практическое значение, запишем его так:
N — это число интервалов разбиения давления от
до измеренного
.
Плотность зависит от давления практически линейно, и считать такую сумму из-за учета одной лишь сжимаемости смысла нет, но я привел здесь эту формулу не просто так.

Сам факт, что плотность зависит от трех параметров — это еще пол беды. Сложность кроется в том, что все эти параметры могут сильно меняться с глубиной. В этом случае принято говорить о профиле температуры и солености. Вот так, к примеру, выглядит профиль из Арктики:
Вот так с северной части тихого океана:
А вот так, для сравнения — с юга атлантики:
Например, если представить, что мы погружается в северной части тихого океана (39°СШ,152°ВД) учитываем атмосферное давление и географическую широту места и сжимаемость воды, а наш датчик давления показывает 100 Бар (~1000 м), а температуру и соленость мы берем в точке измерения, но не учитываем профиль, мы ошибемся с глубиной на 2 метра.
Я специально запилил онлайн-калькулятор и добавил три тестовых профиля (их можно переключать кнопками), чтобы каждый мог сам попробовать.
Если теперь просто переключить профиль на «южноатлантический» и попробовать пересчитать, то мы увидим, что разница выросла до 6-и метров.
 Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.
Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.Естественно, все меняется и со сменой времен года и со сменой времени суток. Летом (в северном полушарии, зимой — в южном) верхний слой прогревается, а зимой — остывает. Шторма перемешивают воду, дожди смывают грязь с суши и реками уносят в моря, таят снега и ледники.
Это я к тому, что нельзя один раз перемерить и выбить в граните все профили температуры и солености для всех морей и океанов — все течет, все меняется. И если вдруг вы собрались погружаться на ощутимые глубины и у вас нет температурного профиля — я не поверю в ваш рекорд )
Матчасть
Как я упомянул в начале статьи, все необходимое для расчета глубины я собрал в библиотеку и
положил на GitHub.
Она в том числе переведена на JavaScript, а в качестве интерактивного примера ее использования привожу онлайн-калькулятор.
P.S.
Благодарю за внимание, буду искренне благодарен за конструктивную критику, сообщения об ошибках, пожелания и предложения.

В следующей статье разберу второй способ определения глубины — по эхолокации.
Давление в физике – виды, формулы и определения с примерами
Содержание:
Давление:
Вы уже знаете, что тело, находящееся на горизонтальной опоре, действует на опору силой давления. Она приложена к опоре и направлена перпендикулярно к ней. Опора деформируется. А от чего зависит степень ее деформации?
Проделаем такой опыт. Поместим столик вверх ножками в ящик с песком, на столик поставим гирю (рис. 166, а). Столик с гирей лишь незначительно погрузится в песок. А теперь перевернем столик ножками вниз и поставим ту же гирю (рис. 166, б). Ножки погрузятся в песок. Результат действия одной и той же силы давления (веса столика с гирей) оказался разным. Почему? Потому, что сила давления действовала на разную площадь поверхности опоры. В первом случае ее действие распределилось на площадь поверхности песка под крышкой, во втором — на площадь поверхности песка под ножками столика.
 Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.
Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.Результат действия силы давления на поверхность можно определить с помощью физической величины — давления. Обозначим давление буквой р. Из опыта следует, что давление тем больше, чем больше сила давления и чем меньше площадь поверхности, на которую она действует.
Что такое давление
Давление — это физическая величина, равная отношению силы давления, действующей перпендикулярно поверхности, к площади поверхности.
Математически это можно выразить так:
В СИ единицей давления является Ее называют паскалем (Па) в честь французского ученого Блеза Паскаля, изучавшего давление в жидкостях и газах.
1 паскаль — это давление на поверхность площадью производимое силой 1 Н, действующей перпендикулярно.

Применяют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа) и мегапаскаль (МПа). Обратите внимание:
Позлее вы познакомитесь и с другими единицами давления.
Силой давления может быть не только вес тела, но и любая сила, перпендикулярная поверхности, на которую она действует.
Простой пример: вы загоняете канцелярскую кнопку в вертикальную доску (рис. 167). Силой давления на кнопку является сила действия руки, направленная горизонтально (перпендикулярно доске). Пружины дивана оказывают давление на сидящего на нем человека. Сила давления (сила упругости пружин) при этом направлена вертикально вверх.
Для практических целей иногда необходимо уменьшить давление, а в ряде случаев, наоборот, — увеличить. Как изменить давление?
Обратимся к формуле Совершенно ясно: чтобы уменьшить давление, нужно уменьшить силу давления или увеличить площадь поверхности.
Например, чтобы увеличить проходимость тяжелых машин (трактора, танка), их снабжают гусеницами (рис.
 168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.
168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.А как увеличить давление? Из формулы давления следует: надо увеличить силу давления или уменьшить площадь поверхности, на которую действует сила. Затачивая лезвия ножей, ножниц (рис. 171), кос, острия игл, зубцы пил и др., мы стараемся уменьшить площадь поверхности. Тем самым, действуя малой силой, можно создать большое давление.
Животному миру природа сама обеспечила возможность создавать большое давление небольшим усилием, вооружив его представителей иглами, клювами и когтями (рис. 172), зубами, клыками, жалами и т. д.
Главные выводы:
- Давление — это физическая величина, равная отношению силы давления к площади поверхности.

- Чем больше действующая на поверхность сила давления, чем меньше площадь поверхности, на которую действует сила давления, тем больше давление.
- В СИ единицей давления является 1 Па.
Для любознательных:
Человек при ходьбе создает давление до 300—400 кПа (определите давление, которое создаете вы, стоя на полу; сравните полу ценные результаты с приведенным значением и объясните причину расхождения этих значений). Гусеничный трактор создает давление на почву в 40—60 кПа, а колеса вагона поезда па рельсы — около 50 МПа.
Пример решения задачи:
Семиклассник массой m = 50 кг стоит на полу. Определите давление, которое он производит на пол, если площадь соприкосновения подошвы его ботинка с полом Коэффициент
Дано:
m = 50 кг
Решение:
Давление, которое производит семиклассник на пол:
Сила давления F равна весу P семиклассника. Вес Тогда:
Ответ: p = 50 кПа.
Давление газа
Газы, как и твердые тела, тоже производят давление. Но твердые тела передают давление в том направлении, в котором действует сила давления. Кнопка (см. рис. 167) передает давление перпендикулярно доске, лопата (рис. 174) — в направлении силы давления ноги и т. д.
А вот газы передают давление во все стороны. Чем обусловлена такая особенность газов? От чего зависит давление газа?
Вам уже известно, что газы, как жидкости и твердые тела, состоят из частиц (атомов, молекул). Но расстояния между частицами у газов больше, чем у жидкостей и твердых тел. Поэтому силы взаимодействия между частицами у газов практически отсутствуют (кроме процессов столкновения). Двигаясь хаотически, они сталкиваются между собой и со стенками сосуда. Так как число частиц газа в сосуде чрезвычайно велико (например, в их примерно ), то стенка воспринимает удары частиц как действие вполне ощутимой силы давления.
В газах среднее число ударов хаотически движущихся частиц и средняя сила ударов на единицу площади поверхности стенки по всем направлениям одинаковы.
 Значит, и среднее давление по всем направлениям одинаково.
Значит, и среднее давление по всем направлениям одинаково.Подтвердим это опытом. Под стеклянный колокол поместим завязанную оболочку резинового шара, внутри которой находится газ (рис. 175). Будем откачивать воздух из-под колокола. Объем шара по мере откачки воздуха увеличивается. Это связано с тем, что давление газа под колоколом становится меньше, чем внутри шара.
Форма оболочки в виде шара — доказательство того, что давление газа по всем направлениям одинаково.
Каким образом можно изменить давление газа? Поскольку давление обусловлено числом ударов частиц и силой удара каждой частицы о стенку, то есть два пути его изменения. Первый из них — изменить число частиц в единице объема.
Подтвердим сказанное опытом. В пробковом пистолете между пробкой и поршнем находится воздух (рис. 176, а), который оказывает давление по всем направлениям. Если будем поршнем сжимать газ, не меняя его температуры, то пробка вылетит из пистолета (рис. 176, б). Почему?
Уменьшая объем газа, мы увеличиваем число частиц в единице объема.
 Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.
Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.Итак, при уменьшении объема (сжатии) газа при постоянной температуре его давление увеличивается, а при увеличении объема (расширении) газа давление уменьшается.
Второй путь изменить (например, увеличить) давление газа — это изменить силу удара частиц о стенки. Для этого газ нужно нагреть. Тогда скорость хаотического движения частиц увеличится, и, следовательно, увеличится и сила ударов их о стенки.
Зависимость давления от температуры можно подтвердить опытом. Если объем газа в пробковом пистолете (рис. 177, а) сохранять постоянным, но повышать температуру газа, подогревая его на спиртовке (рис. 177, б), то пробка вылетит вследствие увеличения давления. Значит, чем выше температура газа, тем больше его давление; чем ниже температура, тем меньше давление.

Главные выводы:
- Давление газа есть результат ударов частиц о стенки сосуда, в котором он находится.
- Давление газа можно увеличить, если уменьшать его объем при постоянной температуре или, сохраняя объем газа, увеличивать его температуру.
- Давление газа можно уменьшить, если увеличивать (расширять) его объем при постоянной температуре или охлаждать газ, сохраняя его объем.
Для любознательных:
Возрастание давления газа при его нагревании вызвано не только увеличением силы отдельных ударов. В холодном и горячем газе будет неодинаковым и среднее число ударов частиц о стенки сосуда за единицу времени (т. е. частота ударов). Подумайте, как влияет этот фактор на давление газа.
На баллоне с лаком для волос написано: «Предохранять от воздействия прямых солнечных лучей и нагревания выше +50 °С!» Объясните необходимость таких мер предосторожности с точки зрения физики.
Передача давления газами и жидкостями. Закон Паскаля
Закон ПаскаляВы уже знаете, что частицы твердых тел (атомы, молекулы) жестко связаны между собой и могут совершать лишь хаотические колебательные движения около положений равновесия. У газов частицы движутся по всему объему хаотически поступательно. У жидкостей они совершают и хаотическое колебательное, и хаотическое поступательное движение. Значит, у газов и жидкостей подвижность частиц значительно выше, чем у твердых тел. Поэтому жидкости и газы не сохраняют своей формы, а принимают форму сосуда, в котором находятся (рис. 178).
Кроме того, некоторые законы для жидкостей и газов одинаковы. Рассмотрим один из них. Проведем опыт. Шар с отверстиями заполним дымом и присоединим к трубке с поршнем. Дым с имеющимся в шаре воздухом займет весь объем шара. Будем перемещать поршень вниз. Мы заметим, что из всех отверстий начнут вытекать струйки дыма (рис. 179). Как объяснить это явление?
Подвижность частиц дыма и молекул воздуха приводит к тому, что они распределяются равномерно по всему объему.
 Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки.
Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки.Аналогичный опыт можно провести с жидкостью, например с водой. При нажатии на поршень струйки воды через отверстия шара будут вытекать но всем направлениям.
Проведем еще опыт. Через пробку в банку с водой вставим четыре трубки (рис. 180). Через трубку 1 будем накачивать в банку воздух, увеличивая там его давление. Увеличение внешнего давления (давления воздуха) на поверхность воды передается водой от слоя к слою по всем направлениям. В результате вода во всех трубках поднимается, причем на одну и ту же высоту.
 Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.
Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.А вспомните, как с одинаковым напором вытекают струйки воды из всех дыр, появившихся в шланге для полива огорода (рис. 181). Давление, производимое внешней силой на жидкость (газ), находящуюся в сосуде, передается жидкостью (газом) во все точки жидкости (газа) без изменения. К такому выводу еще в XVII в. пришел французский ученый Блез Паскаль. Этот вывод называют законом Паскаля.
В твердых телах подвижность частиц ограничена, и эти тела не подчиняются закону Паскаля. Если вы поставите на стол тяжелый предмет, например гирю, то вес гири создаст давление лишь на площадь поверхности стола под гирей, т. е. только в направлении действия силы.
Главные выводы:
- Частицы жидкости и газа обладают подвижностью.
- Благодаря подвижности частиц жидкости и газы передают производимое на них давление во все точки без изменения.

- Твердые тела передают давление только в направлении действия силы давления.
Благодаря подвижности частиц (атомов, молекул) жидкость принимает форму того сосуда, в который она налита. Если на жидкость действует внешняя сила давления, то жидкость передает созданное этой силой давление во все точки. Но жидкость создает давление и за счет своего веса, причем не только на дно сосуда, но и на стенки.
В том, что жидкость давит на стенки и дно сосуда, можно убедиться, используя эластичный полиэтиленовый пакет или трубку, нижний конец которой закрыт резиновой пленкой. Постепенно наливая подкрашенную воду в сосуд, мы обнаружим увеличивающийся прогиб пленки (рис. 182).
Причиной увеличения прогиба является рост давления воды на пленку. Притягиваясь к Земле, жидкость давит своим весом на пленку подобно тому, как давит на стол стопка книг. Давление неподвижной жидкости, обусловленное ее весом, называют гидростатическим (от лат.
 hydros — вода, station — неподвижный).
hydros — вода, station — неподвижный).Гидростатическое давление можно рассчитать. Так, давление столба жидкости высотой h на дно сосуда с вертикальными стенками и площадью дна S (рис. 183) равно Силой давления F является вес жидкости. Для неподвижной жидкости ее вес численно равен силе тяжести:
Запишем массу m жидкости через плотность и объем V. Масса: Объем тогда Подставим в формулу давления, получим:
Итак, давление жидкости на дно сосуда зависит от ее плотности и высоты столба жидкости.
Выведенная формула справедлива для сосуда любой формы, даже если таким «сосудом» является пруд или океан. Чтобы подтвердить формулу, к сосуду с эластичным дном присоединим измерительную систему (рис. 184). При замене цилиндрического сосуда (а) на конические (б и в) (сосуды имеют одинаковую площадь дна и равные высоты столбов жидкости) прибор показывает равные силы давления. Значит, давления жидкости на дно всех сосудов равны, хотя масса жидкости в сосудах разная.

Формула позволяет найти давление не только на дно, но и на боковые стенки. Действительно, давление на стенку на данной глубине, как и на дно, зависит от высоты столба жидкости. Подтвердим это опытом. Нальем в пластиковую бутылку с проколотыми в стенке отверстиями подкрашенную воду (рис. 185). Наблюдения за вытекающими струями показывают, что гидростатическое давление действует и на стенку бутылки. Его величина возрастает по мере увеличения высоты столба воды в бутылке над отверстием, поэтому струя III падает дальше, чем струя I. Чтобы объяснить это явление, разделим мысленно жидкость на слои /, 2> 3, 4. На каждый нижний слой жидкости действует вес верхних ее слоев. Сила тяжести, действующая на слой /, прижимает его к слою 2. Слой 2 передает производимое на него давление слоя 1 по всем направлениям. На слой 3 действует вес слоев 2, 2. Следовательно, давление в слое 3 больше, чем в слое 2. Наибольшим оно будет на дно и стенку у дна сосуда.
Главные выводы:
- Гидростатическое давление обусловлено весом покоящейся жидкости.

- Гидростатическое давление на данной глубине зависит от плотности жидкости и высоты столба жидкости.
- Гидростатическое давление на боковую стенку сосуда и на поверхность находящегося в жидкости тела на глубине h равно
Для любознательных:
Гидростатическое давление — главное препятствие для проникновения людей в глубины Мирового океана. Уже на глубине 2,5 м нетренированный ныряльщик испытывает боль в ушах из-за давления воды на барабанные перепонки. Корпуса подводных лодок, изготовленные из прочнейших сталей, на глубине в несколько сотен метров находятся на грани превышения допустимой прочности. Тогда почему рыбы на большой глубине чувствуют себя комфортно? Оказывается, вода давит на рыб не только извне, но и изнутри, т. е. происходит компенсация сил давления.
Пример №1Определите глубину водоема, на которой давление воды р = 100 кПа. Какая сила давления воды действует на ракушку с площадью поверхности лежащую на дне? Коэффициент примите равным
Дано:
Давление воды на глубине h равно:
откуда где (плотность воды).

Сила давления:
Ответ:
Сообщающиеся сосудыДействие на жидкость силы тяжести и подвижность ее молекул приводят к тому, что в широких сосудах поверхность жидкости устанавливается горизонтально. Это легко проверить с помощью прямоугольного треугольника (рис. 187). Горизонтальной будет поверхность жидкости и в сосудах, соединенных между собой, независимо от их формы.
Возьмем несколько соединенных между собой открытых сосудов. Их называют сообщающимися. Будем наливать в один из них воду. Вода перетечет в остальные сосуды и установится во всех сосудах на одном уровне (рис. 188) (если сосуды не очень узкие). Почему это происходит?
Рассмотрим самые простые сообщающиеся сосуды (рис. 189). Выделим внутри тонкий слой жидкости Как и вся жидкость, он неподвижен. Значит, слева и справа на него действуют силы с равными модулями, но противоположные по направлению. Это силы давления столбов жидкости Но чтобы модули этих сил были равны, необходимо, чтобы были одинаковыми давления, создаваемые левым и правым столбами жидкости, т.
 е.
е.После сокращения получим:
В открытых сообщающихся сосудах поверхности однородной жидкости устанавливаются на одинаковом уровне.
С сообщающимися сосудами вы встречаетесь постоянно: это чайники, лейки для полива (рис. 190, а), водомерные трубки в больших емкостях с водой или топливом (рис. 190, б). На принципе действия сообщающихся сосудов работает, к примеру, безнасосный фонтан (рис. 191).
Сложную систему сообщающихся сосудов используют в дачных поселках и деревнях в башенном водопроводе. Схема простейшего водопровода представлена на рисунке 192. Вода из артезианского источника насосом (1) подается в бак водонапорной башни (2). От бака идут трубы с ответвлениями, вводимыми в дома на все этажи. Концы ответвлений труб закрываются кранами. Давление воды в кране определяется высотой столба воды в башне над уровнем крана. Поэтому чем выше этаж, тем давление воды в кране меньше. Чтобы вода смогла достигать всех этажей, башни строят высокими.

А если вам потребуется строго горизонтально установить поверхность стола или стиральной машины? Как в этом случае вам смогут помочь сообщающиеся сосуды? Приведите еще примеры использования сообщающихся сосудов.
Все полученные в этом параграфе закономерности справедливы для широких сосудов, в которых поверхности жидкости плоские. В очень узких сосудах поверхности жидкости искривляются (рис. 193) и данные закономерности не выполняются.
Главные выводы:
- В широких неподвижных сосудах поверхность жидкости всегда горизонтальна.
- Уровень поверхностей однородной жидкости в открытых сообщающихся сосудах одинаков и не зависит от формы сосудов.
Для любознательных:
Что мы будем наблюдать, если в сообщающиеся сосуды налиты разные жидкости, например ртуть и вода (см. рис.)? В таком случае для равновесия тонкого слоя нужно, чтобы давление, создаваемое левым (ртутным) столбом высотой было равно давлению правого столба воды и ртути высотой , т.
 е. откуда Используя свойства пропорции, запишем окончательно:
е. откуда Используя свойства пропорции, запишем окончательно:Посмотрите в таблицу плотностей жидкостей. Плотность ртути в 13,6 раза больше плотности воды. Значит, будет в 13,6 раза меньше
В открытых сообщающихся сосудах высоты столбов несмешивающихся жидкостей над уровнем их раздела обратно пропорциональны плотностям жидкостей.
Пример №2Поверхность воды в водонапорной башне находится на h = 40 м выше кухонного водопроводного крана. Определите давление воды в кране. Коэффициент примите равным
Дано:
Решение:
Давление в кране создается столбом воды высотой ; где – плотность воды;
Ответ:
Газы и их весТо, что жидкость имеет вес, никого не удивляет. Каждый из вас ощущал вес, держа в руке ведро воды (рис. 197), бутылку растительного масла или напитка. Однако мы не чувствуем изменения веса футбольного мяча при его накачивании воздухом.
 Почему?
Почему?Посмотрите в таблицу плотностей и сравните плотность воздуха и воды. Плотность воздуха почти в 800 раз меньше плотности воды.
Расчеты показывают, что, например, в сильно накачанном мяче вес воздуха находится в пределах 0,1 Н, а его масса около 10 г.
Покажем на опыте наличие у воздуха массы, а следовательно, веса. Уравновесим на весах стеклянный сосуд, заполненный воздухом. Откачаем насосом воздух и взвесим сосуд повторно. Он стал легче (рис. 198). Добавляя на чашку с сосудом разновес, можно узнать массу откачанного воздуха и его вес.
Воздушный слой, окружающий нашу Землю (земная атмосфера), тоже имеет вес. На каждую молекулу этого слоя действует Земля силой тяжести. Молекулы земной атмосферы, если бы на них не действовала сила тяжести, двигаясь хаотично, давно бы покинули нашу планету. Но тяготение Земли стремится расположить их у поверхности, что приводит к неоднородности атмосферы. Ее плотность заметно убывает с высотой. Так, на высоте км плотность воздуха уже в 2 раза меньше, чем у поверхности Земли.
 На высоте км плотность а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность
На высоте км плотность а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность Главные выводы:
- Газы обладают массой и весом.
- Земная атмосфера обладает весом вследствие действия на нее притяжения Земли.
- Действие силы тяжести и хаотичное движение молекул приводят к неодинаковой плотности земной атмосферы.
Для любознательных:
Обратите внимание, что приведенные в таблице 3 плотности газов указаны при нормальных условиях, т. е. при строго определенной температуре и давлении. При сжатии газов (и обычного воздуха) их плотности могут возрастать во много раз. Такие сильно сжатые газы, во-первых, очень удобны при транспортировке, например в баллонах с кислородом для сварки или в баллонах аквалангистов. Во-вторых, сжатые до высокого давления газы удобно использовать при работе отбойного молотка и пневматических (от греч. pneuma — дуновение, дыхание) тормозов, которые устанавливаются на мощных автомобилях, в том числе на автомобилях МАЗ и БелАЗ.
Атмосферное давление Устройства для сжатия различных газов называют компрессорами.
Устройства для сжатия различных газов называют компрессорами.Вы знаете, что атмосфера Земли — газовая оболочка, в состав которой входят азот, кислород, углекислый газ, водяные пары и другие газы (рис. 199).
Всякий газ, если он находится в сосуде, производит давление на стенки сосуда, так как молекулы газа непрерывно бомбардируют эти стенки. А производит ли давление атмосфера Земли? Чем обусловлено это давление?
Атмосфера Земли удерживается силой тяжести, действующей со стороны Земли. В результате действия этой силы верхние слои атмосферы давят на нижние. Поэтому нижний слой оказывается наиболее сжатым. Давление одного слоя атмосферы на другой по закону Паскаля передается по всем направлениям и действует на любое тело: на здания, на растения, на людей. Это давление называют атмосферным. Атмосферное давление по мере удаления от поверхности Земли уменьшается. Уменьшается толщина слоя воздуха, создающего давление, и его плотность.

Атмосферное давление можно рассчитать. Результаты этих расчетов не могут не удивлять. Атмосферное давление равно примерно Значит, на каждый квадратный сантиметр нашего тела действует сила 10 Н, а на всю площадь поверхности тела (примем ее за ) — сила 100 000 Н. Это равно весу десятитонного МАЗа! Как же мы живем под таким гигантским давлением?
Вспомним глубоководных рыб. Подобно им, мы просто не замечаем этой огромной сжимающей силы, так как она компенсируется равной расширяющей силой, создаваемой давлением воздуха внутри нас (он растворен даже в нашей крови).
Так что же, атмосферное давление вообще нельзя обнаружить? Для ответа на этот вопрос обратимся к опыту. Возьмем стакан с водой, накроем его листом бумаги, перевернем, придерживая рукой лист, а затем уберем руку (см. рис. 200). Мы видим, что вода из стакана не выливается, лист не отрывается. Сила атмосферного давления, приложенная к листу бумаги, компенсирует действие веса налитой воды и разреженного воздуха в стакане.

Опустите иглу шприца в подкрашенную воду и поднимайте поршень вверх. Вы увидите, что жидкость поднимается вслед за поршнем (рис. 201) противоположно направлению действия силы тяжести. Сила атмосферного давления заставляет сок подниматься вверх по трубочке (рис. 202). Опытов, в которых проявляется действие атмосферного давления, много.
Как измерить атмосферное давление? Рассмотрим наиболее важный из опытов, проведенный в 1643 г. по предложению итальянского физика и математика Эванджелисты Торричелли.
В этом опыте запаянная с одной стороны метровая стеклянная трубка (рис. 203, а) заполнялась ртутью. Верхний конец трубки закрывался, трубка переворачивалась и опускалась в широкий сосуд со ртутью, после чего отверстие открывалось. Часть ртути вытекала из трубки в сосуд. В трубке оставался столб ртути высотой Н около 76 см (760 мм) (рис. 203, б).
Что же удерживало от вытекания оставшуюся в трубке ртуть? Широкий сосуд и трубка — это, по сути, уже известные вам сообщающиеся сосуды.
 Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб.
Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб.Рассмотрим условия равновесия тонкого слоя ртути (на рисунке 203, б он обозначен желтым цветом). Это условие требует, чтобы сила атмосферного давления снизу и сила гидростатического давления столба ртути сверху были равны. А это значит, что Таким образом, измерив высоту столба ртути Н, мы можем рассчитать его давление по формуле и тем самым определить величину атмосферного давления.
Поскольку атмосферное давление определяется высотой столба ртути, то понятно, почему очень часто его измеряют не в международных единицах (паскалях), а в миллиметрах ртутного столба.
Выразим в паскалях внесистемную единицу давления 1 миллиметр ртутного столба (сокращенно 1 мм рт. ст.):
По договоренности атмосферное давление считают нормальным, если оно равно давлению столба ртути высотой h = 760 мм при температуре t = 20 °С.
 Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм):
Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм):В большинстве случаев мы будем использовать округленное значение:
Атмосферное давление играет важную роль во многих бытовых и технических устройствах. Оно не только позволяет пользоваться пипеткой или шприцом для набора лекарств, но и дает возможность простого, недорогого способа подъема воды. Знакомые многим резиновые присоски (рис. 204) используются как в быту, так и на заводах для переноса сложнейших узлов электроники, прикосновение к которым (даже в перчатках) совершенно недопустимо.
Главные выводы:
- Удерживаемая земным притяжением атмосфера Земли производит давление.
- Человек не ощущает атмосферного давления, так как оно действует как снаружи, так и изнутри него.
- За нормальное атмосферное давление принято давление столба ртути высотой 760 мм.
Для любознательных:
В середине XVII в.
Измерение атмосферного давления. Барометры и манометры в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела.
в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела.Ежедневно мы получаем информацию о величине атмосферного давления и его изменении. Почему оно не является постоянным? Почему на разных территориях Земли давление разное? Как давление зависит от высоты?
Атмосферное давление зависит от состава воздуха. Так, например, при поступлении влажного воздуха, насыщенного водяными парами, давление уменьшается, поскольку масса молекул воды заметно меньше массы других молекул атмосферы — азота и кислорода. Наиболее сжатыми, а значит, более плотными являются прилегающие к поверхности Земли слои атмосферы. Следовательно, значение атмосферного давления зависит от высоты места над уровнем моря.
 На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия.
На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия.Вода, как и другие жидкости, практически несжимаема. Поэтому давление жидкости от высоты столба зависит прямо пропорционально Зависимость же атмосферного давления от высоты описывается гораздо более сложной формулой. Однако для расчетов, не требующих большой точности (при не очень больших высотах), можно считать, что при подъеме на каждые 12 м давление убывает на 1 мм рт. ст. Зависимость давления от высоты можно использовать для измерения высоты подъема (альпинистов, летательных аппаратов).
Так, если при подъеме давление уменьшилось на 20 мм рт. ст., то это значит, что высота подъема:
Приборы, измеряющие высоту по такому принципу, называют альтиметрами (от лат. altius — выше и metron — мера) (рис. 209).
Атмосферное давление измеряют барометра ми (от греч. baros — тяжесть и metron — мера). Простейшим барометром является сосуд со ртутью и трубка, используемые в опыте Торричелли (см.
 рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.
рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.Внешний вид и внутреннее устройство барометра-анероида представлены на рисунке 210, а, б. Главной частью анероида является металлическая коробочка с волнистой (гофрированной) верхней и нижней поверхностями. Воздух из коробочки частично откачан.
При увеличении атмосферного давления увеличивается сила давления на коробочку. Коробочка сжимается и растягивает пружину, прикрепленную к ней. Пружина связана со стрелкой, которая перемещается по шкале в сторону больших значений давления.
Если давление снижается, сила давления на коробочку уменьшается, силы упругости распрямляют коробочку, и стрелка перемешается по шкале в противоположную сторону.
Шкалу анероида предварительно градуируют, т. е. наносят деления по показаниям ртутного барометра.
 Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа).
Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа).Для измерения разности давления в сосуде и атмосферного давления служат манометры. Простейший манометр — жидкостный. Он представляет собой рассмотренную нами ранее U-образную трубку с жидкостью (см. рис. 189). Одно колено трубки (рис. 211) присоединяется к сосуду, давление в котором необходимо измерить. Другое колено открыто. Если уровень поверхности жидкости в колене, соединенном с сосудом, ниже, чем в открытом, значит, давление газа в сосуде больше атмосферного на величину давления столба жидкости высотой h, т. е.
А если давление газа в несколько раз больше атмосферного? Для измерения высоких давлений применяют металлический манометр (рис. 212). Его основным элементом является полая тонкостенная металлическая трубка (/), согнутая в дугу. Один конец трубки (3) закрыт, другой (2) присоединяется к сосуду с газом. Закрытый конец (3) через зубчатый механизм соединен со стрелкой, движущейся относительно шкалы.
 Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).
Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).Главные выводы:
- Атмосферное давление зависит от высоты местности и метеоусловий.
- Зависимость атмосферного давления от высоты и метеоусловий можно использовать для измерения высоты и для прогноза погоды.
- Атмосферное давление измеряют барометрами, а давление газов в сосудах — манометрами.
Для любознательных:
Жидкостными манометрами можно измерять давление, отличающееся от атмосферного лишь незначительно. Так, если в примере на с. 127—128 давление в сосуде будет в 2 раза больше атмосферного, т. е. то, согласно формуле имеем:
откуда
При использовании в манометре воды
Только представьте размеры такого прибора! При использовании ртути размеры уменьшаются в 13,6 раза, но возникают новые проблемы — пары ртути ядовиты.
Пример №3
У подножия горы барометр показывает давление мм рт. ст., а на ее вершине — мм рт. ст. Определите высоту данной горы.
Дано:
Решение:
Разность давлений у подножия горы и на ее вершине:
Учтем, что на 1 мм рт. ст. давление уменьшается при подъеме примерно на высоту Тогда высота горы:
Ответ: H = 120 м.
Формула давления
ОПРЕДЕЛЕНИЕДавление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях.
 Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1
ПРИМЕР 2Задание Высота воды в аквариуме 1 м. Найти давление на дно аквариума. Решение Напоминаем, плотность воды кг/м, а м/с. Таким образом: (Па)
Ответ Давление воды составляет 9800 Паскаль.
Читайте также:Задание Закрытый сосуд устроен так, что его крышка подвижна (см. рисунок). Сосуд наполнен жидкостью, плотность которой известна. На крышку сосуда действует сила . Найти давление на дно сосуда, если известны площадь дна и крышки и объём жидкости в сосуде. 
Решение Пусть: – площадь крышки
– площадь дна
– объём жидкости
– плотность жидкости
Крышка подвижна, значит она давит на жидкость с той силой, с которой внешние силы давят на неё сверху.
Очевидно:
Попробуем найти давление жидкости:
Соберём всё вместе:
Ответ Все формулы по физике
Формула силы выталкивания
Формула напряжённости магнитного поля
Формула силы Ампера
Формула силы Лоренца
Формула ЭДС
Формула длины волны
Обобщающий урок по физике на тему: “Геометрическая оптика”. 11-й класс
Цели урока:
- Повторить основные формулы и законы
геометрической оптики: закон отражения, закон
синуса, формулы тонкой линзы.

- Закрепить у учащихся навыки решения задач темы
- Развивать умение объяснять окружающие явления.
I этап. Задание на доске (оформлены заранее)
Задание 1. Сопоставить (указать стрелками) основные законы и формулы.
Дополнительный вопрос: Докажите, что именно эта формула определяет фокус линзы, т.е. укажите её из основной формулы.
Ответ:
F =Задание 2. Предмет находится двойным фокусным расстоянием линзы. Построить его изображения. (см. Приложение, рисунок 1)
Дополнительный вопрос: Где используется такое изображение?
Ответ: в фотоаппарате.
Задание 3. По положению предмета и его изображению (параллельны) восстановить положение линзы и её главных фокусов.
 (Приложение, рисунок 2.1 (I
способ), рисунок 2.1 (II способ)
(Приложение, рисунок 2.1 (I
способ), рисунок 2.1 (II способ)Дополнительный вопрос: Почему линза располагается именно в такой плоскости. Как можно её наклонить, что бы она тоже проходила через оптический центр?
Ответ: т.к. предмет и его изображение параллельны друг другу, следовательно, и линза находится в плоскости и параллельно им.(Если наклеить линзу, то формула тонкой линзы не будет работать).
Дополнительный вопрос: Какое свойство линзы позволяет широко использовать их в оптических приборах?
Ответ: Свойство изменять направление лучей, или, как говорят, световыми пучками (основано на явлениях отражения и преломления).
Во время решения этих заданий фронтальный опрос:
1. На какие два фундаментальных закона опирается геометрическая оптика?
Ответ: Закон отражения, закон преломления.
2.
 Сформулируйте законы отражения света.
Сформулируйте законы отражения света.Ответ:
- Угол падения, равен углу отражения;
- ;
- Свойство обратимости лучей.
3. Приведите краткие исторические факты из истории открытия закона преломления света.
Ответ: 1620 г. астроном и математик Снеллиус открыл закон. Ранее в трудах Декарта выведен с помощью принципа Гюйгенса.
4. В чём заключается принцип Гюйгенса?
Ответ: Каждая точка среды до которой дошло возмущение, сама становится источником вторичных волн.
5. Сформулируйте закон преломления.
Ответ: = n = =
6. В чём заключается физический смысл показателя преломления?
Ответ: Он равен отношению скоростей света в средах на границы, между которыми происходит преломление.
7. Что показывает абсолютный показатель преломления среды?
Ответ: это показатель преломления среды относительно вакуума.
 n1 =
n1 =– Итак, всё, что мы сейчас с вами повторили, обобщим в задании 1.
Проверка задания на доске.
II этап урока: Решаем задачи на применение законов отражения и преломления
Задача 1. Луч света падает на границу раздела двух сред под углом 30 градусов. Показатель преломления первой среды равен 2,0. Определите показатель преломления второй среды, если известно, что отражённые и преломлённые лучи перпендикулярны друг другу.
Дано:
о;
n1 = 2,0;
= 90о. (см. Приложение, рисунок 3)
________
n2 – ?Решение:
+ + = 180о;
так как = , , = 180о – ( + ) = 180о– ( + ).
Из закона Снеллиуса следует, что , , n2 = n1
Вывод: вторая среда оптически менее плотная.
Дополнительный вопрос: От каких факторов зависит абсолютный показатель преломления среды?
Ответ: Во-первых, абсолютный показатель преломления определяется скоростью распространения света в среде, следовательно, как и его скорость зависит от физического состояния среды: от температуры вещества, его плотности и зависит от характеристик самого света (?).
Задача 2. Кажущаяся глубина водоёма h = 6 м. Определите истинную глубину водоёма h0.
Дано:
h = 6 м;
h = 1,33 м. (см. Приложение, рисунок 4)
________
h0 – ?Решение:
(1)
треугольник КВ‘C KC = h tg;
треугольник КВС КС = h0 tg;
tg= h0 tg
h0 = = h = h n = 6м 1, 33 8 (м)
tgsin
tg sin для малых углов.
Ответ: h0 = 8 м.
Вывод: кажущаяся глубина водоёма меньше истинной глубины.
Дополнительный вопрос: Если поверхность воды колеблется, то изображение предметов в воде принимают причудливые формы. Почему?
Ответ: Колеблющаяся поверхность воды представляет собой ряд вогнутых и выпуклых зеркал самой различной формы, дающие разные изображения.
Учитель показывает сферические зеркала.
Учитель: Источники света, падая на эти зеркала, дают разные изображения. Подобно этим сферическим зеркалам.
Имеются двояковыпуклые и вогнутые линзы, которые имеют радиусы кривизны сферических поверхностей. Мы решали задачи на применение формулы, и рассчитывали радиус кривизны.
Формула: D = (n – 1) ()
Вопрос: Что эта за формула? Что мы рассчитываем по этой формуле?
Ответ: Формула тонкой линзы.

Учитель: Верно. Но есть и другая запись формулы тонкой линзы (где не учитывается R)
III этап: Решения задач (одновременно у доски)
Задача 3 (I вариант)
Рассматривая предмет в собирающую линзу, и располагая его на расстоянии 4 см от неё, получают его линейное изображение, в 5 раз больше самого предмета. Какова оптическая сила линзы?
Дано:
d = 4 см = 0,04 м;
Г = 5
_______________
D – ?Решение:
D = –
D = (1)
Г = (2)
Из (1) следует f =
Г =
Г(1 – Dd) = 1
Г – ГDd = 1
ГDd = Г – 1Ответ: 20 (дптр)
Дополнительный вопрос: В магазине в отделе “Оптика” выставлены очки. Около них находятся таблички с надписями +2 дптр, – 4 дптр.
 Какие
недостатки зрения исправляют эти очки?
Какие
недостатки зрения исправляют эти очки?Ответ: Очки D = + 2 дптр исправляют дальнозоркость, в очках используют собирающие линзы. У дальнозоркого глаза фокус за сетчаткой. Чтобы изображение попало на сетчатку глаза, усиливают оптическую силу, применяют собирающуюся линзу. Очки – 4 дптр исправляют близорукость, в очках используют рассеивающую линзу, уменьшают оптическую силу. У близорукого глаза изображение получается впереди сетчатки, чтобы оно передвинулось на сетчатку, оптическую силу уменьшают, применяют рассеивающую линзу.
Задача 3 (II вариант)
В трубку вставлены две собирающиеся линзы на расстоянии 20 см одна от другой. Фокусное расстояние первой линзы 10 см, второй – 4 см. предмет находится на расстоянии 30 см от первой линзы. На каком расстоянии от второй линзы получится действительное изображение?
Дано:
а = 20 см = 0,2 м;
F1 = 10 см = 0,1 м;
F2 = 4 см = 0, 04 м;
d1= 30 см = 0,3 м
__________________
f2 – ?Решение:
f1=
f1=
d2 = а – f1 = 0,2 м – 0,15 м = 0,05 м
f2=Ответ: f2 = 0,2 м.

Дополнительный вопрос: Почему сидя у горящего костра, мы видим предметы, расположенные по другую сторону костра, колеблющимися?
Ответ: вследствие изменения температуры воздуха, изменяется его показатель преломления, следовательно, изменяется и сама среда.
Домашнее задание: № 1121, № 1124, № 1127. (Рымкевич “Сборник задач по физике”)
Итог урока: тест (4 мин.)
I вариант
1. В каком случае угол преломления равен углу падения?
А. Только тогда, когда показатели преломления двух сред одинаковы.
Б. Только тогда, когда падающий луч перпендикулярен к поверхности раздела.
В. Когда показатели преломления двух сред одинаковы; падающий луч перпендикулярен к поверхности раздела сред.2. Каким равенством выражается закон преломления ?
- ;
- ;
- .

3. При переходе луча в оптически более плотную среду угол падения:
- Меньше угла преломления;
- Больше угла преломления;
- Равен углу преломления.
4. Если истинная глубина дна водоёма 2,66 м, то кажущаяся глубина равна:
А. 2 м;
Б. 1,33 м;
В. 2,66 м.5. Возможно ли полное отражение, если световой луч, падает из воздуха в воду?
А. Нет;
Б. Да;
В. Может, если угол падения больше предельного угла отражения.II вариант
1. Как меняются кажущиеся размеры предмета в воде?
А. Увеличиваются.
Б. Уменьшаются.
В. Не изменяются.2. Каким равенством выражается увеличение линзы?
А. Г = ;
Б. Г = ;
В. Г = .
Г = .3. При переходе луча в оптически менее плотную среду угол падения:
- Меньше угла преломления;
- Равен углу преломления.
- Больше угла преломления;
4. Человек рассматривает дно водоёма глубиной 4 м (истинная глубина), то кажущаяся глубина:
А. Больше 4 м;
Б. Меньше 4 м;
В. Равна 4 м.5. Возможно ли полное отражение, если световой луч падает, из воды в стекло?
А. Да;
Б. Нет;
В. Может, если угол падения больше предельного угла отражения.Ответы:
I вариант 1. В
2. Б
3. Б
4. А
5. АII вариант 1. А
2. В
3. А
4. Б
Б
5. БДавление атмосферное, гидростатическое. Закон Паскаля, сила. Сообщающиеся сосуды, применение
Тестирование онлайн
Давление. Основные понятия
Механика жидкостей
Давление
Это физическая скалярная величина, которая определяется по формуле
Атмосферное давление
Атмосфера – это воздушная оболочка Земли, которая удерживается гравитационными силами. Атмосфера имеет вес и давит на все тела на Земле. Давление атмосферы составляет около 760 мм.рт.ст. или 1 атм., или 101325Па. Миллиметр ртутного столба, атмосфера – это различные внесистемные единицы измерения давления. Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.
Что такое давление в 1 атм? Рукопожатие крепкого мужчины составляет 0,1 атм, удар боксера составляет несколько атмосферных единиц. Давление каблука-шпильки составляет 100 атмосфер.
 Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.
Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.Закон Паскаля
Давление на жидкость или газ передается во всех направлениях одинаково.
Давление внутри жидкости (газа) на одной и той же глубине одинаково во всех направлениях (влево вправо, вниз и вверх!)
Гидростатическое давление
Это давления столбика жидкости на дно сосуда. Какая сила создает давление? Жидкость обладает весом, который давит на дно.
Давление жидкости на дно
Давление на дно сосуда не зависит от формы сосуда, но зависит от площади его дна. При этом сила давления на дно может быть и больше и меньше силы тяжести жидкости в сосуде.
 В этом заключается “гидростатический парадокс”.
В этом заключается “гидростатический парадокс”.На стенку сосуда гидростатическое давление распределено неравномерно: у поверхности жидкости оно равно нулю (без учета атмосферного давления), внутри жидкости изменяется прямо пропорционально глубине и на уровне дна достигает значения . Это переменное давление можно заменить средним давлением
Сообщающиеся сосуды
Это сосуды, которые имеют общий канал внизу.
Однородная жидкость устанавливается в сообщающихся сосудах на одном уровне независимо от формы сосудов, как видно на фотографии.
Разнородные жидкости устанавливаются в сообщающихся сосудах согласно формуле
Гидравлический пресс
Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы. В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.
Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.
Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего.
 Выигрыша в работе гидравлический пресс не дает.
Выигрыша в работе гидравлический пресс не дает.На практике вследствие наличия трения:
Если сила направлена под углом к нормали (перпендикуляру), то давление определяется по формуле
Газы и жидкости, находящиеся под давлением, нашли широкое применение в промышленной технике. Например, пневматический отбойный молоток. При помощи сжатого воздуха работают также двери в автобусах и метро, тормоза поездов и грузовых автомобилей.
Встречаются также механизмы, работающие при помощи сжатой жидкости. Они называются гидравлическими. Например, устройство гидравлического пресса.
Численное значение атмосферного давления было определено опытным путем в 1643 году итальянским ученым Э.Торричелли.
Стеклянную трубку длиной около метра, запаянную с одного конца, наполняют доверху ртутью. Затем, плотно закрыв отверстие пальцем, трубку переворачивают и опускают в чашу со ртутью, после чего палец убирают. Ртуть из трубки начинает выливаться, но не вся: остаётся «столб» » 76 см высотой, считая от уровня в чаше.
 Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.
Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.Атмосферное давление уравновешивает гидростатическое давление столбика ртути. Согласно закону Паскаля давление атмосферы давит вверх на столбик ртути. А столбик ртути давит вниз своим весом. Ртуть перестает опускаться, когда эти давления одинаковые. Вычислив гидростатическое давление ртути известной высоты, определили давление атмосферы.
Трубка Торричелли с линейкой является простейшим барометром – прибором для измерения атмосферного давления
Для измерения атмосферного давления используют также барометр-анероид.
Поскольку атмосферное давление уменьшается по мере удаления от поверхности Земли, то шкалу анероида можно проградуировать в метрах. В этом случае он называется альтиметром.
Пусть прямоугольный металлический брусок площадью основания S и высотой h лежит на дне сосуда, в который налита вода до высоты H, H>h. Как определить силу давления бруска на дно сосуда?
Возможны два случая! Пусть брусок неплотно прилегает ко дну сосуда, тогда снизу на брусок действует сила давления жидкости.
 Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда – результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.
Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда – результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.Используем 2 закон Ньютона:
Рассмотрим второй возможный случай. Пусть брусок прилегает ко дну так плотно, что жидкость под него не подтекает. Снизу отсутствует давление жидкости, следовательно сила Архимеда равна нулю. Сверху же на брусок действует сила давления жидкости и атмосферы.
Используем 2 закон Ньютона для этого случая:
p0 – атмосферное давление,
p – гидростатическое давление столба жидкости высотой H-h.Давление в жидкости и газе
Давление в жидкости и газе
Внутри жидкости в любой ее точке существует давление, обусловленное весом верхних слоев жидкости на нижние. Если рассматривать жидкость в состоянии покоя, т.е. не двигающуюся, то это давление можно назвать “весовым ” или гидростатическим давлением.

На одном и том же уровне оно одинаково по всем направлениям / и вверх в том числе /.
С глубиной давление увеличивается.Когда вы в резиновых сапогах заходите в воду, то чувствуете, как резина плотно прилегает к ногам. А ведь глубина совсем небольшая!
Расчетная формула
для определения давления жидкости в любой ее точке, а также на дно и стенки сосуда:Все вышесказанное справедливо и для газов, в которых тоже существует гидростатическое давление.
КНИЖНАЯ ПОЛКА1.Когда надо открывать рот пошире?………. смотреть
2. Жидкости давят … вверх! ………. смотреть
3. Естественная форма жидкости ………. смотреть
4. Глубины погружения человека …….. смотреть
РЕШИМ ЗАДАЧКИ?1. Почему вода из ванны вытекает быстрее, если в нее погружается человек?
2. Мальчик давит на малый поршень сосуда с водой. Удержит ли другой мальчик большой поршень, если ребята действуют на поршень с одинаковой силой?
3.
 Из небольшого отверстия в боковой стенке сосуда вытекает струйка воды. Что произойдет с этой струёй, если сосуд начнет свободно падать? Сопротивлением окружающего воздуха пренебречь.
Из небольшого отверстия в боковой стенке сосуда вытекает струйка воды. Что произойдет с этой струёй, если сосуд начнет свободно падать? Сопротивлением окружающего воздуха пренебречь.4. Почему водолазу при погружении на глубину необходимо подавать воздух в скафандр под давлением, равным давлению воды на глубине, на которой он находится?
5. Как изменяется объем пузырька воздуха, когда этот пузырек поднимается со дна водоема на поверхность? Почему?
Жду письменные ответы к следующему уроку!
ЭТО ТОЖЕ ИНТЕРЕСНОНа глубинах более 1,5 м разность между давлением воды, сжимающим грудную клетку, и давлением воздуха внутри нее возрастает настолько, что у человека уже не хватает сил увеличивать объем грудной клетки при вдохе и наполнять свежим воздухом легкие. Поэтому при погружении более чем на 1,5м можно дышать только таким воздухом, который сжат до давления, равного давлению воды на этой глубине.
На какую глубину возможно погружение?искатели жемчуга – 30 м
рекордное погружение человека без специального оснащения – 105 м
погружение с аквалангом – 143 м
в мягком скафандре – 180 м
в жестком скафандре – 250 м
в батискафе – 10 919 м.
… Распространено мнение, что суда, затонувшие в океане, не достигают морского дна, а висят неподвижно на некоторой глубине. В романе Ж. Верна рассказывается о кораблях догнивающих, свободно вися в воде. Так ли это?
… Давление воды в глубинах океана огромно. Если порожнюю закупоренную бутылку опустить на значительную глубину, затем извлечь вновь, то обнаружится что давление воды вогнала пробку внутрь бутылки и вся посудина полна воды.
… Был проделан такой опыт. Три стеклянных трубки различных размеров , с обоих концов запаянные, были завернуты в холст и помещены в медный цилиндр с отверстиями для свободного пропуска воды. Цилиндр был опущен на глубину 5 км. Когда его извлекли, оказалось , что холст наполнен снегообразной массой, это было раздробленное стекло.
А если на такую глубину опустить куски дерева, то после поднятия они начинают тонуть в воде, как кирпичи, так их сдавливает.… Вода, как и все жидкости мало поддается сжатию. Поэтому с глубиной плотность воды изменяется незначительно.
 В самом глубоком месте плотность воды увеличивается лишь на 5 процентов. А чтобы в ней плавало железо необходимо уплотнить ее в 8 раз! Не может быть ни малейшего сомнения, что затонувшие суда покоятся на дне океана!
В самом глубоком месте плотность воды увеличивается лишь на 5 процентов. А чтобы в ней плавало железо необходимо уплотнить ее в 8 раз! Не может быть ни малейшего сомнения, что затонувшие суда покоятся на дне океана!Источник: Занимательная физика. В. Шабловский
ВСЕ БЕЖИМ РЕШАТЬ ЗАДАЧИ!
А МОЖЕТ БЫТЬ, БЕЖИМ РЕШАТЬ ВСЕ ЗАДАЧИ?
1.4: Реальная и кажущаяся глубина
Когда мы смотрим в бассейн с водой сверху, бассейн кажется менее глубоким, чем он есть на самом деле. На рисунке I.6 показано формирование виртуального изображения точки на дне бассейна за счет преломления на поверхности.
Диаметр зрачка человеческого глаза находится в диапазоне от 4 до 7 мм, поэтому, когда мы смотрим вниз в бассейн (или действительно смотрим на все, что находится не очень близко к нашим глазам), задействованные углы малы. .Таким образом, на рисунке I.6 вам предлагается представить, что все углы малы; на самом деле, нарисовать их маленькими сделало бы рисунок очень тесным.
 Поскольку углы малы, я могу аппроксимировать закон Снеллиуса:
Поскольку углы малы, я могу аппроксимировать закон Снеллиуса:\ [\ begin {align} n & = \ frac {\ sin \ theta ‘} {\ sin \ theta} \ label {eq2} \\ [4pt] & \ приблизительно \ dfrac {\ tan \ theta’} {\ загар \ theta} \ label {eq: 1.4.1} \ end {align} \]
и, следовательно,
\ [\ frac {\ text {реальная глубина}} {\ text {кажущаяся глубина}} = \ frac {h} {h ‘} = \ frac {\ tan \ theta’} {\ tan \ theta} = n.\ label {eq: 1.4.2} \]
Для воды \ (n \) составляет примерно \ (\ frac {4} {3} \), так что видимая глубина составляет примерно \ (\ frac {3} {4} \) реальной глубины.
Упражнение \ (\ PageIndex {1} \)
Астроном помещает фотопленку или ПЗС-матрицу в основной фокус телескопа. Затем он решает вставить стеклянный фильтр с показателем преломления \ (n \) и толщиной \ (t \) перед пленкой (или ПЗС). В каком направлении он должен двигать пленку или ПЗС-матрицу и на сколько, чтобы изображение оставалось в фокусе?
Теперь, если бы закон Снеллиуса действительно был задан уравнением \ (\ ref {eq: 1.
 2 \ theta}} \ label {eq: 1.4.3} \]
2 \ theta}} \ label {eq: 1.4.3} \]Упражнение \ (\ PageIndex {2} \)
Покажите, что для первого порядка в \ (\ theta \) уравнение \ ref {eq: 1.4.3} становится \ (h / h ‘= n \).
Уравнение \ (\ ref {eq: 1.4.3} \) показывает \ (h ‘\) как функцию \ (\ theta \) – и что преломленные лучи, когда проецируются назад, не все, кажется, исходят от единственная точка. Другими словами, точечный объект не дает точечного изображения. На рисунке I.7 показаны (для \ (n = 1,5 \) – т.е. стекла, а не воды) обратные проекции преломленных лучей для \ (\ theta ‘\) = 15, 30, 45, 60 и 75 градусов вместе с их огибающая или «каустическая кривая».3 \ theta = 0. \ nonumber \]
Здесь \ (y = 0 \) берется за преломляющую поверхность, а \ (\ theta \) и \ (\ theta ‘\) связаны законом Снеллиуса.
Таким образом, преломление на границе раздела плоскостей создает аберрацию в том смысле, что свет от точечного объекта не отклоняется от точечного изображения. Этот тип аберрации в некоторой степени похож на тип аберрации, возникающей при отражении от сферического зеркала, и в этой степени аберрацию можно назвать «сферической аберрацией».
 Если смотреть на точку на дне пруда под углом к поверхности, а не перпендикулярно ей, возникает дополнительная аберрация, называемая «астигматизмом». Это будет обсуждаться в главе 4.
Если смотреть на точку на дне пруда под углом к поверхности, а не перпендикулярно ей, возникает дополнительная аберрация, называемая «астигматизмом». Это будет обсуждаться в главе 4.11.4 Изменение давления в жидкости с глубиной – College Physics
Если у вас когда-либо ломались уши во время полета или болели во время глубокого погружения в бассейне, вы испытали влияние глубины на давление в жидкости. На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами.Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается. Под водой оказываемое на вас давление увеличивается с увеличением глубины. В этом случае оказываемое на вас давление является результатом как веса воды над вами (), так и веса атмосферы над вами (). Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас на много этажей, но вам нужно погрузиться всего на метр или около того ниже поверхности бассейна, чтобы почувствовать повышение давления.
 Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.Рассмотрим контейнер на рис. 11.9. Его дно выдерживает вес находящейся в нем жидкости. Вычислим давление, оказываемое на дно, на вес жидкости. Это давление представляет собой вес жидкости mgmg размером 12 {ital “mg”} {}, деленный на поддерживающую его площадь AA размером 12 {A} {} (площадь дна контейнера):
P = мгA.P = мгА. размер 12 {P = {{ital “mg”} больше {A}}} {}11.12
Мы можем найти массу жидкости по ее объему и плотности:
m = ρV.m = ρV. размер 12 {m = ρV} {}11,13
Объем VV жидкости размером 12 {V} {} зависит от размеров контейнера. Это
V = Ah, V = Ah, размер 12 {V = ital “Ah”} {}11,14
где AA размер 12 {A} {} – это площадь поперечного сечения, а hh размер 12 {h} {} – это глубина. Объединение последних двух уравнений дает
m = ρAh.m = ρAh. размер 12 {m = ρ ital “Ah”} {}11.15
Если ввести это в выражение для давления, получим
P = ρAhgA. P = ρAhgA. размер 12 {P = {{left (ρ ital “Ah” right) g} над {A}}} {}
P = ρAhgA. размер 12 {P = {{left (ρ ital “Ah” right) g} над {A}}} {}11,16
Область сокращается, и перестановка переменных дает
P = hρg.P = hρg. размер 12 {P = hρg} {}11,17
Это значение представляет собой давление , обусловленное весом жидкости . Уравнение имеет общую применимость за пределами особых условий, при которых оно получено здесь. Даже если бы емкости не было, окружающая жидкость все равно оказывала бы это давление, сохраняя статическое состояние жидкости.Таким образом, уравнение P = hρgP = hρg размер 12 {P = hρg} {} представляет давление из-за веса любой жидкости со средней плотностью ρρ размером 12 {ρ} {} на любой глубине hh размер 12 {h} { } под его поверхностью. Для жидкостей, которые почти несжимаемы, это уравнение справедливо до больших глубин. Для газов, которые достаточно сжимаемы, можно применять это уравнение до тех пор, пока изменения плотности на рассматриваемой глубине невелики.
 Пример 11.4 иллюстрирует эту ситуацию.
Пример 11.4 иллюстрирует эту ситуацию.Рисунок 11.9 Дно этого контейнера выдерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать на жидкость восходящую силу (так как она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это.
Пример 11.3
Расчет среднего давления и прилагаемой силы: какую силу должна выдержать плотина?
В примере 11.1 мы вычислили массу воды в большом резервуаре. Теперь мы рассмотрим давление и силу, действующие на удерживающую воду плотину.(См. Рис. 11.10.) Ширина плотины составляет 500 м, а глубина воды у плотины – 80,0 м. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину, и сравните ее с весом воды в плотине (ранее было установлено, что она составляет 1,96 × 1013 Н1,96 × 1013 Н).
Стратегия для (а)
Среднее давление P¯P¯ из-за веса воды давление на средней глубине h¯h¯ 40,0 м, так как давление линейно растет с глубиной.

Решение для (а)
Среднее давление из-за веса жидкости
P¯ = h¯ρg.P¯ = h¯ρg. размер 12 {P = hρg} {}11,18
Вводя плотность воды из таблицы 11.1 и принимая h¯h¯ size 12 {h} {} за среднюю глубину 40,0 м, получаем
P¯ = ( 40,0 м) 103 кгм 39,80 мс2 = 3,92 × 105 Нм2 = 392 кПа. P¯ = (40,0 м) 103 кгм 39,80 мс2 = 3,92 × 105 Нм2 = 392 кПа.11,19
Стратегия для (б)
Сила, оказываемая водой на плотину, равна среднему давлению, умноженному на площадь контакта:
F = P¯A.F = P¯A. размер 12 {F = {overline {P}} A} {}11.20
Решение для (b)
Мы уже нашли значение для P¯P¯ size 12 {{bar {P}}} {}. Площадь плотины A = 80,0 м × 500 м = 4,00 × 104 м2 A = 80,0 м × 500 м = 4,00 × 104 м2 размер 12 {A = «80» «». 0`m умножить на “500” `m = 4″. ” «00» умножить на «10» rSup {размер 8 {4}} `m rSup {размер 8 {2}}} {}, так что
F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н . F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
размер 12 {F = \ (3 “.” “92” умножить на “10” rSup {размер 8 {5}} “” Н / м “rSup {размер 8 {2}} \) \ (4″.”” 00 “умножить на” 10 “rSup {размер 8 {4}}` m rSup {размер 8 {2}} \)} {} #
“” = 1 “.” “57” умножить на “10” rSup {size 8 {“10″}} `N”. ” {}
}} {}
F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
размер 12 {F = \ (3 “.” “92” умножить на “10” rSup {размер 8 {5}} “” Н / м “rSup {размер 8 {2}} \) \ (4″.”” 00 “умножить на” 10 “rSup {размер 8 {4}}` m rSup {размер 8 {2}} \)} {} #
“” = 1 “.” “57” умножить на “10” rSup {size 8 {“10″}} `N”. ” {}
}} {}11.21
Обсуждение
Хотя эта сила кажется большой, она мала по сравнению с 1,96 × 1013N1,96 × 1013N размером 12 {1 “.” “96” умножить на “10” rSup {size 8 {“13”}} `N} {} веса воды в резервуаре – фактически, это всего лишь 0,0800% 0,0800% вес. Обратите внимание, что давление, обнаруженное в части (а), полностью не зависит от ширины и длины озера – оно зависит только от его средней глубины у плотины.Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не , а не от горизонтальной протяженности водохранилища. На диаграмме толщина дамбы увеличивается с глубиной, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.
 Глубина, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.
Глубина, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.Рисунок 11.10 Плотина должна выдерживать силу, прилагаемую к ней удерживаемой водой. Эта сила мала по сравнению с весом воды за плотиной.
Атмосферное давление – еще один пример давления из-за веса жидкости, в данном случае из-за веса воздуха над заданной высотой. Атмосферное давление у поверхности Земли немного меняется из-за крупномасштабного потока атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «минимумы»). Однако среднее давление на уровне моря определяется стандартным атмосферным давлением PatmPatm размером 12 {P rSub {size 8 {“atm”}}} {}, измеренным как
1 атмосфера (атм) = Patm = 1.01 × 105 Н / м2 = 101 кПа 1 атмосфера (атм) = Patm = 1,01 × 105 Н / м2 = 101 кПа. размер 12 {1` “атмосфера” `\ (” атм “\) = P rSub {размер 8 {” атм “}} = 1″. ” «01» умножить на «10» rSup {размер 8 {5}} «Н / м» rSup {size 8 {2}} = «101» «« кПа »} {}11,22
Это соотношение означает, что на в среднем, на уровне моря столб воздуха выше 1,00 м 21,00 м 2 поверхности Земли имеет вес 1,01 × 105 N1,01 × 105 N размером 12 {1 “”.
Рисунок 11.11 Атмосферное давление на уровне моря в среднем составляет 1,01 × 105 Па1,01 × 105 Па размером 12 {1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” Па “} {} (эквивалентно 1 атм.), Поскольку столб воздуха над этим 1м21м2 размером 12 {1`m rSup {размер 8 {2} }} {}, простираясь до верха атмосферы, весит 1,01 × 105 N1,01 × 105 N размером 12 {1 “.” “01” умножить на “10” rSup {размер 8 {5}} “N”} {}. “01” умножить на “10” rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)
“01” умножить на “10” rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)Пример 11.4
Расчет средней плотности: насколько плотен воздух?
Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км.Сравните эту плотность с плотностью воздуха, указанной в таблице 11.1.
Стратегия
Если мы решим для плотности P = hρgP = hρg size 12 {P = hρg} {}, мы увидим, что
ρ¯ = Phg.ρ¯ = Phg. размер 12 {{bar {ρ}} = {{P} over {ital “hg”}}} {}11,23
Затем мы принимаем PP размер 12 {P} {} за атмосферное давление, hh размер 12 {h } {} задан, а размер gg 12 {g} {} известен, поэтому мы можем использовать его для вычисления ρ¯ρ¯ размера 12 {{bar {ρ}}} {}.

Раствор
Ввод известных значений в выражение для ρ¯ρ¯ size 12 {{bar {ρ}}} {} дает
ρ¯ = 1.01 × 105 Н / м2 (120 × 103 м) (9,80 м / с2) = 8,59 × 10–2 кг / м3. Ρ¯ = 1,01 × 105 Н / м2 (120 × 103 м) (9,80 м / с2) = 8,59 × 10–2 кг / м3. размер 12 {{bar {ρ}} = {{1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” N / m “rSup {size 8 {2}}} больше {\ (” 120 “умножить на” 10 “rSup {размер 8 {3}}` m \) \ (9 “.” “80” `” m / s “rSup {size 8 {2}} \)}} = 8″. ” “59” умножить на “10” rSup {размер 8 {- 2}} «кг / м» rSup {размер 8 {3}}} {}11,24
Обсуждение
Этот результат представляет собой среднюю плотность воздуха между поверхностью Земли и верхним слоем атмосферы Земли, которая по существу заканчивается на уровне 120 км.Плотность воздуха на уровне моря, указанная в таблице 11.1, составляет 1,29 кг / м 31,29 кг / м3 размер 12 {1 “”. “29” “” кг / м “rSup {size 8 {3}}} {} – примерно в 15 раз больше среднего значения.
 Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.Пример 11.5
Расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?
Вычислить глубину под поверхностью воды, на которой давление, обусловленное весом воды, равно 1.00 атм.
Стратегия
Начнем с решения уравнения P = hρgP = hρg size 12 {P = hρg} {} для глубины hh size 12 {h} {}:
h = Pρg.h = Pρg. размер 12 {h = {{P} over {ρg}}} {}11,25
Затем мы берем PP размер 12 {P} {} равным 1,00 атм и ρρ размером 12 {ρ} {} как плотность вода, создающая давление.
Решение
Ввод известных значений в выражение для размера hh 12 {h} {} дает
h = 1,01 × 105 Н / м2 (1.00 × 103 кг / м3) (9,80 м / с2) = 10,3 м · ч = 1,01 × 105 Н / м2 (1,00 × 103 кг / м3) (9,80 м / с2) = 10,3 м. размер 12 {h = {{1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” N / m “rSup {size 8 {2}}} больше {\ (1”. “” 00 “умножить на” 10 “rSup {size 8 { 3}} `” кг / м “rSup {размер 8 {3}} \) \ (9”. “” 80 “` “” м / с “rSup {размер 8 {2}} \)}} =” 10 ” “.” 3`m} {}
размер 12 {h = {{1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” N / m “rSup {size 8 {2}}} больше {\ (1”. “” 00 “умножить на” 10 “rSup {size 8 { 3}} `” кг / м “rSup {размер 8 {3}} \) \ (9”. “” 80 “` “” м / с “rSup {размер 8 {2}} \)}} =” 10 ” “.” 3`m} {}11.26
Обсуждение
Всего 10,3 м воды создают такое же давление, как 120 км воздуха. Поскольку вода почти несжимаема, мы можем пренебречь любым изменением ее плотности на этой глубине.
Как вы полагаете, общее давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный. Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы. Таким образом, общее давление на глубине 10,3 м составляет 2 атм – половина от уровня воды выше и половина от воздуха выше. Мы увидим в принципе Паскаля, что давление жидкости всегда увеличивается таким образом.

11.4 Изменение давления в жидкости с глубиной – Физика колледжа, главы 1-17
Сводка
- Определите давление в единицах веса.
- Объясните изменение давления в жидкости с глубиной.
- Рассчитайте плотность с учетом давления и высоты.
Если у вас когда-либо ломались уши во время полета или болели во время глубокого погружения в бассейне, вы испытали влияние глубины на давление в жидкости.На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами. Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается. Под водой оказываемое на вас давление увеличивается с увеличением глубины. В этом случае оказываемое на вас давление является результатом как веса воды над вами , так и веса атмосферы над вами . Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас на много этажей, но вам нужно погрузиться всего на метр или около того ниже поверхности бассейна, чтобы почувствовать повышение давления.
 Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.Рассмотрим контейнер на рисунке 1. Его дно выдерживает вес находящейся в нем жидкости. Вычислим давление, оказываемое на дно, на вес жидкости. Давление – это вес жидкости [латекс] \ boldsymbol {mg} [/ latex], деленный на площадь [латекс] \ boldsymbol {A} [/ latex], на которой он находится (площадь дна контейнера) :
[латекс] \ boldsymbol {P \: =} [/ latex] [латекс] \ boldsymbol {\ frac {mg} {A}}.[/ латекс]
Мы можем найти массу жидкости по ее объему и плотности:
[латекс] \ boldsymbol {m \: = \ rho {V}}. [/ Latex]
Объем жидкости [латекс] \ boldsymbol {V} [/ latex] зависит от размеров контейнера. Это
[латекс] \ boldsymbol {V = Ah}, [/ латекс]
где [latex] \ boldsymbol {A} [/ latex] – это площадь поперечного сечения, а [latex] \ boldsymbol {h} [/ latex] – это глубина. Объединение последних двух уравнений дает
[латекс] \ boldsymbol {m = \ rho {Ah}}.
 [/ латекс]
[/ латекс]Если ввести это в выражение для давления, получим
[латекс] \ boldsymbol {P \: =} [/ latex] [латекс] \ boldsymbol {\ frac {(\ rho {Ah}) g} {A}}. [/ Latex]
Область отменяется, и перестановка переменных дает
[латекс] \ boldsymbol {P = h \ rho {g}.} [/ Латекс]
Это значение – давление из-за веса жидкости . Уравнение имеет общую применимость за пределами особых условий, при которых оно получено здесь. Даже если бы емкости не было, окружающая жидкость все равно оказывала бы это давление, сохраняя статическое состояние жидкости.Таким образом, уравнение [латекс] \ boldsymbol {P = h \ rho {g}} [/ latex] представляет давление из-за веса любой жидкости со средней плотностью [латекс] \ boldsymbol {\ rho} [/ latex] на любой глубине [латекс] \ boldsymbol {h} [/ латекс] под его поверхностью. Для жидкостей, которые почти несжимаемы, это уравнение справедливо до больших глубин. Для газов, которые достаточно сжимаемы, можно применять это уравнение до тех пор, пока изменения плотности на рассматриваемой глубине невелики.
Рисунок 1. Дно этого контейнера выдерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать на жидкость восходящую силу (так как она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это. Пример 2 иллюстрирует эту ситуацию.
Пример 2 иллюстрирует эту ситуацию.Пример 1: Расчет среднего давления и прилагаемой силы: какую силу должна выдержать плотина?
В главе 11.2 Пример 1 мы вычислили массу воды в большом резервуаре. Теперь мы рассмотрим давление и силу, действующие на удерживающую воду плотину.{13} \ textbf {N}} [/ latex]).
Стратегия для (а)
Среднее давление [латекс] \ boldsymbol {\ bar {P}} [/ latex] из-за веса воды – это давление на средней глубине [латекс] \ boldsymbol {\ bar {h}} [/ latex] 40,0 м, так как давление линейно растет с глубиной.
Решение для (a)
Среднее давление из-за веса жидкости
[латекс] \ boldsymbol {\ bar {P} = \ bar {h} \ rho {g}}.
 [/ Latex]
[/ Latex]Введите плотность воды из Таблицы 1 и приняв [латекс] \ boldsymbol {\ bar {h}} [/ latex] за среднюю глубину 40.{13} \ textbf {N}} [/ latex] вес воды в резервуаре – фактически, это только [латекс] \ boldsymbol {0,0800 \%} [/ латекс] веса. Обратите внимание, что давление, обнаруженное в части (а), полностью не зависит от ширины и длины озера – оно зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не , а не от горизонтальной протяженности водохранилища. На диаграмме толщина дамбы увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличения давления.
Рис. 2. Плотина должна выдерживать силу, прилагаемую к ней удерживаемой водой. Эта сила мала по сравнению с весом воды за плотиной.Атмосферное давление – еще один пример давления из-за веса жидкости, в данном случае из-за веса воздуха, над заданной высотой. Атмосферное давление у поверхности Земли немного меняется из-за крупномасштабного потока атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «минимумы»).
Рис. 3. Атмосферное давление на уровне моря в среднем 1,01 × 10 5 Па (эквивалентно 1 атм), поскольку столб воздуха над ним 1 м 2 , простирающийся до верхних слоев атмосферы, весит 1,01 × 10 5 N . 5 \ textbf {N}}, [/ latex] эквивалент [latex] \ boldsymbol {1 \ textbf {atm}}. [/ Latex] (см. Рисунок 3.)
5 \ textbf {N}}, [/ latex] эквивалент [latex] \ boldsymbol {1 \ textbf {atm}}. [/ Latex] (см. Рисунок 3.)Пример 2: Расчет средней плотности: насколько плотен воздух?
Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км.Сравните эту плотность с плотностью воздуха, указанной в Таблице 1.
Стратегия
Если мы решим [латекс] \ boldsymbol {P = h \ rho {g}} [/ latex] для плотности, мы увидим, что
[латекс] \ boldsymbol {\ bar {\ rho} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {P} {hg}}. [/ Latex]
Затем мы принимаем [латекс] \ boldsymbol {P} [/ latex] за атмосферное давление, за [латекс] \ boldsymbol {h} [/ latex] и за [latex] \ boldsymbol {g} [/ latex] известно, и поэтому мы можем использовать это для вычисления [latex] \ boldsymbol {\ bar {\ rho}}.
 3} [/ latex] – примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
3} [/ latex] – примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.Пример 3: Расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?
Вычислите глубину ниже поверхности воды, на которой давление, обусловленное весом воды, равно 1,00 атм.
Стратегия
Начнем с решения уравнения [латекс] \ boldsymbol {P = h \ rho {g}} [/ latex] для глубины [латекс] \ boldsymbol {h}: [/ latex]
[латекс] \ boldsymbol {h \: =} [/ latex] [латекс] \ boldsymbol {\ frac {P} {\ rho {g}}}.2)}} [/ latex] [latex] \ boldsymbol {= \: 10.3 \ textbf {m.}} [/ Latex]
Обсуждение
Всего 10,3 м воды создают такое же давление, как 120 км воздуха. Поскольку вода почти несжимаема, мы можем пренебречь любым изменением ее плотности на этой глубине.
Как вы полагаете, общее давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный.
 Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы.Таким образом, общее давление на глубине 10,3 м составляет 2 атм – половина от воды выше и половина от воздуха выше. В главе 11.5 «Принцип Паскаля» мы увидим, что давление жидкости всегда увеличивается таким образом.
Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы.Таким образом, общее давление на глубине 10,3 м составляет 2 атм – половина от воды выше и половина от воздуха выше. В главе 11.5 «Принцип Паскаля» мы увидим, что давление жидкости всегда увеличивается таким образом.- Давление – это вес жидкости [латекс] \ boldsymbol {мг} [/ латекс], деленный на площадь [латекс] \ boldsymbol {A} [/ latex], на которой она расположена (площадь дна контейнера):
[латекс] \ boldsymbol {P \: =} [/ latex] [латекс] \ boldsymbol {\ frac {mg} {A}}. [/ Latex]
- Давление, связанное с весом жидкости, определяется по формуле
[латекс] \ boldsymbol {P = h \ rho {g}}, [/ latex]
где [латекс] \ boldsymbol {P} [/ latex] – давление, [latex] \ boldsymbol {h} [/ latex] – высота жидкости, [латекс] \ boldsymbol {\ rho} [/ latex] – плотность жидкости, а [латекс] \ boldsymbol {g} [/ latex] – ускорение свободного падения.
Концептуальные вопросы
1: Атмосферное давление оказывает на верхнюю часть тела большую силу (равную весу атмосферы над вашим телом – около 10 тонн), когда вы лежите на пляже и принимаете солнечные ванны.
 Почему ты можешь встать?
Почему ты можешь встать?2: Почему атмосферное давление падает с высотой быстрее, чем линейно?
3: По каким двум причинам в барометрах используется ртуть, а не вода?
4: На рисунке 4 показано, как мешки с песком, размещенные вокруг утечки за пределами речной дамбы, могут эффективно остановить поток воды под дамбой.Объясните, как небольшое количество воды внутри колонны, образованной мешками с песком, может уравновесить гораздо более крупный водоем позади дамбы.
Рис. 4. Поскольку уровень реки очень высок, она начала просачиваться под дамбу. Мешки с песком помещаются вокруг утечки, и удерживаемая ими вода поднимается до уровня реки, после чего вода перестает подниматься.5: Почему в Большом соленом озере сложно плавать под водой?
6: Имеется ли чистая сила на плотине из-за атмосферного давления? Поясните свой ответ.

7: Добавляет ли атмосферное давление давление газа в жестком резервуаре? На воздушном шарике? Когда вообще атмосферное давление , а не влияет на общее давление в жидкости?
8: Вы можете разбить крепкую винную бутылку, вонзив в нее пробку кулаком, но пробка должна давить прямо на жидкость, наполняющую бутылку – между пробкой и жидкостью не должно быть воздуха. Объясните, почему бутылка разбивается и почему нет, если между пробкой и жидкостью есть воздух.
Задачи и упражнения
1: На какой глубине ртути создается давление 1,00 атм?
2: Самые большие глубины океана на Земле находятся в Марианской впадине недалеко от Филиппин. Вычислите давление, создаваемое океаном на дне этой траншеи, учитывая ее глубину 11,0 км и допущение, что плотность морской воды постоянна на всем протяжении всей впадины.
3: Убедитесь, что единицей СИ для [latex] \ boldsymbol {h \ rho {g}} [/ latex] является [latex] \ boldsymbol {\ textbf {N / m} ^ 2}.
 2} [/ latex] область роговицы. а) Что это за давление в мм рт. (b) Находится ли это значение в пределах нормы для глазного давления?
2} [/ latex] область роговицы. а) Что это за давление в мм рт. (b) Находится ли это значение в пределах нормы для глазного давления?6: Какая сила действует на одну сторону листа бумаги размером 8,50 на 11,0 см атмосферой? Как бумага может выдержать такую силу?
7: Какое давление оказывается на дно бензобака шириной 0,500 м и длиной 0,900 м, который может вместить 50,0 кг бензина по весу бензина в нем, когда он заполнен?
8: Рассчитайте среднее давление, оказываемое на ладонь толкателя ядра при выстреле, если площадь контакта [латекс] \ boldsymbol {50.2 \: L / 2}, [/ latex] где [latex] \ boldsymbol {\ rho} [/ latex] – это плотность воды, [latex] \ boldsymbol {h} [/ latex] – ее глубина у плотины. , а [латекс] \ boldsymbol {L} [/ latex] – длина перемычки. Вы можете предположить, что поверхность плотины вертикальная. (Подсказка: рассчитайте среднее оказываемое давление и умножьте его на площадь контакта с водой (см.
Рисунок 5. Рисунок 5.)
Рисунок 5.)Глоссарий
- давление
- вес жидкости, деленный на площадь, поддерживающую ее
Решения
Задачи и упражнения
1:
0.2} [/ латекс]
9:
24,0 с.
Видео с вопросом: Расчет давления жидкости в точке на основе глубины точки и плотности жидкости
Стенограмма видео
Какое давление оказывает вода на глубине 2,5 метра? Используйте значение 1000 килограммов на кубический метр для плотности воды.
Итак, в этом примере скажем, что мы есть столб воды.И мы заинтересованы в давление, оказываемое этой водой на глубине 2,5 метра от поверхности. Итак, давайте скажем, что это точка здесь, в наша водная толща.
 Давление на данный момент мы
метка создается за счет веса всей воды, находящейся выше этой точки в нашем
столб воды. И, кстати, это не делает
Разница в ширине колонны. Какой бы широкой он ни был,
давление будет таким же, пока у нас есть эта определенная глубина, 2.5 метров.
Давление на данный момент мы
метка создается за счет веса всей воды, находящейся выше этой точки в нашем
столб воды. И, кстати, это не делает
Разница в ширине колонны. Какой бы широкой он ни был,
давление будет таким же, пока у нас есть эта определенная глубина, 2.5 метров.Чтобы ответить на этот вопрос о том, что давление, оказываемое водой в этот момент, мы можем вспомнить, что давление созданная жидкостью равна плотности этой жидкости, умноженной на ее высоту под поверхностью жидкости умножает на 𝑔 ускорение свободного падения. Напомним, что 𝑔 составляет 9,8 метра на во втором квадрате, когда дело доходит до плотности нашей жидкости, мы получаем это в нашем постановка задачи, 1000 килограммов на кубический метр.И еще нам дана высота ℎ, 2,5 метра. А это значит, что мы можем сразу перейти к вычисляя это давление.
 Это равно плотности
вода, умноженная на высоту под поверхностью воды, умноженную на ускорение
из-за силы тяжести.
Это равно плотности
вода, умноженная на высоту под поверхностью воды, умноженную на ускорение
из-за силы тяжести.А теперь, прежде чем мы умножим эти числа вместе, обратите внимание на участвующие единицы. Что все единицы в базовом блоке форма. Мы видим, что в числителе нашего единиц, у нас есть эти два фактора, расстояние в метрах.В знаменателе мы имеем метров в кубе. Это означает, что если бы мы умножили всех задействованных единиц вместе, мы получим общий результат в килограммах на метр второй в квадрате. Это эквивалентно ньютону на метр в квадрате. И мы можем вспомнить, что ньютон на метр в квадрате равен паскаль, которая является единицей измерения давления. Это означает, что единицы, которые мы закончим после того, как мы сделаем наш расчет, будут паскалями.Когда мы умножаем эти три вместе мы находим результат 24500 паскалей.
 Это давление со стороны
вода на этой глубине.
Это давление со стороны
вода на этой глубине.% PDF-1.4 % 26 0 obj> эндобдж xref 26 101 0000000016 00000 н. 0000002647 00000 н. 0000002727 00000 н. 0000002906 00000 н. 0000004085 00000 н. 0000004560 00000 н. 0000004921 00000 н. 0000005209 00000 н. 0000005243 00000 н. 0000005485 00000 н. 0000005740 00000 н. 0000005816 00000 н. 0000006532 00000 н. 0000007227 00000 н. 0000007385 00000 н. 0000008018 00000 н. 0000008551 00000 п. 0000009028 00000 н. 0000009618 00000 н. 0000010105 00000 п. 0000010553 00000 п. 0000013222 00000 п. 0000013358 00000 п. 0000013684 00000 п. 0000016719 00000 п. 0000016859 00000 п. 0000016992 00000 п. 0000017132 00000 п. 0000017272 00000 н. 0000017430 00000 п. 0000017585 00000 п. 0000017721 00000 п. 0000017864 00000 п. 0000018013 00000 п. 0000018146 00000 п. 0000018282 00000 п. 0000018440 00000 п. 0000018586 00000 п. 0000018738 00000 п. 0000018878 00000 п.
 0000019018 00000 п.
0000019158 00000 п.
0000019298 00000 п.
0000019438 00000 п.
0000019574 00000 п.
0000019714 00000 п.
0000019854 00000 п.
0000019990 00000 п.
0000020130 00000 н.
0000020266 00000 п.
0000020402 00000 п.
0000020542 00000 п.
0000020682 00000 п.
0000020825 00000 п.
0000020968 00000 н.
0000021108 00000 п.
0000021254 00000 п.
0000021403 00000 п.
0000021543 00000 п.
0000021686 00000 п.
0000021826 00000 п.
0000021966 00000 п.
0000022102 00000 п.
0000022242 00000 п.
0000022382 00000 п.
0000022522 00000 н.
0000022662 00000 п.
0000022802 00000 п.
0000022942 00000 п.
0000023082 00000 п.
0000023222 00000 п.
0000023368 00000 п.
0000023511 00000 п.
0000023657 00000 п.
0000023797 00000 п.
0000023947 00000 п.
0000024088 00000 п.
0000024229 00000 п.
0000024370 00000 п.
0000024507 00000 п.
0000024648 00000 п.
0000024789 00000 п.
0000024945 00000 п.
0000025082 00000 п.
0000025223 00000 п.
0000025364 00000 п.
0000025505 00000 п.
0000025646 00000 п.
0000019018 00000 п.
0000019158 00000 п.
0000019298 00000 п.
0000019438 00000 п.
0000019574 00000 п.
0000019714 00000 п.
0000019854 00000 п.
0000019990 00000 п.
0000020130 00000 н.
0000020266 00000 п.
0000020402 00000 п.
0000020542 00000 п.
0000020682 00000 п.
0000020825 00000 п.
0000020968 00000 н.
0000021108 00000 п.
0000021254 00000 п.
0000021403 00000 п.
0000021543 00000 п.
0000021686 00000 п.
0000021826 00000 п.
0000021966 00000 п.
0000022102 00000 п.
0000022242 00000 п.
0000022382 00000 п.
0000022522 00000 н.
0000022662 00000 п.
0000022802 00000 п.
0000022942 00000 п.
0000023082 00000 п.
0000023222 00000 п.
0000023368 00000 п.
0000023511 00000 п.
0000023657 00000 п.
0000023797 00000 п.
0000023947 00000 п.
0000024088 00000 п.
0000024229 00000 п.
0000024370 00000 п.
0000024507 00000 п.
0000024648 00000 п.
0000024789 00000 п.
0000024945 00000 п.
0000025082 00000 п.
0000025223 00000 п.
0000025364 00000 п.
0000025505 00000 п.
0000025646 00000 п. 0000025787 00000 п.
0000025928 00000 п.
0000026065 00000 п.
0000026212 00000 п.
0000026353 00000 п.
0000026503 00000 п.
0000026644 00000 п.
0000026785 00000 п.
0000026926 00000 п.
0000027067 00000 п.
0000027208 00000 п.
0000027436 00000 н.
0000002316 00000 н.
трейлер
] >>
startxref
0
%% EOF
126 0 obj> поток
xb“f`a`g“cg @
0000025787 00000 п.
0000025928 00000 п.
0000026065 00000 п.
0000026212 00000 п.
0000026353 00000 п.
0000026503 00000 п.
0000026644 00000 п.
0000026785 00000 п.
0000026926 00000 п.
0000027067 00000 п.
0000027208 00000 п.
0000027436 00000 н.
0000002316 00000 н.
трейлер
] >>
startxref
0
%% EOF
126 0 obj> поток
xb“f`a`g“cg @Что такое удельный вес? – Определение, формула, расчет и примеры – Видео и стенограмма урока
Что такое плотность?
Так что же такое плотность? Плотность объекта – это мера того, насколько он компактный или тяжелый в заданном объеме.3), или килограмм на литр (кг / л).
Вот два объекта с разной плотностью. Слева – объект, сильно забитый частицами. Это означает, что у него высокая плотность. Справа объект с низкой плотностью. Вы можете видеть, что частицы не упакованы плотно, но меньше частиц занимает тот же объем. Чтобы найти плотность объекта, мы делим его массу на его объем.
Например, возьмем объект объемом четыре литра и массой один килограмм.
 Мы подставляем эти числа в формулу плотности и обнаруживаем, что его плотность составляет 0,25 кг / л.
Мы подставляем эти числа в формулу плотности и обнаруживаем, что его плотность составляет 0,25 кг / л.Формула удельного веса
Формула удельного веса, учитывая, что эталонным веществом является вода, представляет собой плотность объекта, деленную на плотность воды. Здесь мы используем греческий символ Ро для обозначения плотности.
Удельный вес равен без единицы , потому что единицы числителя и знаменателя совпадают, поэтому они просто компенсируют друг друга.Давайте посмотрим на пример. Здесь плотность объекта 19 г / мл, плотность воды 1 г / мл. Мы отменяем единицу г / мл, потому что эта единица присутствует как в числителе, так и в знаменателе:
Плотность напрямую связана с массой объекта (единица измерения: обычно в граммах, но может быть измерена в килограммах или фунтах), поэтому удельный вес также можно определить, разделив массу объекта на массу объекта.
 вода.
вода.Сама масса напрямую связана с весом объекта, измеряемым в единицах, называемых ньютонами. Таким образом, удельный вес может быть решен путем деления веса объекта и воды.
Обратите внимание, что во всех этих единицах измерения одинаковы, поэтому в результате не будет единиц, поскольку они будут компенсировать друг друга.
Когда мы бросаем пенни в фонтаны с водой, чтобы загадать желание, пенни опускаются на дно.Это потому, что пенни плотнее воды. Если мы подставим копейки в формулу удельного веса в качестве нашего объекта, мы обнаружим, что удельный вес будет больше единицы. Когда удельный вес больше единицы, объект тонет, а когда удельный вес меньше единицы, объект будет плавать. Если удельный вес равен единице, это означает, что объект не будет ни тонуть, ни плавать – он будет зависать в жидкости.
Удельный вес – важный инструмент в ювелирном бизнесе.
 Представим, что Юлия-ювелир хочет изготовить украшение с золотым кольцом. Она покупает золото в Интернете и хочет знать наверняка, что это настоящий металл, а не другой металл, похожий на золото. Если золото настоящее, оно должно быть плотнее воды – плотность золота составляет 19 г / мл, а плотность воды – 1 г / мл. Удельный вес будет больше единицы, поэтому золото должно тонуть в воде и вытеснять определенный объем воды в зависимости от веса золота.
Представим, что Юлия-ювелир хочет изготовить украшение с золотым кольцом. Она покупает золото в Интернете и хочет знать наверняка, что это настоящий металл, а не другой металл, похожий на золото. Если золото настоящее, оно должно быть плотнее воды – плотность золота составляет 19 г / мл, а плотность воды – 1 г / мл. Удельный вес будет больше единицы, поэтому золото должно тонуть в воде и вытеснять определенный объем воды в зависимости от веса золота.Джули может поместить золото в определенное количество воды, понаблюдать, опускается ли оно на дно, и измерить количество вытесненной воды.Это скажет ей, настоящее ли это золото.
В других отраслях также используется удельный вес. Например, это может помочь экологическим группам решить, как лучше всего ликвидировать разливы нефти в озерах, реках или океанах. Нефть менее плотная, чем вода, поэтому удельный вес меньше единицы. Это означает, что он будет плавать на поверхности, и уборщики могут сосредоточиться на снятии масла с воды.
 Кроме того, при строительстве лодок важно знать удельный вес различных материалов. Различные материалы в разных объемах будут либо тонуть, либо плавать, и судостроители могут использовать удельный вес этих материалов, чтобы определить, будет ли конструкция судна удерживать его от погружения.
Кроме того, при строительстве лодок важно знать удельный вес различных материалов. Различные материалы в разных объемах будут либо тонуть, либо плавать, и судостроители могут использовать удельный вес этих материалов, чтобы определить, будет ли конструкция судна удерживать его от погружения.Расчет удельного веса
Давайте немного попрактикуемся в вычислении удельного веса.
Неизвестная жидкость имеет массу 36 г и объем 3 мл. Каков удельный вес этого объекта? Будет ли объект плавать или тонуть в воде? Плотность воды 1 г / мл.
Начнем с определения плотности объекта. Помните, что определение плотности требует деления массы на объем. Если масса 36 граммов, а объем 3 миллилитра, то плотность объекта составляет 12 граммов на миллилитр.Это означает, что удельный вес будет 12. Это больше единицы. Итак, да, объект утонет в воде.
Решение:
Вот еще одно упражнение. Вы нашли минерал с удельным весом 0,8, когда эталонным объектом является вода.
 Какая у этого минерала плотность? Минерал тонет или плавает в воде? Плотность воды 1 г / мл.
Какая у этого минерала плотность? Минерал тонет или плавает в воде? Плотность воды 1 г / мл.Половина из этого легко, потому что удельный вес меньше единицы.Объект будет плавать в воде. Чтобы найти плотность, мы должны проявить творческий подход. Мы начинаем с добавления известной нам информации к формуле удельного веса. Плотность объекта (x), деленная на плотность воды (1), дает нам удельный вес 0,8. Умножение обеих частей на единицу сократит знаменатель и даст нам значение x, нашей плотности. Наш объект имеет плотность 0,8 грамма.
Решение:
Как насчет еще одного?
Каков удельный вес объекта массой 180 фунтов на 70 фунтов воды? Будет ли он тонуть или плавать в данной массе воды? Помните, что мы можем рассчитать удельный вес, используя массы объекта и эталонной жидкости, поэтому нам не нужно ничего преобразовывать.Мы просто делим массу объекта – это 180 фунтов. – по массе воды, в которой он находится, составляет 70 фунтов.
 3.Поскольку плотность напрямую связана с массой, удельный вес также может быть определен из отношения массы объекта к массе воды или отношения веса объекта к весу воды. Удельный вес не имеет единиц.
3.Поскольку плотность напрямую связана с массой, удельный вес также может быть определен из отношения массы объекта к массе воды или отношения веса объекта к весу воды. Удельный вес не имеет единиц.Если значение удельного веса больше единицы, то объект тонет в воде, а если меньше единицы, то объект плавает в воде . Если удельный вес имеет значение, равное единице, то объект не будет ни тонуть, ни плавать.
Удельный вес является очень важным фактором в различных отраслях промышленности. Например, ювелиры могут использовать его для определения подлинности камней и минералов. Он также помогает судостроителям и строителям лодок в определении лучших материалов для строительства своих судов и направляет усилия по очистке разливов нефти или выявлению неизвестных артефактов в воде.
Как кажущаяся глубина и реальная глубина связаны с показателем преломления?
Как кажущаяся глубина и реальная глубина связаны с показателем преломления?- На рисунке показаны две непрозрачные чашки, A и B.
 Чашка A частично заполнена водой, а чашка B полностью заполнена водой. На дно каждой чашки кладется такая же монета.
Чашка A частично заполнена водой, а чашка B полностью заполнена водой. На дно каждой чашки кладется такая же монета. - При наблюдении с того же места монета в чашке A не видна, но монета в чашке B видна.
- При большем количестве воды в чашке изображение монеты в чашке B фактически находится выше, чем в чашке A. Это сделало монету, которую нельзя увидеть в чашке A, видимой в чашке B без изменения положения глаза.
- Это показывает, что положение изображения зависит от глубины воды.
- На рисунке показано, как наблюдатель видит монету в воде. Этот эффект вызван преломлением на поверхности воды.
- Лучи света, исходящие от монеты, отклоняются от нормы при выходе из воды.
- Когда они достигают глаза, кажется, что они исходят от виртуальной монеты, которая находится над реальной монетой.
- Кажущаяся глубина – это расстояние виртуального изображения, I от поверхности воды .
- Реальная глубина – это расстояние до реального объекта, O от поверхности воды .

- Отношение показателя преломления n к реальной глубине и кажущейся глубине определяется по формуле:
Люди также спрашивают
Эксперимент на реальной и кажущейся глубинеЦель: Найти связь между реальной глубиной глубина и видимая глубина объекта, помещенного в воду.
Задача: Как видимая глубина объекта в воде зависит от его реальной глубины?
Гипотеза: Когда реальная глубина объекта в воде увеличивается, его видимая глубина также увеличивается.Переменные:
(a) Управляемая переменная: реальная глубина, d 1
(b) Реагирующая переменная: кажущаяся глубина, d 2
(c) Фиксированная переменная: плотность воды
Материалы: 2 стальных штифта, 1 пробка, кувшин с водой
Аппарат: Высокий стакан, измерительная линейка, подставка для реторты
Метод:- Аппарат настроен, как показано на рисунке.

- Стальной штифт (штифт O) помещается на дно высокого стакана.
- Другой стальной штифт закреплен на пробке, удерживаемой зажимом ретортной стойки. Он используется как поисковый штифт (Pin l).
- Высокий стакан наполнен водой на высоту d 1 = 20 см (реальная глубина).
- Изображение стальной иглы показано вертикально над краем стакана.
- Поисковый штифт, который находится рядом с стаканом, затем перемещается вверх или вниз, пока он не будет выровнен с изображением стального штифта, видимого через воду.
- Положение изображения d 2 (видимая глубина) измеряется с помощью линейки метра.
- Шаги с 4 по 7 повторяются с d 1 = 30 см, 40 см, 50 см и 60 см. Результаты занесены в таблицу.
- Построен график зависимости реальной глубины (d 1 ) от видимой глубины (d 2 ).
Результаты:
1. Табулирование результатов.2. График реальной глубины (d 1 ) в зависимости от кажущейся глубины (d 2 ).

Обсуждение:
- Видимая глубина всегда меньше реальной глубины.
- Когда реальная глубина увеличивается, кажущаяся глубина также увеличивается.
- График реальной глубины d 1 от видимой глубины d 2 представляет собой график с прямой линией, проходящей через начало координат. Это показывает, что видимая глубина прямо пропорциональна реальной глубине.
- Градиент графика реальной глубины d 1 от видимой глубины d 2 – показатель преломления воды.
Выводы:
- Результаты эксперимента подтверждают гипотезу.
- Отношение реальной глубины к кажущейся глубине – это показатель преломления воды.
- Рыба на дне пруда находится на расстоянии 1,2 м от поверхности воды. Какая глубина водоема?
[Показатель преломления воды = 1,33]
Раствор:
- На рисунке изображен мальчик, стоящий в бассейне.

- Давление — это физическая величина, равная отношению силы давления к площади поверхности.


 Т.н WGS-84 Gravity formula.
Т.н WGS-84 Gravity formula.
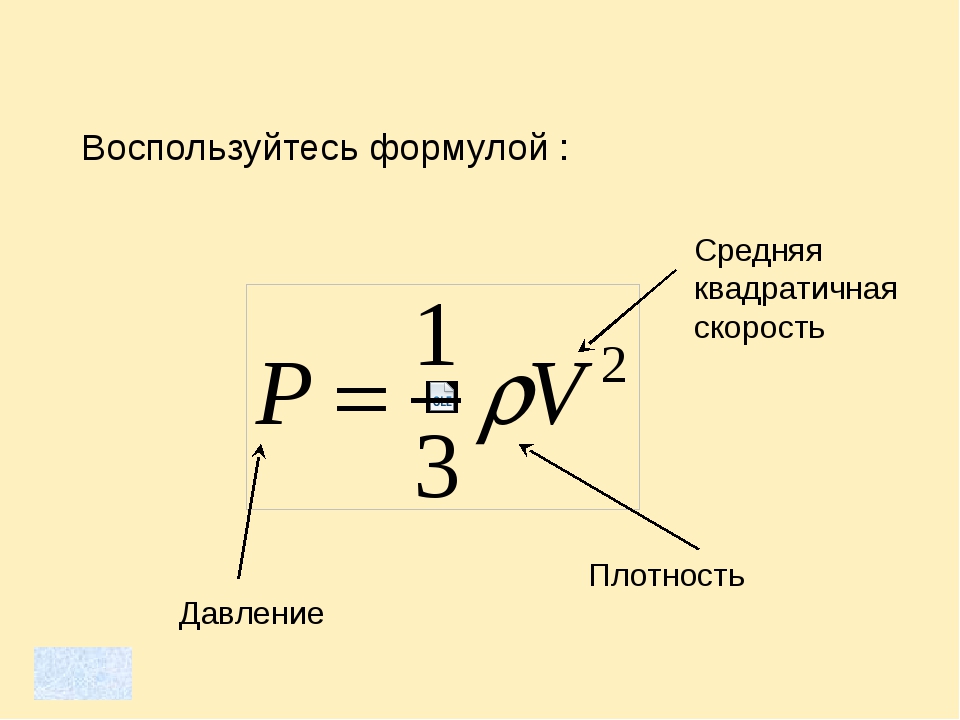
 Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.
Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.
 Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.
Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.
 168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.
168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.

 Значит, и среднее давление по всем направлениям одинаково.
Значит, и среднее давление по всем направлениям одинаково. Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.
Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.
 Закон Паскаля
Закон Паскаля Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки.
Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки. Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.
Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.
 hydros — вода, station — неподвижный).
hydros — вода, station — неподвижный).


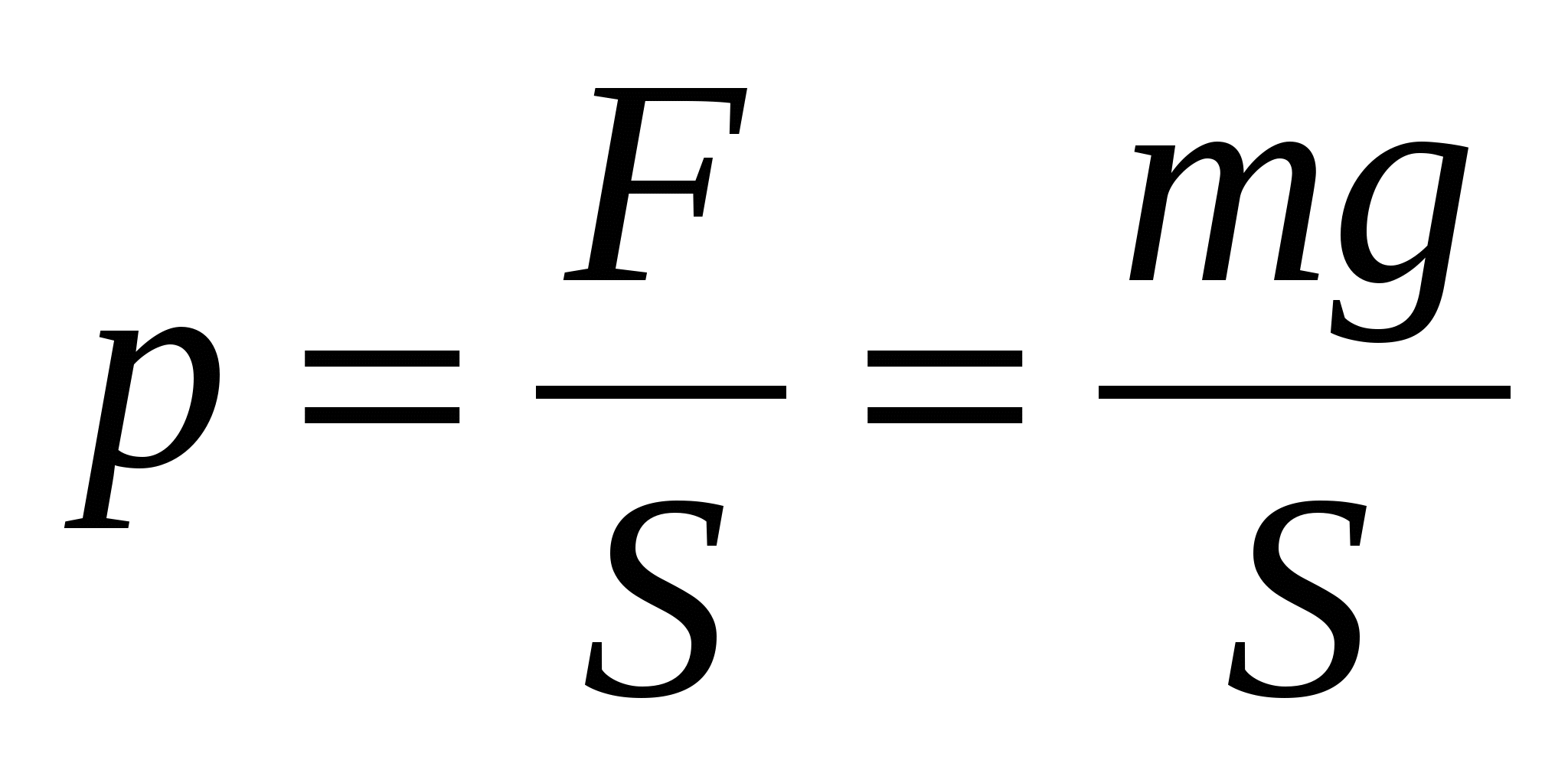 е.
е.
 е. откуда Используя свойства пропорции, запишем окончательно:
е. откуда Используя свойства пропорции, запишем окончательно: Почему?
Почему? На высоте км плотность а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность
На высоте км плотность а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность  Устройства для сжатия различных газов называют компрессорами.
Устройства для сжатия различных газов называют компрессорами.

 Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб.
Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб. Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм):
Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм): в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела.
в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела. На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия.
На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия. рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.
рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.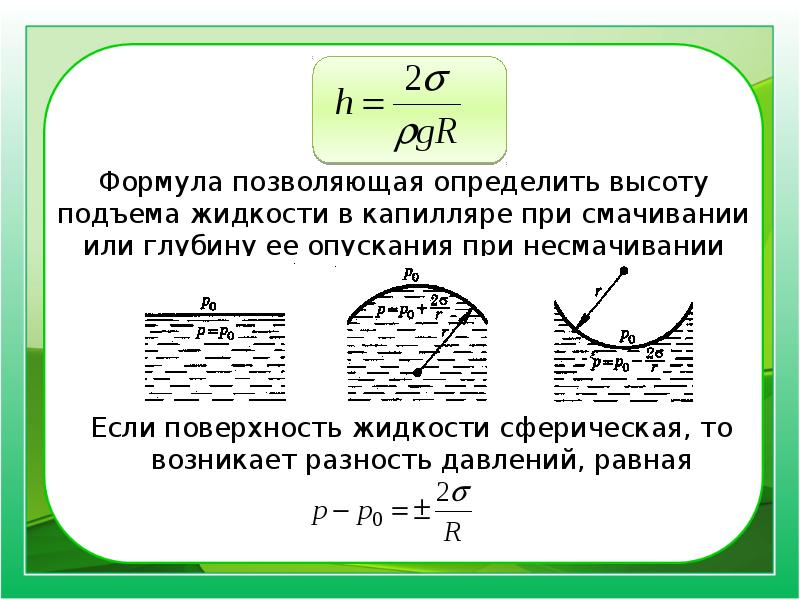 Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа).
Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа). Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).
Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).
 Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:

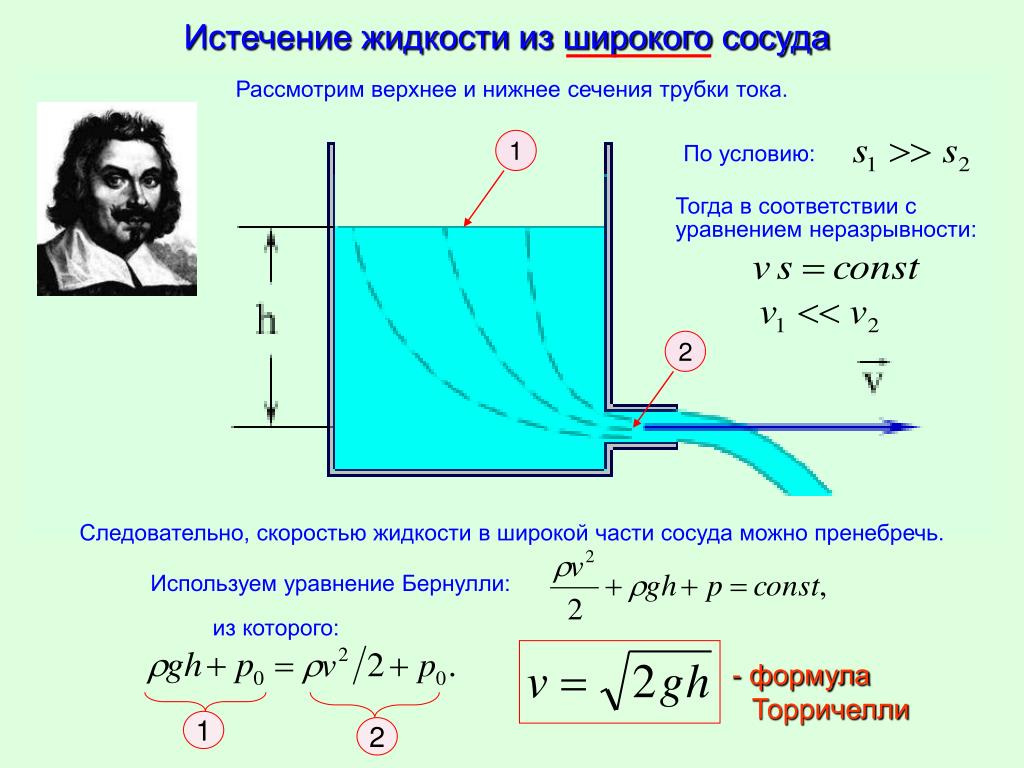 (Приложение, рисунок 2.1 (I
способ), рисунок 2.1 (II способ)
(Приложение, рисунок 2.1 (I
способ), рисунок 2.1 (II способ) Сформулируйте законы отражения света.
Сформулируйте законы отражения света. n1 =
n1 =
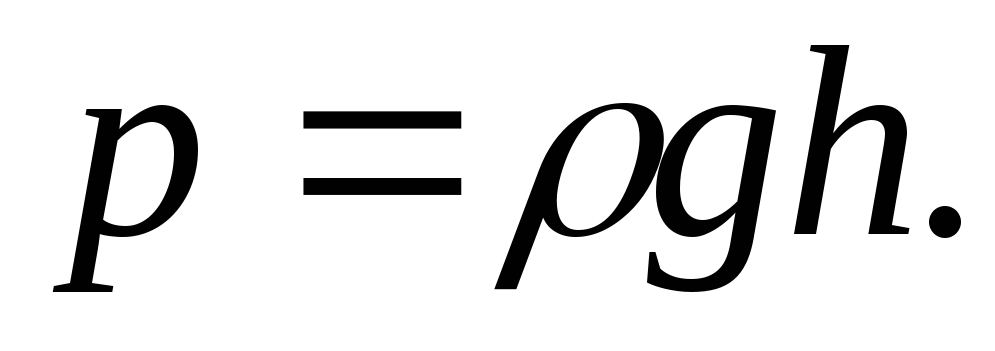
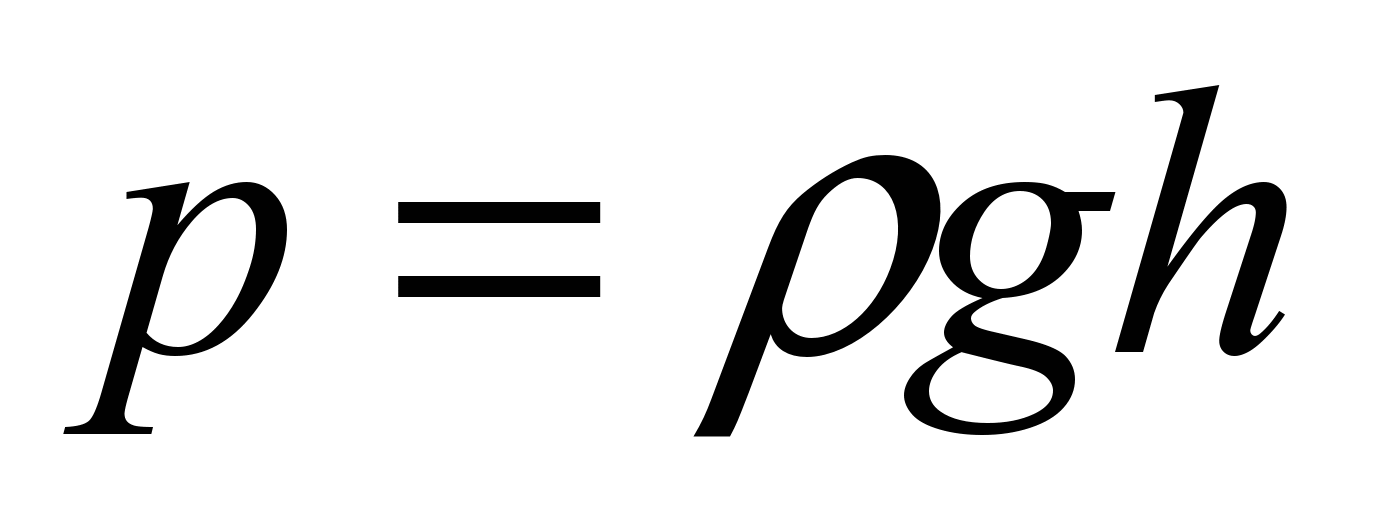
 Какие
недостатки зрения исправляют эти очки?
Какие
недостатки зрения исправляют эти очки?

 Г = .
Г = . Б
Б Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.
Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным. В этом заключается “гидростатический парадокс”.
В этом заключается “гидростатический парадокс”. Выигрыша в работе гидравлический пресс не дает.
Выигрыша в работе гидравлический пресс не дает. Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.
Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения. Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда – результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.
Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда – результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.
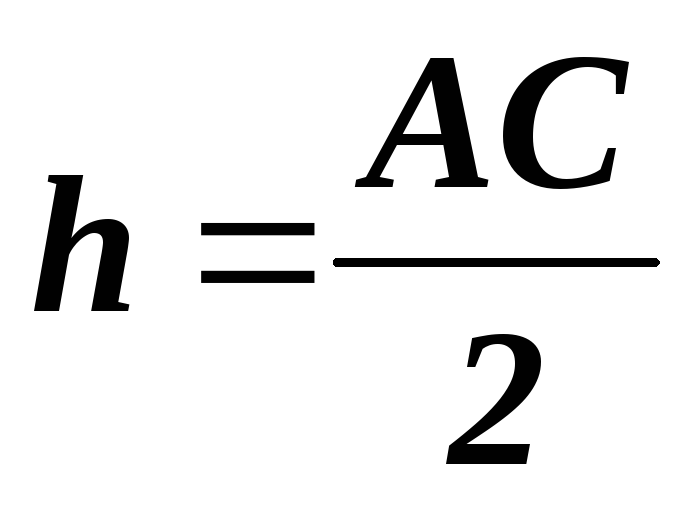 Из небольшого отверстия в боковой стенке сосуда вытекает струйка воды. Что произойдет с этой струёй, если сосуд начнет свободно падать? Сопротивлением окружающего воздуха пренебречь.
Из небольшого отверстия в боковой стенке сосуда вытекает струйка воды. Что произойдет с этой струёй, если сосуд начнет свободно падать? Сопротивлением окружающего воздуха пренебречь.
 В самом глубоком месте плотность воды увеличивается лишь на 5 процентов. А чтобы в ней плавало железо необходимо уплотнить ее в 8 раз! Не может быть ни малейшего сомнения, что затонувшие суда покоятся на дне океана!
В самом глубоком месте плотность воды увеличивается лишь на 5 процентов. А чтобы в ней плавало железо необходимо уплотнить ее в 8 раз! Не может быть ни малейшего сомнения, что затонувшие суда покоятся на дне океана! Поскольку углы малы, я могу аппроксимировать закон Снеллиуса:
Поскольку углы малы, я могу аппроксимировать закон Снеллиуса: 2 \ theta}} \ label {eq: 1.4.3} \]
2 \ theta}} \ label {eq: 1.4.3} \]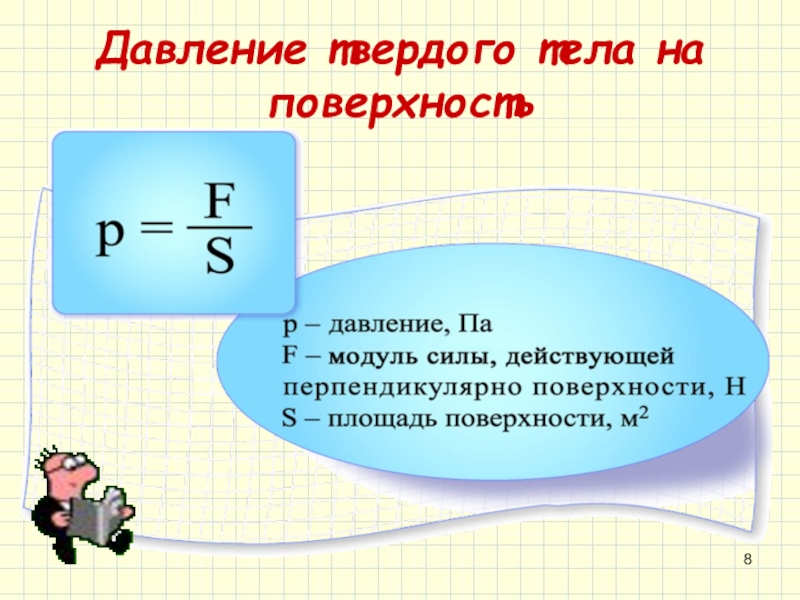 Если смотреть на точку на дне пруда под углом к поверхности, а не перпендикулярно ей, возникает дополнительная аберрация, называемая «астигматизмом». Это будет обсуждаться в главе 4.
Если смотреть на точку на дне пруда под углом к поверхности, а не перпендикулярно ей, возникает дополнительная аберрация, называемая «астигматизмом». Это будет обсуждаться в главе 4. Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.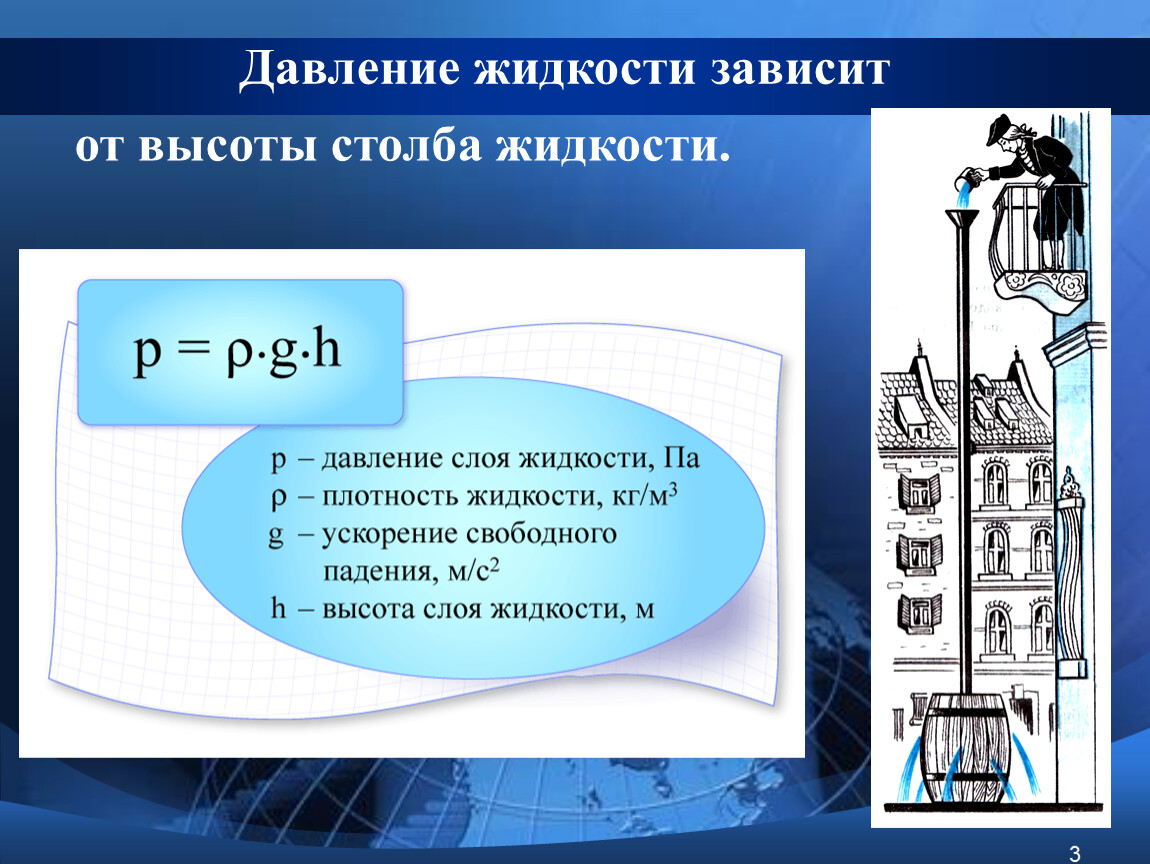 P = ρAhgA. размер 12 {P = {{left (ρ ital “Ah” right) g} над {A}}} {}
P = ρAhgA. размер 12 {P = {{left (ρ ital “Ah” right) g} над {A}}} {} Пример 11.4 иллюстрирует эту ситуацию.
Пример 11.4 иллюстрирует эту ситуацию.
 F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
размер 12 {F = \ (3 “.” “92” умножить на “10” rSup {размер 8 {5}} “” Н / м “rSup {размер 8 {2}} \) \ (4″.”” 00 “умножить на” 10 “rSup {размер 8 {4}}` m rSup {размер 8 {2}} \)} {} #
“” = 1 “.” “57” умножить на “10” rSup {size 8 {“10″}} `N”. ” {}
}} {}
F = (3,92 × 105 Н / м2) (4,00 × 104 м2) = 1,57 × 1010 Н. выравнивание {stack {
размер 12 {F = \ (3 “.” “92” умножить на “10” rSup {размер 8 {5}} “” Н / м “rSup {размер 8 {2}} \) \ (4″.”” 00 “умножить на” 10 “rSup {размер 8 {4}}` m rSup {размер 8 {2}} \)} {} #
“” = 1 “.” “57” умножить на “10” rSup {size 8 {“10″}} `N”. ” {}
}} {} Глубина, чтобы уравновесить увеличивающуюся силу из-за увеличения давления.
Глубина, чтобы уравновесить увеличивающуюся силу из-за увеличения давления. “01” умножить на “10” rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)
“01” умножить на “10” rSup {size 8 {5}} `N} {}, что эквивалентно 1 атм1 атм. (См. Рисунок 11.11.)
 Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой. размер 12 {h = {{1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” N / m “rSup {size 8 {2}}} больше {\ (1”. “” 00 “умножить на” 10 “rSup {size 8 { 3}} `” кг / м “rSup {размер 8 {3}} \) \ (9”. “” 80 “` “” м / с “rSup {размер 8 {2}} \)}} =” 10 ” “.” 3`m} {}
размер 12 {h = {{1 “.” “01” умножить на “10” rSup {размер 8 {5}} “” N / m “rSup {size 8 {2}}} больше {\ (1”. “” 00 “умножить на” 10 “rSup {size 8 { 3}} `” кг / м “rSup {размер 8 {3}} \) \ (9”. “” 80 “` “” м / с “rSup {размер 8 {2}} \)}} =” 10 ” “.” 3`m} {}
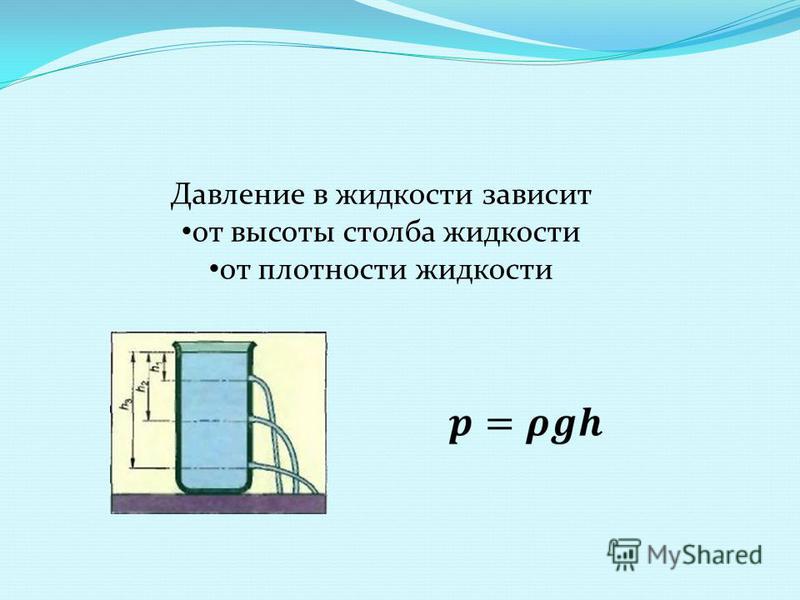 Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.
Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.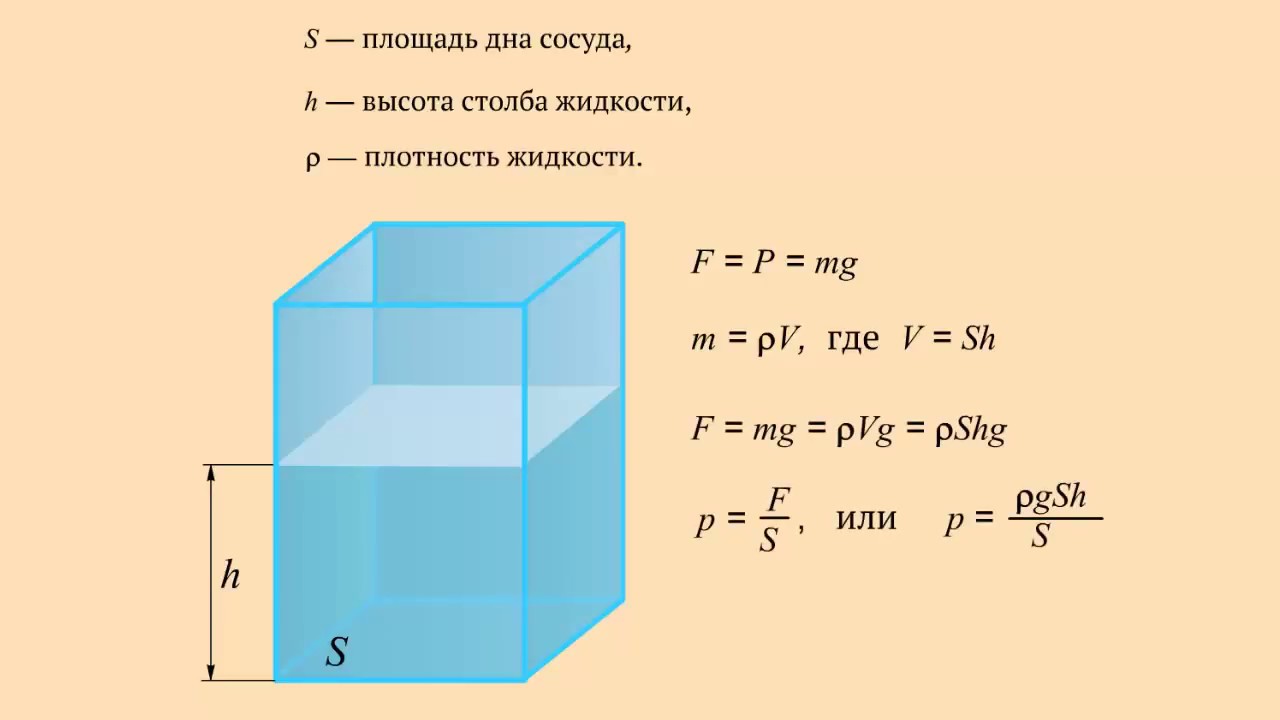 [/ латекс]
[/ латекс] Пример 2 иллюстрирует эту ситуацию.
Пример 2 иллюстрирует эту ситуацию. [/ Latex]
[/ Latex] 5 \ textbf {N}}, [/ latex] эквивалент [latex] \ boldsymbol {1 \ textbf {atm}}. [/ Latex] (см. Рисунок 3.)
5 \ textbf {N}}, [/ latex] эквивалент [latex] \ boldsymbol {1 \ textbf {atm}}. [/ Latex] (см. Рисунок 3.) 3} [/ latex] – примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.
3} [/ latex] – примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой. Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы.Таким образом, общее давление на глубине 10,3 м составляет 2 атм – половина от воды выше и половина от воздуха выше. В главе 11.5 «Принцип Паскаля» мы увидим, что давление жидкости всегда увеличивается таким образом.
Это кажется логичным, поскольку необходимо поддерживать вес воды и атмосферы.Таким образом, общее давление на глубине 10,3 м составляет 2 атм – половина от воды выше и половина от воздуха выше. В главе 11.5 «Принцип Паскаля» мы увидим, что давление жидкости всегда увеличивается таким образом. Почему ты можешь встать?
Почему ты можешь встать?
 2} [/ latex] область роговицы. а) Что это за давление в мм рт. (b) Находится ли это значение в пределах нормы для глазного давления?
2} [/ latex] область роговицы. а) Что это за давление в мм рт. (b) Находится ли это значение в пределах нормы для глазного давления?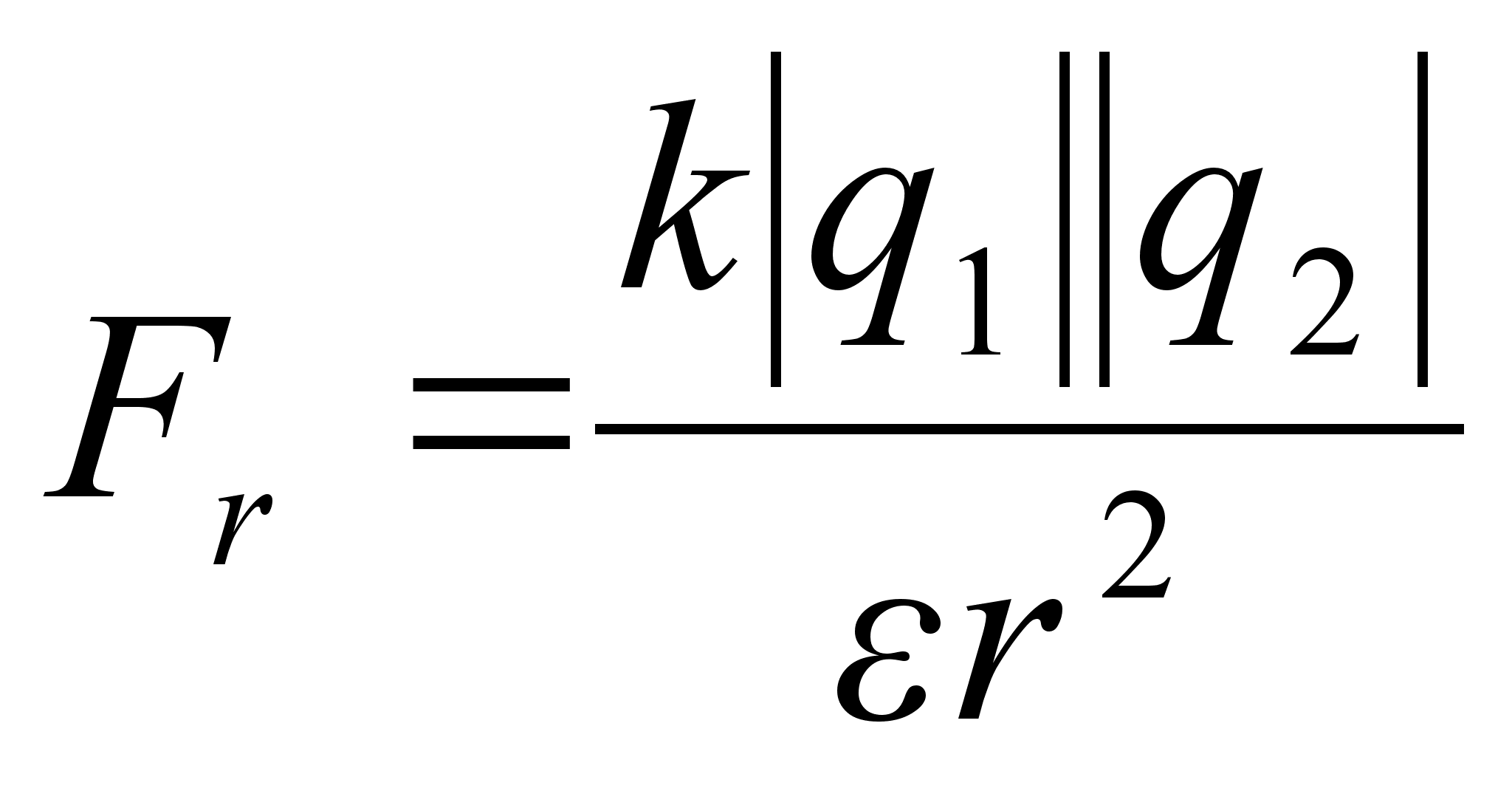 Рисунок 5.)
Рисунок 5.) Давление на данный момент мы
метка создается за счет веса всей воды, находящейся выше этой точки в нашем
столб воды. И, кстати, это не делает
Разница в ширине колонны. Какой бы широкой он ни был,
давление будет таким же, пока у нас есть эта определенная глубина, 2.5 метров.
Давление на данный момент мы
метка создается за счет веса всей воды, находящейся выше этой точки в нашем
столб воды. И, кстати, это не делает
Разница в ширине колонны. Какой бы широкой он ни был,
давление будет таким же, пока у нас есть эта определенная глубина, 2.5 метров. Это равно плотности
вода, умноженная на высоту под поверхностью воды, умноженную на ускорение
из-за силы тяжести.
Это равно плотности
вода, умноженная на высоту под поверхностью воды, умноженную на ускорение
из-за силы тяжести.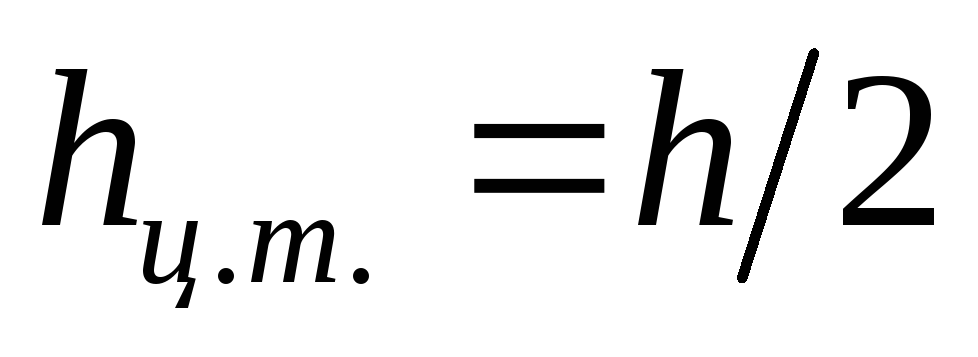 Это давление со стороны
вода на этой глубине.
Это давление со стороны
вода на этой глубине.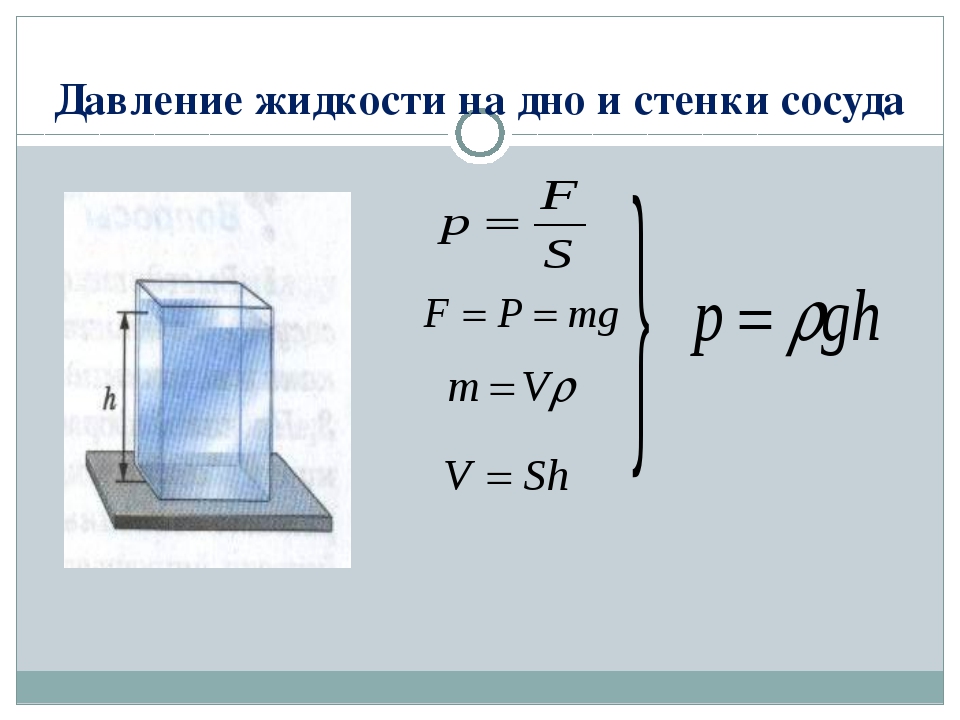 0000019018 00000 п.
0000019158 00000 п.
0000019298 00000 п.
0000019438 00000 п.
0000019574 00000 п.
0000019714 00000 п.
0000019854 00000 п.
0000019990 00000 п.
0000020130 00000 н.
0000020266 00000 п.
0000020402 00000 п.
0000020542 00000 п.
0000020682 00000 п.
0000020825 00000 п.
0000020968 00000 н.
0000021108 00000 п.
0000021254 00000 п.
0000021403 00000 п.
0000021543 00000 п.
0000021686 00000 п.
0000021826 00000 п.
0000021966 00000 п.
0000022102 00000 п.
0000022242 00000 п.
0000022382 00000 п.
0000022522 00000 н.
0000022662 00000 п.
0000022802 00000 п.
0000022942 00000 п.
0000023082 00000 п.
0000023222 00000 п.
0000023368 00000 п.
0000023511 00000 п.
0000023657 00000 п.
0000023797 00000 п.
0000023947 00000 п.
0000024088 00000 п.
0000024229 00000 п.
0000024370 00000 п.
0000024507 00000 п.
0000024648 00000 п.
0000024789 00000 п.
0000024945 00000 п.
0000025082 00000 п.
0000025223 00000 п.
0000025364 00000 п.
0000025505 00000 п.
0000025646 00000 п.
0000019018 00000 п.
0000019158 00000 п.
0000019298 00000 п.
0000019438 00000 п.
0000019574 00000 п.
0000019714 00000 п.
0000019854 00000 п.
0000019990 00000 п.
0000020130 00000 н.
0000020266 00000 п.
0000020402 00000 п.
0000020542 00000 п.
0000020682 00000 п.
0000020825 00000 п.
0000020968 00000 н.
0000021108 00000 п.
0000021254 00000 п.
0000021403 00000 п.
0000021543 00000 п.
0000021686 00000 п.
0000021826 00000 п.
0000021966 00000 п.
0000022102 00000 п.
0000022242 00000 п.
0000022382 00000 п.
0000022522 00000 н.
0000022662 00000 п.
0000022802 00000 п.
0000022942 00000 п.
0000023082 00000 п.
0000023222 00000 п.
0000023368 00000 п.
0000023511 00000 п.
0000023657 00000 п.
0000023797 00000 п.
0000023947 00000 п.
0000024088 00000 п.
0000024229 00000 п.
0000024370 00000 п.
0000024507 00000 п.
0000024648 00000 п.
0000024789 00000 п.
0000024945 00000 п.
0000025082 00000 п.
0000025223 00000 п.
0000025364 00000 п.
0000025505 00000 п.
0000025646 00000 п. 0000025787 00000 п.
0000025928 00000 п.
0000026065 00000 п.
0000026212 00000 п.
0000026353 00000 п.
0000026503 00000 п.
0000026644 00000 п.
0000026785 00000 п.
0000026926 00000 п.
0000027067 00000 п.
0000027208 00000 п.
0000027436 00000 н.
0000002316 00000 н.
трейлер
] >>
startxref
0
%% EOF
126 0 obj> поток
xb“f`a`g“cg @
0000025787 00000 п.
0000025928 00000 п.
0000026065 00000 п.
0000026212 00000 п.
0000026353 00000 п.
0000026503 00000 п.
0000026644 00000 п.
0000026785 00000 п.
0000026926 00000 п.
0000027067 00000 п.
0000027208 00000 п.
0000027436 00000 н.
0000002316 00000 н.
трейлер
] >>
startxref
0
%% EOF
126 0 obj> поток
xb“f`a`g“cg @ Мы подставляем эти числа в формулу плотности и обнаруживаем, что его плотность составляет 0,25 кг / л.
Мы подставляем эти числа в формулу плотности и обнаруживаем, что его плотность составляет 0,25 кг / л. вода.
вода.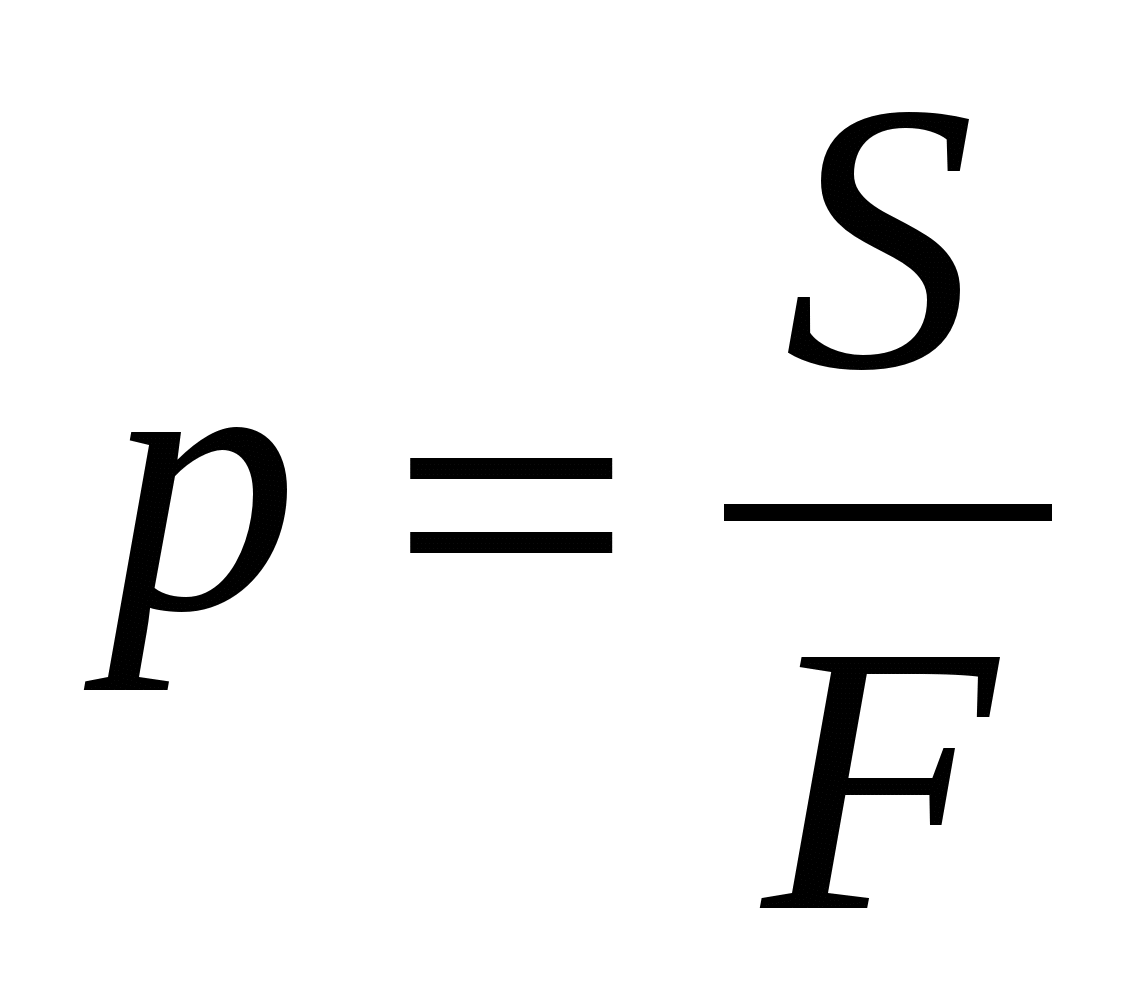 Представим, что Юлия-ювелир хочет изготовить украшение с золотым кольцом. Она покупает золото в Интернете и хочет знать наверняка, что это настоящий металл, а не другой металл, похожий на золото. Если золото настоящее, оно должно быть плотнее воды – плотность золота составляет 19 г / мл, а плотность воды – 1 г / мл. Удельный вес будет больше единицы, поэтому золото должно тонуть в воде и вытеснять определенный объем воды в зависимости от веса золота.
Представим, что Юлия-ювелир хочет изготовить украшение с золотым кольцом. Она покупает золото в Интернете и хочет знать наверняка, что это настоящий металл, а не другой металл, похожий на золото. Если золото настоящее, оно должно быть плотнее воды – плотность золота составляет 19 г / мл, а плотность воды – 1 г / мл. Удельный вес будет больше единицы, поэтому золото должно тонуть в воде и вытеснять определенный объем воды в зависимости от веса золота. Кроме того, при строительстве лодок важно знать удельный вес различных материалов. Различные материалы в разных объемах будут либо тонуть, либо плавать, и судостроители могут использовать удельный вес этих материалов, чтобы определить, будет ли конструкция судна удерживать его от погружения.
Кроме того, при строительстве лодок важно знать удельный вес различных материалов. Различные материалы в разных объемах будут либо тонуть, либо плавать, и судостроители могут использовать удельный вес этих материалов, чтобы определить, будет ли конструкция судна удерживать его от погружения. Какая у этого минерала плотность? Минерал тонет или плавает в воде? Плотность воды 1 г / мл.
Какая у этого минерала плотность? Минерал тонет или плавает в воде? Плотность воды 1 г / мл. 3.Поскольку плотность напрямую связана с массой, удельный вес также может быть определен из отношения массы объекта к массе воды или отношения веса объекта к весу воды. Удельный вес не имеет единиц.
3.Поскольку плотность напрямую связана с массой, удельный вес также может быть определен из отношения массы объекта к массе воды или отношения веса объекта к весу воды. Удельный вес не имеет единиц. Чашка A частично заполнена водой, а чашка B полностью заполнена водой. На дно каждой чашки кладется такая же монета.
Чашка A частично заполнена водой, а чашка B полностью заполнена водой. На дно каждой чашки кладется такая же монета. 


