несколько подходов и примеры проблем
В статье обсуждаются несколько подходов и некоторые примеры проблем о том, как вычислить массу по гравитационной силе.
Каждый объект с массой во Вселенной оказывает гравитационное воздействие на другой. Вот почему сила тяжести прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Узнайте больше о Как рассчитать массу по силе и расстоянию.
Как рассчитать массу по гравитационной силе, используя второй закон движения НьютонаКак рассчитать массу по гравитационной силе?Рассчитаем массу, используя второй закон движения Ньютона:
Во втором законе движения Ньютон описывает, что сила действует на объект с ненулевой массой, чтобы ускорить его в том же направлении. Гравитационная сила – это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил которые действуют на тела. гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ма ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется в соответствии со вторым законом движения. Ускорение, вызванное силой тяжести, постоянно, называется ускорение силы тяжести ‘грамм’. Поскольку гравитация всегда действует на нас, возникла идея нашего «веса» как «mg», который включает нашу массу m и ускорение «a». По этой причине гравитационную силу также называют силой тяжести. сила веса.Сила тяжести как сила веса
(Кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает следующий вид:
Fg = мг …………………………. (1)
Согласно уравнениям (*) и (1),
Чтобы поднять более тяжелое тело, мы должны создать восходящую силу (ма), превышающую силу тяжести (мг).
Поскольку g имеет постоянное значение 9.8 м / с2, гравитационная сила Fg зависит только от массы объекта m. Чем массивнее объект, тем больше силы требуется для его ускорения.
Если к объекту приложена сила тяжести, мы можем вычислить его массу по формуле второго закона движения Ньютона..
Узнайте больше о Законы движения Ньютона.
Сила тяжести, действующая на бегающую в парке девушку, равна 490. Вычислите массу девушки.Данный:
Fg = 490 Н
g = 9.8 м / с
Найти: м =?
Формула:
F = ma
Решение:
Масса девушки рассчитывается с помощью Второй закон движения Ньютона формула,
F = ma
Компания сила гравитации дан кем-то,
Fg = мг
m=Fg/g
м=490/9. 8
8
m = 50 кг …………………………………. а)
Масса бегущей в парке девушки 50 кг.
Как найти массу с гравитационной силой и радиусом?Давайте вычислим массу с гравитационной силой, используя закон тяготения Ньютона следующим образом:
Закон тяготения обнаруживает, что гравитационная сила между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами масс. Если второй объект – Земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону всемирного тяготения Ньютона,
Fg=G(мМ/р2)……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке, в основном в его центральной точке, называемой его центр масс (см). Радиус r измеряет расстояние или разделение между центрами масс двух объектов.
Небольшая масса в 1 кг, разделенная радиусом 1, испытывала небольшую гравитационную силу 6. 67 x 10-11 Нм.2/ кг2, совместимый с каждым объектом. Следовательно, это постоянное значение является значением постоянной пропорциональности в законе всемирного тяготения, также называемой величиной Универсальная гравитационная постоянная G.
67 x 10-11 Нм.2/ кг2, совместимый с каждым объектом. Следовательно, это постоянное значение является значением постоянной пропорциональности в законе всемирного тяготения, также называемой величиной Универсальная гравитационная постоянная G.
Проще вычислить Fg между объектом и Землей как планетой с фиксированной массой M = 5.98 x 1024 кг, а также фиксированный радиус r от центра земли, r = 6.38 x 106m
Сила тяжести, действующая на девушку, бегающую трусцой в парке, равна 490. Вычислите массу девушки, используя закон всемирного тяготения Ньютона.Данный:
Fg = 490 Н
М = 5.98 х 1024 kg
г = 6.38 х 106m
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Решение:
Масса девушки рассчитывается по Закон всемирного тяготения Ньютона является,
Fg=G(мМ/р2)
Переставляем на массу m,
м=Fgr2/ГМ
Подставляя все значения,
Из (а) и (б) мы заметили расчетная масса с использованием второго закона Ньютона и формулы закона всемирного тяготения такая же.
Закон всемирного тяготения может применяться к двум объектам, имеющим одинаковые или разные массы.Сила тяжести между двумя объектами
имея разные массы
(Кредит: Shutterstock)
Данный:
Fg = 3 x 10-7 N
г = 1 м
m1 = 60 кг
G = 6.67 х 10-11 nm2/ кг2
Найти: м2 =?
Формула:
Fg=G(м1m2/r2)
Решение:
Масса коллеги рассчитывается по формуле Закон всемирного тяготения Ньютона является,
Fg=G(м1m2/r2)
Перестановка на массу m2,
m2=Fgr2/Гм1
Подставляя все значения,
Масса вашего коллеги 75 кг.
Рассчитаем массу с гравитационной силой, используя центростремительная сила формула следующим образом:
Когда объект движется по кругу, его скорость постоянно меняется в зависимости от его направления. Направление ускорения – к центру, вызванное центростремительной силой. Поскольку масса всего объекта сосредоточена в его центре, мы можем рассчитать ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона движения Ньютона.
Поскольку ускорение – это круговой путь, нам нужно учитывать радиус; вот почему ускорение становится
v2/r
Следовательно, согласно уравнению (*) центростремительная сила определяется как
Fc=мв2/r
Центростремительная сила – это центристская сила который действует на объект, чтобы двигаться по кругу к его центру. Земля оказывает центростремительное сила, действующая на спутник, чтобы поддерживать его круговое движение вокруг. Центростремительная сила Земли на Спутнике
Земля оказывает центростремительное сила, действующая на спутник, чтобы поддерживать его круговое движение вокруг. Центростремительная сила Земли на Спутнике
Данный:
Fg = 500 Н
Fc = 200 Н
v = 20 м / с
M = масса Земли = 5.98 x 1024 kg
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Fc=мв2/r
Решения:
Масса спутника рассчитывается по формуле закон всемирного тяготения Ньютона,
Fg=G(мМ/р2)
Компания центростремительная сила на спутнике есть,
Fc=мв2/r
Решая формулу для радиуса r,
г=мв2/Fc
Подставляя вышеприведенное уравнение в закон всемирного тяготения Ньютона, получаем
Fg=Fc2[ГМ/мв4]
Решая массу m,
Подставляя все значения,
м=159.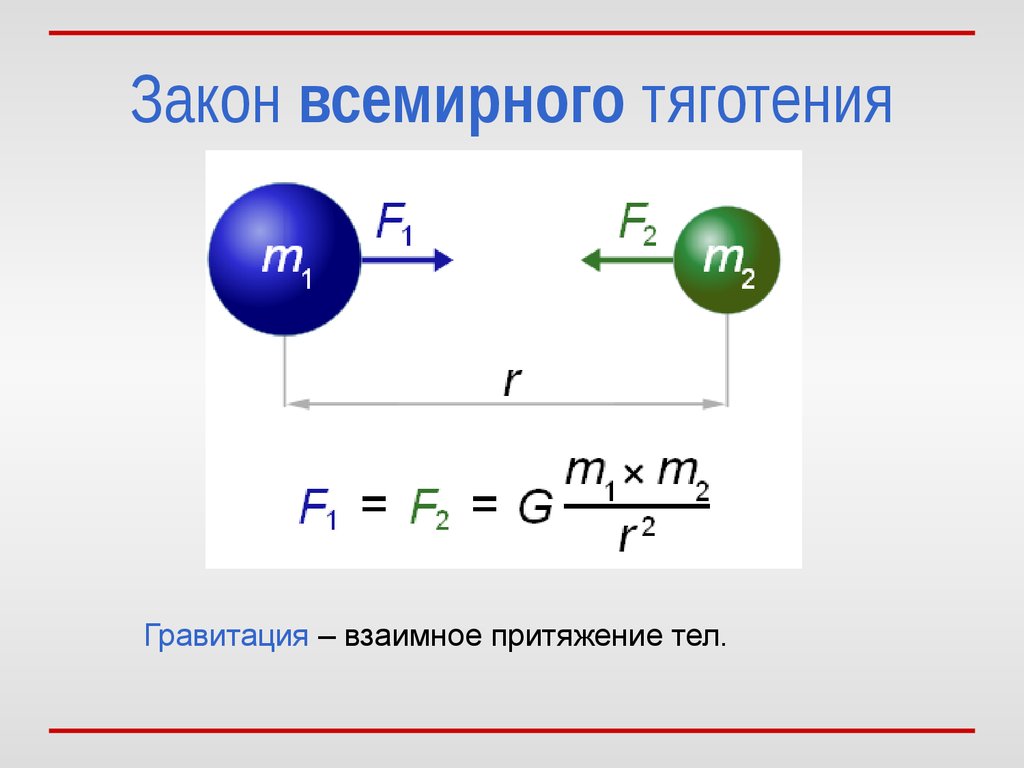 4/8
4/8
м = 19.94 \ примерно 20 кг
Масса спутника, движущегося вокруг Земли, составляет 20 кг.
Закон всемирного тяготения: формула, определение
Содержание
- 1 Что такое всемирное тяготение
- 2 Природа силы всемирного тяготения
- 3 История открытия закона всемирного тяготения
- 4 Вывод закона всемирного тяготения
- 4.1 Притяжение тел к земле
- 4.2 Притяжение Земли и Луны
- 4.3 Ускорение в формуле всемирного тяготения
- 4.4 Второй и третий законы Ньютона в выводе формулы тяготения
- 4.5 Формула всемирного тяготения
- 4.6 В чём измеряется сила притяжения
- 4.7 Гравитационная постоянная
- 4.7.1 Опыт Кавендиша
- 5 Инфографика-вывод закона всемирного тяготения
- 6 Сила тяжести как частный случай закона всемирного тяготения
- 7 В каких случаях справедлив закон всемирного тяготения
- 8 Применение закона всемирного тяготения
- 8.1 Открытие планет с использованием закона всемирного тяготения
- 9 Закон всемирного тяготения.
 Примеры из жизни
Примеры из жизни - 10 Границы применимости
- 11 Дальнейшее развитие
- 12 Выводы
Тяготение – привычное явление для каждого живого существа на Земле, на первый взгляд, не требующее объяснений. Описывает это явление закон всемирного тяготения. Однако стоит углубиться в данную тему чуть больше, так сразу возникает ряд вопросов, для ответа на которые потребуются постулаты классической механики Ньютона, а также теории относительности и базирующейся на ней теории квантовой гравитации.
Что такое всемирное тяготение
Земля — это большой магнит, который притягивает к себе всё, что находится рядом: и карандаш, случайно выскользнувший из пальцев рук, и астероид, пролетающий мимо. С начала развития науки учёные давали своё видение и определение явлению всемирного тяготения, но только в 1687 году в фундаментальной работе Исаака Ньютона «Математические начала натуральной философии» было доказано его существование и воздействие на окружающие объекты.
математические начала натуральной философии
Интересный факт. Одно из первых изданий книги «Principia Mathematica» было продано на аукционных торгах за 3,7 миллиона долларов.
Одно из первых изданий книги «Principia Mathematica» было продано на аукционных торгах за 3,7 миллиона долларов.
Основываясь на известные к тому времени эмпирические соотношения Иоганна Кеплера, описывающие гелиоцентрическую картину мира, Ньютон определил закон, согласно которому все тела притягиваются друг к другу.
гелиоцентрическая система мира
Причём сила взаимодействия растёт с увеличением массы и в то же время связана с расстоянием между объектами обратной квадратичной зависимостью, т.е.:
F = G∙(m1∙m2/ r2)
Несмотря на то, что объектами относительно небольшой массы данное явление практически не воспринимается, именно гравитация управляет движением астрономических тел, а формулировка закона позволяет объяснить, почему планеты движутся вокруг Солнца, а Луна – вокруг Земли.
Природа силы всемирного тяготения
Если важная роль гравитации в работе Вселенной понятна и неоспорима, то дать чёткий ответ на вопрос, откуда эта сила появляется, гораздо сложнее. В первой половине XX века Альберт Эйнштейн предложил специальную и общую теории относительности, в которых раскрыл своё видение природы всемирного тяготения. Согласно учёному, пространство и время представляют собой пространственно-временной континуум – четырёхмерное пространство, одно из измерений которого – время. Но так как люди воспринимают окружающее их пространство и течение времени в отдельности друг от друга, то они видят лишь проекцию континуума. Эйнштейн предположил, что гравитация возникает вследствие того, что тела, обладающие массой, вызывают деформацию пространства при проецировании на него четырёхмерного континуума.
В первой половине XX века Альберт Эйнштейн предложил специальную и общую теории относительности, в которых раскрыл своё видение природы всемирного тяготения. Согласно учёному, пространство и время представляют собой пространственно-временной континуум – четырёхмерное пространство, одно из измерений которого – время. Но так как люди воспринимают окружающее их пространство и течение времени в отдельности друг от друга, то они видят лишь проекцию континуума. Эйнштейн предположил, что гравитация возникает вследствие того, что тела, обладающие массой, вызывают деформацию пространства при проецировании на него четырёхмерного континуума.
деформация пространства телом большой массы
Более понятной идея учёного будет выглядеть, если проиллюстрировать её с помощью двух шаров разной массы и обычного листа бумаги. Допустим, что лист держат за края в горизонтальном положении, а в его центр помещают один из шаров, более тяжёлый. Естественно, бумага прогнётся. Покатив по прямой линии лёгкий шарик, наблюдатель обнаружит, что его траектория является дугообразной, стремящейся к первому, более тяжёлому шару. Причём, с позиции шара меньшей массы, его движение продолжает быть прямолинейным. В этой иллюстрации и заключено упрощённое видение возникновения гравитации как явления.
Причём, с позиции шара меньшей массы, его движение продолжает быть прямолинейным. В этой иллюстрации и заключено упрощённое видение возникновения гравитации как явления.
История открытия закона всемирного тяготения
Существует легенда, согласно которой Ньютон, прогуливаясь по саду и наблюдая за луной, увидел, как падает на землю яблоко (в другой версии, это яблоко упало на голову учёного). В этот же момент он подумал, что, есть вероятность, что одна и та же сила удерживает спутник на небе и заставляет фрукты падать с веток деревьев. Эта догадка и послужила началом работы над законом притяжения.
Сегодня историки сомневаются в этом мифе, что вполне объяснимо, однако главным фактом в истории остаётся то, что Ньютон был первым учёным, который осознал, что тела на Земле и в космосе испытывают на себе воздействие одной и той же силы. До этого момента люди делили гравитацию на два типа: первый отвечал за земное, несовершенное взаимодействие, второй – за небесное, заставляющее планеты двигаться по круговым, совершенным, траекториям.
До этого момента люди делили гравитацию на два типа: первый отвечал за земное, несовершенное взаимодействие, второй – за небесное, заставляющее планеты двигаться по круговым, совершенным, траекториям.
Ньютон математически связал гравитацию и соотношения движения планет, выведенные Кеплером, прекращая тем самым ложное разделение физических устоев Земли и остальной Вселенной.
Интересный факт: существует мнение, что Ньютон вывел закон всемирного тяготения гораздо раньше публикации «Начал». Однако известное на тот момент расстояние от Земли до Луны не подтверждало его теорию, но как только цифры были уточнены и исправлены, всё подтвердилось.
Вывод закона всемирного тяготения
Исаак Ньютон описал свою математическую модель гравитационного воздействия, рассматривая движение Луны вокруг Земли.
Притяжение тел к земле
Известно, что радиус Земли составляет RЗ = 6370 километров, а всякий объект на её поверхности, обладает ускорением свободного падения g = 9,81 м/с2.
Интересный факт: учёными выявлена зависимость g от широты: на экваторе значение меньше принятого – 9,79 м/с2, а на полюсах достигает 9,83 м/с2.
Притяжение Земли и Луны
Известно, что Луна вращается вокруг Земли, двигаясь по круговой орбите радиусом RЛ = 384000 километров, период обращения при этом равен T = 27,3 суток. Для того чтобы численно прикинуть, насколько орбита Луны больше радиуса Земли, требуется разделить имеющиеся величины друг на друга, то есть:
RЛ / RЗ = 384000 / 6370 ≈ 60.
По полученным результатам очевидно, что путь от планеты до спутника включает в себя 60 радиусов Земли.
Ускорение в формуле всемирного тяготения
Луна притягивается к ней с ускорением, которое называют центростремительным. Известно, что центростремительное ускорение находят по формуле:
a = ω2∙R,
где ω – угловая скорость движения;
R – радиус окружности, по которой происходит движение.
Угловая скорость ω и период обращения Т связаны между собой соотношением:
ω = 2π / T.
центростремительное ускорение
Подставляя это равенство в формулу ускорения и преобразуя её путём подстановки индексов к некоторым величинам, получаем:
aЛ = (2π/T)2∙ RЛ,
где aЛ – ускорение Луны;
RЛ – орбита Луны или расстояние от неё до Земли.
Перед тем, как получить численное значение искомого ускорения, требуется перевести размерности всех компонентов в соответствии с Международной системой единиц (СИ):
- период Т = 27,3 суток = 655,2 часа = 39312 минут = 2358720 секунд;
- расстояние R = 384000 километров = 384 ∙106 метров.
Таким образом, спутник движется с ускорением:
aЛ = (2∙3,14 / 2358720)2∙ 384 ∙106 = 2,72∙10-3 м/с2.
ускорение движения луны
Сравнивая полученную величину со значением g, получаем:
g/ aЛ = 9,81 / 2,72∙10-3 ≈ 3600 = 602.
То есть ускорение, получаемое на орбите Луны, в 602 раз меньше ускорения, которое приобретается на поверхности Земли, при этом спутник находится в 60 раз дальше, то есть напрашивается предположение, согласно которому ускорение обратно пропорционально значению расстояния, возведённому в квадрат:
aЛ ~ 1/ (RЛ)2.
Второй и третий законы Ньютона в выводе формулы тяготения
Второй закон Ньютона утверждает, что ускорение a, которое получает тело, прямо пропорционально зависит от равнодействующей сил F, которые приложены к этому телу, и находится в обратной зависимости от его массы m:
a= F / m.
Исходя из этого, напрашивается утверждение, что характер приращения силы идентичен характеру приращения ускорения, то есть:
F ~ a.
второй закон ньютона
А так как уже было выдвинуто предположение, что ускорение имеет обратно пропорциональную зависимость от квадрата расстояния, то у силы, действующей на тело, такой же характер, то есть:
F~ 1/ (RЛ)2.
В это же время известно, что по третьему закону Ньютона взаимодействие тел между собой становится причиной возникновения сил, направленных в противоположные стороны, но одинаковых по модулю:
где F12 – сила, с которой первое тело воздействует на второе;
F21 – сила, действия второго тела на первое.
третий закон ньютона
Таким образом, не только Земля притягивает к себе свой спутник, но и наоборот. А так как по второму закону Ньютона приращение силы прямо зависит не только от приращения ускорения, но и массы, то можно утверждать, что притяжение между Луной и Землёй соответствует записи:
F ~ mЛ∙mЗ,
где mЛ – масса Луны;
mЗ – масса Земли.
Знак умножения здесь получен в результате конъюнкции – логической операции, синонимами которой являются «логическое умножение» и «И» (потому что на притяжение влияет и масса Луны, и масса Земли).
Формула всемирного тяготения
Суммируя полученные вычисления и предположения, можно вывести запись:
F ~ mЛ∙mЗ/ (RЛ)2.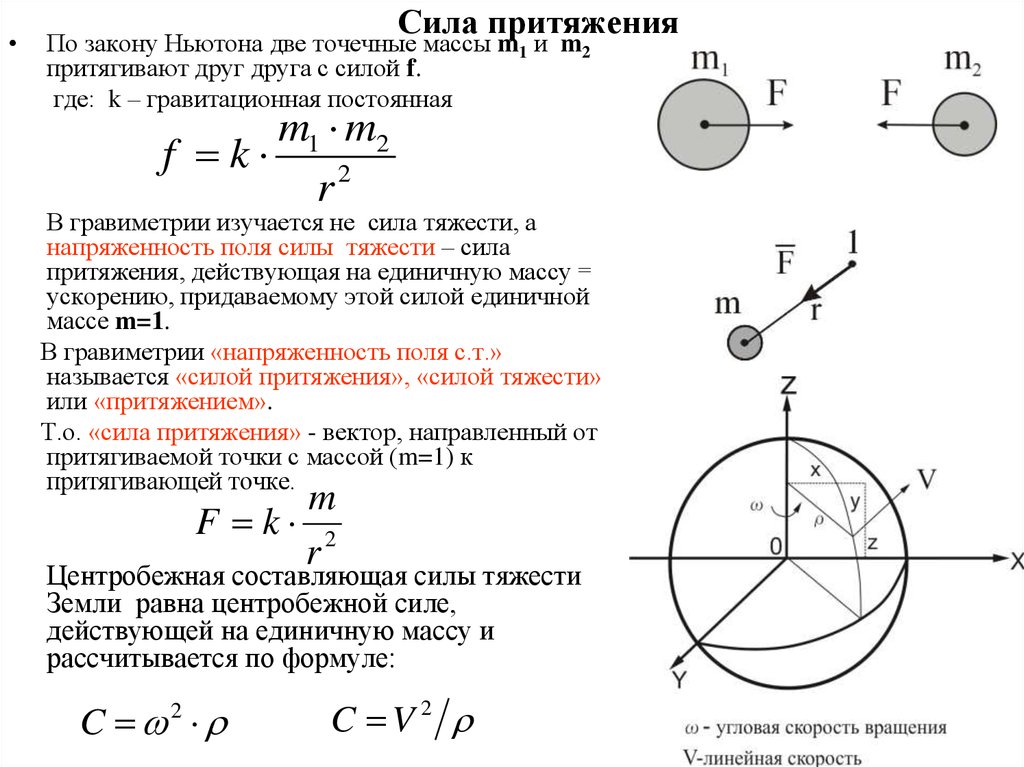
Но так как данное соотношение действует не только на нашу планету и её спутник, а на все объекты, то полученный вид следует слегка преобразовать:
F ~ m1∙m2/ R2,
где F – сила притяжения, возникающая при взаимодействии двух тел;
m1,2 – масса первого и второго тела;
R – расстояние.
определение закона всемирного тяготения
Для того чтобы пропорциональность стала равенством, требуется специальный коэффициент G, называемый гравитационной постоянной. После его введения итог совершённых преобразований получает название формулы закона всемирного тяготения:
F = G∙(m1∙m2/ R2)
В чём измеряется сила притяжения
В СИ размерность любой силы — это ньютоны (Н), следовательно, сила притяжения измеряется в тех же величинах. Ньютоны считаются производными единицами, которые формируются установленными основными. Таким образом, ньютон это отношение килограмма (кг) к отношению метра (м) на секунду в квадрате (с2), то есть Н = кг / (м/с2) .
До 1960 года (дата принятия СИ) использовали СГС (сантиметр-грамм-секунда или абсолютная физическая система единиц), а сила имела размерность дины. По определению 1 дина = 1 г/ (см/с2), следовательно, ньютоны и дины отличаются на пять порядков, то есть: 1 Н = 105 дин.
Гравитационная постоянная
Значение постоянной G приравнивается силе притяжения двух точечных тел, обладающих массой один килограмм и расположенных в одном метре. Согласно СИ,
G = 6,67∙10-11 Н∙м²·кг−2.
Интересный факт: значение коэффициента пропорциональности было определено Генри Кавендишем только в 1798 году, спустя 111 лет после опубликования труда Ньютона.
Опыт Кавендиша
Чтобы определить гравитационную постоянную, был проведён эксперимент, где главную роль играли крутильные весы – устройства, представляющего собой прочную стальную проволоку, на которой расположено горизонтальное коромысло, утяжелённое по краям двумя одинаковыми шарами из свинца.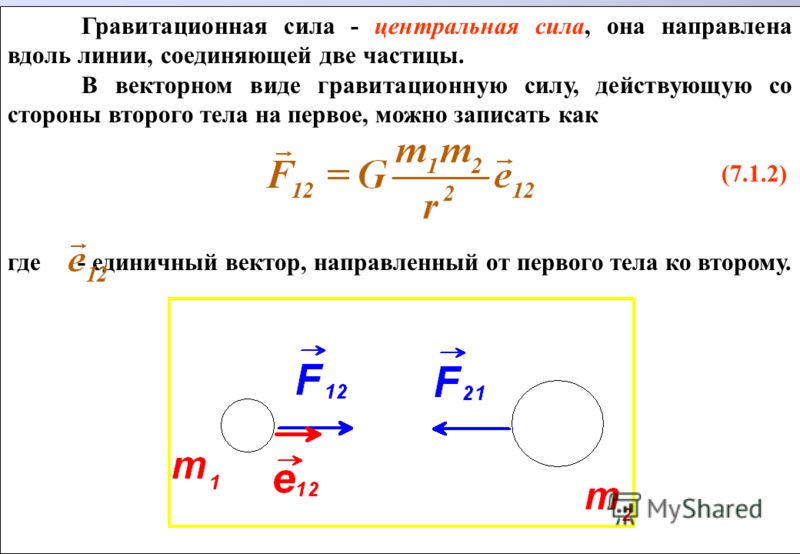 Масса каждого составляла 730 грамм.
Масса каждого составляла 730 грамм.
В ходе эксперимента Кавендиш приближал к маленьким шарикам большие, весом 158 килограмм, подвешенные также на коромысле. При подведении тяжёлых шаров возникала сила взаимного притяжения, поворачивающая коромысло и закручивающая проволоку, что вызывало появление силы упругости, противодействующей притяжению шаров. В определённый момент сила гравитационного взаимодействия уравновешивалась с силой упругости закрученной проволоки. Регистрируя оптическими устройствами отклонения шаров и сравнивая силы, действующие на систему, Кавендиш вычислил значение коэффициента.
Инфографика-вывод закона всемирного тяготения
Сила тяжести как частный случай закона всемирного тяготения
Создав математическую модель притяжения, Ньютон установил, что сила тяжести, чьё влияние видел и испытывал на себе каждый, является лишь одним из проявлений всемирного тяготения, которое утверждает, что все тела во Вселенной, включая планеты, звёзды, астероиды и т. д., воздействуют друг на друга с определённой силой.
д., воздействуют друг на друга с определённой силой.
Чтобы узнать значение этой силы, исходящей от Земли, нужно воспользоваться формулой, выражающей прямо пропорциональную зависимость воздействия и массы объекта:
Fтяж = g∙m,
где g = G∙(mЗ / RЗ2),
сила тяжести
На поверхности значение ускорения свободного падения принимают равным 9,81 м/с2. Если же тело удалено от поверхности Земли, значение g можно найти по формуле:
g = G∙(mЗ / (RЗ+h)2),
где h – расстояние до земли.
Таким образом, действие силы тяжести на тело уменьшается с увеличением высоты.
Интересный факт: если принять силу тяжести, действующую на Земле, за единицу, то можно проанализировать значение притяжения на поверхности других небесных тел. Так, самое большое воздествие тяготения испытает на себе тело на поверхности Юпитера – 2,442, а самое маленькое – на Луне (0,165).
В каких случаях справедлив закон всемирного тяготения
Выявленная Ньютоном зависимость имеет ограничения в области применения. Так, закон справедлив только в случаях, когда:
Так, закон справедлив только в случаях, когда:
- тела можно принять материальными точками, то есть их размеры настолько малы по отношению к расстоянию, что ими можно пренебречь;
- тела обладают сферической формой, что свидетельствует об однородном распределении массы внутри них;
- одно из тел – шар большого диаметра, а второе имеет несопоставимо маленькие размеры.
когда справедлив закон всемирного тяготения
Соотношение неприменимо, если требуется описать взаимодействие шара и стержня бесконечной длины. В этом случае сила притяжения будет пропорциональна не квадрату расстоянию, а его модулю. А если существует потребность определить тяготение между бесконечной плоскостью и телом, расстояние вообще не будет иметь влияния.
Применение закона всемирного тяготения
Закон всемирного тяготения – это фундаментальный закон механики, после формулировки которого стало возможно объяснение и предсказание множества природных явлений. К ним относятся:
- приливы и отливы;
- точное время и место лунных и солнечных затмений;
- масса Солнца и других астрономических тел;
- орбиты движения планет и их спутников.

Открытие планет с использованием закона всемирного тяготения
После открытия явления притяжения астрономы и физики могли, опираясь на закон Ньютона и соотношения Кеплера, определять траектории движения наблюдаемых планет Солнечной системы и указывать их координаты в любой момент времени, причём правильность вычислений подтверждалась эмпирически – результатами астрономических наблюдений.
В 1781 году Уильямом Гершелем была открыта седьмая планета Солнечной системы – Уран. Следуя отработанному алгоритму, астроном рассчитал траекторию своего открытия и его орбиту, однако в первой половине XIX века учёные обнаружили несоответствие вычисленных и реальных координат. Возникло предположение, что, помимо Солнца и шести других планет, на Уран воздействует ещё одна планета, находящаяся за ним.
В 1846 году ночью 23 сентября на основании теоретических расчётов, выполненных по имеющимся отклонениям Урана от рассчитанной траектории, молодым сотрудником Британской обсерватории Иоганном Галле была обнаружена предсказанная планета, названная Нептуном.
планета Нептун
Интересный факт: расчёты, после проведения которых стало возможно открытие, в одно и то же время совершили два учёных, независимо друг от друга – Джон Адамс и Урбен Леверье.
Спустя практически 100 лет, 18 февраля 1930 года, подобным образом была открыта девятая планета – Плутон, которая из-за относительно небольших размеров и массы считается карликовой.
Закон всемирного тяготения. Примеры из жизни
Притяжение испытывает на себе любой объект во Вселенной. В обычной жизни действие этого закона можно наблюдать в каждом явлении падения тел с высоты, будь то листок с дерева, камень, капли дождя, горные обвалы и оползни.
приливы в мировом океане
Кроме этого, тяготение проявляется в наличии веса у каждого объекта – силы, с которой тело воздействует на опору, препятствующую его дальнейшему падению к центру Земли.
Границы применимости
Несмотря на то, что закон всемирного тяготения Ньютона объясняет работу множества явлений, в конце XIX века было выявлено несоответствие наблюдаемого и рассчитанного смещения перигелия Меркурия.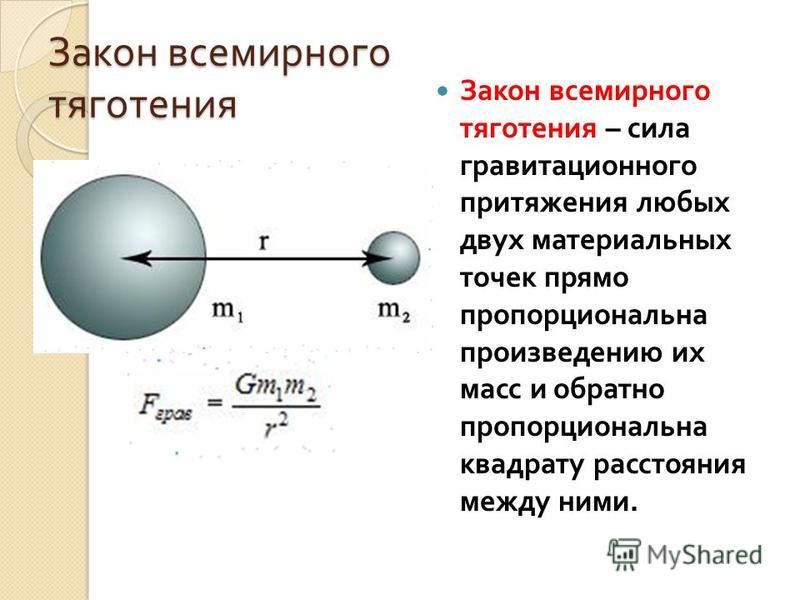 Эта особенность движения планеты не объяснялась известным законом, что потребовало новое понимание гравитации.
Эта особенность движения планеты не объяснялась известным законом, что потребовало новое понимание гравитации.
Кроме того, на рубеже веков применимость классической механики, основанной на законах Ньютона, подверглась ограничениям. Получение точных результатов с её помощью возможно только в случаях, когда:
- скорость тел гораздо меньше скорости звука;
- размеры объектов гораздо больше размеров атомов и молекул;
- скорость распространения гравитации считается бесконечной.
Дальнейшее развитие
С момента создания теории притяжения многие учёные, не разделявшие научных взглядов Ньютона, стремились усовершенствовать его закон. А возникновение трудностей XIX века, подвергших сомнению основы, потребовало внесение коррективов, которые могли бы объяснить расхождение наблюдаемого и рассчитанного. В 1915 году Альберт Эйнштейн создал общую теорию относительности (ОТО), которая объяснила смещение перигелия Меркурия и сегодня является самой перспективной теорией гравитации, доказанной множеством экспериментов.
ОТО имеет чётко выраженные границы применимости, что выражается, например, в невозможности её применения при рассмотрении квантовых эффектов. Поэтому потребовалась новая теория, в которой уже сегодня стремятся объединить теорию относительности Эйнштейна и квантовую механику. Две указанные теории основываются на различных наборах постулатов, но, несмотря на это, квантовая гравитация – одно из основных и перспективных направлений для физических исследований.
Выводы
Все тела во Вселенной взаимно притягиваются, это явление называется гравитацией. Сила притяжения, которая действует между двумя объектами, тем больше, чем больше их массы, в то же время тяготение уменьшается с увеличением расстояния.
После прочтения данной статьи ответ на вопрос, как формулируется закон всемирного тяготения, обязательно будет быстрым и правильным. Однако важно не забывать, что формула, описанная Ньютоном, справедлива только для конкретно описанных случаев.
Более того, несмотря на существование и подтверждение новых гипотез, ньютоновская механика, включая закон всемирного тяготения, является наиболее простой из существующих теорий и верно описывает природные явления в своих границах.
Несколько подходов и примеров задач
В статье обсуждается несколько подходов и некоторые примеры задач о том, как вычислить массу из гравитационной силы.
Каждый объект во Вселенной, имеющий массу, оказывает гравитационное воздействие на другой. Вот почему сила гравитации прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Подробнее о Как рассчитать массу по силе и расстоянию .
Как вычислить массу из силы тяжести, используя второй закон Ньютона Как вычислить массу из силы гравитации?Рассчитаем массу, используя второй закон движения Ньютона, следующим образом:
Во втором законе движения Ньютон описывает, что на объект с ненулевой массой действует сила, которая ускоряет его в том же направлении. Гравитационная сила — это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил, действующих на тела. Гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ma ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется согласно второму закону движения. Ускорение под действием силы тяжести является постоянным и называется ускорением под действием силы тяжести g. Поскольку на нас всегда действует гравитация, возникло представление о нашем «весе» как «mg», включающем в себя нашу массу m и ускорение «a». Вот почему гравитационную силу также называют сила веса . Сила тяжести как сила веса
(кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает следующий вид:
F г = мг ……………………… (1)
В соответствии с уравнениями (*) и (1),
Мы должны создать направленную вверх силу (мА), превышающую силу гравитации (мг), чтобы поднять более тяжелое тело.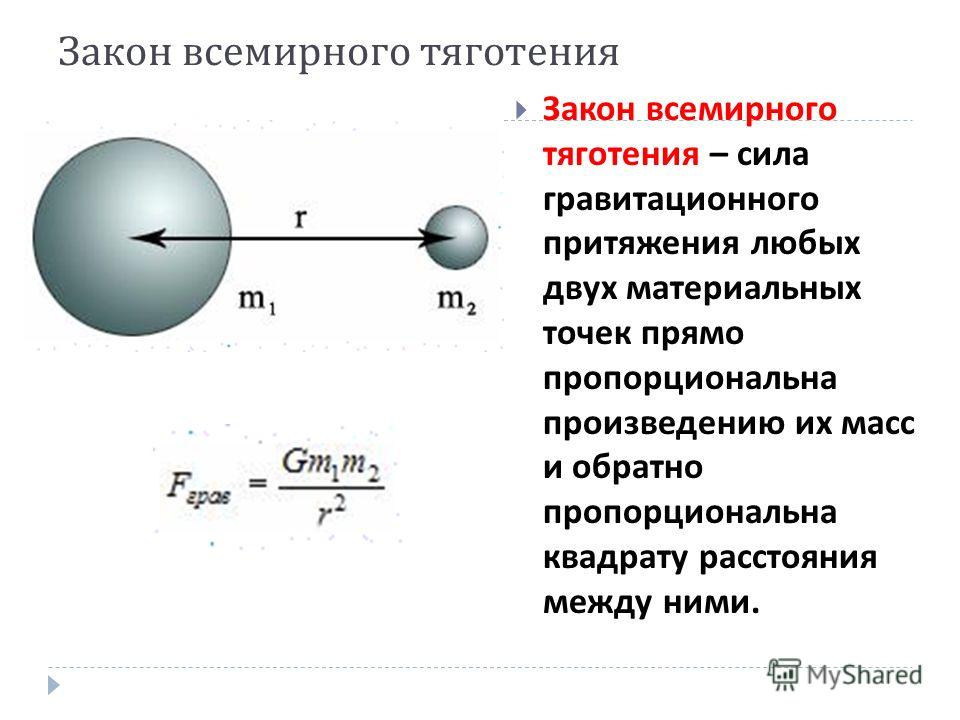
Поскольку g имеет постоянное значение 9,8 м/с 2 , сила гравитации F g зависит только от массы объекта m. Чем массивнее объект, тем больше силы необходимо для его ускорения.
Если к объекту приложена сила гравитации, мы можем вычислить его массу по формуле второго закона Ньютона .
Подробнее о Законах движения Ньютона .
Сила гравитации, действующая на девушку, бегущую по парку, равна 490. Вычислите массу девушки.Дано:
F г = 490 Н
г = 9,8 м/с
Найти: м =?
Формула:
F = MA
Решение:
Масса девушки рассчитывается с использованием Newton’s Second of Motion Formula,
F = MA
гравитационная сила определяется выражением
F г = мг
m= F г /г
m=490/9,8
m = 50 кг ……………………………………. (a)
(a)
Масса бегущей в парке девушки составляет 50 кг.
Как найти массу с помощью гравитационной силы и радиуса?Давайте рассчитаем массу с силой тяжести, используя закон тяготения Ньютона следующим образом:
Закон тяготения обнаруживает, что сила тяготения между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами. масс. Если вторым объектом является земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону тяготения Ньютона,
F г =G(мМ/р 2 )……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке , в основном в его центральной точке, называемой его центром масс (ЦМ) . Радиус r измеряет расстояние или расстояние между центрами масс двух объектов .
Небольшая масса массой 1 кг, разделенная радиусом 1, испытала небольшую гравитационную силу 6,67 x 10-11 Нм 2 /кг 2 , подходит для каждого объекта. Следовательно, это постоянное значение является значением константы пропорциональности в законе тяготения, также называемой универсальной гравитационной постоянной G .
Следовательно, это постоянное значение является значением константы пропорциональности в законе тяготения, также называемой универсальной гравитационной постоянной G .
Легче вычислить F g между объектом и Землей, поскольку планета имеет фиксированную массу M = 5,98 x 10 24 кг, а также фиксированный радиус r от центра своей земли, r = 6,38 x 10 6 м
Сила гравитации, действующая на бегущую в парке девушку, равна 490. Рассчитайте массу девушки, используя закон всемирного тяготения Ньютона.Given :
F g = 490 N
M = 5.98 x 10 24 kg
r = 6.38 x 10 6 m
G = 6.67 x 10 -11 nm 2 /кг 2
Найти: м =?
Формула:
F г =G(мМ/р 2 )
Решение:
Масса девушки вычисляется по закону тяготения Ньютона is,
F g =G(mM/r 2 )
Перестановка для массы m,
r 5 F g 2 /GM
Подставив все значения,
Из (a) и (b) мы заметили, что масса, рассчитанная с использованием второго закона Ньютона и формулы закона всемирного тяготения, одинакова.
Закон всемирного тяготения можно применить к двум объектам, имеющим одинаковую или разную массу. Сила притяжения между двумя объектами
с разными массами
(фото: Shutterstock)
Дано :
F G = 3 x 10 -7 N
R = 1 M
M 1 = 60 KG
G = 6,67 x 10 -11 нм 2 /кг 2
Найти : m 2 =?
Formula :
F G = G (M 1 M 2 /R 2 )
Расчет: 9
. Закон всемирного тяготения Ньютона is,
F g = G(m 1 m 2 /r 2 )
перестройка для MASS M 2 ,
M 2 = F G R 2 /GM 1
СЛУЖИТ ВСЕ ЗНАЧЕНИЯ,
Mass of Your Collegue 75 KG.
Давайте рассчитаем массу с гравитационной силой, используя формулу центростремительной силы следующим образом:
Когда объект движется по окружности, его скорость продолжает изменяться в зависимости от его направления. Направление ускорения к центру, вызванное центростремительной силой. Поскольку вся масса объекта сосредоточена в его центре, мы можем вычислить ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона Ньютона.
Поскольку ускорение представляет собой круговой путь, нам нужно учитывать радиус; поэтому ускорение становится равным
v 2 /r
Следовательно, согласно уравнению (*), центростремительная сила определяется как
F c = mv 2 /r
сила поиска центра , которая действует на объект, чтобы двигаться по кругу к его центру. Земля воздействует на спутник этой центростремительной силой, поддерживая его круговое движение. Центростремительная сила Земли на спутнике
Земля воздействует на спутник этой центростремительной силой, поддерживая его круговое движение. Центростремительная сила Земли на спутнике
Дано :
F G = 500 N
F C = 200 N
V = 20 м/с
M = Масса Земля = 5,98 x 10 24 9
M =0055 кг
G = 6,67 x 10 -11 нм 2 /кг 2
Найти : m =?
Formula :
F g =G(mM/r 2 )
F c =mv 2 /r
Solution :
The mass of спутник рассчитан по закону всемирного тяготения ньютонов ,
F г =G(мМ/р 2 )
Центрипетальная сила на спутнике IS,
F C = MV 2 /R
Решение для Radius R,
R = MV 2 /F C R = MV 2 /F
R = MV 2 /F 4444444444444499000 2
R = MV 2 /F 4444444449.
R = MV 2 /F
замена выше уравнения в Закон Гравитации Ньютона, мы получаем
F G = F C 2 [GM/MV 4 ]
Решение для массы M,
. =159,4/8
м = 19.94 \приблизительно 20 кг
Масса спутника, движущегося вокруг Земли, составляет 20 кг.
Как решать задачи гравитационного взаимодействия
••• Jupiterimages/BananaStock/Getty Images
Обновлено 25 апреля 2017 г. Из всех его многочисленных вкладов одним из самых далеко идущих была его теория гравитации. Хотя гравитация является самой слабой из четырех основных сил, она также играет огромную роль в нашей повседневной жизни, потому что при всей ее слабости масса Земли настолько велика, что ее притяжение к нам очень велико. Мы можем рассчитать силу гравитационного притяжения между двумя объектами, используя уравнения Ньютона. 9-11 ньютон-метров в квадрате на килограмм в квадрате. Единицы в конце константы сокращаются с единицами в уравнении, так что ваш ответ всегда в ньютонах, стандартной единице силы.
Определите расстояние между центрами двух объектов. если вы работаете над задачей викторины, вам, вероятно, будет предоставлена эта информация. Если вы выполняете расчет для объекта на поверхности Земли или вблизи нее, вы можете использовать средний радиус Земли, 6371 км, и добавить высоту объекта над землей. 93 метра) в квадрате = 785,3 ньютона. Умножьте свой ответ в ньютонах на 0,224809, чтобы получить 177 фунтов — фактически столько вы весите. Обратите внимание, что вес — это просто измерение силы, поэтому, когда мы говорим о фунтах, мы на самом деле говорим о силе, которую Земля оказывает на вас, которая варьируется в зависимости от вашей массы.
Заметили кое-что интересное? Не только Земля воздействует на вас, но и вы действуете на Землю. Однако вспомните уравнение Ньютона для силы:
Сила = масса x ускорение
Если вы разделите силу, которую вы оказываете на Землю (785,3 ньютона в нашем примере), на массу Земли, вы получите ускорение Земли из-за вашего гравитационного притяжения.
