Формула внутренней энергии идеального газа. Изменение внутренней энергии газа: формула
Изучая поведение газов в физике, часто возникают задачи на определение запасенной в них энергии, которую теоретически можно использовать для совершения некоторой полезной работы. В данной статье рассмотрим вопрос, по каким формулам внутренняя энергия идеального газа может быть рассчитана.
Понятие о газе идеальном
Четкое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. Любой газ принимает форму и объем сосуда, в который его помещают, однако, не всякий газ является идеальным. Например, воздух можно считать смесью идеальных газов, в то же время водяной пар не является таковым. В чем же заключается принципиальная разница между реальными газами и их идеальной моделью?
Ответом на поставленный вопрос будут две следующие особенности:
- соотношение между кинетической и потенциальной энергией молекул и атомов, составляющих газ;
- соотношение между линейными размерами частиц газа и средним расстоянием между ними.
Газ считается идеальным только в том случае, когда средняя кинетическая энергия его частиц несоизмеримо больше энергии связи между ними. Разница между этими энергиями такова, что можно считать, что взаимодействие между частицами полностью отсутствует. Также для идеального газа характерно отсутствие размеров у его частиц, вернее эти размеры можно не учитывать, поскольку они намного меньше средних межчастичных расстояний.
Хорошими эмпирическими критериями, позволяющими определить идеальность газовой системы, являются такие ее термодинамические характеристики, как температура и давление. Если первая больше 300 К, и второе меньше 1 атмосферы, то любой газ может полагаться идеальным.
Что это внутренняя энергия газа?
Прежде чем записать формулу внутренней энергии газа идеального, необходимо познакомится с этой характеристикой ближе.
В термодинамике внутреннюю энергию, как правило, обозначают латинской буквой U. Определяется в общем случае она по следующей формуле:
U = H – P*V
Где H – энтальпия системы, P и V – давление и объем.
По своему физическому смыслу внутренняя энергия состоит из двух составляющих: кинетической и потенциальной. Первая связана с различного рода движением частиц системы, а вторая – с силовым взаимодействием между ними. Если применить это определение к концепции газа идеального, у которого отсутствует потенциальная энергия, то величина U при любом состоянии системы будет точно равна его кинетической энергии, то есть:
U = Ek.
Вывод формулы внутренней энергии
Выше мы установили, что для ее определения у системы с идеальным газом необходимо рассчитать его кинетическую энергию. Из курса общей физики известно, что энергия частицы массой m, которая поступательно движется в некотором направлении со скоростью v, определяется по формуле:
Ek1 = m*v2/2.
Ее также можно применить для газовых частиц (атомов и молекул), однако, необходимо сделать некоторые замечания.
Во-первых, под скоростью v следует понимать некоторую среднюю величину.
Дело в том, что газовые частицы движутся с разными скоростями согласно распределению Максвелла-Больцмана. Последнее позволяет определить среднюю скорость, которая с течением времени не изменяется, если отсутствуют внешние воздействия на систему.
Во-вторых, формула для Ek1 предполагает энергию на одну степень свободы. Газовые частицы могут двигаться во всех трех направлениях, а также вращаться в зависимости от их строения. Чтобы учесть величину степени свободы z, следует ее умножить на Ek1, то есть:
Ek1z = z/2*m*v2.
Кинетическая энергия всей системы Ek в N раз больше, чем Ek1z, где N – общее число газовых частиц. Тогда для U получаем:
U = z/2*N*m*v2.
Согласно этой формуле, изменение внутренней энергии газа возможно только в том случае, если поменять число частиц N в системе, либо их среднюю скорость v.
Внутренняя энергия и температура
Применяя положения молекулярно-кинетической теории идеального газа, можно получить следующую формулу связи между средней кинетической энергией одной частицы и абсолютной температурой:
m*v2/2 = 1/2*kB*T.
Здесь kB – постоянная Больцмана. Подставляя это равенство в формулу для U, полученную в пункте выше, приходим к следующему выражению:
U = z/2*N*kB*T.
Данное выражение можно переписать через количество вещества n и газовую постоянную R в следующем виде:
U = z/2*n*R *T.
В соответствии с этой формулой, изменение внутренней энергии газа возможно, если поменять его температуру. Величины U и T зависят друг от друга линейно, то есть график функции U(T) представляет собой прямую линию.
Как строение газовой частицы влияет на внутреннюю энергию системы?
Под строением частицы газа (молекулы) имеется в виду количество атомов, которое ее составляет. Оно играет определяющую роль при подстановке соответствующей степени свободы z в формулу для U. Если газ является одноатомным, формула внутренней энергии газа принимает такой вид:
U = 3/2*n*R*T.
Откуда взялась величина z=3? Ее появление связано всего с тремя степенями свободы, которыми обладает атом, поскольку он может двигаться только в одном из трех пространственных направлений.
Если рассматривается двухатомная молекула газа, то внутреннюю энергию следует вычислять по такой формуле:
U = 5/2*n*R*T.
Как видим, двухатомная молекула уже имеет 5 степеней свободы, 3 из которых являются поступательными и 2 вращательными (в соответствии с геометрией молекулы, она может вращаться вокруг двух взаимно перпендикулярных осей).
Наконец, если газ является трех- и более атомным, то справедливо следующее выражение для U:
U = 3*n*R*T.
Сложные молекулы имеют 3 поступательных и 3 вращательных степени свободы.
Пример задачи
Под поршнем находится одноатомный газ при давлении 1 атмосфера. В результате нагрева газ расширился так, что его объем увеличился от 2-х литров до 3-х. Как при этом изменилась внутренняя энергия газовой системы, если процесс расширения был изобарным.
Чтобы решить эту задачу, недостаточно приведенных в статье формул. Необходимо вспомнить об уравнении состояния идеального газа.
Оно имеет вид, представленный ниже.
Поскольку поршень закрывает цилиндр с газом, то в процессе расширения количество вещества n остается постоянным. Во время изобарного процесса температура изменяется прямо пропорционально объему системы (закон Шарля). Это означает, что формула выше запишется так:
P*ΔV = n*R*ΔT.
Тогда выражение для внутренней энергии одноатомного газа примет форму:
ΔU = 3/2*P*ΔV.
Подставляя в это равенство значения давления и изменения объема в единицах СИ, получаем ответ: ΔU ≈ 152 Дж.
Лекция №16 внутренняя энергия идеального газа
Рассмотрим внутреннюю энергию идеального
газа. В идеальном газе притяжение между
молекулами отсутствует. Поэтому их
потенциальная энергия равна нулю. Тогда
внутренняя энергия этого газа будет
складываться только из кинетических
энергий отдельных молекул. Вычислим
сначала внутреннюю энергию одного моля
газа. Известно, что число молекул,
находящихся в одном моле вещества, равно
числу Авогадро NА.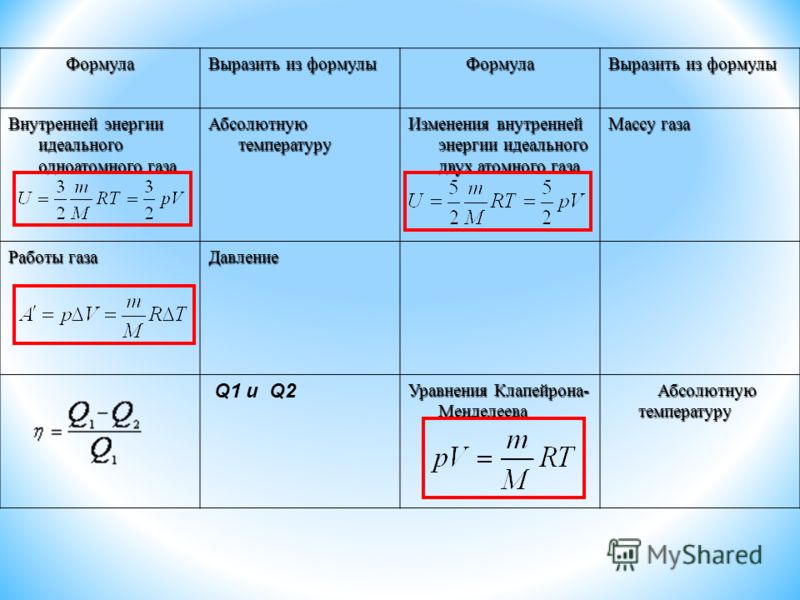
Средняя
кинетическая энергия молекулы находится
по формуле.
Следовательно, внутренняя энергияUодного моля идеального газа равна:
(1)
так как kNA = R — универсальная газовая постоянная. Внутренняя энергия U произвольной массы газа M равна внутренней энергии одного моля, умноженной на число молей , равной = M / , где — молярная масса газа, т.е.
(2)
Таким образом, внутренняя энергия данной массы идеального газа зависит только от температуры и не зависит от объёма и давления.
Количество теплоты
Внутренняя энергия
термодинамической системы под воздействием
ряда внешних факторов может меняться,
о чём как видно из формулы (2), можно
судить по изменению температуры этой
системы. Например, если быстро сжать
газ, то его температура повышается. При
сверлении металла также наблюдается
его нагревание.
Если привести в контакт
два тела, имеющих разные температуры,
то температура более холодного тела
повышается, а более нагретого —
понижается. В первых двух случаях
внутренняя энергия изменяется за счёт
работы внешних сил, а в последнем —
происходит обмен кинетическими энергиями
молекул, в результате чего суммарная
кинетическая энергия молекул нагретого
тела уменьшается, а менее нагретого —
возрастает. Происходит передача энергии
от горячего тела к холодному без
совершения механической работы. Процесс
передачи энергии от одного тела к другому
без совершения механической работы
получил название
Первый закон термодинамики
В природе существует закон сохранения
и превращения энергии, согласно
которомуэнергия не исчезает и не
возникает вновь, а лишь переходит из
одного вида в другой.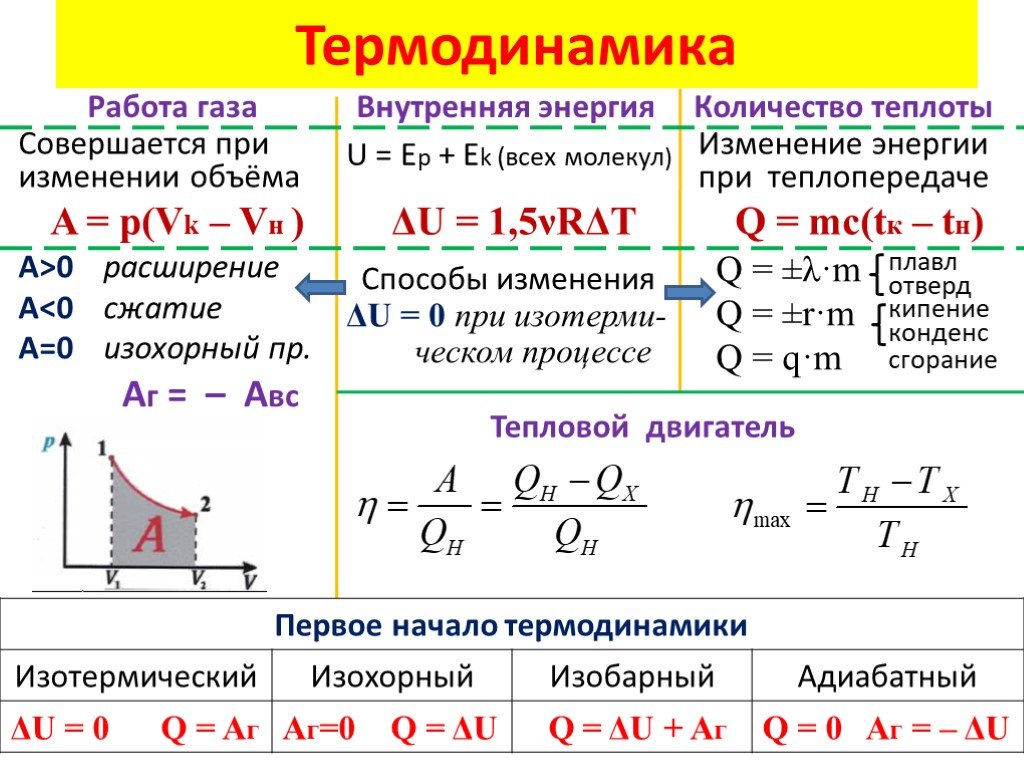
Этот закон
применительно ктепловым процессам,
т.е. процессам, связанным с изменением
температуры термодинамической системы,
а также с изменением агрегатного
состояния вещества, получил название
первого закона термодинамики.
Если термодинамической системе сообщить некоторое количество теплоты Q, т.е. некоторую энергию, то за счёт этой энергии в общем случае происходит изменение её внутренней энергииUи система, расширяясь, совершает определённую механическую работуA. Очевидно, что, согласно закону сохранения энергии, должно выполняться равенство:
(3)
т.е. количество теплоты, сообщённое термодинамической системе, расходуется на изменение её внутренней энергии и на совершение системой механической работы при её расширении. Соотношение (4) носит название первого закона термодинамики.
Выражение первого закона удобно
записывать для малого изменения состояния
системы при сообщении ей элементарного
количества теплоты dQи совершения
системой элементарной работыdA,
т.
е.
(4)
где dU — элементарное изменение внутренней энергии системы. Формула (4) представляет собой запись первого закона термодинамики в дифференциальной форме.
3.1: Расчет изменений внутренней энергии
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 414042
- Роберто Певерати
- Технологический институт Флориды
Внутренняя энергия (\(U\)) системы представляет собой термодинамическую функцию состояния, определяемую как:
Определение: Внутренняя энергия
Свойство системы, которое может быть передано или преобразовано.
В отсутствие химических превращений теплота и работа являются единственными двумя формами энергии, которыми занимается термодинамика.
\[ U = Q + W, \label{3.1.1} \]
, которое мы можем записать в дифференциальной форме, учитывая, что внутренняя энергия является функцией состояния, как: \[ dU = đ Q + đ W, \label{3.1.2} \]
, который, используя ур. 2.4.4 становится:
\[ dU = đ Q – PdV. \метка{3.1.3} \]
Внутренняя энергия в изотермических процессах
Для изучения поведения внутренней энергии в процессе при постоянной температуре (\(dT=0\)) Джеймс Прескотт Джоуль (1818–1889) создал аппарат, изображенный на рисунке \(\PageIndex {1}\).
Рисунок \(\PageIndex{1}\): Эксперимент по расширению Джоуля. Левая часть внутренней камеры аппарата Джоуля заполнена идеальным газом, а в правой камере создается вакуум. Обе камеры погружены в водяную баню, чтобы гарантировать изоляцию от окружающей среды. Когда канал связи между камерами открыт, газ расширяется и уравновешивается.
Работа, связанная с преобразованием, составляет:
\[ đ W=-P_{\text{ext}}dV = 0, \label{3.1.4} \]
, так как камеры не сообщаются с окружающей средой, \(P_{\text{ext}}=0\). Таким образом, изменение внутренней энергии связано с теплообменом процесса, который можно измерить, наблюдая за температурой газа в начале \(T_i\) и в конце опыта \(T_f\). Джоуль экспериментально заметил, что если бы он использовал для этого эксперимента идеальный газ, то температура не изменилась бы \(T_i = T_f\). Поскольку температура не меняется, теплопередача отсутствует, поэтому внутренняя энергия остается постоянной:
\[ dU = đ Q = 0. \label{3.1.5} \]
Примечание
Обратите внимание, что вывод Джоуля справедлив только для идеального газа. Если мы расширим реальный газ, мы заметим изменение температуры, связанное с расширением. Типичным примером такого поведения является использование баллончика с распылителем под давлением и длительное время выпускание его содержимого в воздух.
Контейнер обычно становится холоднее. Мы обсудим это поведение в главе 11, когда будем изучать неидеальные газы.
Из этого простого опыта можно сделать вывод, что внутренняя энергия идеального газа зависит только от его температуры.
Внутренняя энергия в адиабатических процессах
Адиабатический процесс определяется как процесс, протекающий без теплообмена. Таким образом, \(đ Q=0\), а работа, связанная с адиабатическим процессом, становится функцией состояния:
\[ dU=đ W=-PdV, \label{3.1.6} \]
, которая может затем рассчитать по формулам, которые мы вывели в разделе 2.4. Обратите внимание, что изотермический и адиабатический — это два совершенно разных процесса. Если адиабатический процесс происходит без теплообмена через границы системы, это не означает, что температура системы не изменяется. Изотермические процессы обычно связаны с переносом тепла через границы для поддержания постоянной температуры системы. Для адиабатических процессов все наоборот, поскольку они обычно связаны с изменением температуры.
Внутренняя энергия в изохорных процессах
Изохорный процесс – это процесс, при котором объем не изменяется. Следовательно, \(đ W=0\) и \(dU = đ Q_V\), которые, используя уравнение 2.3.1, становятся:
\[ dU = đ Q_V = n C_V dT. \label{3.1.7} \]
Поскольку при этих условиях работа не совершается, тепло становится функцией состояния. Уравнение \ref{3.1.7} также дает математическое обоснование концепции теплоемкости при постоянном объеме. \(C_V\) теперь можно интерпретировать как частную производную (коэффициент) функции состояния (внутренней энергии):
\[ C_V = \left( \dfrac{\partial U} {\partial T} \right)_{V,n=1}, \label{3.1.8} \]
где мы заменили общее производная \(d\) с частной \(\partial\), и мы указали, что производная происходит при постоянном объеме и числе молей. Уравнение \ref{3.1.8} дает строгое определение теплоемкости при постоянном объеме 1 моль вещества:
Определение: Теплоемкость
Теплоемкость вещества \(C_V\) представляет его способность поглощать энергию при постоянном объеме.
Внутренняя энергия в изобарических процессах
В изобарическом процессе давление не меняется, следовательно \(dP=0\). К сожалению, уравнение \ref{3.1.2} для этого случая не упрощается дальше, как это произошло в двух предыдущих случаях. Однако в разделе 2.3 мы ввели полезное понятие теплоемкости при постоянном \(P\). \(C_P\) использовалось в адиабатическом процессе так же, как \(C_V\) использовалось в изохорном случае. То есть как коэффициент для измерения количества тепла, поглощаемого при постоянном давлении. Уравнение \ref{3.1.8} дало математическое определение \(C_V\) как частной производной функции состояния (внутренней энергии). Но если теплоемкости — это коэффициенты, а коэффициенты — это частные производные функций состояния, то как мы объясним \(C_P\)? Для этого мы можем ввести новую функцию состояния, называемую энтальпией (\(H\)), как:{0}, \label{3.1.10} \]
, которые можно переставить следующим образом:
\[ dU = dH -PdV, \label{3.1.11} \]
Замена уравнения \ref{3.
1.11 } в уравнение \ref{3.1.3}:
\[ dH -PdV = đ Q_P – PdV, \label{3.1.12} \]
, которое упрощается до:
\[ dH = đ Q_P. \label{3.1.13} \]
Уравнение \ref{3.1.13} устанавливает, что теплообмен при постоянном давлении равен новой функции состояния, называемой энтальпией, определяемой уравнением \ref{3.1.9}. Также устанавливается математическое обоснование понятия теплоемкости при постоянном давлении. Аналогично \(C_V\), \(C_P\) теперь можно интерпретировать как частную производную (коэффициент) новой функции состояния (энтальпии):
\[ C_P = \left( \dfrac{\partial H } {\partial T} \right)_{P,n=1}, \label{3.1.14} \]
Уравнение \ref{3.1.14} дает также строгое определение теплоемкости при постоянном давлении для 1 моль вещества:
Определение: Теплоемкость
Теплоемкость вещества \(C_P\) представляет его способность поглощать энтальпию при постоянном давлении.
Эта страница под названием 3.1: Расчет изменений внутренней энергии распространяется под лицензией CC BY-SA 4.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Автор
- Роберто Певерати
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги
- источник@https://peverati.github.io/pchem1/
Калькулятор комбинированного газового закона
Создано Wojciech Sas, PhD
Отредактировано Bogna Szyk и Steven Wooding
Последнее обновление: 06 декабря 2022 г.
Содержание:- Что такое термодинамические процессы? Комбинированный закон о газе Формула
- Первый закон термодинамики
- Изохорический процесс
- Изобарический процесс
- Изотермический процесс
- Adiabatic Process
- Вычислительный пример
- Carnot Cycle
. Этот комбинированный газовый калькулятор является отличным инструментом для решения с отличным инструментом для решения с отличным относящиеся к наиболее распространенные превращения газов . Прочтите об изобарических, изохорных, изотермических и адиабатических процессах идеальных газов (газов, которые можно описать уравнением идеального газа) и о том, как идеальные газы могут совершать работу или выделять/поглощать тепло.
Проверьте точные значения для реальных газов, используя наш калькулятор уравнения Ван-дер-Ваальса, и забудьте о термодинамических упражнениях!
Что такое термодинамические процессы? Формула комбинированного газового закона
Мы можем описать идеальный газовый баллон несколькими параметрами: давлением p , объемом V , температурой T и числом частиц n . Их можно соотнести уравнением: p·V = n·R·T , где R обозначает постоянную идеального газа и равен 8,3144598 Дж/(моль·К) .
Во время любого процесса по крайней мере два из этих свойств изменяются , что мы можем скомпилировать в формулу комбинированного газового закона: p·V/T = k
Из всех трансформаций мы можем выделить несколько, которые охватывают подавляющее большинство примеров из повседневной жизни, или мы можем рассматривать их как хорошие приближения.
В этом калькуляторе комбинированного газового закона мы рассматриваем процессы, в которых количество частиц постоянно . Таким образом, мы можем представить себе газ в закрытом сосуде. К ним относятся:
- Изохорный процесс;
- Изобарический процесс;
- Изотермический процесс; и
- Адиабатический процесс.
Первый закон термодинамики
Внутренняя энергия U представляет собой сумму всех видов энергии, присутствующих в системе. Довольно сложно оценить точное значение внутренней энергии. Тем не менее, можно найти изменений тепловой энергии ΔU , которые описываются первым законом термодинамики: ΔU = Q – W , где Q обозначает теплоты, поглощаемой , а W равно работе, совершаемой газом .
Изменение внутренней энергии пропорционально изменению температуры ΔT и типу газа по следующей формуле: ΔU = Cv·n·ΔT , где Cv
Для идеального газа принимает значения:- 3/2·R для одноатомного газа;
- 5/2·R для двухатомного газа; и
- 3·R для газов с более сложными молекулами.
Эти параметры в реальных газах отличаются от теоретических, но они уже есть в нашем калькуляторе термодинамических процессов.
Общая формула для работы, совершаемой газом, выражается как ∫p(V)dV , если мы рассматриваем давление как функцию объема . Хотя в целом это нетривиально, вы можете проверить, как формула упрощается для процессов, упомянутых ниже.
Изохорический процесс
во время этого перехода Объем является постоянным параметром , так что начальные свойства P₁ , T₁ .
Неизменность объема означает, что газ не совершает никакой работы и теплота, поглощаемая газом, в точности равна изменению внутренней энергии: ΔU = Q = Cv·n·ΔT .
Мы можем визуализировать этот процесс для газа, хранящегося в жестком контейнере, который может обмениваться теплом с окружающей средой. Вы можете попробовать наш калькулятор закона Гей-Люссака, так как закон Гей-Люссака соответствует этому термодинамическому процессу.
Изобарический процесс
Мы предполагаем, что давление является постоянным параметром газа во время этого перехода. Поэтому начальные параметры V₁ , T₁ преобразуются в V₂ , T₂ со следующей формой формулы комбинированного газового закона: V₁ / T₁ = V₂ / T₂ .
Поскольку давление неизменно, формула работы, совершаемой газом, будет следующей: Вт = p·ΔV . Теплота, однако, может быть рассчитана как: Q = ΔU + W = Cv·n·ΔT + p·ΔV = Cp·n·ΔT .
Cp известна как молярная теплоемкость при постоянном давлении, а для идеального газа она связана с Cv , так что Cp = Cv + R .
Проверьте калькулятор закона Чарльза Омни, так как закон Чарльза связан с изобарическим переходом.
Изотермический процесс
Постоянным параметром в этом переходе является температура , так что начальные свойства p₁ , В₁ изменяются на p₂ , V₂ , и соотношение: p₁·V₁ = p₂·V₂ . В представленном примере видно, что согласно уравнению идеального газа давление является следующей функцией объема: p(V) = n·R·T / V = A / V , где A постоянным на протяжении всего процесса.
Общее выражение для работы, совершаемой газом, можно оценить как W = n·R·T·ln(V₂ / V₁) , где ln обозначает натуральный логарифм заданного числа. Из-за постоянства температуры начальная энергия не меняет , откуда следует равенство: Q = W . Можно сказать, что мы превращаем всю теплоту, поглощаемую газом, в совершаемую им работу, но, с другой стороны, этот переход, как известно, очень медленный на практике.
Для более подробного объяснения обратитесь к нашему калькулятору закона Бойля, который описывает термодинамические процессы такого рода.
Адиабатический процесс
При этом переходе изменяются все три параметра, но одновременно газ не обменивается теплом с окружающей средой . Справедлива следующая формула: p₁V₁ γ = p₂·V₂ γ , где γ = Cp / Cv известно как отношение теплоемкости . Работа, совершаемая газом, противоположна его начальному изменению внутренней энергии Вт = -ΔU . Этот процесс описывает переходы, которые происходят быстро , и газ не успевает поглотить или отдать какое-либо тепло.
Расчетный пример
Предположим, что вы хотите найти изменение внутренней энергии , поглощенное тепло и работу, выполненную азотом, хранящимся внутри гибкого контейнера объемом 0,5 м³ при атмосферном давлении и температуре 250 К, который мы нагреваем до 300 К.
В этом случае мы рассматриваем изобарический процесс.
Рассчитать конечный объем:
V₂ = V₁·T₂ / T₁
= 0,5 м³ · 300 K / 250 K
= 0,6 м³Определите количество молекул:
n = p·V₁ / (R·T₁)
= 101,325 кПа · 0,5 м³ / (8,314 Дж/(моль·K) · 250 K)
= 24,375 мольНайти теплоемкость Cv азота, которая равна 20,814 Дж/(моль·К) (для идеального двухатомного газа она должна быть равна 20,786 Дж/(моль·К) ).
Оценка изменения внутренней энергии:
ΔU = 20,814 Дж/(моль·К) · 24,375 моль · 50 К
= 25,367 кДжОпределить работу, совершаемую газом:
Вт = 101,325 кПа · 0,1 м³
= 10,133 кДжОцените тепло, поглощенное азотом:
Q = 25,367 кДж + 10,133 кДж
= 35,500 кДж .
