Магнитный поток формула единица измерения. Базовые формулы
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь
МАГНИТНЫЙ ПОТОК – (поток магнитной индукции), поток Ф вектора магн. индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия
магнитный поток – Скалярная величина, равная потоку магнитной индукции. [ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика
МАГНИТНЫЙ ПОТОК – (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ.
МАГНИТНЫЙ ПОТОК – поток Ф вектора магнитной индукции (см. (5)) В через поверхность S, нормальную вектору В в однородном магнитном поле. Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия
МАГНИТНЫЙ ПОТОК – величина, характеризующая магнитное воздействие на данную поверхность. М. п. измеряется количеством магнитных силовых линий, проходящих через данную поверхность. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
Магнитный поток – скалярная величина, равная потоку магнитной индукции… Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
магнитный поток – поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
магнитный поток – , поток магнитной индукции поток вектора магнитной индукции через какую либо поверхность. Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии
Магнитный поток – 12. Магнитный поток Поток магнитной индукции Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа 12 магнитный по … Словарь-справочник терминов нормативно-технической документации
Книги
- , Миткевич В. Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было… Купить за 2252 грн (только Украина)
- Магнитный поток и его преобразование , Миткевич В.
 Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
МАГНИТНЫЙ ПОТОК
МАГНИТНЫЙ ПОТОК (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m – магнитная ПРОНИЦАЕМОСТЬ среды, а Н – интенсивность магнитного поля. Плотность магнитного потока – это поток на единицу площади (символ В), который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.
Научно-технический энциклопедический словарь .
Смотреть что такое “МАГНИТНЫЙ ПОТОК” в других словарях:
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь
– (поток магнитной индукции), поток Ф вектора магн.
магнитный поток – Скалярная величина, равная потоку магнитной индукции. [ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика
МАГНИТНЫЙ ПОТОК – поток Ф вектора магнитной индукции (см. (5)) В через поверхность S, нормальную вектору В в однородном магнитном поле. Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия
Величина, характеризующая магнитное воздействие на данную поверхность. М. п. измеряется количеством магнитных силовых линий, проходящих через данную поверхность. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
Магнитный поток – скалярная величина, равная потоку магнитной индукции. .. Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
.. Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
Классическая электродинамика … Википедия
магнитный поток – , поток магнитной индукции поток вектора магнитной индукции через какую либо поверхность. Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии
Магнитный поток – 12. Магнитный поток Поток магнитной индукции Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа 12 магнитный по … Словарь-справочник терминов нормативно-технической документации
Книги
- , Миткевич В.
 Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было…
Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было… - Магнитный поток и его преобразование , Миткевич В. Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
магнитная индукция – является плотностью магнитного потока в данной точке поля. Единицей магнитной индукции является тесла (1 Тл = 1 Вб/м 2).
Возвращаясь к полученному ранее выражению (1), можно количественно определить магнитный поток через некоторую поверхность как произведение величины заряда, протекающего через проводник совмещенный с границей этой поверхности при полном исчезновении магнитного поля, на сопротивление электрической цепи, по которой протекают эти заряды
.
В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля.
Ф + Δ Ф = r (q – Δ q ) => Δ Ф = –rΔ q => Δ q = -Δ Ф/r |
где Δ Ф и Δ q – приращения потока и количества зарядов. Разные знаки приращений объясняются тем, что положительный заряд в опытах с удалением витка соответствовал исчезновению поля, т.е. отрицательному приращению магнитного потока.
С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции B (рис. 3)
Эти линии называются линиями вектора магнитной индукции или магнитными линиями .
Пространство магнитного поля можно мысленно разделить трубчатыми поверхностями, образованными магнитными линиями, причем, поверхности можно выбрать таким образом, чтобы магнитный поток внутри каждой такой поверхности (трубки) численно был равен единице и изобразить графически осевые линии этих трубок.
Магнитные линии непрерывны и этот принцип можно математически представить в виде
т.е. магнитный поток, проходящий через любую замкнутую поверхность равен нулю .
Выражение (4) справедливо для поверхности s любой формы. Если рассматривать магнитный поток проходящий через поверхность, образованную витками цилиндрической катушки (рис. 4), то ее можно разделить на поверхности, образованные отдельными витками, т.е. s =s 1
+s 2
+. ..+s 8
. Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.
..+s 8
. Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.
Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф 1 =4; Ф 2 =4; Ф 3 =6; Ф 4 =8. Также, зеркально-симметрично с нижними.
Потокосцепление –
виртуальный (воображаемый общий) магнитный поток Ψ, сцепляющийся со всеми витками катушки, численно равен сумме потоков, сцепляющихся с отдельными витками: Ψ = w э Ф m , где Ф m – магнитный поток, создаваемый током, проходящим по катушке, а w э – эквивалентное или эффективное число витков катушки. Физический смысл потокосцепления – сцепление магнитных полей витков катушки, которое можно выразить коэффициентом (кратностью) потокосцепления k = Ψ/Ф = w э.
Физический смысл потокосцепления – сцепление магнитных полей витков катушки, которое можно выразить коэффициентом (кратностью) потокосцепления k = Ψ/Ф = w э.
То есть для приведенного на рисунке случая, двух зеркально-симметричных половинок катушки:
Ψ = 2(Ф 1 + Ф 2 + Ф 3 + Ф 4) = 48 |
Виртуальность, то есть воображаемость потокосцепления проявляется в том, что оно не представляет собой реального магнитного потока, который никакая индуктивность не может кратно увеличивать, но поведение импеданса катушки таково, что кажется, что магнитный поток увеличивается кратно эффективному количеству витков, хотя реально – это просто взаимодействие витков в том же самом поле. Если бы катушка увеличивала магнитный поток своим потокосцеплением, то можно было бы создавать умножители магнитного поля на катушке даже без тока, ибо потокосцепление не подразумевает замкнутости цепи катушки, но лишь совместную геометрию близости витков.
Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков w э, сохраняя при этом величину потокосцепления Ψ = w э Ф m , где Ф m – поток, сцепляющийся с внутренними витками катушки, а w э – эквивалентное или эффективное число витков катушки. Для рассмотренного на рис. 4 случая w э = Ψ/Ф 4 =48/8=6.
Что такое магнитный поток?
Для того чтобы дать точную количественную формулировку закона электромагнитной индукции Фарадея, нужно ввести новую величину – поток вектора магнитной индукции .
Вектор магнитной индукции характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значений вектора не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром.
Для этого рассмотрим плоский замкнутый проводник (контур), ограничивающий поверхность площадью S и помещенный в однородное магнитное поле (рис.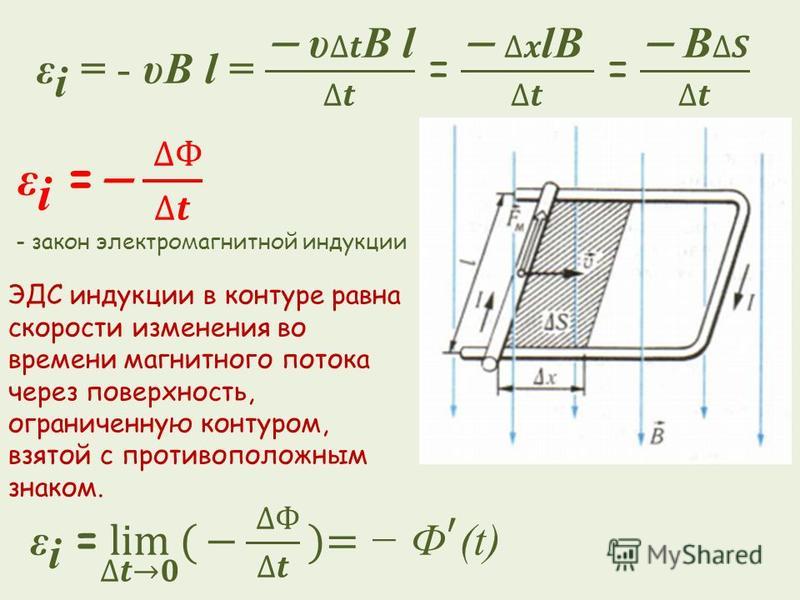 2.4). Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол с направлением вектора магнитной индукции . Магнитным потоком Ф (потоком Вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла между векторами и :
2.4). Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол с направлением вектора магнитной индукции . Магнитным потоком Ф (потоком Вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла между векторами и :
Произведение представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому
Магнитный поток тем больше, чем больше В n и S. Величина Ф названа «магнитным потоком» по аналогии с потоком воды, который тем больше, чем больше скорость течения воды и площадь сечения трубы.
Магнитный поток графически можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.
Единицей магнитного потока является вебер. в 1 вебер (1 Вб) создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции.
Магнитный поток зависит от ориентации поверхности, которую пронизывает магнитное поле.
Обобщенные сведения о магнитном потоке
Сегодняшний урок по физике у нас с вами посвящен теме о магнитном потоке. Для того чтобы дать точную количественную формулировку закона электромагнитной индукции Фарадея нам нужно будет ввести новую величину, которая собственно называется магнитный поток или поток вектора магнитной индукции.
Из предыдущих классов вы уже знаете, что магнитное поле описывается вектором магнитной индукции B. Исходя из понятия вектор индукции B, мы и можем найти магнитный поток. Для этого мы с вами рассмотрим замкнутый проводник или контур с площадью S. Допустим, через него проходит однородное магнитное поле с индукцией B. Тогда магнитным потоком F вектор магнитной индукции через поверхность площадью S называют величину произведения модуля вектора магнитной индукции B на площадь контура S и на cos угла между вектором B и нормалью cos альфа:
В общем, мы с вами пришли к такому выводу, что если поместить в магнитное поле контур с током, то все линии индукции этого магнитного поля будут проходить через контур. То есть, можно смело говорить, что линия магнитной индукции и есть этой самой магнитной индукцией, которая находится в каждой точке этой линии. Или же можно сказать, что линии магнитной индукции являются потоком вектора индукции по ограниченному и описываемому этими линиями пространству, т.е магнитным потоком.
То есть, можно смело говорить, что линия магнитной индукции и есть этой самой магнитной индукцией, которая находится в каждой точке этой линии. Или же можно сказать, что линии магнитной индукции являются потоком вектора индукции по ограниченному и описываемому этими линиями пространству, т.е магнитным потоком.
А теперь давайте вспомним, чему равняется единица магнитного потока:
Направление и количество магнитного потока
Но необходимо так же знать, что каждый магнитный поток имеет свое направление и количественное значение. В этом случае можно сказать, что контур проникает в определенный магнитный поток. И также, следует отметить, что от величины контура зависит и величина магнитного потока, то есть, чем больше размер контура, тем больший магнитный поток будет проходить через него.
Здесь можно подвести итог и сказать, что магнитный поток зависит от площади пространства, через которую он проходит. Если мы, например, возьмем неподвижную рамку определенного размера, которая пронизана постоянным магнитным полем, то в этом случае магнитный поток, который проходит через эту рамку, будет постоянным.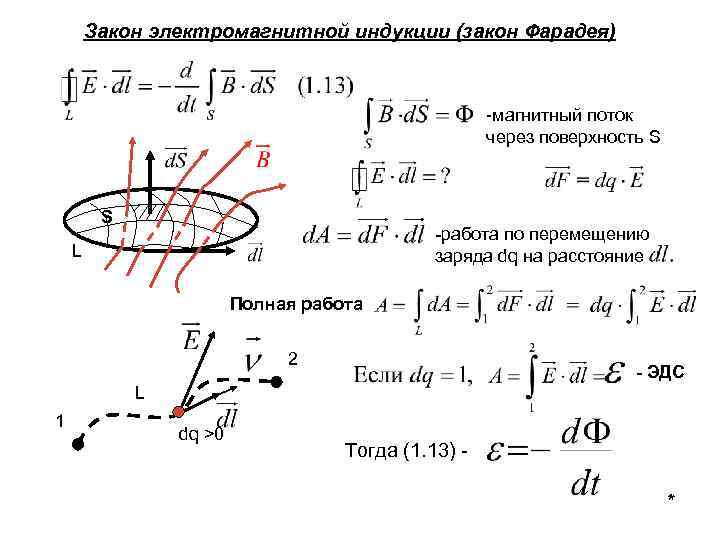
При увеличении силы магнитного поля, естественно и увеличится магнитная индукция. Кроме того и пропорционально возрастет величина магнитного потока в зависимости от возросшей величине индукции.
Практическое задание
1. Посмотрите внимательно на данный рисунок и дайте ответ на вопрос: Как может измениться магнитный поток, если контур будет вращаться вокруг оси ОО”?
2. Как вы думаете, как может измениться магнитный поток, если взять замкнутый контур, который расположен под некоторым углом к линиям магнитной индукции и его площадь уменьшить в два раза, а модуль вектора увеличить в четыре раза?
3. Посмотрите на варианты ответов и скажите, как нужно сориентировать рамку в однородном магнитном поле, чтобы поток через эту рамку равнялся нулю? Какой из ответов будет правильным?
4. Внимательно посмотрите на рисунок изображенных контуров I и II и дайте ответ, как при их вращении может измениться магнитный поток?
5. Как вы думаете, от чего зависит направление индукционного тока?
Как вы думаете, от чего зависит направление индукционного тока?
6. В чем отличие магнитной индукции от магнитного потока? Назовите эти отличия.
7. Назовите формулу магнитного потока и величины, которые входят в эту формулу.
8. Какие вы знаете способы измерения магнитного потока?
Это интересно знать
А известно ли вам, что повышенная солнечная активность влияет на магнитное поле Земли и приблизительно каждые одиннадцать с половиной лет она возрастает так, что может нарушить радиосвязь, вызвать сбой работы компаса и отрицательно сказываться на самочувствии человека. Такие процессы называют магнитными бурями.
Мякишев Г. Я., Физика . 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.
1.Принцип активной радиолокации.
2.Импульсная РЛС. Принцип работы.
3. Основные временные соотношения работы импульсной РЛС.
Основные временные соотношения работы импульсной РЛС.
4.Виды ориентации РЛС.
5.Формирование развертки на ИКО РЛС.
6.Принцип функционирования индукционного лага.
7.Виды абсолютных лагов. Гидроакустический доплеровский лаг.
8.Регистратор данных рейса. Описание работы.
9.Назначение и принцип работы АИС.
10.Передаваемая и принимаемая информация АИС.
11.Организация радиосвязи в АИС.
12.Состав судовой аппаратуры АИС.
13.Структурная схема судовой АИС.
14.Принцип действия СНС GPS.
15.Сущность дифференциального режима GPS.
16.Источники ошибок в ГНСС.
17.Структурная схема приемника GPS.
18.Понятие об ECDIS.
19.Классификация ЭНК.
20.Назначение и свойства гироскопа.
21.Принцип работы гирокомпаса.
22.Принцип работы магнитного компаса.
Электронные термометры получили широкое распространение в качестве измерителей температуры. Ознакомиться с контактными и бесконтактными цифровыми термометрами можно на сайте http://mera-tek. ru/termometry/termometry-elektronnye . Этими приборами в основном и обеспечивается измерение температуры на технологических установках благодаря высокой точности измерения и большой скорости регистрации.
ru/termometry/termometry-elektronnye . Этими приборами в основном и обеспечивается измерение температуры на технологических установках благодаря высокой точности измерения и большой скорости регистрации.
В электронных потенциометрах, как показывающих, так и регистрирующих, применяются автоматическая стабилизация тока в цепи потенциометра и непрерывная компенсация термопары.
Соединение токопроводящих жил — часть технологического процесса соединения кабеля. Многопроволочные токопроводящие жилы с площадью сечения от 0,35 до 1,5 мм 2 соединяют пайкой после скрутки отдельных проволок (рис. 1). Если восстанавливают изоляционными трубками 3, то перед скруткой проволок их необходимо надеть на жилу и сдвинуть к срезу оболочки 4.
Рис. 1. Соединение жил скруткой: 1 — жила токопроводящая; 2 — изоляция жилы; 3 — трубка изоляционная; 4 — оболочка кабеля; 5 — луженые проволоки; 6 — паяная поверхность
Однопроволочные жилы соединяют внахлест, скрепляя перед пайкой двумя бандажами из двух-трех витков медной луженой проволоки диаметром 0,3 мм (рис. 2). Также можно использовать специальные клеммы wago 222 415 , которые сегодня стали очень популярны за счет простоты использования и надежности эксплуатации.
2). Также можно использовать специальные клеммы wago 222 415 , которые сегодня стали очень популярны за счет простоты использования и надежности эксплуатации.
При монтаже электрических исполнительных механизмов корпус их необходимо заземлять проводом сечением не менее 4 мм 2 через винт заземления. Место присоединения заземляющего проводника тщательно зачищают, а после присоединения наносят на него слой консистентной смазки ЦИАТИМ-201 для предохранения от коррозии. По окончании монтажа с помощью проверяют значение , которое должно быть не менее 20 МОм, и заземляющего устройства, которое не должно превышать 10 Ом.
Рис. 1. Схема электрических соединений блока датчиков однооборотного электрического механизма. А — блок усилителя БУ-2, Б — блок магнитного датчика, В — электрический исполнительный механизм
Монтаж блока датчиков однооборотных электрических исполнительных механизмов производится по схеме электрических соединений, показанной на рис.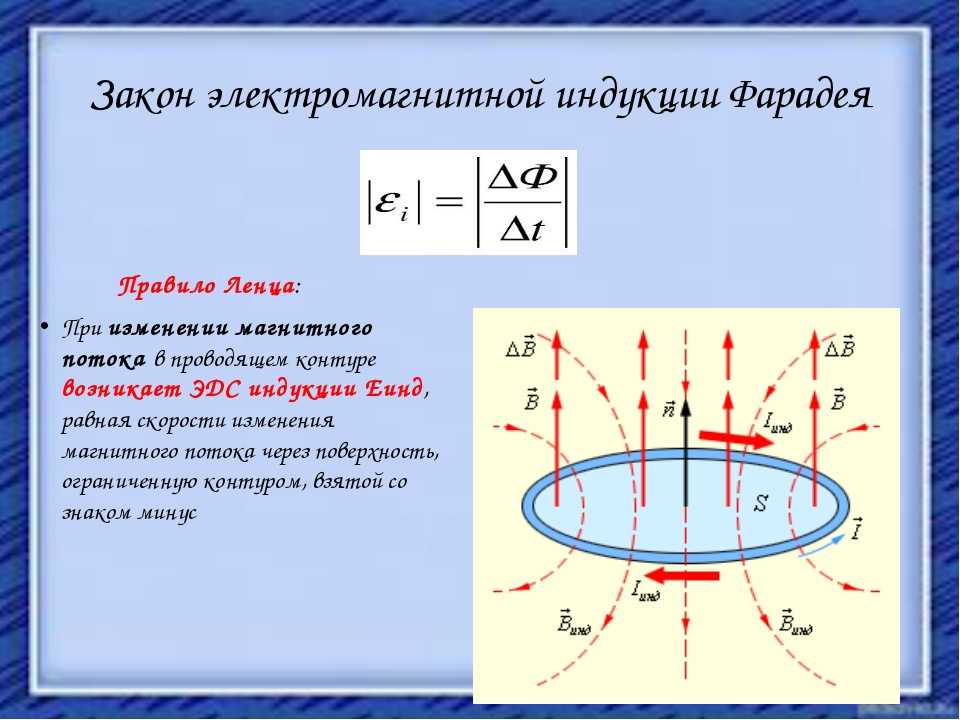 1, проводом сечением не менее 0,75 мм 2 . Перед установкой датчика необходимо проверить его работоспособность по схеме, изображенной на рис. 2.
1, проводом сечением не менее 0,75 мм 2 . Перед установкой датчика необходимо проверить его работоспособность по схеме, изображенной на рис. 2.
21.03.2019
Типы газоанализаторов
Используя газ в печах, различных устройствах и установках, необходимо контролировать процесс его сжигания, чтобы обеспечить безопасную эксплуатацию и эффективную работу оборудования. При этом качественный и количественный состав газовой среды определяется с помощью приборов, называемых
Единица измерения магнитного потока, теория и онлайн калькуляторы
Единица измерения магнитного потока, теория и онлайн калькуляторыОпределение
Элементарный магнитный поток ($dФ$) сквозь малую поверхность $dS$ равен произведению проекции вектора магнитной индукции ($B_n$) на нормаль к элементарной площадке $dS$ на величину этой площадки:
\[dФ=B_ndS\ \left(1\right).\]
Полный поток сквозь всю поверхность $S$ будет равен:
\[Ф=\int\limits_S{B_ndS\ \left(2\right).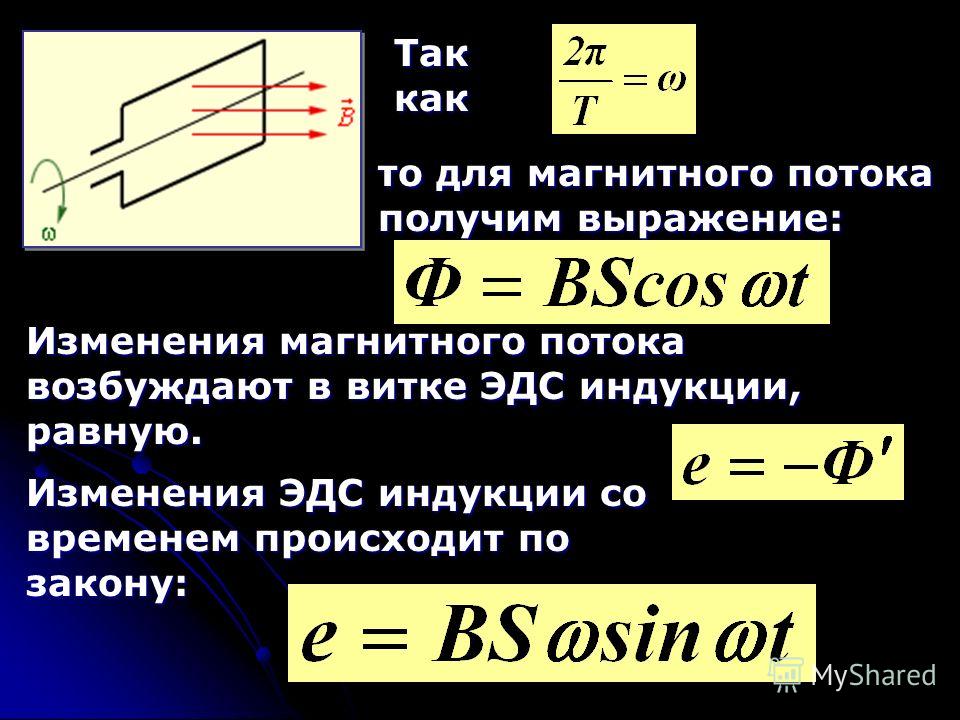 5Мкс$
5Мкс$
Читать дальше: единица измерения магнитной индукции.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Магнитный поток формула через напряженность. Поток индукции магнитного поля
На картинке показано однородное магнитное поле. Однородное означает одинаковое во всех точках в данном объеме. В поле помещена поверхность с площадью S. Линии поля пересекают поверхность.
Определение магнитного потока :
Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.
Формула магнитного потока:
здесь α – угол между направлением вектора магнитной индукции B и нормалью к поверхности S.
Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S. Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 10 8 мкс. Соответственно 1 мкс = 10 -8 вб.
Магнитный поток является скалярной величиной.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля. Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? – выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность
Основные формулы
· Закон электромагнитной индукции (закон Фарадея):
, (39)
где – эдс индукции;– полный магнитный поток (потокосцепление).
· Магнитный поток, создаваемый током в контуре,
где – индуктивность контура;– сила тока.
· Закон Фарадея применительно к самоиндукции
· Эдс индукции, возникающая при вращении рамки с током в магнитном поле,
где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.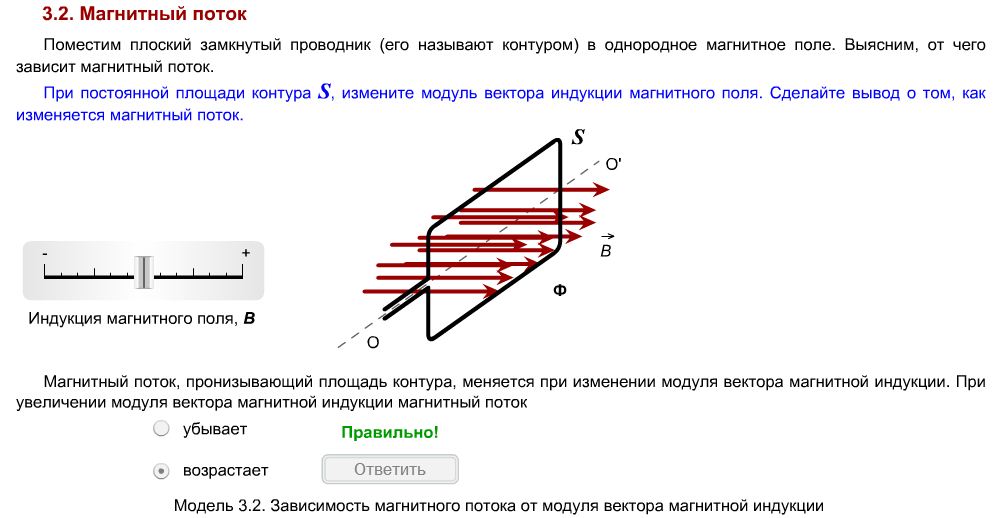
· Индуктивность соленоида
, (43)
где – магнитная постоянная;– магнитная проницаемость вещества;– число витков соленоида;– площадь сечения витка;– длина соленоида.
· Сила тока при размыкании цепи
где – установившаяся в цепи сила тока;– индуктивность контура,– сопротивление контура;– время размыкания.
· Сила тока при замыкании цепи
. (45)
· Время релаксации
Примеры решения задач
Пример 1.
Магнитное поле изменяется по закону , где= 15 мТл,. В магнитное поле помещен круговой проводящий виток радиусом = 20 см под угломк направлению поля (в начальный момент времени). Найти эдс индукции, возникающую в витке в момент времени= 5 с.
Решение
По закону электромагнитной индукции возникающая в витке эдс индукции , где– магнитный поток, сцепленный в витке.
где – площадь витка,;– угол между направлением вектора магнитной индукциии нормалью к контуру:.
Подставим
числовые значения: =
15 мТл,,= 20
см = = 0,2 м,.
Вычисления дают .
Пример 2 В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре. Решение При движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции. |
По закону Фарадея , где, тогда, но, поэтому.
Знак «–» показывает, что эдс индукции и индукционный ток направлены против часовой стрелки.
САМОИНДУКЦИЯ
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл. поля и в цепи появляется
ЭДС индукции.
Это
явление называется самоиндукцией.Самоиндукция –
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
поля и в цепи появляется
ЭДС индукции.
Это
явление называется самоиндукцией.Самоиндукция –
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
Проявление явления самоиндукции
Замыкание цепи При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результатеЛ1 загорается позже, чем Л2.
Размыкание
цепи
При
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
(стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает. Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл. ток пропадает не сразу).
ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От чего зависит ЭДС самоиндукции? Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике (B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью. Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:
где Ф – магнитный поток через контур, I – сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(возможен сердечник).
ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
Для характеристики намагниченности вещества в магнитном поле используетсямагнитный момент (Р м ). Он численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл.
Магнитный момент единицы объема вещества характеризует его намагниченность – I , определяется по формуле:
I = Р м /V , (2.4)
где V – объем вещества.
Намагниченность в системе СИ измеряется, как и напряженность, в А/м , величина векторная.
Магнитные свойства веществ характеризуются объемной магнитной восприимчивостью – c о , величина безразмерная.
Если
какое-либо тело поместить в магнитное
поле с индукцией В 0 ,
то происходит его намагничивание.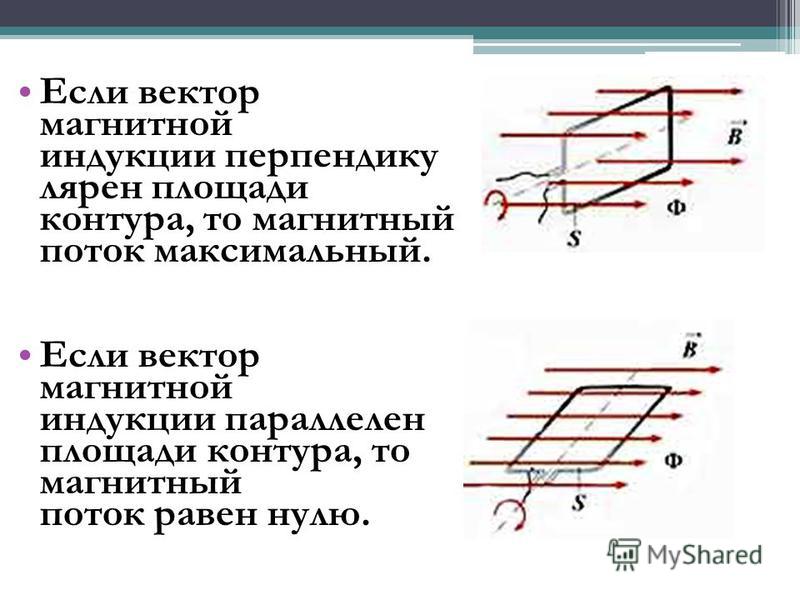 Вследствие этого тело создает свое
собственное магнитное поле с индукцией В ” ,
которое взаимодействует с намагничивающим
полем.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В ” ,
которое взаимодействует с намагничивающим
полем.
В этом случае вектор индукции в среде (В) будет слагаться из векторов:
В = В 0 + В ” (знак вектора опущен), (2.5)
где В ” – индукция собственного магнитного поля намагнитившегося вещества.
Индукция собственного поля определяется магнитными свойствами вещества, которые характеризуются объемной магнитной восприимчивостью – c о , справедливо выражение:В ” = c о В 0 (2.6)
Разделим на m 0 выражение (2.6):
В ” / m о = c о В 0 /m 0
Получим: Н ” = c о Н 0 , (2. 7)
7)
но Н ” определяет намагниченность вещества I , т.е. Н ” = I , тогда из (2.7):
I = c о Н 0 . (2.8)
Таким образом, если вещество находится во внешнем магнитном поле с напряженностьюН 0 , то внутри него индукция определяется выражением:
В=В 0 + В ” = m 0 Н 0 +m 0 Н ” = m 0 (Н 0 + I) (2.9)
Последнее выражение строго справедливо, когда сердечник (вещество) находится полностью во внешнем однородном магнитном поле (замкнутый тор, бесконечно длинный соленоид и т.д.).
МАГНИТНОЕ ПОЛЕ
Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.
В – физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).
Магнитная индукция – векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:
Единица магнитной индукции . В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:
СИЛА ЛОРЕНЦА
Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F А = IBlsin a , а сила Лоренца действует на движущийся заряд:
где a – угол между векторами B и v .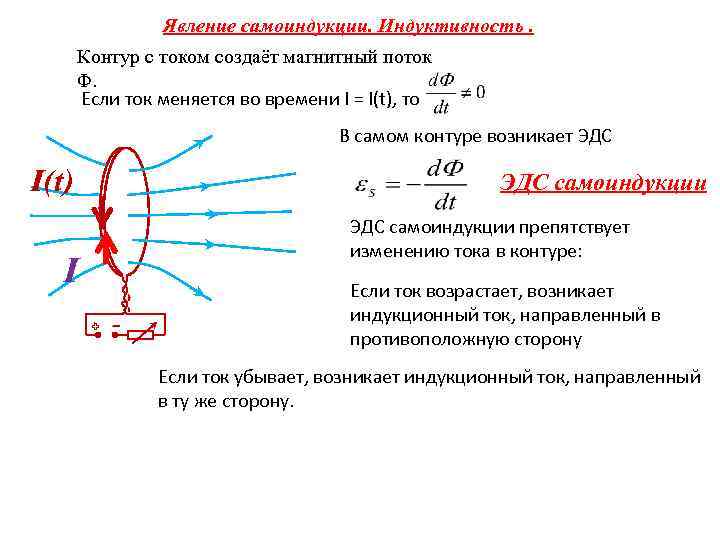
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила м, постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:
В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,
Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.
Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м:
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.
МАГНИТНЫЙ ПОТОК
Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S – величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:
Ф=BScos
В СИ единица магнитного потока 1 Вебер (Вб) – магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:
Электромагнитная индукция -явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.
Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.
Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε i .
По закону Ома для замкнутой цепи
Так как R не зависит от , то
ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:
САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:
Ф = L*I .
Индуктивность контура L – коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.
Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.
Самоиндукция – явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.
Самоиндукция – частный случай электромагнитной индукции.
Индуктивность – величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.
Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :
Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.
ЭДС самоиндукции имеет в этом случае постоянное значение:
где I – начальное значение тока, t – промежуток времени, за который сила тока убывает от I до 0.
За время t в цепи проходит электрический заряд q = I cp t . Так как I cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:
Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:
Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?
Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1 . Следовательно,
МАГНИТНЫЙ ПОТОК
МАГНИТНЫЙ ПОТОК (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m – магнитная ПРОНИЦАЕМОСТЬ среды, а Н – интенсивность магнитного поля. Плотность магнитного потока – это поток на единицу площади (символ В), который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.
Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m – магнитная ПРОНИЦАЕМОСТЬ среды, а Н – интенсивность магнитного поля. Плотность магнитного потока – это поток на единицу площади (символ В), который равен Н. Изменение магнитного потока через электрический проводник наводит ЭЛЕКТРОДВИЖУЩУЮ СИЛУ.
Научно-технический энциклопедический словарь .
Смотреть что такое “МАГНИТНЫЙ ПОТОК” в других словарях:
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь
– (поток магнитной индукции), поток Ф вектора магн. индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия
магнитный поток – Скалярная величина, равная потоку магнитной индукции. [ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика
[ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика
МАГНИТНЫЙ ПОТОК – поток Ф вектора магнитной индукции (см. (5)) В через поверхность S, нормальную вектору В в однородном магнитном поле. Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия
Величина, характеризующая магнитное воздействие на данную поверхность. М. п. измеряется количеством магнитных силовых линий, проходящих через данную поверхность. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
Магнитный поток – скалярная величина, равная потоку магнитной индукции… Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
Классическая электродинамика … Википедия
магнитный поток – , поток магнитной индукции поток вектора магнитной индукции через какую либо поверхность. Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии
Магнитный поток – 12. Магнитный поток Поток магнитной индукции Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа 12 магнитный по … Словарь-справочник терминов нормативно-технической документации
Книги
- , Миткевич В. Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было…
- Магнитный поток и его преобразование , Миткевич В.
 Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Что такое магнитный поток?
Для того чтобы дать точную количественную формулировку закона электромагнитной индукции Фарадея, нужно ввести новую величину – поток вектора магнитной индукции .
Вектор магнитной индукции характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значений вектора не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром.
Для этого рассмотрим плоский замкнутый проводник (контур), ограничивающий поверхность площадью S и помещенный в однородное магнитное поле (рис. 2.4). Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол с направлением вектора магнитной индукции . Магнитным потоком Ф (потоком Вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла между векторами и :
Произведение представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому
Поэтому
Магнитный поток тем больше, чем больше В n и S. Величина Ф названа «магнитным потоком» по аналогии с потоком воды, который тем больше, чем больше скорость течения воды и площадь сечения трубы.
Магнитный поток графически можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.
Единицей магнитного потока является вебер. в 1 вебер (1 Вб) создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции.
Магнитный поток зависит от ориентации поверхности, которую пронизывает магнитное поле.
Обобщенные сведения о магнитном потоке
Сегодняшний урок по физике у нас с вами посвящен теме о магнитном потоке. Для того чтобы дать точную количественную формулировку закона электромагнитной индукции Фарадея нам нужно будет ввести новую величину, которая собственно называется магнитный поток или поток вектора магнитной индукции.
Из предыдущих классов вы уже знаете, что магнитное поле описывается вектором магнитной индукции B. Исходя из понятия вектор индукции B, мы и можем найти магнитный поток. Для этого мы с вами рассмотрим замкнутый проводник или контур с площадью S. Допустим, через него проходит однородное магнитное поле с индукцией B. Тогда магнитным потоком F вектор магнитной индукции через поверхность площадью S называют величину произведения модуля вектора магнитной индукции B на площадь контура S и на cos угла между вектором B и нормалью cos альфа:
В общем, мы с вами пришли к такому выводу, что если поместить в магнитное поле контур с током, то все линии индукции этого магнитного поля будут проходить через контур. То есть, можно смело говорить, что линия магнитной индукции и есть этой самой магнитной индукцией, которая находится в каждой точке этой линии. Или же можно сказать, что линии магнитной индукции являются потоком вектора индукции по ограниченному и описываемому этими линиями пространству, т. е магнитным потоком.
е магнитным потоком.
А теперь давайте вспомним, чему равняется единица магнитного потока:
Направление и количество магнитного потока
Но необходимо так же знать, что каждый магнитный поток имеет свое направление и количественное значение. В этом случае можно сказать, что контур проникает в определенный магнитный поток. И также, следует отметить, что от величины контура зависит и величина магнитного потока, то есть, чем больше размер контура, тем больший магнитный поток будет проходить через него.
Здесь можно подвести итог и сказать, что магнитный поток зависит от площади пространства, через которую он проходит. Если мы, например, возьмем неподвижную рамку определенного размера, которая пронизана постоянным магнитным полем, то в этом случае магнитный поток, который проходит через эту рамку, будет постоянным.
При увеличении силы магнитного поля, естественно и увеличится магнитная индукция. Кроме того и пропорционально возрастет величина магнитного потока в зависимости от возросшей величине индукции.
Практическое задание
1. Посмотрите внимательно на данный рисунок и дайте ответ на вопрос: Как может измениться магнитный поток, если контур будет вращаться вокруг оси ОО”?
2. Как вы думаете, как может измениться магнитный поток, если взять замкнутый контур, который расположен под некоторым углом к линиям магнитной индукции и его площадь уменьшить в два раза, а модуль вектора увеличить в четыре раза?
3. Посмотрите на варианты ответов и скажите, как нужно сориентировать рамку в однородном магнитном поле, чтобы поток через эту рамку равнялся нулю? Какой из ответов будет правильным?
4. Внимательно посмотрите на рисунок изображенных контуров I и II и дайте ответ, как при их вращении может измениться магнитный поток?
5. Как вы думаете, от чего зависит направление индукционного тока?
6. В чем отличие магнитной индукции от магнитного потока? Назовите эти отличия.
7. Назовите формулу магнитного потока и величины, которые входят в эту формулу.
8. Какие вы знаете способы измерения магнитного потока?
Это интересно знать
А известно ли вам, что повышенная солнечная активность влияет на магнитное поле Земли и приблизительно каждые одиннадцать с половиной лет она возрастает так, что может нарушить радиосвязь, вызвать сбой работы компаса и отрицательно сказываться на самочувствии человека. Такие процессы называют магнитными бурями.
Мякишев Г. Я., Физика . 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.
Поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Большой Энциклопедический словарь
МАГНИТНЫЙ ПОТОК – (поток магнитной индукции), поток Ф вектора магн. индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия
индукции В через к. л. поверхность. М. п. dФ через малую площадку dS, в пределах к рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на… … Физическая энциклопедия
магнитный поток – Скалярная величина, равная потоку магнитной индукции. [ГОСТ Р 52002 2003] магнитный поток Поток магнитной индукции через перпендикулярную магнитному полю поверхность, определяемый как произведение магнитной индукции в данной точке на площадь… … Справочник технического переводчика
МАГНИТНЫЙ ПОТОК – (символ Ф), мера силы и протяженности МАГНИТНОГО ПОЛЯ. Поток через площадь А под прямым углом к одинаковому магнитному полю есть Ф=mНА, где m магнитная ПРОНИЦАЕМОСТЬ среды, а Н интенсивность магнитного поля. Плотность магнитного потока это поток… … Научно-технический энциклопедический словарь
МАГНИТНЫЙ ПОТОК – поток Ф вектора магнитной индукции (см. (5)) В через поверхность S, нормальную вектору В в однородном магнитном поле. Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия
Единица магнитного потока в СИ (см.) … Большая политехническая энциклопедия
МАГНИТНЫЙ ПОТОК – величина, характеризующая магнитное воздействие на данную поверхность. М. п. измеряется количеством магнитных силовых линий, проходящих через данную поверхность. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
Магнитный поток – скалярная величина, равная потоку магнитной индукции… Источник: ЭЛЕКТРОТЕХНИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
магнитный поток – поток вектора магнитной индукции В через какую либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = BndS, где Вn проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную… … Энциклопедический словарь
магнитный поток – , поток магнитной индукции поток вектора магнитной индукции через какую либо поверхность. Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии
Для замкнутой поверхности суммарный магнитный поток равен нулю, что отражает соленоидный характер магнитного поля, т. е. отсутствие в природе … Энциклопедический словарь по металлургии
Магнитный поток – 12. Магнитный поток Поток магнитной индукции Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа 12 магнитный по … Словарь-справочник терминов нормативно-технической документации
Книги
- , Миткевич В. Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было… Купить за 2252 грн (только Украина)
- Магнитный поток и его преобразование , Миткевич В. Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Расчет плотности магнитного потока (формула)
Плотность магнитного потока также называется «полем В» или «магнитной индукцией». Поле B наших супермагнитов можно рассчитать по оси север-юг полюса, используя приведенные здесь формулы.
Кроме того, мы также предоставляем вам таблицы (Excel/OpenOffice), которые вы можете использовать для автоматического расчета плотности магнитного потока.
Напротив, вычисление полей B всего пространства намного сложнее и требует использования компьютерных программ.
Поле B наших супермагнитов можно рассчитать по оси север-юг полюса, используя приведенные здесь формулы.
Кроме того, мы также предоставляем вам таблицы (Excel/OpenOffice), которые вы можете использовать для автоматического расчета плотности магнитного потока.
Напротив, вычисление полей B всего пространства намного сложнее и требует использования компьютерных программ.
Содержание
Плотность магнитного потока магнита также называется «полем В» или «магнитной индукцией». Он измеряется в теслах (единица СИ) или гауссах (10 000 гаусс = 1 тесла).
Постоянный магнит создает поле В в своем ядре и во внешнем окружении. Направленная напряженность поля B может быть приписана каждой точке внутри и снаружи магнита. Если вы поместите маленькую стрелку компаса в поле B магнита, она ориентируется в направлении поля. Воздействующая сила пропорциональна напряженности поля В.
Не существует простых формул для расчета плотности магнитного потока различных магнитных форм. Для этого были разработаны компьютерные программы (см. ниже).
Однако для менее сложной симметричной геометрии существуют простые формулы, позволяющие рассчитать поле B на оси симметрии в направлении полюса север-юг.
Мы рады поделиться с вами этими формулами для расчета плотности магнитного потока ниже.
Для этого были разработаны компьютерные программы (см. ниже).
Однако для менее сложной симметричной геометрии существуют простые формулы, позволяющие рассчитать поле B на оси симметрии в направлении полюса север-юг.
Мы рады поделиться с вами этими формулами для расчета плотности магнитного потока ниже.
Формула для плотности магнитного потока блока
Формула для поля B на оси симметрии аксиально намагниченного блочного или кубического магнита: 92}}\bigg)\right]\end{выровнено}\)B R : Поле Remanence, независимо от геометрии магнита (см. Данные физического магнита)
Z : Расстояние от полюсной поверхности на оси симметрии
L : длина. блока
W : Ширина блока
D : Толщина (или высота) блока
Единица длины может быть выбрана произвольно, если она одинакова для все длины. 92}}\справа)\конец{выровнено}\)
B r : Remanence field, independent of the magnet’s geometry (see physical magnet data)
z : Distance from a pole face on the symmetrical axis
D : Thickness (или высота) цилиндра
R : Полудиаметр (радиус) цилиндра
Единица длины может быть выбрана произвольно, если она одинакова для всех длин.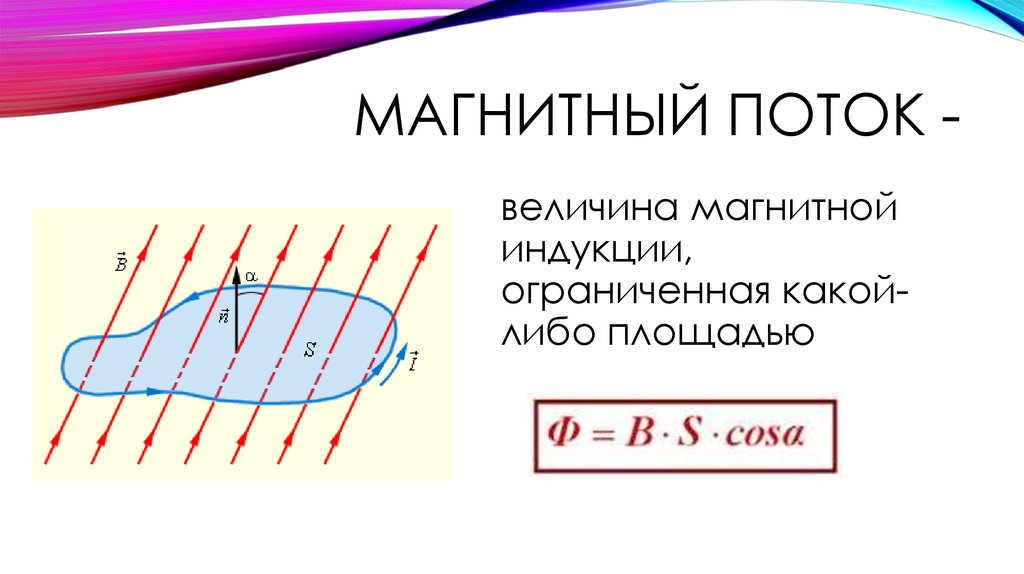 92}}\справа)\справа]\конец{выровнено}\)
92}}\справа)\справа]\конец{выровнено}\)
B R : Поле Remanence, независимо от геометрии магнита (см. Данные физического магнита)
Z : Расстояние от полюсной поверхности на оси симметрии
D :: Голотия
D :: Голова
D :: Голова (или высота) кольца
R a : Внешний радиус кольца
R i : Внутренний радиус кольца
Единица длины может быть выбрана произвольно, если она одинакова для всех длин.
Формула для кольцевых магнитов показывает, что поле B для кольцевого магнита состоит из поля большего цилиндрического магнита с радиусом R a минус поле меньшего цилиндрического магнита с радиусом R i .
Формула для плотности магнитного потока сферы
Формула для поля B на оси симметрии аксиально намагниченного сферического магнита: 93}\конец{выровнено}\) B R : Поле Remanence, независимо от геометрии магнита (см. -диаметр (радиус) сферы
-диаметр (радиус) сферы
Единицу длины можно выбирать произвольно, главное, чтобы она была одинаковой для всех длин.
Упомянутые выше формулы плотности потока также удобно рассчитать в таблице. Введите сведения о магните в желтые поля, и плотность потока будет рассчитана автоматически. Доступны следующие версии:
Расчет полей B всего пространства
Для расчета полей В помимо осей симметрии или полей различных магнитных форм существуют очень сложные и часто очень дорогие компьютерные программы , , который может вычислять поля B и многое другое.Бесплатное программное обеспечение, ограниченное вращательно-симметричными магнитами, называется FEMM. («Магнетизм метода конечных элементов»).
Как и другие инструменты, FEMM рассчитывает и отображает только одну половину магнита, поскольку поля B симметричны. Вы должны представить другую половину, отраженную слева.
B поле половины магнита (дискового магнита), проиллюстрировано с помощью FEMM
Формула магнитного потока | Определения и практические вопросы
Это общая для всех составляющая потока, проходящего через катушку. Магнитный поток представлен символом B, где B может быть полем, поэтому единицей измерения является Вебер (Вб). Значение магнитного потока может быть векторной величиной, зависящей от направления потока.
Магнитный поток представлен символом B, где B может быть полем, поэтому единицей измерения является Вебер (Вб). Значение магнитного потока может быть векторной величиной, зависящей от направления потока.
Магнитный поток относится к общему числу силовых линий магнитного поля, пронизывающих любую поверхность, расположенную перпендикулярно магнитному полю. Он рассчитывается как произведение средней силы магнитного поля на перпендикулярную площадь, через которую оно проходит.
Магнитный поток обозначается ΦB, где B представляет собой магнитное поле, а его единицей измерения является тесла-метр2 или вебер (Вб).
Математически формула магнитного потока выглядит следующим образом:
\[\Phi B=\vec{B}.\vec{A}\Phi B=B\rightarrow .A\rightarrow \]
Или,
\[\Phi B=BAcos\theta \]
Где B — магнитное силовое поле, A — площадь или протяженность поверхности, а θ — угол между нормалью к поверхности и магнитным полем.
Если катушку с n витками и площадью поперечного сечения A поместить в магнитное поле напряженностью B, то общий поток, связанный с катушкой, составит: 9{\circ}=0,5Wb\]
Когда катушка вращается между полюсными наконечниками магнита, как показано, в течение одного полного оборота катушки, как часто магнитный поток, связанный с катушкой, будет максимальным и минимальным ?
Варианты:
(a) максимум и минимум один раз
(b) максимум и минимум дважды каждый
(c) максимум один раз, минимум два раза
(d) максимум два раза, минимум один раз
Ответ: (b)
Магнитные свойства электричества, протекающего по проводу
В детстве вы наверняка играли с магнитом. Это материал, который притягивает железо или железные предметы. Хром и никель — два других объекта, которые притягиваются к магнитам. Позже, когда были открыты характеристики магнита, было обнаружено, что в магните существуют два полюса на обоих концах. Один полюс известен как северный полюс, а другой – южный полюс. Позднее также было обнаружено, что электричество, проходящее через металлическую проволоку, также обладает свойствами магнетизма. А если проволоку свернуть в виде пружины или селена и через нее пропустить электрический ток, то пружина ведет себя как настоящий магнит. Северный полюс и южный полюс этого типа магнита можно легко определить с помощью компаса.
Позже, когда были открыты характеристики магнита, было обнаружено, что в магните существуют два полюса на обоих концах. Один полюс известен как северный полюс, а другой – южный полюс. Позднее также было обнаружено, что электричество, проходящее через металлическую проволоку, также обладает свойствами магнетизма. А если проволоку свернуть в виде пружины или селена и через нее пропустить электрический ток, то пружина ведет себя как настоящий магнит. Северный полюс и южный полюс этого типа магнита можно легко определить с помощью компаса.
Магнитная сила любого обычного магнита или электромагнита может быть представлена магнитными линиями. Эти магнитные линии берут начало от северного полюса магнитов и заканчиваются на южном полюсе магнита, замыкая замкнутую цепь через корпус магнита. Когда железный предмет подносится к магнитному предмету, он также ведет себя как магнит. Качество магнитных свойств такого магнита зависит от количества магнитных силовых линий, проходящих через этот объект и исходящих из самого магнита. Измерение количества магнитной силы, испытываемой любым объектом, измеряется магнитными силовыми линиями, входящими в него и выходящими из него. Термин, используемый для описания этого измерения, известен как магнитный поток.
Измерение количества магнитной силы, испытываемой любым объектом, измеряется магнитными силовыми линиями, входящими в него и выходящими из него. Термин, используемый для описания этого измерения, известен как магнитный поток.
Практические вопросы
Когда катушка вращается между полюсными наконечниками магнита, как показано на рисунке, как часто магнитный поток, связанный с катушкой, будет максимальным и минимальным в течение одного полного оборота катушки?
Ответ: Согласно закону Фарадея, когда магнитный поток, связывающий цепь, изменяется, в цепи индуцируется электродвижущая сила, пропорциональная скорости изменения потокосцепления.
Итак, при вращении прямоугольной катушки в однородном магнитном поле вокруг оси, проходящей через ее центр и перпендикулярной направлению поля, наведенное напряжение в катушке =dtdϕ ⇒ э.д.с. = dϕ
⇒ э. д.с. = NABωcosθ
д.с. = NABωcosθ
, где θ — угол между плоскостью катушки и силовыми линиями.
Итак, ЭДС индукции в катушке максимальна, когда cosθ максимален или θ равен нулю, значит, когда плоскость катушки параллельна полю.
Прямоугольная петля имеет размеры 0,50 м и 0,60 м. Значения B равны 0,02T и 45° соответственно. Вычислите магнитный поток на поверхности.
Ответ: Дано:
Размеры прямоугольной петли = 0,50 м и 0,60 м,
B = 0.02T
θ = 45°
Magnetic flux formula is given by
ΦB = B A Cosθ
Area, A = 0.50 × 0.60
= 0.3 m2
ΦB = 0.02 × 0.3 × Cos 45
ΦB = 0,00312 Wb
Перпендикулярное силовое поле магнитудой 0,1 Тл приложено к продолговатой петле размерами 3 см на 5 см.
 Как рассчитать магнитный поток через петлю?
Как рассчитать магнитный поток через петлю?
Ответ: По формуле ΦB = BACosθ магнитный поток определяется как произведение поля, площади и, следовательно, угла между B и единичным вектором, перпендикулярным поверхности.
Здесь петля расположена перпендикулярно силовому полю B, а именно угол между B и единичным вектором, нормальным к поверхности n, равен нулю θ = 0⁰. Следовательно, применяя формулу, мы получаем
= (0,1) (0,03 × 0,05) cos0 ∘
= 15 × 10⁻⁻⁵
Вб = 0,15 Вб
Электрическая и магнитная индукция, плотность Формулы
Электрический поток, магнитный поток, электрическая плотность, магнитная плотность, электрическая и магнитная напряженность, формулы и уравнения
Содержание
Формула электрического потока:
Электрический поток — это линии электрического поля, проходящие через площадь A . Это векторная величина.
Это векторная величина.
Φ E = EA
Φ E = EA cosθ
Где
- Flux 2×9 E 900
- E = электрическое поле
- А = площадь поверхности
- θ = угол между E и A
- Φ E = Электрический поток
- E = электрическое поле
- А = площадь поверхности
- Q = электрический заряд внутри поверхности A
- ε 0 = диэлектрическая проницаемость свободного пространства (также известная как универсальная или электрическая постоянная, равная ε 0 ≈ 8,854 187 817… x 10 −12 Ф·м −1 .
 )
) - Разница между электрическим полем и магнитным полем
- Разница между электрической и магнитной цепью
- D = Плотность
- Φ E = Электрический поток
- А = Зона
- E = напряженность электрического поля
- Ф = Сила
- Q = Электрический заряд
- Φ b = магнитный поток
- B = Магнитное поле
- А = область
- θ = угол между B и A
- Определение основных магнитных терминов с помощью формул
- Что такое закон Фарадея? Законы электромагнитной индукции
- Закон электромагнитной индукции Ленца
Не однородная электрическая подача
D φ E = E D A
Electric Flux для поверхности GAUSSIAN
Electric Froue для поверхности GAUSSIAN
. d A = Q/ε 0
Где
Приведенное выше уравнение является одним из четырех уравнений Максвелла, также известных как закон Гаусса, относящихся к электрическому полю.
Похожие сообщения:
Электрический поток на единицу площади называется плотностью электрического потока.
D = φ E /A
Другие формы уравнений для плотности электрического потока следующие:
D = εE = Q/4πr 2
28 E = Q/4π407 2 29047 29047 29047 2 2
281.
E = q/4πε r ε 0 r 2
D = ε r ε 0 E
Где:
Это скалярная величина, единицей измерения которой является Кл/м 2 , т. е. поверхностная плотность заряда «σ».
е. поверхностная плотность заряда «σ».
Сила на единицу заряда известна как напряженность электрического поля.
E = F/Q
Где:
Формула напряженности электрического поля в вольтах на метр выглядит следующим образом:
ε = e/d
Формула магнитного потока:
Число магнитных линий, проходящих через площадь A , известно как магнитный поток.
Φ b = BA cosθ
Где
Это векторная величина, и общую форму магнитного потока можно рассчитать с помощью следующего уравнения:
Плотность магнитного потока Формула:
Магнитный поток на единицу площади называется плотностью магнитного потока в Теслах (веберов на метр 2 ) и является векторной величиной.

 Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о… Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было…
Ф.. В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о магнитном потоке, и что не было до сих пор достаточно определенно высказано или не было… Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о…
Ф.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand.
В этой книге содержится многое, на что не всегда обращается должное внимание, когда речь идет о… Как рассчитать магнитный поток через петлю?
Как рассчитать магнитный поток через петлю? )
)