Как найти Объем Параллелепипеда?
Поможем понять и полюбить математику
Начать учиться
316.1K
В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила.
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
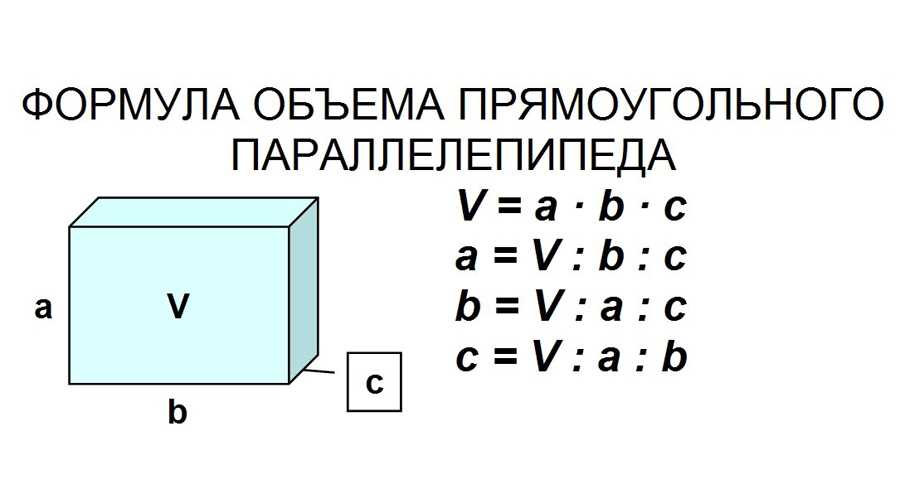
Объем прямоугольного параллелепипеда

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.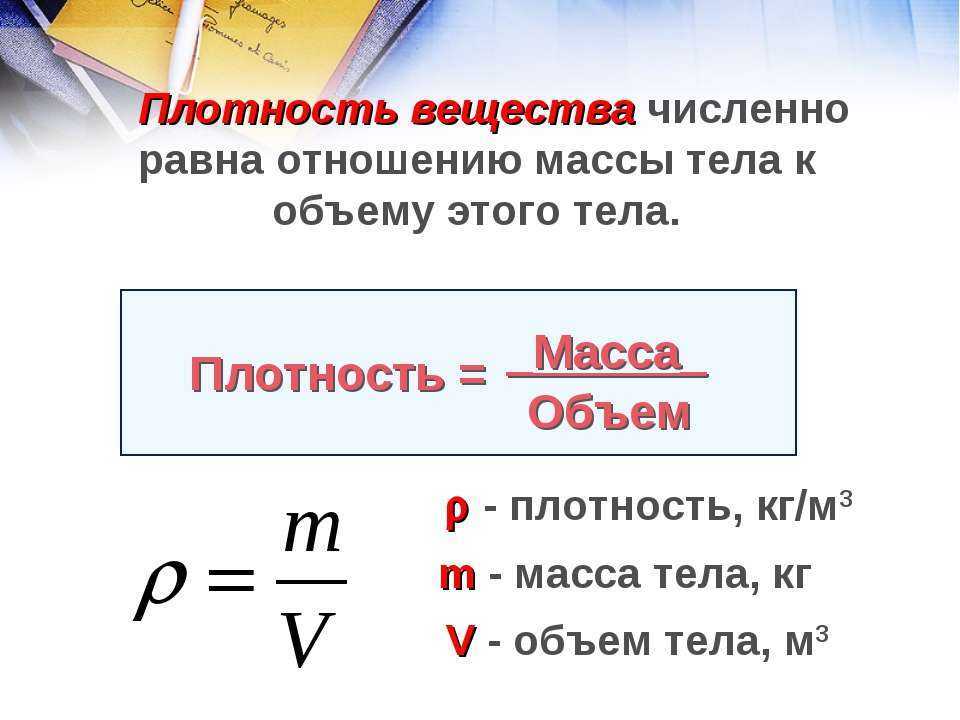
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.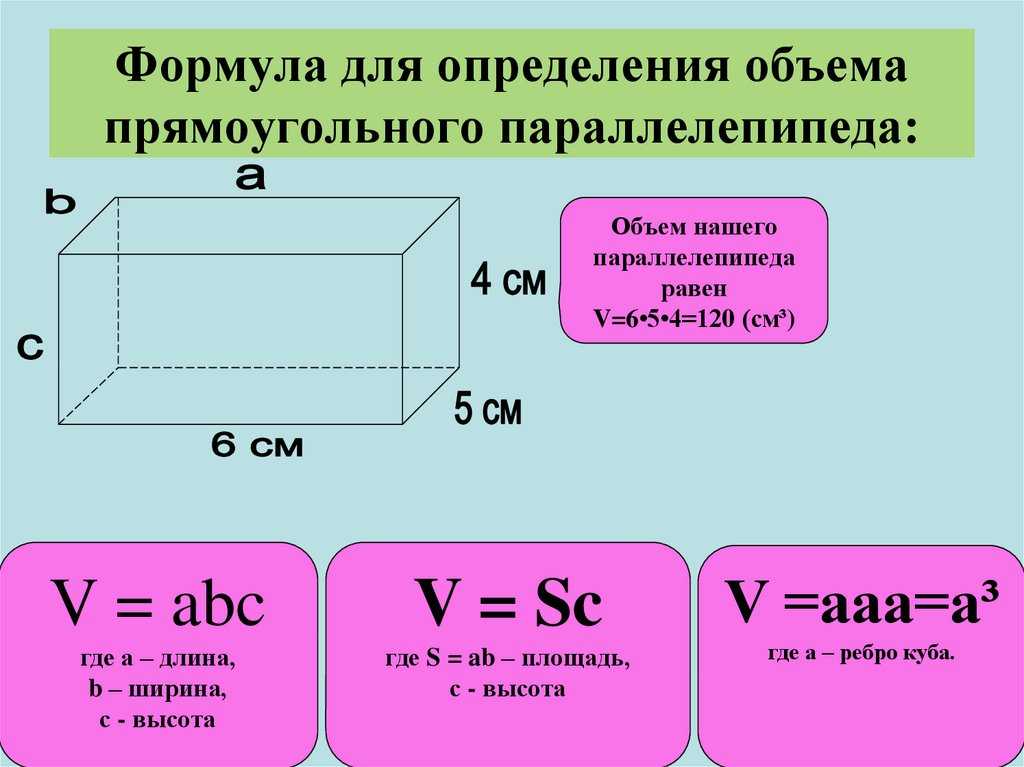
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.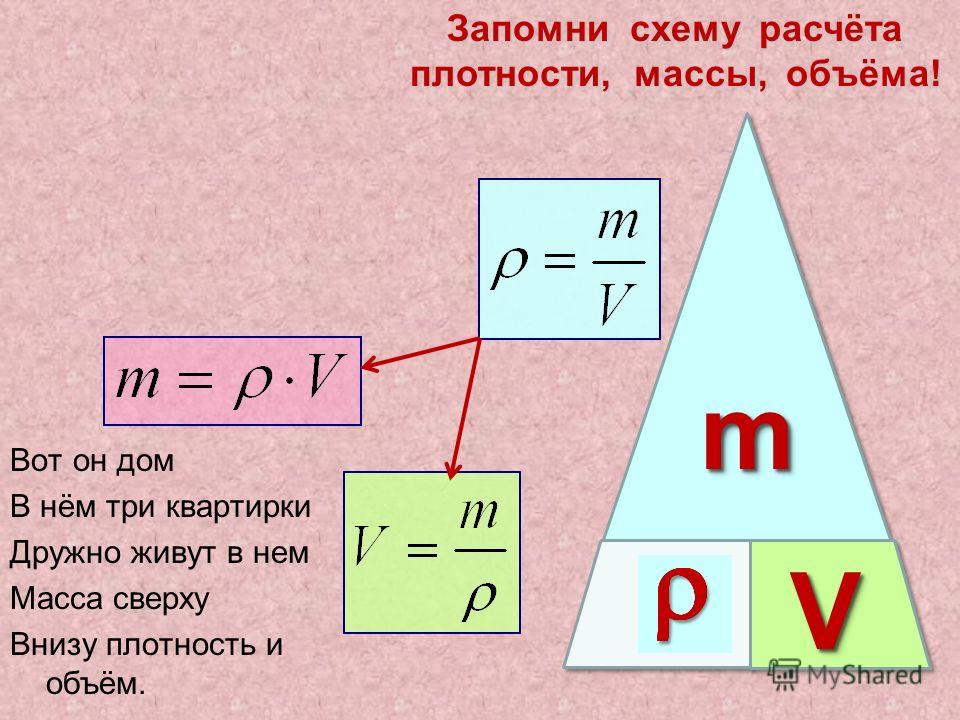
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. п. = 2 (ac + bc) |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
412.8K
Время, скорость, расстояние
К следующей статье
501. 5K
5K
Порядок действий в математике
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Как находится объем
Статьи › Находится
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
- Как найти объем формула
- Что такое объем и как его вычислить
- Как найти объем фигуры
- Как найти объем 5 класс формула
- Как вычислить V
- Чему равно V в физике объем
- Чему равен объем
- Как определить объем 7 класс
- Как рассчитать объем по размерам
- Как вычислить объем по массе
- Чему равен объем куба
- Как найти объем по массе
- Как находить объем 6 класс
- Как определить объем вещества
- В чем измеряется объем
- Как найти объем воды
- Как найти объем фигуры из кубиков
- Как вычислить объем в м3
- Как вычислить объем куба
- Как найти объем в математике 4 класс
- Как измеряется объем
Как найти объем формула
Следствие.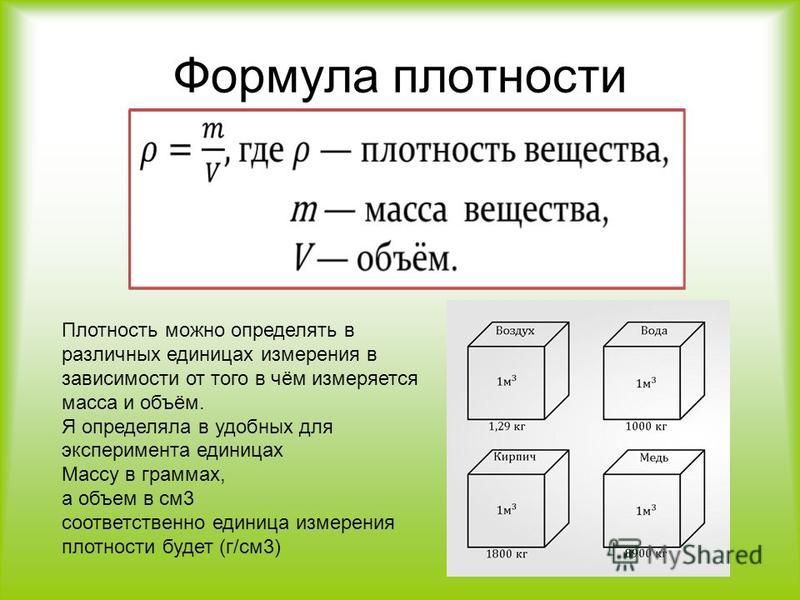 Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. V = S (основания) ⋅ h.
Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. V = S (основания) ⋅ h.
Что такое объем и как его вычислить
Объём — это количественная характеристика пространства, занимаемого телом или веществом. Другими словами, это то, сколько места занимает предмет. Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
Как найти объем фигуры
Чтобы вычислить объем, применяйте следующее правило — длину, ширину и высоту нужно перемножить между собой.
Как найти объем 5 класс формула
V = а · b · c = S · с
Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.
Как вычислить V
Формулы:
- V=a*b*h, где:
- a — длина основания (м),
- b — ширина основания (м),
- h — высота (м),
- V — объем (м3).

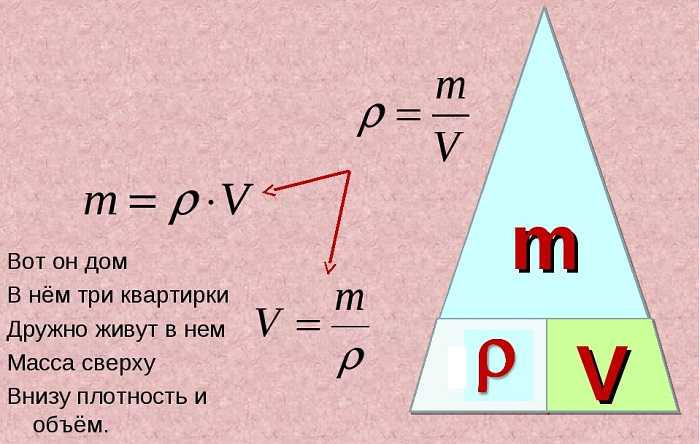
Чему равно V в физике объем
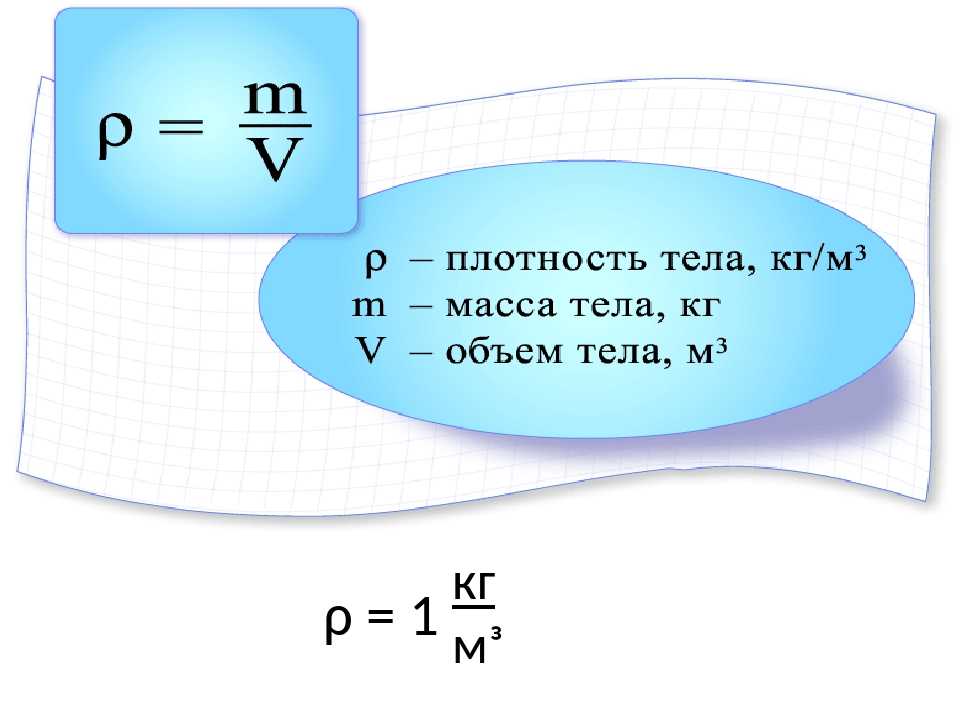
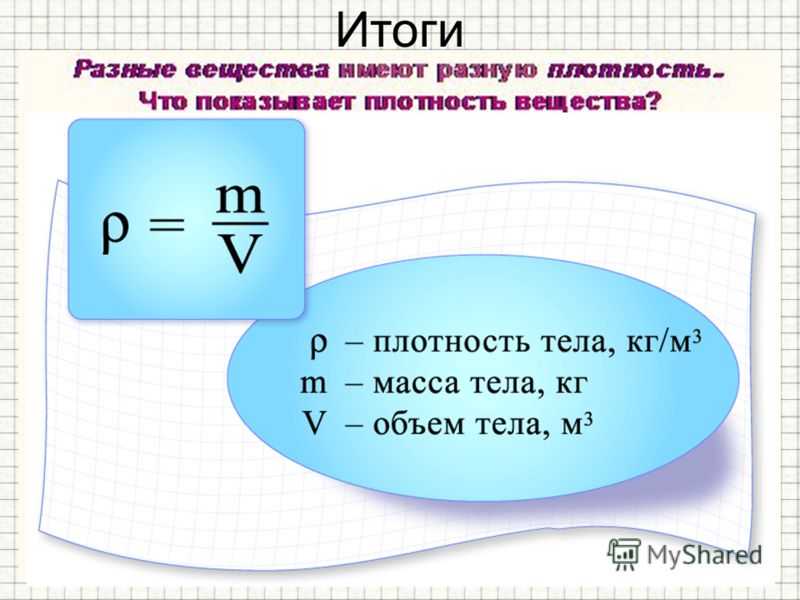
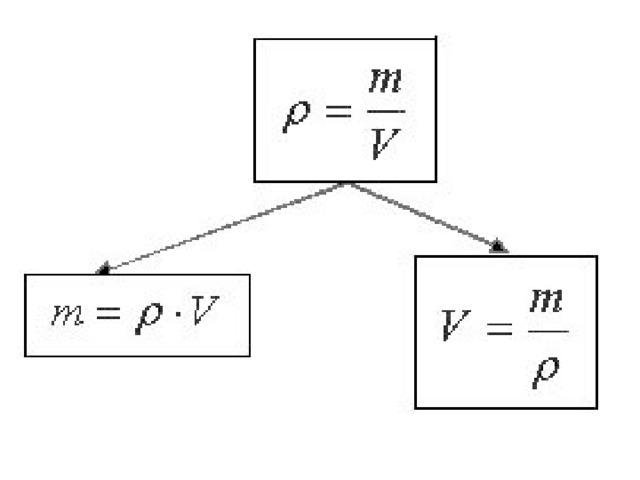
Для того, чтобы узнать массу нужно объем (х) поделить на плотность. Объем неизвестен, поэтому его отмечаем буквой х. Формула: V=m/p.
Чему равен объем
Формула объема.
Фигура | Формула |
|---|---|
Куб. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3. | V = s3 |
Как определить объем 7 класс
Если длина равна l 1, ширина l 2, высота l 3, тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3.
Как рассчитать объем по размерам
Расчет объема коробок
Размеры можно измерить с помощью обычной линейки или рулетки. Расчет объема, исходя из размера коробки, можно произвести по формуле: Формула для подсчета: V=a*b*h.
Как вычислить объем по массе
Вес можно рассчитать по формуле: m=V*p, где р — плотность, V — объем материала. 3. Ответ: Объем = масса / плотность.
3. Ответ: Объем = масса / плотность.
Как находить объем 6 класс
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. V = a * b * c; 2.
Как определить объем вещества
Ответы1. 1. Объём газов находится по формуле: V = n * Vm, где V — объём, n — количество вещества (в молях), Vm — молярный объём газа.
В чем измеряется объем
Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
Как найти объем воды
V — обьем воды, S — скорость наполнения, t — время:
- Чтобы найти обьем воды V, перемножим скорость наполнения (л/ч) — d на время t. V = d * t.
- Для нахождения времени t, необходимо разделить обьем воды на скорость наполнения p.
- Чтобы вычислить скорость наполнения S, разделим обьем V на скорость наполнения t.
 3=a*a*a — то есть сторона куба, возведенная в третью степень.
3=a*a*a — то есть сторона куба, возведенная в третью степень.Как найти объем в математике 4 класс
Как измеряется объем
Единицей объема в СИ считается кубический метр, его производные — кубический сантиметр, кубический дециметр и т. д. Жидкость измеряется в литрах. Для жидких и сыпучих веществ в разных странах используют различные внесистемные единицы — галлон, баррель.
- В чем измеряется объем
- Как вычислить V
- Как вычислить объем в м3
- Как вычислить объем куба
- Как вычислить объем по массе
- Как измеряется объем
- Как найти объем 5 класс формула
- Как найти объем воды
- Как найти объем по массе
- Как найти объем фигуры
- Как найти объем фигуры из кубиков
- Как найти объем формула
- Как находить объем 6 класс
- Как определить объем 7 класс
- Как определить объем вещества
- Как рассчитать объем по размерам
- Чему равен объем
- Чему равен объем куба
- Чему равно V в физике объем
- Что такое объем и как его вычислить
Плотность | Определение, символ, единицы измерения, формула и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
- Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Объем – формула, определение, расчет, примеры
Объем – это мера емкости, которую держит объект.
 Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:- Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
- Соедините противоположные стороны листа бумаги, не сгибая лист.
- Вы создали трехмерный объект, заключающий внутри себя пространство, из двухмерного листа.
1. Определение тома 2. Объем трехмерных фигур 3. 
Список формул объема 4. Как рассчитать объем? 5. Единицы объема 6. Калькулятор объема 7. Часто задаваемые вопросы по тому Определение тома
Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Объем 3D-фигур
Каждый объект в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами.
 Давайте посмотрим на объем этих твердых фигур в деталях.
Давайте посмотрим на объем этих твердых фигур в деталях.Объем кубоида
Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, ч . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.
Чтобы вычислить объем пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем кубоида = l × b × h
Объем куба
Куб является частным случаем параллелепипеда, все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³. Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.

Объем цилиндраТочно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.
Цилиндр представляет собой трубчатую конструкцию с двумя параллельными круглыми основаниями, соединенными изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h
Объем пирамиды
Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине. Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.
Объем конуса
Разница между конусом и пирамидой заключается в том, что основание конуса круглое, тогда как основание пирамиды представляет собой многоугольник.
 Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.Объем сферы
Объем сферы – это занимаемое ею пространство.
Объем сферы, радиус которой r равен 4/3 πr³.Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.
Список формул объема
Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (твердых) форм.
Как рассчитать объем?
Вот шаги для расчета объема любой твердой формы:
- Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т. д.
- Убедитесь, что все параметры имеют одинаковые единицы измерения.
- Подставьте значения в формулу объема соответствующих форм.

- Запишите единицы измерения в кубических единицах.
Давайте разберемся с шагами на примере.
Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr 2 h = (3,142)(25) 2 (1) = 1963,75 м 3 .
Объем баллона 1963,75 куб.м.Единицы объема
Единицей объема в СИ является кубический метр (м 3 ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.

Боковой блок Единица объема Метрический эквивалент Дюйм Кубические дюймы (в 3 ) 1 куб. дюйм = 16,387064 мл Ножка Кубические футы (футы 3 ) 1 куб. фут = 28,316846592 л см Кубический сантиметр (см 3 ) 1 кубический сантиметр = 1 мл Двор Кубический ярд (ярд 3 ) 1 куб.ярд = 764,554857984 л
1 куб.ярд = 0,764554857984 м 3Хотя стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.
Блок Эквивалентное преобразование 1 пинта (pt) 2 чашки 1 кварта (кварт) 2 балла 1 галлон 3,78 литра 1 литр 1000 кубических сантиметров Калькулятор объема
Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы.
 Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.☛Также проверьте:
- Калькулятор объема цилиндра
- Калькулятор объема сферы
- Калькулятор объема куба
- Калькулятор объема прямоугольного параллелепипеда
☛Статьи по теме
Ознакомьтесь со статьями, посвященными объему различных объемных форм.
- Объем конуса
- Объем цилиндра
- Объем кубоида
- Том Пирамиды
Примеры томов
Пример 1: Эдвин имеет конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.
Раствор.
Сосуд имеет форму конуса.
Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
∴ Объем судна 264 куб. дюйм
дюймПример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?
Раствор.
Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
В его структуре 15 кубиков. Итак, объем всей конструкции:
Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
∴ Объем конструкции 405 дюймов³.Пример 3: Если диаметр мяча 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14
Решение.
Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
Радиус шара 14/2 дюйма = 7 дюймов
Объем шара = 4/3 πr³
= [4/3 × 3,14 × (7)³]
= 1436,02 дюйма³
∴ Мяч содержит 1436,02 дюйма³ воздуха.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы в томе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по тому
Что означает объем?
Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
☛Загрузите прямо сейчас, чтобы попрактиковаться.
- Объемные листы
- Объем кубов Рабочие листы
- Объем конуса Рабочие листы
- Объем цилиндра Рабочие листы
Какая формула объема частичного конуса?
Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» – радиус верхней поверхности.

☛ Прочтите основы здесь:
- Объем правого кругового конуса
- Объем частичного конуса
- Объем конуса в числах Пи
Как найти объем пирамид?
Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.
☛ Также проверьте:
- Объем прямоугольной пирамиды
- Объем треугольной пирамиды
- Объем прямоугольной пирамиды
Как найти объем конуса?
Объем конуса составляет 1/3 объема цилиндра той же высоты и того же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Как найти объем цилиндра?
Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.
В чем разница между объемом и площадью?
Объем фигуры или твердого тела – это пространство, занимаемое им, которое также включает его высоту или глубину.
 Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.☛ Проверьте список важных математических формул:
- Формулы площади
- Формулы площади поверхности
- Геометрические формулы
- Формулы измерения
Каков объем мяча?
Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Какая формула объема цилиндра?
Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.
Как найти объем призмы?
Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» – это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).
☛Чек:
- Объем призмы
- Объем призм.


 п.)
п.)
 3=a*a*a — то есть сторона куба, возведенная в третью степень.
3=a*a*a — то есть сторона куба, возведенная в третью степень.

 Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
 Давайте посмотрим на объем этих твердых фигур в деталях.
Давайте посмотрим на объем этих твердых фигур в деталях.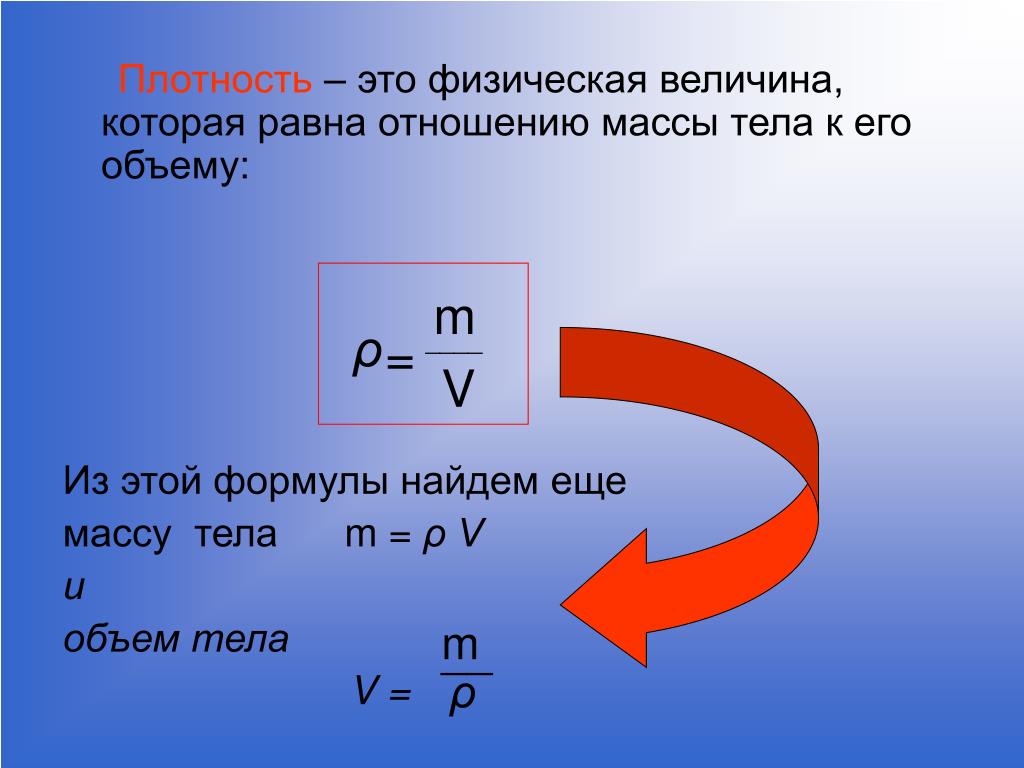
 Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
 Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов. дюйм
дюйм

 Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.