Главная
Формула как найти скорость по физике: 404 – Страница не найдена

Формула как найти скорость по физике: 404 – Страница не найдена

Содержание

Скорость в физике. Формула скорости

Эта тема будет полезна не только учащимся средней школы, но даже взрослым. Кроме того, статья будет интересна родителям, желающим объяснить своим детям простые вещи из естественных наук. Среди очень важных тем – это скорость в физике.

Довольно часто ученики не могут разобраться в решении задач, отличить имеющиеся виды скоростей, а еще сложнее понять научные определения. Здесь мы рассмотрим все на более доступном языке, чтобы было не только все ясно, но даже интересно. А вот запомнить некоторые вещи все же придется, так как технические науки (физика и математика) требуют заучивать наизусть формулы, единицы измерения и, конечно же, значения символов в каждой формуле.

Где встречается?

Для начала вспомним, что данная тема относится к такому разделу физики как механика, подразделу «Кинематика». Кроме того, изучение скорости на этом не заканчивается, оно будет и в последующих разделах:

  • оптика,
  • колебания и волны,
  • термодинамика,
  • квантовая физика и так далее.

Также понятие скорость встречается в химии, биологии, географии, информатике. В физике тема «скорость» встречается чаще всего и изучается углубленно.

Кроме того, данное слово употребляется в повседневной жизни всеми нами, особенно среди автомобилистов, водителей транспортной техники. Даже опытные кулинары иногда используют фразу, например, «взбить яичные белки миксером на средней скорости».

Что такое скорость?

Скорость в физике – это кинематическая величина. Означает расстояние, которое преодолевается телом за какой-то промежуток времени. Допустим, молодой человек движется от дома к магазину, преодолевая двести метров за одну минуту. Напротив, его старенькая бабушка пройдет тем же маршрутом за шесть минут мелкими шажками. То есть парень перемещается намного быстрее своей пожилой родственницы, так как развивает скорость гораздо больше, делая очень быстрые длинные шаги.

То же самое стоит сказать про автомобиль: одна машина едет быстрее, а другая медленнее, потому что скорости движения разные. Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.

Формула

На уроке в школе обязательно рассматривается формула скорости в физике для того, чтобы было удобно решать задачи.

  • V – это, соответственно, скорость движения;
  • S – расстояние, которое преодолевается телом при перемещении от одной точки в пространстве до другой;
  • t – время перемещения.

Следует запомнить формулу, потому что она пригодится в будущем при решении множества задач и не только. Например, вам может стать интересно, с какой скоростью дойдете от дома до работы или места учебы. Но вы заранее можете узнать расстояние по карте в смартфоне или на компьютере, либо по бумажному варианту, зная масштаб и имея при себе линейку. Далее вы засекаете время, перед тем, как начать движение. Придя на место назначения, смотрите, сколько минут или часов потребовалось пройти без остановки.

В чем измеряется?

Скорость чаще всего измеряется по системе единиц СИ. Ниже представлены не только единицы, но и примеры того, где они применяются:

  • км/ч (километр в час) – транспорт;
  • м/с (метр в секунду) – ветер;
  • км/с (километр в секунду) – космические объекты, ракеты;
  • мм/ч (миллиметр в час) – жидкости.

Давайте для начала разберемся, откуда взялась дробная черта и почему единица измерения именно такая. Обратите внимание по физике на формулу скорости. Что вы видите? В числителе стоит S (расстояние, путь). В чем измеряется расстояние? В километрах, метрах, миллиметрах. В знаменателе, соответственно, t (время) – часы, минуты, секунды. Отсюда и единицы измерения величины именно такие, как представлены в начале данного раздела.

Закрепим с вами изучение формулы скорости в физике следующим образом: какое расстояние преодолеет тело за конкретный промежуток времени? Например, человек пройдет 5 километров за 1 час. Итого: скорость движения человека – 5 км/ч.

От чего зависит?

Нередко учителя задают ученикам вопрос: “От чего зависит скорость?”. Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.

Во многих задачах по кинематике приходится строить графики зависимости, где по оси Х – время, а по оси Y – расстояние, путь. По таким изображениям можно легко оценить характер скорости движения. Стоит отметить, что во многих профессиях, связанных с транспортом, электрическими машинами часто применяются графики. Например, на железной дороге.

В нужный момент измеряем скорость

Есть еще одна тема, которая пугает учеников средней школы, – мгновенная скорость. В физике это понятие встречается как определение величины скорости в мгновенный промежуток времени.

Давайте рассмотрим простой пример: машинист ведет поезд, его помощник наблюдает за скоростью движения время от времени. Вдалеке виднеется знак ограничения скорости. Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.

Начало движения

Без начальной скорости физика не представляет практически ни одно движение транспортной техники. Что это за параметр? Это скорость, с которой начинает движение объект. Допустим, машина не может начинать движение моментально со скоростью 50 км/ч. Ей нужно разогнаться. Когда водитель нажимает педаль, автомобиль плавно начинает движение, например, со скоростью сначала 5 км/ч, потом постепенно 10 км/ч, 20 км/ч и так далее (5 км/ч и есть начальная скорость).

Конечно, можно совершить резкий старт, какой бывает у бегунов-спортсменов, при ударе теннисного мяча ракеткой, но все равно всегда существует начальная скорость.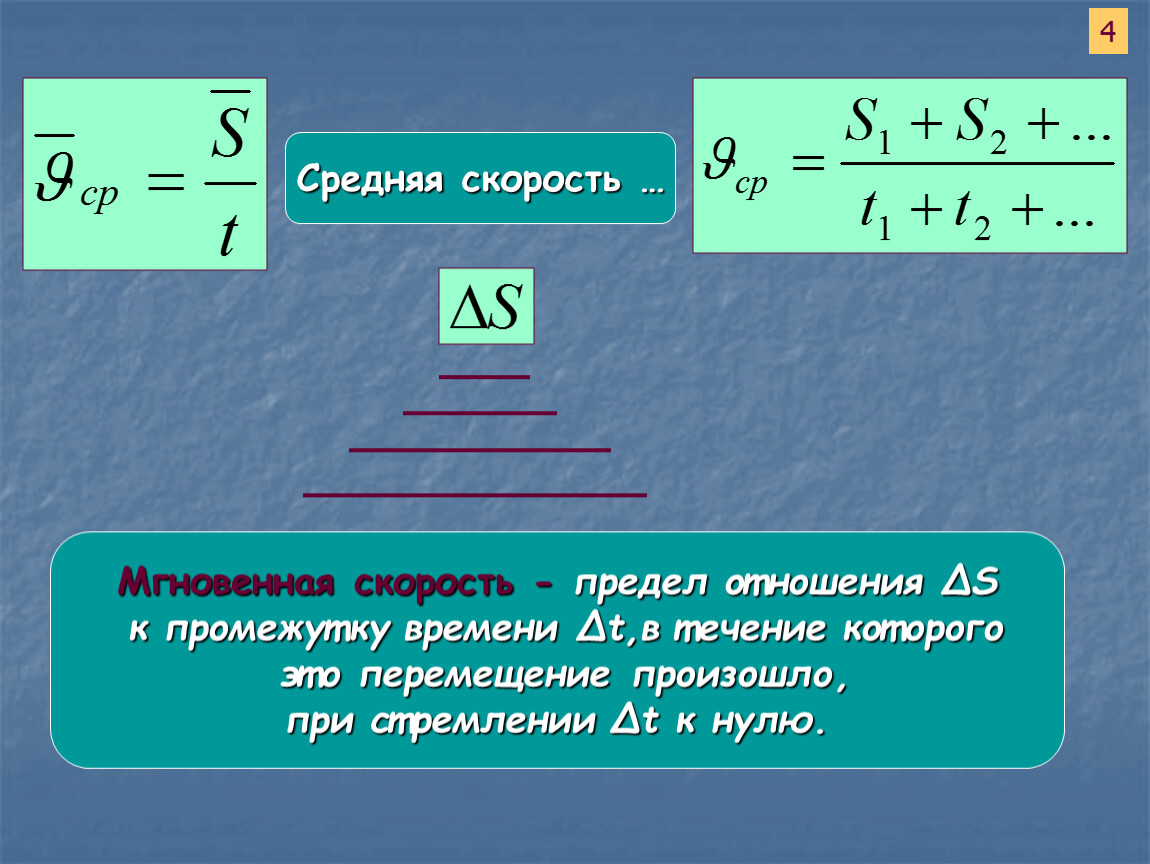 Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.

Равномерная скорость

Скорость в физике – это совокупность отдельных явлений и характеристик. Различают также равномерное и неравномерное движение, криволинейное и прямолинейное. Давайте приведем пример: человек идет по прямой дороге с одинаковой скоростью преодолевая из точки А в точку В расстояние 100 метров.

С одной стороны, это можно назвать прямолинейной и равномерной скоростью. Но если присоединить человеку очень точные датчики скорости, маршрута, то можно заметить, что разница все же есть. Неравномерная скорость – это когда скорость регулярно или постоянно меняется.

В быту и технике

Скорость движения в физике существует всюду. Даже микроорганизмы перемещаются, пусть и с очень медленной скоростью. Стоит отметить, что существует вращение, которое характеризуется также скоростью, но имеет единицу измерения – об/мин (обороты в минуту). Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).

В географии и химии

Даже вода имеет скорость движения. Физика всего лишь является дочерней наукой в сфере процессов, происходящих в природе. Допустим, скорость ветра, волны в море – это все измеряется привычными физическими параметрами, величинами.

Наверняка, многие из вас знакомы с фразой «скорость химической реакции». Только в химии это имеет иное значение, так как имеется в виду, за какое время произойдет тот или иной процесс. Например, марганцовка быстрее растворится в воде, если взболтать сосуд.

Скорость-невидимка

Существуют невидимые явления. Например, мы не можем видеть, как перемещаются частицы света, различных излучений, как распространяется звук. Но если бы не было движения их частиц, то никакое бы из этих явлений не существовало в природе.

Информатика

Практически каждый современный человек сталкивается с понятием «скорость» во время работы на компьютере:

  • скорость Интернета;
  • скорость загрузки страниц;
  • быстрота загрузки процессора и так далее.

Примеров скорости движения в физике можно привести огромное множество.

Внимательно прочитав статью, вы познакомились с понятием скорости, узнали, что она из себя представляет. Пусть данный материал поможет вам углубленно изучить раздел «Механика», проявить к нему интерес и побороть страх при ответах на уроках. Ведь скорость в физике – это часто встречающееся понятие, которое легко запомнить.

Академия занимательных наук. Физика – Формула расчёта скорости. Определение вектора скорости. Видеоуроки физики

Формула расчёта скорости. Определение вектора скорости. Видеоуроки физики

Выпуск 13

В видеоуроке физики от Академии занимательных наук профессор Кварк со своими ассистентами познакомят ребят с понятием скорости. Это очень нужное знание, которое может здорово пригодиться в жизни. Речь пойдет о формуле расчёта скорости и её применении на практике, а также про определение вектора скорости, которое может понадобиться, если от цели нас начнёт отклонять какая-нибудь сила.

Формула расчёта скорости

Как узнать, за сколько минут нужно выйти из дома, чтобы не опоздать в школу? При решении этой задачи на помощь приходит формула расчёта скорости. Формула расчёта скорости выглядит так: V=S/t Это означает, что для того, чтобы найти скорость, нужно пройденное расстояние разделить на время, за которое оно было пройдено. Достаточно лишь немного изменить  формулу расчёта скорости и мы получим формулу для расчёта необходимого на дорогу времени. Скорость идущего человека равна приблизительно 5 километров в час. Длина одного квартала составляет около 200 метров. Если, к примеру, школа находится в пяти кварталах от дома, время, за которое мы дойдём до неё равно примерно за 10 минут. А что если нам нужно вычислить, за какое время мы доберёмся до пункта назначения по реке, на пароходе? Казалось бы, в этом случае формула расчёта скорости должна быть той же самой. Но на самом деле формула расчёта скорости должна быть немного дополнена. Дело в том, что у реки есть течение.

И в зависимости от того, в какую сторону плывёт пароход (вверх по течению или вниз), нужно отнять от его скорости скорость течения или прибавить её. Если пароход плывёт по течению, формула расчёта времени его пути будет такой: t=  S/(Vпар.+Vтеч.)

Определение вектора скорости

А как же быть в случаях, когда мы плывём не против течения и не по течению? В этих случаях течение вмешивается в наши планы и мы можем оказаться совсем не там, где рассчитывали. Дело в том, что скорость это векторная величина. Это значит, что скорость не существует без направления. Вектор как раз и означает направление. Определение вектора скорости поможет нам рассчитать, какое действие окажет течение на нас. Благодаря такому расчёту станет возможным внести поправку в вектор нашего движения и мы прибудем точно в то место, в какое собирались.Таким образом, можно сказать, что скорость — это векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта.

Средняя скорость молекул

В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.

Средняя скорость движения молекул

Средняя скорость движения молекул называется также скоростью теплового движения молекул.

Определение 1

Формула средней относительной скорости молекул в физике представлена следующим выражением:

υotn=28kTπm0=2υ.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Средняя квадратичная скорость

Средняя квадратичная скорость движения молекул газа это следующая величина:

υkυ=1N∑i=1Nυi2

Формулу средней квадратичной скорости можно переписать так:

υkυ2=∫0∞υ2Fυdυ.

Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:

υkυ=3kTm0=3RTμ

Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:

p=13nm0υkυ,

где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.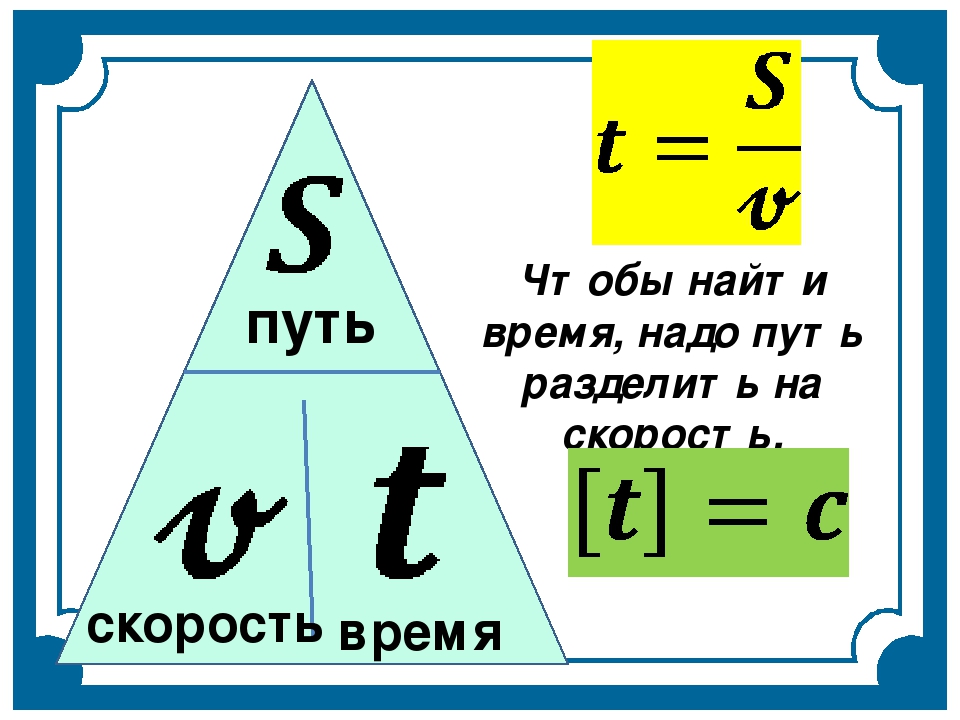

Пример 1

Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).

Рисунок 1

Решение

Запишем выражение для средней скорости движения молекул газа следующим образом:

υ=8kTπm0

Из графика видно, что p~ρ или p=Cρ,  где C – это некоторая константа.

m0=ρn, p=nkT=Cρ→kT=Cρn

Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:

υ=8kTπm0=8Cρπnnρ=8Cπ

Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.

Пример 2

Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?

Решение

Применим выражение для υkυ:

υkυ=3RTμ

Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:

pV=mμRT=NNART.

Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:

p=nNART→RT=pNAn

Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:

υkυ=3pNAμn

Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.

Автор: Роман Адамчук

Преподаватель физики

Текстовые задачи на среднюю скорость

Средняя скорость – есть отношение всего пройденного пути ко всему затраченному времени.

Задача 1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью км/ч, а вторую половину времени – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть t часов – полное время движения автомобиля, тогда средняя скорость равна:

км/ч.

Ответ: 70.

Задача 2. Первые два часа автомобиль ехал со скоростью км/ч, следующий час – со скоростью км/ч, а затем два часа – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Тогда

км/ч.

Ответ:

Задача 3. Первую треть трассы автомобиль ехал со скоростью км/ч, вторую треть – со скоростью км/ч, а последнюю – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть км – весь путь автомобиля, тогда средняя скорость равна:

км/ч.

Ответ:

Задача 4. Пу­те­ше­ствен­ник пе­ре­плыл море на яхте со сред­ней ско­ро­стью км/ч. Об­рат­но он летел на спор­тив­ном са­мо­ле­те со ско­ро­стью км/ч. Най­ди­те сред­нюю ско­рость пу­те­ше­ствен­ни­ка на про­тя­же­нии всего пути. Ответ дайте в км/ ч.

Решение: + показать

Пусть путь, что проделал путешественник –

Время, затраченное на путь в один конец, – ч,

время, затраченное на путь в другой конец,  – ч.

Тогда

км/ч.

Ответ:

Вы можете пройти тест по теме «Задачи на среднюю скорость»

Примеры решенных задач по физике -Контрольная 1(гармонические колебания, плоские волны, кольца Ньютона, дифракция, поляризация света)

Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд. 

    № 304

    Точка совершает гармонические колебания с амплитудой А=10 см и периодом Т=5 с. Определите для точки : 1) максимальную скорость, 2) максимальное ускорение.

    Дано : A=10 см=0.1 м

                 Т=5 с

    Найти : vmax , amax

                                                                 Решение.

    Уравнение гармонического колебания точки имеет вид :

                              x=Acos(ωt+φ)                                                        (1)

    Формулу скорости получим, взяв первую производную по времени от смещения :

                            v==dx/dt=-Aωsin(ωt+φ)

    Максимальная скорость точки равна :

                            vmax=-Aω                                            (2)  ,  где А – амплитуда колебаний ; ω – круговая частота колебаний.

    Круговая частота колебаний ω связана с периодом колебаний Т выражением :

                               ω=2π/T                                            (3)

    С учётом (3) формула (2) примет вид :

                                 vmax=-2πA/T                                  (4)

    Ускорение точки найдём, взяв производную по времени от скорости :

                                 a==dv/dt=-Aω2cos(ωt+φ)             

    Максимальное ускорение, равно :

                                 amax=-Aω2                                      (5)

    С учётом (3) перепишем формулу (5) в виде :

                                 amax=-4π2A/T2                               (6)

    Производя вычисления по формулам (4) и (6), найдём максимальные скорость и ускорение точки.

                                  vmax=-2×3.14×0.1/5=-0.13 м/с

                                  amax=-4×3.142×0.1/52=-0.16 м/с2

    Ответ : vmax=-0.13 м/с ; amax=-0.16 м/с2

 

                № 314

    Волна с периодом Т=1.2 с и амплитудой колебания А=2 см распространяется со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 45 м от источника волн в тот момент, когда от начала колебаний источника прошло время t=4 с?  

    Дано :  T=1.2 c

                 A=2 см=0.02 м

                 v=15 м/с

                  x=45 м

                  t=4 c

    Найти : y

                                                                       Решение.

    Уравнение плоской волны имеет вид :

                            y(x,t)=Acos(ωt-kx)                               (1)  ,  где y – смещение точек среды с координатой x в момент времени t ; ω – круговая частота ; k – волновое число.

    Волновое число k связано с длиной волны λ выражением :

                              k=2π/λ                   (2)  , где λ=vT ; v – скорость распространения колебаний ; T – период колебаний.

    Циклическая частота ω связана с периодом Т выражением :

                             ω=2π/T                  (3)

    С учётом (2) и (3) уравнение (1) примет вид :

                            y(x,t)=Acos(2πt/T-2πx/(vT))=Acos            (4)

    Вычисления по формуле (4), дают :

                            y(45 ; 4)=0.02×cos=0.01 м=1 см

    Ответ : y(45 ; 4)=1 см.

 

 

 

№ 324

    Определить радиус второго темного кольца Ньютона в отраженном свете, если прибор, состоящий из плосковыпуклой линзы с радиусом кривизны 8 м и плоской пластины освещается монохроматическим светом с длиной волны 640 нм.

    Дано: λ=640 нм=6.5×10-7 м

                 R=8 м

                 k=2

    Найти: r2.

                                                                       Решение.

    Радиус темных колец Ньютона в отражённом свете определяется формулой:

                      rk=                                                       (1)

    где k – номер кольца; R – радиус кривизны линзы; λ – длина волны.

    3,2∙10-3 м.

    Ответ: r2=3,2∙10-3 м.

 

 

№ 334

    Постоянная дифракционной решётки в n=4 раза больше длины световой волны монохроматического света, нормально падающего на её поверхность. Определить угол α между двумя  первыми симметричными дифракционными максимумами.

    Дано: n=4                                                           

                k=1

    Найти: α

                                                                        Решение.

    Постоянная дифракционной решётки d , длина волны λ и угол  отклонения лучей соответствующий К – му дифракционному максимуму, связаны соотношением

                       dsin=kλ , или  sin=kλ/d                                             (1)

где к – порядок максимума (в данном случае к=1). Учитывая, что λ/d=1/n перепишем формулу (1) в виде:

                        sin=k/n                                                                           (2)

    Из рисунка видно, что угол α равен удвоенному углу . Тогда формула (2) примет вид:

               sin(α/2)=k/n , откуда   α=2arcsin(k/n)

    Подставим в последнюю формулу числовые значения и вычислим:

                   α=2arcsin(1/4)=29°

    Ответ: α=29°.

№ 346

    На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10%?

    Дано : k=0.1

    Найти : n%

                                                                     Решение.

 

        

    Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного лучепреломления на два пучка : обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа. Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок (о) вследствие полного отражения от грани AB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму. При этом интенсивность света уменьшается вследствие поглощения в веществе николя. Таким образом, интенсивность света, прошедшего через призму :

                                      I1=0.5I0(1-k)

    где k=0.1 – относительная потеря интенсивности света в николе ; I0 – интенсивность естественного света, падающего на николь.

    Относительное уменьшение интенсивности света получим, разделив интенсивность I0 естественного света, падающего на первый николь, на интенсивность I1 поляризованного света :

                                                             (1)

    Вычисления по формуле (1) дают :

                                       =2.2

    Процентное уменьшение интенсивности :

                          n%==54. 5%

    Ответ : при прохождения света через призму интенсивность уменьшится на 54.5%.

 

 

 

 

 

 

 

 

№ 356

 

Найти длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.

    Дано : n=1

    Найти : λ

                                                                   Решение.

    Длина волны де Бройля λ частицы зависит от её импульса p и определяется формулой :

                                  λ=2πħ/p                                                     (1)

    Импульс частицы можно определить, если известна её скорость v. Связь импульса со скоростью для нерелятивистского (когда v<<c) и для релятивистского (когда v≈c) случаев соответственно выражается формулами :

                    p=m0v        (2)   ;                        p=        (3)

    Формула (1) с учётом соотношений (2) и (3) запишется соответственно в нерелятивистском и релятивистском случаях :

                    λ=     (4)   ;                     λ=     (5)

    Найдём скорость электрона на круговой орбите атома водорода, находящегося в основном состоянии, из следующих соображений. Согласно теории Бора, радиус r электронной орбиты и скорость v электрона на ней связаны равенством mvr=nħ. Так как нам требуется скорость электрона на первой орбите, то главное квантовое число n=1 и равенство примет вид :

                            mvr=ħ

    Откуда скорость электрона :

                            v=                                                              (6)

    где ħ – постоянная Планка (ħ=1.05×10-34 Дж·с) ; m – масса покоя электрона

(m=9.11×10-31 кг) ; a – радиус первой орбиты (а=5.29×10-11 м – Боровский радиус).

    Найдём скорость электрона, произведя вычисления по формуле (6) :

                            v= м/с

    Следовательно, можно применить формулу (4). С учётом (6) формула (4) примет вид :

                            λ=2πa                                                                 (7)

    Вычисления по формуле (7)  дают :

                            λ=2×3.14×5.29×10-11=3. 3×10-10 м

    Ответ : λ=3.3×10-10 м.=0.33 нм.

 

 

Скорость и скорость – Практика – Гипертекст по физике

Практика

практическая задача 1

Однажды я пошел гулять. Я шел на север 6,0 км со скоростью 6,0 км / ч, а затем на запад 10 км со скоростью 5,0 км / ч. Определите среднее…
  1. скорость
  2. скорость
… На весь путь.
раствор

  1. Средняя скорость

    Эта проблема обманчиво проста. Усреднение преподается в начальной школе, что делает это элементарной проблемой.Верно?

    6,0 км / ч + 5,0 км / ч = 5,5 км / ч
    2
    Неправильный метод усреднения

    Метод сложения и разделения работает только при усреднении элементов равного веса. Средний возраст учеников в классе – это сумма их возрастов, деленная на количество учеников только потому, что каждый ученик имеет одинаковую значимость (ученик, ученик, ученик,…). Однако в этой задаче два отрезка прогулки существенно различаются. Вторая «половина» была фактически большей частью прогулки. Он несет больший вес, чем более короткая первая «половина». Таким образом, метод сложения и разделения работать не будет.

    Вернемся к нашему определению. Поскольку скорость – это скорость изменения расстояния во времени, нам понадобится как пройденное расстояние, так и время, необходимое для завершения прогулки. После того, как мы определим оба этих числа, остальное будет несложно.

    ∆ т =
    ∆ т 1 = 6.0 км = 1,0 ч
    6,0 км / ч
    ∆ т 2 = 10 км = 2,0 ч
    5,0 км / ч
    v =
    v = 6. 0 км + 10 км
    1,0 ч + 2,0 ч
    v = 5.3 км / ч

    Посмотрите внимательно на расчеты справа. Обратите внимание, что формула содержит символы ∆ (дельта), но я добавил расстояния в числителе и время в знаменателе. Это потому, что ∆ не означает разницу, это означает изменение. Во время прогулки моя позиция не изменилась: с 6,0 км, на 10 км, сначала на 6,0 км и , затем на 10 км, итого изменение на 16 км.

  2. Средняя скорость

    Скорость – это скорость изменения смещения во времени. Скорость – это вектор, а значит, задача должна решаться графически. Нарисуйте стрелку, указывающую на верх страницы (север). Обозначьте это 6 км. Нарисуйте еще одну стрелку влево (на запад), начиная с предыдущей (расположенной головой к хвосту). Сделайте его немного длиннее и обозначьте 10 км. Нарисуйте третью стрелку, начиная с хвоста первой и заканчивая головкой второй.Поскольку север и запад расположены под прямым углом друг к другу, результирующее смещение является гипотенузой прямоугольного треугольника. Используйте теорему Пифагора, чтобы найти его величину и касательную, чтобы определить направление.

    r = √ [(6,0 км) 2 + (10 км) 2 ]
    r = 11,6619… км
    тангенс угла θ = напротив = 10 км
    смежный 6.0 км
    θ = 59 ° на западной стороне севера

    Разделите смещение на время, чтобы получить скорость.

    против =
    против =
    11,6619… км при 59 ° з.д. от с.ш.
    3.0 ч.
    v = 3,9 км / ч при 59 ° з.д. от с.ш.

практическая задача 2

Как быстро точка на экваторе движется из-за вращения Земли?

раствор

Обратите внимание, что в этой задаче не указаны числа. Когда для решения проблемы требуется числовое значение, а это число не указано, это может означать одно из нескольких.

  • Посмотри! Он может появиться где-нибудь в учебнике, который вы используете – на внутренней стороне обложки, в приложении или в тексте главы, над которой вы сейчас работаете. Его можно найти в справочной таблице, которую раздают некоторые учителя. Стандартизированные экзамены обычно имеют собственную справочную таблицу.
  • Знай! Некоторые числа – это числа, которые вам просто необходимо знать. В этой задаче есть одно релевантное число, которое знает почти каждый. Вы также можете запомнить определенные числа от преподавателя или профессора.
  • Посчитайте! Возможно, есть способ найти номер, который вам нужно знать, используя другие числа, указанные в задаче.
  • Забудьте об этом! Может быть, вам действительно не нужен номер, который, как вы думаете, вам нужен. Может, вы ошиблись. Особенно в условиях тестирования очень маловероятно, что вам могут задать вопрос, требующий числового значения, которое вы не можете найти, не знаете или не можете вычислить. Возможно, есть другой способ решения этой проблемы.

Чтобы рассчитать скорость, вам понадобится расстояние и время.На какое расстояние переместится точка на экваторе за удобный промежуток времени? Что ж, надеюсь, вы знаете, что Земля один раз вращается вокруг своей оси каждый день. Вы также должны знать, как рассчитать продолжительность дня в секундах. (Сутки – это период вращения Земли, для которого заглавными буквами является T .) В течение дня точка на экваторе Земли прошла бы расстояние, равное окружности Земли. Радиус Земли – это число, которое обычно встречается в учебниках и справочных таблицах.Теперь проблему можно решить.

v =
v =
2π (6,37 × 10 6 м)
24 × 3600 с
v = 463 м / с

Это примерно на 75% быстрее, чем скорость звука в воздухе при комнатной температуре (343 м / с).Позже предстоит решить интересную проблему: если Земля вращается так быстро, почему предметы на экваторе не улетают в космос?

практическая задача 3

Обычная мера астрономических расстояний – световой год. Это расстояние, на которое луч света прошел бы в вакууме за один год. Определите размер светового года в метрах.

раствор

Астрономические расстояния настолько велики, что использование метров затруднительно. Для действительно больших расстояний световой год – лучшая единица измерения. световых лет. – это расстояние, которое свет прошел бы за один год в вакууме. Поскольку скорость света велика, а год длинный, световой год – довольно хорошая единица измерения для астрономии. Один световой год составляет около десяти петаметров (десять квадриллионов метров), как показывает следующий расчет.

Начните с определения скорости и решите ее для расстояния. Традиционный символ скорости света – c от латинского слова быстрота – celeritas .

Номера на входе, на выходе.

∆ с = c ∆t
∆ с = (3,00 × 10 8 м / с) (365,25 × 24 × 3600 с)
∆ с = 9,46 × 10 15 м
Δ с ≈ 10 петаметров

Поскольку и скорость света, и год имеют точно определенные значения в Международной системе единиц, световой год может быть указан с излишне большим количеством значащих цифр.

Некоторые расстояния в световых годах указаны ниже.

  • Расстояние до Проксимы Центавра (ближайшей к Солнцу звезды) составляет 4,3 световых года.
  • Диаметр Млечного Пути (совокупность звезд, включающая Солнце и все звезды, видимые невооруженным глазом) составляет около 100 000 световых лет.
  • Расстояние до Андромеды (ближайшей галактики за пределами Млечного Пути) составляет около 2 миллионов световых лет.
  • Расстояние до края Вселенной (наблюдаемой ее части) 13.8 миллиардов световых лет.

практическая задача 4

Проблема только для жителей США. Преобразуйте 60 миль в час (обычная скорость на шоссе) в…
  1. км / ч
  2. м / с
раствор

Каждый должен знать (или хотя бы осознать после небольшого размышления), что есть…

∆ т = 60 × 60 = 3600 с

в час. Многие американцы, любители легкой атлетики, знают, что четыре круга вокруг 400-метровой открытой трассы – это почти одна миля.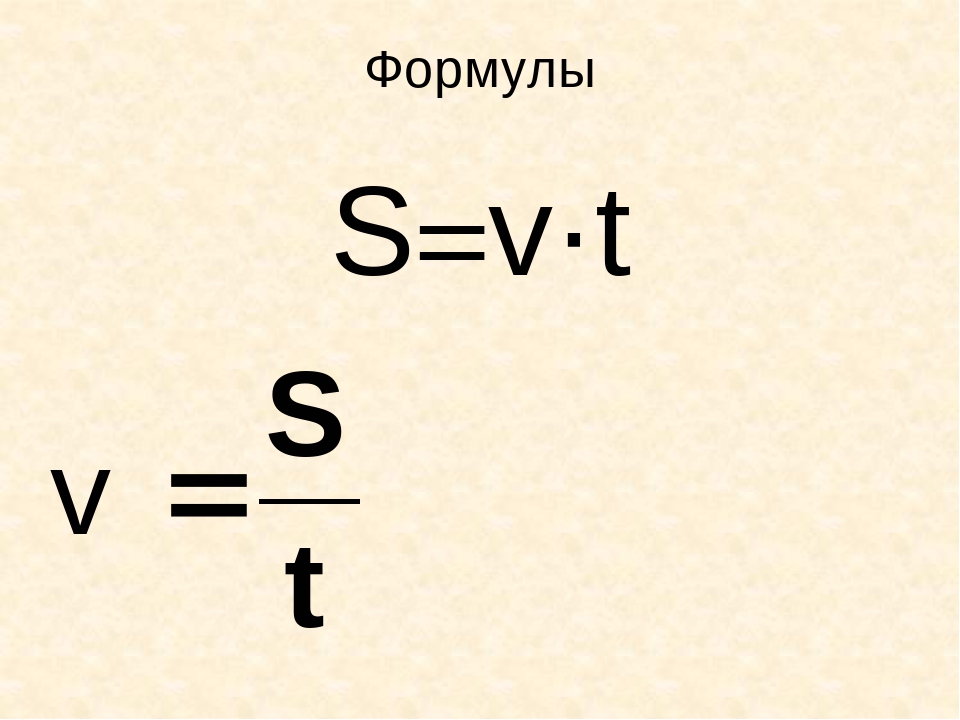

∆ с = 1 миля ≈ 4 × 400 м = 1600 м = 1,6 км

Точнее точно… на самом деле, самое точно… собственно, точно по определению…

∆ с = 1 миля = 1609,344 м = 1,609344 км

  1. Первый ответ…

    v =
    v =
    v = 60 (1.609344 км)
    1 ч
    v = 96,6 км / ч

    Для сравнения: ограничение скорости на многих канадских шоссе составляет 100 км / ч.

  2. Ответ второй…

    v =
    v =
    v = 60 (1609. 344 м)
    3600 с
    v = 26,8 м / с

    Обратите внимание, что число с международными единицами измерения немного меньше половины значения числа с британо-американскими единицами. Я привык к милям в час, но для работы мне нужно хорошо разбираться в м / с. Хорошее практическое правило для сравнения скоростей -…

    разделите на 2 и вычтите немного при преобразовании из миль в час в м / с

    или…

    умножьте на 2 и добавьте немного при преобразовании из м / с в миль / ч.

Скорость и скорость – Ресурсы – Гипертекст по физике

  • … смещение
  • скорость
  • ускорение…
Гипертекст по физике
© 1998–2021 Гленн Элерт
Автор, иллюстратор, веб-мастер

Нет постоянных условий.

  1. Механика
    1. Кинематика
      1. Движение
      2. Расстояние и перемещение
      3. Скорость и скорость
      4. Разгон
      5. Уравнения движения
      6. Свободное падение
      7. Графики движения
      8. Кинематика и расчет
      9. Кинематика в двух измерениях
      10. Снарядов
      11. Параметрические уравнения
    2. Динамика I: Сила
      1. Силы
      2. Сила и масса
      3. Действие-реакция
      4. Масса
      5. Динамика
      6. Статика
      7. Трение
      8. Силы в двух измерениях
      9. Центростремительная сила
      10. Кадры справки
    3. Энергия
      1. Работа
      2. Энергия
      3. Кинетическая энергия
      4. Потенциальная энергия
      5. Сохранение энергии
      6. Мощность
      7. Простые машины
    4. Dynamics II: Импульс
      1. Импульс и импульс
      2. Сохранение импульса
      3. Импульс и энергия
      4. Импульс в двух измерениях
    5. Вращательное движение
      1. Кинематика вращения
      2. Инерция вращения
      3. Вращательная динамика
      4. Статика вращения
      5. Угловой момент
      6. Энергия вращения
      7. Прокатный
      8. Вращение в двух измерениях
      9. Сила Кориолиса
    6. Планетарное движение
      1. Геоцентризм
      2. Гелиоцентризм
      3. Вселенская гравитация
      4. Орбитальная механика I
      5. Гравитационная потенциальная энергия
      6. Орбитальная механика II
      7. Плотность вытянутых тел
    7. Периодическое движение
      1. Пружины
      2. Генератор простых гармоник
      3. Маятники
      4. Резонанс
      5. Эластичность
    8. Жидкости
      1. Плотность
      2. Давление
      3. Плавучесть
      4. Расход жидкости
      5. Вязкость
      6. Аэродинамическое сопротивление
      7. Режимы потока
  2. Теплофизика
    1. Тепло и температура
      1. Температура
      2. Тепловое расширение
      3. Атомная природа вещества
      4. Закон о газе
      5. Кинетико-молекулярная теория
      6. Фазы
    2. Калориметрия
      1. Явное тепло
      2. Скрытое тепло
      3. Химическая потенциальная энергия
    3. Теплопередача
      1. Проводимость
      2. Конвекция
      3. Радиация
    4. Термодинамика
      1. Тепло и работа
      2. Диаграммы давление-объем
      3. Двигатели
      4. Холодильники
      5. Энергия и энтропия
      6. Абсолютный ноль
  3. Волны и оптика
    1. Волновые явления
      1. Природа волн
      2. Периодические волны
      3. Интерференция и суперпозиция
      4. Интерфейсы и барьеры
    2. Звук
      1. Природа звука
      2. Интенсивность
      3. Эффект Доплера (звук)
      4. Ударные волны
      5. Дифракция и интерференция (звук)
      6. Стоячие волны
      7. ударов
      8. Музыка и шум
    3. Физическая оптика
      1. Природа света
      2. Поляризация
      3. Эффект Доплера (световой)
      4. Черенковское излучение
      5. Дифракция и интерференция (свет)
      6. Тонкопленочная интерференция
      7. Цвет
    4. Геометрическая оптика
      1. Отражение
      2. Преломление
      3. Зеркала сферические
      4. Сферические линзы
      5. Аберрация
  4. Электричество и магнетизм
    1. Электростатика
      1. Электрический заряд
      2. Закон Кулона
      3. Электрическое поле
      4. Электрический потенциал
      5. Закон Гаусса
      6. Проводников
    2. Электростатические приложения
      1. Конденсаторы
      2. Диэлектрики
      3. Батареи
    3. Электрический ток
      1. Электрический ток
      2. Электрическое сопротивление
      3. Электроэнергия
    4. цепей постоянного тока
      1. Резисторы в цепях
      2. Батареи в цепях
      3. Конденсаторы в цепях
      4. Правила Кирхгофа
    5. Магнитостатика
      1. Магнетизм
      2. Электромагнетизм
      3. Закон Ампера
      4. Электромагнитная сила
    6. Магнитодинамика
      1. Электромагнитная индукция
      2. Закон Фарадея
      3. Закон Ленца
      4. Индуктивность
    7. цепей переменного тока
      1. Переменный ток
      2. RC цепи
      3. Цепи РЛ
      4. Цепи LC
    8. Электромагнитные волны
      1. Уравнения Максвелла
      2. Электромагнитные волны
      3. Электромагнитный спектр
  5. Современная физика
    1. Относительность
      1. Пространство-время
      2. Масса-энергия
      3. Общая теория относительности
    2. Quanta
      1. Излучение черного тела
      2. Фотоэффект
      3. Рентгеновские снимки
      4. Антиматерия
    3. Волновая механика
      1. Волны материи
      2. Атомарные модели
      3. Полупроводники
      4. Конденсированные вещества
    4. Ядерная физика
      1. Изотопы
      2. Радиоактивный распад
      3. Период полураспада
      4. Энергия связи
      5. Деление
      6. Fusion
      7. Нуклеосинтез
      8. Ядерное оружие
      9. Радиобиология
    5. Физика элементарных частиц
      1. Квантовая электродинамика
      2. Квантовая хромодинамика
      3. Квантовая динамика вкусов
      4. Стандартная модель
      5. Помимо стандартной модели
  6. Фонды
    1. квартир
      1. Международная система единиц
      2. Гауссова система единиц
      3. Британо-американская система единиц
      4. Разные единицы
      5. Время
      6. Преобразование единиц
    2. Измерение
      1. Значащие цифры
      2. По порядку величины
    3. Графики
      1. Графическое представление данных
      2. Линейная регрессия
      3. Подгонка кривой
      4. Исчисление
    4. Векторы
      1. Тригонометрия
      2. Сложение и вычитание векторов
      3. Векторное разрешение и компоненты
      4. Умножение векторов
    5. ссылку
      1. Специальные символы
      2. Часто используемые уравнения
      3. Физические константы
      4. Астрономические данные
      5. Периодическая таблица элементов
      6. Люди в физике
  7. Назад дело
    1. Предисловие
      1. Об этой книге
    2. Связаться с автором
      1. гленнелерт. нас
      2. Behance
      3. Instagram
      4. Твиттер
      5. YouTube
    3. Аффилированные сайты
      1. hypertextbook.com
      2. midwoodscience.org

Измерение скорости объекта: физическая лаборатория – стенограмма видео и урока

Шаги физической лаборатории

Для этой физической лаборатории вам понадобятся:

  • Бейсбольный мяч или другой маленький мяч
  • Автомобиль с постоянной скоростью (или любой моторизованный автомобиль с батарейным питанием, который движется сам по себе)
  • Секундомер
  • Рулетка или линейка
  • Клейкая лента

Шаг 1. Поместите кабину постоянной скорости на поверхность так, чтобы перед ней оставалось достаточно места.Изолентой отметьте стартовую позицию автомобиля, поместив кусок прямо за задние колеса.

Шаг 2: Измерьте расстояние от ленты, несколько метров вдоль пола (чем длиннее, тем лучше), и поместите второй кусок изоленты. Запишите общее расстояние.

Шаг 3: Включите моторизованный автомобиль, поместите его перед стартовой лентой и отпустите, одновременно запустив секундомер.

Шаг 4. Остановите секундомер, когда он достигнет второго отрезка ленты, и запишите время в таблице данных, которая выглядит примерно так:

Пример таблицы данных

Шаг 5. Повторите эксперимент не менее пяти раз и запишите все испытания.

Шаг 6: Найдите среднее значение пяти или более испытаний, сложив числа и разделив их на количество выполненных вами испытаний.

Шаг 7: Рассчитайте скорость вашего автомобиля по формуле: скорость равна расстоянию, разделенному на время.

И все; вы измерили скорость машины. Чтобы сделать это как можно точнее, вам следует попытаться добраться до второго отрезка ленты раньше, чем это сделает машина – для точных измерений важна линия глаз. Когда вы что-то измеряете, ваш глаз должен быть прямо над предметом, на который вы смотрите, или рядом с ним.

Теперь мы можем попробовать сделать то же самое с бейсбольным мячом, сбросив его с высоты.

Итак, Шаг 8: Измерьте высоту вдоль стены или ножки стола и отметьте ее куском изоленты.

Шаг 9: Отпустите бейсбольный мяч нижним краем вдоль отметки и одновременно включите секундомер.

Шаг 10: Остановите секундомер, когда мяч ударяется о землю (используйте глаза, а не звук, потому что скорость света выше скорости звука) и запишите время.

Шаг 11: Найдите среднее значение пяти испытаний и выполните те же вычисления, что и для автомобиля постоянной скорости.

Здесь важно отметить, что на этот раз ваш ответ – СРЕДНЯЯ скорость мяча. Падающий объект ускоряется – его скорость постоянно меняется. Таким образом, все, что вы можете сделать с помощью этого эксперимента, – это определить среднюю скорость падения.

Краткое содержание урока

Скорость – это скорость изменения положения объекта, измеряемая в метрах в секунду.Уравнение скорости простое: расстояние, разделенное на время. Вы берете пройденное расстояние (например, 3 метра) и делите его на время (три секунды), чтобы получить скорость (один метр в секунду).

Следовательно, для вычисления скорости объекта необходимо измерить расстояние и время, необходимое для прохождения этого расстояния. Измерение скорости объекта легко, если вы проводите тщательные измерения и используете линию взгляда, чтобы сделать ее как можно более точной. Если скорость объекта постоянна, вы сможете рассчитать эту постоянную скорость.Если скорость меняется, вы можете узнать среднюю скорость во время движения. И это действительно все.

Результаты обучения

Этот урок может помочь вам:

  • Прочтите определение скорости
  • Определите уравнение для скорости
  • Запомните и выполните шаги физической лаборатории, необходимые для определения средней скорости объекта
Формула средней скорости

– что такое формула средней скорости? Примеры

Средняя скорость – это среднее значение скорости тела за определенный период времени. Формула для средней скорости необходима, поскольку скорость движущегося тела непостоянна и изменяется в течение определенного периода времени. Даже при переменной скорости можно использовать значения общего времени и общего пройденного расстояния, а с помощью формулы для средней скорости мы можем найти одно значение, представляющее все движение.

Что такое формула средней скорости?

Средняя скорость тела равна общей пройденной дистанции, деленной на общее затраченное время. Формула для средней скорости имеет следующий вид:

Формула средней скорости:

Средняя скорость = Общее пройденное расстояние ÷ Общее время

Особые случаи формулы средней скорости

Случай 1: Для тела или объекта, движущегося со скоростью \ (s_1 \) для времени \ (t_1 \), и скоростью \ (s_2 \) для времени \ (t_2 \), формула для среднего скорость указана в приведенном ниже выражении.Произведение \ (s_1 \ times t_1 \) и \ (s_2 \ times t_2 \) дает расстояния, пройденные за интервалы времени \ (t_1 \) и \ (t_2 \) соответственно.

Формула средней скорости \ (= \ frac {s_1 \ times t_1 + s_2 \ times t_2} {t_1 + t_2} \)

Случай 2: Точно так же, когда ‘n’ разных скоростей, \ (s_ {1}, s_ {2}, s_ {3}, … s_ {n} \), даны для ‘n’ соответствующего человека временные интервалы, \ (t_ {1}, t_ {2}, t_ {3}, … t_ {n} \) соответственно, формула средней скорости задается как:

Формула средней скорости \ (= \ frac {s_1 t_1 + s_2 t_2 +… + s_n t_n} {t_1 + t_2 + … + t_n} \)

Случай 3: Средняя скорость, когда разные расстояния, \ (d_ {1}, d_ {2}, d_ {3}, … d_ {n} \), пройдены за разные промежутки времени, \ (t_ {1}, t_ {2}, t_ {3}, … t_ {n} \) соответственно задается как:

Формула средней скорости \ (S_ {avg} \) \ (= \ frac {d_1 + d_2 + d_3 + … + d_n} {t_1 + t_2 + t_3 + …. + t_n} \)

Случай 4: Средняя скорость, когда разные скорости, \ (s_ {1}, s_ {2}, s_ {3}, … s_ {n} \), указаны для разных расстояний, \ (d_ {1 }, d_ {2}, d_ {3} ,. .. d_ {n} \) соответственно задается как:

Формула средней скорости \ (S_ {avg} \) \ (= \ frac {d_1 + d_2 + d_3 + … + d_n} {\ dfrac {d_1} {s_1} + \ dfrac {d_2} {s_2} + \ dfrac {d_3} {s_3} + …. + \ dfrac {d_n} {s_n}} \)

Случай 5: Формула средней скорости, когда заданы две или более скорости (\ (s_ {1}, s_ {2}, s_ {3}, … s_ {n} \)), при которых эти скорости были пройдены за такое же количество времени (\ (t_ {1} = t_ {2} = t_ {3} = … t_ {n} = t) \) задается как:

Формула средней скорости, \ (S_ {avg} \) \ (= \ frac {s_ {1} t + s_ {2} t +… + s_ {n} t} {t \ times n} = \ frac {s_ {1} + s_ {2} + … + s_ {n}} {n} \)

Случай 6: Средняя скорость при заданных разных скоростях (\ (s_ {1}, s_ {2}, s_ {3}, … s_ {n}) \) на одинаковом расстоянии (\ (d_ {1} = D_ {2} = d_ {3} = … d_ {n} = d) \) задается как:

Формула средней скорости \ (S_ {avg} \) \ (= \ frac {n \ times d} {d \ times \ left [\ dfrac {1} {s_1} + \ dfrac {1} {s_2} + \ dfrac {1} {s_3} + . … + \ dfrac {1} {s_n} \ right]} = \ frac {n} {\ left [\ dfrac {1} {s_1} + \ dfrac {1} {s_2 } + \ dfrac {1} {s_3} + …. + \ dfrac {1} {s_n} \ right]} \)

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.Cuemath находит решения простым и легким способом.

Забронируйте бесплатную пробную версию класса

Примеры формулы средней скорости

Давайте рассмотрим несколько примеров, чтобы лучше понять формулу средней скорости.

Пример 1: Используя формулу средней скорости, найдите среднюю скорость Сэма, который преодолевает первые 200 километров за 4 часа и следующие 160 километров за следующие 4 часа.

Раствор:

Чтобы найти среднюю скорость, нам нужно общее расстояние и общее время.
Общее расстояние, пройденное Сэмом = 200 км + 160 км = 360 км
Общее время, затраченное Сэмом = 4 часа + 4 часа = 8 часов
Средняя скорость = Общее пройденное расстояние ÷ Общее время
Средняя скорость = 360 ÷ 8 = 45 км / ч

Ответ: Средняя скорость Сэма 45 км / час.

Пример 2: Поезд движется со скоростью 80 миль в час в течение первых 4 часов и 110 миль в час в течение следующих 3 часов. Найдите среднюю скорость поезда с помощью формулы средней скорости.

Раствор:

Принято, что первые 4 часа поезд движется со скоростью 80 миль в час.
Здесь \ (S_1 \) = 80 и \ (T_1 \) = 4.
И следующие 3 часа поезд движется со скоростью 110 миль в час.
Следовательно, \ (S_2 \) = 110 и \ (T_2 \) = 3.
Формула средней скорости = \ (\ frac {S_1 \ times T_1 + S_2 \ times T_2} {T_1 + T_2} \)
Средняя скорость = (80 × 4 + 110 × 3) ÷ (4 + 3)
= (650) ÷ (7) = 92.86 миль / час

Ответ: Средняя скорость поезда 92,86 миль / час.

Пример 3: Автомобиль движется со скоростью 45 км / ч в течение 5 часов, а затем решает снизить скорость до 40 км / ч в течение следующих 2 часов. Рассчитайте среднюю скорость по формуле средней скорости.

Раствор:

Расстояние I = 45 × 5 = 225 миль
Расстояние II = 40 × 2 = 80 миль
Общее расстояние = Расстояние 1 + Расстояние 2
D = 225 + 80 = 305 миль
Используя формулу средней скорости = Общее пройденное расстояние ÷ Общее затраченное время
Средняя скорость = 305 ÷ 7 = 43.57 м / с.

Ответ: Средняя скорость автомобиля 43,57 м / с.

Часто задаваемые вопросы по формуле средней скорости

Как рассчитать расстояние по формуле средней скорости?

Общая формула для средней скорости имеет вид [Средняя скорость = пройденное расстояние ÷ общее время]
Для расчета расстояния формулу средней скорости можно представить в виде [Расстояние = Средняя скорость × Время].

Как рассчитать время по формуле средней скорости?

Общая формула средней скорости имеет вид [Средняя скорость = Расстояние ÷ Время]
Для расчета времени формула средней скорости будет иметь вид [Время = пройденное расстояние ÷ средняя скорость].

Как использовать формулу для средней скорости?

Чтобы понять, как использовать формулу для средней скорости, давайте рассмотрим пример.
Пример: бегун преодолевает 100-метровый круг за 40 секунд. После финиша первого круга он вернулся к исходной точке. Рассчитайте среднюю скорость бегуна.
Решение: Общее расстояние, пройденное бегуном = 100 метров
Общее время = 40 сек
Итак, применяя общую формулу для средней скорости
у нас есть,
Средняя скорость = Расстояние ÷ Время
Средняя скорость = 100 ÷ 40 = 2.5 м / с.
Средняя скорость бегуна 2,5 м / с.

Какой будет формула общей средней скорости объекта?

Общая формула средней скорости для объекта имеет вид [Средняя скорость = Общее пройденное расстояние ÷ Общее время]. Единица измерения средней скорости в системе СИ – м / с.

Speed ​​& Velocity – Определения, Формулы, Типы, Различия, Проблемы

HelpYouBetter »Физика» Одномерное движение »Speed ​​& Velocity – Определения, Формулы, Типы, Различия, Проблемы

Проходя эту статью, вы получите глубокие знания об определениях, уравнениях, классификациях и различиях между скоростью и скоростью, шаги для расчета скорости и скорости движущегося тела с помощью решенных задач.

Что такое скорость и какова ее формула?

Скорость частицы определяется как расстояние, которое она преодолевает за единицу времени, или скорость изменения расстояния во времени.

Единица измерения скорости в системе СИ – метр в секунду, а ее размерная формула: [M 0 L 1 T -1 ]

Скорость дает только количественное представление о том, насколько быстро или медленно движется объект. движущийся. Направление движения не учитывается. Следовательно, скорость является скалярной величиной и никогда не может быть отрицательной величиной.

Различные типы скорости

По сути, в физике существует четыре различных типа скорости, каждый из которых объясняется ниже:

  1. Единая скорость:

    Если тело преодолевает равные расстояния за равные промежутки времени, говорят двигаться с постоянной скоростью.

  2. Переменная скорость:

    Если тело преодолевает равные расстояния за неравные промежутки времени, считается, что оно движется с переменной скоростью.

  3. Мгновенная скорость:

    Скорость объекта в определенный момент времени называется его мгновенной скоростью.

  4. Средняя скорость:

    Отношение общего расстояния, пройденного телом к ​​общему затраченному времени, называется средней скоростью.

      • Если частица движется со скоростью s 1 , за интервал времени t 1 и со скоростью s 2 за интервал времени t 2 ,
        , то, общее расстояние = s 1 t 1 + s 2 t 2
        общее время = t 1 + t 2
      • Если частица преодолевает расстояние d 1 со скоростью s 1 , а затем d 2 с s 2 ,
        , тогда общее расстояние = d 1 + d 2

Что означает скорость и какова формула для определения скорости ?

Скорость движущейся частицы – это расстояние, которое она проходит за единицу времени в заданном направлении, или, другими словами, скорость – это скорость перемещения тела.

Если x 1 и x 2 являются координатами положения частицы, находящейся в равномерном движении в моменты времени t 1 и t 2 соответственно, ее скорость определяется как,

СИ единица измерения скорости – метр / секунда, а ее размерная формула – [M 0 L 1 T -1 ]

Скорость – это векторная величина. Он может иметь положительное, отрицательное или нулевое значение. Он положительный, когда смещение положительное (т.е.е., когда частица движется в направлении увеличения координаты положения) и отрицательная, когда смещение отрицательное.

Типы скорости

Различные типы скоростей: равномерная скорость, переменная скорость, средняя скорость и мгновенная скорость. Теперь давайте подробно обсудим каждый из них.

  1. Равномерная скорость

    Говорят, что частица движется с постоянной скоростью, если она совершает равные перемещения за равные промежутки времени, то есть скорость остается постоянной на протяжении всего движения. То есть, когда тело движется с постоянной скоростью, величина и направление скорости остаются неизменными в любой точке.
    В этом случае смещение «s» частицы в течение заданного временного интервала «t» получается как произведение скорости «v» и временного интервала «t».
    , т.е. смещение = скорость × интервал времени
    или, s = vt

  2. Переменная скорость или неоднородная скорость

    Тело считается движущимся с переменной скоростью, если его скорость, направление или оба меняются со временем.
    Например, представьте, что тело движется по кругу с постоянной скоростью. Его скорость может изменяться, так как его направление меняется с движением.

  3. Средняя скорость

    Рассмотрим тело, движущееся с переменной скоростью. Тогда отношение полного смещения к общему интервалу времени называется средней скоростью.

    То есть, мы можем сказать, что средняя скорость объекта в течение данного интервала времени – это отношение его смещения в течение этого интервала к затраченному времени.
    Рассмотрим объект, движущийся по оси X. Пусть x (t 1 ) и x (t 2 ) будут координатами его положения в моменты времени t 1 и t 2 соответственно. Тогда

  4. Мгновенная скорость

    Рассмотрим тело, движущееся с переменной скоростью. Скорость объекта в определенный момент времени называется его мгновенной скоростью.
    Для объекта, движущегося в направлении X, пусть x (t) и x (t + Δt) будут координатами положения в моменты времени t и (t + Δt) соответственно.Тогда его средняя скорость за интервал времени t равна,

    . Тогда мгновенная скорость определяется как

    , где Δx – смещение тела за бесконечно малый интервал времени Δt.
    Здесь время Δt в пределе стремится к нулю. Направление мгновенной скорости – по касательной к траектории в точке.
    Также – производная x по времени t. Другими словами, скорость частицы в любой момент является производной координаты положения частицы по времени.

Запишите разницу между скоростью и скоростью в табличной форме.

Скорость

Скорость

Скорость – это скорость изменения расстояния частицы Скорость – это скорость смещения
Скорость – скалярная величина Скорость – это векторная величина
Скорость может иметь только положительные значения Скорость может иметь положительные, отрицательные или нулевые значения.
Скорость ничего не говорит о направлении движения тела Скорость определяет направление движения тела
Ее единица СИ – м / с и имеет размерность [M 0 L 1 T -1 ] Его единица измерения и размер такие же, как и у скорости, которая составляет м / с и [M 0 L 1 T -1 ]

Проблемы скорости и скорости с Решения

Задача 1:
Мотоцикл движется со скоростью 40 км / ч в течение 20 минут, а затем со скоростью 50 км / ч в течение 5 минут.Найдите общее пройденное расстояние и среднюю скорость автомобиля.

Решение:
Учитывая v 1 = 40 км / ч
t 1 = 20 мин = 20/60 = 0,333 часа
v 2 = 50 км / час
t 2 = 5 мин = 5 / 60 = 0,083 час

Расстояние, пройденное при скорости 40 км / час, d 1 = v 1 t 1 = 40 × 0,333 = 13,32 км
Расстояние, пройденное при скорости 50 км / час, d 2 = v 2 t 2 = 50 × 0.083 = 4,15 км
∴ Общее пройденное расстояние, D = d 1 + d 2 = 13,32 + 4,15 = 17,47 км

Средняя скорость = Общее расстояние / Общее время = D / (t 1 + t 2 )
т.е. S avg = 17,47 / (0,333 + 0,083) = 41,995 км / час

Задача 2:
Автобус преодолевает первую половину расстояния между двумя местами со скоростью 70 км / час и вторая половина на скорости 40 км / час. Какая средняя скорость автомобиля?

Ответ:
Дано s 1 = 70 км / час
s 2 = 40 км / час

Задача 3:
Транспортное средство преодолевает 1/3 части общего расстояния со скоростью 15 км. / час, вторая 1/3 часть со скоростью 25 км / час и последняя 1/3 часть со скоростью 50 км / час.Найдите среднюю скорость автомобиля.

Решение:
Дано с 1 = 15 км / ч
с 2 = 25 км / ч
с 3 = 50 км / ч

Пусть D будет общим пройденным расстоянием.

Тогда время, чтобы преодолеть первое расстояние D / 3,

Точно так же время, чтобы преодолеть второе расстояние D / 3,

Точно так же время, чтобы преодолеть третье расстояние D / 3,

Следовательно, средняя скорость равна,

Задача 4
Объект движется по прямой линии вдоль оси X, его смещение от начала координат задается уравнением x = 5t 3 – 4t 2 + 2t, где x в метрах, а t в секундах.Найти среднюю скорость тела в интервале времени от t = 0 до t = 2 секунды.

Ответ:
Дано, x = 5t 3 – 4t 2 + 2t
Пусть x 0 обозначает начальную позицию.

При t = 0, x 0 = 5 × 0 – 4 × 0 + 2 × 0 = 0 (x 0 обозначает начальное положение)
При t = 2, x 1 = 5 × 2 3 – 4 × 2 2 + 2 × 2 = 40-16 + 4 = 28 м
∴ Полное перемещение = x 1 – x 0 = 28-0 = 28 м
Общее время = 2 секунды.

∴ Средняя скорость = Общее перемещение / Общее время = 28/2 = 14 м / с

Задача 5
Мальчик ходит 1 минуту со скоростью 1 м / с, а затем бежит 2 минуты со скоростью 4 м / с по прямой дороге. Какая средняя скорость у мальчика?

Ответ:
Учитывая v 1 = 1 м / с
t 1 = 1 мин = 60 с
v 2 2 = 4 м / с
t 2 = 2 мин = 2 × 60 = 120 s

Расстояние, пройденное мальчиком со скоростью 1 м / с, d 1 = v 1 t 1 = 1 × 60 = 60 м
Расстояние, пройденное мальчиком со скоростью 4 м / с, d 2 = v 2 t 2 = 4 × 120 = 480 м
∴ Общее пройденное расстояние, D = d 1 + d 2
= 60 + 480
= 540 м

Средняя скорость, S avg = Общее расстояние / Общее время
= D / (t 1 + t 2 )
i.е., S ср. = 540 / (60 + 120)
= 3 м / с

Задача 6
Автобус движется со скоростью 55 км / ч. Автобус должен преодолеть расстояние 85 километров. Сколько времени потребуется автобусу, чтобы добраться до места назначения?

Решение:
Заданная скорость, s = 55 км / час
Расстояние, d = 85 км
Время, t =?

Мы знаем, что скорость = расстояние / время
∴ время = расстояние / скорость
= 85/55
= 1.545 часов

т.е. автобусу нужно 1,545 часа, чтобы добраться до места назначения.

Задача 7
Транспортное средство описывается функцией x = 8t 2 + 20t + 12. Вычислите мгновенную скорость транспортного средства в момент времени t = 8 секунд.

Ответ:
Учитывая функцию, x = 8t 2 + 20t + 12

Скорость в любой момент времени может быть определена путем дифференцирования заданной функции по времени.

то есть мгновенную скорость в момент времени t = 8 секунд можно рассчитать как,

v (t) = 16t + 20
∴ При t = 8 s,
v (8) = 16 × 8 + 20
= 128 + 20
= 148 м / с

i.е., мгновенная скорость транспортного средства в момент времени 8 секунд составляет 148 м / с.

Задача 8
Автобус проезжает 98 км за 3 часа и 100 км за 2 часа в том же направлении. а) Найдите среднюю скорость автобуса за всю поездку. б) Найдите среднюю скорость автобуса за всю поездку.

Решение:

a) Здесь Общее пройденное расстояние = 98 + 100 = 198 км
Общее затраченное время = 3 + 2 = 5 часов
∴ Средняя скорость автобуса за всю поездку = Общее расстояние / Общее затраченное время
= 198/5
= 39.6 км / час

б) Учитывая, что весь путь проходит в одном направлении.
∴ Общее водоизмещение = 98 + 100 = 198 км
Общее затраченное время = 3 + 2 = 5 часов
∴ Средняя скорость автобуса за всю поездку = Общее перемещение / Общее затраченное время
= 198/5
= 39,6 км / час

Задача 9
Автобус перемещается на 90 км на восток за 3 часа и на 50 км на запад за 2 часа.а) Найдите среднюю скорость автобуса за всю поездку. б) Найдите среднюю скорость автобуса за всю поездку.

Ответ:

a) Здесь Общее пройденное расстояние = 90 + 50 = 140 км
Общее затраченное время = 3 + 2 = 5 часов
∴ Средняя скорость автобуса за всю поездку = Общее расстояние / Общее время принято
= 140/5
= 28 км / час

б) Учитывая, что вся поездка проходит в противоположных направлениях.
∴ Общее водоизмещение = 90-50 = 40 км
Общее затраченное время = 3 + 2 = 5 часов
∴ Средняя скорость автобуса за весь путь = Общее перемещение / Общее затраченное время
= 40/5
= 8 км / час

Задача 10
Мальчик начинает бежать с точки по круговой дорожке радиусом 400 метров и возвращается к той же точке через 30 минут.а) Узнайте среднюю скорость бегущего мальчика. б) Узнайте среднюю скорость бегущего мальчика.

Решение:
a) Мальчик бежит из точки по круговой траектории и возвращается в ту же точку, что означает, что он преодолел расстояние, равное длине окружности круга.

Здесь радиус круговой траектории, r = 400 м
Затраченное время = 30 минут
= 30 × 60 секунд
= 1800 с
∴ Пройденное расстояние = окружность круга
= 2πr
= 2 × 3.14 × 400
= 2512 метров

∴ Средняя скорость бегущего мальчика = Общее расстояние / Общее затраченное время
= 2512/1800
= 1,395 м / с

б) Мальчик бежит из точки по круговой дорожке и возвращается в ту же точку означает, что смещение равно нулю.

∴ Средняя скорость бегущего мальчика = Общее перемещение / Общее затраченное время
= 0/1800
= 0 м / с

Задача 11
Автомобиль движется на север 160 км со скоростью 70 км / ч, а затем на запад 130 км со скоростью 80 км / час.
а) Найдите среднюю скорость автомобиля.
б) Найдите среднюю скорость автомобиля.

Ответ:
Мы знаем,
скорость = расстояние / время
∴ время = расстояние / скорость

a) Пусть t 1 будет временем, чтобы преодолеть 160 км со скоростью 70 км / ч и выражается выражением,
t 1 = 160/70
= 2,286 часа

Аналогичным образом, пусть t 2 будет временем для преодоления 130 км со скоростью 80 км / час и определяется как,
t 2 = 130 / 80
= 1.625 часов

∴ Средняя скорость автомобиля = Общее расстояние / Общее затраченное время
= (160 + 130) / (2,286 + 1,625)
= 290 / 3,911
= 74,149 км / час

b) Водоизмещение самое короткое расстояние AC между начальной точкой и конечной точкой рассчитывается следующим образом.

По теореме Пифагора AC 2 = AB 2 + BC 2
i.е., AC = √ (AB 2 + BC 2 )
= √ (160 2 + 130 2 )
= √ (25600 + 16900)
= √ (42500)
= 206,155

∴ Средняя скорость автомобиля = Общий водоизмещение / Общее затраченное время
= 206,155 / (т 1 + т 2 )
= 206.155 / (2,286 + 1,625)
= 206,155 / 3,911
= 52,711 км / час

Задача 12
Средняя скорость автомобиля составляет 75 км / час. Сколько километров машина преодолеет за 4 часа.

Ответ:
Мы знаем, Средняя скорость = Общее расстояние / Общее время
∴ Общее расстояние = Средняя скорость × Общее время

Учитывая, средняя скорость = 75 км / час
Затраченное время = 4 часа
∴ Общее расстояние = Средняя скорость × Общее затраченное время
= 75 × 4
= 300 км

В этой статье были изучены определения, типы и различия между скоростью и скоростью движущегося объекта.Теперь вы можете рассчитать скорость и скорость движущегося тела.

Ваши мысли и отзывы о прочитанном! Оставьте мне комментарий в разделе ниже и подумайте о том, чтобы поделиться этой статьей на facebook и twitter.

Также изучите расстояние и смещение.

Скорость звука в температуре воздуха Калькулятор атмосферного давления без таблицы Расчет плотности воздуха по формуле температуры Мах 1 акустический импеданс Распространение температуры в помещении Плотность воздуха на уровне моря скорость идеальный газ 20 градусов или 21 градус Цельсия C холодный теплый

Скорость звука в калькуляторе атмосферного давления без таблицы плотность воздуха формула расчета температуры мах 1 акустический импеданс распространение температуры в помещении плотность воздуха скорость на уровне моря идеальный газ 20 градусов или 21 градус Цельсия C холодный теплый – sengpielaudio Sengpiel Berlin

● Расчет Скорость звука
в Воздух и эффективная температура ●
33 Важная температура воздуха и не относящиеся к делу давление = Давление воздуха = Барометрическое давление
Забудьте о высоте (высоте).Думайте только о температуре на этой высоте.

Ошибочное предположение, что скорость звука уменьшается
с высотой над уровнем моря, т.к. плотность воздуха
убывает с высотой. Изменение атмосферного давления
не меняет скорость звука.
Только более низкая температура (!) Позволяет снизить скорость
звук на больших высотах.
Скорость звука не имеет ничего общего с «уровнем моря».
Для звукового давления без воздуха среды нет скорости
звука.
Скорость звука зависит почти только от его температуры.
Не зависит от амплитуды звука , частоты или
длины волны .

скорость распространения или скорость звука в воздухе

При 0 ° C ρ 0 = 1.293 кг / м 3 , Z 0 = 428 Н · с / м 3 и c 0 = 331,3 м / с
При 15 ° C ρ 15 = 1,225 кг / м 3 , Z 15 = 417 Н · с / м 3 и c 15 = 340 м / с
При 20 ° C составляет ρ 20 = 1,204 кг / м 3 , Z 20 = 413 Н · с / м 3 и c 20 = 343 м / с
При 25 ° C ρ 20 = 1.184 кг / м 3 , Z 25 = 410 Н · с / м 3 и c 25 = 346 м / с

Плотность воздуха или плотность воздуха ρ (rho), импеданс воздуха Z , скорость звука c c Скорость звука в воздухе c определяется самим воздухом и не зависит от
на амплитуде , частоте или длине волны звука .
Для идеального газа скорость звука зависит только от его температуры и составляет
не зависит от давления газа. Эта зависимость относится и к воздуху, в хорошем
приближении и может рассматриваться как идеальный газ.

Сайт для звукорежиссеров и музыкантов. Нас интересует
скорость звука воздуха (!) на Земле в местах нахождения акустических музыкальных инструментов
или используются голоса, обычно в комнатах или холлах. Скорость звука
слои атмосферы, как на высоте 100 км (высота), так и близкие к вакууму, не
представляет интерес.
Также мы не заботимся о повышенном давлении воздуха в автомобильных шинах.
Какая скорость у звука в обычной жизни?

Используемый браузер не поддерживает Javascript.
Программа указана, но фактическая функция отсутствует.


Примечание для музыкантов и технических специалистов (не для профессоров физики):
Скорость звука в воздухе явно изменяется с температурой, немного с
влажность – но не с давлением воздуха (атмосферное) и высотой.
Слова «звуковое давление на уровне моря» неверны и вводят в заблуждение в
случай «скорость звука». Индикация температуры –
. абсолютно необходимо.
Изменение атмосферного давления не влияет на звук
музыкальных инструментов в концертном зале или в комнате.
Это влияет на изменение температуры.

Среднее давление воздуха на уровне моря составляет 101325 Па.Однако эта информация
несущественно для скорости звука. Нам всегда требуется указание температуры.


В единицах СИ с сухим воздухом при 20 ° C (68F) скорость звука c составляет 343 метра в секунду (м / с).
Это также равно 1235 км / ч, 1125 футов в секунду (фут / с или кадр / с), 666 узлов, 767,3 миль
в час (миль / ч или миль / ч) , 12,79 миль в минуту (миль / мин), 0,2131 мили в секунду (миль / с),
То есть 0.343 километра в секунду (км / с) или 20,58 километра в минуту (км / мин).

Нет смысла давать скорость звука, добавляя слова «стандартная атмосфера на уровне моря».
Для получения скорости звука важна температура , а не барометрическое давление.

Заявление: Статическое давление воздуха p_ и плотность воздуха ρ (плотность воздуха) пропорциональны при одном и том же
температура, потому что отношение p_ / ρ всегда постоянно, на высокой горе или даже на высоте уровня моря.
Примечание: Отношение p_ / ρ (статическое давление воздуха к плотности воздуха) действительно всегда постоянно. Формула:

Скорость звука


Это означает, отношение p_ / ρ всегда постоянно на высокой горе,
и даже на «уровне моря». Статическое атмосферное давление p _ и
плотность воздуха ρ всегда идут вместе.Соотношение остается постоянным.

При расчете скорости звука забудьте атмосферное давление ,
но посмотрите внимательно на очень важную температуру.
Скорость звука меняется с высотой (высотой) только из-за
изменение температуры там.

Давление зависит от температуры и косвенно от высоты.

Индекс адиабаты или отношение удельных теплоемкостей κ (каппа) = c p / c v = 1.402 для воздуха.
Удельная теплоемкость в процессе постоянного давления = c p ; Удельная теплоемкость в процессе постоянного объема = c v

Обычно мы берем с достаточной точностью формулу (уравнение) для скорости звука в воздухе
в м / с в зависимости от температуры ϑ (тета) в градусах Цельсия (Цельсия):


Скорость звука c ≈ 331,3 + (0,6 × ϑ ) в м / с.

Это дает, например, при температуре ϑ = 20 ° C скорость звука:
c ≈ 331,3 + (0,6 × ϑ ) = 331,3 + (0,6 × 20) = 343,3 м / с.


Изменение температуры на Δ ϑ = 1 ° C равно
изменение скорости звука Δ c = 60 см / с.

Существует полезная формула (практическое правило) для получения температуры ϑ в ° C
, когда вы знаете скорость звука c в воздухе (м / с).

Формула: Температура воздуха ϑ ≈ ( c – 331,3) / 0,6 ° C.

С помощью следующей формулы вы можете точно рассчитать скорость звука.

Скорость звука в м / с;
температура ϑ в ° C.

Скорость звука в зависимости от высоты и температуры?
Забудьте о высоте и позаботьтесь только о температуре.


При температуре ϑ = 0C скорость звука в сухом воздухе была определена равной
c = 331.3 м / с. 0 ° C равняется 32 ° F.

Точные уравнения для скорости звука и температуры:

Для точного расчета скорости звука в м / с:
c = 331,3 × √ (1+ ( ϑ / 273,15))
, если используется известная температура воздуха ϑ ° C.

Для точного расчета температуры воздуха в ° C:
ϑ = 273,15 × (0,00000
  • 1216350702156684298215 × c 2 – 1)
    , если использовать известную скорость звука c в м / с.

    Упрощенные формулы (для от + 35 ° C до -35 ° C):

    Скорость звука в воздухе в м / с: c = 331,3 + 0,6 × ϑ

    Температура в ° C: ϑ = ( c – 331,3) / 0,6

    • Расчет и преобразование: Температура и скорость звука

    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака ↔ .

    Скорость звука c зависит от температуры воздуха ϑ , а не от давления воздуха!
    Влажность воздуха незначительно влияет на скорость звука. Давление воздуха
    и плотность воздуха (плотность воздуха) пропорциональны друг другу при одинаковой температуре.
    Применяется всегда p / ρ = постоянный. rho – плотность ρ и p – звуковое давление.
    Следовательно, давление воздуха не учитывается при расчете скорости звука воздуха.


    Примечание: скорость звука одинакова и на вершине горы
    как на уровне моря при такой же температуре воздуха.

    Можно предположить, что это верно даже на высоте 100 км.
    С понижением давления плотность воздуха уменьшается.

    При какой температуре скорость звука вдвое превышает значение 0 ° C?

    При какой температуре скорость звука 331.3 м / с (скорость звука) увеличится вдвое?
    Температура 819,45 ° C удвоит скорость звука до 662,6 м / с.

    Найдите следующий ответ на вопрос: «Какая скорость звука?»

    Скорость звука – имеет значение температура, а не давление воздуха

    Плотность воздуха (плотность воздуха) ρ = давление воздуха p_ (газовая постоянная R × температура в Кельвинах)
    ρ = p_ / R × T в кг / м 3 .

    Удельная газовая постоянная для сухого воздуха составляет R = 287,058 Дж / кг × K
    Джоуль Дж = ньютон × метр = N · м и T в Кельвинах = ° C + 273,15
    Атмосферное давление p 0 = 101325 Па = 1013,25 мбар = 1013,25 гПа
    R = 287,058 Дж / кг × K
    T 0 = 273.15 K при 0 ° C
    ρ 0 = 101325 / (287,058 × 273,15) = 1,2922 кг / м³
    T 20 = 293,15 K при 20 ° C
    ρ 20 = 101325 / (287,058 × 293,15) = 1,2041 кг / м³

    Иногда ошибочно принимают, что давление и плотность воздуха одинаковы.

    Скорость звука c не является скоростью частицы v .
    Скорость звука v лучше называть скоростью частицы v .
    Скорость звука c лучше называть скоростью звука c .


    Скорость звука называется Мах 1
    Мах обычно используется для обозначения скорости объекта, например самолета
    или ракета, когда она движется со скоростью звука или кратной ей.
    Скорость выше 1 Маха называется сверхзвуковой.

    Число Маха ниже 1 означает, что скорость потока ниже скорости звука – а скорость дозвуковая .
    Число Маха 1 означает, что скорость потока – это скорость звука, а скорость вокруг нее равна околозвуковой .
    Число Маха выше 1 означает, что скорость потока выше скорости звука – а скорость составляет сверхзвуковой .
    Более чем число Маха 5 называется гиперзвуковым . «Число Маха» – это безразмерное отношение.


    Примечание: скорость звука c не зависит от частоты и
    амплитуда звуковой волны и давление воздуха.Но скорость
    звук зависит от температуры.

    При температуре 819,45 мы получаем скорость звука 662,6 м / с.
    Это вдвое больше скорости звука, которое мы находим при 0 ° C с 331,3 м.

    Сверхзвуковая скорость имеет абсолютно
    не имеет отношения к давлению воздуха – но
    с температурой!

    Плотность воздуха ρ также не влияет,
    потому что соотношение давления воздуха p до
    плотность ρ то есть p / ρ всегда
    постоянный.Посмотрите на эту важную формулу:
    Скорость звука

    Таблица (диаграмма): Воздействие температуры
    Плотность воздуха, скорость звука, характеристика акустики
    сопротивление и зависимость температуры воздуха

    Температура
    воздуха ϑ в ° C    		 Скорость звука
    c м / с    		 Время на 1 м
    Δ t в мс / м    		 Плотность воздуха
    ρ в кг / м 3     		Импеданс
    воздуха Z в Н · с / м 3
    +40 354.94 2,817 1,1272 400,0
    +35 351,96 2,840 1,1455 403,2
    +30 349,08 2,864 1,1644 406,5
    +25 346,18 2,888 1,1839 409,4
    +20 343.26 2,912 1,2041 413,3
    +15 340,31 2,937 1,2250 416,9
    +10 337,33 2,963 1,2466 420,5
    +5 334,33 2,990 1,2690 424,3
    0 331.30 3,017 1,2920 428,0
    −5 328,24 3,044 1,3163 432,1
    −10 325,16 3,073 1,3413 436,1
    −15 322,04 3,103 1,3673 440,3
    −20 318.89 3,134 1,3943 444,6
    −25 315,72 3,165 1.4224 449,1

    Примечание: Давление воздуха p и плотность воздуха ρ не совпадают.
    В газах, чем выше скорость звука в этой среде, тем выше будет высота звука при пении.

    Только из-за понижающейся температуры воздуха, которая уменьшается с высотой (высотой), скорость звука уменьшается.

    В общепринятом использовании и в научной литературе скорость звука совпадает с скоростью звука или скоростью звука.
    Скорость звука c не следует путать со скоростью звуковых частиц v , которая является скоростью отдельных частиц.

    Приблизительная скорость звука
    в обычных материалах
    Средний Скорость звука
    м / с фут / с
    Воздух, сухой при 20 ° C 343 1 125
    Водород при 0 ° C 1 280 4 200
    Вода при 15 ° C 1 500 4 920
    Свинец 2 160 7 090
    Бетон 3 100 10 200
    Дерево (мягкое – по волокну) 3 800 12 500
    Стекло 5 500 18 500
    Сталь 5 800 19 000

    В данном идеальном газе скорость звука зависит только от его температуры.
    Скорость звука в неподвижном сухом воздухе при температуре ϑ = 0 градусов
    Цельсия c = 331,3 м / с.
    Это зависит от температуры и материала. Так как звук передается
    легко проходит через плотно упакованные молекулы, быстрее через плотные
    вещества.
    Таким образом, скорость звука увеличивается с увеличением жесткости материала.

    На частый вопрос: “Сколько стоит скорость звука?” всегда должен следовать
    требование: “При какой температуре, пожалуйста?”
    Кто упоминает о барометрическом давлении, есть чему поучиться.

    Скорость звука и акустическая скорость (скорость звука)

    Скорость – это скорость изменения расстояния во времени.
    Скорость – это мера скорости и направления движущегося объекта.
    Скорость – это скорость изменения смещения во времени.
    Скорость – это расстояние, на которое проходит объект, скорость – это измерение скорости И направления.

    В данном идеальном газе скорость звука зависит только от его температуры.Скорость
    звук в неподвижном воздухе при 0 градусах Цельсия составляет 331,3 м / с. Это зависит от температуры, а
    материал. Поскольку звук легче передается между близкими молекулами, он распространяется
    быстрее в более плотном веществе. Таким образом, скорость звука увеличивается с жесткостью
    материал.

    Действительно неправильные ответы в Yahoo! Answers

    Как скорость звука в воздухе зависит от давления воздуха?

    1 st неправильный ответ: лучший ответ – выбран избирателями
    В более тонком воздухе плавает меньше атомов, чем в более плотном (более высоком давлении).
    Поскольку звуковые волны беспрепятственно распространяются быстрее, меньшее давление воздуха составляет
    более высокая скорость из-за пониженной атмосферной «вязкости».

    2 nd неправильный ответ: скорость звука в воздухе прямо пропорциональна квадратному корню
    давления.

    Правильный ответ: скорость звука не зависит от давления воздуха, а
    по температуре. Давление воздуха – это не то же самое, что плотность воздуха.

    Свойства звука в воздухе, частота и длина волны

    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака ↔ .

    При 0 ° C скорость звука в учебниках США составляет 331,3 м / с.
    При 20 ° Цельсия скорость звука равна 343.21 м / с, округлено 343 м / с.
    При 0 ° C скорость звука в немецких учебниках составляет 331,5 м / с.
    При 20 ° C скорость звука тогда составляет 343,42 м / с, округленное значение – 343 м / с.

    Скорость и скорость – разница

    Скорость – это расстояние за определенный период времени.
    Скорость – это мера скорости и направления движущегося объекта.
    Разница: скорость – это расстояние, на которое объект проходит за единицу времени.
    Скорость – это перемещение за единицу времени.
    Разница: скорость – это скалярная величина, она имеет только величину и не может
    быть нулевым.
    Скорость – это векторная величина, она имеет как величину, так и направление, и это
    может быть нулевым.

    Конвертер: Фаренгейт в Цельсий и Цельсий в Фаренгейт

    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака ↔ .

    Звуковое давление или акустическое давление – это локальное отклонение давления от окружающего
    атмосферное давление, вызванное звуковой волной. Звуковое давление можно измерить с помощью
    микрофон в воздухе. Единица СИ для звукового давления p – это паскаль – символ: Па.

    НАСА говорит: Скорость звука зависит от температуры воздуха .
    Он меняется с высотой (высотой) только , потому что меняющейся температуры!
    Атмосферное давление пропорционально плотности воздуха.1/2 = 343,24 м / с.

    Зональный средний вертикальный профиль температуры в
    атмосфера в июне на 45 ° северной широты

    Температура в зависимости от высоты (атмосферное давление)

    Неправильное мышление:
    Рассчитайте скорость звука на большой высоте.
    Вы чувствуете предположение, что это должно быть связано с ростом. Это не правильно.
    Только температура имеет отношение к скорости звука.
    Там наверху довольно холодно.
    Звуковое давление или акустическое давление (переменные изменения давления)
    динамическое давление. Однако давление воздуха (равное атмосферное давление) составляет
    статическое давление. Динамическое звуковое давление накладывается на статическое
    . давление воздуха.


    Примечание. Время, частота и фаза тесно связаны.
    Высота амплитуды не влияет на эти параметры.

    Амплитуда A не имеет ничего общего с частотой, длиной волны,
    продолжительность времени и скорость звука .


    4 формулы средней скорости, которые необходимо знать для GMAT

    Многие люди просили нас устранить путаницу, связанную с различными формулами средней скорости. Мы начнем с подведения итогов – существует одна универсальная формула для ВСЕХ вопросов о средней скорости, а именно

    .

    Средняя скорость = Общее расстояние / Общее время

    Независимо от того, какую формулу вы выберете, она всегда будет сводиться к этой.Имея это в виду, давайте обсудим различные формулы, с которыми мы сталкиваемся:

    1. Средняя скорость = (a + b) / 2

    Применяется, когда кто-то движется со скоростью a половину времени и скорость b вторую половину времени. В этом случае средняя скорость – это среднее арифметическое двух скоростей.

    2. Средняя скорость = 2ab / (a ​​+ b)

    Применяется, когда человек едет на скорости a половину расстояния и скорость b на другой половине расстояния. В этом случае средняя скорость – это среднее гармоническое значение двух скоростей.Аналогичным образом вы можете изменить эту формулу для одной трети расстояния.

    3. Средняя скорость = 3abc / (ab + bc + ca)

    Применяется, когда человек движется со скоростью a одну треть расстояния, со скоростью b еще одну треть расстояния и скоростью c на оставшейся трети расстояния.

    Обратите внимание, что общая формула среднего гармонического для n чисел –

    Среднее гармоническое значение = n / (1 / a + 1 / b + 1 / c +…)

    4. Вы также можете использовать средневзвешенные значения.Обратите внимание, что в случае средней скорости вес всегда равен «времени». Итак, если вам дана средняя скорость, вы можете найти отношение времени как

    t1 / t2 = (a – средн.) / (Средн – b)

    Как вы уже знаете, это всего лишь наша формула средневзвешенного значения.

    Теперь давайте рассмотрим несколько простых вопросов, в которых вы можете использовать эти формулы.

    Вопрос 1: Майра ехала со средней скоростью 30 миль в час в течение T часов, а затем со средней скоростью 60 миль в час в течение следующих T часов.Если она не делала остановок во время поездки и достигла пункта назначения за 2T часов, какова была ее средняя скорость в милях в час за всю поездку?

    (А) 40

    (В) 45

    (К) 48

    (Г) 50

    (E) 55

    Решение: Здесь время, в течение которого Майра двигалась на двух скоростях, одинаково.

    Средняя скорость = (a + b) / 2 = (30 + 60) / 2 = 45 миль в час

    Ответ (B)

    Вопрос 2: Майра ехала со средней скоростью 30 миль в час первые 30 миль пути, а затем со средней скоростью 60 миль / час на протяжении оставшихся 30 миль пути.Если она не останавливалась во время поездки, какова была ее средняя скорость в милях / час за всю поездку?

    (А) 35
    (В) 40
    (В) 45
    (Г) 50
    (Д) 55

    Решение: Здесь расстояние, которое Майра проехала на двух скоростях, одинаково.

    Средняя скорость = 2ab / (a ​​+ b) = 2 * 30 * 60 / (30 + 60) = 40 миль / ч

    Ответ (B)

    Вопрос 3: Майра ехала со средней скоростью 30 миль в час в течение первых 30 миль поездки, со средней скоростью 60 миль в час в течение следующих 30 миль и со средней скоростью 90 миль в час в течение следующих 30 миль. оставшиеся 30 миль пути.Если во время поездки она не делала остановок, средняя скорость Майры в милях / час за всю поездку была близка к

    (А) 35
    (В) 40
    (В) 45
    (Г) 50
    (Д) 55

    Решение: Здесь Майра проехала на трех скоростях по одной трети расстояния каждая.

    Средняя скорость = 3abc / (ab + bc + ca) = 3 * 30 * 60 * 90 / (30 * 60 + 60 * 90 + 30 * 90)

    Средняя скорость = 3 * 2 * 90 / (2 + 6 + 3) = 540/11

    Это немного меньше 50, поэтому ответьте (D).

    Вопрос 4: Майра какое-то время ехала со средней скоростью 30 миль в час, а затем со средней скоростью 60 миль в час на протяжении оставшейся части пути.Если она не делала остановок во время поездки и ее средняя скорость за все время поездки составляла 50 миль в час, в течение какой части общего времени она ехала со скоростью 30 миль / час?

    (A) 1/5
    (B) 1/3
    (C) 2/5
    (D) 2/3
    (E) 3/5

    Решение: мы знаем среднюю скорость и должны найти долю времени, затраченного на определенную скорость.

    t1 / t2 = (A2 – Aavg) / (Aavg – A1)

    t1 / t2 = (60-50) / (50-30) = 1/2

    Итак, из всего 3 частей времени в пути она ехала со скоростью 30 миль в час 1 часть и 60 миль в час 2 части времени.Доля общего времени, в течение которого она проехала со скоростью 30 миль в час, составляет 1/3.

    Оставить комментарий