Формула как найти время физика: Формула скорости пути времени и их единицы измерения

Как найти время равномерного движения?

Статьи › Чем отличается › Чем отличается равномерное и неравномерное движение?

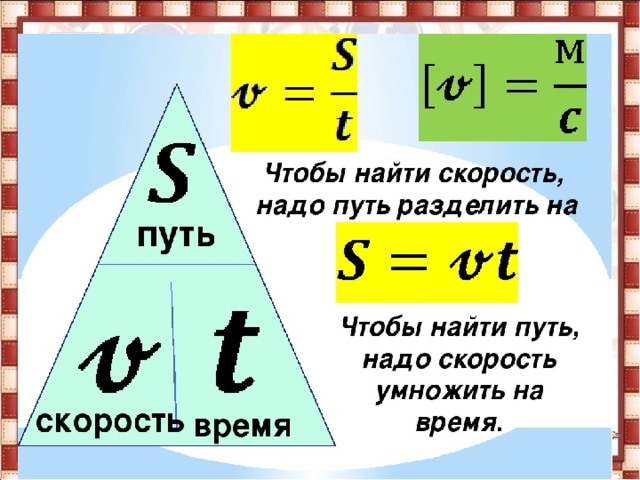
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.

1. Как найти время движения физика?
2. Как найти равномерное движение?
3. Как рассчитать скорость при равномерном движении?
4. Как рассчитать путь s при равномерном движении?
5. Какая формула как найти время?
6. Как найти время?
7. Как зависит скорость от времени при равномерном движении?
8. Как найти перемещение при равномерном движении?
9. Чему равна сила при равномерном движении?
10. Как найти путь за промежуток времени?
11. Что такое равномерное движение и формула?
12. Как найти перемещение формула?
13. Чему равна T в физике?
14. Как найти V?
15. Как узнать время в задачах на движение?
16. Как направлена скорость при равномерном движении?
17. Чему равна скорость при равноускоренном движении?
18. Как можно найти скорость при неравномерном движении?
19. Как найти Равнозамедленное движение?

Как найти время движения физика?

Чтобы найти время движения, необходимо путь разделить на скорость.

Как найти равномерное движение?

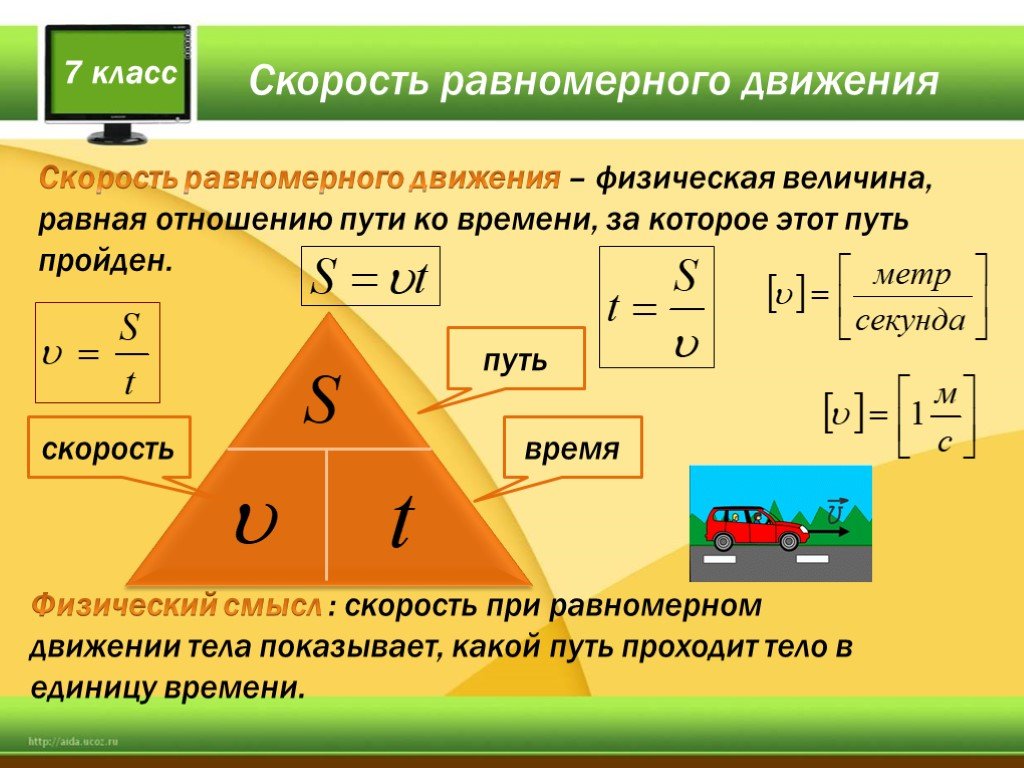
Теория: Равномерное движение — это движение, при котором тело проходит равные расстояния за небольшие равные промежутки времени. При равномерном движении скорость тела постоянна. Её легко вычислить: нужно пройденное расстояние поделить на время пути.

Как рассчитать скорость при равномерном движении?

Ответы1. Скорость при равномерном движении показывает какой путь прошло тело за единицу времени. Скорость обозначается — v. Формула v=S/t, где S — путь пройденный телом, t — время, за которое тело прошло путь.

Как рассчитать путь s при равномерном движении?

Пройдённым путём S называется длина линии, которую описывает тело при движении. При движении тела с постоянным ускорением а, путь тела S определяется формулой: S = V0 * t + a * t2 / 2, где V0 — начальная скорость движения тела, t — время движения тела.

Какая формула как найти время?

Если известны скорость и расстояние, то можно найти время: t = s: v.

Как найти время?

Чтобы найти время, нужно расстояние разделить на скорость.

Как зависит скорость от времени при равномерном движении?

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени. Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) — прямая линия, параллельная оси времени.

Как найти перемещение при равномерном движении?

Для нахождения перемещения тела достаточно умножить его скорость на время движения. Для нахождения перемещения удобно воспользоваться нашим онлайн калькулятором. Просто подставьте скорость и время в пути и получите искомое значение перемещения.

Чему равна сила при равномерном движении?

При равномерном движении бруска равнодействующая всех сил равна нулю.

Как найти путь за промежуток времени?

Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.

Что такое равномерное движение и формула?

Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением: x (t) = x0 + υt. В этом уравнении υ = const — скорость движения тела, x0 — координата точки, в которой тело находилось в момент времени t = 0.

Как найти перемещение формула?

Так как тело двигается рано ускоренно с ускорением а, то его перемещение определяется формулой: S = V0 * t + а * t2 / 2, где V0 — начальная скорость тела, t — время его движения.

Чему равна T в физике?

V = S / t, где S — путь тела, t — время, за которое этот путь пройден.

Как найти V?

Следствие. Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. V = S (основания) ⋅ h.

Как узнать время в задачах на движение?

Движение скорость v=s/t. время t=s/v. расстояние s=v∗t.В таких задачах важно понимать:

• если мы умножаем скорость на время, то получаем расстояние;
• если расстояние делим на время, то получаем скорость;
• если расстояние делим на скорость, то получаем время;

Как направлена скорость при равномерном движении?

Вектор скорости равномерного прямолинейного движения материальной точки направлен вдоль ее траектории в сторону движения.

Чему равна скорость при равноускоренном движении?

При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.

Как можно найти скорость при неравномерном движении?

Для описания неравномерного движения вводится понятие средней скорости. Средняя скорость это физическая величина, равная отношению всего пути, пройденного телом, ко всему времени его движения на рассматриваемом участке: где L — весь путь, а t — все время движения на рассматриваемом участке.

Как найти Равнозамедленное движение?

В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.

Простая физика – EASY-PHYSIC

Вашему вниманию предлагаются самые простые задачи на движение с постоянной скоростью.

Мы научимся по условию задачи записывать уравнение движения тела, вспомним, что путь можно определить как площадь фигуры под графиком скорости.

Задача 1.

По оси движутся две точки: первая по закону , вторая по закону . В какой момент времени они встретятся? Решить аналитически и графически.

Для того, чтобы решить эту задачу аналитически, нужно приравнять два выражения, определяющие законы движения тел (то есть координата и у первого, и у второго одна и та же, потому что они встретились):

Решим задачу графически. Для этого построим два графика зависимостей на одной координатной плоскости, и найдем точку их пересечения:

Задача 1.

Ответ:

 

Задача 2.

Из пункта А в пункт В выехала автомашина с постоянной скоростью км/ч. Спустя мин из пункта В в пункт А выехал велосипедист с постоянной скоростью км/ч.

а) написать закон движения автомашины и велосипедиста, считая, что начало координат находится в пункте А, а начало отсчета времени – выезд автомашины.

б) Найти время и место встречи аналитически и графически. Расстояние между пунктами А и В км.

1. a) Запишем закон движения автомашины: она движется по самому обычному закону для движения с постоянной скоростью: . Так как начальная координата автомашины равна нулю, то можно записать: . Велосипедист выехал из пункта , и его начальная координата равна 55 (км). Расстояние до пункта А постоянно уменьшается, следовательно, скорость его «отрицательна» – то есть отрицательна ее проекция на ось . Тогда закон движения велосипедиста .

Найдем время встречи, приравняв координаты обоих участников:

Место встречи:

Решим теперь задачу графически:

Задача 2. Графическое решение

Ответ: встреча произойдет через 0,55 часа на 44 километре шоссе.

 

Задача 3.

Координата тела, движущегося вдоль оси , изменяется со временем по закону, представленному на рисунке.

Задача 3. График зависимости координаты от времени

Построить график зависимости скорости и пути тела от времени. Чему равны перемещение и путь за первые с движения тела? Найти среднюю путевую скорость и среднюю скорость по перемещению за первые с движения.

В отличие от координаты и перемещения, путь всегда только растет со временем. Поэтому график пути будет следующим:

Задача 3. Путь от времени

Скорость постоянна,  проекция скорости на ось на промежутках времени 0-2 с и 4-5 с отрицательна (координата уменьшается), на промежутке 2-4 с – положительна (координата растет).

Задача 3. Зависимость скорости от времени

Определим  путь за 3 с. Это можно сделать по графику пути, определив ординату по известной абсциссе:

Задача 3. Определяем путь по графику пути

А можно определить путь как площадь под графиком скорости:

Задача 3. Определяем путь и перемещение по графику скорости

Определим перемещение . Это как раз удобно сделать по графику скорости, нужно вычесть из площади   площадь :

Средней путевой скоростью называется средняя скорость на всем пути, то есть частное от деления длины пути на время, а средней скоростью по перемещению называется частное от деления перемещения на время.

Найдем среднюю путевую скорость:

Найдем среднюю скорость по перемещению:

 

Ответ: , , , .

По какой формуле найти время в физике? – Reviews Wiki

Формула для времени дается как [Время = Расстояние ÷ Скорость] . Для расчета скорости формула времени будет иметь вид [Скорость = Пройденное расстояние ÷ Время].

Отсюда самый простой способ рассчитать время?

1. Преобразуйте оба времени в 24-часовой формат, добавив 12 к любым часам после полудня. 8:55 утра становится 8:55 часами (время начала) …
2. Если минуты начала больше, чем минуты окончания… …
3. Вычесть минуты времени окончания из минут времени начала… …
4. Вычесть часы… …
5. Сложить (не складывать) часы и минуты – 6:45 (6 часов 45 минут)

Дополнительно Как сделать вы находите время в физике без расстояния? В сторону: вообще, вы можете вычислить время, не зная расстояния (т. е. пройденного расстояния), если у вас достаточно другой информации. d = (v — u)T/2 и v = u+ aT (из этих двух можно вывести все остальные уравнения).

Как рассчитать время вручную? Как вручную рассчитать количество рабочих часов

1. Преобразовать все время в 24-часовой формат (военное время): преобразовать 8:45 утра в 08:45 часов. …
2. Далее, вычтите время начала из времени окончания.
3. Теперь у вас есть фактические часы и минуты, отработанные за день.
4. Наконец, чтобы определить общую заработную плату, вам нужно будет преобразовать ее в десятичный формат.

Как найти расстояние?

Может ли скорость быть отрицательной в физике? Скорость = Пройденное расстояние/Затраченное время

Поскольку расстояние и время являются положительными величинами, а скорость получается отношением этих двух величин, скорость не может быть отрицательной .

Как найти время, зная только расстояние?

Чтобы найти время, разделите пройденное расстояние на скорость . Например, если Коул едет на своей машине со скоростью 45 км в час и проезжает в общей сложности 225 км, то он проехал 225/45 = 5 часов.

Также Как найти время в физике без скорости? Решите для времени после того, как окончательная скорость найдена. Для этого вы можете изменить следующее уравнение: (Конечная скорость) = (Начальная скорость) + (Ускорение)*(Время). Таким образом, в этом случае (Время) = (Конечная скорость – Начальная скорость)/(Ускорение) . Тогда время равно (10,25 – 5)/(4) = 1,31 секунды.

Как найти конечную скорость с расстоянием и временем?

Как рассчитать скорость – скорость против скорости

1. Преобразование минут в секунды (чтобы окончательный результат был в метрах в секунду). 3 минуты = 3 * 60 = 180 секунд,
2. Разделите расстояние на время: скорость = 500/180 = 2,77 м/с.

Как добавить время в табель учета рабочего времени? Добавьте ежедневных рабочих часов за неделю.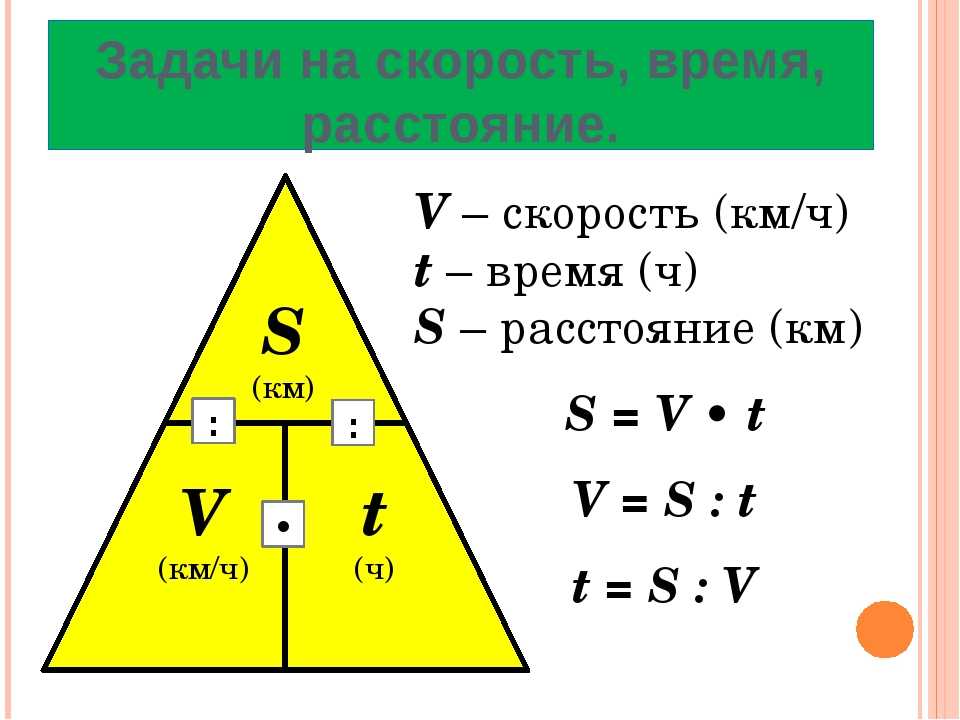 Например, с понедельника по пятницу на карточке учета рабочего времени отображается «В 8:00; на обед – 12:15, на обед – 13:15, на выход – 17:00». Вычтите один час за неоплачиваемый обед и оплатите работнику восемь рабочих часов за каждый день, что равняется 40 часам в неделю.

Как рассчитать 15 минут?

Ответ: 15 минут в десятичной форме выражается как 0,25 часа .

Как рассчитать часы часов?

Возьмите количество минут и разделите на 60.

1. Возьмите количество минут и разделите на 60. В этом примере ваш неполный час равен 15 минутам: …
2. Прибавьте обратно целые часы, чтобы получить 41,25 часа. . Итак, 41 час 15 минут равняется 41,25 часа.
3. Умножьте свою ставку заработной платы на десятичные часы, чтобы получить общую сумму заработной платы до вычета налогов.

Что такое формула расстояния в физике? Чтобы определить расстояние, используйте формулу для расстояния d = st , или расстояние равно скорости, умноженной на время. расстояние = скорость х время. Скорость и скорость похожи, поскольку они оба представляют некоторое расстояние в единицу времени, например мили в час или километры в час. Если скорость r такая же, как скорость s, r = s = d/t.

Что такое расстояние в физике? Расстояние 92} , где c — самая длинная сторона прямоугольного треугольника (также известная как гипотенуза), а a и b — другие более короткие стороны (известные как катеты прямоугольного треугольника).

Как найти время, зная только расстояние? Чтобы найти время, разделите пройденное расстояние на скорость . Например, если Коул едет на своей машине со скоростью 45 км в час и проезжает в общей сложности 225 км, то он проехал 225/45 = 5 часов. Создано Салом Ханом.

Как найти скорость, зная только расстояние?

Чтобы найти скорость, рассчитайте расстояние во времени в треугольнике, поэтому скорость равна пути, деленному на время . Чтобы найти расстояние, скорость не зависит от времени, поэтому расстояние равно скорости, умноженной на время.

Уменьшает ли скорость время? Скорость никогда не уменьшается со временем .

Расстояние уменьшает время?

1) Кратчайшее расстояние между конечной позицией и начальной позицией движения объекта. … 4) Расстояние не уменьшается со временем .

Почему скорость частицы не может быть отрицательной? Ответ Эксперт проверен

СКОРОСТЬ = пройденное расстояние/затраченное время . Скорость является скалярной величиной. КАК РАССТОЯНИЕ не может быть отрицательным для движущейся частицы, так и скорость для частицы не может иметь отрицательного значения.

4.4: Движение снаряда – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3987

• OpenStax
• OpenStax

Цели обучения

• Использовать одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
• Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
• Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
• Рассчитать траекторию снаряда.

Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются

снарядов и их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой линии», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.

Наиболее важным фактом, который следует здесь помнить, является то, что движения вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, возникающее в результате силы тяжести, является вертикальным; таким образом, ускорение вдоль горизонтальной оси отсутствует, когда сопротивлением воздуха можно пренебречь.) Как обычно, мы называем горизонтальную ось осью x, а вертикальную ось Y-ось. Мы не обязаны использовать этот выбор осей; это просто удобно в случае гравитационного ускорения. В других случаях мы можем выбрать другой набор осей. На рисунке \(\PageIndex{1}\) показано обозначение смещения, где мы определяем \(\vec{s}\) как общее смещение, а \(\vec{x}\) и \(\vec{ y}\) — его составляющие векторы вдоль горизонтальной и вертикальной осей соответственно.

Величины этих векторов равны s, x и y.

Рисунок \(\PageIndex{1}\): Полное перемещение s футбольного мяча в точке на его пути. Вектор \(\vec{s}\) имеет компоненты \(\vec{x}\) и \(\vec{y}\) вдоль горизонтальной и вертикальной осей. Его величина равна s, и он составляет угол \(\phi\) с горизонтом.

Чтобы полностью описать движение снаряда, мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты по осям x и y. Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми: 9{2}) \ldotp\]

Поскольку гравитация вертикальна, a _x = 0. Если a _x = 0, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x, или v

x = v _0x . С этими условиями на ускорение и скорость мы можем записать кинематическое уравнение 4. 11 через уравнение 4.18 для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из движения с постоянным ускорением. Кинематические уравнения движения в однородном гравитационном поле переходят в кинематические уравнения с 9{2} + 2g(y – y_{0}) \label{4.23}\]

Используя этот набор уравнений, мы можем проанализировать движение снаряда, помня о некоторых важных моментах.

Стратегия решения проблем: Движение снаряда

1. Разделите движение на горизонтальную и вертикальную составляющие вдоль осей x и y. Величины компонентов смещения \(\vec{s}\) вдоль этих осей равны x и y. Величины компонентов скорости \(\vec{v}\) равны v _x = vcos\(\theta\) и v _y = vsin\(\theta\), где v — величина скорости, а \(\theta\) — ее направление относительно горизонтали, как показано на рисунке \(\PageIndex{2}\).
2. Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
3. Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t. Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах. 9{2}} \ldotp$$, где \(\phi\) — направление смещения \(\vec{s}\).

Рисунок \(\PageIndex{2}\): (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей. (b) Горизонтальное движение простое, потому что a _x = 0, а v _x является константой. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (d) Движения x и y рекомбинируются, чтобы получить общую скорость в любой заданной точке траектории.

Пример 4.7: Снаряд фейерверка взрывается высоко и далеко

Во время фейерверка снаряд выстреливается в воздух с начальной скоростью 70,0 м/с под углом 75,0° над горизонталью, как показано на рисунке \( \ИндексСтраницы{3}\). Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?

Рисунок \(\PageIndex{3}\): Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.

Стратегия

Движение можно разбить на горизонтальное и вертикальное, в которых _x = 0 и _y = −g. Затем мы можем определить x ₀ и y ₀ равными нулю и найти нужные величины.

Решение 9{2})} \ldotp$$ Таким образом, имеем $$y = 233\; м \ldotp$$Обратите внимание, что, поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение, вызванное силой тяжести, отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты. 9{2}} = 6,90\; s \ldotp$$Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется.

Другой способ найти время — использовать y = y ₀ + \(\frac{1}{2}\)(v _0y + v _y )t. Это оставлено вам в качестве упражнения для выполнения.

Поскольку сопротивлением воздуха можно пренебречь, _x = 0, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение – это горизонтальная скорость, умноженная на время, как указано x = x 9{о} = 18,1\; м/с \ldotp$$Время t для обоих движений одинаково, поэтому x равен $$x = (18,1\; м/с)(6,90\; с) = 125\; м \ldotp$$Горизонтальное движение – это постоянная скорость при отсутствии сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, большое влияние оказывает сопротивление воздуха, и многие осколки приземляются прямо под ним.

Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что нужно здесь, это найти величину и направление смещения в самой высокой точке: $$\vec{s} = 125 \hat{i} + 233 \шляпа{j}$$$$|\vec{s}| = \sqrt{125^{2} + 233^{2}} = 264\; m$$$$\theta = \tan^{-1} \left(\dfrac{233}{125}\right) = 61,8^{o} \ldotp$$Обратите внимание, что угол вектора смещения меньше начальный угол запуска. {2}}{2g} \ldotp$$Это уравнение определяет максимальная высота снаряда над стартовой позицией и зависит только от вертикальной составляющей начальной скорости.

Упражнение 4.3

Камень брошен горизонтально со скалы высотой 100,0 м со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?

Пример 4.8: Расчет движения снаряда — теннисист

Теннисист выиграл матч на стадионе имени Артура Эша и ударил мячом по трибунам со скоростью 30 м/с под углом 45° над горизонтом (рис. \(\PageIndex{4}\)). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?

Рисунок \(\PageIndex{4}\): траектория удара теннисного мяча о трибуны.

Стратегия

Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала находим t. Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить \(\vec{v}\) в конечное время t, определенное в первой части примера. 9{2} − (21,2\; м/с)t + 10,0\; m = 0 \ldotp$$Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Так как мяч находится на высоте 10 м два раза на своем пути — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя: $$t = 3,79\; с \ldotp$$Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, тратит 3,79с в воздухе.

Мы можем найти конечные горизонтальную и вертикальную скорости v _x и v _y , используя результат (а). {o} = 21,2\; м/с \ldotp$$Конечная вертикальная скорость определяется уравнением \ref{4.21}: $$v_{y} = v_{0y} − gt \ldotp$$Поскольку \(v_{0y}\) было найдено части (а) равной 21,2 м/с, имеем $$v_{y} = 21,2\; м/с − (9{o} \ldotp$$

Значение

1. Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с.
2. Отрицательный угол означает, что скорость на 53,1° ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательную компоненту y скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.

Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на эту же поверхность. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.

Время полета

Мы можем найти время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполняя некоторые манипуляции с кинематическими уравнениями. Отметим, что положение и перемещение по y должны быть равны нулю при пуске и при ударе о ровную поверхность. Таким образом, приравняем смещение по y к нулю и найдем 9{2} = 0 \ldotp\]

Факторинг, мы имеем

\[t \left(v_{0} \sin \theta_{0} – \dfrac{gt}{2}\right) = 0 \ldotp \]

Решение для t дает нам

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

Это время полета снаряда, выпущенного и ударившегося о плоскую горизонтальную поверхность. Уравнение \ref{4.24} не применяется, когда снаряд приземляется на высоте, отличной от той, на которой он был запущен, как мы видели в примере 4.8, где теннисист отбивает мяч в трибуны. Другое решение, t = 0, соответствует моменту запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g. Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.

Траектория

Траекторию снаряда можно найти, исключив временную переменную t из кинематических уравнений для произвольного t и решив для y(x). Мы берем x ₀ = y ₀ = 0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для x дает

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0} } \ldotp\]

Подставляя выражение для t в уравнение для положения y = (v 9{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

Обратите особое внимание на то, что уравнение \ref{4.26} действительно только для запуска и удара о горизонтальную поверхность. Мы видим, что диапазон прямо пропорционален квадрату начальной скорости v ₀ и sin ² \(\theta_{0}\) и обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости. Кроме того, мы видим из множителя sin ² \(\theta_{0}\), что диапазон максимален при 45°. Эти результаты показаны на рисунке \(\PageIndex{5}\). В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (б) мы видим, что диапазон максимален при 45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон обнаруживается для двух начальных углов запуска, которые в сумме составляют 90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.

Рисунок \(\PageIndex{5}\): Траектории снарядов на ровной поверхности. (a) Чем больше начальная скорость v ₀ , тем больше диапазон для данного начального угла. (b) Влияние начального угла (\theta_{0}\) на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов 15° и 75°, хотя максимальная высота этих путей различна.

Пример 4.9: Сравнение ударов в гольфе

Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет ударить по мячу 90 м и дайте ей выбежать на грин. Он направляет удар низко к земле под углом 30° к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом 70° к горизонтали, чтобы свести к минимуму перекатывание после удара. Оба выстрела попали в ровную поверхность. а) Какова начальная скорость мяча у второй лунки? б) Какова начальная скорость мяча у четвертой лунки? (c) Напишите уравнение траектории для обоих случаев. (d) Нарисуйте траектории. 9{2}$$

Используя графическую утилиту, мы можем сравнить две траектории, показанные на рисунке \(\PageIndex{6}\).

Рисунок \(\PageIndex{6}\): две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка запуска.

Значение

Начальная скорость выстрела под углом 70° больше, чем начальная скорость выстрела под углом 30°. Обратите внимание на рисунок \(\PageIndex{6}\), что два снаряда, запущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска в сумме составляют 9.0°. Углы запуска в этом примере складываются, чтобы получить число больше 90 °. Таким образом, выстрел под углом 70° должен иметь большую скорость пуска, чтобы достичь 90 м, иначе он приземлится на более коротком расстоянии.

Упражнение 4.4

Если бы два удара для гольфа в примере 4.9 были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?

Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мало по сравнению с окружностью Земли. Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рисунке \(\PageIndex{7}\), который основан на рисунке в 9 Ньютоне.0183 Принципы . Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля “Шаттл” на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».