Формула касательного ускорения: Напишите формулу для определения касательного ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю? — Мегаобучалка

Чему равны проекции вектора скорости точки на естественные оси? Запишите соответствующие формулы.

, ,

8. Чему равны проекции вектора ускорения точки на естественные оси? Запишите соответствующие формулы.

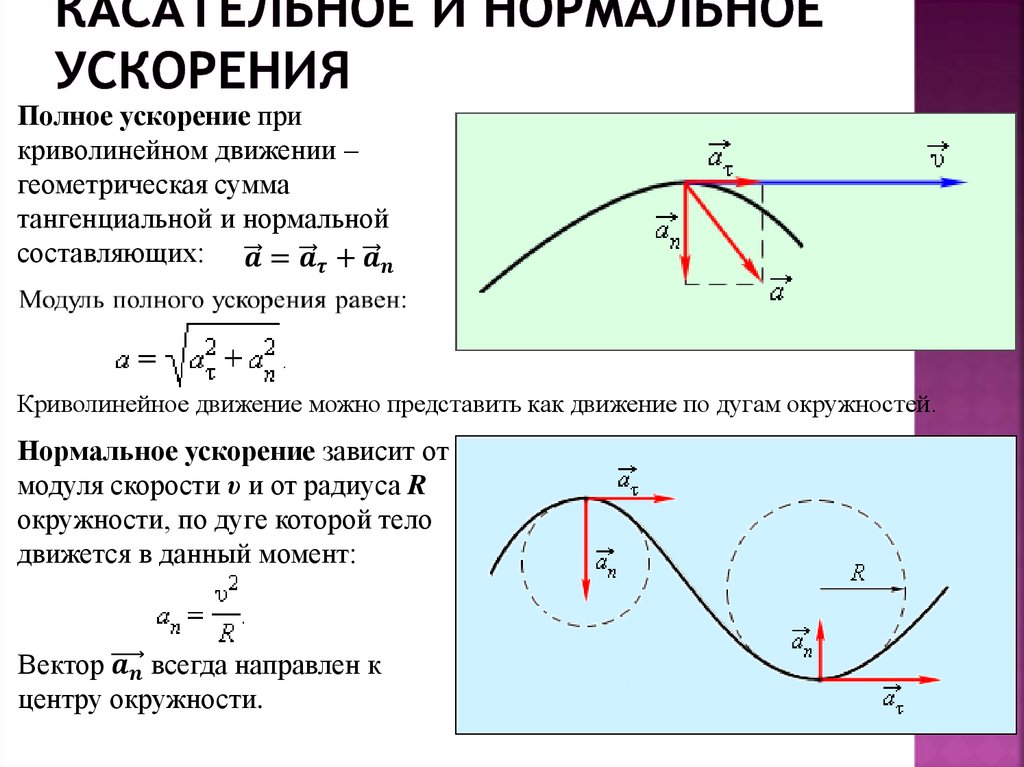
Формула представляет собой разложение ускорения точки М по ортам естественного трёхгранника. Составляющие вектора ускорения по направлениям и соответственно равны: , . Проекция ускорения на направление касательной: , называется касательным или тангенциальным ускорением. Проекция ускорения на главную нормаль: , называется нормальным ускорением. Так как ускорение точки лежит в соприкасающейся плоскости, то проекция ускорения точки на бинормаль равна нулю.

9. Напишите формулу для определения касательного ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю?

Касательное ускорение характеризует изменение скорости по величине. Касательное ускорение равно нулю, при движении точки с постоянной по модулю скоростью и в моменты времени, когда скорость достигает экстремальных значений. При движение равномерное.

Формула для определения касательного ускорения (проекция ускорения на направление касательной): . Или, если единичный вектор касательной определяем формулой: , то запишем:

10. Напишите формулу для определения нормального ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю?

Нормальное ускорение характеризует изменение скорости по направлению. Нормальное ускорение равно нулю при прямолинейном движении (), в точках перегиба криволинейной траектории и с в моменты, когда скорость точки обращается в нуль.

Формула для определения нормального ускорения (проекция ускорения на направление нормали): . Или, если единичный вектор касательной определяем формулой: , то запишем:

11. Чему равно ускорение точки при равномерном криволинейном движении. Как это ускорение направлено и по какой формуле вычисляется?

Формула для определения касательного ускорения (проекция ускорения на направление касательной): .

Формула для определения нормального ускорения (проекция ускорения на направление нормали): . Модуль полного ускорение точки вычисляется по теореме Пифагора: . Определим направление вектора : – угол между вектором полного ускорения и нормалью.

12. Какое движение твердого тела называется поступательным? Перечислите свойства поступательного движения твёрдого тела.

– Поступательным движением твёрдого тела называется такое движение, при котором любая прямая, проведённая в теле во всё время движения, остаётся параллельной своему первоначальному направлению.

СВ1: При поступательном движении твёрдого тела всё его точки описывают одинаковые траектории, которые при параллельном переносе совпадают.

СВ2: При поступательном движении всё точки твёрдого тела движутся с одинаковыми скоростями и ускорениями для любого момента времени.

13. Какое движение твердого тела называется движением вокруг неподвижной оси? Запишите уравнение вращательного движения.

    Сделайте соответствующий рисунок.

Вращательное движение. Это такое движение твёрдого тела, при котором все точки этого тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения. Уравнение или закон вращательного движения вокруг неподвижной оси: .

Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)

Регистрация на конференцию ИТЭС

Регистрация на конференцию «Актуальные проблемы теории и практики современной науки»

Регистрация на конференцию «Архитектура и строительство: традиции и инновации»

Как поступить в БелГУТ

Как получить место

в общежитии БелГУТа

Как поступить иностранному гражданину

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
	1	2	3	4	5 Дата : 2022-11-05	6 Дата : 2022-11-06
7	8 Дата : 2022-11-08	9	10	11	12 Дата : 2022-11-12	13
14	15	16 Дата : 2022-11-16	17 Дата : 2022-11-17	18	19 Дата : 2022-11-19	20
21 Дата : 2022-11-21	22	23	24 Дата : 2022-11-24	25 Дата : 2022-11-25	26 Дата : 2022-11-26	27
28 Дата : 2022-11-28	29	30

Все анонсы

• Набор в Студенческий совет БелГУТа . ..
• Кастинг видеоблогеров, теле- и радиоведущих…
• Республиканская викторина «Я хочу быть таможеннико…
• Билеты на премьерный спектакль «451° по Фаренгейту…
• Финал игр спартакиады по мини-футболу…
• ПРОГРАММА. XII Международная научно-практическая к…
• Приглашаем в бассейн
• V Международная научно-практическая конференция ст…
• Олимпиада по высшей математике для студентов…
• Навстречу Дню освобождения г. Гомеля от немецко-…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Набор в Студенческий совет БелГУТа …

Кастинг видеоблогеров, теле- и радиоведущих…

Республиканская викторина «Я хочу быть таможеннико…

Билеты на премьерный спектакль «451° по Фаренгейту…

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений



• Университет

Круглый стол «Об изменениях Закона Республики Беларусь «О железнодорож. ..
25 ноября 2022

• Университет

Митинг на «Аллее героев»
25 ноября 2022

Работа секции № 5 «Безопасность транспортной инфраструктуры»…
25 ноября 2022

• Университет

Работа секции № 6 «Надежность и безопасность зданий и сооружений»…
25 ноября 2022

• Университет

XII Международная научно-практическая конференция «Проблемы безопаснос…
24 ноября 2022

• Студенческая жизнь

Студенты читают свои стихи, посвященные Дню освобождения Гомеля…
24 ноября 2022

• Воспитательная работа

Открытый диалог в канун празднования 79-й годовщины освобождения город. ..
24 ноября 2022

• Воспитательная работа

«Пойти и не вернуться»
24 ноября 2022

• Университет

Лауреаты конкурса «Лучшая научная работа 2022»…
24 ноября 2022

Другие новости

• Студотряды БелГУТа – лучшие студотряды Гомельской области…
• У памятника братьям Лизюковым
• Материалы XII Международной научно-практической конференции «Проблемы …
• В музыке не существует границ
• Телемост двух государств «Поезд памяти»…
• Встреча ректора БелГУТа с коллективом локомотивного депо Гомель…
• Братские могилы на Лещинском кладбище
• Экскурсия на участок обороны Гомельского народного ополчения…
• Будь в теме!
• Наши студотрядовцы – лучшие!
• Лучший молодой специалист года!

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Формула тангенциального ускорения – GeeksforGeeks

Тангенциальное ускорение — это скорость изменения тангенциальной скорости при вращательном движении любого объекта.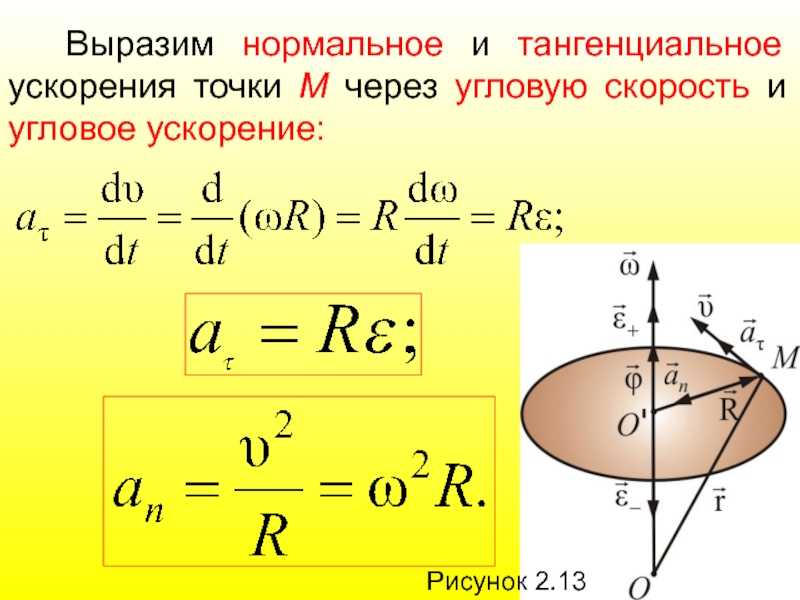 Он действует в направлении касательной в точке движения объекта. Тангенциальная скорость также действует в том же направлении для объекта, совершающего круговое движение. Тангенциальное ускорение существует только тогда, когда объект движется по круговой траектории. Она положительна, если тело вращается с большей скоростью, отрицательна, когда тело замедляется, и равна нулю, когда тело движется равномерно по орбите.

 

Формула

Тангенциальное ускорение обозначается символом a _t . Его единица измерения такая же, как и линейное ускорение, то есть метры в секунду в квадрате (м/с ² ). Его размерная формула задается как [M ⁰ L ¹ T ^-2 ]. Его формула определяется произведением радиуса окружности на угловое ускорение вращающегося объекта.

а _t = r α

где,

a _t — тангенциальное ускорение,

r — радиус окружности,

α — угловое ускорение.

Формула для угловой скорости и времени имеет вид ω — угловая скорость,

t — затраченное время.

В терминах углового перемещения и времени формула имеет вид:

A _T = R (θ/T ² )

, где,

A _T – это касательное ускорение,

θ – угловое смещение или угол вращения,

T IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS. затраченное время.

Примеры задач

Задача 1. Вычислить тангенциальное ускорение, если тело совершает круговое движение радиусом 5 м и угловым ускорением 2 рад/с ² .

Решение:

Мы имеем,

R = 5

α = 2

Используя формулу, которую мы получаем,

A _T = R α

= 5 (2)

= 10 м/ М/ М/ М/ М/ М/ М/ s ²

Задача 2. Вычислить тангенциальное ускорение, если тело совершает круговое движение для радиуса 12 м и углового ускорения 0,5 рад/с ² .

Решение:

Имеем,

r = 12

α = 0,5

с использованием формулы, которую мы получаем. если объект совершает круговое движение с радиусом 20 м и тангенциальным ускорением 40 м/с ² .

Решение:

Имеем,

r = 20

a _t = 40

Используя формулу получаем,

A _T = R α

=> α = A _T /R

=> α = 40/20

=> α = 2 RAD/S ²

Проблема 4. Вычислите угловое ускорение, если объект совершает круговое движение с радиусом 2 м и тангенциальным ускорением 20 м/с ² .

Решение:

Имеем,

r = 2

a _t = 20

Используя формулу получаем,

A _T = R α

=> α = A _T /R

=> α = 20/2

=> α = 10 RAD/S ²

Проблема 5. Вычислите радиус, если объект совершает круговое движение с угловым ускорением 4 рад/с ² и тангенциальным ускорением 20 м/с ² .

Решение:

Имеем,

α = 4

a _t = 20

Используя формулу получаем,

a _t = r α

=> r = a _t /α

=> r = 20/4

=> r = 5 м 

2 Задача вычислить угловое ускорение 6. объект совершает круговое движение радиусом 12 м, угловой скоростью 3 рад/с и временем 9 с.

Решение:

Имеем,

r = 12

ω = 3

t = 9

9002 90 a 2 = r (ω/t)

= 12 (3/9)

= 12/3

= 4 м/с ²

Задача 7. Вычислить тангенциальное ускорение, если объект движется по окружности движение по радиусу 5 м, угловое смещение 30 радиан и время 5 с.

Решение:

. )

= 5 (30/5 ² )

= 30/5

= 6 м/с ²

ТАНГАВИНДА

В круговом движении мы обычно связываем термин ускорение с радиальным и тангенциальным ускорением. Этот тип ускорения измеряет, насколько быстро изменяется тангенциальная скорость. Они всегда действуют перпендикулярно центростремительному ускорению вращающегося объекта. Тангенциальное ускорение определяется как скорость изменения тангенциальной скорости вещества на круговом пути.

Определение тангенциального ускорения

Тангенциальное ускорение можно определить как изменение скорости, происходящее по касательной при круговом движении.

Формула тангенциального ускорения

Математически представляется как

a _t = v ₂ – v ₁ / t ₂ -t ₁ ——————-(1)

Где а — тангенциальная составляющая 

t = t ₂ -t ₁ — период времени

и V ₁ и V ₂ являются соответствующими скоростями двух объектов

. Блок представлен как MS ^-2

Другие формы Формулы для тангенциального ускорения 7

. Использование Очисти формуле физики, мы можем преобразовать уравнение (1) в терминах расстояния как:

Опять же, используя формулу скорость = расстояние по времени:

Формула тангенциального ускорения через скорость и расстояние.

Численные задачи на тангенциальное ускорение

Мальчик бежит со скоростью 10 км/ч по равномерному круговому пути и пытается разогнаться до скорости 20 км/ч (в два раза больше текущей скорости). ). Вычислите тангенциальное ускорение, необходимое для достижения этого за 30 секунд.

а _т = v ₂ – v ₁ / t ₂ -t ₁ (Формула тангенциального ускорения)

Здесь изменение скорости равно 10 км/ч (2,77 м/с), а время занимает 30 секунд. Используя формулу для тангенциального ускорения, имеем:

a _t = 2,77/30 = 0,092 м/с

Итак, тангенциальное ускорение при изменении скорости на 10 км/ч за 30 с составляет 0,092 м/с.

Корова, движущаяся по равномерному круговому пути, имеет тангенциальное ускорение 1 м/с. Найдите изменение скорости, которое он может достичь за 1 мин.

снова, используя формулу для тангенциального ускорения (A _T = V ₂ -V ₁ / T ₂ -T ₁ ) Мы имеем:

1 = V ₂ -V _{). 1} / 60.

Следовательно, изменение скорости, которое может развить корова, составляет 60 м/с или 216 км/ч (что практически невозможно! :))

См. также Радиальное ускорение

Расчет конечной скорости

Определение скорости дрейфа

Типы переключателей

Плохие проводники электричества

Предыдущая статьяВывод скорости дрейфа

Следующая статьяЗакон Гука – Определение | формула | Примеры

Поиск

DewWool Видео дня

Поддержите нас

Мы хотим сделать науку интересной и в то же время бесплатной! Ваш вклад в эту страницу поможет нам донести качественный контент до детей, которые больше всего в нем нуждаются. Если вам нравится, что мы делаем, и вы хотите поддержать нас, вы можете посетить нашу страницу пожертвований ko-fi на www.ko-fi.com/dewwool.

Категории

• Анимация
• Биология
• Блог
• Химия
  • Органическая химия
• Математика
• Физика
  • Оптика и акустика
• Викторина
• Без категории
• Рабочие листы

Комикс дня

Архивы

Архивы Выбрать месяц Ноябрь 2022 Октябрь 2022 Август 2022 Июль 2022 Июнь 2022 Май 2022 Апрель 2022 Март 2022 Январь 2022 Декабрь 2021 Ноябрь 2021 Октябрь 2021 Сентябрь 2021 Август 2021 Июль 2021 Июнь 2021 Май 2021 Апрель 2021 Сентябрь 2020 г. Август 2020 г. Июль 2020 г. Июнь 2020 г. Май 2020 г. Март 2020 г.

Последние сообщения

10 примеров равнобедренных треугольников

админ – 24 ноября 2022 0

Равнобедренные треугольники — это треугольники, у которых две стороны одинаковой длины, а третья сторона разной длины. Кроме того, два угла заключены…

10 примеров равностороннего треугольника

админ – 18 ноября 2022 0

Все мы знаем, что у равностороннего треугольника все три стороны равны, а все три угла равны 60 градусам. Но помните…

30 Примеры семян двудольных растений

админ – 16 ноября 2022 0

Как мы все знаем, семя является самой основной и важной частью растения. Они находятся внутри фрукта, который превращает.