Энергия кинетическая молекул идеального газа
Для одноатомного идеального газа внутренняя энергия определяется кинетической энергией его молекул. Для одного моля она равна [c.35]Согласно кинетической теории средняя кинетическая энергия молекул идеального газа [c.34]
Для любой системы, находящейся в равновесии и подчиняющейся законам классической механики, число молекул, обладающих энергией больше е, пропорционально фактору Больцмана g-e/fer g-EiR-r рде E-=Ne. Для идеального газа, молекулы которого (по предположению) обмениваются толька кинетической энергией, выполняется закон Максвелла — Больцмана для распределения молекул по скоростям доля молекул, скорость которых лежит в пределах от и до u + du, равна [c.57]
Молекулярно-кинетическая теория также позволяет делать предсказания относительно диффузии, вязкости и теплопроводности газов, т.


Отношение /2кТ = показывает, что абсолютная температура пропорциональна средней кинетической энергии перемещения молекулы идеального газа. [c.97]
Так как кинетическая энергия поступательного движения молекул газа, налетающих на удаляющийся от них поршень, уменьшается, то слой газа, прилегающий к поршню, непрерывно охлаждается. Однако вследствие хаотического движения и столкновения молекул температура газа при медленном его расширении будет выравниваться по всей массе. Чтобы температура газа при его рабочем расширении оставалась неизменной, необходимо пополнять энергию газа путем подвода к нему теплоты. В результате работа расширения газа будет производиться за счет теплоты, сообщаемой газу.
Среднюю квадратичную скорость можно теперь записать в виде с = = ЗкТ/ту/ , а среднюю кинетическую энергию молекулы идеального газа — [c.29]
Таким образом, абсолютная температура пропорциональна средней кинетической энергии в молекул идеального газа и поэтому служит мерой энергии. С точки зрения молекулярно-кинетической теории абсолютный нуль температуры может быть определен как температура, при которой кинетическая энергия молекул равна нулю.
Определите молекулярный вес этого соединения. Используя закон Максвелла о распределении молекул по энергиям = /е напишите выражение для доли молекул идеального газа, трансляционная кинетическая энергия которых больше некоторой величины 8о.
Энергия молекул идеального газа, по определению, является только кинетической. Таким образом, в уравнении (21) величина т равна нулю, и энергия молекулы, выраженная через компоненты импульсов р и скоростей и, имеет вид [c.41]
При небольших смещениях атомов из положения равновесия в узлах кристаллической решетки можно в первом приближении потенциальной энергии пренебречь ангармонизмом (энергия, связанная с ангармонизмом, мала). Покажем, что при этом условии в случае всестороннего сжатия и расширения (ниже макроскопического предела текучести) химический потенциал атомов металла, возбужденных деформацией, будет одинаково возрастать независимо от знака деформации (т. е. знака, приложенного извне гидростатического давления) в отличие от кинетической модели системы свободных молекул (идеального газа), где знак приращения давления определяет направление изменения химического потенциала. Напротив, термоупругие эффекты в твердых телах связаны с ангармоническими членами в выражении потенциальной энергии взаимодействия атомов, но здесь они не рассматриваются. В литературе этому вопросу не уделено должного внимания, так как все опыты по изучению поведения твердых тел под высоким давлением относятся к деформации тела сжатием.
Покажем, что при этом условии в случае всестороннего сжатия и расширения (ниже макроскопического предела текучести) химический потенциал атомов металла, возбужденных деформацией, будет одинаково возрастать независимо от знака деформации (т. е. знака, приложенного извне гидростатического давления) в отличие от кинетической модели системы свободных молекул (идеального газа), где знак приращения давления определяет направление изменения химического потенциала. Напротив, термоупругие эффекты в твердых телах связаны с ангармоническими членами в выражении потенциальной энергии взаимодействия атомов, но здесь они не рассматриваются. В литературе этому вопросу не уделено должного внимания, так как все опыты по изучению поведения твердых тел под высоким давлением относятся к деформации тела сжатием.
При какой температуре поступательная кинетическая энергия молекул идеального газа равна 5 ккал/моль [c.280]
С микроскопической точки зрения, представляемой квантовой механикой и приложениями классической механики к кинетической теории, поведение отдельных молекул можно описать, рассматривая строение этих молекул и механизмы их взаимодействия с другими молекулами. Мы уже показали, как с помощью кинетической теории описать давление, энергию и теплоемкости идеальных газов, не обладающих внутренними степенями свободы. Но мы также видели, что кинетическая теория не может объяснить изменение теплоемкостей молекул или кристаллов с температурой. В идеальном случае хотелось бы, чтобы можно было предсказывать термодинамическое поведение веществ на основе сведений об отдельных молекулах, полученных из спектроскопических измерений И из теоретических расчетов, таких, как расчеты, рассмотренные в гл. 14.
Мы уже показали, как с помощью кинетической теории описать давление, энергию и теплоемкости идеальных газов, не обладающих внутренними степенями свободы. Но мы также видели, что кинетическая теория не может объяснить изменение теплоемкостей молекул или кристаллов с температурой. В идеальном случае хотелось бы, чтобы можно было предсказывать термодинамическое поведение веществ на основе сведений об отдельных молекулах, полученных из спектроскопических измерений И из теоретических расчетов, таких, как расчеты, рассмотренные в гл. 14.
Теплота и работа, Согласно молекулярно-кинетической теории каждое тело располагает определенным запасом внутренней энергии, который слагается из энергии движения молекул (поступательного и вращательного), называемой внутренней кинетической энергией, и энергии взаимного притяжения молекул — внутренней потенциальной энергии (в идеальных газах отсутствует).
В идеальном газе молекулы рассматриваются как материальные точки, размеры которых бесконечно малы по сравнению с расстояниями между ними. Кроме того, считается, что столкновения молекул идеально упруги, т. е. кроме передачи кинетической энергии никаких других взаимодействий между молекулами идеального газа не существует. [c.76]
Кроме того, считается, что столкновения молекул идеально упруги, т. е. кроме передачи кинетической энергии никаких других взаимодействий между молекулами идеального газа не существует. [c.76]
Постоянная k = R/Na называется постоянной Больцмана ее можно рассматривать как газовую постоянную, отнесенную к одной молекуле идеального газа. Универсальная газовая постоянная / равна 2/з кинетической энергии молекул 1 кмоль вещества, приобретаемой при нагревании на 1 К.
Величину tv легко оценить, используя формулу (1.4.26) для кинетической энергии молекул идеального газа еу где [c.155]
Так как 1 эв при температурном пересчете соответствует 11600 грай, по средней энергии осколков можно оценить создаваемую ими кинетическую температуру. Получается, что непосредственно в зоне деления она составляет 900 миллиардов градусов. Если допустить, что концентрация осколков такова же, как молекул идеального газа при обычных условиях, то в зоне деления создается давление около 2 миллиардов атмосфер. Реальные значения и температуры, и давления должны быть гораздо ниже (из-за относительно малой концентрации осколков и их неподчинения законам идеальных газов). Однако они все же очень велики (по ориентировочным данным —50 млн. град и 1 млн. атм), чем и обусловлен взрывной эффект атомной бомбы.
Реальные значения и температуры, и давления должны быть гораздо ниже (из-за относительно малой концентрации осколков и их неподчинения законам идеальных газов). Однако они все же очень велики (по ориентировочным данным —50 млн. град и 1 млн. атм), чем и обусловлен взрывной эффект атомной бомбы.
Кинетическая энергия молекул идеального газа. В кинетической теории газов молекулы рассматриваются как упругие шары, имеющие исключительно малый объем по сравнению с общим объемом газа (как материальные точки). Предполагается также, что молекулы газов не притягиваются и не отталкиваются друг от друга, т. е. столкновения между ними абсолютно упруги. [c.43]
Эффект Джоуля — Томсона. Согласно кинетической теории газов кинетическая энергия молекул идеального газа не зависит от объема. Если газ (например, воздух), находящийся в сосуде почти в идеальных условиях (при атмосферном давлении), может выходить из него в эвакуированный сосуд, то его температура не изменяется (см. опыт Гей-Люссака и Джоуля, описанный на стр. 42). [c.137]
опыт Гей-Люссака и Джоуля, описанный на стр. 42). [c.137]
Рассмотрим полость со стенками, не имеющими никаких специфических свойств и полностью отражающих всякую падающую радиацию. Внутри полости находится разреженный электронный газ. Если газ разрежен достаточно, то мы знаем из рассуждений, аналогичных тем, которые приведены Ричардсоном при рассмотрении термоионной эмиссии, что электроны ведут себя подобно молекулам идеального газа. Эффектом пространственного распределения заряда можно пренебречь в сравнении с силами, определяемыми столкновениями частиц. Пусть электронный газ в полости находится при температуре в. На электроны действуют силы двух родов силы столкновения с другими электронами, природа которых такая же, как у атомов в обычной кинетической теории и силы поля радиации в эфире. Электроны постоянно ускоряются, поэтому они непрерывно излучают и поглощают энергию из эфирного поля радиации. Система должна рано или поздно прийти в равновесие, достигая некоторой плотности энергии в эфире, причем электроны должны обладать кинетической энергией, свойственной атомам газа при температуре полости. Подробное решение задачи требует, разумеется, весьма сложного статистического анализа, но и анализ размерностей приводит к некоторым заключениям о форме результата. [c.105]
Подробное решение задачи требует, разумеется, весьма сложного статистического анализа, но и анализ размерностей приводит к некоторым заключениям о форме результата. [c.105]
Это выражение показывает, что химический потенциал идеального трехмерного газа при данной температуре Т определяется его концентрацией [c.509]
Таким образом, при описании фазовых переходов в газовых смесях необходим учет энергии взаимодействия между молекулами пара и конденсата при выполнении условия насыщенности конденсирующейся смеси и проявления в ней ван-дер-вааль-совых сил и водородных связей. Уравнения состояния, построенные с учетом ассоциации, описывают процессы в газах с большой точностью. Это объясняется тем, что присутствие молекулярных комплексов является одной из причин отклонения в поведении реальных газов по сравнению с идеальным газом. При сложных столкновениях может случиться, что молекулы после соударения не смогут преодолеть силы притяжения и будут двигаться совместно. Образующиеся комплексы могут быть достаточно устойчивыми и продолжают дальнейшее движение уже за счет собственной кинетической энергии. [c.101]
Образующиеся комплексы могут быть достаточно устойчивыми и продолжают дальнейшее движение уже за счет собственной кинетической энергии. [c.101]
Вычислите кинетическую энергию молекул 1 моля идеального газа при [c.161]
При повышении температуры идеального газа теплота расходуется только на увеличение кинетической энергии поступательного и вращательного движения его молекул и на усиление колебательного движения атомов, составляющих молекулы, и внутреннего вращения ( 35). Все эти формы движения не зависят от давления газа, и при данной температуре энергия их постоянна. Поэтому не зависит от давления и теплоемкость каждого данного газа. Отсюда следует, что и внутренняя энергия идеального газа не изменяется с изменением давления, [c.231]
Первое начало термодинамики ничего не говорит о возможных направлениях передачи энергии, тогда как второе начало предопределяет это направление. Внутренняя энергия системы слагается из кинетической и потенциальной энергий. Кинетическая энергия — это энергия беспорядочного движения атомов и молекул, потенциальная энергия — энергия их взаимного притяжения и отталкивания. Для идеального газа энергия при-тяжЕния и отталкивания пренебрежимо мала, и поэтому энергия идеального газа однозначно определяется так называемым уравнением состояния. [c.23]
Кинетическая энергия — это энергия беспорядочного движения атомов и молекул, потенциальная энергия — энергия их взаимного притяжения и отталкивания. Для идеального газа энергия при-тяжЕния и отталкивания пренебрежимо мала, и поэтому энергия идеального газа однозначно определяется так называемым уравнением состояния. [c.23]
Внутренняя энергия идеального газа и представляет собой сумму кинетической энергии отдельных молекул. Для одноатомного газа (например, инертного) кинетическая энергия определяется только поступательным движением. Поэтому для одной молекулы газа из уравнения (7) получим [c.20]
Если же сравнить этот результат, полученный на основании молеку-лярно-кинетической теории, с экспериментально установленным уравнением состояния идеального газа (уравнение 3-8), можно сделать вывод, что кинетическая энергия 1 моля газа пропорциональна его температуре. Но представляет интерес воспользоваться этим выводом, наоборот, для того, чтобы осмыслить понятие температуры газа. Абсолютная температура Т газа-не что иное, как проявление кинетической энергии газовых молекул, точнее температура-это мера среднеквадратичной скорости мoлeкyJl. Для 1 моля идеального газа имеем РУ = КТ. Подстановка в это равенство значения РУ, соответствующего формуле (3-25), дает [c.138]
Абсолютная температура Т газа-не что иное, как проявление кинетической энергии газовых молекул, точнее температура-это мера среднеквадратичной скорости мoлeкyJl. Для 1 моля идеального газа имеем РУ = КТ. Подстановка в это равенство значения РУ, соответствующего формуле (3-25), дает [c.138]
Идеальный газ. Модель идеального газа рассматривает молекулы как упругие шарики, между которыми отсутствуют силы притяжения и которые при столкновении ведут себя как идеально упругие тела (суммарная кинетическая энергия сталкивающихся молекул не меняется в результате столкновения). Занимаемый ими объем пренебрежимо мал по сравнению с объемом газа. [c.56]
Кинетическая теория газов показывает, что температура определяется средней кинетической энергией поступательного двин ения, хотя кинетическая энергия отдельных частиц-молекул может и значительно отличаться от этой величины. Давление газа выражает суммарный эффект столкновений молекул со стенкой сосуда и является величиной, усредненной по большому числу ударов. Молекулы могут обладать при этом самыми различными количествами движения и ударяться о стенку под самыми различными углахги. Чтобы выбранная модель соответствовала реальному газу, общая энергия всех молекул идеального газа должна равняться фактической. Молекулы в газе движутся, но взаимодействие между ними отсутствует, поэтому энергия газа — это сумма кинетических энергий всех молекул [c.16]
Молекулы могут обладать при этом самыми различными количествами движения и ударяться о стенку под самыми различными углахги. Чтобы выбранная модель соответствовала реальному газу, общая энергия всех молекул идеального газа должна равняться фактической. Молекулы в газе движутся, но взаимодействие между ними отсутствует, поэтому энергия газа — это сумма кинетических энергий всех молекул [c.16]
Когда в гл. 3 молярная энергия Е одноатомного идеального газа определялась как сумма кинетической энергии индивидуальных молекул или как авогадрово число средних молекулярных энергий, молчаливо предполагалось, что Е является функцией состояния. Так ли это [c.37]
В молекулярно-кинетической теории газов, подробно рассматриваемой в курсах физики, под идеальным газом понимается вещество, состоящее из беспорядочно движущихся сферических упругих частиц, размеры которых пренебрежимо малы по сравнению с рас-стояниём между 1[йми. Взаимодействие этих частиц заключается только в упругом соударении друг с другом. Никакого специфического взаимодействия между молекулами идеального газа нет, поэтому внутренняя энергия определенного количества газа не зависит от расстояния между молекулами, а определяется исключительно интенсивностью теплового движения молекул, зависящей от температуры. Поэтому с термодинамической точки зрения идеальный газ можно определить как такое вещество, внутренняя энергия которого при постоянной температуре не зависит от объема, т. е. [c.43]
Никакого специфического взаимодействия между молекулами идеального газа нет, поэтому внутренняя энергия определенного количества газа не зависит от расстояния между молекулами, а определяется исключительно интенсивностью теплового движения молекул, зависящей от температуры. Поэтому с термодинамической точки зрения идеальный газ можно определить как такое вещество, внутренняя энергия которого при постоянной температуре не зависит от объема, т. е. [c.43]
Однако законы идеальных газов применимы не всегда. Они точно соблюдаются лишь тогда, когда мы имеем дело с не очень высоким давлением и температурой, достаточно удаленной от критической точки сжижения газов. При выведении уравнения Клапейрон не учитывал двух важных обстоятельств 1) объемов, занимаемых самими молекулами, допуская, что они свободно движутся во всем объеме, и 2) взаимодействия между самнлш молекул а.ми, предполагая тем самым, что давление зависит исключительно от кинетической энергии движущихся молекул. Если газы достаточно разрежены, то эти факторы практического значения не имеют и ими можно пренебречь. [c.118]
Если газы достаточно разрежены, то эти факторы практического значения не имеют и ими можно пренебречь. [c.118]
В основе кинетической теории идеальных газов лежит представление о том, что молекулы его являются твердыми, шарообразными частицами одного размера. Скорость движения молекул и величина средней кинетической энергии системы определяются внешним энергетическим воздействием — величиной температуры среды, а характер распределения — механическим взаимодействием частиц газа (столкновениехм) между собой. [c.184]
Рассмотрим далее распределение молекул по скоростям. Распределение по скоростям было впервые выведено Максвеллом (1860 г.) на основании молекулярно-кинетического подхода. Здесь мы выведем распрёделение Максвелла из формул (IV. 10), (IV. 1 5), (IV.17). Энергию молекулы идеального газа можем представить в виде суммы [c.100]
Согласно молекулярно-кинетической теории, давление представляет собой просто результат столкновений молекул со стенками сосуда, которым передается импульс движущихся молекул. Произведение давления на объем газа равно двум третям кинетической энергии движения молекул [уравнение (3-25)]. Этот факт в сочетании с экспериментально установленным объединенным законом состояния идеального газа приводит к важному выводу, что кинетическая энергия движения молекул газа прямо пропорциональна его абсолютной температуре [уравнение (3-26)], т.е. что температура представляет собой прпгто меру интенсивности молекулярного движения. [c.156]
Произведение давления на объем газа равно двум третям кинетической энергии движения молекул [уравнение (3-25)]. Этот факт в сочетании с экспериментально установленным объединенным законом состояния идеального газа приводит к важному выводу, что кинетическая энергия движения молекул газа прямо пропорциональна его абсолютной температуре [уравнение (3-26)], т.е. что температура представляет собой прпгто меру интенсивности молекулярного движения. [c.156]
Согласно кинетической теории газон ннутренняя энергия идеального газа совпадает с кинетической энергией составляющих его молекул, нри этом пренебрегают колебаниями атомов внутри молекул, а также энергией взаимодействия молекул, которая является функцией расстояния между ними. [c.155]
Реальная удельная теплоемкость одноатомных газов при температурах, существенно больших температуры насыщения, действитель]ю имеет значения, предсказываемые кинетической теорией газов. Двухатомные и многоатомные газы имеют, од]]ако, более высокие удельные теплоемкости вследствие упругих колеба] ий молекул, которыми пренебрегает эта теория. Такие колебания возбуждаются столк]]овениямн, которые передают минимальный квант энергии /ге (где к — постоян]1ая Планка, равная 6,6253 10- Дж-с, а Л) — частота колебаний молекулы как упругого вибратора, с ). С ростом температуры число столк1]овений, удовлетворяющих этому требованию, также растет, таким образом увеличивая вклад к0лебателы]0й энергии в полную энергию многоатомного (но по-прел[c.155]
Такие колебания возбуждаются столк]]овениямн, которые передают минимальный квант энергии /ге (где к — постоян]1ая Планка, равная 6,6253 10- Дж-с, а Л) — частота колебаний молекулы как упругого вибратора, с ). С ростом температуры число столк1]овений, удовлетворяющих этому требованию, также растет, таким образом увеличивая вклад к0лебателы]0й энергии в полную энергию многоатомного (но по-прел[c.155]
Использование анализа размерностей в разделе «Молекулярно-кинетическая теория. Законы идеального газа»
Библиографическое описание:Мазейкина, М. Ю. Использование анализа размерностей в разделе «Молекулярно-кинетическая теория. Законы идеального газа» / М. Ю. Мазейкина. — Текст : непосредственный // Педагогическое мастерство : материалы II Междунар. науч. конф. (г. Москва, декабрь 2012 г.). — Москва : Буки-Веди, 2012. — С. 124-126. — URL: https://moluch.ru/conf/ped/archive/65/3168/ (дата обращения: 22. 04.2021).
04.2021).
В работах [1-2] были представлены примеры использования анализа размерностей (далее АР) в геометрии и механике на уровне, доступном ученикам средней школы. Предлагаемую работу можно рассматривать как продолжение указанных работ. Здесь представлен пример использования АР в разделе «Молекулярно-кинетическая теория. Законы идеального газа».
ПОСТАНОВКА ЗАДАЧИ
Задача №МКТ1. Найти формулу давления идеального газа в сосуде (формулу основного уравнения молекулярно-кинетической теории).
Механической моделью идеального газа в рамках молекулярно-кинетической теории (далее МКТ) может служить замкнутое в сосуде ограниченное множество абсолютно упругих одинаковых точечных физических объектов (молекул).
Сосуд – это абсолютно упругая оболочка.
Сосуд может иметь
дополнительные свойства, отраженные в условиях конкретной задачи.
Исходя из этой модели, давление на стенки сосуда есть следствие абсолютно упругого взаимодействия молекул газа со стенками сосуда. Следовательно, можно попытаться составить перечень физических параметров, от которых может зависеть давление.
1. Давление газа (p) может зависеть от концентрации (n) молекул – числа молекул в единице объема.
Логично предположить, что давление газа тем больше, чем больше молекул в сосуде заданного объема.
2. Естественным было бы и предположение о зависимости давления газа от массы молекулы (m1).
Было бы логичным предположить, что чем больше масса молекул, тем больше будет давление при прочих постоянных величинах.
3. Предположим, что давление газа зависит от осредненной скорости (v) молекул газа.
Логично
предположить, что при увеличении скоростей молекул газа давление газа
будет возрастать при равных прочих величинах.
Указанные соображения (предположения) носят качественный характер. Они основаны на логике и интуиции исследователя (в данном случае ученика). Тем не менее, они позволяют поставить задачу в обобщенной форме: найти функциональную зависимость давления газа от концентрации молекул, их массы и скорости:
p = f (n, m1, v). (1)
РЕШЕНИЕ ЗАДАЧИ
Для того, чтобы выявить функциональную зависимость (1), воспользуемся известным алгоритмом анализа размерностей (далее АР), представленным в работах [2-4].
За определяемый физический параметр примем давление газа. Тогда определяющими физическими параметрами будут служить: концентрация молекул, их масса и осредненная скорость.
Искомую функциональную зависимость будем искать в виде степенного одночлена:
p = K nxm1yvz, (ИФ2)
К = Сonst,
[К] = 1. (3)
(3)
Здесь и далее ИФ – итоговая формула.
За базисную систему размерностей примем систему LTM.
L – размерность длины, T– размерность времени, M – размерность массы, К – безразмерная постоянная величина.
Формулы размерностей концентрации, массы и скорости в системе LTM имеют вид:
[p] = L-1 T-2M; [n] = L-3; [m1] = M; [v] = L T-1. (4)
Используя (2) и (3), составим уравнение размерностей:
L-1T-2M = L-3х Mу LzT–z. (5)
После упрощения уравнение размерностей (5) примет вид
L-1T-2M= L-3х+zT–zMу. (6)
Приравнивание показателей степеней при одинаковых основаниях обеих частей уравнения размерностей (6) дает систему линейных уравнений
-3х+z = -1
у = 1 (7)
-z
= -2.
Решение системы (7) есть решение уравнения размерностей (6). Решая систему (7), получим:
х = у = 1, z = 2. (8)
Подставляя (8) в (ИФ2), получим итоговую формулу
- р = K n m1 v2. (ИФ9)
Мы получили с точностью до постоянного безразмерного множителя (К) выражение (ИФ9), называемое основным уравнением МКТ.
Эксперимент и решение задачи иными методами дают для одноатомного газа следующее значение К:
- К = (ИФ10)
АНАЛИЗ РЕШЕНИЯ ЗАДАЧИ
Давление газа, используя (ИФ9), можно выразить и так:
- р = Kρv2 (ИФ11)
ρ = nm1= m / V, (12)
m = nm1V = N m1, (13)
где ρ
– плотность газа, m
– масса газа, V
– объем газа (сосуда), N
– число молекул газа.
Формулу (ИФ11) можно получить, если решать эту же задачу анализом размерностей, предполагая, что параметрами, определяющими давление, являются плотность газа (ρ) и осредненная скорость молекул (v).
Из (ИФ11) и (12) получим
p = Kmv2 / V. (14)
Эту формулу можно записать иначе
p = K1mv2 / (2V), (15)
К1 = 2K = , (16)
- p = K1Е/V= K1U/V= K1= K1 (ИФ17)
где Е – суммарная кинетическая энергия молекул газа,
– объемная плотность суммарной кинетической энергии молекул газа, – объемная плотность внутренней энергии идеального газа, К1 – безразмерная постоянная (равная для одноатомного газа).
Определение. Суммарная
кинетическая энергия молекул газа (Е) называется внутренней энергией
газа (U).
Суммарная
кинетическая энергия молекул газа (Е) называется внутренней энергией
газа (U).
Е = U. (18)
Из (ИФ17) и (18) следует
- pV = K1Е = K1U (ИФ19)
Из формулы (ИФ17) следует теорема 1, а из (ИФ19) – теорема 2.
Теорема 1. Давление идеального газа пропорционально объемной плотности суммарной кинетической энергии молекул газа (или объемной плотности внутренней энергии идеального газа).
Теорема 2. Произведение давления идеального газа на его объем пропорционально суммарной кинетической энергии молекул газа (или внутренней энергии идеального газа).
ЧАСТНЫЕ СЛУЧАИ ФОРМУЛЫ (ИФ19)
Если предположить, что суммарная кинетическая энергия (Е) молекул газа данной массы (m) величина постоянная, то формула (ИФ19) примет вид
pV
= const1.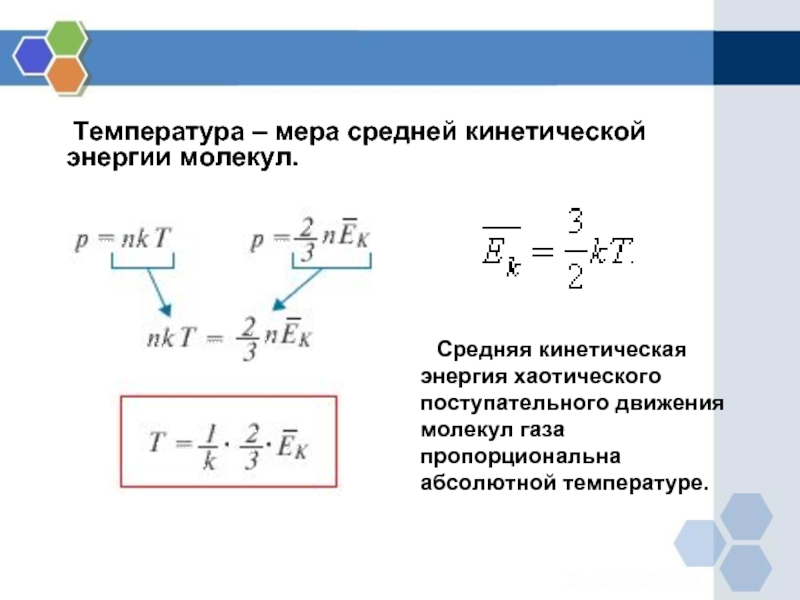 (ИФ20)
(ИФ20)
Если объем газа (V) данной массы газа (m) величина постоянная, то формула (ИФ19) примет вид
p/Е = const2. (ИФ21)
Если давление газа (р) данной массы газа (m) величина постоянная, то формула (ИФ19) примет вид
V/Е = ( )-1 = = const3. (ИФ22)
В этом случае объемная плотность () суммарной кинетической энергии всех молекул газа есть величина постоянная.
Постоянные const1 – const3 имеют размерности левых частей формул.
Из трех термодинамических макроскопических параметров газа (объем, давление и температура), измеряемых простейшими приборами, в формулах (ИФ20-ИФ22) явным образом не содержится лишь температура.
Однако
температура содержится в указанных формулах косвенно. Это можно
установить, если поставить вопрос: «А не связана ли суммарная
кинетическая энергия (Е) всех молекул газа с температурой газа?».
На постановку этого вопроса указывает качественный анализ частных
случаев формулы (ИФ19) – формул (ИФ20-22).
Это можно
установить, если поставить вопрос: «А не связана ли суммарная
кинетическая энергия (Е) всех молекул газа с температурой газа?».
На постановку этого вопроса указывает качественный анализ частных
случаев формулы (ИФ19) – формул (ИФ20-22).
При этом следующие два предположения представляются вполне логичными.
Предположение П1. Предположим, что осредненная кинетическая энергия молекул газа (Е1) есть функция абсолютной температуры (Т)
Е1 = = = f (Т). (П1)
Предположение П2. Предположим, что эта функция – степенная и простейшая.
Т. е.
Е1 = const4 Т, (П2)
где const4 – константа, имеющая размерность, удовлетворяющую требованиям АР.
Для того, чтобы формула (П2) удовлетворяла предельному случаю
Е1 = 0 → Т = 0, (23)
необходимо, чтобы
температура (Т) являлась «абсолютной температурой»,
измеряемой по шкале Кельвина.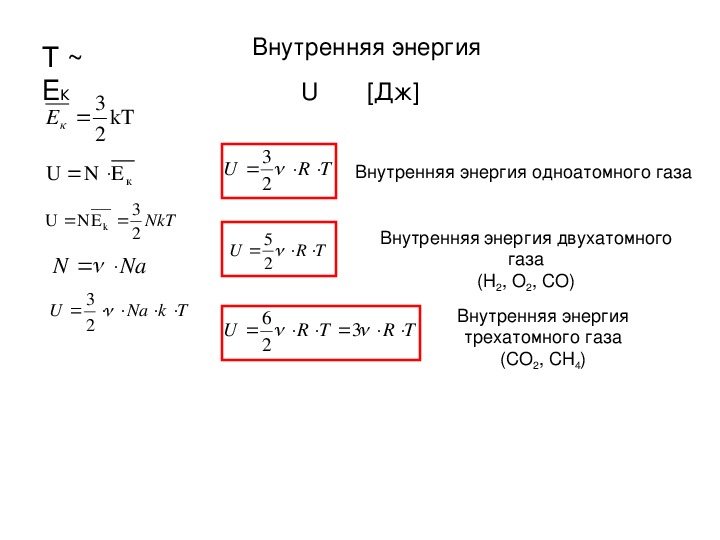
Константа (const4) определяется формулой Больцмана (для одноатомного газа):
Е1= = k ·Т, (24)
где k – постоянная Больцмана (Дж/К – в системе SI).
Формула размерности постоянной Больцмана в системе размерностей LTMT°.
[k] = L2T-2M/T°, где T°-1 – размерность температуры, измеряемой в кельвинах.
Из (24) получим выражение для константы (const4):
const4 = k. (25)
Для двухатомного газа выражение для константы (const4) таково:
const4 = k. (26)
С учетом предположений П1 и П2 понятие «осредненной скорости» молекул обретает конкретный смысл: это средняя квадратичная скорость всех молекул.
v
= (Σvi2
/N)0. 5,
(27)
5,
(27)
где i – текущий номер молекулы; суммирование производится по числу (N) всех молекул газа.
В этом случае замена скоростей молекул на среднеквадратичную скорость не приведет к изменению суммарной кинетической энергии всех молекул газа, т. е. кинетическая энергия рассматриваемой системы абсолютно упругих частиц не изменится.
Предположения П1 и П2 (и соответствующие им формулы П1 и П2) отражают физический смысл понятия «абсолютная температура»: абсолютная температура – это осредненная кинетическая энергия молекул газа.
Из формул (П1), (П2), (24), (25) следует формула внутренней энергии для одноатомного газа
Е = U = N Е1 = N k Т. (28)
Заметим, что для двухатомного газа аналогичная формула такова
Е = U
= N
Е1
=
N
k
Т. (29)
(29)
Подставляя (28) в формулы (ИФ19-ИФ22), получим
-
p V / Т
= const, (ИФ19.1)
- p V = const, (ИФ20.1)
- p / Т = const, (ИФ21.1)
- V / Т = const, (ИФ22.1)
- p V = const, (ИФ20.1)
где const – константы, имеющие размерности левых частей формул.
Формулы (ИФ19.1 – ИФ22.1) есть выражение законов идеального газа с позиций МКТ.
Полученные формулы законов идеального газа представлены в таблице.
|
№ п/п |
№ формулы |
Формула, выражающая закон |
Наименование газового процесса, выраженного формулой |
Наименование закона |
|
1 |
(ИФ19. |
p V / Т = const |
Для любого процесса |
Уравнение Клапейрона состояния идеального газа |
|
2 |
(ИФ20.1) |
p V = const |
Изотермический процесс |
Бойля-Мариотта |
|
3 |
(ИФ21.1) |
p / Т = const |
Изохорный процесс |
Шарля |
|
4 |
(ИФ22.1) |
V / Т = const |
Изобарный процесс |
Гей-Люссака |
|
5 |
(ИФ19. |
pV/Т= νR = const |
Для любого процесса |
Уравнение Клапейрона-Менделеева состояния идеального газа |
Д. И. Менделеев придал формуле (ИФ19.1) более содержательный вид, установив физический смысл константы правой части (см. формулу 19.2):
- p V / Т = ν R = const (ИФ19.2)
ν = m / M, (30)
где ν – число молей газа, m – масса газа, М – молярная масса газа,
R – универсальная газовая постоянная.
Отметим, что все формулы, представленные в таблице, справедливы для любого идеального газа: одноатомного, двухатомного, трехатомного. Специфика газа, определяемая его химическим составом, в формуле (ИФ19.2) отражена его молярной массой (М).
Заметим,
что формула (ИФ11) представляет собой частный случай уравнения
Бернулли для идеальной жидкости, если положить К=
. В этом случае буква (v) означает скорость молекул в поперечном
сечении струи. При этом предполагается, что скорости всех молекул в
поперечном сечении струи одинаковы. В этой формуле давление,
обозначенное буквой p, в аэродинамике называется динамическим
давлением.
В этом случае буква (v) означает скорость молекул в поперечном
сечении струи. При этом предполагается, что скорости всех молекул в
поперечном сечении струи одинаковы. В этой формуле давление,
обозначенное буквой p, в аэродинамике называется динамическим
давлением.
Таким образом, АР позволяет выявлять аналогии между формулами различных разделов физики. Часто эти аналогии имеют глубокий физический смысл. При этом выявляется новый уровень обобщения. В таких случаях АРП служит звеном, укрепляющим связи между разделами физики.
Литература:
Неграш А. С., Мазейкина М.Ю. Использование анализа размерностей в геометрии /А.С. Неграш, М.Ю. Мазейкина// Педагогическое мастерство: материалы междунар. заоч. науч. конф. (г. Москва, апрель 2012 г.). – М.: Буки-Веди, 2012. – С.165-169.
Неграш А. С., Мазейкина М.Ю. Использование алгоритма анализа размерностей физических величин в школе / А.
 С. Неграш, М.Ю. Мазейкина// Молодой учёный. –
2012. – №6. – С. 411 – 417
С. Неграш, М.Ю. Мазейкина// Молодой учёный. –
2012. – №6. – С. 411 – 417Дешковский А., Койфман Ю. Метод размерностей в решении задач //ФПВ. – 2002. – № 2. – С. 71–81.
Неграш, А. С. Алгоритм решения задач физики анализом размерностей с использованием линейной алгебры / Неграш, А.С., Мазейкина М.Ю. // Бюллетень лаборатории математического, естественнонаучного образования и информатизации: Реценз. сб. науч. тр.–М.: Научная книга. – 2012. Том III. – С. 232-235.
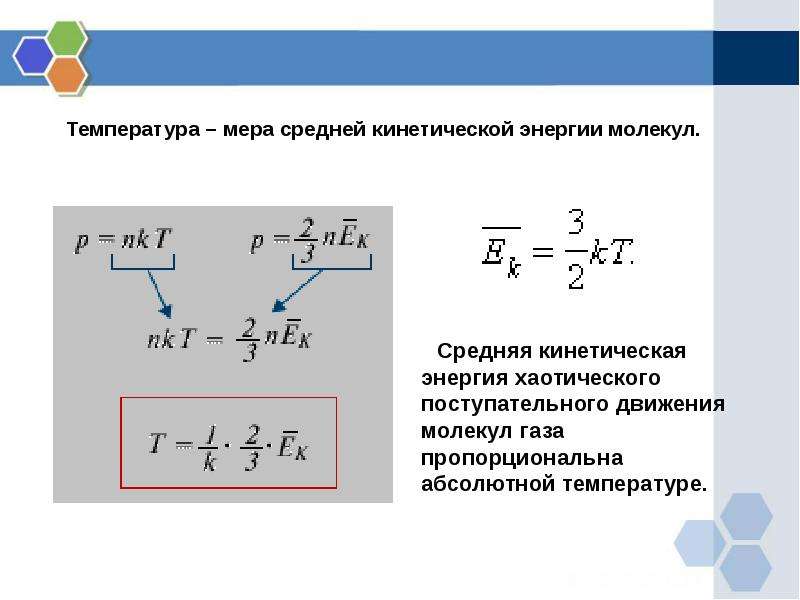
Температура как мера средней кинетической энергии молекул
Представляем формулу основного уравнения молекулярно-кинетической теории (МКТ) газов:
(где n=NV – это концентрация частиц в газе, N – это число частиц, V – это объем газа, 〈E〉 – это средняя кинетическая энергия поступательного движения молекул газа, υkv – это средняя квадратичная скорость, m0 – это масса молекулы) связывает давление – макропараметр, достаточно просто измеряющийся с такими микропараметрами, как средняя энергия движения отдельной молекулы (или в другом выражении), как масса частицы и ее скорость.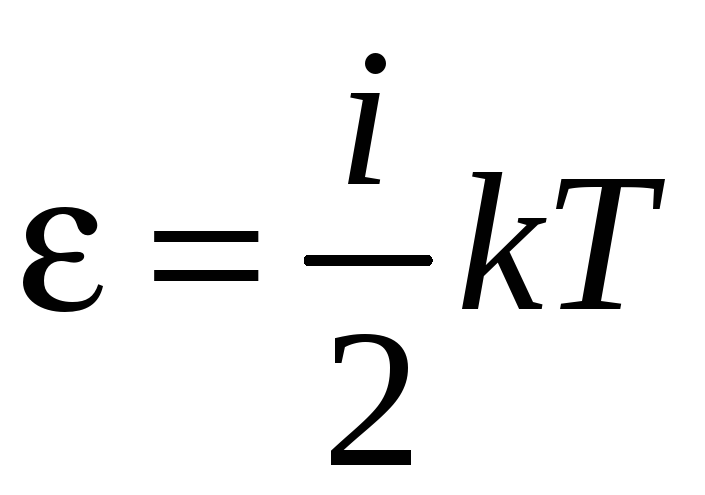 Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.
Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.
Газовая температура
Для определения газовой температуры нужно вспомнить важное свойство, которое сообщает о том, что в условиях равновесия средняя кинетическая энергия молекул в смеси газов одинаковая для различных компонентов данной смеси. Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:
С учетом вышесказанного, используем (1) и (2) и получаем:
Из уравнения (3) следует, что величина θ, которой мы обозначили температуру, вычисляется в Дж, в чем измеряется также и кинетическая энергия. В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:
В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:
θ=kT (4), где T – это термодинамическая температура в кельвинах.
Связь термодинамической температуры и средней кинетической энергией теплового движения молекул газа выражается формулой:
E=32kT (5).
Из уравнения (5) видно, что средняя кинетическая энергия теплового движения молекул прямо пропорциональна температуре газа. Температура является абсолютной величиной. Физический смысл температуры заключается в том, что она, с одной стороны, определяется средней кинетической энергией, которая приходится на 1 молекулу. А с другой стороны, температура – это характеристика системы в целом. Таким образом, уравнение (5) показывает связь параметров макромира с параметрами микромира.
Известно, что температура – это мера средней кинетической энергии молекул.
Можно установить температуру системы, а затем рассчитать энергию молекул.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеАбсолютный ноль температур
В условиях термодинамического равновесия все составляющие системы характеризуются одинаковой температурой.
Определение 3Температура, при которой средняя кинетическая энергия молекул равняется 0, давление идеального газа равняется 0, называется абсолютным нулем температур. Абсолютная температура никогда не является отрицательной.
Пример 1Необходимо найти среднюю кинетическую энергию поступательного движения молекулы кислорода, если температура T=290 K. А также найти среднюю квадратичную скорость капельки воды диаметра d=10-7 м, взвешенной в воздухе.
Решение
Найдем среднюю кинетическую энергию движения молекулы кислорода по уравнению, связывающему энергию и температуру:
E=32kT (1. 1).
1).
Поскольку все величины заданы в системе измерения, проведем вычисления:
E=32·1,38·10-23·10-7=6·10-21 Дж.
Перейдем ко второй части задания. Положим, что капелька, взвешенная в воздухе, – это шар (рисунок 1). Значит, массу капельки можно рассчитать как:
m=ρ·V=ρ·πd36.
Рисунок 1
Найдем массу капельки воды. Согласно справочных материалов, плотность воды в нормальных условиях равняется ρ=1000 кгм3, тогда:
m=1000·3,14610-73=5,2·10-19 (кг).
Масса капельки чрезмерно маленькая, поэтому, сама капелька сравнима с молекулой газа, и тогда можно использовать при расчетах формулу средней квадратичной скорости капли:
E=mυkυ22 (1.2),
где 〈E〉 мы уже установили, а из (1.1) понятно, что энергия не зависит от разновидности газа, а зависит только лишь от температуры. Значит, мы можем применить полученную величину энергии. Найдем из (1.2) скорость:
υkυ=2Em=6·2Eπρd3=32kTπρd3 (1.3).
Рассчитаем:
υkυ=2·6·10-215,2·10-19=0,15 мс
Ответ: Средняя кинетическая энергия поступательного движения молекулы кислорода при заданной температуре равняется 6·10-21 Дж. Средняя квадратичная скорость капельки воды при заданных условиях равняется 0,15 м/с.
Средняя квадратичная скорость капельки воды при заданных условиях равняется 0,15 м/с.
Средняя энергия поступательного движения молекул идеального газа равняется 〈E〉, а давление газа p. Необходимо найти концентрацию частиц газа.
Решение
В основу решения задачи положим уравнение состояния идеального газа:
p=nkT (2.1).
Прибавим к уравнению (2.1) уравнение связи средней энергии поступательного движения молекул и температуры системы:
E=32kT (2.2).
Из (2.1) выражаем необходимую концентрацию:
n=pkT 2.3.
Из (2.2) выражаем kT:
kT=23E (2.4).
Подставляем (2.4) в (2.3) и получаем:
n=3p2E
Ответ: Концентрацию частиц можно найти по формуле n=3p2E.
Формула внутренней энергии в физике
Содержание:
Определение и формула внутренней энергии
Определение
Внутренней энергией тела (системы) называют энергию, которая связана со всеми видами движения и взаимодействия частиц,
составляющих тело (систему), включая энергию взаимодействия и движения сложных частиц.
Из выше сказанного следует, что к внутренней энергии не относят кинетическую энергию движения центра масс системы и потенциальную энергию системы, вызванную действием внешних сил. Это энергия, которая зависит только от термодинамического состояния системы.
Внутреннюю энергию чаще всего обозначают буквой U. При этом бесконечно малое ее изменение станет обозначаться dU. Считается, что dU является положительной величиной, если внутренняя энергия системы растет, соответственно, внутренняя энергия отрицательна, если внутренняя энергия уменьшается.
Внутренняя энергия системы тел равна сумме внутренних энергий каждого отдельного тела плюс энергия взаимодействия между телами внутри системы.
Внутренняя энергия – функция состояния системы. Это означает, что изменение внутренней энергии системы при переходе системы из одного состояния в другое не зависит от способа перехода (вида термодинамического процесса при переходе) системы и равно разности внутренних энергий конечного и начального состояний:
$$\Delta U=U_{2}-U_{1}(1)$$Для кругового процесса полное изменение внутренней энергии системы равно нулю:
$$\oint d U=0(2)$$Для системы, на которую не действуют внешние силы и находящуюся в состоянии макроскопического покоя, внутренняя энергия – полная энергия системы.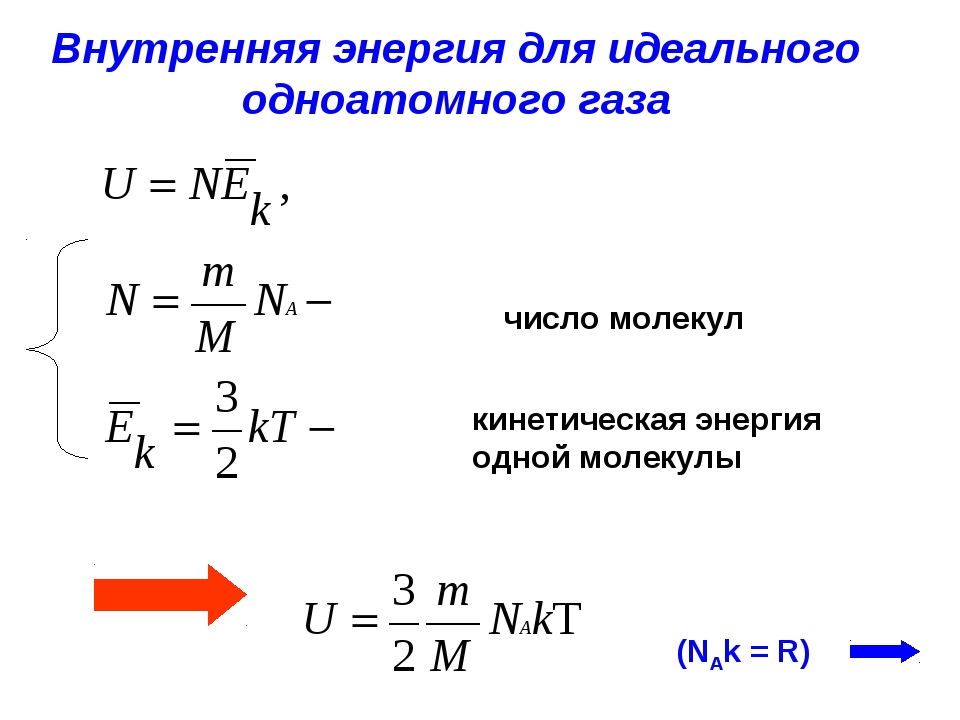 {T} c_{V} d T+u_{0}\right)$$
{T} c_{V} d T+u_{0}\right)$$
где CV – теплоемкость газа в изохорном процессе; cV – удельная теплоемкость газа в изохорном процессе; $u_{0}=\frac{U_{0}}{m}$ – внутренняя энергия, приходящаяся на единицу массы газа при абсолютном нуле температур. Или:
$$d U=\frac{i}{2} \nu R d T(4)$$i – число степеней свободы молекулы идеального газа, v – число молей газа, R=8,31 Дж/(моль•К) – универсальная газовая постоянная.
Первое начало термодинамики
Как известно первое начало термодинамики имеет несколько формулировок. Одна из формулировок, которую предложил К.
Каратеодори говорит о существовании внутренней энергии как составляющей полной энергии системы.Она является функцией состояния,
в простых системах зависящей от объема (V), давления (p), масс веществ (mi), которые составляют данную систему:
$U=U\left(p, V, \sum m_{i}\right)$ . В формулировке, которую дал Каратеодори внутренняя
энергия не является характеристической функцией своих независимых переменных.
В более привычных формулировках первого начала термодинамики, например, формулировке Гельмгольца внутренняя энергия системы вводится как физическая характеристика системы. При этом поведение системы определено законом сохранения энергии. Гельмгольц не определяет внутреннюю энергию как функцию конкретных параметров состояния системы:
$$\Delta U=Q-A(5)$$$\Delta U$ – изменение внутренней энергии в равновесном процессе, Q – количество теплоты, которое получила система в рассматриваемом процессе, A – работа, которую система совершила.
Единицы измерения внутренней энергии
Основной единицей измерения внутренней энергии в системе СИ является: [U]=Дж
Примеры решения задач
Пример
Задание. Вычислите, на какую величину изменится внутренняя энергия гелия имеющего массу 0,1 кг, если его температура увеличилась на 20С.
Решение. При решении задачи считаем гелий одноатомным идеальным газом, тогда для расчетов можно применить формулу:
$$d U=\frac{i}{2} \nu R d T(1. {3}$ (Дж)
{3}$ (Дж)Слишком сложно?
Формула внутренней энергии не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Идеальный газ расширили в соответствии с законом, который изображен графиком на рис.1. от начального объема V0. При расширении объем сал равен $V=\tau V_{0}$ . Каково приращение внутренней энергии газа в заданном процессе? Коэффициент адиабаты равен $\gamma$.
Решение. Исходя из рисунка, уравнение процесса можно представить аналитически как:
$$p=\alpha V(2.1)$$Показатель адиабаты связан с числом степеней свободы газа выражением:
$$\gamma=\frac{i+2}{i}(2.2)$$Выразим число степеней свободы из (2.2):
$$i=\frac{2}{\gamma-1}$$Приращение внутренней энергии для постоянной массы газа (см. Пример 1) найдем в соответствии с формулой:
$$\Delta U=\frac{i}{2} \nu R \Delta T(2.4)$$Запишем уравнения состояний идеального газа для точек (1) и (2) рис. {2}-1\right)$
{2}-1\right)$
Читать дальше: Формула времени.
Формулы МКТ / Блог / Справочник :: Бингоскул
Молекулярная физика: основные формулы для решения задач
| НАЗВАНИЕ | ФОРМУЛА |
| Основы молекулярно-кинетической теории |
|
| Основное уравнение МКТ | |
| Основное уравнение МКТ идеального газа |
|
| Уравнение Клайперона-Менделеева (уравнение состояния идеального газа) |
|
| Уравнение состояния идеального газа: |
|
| Изотермический закон (закон Бойля-Мариотта) |
|
| Изохорный закон (закон Шарля) |
|
| Изобарный закон (закон Гей-Люссака) |
|
| Закон Дальтона |
|
| Средняя квадратичная скорость движения молекул газа |
|
| Средняя кинетическая энергия поступательного движения молекул |
|
| Средняя кинетическая энергия молекул газа |
|
| Давление идеального газа на стенки сосуда |
|
| Абсолютная температура | |
| Плотность |
Смотри так же:
Идеальный газ, параметры состояния, давление, температура, средняя квадратичная скорость. Основное уравнение молекулярно-кинетической теории
Тестирование онлайн
Идеальный газ
Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.
Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.
Параметры состояния газа
Давление, температура и объем – параметры состояния газа. Или их называют макропараметрами. Температура – внешняя характеристика скоростей частиц газа. Давление – внешняя характеристика соударений со стенками, например, сосуда. Объем – место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.
Микропараметры (маленькие, внутренние характеристики) газа – это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.
Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.
Основное уравнение молекулярно-кинетической теории
Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.
Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.
Основное уравнение мкт имеет вид
Средний квадрат скорости молекул
Средняя квадратичная скорость vкв молекул это квадратный корень из среднего квадрата скорости
Средняя кинетическая энергия молекул
Можно вывести формулы
Температура
Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.
Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.
Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.
Связь между температурами по шкале Цельсия и по шкале Кельвина
Физика в школе 867
Модель идеального газа
Идеальный газ – это теоретическая модель газа, для которой верны следующие три тезиса:
- Размеры молекул газа пренебрежимо малы по сравнению с расстоянием между ними
- Потенциальная энергия взаимодействия между собой молекул пренебрежимо мала
- Столкновения молекул газа абсолютно упругие
Основное уравнение МКТ
Основное уравнение молекулярно-кинетической теории является первым полученным количественным соотношением в МКТ.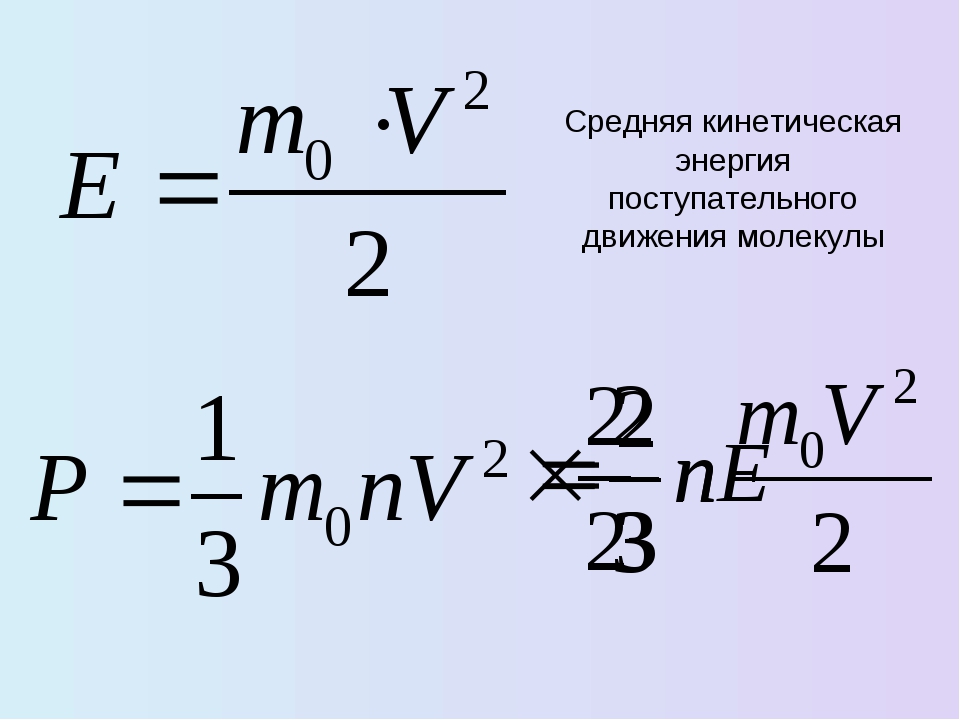
Давление газа равно:
Здесь p – давление газа, m0 – масса одной молекулы газа, n – концентрация и v2 с палочкой наверху означает средний квадрат скорости молекул (то есть среднее арифметическое квадратов скоростей всех молекул газа).
Если воспользоваться формулой кинетической энергии, мы получим иную запись основного уравнения МКТ:
Как видим, давление газа прямо пропорционально кинетической энергии его молекул. Важно заметить, что Eкин в данной формуле является кинетической энергией не всего газа, а лишь одной молекулы.
Также давление прямо пропорционально температуре по формуле:
Температура
Так как в молекулярной физике величины связаны математическими формулами и не отрицательны (давление, объем, концентрация и т.д.), а температура может принимать отрицательные значения, например, – 100 °C, физики решили использовать иную шкалу температур, где выполняется T > 0, и ввели шкалу Кельвина.
Связь шкалы Цельсия и шкалы Кельвина:
Абсолютный нуль есть значение T = 0 K = – 273,15 °C. При таком значении температуры движение молекул прекращается (это следует из формулы связи кинетической энергии молекулы и температуры, см. ниже). Это теоретическое значение, так как на практике быть полученным не может, но возможна температура, сколь угодно близкая к абсолютному нулю.
Средняя кинетическая энергия одной молекулы прямо пропорциональна абсолютной температуре:
Среднюю квадратичную скорость молекул можно рассчитать по формуле:
Уравнение Менделеева-Клапейрона
Уравнение Клапейрона
В 1834 г. французский ученый Бенуа Поль Эмиль Клапейрон вывел формулу:
Здесь p – давление, V – объем, T – абсолютная температура и значение A – некая переменная, которая зависит от массы газа m и молекулярной массы газа M.
Уравнение Менделеева
В 1874 г. русский ученый Дмитрий Иванович Менделеев вывел формулу для одного моля идеального газа:
Здесь p – давление, V – объем, T – абсолютная температура и значение R = kNA = 8,31 есть газовая постоянная.
Уравнение Менделеева-Клапейрона
Объединив вышенаписанные уравнения, физики получили уравнение Менделеева-Клапейрона, которое характеризует состояние идеального газа произвольного количества молей:
Воспользовавшись тождеством , мы получим более компактную запись:
Если рассмотреть один и тот же газ (ν = const), то заметим, что произведение νR = const. Таким образом, если выразить это произведение, поделив на T, мы получим уравнение, полезное в случае изменения определенных параметров одного и того же газа:
Кинетическая теория идеальных газов
Кинетическая теория идеальных газовКинетическая теория идеальных газов
ТЕОРИЯ
Идеальный газ – это газ, в котором атомы не действуют друг на друга, но сталкиваются со стенками контейнера (в упругих столкновениях). Основываясь на здравом смысле и эксперименте, закон идеального газа связывает давление, температуру, объем и количество молей идеального газа:
PV = nRT,
где R – постоянная, известная как универсальная газовая постоянная.
Комментарии:
- Будьте осторожны, все величины выражены в одной системе единиц!
- Температура T, должна быть выражена как абсолютная температура, Кельвин.
- n – количество молей газа, определяемое как
n º м образец / М
м º N A м атом
, где m sample – масса всей пробы газа, N A – число Авогадроса, а m atom – масса одного атома газа.M называется молекулярной массой газа (массой одного моля газа). Если под N мы подразумеваем общее количество атомов газа, то мы также можем написать
n = нет данных A
Это означает, что 1 моль состоит из N A атомов газа.
В классе I докажу на основе второго закона Ньютона и закона идеального газа
E int = 3/2 n R T (для одноатомного идеального газа = «m.i.g.»)
Следовательно,
- внутренняя энергия идеального газа зависит только от его абсолютной температуры, а
- температура – это мера случайной кинетической энергии атомов.
- Это уравнение – замечательное уравнение, поскольку оно обеспечивает связь между макроскопическим миром (n, T) и микроскопическим миром (E int газа атомов)
Поскольку внутренняя энергия m.i.g. полностью кинетический у нас также есть
E int = m образец
, что дает среднеквадратичную скорость атома газа
против RMS = [3RT / M] 1/2 .
Внимание: держитесь прямо n, N, N A , m atom , m sample и M. Это шесть различных величин.
ПРИМЕРЫ
[в классе]
Кинетическая теория | Безграничная физика
Источник давления
Согласно кинетической теории, давление возникает из-за силы, оказываемой молекулами или атомами на стенки контейнера.
Цели обучения
Выразите связь между давлением и средней кинетической энергией молекул газа в виде уравнения
Основные выводы
Ключевые моменты
- Мы можем лучше понять давление (а также температуру) из кинетической теории газов, которая предполагает, что атомы и молекулы находятся в непрерывном беспорядочном движении. 2}} {3} [/ латекс].2} / 3 [/ латекс].
Ключевые термины
- кинетическая теория газов : Кинетическая теория газов описывает газ как большое количество мелких частиц (атомов или молекул), все из которых находятся в постоянном случайном движении.
- Ньютоновская механика : Ранняя классическая механика, предложенная Исааком Ньютоном, особенно основанная на его законах движения и теории гравитации.
В механике Ньютона, если давление – это сила, деленная на площадь, на которую действует сила, то каково происхождение давления в газе? Какие силы создают давление? Мы можем лучше понять давление (а также температуру) из кинетической теории газов, которая предполагает, что атомы и молекулы находятся в непрерывном беспорядочном движении.
Микроскопическое происхождение давления
Согласно кинетической теории давление возникает из-за силы, действующей со стороны молекул или атомов на стенки контейнера, как показано на рисунке ниже. Рассмотрим газ из N молекул, каждая массой m, заключенный в кубический контейнер объемом V = L 3 . Когда молекула газа сталкивается со стенкой контейнера, перпендикулярной оси координат x, и отскакивает в противоположном направлении с той же скоростью (упругое столкновение), то импульс, потерянный частицей и приобретенный стенкой ([латекс] \ Delta \ text {p} [/ latex]):
Поступательное движение гелия : Реальные газы не всегда ведут себя в соответствии с идеальной моделью при определенных условиях, таких как высокое давление.Здесь размер атомов гелия относительно их расстояния показан в масштабе при давлении 1950 атмосфер.
[латекс] \ begin {align} \ Delta \ text {p} & = \ text {p} _ {\ text {i}, \ text {x}} – \ text {p} _ {\ text {f} , \ text {x}} = \ text {p} _ {\ text {i}, \ text {x}} – (- \ text {p} _ {\ text {i}, \ text {x}}) \\ & = 2 \ text {p} _ {\ text {i}, \ text {x}} = 2 \ text {mv} _ \ text {x} \ end {align} [/ latex]
, где v x – x-компонента начальной скорости частицы.
Частица ударяется об одну конкретную боковую стену один раз каждые [латекс] \ Delta \ text {t} = \ frac {2 \ text {L}} {\ text {v} _ \ text {x}} [/ latex],
(где L – расстояние между противоположными стенами).2}} {\ text {L}} [/ latex],
, где полоса обозначает среднее значение по N частицам. Поскольку предполагается, что частицы движутся в случайных направлениях, если мы разделим векторы скорости всех частиц в трех взаимно перпендикулярных направлениях, среднее значение квадрата скорости вдоль каждого направления должно быть одинаковым. (Это не означает, что каждая частица всегда движется под углом 45 градусов к осям координат.)
Давление : Давление возникает из-за силы, оказываемой молекулами или атомами на стенки контейнера.2}} {3} [/ latex],
где V = L 3 – объем ящика. Доля n = N / V – это плотность газа. Это первый нетривиальный результат кинетической теории, поскольку он связывает давление (макроскопическое свойство) со средней (поступательной) кинетической энергией на молекулу, которая является микроскопическим свойством. 2)} {2 \ text {kT}} \ right] [/ latex].2} {2 \ text {kT}} \ right) [/ latex]. Это просто называется распределением Максвелла.
Ключевые термины
- среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
Движение молекул в газе является случайным по величине и направлению для отдельных молекул, но газ, состоящий из многих молекул, имеет предсказуемое распределение молекулярных скоростей, известное как распределение Максвелла-Больцмана (показано на рисунке). Распределение имеет длинный хвост, потому что скорость некоторых молекул может в несколько раз превышать среднеквадратичную скорость.Наиболее вероятная скорость v p (на пике кривой) меньше действующей скорости v rms . Как показано на, кривая смещается в сторону более высоких скоростей при более высоких температурах с более широким диапазоном скоростей.
Распределение Максвелла-Больцмана при более высоких температурах : Распределение Максвелла-Больцмана смещается в сторону более высоких скоростей и расширяется при более высоких температурах. 2)} {2 \ text {kT}} \ right] [/ latex],
где fv – функция плотности вероятности скорости.(Вывод формулы выходит за рамки вводной физики.) Формула вычисляет вероятность нахождения частицы со скоростью в бесконечно малом элементе [ dv x , dv y , dv z ] о скорости v = [ v x , v y , v z ]:
[латекс] \ text {f} _ \ mathbf {\ text {v}} \ left (\ text {v} _ \ text {x}, \ text {v} _ \ text {y}, \ text {v } _ \ text {z} \ right) \, \ text {dv} _ \ text {x} \, \ text {dv} _ \ text {y} \, \ text {dv} _ \ text {z} [ /латекс].
Также можно показать, что распределение скорости Максвелла – Больцмана для векторной скорости [ v x , v y , v z ] является продуктом распределений для каждого из трех направления:
[латекс] \ text {f} _ \ text {v} \ left (\ text {v} _ \ text {x}, \ text {v} _ \ text {y}, \ text {v} _ \ text {z} \ right) = \ text {f} _ \ text {v} (\ text {v} _ \ text {x}) \ text {f} _ \ text {v} (\ text {v} _ \ текст {y}) \ text {f} _ \ text {v} (\ text {v} _ \ text {z}) [/ latex],
, где распределение для одного направления равно,
[латекс] \ text {f} _ \ text {v} (\ text {v} _ \ text {i}) = \ sqrt {\ frac {\ text {m}} {2 \ pi \ text {kT} }} \ exp \ left [\ frac {- \ text {mv} _ \ text {i} ^ 2} {2 \ text {kT}} \ right] [/ latex]. 2} {2 \ text {kT}} \ right) [/ latex] для скорости v.
Температура
Температура прямо пропорциональна средней поступательной кинетической энергии молекул в идеальном газе.
Цели обучения
Описать взаимосвязь между температурой и энергией молекул в идеальном газе
Основные выводы
Ключевые моменты
- Средняя поступательная кинетическая энергия молекулы эквивалентна [латексу] \ frac {3} {2} \ text {kT} [/ latex] и называется тепловой энергией.
- В кинематической теории газов макроскопические величины (такие как давление и температура) объясняются путем рассмотрения микроскопического (случайного) движения молекул.
- Среднеквадратичная скорость молекул в газе задается как [латекс] \ sqrt {\ frac {3 \ text {kT}} {\ text {m}}} [/ latex].
Ключевые термины
- кинетическая теория газов : Кинетическая теория газов описывает газ как большое количество мелких частиц (атомов или молекул), все из которых находятся в постоянном случайном движении.
- идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
Интуитивно более горячий воздух предполагает более быстрое движение молекул воздуха. В этом атоме мы выведем уравнение, связывающее температуру газа (макроскопическая величина) со средней кинетической энергией отдельных молекул (микроскопическая величина). Это основное и чрезвычайно важное соотношение в кинетической теории газов.
Вид под микроскопом
Мы предполагаем, что молекула мала по сравнению с разделением молекул в газе (заключенным в трехмерный контейнер), и что ее взаимодействием с другими молекулами можно пренебречь.Кроме того, мы предполагаем упругие столкновения, когда молекулы ударяются о стенку контейнера, как показано на.
Упругие столкновения, когда молекулы ударяются о стенку контейнера : Газ в контейнере оказывает внешнее давление на его стенки. Молекула, сталкивающаяся с жесткой стенкой, меняет направление своей скорости и импульса в x-направлении. Это направление перпендикулярно стене. Компоненты его скорости движения в направлениях y и z не изменяются, что означает отсутствие силы, параллельной стенке.2} [/ латекс] (уравнение 1).
Что мы можем узнать из этой атомно-молекулярной версии закона идеального газа? Мы можем вывести связь между температурой и средней поступательной кинетической энергией молекул в газе. Напомним макроскопическое выражение закона идеального газа:
[латекс] \ text {PV} = \ text {NkT} [/ latex] (уравнение 2),
где N – количество молекул, T – температура газа, а k – постоянная Больцмана.
Приравнивая правые части макроскопической и микроскопической версий закона идеального газа (ур.2} = \ frac {3} {2} \ text {kT} [/ latex], (уравнение 3).
Средняя поступательная кинетическая энергия молекулы называется тепловой энергией.
RMS Скорость
Ур. 2}} = \ text {v} _ {\ text {rms}} = \ sqrt {\ frac {3 \ text {kT}} {\ text {m}}} [/ latex],
, где v rms обозначает среднеквадратичную (среднеквадратичную) скорость.
Внутренняя энергия идеального газа
Внутренняя энергия – это полная энергия, содержащаяся в термодинамической системе, и состоит из двух основных компонентов: кинетической энергии и потенциальной энергии.
Цели обучения
Определите количество степеней свободы и вычислите внутреннюю энергию для молекулы идеального газа
Основные выводы
Ключевые моменты
- В идеальных газах нет межчастичного взаимодействия. Следовательно, только кинетическая энергия дает вклад во внутреннюю энергию.
- Каждая степень свободы вносит [латекс] \ frac {1} {2} \ text {kT} [/ latex] на атом во внутреннюю энергию.
- Для одноатомного идеального газа с N атомами его полная внутренняя энергия U задается как [latex] \ text {U} = \ frac {3} {2} \ text {NkT} [/ latex]. Для двухатомных газов U = [латекс] \ frac {5} {2} \ text {NkT} [/ latex].
Ключевые термины
- Постоянная Больцмана : Физическая постоянная, связывающая энергию на уровне частиц с температурой, наблюдаемой на объемном уровне.Это газовая постоянная R, деленная на число Авогадро, NA.
- момент инерции : Мера сопротивления тела изменению его угловой скорости вращения
- благородный газ : Любой из элементов 18 группы Периодической таблицы, одноатомный и (за очень ограниченными исключениями) инертный.
В термодинамике внутренняя энергия – это полная энергия, содержащаяся в термодинамической системе. Внутренняя энергия состоит из двух основных компонентов: кинетической энергии и потенциальной энергии.Кинетическая энергия обусловлена движением частиц системы (например, перемещениями, вращениями, колебаниями). В идеальных газах нет межчастичного взаимодействия. Поэтому мы не будем принимать во внимание потенциальную энергию и сосредоточимся только на вкладе кинетической энергии во внутреннюю энергию.
Одноатомные газы
Одноатомный газ – это газ, в котором атомы не связаны друг с другом. Благородные газы (He, Ne и др.) Являются типичными примерами. Гелиевый шар показан на следующем рисунке. В этом случае кинетическая энергия состоит только из поступательной энергии отдельных атомов.Одноатомные частицы не колеблются, и их вращательной энергией можно пренебречь, потому что атомный момент инерции очень мал. Кроме того, они не возбуждаются электронным способом до более высоких энергий, за исключением очень высоких температур. Следовательно, практические изменения внутренней энергии в идеальном газе можно описать исключительно изменениями его поступательной кинетической энергии.
Helium Blimp : Гелий, как и другие благородные газы, является одноатомным газом, который часто можно описать с помощью закона идеального газа.2} = \ frac {3} {2} \ text {kT} [/ latex],
где k – постоянная Больцмана. (См. Атом в разделе «Температура» в кинетической теории.) С атомами N в газе его полная внутренняя энергия U определяется как:
[латекс] \ text {U} = \ frac {3} {2} \ text {NkT} [/ latex],
где N – количество атомов в газе. Обратите внимание, что в одноатомных газах есть три степени свободы: перемещение в направлениях x, y и z.
Поскольку движение атомов является случайным (и, следовательно, изотропным), каждая степень свободы вносит вклад [латекс] \ frac {1} {2} \ text {kT} [/ latex] на атом во внутреннюю энергию.
Двухатомные газы
Двухатомная молекула (H 2 , O 2 , N 2 и т. Д.) Имеет 5 степеней свободы (3 для перемещения в направлениях x, y и z и 2 для вращения). Следовательно, внутренняя энергия для двухатомных газов равна U = 52NkTU = \ frac {5} {2} NkT.
9.14: Кинетическая теория газов – полная молекулярная кинетическая энергия
Уравнение (1) из постулатов кинетической теории, однако, может сказать нам гораздо больше, чем это, о газах.{\ text {2}}) _ {\ text {ave}} \]
Подставляя из уравнения.
\ [E_ {k} = \ tfrac {\ text {3}} {\ text {2}} PV \]
или
\ [PV = \ tfrac {\ text {2}} {\ text {3}} E_ {k} \]
Произведение давления на объем газа составляет две трети общей кинетической энергии молекул газа . Теперь мы можем понять, почему PV выражается в джоулях – это действительно энергия. Согласно постулату 4 кинетической теории, молекулы газа имеют постоянную полную кинетическую энергию.На макроскопическом уровне это отражается постоянством PV , или, другими словами, законом Бойля. Кинетическая теория также дает важное понимание того, что означает температура газа на микроскопическом уровне. Из закона идеального газа мы знаем, что PV = nRT . Подставляя это в уравнение. \ (\ ref {6} \),
\ [nRT = \ tfrac {2} {3} E_ {k} \ label {6} \]
Если мы разделим обе части уравнения. \ (\ ref {7} \) на n и умножить на \ (\ tfrac {3} {2} \),
\ [\ frac {E_ {k}} {n} = \ tfrac {\ text {3}} {2} RT \ label {7} \]
Член E k / n – это полная кинетическая энергия, деленная на количество вещества, то есть молярная кинетическая энергия .Представляя молярную кинетическую энергию E m , мы имеем
\ [E _ {\ text {m}} = \ tfrac {\ text {3}} {2} RT \]
Молярная кинетическая энергия газа пропорциональна его температуре, а константа пропорциональности в \ (\ tfrac {3} {2} \) умножена на газовую постоянную R .
Видео ниже демонстрирует взаимосвязь между молярной кинетической энергией и температурой. Демонстрация подчеркивает тот факт, что более высокая температура означает более высокую молярную кинетическую энергию.
Когда пищевой краситель помещается в воду с разной температурой, он ведет себя по-разному. Пищевой краситель в горячей воде быстро диспергируется из-за его высокой молярной кинетической энергии / температуры. С другой стороны, холодная вода имеет низкую молярную кинетическую энергию, поэтому пищевой краситель медленно распространяется по ней.
Кинетическая температура, тепловая энергия
Статистические методы становятся более точным способом изучения природы при большом количестве частиц.Таким образом, мы ожидаем, что описание скоростей молекул в газе на самом деле будет наиболее вероятным распределением, поскольку мы имеем дело с числами частиц в диапазоне числа Авогадро. Но это наиболее вероятное распределение (распределение Максвелла-Больцмана) подчиняется ограничениям, а именно, что количество частиц постоянно и что полная энергия постоянна (закон сохранения энергии). Максимизация вероятностного распределения с учетом этих ограничений в целом является сложной математической задачей (см. Richtmyer, et al., Например). Один из способов подойти к решению более интуитивно – это рассмотреть известный нам физический пример, а именно физику атмосферы под действием силы тяжести, отраженную в барометрической формуле. Следующее лечение следует за разработкой Rohlf.
В этом подходе мы используем тот факт, что средняя кинетическая энергия молекул может быть выражена через кинетическую температуру. Кроме того, мы знаем, что сохранение энергии в этом случае включает просто баланс кинетической энергии и гравитационной потенциальной энергии, если мы рассматриваем атмосферу как идеальный газ.
Из выражения для кинетической температуры
у нас есть экспериментально проверенное выражение для молекулярной кинетической энергии. В барометрической формуле:
у нас есть описание идеальной газовой системы, которое можно использовать, чтобы помочь разработать аргумент правдоподобия для распределения Максвелла по скоростям. Шаги в этом процессе следующие:
Для одного направления в пространстве этот процесс дает выражение:
, а когда включены все направления скорости, получается соотношение распределения скоростей Максвелла:
Следует отметить, что хотя мы использовали физическую ситуацию, зависящую от гравитации, для получения распределения скоростей, гравитация не появляется в конечном результате.То есть полученный результат является общим, не содержащим g. Барометрическая формула использовалась просто как конструкция, чтобы связать распределение скоростей с ограничениями по энергии и количеству частиц.
Кинетическая теория газов
18.1. Константа Авогадро
законы классической термодинамики не показывают прямой зависимости наблюдаемые макроскопические переменные на микроскопических аспектах движения атомы и молекулы.Однако ясно, что давление оказывало газом связана с импульсом атомов и молекул, и что температура газа связана с кинетической энергией атомы и молекулы. В связи с последствиями движения атомы и молекулы до макроскопических наблюдаемых, таких как давление и температура, мы должны определить количество молекул в газе. моль – это мера количества молекул в образец, и он определяется как
” количество любого вещества, которое содержит столько атомов / молекул, сколько существует атомы в
а 12-граммовый образец 12С “
Лаборатория Эксперименты показывают, что количество атомов в образце 12С массой 12 г равно 6.02 х 1023 моль-1. Этот номер называется постоянной Авогадро , NA. Количество родинок в образец n определяется легко:
18.2. Идеальный газ
Авогадро сделал предположение, что все газы – при одинаковых температурных условиях и давление – содержат одинаковое количество молекул. Наоборот, если отбираем пробы различных газов объемом 1 моль, помещаем их в коробки одинаковых объема и удерживая их при той же температуре, мы обнаруживаем, что их измеренные давления почти одинаковы.Эксперименты показали, что газы подчиняются следующему соотношению (закон идеального газа ):
где n – количество молей газа, а R – газовая постоянная . R имеет одинаковое значение для всех газов:
Температура газа всегда должна выражаться в абсолютных единицах (Кельвинах).
Использование По закону идеального газа мы можем рассчитать работу, совершаемую идеальным газом.Предполагать образец n молей идеального газа заключен в начальный объем Vi. Газ расширяется перемещая поршень. Его окончательный объем – Vf. Во время расширения температура T газ поддерживается постоянным (этот процесс называется изотермическое расширение ). Дается работа, выполняемая расширяющимся газом. по
Закон идеального газа дает нам связь между давлением и том
С T остается постоянным, проделанная работа может быть легко рассчитана
Примечание:
Образец Задача 18-1
А баллон содержит кислород при температуре 20С и давлении 15 атм.при объеме 12 л. В температура повышается до 35С, а объем уменьшен до 8,5 л. Какое конечное давление газа ?
Закон идеального газа гласит, что
начальное состояние газа определяется Vi, pi и Ti; конечное состояние газа определяется Vf, pf и Tf. Делаем вывод, что
Таким образом,
температура T в этой формуле должна быть выражена в Кельвинах:
Ti = 293 К
Tf = 308 К
единицы объема и давления можно оставить в л и атм.так как только их соотношение входит в уравнение. Делаем вывод, что pf = 22 атм.
18,3. Давление и температура: взгляд на молекулы
Пусть n моль идеального газа заключено в кубический ящик объемом V. молекулы в ящике движутся во всех направлениях с разной скоростью, сталкиваясь друг с другом и со стенками ящика. На рисунке 18.1 показано молекула движется в коробке. Молекула столкнется с правая стена.Результатом столкновения является изменение направления движения на противоположное. x-компоненты импульса молекулы:
Рисунок 18.1. Молекула движется в коробке. |
y- и z-компоненты импульса молекулы не изменяются. В изменение импульса частицы, следовательно,
После молекула разлетелась по правой стенке, она столкнется с левой стена и, наконец, вернитесь к правой стене.Время, необходимое для завершить этот путь дается
Каждый когда молекула сталкивается с правой стенкой, она изменяет импульс стены по п. Сила, действующая на стену со стороны этой молекулы легко вычисляется
Для n моль газа, соответствующая сила равна
давление, оказываемое газом, равно силе на единицу площади, и, следовательно,
член в скобках можно переписать в терминах средней квадратичной скорости:
Таким образом, заключаем, что
где M – молекулярный вес газа.Для каждой молекулы общее скорость вычисляется легко
С есть много молекул, и поскольку нет предпочтительного направления, средний квадрат скоростей в направлениях x, y и z равен
и таким образом
Использование Из этого соотношения выражение для давления p можно переписать как
где vrms называется среднеквадратичной скоростью молекулы.Закон идеального газа говорит нам, что
Объединение последние два уравнения заключаем, что
и
Для H при 300 K vrms = 1920 м / с; для 14N vrms = 517 м / с. Скорость звука в этих двух газах составляет 1350 м / с и 350 м / с соответственно. Скорость звука в газе всегда будет меньше v среднеквадратичного значения , поскольку звук распространяется через газ, вызывая возмущение. движение молекул .В возмущение передается от молекулы к молекуле посредством столкновений; а поэтому звуковая волна никогда не может двигаться быстрее, чем средняя скорость молекулы .
18,4. Поступательная кинетическая энергия
средняя поступательная кинетическая энергия молекулы, обсуждаемая в предыдущем разделе дается
Использование полученное ранее выражение для vrms, получаем
постоянная k называется постоянной Больцмана и равна отношению газовой постоянной R и постоянная Авогадро NA
Расчет показывает, что для данной температуры все молекулы газа – независимо от их массы – имеют одинаковую среднюю кинетическую поступательную энергия , а именно (3/2) кТ .Когда мы измеряем температуру газа, мы измеряем средняя поступательная кинетическая энергия его молекул.
18,5. Средняя длина свободного пробега
движение молекулы в газе затруднено. Помимо столкновения с в стенках удерживающего сосуда молекулы сталкиваются друг с другом. А Полезным параметром для описания этого движения является длина свободного пробега л. В длина свободного пробега l – средняя расстояние, которое проходит молекула между столкновениями.Средне бесплатно путь молекулы связан с ее размером; чем больше размер тем короче его длина свободного пробега.
Предположим молекулы газа имеют сферическую форму и диаметр d. Две молекулы газа столкнутся, если их центры разделены менее чем на 2d. Предполагать среднее время между столкновениями t. За это время молекула путешествует на расстояние v. т, и подметает объем равный
Если в среднем он испытывает одно столкновение, количество молекул в объем V должен быть 1.Если N – количество молекул в единице объема, это означает, что
или
интервал времени t, определенный таким образом, является средним временем между столкновениями, а длина свободного пробега l равна
Здесь мы предположили, что движется только одна молекула, а все остальные неподвижны. Если проводим расчет правильно (все молекулы движутся), следующее для длины свободного пробега получено соотношение:
связь, полученная между макроскопическим давлением и микроскопическими аспектами движения молекул зависят только от средней среднеквадратичной скорости молекул в газе.Часто уходите, нам нужна дополнительная информация чем просто средняя среднеквадратичная скорость. Например, вопросы например, какая часть молекул имеет скорость больше v0, может иметь значение (ядерная реакция сечения резко увеличиваются с увеличением скорости). Это можно показать, что распределение скоростей молекул в газе описывается так называемым распределением скоростей Максвелла
product P (v) dv – доля молекул, скорость которых лежит в диапазоне от v до v + дв.Распределение нормализовано, а это значит, что
наиболее вероятная скорость , вп. пики распределения скорости. Наиболее вероятная скорость получается требуя, чтобы dP / dv = 0
ср заключаем, что dP / dv = 0, когда
и таким образом
Среднее значение скорость молекул газа можно рассчитать следующим образом:
Среднее значение квадратная скорость молекул может быть получена аналогичным манера.
Среднеквадратичное значение скорость , vrms, теперь можно получить
ср
обратите внимание, что vp внутренняя энергия газа связана с кинетической энергией
его молекулы. Предположим пока, что мы имеем дело с одноатомным
газ. В этом случае средняя поступательная кинетическая энергия каждого
молекула газа просто равна 3kT / 2.Если образец содержит n молей
такого газа он содержит молекулы нНК. В
полная внутренняя энергия газа равна ср
заметьте, что полная внутренняя энергия газа является функцией только
температура газа и не зависит от других переменных, таких как давление
и плотность. Для более сложных молекул (двухатомный N 2 и т. Д.) Ситуация осложняется тем, что
что кинетическая энергия молекул будет состоять не только из поступательного
движение, но и вне вращательного движения . Предположим
мы нагреваем n молей газа, сохраняя его объем постоянным. В
результатом добавления тепла в систему является повышение ее температуры Здесь,
CV – молярная теплоемкость при постоянном объеме , Q – добавленное тепло, а T – результирующее увеличение.
в температуре системы. Первый закон термодинамики
показывает, что С
объем остается постоянным (V = 0), мы заключаем, что и Использование
ранее полученное уравнение для U через T, мы можем показать, что и
таким образом Предположим
что при добавлении тепла в систему объем изменяется таким образом, что
давление газа не меняется. Опять же, изменение внутреннего
энергия системы дается где
Cp – молярная теплоемкость при постоянном давлении . Это выражение можно переписать как Для
идеальный газ (pV = nRT) мы можем связать V с T, если мы примем постоянную
давление Использование
это соотношение, первый закон термодинамики можно переписать как или Однако
внутренняя энергия U зависит только от температуры, а не от того, как
объем и / или давление меняется.Таким образом, U / T = 3/2 n R = n CV. Таким образом, предыдущее уравнение может
переписать как или ср
увидеть, что Cp CV. Во время адиабатическое расширение идеального газа без добавления или отвода тепла
из системы. Этого можно добиться, расширив газ.
очень быстро (так, что не успевает течь тепло) или очень быстро
хорошо изолирующая система.Первый закон термодинамики говорит
нам, что Закон идеального газа можно использовать, чтобы переписать p V: или удельная теплоемкость CV относится к U Использование
первый закон термодинамики мы можем написать или Объединение
два выражения, полученные для n. T получаем или Это
выражение можно переписать как Для
небольшие изменения это можно переписать как где
мы определили g как (Cp / CV).После интеграции этого
выражение получаем или Использование
закон идеального газа, чтобы исключить p из выражения, получаем Таким образом, Пытаясь понять, что мы видим на макроскопическом уровне с точки зрения микроскопических свойств системы, состоящей из атомов и молекул, мы начнем с рассмотрения закона идеального газа.Мы выбираем идеальные газы, потому что они сравнительно просты. Поскольку молекулы расположены относительно далеко друг от друга, вам действительно не нужно слишком беспокоиться о взаимодействиях между молекулами – за исключением того, что нужно понимать, что они позволяют молекулам делиться энергией посредством столкновений. В основном это движение свободных частиц (гравитация играет очень небольшую роль, поскольку молекулы движутся очень быстро). И вы уже знакомы с макроскопической формой закона идеального газа, pV = nRT , из химии. Что такое газ? Согласно идее, разработанной Джеймсом Клерком Максвеллом в середине 19 века, это множество отдельных молекул, которые свободно перемещаются и отскакивают от стенок контейнера (или комнаты и т. Д.). Каждая отдельная молекула в основном подчиняется законам Ньютона. Так что, если бы мы захотели, мы могли бы смоделировать поведение газа, рассматривая каждую молекулу отдельно, и выяснить положение и скорость каждой из них. Но есть одна проблема: мы говорим о партии молекул.Один моль газа (или чего-либо еще) содержит 6×10 23 молекул. Чтобы упростить задачу, полезно подумать об объемных величинах, таких как температура и давление, которые представляют собой средние значения для всей совокупности молекул. Чтобы установить связь между микро- и макроизображениями, мы можем посмотреть на одну репрезентативную частицу и рассматривать ее так, как если бы она двигалась в случайном направлении. Движение этой частицы на самом деле не является случайным: оно очень определенно и находится под влиянием сил, действующих на эту одну частицу.Но поскольку мы случайным образом выбираем его из большего набора частиц (движущихся во всех возможных направлениях), его движение выглядит случайным. Эти идеи случайности и вероятности станут очень важными в ближайшие недели. Откуда давление? В нашей модели, когда многие молекулы движутся очень быстро, это происходит из-за ударов молекул газа о стену. Представьте себе одиночную молекулу газа, сталкивающуюся со стеной. Он отскакивает и меняет направление, что означает, что стенка оказывает на молекулу силу, изменяющую ее скорость.Согласно 3-му закону Ньютона мы знаем, что молекула должна оказывать на стену равную и противоположную силу. Сумма всех сил, действующих на стену, со стороны всех молекул (на единицу площади) и есть давление газа. Все, что нам нужно сделать, это вычислить: Для этого все, что нам нужно, это наше основное уравнение скорости, второй и третий законы Ньютона, а также модель случайности движения многих молекул.Вот единственные уравнения, которые нам нужны. (Кроме того, нам нужно знать закон идеального газа, pV = nRT .) $$ F_ {стена \ правая стрелка молекула} = m {{\ Delta v_x} \ over {\ Delta t}} = -F_ {молекула \ rightarrow wall} $$ $$ \ langle v_x \ rangle = {\ Delta x \ over \ Delta t} $$ А теперь воспользуемся ими. Представьте себе стену с газом слева. Теперь представьте, что одна молекула отскакивает от стены.На рисунке справа путь молекулы выделен красным. Мы выбрали наши координаты так, чтобы положительное направление x было в направлении нормали к стене, направленной наружу от области, где находится газ. Когда молекула ударяется о стенку, компонент x ее скорости меняет местами, но компоненты y и z остаются прежними. Поскольку столкновение считается упругим, молекула сохраняет то же количество кинетической энергии, поэтому величина скорости остается неизменной; меняется только направление. Теперь давайте найдем величину силы, которую молекула оказывает на стену. Оно равно массе молекулы, умноженной на ее ускорение во время столкновения, а ускорение – это изменение ее скорости, деленное на время одного столкновения $$ F_ {стена \ правая стрелка молекула} = m {{\ Delta v_x} \ over {\ Delta t}} = -F_ {молекула \ rightarrow wall} $$ Насколько велик $ \ Delta v_ {x} $? Если перед столкновением оно имело какое-то значение $ v_ {x} $, то оно было $ -v_ {x} $ после столкновения (такая же величина, противоположное направление), поэтому величина изменения равна $ -v_ {x} – (v_ {x}) = -2v_ {x} долларов. Таким образом, величина силы, действующей на стену от каждого столкновения, составляет $ {2mv_ {x} \ over \ Delta t} $. Наш результат выше получен только для одной молекулы. Как мы можем определить, сколько молекул ударяется о стену? Результат зависит от плотности молекул. Пусть n – количество молекул в единице объема, $ A $ – площадь рассматриваемой стенки, и рассмотрим небольшой интервал времени $ Δt $ . Это время должно быть достаточно длинным, чтобы многие молекулы столкнулись с стенкой, но достаточно коротким, чтобы не сильно измениться в макроскопическом смысле за это время. Чтобы выяснить, сколько молекул ударится в нашу область за время Δ t, посмотрите на молекулы, движущиеся у стены. Только те, кто движется к стене, могут попасть в нее. И попадут только те, кто находится достаточно близко. Чтобы увидеть, как это работает, давайте сделаем еще более простую модель. Вместо того чтобы молекулы беспорядочно перемещались во всех направлениях, давайте возьмем, что все молекулы движутся случайным образом влево или вправо. Далее мы придадим всем молекулам одинаковую скорость.Хотя это кажется слишком упрощенным, движения вверх и вниз (направление y) не влияют на силу, поэтому мы можем их игнорировать. Позже мы справимся со случайностью скорости, заменив предполагаемую постоянную скорость средней скоростью. Итак, наша модель следующая: множество молекул, рассредоточенных в направлении y, но движущихся только влево или вправо с постоянной скоростью $ v_x $ и с плотностью $ n $ молекул на единицу объема. В этой упрощенной модели наши молекулы у стены выглядят как на рисунке справа. В этой упрощенной модели только молекулы в цилиндре с площадью $ A $ и высотой $ v_xΔt $ смогут попасть в область $ A $ за время $ Δt $ . Поскольку объем цилиндра равен $ Av_xΔt $, количество молекул в цилиндре составляет $ nAv_xΔt $ , , а количество, которое попадет за время $ Δt $, равно $ ½nAv_xΔt $ . (Это тот же самый $ Δt $, который мы использовали раньше? Да, если это средняя сила , усредненная за все время, понимая «время одного столкновения», чтобы также включить время между столкновениями.2_x A $$ Не все молекулы в газе движутся с одинаковой скоростью и не все движутся в направлении x. Как мы с этим справимся? Что ж, направления y (и z) не имеют значения. Некоторые из наших молекул будут иметь скорости $ v_y $. Так что некоторые выйдут из нашей коробки за время $ Δt $. Но въезжает столько же, сколько уезжает, поэтому мы можем это игнорировать. Но как насчет того факта, что все наши молекулы не движутся с одинаковой скоростью? Что ж, поскольку некоторые будут двигаться быстрее, а некоторые – медленнее, мы можем попробовать работать со средней скоростью молекулы $ \ langle v \ rangle $.2 \ вправо) $$ Что у нас здесь? $ pV $ = количество молекул, умноженное на что-то пропорциональное средней кинетической энергии каждой молекулы! Где мы раньше видели что-нибудь подобное? Да ладно, каждый, кто когда-либо занимался химией, знает Закон идеального газа в том, что мы называем химической формой : $$ pV = n_ {моль} RT, $$ , где $ R $ – константа, не зависящая от типа газа, а $ T $ – температура. Это соотношение было установлено экспериментально из макроскопических экспериментов.Возможно, вы проделали этот эксперимент (с воздушными шарами или чем-то в этом роде) в химической лаборатории. Поскольку это представление закона идеального газа включает количество молей, нам нужно преобразовать его в количество молекул , если мы хотим сопоставить его с тем, что мы имеем в нашем уравнении. Вы можете вспомнить, что моль газа (или моль чего-либо) содержит 6,02×10 23 молекул (число Авогадро, $ N_A $), поэтому количество молей равно $ N $ (количество молекул), разделенное на $ N_A $.Итак, закон идеального газа теперь выглядит как $$ pV = \ left ({{N} \ over {N_ {A}}} \ right) RT. Чтобы упростить это, мы объединим две константы и запишем их в том, что мы называем формулой для физиков закона идеального газа: $$ pV = N k_B T, $$ где $ k_B $ (известная как постоянная Больцмана) – газовая постоянная $ R $, деленная на число Авогадро. 2 $ каждой молекулы равна $ {3 \ over2} k_B T $, а полная кинетическая энергия всех $ N $ молекул равна $ { 3 \ over2} N k_B T $.Не теряйте сон из-за фактора 3/2; это просто артефакт жизни в трехмерном мире. Дело в том, что мы можем построить мост между температурой (макроскопическое свойство) и кинетической энергией (свойство отдельных молекул). Постоянная Больцмана (которую мы увидим в нескольких других местах) функционирует как этот мост. Чтобы найти его значение, просто разделите $ R $ на $ N_A $. Возможно, вы видели это в других единицах, но в единицах СИ, $ R $ = 8,31 Дж / моль-К. (Да, объем давления-времени имеет единицы энергии! Поработайте над этим сами, если хотите больше попрактиковаться в анализе измерений.{-23} \ mathrm {J / K} $. Он измеряется в джоулях на кельвин, так что это как коэффициент преобразования энергии в температуру. Это похоже на очень маленькое число, но не забывайте, что это энергия отдельной молекулы! Эта кинетическая энергия всех молекул вместе и есть то, что мы называем «тепловой энергией». На самом деле это не другой тип энергии – в глубине души это просто кинетическая энергия (точно так же, как «химическая энергия» – это просто потенциальная энергия), но мы даем ей другое название, потому что если вы просто посмотрите на объект с тепловой энергией , не похоже, что он движется! Помните, что энергия – это скаляр, а не вектор (энергия не имеет направления), поэтому, когда вы складываете энергии всех молекул, даже если они движутся во всех разных направлениях, они не в сумме дают ноль, величины просто складываются. Этот подробный анализ был специально для газов, но это та же общая идея для жидкостей и твердых тел. Математика более сложная, поскольку молекулы расположены близко друг к другу и взаимодействуют – «Закона идеальной жидкости» не существует. Но и в этих случаях температура по-прежнему пропорциональна средней кинетической энергии молекул. Таким образом, общая тепловая энергия пропорциональна температуре, умноженной на количество молекул. В твердых телах молекулы не могут свободно перемещаться, поэтому кинетическая энергия, о которой мы говорим, связана с вибрацией. Бен Дрейфус и Джо Редиш 26.11.11 По мере увеличения температуры и средней кинетической энергии увеличивается и средняя скорость молекул воздуха. Однако не все молекулы движутся с одинаковой скоростью. Один из способов приблизиться к средней скорости молекул в газе – это вычислить нечто, называемое среднеквадратичным значением или среднеквадратичной скоростью.Среднеквадратичная скорость молекул – это квадратный корень из среднего значения каждой отдельной скорости в квадрате. Например, если три объекта имеют скорости 10 м / с, 5 м / с и 7 м / с соответственно, то среднеквадратичная скорость группы будет 7,6 м / с. Конечно, в гостиной Эми гораздо больше, чем трех частиц газа! Поскольку движущиеся частицы обладают кинетической энергией, а кинетическая энергия увеличивается с увеличением скорости, существует связь между среднеквадратичной скоростью молекул газа и средней кинетической энергией в газе.Это означает, что существует взаимосвязь между среднеквадратичной скоростью и температурой. Средняя кинетическая энергия ( K ) равна половине массы ( м ) каждой молекулы газа, умноженной на среднеквадратичную скорость ( vrms) в квадрате. Итак, какова среднеквадратичная скорость молекул газа в гостиной Эми? Помните, что средняя кинетическая энергия составляла 6,15х10-21 Дж / атом. Хотя воздух в атмосфере Земли содержит много разных газов, почти 78% атмосферы – это азот.Поэтому воспользуемся массой молекулы азота N2. Поскольку молекула газообразного азота содержит два атома азота, мы можем найти массу молекулы, сначала умножив атомную массу одного атома азота (0,014 г / моль) на два, чтобы получить молекулярную массу 0,028 г / моль. Затем разделите на число Авоградро, чтобы определить, что масса одной молекулы газообразного азота составляет 4,65х10-26 кг. Получив массу молекулы азота и среднюю кинетическую энергию, мы можем найти среднеквадратичную скорость молекул в комнате. Таким образом, мы можем вычислить, что среднеквадратичная скорость молекул в гостиной Эми составляет около 514 м / с. Довольно быстро, правда ?! Если вы не знаете индивидуальные скорости каждой молекулы газа, есть другой способ определить среднеквадратичную скорость. Один из способов сделать это – посмотреть на график, показывающий распределение скоростей в газе. Большинство молекул газа будут иметь скорости, близкие к среднеквадратичной скорости, с пропорционально меньшим количеством молекул, движущихся как с более высокими, так и с более низкими скоростями.Это придает распределению всех скоростей молекул газа форму колоколообразной кривой. Пик колоколообразной кривой покажет нам скорость, с которой движется большинство молекул, что соответствует среднеквадратичной скорости. Диффузия – это перемещение молекул из областей с высокой концентрацией в области с низкой концентрацией. Скорость диффузии газов зависит от температуры газа.С повышением температуры скорость диффузии увеличивается. Почему это происходит? Давайте подумаем о том, что мы знаем о взаимосвязи между температурой и среднеквадратичной скоростью молекул. Температура газа увеличивается, когда увеличивается среднеквадратичная скорость молекул. Когда молекулы движутся быстрее, они могут распространяться быстрее, чем при более низкой температуре. Согласно кинетической теории газов , все газы состоят из микроскопических молекул, которые движутся по прямым линиям, пока не сталкиваются с другой молекулой газа или объектом. Температура – это мера средней кинетической энергии всех молекул в газе. По мере изменения температуры и, следовательно, кинетической энергии газа, среднеквадратичная скорость молекул газа также изменяется. Среднеквадратичная скорость молекул – это квадратный корень из среднего значения каждой отдельной скорости в квадрате. 18,6. Теплоемкость идеального газа
18.6.1. Молярная теплоемкость при постоянном объеме
18.6.2. Молярная теплоемкость при постоянном давлении
18,7. Адиабатическое расширение идеального газа
Кинетическая теория: Закон идеального газа
Простая модель газа
Сколько силы одиночная молекула оказывает на стену, когда отскакивает от нее?
Сколько молекул ударяется о стену в секунду?
Обработка случайности
Средняя кинетическая энергия и температура системы – класс AP [видео 2021 года]
Кинетическая энергия и средняя скорость
Распределение скоростей
Диффузия газов
Краткое содержание урока

 1)
1) 2)
2)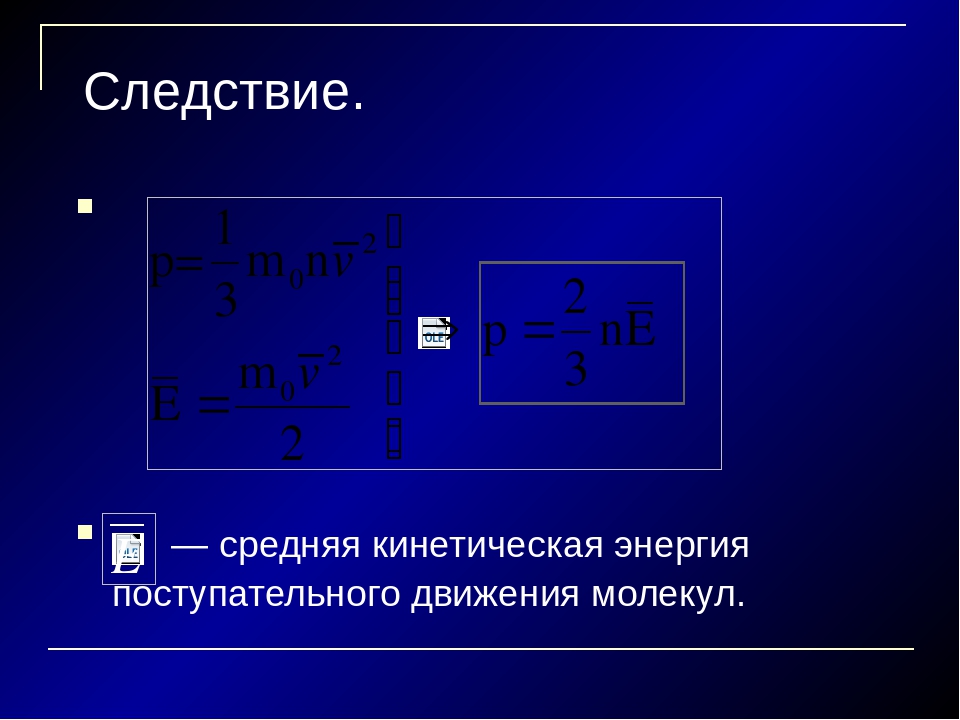 С. Неграш, М.Ю. Мазейкина// Молодой учёный. –
2012. – №6. – С. 411 – 417
С. Неграш, М.Ю. Мазейкина// Молодой учёный. –
2012. – №6. – С. 411 – 417