Формула лопиталя: Правило Лопиталя: формула, примеры решения - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Электронный учебник по математическому анализу

4.3 Свойства дифференцируемых функций

Рассмотрим отношение двух функций $f(x)/g(x)$. Иногда возникает ситуация, когда $f(x)\rightarrow 0$, $g(x)\rightarrow 0$ при $x \rightarrow c$, где $c$ – конечное число. В этом случае говорят о неопределенности типа $0/0$ при $x \rightarrow c$. Вычисление значения $\lim _{x \to c}f(x)/g(x)$ называется раскрытием неопределенности. Такого типа задачи можно решать с помощью следующей теоремы.

Теорема (Правило Лопиталя). Пусть $f(x), g(x)$ дифференцируемы на интервале $(a,b)$, и в некоторой точке $c\in (a,b)$ выполняются равенства: $f(c)=g(c)=0$. Предположим, что существует предел $\lim _{ x \to c} \left (f'(x)/g'(x)\right )$. Тогда существует и предел $\lim _{ x \to c}\left ( f(x)/g(x)\right )$, причем \[ \lim _{ x \to c} \frac{f(x)}{g(x)}=\lim _{ x \to c} \frac{f'(x)}{g'(x)}. \]

Доказательство.

Возьмем какую-нибудь точку $x \in (a,b)$, $x >c$, и применим к интервалу $(c,x)$ теорему Коши (все условия ее выполняются).

Согласно этой теореме существует точка $\xi \in (c,x)$ такая, что

\[ \frac{f(x)-f(c)}{g(x)-g(c)}=\frac{f'(\xi)}{g'(\xi)}. \]

Так как $f(c)=g(c)=0$, имеем:

\[ \frac{f(x)}{g(x)}=\frac{f'(\xi)}{g'(\xi)}. \]

При $x \to c$ имеем: $\xi \to c$. Устремим в последнем равенстве значение $x$ к $c$. Согласно условию теоремы, выражение в правой части имеет предел, так что и выражение в левой части имеет тот же предел.

Пример.

Рассмотрим неопределенность $\sin(2x)/\sin(5x)$ при $x \to 0$. Применим правило Лопиталя. Вычисляем производные от числителя и знаменателя: $(\sin (2x))’=2\cos (2x)$, $(\sin (5x))’=5\cos (5x)$. При этом отношение производных имеет при $x \to 0$ конечный предел,

\[ \lim _{x \to 0} \frac{\sin (2x)’}{\sin (5x)’}=\lim _{x \to 0} \frac{2\cos (2x)}{5\cos (5x)}=\frac{2}{5}. \] \[ В соответствии с правилом Лопиталя имеем: \] \[ \lim _{x \to 0} \frac{\sin (2x)}{\sin (5x)}=\lim _{x \to 0} \frac{\sin (2x)’}{\sin (5x)’}=\frac{2}{5}. 2x\right ). \]

4.3 Свойства дифференцируемых функций

Правило Лопиталя

Производные позволяют не только исследовать функции на возрастание, убывание или выпуклость. Ещё с их помощью можно находить пределы, раскрывая неопределенности.

20.1Раскрытие неопределенности 0/0

Правило Лопиталя позволяет раскрывать неопределенности с помощью дифференцирования. Существует много разных версий этого правила — для начала, я сформулирую ту, которую проще доказывать.

Теорема 1. (Правило Лопиталя для неопределенности 0/0 в конечной точке). Пусть функции f и g определены на интервале (a,b),

limx→a+f(x)=0,limx→a+g(x)=0,

существуют производные f′(x) и g′(x) для всех x∈(a,b), g′(x) не обращается в ноль на (a,b), и существует предел

limx→a+f′(x)g′(x)=:L.

Тогда существует предел

limx→a+f(x)g(x),

и он равен L.

Иными словами, теорема 1 позволяет раскрывать неопределенность 0/0 путём дифференцирования числителя и знаменателя дроби. Неформально можно думать об этой теореме так: она показывает, что если две величины стремятся к нулю, то предел их отношения совпадает с пределом их скоростей. Что звучит довольно логично.

20.1.1Теорема Коши

Для доказательства теоремы 1 нам понадобится вспомогательное утверждение, известное как теоремы Коши.

Теорема 2. (Коши). Пусть функции f и g непрерывны на отрезке [a,b] и дифференцируемы на интервале (a,b). Пусть g′(x)≠0 при всех x∈(a,b). Тогда существует такая точка c∈(a,b), что

f(a)−f(b)g(a)−g(b)=f′(c)g′(c)

Доказательство. Рассмотрим функцию

H(x)=f(x)−f(a)−f(b)g(a)−g(b)(g(x)−g(b)).

Это похоже на то, как мы доказывали теорему Лагранжа, только вместо линейной функции вычитаем функцию g(x) с подходящим коэффициентом.

Заметим, что

H(a)=f(b)=H(b).

Применим к H теорему Ролля. Существует такая точка c∈(a,b), что H′(c)=0. Запишем производную H:

H′(x)=f′(x)=f(a)−f(b)g(a)−g(b)g′(x).

Следовательно

0=H′(c)=f′(c)−f(a)−f(b)g(a)−g(b)g′(c).

Поскольку g′(c)≠0 (т.к. g′(x)=0 для всех x∈(a,b)), можно на него поделить и получить искомое равенство.∎

Вопрос 1. А почему при определении функции H можно делить на (g(a)−g(b)), почему эта штука не обращается в ноль?

Узнать ответ

Верный ответ. Если бы она обращалась в ноль, то g(a) было бы равно g(b) и функция g удовлетворяла бы условиям теоремы Ролля, а значит нашлась бы точка на интервале (a,b), в которой производная g обнуляется. А это ей запрещено условием нашей теоремы.

20.1.2Доказательство правила Лопиталя

Доказательство теоремы 1. До- или переопределяя функции f и g в точке a, можно считать, что f(a)=g(a)=0. На пределы и производные это никак не повлияет, поскольку они не зависят от того, чему равны функции в точке a. Тогда

limx→a+f(x)g(x)=limx→a+f(x)−f(a)g(x)−g(a)=…

Применим теорему Коши к отрезку [a,x]. Существует такая точка c(x)∈(a,x), что дробь под знаком предела равна f′(c(x))/g′(c(x)). (Теорема Коши для фиксированного отрезка даёт фиксированную точку c, а в нашем случае для каждого x свой отрезок, поэтому точка c зависит от x.)

Можно продолжить равенство:

…=limx→a+f′(c(x))g′(c(x))=…

Заметим, что c(x)→a+ при x→a+ и c(x)≠a, поскольку c(x)∈(a,x) (по теореме о двух милиционерах). Значит, можно использовать теорему о пределе сложной функции (см. упражнение 2 в лекции 13). Имеем:

…=limc→a+f′(c)g′(c)=L.

∎

20.2Другие версии и примеры

Конечно, можно доказать утверждение, аналогичное теореме 1 с пределом слева, а также с двусторонним пределом (в этом случае требуется, что f и g были дифференцируемы в проколотой окрестности точки a).

Доказательства полностью аналогичны.

20.2.1Предел в бесконечности

Случай x→+∞ или x→−∞ легко сводится к теореме 1.

Теорема 3. Пусть функции f и g определены на луче (a,+∞),

limx→+∞f(x)=0,limx→+∞g(x)=0,

существуют производные f′(x) и g′(x) для всех x∈(a,+∞), g′(x) не обращается в ноль на (a,+∞) и существует предел

limx→+∞f′(x)g′(x)=:L.

Тогда существует предел

limx→+∞f(x)g(x).

и он равен L.

Доказательство. Пусть t=1/x. Тогда при x→+∞, t→0+. По теореме о пределе сложной функции (похожая была в домашнем задании),

limx→+∞f(x)g(x)=limt→0+f(1/t)g(1/t)=…(20.1)

Рассмотрим функции

~f(t):=f(1/t),~g(t):=g(1/t).

Равенство (20.1) можно продолжить:

limt→0+~f(t)~g(t)=…

Применим теорему 1 к получившемуся пределу и интервалу (0,1/a) (можно считать, что a>0).

Для вычисления производных f(1/t) и g(1/t) применим теорему о производной сложной функции.

…=limt→0+~f′(t)~g′(t)=limt→0+f′(1/t)⋅(−1t2)g′(1/t)⋅(−1t2)=limt→0+f′(1/t)g′(1/t=…

…=limt→0+~f′(t)~g′(t)==limt→0+f′(1/t)⋅(−1t2)g′(1/t)⋅(−1t2)==limt→0+f′(1/t)g′(1/t=…

Теперь можно снова применить теорему о пределе сложной функции, делая обратную замену x=1/t, и получить:

…=limx→+∞f′(x)g′(x).

∎

Аналогично можно разобрать случай x→−∞ и x→∞.

20.2.2Примеры раскрытия неопределенности 0/0

Пример 1. Найдём предел

limx→0sinxx+x2.

Перед нами неопределенность 0/0, производная знаменателя не обнуляется вблизи нуля, продифференцируем числитель и знаменатель. Имеем:

limx→0cosx1+2x.

Теперь неопределенности нет, этот предел существует и равен 1 (в силу непрерывности косинуса и теоремы о пределе частного). Значит, исходный предел также существует и равен 1.

Пример 2. Найдём предел

limx→01−cosxsin(x2).(20.2)

Снова неопределенность 0/0. Производная знаменателя не обнуляется вблизи нуля. Продифференцируем числитель и знаменатель.

limx→0sinx2xcosx2.(20.3)

Снова получили неопределенность 0/0. Можно попробовать к новому пределу также применить правило Лопиталя.

limx→0cosx2cosx2+4x2sinx2.

Теперь неопределенности нет, и в силу непрерывности косинуса и синуса и арифметики пределов, предел равен 1/2. Значит, правило Лопиталя применимо для вычисления предела (20.3), он существует и равен 1/2. Значмт, правило Лопиталя применимо для вычисления предела (20.2), он существует и равен 1/2.

Пример 3. Найдём предел

limx→0sinxx.

В принципе, можно было бы формально применить правило Лопиталя и получить верный ответ, но тут возникает логическая ошибка. Дело в том, что это первый замечательный предел. При доказательстве дифференцируемости синуса и вычислении его производной мы воспользовались тем, что этот предел существует и равен 1. (Это мы доказывали на семинарах из геометрических соображений.) Чтобы воспользоваться правилом Лопиталя сейчас, нам нужно продифференцировать синус, но сделать мы это можем только если уже как-то доказали, что данный предел равен 1.

20.2.3Раскрытие неопределенности ∞/∞

Вместо условия, что f и g одновременно стремятся к нулю, можно использовать условие, что они одновременно стремятся к бесконечности. Доказательство этого утверждения довольно громоздкое, и мы его приводить не будем, а вот пример разберём.

Пример 4. Найдём предел

limx→+∞lnx√x.

Это неопределенность вида ∞/∞, производная знаменателя не обращается в ноль. Попробуем продифференцировать числитель и знаменатель. Имеем:

limx→+∞1/x1/(2√x)=limx→+∞2√x=0.

Предел существует и равен нулю, значит, правило Лопиталя применимо, исходный предел также существует и равен нулю.

20.3Заключение

Правило Лопиталя часто (хотя и не всегда) позволяет раскрывать неопределенности вида 0/0 или ∞/∞ без особых раздумий — если после первого дифференцирования снова получили неопределенность, не беда — можно продифференцировать ещё раз, и так пока не получим какой-нибудь конкретный предел. (Главное не забывать проверить, что условия соответствующих теорем применимы.) Студенты его очень любят. А я нет. Потому что на практике вместо правило Лопиталя быстрее использовать другую штуку — разложение функций в ряд Тейлора. Об этом мы поговорим в следующий раз.

← Предыдущая глава Следующая глава →

Доказательство правила Лопиталя | Правило Лопиталя

Математические сомнения
Ограничения
Методы

Правило Лопиталя — это метод оценки предела рационального выражения, когда предел рационального выражения неопределим, когда вход функции приближается к некоторому значению.

$\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f'(x)}{g'(x)}}$

В исчислении формула Лопиталя может быть получена математически в три шага.

Предел рациональной функции

Пусть $f(x)$ и $g(x)$ — две функции из $x$. Предположим, что $c$ — константа. Две функции образовали функцию в рациональной форме. Предел отношения $f(x)$ к $g(x)$ при приближении $x$ к $c$ записывается в следующей математической форме.

$\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$

Условие доказательства правила

Если $f(x)$ и $g(x)$ непрерывно дифференцируемы в вещественном числе $c$ и $f(c) \,=\, g(c) \,=\, 0$, тогда $f(x) \,=\, f(x)-f(c)$ и $g(x) \,=\, g(x)-g(c)$

$\implies$ $\ displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\,c}{\normalsize \dfrac{f(x)-f(c)}{g(x)-g(c)}}$

Предел рационального выражения равен неопределенности при $ x$ приближается к $c$.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \dfrac{f(c)-f(c)}{g(c)-g(c)}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \dfrac{0}{0}$

Понятно, что условие, которое мы приняли выше, делает предел рационального выражения математически неопределенным, когда вход функции приближается к значению.

Предел функции в форме дифференцирования

Теперь вернемся к следующему математическому уравнению, чтобы доказать правило Лопиталя.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)-f(c)}{g(x)-g(c)}}$

Каждое выражение в рациональной функции должно иметь выражение $x-c$ в качестве знаменателя для выражения каждого выражения в рациональной функции, и оно будет нам полезно для получения его в форме дифференцирования. Итак, давайте сделаем это математически приемлемым способом.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \displaystyle \large \lim_{x\,\to\,c}{\normalsize \Bigg(\dfrac{f(x)-f(c)}{g(x)-g(c)} \times 1\ Bigg)}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,= \, $ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \Bigg(\dfrac{f(x)-f(c)}{g(x)-g(c)} \times \dfrac{x-c}{x-c}\Bigg)}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \ displaystyle \ large \ lim_ {x \, \ to \, c} {\ normalsize \ dfrac {\ Big (f (x) -f (c) \ Big) (xc)} {\ Big (g (x) – g(c)\Big)(x-c)}}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g( х)}}$ $\,=\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{\Big(f(x)-f(c)\Big) (xc)}{\Big(g(x)-g(c)\Big)(xc)}}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{ \normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f( х)-f(c)}{\dfrac{\Big(g(x)-g(c)\Big)(xc)}{xc}}}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \ displaystyle \ large \ lim_ {x \, \ to \, c} {\ normalsize \ dfrac {f (x) -f (c)} {(xc) \ times \ dfrac {\ Big (g (x) -g) (c)\Big)}{x-c}}}$

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g( х)}}$ $\,=\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{\dfrac{f(x)-f(c)}{xc }}{\dfrac{g(x)-g(c)}{x-c}}}$

Теперь воспользуемся правилом частных пределов, чтобы вывести математическое доказательство на следующий уровень.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \ dfrac {\ Displaystyle \ большой \ lim_ {х \, \ к \, с} {\ normalsize \ dfrac {f (х) -f (с)} {хс}}} {\ Displaystyle \ большой \ lim_ {х \ ,\to\,c}{\normalsize \dfrac{g(x)-g(c)}{x-c}}}$

Выражения $f(x)-f(c)$ и $g(x) -g(c)$ выражают изменение функции $f(x)$ и изменение функции $g(x)$ соответственно. Точно так же выражение $x-c$ также выражает шанс в переменной $x$.

Согласно основному определению производной, частное $f(x)-f(c)$ на $x-c$ называется производной функции $f(x)$. Точно так же частное $g(x)-g(c)$ на $x-c$ называется производной функции $g(x)$

$x\,\to\,c$ означает, что значение $x$ ближе к $c$. Итак, изменение значений функций и изменение переменной бесконечно малы. Следовательно, производные обеих функций выражаются следующим образом.

$(1).\,\,\,$ $\dfrac{df(x)}{dx}$ $\,=\,$ $\dfrac{f(x)-f(c)}{x-c }$

$(2).\,\,\,$ $\dfrac{dg(x)}{dx}$ $\,=\,$ $\dfrac{g(x)-g(c)} {x-c}$

Теперь мы можем заменить выражения в числителе и знаменателе их соответствующими производными функций.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \dfrac{\displaystyle \large \lim_{x\,\to\,c}{\normalsize\dfrac{d}{dx}f(x)}}{\displaystyle \large\lim_{x\,\to\ ,c}{\normalsize \dfrac{d}{dx}g(x)}}$

В дифференциальном исчислении выражения $\dfrac{df(x)}{dx}$ и $\dfrac{dg(x )}{dx}$ просто обозначаются $f'(x)$ и $g'(x)$ соответственно.

$\implies$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x)}{g(x)}}$ $\,=\,$ $ \dfrac{\displaystyle \large \lim_{x\,\to\,c}{\normalsize f'(x)}}{\displaystyle \large \lim_{x\,\to\,c}{\normalsize g ‘(х)}}$

Теперь используйте правило частных пределов для упрощения выражения правой части уравнения.

$\,\,\,\поэтому\,\,\,\,\,\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f(x )}{g(x)}}$ $\,=\,$ $\displaystyle \large \lim_{x\,\to\,c}{\normalsize \dfrac{f'(x)}{g'( x)}}$

Видео-урок: Правило Лопиталя | Nagwa

Стенограмма видео

Правило Лопиталя.

В этом видео мы научимся применить правило Лопиталя для оценки пределов неопределенных форм нуля над нулем, бесконечность над бесконечностью и отрицательная бесконечность над отрицательной бесконечностью. Мы рассмотрим несколько примеров того, как мы можем использовать правило Лопиталя.

Начнем с рассмотрения предел. И это предел, поскольку 𝑥 стремится к нулю 𝑥 над грехом пяти 𝑥. Если мы хотим оценить этот предел, мы можем начать с попытки использовать прямую замену. Мы получаем ноль над грехом пяти раз ноль. Поскольку пять раз ноль — это просто ноль, это то же самое, что ноль над грехом нуля. Грех нуля дает ноль. Таким образом, это должно быть равно нулю в течение ноль, который не определен. Поэтому этот предел не может быть оценивается непосредственно с помощью прямой замены.

На самом деле, любой из методов, которые мы известно до сих пор не могут быть использованы для оценки этого предела. Вот где правит L’Hopital Правило Лопиталя говорит нам, что если предел при приближении 𝑥 к 𝑎 некоторого 𝑓 из 𝑥 по 𝑔 из 𝑥 равен нулю по ноль или предел при приближении 𝑥 к 𝑎 из 𝑓 из 𝑥 по 𝑔 из 𝑥 равен положительному или отрицательная бесконечность над положительной или отрицательной бесконечностью. Где 𝑎 может быть любым действительным числом, положительная бесконечность или отрицательная бесконечность. Тогда предел при приближении 𝑥 к 𝑎 𝑓 из 𝑥 над 𝑔 из 𝑥 равно пределу, когда 𝑥 приближается к 𝑎 из 𝑓 простого числа 𝑥 над 𝑔 простым числом 𝑥.

Обратите внимание на L’Hopital’s правило состоит в том, что для того, чтобы это работало, оба 𝑓 из 𝑥 и 𝑔 из 𝑥 должны быть дифференцируемый. А также с нашим состоянием, когда мы говорим, что предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥 по 𝑔 из 𝑥, может быть равен положительная или отрицательная бесконечность над положительной или отрицательной бесконечностью. Он должен быть равен положительному бесконечность над положительной бесконечностью или отрицательная бесконечность над отрицательной бесконечностью. Правило не работает, когда предел равен положительной бесконечности над отрицательной бесконечностью или отрицательной бесконечности над положительная бесконечность.

Теперь, когда мы рассмотрели определение правила Лопиталя, давайте применим его к пределу, который мы пытаемся найти.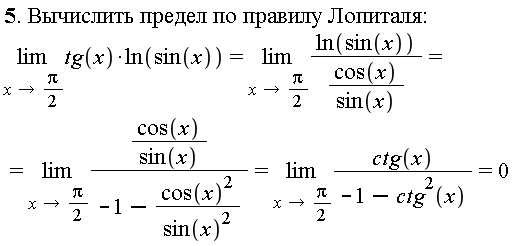 Так что это предел, как 𝑥 приближается к нулю 𝑥 по греху пяти 𝑥. И мы видели, что с помощью прямого замена, наш предел равен нулю над нулем. Следовательно, он удовлетворяет первому условие правила Лопиталя. Мы видим, что значение 𝑎 в наш предел равен нулю. Поскольку 𝑎 — действительное число, оно также удовлетворяет второму условию. Теперь мы можем сказать, что 𝑓 из 𝑥 равно равно 𝑥, а 𝑔 от 𝑥 равно греху пяти 𝑥. Ясно, что обе эти функции, 𝑓 и 𝑔 дифференцируемы. Поэтому мы готовы подать заявку Правило Лопиталя.

Сначала нам нужно найти 𝑓 простое число 𝑥 и 𝑔 простое число 𝑥. Дифференцируя 𝑥 по 𝑥, мы находим, что 𝑓 простое число 𝑥 равно единице. Чтобы найти 𝑔 простое число 𝑥, мы нужно дифференцировать грех пяти 𝑥. Это составная функция. Поэтому мы должны использовать цепочку правило. Мы различаем внутреннюю часть функция — так что пять 𝑥 — чтобы получить константу пять. Затем дифференцируем синус получить cos из пяти 𝑥, давая нам, что 𝑔 простое число 𝑥 равно пяти cos из пяти 𝑥.

Применяя правило Лопиталя, мы можем говорят, что предел, когда 𝑥 приближается к нулю 𝑥 по греху пяти 𝑥, равен предел, когда 𝑥 приближается к нулю из одного из пяти, потому что из пяти 𝑥. И теперь мы можем просто использовать прямой замена. И мы видим, что наш предел равен до единицы более пяти раз, потому что пять раз ноль. Пять раз ноль — это просто ноль. А потому что ноль – это просто единица. Таким образом, мы можем сказать, что наша предел равен единице на пять, умноженной на единицу, что составляет просто одну пятую.

Правило Лопиталя может быть очень полезным для нахождения пределов функций, которые кажутся несуществующими. Давайте посмотрим на пример.

Найдите предел по мере приближения 𝑥 ноль семи 𝑒 до пяти 𝑥 минус семь сверх отрицательного 𝑒 до восьми 𝑥 плюс один.

Мы начнем с попытки решить этот предел с помощью прямой замены. Получаем семь раз 𝑒 к степень пяти раз ноль минус семь над отрицательным 𝑒 в степени восемь раз ноль плюс один. Так как 𝑒 в степени нуля равно равно единице, мы находим, что это равно семи минус семь плюс минус один плюс один, который упрощается до нуля над нулем. Однако это не определено. Хотя мы получаем, что наш предел не определен с помощью прямой замены, он равен нулю над нулем. И это говорит нам о том, что мы можем быть можно использовать правило Лопиталя.

Правило Лопиталя говорит нам, что если предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥 по 𝑔 из 𝑥, равен нулю выше нуля, положительная бесконечность над положительной бесконечностью или отрицательная бесконечность над отрицательной бесконечность. Где 𝑎 – действительное число, положительное бесконечность или отрицательная бесконечность. Тогда предел при приближении 𝑥 к 𝑎 𝑓 из 𝑥 над 𝑔 из 𝑥 равно пределу, когда 𝑥 приближается к 𝑎 из 𝑓 простого числа 𝑥 над 𝑔 простым числом 𝑥.

Теперь наш предел удовлетворяет при условии, что наш предел равен нулю над нулем. И так как мы берем предел как 𝑥 стремится к нулю, значит, наше 𝑎 равно нулю, что является реальным количество. Поэтому мы можем использовать L’Hopital’s правило. 𝑓 из 𝑥 является числителем функция, для которой мы берем предел. Итак, с семи 𝑒 до пяти 𝑥 минус семь. И 𝑔 из 𝑥 является знаменателем. Так что это минус 𝑒 в степени восемь 𝑥 плюс один.

Теперь мы должны найти 𝑓 простое число 𝑥 и 𝑔 премьера 𝑥. Поскольку мы будем различать экспоненциальные члены, мы можем использовать правило, которое говорит нам, что дифференциал 𝑒 к мощность 𝑘𝑥 по отношению к 𝑥 равна 𝑘 раз 𝑒 степени 𝑘𝑥. Продифференцируем 𝑓 от 𝑥 термина по сроку. Семь 𝑒 в степени пять 𝑥 равно экспоненциальный член. Поэтому мы будем использовать правило, которое мы только что заявили. Наше значение 𝑘 равно пяти. И мы замечаем, что у нас есть постоянная семи, умножающая наш экспоненциальный член. Так что должно остаться два, давая нам семь раз по пять 𝑒 до пяти 𝑥. Тогда семь раз пять будет 35. Таким образом, мы можем записать это как 35𝑒 в степень пяти 𝑥.

Второй член в 𝑓 числа 𝑥 равен минус семь, что является просто константой. И когда мы различаем любой константа, мы просто получаем ноль. Итак, мы обнаружили, что 𝑓 простое число 𝑥 равно равно 35𝑒 в пятой степени 𝑥. Первый член в 𝑔 из 𝑥 равен отрицательное 𝑒 в степени восемь 𝑥, что снова является экспоненциальным членом. Используя наше правило, получаем, что дифференциал этого члена равен восьми 𝑒 в восьмой степени 𝑥. Второй член в 𝑔 из 𝑥 равен единице, что опять константа. И поэтому это будет отличаться от дать ноль.

Теперь мы готовы подать заявку Правило Лопиталя. Получаем, что предел как 𝑥 приближается к нулю из семи 𝑒 в степени пять 𝑥 минус семь по отрицательному 𝑒 к сила восьми 𝑥 плюс один. Равен пределу как 𝑥 приближается к нулю в 35 раз 𝑒 в степени пять 𝑥 по восьми отрицательным числам 𝑒 в степени восемь 𝑥. Теперь мы можем подать заявку напрямую подстановка, дающая нам 35 умноженное на 𝑒 в степени нуля над отрицательными восемью умноженное на 𝑒 в степени нуля. Так как 𝑒 в степени нуля равно равным единице, мы получаем решение, что наш предел должен быть равен минус 35 в течение восемь. Далее рассмотрим пример что удовлетворяет другому условию правила Лопиталя.

Найдите предел, когда 𝑥 стремится к бесконечность в два раза, умноженная на 𝑒 в степени три 𝑥 минус пять более чем в три раза 𝑒 в степени три 𝑥 минус один.

Мы можем начать с попытки найти это ограничение с помощью прямой замены. Мы будем использовать тот факт, что предел при стремлении 𝑥 к бесконечности 𝑒 в степени 𝑥 равен положительному бесконечность. Отсюда получаем, что предел так как 𝑥 стремится к бесконечности 𝑒 в степени три 𝑥 также равно положительному бесконечность. И это говорит нам о том, что когда мы используем прямой подстановкой, чтобы найти наш предел, мы находим, что он равен положительному бесконечность над положительной бесконечностью. И это не определено. Поэтому мы еще не нашли решение.

Однако тот факт, что он равен к положительной бесконечности над положительной бесконечностью говорит нам, что мы можем использовать Правило Лопиталя. Правило Лопиталя говорит нам, что если предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥 по 𝑔 из 𝑥, равен нулю выше нуля, положительная бесконечность над положительной бесконечностью или отрицательная бесконечность над отрицательной бесконечность. Где 𝑎 – действительное число, положительное бесконечность или отрицательная бесконечность. Тогда предел при приближении 𝑥 к 𝑎 𝑓 из 𝑥 над 𝑔 из 𝑥 равно пределу, когда 𝑥 приближается к 𝑎 из 𝑓 простого числа 𝑥 над 𝑔 простым числом 𝑥.

Теперь наш лимит равен бесконечности над бесконечностью. И мы берем лимит как 𝑥 стремится к положительной бесконечности. Поэтому нам разрешено использовать Правило Лопиталя. В нашем случае 𝑓 из 𝑥 равно два раза 𝑒 в степени три 𝑥 минус пять. А 𝑔 из 𝑥 равно трем умноженное на 𝑒 в степени три 𝑥 минус один.

Находим 𝑓 простое и 𝑔 простое по дифференцируя 𝑓 и 𝑔. Дифференцирование двух 𝑒 в степени из трех 𝑥 минус пять относительно 𝑥, мы получаем, что 𝑓 простое число 𝑥 должно быть равно шести 𝑒 в степени три 𝑥. И дифференцируя три раза 𝑒 в степени трех 𝑥 минус один относительно 𝑥, мы получаем, что 𝑔 простое число 𝑥 должно быть равно девяти 𝑒 трем 𝑥. Получаем, что наш предел должен быть равно пределу, поскольку 𝑥 стремится к бесконечности в шесть раз, умноженное на 𝑒 на три 𝑥 за девять раз на 𝑒 к трем 𝑥.

Здесь мы замечаем, что у нас есть множитель, умноженный на 𝑒 на три 𝑥 как в числителе, так и знаменатель. Поскольку мы можем записать наш числитель как умножить на три 𝑒 в степени три 𝑥 и наш знаменатель равен трем умноженное на три 𝑒 в степени три 𝑥. Таким образом, эти три фактора умноженное на 𝑒 в степени 3 𝑥, уравновешивается, оставляя нам предел как 𝑥 стремится к бесконечности от двух до трех. Поскольку нет зависимости 𝑥 внутри нашего предела, наш предел просто равен двум третям. И это решение задачи вопрос. Множество различных пределов дают один из неопределенные формы, необходимые для использования правила Лопиталя. Рассмотрим следующее Примеры.

Определить лимит как 𝑥 приближается к одному из отрицательных 11-кратного натурального логарифма 𝑥 по отрицательным девяти 𝑥 плюс девять.

Давайте начнем с поиска этого ограничение с помощью прямой замены. Получаем минус 11 умноженный на натуральный логарифм единицы на минус девять плюс девять. Мы будем использовать тот факт, что натуральный логарифм единицы равен нулю. И это дает нам, что наш предел должен быть равен нулю больше нуля, что не определено. Однако это основное условие которому мы должны удовлетворить, чтобы использовать правило Лопиталя.

Это правило Лопиталя. А так как наш предел равен нулю выше нуля, мы видим, что мы выполнили первое условие. Мы берем лимит как 𝑥 подходит к одному. Таким образом, мы можем сказать, что 𝑎 равно один. И один – действительное число. Таким образом, мы удовлетворили второе условие. И это говорит нам о том, что мы способны использовать правило Лопиталя. Мы можем сказать, что 𝑓 из 𝑥 равно в минус 11, умноженный на натуральный логарифм 𝑥. И 𝑔 из 𝑥 равно отрицательному девять 𝑥 плюс девять.

Чтобы отличить 𝑓 от относительно 𝑥 мы будем использовать тот факт, что дифференциал натурального логарифм 𝑥 по 𝑥 равен единице по 𝑥. Поскольку 𝑓 of 𝑥 просто константа умножается на натуральный логарифм 𝑥, где константа равна отрицательному 11, получаем, что 𝑓 простое число 𝑥 равно минусу 11 над 𝑥. Теперь 𝑔 из 𝑥 равно отрицательному девять 𝑥 плюс девять, что является простым многочленом. И поэтому мы можем различать это используя правило степени для дифференцирования, давая нам, что 𝑔 простое число 𝑥 равно отрицательная девятка.

Теперь мы можем применить формулу для Правило Лопиталя, заключающееся в том, что предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥 по 𝑔 из 𝑥 равно пределу, когда 𝑥 приближается к 𝑎 из 𝑓 простого числа 𝑥 по 𝑔 простого числа 𝑥. Что говорит нам о том, что предел как 𝑥 приближается к одному из отрицательных 11-кратного натурального логарифма 𝑥 по отрицательным девяти плюс девять. Равен пределу как 𝑥 приближается к одному из отрицательных 11 над отрицательными девятью 𝑥. Мы видим, что у нас есть коэффициент минус единица как в числителе, так и в знаменателе. И поэтому их можно отменить, давая нам предел, когда 𝑥 приближается к одному из 11 из девяти 𝑥. И здесь мы можем применить прямое замена, что дает нам 11 на девять, умноженное на один. Это дает нам решение, которое наша предел должен быть равен 11 больше девяти.

В следующем примере мы будем увидеть, как мы можем использовать правило Лопиталя, чтобы найти другой результат.

Данные функции строчные 𝑓 и капитала 𝐹, которые положительны при больших значениях 𝑥, мы говорим, что капитал 𝐹 доминирует над строчной 𝑓, так как 𝑥 стремится к бесконечности, если предел как 𝑥 стремится к бесконечности строчной 𝑓 из 𝑥 над прописной 𝐹 из 𝑥 равно нулю. Используйте правило Лопиталя, чтобы определить который является доминирующим, поскольку 𝑥 стремится к бесконечности. Натуральный логарифм 𝑥 или квадратный корень из 𝑥.

Использование определения доминирующего заданный в вопросе, чтобы сказать, является ли натуральный логарифм 𝑥 или квадратный корень из 𝑥 является доминирующим. Нам нужно показать, что либо предел, поскольку 𝑥 стремится к бесконечности натурального логарифма 𝑥 по квадратному корню из 𝑥 равно нулю. Или предел, поскольку 𝑥 стремится к бесконечность квадратного корня из 𝑥 над натуральным логарифмом 𝑥 равна нуль.

Начнем с рассмотрения последний из этих двух вариантов. Нам нужно найти предел как 𝑥 стремится к бесконечности квадратного корня из 𝑥 по натуральному логарифму 𝑥. Поскольку квадратный корень из 𝑥 и натуральный логарифм 𝑥 являются возрастающими функциями, мы знаем, что предел каждый из них в отдельности, поскольку 𝑥 стремится к положительной бесконечности, будет положительным бесконечность. Следовательно, предел при 𝑥 стремится к бесконечность квадратного корня из 𝑥 над натуральным логарифмом 𝑥 равна бесконечность над бесконечностью. И это не определено. Тем не менее, это дает нам главное Условия использования правила Лопиталя.

Теперь, поскольку наш предел равен положительная бесконечность над положительной бесконечностью, мы выполнили первое условие. И мы берем лимит как 𝑥 стремится к положительной бесконечности. Таким образом, мы также удовлетворили второе условие. Таким образом, мы можем использовать L’Hopital’s правило.

Имеем, что 𝑓 из 𝑥 равно квадратный корень из 𝑥 и 𝑔 из 𝑥 равен натуральному логарифму 𝑥. Квадратный корень из 𝑥 также равен в 𝑥 в половинной степени. Итак, чтобы найти 𝑓 простое число 𝑥, мы будем использовать степенное правило для дифференцирования. Умножаем на мощность и уменьшите степень на единицу, давая нам, что 𝑓 простое число 𝑥 равно половине умножить на 𝑥 в степени отрицательной половины.

Чтобы отличить 𝑔 от 𝑥 относительно 𝑥 воспользуемся тем, что дифференциал натурального логарифма 𝑥 по отношению к 𝑥 равно единице по 𝑥. Итак, 𝑔 простое число 𝑥 равно один над 𝑥. Применяя правило Лопиталя, находим что наш предел равен пределу при стремлении 𝑥 к бесконечности 𝑥 в степени отрицательная половина более чем в два раза умноженная на единицу более 𝑥.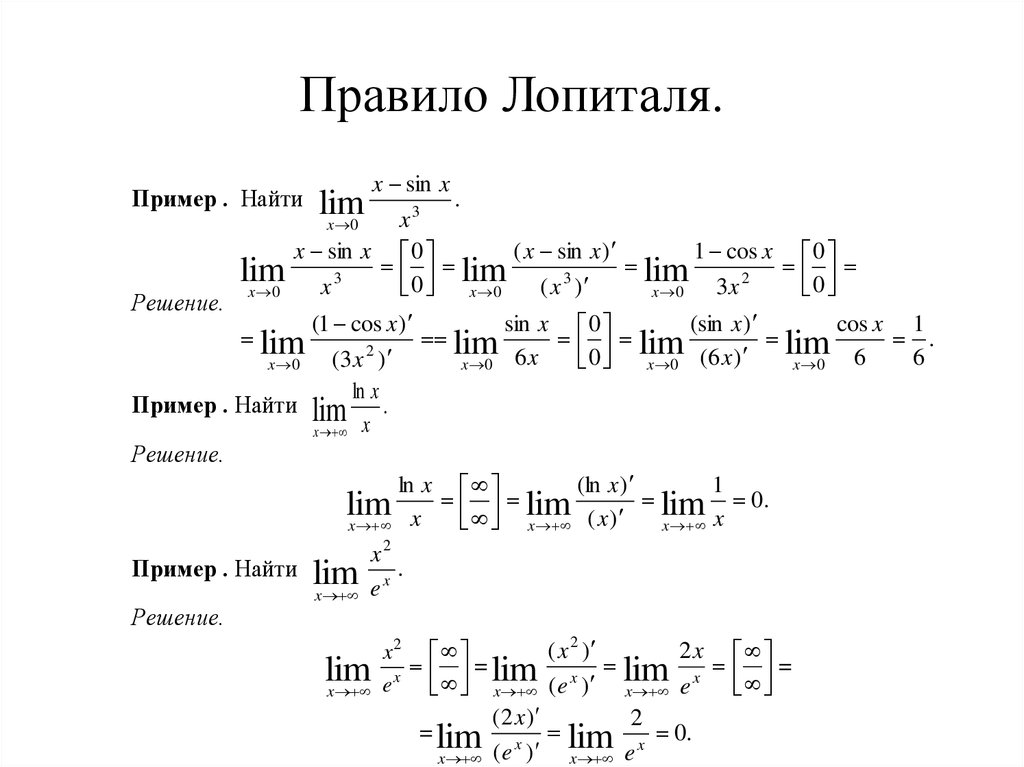

Упрощая, получаем предел, поскольку 𝑥 стремится к бесконечности 𝑥 более чем в два раза на 𝑥 в степени одна половина. Теперь мы можем сократить множитель 𝑥 до сила пополам сверху и снизу. Мы получаем предел, когда 𝑥 стремится к бесконечность 𝑥 в степени половины над двумя. И единственный термин 𝑥 здесь имеет положительная сила. И это в числителе дробная часть. Следовательно, этот предел должен быть равен до бесконечности. И поэтому он не равен нулю. И отсюда мы можем сделать вывод, что натуральный логарифм 𝑥 не доминирует над квадратным корнем из 𝑥.

Теперь проверим, соответствует ли лимит 𝑥 стремится к бесконечности натурального логарифма 𝑥 над квадратным корнем из 𝑥 равно равен нулю. Теперь натуральный логарифм 𝑥 закончился квадратный корень из 𝑥 является обратной величиной квадратного корня из 𝑥 над естественным логарифм 𝑥. И поэтому, когда мы используем прямой подстановки для нахождения предела при стремлении 𝑥 к бесконечности снова получим бесконечность над бесконечностью. Таким образом, мы можем сказать, что предел как 𝑥 стремится к бесконечности натуральный логарифм 𝑥 над квадратным корнем из 𝑥 должен быть равно бесконечности над бесконечностью, которая снова не определена. Однако это позволило нам использовать Правило Лопиталя, так как эти два условия выполняются.

Наш лимит равен положительному бесконечность над положительной бесконечностью. И мы берем лимит как 𝑥 стремится к положительной бесконечности. Так как мы берем предел обратной функции, наши 𝑓 и 𝑔 будут наоборот. Поэтому для нашей последней строки работая, мы просто будем брать предел обратной функции. А так как предел как 𝑥 стремится к бесконечность квадратного корня из 𝑥 над натуральным логарифмом 𝑥 равна предел, поскольку 𝑥 стремится к бесконечности 𝑥 в степени половины над двумя. Это говорит нам о том, что предел как 𝑥 стремится к бесконечности натуральный логарифм 𝑥 по квадратному корню из 𝑥 будет равен пределу, когда 𝑥 стремится к бесконечности обратной величины 𝑥 в степени половина больше двух. И это предел, поскольку 𝑥 стремится бесконечность двух над 𝑥 в половинной степени.

В этом пределе наш 𝑥 имеет положительная степень половины. Однако она находится в знаменателе дробь. И поэтому, если мы возьмем предел при стремлении 𝑥 к бесконечности оно будет равно нулю. Итак, мы показали, что предел поскольку 𝑥 стремится к бесконечности натурального логарифма 𝑥 по квадратному корню из 𝑥 равно равен нулю. Отсюда мы можем сделать вывод, что квадратный корень из 𝑥 доминирует над натуральным логарифмом 𝑥. Как мы видели из этого примера, Правило Лопиталя может быть полезно для демонстрации почти всего, что связано с пределом, поскольку это позволяет нам найти пределы, которые в противном случае были бы неопределенными.

Мы уже видели множество примеры, связанные с правилом Лопиталя. Рассмотрим некоторые ключевые моменты Видео. Ключевые моменты. По правилу Лопиталя можно найти пределы неопределенных форм ноль над нулем, положительная бесконечность над положительной бесконечность и отрицательная бесконечность над отрицательной бесконечностью.