Формула момент инерции круга: Полярный момент инерции круга в технической механике с примерами

Момент осевой кругов – Энциклопедия по машиностроению XXL

Исходя из соотношения (10.14, а), находим осевые моменты инерции круга и кругового кольца  [c.170]

Выше были рассмотрены осевые моменты инерции некоторых простейших сечений. Для определения осевого момента инерции круга предварительно следует ознакомиться с понятием полярный момент инерции и установить формулу для его вычисления.  [c.253]

Установим связь между полярным и осевыми моментами инерции круга и кругового кольца.  [c.254]

Итак, осевой момент инерции круга относительно диаметра равен половине его полярного момента инерции относительно центра. Применив формулу (2.32), получим  [c.255]

Определим осевые моменты сопротивления круга и кругового кольца относительно их центральных осей. Разделив выражения для осевых моментов инерции на 0,5 й, получим для круга  

[c. 255]

Для определения осевых моментов инерции круга и кольца воспользуемся зависимостью между полярным и осевыми моментами инерции  [c.250]

При помощи выражения (3.9), в частности, легко определить осевой момент инерции круга относительно диаметра. Так как в силу симметрии Jx = Jy, получаем = Jy = Jp/2, но, как известно, Jp = irD /32, следовательно, для круга  [c.153]

Чему равны осевые моменты инерции круга и кольца относительно осей, проходящих через их центры тяжести  [c.164]

Как изменится осевой момент инерции круга, если его диаметр увеличить в два раза  

[c.59]

Определить осевой момент инерции круга (см. рис. 50, б) относительно вертикальной оси, касательной к его периметру.  [c.280]

Чему равны осевые центральные моменты инерции круга и кругового кольца  [c.185]

Относительно осей и О у , которые являются главными осями для полукруга, осевые моменты инерции равны половине моментов инерции круга  [c. 33]

Зная полярный момент инерции круга относительно центра, легко найти его момент инерции относительно диаметра. Поскольку осевые моменты инерции одинаковы для всех диаметров, из (А.12) получим  

[c.600]

Определим осевой момент инерции круга относительно любой оси 2, проходящей через его центр тяжести. Из рис. 16.5,а следует  [c.163]

Формулу осевого момента инерции круга можно получить более простым путем, если предварительно вывести рмулу для  [c.164]

Чему равен полярный момент инерции круга, если его осевой момент инерции относительно центральной оси составляет 200 см 7  [c.118]

А. Неправильно. Существует зависимость между полярным и осевым моментами инерции, поэтому, зная центральный осевой момент инерции круга, можно определить полярный момент инерции.  

[c.119]

Б. Неправильно. Чтобы определить, как изменится осевой момент инерции круга с изменением диаметра, нужно учесть, что осевой момент инерции круга пропорционален четвертой степени диаметра.  [c.119]

Б. Неправильно. Полярный момент инерции круга в два раза больше осевого момента инерции круга относительно оси, проходящей через его центр.  [c.119]

Определим осевой и полярный моменты инерции круга относительно центральных осей. Сразу отметим равенство осевых моментов инерции между собой I,, = 1 . А посколь-   [c.240]

Ha основании формулы (2.45) видим, что ОК = Jf Таким образом, в соответствующем масштабе абсциссы точек круга инерции дают нам значения осевых моментов инерции, а ординаты — центробежных.  [c.28]

Круг, кольцо. Для круга или кольца (рис. 2.57) главные центральные моменты инерции относительно осей хну равны между собой. Поэтому из равенства (2.62), выражающего зависимость между осевыми и полярным моментами инерции, получаем  [c.197]

У круга любая центральная ось главная, потому момент сопротивления круглого сечения отмечен индексом ос — осевой, а изгибающий момент ин-

[c. 241]

В 5.5 были получены формулы, по которым можно вычислять осевые моменты инерции некоторых простейших сечений — пpя ю-угольника, круга, кольца.  [c.255]

Вероятно, наиболее удачно говорить, что главными называют оси, относительно которых осевые моменты инерции экстремальны, и равенство нулю центробежного момента инерции относительно этих осей — удобный признак для их отыскания (распознавания). Причина, по которой в техникумах такое определение не подходит, была указана выше. Выводы формул для опр -деления главных центральных моментов круга, прямоугольника и равнобедренного треугольника должны быть даны.  

[c.115]

Круг (рис. 2.4.3). Для круглого поперечного сечения полярный момент инерции 1р = ж1 /32, а осевые моменты инерции — I, = 1у = яВ 64.  [c.32]

Найти полярный Ур и осевой У моменты инерции сечения круглой трубы, приближенно рассматривая сечение как тонкое кольцо толщиной и длиной nd по средней линии. Выразить точное значение У “, полученное как разность моментов инерции наружного (di=d+0 и внутреннего d =d—i) кругов, через и отношение t/d. Насколько отличается приближенное значение от точного при отношении tjd=0, 1  

[c.80]

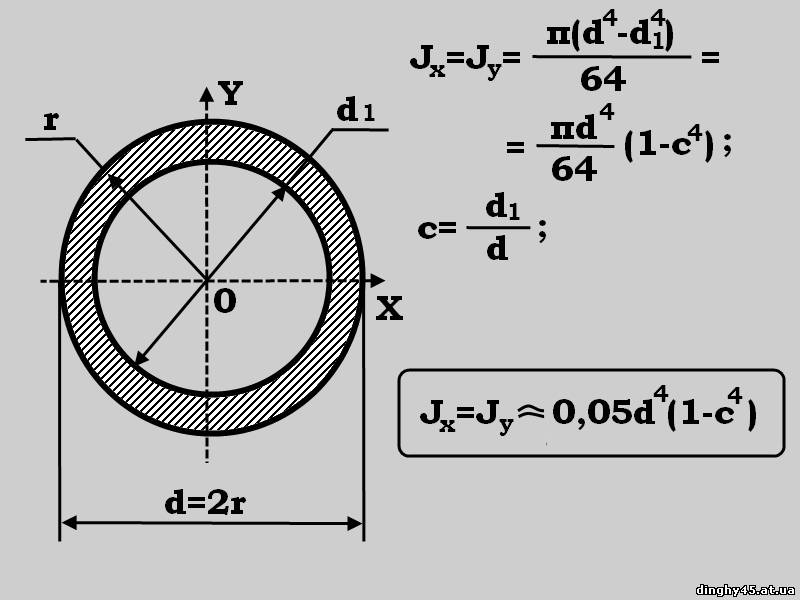
Моменты инерции (полярный i осевые) сечения, имеющего форму кругового кольца с наружным диг -метром с1 и внутренним (рис. 5.13 , можно определить как разности мея -ду соответствующими моментам и инерции наружного и внутреннего кругов.  [c.146]

Чему равен осевой момент сопротивления прямоугольника и круга  [c.112]

Вычислить центральные осевые моменты инерции а) круга d = 98 мм б) кольца d = 100 мм, а = – = 0,8 в) квадрата а = 120 мм, г) прямоуголь-  [c.280]

Вернемся к уравнению (17.23). Если = Jy, что означает равенство главных осевых моментов инерции, то угол между силовой и нулевой линиями будет прямой, а значит, и изгиб будет прямым. Такой случай возможен для сечений, у которых все центральные оси главные (например, круг, кольцо).

 [c.171]

При помощи выраасения (3.9), в частности, легко определяется осевой момент инерции круга относительно диаметра. Так как в силу симметрии = получаем  [c.114]

Кольцо (рис. IV.5, в). Осевой момент инерции в этом случае равен разности моментов инерции внещнего и внутреннего кругов  

[c.98]

Осевой момент инерции сечения в виде круга увеличился в 8 раз. Во сколько раз измешьчась площадь сечения круга  [c.250]

Круг. Все осевые моменты, инерции площади круга отдосительно осей, проходящих через щентр тяжести сечения одинаковы,  [c.171]

Найти осевой момент инерции для круга, ослабДенно-го отверстиями в форма равносторонних треугольников со стороной, равной К/4.  [c.50]

Круг для моментов инерции дает зависимость между моментами инерции рассматриваемого сечения по отношению к различным осям, проходящим через данную точку, и вычерчивается по осевым и центробежному моментам инерции по отношению к двум взаимно-пернендикулярным осям.

Координаты каждой точки окружности дают  [c.45]

---

Лекция на тему “Характеристики плоских сечений”

Геометрические характеристики плоских сечений

Иметь представление о физическом смысле и порядке определения осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.

Знать формулы моментов инерции простейших сечений, способы вычисления моментов инерции при параллельном переносе осей.

При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь геометрической характеристикой сечения является площадь.

При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометрические характеристики сечения, влияющие на сопротивления сечения деформированию.

Статический момент площади сечения

Рассмотрим произвольное сечение (рис. 1).

Если разбить сечение на бесконечно малые площадки аА и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:

Для симметричного сечения статические моменты каждой половины площади равны по величине и имеют разный знак. Следовательно, статический момент относительно оси симметрии равен нулю.

Статический момент используется при определении положения центра тяжести сечения:

Формулы для определения положения центра тяжести можно записать в виде

Центробежным моментом инерции сечения называется взятая по всей площади сумма произведений элементарных площадок на обе координаты:

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. й площади сумма произведений элементарных площадок на квадрат их расстояния до этой точки:

где р — расстояние до полюса (центра поворота) (рис. 25.1).

Поскольку , получим: полярный момент инерции
сечения равен сумме осевых:

Осевые моменты инерции характеризуют сопротивление сечения повороту относительно соответствующей оси.

Полярный момент инерция характеризует сопротивление сечения повороту вокруг полюса (начала координат). Единицы измерения моментов инерции: м⁴; см⁴; мм⁴.

Моменты инерции простейших сечений

Осевые моменты инерции прямоугольника (рис. 25.2)

Представим прямоугольник высотой Н и шириной Ъ в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы: Ъбу — аА. Подставим в формулу осевого момента инерции относительно оси Ох:

По аналогии, если разбить прямоугольник на вертикальные по лосы, рассчитать площади полос и подставить в формулу для осевого момента инерции относительно оси Оу, получим:

Очевидно, что при /г > Ъ сопротивление повороту относительно

оси Ох больше, чем относительно Оу.

Для квадрата:

Полярный момент инерции круга

Для круга вначале вычисляют полярный момент инерции, затем — осевые.

Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3).

Площадь каждого кольца можно рассчитать как площадь прямоугольника с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца:

Подставим это выражение для площади в формулу для полярного момента инерции:

Получим формулу для расчета полярного момента инерции круга:

Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:

где а — наружный диаметр кольца; а_ън — внутренний диаметр кольца

Если обозначить й_вн/^ = с, то

Осевые моменты инерции круга и кольца

Используя известную связь между осевыми и полярным моментами инерции, получим:

Моменты инерции относительно параллельных осей

Оси Охо и Ох параллельны (рис.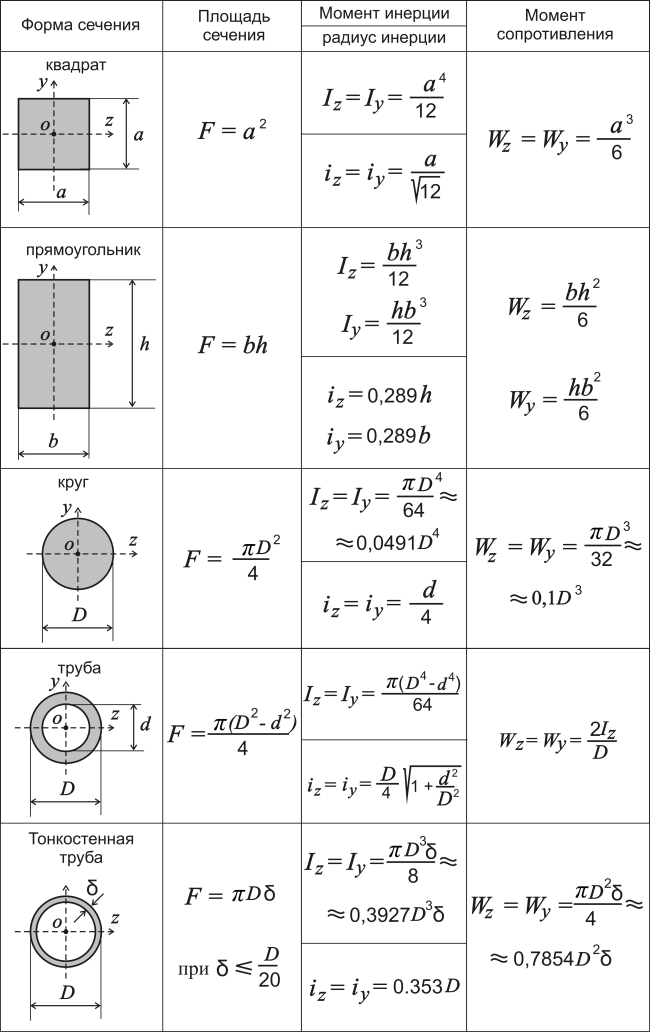 _Xй — момент инерции относительно оси

Ох₀;

А — площадь сечения; а — расстояние между осями Ох и Охо-

Главные оси и главные моменты инерции

Главные оси — это оси, относительно которых осевые моменты инерции принимают экстремальные значения: минимальный и максимальный.

Главные центральные моменты инерции рассчитываются относительно главных осей, проходящих через центр тяжести.

Примеры решения задач

Пример 1. Определить величину осевых моментов инерции плоской фигуры относительно осей Ох и Оу (рис. 25.5).

Решение

1. Определим осевой момент инерции относительно оси Ох. Используем формулы для главных центральных моментов. Представим момент инерции сечения как разность моментов инерции круга и прямоугольника.

Для круга

Для прямоугольника

Для прямоугольника ось Ох не проходит через ЦТ. Момент инерции прямоугольника относительно оси Ох:

где А — площадь сечения; а — расстояние между осями Ох и Охо.

Момент инерции сечения

2. Осевой момент инерции относительно оси Оу:

Момент инерции сечения

решение задач. Лекции. Геометрические характеристики сечений. Моменты инерции простых сечений.

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW – считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн – построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW – эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции – теория, практика, задачи… Примеры решения задач Справочная информация – ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги – разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи. ::Оглавление:: 1. Геометрические характеристики сечений. 1.3. Моменты инерции простых сечений. 1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию. За dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда Итак,           (1.11) Аналогично, получим           (1.12) 2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга За dA принимаем площадь бесконечно тонкого кольца толщиной dp тогда Следовательно,           (1.13) Теперь легко найдем Ixo. Действительно, для круга согласно формуле (1.9.), имеем Iр = 2Iхо = 2Iуо, откуда           (1.14) 2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов           (1. 15) где c = d/D. Аналогично полярный момент инерции           (1.16) 2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника: dA = bydy, где by – длина прямоугольника. Легко получить из подобия треугольников by = yb/h; тогда           (1.17) Определим момент инерции относительно центральной оси; для этого используем формулу (1.10)           (1.18) Определим момент инерции относительно оси, проходящей через основание:           (1.19) ::Оглавление::

Сообщество Вход Решение задач Расчет редукторов Для Android (рекомендую) NEW Mobile Beam 2. 0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME

Определение момента инерции диска. Проверка теоремы Штейнера. | Учителю.

Определение момента инерции диска. Проверка теоремы Штейнера.

ЦЕЛЬ: определить момент инерции диска расчётным и экспериментальным методами

ОБОРУДОВАНИЕ: специальная установка, набор гирь, штангенциркуль, секундомер

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Работа, которую совершает постоянный момент силы М при повороте тела на угол φ (в радианах),
А = Мφ (1)
Работа сил трения или сопротивления равна изменению механической энергии системы: А = Е1 – Е2 (2) Кинетическая энергия тела массой m, которое движется поступательно со скоростью υ и одновременно вращается с угловой скоростью ω относительно центра масс,

Эта энергия равна кинетической энергии вращательного движения относительно мгновенной оси (MOB):

В этих формулах Jс – момент инерции тела относительно оси, проходящей через центр масс, J – момент инерции относительно MOB.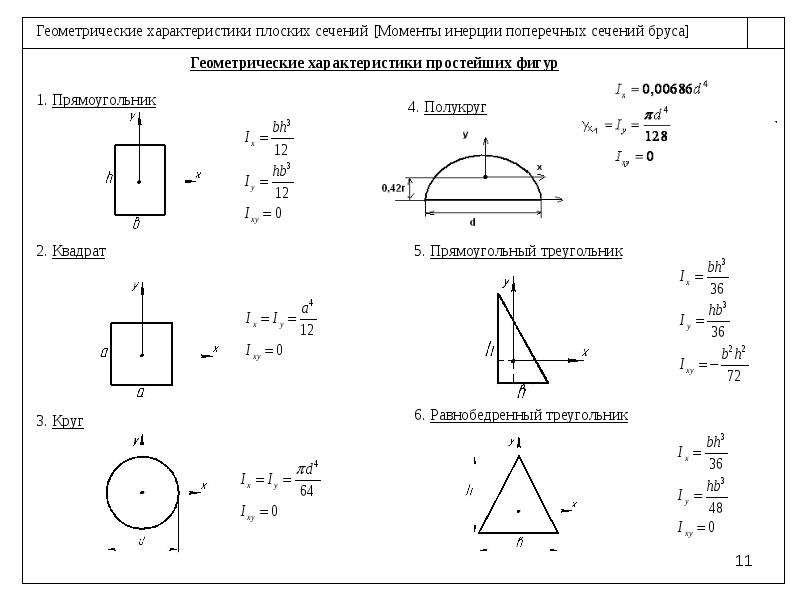
Если эти оси параллельны друг другу, то согласно теореме Штейнера

где m – масса тел, а – расстояние между осями.

ОПИСАНИЕ УСТАНОВКИ

Диск 1 с резьбовыми отверстиями насажен на ось (рис. 1) и может вращаться с малым трением. На той же оси находится шкив 2 радиусом г, на который наматывается нить. К другому концу нити привязан груз 4 массой m, под действием которого система приводится во вращение.
Путь, пройденный грузом до своего нижнего положения (когда нить полностью размотается), определяется по шкале 3, вдоль которой груз движется.
В резьбовые отверстия диска могут вворачиваться дополнительные грузы 5 цилиндрической формы (радиуса R) и массы m0.
В установке предусмотрено автоматическое измерение времени движения груза до нижней точки и расстояния h, на которое поднимается груз по инерции после прохождения нижнего положения.

ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ

Если намотать нить на шкив, подняв на высоту груз m, то он будет обладать потенциальной энергией При падении груза его потенциальная энергия переходит в кинетическую энергию поступательного движения груза и энергию вращения диска . Зная время t падения груза до нижней точки, можно определить конечную скорость движения груза и угловую скорость вращения диска , где r – радиус шкива.

При движении в подшипниках действует момент сил трения Мтр, для преодоления которого на пути совершается работа А = Мφ

Где φ0- угол поворота диска (угловое перемещение).

В соответствии с законом сохранения энергии и равенством (2)

Момент сил трения Мтр найдём из следующих соображений. После того, как груз опустится до нижней точки, маховик, продолжая вращение по инерции, поднимет груз на высоту h; там его потенциальная энергия mgh меньше, чем начальная, на величину работы, совершенной против сил трения на всём пути . Из закона сохранения энергии и формулы (2) следует

Решая совместно уравнения (7), (8), получаем расчётную формулу для момента инерции вращающегося тела:

ВОПРОСЫ К ДОПУСКУ

1. Чему равен момент инерции материальной точки?
2. От каких величин зависит момент инерции диска?
3. Чему равен момент инерции твёрдого тела относительно оси?
4. В каких единицах измеряют момент инерции?
5. Чему равен момент инерции системы тел относительно какой-то оси?
6. Запишите закон сохранения энергии для системы “диск—груз”.
7. На что расходуется механическая энергия в системе:
а) потенциальная энергия груза при его опускании;
б) кинетическая энергия системы при движении груза вверх?
8. Какое положение груза соответствует наибольшей кинетической энергии маховика?
9. По какой формуле определяют работу, затраченную на преодоление сил трения?
10. Чему равна работа постоянного момента силы?

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит метод определения момента инерции диска в данной работе? По какой формуле его рассчитывают в опытах?
2. Чем обусловлена погрешность в данной работе?
3. От каких величин зависит кинетическая энергия тела при поступательном и вращательном движениях?
4. Что характеризует момент инерции материальной точки, тела?
5. От каких величин зависит момент инерции тела?
6. Сформулируйте и докажите теорему Штейнера.
7. Как рассчитывают момент инерции твёрдого тела сложной формы?
8. Найти момент инерции однородной пирамиды, основанием которой служит квадрат со стороной a, относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.
9. Две материальные точки с массами m1 и m2 соединены жестким невесомым стержнем длины l. Найти момент инерции этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.

Момент инерции окружности – объяснение, формулы и важные часто задаваемые вопросы

Момент инерции окружности

Прежде всего, давайте простыми словами обсудим основную концепцию момента инерции.

Можно сделать вывод, что инерция связана с массой тела. Когда тело начинает вращаться вокруг постоянной оси, каждый элемент тела движется по петле с линейной скоростью, что означает, что каждая частица движется с угловым ускорением.

Да, правильное определение момента инерции состоит в том, что тело стремится бороться с угловым ускорением. Математически это сумма произведения массы каждой частицы в теле на квадрат ее длины от оси вращения.

Формула момента инерции может быть представлена ​​как:

I = момент инерции = Σ miri2

Здесь m = масса тела

r = радиус круговой траектории

[Изображение будет загружено в ближайшее время]

Момент инерции = I = πR4 / 4

[Изображение будет загружено в ближайшее время]

Момент инерции = I = 5πR4 / 4

[Изображение будет загружено в ближайшее время]

Момент инерции = I = 5πR4 / 2

[Изображение будет загружено в ближайшее время]

Момент инерции = I = πR4 / 8

[Изображение будет загружено в ближайшее время]

Момент инерции = I = πR4 / 16

Момент инерции Инерция окружности относительно ее диаметра

Если мы рассмотрим диаметр окружности D, то мы должны также принять радиус r как D / 2.

Ось проходит через центр.

Это выражение для момента инерции окружности относительно ее диаметра можно представить как

I = π D4 / 64.

Момент инерции окружности

Вы знаете, как найти момент инерции окружности? Чтобы узнать об этом, нам нужно понять вывод момента инерции круга, как описано ниже. С этим выводом будет легче понять, как найти момент инерции окружности.

Формула момента инерции окружности, согласно получению, круглое поперечное сечение будет вычислено с радиусом и осью, проходящей точно через центр. Это объяснение включает определенные шаги, например:

1. Опишите систему координат.

2. Откройте для себя область дифференциала.

3. Наконец, интегрируйте его.

[Изображение будет загружено в ближайшее время]

Шаг: 1

Давайте начнем с запоминания уравнения для области второго момента. Это уравнение выражено ниже:

A∫ z2 dy dz = Iy

∫ z2 da = Iy

Iy – компонент MOI по оси ординат.

А пока просто опишем координаты, применив полярную систему.

После подачи заявки приобретаем;

r sin θ = z

r cos θ = y

Шаг: 2

После завершения шага 1 нам нужно вычислить дифференциальную площадь, которую можно получить, объявив площадь сектора.

Изображение нарисовано ниже:

[Изображение будет загружено в ближайшее время]

На основании изображения площадь сектора может быть выражена как;

A = ½r2dθ

Теперь после дифференцирования выражение будет получено как;

dA = rdrdθ

Шаг: 3

Теперь давайте просто запишем интеграл для момента инерции окружности.

Выражение будет;

o∫2πo∫r (r sin θ) 2rdrdθ = Iy

Давайте просто упростим это интегрирование с помощью соответствующих шагов:

o∫2πo∫r r3 sin2θ dr dθ = Iy

o∫2πsin2θ [o∫r r3dr ] dθ = Iy

o∫2π sin2θ [r4 / 4] ordθ = Iy

r4 / 4o∫2πsin2θ = Iy

Как мы знаем о тригонометрическом тождестве i. е.

sin2θ = 1 – cos2θ / 2 ——- eq (1)

Давайте просто подставим значение в интеграл. Выражение будет следующим:

r4 / 4 o∫2π1 – cos 2θ / 2 x dθ = Iy

r4 / 4 o∫2π½ – ½cos (2θ) dθ = Iy

r4 / 4 [½θ – ½sin (2θ) ] o2π = Iy

r4 / 4 [½ (2π) – ¼sin (4π) – ½ (0) + ¼sin (0)] o2π = Iy

r4 / 4 (π – 0 – 0 + 0) = Iy

πr4 / 4 = Iy

В некоторых случаях есть возможность вычислить MOI круга относительно его оси, касательной к периметру, тогда мы будем практиковать теорему о параллельной оси.

По теореме;

I + Ad2 = II

Что ж, нам нужно принять во внимание некоторые факторы, такие как,

d = r

I = πR4 / 4

A = πR2

Давайте просто поместим значение в уравнение ( 1):

πR4 / 4 + πR2 / 4 = II

5πR4 / 4 = II

Момент инерции круговой формулы

1. I = πR4 / 4 – MOI круга

2. I = πD4 / 64 – МОИ кругового сечения вокруг оси, перпендикулярной сечению

3. I = 5πR4 / 4 – МОИ окружности вокруг оси, касательной к периметру (окружности)

4. I = 5πR4 / 2 – Полярный момент инерции

5. I = πR4 / 8 – Случай полукруга

6. I = πR4 / 16 – Случай четверти круга

[Решено] Момент инерции четверти окружность радиуса ‘r’ ab

Концепция:

Теорема о параллельной оси:

Момент инерции тела относительно оси, параллельной телу, проходящей через его центр, равен сумме момента инерции тела относительно оси, проходящей через центр, и произведению площади тела, умноженной на квадрат расстояния между двумя осями

I = I _ком + Ax ²

Расчет:

Момент инерции окружности вокруг центральной оси равен:

\ ({I_ {xx}} = {I_ {yy}} = \ frac {{\ pi {d ^ 4}}} {{64}} \ Rightarrow \ frac {{\ pi {r ^ 4}}}} {4} \)

Момент инерции четверти круга относительно его основания определяется как:

\ ({I_ {AB}} = \ frac {{\ pi {d ^ 4}}} {{4 \; \ times \; 64}} \ Rightarrow \ frac {{\ pi {r ^ 4}}}} {{4 \; \ times \; 4}} \)

Момент инерции четверти окружности вокруг центральной оси определяется по формуле:

\ ({{\ rm {I}} _ {{\ rm {xx}}}} = {\ rm {I_ {AB}}} \; – {\ rm {A}} \ times {\ left ({ {\ rm {\ bar x}}} \ right) ^ 2} \)

\ (A = \ frac {{\ pi {r ^ 2}}} {4} \)

Мы знаем, что центр тяжести четверти окружности находится по адресу:

. 4}}} {{144 \ pi}} \)

∴ I _xx = 0.4} \)

Калькулятор момента инерции | Pi Day

Калькулятор момента инерции определит второй момент площади (также известный как момент инерции плоской площади или момент инерции площади) обычных геометрических фигур.

Перед тем, как вычислить второй момент площади, нам нужно понять концепцию. Так что же такое момент инерции плоской поверхности?
Это объяснение того, как область распределена по оси x или оси y.По окончании расчетов единицы будут в 4-й степени.
При определении момента инерции вдоль оси мы обычно рассматриваем «основание» как расстояние по оси x, а «высоту» как вертикальное расстояние по оси y.

Вычисление второго момента площади геометрических фигур вручную может быть запутанным и трудоемким, поэтому позвольте этому калькулятору сделать всю работу за вас. Но формулы будут даны, поэтому, если вам действительно нужно рассчитать вручную, калькулятор станет отличным ресурсом для проверки вашей работы. {3} \)

Очень важно отметить, что эти формулы работают, только если рассматриваемая форма имеет обе оси, пересекающие центроид. Центроид расположен на 2/3 пути от каждой вершины многоугольника до середины противоположной стороны. Это также относится к центру масс геометрического объекта.

Приведенные выше формулы хороши, если начало координат и центроид совпадают, но на самом деле это не всегда так. Чтобы найти момент площади в этом случае, рассмотрите следующую информацию:

l: момент инерции относительно оси, параллельной оси x

A: площадь формы

лк: момент площади вокруг оси x

a: расстояние между параллельными осями.{2}) \)

Вы можете попрактиковаться в определении момента площади, вручную проведя вычисления, а затем проверить свои ответы с помощью нашего удобного калькулятора. Или, если вы хотите получить почти мгновенный ответ, переходите прямо к нашему калькулятору. Попробуйте, и вы останетесь довольны результатом!

Площадь Момент инерции или второй момент площади плоских сечений элементов конструкции

Оси x-x и y-y проходят через центроид и ось x-x параллельна ширине секции, а y-y параллельно глубине.

2. Циркулярный раздел

я _хх = I _гг = (πD ⁴ ) / 64,

где D – диаметр сечения, а x-x и оси y-y проходят через центроид.

Момент инерции полых профилей также может определяется путем вычитания момента инерции снятого площадь с момента инерции исходной площади.

Мы можем использовать теорему о параллельных осях , чтобы найти момент инерции относительно оси, параллельной x-x или y-y,

Например, если p-q – ось, параллельная x-x и он находится на расстоянии «h» от оси x-x.Тогда момент инерция I _pq относительно оси p-q может быть определена как указано ниже;

I _pq = I _xx + Ач ²

где A = площадь сечения

Теорема

о параллельных осях также используется для определения момента инерции составных секций .

Полярный момент инерции требуется в случай кручения конструктивного элемента. Полярный момент инерции определяется как момент инерции относительно оси, перпендикулярной к плоскость сечения и может быть рассчитана путем применения теорема о перпендикулярных осях , которая говорит, что

я _хх + I _yy = I _zz , где ось zz перпендикулярна оси xx и оси yy.

Используйте наш Момент калькулятора инерции для определения центра тяжести, момента инерции, модуль упругости сечения и радиус инерции для различные сечения, включая угол, круг, прямоугольник, канал, двутавровое или двутавровое сечение, тавровое сечение, пятиугольник, шестиугольник. Момент инерции необходим для определения напряжения изгиба, напряжения сдвига и прогиб луча.

Вы можете выбрать из списка плоских сечений, приведенного ниже, или посетить Инструкцию по вычислению момента инерции, чтобы ознакомиться с инструкциями по использованию этого калькулятора.

Проблемы прочности материалов – Sanfoundry

Этот набор задач по прочности материалов посвящен «Моменту инерции сечения».

1. Каков момент инерции круглого сечения?
a) πD ⁴ /64
b) πD ³ /32
c) πD ³ /64
d) πD ⁴ /32
Посмотреть ответ

Ответ: a
Пояснение: Момент инерция круглого сечения πD ⁴ /64.

2. Каков момент инерции прямоугольного сечения относительно горизонтальной оси через ЦТ?
a) bd ³ /6
b) bd ² /12
c) b ² d ² /12
d) bd ³ /12
Посмотреть ответ

Ответ: d
Пояснение : Момент инерции прямоугольного сечения относительно горизонтальной оси, проходящей через C.G is bd ³ /12.

3. Каков момент инерции прямоугольного сечения относительно горизонтальной оси, проходящей через основание?
a) bd ³ /12
b) bd ³ /6
c) bd ³ /3
d) bd ² /3
Посмотреть ответ

Ответ: c
Пояснение: Момент инерция прямоугольного сечения относительно горизонтальной оси, проходящей через основание, равна bd ³ /3.

4. Каков момент инерции треугольного сечения относительно основания?
a) bh ² /12
b) bh ³ /12
c) bh ³ /6
d) bh ² /6
Посмотреть ответ

Ответ: b
Пояснение: Момент инерция треугольного сечения относительно основания bh ³ /12.

5. Каков момент инерции треугольного сечения относительно оси, проходящей через C.G. а параллельно базе?
a) bh ³ /12
b) bh ³ /24
c) bh ³ /36
d) bh ³ /6
Посмотреть ответ

Ответ: c
Пояснение: Момент инерция треугольного сечения относительно оси, проходящей через ЦТ а параллельно основанию – bh ³ /36.

Подписаться на информационный бюллетень прочности материалов

6.Каким будет момент инерции круга в см4 диаметром 10 см?
a) a340
b) 410
c) 460
d) 490
Посмотреть ответ

Ответ: d
Пояснение: Момент инерции окружности = πD ⁴ /64
= 491,07 см ⁴ .

7. Каким будет момент инерции данного прямоугольника относительно горизонтальной оси, проходящей через основание?

a) 1500 мм ⁴
b) 1650 мм ⁴
c) 1666 мм ⁴
d) 1782 мм ⁴
Посмотреть ответ

Ответ: c
Пояснение: Момент инерции a прямоугольное сечение вокруг горизонтальной оси, проходящей через базу = bd ³ /3
= 5x10x10x10 / 3
= 1666.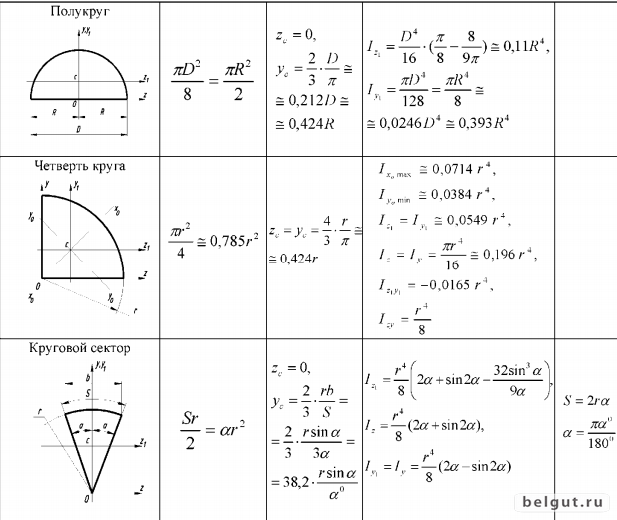 66 мм ⁴ .

8. Каким будет момент инерции данного прямоугольного сечения относительно горизонтальной оси через ЦТ?

a) 350 мм ⁴
b) 379 мм ⁴
c) 416 мм ⁴
d) 500 мм ⁴
View Ответ

Ответ: c
Пояснение: Момент инерции прямоугольного сечения около горизонтальная ось через CG = bd ³ /12
= 5x10x10x10 / 12
= 416,67 мм ⁴ .

9. Каким будет момент инерции данного треугольника относительно основания?

a) 20,33 мм ⁴
b) 21,33 мм ⁴
c) 24,33 мм ⁴
d) 22,33 мм ⁴
Посмотреть ответ

Ответ: b
Пояснение: Момент инерции треугольное сечение около цоколя = bh ³ /12.
= 4x4x4x4 / 12
= 21,33 мм ⁴ .

10. Каким будет момент инерции данного треугольника относительно оси, проходящей через C.G и параллельно базе?

a) 6,1 мм ⁴
b) 7,1 мм ⁴
c) 8,1 мм ⁴
d) 7,56 мм ⁴
Посмотреть ответ

Ответ: b
Пояснение: Момент инерции a треугольное сечение вокруг оси, проходящей через ЦТ и параллельно основанию = bh ³ /36.
= 4x4x4x4 / 36
= 7,11 мм ⁴ .

11. Какая разница между MOI двух сечений треугольника в 1-м, MOI берется относительно его основания, а во 2-ом MOI берется относительно его центроида?
a) bh ³ /12
b) bh ³ /18
c) bh ³ /36
d) bh ³ /24
Посмотреть ответ

Ответ: b
Пояснение: Момент Инерция треугольного сечения относительно основания bh ³ /12
Момент инерции треугольного сечения относительно оси, проходящей через C.G. is bh ³ /36
Итак, разница = bh ³ /12 – bh ³ /36 = bh ³ /18.

Серия Sanfoundry Global Education & Learning – Прочность материалов.

Чтобы практиковаться во всех областях проблемы прочности материалов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .

Следующие шаги:

• Получить бесплатно Почетную грамоту в области сопротивления материалов
• Примите участие в конкурсе по сертификации прочности материалов
• Стать лидером в области сопротивления материалов
• Подать заявку на вакансию в области сопротивления материалов


• Принять испытания на прочность материалов
• Практические тесты по главам: Глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
• Мок-тесты по главам: Глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Момент инерции

Момент инерции
следующий: крутящий момент Up: Вращательное движение Предыдущее: Центр масс

Момент инерции Рассмотрим расширенный объект, состоящий из элементов. Пусть th элемент обладают массой, вектором положения и скоростью. В полная кинетическая энергия объекта записывается

(334)

Предположим, что движение объекта состоит просто из жесткого вращения на угловой скорость . Как следует из разд. 8.4, что

(335)

Напишем

(336)

где – единичный вектор, выровненный вдоль оси вращения (которая предполагается, что проходит через начало нашей системы координат).Это следует из приведенные выше уравнения, что кинетическая энергия вращения объекта принимает форма

(337)

или

(338)

Здесь величина называется моментом инерции объекта, и написано

(339)

где расстояние по перпендикуляру от th элемента до оси вращение. Обратите внимание, что для поступательного движения мы обычно пишем

(340)

где представляет собой массу и представляет собой скорость. Сравнение Уравнения. (338) и (340) предполагают, что момент инерции играет та же роль во вращательном движении, что и масса в поступательном движении.

Для непрерывного объекта аргументы, аналогичные тем, которые используются в разд. 8,5 урожай

(341)

где – массовая плотность объекта, является расстояние по перпендикуляру от оси вращения, и является элементом объема.Наконец, для объекта постоянной плотности приведенное выше выражение сводится к

(342)

Здесь – полная масса объекта. Отметим, что интегралы берутся по всей объем объекта.

Момент инерции однородного объекта зависит не только от его размера и формы. объект, но на месте оси, вокруг которой объект вращается. Особенно, один и тот же объект может иметь разные моменты инерции при вращении вокруг разные оси.

К сожалению, оценка момента инерции данного тела относительно данной оси неизменно вовлекает выполнение неприятного интеграла объема. На самом деле есть только один тривиальный момент инерции расчета, а именно момент инерции тонкого круговое кольцо вокруг оси симметрии, проходящей перпендикулярно в плоскость кольца. См. Рис. 75. Предположим, что это масса кольца, а это его радиус. Каждый элемент кольца разделяет общее перпендикулярное расстояние от ось вращения – i.е. , г. Следовательно, уравнение. (342) сводится к

(343)

Рисунок 75: Момент инерции кольца относительно перпендикулярной оси симметрии.

В общем, моменты инерции вычислять довольно утомительно. К счастью, есть две мощные теоремы, которые позволяют нам просто связать момент инерции данного тела относительно данной оси до момента инерции того же тела относительно другой оси.Первый из Эти теоремы называются теоремой о перпендикулярной оси и применимы только к однородная ламинарная предметов. Рассмотрим ламинарный объект (, т.е. , тонкий плоский объект). однородной плотности. Предположим, для простоты, что объект лежит в плоскости -. Момент инерции объекта относительно -ось задается

(344)

где мы убрали тривиальное -интегрирование, а интеграл берется по протяженности объекта в плоскости.Между прочим, Вышеприведенное выражение следует из наблюдения, что когда ось вращения совпадает с осью. Точно так же моменты инерция объекта относительно осей – и – принимает вид

соответственно. Здесь мы использовали тот факт, что внутри объекта. Отсюда следует при осмотре из предыдущих трех уравнений, которые

(347)

См. Рис.76.

Рисунок 76: Теорема о перпендикулярной оси.

Воспользуемся теоремой о перпендикулярной оси, чтобы найти момент инерции тонкого кольца относительно ось симметрии, лежащая в плоскости кольца. Принятие системы координат, показанной на Рис. 77, из симметрии ясно, что. Теперь мы уже знаем, что где – масса кольца, – его радиус. Следовательно, перпендикулярная ось Теорема говорит нам, что

(348)

или

(349)

Конечно, потому что, когда кольцо вращается вокруг оси -оси, его элементы в среднем составляют дальше от оси вращения, чем когда он вращается вокруг оси.

Рисунок 77: Момент инерции кольца относительно компланарной оси симметрии.

Вторая полезная теорема относительно моментов инерции называется параллелью . Теорема оси . Теорема о параллельности оси, которая носит довольно общий характер, утверждает, что если момент инерции данного тела относительно оси, проходящей через центр масс этого тела, то момент инерции того же тела относительно второй оси который параллелен первому

(350)

где – масса тела, а – перпендикулярное расстояние между две оси.

Чтобы доказать теорему о параллельности осей, выберем начало координат нашего систему координат, чтобы она совпадала с центром масс рассматриваемого тела. Кроме того, давайте сориентируем оси нашей системы координат так, чтобы ось совпадает с первой осью вращения, а вторая ось ось кусочков – плоскость. Из уравнения. (328), тот факт, что центр масс расположен в начале координат означает, что

(351)

где интегралы берутся по объему тела.Из уравнения. (342), выражение для первого момента инерции:

(352)

поскольку – это перпендикулярное расстояние общей точки от оси -оси. Точно так же выражение для второго момента инерции принимает форма

(353)

Приведенное выше уравнение можно расширить, чтобы получить

Из Ур. (351) и (352) следует, что

(355)

что доказывает теорему.

Воспользуемся теоремой о параллельности осей, чтобы вычислить момент инерции тонкого кольцо вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит по окружности кольца. Мы знаем, что момент инерции кольца массы и радиус вокруг оси, которая проходит перпендикулярно плоскости кольца и проходит через центр кольца – который совпадает с центром массы кольца – есть. Наша новая ось параллельна этой первоначальной оси, но смещена боком на перпендикулярное расстояние.Следовательно, параллель теорема оси говорит нам, что

(356)

См. Рис.78.

Рисунок 78: Применение теоремы о параллельности осей.

В качестве иллюстрации прямого применения формулы (342) позвольте нам вычислить момент инерции тонкого круглого диска массы и радиуса, вокруг оси, которая проходит через центр диска и проходит перпендикулярно к плоскость диска. Выберем нашу систему координат так, чтобы диск лежит в плоскости – с центром в начале координат. Ось вращения, следовательно, совпадает с осью. Следовательно, формула (342) сводится к

(357)

где интегралы берутся по площади диска, а избыточное -интегрирование был подавлен. Разобьем диск на тонкие кольца. Рассмотрим кольцо радиуса и радиальная толщина.Площадь этого кольца просто . Следовательно, мы можем заменить в приведенных выше интегралах на , чтобы дать

(358)

Вышеприведенное выражение дает

(359)

Расчеты, аналогичные приведенным выше, дают следующие стандартные результаты:

---

следующий: крутящий момент Up: Вращательное движение Предыдущее: Центр масс

Ричард Фицпатрик 2006-02-02

Момент инерции четверти окружности

Момент инерции четверти окружности обычно находят или рассчитывают по данной формуле;

На этом уроке мы узнаем, как выводить формулу, а также как ее применять в задачах.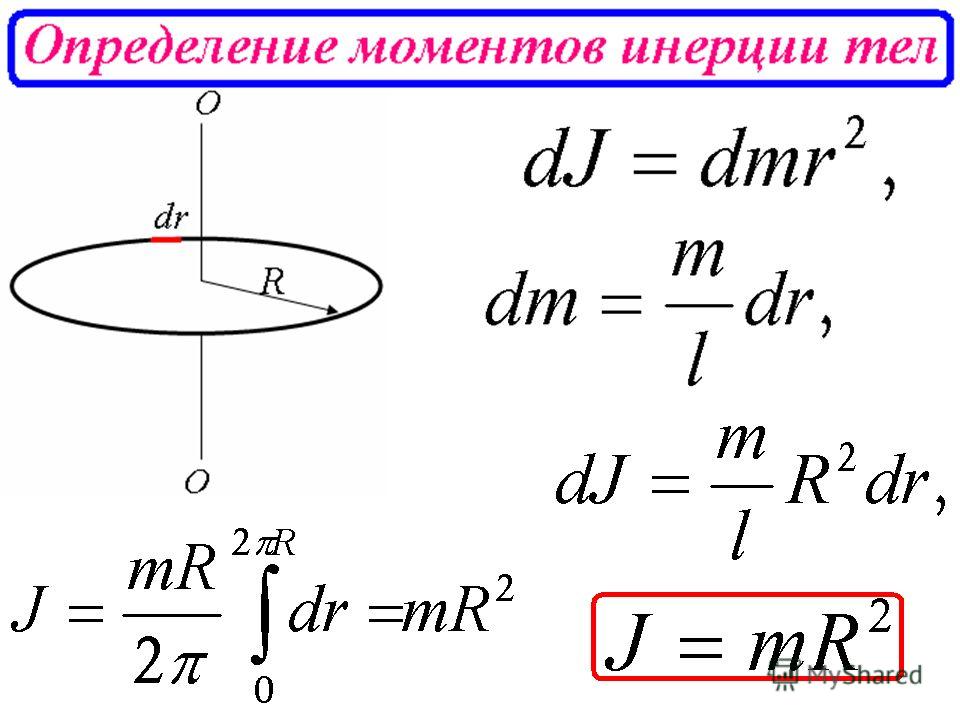

Вывод момента инерции четверти круга

Когда мы выводим выражение момента инерции для четверти круга, мы можем частично использовать тот же вывод, который используется для определения момента инерции круга. Концепция более-менее такая же.

1. Сначала мы рассмотрим формулу полного круга. Это дается как;

I = πr ⁴ /4

Если мы хотим вывести уравнение для четверти круга, то в основном мы должны разделить результаты, полученные для полного круга, на два и получить результат для четверти круга.Примечательно, что в полном круге момент инерции относительно оси x совпадает с осью y.

С этой концепцией мы получаем;

I _x = I _y = ¼ πr ⁴ = ¼ πr ² ) R ²

J _o = I _x + I _y = ¼ πr2 + ¼ πr ⁴ = ½ πr ⁴

Нам также нужно будет определить площадь круга. Когда мы решаем это выражение, мы обычно заменяем M на Area, A.

J _o = ½ (πr ² ) R ²

J _o = ½ (πr ² ) R ₂

Теперь, если взять четверть окружности, момент инерции относительный. относительно оси x и оси y будет составлять четверть момента инерции полного круга. Однако часть круга, вращающаяся вокруг оси, будет симметричной, и значения будут одинаковыми для осей y и x. С этим мы решим уравнение ниже.

I _x = I _y = 1/16 πr ⁴

= 1/16 (πr ² ) R ²

= 1/16 (A) R ²

= ¼ (¼ A _o ) R ²

Следующий шаг включает определение момента инерции четверти окружности.Для этого мы просто добавим значения по осям x и y.

MOI относительно начала координат, J _o = I _x + I _y

= 1/16 (A) R ² + 1/16 (A) R ²

= ⅛ (A) R ²

= ⅛ (πr ² ) R ²

= ⅛ πr ⁴

⇒ Проверить момент инерции другого объекта:

.