Формула момент инерции материальной точки: 20. Момент инерции материальной точки, системы материальных точек, твердого тела относительно оси.

формулы, теорема Штейнера, пример решения задачи — OneKu

Содержание статьи:

• Общие сведения о физической величине
• Величина I для тел разной формы
• Теорема Штейнера и формула
• Уравнение моментов
• Пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫m(r² * dm) = ρ * ∫V(r² * dV).

Где ρ – плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Теорема Штейнера и формула

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = IO + M * h3.

Здесь M – масса тела, h – расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r0 + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M – момент силы, α – угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d – плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см.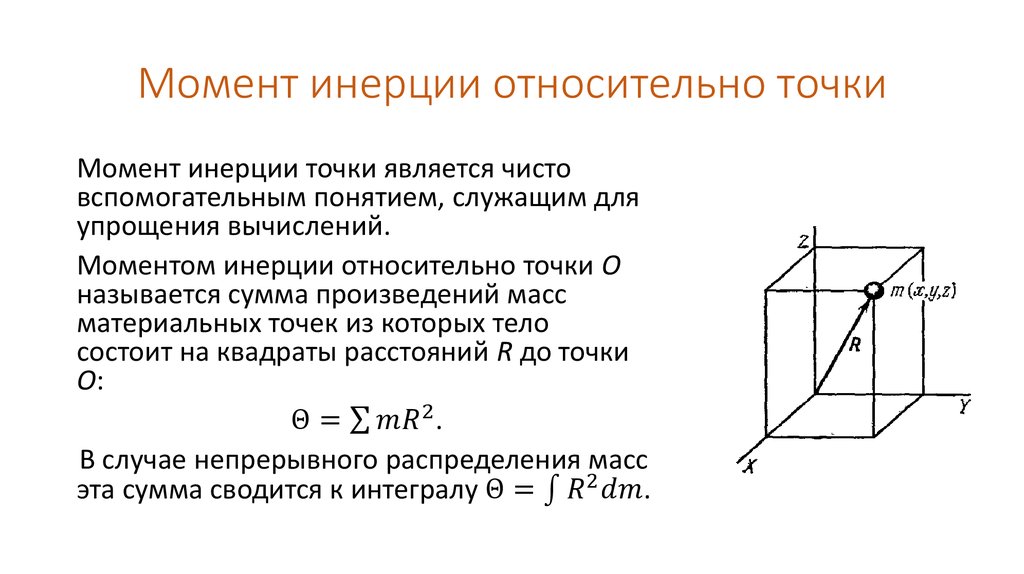 На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

формулы, теорема Штейнера, пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫_m(r² * dm) = ρ * ∫_V(r² * dV).

Где ρ – плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину I_O тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром I_O и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = I_O + M * h².

Здесь M – масса тела, h – расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r₀ + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = I_O + M * (L / 2)² = 1 / 12 * M * L² + M * L² / 4 = M * L² / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M – момент силы, α – угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d – плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = I_O + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

Сопротивление материалов | Механика материалов

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

---

Сопротивление материалов , также известный как механика материалов , ориентирован на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки.

Стресс и напряжение

Когда сила приложена к элементу конструкции, этот элемент будет испытывать как напряжение, так и деформацию в результате действия силы. Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила/дюйм ² (psi) для обычных единиц США и Н/м ² (Па) для единиц СИ:

где F — приложенная сила, а A — площадь поперечного сечения, на которое действует сила. Приложенная сила заставит элемент конструкции деформироваться на некоторую длину пропорционально его жесткости. Деформация – это отношение деформации к исходной длине детали:

где L — деформированная длина, L ₀ — исходная недеформированная длина, а δ — деформация (разница между ними).

Существуют различные типы нагрузки, которые приводят к различным типам напряжения, как указано в таблице ниже:

Тип загрузки	Тип напряжения	Иллюстрация
Осевая сила	Осевое напряжение (общий случай) Растягивающее напряжение (если сила растягивающая) Напряжение сжатия (если сила сжимающая)
Сила сдвига	Напряжение поперечного сдвига
Изгибающий момент	Напряжение при изгибе
Торсион	Напряжение кручения

Осевое напряжение и напряжение изгиба являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно площади, противодействующей силе. Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.

Нормальное напряжение
Осевое напряжение:
Напряжение при изгибе:

Напряжение сдвига
Поперечное напряжение:
Напряжение при кручении:

В уравнениях для осевого напряжения и поперечного напряжения сдвига F — сила, а A — площадь поперечного сечения элемента. В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I _c – центральный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения кручения T — это кручение, r — радиус, а J — полярный момент инерции поперечного сечения.

В случае осевого напряжения на прямолинейном участке напряжение распределяется равномерно по всей площади. В случае касательного напряжения распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F/A, и это среднее напряжение сдвига обычно используется при расчете напряжения. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и напряжения кручения максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.

---

---

Так же, как первичными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига . В случае нормальной деформации деформация нормальна к области, воспринимающей силу:

В случае деформации поперечного сдвига деформация параллельна площади, несущей силу:

где γ – деформация сдвига (безразмерная), а ϕ – деформированный угол в радианах.

В случае деформации кручения элемент скручивается на угол ϕ вокруг своей оси. Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется по формуле:

где ϕ — угол закручивания, r — радиус стержня, а L — длина.

Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:

где ρ — радиальное расстояние от оси стержня.

Закон Гука

Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, где кривая является линейной).

Нормальный стресс и деформация связаны:

σ = E ϵ

где E — модуль упругости материала, σ — нормальное напряжение, ϵ это нормальное напряжение.

Касательное напряжение и деформация связаны соотношением:

τ = G γ

где G — модуль сдвига материала, τ — касательное напряжение, γ — сдвиговая деформация. Модуль упругости и модуль сдвига связаны соотношением:

где ν — коэффициент Пуассона.

Закон Гука аналогичен уравнению силы пружины, F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно изменить, чтобы получить деформацию (удлинение) материала:

Осевое удлинение (от нормального напряжения)
Угол закручивания (от напряжения сдвига/кручения)

Энергия деформации

Когда к элементу конструкции прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина. Энергия деформации (т. е. количество потенциальной энергии, накопленной в результате деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и выражается в дюймо-фунтах в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах предела упругости, то вся энергия деформации может быть восстановлена.

Энергия деформации рассчитывается как:

Общая форма:	U = Работа = ∫ F дл	(площадь под кривой нагрузки-прогиба)
В пределах эластичности:		(площадь под кривой нагрузки-прогиба)
		(потенциальная энергия пружины)

Обратите внимание, что есть два уравнения для энергии деформации в пределе упругости. Первое уравнение основано на площади под кривой отклонения нагрузки. Второе уравнение основано на уравнении потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.

Более подробную информацию об энергии деформации можно найти здесь.

---

---

Жесткость

Жесткость, обычно называемая жесткостью пружины, представляет собой усилие, необходимое для деформации элемента конструкции на единицу длины. Все конструкции можно рассматривать как наборы пружин, а силы и деформации в конструкции связаны уравнением пружины:

F = k δ _макс.

где k — жесткость, F — приложенная сила и δ _max — максимальный прогиб элемента.

Если прогиб известен, то жесткость элемента можно найти, решив k = F/δ _max . Однако максимальное отклонение обычно неизвестно, поэтому жесткость необходимо рассчитывать другими способами. Таблицы прогиба балки можно использовать для общих случаев. Два наиболее полезных уравнения жесткости, которые нужно знать, — это уравнения жесткости для балки с осевой нагрузкой и для консольной балки с торцевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.

	Жесткость [фунт-сила/дюйм]	Макс. отклонение [дюйм]	Иллюстрация
Балка с осевой нагрузкой:
Консольная балка с торцевой нагрузкой:

Крутильный эквивалент уравнения пружины:

T = k ϕ

Особый интерес представляет жесткость вала при нагрузке на кручение:

	Жесткость [дюйм*фунт-сила/рад]	Максимальное отклонение [рад]	Иллюстрация
Вал с торсионной нагрузкой:

Конструкция с несколькими путями нагрузки

Если в конструкции имеется несколько путей прохождения нагрузки (т. е. в конструкции есть несколько элементов, которые распределяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.

	Пружины параллельно	Пружины серии
Иллюстрация:
Эквивалент жесткости конструкции:	k eq = k 1 + к 2 + к 3 + …
Сила в отдельном члене:		F 1 = k eq δ tot = F app
Прогиб отдельного элемента:
Общая сила в конструкции:	Ф to = F 1 + F 2 + F 3 + . ..	F to = F 1 = F 2 = F 3 = …
Общий прогиб конструкции:	δ tot = δ 1 = δ 2 = δ 3 = …	δ to = δ 1 + δ 2 + δ 3 + …

Если элементы на пути нагрузки нельзя рассматривать просто как пружины, соединенные последовательно или как пружины, соединенные параллельно, а скорее они представляют собой комбинацию пружин, соединенных последовательно и параллельно, то проблему необходимо будет решать итеративно. Найдите подгруппу стержней, которые либо чисто последовательно, либо параллельно, и используйте предоставленные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одну пружину с рассчитанными жесткостью, силой и прогибом, и эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.

Концентрация стресса

Можно представить, что силы и напряжения протекают через материал, как показано на рисунке ниже. Когда геометрия материала изменяется, линии потока перемещаются ближе или дальше друг от друга, чтобы приспособиться. Если в материале есть разрыв, такой как отверстие или выемка, напряжение должно течь вокруг разрыва, и линии потока будут собираться вблизи этого разрыва. Эта внезапная упаковка линий потока вызывает резкий скачок напряжения – это пиковое напряжение называется концентрация стресса . Элемент, вызывающий концентрацию напряжений, называется концентраторами напряжений .

Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в непосредственной близости от несплошности, рассчитайте номинальное напряжение в этой области, а затем масштабируйте его с помощью соответствующего коэффициента концентрации напряжения:

σ _макс. = K σ _ном.

где о _max — фактическое (масштабированное) напряжение, σ _nom — номинальное напряжение, а K — коэффициент концентрации напряжения. При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше следует использовать наименьшую площадь в основании скругления.

Многие справочники содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрий. Двумя наиболее полными наборами факторов концентрации стресса являются факторы концентрации стресса Петерсона и формулы Рорка для стресса и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации напряжений.

Концентрация напряжения будет рассеиваться по мере удаления от источника напряжения. Принцип Сен-Венана – это общее практическое правило, согласно которому расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.

Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах локальная текучесть позволит перераспределить напряжения и уменьшит напряжение вокруг райзера. По этой причине коэффициенты концентрации напряжений обычно не применяются к конструктивным элементам, изготовленным из пластичных материалов. Коэффициенты концентрации напряжения также обычно не применяются при наличии избыточного пути нагрузки, и в этом случае текучесть одного элемента позволит перераспределить силы на элементы на других путях нагрузки. Примером этого является шаблон болтов. Если один болт начнет прогибаться, то другие болты в схеме примут на себя большую нагрузку.

Комбинированные напряжения

В любой точке нагруженного материала общее напряженное состояние можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью касательными напряжениями (по два в каждом направлении):

Нижние индексы нормальных напряжений σ указывают направление нормальных напряжений. Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.

Обычно напряжения в одном направлении равны нулю, так что полное напряженное состояние возникает в одной плоскости, как показано на рисунке ниже. Это называется плоскостное напряжение . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Поверхностные напряжения обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и напряжение кручения максимальны на поверхности.

На рисунке выше σ _x и σ _y — нормальные напряжения, τ — касательное напряжение. Напряжения уравновешиваются так, что точка находится в статическом равновесии. Поскольку все напряжения сдвига равны по величине, индексы для простоты опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y . )

Надлежащие соглашения о знаках показаны на рисунке. При нормальном напряжении растягивающее напряжение положительно, а сжимающее отрицательно. Для касательного напряжения направление по часовой стрелке является положительным, а против часовой стрелки — отрицательным.

Если напряжения на рисунке выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ по отношению к горизонтали, как показано на рисунке ниже. Приведенные ниже уравнения преобразования дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.

Нормальное напряжение:
Напряжение сдвига:

Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.

В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимальны и минимальны. Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.

Углы главных напряжений:
Углы предельного напряжения сдвига:

Приведенные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и предельных касательных напряжений:

Главные напряжения:
Экстремальные напряжения сдвига:

Углы, под которыми возникают главные напряжения, составляют 90 ^° друг от друга. Главные напряжения всегда сопровождаются нулевым касательным напряжением. Углы, под которыми возникают предельные касательные напряжения, составляют 45 ^° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ _x + σ _y ) / 2.

Пара полезных отношений:

σ 1 +плюс; σ 2 = σ x +плюс; о г	Сумма нормальных напряжений постоянна.
	Максимальное касательное напряжение равно половине разности главных напряжений.

Круг Мора

Круг Мора — это способ визуализации напряженного состояния в точке нагруженного материала. Это дает интуитивное представление об уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы главные напряжения, экстремальные касательные напряжения и углы, под которыми эти напряжения возникают. Пример круга Мора показан на рисунке ниже:

Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:

Поместите точки на круге, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты ( σ _x , −τ ), а напряжения на грани y будут иметь координаты ( σ _y , τ ). Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты ( σ ₁ , 0 ), а минимальное главное напряжение будет иметь координаты ( σ ₂ , 0 ). Поместите точки на окружность для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты ( σ _c , τ ₁  ), а минимальное экстремальное напряжение сдвига будет иметь координаты ( σ _c , τ ₂  ).

Все точки будут лежать на периметре окружности. Окружность имеет радиус, равный величине предельных касательных напряжений:

Напряженное состояние на x и y гранях напрягаемого элемента представлено черной линией в круге Мора, соединяющей точки ( σ _x , −τ ) и ( σ _y , τ ). Эта линия в круге Мора соответствует невращенному элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек в конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента. Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, очки за 9Грань 0006 x и грань y отстоят друг от друга на 180 градусов на круге Мора, но только на 90 градусов на элементе напряжения.

Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в нагруженном элементе и как меняется напряженное состояние в зависимости от угла поворота, см. прилагаемый калькулятор круга Мора.

Приложения

Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:

• Балки
• Столбцы
• Болтовые соединения
• Подъемные проушины
• Сосуды под давлением
• Валы

---

---

Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции. Предел текучести материала обычно выбирают в качестве предела прочности, с которым сравнивают расчетные напряжения.

Коэффициент безопасности , FS, рассчитывается как:

где σ _{фактическое} — расчетное напряжение в конструкции, а σ _предел — максимальный предел напряжения, обычно прочность материала, такая как предел текучести (S _{ty). Коэффициент безопасности показывает, насколько фактическое напряжение ниже предельного напряжения. Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию. Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10.}

Запас прочности рассчитывается как:

В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы безопасности обычно представляются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции в 1,5 раза превышает фактическое напряжение, запас составляет 50 % (MS = 0,5).

При сообщении коэффициентов безопасности и пределов безопасности иногда требуемый коэффициент безопасности будет «запекаться» в сообщаемых факторах. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, чтобы FS _req = 2. Для достижения необходимого коэффициента запаса прочности сообщаемые значения FS и MS рассчитываются как:

Обратите внимание, что при включении требуемого запаса прочности, FS _req , сообщаемые FS и MS на самом деле представляют собой запасы по отношению к FS _req , а не по отношению к напряжению.

---

PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице прочности материалов. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!

Просмотреть курс сейчас:

Просмотреть курс

---

Каталожные номера

1. Будинас-Нисбетт, «Машиностроение Шигли», 8-е издание.
2. Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е издание.
3. Гир, Джеймс М., «Механика материалов», 6-е издание.
4. Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е издание.
5. Пилки, Уолтер Д. и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
6. «Формулы Рорка для стресса и напряжения», 8-е издание.

Как рассчитать момент инерции различных форм и твердых тел

В физике при расчете момента инерции объекта необходимо учитывать не только массу объекта, но и распределение массы. Например, если два диска имеют одинаковую массу, но у одного вся масса приходится на ободок, а другой твердый, то диски будут иметь разные моменты инерции.

Вычисление моментов инерции довольно просто, если вам нужно исследовать орбитальное движение небольших точечных объектов, где вся масса сосредоточена в одной конкретной точке на заданном радиусе r . Например, для мяча для гольфа, который вы вращаете на веревке, момент инерции зависит от радиуса круга, по которому вращается мяч:

I = мр ²

Здесь r — радиус окружности от центра вращения до точки, в которой сосредоточена вся масса мяча для гольфа.

Однако, когда вы входите в мир без мячей для гольфа, считывание чисел может стать немного затруднительным, потому что вы можете не знать, какой радиус использовать. Что делать, если вы крутите удочку? Вся масса стержня не сосредоточена на одном радиусе. Когда у вас есть протяженный объект, такой как стержень, каждая частица массы находится на другом радиусе. У вас нет простого способа справиться с этим, поэтому вы должны суммировать вклад каждой частицы массы на каждом радиусе следующим образом:

Вы можете использовать эту концепцию суммирования моментов инерции всех элементов, чтобы получить сумму, чтобы вычислить момент инерции любого распределения массы. Вот пример использования двух точечных масс, который немного сложнее, чем одна точечная масса. Скажем, у вас есть два мяча для гольфа, и вы хотите узнать, каков их суммарный момент инерции. Если у вас есть мяч для гольфа с радиусом r ₁ и еще один с радиусом r ₂ , общий момент инерции равен

Так как же найти момент инерции, скажем, диска, вращающегося вокруг оси, проходящей через его центр? Вы должны разбить диск на крошечные шарики и сложить их все вместе. Вы завершаете это, используя исчисление процесса интегрирования.

Формы, соответствующие моментам инерции в таблице.

Надежные физики уже выполнили эту задачу для многих стандартных форм; В следующей таблице приведен список объектов, с которыми вы, вероятно, столкнетесь, и их моменты инерции. На рисунке изображены формы, которым соответствуют эти моменты инерции.

Эта статья из книги:

• Физика I для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию.