Момент инерции тела.
При описании поступательного движения тел мы вводили понятие массы тела – меры инертности тела при действии на него кокой – либо силой. Именно масса тела определяет ускорение, с которым будет двигаться тело под воздействием силы.
А достаточно ли знания массы тела, чтобы описать вращательное движение тела вокруг какой либо оси? Оказывается, что для описания вращательного движения кроме массы тела необходимо знать и его момент инерции относительно выбранной оси вращения.
Пусть тело вращается относительно оси, проходящей через точку О (см. рис. 6.3). При вращательном движении точки, обладающие одинаковой массой, но находящиеся на разном расстояние от оси вращения, будут иметь разную инертность.
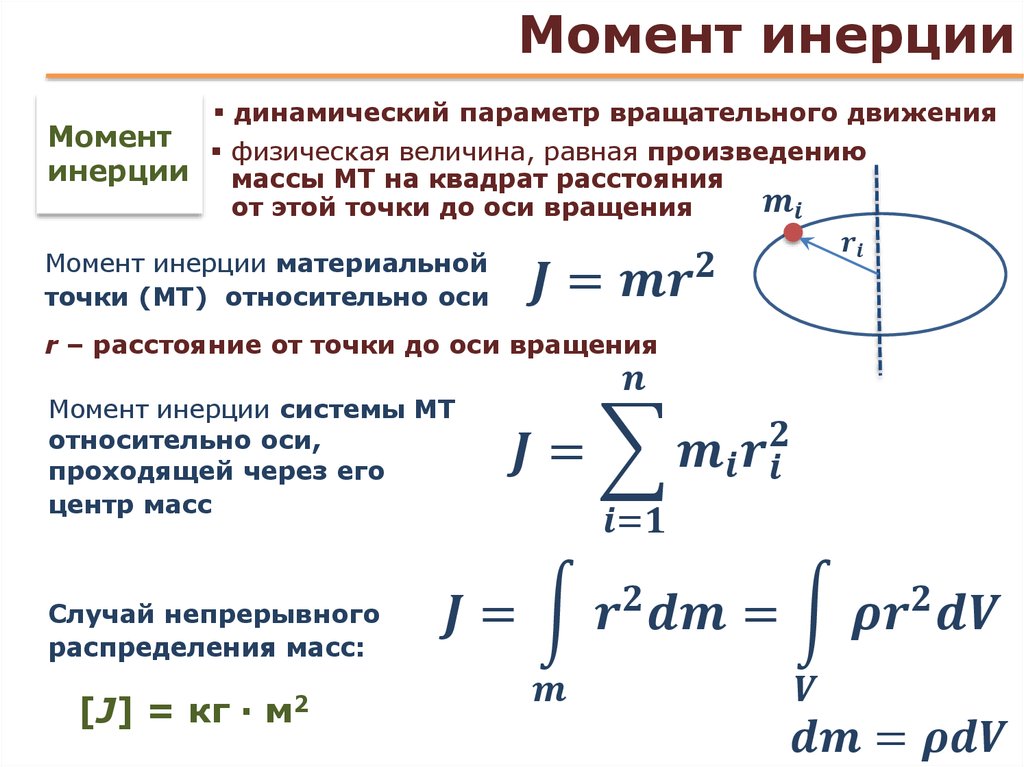
Во вращательном движении материального тела мерой его инертности является момент инерции. Моментом инерции материальной точки относительно оси вращения
. .( 6.2 )
.( 6.2 )
Рис. 6.3. К понятию инертности тела.
Чтобы найти момент инерции всего материального тела, необходимо сложить моменты инерции всех материальных точек, составляющих это материальное тело:
. ( 6.3 )
Выражения
( 6.2 ) и ( 6.3 ) показывают, что момент инерции
любого материального тела есть величина
Если
в формуле ( 6. 3 ) сделать предельный
переход, учитывая, что суммирование
производится по непрерывно меняющейся
величине, то суммирование заменится
интегрированием, т.е. для точки с
3 ) сделать предельный
переход, учитывая, что суммирование
производится по непрерывно меняющейся
величине, то суммирование заменится
интегрированием, т.е. для точки с
, ( 6.4 )
где интегрирование производится по всему объему однородного материального тела. Величина r в этом случае есть функция положения точки с координатами (x, y, z ).
Выражение ( 6.4 ) однако несколько некорректно, поскольку не вполне понятно, как вычислять элементы dm . В случае,если плотность материального тела однородна, т.е. , где
. ( 6.5 )
( 6.5 )
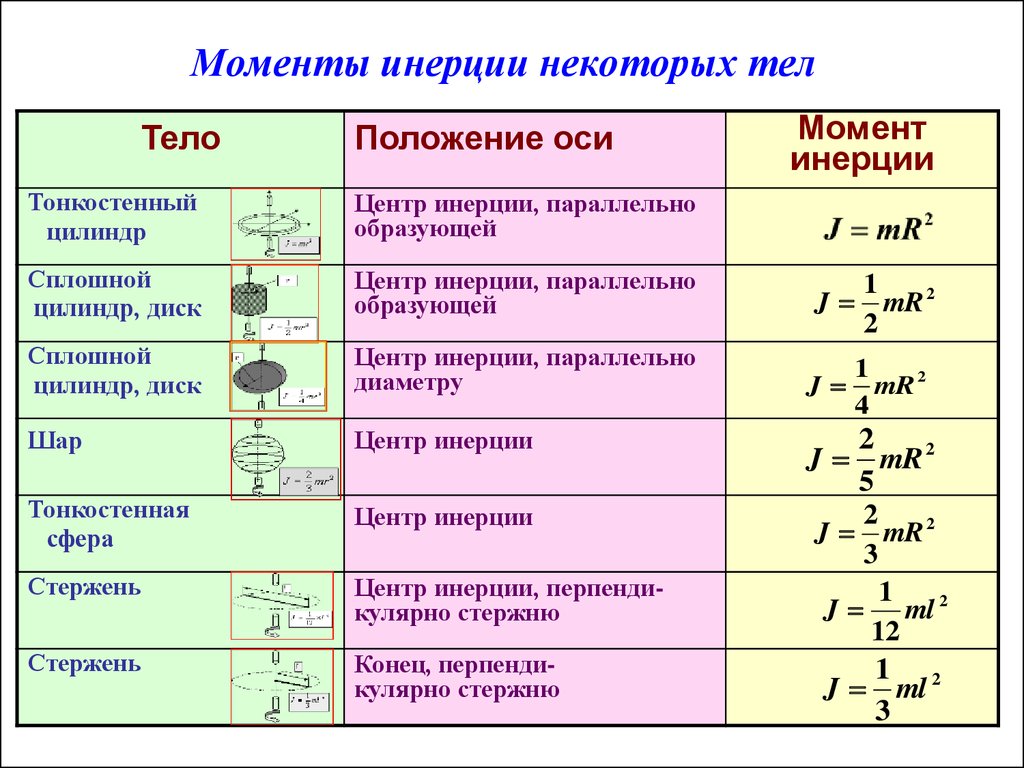
В качестве примера применения формул ( 6.4 ) и ( 6.5 ) рассмотрим случаи вычисления момента инерции конкретных материальных тел.
1.Момент инерции однородного стержня относительно оси, проходящей через центр масс.
Рис. 6.4. К вычислению момента инерции однородного стержня.
Выберем на расстояние r от оси вращения участок стержня толщиной dr, имеющий объем dV=Sdr. Поскольку стержень предполагается однородным то:
, (6.6)
т.к. Sl = m.
2.
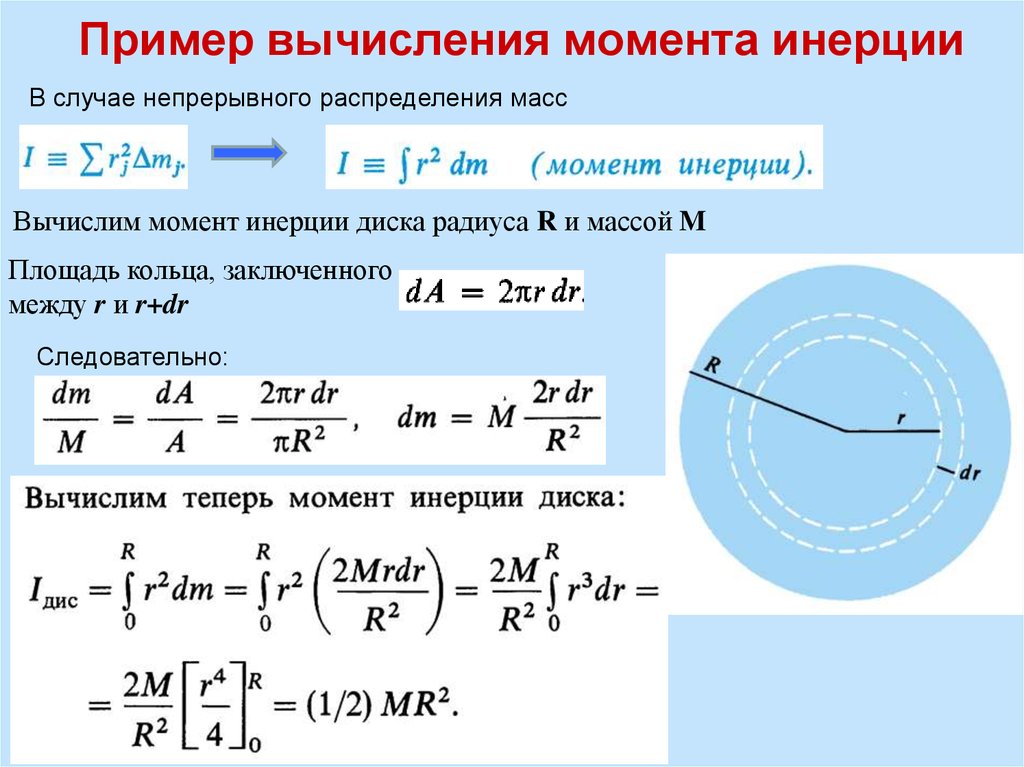
На расстоянии r от оси ОО вращение цилиндра выберем слой толщиной dr (см. рис 6.5 ). Объем этого бесконечно тонкого слоя будет равен:
. ( 6.7 )
Подставим это выражение в формулу (6.5) и получим::
( 6.8 )
Рис. 6.5. К вычислению момента инерции однородного цилиндра.
Момент вращения и момент инерции: формулы, пример решения задачи
Тела, совершающие круговые движения, в физике принято описывать с помощью формул, включающих в себя угловую скорость и угловое ускорение, а также такие величины, как моменты вращения, сил и инерции. Рассмотрим подробнее эти понятия в статье.
Момент вращения относительно оси
Эту физическую величину также называют моментом импульса.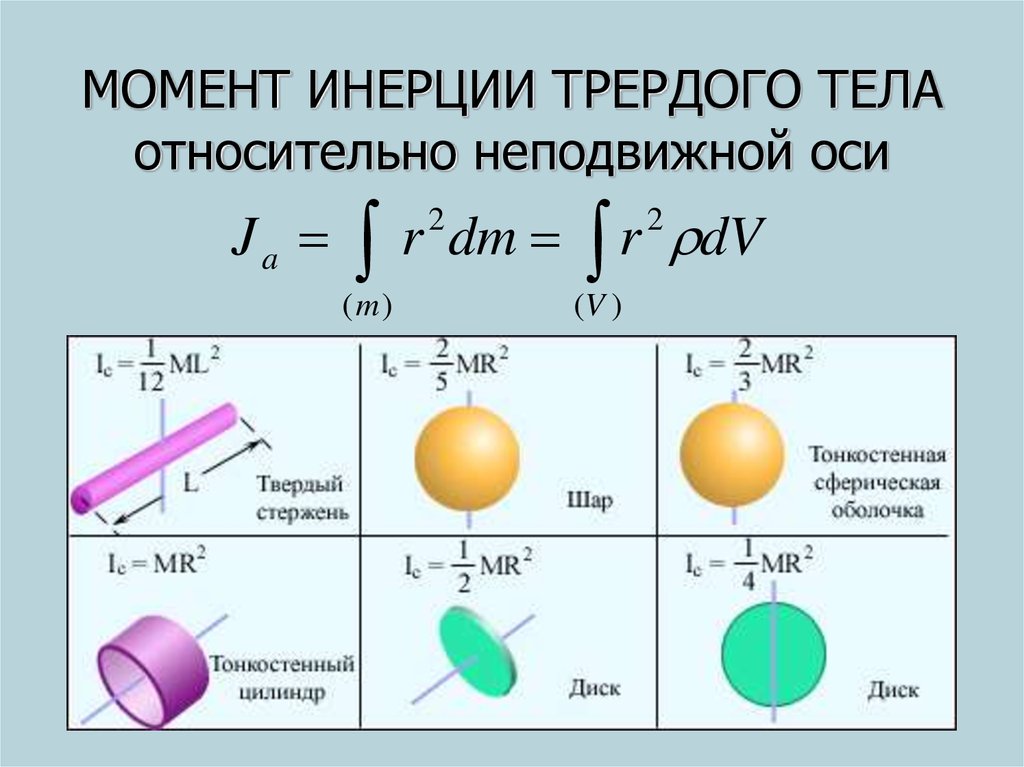 Слово “момент” означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:
Слово “момент” означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:
L¯ = r¯*m*v¯ = r¯*p¯, где p¯ – импульс частицы.
Знак “¯” указывает на векторный характер соответствующей величины. Направление вектора момента вращения L¯ определяется по правилу правой руки (четыре пальца направлены от конца вектора r¯ к концу p¯, и отставленный большой палец показывает, куда будет направлен L¯). Направления всех названных векторов можно посмотреть на главном фото статьи.
При решении практических задач пользуются формулой для момента импульса в форме скалярной. Кроме того, линейную скорость заменяют угловой. В этом случае формула для L будет выглядеть так:
L = m*r2*ω, где ω = v*r – угловая скорость.
Величина m*r2 обозначается буквой I и называется моментом инерции. Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:
Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:
L = I*ω.
Эта формула справедлива не только для вращающейся частицы массой m, но и для любого тела произвольной формы, которое совершает круговые перемещения относительно некоторой оси.
Момент инерции I
В общем случае введенная в предыдущем пункте величина I рассчитывается по формуле:
I = ∑i(mi*ri2).
Здесь i указывает на номер элемента с массой mi, расположенном от оси вращения на расстоянии ri. Это выражение позволяет произвести расчет для неоднородного тела произвольной формы. Для большинства идеальных объемных геометрических фигур этот расчет уже произведен, и полученные значения момента инерции внесены в соответствующую таблицу. Например, для однородного диска, который совершает круговые движения вокруг оси, перпендикулярной его плоскости и проходящей через центр масс, I = m*r2/2.
Чтобы понять физический смысл момента инерции вращения I, следует ответить на вопрос, относительно какой оси легче раскрутить швабру: той, которая проходит вдоль швабры или той, которая ей перпендикулярна? Во втором случае придется приложить больше усилий, поскольку момент инерции для этого положения швабры имеет большую величину.
Закон сохранения величины L
Изменение момента вращения во времени описывается приведенной ниже формулой:
dL/dt = M, где M = r*F.
Здесь M – это момент результирующей внешней силы F, приложенной к плечу r относительно оси вращения.
Формула показывает, если M=0, тогда изменение момента импульса L не будет происходить, то есть он будет оставаться сколь угодно длительное время неизменным независимо от внутренних изменений в системе. Этот случай записывают в виде выражения:
I1*ω1 = I2*ω2.
То есть любые изменения внутри системы момента I будут приводить к изменениям угловой скорости ω таким образом, что их произведение будет оставаться постоянным.
Примером проявления этого закона является спортсмен в фигурном катании, который, выбрасывая руки и прижимая их к телу, меняет свой I, что отражается на изменении его скорости вращения ω.
Задача на вращение Земли вокруг Солнца
Решим одну интересную задачу: используя приведенные выше формулы, необходимо рассчитать момент вращения нашей планеты по своей орбите.
Поскольку притяжением остальных планет можно пренебречь, а также учитывая, что момент гравитационной силы, действующей со стороны Солнца на Землю, равен нулю (плечо r=0), то L=const. Для вычисления L воспользуемся следующими выражениями:
L = I*ω; I = m*r2; ω = 2*pi/T.
Здесь мы приняли, что Землю можно считать материальной точкой с массой m=5,972*1024 кг, поскольку ее размеры намного меньше расстояния до Солнца r=149,6 млн км. T = 365,256 дня – период обращения планеты вокруг своей звезды (1 год). Подставляя все данные в выражение выше, получаем :
L = I*ω = 5,972*1024*(149,6*109)2*2*3,14/(365,256*2 3600) = 2,66*1040 кг*м2/с.
Рассчитанное значение момента импульса является гигантским, что обусловлено большой массой планеты, высокой скоростью ее вращения по орбите и огромным астрономическим расстоянием.
Теорема о параллельных осях
Теорема о параллельных осях
| Назад |
Выражение для момента инерции сплошного цилиндра можно построить из момента инерции тонких цилиндрических оболочек.
Показать форму интеграла | Индекс | ||
| Назад |
| Индекс Понятия момента инерции | ||
|
При построении выражения для момента инерции цилиндра относительно диаметра на его конце (ось x на диаграмме) используются как теорема о параллельной оси, так и теорема о перпендикулярной оси. Получение момента инерции полного цилиндра около диаметра на его конце включает суммирование по бесконечному числу тонких дисков на различных расстояниях от этой оси. Это включает интеграл от z=0 до z=L. Для любого заданного диска на расстоянии z от оси x использование теоремы о параллельной оси дает момент инерции относительно оси x. Теперь, выражая элемент массы dm через z, мы можем проинтегрировать по длине цилиндра. Эта форма может показаться правдоподобной, если вы заметите, что она представляет собой сумму выражений для тонкого диска около диаметра плюс выражение для тонкого стержня на его конце. Если вы возьмете предельный случай R = 0, вы получите выражение тонкого стержня, а если вы возьмете случай, когда L = 0, вы получите выражение тонкого диска. На последних шагах используются полиномиальные формы интегралов. Моменты инерции тонкого диска | Индекс Понятия момента инерции | |
|
Как рассчитать момент инерции?
Момент инерции, называемый угловой массой или инерцией вращения относительно оси вращения, представляет собой величину, определяющую величину крутящего момента, необходимого для достижения желаемого углового ускорения, или характеристику тела, препятствующую угловому ускорению. Момент инерции рассчитывается как произведение массы каждой частицы на квадрат ее расстояния от оси вращения.
Момент инерции
Термин «момент инерции» относится к величине, которая описывает, как тело сопротивляется угловому ускорению, и рассчитывается как произведение массы каждой частицы на квадрат расстояния частицы от оси вращения. Или, другими словами, можно сказать, что это величина, определяющая, какой крутящий момент требуется для определенного углового ускорения вращающейся оси. Момент инерции часто называют вращательной инерцией или угловой массой. кг·м 2 — единица момента инерции в системе СИ.
Или, другими словами, можно сказать, что это величина, определяющая, какой крутящий момент требуется для определенного углового ускорения вращающейся оси. Момент инерции часто называют вращательной инерцией или угловой массой. кг·м 2 — единица момента инерции в системе СИ.
Момент инерции системы n частиц
Момент инерции системы точечных частиц, вращающихся вокруг неподвижной оси, равен:
где,
r i — расстояние между осью i th и
m i — масса i th частица.
Как рассчитать момент инерции?
Для расчета момента инерции любого вращающегося объекта используется несколько способов.
- Для однородных объектов момент инерции рассчитывается путем произведения массы объекта на квадрат расстояния от оси вращения (r 2 ).
- Для неоднородных объектов мы вычисляем момент инерции, взяв сумму произведений масс отдельных точек на каждом другом радиусе, для этого используется формула
I = ∑M I R I 2
Формулы для некоторого Symporting Sommanting Sommance Asemition Obsemation Obsemation Somextation Somections Somections Symempation Symemportaition Somemrismition на втором виде наносимым наряду с Asemition Asemation Somecrita.
 в этой таблице.
в этой таблице.
| Объект | Ось | Выражение момента инерции | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0004 Central | I = MR 2 | ||||||||||
| Тонкое кольцо | Диаметр | I = 1/2 MR 2 | |||||||||
| Ennulal Ring Or Hollow Cylind (r 2 2 + r 1 2 ) | |||||||||||
| Solid Cylinder | Central | I = 1/2 Mr 2 | |||||||||
| Uniform Disc | Diameter | I = 1/4 м 2 | |||||||||
| Hollow Sphere | Центральный | I = 2/3 MR 2 | |||||||||
| SOLID SPHEERE | Central | I = 2/5 MR 2 4 | I = 2/5 MR 2 4 | 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 | . Shell | Central | |||||
| Однородная пластина или прямоугольная параллелепипена | Central | I = 1/12 м (A 2 + B 2 ) | |||||||||
| Shind Rod ) | |||||||||||
. 0014 0014 | Central | I = 1/12 MR 2 | |||||||||
| Тонкий стержень | в конце стержня | I = 1/3 MR 2 |
.
Пример 1: Определить момент инерции твердого шара массой 22 кг и радиусом 5 м.
Ответ :
Дано:
M = 22 кг, R = 5 мДля твердой сферы имеем MOI (I) = 2/5 MR 2
I = 2/5 × 22 × 25
I = 220 кг·м 2
2 и радиусом 10 м.
Ответ :
Дано:
I = 110 кг м 2 , R = 10 мИмеем для однородного диска (I) = 1/4 MR
0 1 0 2 R 2
М = 4 × 110 / 10 2
M = 440 / 100
M = 4,4 кг
Пример 3. Если однородная плита имеет массу 23 кг, длину 10 м и ширину 7 м, определить его момент инерции.

Answer :
Given: M = 23 kg, L = 10 m, b = 7 m
We have for uniform plate MOI
I = 285 kg m 2
Пример 4: Когда однородный полый прямоугольный круговой конус имеет момент инерции 98 кг m 2 и масса 20 кг определяют радиус конуса.
Ответ :
Дано:
I = 98 кг м 2 , M = 20 кгИмеем для прямого кругового конуса, MOI (I) = 9 1/2 R 1/2 MR 4
0 2 = 2i / m R 2 = 2 × 98 /20
R 2 = 9,8
R = √9.8
R = 3,13 M
5920202020202020243434343 3.13 M 9202020202020202020243 4: 3,13 M 202020202020202024343434343434343434343434343 3. масса 10 кг и радиус 7 м, определить момент инерции полого цилиндра.


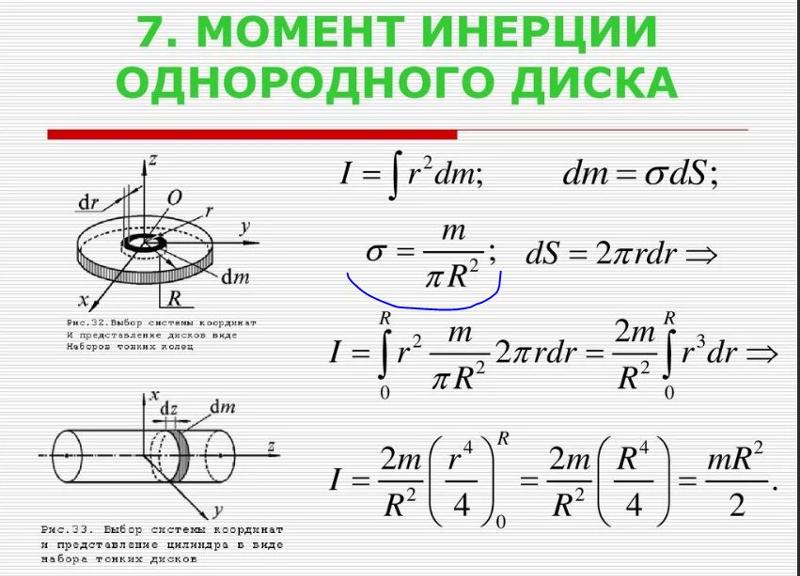
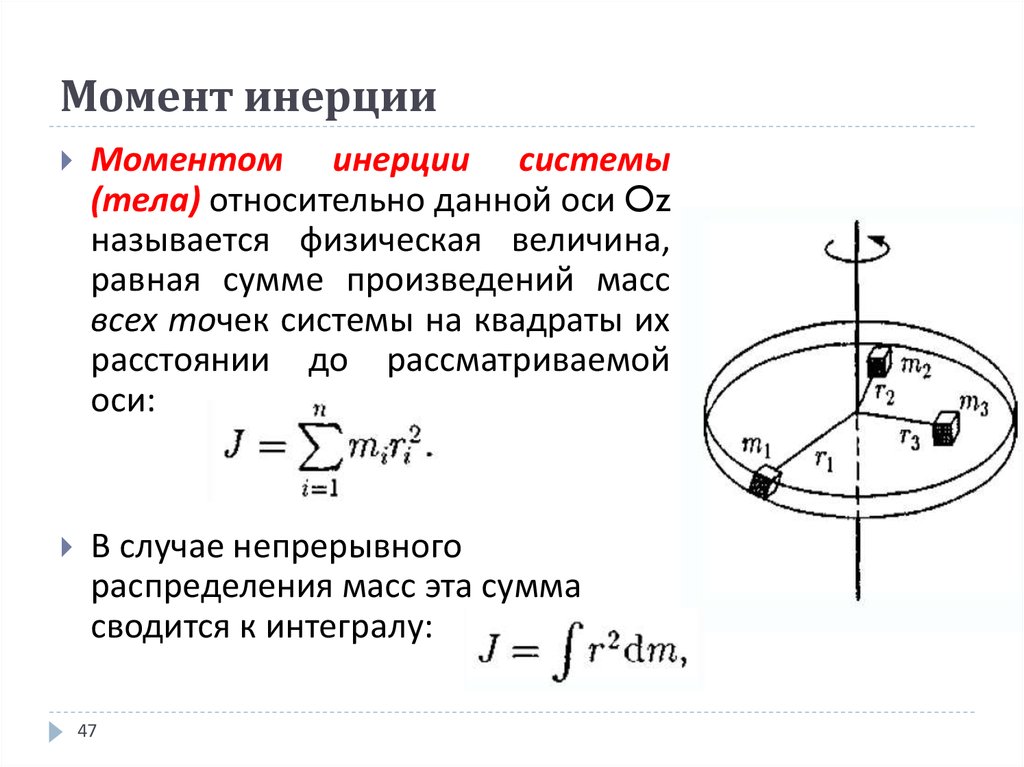 Подход включает в себя нахождение выражения для тонкого диска на расстоянии z от оси и суммирование по всем таким дискам.
Подход включает в себя нахождение выражения для тонкого диска на расстоянии z от оси и суммирование по всем таким дискам.