Формула момент инерции обруча: Помогите решить / разобраться (Ф)

Помогите решить / разобраться (Ф)

Сообщения без ответов | Активные темы | Избранное

Aden	Момент инерции обруча 01.01.2013, 22:09
10/02/10 268	Здраствуйте. Поздравлю всех форумчан с 2013г. Удачи и здоровья. Прошу помочь разобраться с задачкой. Определить момент инерции стального маховика относительно оси вала. Радиусы R1=6м, R2=4м. Дан обруч со спицами. Количество спиц равно 24. Масса каждой спицы m1=20г, масса обруча m2=300г, длина втулки равна 0,02 м. Спицы и обруч считать тонкими. http://restoran-modern.by/moment_in.jpg

kw_artem	Re: Момент инерции обруча 02.01.2013, 00:02
17/01/12 445	Обруч = окружность, Спица = тонкий стержень, поэтому ваша формула: Момент инерции = момент инерции окружности относительно ее центра + 24 момента инерции тонкого стержня относительно конца стержня. Так как все стержни одинаковые, то в последнем слагаемом можно просто взять этот момент для одного стержня и умножить на 24. — 02.01.2013, 01:04 — Формулы мом.инерции для окружности и стержня можете в Википедии подсмотреть.

larkova_alina	Re: Момент инерции обруча 02.01.2013, 00:20
20/04/12 250	– момент инерции относительно некоторой оси. Данный интеграл – это интеграл по объему. Отсюда и надо плясать. Еще важный момент. Момент инерции является аддитивной величиной. kw_artem , думаю нужно найти нужные моменты инерции, исходя из определения.

Aden	Re: Момент инерции обруча 02.01.2013, 13:26
10/02/10 268	А зачем в задаче дана длина втулки ?

kw_artem	Re: Момент инерции обруча 02. 01.2013, 19:47
17/01/12 445	А где эта длина втулки на рисунке? Не длина ли это окружности внутреннего отверстия?

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 5 ]

Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Вычисление момента инерции некоторых тел

J = ;

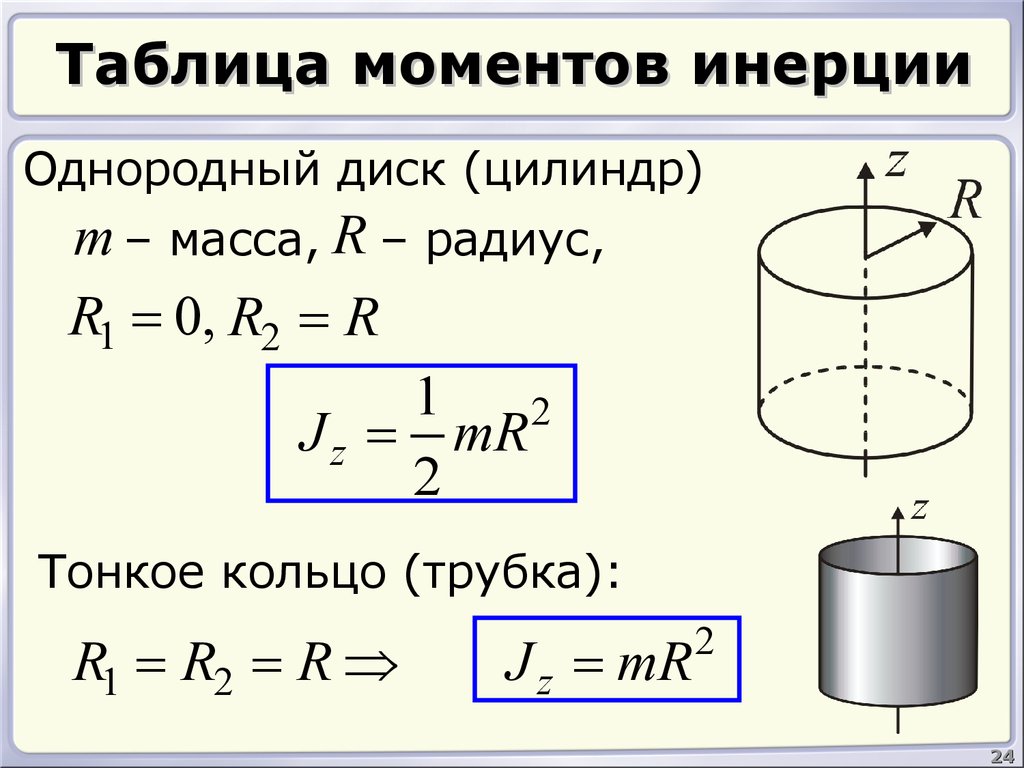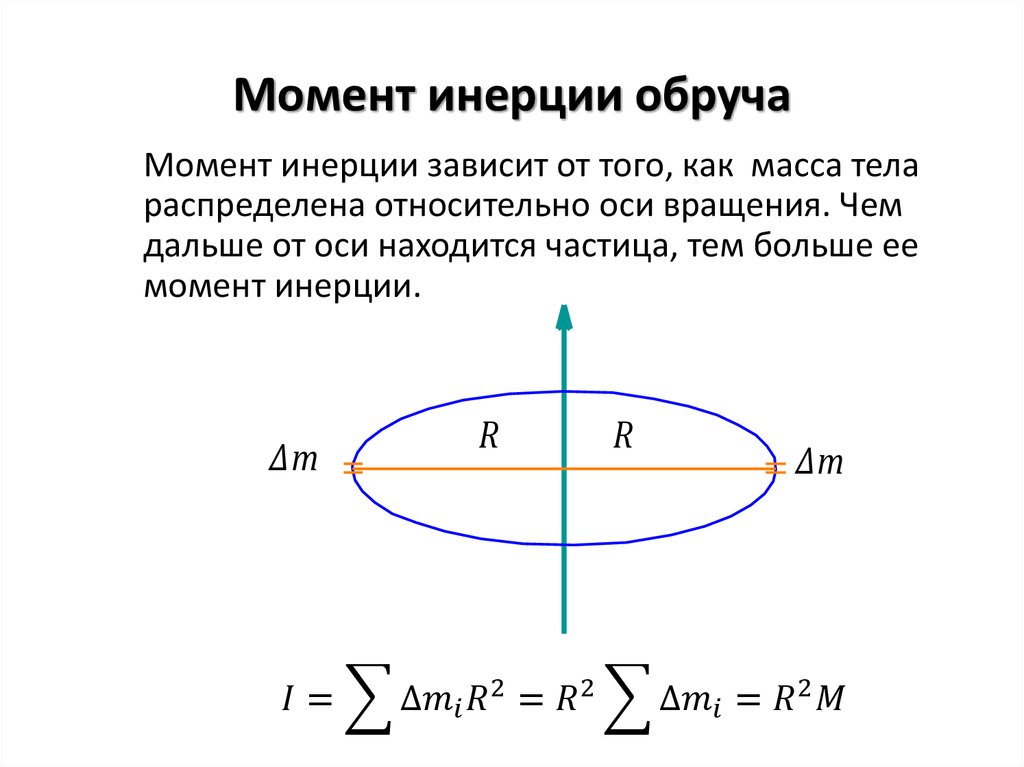
1. Момент инерции однородного обруча относительно оси, перпендикулярной к плоскости обруча и прохо­дящей через его центр

.

Будем считать толщину обруча посто­янной, разобьем обруч на малые элементы m_i;. Момент инерции относительно оси вы­разится выражениями ,

;

2. Момент инерции стержня относительно оси, перпен­дикулярной стержню и проходящей через центр масс и через один из концов стержня.

Разобьем стержень на малые элементы. Момент инерции относи­тельно оси одной половины стержня равен , а всего стержня,.

Если S – сечение стержня,  – плотность материала, то m = Sr;

J_C=2

Sr_i²r=2Sr_i²r в пределе операция суммирования переходит в интегрирование ;

Так как m = Sl – масса стержня, то момент инерции стержня относительно центра

J_C = ;

Момент инерции шара

Момент инерции сплошного цилиндра или диска

Момент инерции тела зависит от формы тела, относительно какой оси вращается тело и от распределения массы по объему тела.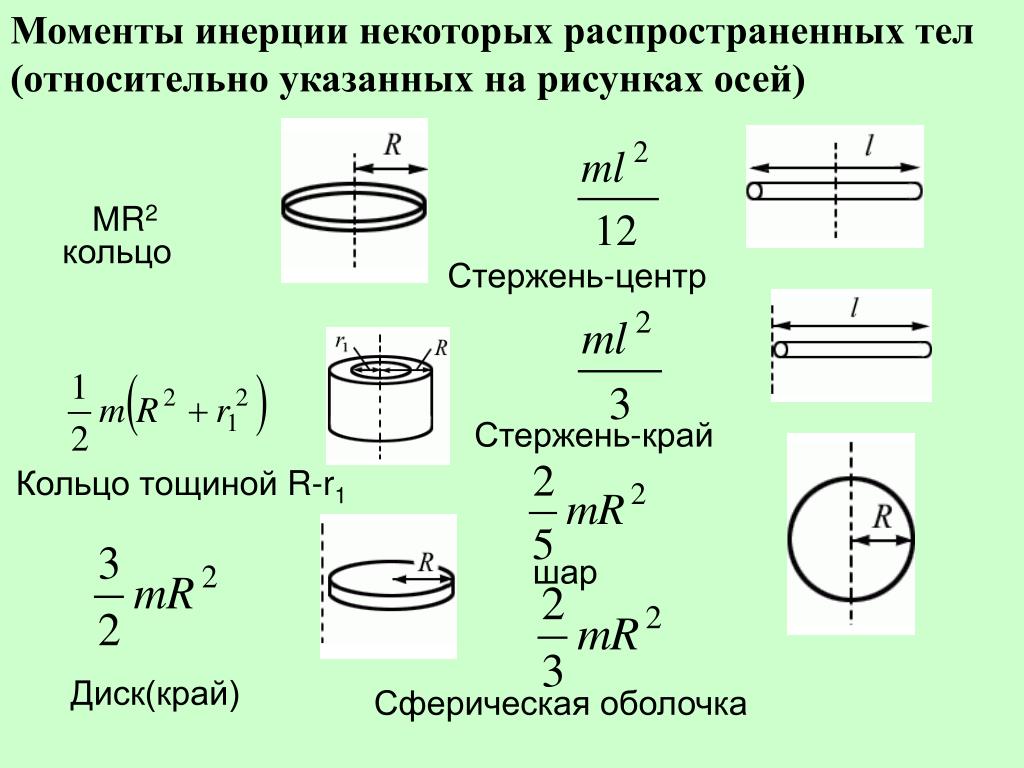

Теорема Штейнера: Момент инерции тела J относительно произвольной оси равен моменту инерции J_C относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела m на квадрат расстояния между осями d.

2. Кинетическая энергия вращающегося твердого тела.

1. Работа внешних сил при вращении твердого тела.

Рассмотрим теперь вращение тела с энергетической точки зрения. Допустим, что в некоторой точке тела приложена сила (в плоскости, перпендикулярной оси вращения), направление кото­рой совпадает с вектором линейной скорости этой точки. Поэтому речь идет о силе = _.

Элементарная работа этой силы равна

dA = F_ds,

где ds — элемент дуги окружности, связанный, как известно, с ее радиусом и углом поворота следующим образом:

dS = rd;

Тогда

dA = F_rd или

dA = Md .

Если М = const, то при повороте тела на конечный угол , формула для работы имеет вид

A = M;

Найдем теперь кинетическую энергию вращающегося тела. Очевидно, эта энергия должна быть равна сумме кинетических энергий отдельных материальных точек, т.е.

W_К = ,

_i = r_i и, принимая во внимание, что момент инерции тела относительно оси вращения

W_K =

Сравнивая полученное выражение с выражением для кине­тической энергии тела, движущегося поступательно W_K = , приходим к выводу, что момент инерции вращательного движе­ния – мера инертности тела.

Работа А, совершенная моментом внешних сил на протяжении угла поворота  = ₂ – ₁, связана с изменением кине­тической энергии вращения тела следующим образом

A = ;

где ₂ и ₁— угловые скорости тела в моменты, когда его угловые координаты равны соответственно ₂ и ₁.

В случае, например, скатывающегося цилиндра с наклонной плоскости без скольжения энергия движения складывается из энергии поступательного движения и энергии вращения

W_K = +

где т — масса катящегося тела; _C — скорость центра масс тела;

J_c — момент инерции тела относительно оси, проходящей через его центр масс;  – угловая скорость тела.

5. Элементы механики жидкостей и газов.

1. Давление в жидкости и газе.

Молекулы газа, совершая беспорядочное, хаотическое дви­жение, не связаны или слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стре­мятся разлететься во все стороны, заполняя весь предоставленный им объем, т.е. объем газа определяется объемом того сосуда, кото­рый газ занимает.

Как и газ, жидкость принимает форму того сосуда, в кото­рый она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.

Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинако­выми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика — раздел механики, изучающий равновесие и дви­жение жидкостей и газов, их взаимодействие между собой и обтекаемыми или твердыми телами — использует единый подход к изучению жидкостей и газов.

В механике жидкости и газы рассматриваются как сплош­ные, непрерывно распределенные тела в занятой ими части про­странства.

Плотность жидкости мало зависит от давления и во многих задачах можно пользоваться понятием несжимаемой жид­кости — жидкости, плотность которой всюду одинакова и не из­меняется со временем.

Жидкости имеют следующие наиболее характерные свойства.

Типичные жидкости (вода, бен­зин, спирт и т.п.) не имеют трения покоя, частицы их очень подвижны.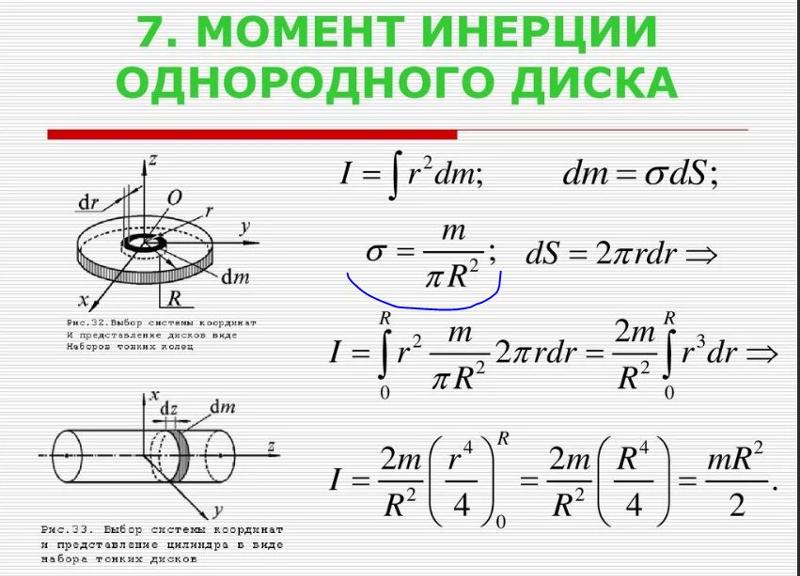 В других жидкостях имеется вязкость (внутреннее трение) — это мед, масло, вар и т.п. Однако при продолжитель­ном действии силы частицы вязкой жидкости тоже становятся подвиж­ными. Это свойство выражается так: жидкости не имеют упругости формы, для них модуль сдвига равен нулю.

Практически все жидкости не­сжимаемы. Это значит, что для них коэффициенты сжатия имеют очень малые значения. Следовательно,

приближенно можно считать все жид­кости невязкими и несжимаемыми: такие жидкости назы­ваются идеальными.

[P]=Па=н/м²

Действие силы тяжести приводит к возникновению разности давлений между горизон­тальными слоями жидкости находящимися на различной глубине. Разность сил давления в слоях АВ и СД (рис. 1.27) равна весу вертикального столба жидкости с основанием S и высотой h₁. При поперечном сечении S столба жидкости, его высоте h и плотности  сила давления на слой находящийся на глубине h находится по формуле:

F =ghS, а давление на нижнее основание

_{давление столба жидкости}

_{(1. 2)}

Если давление на поверхности P₀, то в любом го­ризонтальном слое давление постоянно и будет зависеть от глубины слоя АВ:

_(1.2)

Согласно формуле (1.82) сила давления на нижние слои жид­кости будет больше, чем на верхние, поэтому на тело, погружен­ное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), дей­ствует со стороны этой жидкости (газа) направленная вверх вы­талкивающая сила, равная весу жидкости (газа) вытесненной телом.

_(1.2)

где — плотность жидкости,V — объем погруженного в жид­кость тела.

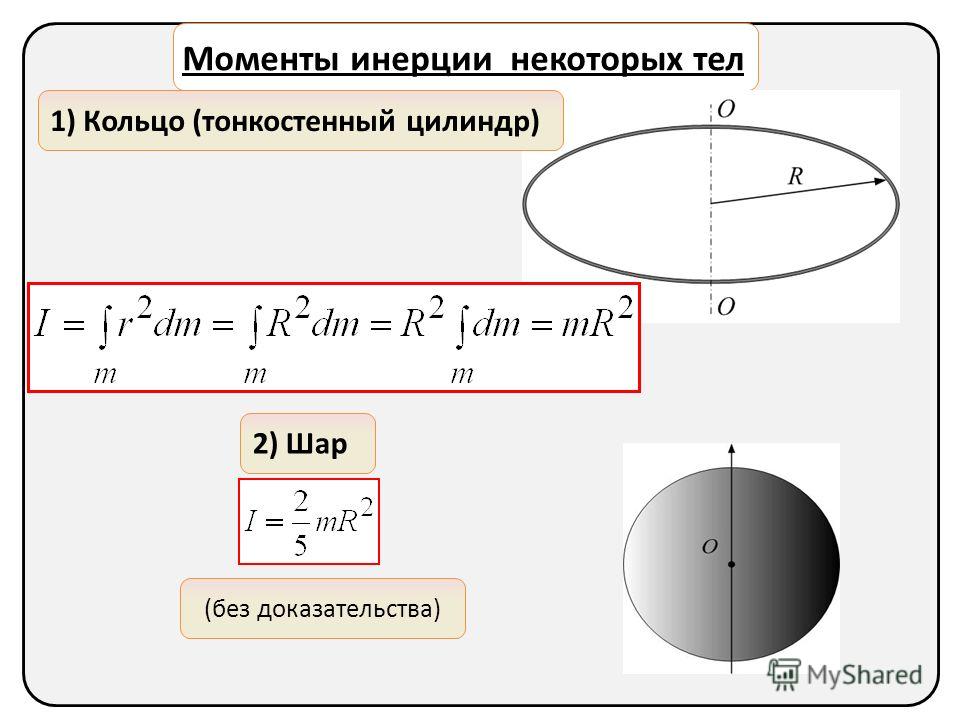
домашнее задание и упражнения – Момент инерции тонкого круглого обруча

спросил 6 лет, 2 месяца назад

Изменено 6 лет, 2 месяца назад

Просмотрено 4к раз

$\begingroup$

Почему тонкий круглый обруч радиуса $r$ и массы $m$ имеет следующие моменты инерции? 92$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.