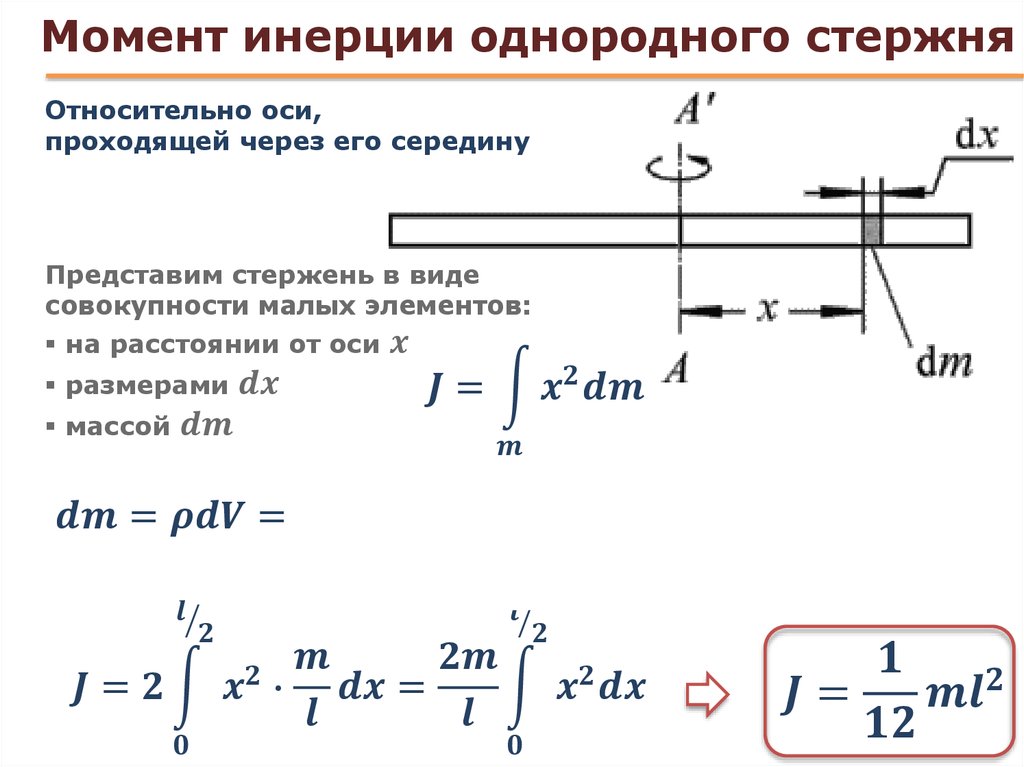
Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр Калькулятор
✖Масса тела – это количество вещества в теле независимо от его объема или действующих на него сил.ⓘ Масса тела [M] | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Длина стержня – это размер стержня от одного конца до другого конца (длина стержня). | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Момент инерции — это мера сопротивления тела угловому ускорению относительно данной оси. |
Грамм квадратный сантиметрГрамм квадратный миллиметрКилограмм квадратный сантиметрКилограмм квадратный метрКилограмм квадратный миллиметрКилограмм-сила, метр в квадрате, секундаУнция квадратный дюймУнция-сила, дюйм в квадрате, секундаФунт квадратный футфунт квадратный дюймФунт-сила-фут-квадрат-секундаФунт-сила, дюйм в квадрате, секундаСлаг Квадратный фут |
⎘ копия |
👎
Формула
сбросить
👍
Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.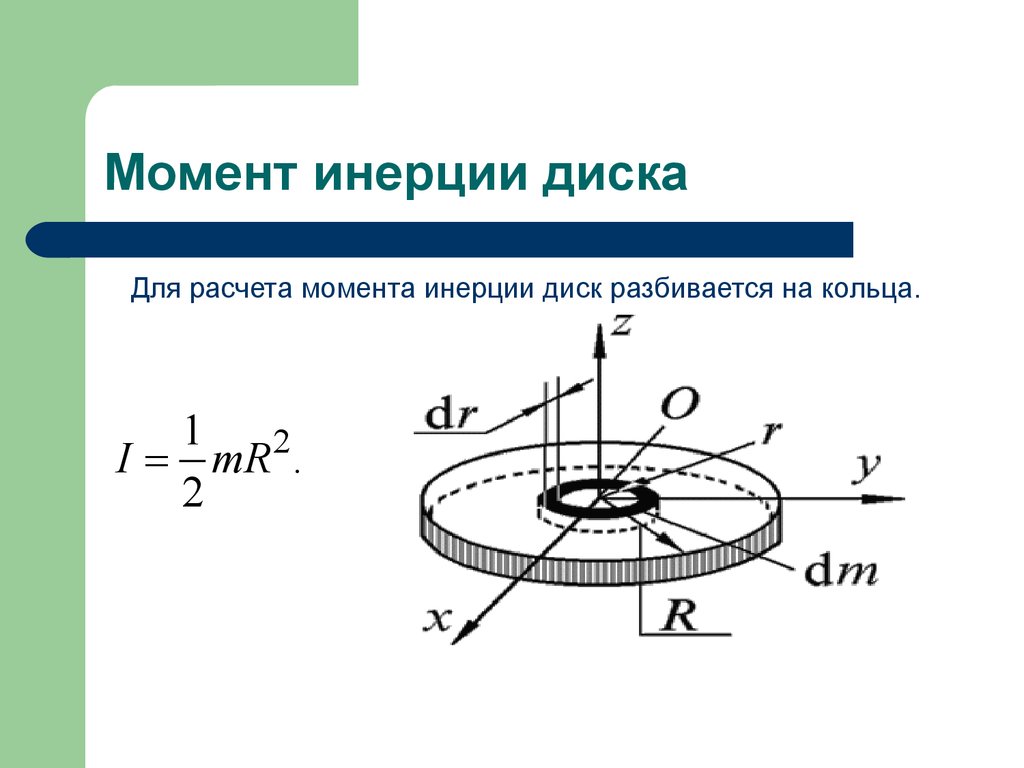 2))/12
2))/12
Почему важен момент инерции?
Это неотъемлемое свойство материи. При вращательном движении момент инерции тела является мерой его инерции. Чем больше момент инерции, тем больше крутящий момент, необходимый для создания в нем заданного углового ускорения.
Share
Copied!
Момент инерции различных тел. Теорема Штейнера, страница 2
j | F | l | M |
p/2 | |||
p | |||
3p/2 | |||
2p |
Проделайте эти
измерения для углов j, равных 180о,
270о, 360о. Полученные данные занесите в таблицу.
Полученные данные занесите в таблицу.
По полученным данным постройте график зависимости М от j.
Тангенс угла наклона прямой будет численно равен модулю кручения
Далее следует измерить период колебаний системы с исследуемым телом. Для измерения периода используется устройство называемое световым барьером. Оно состоит из источника света и приемника света. На ось пружины насажена непрозрачная полоска, размещаемая между источником и приемником света. При колебаниях эта пластинка периодически перекрывает луч света. Световой барьер может работать в нескольких режимах, которые устанавливаются с помощью переключателя. Он может измерять или число колебаний, или полпериода, или целый период колебаний. Удобнее использовать режим измерения периода колебаний. Для этого переключатель устанавливают в положение, при котором на индикаторе высвечиваются четыре точки.
Процедура измерения периода следующая.
1. Насадите
на ось пружины исследуемое тело.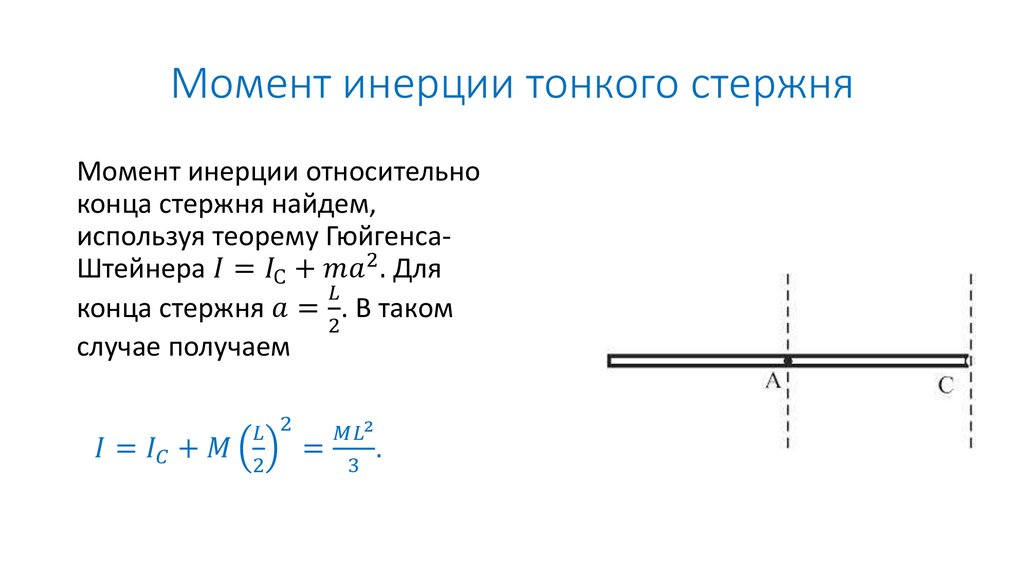
2. Расположите всю систему так, чтобы непрозрачная полоска перекрывала луч света от источника.
3. Закрутите пружину на 180о и отпустите.
4. После того как на индикаторе появится значение периода, запишите это значение и нажмите кнопку на световом барьере (обнулите показания индикатора).
5. Повторите измерения периода 5 – 10 раз.
6. Найдите среднее значение периода.
В данной работе можно выполнять несколько заданий.
А. Определение моментов инерции различных тел относительно оси, проходящей через центр симметрии.
1. Выберите определенное тело и насадите его на ось пружины.
2. Измерьте период колебаний системы описанным выше способом.
3. По измеренным D и T по формуле (9) вычислите экспериментальное значение момента инерции.
4. Измерьте радиус тела и определите его массу (взвесив тело).
5. По одной из формул (1 – 5) вычислите теоретическое значение момента инерции для данного тела.
Проведите
измерения для различных тел (по указанию преподавателя).
В. Изучение зависимости момента инерции от расстояния масс от оси вращения.
1. Насадите на ось пружины стержень с симметрично расположенными грузами.
2. Расположите грузы на ближайшем расстоянии от оси вращения. Измерьте расстояние r от оси вращения до центров грузов.
3. Измерьте период колебаний системы.
4. Последовательно смещайте грузы на 2 см и измеряйте период.
5. По формуле (9) рассчитайте момент инерции для каждого положения грузов.
6. Составьте таблицу.
r, (м) | ||||||
r2, (м2) | ||||||
T, (с) | ||||||
J, (кг. |
7. По данным таблицы постройте график зависимости J=f(r2).
8. Теоретическую формулу для момента инерции стержня с грузами можно записать в виде
Здесь Jст–момент инерции стержня, m –масса одного груза.
В параметрах J=f(r2) это уравнение прямой, не проходящей через начало координат. Отрезок, осекаемый экспериментальным графиком на оси ординат равен моменту инерции стержня Jст. Сравните это значение с теоретическим значением Jст .
Здесь m1 –масса стержня, l – длина стержня.
С. Проверка теоремы Штейнера.
1. Насадите
на ось пружины стержень без грузов. Ось пружины должна совпадать с центром
стержня.
2. Измерьте период колебаний и вычислите момент инерции Joформуле (9).
3. Сместите стержень на некоторое расстояние d от центра.
4. Измерьте период колебаний и вычислите момент инерции J .
5. Согласно теореме Штейнера
где l –длина стержня, m – масса стержня.
6. Измерьте массу стержня, его длину и расстояние d.
7. Вычислите теоретическое значение J по этой формуле и сраните его с экспериментальным значением J.
Что такое Момент инерции стержня? Расчет, пример
В этой статье мы изучим момент инерции стержня, а также примеры, расчет и т. Д. Давайте исследуем!
Что такое момент инерции стержня?
Попробуем разобраться в моменте инерции стержневых основ.
Момент инерции стержня Основы
Попробуем понять момент инерции стержня. Когда цилиндрический стержень вращается, мы можем сказать, совершает ли он угловое движение, и что мы хотим вычислить точную точку, где находится максимальная масса, можно сказать или предположить, что это будет ось вращения, от которой вращается все тело.
Но здесь мы все ошибаемся. Не обязательно думать, что массовый элемент стержня часто находится в центральной точке или оси, и именно здесь появляется момент инерции стержня.
Какой момент инерции пример расчета стержня основы- Как правило, когда стержень находится в угловом движении, элементы массы элемента обычно изменяются в чрезвычайно отличном месте от центра тела.
- Говоря техническими словами, момент инерции стержня представляет собой количественную сумму вращательной инерции (движения) стержня, т. е. сопротивления, оказываемого вращающимся телом в пределах фронта крутящего момента, который можно просто назвать вращающей силой.
- Ось вращения тела будет внешней или внутренней, или будем считать ее ограничением или изменением. Хотя момент инерции часто задается с осью вращения тела в гораздо более простом состоянии.
Момент инерции стержня Определение
Момент инерции стержня может быть определен как сумма произведений, которые мы получаем из всей массы каждого прикрепленного элемента стержня, и затем это целое умножается на квадрат частицы относительно ее расстояния от центра.
- Момент инерции стержня, который обычно имеет форму, часто определяется с помощью более простых математических формул и обычно упоминается как исчисление.
- В случае анонимных форм тел мы можем определить момент инерции опытным путем.
- Одна из наиболее часто используемых экспериментальных процедур устанавливает связь между временем вращения и, следовательно, массой подвешенного элемента.
Момент инерции стержня – ось проходит через центр
Момент инерции стержня, ось которого проходит через центр стержня, имеющего массу (M) и длину (L), обычно выражается как; I = (1/12) ML 2
Как определить момент инерции стержня – ось, проходящая через центр?
Мы должны помнить некоторые вещи; мы должны представить, что стержень расколот на множество бесконечно тонких кусочков. Нам нужно определить переменную для суммирования. В первом случае нужно считать, что стержень обладает бесконечным числом точечных масс.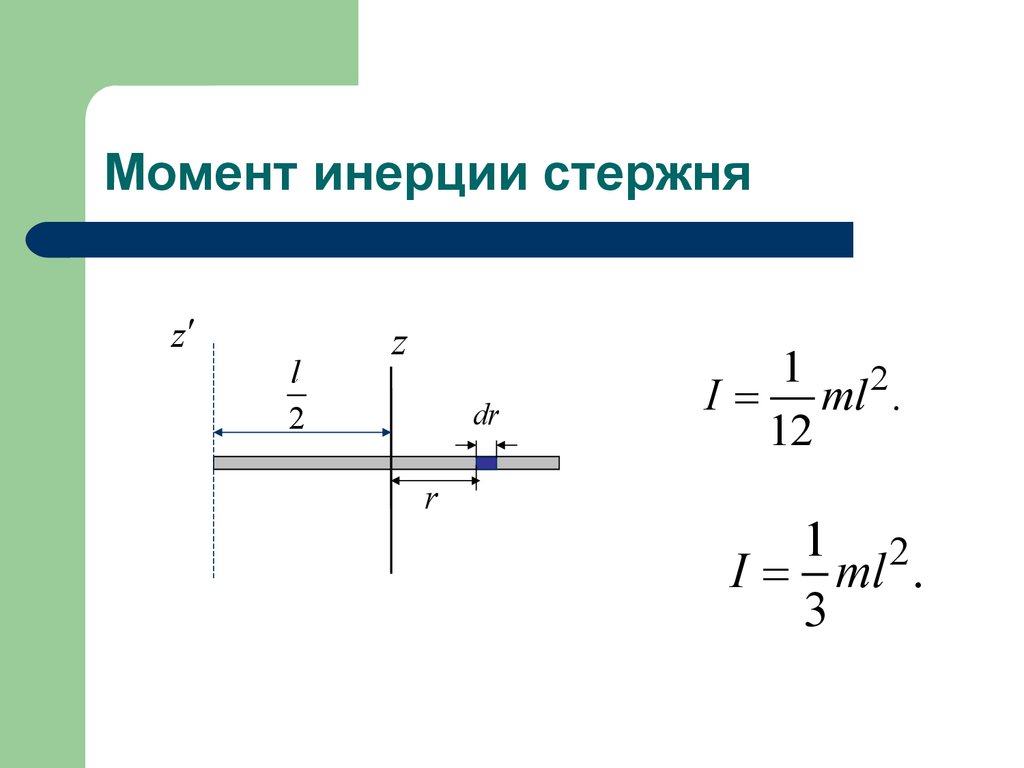 Все их выездные произведения получаются путем умножения квадрата зазора от оси. Нам даже нужно рассмотреть чрезвычайно малый элемент длины dl, соответствующий массе dm.
Все их выездные произведения получаются путем умножения квадрата зазора от оси. Нам даже нужно рассмотреть чрезвычайно малый элемент длины dl, соответствующий массе dm.
Кроме того, после того, как мы изобразим или обозначим начало координат в центре масс, лежащем на пути оси, мы увидим, что расстояние от стержня слева равно -L/2, в то время как разрыв от начала координат справа от него равен +L/2. Теперь нам нужно переключить значение «dm» в выражении; Момент инерции стержня:
- I = O ∫ M l 2 дм
Теперь, поскольку стержень цилиндрический и однородный, можно сказать, что его линейная плотность одинакова по всей длине.
- Линейная плотность = Масса на единицу длины
- Линейная плотность стержня (M/L) = Линейная плотность наименьшей части (дм/дл) [поскольку плотность одинакова по всему стержню]
Итак, мы можем написать,
- М/л = дм/дл
- или, dm = (M/L) dl
Момент инерции стержня:
- I = O ∫ M l 2 дм
- I = -L/2 ∫ L/2 l 2 (M/L) dl [как dm = (M/L) dl ]
- I = M/L -L/2 ∫ L/2 l 2 dl
- I = M / L [l 3 /3] -L/2 L/2
Здесь переменной смешивания является длина (dl). Границы изменились с M на желаемую долю L.
Границы изменились с M на желаемую долю L.
- I = M/3L, [(L/2) 3 – (-L/2) 3 ]
- I = M/3L [L 3 /8 + L 3 /8]
- I = (М/3л) . 2л 3 /8
- I = (М/3л) . L 3 /4
- I = (1/12) ML 2
Момент инерции стержня – ось через конец
Когда ось стержня проходит через лучшую часть стержня, для объяснения момента инерции можно использовать другую формулу. В этом случае мы используем; I = ⅓ ML 2
Как определить момент инерции стержня – ось через наконечник?
Для расчета, когда ось находится вверху, мы должны нарисовать начало координат на этом отдельном конце. Часто используется то же выражение, но с другим пределом. Поскольку ось опирается на кончик, предел, используемый при интегрировании, равен 0,9.0003 в какой момент оси инерционной стержни до конца кончика
I = O ∫ M L 2 DM
I = O ∫ L L 2 (м/л) DL L 2 (м/л) интеграция;
- L (конец) = (M/L) O ∫ L l 2 dl
- L (конец) = (M/L) [l 3 /3] 0 L
- L (конец) = (M/3L) [(L 3 /3) – (/3)]
- I (конец) = (M/3L) [ L 3 – 0 3 ]
- L (конец) = (⅓) ML 2
В качестве альтернативы можно использовать теорему о параллельных осях для определения выражения. У нас есть;
У нас есть;
- Iпараллельная ось=Iцентр масс+Md 2 .
- I = L (см) + Md 2
Теперь, если мы поместим значение в данное уравнение, оно станет таким:
- L (конец) = (1/12) ML 2 + M (L/2) 2
- L (конец) = (1/12) ML 2 + ( ¼) ОД 2
- L (конец) = (⅓) ML 2 .
Расчет момента инерции стержня
Вопрос № 1 Момент инерции стержня M и L Дано
Задача : Цилиндрический стержень вращается вокруг оси. Ось перпендикулярна его длине, проходящей через один из его концов. Каков момент инерции этого стержня? Где Масса, m = 5 кг, Длина, L = 2,5 м.
Решение: Приведены входные данные:
- Масса, m=5 кг
- Длина, Д = 2,5 м
Узнать: Момент инерции, I =?
Расчет : Мы уже узнали из нашего расчета момента инерции для стержня,
Момент инерции, I = 1/12 ML 2
Теперь применим теорему о параллельных осях, момент инерции стержня относительно параллельной оси, проходящей через один конец стержня, можно записать как
- I’ = I + M (L/2) 2
- I’ = 1/12 ML 2 + M (L/2) 2
- I’ = 1/12 ML 2 + ¼ ML 2
- I’ = 4/12 ML 2
- I’ = 1/3 ML 2
Теперь представим значение m = 5 кг и L = 2,5 м
- I’ = 1/3 x 5 x 2,5 2
- I’ = 10,4 кг·м 2
Следовательно, это значение момента инерции этого стержня.
Вопрос № 2 Момент инерции стержней и кинетическая энергия вращения – M, L и ω Дано
Задача : Однородный цилиндрический стержень массой и длиной 3 кг и длиной 1,5 м соответственно вращается вокруг оси. Ось перпендикулярна его длине, проходящей через один из его концов. Мгновенная угловая скорость цилиндрического стержня 70 град/с
- Каков момент инерции этого стержня?
- Каково значение кинетической энергии вращения?
Решение: Исходные данные:
- Масса, m =3 кг
- Длина, L = 1,5 м
- Угловая скорость, ω =70 град/с
Узнать:
- Момент инерции, I =?
- Вращение Кинетическая энергия, К.Э =?
Расчет : Мы уже узнали из нашего расчета момента инерции для стержней,
Момент инерции, I = 1/12 ML 2
Теперь применим теорему о параллельной оси, момент инерции стержня о параллельная ось, проходящая через один конец стержня, может быть записана как
- I’ = I + M (L/2) 2
- I’ = 1/12 ML 2 + M (L/2) 2
- I’ = 1/12 ML 2 + ¼ ML 2
- I’ = 4/12 ML 2
- I’ = 1/3 ML 2
Теперь представим значение m = 3 кг и L = 1,5 м
- I’ = 1/3 x 3 x 1,5 2
- I’ = 3,38 кг·м 2
Следовательно, это значение момента инерции этого стержня. Теперь у нас есть угловая скорость в град/с, поэтому мы должны сначала преобразовать ее в рад/с.
Теперь у нас есть угловая скорость в град/с, поэтому мы должны сначала преобразовать ее в рад/с.
- 180 град/с = π рад/с
- 1 град/с = π/180 рад/с
- 70 град/с = π/180 x 70 рад/с = 1,22 рад/с
- ω = 1,22 рад/с
Что такое кинетическая энергия вращения? Мы знаем формулу,
Вращение Кинетическая энергия, K.E
- K.E = ½ I’ ω 2
- K.E = ½ x 3,38 x 1,22 2
- КЭ = 2,52 Дж
Следовательно, значение кинетической энергии вращения равно 2,52 Дж.
Вопрос № 3 Момент инерции стержня при его изгибе – M, L и заданный угол
Задача : Однородный цилиндрический стержень массой и длиной M кг и L м соответственно вращается вокруг центра своей оси. Теперь, если стержень согнут в середине под углом 60 градусов, каков будет момент инерции того же стержня относительно той же оси?
Решение: Исходные данные:
- Масса = M кг
- Длина = L м
- Угол между двумя половинками = 60 град.

Узнать: Момент инерции, I =?
Расчет : Мы уже узнали из нашего расчета момента инерции стержней,
Момент инерции, I = 1/12 ML параллельная ось, проходящая через один конец стержня, может быть записана как
- I’ = I + M (L/2) 2
- I’ = 1/12 ML 2 + M (L/2) 2
- I’ = 1/12 ML 2 + ¼ ML 2
- I’ = 4/12 ML 2
- I’ = 1/3 ML 2
Теперь, если стержень согнуть пополам,
- Длина каждой части L’ = L/2 м
Итак, каким будет момент инерции у этих изогнутых Стержней?
- I’’ = 2 x I’
- I’’ = 2 x 1/3 M’L’ 3
- I’ = 2 x 1/3 M x (L/2) 3
- I’ = 2 x 1/3 М x Д 3 /8
- I’ = 1/12 ML 3
Следовательно, момент инерции этого стержня станет 1/12 ML 3 кг·м 2
Заключение
Следовательно, мы узнали основы момента инерции стержней, а также научились вычислять это значение вместе с расчетом образца.
Момент инерции прямоугольника
Калькулятор момента инерции прямоугольника для расчета момента инерции площади, модуля сечения, площади поперечного сечения и радиуса вращения прямоугольного сечения.
Стальные прямоугольные стержни соответствуют стандарту ASTM A108 «Стандартная спецификация». для стальных стержней, углеродистых и легированных, холоднодеформированных», A36/A36m «Стандартный Спецификация для углеродистой конструкционной стали» и ASTM A276 «Стандартная спецификация для стержней и профилей из нержавеющей стали».
Калькулятор момента инерции прямоугольника:
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота [В] | ||
| Ширина [В] | ||
| Длина [л] | ||
| Плотность [п] | 93 | |
| | ||
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения [A] | — 92 | |
| Масса [М] | — | кгфунт |
| Второй момент площади [I xx ] | — | 94|
| Второй момент площади [I yy ] | — | |
| Модуль упругости [S xx ] | — | мм^3см^3дюйма^3фута^3 |
| Модуль упругости [S yy ] | — | |
| Радиус вращения [r x ] | — | |
| Радиус вращения [r y ] | — | |
| Расстояние до центра тяжести в направлении x [x c ] | — | |
| Расстояние до центра тяжести в направлении Y [y c ] | — | |
Примечание.

 ⓘ Длина стержня [Lrod]
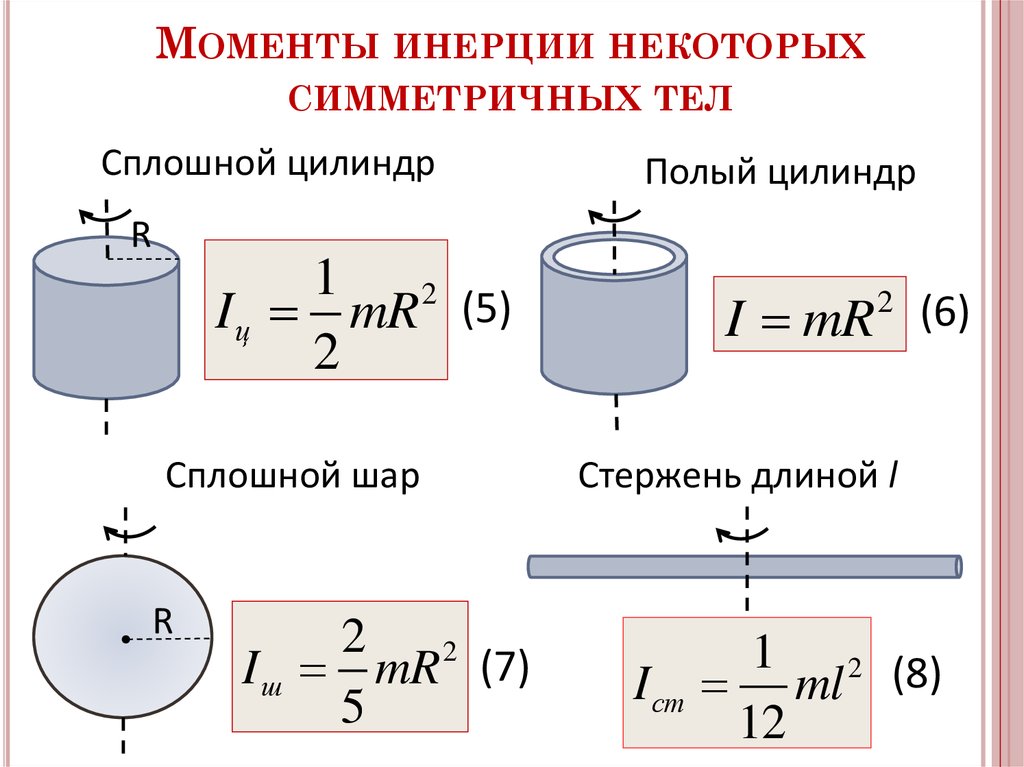
ⓘ Длина стержня [Lrod] ⓘ Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр [I]
ⓘ Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр [I]
 *м2)
*м2)