Формула момент инерции тела: Корпоративный портал ТПУ - Ошибка - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Формула момента инерции, J

Момент инерции тела

Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек () (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний () от них до оси вращения:

Если тело считают непрерывным, то суммирование в выражении (1) заменяется интегрированием, массы элементов тела обозначают как :

где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Если тело является однородным:

Момент инерции материальной точки

Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:

где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной.

Момент инерции является аддитивной величиной.

Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции () отдельных точек:

Примеры моментов инерции некоторых тел

Момент инерции тонкого стержня вращающегося около оси, проходящей через его один конец и перпендикулярно стержню, равен:

Момент инерции прямого круглого конуса, массы высоты h и радиуса r вращающегося около своей оси:

Момент инерции однородного твердого параллелепипеда, c геометрическими параметрами и массой m вращающегося относительно своей самой длинной диагонали, вычисляют по формуле:

Момент инерции тонкой прямоугольной пластины массы m, ширины w и длины d, вращающейся относительно оси, которая проходит через точку пересечения диагоналей этого прямоугольника перпендикулярно плоскости пластины:

где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.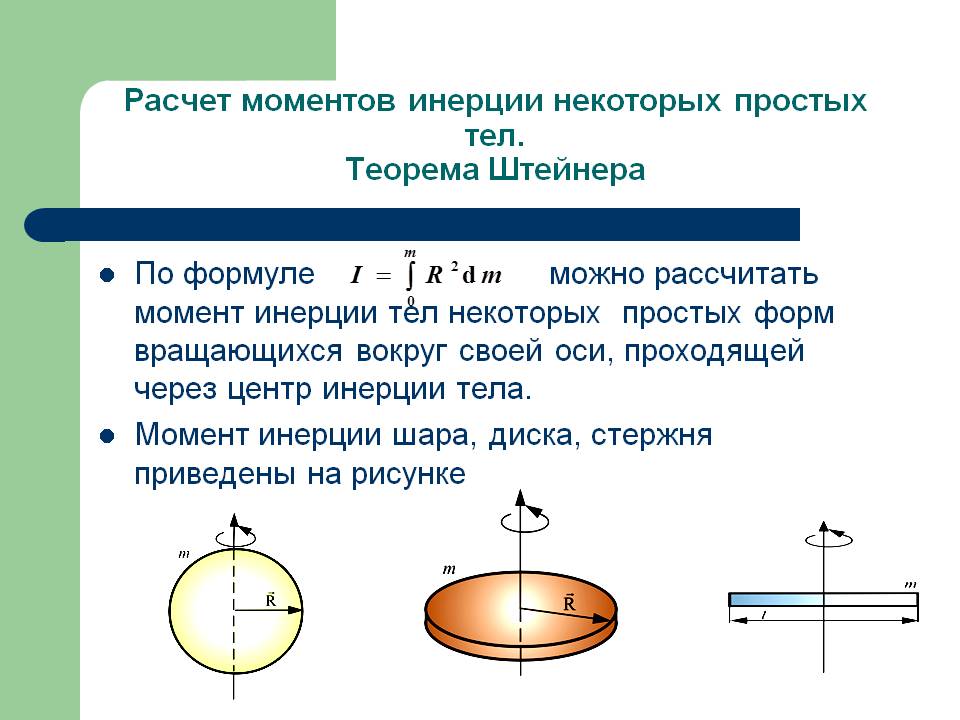

Примеры формул для вычисления моментов инерции других тел можно посмотреть в разделе «Момент инерции». В этом же разделе можно ознакомиться с теоремой Штейнера.

Примеры решения задач по теме «Момент инерции»

Новосибирский государственный архитектурно-строительный университет – Сибстрин

Студенты-гидротехники посетили с экскурсией гидроузел на реке Тула

В период обучения на втором курсе студенты кафедры гидротехнического строительства, безопасности и экологии НГАСУ (Сибстрин), обучающиеся по профилю «Гидротехническое строительство», проходят летнюю технологическую практику, которая дает представление о специфике их будущей профессии. В рамках данной практики студенты 271 группы посетили с обзорной экскурсией гидроузел на реке Тула. Этот объект недавно был реконструирован и отремонтирован. Казалось бы, Тула – небольшая речка, но весной там бывают очень высокие паводки. Уровень воды поднимается на несколько метров, возрастает нагрузка на плотину, во много раз увеличиваются расходы воды через водосливную плотину, которые могут нанести большой вред прилегающей территории.

Идет набор в сборную команду НГАСУ (Сибстрин) по киберспорту

Студент, внимание! Если ты увлекаешься киберспортом, подавай заявку на вхождение в состав команды НГАСУ (Сибстрин)! Киберспорт – это быстро развивающаяся мировая индустрия, в которой геймеры участвуют в командных и индивидуальных соревнованиях по компьютерным играм. Если у тебя есть опыт участия или желание попробовать свои силы в студенческом киберспорте и побеждать в своей любимой игре, то подавай заявку прямо сейчас! До следующего сезона Студенческой лиги Quazar еще 1-2 месяца, а до Всероссийской киберспортивной студенческой лиге более полугода, однако прием заявок по дисциплинам Dota 2, CS:GO, Hearthstone уже стартовал.

Повышение стипендии для успешных студентов-первокурсников набора 2021!

Ученый совет НГАСУ (Сибстрин) принял решение ОБ УВЕЛИЧЕНИИ РАЗМЕРА СТИПЕНДИИ НА100 % С 1 сентября 2021 года: студентам бакалавриата и специалитета 1 курса в 1 семестре, поступившим в университет на бюджетной основе с суммой баллов ЕГЭ от 240 и выше (для студентов направления 07.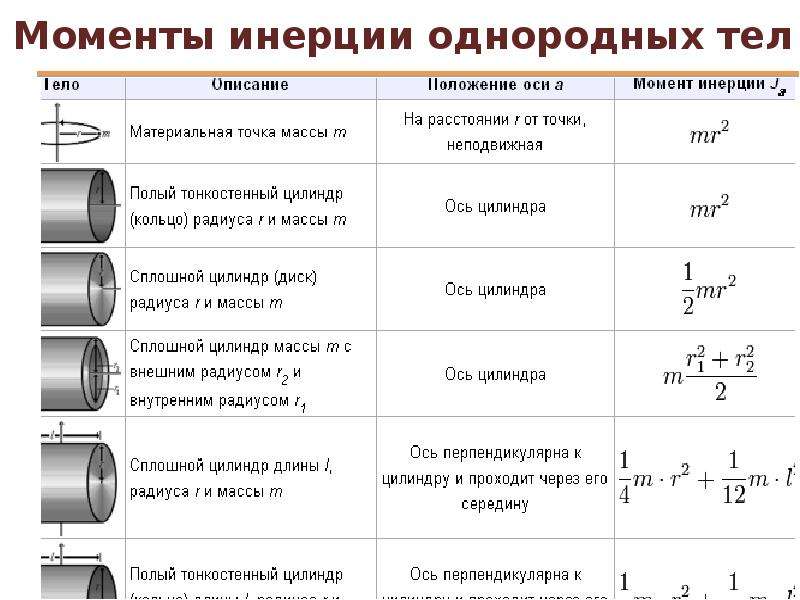

00.00 Архитектура – средний балл по ЕГЭ от 80 и выше). студентам бакалавриата и специалитета 1 курса в 1 семестре, поступившим в университет на бюджетной основе – победителям (призерам) заключительного этапа всероссийской олимпиады по общеобразовательным предметам. Таким образом, для перечисленных категорий студентов академическая стипендия составит 7400.

Второкурсники кафедры ТГиВ закрепляют теорию на технологической практике

В июле у студентов второго курса кафедры теплогазоснабжения и вентиляции НГАСУ (Сибстрин) состоялись мероприятия летней технологической практики. В процессе ее прохождения студенты получают необходимые практические навыки, без которых невозможно обойтись будущему специалисту. 21-22 июля 241 и 242 студенческие группы посетили с экскурсией ООО «Генерация Сибири». Это энергоснабжающаяяя организация строительного концерна «Сибирь», осуществляющая электро и теплоснабжение потребителей жилищной, социальной и производственной сферы в Первомайском районе Новосибирска.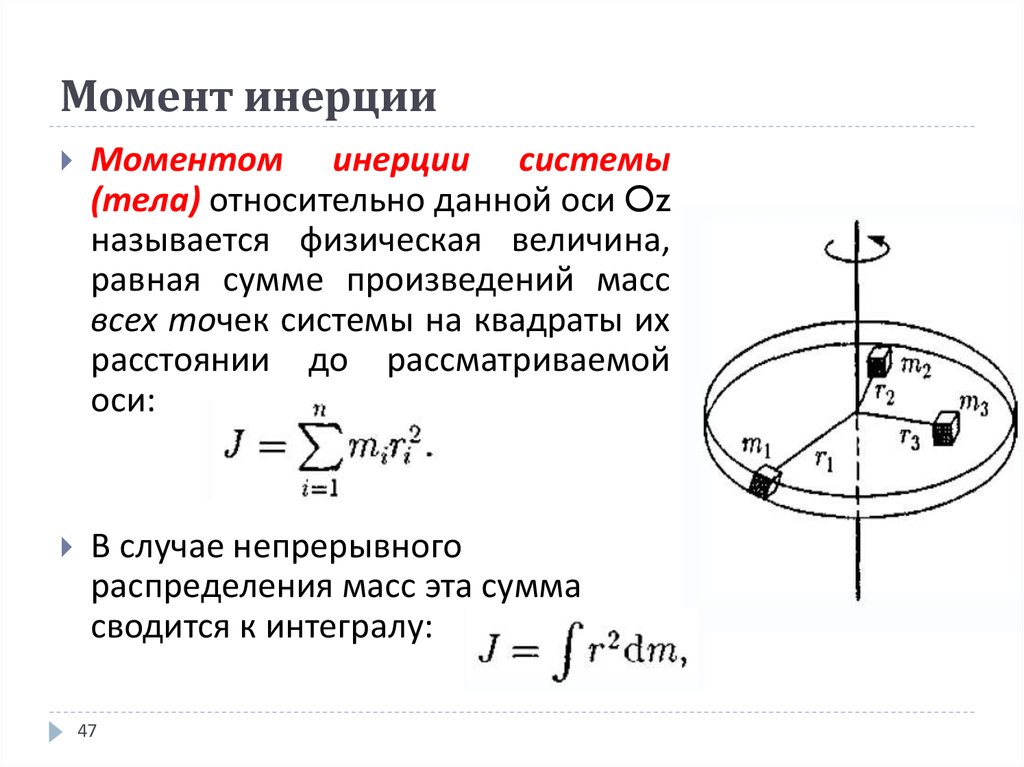

Целью поездки стало ознакомление с работой тепловой электрической станции.

лабораторная работа 109

Цель работы: Экспериментальное определение момента инерции диска методом крутильных колебаний.

Приборы и принадлежности: диск на упругой проволоке, секундомер, линейка, штангенциркуль, шары, цилиндры, технические весы.

Теоретическое введение

Как известно из динамики, момент инерции является физической величиной, характеризующей распределение масс в теле и являющейся мерой инертности тела при вращательном движении.

Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния до этой оси

Момент инерции твердого тела относительно некоторой оси ОО, проходящей через его центр масс, равен сумме моментов инерции всех точек тела относительно этой оси (рис. 1)

Момент инерции тела, плотностью r, вычисляется по формуле

где dV– элемент объема. Как видно из формул (1) и (2), момент инерции относительно данной оси, как и масса тела, не зависит от характера движения, а зависит от размеров, форм и плотности тела.

Если момент инерции относительно оси, проходящей через центр масс, равен J₀, то момент инерции тела относительно любой другой оси, параллельной первой, может быть определен на основании теоремы Штейнера

где m – масса тела, d – расстояние между осями.

Основной закон динамики вращательного движения имеет вид:

Момент импульса тела при вращательном движении вычисляют по формуле , тогда

где – величина суммарного момента внешних сил, действующих на тело, – угловая скорость тела. Если = 0, то = const. Таким образом, если момент сил, действующих на тело, равен нулю, т.е. система замкнута, то тело будет покоится или вращаться бесконечно долго, сохраняя постоянный момент импульса. Это утверждение, в сущности, является одной из формулировок закона сохранения момента импульса, то есть математически закон сохранения момента импульса запишется в виде

при

В случае вращательного движения момент инерции играет ту же роль, что и масса при поступательном движении, а угловая скорость – роль линейной.

Ниже приведена таблица 1, в которой сопоставлены величины и соотношения, являющиеся эквивалентными при поступательном и вращательном движении.

Таблица 1

Поступательное движение

Вращательное движение

Линейная скорость

Линейное ускорение

Масса m

Сила F

Импульс

Второй закон Ньютона:

Кинетическая энергия

Угловая скорость

Угловое ускорение

Момент инерции J

Момент силы M

Момент импульса

Основной закон динамики:

Кинетическая энергия

Описание рабочей установки и метода измерений

Момент инерции тела правильной геометрической формы может быть вычислен теоретически по формуле (2).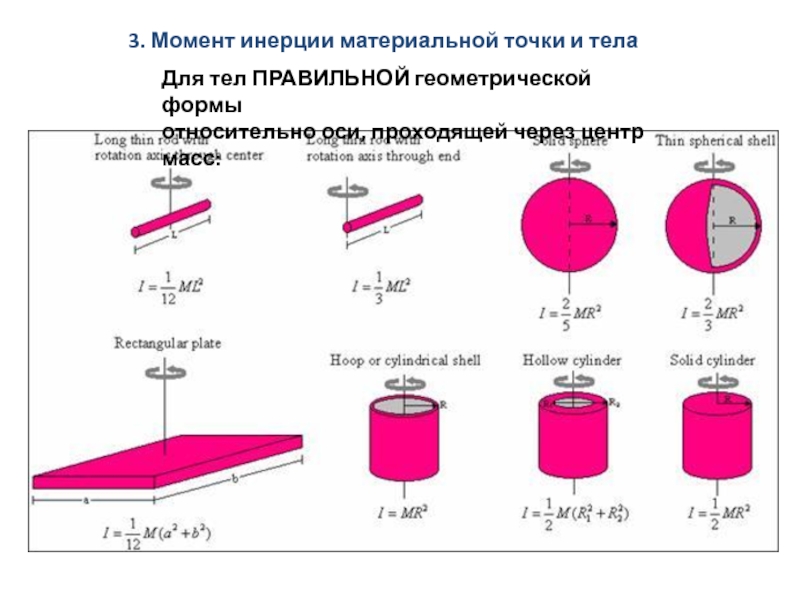 Если же тело имеет сложную форму (маховое колесо, коленчатый вал, винт и др.), то теоретическое определение его момента инерции представляет значительные трудности.

Одним из методов экспериментального определения момента инерции является метод крутильных колебаний. Подвесим испытуемое тело (диск 1) на упругой металлической проволоке 2 так, чтобы один конец проволоки проходил через центр масс тела, а другой был закреплен неподвижно в точке подвеса (рис.2). Если повернуть диск на небольшой угол около оси, совпадающей с осью проволоки, после чего предоставить его самому себе, то тело начнет совершать колебательное движение в горизонтальной плоскости. Вращательный момент М, закручивающий проволоку на угол a, равен

где D – модуль кручения материала проволоки. Знак минус показывает, что реакция сил упругости в проволоке, возрастающая с увеличением угла a, направлена в сторону, противоположную действию вращательного момента.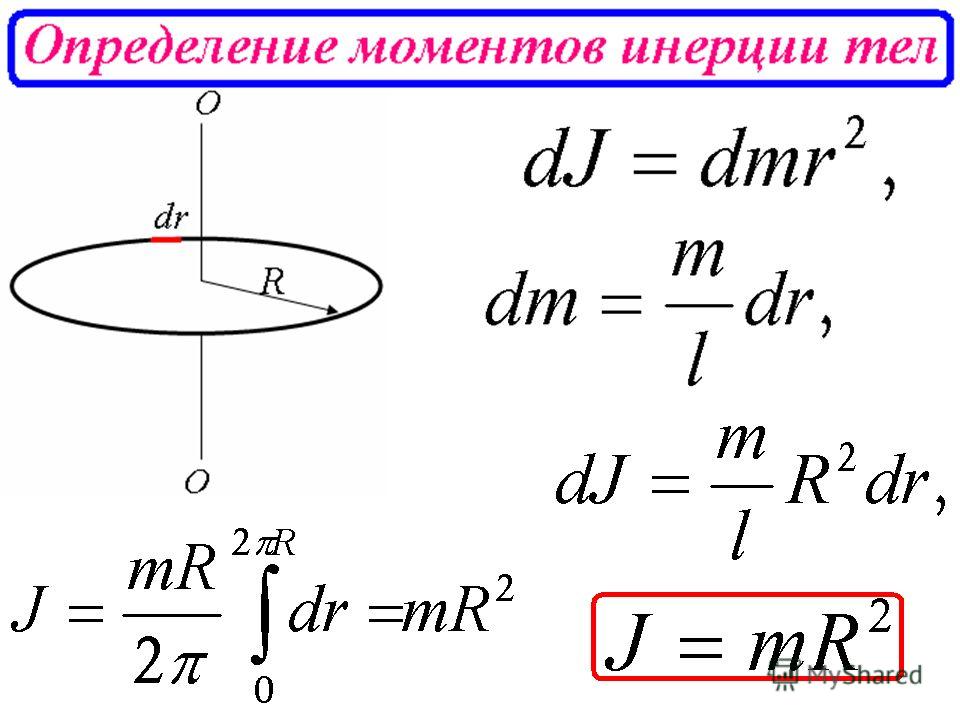

С другой стороны, из основного уравнения динамики вращательного движения (4) при J=const

где J – момент инерции тела относительно оси вращения, – угловое ускорение тела.

Из формул (5) и (6) имеем

Сравнивая с дифференциальным уравнением гармонических колебаний

приходим к выводу, что угловая частота крутильных колебаний w может быть определена, как

Период колебаний маятника:

откуда

Исключим из формулы (8) неизвестную величину D. Для этого на тело, симметрично оси колебаний ОО^/ поместим добавочные грузы 3 (например, два равных цилиндра или шара). Тогда период колебаний этой системы будет равен

откуда

Приравняв выражения для D, получим

где Т₁ и Т – периоды крутильных колебаний соответственно с добавочными грузами и без них, J₁ – момент инерции двух добавочных грузов одинаковой массы (цилиндров или шаров) относительно оси вращения ОО^/.

Момент инерции цилиндра относительно оси О₁О₁^/, проходящий через его центр масс

де т – масса цилиндра, r – его радиус. По теореме Штейнера (3) момент инерции двух цилиндров относительно оси ОО^/

где d – расстояние между ОО^/ и О₁О₁^/.

Из уравнений (9) и (10) момент инерции исследуемого тела в случае использования в качестве дополнительных грузов цилиндров определяется по формуле

Момент инерции шара относительно оси О₁О₁^/, проходящей через центр масс:

где т – масса шара, r – его радиус. По формуле (3) момент инерции двух шаров относительно оси ОО^/ выразится:

где d – расстояние между ОО^/ и О₁О₁^/.

Исследуемое тело представляет собой диск, который можно считать приближенно сплошным и однородным. Момент инерции сплошного однородного диска относительно оси ОО^/ определяется по формуле

где т₁ – масса диска, R – его радиус. Формула (14) будет являться проверочной при определении момента инерции диска методом крутильных колебаний.

Ход работы

1. Исследуемое тело привести в крутильное колебание. Для этого тело поворачивается относительно оси ОО^/ на малый угол (не более 6^о) и после этого его предоставить самому себе. Секундомером измерить время t 30-50 полных колебаний. Опыт повторить не менее 5 раз с одним и тем же выбранным числом колебаний. Найти среднее значение <t>. Определить период колебаний: , где п – число крутильных колебаний.

2. На одинаковом расстоянии от проволоки на диск поставить добавочные грузы (шары или цилиндры), проделав 5 опытов для того же числа колебаний п, найти период колебаний диска с добавочными грузами

3. Линейкой измерить расстояние между осями ОО^/ и О₁О₁^/.

4. Штангенциркулем измерить диаметр 2r добавочного груза.

5. В зависимости от вида используемых добавочных грузов вычислить момент инерции исследуемого тела по формуле (11) или (13).

6. Измерить радиус исследуемого диска R и найти значение момента инерции по проверочной формуле (14). Масса диска т₁=1.570кг.

7. Методом расчета погрешностей косвенных измерений найти абсолютную погрешность результата DJ.

8. Данные результатов измерений занести в таблицу.

Таблица

№

<t>

t₁

<t₁>

T₁

m₁

J_пр

п/п

кг

кг×м²

кг

кг×м²

Вопросы для допуска к работе

1. Какова цель работы?

2. Что называется моментом инерции материальной точки? Каков физический смысл данного понятия?

3. Опишите рабочую установку и ход эксперимента. Каково назначение в работе добавочных грузов?

4. Запишите формулу для периода колебаний крутильного маятника. При каких условиях справедлива эта формула?

5. Оцените погрешность метода измерений момента инерции.

Вопросы для защиты работы

1. Выведите формулу периода колебаний крутильного маятника.

2. Сформулируйте теорему Штейнера и покажите, как она применяется в проделанной работе.

3. Пользуясь дифференциальным методом, получите формулу относительной погрешности DJ/J.

4. Как повысить точность эксперимента, проведенного на данной установке?

5. Выведите формулу момента инерции сплошного диска, кольца, стержня.

6. Сформулируйте закон сохранения момента импульса, основной закон динамики вращательного движения.

17. Момент инерции тела и его физический смысл. Примеры вычисления момента инерции твердых тел. Теорема Штейнера .

Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

2. Физический смысл момента инерции. Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу. Сравните. Вращательное движение. Поступательное движение. Момент инерции представляет собой меру инерции тела во вращательном движении

Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:

Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :

18. Момент импульса твердого тела. Вектор угловой скорости и вектор момента импульса. Гироскопический эффект. Угловая скорость прецессии

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим .

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): . Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:.

угловую скорость как вектор, величина которого численно равна угловой скорости, и направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось², что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») − если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.

Вращающееся тело ( колесо мотоцикла ) стремиться сохранять положение оси вращения в пространстве неизменным .( гироскопический эффект ) Поэтому возможно движение на 2-х колёсах, но не возможно стояние на двух колёсах Этот эфект используется в корабельных и танковых системах наведения орудий. ( корабль качается на волнах, а орудие смотрит в одну точку ) В навигации и др.

Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.

Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно.

19. Идеальная и вязкая жидкость. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бирнулли.

Идеальной жидкостью назвается воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность. Так как в ней отсуствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.

вязкая жидкость характеризуется наличием сил трения, которые возникают при ее движении. вязкой наз. жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения

Рассматриваемые в Г. ур-ния относит. равновесия несжимаемой жидкости в поле сил тяжести (относительно стенок сосуда, совершающего движение по нек-рому известному закону, напр. поступательное или вращательное) дают возможность решать задачи о форме свободной поверхности и о плескании жидкости в движущихся сосудах – в цистернах для перевозки жидкостей, топливных баках самолётов и ракет и т. п., а также в условиях частичной или полной невесомости на космич. летат. аппаратах. При определении формы свободной поверхности жидкости, заключённой в сосуде, кроме сил гидростатич. давления, сил инерции и силы тяжести необходимо учитывать поверхностное натяжение жидкости. В случае вращения сосуда вокруг вертик. оси с пост. угл. скоростью свободная поверхность принимает форму параболоида вращения, а в сосуде, движущемся параллельно горизонтальной плоскости поступательно и прямолинейно с пост. ускорением а, свободной поверхностью жидкости является плоскость, наклонённая к горизонтальной плоскости под углом

Момент инерции геометрического тела – Энциклопедия по машиностроению XXL

МОМЕНТ ИНЕРЦИИ ГЕОМЕТРИЧЕСКОГО ТЕЛА — сумма произведений элементарных объемов на квадраты их расстояний до плоскости, оси или точки. [c.187]

Формулы для вычисления моментов инерции геометрических тел [c.234]

Формулы для вычисления моментов инерции геометрических тел 234—236 Роботы промышленные 81—86 — Технологическая классификация 83 [c.400]

В качестве примера на рис. 4.8 приведена эквивалентная схема плоского сложного элемента шарнирная связь двух твердых тел , где С/, С2 — массы, а СЗ, С4 — моменты инерции соединенных тел. Математическая модель представляет собой систему уравнений, отражающих геометрические соотношения, действующие в системе шарнирно связанных тел [c. 172]

Вычисление моментов инерции однородных тел правильной геометрической формы производится с помощью методов интегрального исчисления. В случае тел, не имеющих правильной формы, моменты инерции определяются или экспериментально, или приближенно путем вычислений, для чего данное тело разбивают на несколько тел, имеющих правильную геометрическую форму. О способах экспериментального определения моментов инерции будет сказано ниже. [c.163]

Из равенства (9) следует, что радиус инерции геометрически равен расстоянию от оси г той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела относительно оси 2. [c.553]

Моменты инерции других тел могут быть найдены принципиально тем же путем. Однако практически расчет получается достаточно простым только для тел вращения, особенно для тел цилиндрической формы. Например, для полого цилиндра момент инерции относительно геометрической оси вычисляется так же, как и для сплошного [c. 405]

Формулы для вычисления моментов инерции однородных тел различной геометрической формы можно найти в технических справочниках. Вывод этих формул для некоторых однородных тел простейшей геометрической формы дан ниже, в 98. Для тел неоднородных или имеющих сложное очертание моменты инерции находятся обычно экспериментальным путем. [c.322]

Моменты инерции некоторых тел правильной геометрической формы (т — масса тела) [c.61]

Вычислим моменты инерции некоторых тел простейшей геометрической формы. [c.504]

Определение моментов инерции производится аналитически и экспериментально. Аналитически можно определять моменты инерции однородных тел правильной геометрической формы (табл. 6) для деталей и частей строительных машин сложной формы моменты инерции определяются экспериментально. [c.91]

Переход от произвольной системы координат К, в которой тензор инерции недиагонален, к системе К осуществляется с помощью некоторого линейного и ортогонального преобразования координат, называемого преобразованием к главным осям. В справедливости этого утверждения проще всего убедиться, исходя из геометрических соображений. Рассмотрим с этой целью момент инерции твердого тела относительно некоторой оси, проходящей [c.285]

Инварианты. Эллипсоид инерции был определен из геометрического условия, что длина любого его радиуса-вектора равна некоторой постоянной, деленной на квадратный корень из момента инерции твердого тела относительно оси, на которой расположен этот радиус-вектор. Следовательно, какие бы оси координат ни были взяты, эллипсоид инерции должен всегда оставаться тем же самым, а поэтому в произвольных прямоугольных осях координат коэффициенты при —2YZ, —2ZX, —2XV в уравнении эллипсоида инерции будут по-прежнему представлять собой моменты и произведения инерции относительно этих осей. [c.28]

Моменты инерции однородных тел простейших и наиболее часто встречаюш их я геометрических форм могут быть подсчитаны с помощью элементарной математики.

[c.54]

Вычисление моментов инерции неоднородных и однородных тел неправильной геометрической формы в ряде случаев бывает сложным. [c.218]

Таким образом, геометрическим местом концов указанных отрезков, т. е. геометрическим местом точек N, является поверхность второго порядка. По самому построению длина отрезка ON на рис. V.4 отлична от нуля и ограничена, так как для любого конечного тела момент инерции У —величина, отличная от нуля и ограниченная. Среди поверхностей второго порядка ограничены лишь эллипсоиды (в частности, сферы). Следовательно, геометрическим местом точек N является эллипсоид i). Построенный так эллипсоид называется эллипсоидом инерции для точки О. Уравнение (29) является уравнением эллипсоида инерции для этой точки. Непосредственно видно, что задание тензора инерции однозначно задает эллипсоид инерции. [c.178]

Этой формулой можно пользоваться для определения моментов инерции тел, имеющих геометрическую форму тел вращения. [c.326]

Если тело, момент инерции которого определяют, имеет правильную геометрическую форму и масса в нем распределена непрерывно, то сумму (200) следует заменить интегралом [c.337]

Этому уравнению удовлетворяют координаты точек М, а следовательно, геометрическое место этих точек есть поверхность второго порядка. Из всех поверхностей второго порядка только эллипсоид не имеет бесконечно удаленных точек, следовательно, концы отложенных отрезков лежат на поверхности эллипсоида. Его называют эллипсоидом инерции . Заметим, что при построении этого эллипсоида мы взяли начало координат в произвольной точке О. Следовательно, для каждого тела в каждой точке пространства можно построить свой эллипсоид инерции с центром в этой точке. Момент инерции тела относительно любой оси, проходящей через эту точку, обратно пропорционален квадрату отрезка оси, лежащей внутри эллипсоида инерции. Ясно, что наибольшей оси эллипсоида соответствует наименьший момент инерции и, наоборот, наименьшей оси эллипсоида — максимальный момент инерции.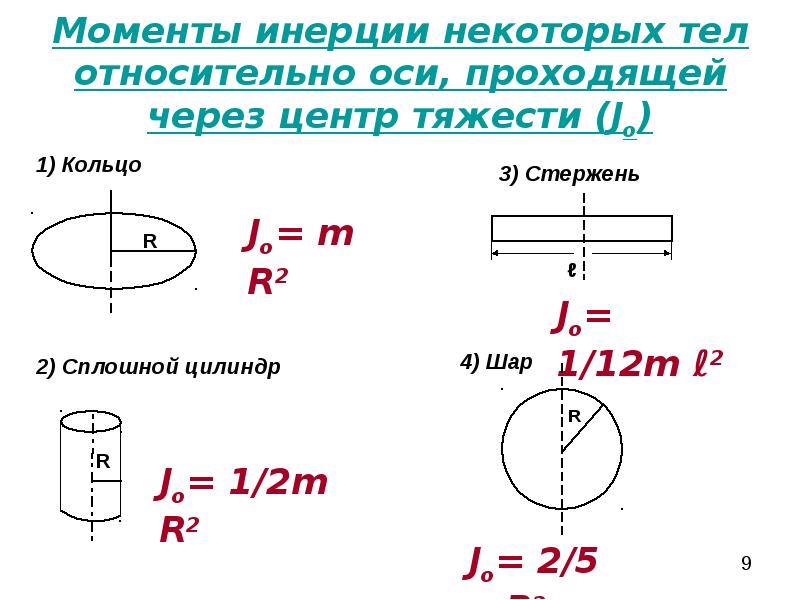 Напомним, что в эллипсоиде имеются обычно три взаимно перпендикулярные оси, называемые главными. Можно совместить координатные оси с главными осями эллипсоида инерции. Из математики известно, что уравнение эллипсоида, отнесенного к главным осям, не содержит членов с произведениями координат. Следовательно, центробежные моменты инерции относительно этих осей равны нулю. Их называют главными осями инерции в данной точке О, а моменты инерции тела относительно этих осей называют главными моментами инерции. Формула (204) принимает. вид [c.341]

Таким образом, приходим к следующей, полученной Пуансо, геометрической интерпретации движения твердого тела в случае Эйлера эллипсоид инерции для неподвижной точки катится без скольжения по плоскости, неподвижной в пространстве-, эта плоскость перпендикулярна кинетическому моменту угловая скорость тела пропорциональна длине радиуса-вектора точки касания, а по направлению с ним совпадает. [c.162]

Реальные детали мы разделяем на простые геометрические тела, момент инерции которых легко определяется, или на небольшие элементы объема, причем интеграл заменяем приближенным суммированием, после чего [c. 295]

Моменты инерции некоторых правильных геометрических тел приведены в т. 1, стр. 394, табл. 8. [c.358]

При отсутствии внешних моментов КА будет устойчиво вращаться вокруг оси максимального или минимального момента инерции, совершая короткопериодические (нутационные) движения, причинами которых могут быть 1) наличие ненулевых начальных условий,по угловой скорости в плоскости, перпендикулярной оси вращения 2) несовпадение строительных осей с главными центральными осями инерции объекта. Наглядную геометрическую картину свободного движения дает разработанный Пуан-со графический метод анализа, динамики вращающихся твердых тел. [c.37]

Момент инерции всегда величина положительная, размерность его KIM etfi. При однородных телах постоянную плотность можно вынести в качестве множителя перед суммой или интегралом, и тогда остается момент инерции геометрических тел J а- dv, или J г- dv (стр. 268). [c. 265]

I. Моменты инерции однородных тел простейших геометрических форм [c.143]

МОМЕНТ инерции (относительно оси — мера инертности тела во вращательном движении вокруг этой оси системы механической относительно оси равен сумме произведений масс всех малых частей тела на квадраты их расстояний до оси центробежный характеризует динамическую неуравновешенность масс при вращении тела экваториальный есть момент инерции однородного тела вращения относительно оси, перпендикулярной к оси симметрии и проходящей через центр масс тела) крутящий является силовым фактором, вызывающим деформацию кручения магнитный [атома орбитальный равен геометрической сумме орбитальных магнитных моментов всех электронов атома нлоского контура с током перпендикулярен ему и равен произведению силы электрического тока и площади котура соленоида равен векторной сумме магнитных моментов всех его витков [c.251]

Корни характеристического уравнения (22) были вычислены обычным образом при помощи вычислительного устройства. При этом использовались значения параметров, которые считались характерными для системы SAS-A на ранней стадии ее разработки. Масса спутника принята равной 114 кг, полярный момент инерции 20,4 кг м , а экваториальный момент инерции 20,0 кг-м . Моменты инерции маховика были приняты 0,015 кг-м (полярный) и 0,00775 кг-м (экваториальный). Масса маховика, по предположению, входит в указанные 114 кг. При этих значениях отношение всего полярного момента инерции обоих тел спутника ко всему их экваториальному моменту инерции оказалось равным 1,02 (данное отношение обозначено через В А). Длина маятника стержня демпфера выбрана равной 20 см, а расстояние от оси подвеса демпфера до полярной (геометрической) оси — равным 2 см. Следовательно, Го/г1 = 0,1. Масса концевого груза маятника составила [c.67]

Вымисление моментов инерции неоднородных и однородных тел неправильной геометрической формулы в ряде случаев бывает сложным. Поэтому моменты инерции таких тел определяют обычно опытным путем.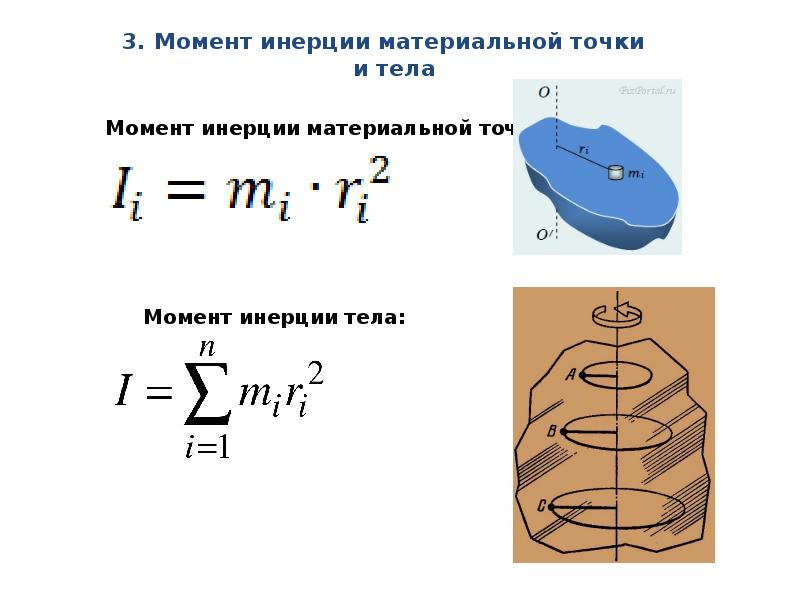 Опытное определение моментов инерции основывается на наблюдении того илн иного вида вращения твердого тела вокруг неподвижной оси, т. к. момент инерции тела — это характеристика его инертности во вращательном движении. [c.443]

Задача определения приведенной длины маятника была поставлена Мерсе-ном (1646 г.). Над цею работали многие ученые (Декарт, Роберваль, Кавендиш, Пикар и др.). Полное и точное решение этой задачи Гюйгенсом (1673 г.) явилось едва ли не первым случаем геометрического интегрирования, первым точным решением задачи по динамике твердого тела, первым введением понятия момента инерции и, безусловно, создало эпоху в развитии физико-математических наук., [c.335]

Опытное определение момента инерции (метод маятниковых колебаний). Как видно из 101, вычисление моментсв инерции неоднородных тел, а также однородных тел сложной геометрической формы практически невозможно. Однако знание этих моментов оказывается необходимым во всех случаях, когда приходится исследовать вращательное или плоское движение деталей механизмов и машин.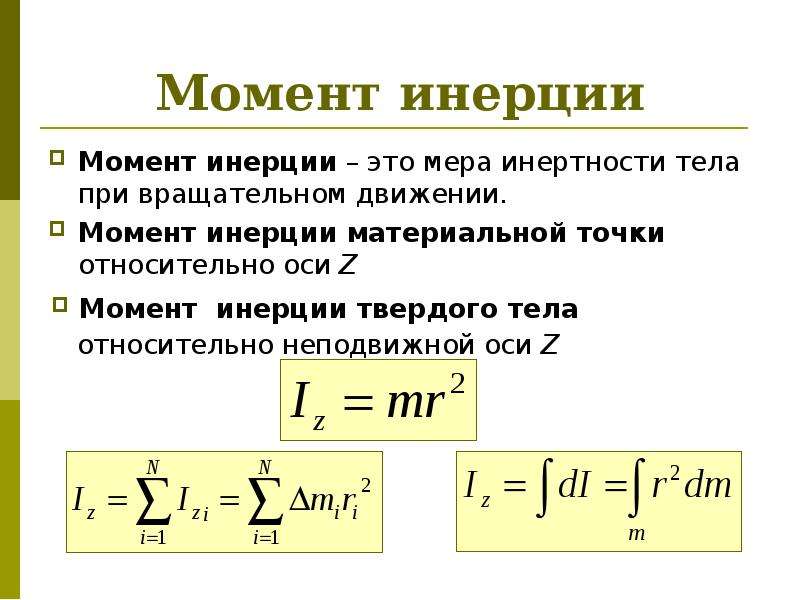 [c.685]

Это уравнение геометрического места точек Р, удаленных от начала координат на расстояние, обратное корню квадратнол1у из момента инерции относительно оси 01. Поскольку Ji ибо тело расположено в конечной части пространства, и Л О, так как точки тела не лежат на одной прямой, то ОР =0 а ОР Единственной поверхностью второго порядка, пе имеющей бесконечно удаленных точек, является эллипсоид. Поэтому уравнение (22.3) есть уравнение эллипсоида, называемого эллипсоидом инерции тела для точки О. [c.395]

Положим, что тело представляет собой сплошной однородный цилиндр высоты h. Найдем момент инерции цилиндра относительно его геометрической оси. Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr (элементарные цилиндры) с внутренним радиусом г и внешним r+dr (рис. 194). Момент инерции каждого такого полого цилиндра мы можем вычислить, пренебрегая dr по сравнению с г, т. е. считая, что расстояние от всех точек одного элементарного полого цилиндра до оси равно г. Поэтому для каждого отдельного цилиндра момент инерции равен 5]Дтг =г Х1Дт, где ЦАт — масса всего элементарного цилиндра. Сечение стенки полого цилиндра есть h dr н ее длина 2лг поэтому объем элементарного цилиндра равен 2nrh dr, и если материал однороден, то масса всего полого цилиндра 1 Дт = р2яг/г dr, где р — плотность [c.405]

Теория моментов инерции плоских фигур предстанляет собою чисто геометрическую теорию, оиа строится совершенно подобно теории моментов инерции масс в механике твердого тела и здесь излагаться не будет. Заметим только следующие свойства введенных величин. [c.82]

Формула (1) выражает момент инерции I в виде функции трех переменных параметров я, р, у, определяющих направление оси OR в теле. Она дает закон изменения момента инерции при изменении направления этой оси. Геометрически этот закон интерпретируется при помощи следующего очень про-хтого, но имеющего фундаментальное значение построения. [c. 56]

Момент инерции маховика можно вычислить как сумму моментов 1инерции Т Ш геометрически простых тел, -составляю- [c.388]

Расчетные динамические модели, а также антропоморфные манекены должны быть эквивале1гтными телу человека по следующим основным показателям а) геометрическим размерам и формам, б) распределению масс частей тела (в частности, по расположению центров масс частей тела, значениям этих масс и моментов инерции), в) видам соединений отдельных звеньев, г) упругим и демпфирующим свойствам. [c.373]

Постановка задачи Сен-Венана. Призматический стержень— тело, образуемое при поступательном движении плоской фигуры S по прямой, перпендикулярной плоскости фигуры фигура S представляет поперечное сечение стержня. Осью стержня Oz называется прямая, являющаяся геометрическим местом центров инерции поперечных сечений оси Ох, Оу, расположенные в плоскости поперечного сечения, направлены по его главным осям инерции.

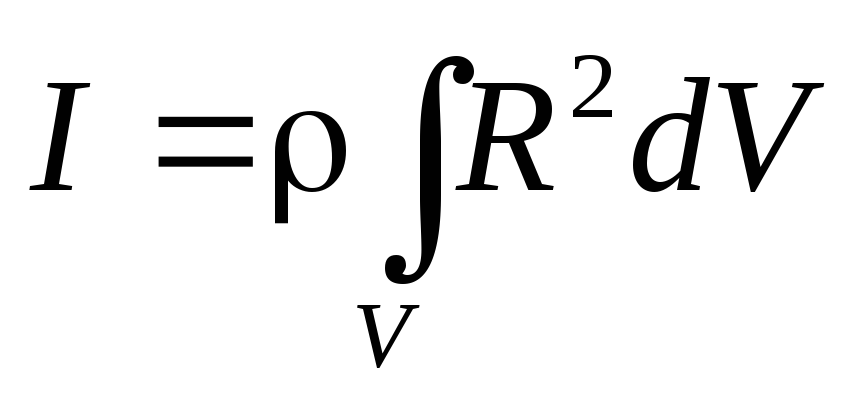Начало О системы осей Оху расположено в одном из поперечных сечений (в сечении 2 = onst) начальное = 0) и конечное (z = I) поперечные сечения называются торцами стержня, их центры инерции обозначаются 0-, 0+. Через 1ос, 1у назовем моменты инерции поперечного сечения относительно расположенных в нем осей, через S — его площадь. Итак, [c.366]

Динамика системы материальных точек. Кинетическая энергия твердого тела.

Динамика системы материальных точек

Уравнение поступательного движения твердого тела

Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, – внешними.

Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1).

Разобьем тело на ряд материальных точек с массами m₁ и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции F_i^ин = – m_ia и составим уравнение равновесия:

ΣX = 0; F – ΣF_i^ин = 0,

откуда:

F = ΣF_i^ин = Σ(m_ia).

Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.

F = ΣF_i^ин = аΣm_i = am.

Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:

F = ma.

Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.

***

Уравнение вращательного движения твердого тела

Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2).

Разобьем тело на ряд материальных точек с массами m_i и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:

ΣМ_z = 0; ΣM_zi(F_i) – ΣM_z(F_τi^ин) = 0.

Моменты реакций подшипника и подпятника, а также сил F_τi^ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом.
Тогда

ΣM_z(F_i) = T = ΣM_z(F_τi^ин) = Σ(m_ir_i²α) = αΣ(m_ir_i²).

Выражение Σ(m_ir_i²) называют моментом инерции тела относительно оси и обозначают J:

J = Σ(m_ir_i²).

Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.

В результате получим формулу:

Т = Jα,

которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.

Единица момента инерции – [J] = [mr²] = [m][r²] = кг×м².

Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.

В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R, толщина s, масса m, относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3).

Разобьем диск на элементарные кольца переменного радиуса r, шириной dr и толщиной s. Согласно определению момент инерции такого кольца равен

dJ = dΣ(m_ir²) = r² dΣm_i = r² dm = r² 2πr drsρ = 2πsρ r³ dr ,

где ρ – плотность материала диска.

Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:

J = ∫ 2πsρ r³ dr = 2πsρ ∫ r³ dr = 2πsρ r⁴/4 = πsρ r⁴/2.

Так как масса диска m = πr²sρ, то можно записать: J = mR²/2.

Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.

***

Моменты инерции тел вращения

На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле

J = mR²/2.

Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.

Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.

Шар массой m, радиусом R относительно диаметра:

J = 2/5 mR²;

Тонкий стержень массой m, длиной l относительно оси, проходящей перпендикулярно стержню через его конец:

J = ml²/3;

Тонкая сферическая оболочка массой m, радиусом R относительно диаметра:

J = 2mR²/3;

Пустотелый вал массой m, наружным радиусом R и радиусом отверстия r относительно оси:

J = m(R² + r²)/2.

Момент инерции Jz тела относительно какой-либо оси z, параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:

Jz = Jc + ma².

Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси, т. е. центральный момент инерции.

Иногда момент инерции определяют по формуле: J = mr_и², где r_и – радиус инерции тела:

r_и = √(J/m).

Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.

Удвоенный радиус инерции тела называется диаметром инерции: D_и = 2r_и.

В практике иногда вместо момента инерции пользуются понятием махового момента GD_и².

Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.

Единица махового момента – Н×м².

Между маховым моментом и моментом инерции существует простая зависимость:

GD_и² = 4g J = 39,24 J.

***

Кинетическая энергия твердого тела

Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:

К = Σ(m_iv_i²)/2.

Определим выражения для кинетической энергии твердого тела для трех случаев движения.

Тело движется поступательно

Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:

К_пост = Σ(m_iv_i²)/2 = v_i²/2 Σ m_i, или К_пост = mv²/2.

Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.

Тело вращается вокруг неподвижной оси

Запишем:

К_вр = Σ(m_iv_i²)/2 = Σ[m_i(ωr_i)²]/2 = (ω²)/2 Σ (m_ir_i)² или К_вр = Jω²/2.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

Тело движется плоскопараллельно

Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей).
Допустим, что известна скорость v_с центра тяжести тела, тогда мгновенная угловая скорость

ω = v_с/ОС,

где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О.

Момент инерции J_о относительно мгновенной оси вращения определяют по формуле:

J_о = J_с + mОС²,

где J_с – момент инерции относительно центральной оси или центральный момент инерции.

Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:

К_пп = J_оω²/2 = (J_с + mОС²) ω²/2 = (J_сω²)/2 + mOC²/2×v_с²/ОС²,

или

К_пп = mv_с²/2 + J_сω²/2.

Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.

В заключение сформулируем теорему об изменении кинетической энергии системы тел:

Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:

ΣК – ΣК₀ = ΣW.

Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.

Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.

***

Балансировка вращающихся тел

Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

10,4 Момент инерции и вращательной кинетической энергии – University Physics Volume 1

10,4 Момент инерции и вращательная кинетическая энергия.

Цели обучения

К концу этого раздела вы сможете:

Опишите разницу между вращательной и поступательной кинетической энергией
Определите физическое понятие момента инерции в терминах распределения массы от оси вращения
Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
Использование сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил

До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения.В этом разделе мы определяем две новые величины, которые полезны для анализа свойств вращающихся объектов: момент инерции и кинетическая энергия вращения. Определив эти свойства, мы получим два важных инструмента, которые нам понадобятся для анализа динамики вращения.

Кинетическая энергия вращения

Фигура 10,17 Кинетическая энергия вращения точильного камня преобразуется в тепло, свет, звук и вибрацию. (Источник: Захари Дэвид Белл, ВМС США)

Энергия во вращательном движении – не новая форма энергии; скорее, это энергия, связанная с вращательным движением, такая же, как кинетическая энергия в поступательном движении. Однако, поскольку кинетическая энергия определяется выражением K = 12mv2K = 12mv2, а скорость является величиной, которая различается для каждой точки вращающегося тела вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную ωω , что одинаково для всех точек твердого вращающегося тела.Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение vt = ωrvt = ωr, где r – расстояние частицы от оси вращения, а vtvt – ее тангенциальная скорость. Подставляя в уравнение для кинетической энергии, находим

K = 12mvt2 = 12m (ωr) 2 = 12 (mr2) ω2. K = 12mvt2 = 12m (ωr) 2 = 12 (mr2) ω2.

В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая с массой mjmj и расстоянием до оси вращения rjrj, так что общая масса тела равна сумма индивидуальных масс: M = ∑jmjM = ∑jmj.Каждая меньшая масса имеет тангенциальную скорость vjvj, где на данный момент мы опустили индекс t . Полная кинетическая энергия твердого вращающегося тела

К = ∑j12mjvj2 = ∑j12mj (rjωj) 2K = ∑j12mjvj2 = ∑j12mj (rjωj) 2

, а поскольку ωj = ωωj = ω для всех масс,

K = 12 (∑jmjrj2) ω2.K = 12 (∑jmjrj2) ω2.

10,16

В уравнении 10.16 используются джоули (Дж). Уравнение в этой форме полное, но неудобное; нам нужно найти способ его обобщить.

Момент инерции

Если мы сравним уравнение 10.16 к тому, как мы записали кинетическую энергию в работе и кинетической энергии, (12mv2) (12mv2), это говорит о том, что у нас есть новая вращательная переменная, которую нужно добавить в наш список наших отношений между вращательными и поступательными переменными. Величина ∑jmjrj2∑jmjrj2 является эквивалентом массы в уравнении для вращательной кинетической энергии. Это новый важный термин для обозначения вращательного движения. Эта величина называется моментом инерции I , в единицах кг · м2 · кг · м2:

. Я = ∑jmjrj2.I = ∑jmjrj2.

10,17

А пока оставим выражение в форме суммирования, представляющее момент инерции системы точечных частиц, вращающихся вокруг фиксированной оси.Отметим, что момент инерции одиночной точечной частицы относительно фиксированной оси равен просто mr2mr2, где r – это расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для вычисления момента инерции некоторых твердых тел правильной формы.

Момент инерции – это количественная мера инерции вращения, как и в поступательном движении, а масса – это количественная мера линейной инерции, то есть чем массивнее объект, тем больше у него инерции и тем больше у него сопротивление изменению линейной скорости.Точно так же, чем больше момент инерции твердого тела или системы частиц, тем больше его сопротивление изменению угловой скорости вокруг фиксированной оси вращения. Интересно посмотреть, как момент инерции изменяется в зависимости от r, расстояния до оси вращения массовых частиц в уравнении 10.17. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, имеют большие моменты инерции, чем тела и системы той же массы, но сосредоточенные около оси вращения.Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя уравнение 10.17 в уравнение 10.16, выражение для кинетической энергии вращающегося твердого тела становится

Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в устройствах накопления энергии маховиком, которые предназначены для хранения большого количества кинетической энергии вращения.Многие автопроизводители сейчас тестируют в своих автомобилях маховик-накопители энергии, такие как маховик или система рекуперации кинетической энергии, показанные на рис. 10.18.

Фигура 10,18 Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville» / Flickr)

Вращательные и поступательные величины кинетической энергии и инерции приведены в Таблице 10.4. Столбец отношений не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных в Таблице 10.3.

Вращательный	Переводческое
I = ∑jmjrj2I = ∑jmjrj2	мм
К = 12Iω2K = 12Iω2	К = 12 мв2 К = 12 мв2

Таблица 10,4 Вращательная и поступательная кинетическая энергия и инерция

Пример 10,8

Момент инерции системы частиц

Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и 0.Длина 5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на рисунке 10.19. а) Каков момент инерции системы? (b) Если снять две ближайшие к оси шайбы, каков момент инерции остальных четырех шайб? (c) Если система с шестью шайбами вращается со скоростью 5 об / с, какова ее кинетическая энергия вращения?

Фигура 10,19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.

Стратегия

Мы используем определение момента инерции для системы частиц и выполняем суммирование, чтобы оценить эту величину. Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
Делаем аналогичный расчет.
Подставим результат из (а) в выражение для кинетической энергии вращения.

Решение

I = ∑jmjrj2 = (0,02 кг) (2 × (0,25 м) 2 + 2 × (0,15 м) 2 + 2 × (0,05 м) 2) = 0.0035 кг · м2I = ∑jmjrj2 = (0,02 кг) (2 × (0,25 м) 2 + 2 × (0,15 м) 2 + 2 × (0,05 м) 2) = 0,0035 кг · м2.
I = ∑jmjrj2 = (0,02 кг) (2 × (0,25 м) 2 + 2 × (0,15 м) 2) = 0,0034 кг · м2I = ∑jmjrj2 = (0,02 кг) (2 × (0,25 м) 2 + 2 × (0,15 м) 2) = 0,0034 кг · м2.
K = 12Iω2 = 12 (0,0035 кг · м2) (5,0 × 2πрад / с) 2 = 1,73JK = 12Iω2 = 12 (0,0035 кг · м2) (5,0 × 2πрад / с) 2 = 1,73Дж.

Значение

Мы можем видеть индивидуальные вклады в момент инерции. Массы, близкие к оси вращения, вносят очень небольшой вклад. Когда мы их сняли, это очень мало повлияло на момент инерции.

В следующем разделе мы обобщаем уравнение суммирования для точечных частиц и разрабатываем метод вычисления моментов инерции для твердых тел. На данный момент, однако, на рис. 10.20 приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.

Фигура 10.20 Значения инерции вращения для обычных форм объектов.

Применение кинетической энергии вращения

Теперь давайте применим идеи вращательной кинетической энергии и таблицы моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами.Следующие ниже примеры также помогут вам освоить эти уравнения. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.

Стратегия решения проблем

Вращательная энергия

Определите, какая энергия или работа задействованы во вращении.
Определите интересующую систему. Обычно помогает набросок.
Проанализируйте ситуацию, чтобы определить виды работ и задействованные энергии.
Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть Ki + Ui = Kf + UfKi + Ui = Kf + Uf.
Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее. Определите, что это такое, и при необходимости рассчитайте их.
По возможности исключите термины, чтобы упростить алгебру.
Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.

Пример 10.9

Расчет энергии вертолета

Типичный небольшой спасательный вертолет имеет четыре лопасти: по четыре лопасти в каждой.00 м и имеет массу 50,0 кг (рис. 10.21). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную массу в снаряженном состоянии 1000 кг. (а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об / мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м / с, и сравните ее с энергией вращения лопастей.

Фигура 10.21 (а) Эскиз четырехлопастного вертолета.(b) Спасательная операция на воде с участием вертолета спасательной службы Окленда Вестпак. (кредит b: модификация работы «111 Emergency» / Flickr)

Стратегия

Вращательная и поступательная кинетические энергии могут быть рассчитаны по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетической энергии.

Решение

Кинетическая энергия вращения равна Мы должны преобразовать угловую скорость в радианы в секунду и вычислить момент инерции, прежде чем сможем найти K .Угловая скорость ωω равна ω = 300об1.00мин2πрад1 оборот1.00мин60.0с = 31,4рад. ω = 300об1.00мин2πрад1 оборот1.00мин60.0с = 31,4рад. Момент инерции одной лопасти – это момент инерции тонкого стержня, вращающегося вокруг своего конца, как показано на рисунке 10.20. Общий I в четыре раза больше этого момента инерции, потому что имеется четыре лопасти. Таким образом, I = 4Ml23 = 4 × (50,0 кг) (4,00 м) 23 = 1067,0 кг · м2. I = 4Ml23 = 4 × (50,0 кг) (4,00 м) 23 = 1067,0 кг · м2. Ввод ωω и I в выражение для кинетической энергии вращения дает K = 0,5 (1067 кг · м2) (31.4 рад / с) 2 = 5,26 × 105 Дж. K = 0,5 (1067 кг · м2) (31,4 рад / с) 2 = 5,26 × 105 Дж.
Вводя данные значения в уравнение для поступательной кинетической энергии, получаем K = 12 мв2 = (0,5) (1000,0 кг) (20,0 м / с) 2 = 2,00 × 105 Дж. K = 12 мв2 = (0,5) (1000,0 кг) (20,0 м / с) 2 = 2,00 × 105 Дж. Чтобы сравнить кинетические энергии, мы берем отношение поступательной кинетической энергии к вращательной кинетической энергии. Это соотношение 2,00 × 105 Дж 5,26 × 105 Дж = 0,380 2,00 × 105 Дж 5,26 × 105 Дж = 0,380.

Значение

Отношение поступательной энергии к вращательной кинетической энергии составляет всего 0.380. Это соотношение говорит нам о том, что большая часть кинетической энергии вертолета находится в его вращающихся лопастях.

Пример 10.10

Энергия в бумеранге

Человек бросает бумеранг в воздух со скоростью 30,0 м / с под углом 40,0 ° 40,0 ° по отношению к горизонту (рис. 10.22). Он имеет массу 1,0 кг и вращается со скоростью 10,0 об / с. Момент инерции бумеранга определяется как I = 112mL2I = 112mL2, где L = 0,7mL = 0,7м. а) Какова полная энергия бумеранга, когда он покидает руку? б) Насколько высоко бумеранг идет от высоты руки, если не учитывать сопротивление воздуха? Фигура 10.22 Бумеранг подбрасывается в воздух под начальным углом 40 ° 40 °.

Стратегия

Мы используем определения вращательной и линейной кинетической энергии, чтобы найти полную энергию системы. Задача состоит в том, чтобы пренебречь сопротивлением воздуха, поэтому нам не нужно беспокоиться о потере энергии. В части (b) мы используем закон сохранения механической энергии, чтобы найти максимальную высоту бумеранга.

Решение

Момент инерции: I = 112 мл 2 = 112 (1,0 кг) (0,7 м) 2 = 0,041 кг · м2 I = 112 мл 2 = 112 (1.0 кг) (0,7 м) 2 = 0,041 кг · м2.
Угловая скорость: ω = (10,0 об / с) (2π) = 62,83рад / с ω = (10,0 об / с) (2π) = 62,83рад / с.
Таким образом, кинетическая энергия вращения равна KR = 12 (0,041 кг · м2) (62,83рад / с) 2 = 80,93Дж. KR = 12 (0,041 кг · м2) (62,83рад / с) 2 = 80,93Дж. Поступательная кинетическая энергия равна KT = 12 мв2 = 12 (1,0 кг) (30,0 м / с) 2 = 450,0 Дж. KT = 12 мв2 = 12 (1,0 кг) (30,0 м / с) 2 = 450,0 Дж. Таким образом, полная энергия бумеранга равна K Итого = KR + KT = 80,93 + 450,0 = 530,93 Дж. K Итого = KR + KT = 80,93 + 450,0 = 530,93 Дж.
Мы используем консервацию механической энергии.Поскольку бумеранг запускается под углом, нам нужно записать полную энергию системы в терминах ее линейной кинетической энергии, используя скорость в направлениях x и y . Общая энергия, когда бумеранг покидает руку, составляет EBefore = 12mvx2 + 12mvy2 + 12Iω2.EBefore = 12mvx2 + 12mvy2 + 12Iω2. Полная энергия на максимальной высоте составляет EFinal = 12mvx2 + 12Iω2 + mgh.EFinal = 12mvx2 + 12Iω2 + mgh. По закону сохранения механической энергии EBefore = EFinalEBefore = EFinal, поэтому после исключения подобных условий мы имеем Поскольку vy = 30.0 м / с (sin40 °) = 19,28 м / св = 30,0 м / с (sin40 °) = 19,28 м / с, находим h = (19,28 м / с) 22 (9,8 м / с2) = 18,97 м. h = (19,28 м / с) 22 (9,8 м / с2) = 18,97 м.

Значение

В части (b) решение демонстрирует, что сохранение энергии является альтернативным методом решения проблемы, которая обычно решается с использованием кинематики. В отсутствие сопротивления воздуха кинетическая энергия вращения не учитывалась при расчете максимальной высоты.

Проверьте свое понимание 10,4

Винт атомной подводной лодки имеет момент инерции 800.0 кг · м 2800,0 кг · м2. Если погружной гребной винт имеет скорость вращения 4,0 об / с при выключенном двигателе, какова скорость вращения гребного винта через 5,0 с, когда водонепроницаемость системы снизилась на 50 000 Дж?

10.5 Расчет моментов инерции – University Physics Volume 1

В предыдущем разделе мы определили момент инерции, но не показали, как его вычислить. В этом разделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта.Этот раздел очень полезен для того, чтобы увидеть, как применить общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии).

Момент инерции

Мы определили момент инерции I объекта как I = ∑imiri2I = imiri2 для всех точечных масс, составляющих объект. Поскольку r – это расстояние до оси вращения от каждой части массы, составляющей объект, момент инерции для любого объекта зависит от выбранной оси.Чтобы убедиться в этом, давайте возьмем простой пример двух масс на конце безмассового (пренебрежимо малая масса) стержня (рис. 10.23) и вычислим момент инерции относительно двух разных осей. В этом случае суммирование по массам является простым, потому что две массы на конце штанги могут быть аппроксимированы как точечные массы, и поэтому сумма имеет только два члена.

В случае с осью в центре штанги, каждая из двух масс м находится на расстоянии R от оси, что дает момент инерции

I1 = mR2 + mR2 = 2mR2.I1 = mR2 + mR2 = 2mR2.

В случае с осью на конце штанги, проходящей через одну из масс, момент инерции равен

. I2 = m (0) 2 + m (2R) 2 = 4mR2. I2 = m (0) 2 + m (2R) 2 = 4mR2.

Из этого результата можно сделать вывод, что вращать штангу вокруг конца в два раза сложнее, чем вокруг ее центра.

Фигура 10,23 а) штанга с осью вращения, проходящей через ее центр; (б) штанга с осью вращения, проходящей через один конец.

В этом примере у нас было две точечные массы, и сумму было просто вычислить.Однако, чтобы иметь дело с объектами, которые не являются точечными, нам нужно тщательно продумать каждый из членов уравнения. Уравнение просит нас суммировать каждый «кусок массы» на определенном расстоянии от оси вращения. Но что именно означает каждый «кусок массы»? Напомним, что при выводе этого уравнения каждая часть массы имела одинаковую величину скорости, что означает, что вся часть должна находиться на одном расстоянии r от оси вращения. Однако это невозможно, если мы не возьмем бесконечно маленький кусок массой дм , как показано на рисунке 10.24.

Фигура 10,24 Использование бесконечно малой массы для вычисления вклада в общий момент инерции.

Необходимость использовать бесконечно малый кусок массы дм предполагает, что мы можем записать момент инерции, вычисляя интеграл по бесконечно малым массам, а не делая дискретную сумму по конечным массам:

I = imiri2becomesI = ∫r2dm.I = ∑imiri2becomesI = ∫r2dm.

10,19

Фактически, это та форма, которая нам нужна для обобщения уравнения для сложных форм.Лучше всего подробно проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Этому посвящена большая часть остальной части этого раздела.

Однородный тонкий стержень с осью через центр

Рассмотрим однородный (по плотности и форме) тонкий стержень массой M и длиной L , как показано на рисунке 10.25. Нам нужен тонкий стержень, чтобы мы могли предположить, что площадь поперечного сечения стержня мала и стержень можно представить как набор масс вдоль одномерной прямой линии.В этом примере ось вращения перпендикулярна стержню и для простоты проходит через среднюю точку. Наша задача – вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила по длине стержня, как показано на рисунке. Это удобный выбор, потому что затем мы можем интегрировать по оси x .

Фигура 10,25 Расчет момента инерции I для однородного тонкого стержня вокруг оси, проходящей через центр стержня.

Мы определяем дм как небольшой элемент массы, составляющий стержень. Интеграл момента инерции является интегралом по распределению масс. Однако мы знаем, как интегрироваться по пространству, а не по массе. Поэтому нам нужно найти способ связать массу с пространственными переменными. Мы делаем это, используя линейную плотность массы объекта λλ, которая является массой на единицу длины. Поскольку массовая плотность этого объекта однородна, мы можем написать

λ = mlorm = λl. λ = mlorm = λl.

Если мы возьмем дифференциал каждой части этого уравнения, мы найдем

dm = d (λl) = λ (dl) dm = d (λl) = λ (dl)

, поскольку λλ постоянно.Для удобства мы решили сориентировать штангу по оси x – именно здесь такой выбор становится очень полезным. Обратите внимание, что кусок стержня dl полностью лежит вдоль оси x и имеет длину dx ; фактически, в этой ситуации dl = dxdl = dx. Поэтому мы можем написать dm = λ (dx) dm = λ (dx), что даст нам переменную интегрирования, с которой мы знаем, как обращаться. Расстояние каждого куска массой дм и от оси задается переменной x , как показано на рисунке.Собирая все вместе, получаем

I = ∫r2dm = ∫x2dm = ∫x2λdx.I = ∫r2dm = ∫x2dm = ∫x2λdx.

Последний шаг – быть осторожным с нашими пределами интеграции. Стержень простирается от x = −L / 2x = −L / 2 до x = L / 2x = L / 2, поскольку ось находится в середине стержня в точке x = 0x = 0. Это дает нам

I = ∫ − L / 2L / 2×2λdx = λx33 | −L / 2L / 2 = λ (13) [(L2) 3 – (- L2) 3] = λ (13) L38 (2) = ML (13) L38 (2) = 112ML2.I = ∫ − L / 2L / 2×2λdx = λx33 | −L / 2L / 2 = λ (13) [(L2) 3 – (- L2) 3] = λ (13) L38 (2) = ML (13) L38 (2) = 112ML2.

Затем мы вычисляем момент инерции для того же однородного тонкого стержня, но с другим выбором оси, чтобы мы могли сравнить результаты.Мы ожидаем, что момент инерции будет меньше относительно оси, проходящей через центр масс, чем ось конечной точки, как это было в примере со штангой в начале этого раздела. Это происходит потому, что больше массы распределяется дальше от оси вращения.

Однородный тонкий стержень с осью на конце

Теперь рассмотрим тот же однородный тонкий стержень массой M и длиной L , но на этот раз переместим ось вращения на конец стержня. Мы хотим найти момент инерции относительно этой новой оси (рисунок 10.26). Количество дм снова определяется как небольшой элемент массы, составляющий стержень. Как и раньше, получаем

I = ∫r2dm = ∫x2dm = ∫x2λdx.I = ∫r2dm = ∫x2dm = ∫x2λdx.

Однако на этот раз у нас другие пределы интеграции. Стержень простирается от x = 0x = 0 до x = Lx = L, так как ось находится на конце стержня в точке x = 0x = 0. Таким образом, мы находим

I = ∫0Lx2λdx = λx33 | 0L = λ (13) [(L) 3− (0) 3] = λ (13) L3 = ML (13) L3 = 13ML2.I = ∫0Lx2λdx = λx33 | 0L = λ ( 13) [(L) 3− (0) 3] = λ (13) L3 = ML (13) L3 = 13ML2.

Фигура 10.26 Расчет момента инерции I для однородного тонкого стержня вокруг оси, проходящей через конец стержня.

Обратите внимание, что инерция вращения стержня вокруг его конца больше, чем инерция вращения относительно его центра (в соответствии с примером штанги) в четыре раза.

Теорема о параллельных осях

Сходство между процессом определения момента инерции стержня вокруг оси, проходящей через его середину, и вокруг оси, проходящей через его конец, поразительно, и предполагает, что может существовать более простой метод определения момента инерции стержня, проходящего через его середину. любая ось параллельна оси, проходящей через центр масс.Такая ось называется параллельной осью. Для этого есть теорема, называемая теоремой о параллельных осях, которую мы формулируем здесь, но не выводим в этом тексте.

Теорема о параллельных осях

Пусть m будет массой объекта и пусть d будет расстоянием от оси, проходящей через центр масс объекта, до новой оси. Тогда у нас

Параллельная ось = центр массы + md2. Параллельная ось = центр массы + md2.

10.20

Давайте применим это к примерам стержней, решенным выше:

Iend = Центр массы + md2 = 112mL2 + m (L2) 2 = (112 + 14) mL2 = 13mL2.Iend = Центр массы + md2 = 112mL2 + m (L2) 2 = (112 + 14) mL2 = 13mL2.

Этот результат согласуется с нашим более длинным вычислением, приведенным выше. Это полезное уравнение, которое мы применяем в некоторых примерах и задачах.

Проверьте свое понимание 10,5

Каков момент инерции цилиндра радиусом R и массой м относительно оси, проходящей через точку на поверхности, как показано ниже?

Единый тонкий диск вокруг оси, проходящей через центр

Интегрирование для определения момента инерции двумерного объекта немного сложнее, но на этом уровне исследования обычно делается одна форма – однородный тонкий диск вокруг оси, проходящей через его центр (рис.27).

Фигура 10,27 Вычисление момента инерции тонкого диска вокруг оси, проходящей через его центр.

Поскольку диск тонкий, мы можем считать массу распределенной полностью в плоскости xy . Мы снова начнем с соотношения для поверхностной плотности массы, которая представляет собой массу на единицу площади поверхности. Поскольку он однороден, поверхностная плотность массы σσ постоянна:

σ = mA или σA = m, sodm = σ (dA). σ = mA или σA = m, sodm = σ (dA).

Теперь мы используем упрощение для области.Область можно представить как состоящую из серии тонких колец, где каждое кольцо представляет собой приращение массы дм радиуса r , равноудаленного от оси, как показано в части (b) рисунка. Бесконечно малая площадь каждого кольца dA , таким образом, определяется длиной каждого кольца (2πr2πr), умноженной на бесконечно малую ширину каждого кольца dr :

A = πr2, dA = d (πr2) = πdr2 = 2πrdr.A = πr2, dA = d (πr2) = πdr2 = 2πrdr.

Полная площадь диска складывается из всех тонких колец с радиусом от 0 до R .Затем этот диапазон радиусов становится нашими пределами интегрирования для dr , то есть мы интегрируем от r = 0r = 0 до r = Rr = R. Собирая все вместе, получаем

I = ∫0Rr2σ (2πr) dr = 2πσ∫0Rr3dr = 2πσr44 | 0R = 2πσ (R44−0) = 2πmA (R44) = 2πmπR2 (R44) = 12mR2. | 0R = 2πσ (R44−0) = 2πmA (R44) = 2πmπR2 (R44) = 12mR2.

Обратите внимание, что это соответствует значению, приведенному на рисунке 10.20.

Расчет момента инерции для составных объектов

Теперь рассмотрим составной объект, такой как на рисунке 10.28, на котором изображен тонкий диск на конце тонкого стержня. Это не может быть легко интегрировано, чтобы найти момент инерции, потому что это объект неоднородной формы. Однако, если мы вернемся к первоначальному определению момента инерции как суммы, мы можем заключить, что момент инерции составного объекта может быть найден из суммы каждой части объекта:

Itotal = ∑iIi.Itotal = ∑iIi.

10.21

Важно отметить, что моменты инерции объектов в уравнении 10.21 – это вокруг общей оси . В случае этого объекта это был бы стержень длиной L , вращающийся вокруг своего конца, и тонкий диск радиусом R , вращающийся вокруг оси, смещенной от центра на расстояние L + RL + R, где R – радиус диска. Давайте определим массу стержня как mrmr, а массу диска как md.md.

Фигура 10,28 Составной объект, состоящий из диска на конце стержня. Ось вращения расположена на A .

Момент инерции стержня равен просто 13mrL213mrL2, но мы должны использовать теорему о параллельных осях, чтобы найти момент инерции диска относительно показанной оси. Момент инерции диска относительно его центра равен 12mdR212mdR2, и мы применяем теорему о параллельных осях: Iparallel-axis = Icenter of mass + md2Iparallel-axis = Icenter of mass + md2, чтобы найти

. Параллельная ось = 12mdR2 + md (L + R) 2. Параллельная ось = 12mdR2 + md (L + R) 2.

Складывая момент инерции стержня плюс момент инерции диска со смещенной осью вращения, мы получаем, что момент инерции составного объекта равен

. Itotal = 13mrL2 + 12mdR2 + md (L + R) 2.Itotal = 13mrL2 + 12mdR2 + md (L + R) 2.

Применение расчета момента инерции для решения проблем

Теперь давайте рассмотрим некоторые практические применения расчета момента инерции.

Пример 10.11

Человек на карусели

Ребенок весом 25 кг стоит на расстоянии r = 1,0 м = 1,0 м от оси вращающейся карусели (рис. 10.29). Карусель можно представить как сплошной однородный диск массой 500 кг и радиусом 2,0 м. Найдите момент инерции этой системы.

Фигура 10.29 Расчет момента инерции ребенка на карусели.

Стратегия

Эта задача включает вычисление момента инерции. Нам даны масса и расстояние до оси вращения ребенка, а также масса и радиус карусели. Поскольку масса и размер ребенка намного меньше, чем у карусели, мы можем аппроксимировать ребенка как точечную массу. Мы используем следующие обозначения: mc = 25kg, rc = 1.0m, mm = 500kg, rm = 2.0mmc = 25 кг, rc = 1,0 м, мм = 500 кг, rm = 2,0 м.

Наша цель – найти Itotal = ∑iIiItotal = ∑iIi.

Решение

Для ребенка Ic = mcr2Ic = mcr2, а для карусели Im = 12mmr2Im = 12mmr2. Следовательно Итого = 25 (1) 2 + 12 (500) (2) 2 = 25 + 1000 = 1025 кг · м2. Итого = 25 (1) 2 + 12 (500) (2) 2 = 25 + 1000 = 1025 кг · м2.

Значение

Значение должно быть близко к моменту инерции карусели, потому что она имеет гораздо большую массу, распределенную от оси, чем ребенок.

Пример 10.12

Жезл и твердая сфера

Найдите момент инерции стержня и твердой сферы вокруг двух осей, как показано ниже. Удочка имеет длину 0,5 м и массу 2,0 кг. Радиус сферы 20,0 см, масса 1,0 кг.

Стратегия

Поскольку в обоих случаях у нас есть составной объект, мы можем использовать теорему о параллельных осях, чтобы найти момент инерции относительно каждой оси. В (а) центр масс сферы расположен на расстоянии L + RL + R от оси вращения.На (b) центр масс сферы расположен на расстоянии R от оси вращения. В обоих случаях момент инерции стержня действует относительно оси на одном конце. Обратитесь к Таблице 10.4, где указаны моменты инерции для отдельных объектов.

Itotal = ∑iIi = IRod + ISphereItotal = ∑iIi = IRod + ISphere;
ISphere = Icenter массы + mSphere (L + R) 2 = 25mSphereR2 + mSphere (L + R) 2ISphere = Icenter массы + mSphere (L + R) 2 = 25mSphereR2 + mSphere (L + R) 2;
Itotal = IRod + ISphere = 13mRodL2 + 25mSphereR2 + mSphere (L + R) 2; Itotal = IRod + ISphere = 13mRodL2 + 25mSphereR2 + mSphere (L + R) 2;
Итого = 13 (2.0 кг) (0,5 м) 2 + 25 (1,0 кг) (0,2 м) 2+ (1,0 кг) (0,5 м + 0,2 м) 2; Itotal = 13 (2,0 кг) (0,5 м) 2 + 25 (1,0 кг) (0,2 м) 2+ (1,0 кг) (0,5 м + 0,2 м) 2;
Итого = (0,167 + 0,016 + 0,490) кг · м2 = 0,673 кг · м2. Итого = (0,167 + 0,016 + 0,490) кг · м2 = 0,673 кг · м2.
ISphere = 25mSphereR2 + mSphereR2ISphere = 25mSphereR2 + mSphereR2;
Itotal = IRod + ISphere = 13mRodL2 + 25mSphereR2 + mSphereR2Itotal = IRod + ISphere = 13mRodL2 + 25mSphereR2 + mSphereR2;
Итого = 13 (2,0 кг) (0,5 м) 2 + 25 (1,0 кг) (0,2 м) 2+ (1,0 кг) (0,2 м) 2 Итого = 13 (2,0 кг) (0,5 м) 2 + 25 (1,0 кг) (0,2 м) 2+ (1.0 кг) (0,2 м) 2;
Итого = (0,167 + 0,016 + 0,04) кг · м2 = 0,223 кг · м2. Итого = (0,167 + 0,016 + 0,04) кг · м2 = 0,223 кг · м2.

Значение

Использование теоремы о параллельных осях упрощает вычисление момента инерции составных объектов. Мы видим, что момент инерции больше в (а), чем в (б). Это потому, что ось вращения находится ближе к центру масс системы в (b). Простая аналогия – это стержень. Момент инерции относительно одного конца составляет 13mL213mL2, но момент инерции через центр масс по его длине равен 112mL2112mL2.

Пример 10,13

Угловая скорость маятника

Маятник в форме стержня (рис. 10.30) выходит из состояния покоя под углом 30 ° 30 °. Он имеет длину 30 см и массу 300 г. Какова его угловая скорость в самой низкой точке? Фигура 10.30 Маятник в виде стержня выходит из состояния покоя под углом 30 ° 0,30 °.

Стратегия

Используйте сохранение энергии для решения проблемы. В момент срабатывания маятник обладает гравитационной потенциальной энергией, которая определяется по высоте центра масс над его самой низкой точкой при качании.В нижней части качелей вся потенциальная гравитационная энергия преобразуется в кинетическую энергию вращения.

Решение

Изменение потенциальной энергии равно изменению кинетической энергии вращения, ΔU + ΔK = 0ΔU + ΔK = 0.

В верхней части колебания: U = mghcm = mgL2 (cosθ) U = mghcm = mgL2 (cosθ). В нижней части колебания U = mgL2.U = mgL2.

В верхней части качелей кинетическая энергия вращения K = 0K = 0. Внизу качелей K = 12Iω2K = 12Iω2. Следовательно:

ΔU + ΔK = 0⇒ (mgL2 (1 − cosθ) −0) + (0−12Iω2) = 0ΔU + ΔK = 0⇒ (mgL2 (1 − cosθ) −0) + (0−12Iω2) = 0

или

12Iω2 = mgL2 (1 – cosθ).12Iω2 = mgL2 (1 – cosθ).

Решая относительно ωω, имеем

ω = mgLI (1 − cosθ) = mgL1 / 3mL2 (1 − cosθ) = g3L (1 − cosθ). ω = mgLI (1 − cosθ) = mgL1 / 3mL2 (1 − cosθ) = g3L (1 − cosθ).

Подставляя числовые значения, получаем

ω = 9,8 м / с 230,3 м (1-cos30) = 3,6рад / с. ω = 9,8 м / с 230,3 м (1-cos30) = 3,6рад / с.

Значение

Обратите внимание, что угловая скорость маятника не зависит от его массы.

10,4 Момент инерции и кинетической энергии вращения

Цели обучения

К концу этого раздела вы сможете:

Опишите разницу между вращательной и поступательной кинетической энергией
Определите физическое понятие момента инерции в терминах распределения массы от оси вращения
Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
Использование сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил

Кинетическая энергия вращения

Любой движущийся объект обладает кинетической энергией. Мы знаем, как рассчитать это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость.Однако мы можем использовать угловую скорость – которая одинакова для всего твердого тела – для выражения кинетической энергии вращающегося объекта. (Рисунок) показывает пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникает шум и вибрация. Эта система обладает значительной энергией, в том числе в виде тепла, света, звука и вибрации. Однако большая часть этой энергии находится в форме кинетической энергии вращения .{2} [/ latex], а скорость – это величина, которая различна для каждой точки на вращающемся теле вокруг оси, имеет смысл найти способ записать кинетическую энергию в единицах переменной [latex] \ omega [/ латекс], который одинаков для всех точек твердого вращающегося тела. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex] {v} _ {\ text {t}} = \ omega r [/ latex], где r – расстояние от частицы до ось вращения и [латекс] {v} _ {\ text {t}} [/ latex] – его тангенциальная скорость.{2}. [/ латекс]

В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [латекс] {m} _ {j} [/ latex] и расстояние до оси вращения [ latex] {r} _ {j} [/ latex], так что общая масса тела равна сумме индивидуальных масс: [latex] M = \ sum _ {j} {m} _ {j} [/латекс]. {2}.{2} [/ latex], где r – это расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для вычисления момента инерции некоторых твердых тел правильной формы.

Момент инерции – это количественная мера инерции вращения, как и в поступательном движении, а масса – это количественная мера линейной инерции, то есть чем массивнее объект, тем больше у него инерции и тем больше у него сопротивление изменению линейной скорости.Точно так же, чем больше момент инерции твердого тела или системы частиц, тем больше его сопротивление изменению угловой скорости вокруг фиксированной оси вращения. Интересно посмотреть, как момент инерции изменяется с r, расстоянием до оси вращения массовых частиц (рисунок). Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, имеют большие моменты инерции, чем тела и системы той же массы, но сосредоточенные около оси вращения.{2}. [/ латекс]

Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в устройствах накопления энергии маховиком , которые предназначены для хранения большого количества кинетической энергии вращения. Многие автопроизводители сейчас тестируют в своих автомобилях маховик-накопители энергии, такие как маховик или система рекуперации кинетической энергии, показанные на (Рисунок).

Рисунок 10.18 A Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville» / Flickr)

Вращательные и поступательные величины кинетической энергии и инерции приведены на (Рисунок). Столбец отношений не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на (рисунок).

Пример

Момент инерции системы частиц

Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и 0.Длина 5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на (Рисунок). а) Каков момент инерции системы? (b) Если снять две ближайшие к оси шайбы, каков момент инерции остальных четырех шайб? (c) Если система с шестью шайбами вращается со скоростью 5 об / с, какова ее кинетическая энергия вращения?

Рисунок 10.19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и вращаются вокруг вертикальной оси.{2} = 1,73 \, \ text {J} [/ latex].

Значение

В следующем разделе мы обобщаем уравнение суммирования для точечных частиц и разрабатываем метод вычисления моментов инерции для твердых тел. На данный момент, однако, (рисунок) дает значения инерции вращения для обычных форм объектов вокруг заданных осей.

Рисунок 10.20 Значения инерции вращения для объектов общей формы

Применение кинетической энергии вращения

Теперь давайте применим идеи вращательной кинетической энергии и таблицы моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие ниже примеры также помогут вам освоить эти уравнения. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.

Стратегия решения проблем: энергия вращения

Определите, какая энергия или работа задействованы во вращении.
Определите интересующую систему. Обычно помогает набросок.
Проанализируйте ситуацию, чтобы определить виды работ и задействованные энергии.
Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} = {K} _ {\ text {f}} + {U} _ {\ text {f}} [/ latex].
Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее.Определите, что это такое, и при необходимости рассчитайте их.
По возможности исключите термины, чтобы упростить алгебру.
Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.

Пример

Расчет энергии вертолета

Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая длиной 4,00 м и массой 50,0 кг ((Рисунок)). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине.Вертолет имеет полную массу в снаряженном состоянии 1000 кг. (а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об / мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м / с, и сравните ее с энергией вращения лопастей.

Рис. 10.21 (a) Эскиз четырехлопастного вертолета. (b) Спасательная операция на воде с участием вертолета спасательной службы Окленда Вестпак. (кредит b: «111 Emergency» / Flickr)

Стратегия

Вращательная и поступательная кинетические энергии могут быть рассчитаны по их определениям.{2}. [/ латекс]

Мы должны преобразовать угловую скорость в радианы в секунду и вычислить момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс] \ омега [/ латекс] составляет

[латекс] \ omega = \ frac {300 \, \ text {rev}} {1,00 \, \ text {min}} \, \ frac {2 \ pi \, \ text {rad}} {\ text {1 rev}} \, \ frac {1.00 \, \ text {min}} {60.0 \, \ text {s}} = \, 31.4 \, \ frac {\ text {rad}} {\ text {s}}. [/ латекс]

Момент инерции одной лопасти – это момент инерции тонкого стержня, вращающегося вокруг своего конца, указанного на (Рисунок).{5} \, \ text {J}} = 0,380. [/ латекс]

Значение

Отношение поступательной энергии к вращательной кинетической энергии составляет всего 0,380. Это соотношение говорит нам о том, что большая часть кинетической энергии вертолета находится в его вращающихся лопастях.

Пример

Энергия в бумеранге

Человек бросает бумеранг в воздух со скоростью 30,0 м / с под углом [латекс] 40,0 \ text {°} [/ latex] по отношению к горизонтали ((Рисунок)).{2} [/ latex], где [latex] L = 0,7 \, \ text {m} [/ latex]. а) Какова полная энергия бумеранга, когда он покидает руку? б) Насколько высоко бумеранг идет от высоты руки, если не учитывать сопротивление воздуха?

Рис. 10.22 Бумеранг подбрасывается в воздух под начальным углом [латекс] 40 \ text {°} [/ latex].

Стратегия

Таким образом, полная энергия в бумеранге равна

. {2} [/ latex].{2} [/ latex], момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции – это вращательный аналог массы при линейном движении.

В системах, которые одновременно вращаются и поступательно, можно использовать сохранение механической энергии, если нет действующих неконсервативных сил. Полная механическая энергия сохраняется и является суммой вращательной и поступательной кинетической энергии и гравитационной потенциальной энергии.

Концептуальные вопросы

Что, если бы другая планета того же размера, что и Земля, была выведена на орбиту вокруг Солнца вместе с Землей. Будет ли момент инерции системы увеличиваться, уменьшаться или оставаться прежним?

Твердая сфера вращается вокруг своей оси с постоянной скоростью. Другая полая сфера той же массы и радиуса вращается вокруг своей оси через центр с той же скоростью вращения. Какая сфера имеет большую кинетическую энергию вращения?

Показать решение

Полая сфера, поскольку масса распределена дальше от оси вращения.

Проблемы

Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг, и все они лежат в одной плоскости. а) Каков момент инерции системы относительно данной оси? (b) Если система вращается со скоростью 5 об / с, какова ее кинетическая энергия вращения?

(а) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца?

Показать решение

а.{33} \, \ text {J} [/ латекс]

Рассчитайте кинетическую энергию вращения колеса мотоцикла весом 12 кг, если его угловая скорость составляет 120 рад / с, а его внутренний радиус равен 0,280 м, а внешний радиус – 0,330 м.

Бейсбольный питчер бросает мяч движением, при котором предплечье вращается вокруг локтевого сустава, а также другие движения. Если линейная скорость мяча относительно локтевого сустава составляет 20,0 м / с на расстоянии 0,480 м от сустава, а момент инерции предплечья составляет [латекс] 0. {30} \, \ text {kg} [/ latex] и радиусом 10 км вращается с периодом 0.{42} \, \ text {J} [/ латекс]

Электрическая шлифовальная машинка, состоящая из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об / сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Какова конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?

Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором установлен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см. Ниже).{2} [/ латекс]; б. [латекс] K = 621,8 \, \ text {J} [/ латекс]

Глоссарий

момент инерции: масса вращения твердого тела, которая относится к тому, насколько легко или сложно будет изменить угловую скорость вращающегося твердого тела

кинетическая энергия вращения: кинетическая энергия за счет вращения объекта; это часть его полной кинетической энергии

Кинетическая энергия вращения | Безграничная физика

Кинетическая энергия вращения: работа, энергия и сила

Кинетическая энергия вращения – это кинетическая энергия вращения объекта, которая является частью его общей кинетической энергии.{2} [/ latex], где [latex] \ omega [/ latex] – угловая скорость, а [latex] \ text {I} [/ latex] – момент инерции вокруг оси вращения.

Механическая работа, прикладываемая во время вращения, равна крутящему моменту, умноженному на угол поворота: [latex] \ text {W} = \ tau \ theta [/ latex].

Мгновенная мощность тела с угловым ускорением равна крутящему моменту, умноженному на угловую скорость: [latex] \ text {P} = \ tau \ omega [/ latex].

Существует тесная взаимосвязь между результатом для вращательной энергии и энергией, удерживаемой линейным (или поступательным) движением.

Ключевые термины

крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
инерция : свойство тела сопротивляться любому изменению его равномерного движения; эквивалент его массе.
угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.

Кинетическая энергия вращения – это кинетическая энергия вращения объекта, являющаяся частью его общей кинетической энергии. Рассмотрение энергии вращения отдельно вокруг оси вращения объекта дает следующую зависимость от момента инерции объекта:

Кинетическая энергия вращения : Вещи, которые катятся без скольжения, имеют некоторую часть своей энергии как поступательную кинетическую, а остальную часть – как кинетическую вращательную.{2} [/ латекс],

где [latex] \ omega [/ latex] – угловая скорость, а [latex] \ text {I} [/ latex] – момент инерции вокруг оси вращения.

Механическая работа, прикладываемая во время вращения, равна крутящему моменту ([latex] \ tau [/ latex]), умноженному на угол поворота ([latex] \ theta [/ latex]): [latex] \ text {W} = \ tau \ theta [/латекс]. {2} [/ latex].

Во вращающейся системе момент инерции играет роль массы, а угловая скорость играет роль линейной скорости.

В качестве примера давайте вычислим кинетическую энергию вращения Земли (показано на рисунке 1). Поскольку Земля имеет период около 23,93 часа, она имеет угловую скорость 7,29 × 10 ⁻⁵ рад / с. У Земли есть момент инерции I = 8,04 × 10 ³⁷ кг · м2. Следовательно, он имеет кинетическую энергию вращения 2,138 × 10 ²⁹ Дж.

Вращающаяся Земля : Вращение Земли является ярким примером кинетической энергии вращения.

Частично это можно использовать с помощью приливной энергии. Дополнительное трение двух глобальных приливных волн создает физическую энергию, бесконечно замедляя угловую скорость Земли. Благодаря сохранению углового момента этот процесс передает угловой момент орбитальному движению Луны, увеличивая ее расстояние от Земли и ее орбитальный период.

Момент инерции

Момент инерции – это свойство массы, которое измеряет ее сопротивление вращательному ускорению вокруг одной или нескольких осей.

Цели обучения

Определить свойство массы, описываемое моментом инерции

Ключевые выводы

Ключевые моменты

Первый закон Ньютона, который описывает инерцию тела при линейном движении, может быть расширен до инерции тела, вращающегося вокруг оси, с использованием момента инерции.
Объект, который вращается с постоянной угловой скоростью, будет продолжать вращаться, если на него не действует внешний крутящий момент.
Чем больше крутящий момент, тем больше угловое ускорение.

Ключевые термины

крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
инерция : свойство тела сопротивляться любому изменению его равномерного движения; эквивалент его массе.

Момент инерции

Момент инерции – это свойство распределения массы в пространстве, которое измеряет сопротивление массы вращательному ускорению вокруг одной или нескольких осей.Первый закон Ньютона, который описывает инерцию тела при линейном движении, может быть распространен на инерцию тела, вращающегося вокруг оси, с использованием момента инерции. То есть объект, который вращается с постоянной угловой скоростью, будет продолжать вращаться, если на него не действует внешний крутящий момент. Таким образом, момент инерции играет во вращательной динамике ту же роль, что и масса в линейной динамике: он описывает взаимосвязь между угловым моментом и угловой скоростью, а также крутящим моментом и угловым ускорением.

Момент инерции : Краткое введение в момент инерции (вращательной инерции) для студентов, изучающих математические науки.

Момент инерции I объекта можно определить как сумму mr ² для всех точечных масс, из которых он состоит, где m – масса, а r – расстояние массы от центра объекта. 2 [/ latex], где r теперь расстояние между двумя осями, а [latex] \ text {I} _ {\ text {cm}} [/ latex] – это момент инерции при вращении вокруг центра масс, который вы научились рассчитывать в предыдущем абзаце.

Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением: net τ = I α, или α = (net τ) / I. Net τ – это общий крутящий момент от всех сил относительно выбранной ось. Такие моменты могут быть положительными или отрицательными и складываются как обычные числа. Соотношение τ = Iα является вращательным аналогом второго закона Ньютона и очень применимо. Это уравнение действительно для любого крутящего момента, приложенного к любому объекту и относительно любой оси.

Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем медленнее он разгоняется с тем же крутящим моментом. Основное соотношение между моментом инерции и угловым ускорением состоит в том, что чем больше момент инерции, тем меньше угловое ускорение. Момент инерции зависит не только от массы объекта, но и от его распределения массы относительно оси, вокруг которой он вращается.Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять у внешнего края.

Момент инерции карусели : Отец толкает карусель на детской площадке за край и перпендикулярно ее радиусу для достижения максимального крутящего момента.

Массовый момент инерции

Массовый момент инерции (момент инерции) – I – это мера сопротивления объекта изменению направления вращения.Момент инерции имеет такое же отношение к угловому ускорению, как масса к линейному ускорению.

Момент инерции тела зависит от распределения массы в теле относительно оси вращения

Для точечной массы Момент инерции равен массе, умноженной на квадрат перпендикулярного расстояния к вращению. отсчетной оси и может быть выражено как

I = mr ² (1)
где
I = момент инерции ( кг · м ² , фут ^{909 2}, фунт _f фут ²)

м = масса (кг, снаряды)
r = расстояние между осью и масса вращения (м, футы)

Пример – Момент инерции одиночной массы

Создание трехмерных моделей с помощью бесплатного расширения Engineering ToolBox Sketchup Extension

Момент инерции с учетом для вращения вокруг оси z одной массы 1 кг , распределенной в виде тонкого кольца, как показано на рисунке выше, можно рассчитать как

I _z = (1 кг) ((1000 мм) ( 0.001 м / мм)) ²

= 1 кг м ²

Момент инерции – распределенные массы

Точечная масса является основой для всех других моментов инерции, поскольку любой объект может быть “построен”. “из набора точечных масс.

I = ∑ _i m _i r _i ² = m ₁ r ₁ ² + m ₂ r ₂ ^{+ 22 909…..} + m _n r _n ² (2)

Для твердых тел с непрерывным распределением соседних частиц формулу лучше выразить в виде интеграла

I = ∫ r ² дм (2b)
где
дм = масса бесконечно малой части тела

Преобразование между единицами измерения момента инерции

00 Умножьте 999 на
от

до
кг · м ²	г · см ²	фунтов _м футов ²	фунтов 9076 9027 1 ^{пуля футов ²}	пуля в ²
кг м ²	1	1 10 ⁷	2.37 10 ¹	3,42 10 ³	7,38 10 ^-1	1,06 10 ²
г см ²	1 10 ^-7	2,37 10 ^-6	3,42 10 ^-4	7,38 10 ^-8	1,06 10 ⁵
фунтов _м футов ² – 1 4,2 900 2	4.21 10 ⁵	1	1,44 10 ²	3,11 10 ^-2	4,48
фунтов _м дюйм ²	4 2,93 278 ^{2,93 10 ³}	6,94 10 ^-3	1	2,16 10 ^-4	3,11 10 ^-2
отрывной фут ² 1	1,336 10 ⁷	3,22 10 ¹	4,63 10 ³	1	1,44 10 ²
заглушка в ²	1 9,42	9,42 9,42 10 ⁴	2,23 10 ^-1	3,22 10 ¹	6,94 10 ^-3	1

Момент инерции – общая формула

Общее выражение инерции уравнение:

I = kmr ² (2c)
где
k = инерционная постоянная – в зависимости от формы корпуса

Радиус вращения )

Радиус вращения – это расстояние от оси вращения, где сосредоточенная точечная масса равна Моменту инерции переменного тока. Туальное тело.Радиус вращения тела может быть выражен как

r _g = (л / м) ^1/2 (2d)

, где

r _g = радиус вращения ( м, футы)

I = момент инерции корпуса ( кг · м ² , футы ²)

м = масса кузова (кг, снаряды)

Некоторые типичные тела и их моменты инерции

Цилиндр

Тонкостенный полый цилиндр

Моменты инерции для полого тонкостенного цилиндра сравнимы с точечной массой (1) и могут быть выражены как :

I = mr ² (3a)
где
m = масса полости (кг, снаряды)
r = расстояние между ось и тонкостенная полость (м, футы)
r _o = расстояние между осью и внешней полостью (м, футы)

Полый цилиндр

I = 1/2 м (r _i ² + r _o ²) (3b)
где
m = масса полости (кг, снаряды)
r _i = расстояние между осью и внутренней частью полый (м, футы)
r _o = расстояние между осью и внешней полостью (м, футы)

Сплошной цилиндр

I = 1/2 mr ² (3c)
, где
m = масса цилиндра (кг, снаряды)
r = расстояние между осью и внешним цилиндром (м, футы)

Круглый диск

900 06 I = 1/2 mr ² (3d)
где
m = масса диска (кг, снаряды)
r = расстояние между осью и внешним диском (м, футы)

Сфера

Тонкостенная полая сфера

I = 2/3 mr ² (4a)
где
m = масса полой сферы000 (кг, 9 штекеров)
r = расстояние между осью и полостью (м, фут)

Сплошная сфера

I = 2/5 mr ² (4b)
где
m = масса сферы (кг, снаряды)
r = радиус в сфере (м, футы)

Прямоугольная плоскость

Моменты инерции для прямоугольной плоскости с xis через центр можно выразить как

I = 1/12 м (a ² + b ²) (5)
, где
a, b = короткая и длинная стороны

Моменты инерции для прямоугольной плоскости с осью вдоль кромки могут быть выражены как

I = 1/3 ма ² (5b)

Slender Rod

Моменты инерции для тонкого стержня с осью через центр можно выразить как

I = 1/12 м L ² (6)
где
L = длина стержня

Моменты инерции для тонкого стержня с осью сквозной конец может быть выражен как

I = 1/3 м L ² (6b)

How to Ca lculate Moment of Inertia

Как рассчитать момент инерции (MOI) в реальном мире

Первым шагом для вычисления момента инерции массы является определение местоположения осей X, Y и Z.Точность расчетов (и измерений для проверки расчетов) будет во многом зависеть от того, насколько хорошо определены оси. Теоретически эти оси могут находиться в любом месте относительно рассматриваемого объекта при условии, что оси взаимно перпендикулярны. Однако в реальной жизни, если оси не определены четко и не могут быть точно привязаны, вычисления момента инерции бессмысленны.

Момент инерции аналогичен инерции, за исключением того, что он применяется к вращению, а не к линейному движению.Инерция – это тенденция объекта оставаться в покое или продолжать движение по прямой с той же скоростью. Инерцию можно рассматривать как другое слово для обозначения массы. Следовательно, момент инерции – это масса вращения. В отличие от инерции, MOI также зависит от распределения массы в объекте. Чем больше расстояние между массой от центра вращения, тем больше момент инерции.

Формула, аналогичная второму закону движения Ньютона, может быть записана для вращения:
F = Ma (F = сила; M = масса; a = линейное ускорение)
T = IA (T = крутящий момент; I = момент инерции; A = ускорение вращения)

Выбор местоположения опорной оси даже для сложной формы

Для вычисления центра тяжести необходимы три опорные оси, но только одна ось необходима для определения момента инерции.Хотя в качестве опорной можно выбрать любую ось, обычно желательно выбрать ось вращения объекта. Если объект установлен на подшипниках, то эта ось определяется средней линией подшипников. Если объект летит в пространстве, то эта ось является «главной осью» (осью, проходящей через центр тяжести и ориентированной таким образом, что произведение инерции относительно этой оси равно нулю (см. Обсуждение произведения инерции). будет использоваться для расчета момента инерции сложной формы, выберите ось симметрии, чтобы упростить расчет.Затем эту ось при желании можно переместить на другую ось, используя правила, изложенные в разделе «Теорема о параллельной оси».

Полярность момента инерции

Значения центра тяжести могут быть как положительными, так и отрицательными, и фактически их полярность зависит от выбора местоположения опорной оси. Значения момента инерции могут быть только положительными, так же как масса может быть только положительной.

Единицы момента инерции

В Соединенных Штатах слово «фунт» часто неправильно используется для обозначения как массы, так и веса.Если единицей веса является фунт, то единицей массы также не может быть фунт, поскольку это нарушит второй закон Ньютона. Однако по причинам, которые были потеряны в древности, в США объект весом 1 фунт часто упоминается как имеющий массу 1 фунт. Это приводит к единицам момента инерции, таким как фунт-дюйм ², где «фунт» относится к весу объекта, а не к его массе. Правильные единицы измерения момента инерции (а также произведения инерции): МАССА x РАССТОЯНИЕ ².Когда фунт-дюйм ² или фунт-фут ² используются для определения MOI или POI, величина ДОЛЖНА быть разделена на соответствующее значение «g», чтобы обеспечить правильность размеров в инженерных расчетах. Опять же, анализ размеров подтвердит, используются ли правильные единицы измерения. В следующей таблице показаны некоторые из используемых сегодня единиц для определения момента инерции и произведения инерции:

УСТРОЙСТВО КОММЕНТАРИИ
фунт-дюйм ² фунт = вес; нужно разделить на g = 386.088 дюйм / сек ²
фунт-дюйм-сек ² фунт-дюйм-сек ² = расстояние ² x вес / г; вес / г = масса; правильные размеры
снаряд-фут ² снаряд = масса; правильные размеры
кг-м ² кг = масса; правильные размеры

Наиболее распространенными единицами измерения в США являются фунт-дюйм ², даже если это неверно по размерам.

ПРАВИЛО 1 . Если момент инерции или произведение инерции выражены в следующих единицах, то их значения могут использоваться в инженерных расчетах как есть:
Slug-ft ², фунт-дюйм-сек ², кг-м ², фунт-фут-сек ², унция-дюйм-сек ²

ПРАВИЛО 2 .Если момент инерции или произведение инерции выражены в следующих единицах, то их значения должны быть разделены на соответствующее значение «g», чтобы сделать их размерно правильными.

фунт-фут ², фунт-дюйм ², унция-дюйм ²

Значение g: 32,17405 фут / сек ² или 386,088 дюйм / сек ²
Не использовать местное значение г, чтобы преобразовать в массу!

Какова формула момента инерции?

MOI, иногда называемый вторым моментом, для точечной массы вокруг любой оси: I = Mr ²
, где I = MOI (снаряд-фут ² или другая масса-длина ² единиц)
M = масса элемента (пули или другая единица массы)
r = расстояние от точечной массы до исходной оси

Определение радиуса вращения

Момент инерции любого объекта относительно оси через его ЦТ можно выразить следующим образом: формула: I = Mk ², где I = момент инерции
M = масса (снаряд) или другая правильная единица массы
k = длина (радиус вращения) (футы) или любая другая единица длины

Расстояние (k) называется радиусом вращения.Метод расчета радиуса инерции описан в следующих разделах. Рассмотрим сначала тело, состоящее из двух точечных масс, каждая с массой M / 2, разделенных расстоянием 2r. Ось отсчета проходит через точку, равноудаленную от двух масс. У каждой массы есть MOI Mr ²/2. Таким образом, их объединенный MOI – Mr ². Второй пример показывает тонкостенную трубку радиуса r. По симметрии ЦТ лежит на средней линии трубы. Опять же, вся масса расположена на расстоянии r от оси отсчета, поэтому ее MOI = Mr ².В этих примерах радиус вращения k = r. Это приводит к определению: «Радиус вращения объекта относительно оси, проходящей через ЦТ, – это расстояние от оси, на котором вся масса объекта может быть сосредоточена без изменения его момента инерции. Радиус вращения всегда отсчитывается от центра тяжести ».

Теорема о параллельной оси для вычисления момента инерции

Если в приведенном выше примере мы хотели определить MOI объекта относительно оси X _a, а не оси X, через CG, то значение можно определить с помощью теорема о параллельной оси:

Ia = I + d ² M, Поскольку I = k ² M, тогда Ia = M (d ² + k ²)
, где k – радиус вращения.

Эта теорема о параллельных осях часто используется при вычислении MOI ракеты или другого аэрокосмического объекта. MOI каждого компонента в ракете сначала измеряется или вычисляется вокруг оси через ее CG, а затем используется теорема о параллельных осях для определения MOI всего транспортного средства с этими компонентами, установленными в их надлежащем месте. Смещение «d» – это расстояние от ЦТ компонента до центральной линии ракеты.

Полезные приближения

Поскольку момент инерции объекта, смещенного относительно его базовой оси, пропорционален (d ² + k ²), мы можем сделать два наблюдения, которые упростят вычисление MOI:

ПРАВИЛО 1.Если радиус вращения объекта составляет менее 1% от расстояния смещения «d», то MOI объекта вокруг его центра тяжести может быть проигнорирован при вычислении общего MOI, и значение станет d ² M. Например если гироскоп с массой 0,1 снаряда расположен около внешней поверхности ракеты и смещение к центру тяжести гироскопа составляет 3 фута, в то время как радиус вращения гироскопа составляет всего 0,02 фута, то MOI относительно центра Линия ракеты за счет гироскопа составляет d ² M = 0,9 снаряда-фут ².Погрешность при использовании этого приближения составляет менее 0,01%.

ПРАВИЛО 2. Если радиус вращения объекта более чем в 100 раз превышает расстояние смещения «d», то смещение объекта можно игнорировать при вычислении общего MOI, и значение становится равным k ² M. Для Например, если ракетный двигатель массой 100 фунтов расположен рядом с центральной линией ракеты, а смещение к ЦТ ракетного двигателя составляет 0,100 дюйма, а радиус вращения ракетного двигателя составляет 12 дюймов, то MOI относительно центральной линии ракеты из-за ракетного двигателя k ² M = 14400 фунт-дюйм ² (точнее 37.3 фунта в секунду ²). Опять же, ошибка аппроксимации составляет менее 0,01%. Правило 2 также может применяться к ошибкам выравнивания при вычислении или измерении MOI. Если смещение или несовпадение составляет менее 1% радиуса инерции, то ошибка центровки незначительна.

Эта страница представляет собой отрывок из статьи Ричарда Бойнтона и Курта Вайнера из Space Electronics в 2001 году, которая четыре раза цитировалась в других статьях .

Щелкните здесь, чтобы получить доступ к полной статье Как рассчитать массовые характеристики – Практическое руководство инженера НЕ ТРЕБУЕТСЯ ВХОД

Дополнительную информацию можно увидеть в полном PDF:

Объединение момента инерции двух объектов
Основная формула с использованием дифференциальных элементов массы
Объединение осевых значений MOI
Объединение значений MOI в поперечном направлении
Пример составного MOI
Влияние несоосности
Влияние несоосности
Преобразование прямоугольной формы в полярную
Разница между смещением ЦТ и произведением инерции
Теорема о параллельной оси POI
Сравнение между MOI и POI И еще 13 страниц после этого

Расчет момента инерции

🕑 Время чтения: 1 минута

Что такое момент инерции? Момент инерции , также называемый моментом инерции массы или угловой массой (единицы СИ кг м ²), является мерой сопротивления объекта изменениям скорости его вращения.Это вращательный аналог массы. То есть это инерция твердого вращающегося тела по отношению к его вращению. Момент инерции играет во вращательной динамике почти ту же роль, что и масса в базовой динамике, определяя взаимосвязь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также рядом других величин. Хотя простой скалярной обработки достаточно для многих ситуаций, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как волчки и движение гироскопа. Символ I и иногда J обычно используется для обозначения момента инерции. Момент инерции объекта относительно данной оси описывает, насколько сложно изменить его угловое движение вокруг этой оси. Например, рассмотрим два диска (A и B) одинаковой массы. Диск A имеет больший радиус, чем диск B. Предполагая, что существует однородная толщина и распределение массы, требуется больше усилий для ускорения диска A (изменения его угловой скорости), потому что его масса распределена дальше от его оси вращения: масса, которая находится дальше выходящая из этой оси должна при данной угловой скорости двигаться быстрее, чем масса ближе внутрь.В этом случае диск A имеет больший момент инерции, чем диск B. Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, которая не требует знания оси вращения. Скалярная форма I (часто называемая просто «моментом инерции») позволяет кратко проанализировать многие простые проблемы в динамике вращения, такие как скатывание объектов по склону и поведение шкивов. Например, в то время как блок любой формы будет скользить вниз с уменьшением трения с той же скоростью, катящиеся объекты могут спускаться с разной скоростью, в зависимости от их моментов инерции.Обруч будет опускаться медленнее, чем твердый диск той же массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения, и, следовательно, ему нужно двигаться быстрее, если обруч катится с той же угловой скоростью. Однако для (более сложных) задач, в которых ось вращения может измениться, скалярная обработка неадекватна, и необходимо использовать тензорную обработку (хотя в особых случаях возможны сокращения). Примеры, требующие такой обработки, включают гироскопы, вершины и даже спутники, все объекты, выравнивание которых может изменяться.Момент инерции не следует путать с полярным моментом инерции, который является мерой способности объекта сопротивляться скручиванию (скручиванию).

Формула момента инерции: Простая формула момента инерции любого объекта, будь то точечная масса или 3D-структура, задается следующим образом: куда dm – масса бесконечно малой части тела и r – (перпендикулярное) расстояние от точечной массы до оси вращения.

Детальный анализ (Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется выражением I является аддитивным.Таким образом, для твердого тела, состоящего из N точечных масс м _i с расстояниями r _i до оси вращения, сумма I равна сумме моментов инерции точечной массы: Для твердого тела, описываемого непрерывной функцией плотности массы? ( r ), I относительно известной оси может быть вычислено путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки в теле до вращения. ось: куда V – объем, занимаемый объектом.? – пространственная функция плотности объекта, а – координаты точки внутри тела. Диаграмма для расчета I. диска. Здесь k составляет 1/2, а r – радиус, используемый для определения момента. Основываясь только на размерном анализе, I неточечного объекта должен принимать форму: куда M – масса R – радиус объекта от центра масс (в некоторых случаях вместо него используется длина объекта). k – это безразмерная константа, называемая константой инерции , которая изменяется в зависимости от рассматриваемого объекта.Инерционные константы используются для учета различий в размещении массы относительно центра вращения. Примеры включают: k = 1, тонкое кольцо или тонкостенный цилиндр вокруг его центра, k = 2/5, сплошная сфера вокруг центра k = 1/2, сплошной цилиндр или диск вокруг его центра.

Теорема о параллельной оси После того, как момент инерции был вычислен для вращений вокруг центра масс твердого тела, его можно удобно пересчитать и для всех параллельных осей вращения, не прибегая к формальному определению.Если ось вращения смещена на расстояние R от центра масс оси вращения (например, вращение диска вокруг точки на его периферии, а не через его центр), смещение и центр-момент инерции связаны следующее: Эта теорема также известна как правило о параллельных осях и является частным случаем теоремы Штейнера о параллельных осях .

Теорема о перпендикулярной оси Теорема о перпендикулярной оси для плоских объектов может быть продемонстрирована, если посмотреть на вклад в трёхосные моменты инерции от произвольного элемента массы.По моменту точечной массы вклады в каждый из осевых моментов инерции равны

Композитные тела Если тело можно разложить (физически или концептуально) на несколько составных частей, то момент инерции тела относительно данной оси получается путем суммирования моментов инерции каждой составной части вокруг той же заданной оси.

Моменты инерции общих форм .