Расчеты на прочность и жесткость при кручении.
Сопротивление материалов
Деформация кручения
Расчеты на прочность и жесткость при кручении
Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:
τmax = Мкр / Wr≤ [τкр],
где [τкр] – предельное допускаемое напряжение.
При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид:
для стали – [τкр] = 0,55….0,6 [σр]
для чугуна – [τкр] = 1,0….1,2 [σр])
(здесь [σр] – справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).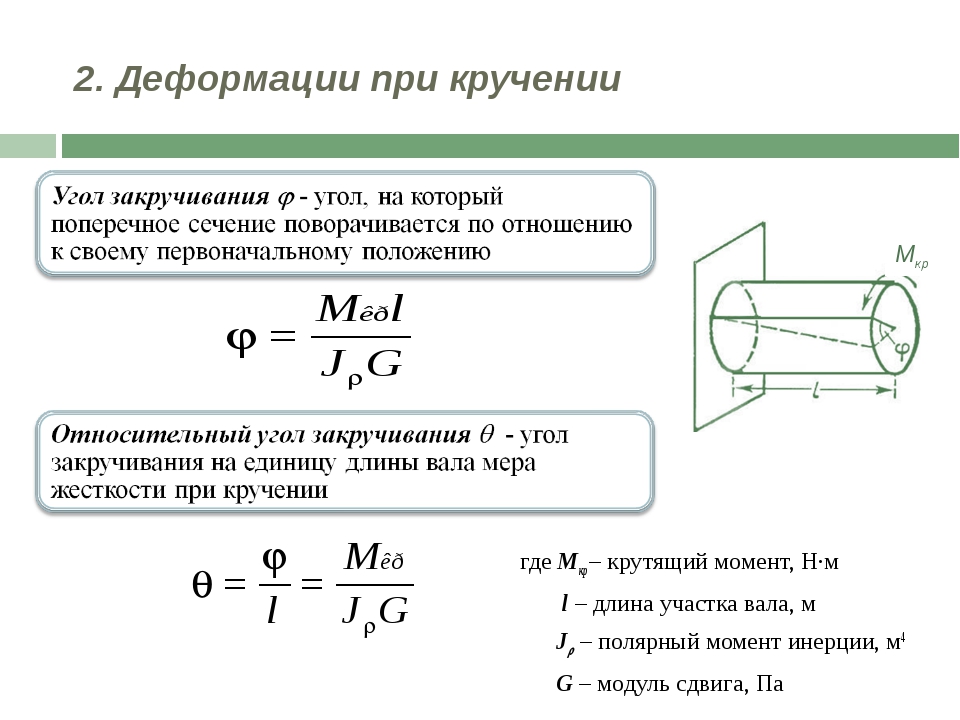
Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции.
Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0°].
Расчетная формула на жесткость при кручении имеет вид:
φ0° = 180 Мкр / (пGIr) ≤ [φ0°]
В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ0°] = 0,25…1 градус/м.
Пример решения задачи на кручение
Определить минимальный допустимый диаметр вала d, передающего крутящий момент М
Решение
По известному передаваемому крутящему моменту можно определить момент сопротивления кручению:
Wr = Мкр / [τкр] = 464 / 30 х 106 = 15,6 х 10-6 м3.
Из зависимости между моментом сопротивления кручению и диаметром вала Wr ≈ 0,2D3 находим минимальный допустимый диаметр:
D ≈ 3√(Wr / 0,02) ≈ 43 мм (здесь и далее √ – знак корня)
Округляя найденное значение диаметра до стандартной величины (в большую сторону), принимаем D = 45 мм.
***
Потенциальная энергия деформации при кручении
Представим себе круглый цилиндрический брус (вал) постоянного сечения, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-либо значения Т.
Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.
Момент Т вызывает в брусе деформацию кручения и при этом совершает работу W, которая аккумулируется в виде потенциальной энергии деформации U, причем пренебрегая незначительными потерями энергии (например, на нагрев бруса), можно считать, что W = U.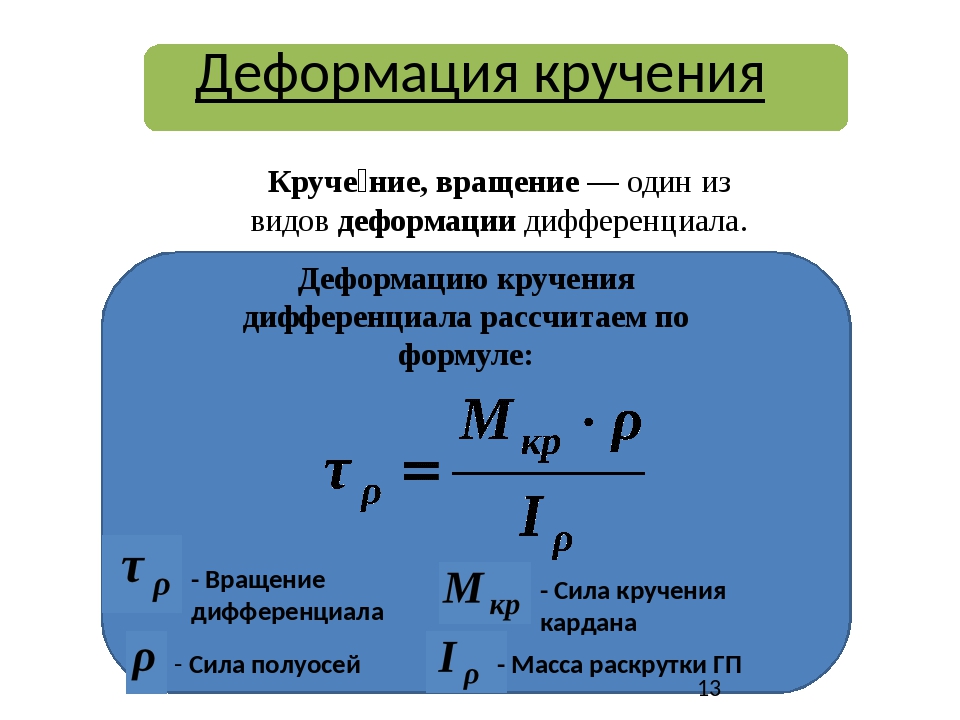
Работа в случае статического нагружения равна: W = Т φ / 2, где φ – полный угол закручивания бруса.
Так как Т = Мкр, то справедливо равенство:
U = W = Т φ / 2 = Мкр2 l / (2Glr).
При одновременном действии нескольких моментов или ступенчатом изменении размеров поперечного сечения брус разбивают на однородные участки и потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий этих участков.
***
Материалы раздела “Деформация кручения”:
Деформация среза
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
| ⇐ ПредыдущаяСтр 14 из 28Следующая ⇒ Иметь представление о напряжении и деформациях при кручении, о моменте сопротивления при кручении. Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении. Напряжения при кручении Проводим на поверхности бруса сетку из продольных и поперечных линий и рассмотрим рисунок, образовавшийся на поверхности после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол (р, продольные линии искривляются, прямоугольники превращаются в параллелограммы. Рассмотрим элемент бруса 1234 после деформации. При выводе формул используем закон Гука при сдвиге и гипотезы плоских сечений и неискривления радиусов поперечных сечений. При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.1б ). При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1 г). Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига. Закон Гука при сдвиге G — модуль упругости при сдвиге, Н/мм2; Напряжение в любой точке поперечного сечения Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2). где τ — касательное напряжение; В силу симметрии сечения силы dQ образуют пары (см. лекцию 26). Элементарный момент силы dQ относительно центра круга где ρ — расстояние от точки до центра круга. Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов: После преобразования получим формулу для определения напряжений в точке поперечного сечения: При ρ = 0 (лекция 25) называется полярным моментом инерции сечения. Анализ полученной формулы для Jv показывает, что слои, расположенные дальше от центра, испытывают большие напряжения. Эпюра распределения касательных напряжений при кручении (рис. 27.3) Мк — крутящий момент в сечении; рв — расстояние от точки тв — напряжение в точке Максимальные напряжения при кручении Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности. Определим максимальное напряжение, учитывая, что ρта х Для круглого сечения полярный момент инерции рассчитывается по формуле (см. лекцию 25). Максимальное напряжение возникает на поверхности, поэтому имеем Обычно JP/pmax обозначают Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу Для круглого сечения Для кольцевого сечения Условие прочности при кручении Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности где [τ к] — допускаемое напряжение кручения. Виды расчетов на прочность Существует два вида расчета на прочность. 1. Проектировочный расчет — определяется диаметр бруса (вала) в опасном сечении: Откуда 2. Проверочный расчет — проверяется выполнение условия прочности 3. Расчет на жесткость При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4). При кручении деформация оценивается углом закручивания (см. лекцию 26): Здесь φ — угол закручивания; Закон Гука имеет вид τ к = Откуда Произведение GJP называют жесткостью сечения. Модуль упругости можно определить как G = 0,4 Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ o. Условие жесткости при кручении можно записать в виде где φ o — относительный угол закручивания, Примеры решения задач Пример 1. Из расчетов на прочность и жесткость определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φо] = 0,02рад/м; модуль упругости при сдвиге Решение 1. Определение размеров поперечного сечения из расчета на прочность. Условие прочности при кручении: Определяем вращающий момент из формулы мощности при вращении: Из условия прочности определяем момент сопротивления вала при кручении Значения подставляем в ньютонах и мм. Определяем диаметр вала: 2. Условие жесткости при кручении: Из условия жесткости определяем момент инерции сечения при кручении: Определяем диаметр вала: 3. Выбор потребного диаметра вала из расчетов на прочность и жесткость. Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее. Полученное значение следует округлить, используя ряд предпочтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение dвала = 75 мм. Для определения диаметра вала желательно пользоваться стандартным рядом диаметров, приведенном в Приложении 2. Пример 2. В поперечном сечении бруса d = 80 мм наибольшее касательное напряжение Решение Эпюра касательных напряжений в поперечном сечении представлена на рис. . Очевидно, откуда Пример 3. В точках внутреннего контура поперечного сечения трубы (d0 = 60 мм; d = 80 мм) возникают касательные напряжения, равные 40 Н/мм2. Определить максимальные касательные напряжения, возникающие в трубе. Решение Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, в . Очевидно, Откуда Пример 4. В кольцевом поперечном сечении бруса (d0 = 30 мм; Решение Касательное напряжение в произвольной точке поперечного сечения вычисляется по формуле В рассматриваемом примере Мz = 3 кН-м = 3-106 Н• мм, Подставляя числовые значения, получаем Пример 5. Стальная труба (d0 = l00 мм; d = 120 мм) длиной l = 1,8 м закручивается моментами Решение Угол закручивания (в град/м) для одного участка вычисляется по формуле тогда В данном случае Подставляя числовые значения, получаем Вычисляем максимальные касательные напряжения: Пример 6. Для заданного бруса (рис. 2.38, а ) построить эпюры крутящих моментов, максимальных касательных напряжений, углов поворота поперечных сечений. Решение Заданный брус имеет участки I, II, III, IV, V (рис. 2. 38, Пользуясь соотношением строим эпюру крутящих моментов. Построение эпюры Мz начинаем со свободного конца бруса: для участков III и Эпюра крутящих моментов представлена на рис, 2. . Строим эпюру максимальных касательных напряжений по длине бруса. Условно приписываем на участке III на участке IV на участке V Эпюра максимальных касательных напряжений показана на рис. 2.38, в . Угол поворота поперечного сечения бруса при постоянных (в пределах каждого участка) диаметре сечения и крутящем моменте определяется по формуле Строим эпюру углов поворота поперечных сечений. Угол поворота сечения А φ л = 0, так как в этом сечении брус закреплен. Эпюра углов поворота поперечных сечений изображена на рис. 2.38, г . Пример 7. На шкив В ступенчатого вала (рис. 2.39, Решение Вычислим внешние (скручивающие) моменты, приложенные к валу: где Строим эпюру крутящих моментов. При этом, двигаясь от левого конца вала, условно считаем момент, соответствующий N А, положительным, что меньше [тк] на Относительный угол закручивания участка АВ что значительно больше [Θ] ==0,3 град/м. Максимальные напряжения в поперечных сечениях участка ВС что меньше [тк] на Относительный угол закручивания участка ВС что значительно больше [Θ] = 0,3 град/м. Следовательно, прочность вала обеспечена, а жесткость — нет. Пример 8. От электродвигателя с помощью ремня на вал 1 передается мощность Решение Нарис. 2.40, б изображен вал и внешние скручивающие моменты ). При этом, двигаясь от левого конца вала, условно считаем моменты, соответствующие Диаметр вала 1 из условия прочности Диаметр вала 1 из условия жесткости ([Θ], рад/мм) Окончательно принимаем с округлением до стандартного значения d1 = 58 мм. Частота вращения вала 2 На рис. 2.40, г изображен вал Эпюра крутящих моментов для вала 2 показана на рис. Диаметр вала 2 из условия прочности Диаметр вала 2 из условия жесткости Окончательно принимаем d2= 62 мм. Пример 9. Определить из условий прочности и жесткости мощность N (рис. 2.41, Решение Вычислим внешние моменты, приложенные к валу: где Расчетная схема вала показана на рис. 2.41, б . На рис. 2.41, в представлена эпюра крутящих моментов. Расчетный (максимальный) крутящий момент откуда Условие жесткости откуда Лимитирующим является условие жесткости. Следовательно, допускаемое значение передаваемой мощности [N] = 82,3 кВт. ⇐ Предыдущая14Следующая ⇒ Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам… ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования… ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между… Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор… Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: |
Момент инерции при кручении – Энциклопедия по машиностроению XXL
Здесь F – площадь поперечного сечения I – длина стержня, балки -момент сопротивления при изгибе 7 — о.севой момент инерции сечения – момент сопротивления при кручении – момент инерции при кручении h — толщина оболочки, пластины г — радиус оболочки, пластины Е, G – moj h упругости при растяжении и сдвиге соответственно а, а, 1, oi2, а% — коэффициенты, зависящие от условий закрепления, нагружения и коэффициента Пуассона /i.Здесь и UJ k — некоторые геометрические характеристики, которые условно называют моментом инерции при кручении и моментом сопротивления при кручении, см и см соответственно.
 [c.220]
[c.220]Условный момент инерции при кручении для эллипса [c.221]
Момент инерции при Кручении 7 см [c.222]
Момент инерции при кручении Jr., -lf [c.176]
Момент инерции при кручении м [c.178]
Момент инерции при кручении определяем по формуле J = ab, где коэффициент а берется по табл. 6.9 в зависимости от соотношения сторон сече-
В формулах (115) и (116) введены обозначения Е — модуль нормальной упругости G — модуль сдвига р — плотность материала Jp — полярный момент инерции — момент инерции при кручении V — коэффициент частоты [c.400]
При расчете на прочность, жесткость и устойчивость элементов машиностроительных конструкций одним из обязательных этапов является установление основных геометрических характеристик поперечного сечения рассчитываемой детали — координат центра тяжести, площади, главных осевых моментов инерции, момента инерции при кручении, минимального радиуса инерции и т.
Если момент инерции при кручении равен нулю, элемент не имеет вращательных степеней свободы в узлах и, следовательно, в модель не требуется вводить закрепления по углам поворота. При задании ненулевого момента инерции при кручении требуется вводить закрепления, исключающие вращение элемента вокруг своей оси как твердого тела.
Замечание. Момент инерции при кручении в этом элементе всегда определен, поэтому в модель требуется вводить закрепления, исключающие вращение элемента вокруг своей оси как твердого тела. [c.191]
Из сравнения этого выражения с (8.53) следует, что момент инерции при кручении стержня с поперечным сечением в виде узкого прямоугольника равен
[c. 177]
177]
Момент инерции при кручении (У ) Для двутаврового профиля может быть подсчитан по формуле (9.38 ) [c.479]
Момент инерции при кручении /к, см Момент сопротивления при кручении см
Момент инерции при кручении Л. СМ+ [c.49]
Момент инерции при кручении /к, см Момент сопротивления при кручении WYi, см Положение точки, в которой возникает наибольшее М напряжение т = [c.51]
Момент инерции при кручении /к- см [c.52]
Вычисление момента инерции при кручении сечения с тонкостенным многосвязным профилем. Для сечения, состоящего из [c.66]
Одновременно с преобразованием расчетных фрагментов рассчитываются необходимые геометрические и жесткостные характеристики элементов, определяются эксцентриситеты связей и оболочек. Для шпангоутов рассчитываются площадь продольного сечения, осевые моменты инерции сечения относительно центра тяжести шпангоута, центробежный момент инерции, момент инерции при кручении.
В табл. 7.2 и 7.3 для тонкостенных поперечных сечений приведены формулы моментов инерции при кручении J и изгибе / . [c.167]
Формулы моментов инерции при кручении J и изгибе [c.169]
Моменты инерции при кручении Ун прокатных двутавров (по ГОСТ 8239—72) [c.387]
Так называемый момент инерции при кручении [c.171]
Для сечений, составленных из тонких прямоугольников, а именно — двутавровых, тавровых, швеллерных и уголковых, условный момент инерции при кручении -можно на-. ходить ло формуле
ходить ло формуле
У н Ц — осевые моменты инерции и еопротивления (при изгибе) J = 2J — полярный момент инерции (при кручении) [c.584]
Смысл выходных параметров следующий Z0, Y0 — координаты центра тяжести сечения z , Уо (11) F — площадь сечения F (9) IZ , IY , IZY — осевые и центробежный центральные моменты инерции 1ц , (12), (13) IP — момент инерции при кручении [р (17) II, 12 — главные центральные моменты инерции /], (14) AL1 — угол наклона первой главной оси к исходной оси 2 — 01 (15) RMIN — минимальный радиус инерции сечения / min (16). [c.324]
Здесь V, w — составляющие полного прогиба стержня в направлении главных осей у, г Q — угол закручивания сечения относительно линии центров изгиба х Е, G — модули упругости первого и второго рода йу, — координаты центра изгиба (рис. 7,18) Jy, JZ, Jh> J i> — главные осевые моменты инерции, момент инерции при кручении и секториальный момент инерции сечения (О — секториальная площадь (rf o = р ds) р — расстояние по нормали между центром изгиба и касательной к контуру = = (Jy + Jz) + al + at F — площадь сечения стержня (dF = h ds) h — толщина стенки s — длина дуги контура.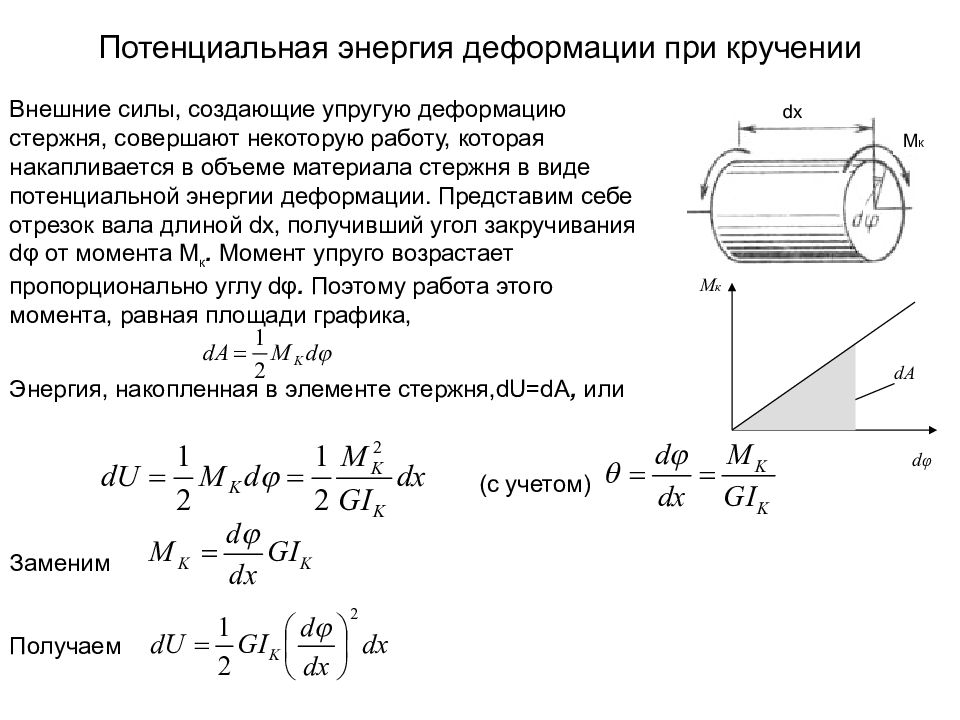 [c.160]
[c.160]
Определение крутящих моментов и построение эпюры
Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент Mк.
Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня.
Правило знаков для крутящих моментов.
Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.
Крутящий момент для сечения можно выразить так: $$M _к(x) = \sum M _{кi} + \sum \int m _i(x)\cdot dx$$
Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид: $$M _к(x) = \sum M _{кi} + \sum m _i(x)\cdot (x- L_{mн}) – \sum m _i(x)\cdot (x- L_{mк})$$
где Lmн и Lmк – расстояние от начала координат до начала и до конца распределенного момента соответственно.
Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:
dMк = m·dx
Общий порядок расчета и построения эпюры.
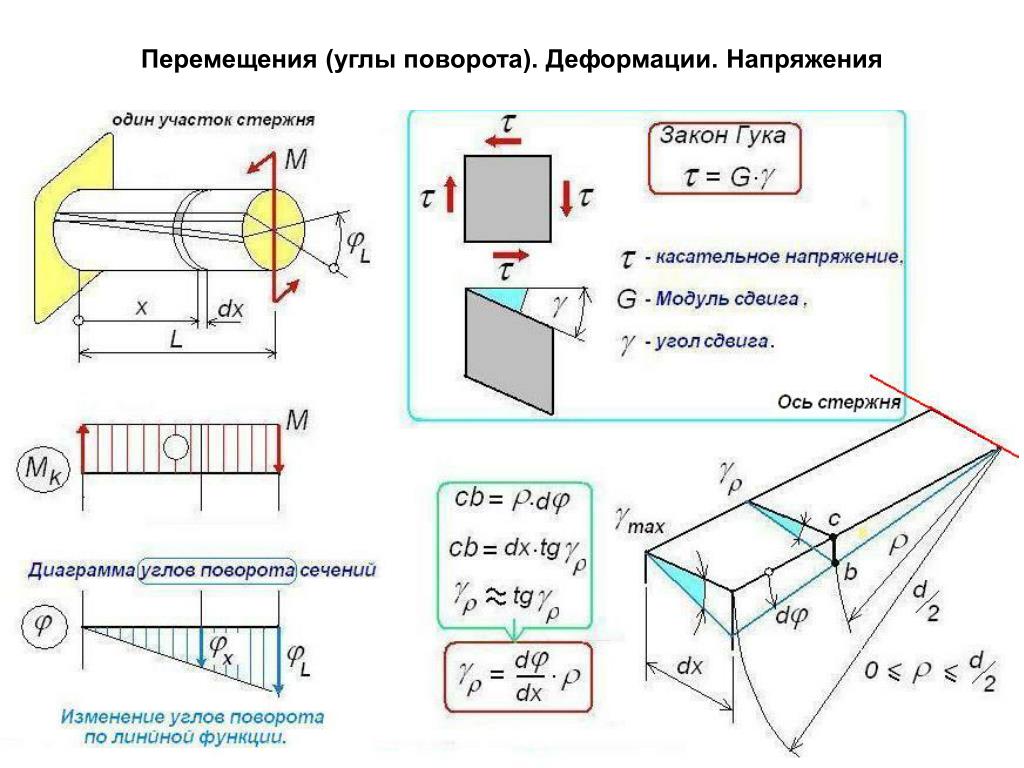
- Намечаем характерные сечения стержня.
- Определяем крутящий момент в каждом характерном сечении.
- По найденным значениям моментов строим эпюру.
Построение эпюр крутящих моментов (пример)
Построить эпюру крутящих моментов для жестко защемленного стержняПусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1=-30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).
1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.
2. Проведем сечение 1. Определим крутящий момент в текущем сечении:
Mк1= Mкв2= 50 кНм
3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом Mк2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:
Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:
Mк2 = Mк1 = Mкв2 = 50 кНм
3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:
Mк3 = Mкв2 – m1*4 = 50 – 10*4 = 10 кНм
4. Аналогично для сечения 4:
Mк4 = Mк3 = 10 кНм
5. Также для сечения 5:
Mк5= Mк4-Mкв1= 10 – 30 = -20 кНм
6. Для сечения 6:
Mк6= Mк5 =-20 кНм
7. По полученным значения строим эпюру крутящих моментов (см. рис.).
Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) Mк6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
Правила контроля правильности эпюр крутящих моментов
Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.
- Эпюры крутящих моментов всегда прямолинейные.
- На участке, где нет распределенных моментов, эпюра Mк – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
- Под точкой приложения сосредоточенного момента на эпюре Mк будет скачок на величину этого момента.
Дополнительно
Еще один вариант построения эпюры крутящих моментов с использованием компьютера найдете на этой странице.
Пример из пособия МИИТ Построение эпюры крутящих моментов (формат pdf).
метки: внутренние усилия, кручение
Крутящий момент и зависимость крутящего момента
Как рассчитать крутящий момент, зная обороты и мощность двигателя?
Крутящий момент напрямую зависит от мощности и числа оборотов двигателя в минуту. Имеется общепринятая формула расчета крутящего момента, выражаемого в Ньютон-метрах ( русское обозначение Н·м, международное N·m )
Имеется общепринятая формула расчета крутящего момента, выражаемого в Ньютон-метрах ( русское обозначение Н·м, международное N·m )
M = P х 9550 / N
Где P – это мощность двигателя в киловаттах (кВт)
N – обороты вала в минуту
Как рассчитать мощность двигателя, зная крутящий момент и обороты?
Для такого расчета существует формула:
P = M х N / 9550
Где M – это крутящий момент двигателя
N – это обороты двигателя
Для скорости и простоты расчета воспользуйтесь удобным калькулятором крутящего момента. Впишите в ячейки калькулятора имеющиеся значения и калькулятор автоматически проставит результаты расчета.
Впишите в ячейки калькулятора имеющиеся значения и калькулятор автоматически проставит результаты расчета.
Калькулятор крутящего момента
Что такое крутящий момент электродвигателя
Одним из важных параметров электродвигателя, который так же важен при его выборе, является крутящий момент. Эта величина определяется произведением приложенной к плечу рычага силы и зависит исключительно от степени нагрузки. Если в двигателях внутреннего сгорания данную нагрузку задаётся коленчатым валом, то асинхронные электродвигатели получают величину крутящего момента от токов возбуждения. При этом величина этого момента будет зависеть от скорости вращающегося в магнитном поле статора устройства, называемого ротор. В зависимости от периода и способа определения, крутящий момент разделяют на:
В зависимости от периода и способа определения, крутящий момент разделяют на:
- статический (пусковой) – минимальный момент холостого хода;
- промежуточный – развивает значение при работе двигателя от 0 величины оборотов до максимального значения в номинальной величине напряжения;
- максимальный – развивающийся при эксплуатации двигателя;
- номинальный – соответствует номинальным значениям мощности и оборотов.
Для вычисления величины крутящего момента, определяющегося в «кгм» (килограмм на метр) или «Нм» (ньютон на метр), многие электротехнические пособия предлагают специальные формулы, учитывающие кроме основного действия вращающегося магнитного поля ряд всевозможных факторов, например:
- напряжения сети;
- величину индуктивного и активного сопротивления;
- зависимость от увеличения скольжения.
Но, рост скольжения не всегда приносит высокий момент. Зачастую, при достижении критических значений, наблюдается его резкое снижение. Такое явление обозначается как опрокидывающий момент. Одним из устройств, стабилизирующих скорость вращения ротора, а значит и величину момента кручения является частотный преобразователь, применение которого сейчас очень распространено во всех сферах, где от контроля работы двигателя зависит и успешность выполнения множественных производственных задач.
Зачастую, при достижении критических значений, наблюдается его резкое снижение. Такое явление обозначается как опрокидывающий момент. Одним из устройств, стабилизирующих скорость вращения ротора, а значит и величину момента кручения является частотный преобразователь, применение которого сейчас очень распространено во всех сферах, где от контроля работы двигателя зависит и успешность выполнения множественных производственных задач.
Выбираем электродвигатель по крутящему моменту
Для выбора, требуемого к выполнению тех или иных задач электродвигателя, берут в учёт практически все его характеристики, начиная от показателей мощности и заканчивая массогабаритными параметрами. Каждый из элементов по-своему важен в решении нюансов. Не меньшее значение припадает и на крутящий момент. Благодаря тому, что момент кручения напрямую связан с оборотами в соотношении: чем больше сами обороты, тем меньше будет момент, выбор электродвигателя будет исходить из следующих нюансов:
- из скоростных требований.
 В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях;
В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях; - по пусковым напряжениям. Здесь учитывается первичное усилие, например, для управления лифтом следует подбирать двигатели высокого пускового момента, способного поднимать большие грузы со старта. Хотя, многие статьи про электродвигатели рекомендуют так же применять устройства плавного пуска, умеющие обезопасить от нежелательных перегрузов.
Стоит помнить, что выбор осуществляется не по одному из показателей, даже при ориентировании относительно крутящего момента, ведь каждый из показателей ориентируется по рабочей предрасположенности электротехнического приводного устройства и его рабочих нагрузок в статистических и динамических эксплуатационных условиях, задаваемых самим предприятием.
Электродвигатели Остались вопросы?
Специалисты ЭНЕРГОПУСК ответят на Ваши вопросы:
8-800-700-11-54 (8-18, Пн-Вт)
| ⇐ ПредыдущаяСтр 14 из 28Следующая ⇒ Иметь представление о напряжении и деформациях при кручении, о моменте сопротивления при кручении. Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении. Напряжения при кручении Проводим на поверхности бруса сетку из продольных и поперечных линий и рассмотрим рисунок, образовавшийся на поверхности после деформации (рис. продольные линии искривляются, прямоугольники превращаются в параллелограммы. Рассмотрим элемент бруса 1234 после деформации. При выводе формул используем закон Гука при сдвиге и гипотезы плоских сечений и неискривления радиусов поперечных сечений. При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.1б ). При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1 г).
Закон Гука при сдвиге G — модуль упругости при сдвиге, Н/мм2; Напряжение в любой точке поперечного сечения Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. где τ — касательное напряжение; В силу симметрии сечения силы dQ образуют пары (см. лекцию 26). Элементарный момент силы dQ относительно центра круга где ρ — расстояние от точки до центра круга. Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов: После преобразования получим формулу для определения напряжений в точке поперечного сечения: При ρ = 0 (лекция 25) называется полярным моментом инерции сечения. Анализ полученной формулы для Jv показывает, что слои, расположенные дальше от центра, испытывают большие напряжения. Эпюра распределения касательных напряжений при кручении (рис. 27.3) Мк — крутящий момент в сечении; рв — расстояние от точки тв — напряжение в точке Максимальные напряжения при кручении Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности. Определим максимальное напряжение, учитывая, что ρта х Для круглого сечения полярный момент инерции рассчитывается по формуле (см. лекцию 25). Максимальное напряжение возникает на поверхности, поэтому имеем Обычно JP/pmax обозначают Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу Для круглого сечения Для кольцевого сечения Условие прочности при кручении Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности где [τ к] — допускаемое напряжение кручения. Виды расчетов на прочность Существует два вида расчета на прочность. 1. Проектировочный расчет — определяется диаметр бруса (вала) в опасном сечении: Откуда 2. Проверочный расчет — проверяется выполнение условия прочности 3. Определение нагрузочной способности (максимального крутящего момента) Расчет на жесткость При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4). При кручении деформация оценивается углом закручивания (см. лекцию 26): Здесь φ — угол закручивания; Закон Гука имеет вид τ к = Откуда Произведение GJP называют жесткостью сечения. Модуль упругости можно определить как G = 0,4 Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ o. Условие жесткости при кручении можно записать в виде где φ o — относительный угол закручивания, Примеры решения задач Пример 1. Из расчетов на прочность и жесткость определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φо] = 0,02рад/м; модуль упругости при сдвиге Решение 1. Определение размеров поперечного сечения из расчета на прочность. Условие прочности при кручении: Определяем вращающий момент из формулы мощности при вращении: Из условия прочности определяем момент сопротивления вала при кручении Значения подставляем в ньютонах и мм. Определяем диаметр вала: 2. Определение размеров поперечного сечения из расчета на жесткость. Условие жесткости при кручении: Из условия жесткости определяем момент инерции сечения при кручении: Определяем диаметр вала: 3. Выбор потребного диаметра вала из расчетов на прочность и жесткость. Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее. Полученное значение следует округлить, используя ряд предпочтительных чисел. Практически округляем полученное значение так, чтобы число заканчивалось на 5 или 0. Принимаем значение dвала = 75 мм. Для определения диаметра вала желательно пользоваться стандартным рядом диаметров, приведенном в Приложении 2. Пример 2. В поперечном сечении бруса d = 80 мм наибольшее касательное напряжение Решение Эпюра касательных напряжений в поперечном сечении представлена на рис. . Очевидно, откуда Пример 3. В точках внутреннего контура поперечного сечения трубы (d0 = 60 мм; d = 80 мм) возникают касательные напряжения, равные 40 Н/мм2. Определить максимальные касательные напряжения, возникающие в трубе. Решение Эпюра касательных напряжений в поперечном сечении представлена на рис. 2.37, в . Очевидно, Откуда Пример 4. В кольцевом поперечном сечении бруса (d0 = 30 мм; Решение Касательное напряжение в произвольной точке поперечного сечения вычисляется по формуле В рассматриваемом примере Мz = 3 кН-м = 3-106 Н• мм, Подставляя числовые значения, получаем Пример 5. Стальная труба (d0 = l00 мм; d = 120 мм) длиной l = 1,8 м закручивается моментами Решение Угол закручивания (в град/м) для одного участка вычисляется по формуле тогда В данном случае Подставляя числовые значения, получаем Вычисляем максимальные касательные напряжения: Пример 6. Для заданного бруса (рис. 2.38, а ) построить эпюры крутящих моментов, максимальных касательных напряжений, углов поворота поперечных сечений. Решение Заданный брус имеет участки I, II, III, IV, V (рис. 2. 38, Пользуясь соотношением строим эпюру крутящих моментов. Построение эпюры Мz начинаем со свободного конца бруса: для участков III и Эпюра крутящих моментов представлена на рис, 2. . Строим эпюру максимальных касательных напряжений по длине бруса. Условно приписываем на участке III на участке IV на участке V Эпюра максимальных касательных напряжений показана на рис. 2.38, в . Угол поворота поперечного сечения бруса при постоянных (в пределах каждого участка) диаметре сечения и крутящем моменте определяется по формуле Строим эпюру углов поворота поперечных сечений. Угол поворота сечения А φ л = 0, так как в этом сечении брус закреплен. Эпюра углов поворота поперечных сечений изображена на рис. 2.38, г . Пример 7. На шкив В ступенчатого вала (рис. 2.39,
Вычислим внешние (скручивающие) моменты, приложенные к валу: где Строим эпюру крутящих моментов. При этом, двигаясь от левого конца вала, условно считаем момент, соответствующий N А, положительным, что меньше [тк] на Относительный угол закручивания участка АВ что значительно больше [Θ] ==0,3 град/м. Максимальные напряжения в поперечных сечениях участка ВС что меньше [тк] на Относительный угол закручивания участка ВС что значительно больше [Θ] = 0,3 град/м. Следовательно, прочность вала обеспечена, а жесткость — нет. Пример 8. От электродвигателя с помощью ремня на вал 1 передается мощность Решение Нарис. 2.40, б изображен вал и внешние скручивающие моменты ). При этом, двигаясь от левого конца вала, условно считаем моменты, соответствующие Диаметр вала 1 из условия прочности Диаметр вала 1 из условия жесткости ([Θ], рад/мм) Окончательно принимаем с округлением до стандартного значения d1 = 58 мм. Частота вращения вала 2 На рис. 2.40, г изображен вал Эпюра крутящих моментов для вала 2 показана на рис. Диаметр вала 2 из условия прочности Диаметр вала 2 из условия жесткости Окончательно принимаем d2= 62 мм. Пример 9. Определить из условий прочности и жесткости мощность N (рис. 2.41, Решение Вычислим внешние моменты, приложенные к валу: где Расчетная схема вала показана на рис. 2.41, б . На рис. 2.41, в представлена эпюра крутящих моментов. Расчетный (максимальный) крутящий момент откуда Условие жесткости откуда Лимитирующим является условие жесткости. Следовательно, допускаемое значение передаваемой мощности [N] = 82,3 кВт. ⇐ Предыдущая14Следующая ⇒ Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)… Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все… Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем… Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право… Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: |
Крутящий момент
Загрузка
Мощность — это скорость, с которой совершается работа, то есть скорость, с которой энергия передается силой. Сила вращения, создаваемая двигателем (с помощью которой передается энергия), называется крутящим моментом.
об/мин — это сокращение от «оборотов в минуту». Это скорость, с которой двигатель вращает маховик.
Это скорость, с которой двигатель вращает маховик.
Двигатели внутреннего сгорания (ДВС) не производят одинаковую мощность на всех скоростях двигателя, следовательно, будет частота вращения двигателя (об/мин), при которой двигатель будет генерировать максимальную мощность.То же самое и с крутящим моментом.
В качестве характеристики двигателя внутреннего сгорания максимальный крутящий момент обычно создается при меньшей частоте вращения двигателя, чем при максимальной мощности.
Гораздо проще.
Мощность – это количество энергии, которое двигатель может передать за время… (Вот откуда вы берете пикап)
Крутящий момент – это грузоподъемность.
Так что это зависит от ваших потребностей. Чем большее ускорение вы хотите, тем больше мощности вам нужно… в то время как в случае, если вам нужно нести груз, вам нужен больший крутящий момент.
Об/мин указывает, при каких оборотах двигатель может развивать максимальную мощность/крутящий момент.
Бензиновые автомобили лучше развивают мощность, а дизельные двигатели — крутящий момент.
Для ускорения нужны и мощность, и крутящий момент. Проще говоря, крутящий момент — это скорость, с которой двигатель может производить мощность. Помните, что ускорение — это скорость, с которой изменяется скорость, поэтому для поддержания скорости вам нужна мощность для преодоления сопротивления (трение о дорогу, трение о воздух, а также трение в движущихся частях двигателя автомобиля и трансмиссии).Как правило, число оборотов в минуту между максимальным крутящим моментом и максимальной мощностью является диапазоном мощности автомобиля, нижний предел этого диапазона соответствует диапазону, в котором вы будете двигаться, а верхний предел соответствует диапазону, в котором вы участвуете в гонках.
А теперь немного подробнее.
Крутящий момент (Тл, Нм) является произведением массы вращения (Дж, инерции) x (угловое ускорение, изменение скорости в зависимости от изменения во времени, dw/dt). 2).Радиус F x станет
более важно позже.
2).Радиус F x станет
более важно позже.
Крутящий момент — это мера того, какая сила, действующая на объект, заставляет этот объект вращаться. Объект вращается вокруг оси, которую мы назовем точкой вращения и обозначим буквой «О». Мы назовем силу «F». Расстояние от точки вращения до точки, в которой действует сила, называется плечом момента и обозначается буквой «r». Обратите внимание, что это расстояние «r» также является вектором и указывает от оси вращения до точки, где действует сила.(Обратитесь к рисунку 1 для графического представления этих определений.)
Вы создаете крутящий момент каждый раз, когда применяете силу с помощью гаечного ключа. Хорошим примером является затяжка гаек на колесах. Когда вы используете гаечный ключ, вы прикладываете усилие к рукоятке. Эта сила создает крутящий момент на гайке, который стремится провернуть гайку.
Единицей СИ для крутящего момента является ньютон-метр (Нм). В имперских и американских единицах измерения он измеряется в фут-фунтах (фут-фунт-сила) (также известный как «фунт-фут»), а для меньшего измерения крутящего момента: в дюйм-фунтах (дюйм-фунт-сила) или даже в дюйм-унциях (дюйм-унция). .
.
Крутящий момент определяется как:
| r X F = r F sin |
Обратите внимание, что единицы крутящего момента содержат расстояние и силу. Чтобы рассчитать крутящий момент в имперских единицах, вы просто умножаете силу на расстояние от центра. В случае с зажимными гайками, если ключ имеет длину в фут и вы прикладываете к нему усилие в 200 фунтов, вы создаете крутящий момент в 200 фунт-футов.Если вы используете 2-футовый ключ, вам нужно приложить к нему всего 100 фунтов силы, чтобы создать такой же крутящий момент.
В единицах СИ сила в три ньютона, приложенная, например, в двух метрах от зажимных гаек, создает такой же крутящий момент, как один ньютон, приложенный в шести метрах от зажимных гаек. Это предполагает, конечно, в обоих случаях, что сила направлена под прямым углом к прямому рычагу.
Автомобильный двигатель создает крутящий момент и использует его для вращения коленчатого вала. Этот крутящий момент создается точно так же: сила прикладывается на расстоянии.Давайте внимательно посмотрим на некоторые детали двигателя:
Этот крутящий момент создается точно так же: сила прикладывается на расстоянии.Давайте внимательно посмотрим на некоторые детали двигателя:
Сгорание газа в цилиндре создает давление на поршень. Это давление создает силу на головке поршня, которая толкает ее вниз. Усилие передается от поршня к шатуну, а от шатуна к коленчатому валу. Обратите внимание, что точка крепления шатуна к коленчатому валу находится на некотором расстоянии от центра вала. Горизонтальное расстояние изменяется по мере вращения коленчатого вала, поэтому изменяется и крутящий момент, поскольку крутящий момент равен силе, умноженной на расстояние.
Вам может быть интересно, почему только горизонтальное расстояние важно для определения крутящего момента в этом двигателе. Вы можете видеть, что когда поршень находится в верхней или нижней части своего хода, шатун указывает прямо вниз или вверх в центре коленчатого вала. В этом положении крутящий момент не создается, потому что только сила, действующая на рычаг в направлении, перпендикулярном рычагу, создает крутящий момент.
Таким же образом можно описать работу двигателя Roto Wankel.На изображении выше вы можете видеть синий «шатун», соединенный с центральным валом. При изменении угла изменяется крутящий момент, но редко случается, что «синий шатун» указывает прямо на центр коленчатого вала. Точнее, каждое третье вращение. Двигатель Отто делает это дважды за каждый оборот. И, как я объяснял ранее, это момент, когда крутящий момент равен 0. Вот почему двигатель Ванкеля имеет лучший крутящий момент и мощность, чем двигатель Отто.
Крутящий момент в физике — это псевдовектор, который измеряет тенденцию силы вращать объект вокруг некоторой оси (или точки опоры, или точки поворота).Точно так же, как сила представляет собой толчок или тягу, крутящий момент можно рассматривать как крутящий момент. Символом крутящего момента является греческая буква тау.
Крутящий момент также называют моментом или моментом силы. Это не следует путать с различными другими определениями «момент» в физике. В контексте машиностроения термины «момент» и «крутящий момент» не обязательно взаимозаменяемы; скорее, тот или иной предпочтительнее в конкретном контексте. Например, «крутящий момент» обычно используется для описания силы вращения на валу, например, с помощью гаечного ключа, тогда как «момент» чаще используется для описания изгибающей силы, действующей на балку.
В контексте машиностроения термины «момент» и «крутящий момент» не обязательно взаимозаменяемы; скорее, тот или иной предпочтительнее в конкретном контексте. Например, «крутящий момент» обычно используется для описания силы вращения на валу, например, с помощью гаечного ключа, тогда как «момент» чаще используется для описания изгибающей силы, действующей на балку.
Величина крутящего момента зависит от трех величин: во-первых, приложенной силы; во-вторых, длина плеча рычага, соединяющего ось с точкой приложения силы; и в-третьих, угол между ними. Опять же условными обозначениями:
Где
Особенно важна длина плеча рычага; Правильный выбор этой длины лежит в основе работы рычагов, шкивов, шестерен и большинства других простых механизмов, требующих механического преимущества
Направление крутящего момента можно определить с помощью правила захвата правой рукой: согните пальцы правой руки, чтобы указать направление вращения, и вытяните большой палец так, чтобы он совпадал с осью вращения. Ваш большой палец указывает в направлении вектора крутящего момента.
Ваш большой палец указывает в направлении вектора крутящего момента.
Крутящий момент является частью базовой спецификации двигателя: выходная мощность двигателя выражается как его крутящий момент, умноженный на его скорость вращения оси. Двигатели внутреннего сгорания создают полезный крутящий момент только в ограниченном диапазоне скоростей вращения (обычно от 2000 до 5000 об / мин для небольшого автомобиля). Изменение выходного крутящего момента в этом диапазоне можно измерить с помощью динамометра и показать в виде кривой крутящего момента. Пик этой кривой крутящего момента находится несколько ниже общего пика мощности.Пик крутящего момента не может по определению появляться при более высоких оборотах, чем пик мощности.
Понимание взаимосвязи между крутящим моментом, мощностью и частотой вращения двигателя имеет жизненно важное значение в автомобилестроении, поскольку оно связано с передачей мощности от двигателя через трансмиссию к колесам. Мощность обычно зависит от крутящего момента и частоты вращения двигателя.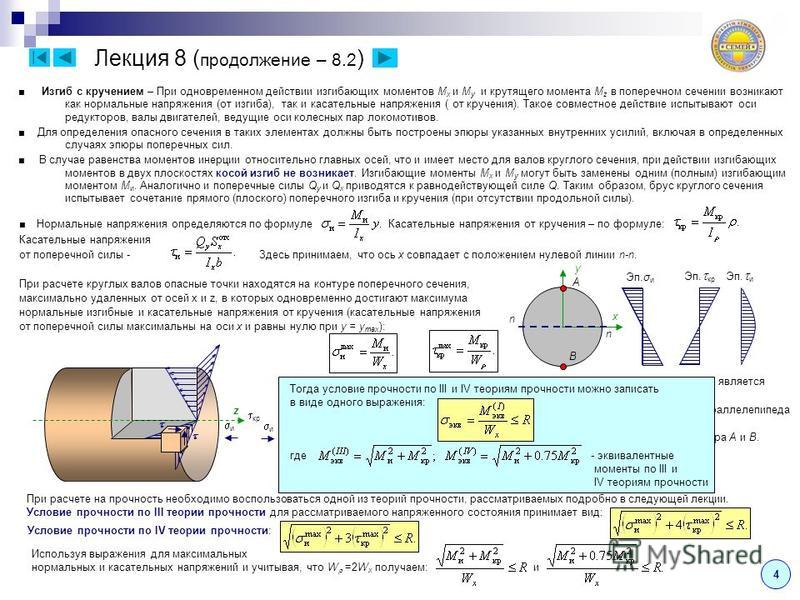 Зубчатая передача трансмиссии должна быть выбрана соответствующим образом, чтобы максимально использовать характеристики крутящего момента двигателя.
Зубчатая передача трансмиссии должна быть выбрана соответствующим образом, чтобы максимально использовать характеристики крутящего момента двигателя.
Как правило, кривая крутящего момента двигателя с турбонаддувом представляет собой крутой подъем, а затем пологую почти до максимальных оборотов.Типичный атмосферный двигатель очень отличается, с очень низким крутящим моментом на низких оборотах, а затем быстрым ростом оборотов до пикового крутящего момента, а затем снова быстрым падением. Область под кривой крутящего момента Turbo намного больше у турбодвигателя. И если вы удвоите крутящий момент, вы удвоите ускорение, уберите из него коробку передач. Крутящий момент играет роль в улучшении ускорения именно по тем причинам, которые я изложил в отношении кривой крутящего момента: большее количество передач позволяет разработчику удерживать двигатель в более точном диапазоне оборотов, обеспечивающих максимальный крутящий момент.Атмосферному двигателю нужны обороты для производства мощности.
Если сила действует на расстоянии, она совершает механическую работу. Точно так же, если крутящему моменту позволено действовать через расстояние вращения, он совершает работу. Мощность – это работа в единицу времени. Однако время и расстояние вращения связаны угловой скоростью, где каждый оборот приводит к тому, что длина окружности проходит под действием силы, создающей крутящий момент.
Мощность, инжектируемая приложенным крутящим моментом, может быть рассчитана как:
Мощность = крутящий момент x угловая скорость
Как видите, крутящий момент и мощность напрямую связаны.Мощность — это просто приложение X количества крутящего момента в течение Y времени. Необходимо использовать согласованные единицы. Для метрических единиц СИ мощность – это ватты, крутящий момент – это ньютон-метры, а угловая скорость – это радианы в секунду (не об/мин и не обороты в секунду).
В правой части это скалярное произведение двух векторов, дающее скаляр в левой части уравнения.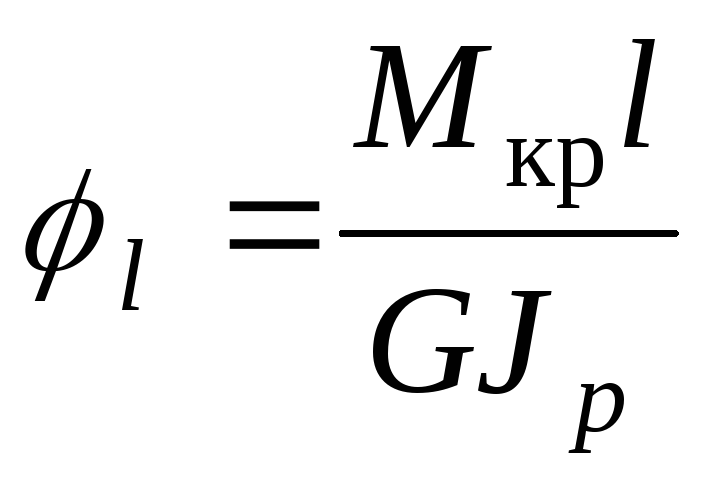 Математически уравнение можно изменить, чтобы вычислить крутящий момент для заданной выходной мощности. Обратите внимание, что мощность, подаваемая крутящим моментом, зависит только от мгновенной угловой скорости, а не от того, увеличивается ли угловая скорость, уменьшается или остается постоянной во время приложения крутящего момента (это эквивалентно линейному случаю, когда мощность, подаваемая силой зависит только от мгновенной скорости, а не от результирующего ускорения, если таковое имеется).
Математически уравнение можно изменить, чтобы вычислить крутящий момент для заданной выходной мощности. Обратите внимание, что мощность, подаваемая крутящим моментом, зависит только от мгновенной угловой скорости, а не от того, увеличивается ли угловая скорость, уменьшается или остается постоянной во время приложения крутящего момента (это эквивалентно линейному случаю, когда мощность, подаваемая силой зависит только от мгновенной скорости, а не от результирующего ускорения, если таковое имеется).
Для различных единиц мощности, крутящего момента или угловой скорости в уравнение необходимо ввести коэффициент преобразования. Кроме того, если скорость вращения (оборот за время) используется вместо угловой скорости (радианы за время), необходимо добавить коэффициент преобразования 2Pi, поскольку в одном обороте 2Pi радиан:
Мощность = крутящий момент X 2π X скорость вращения
, где скорость вращения выражается в оборотах в единицу времени.
Теперь вы можете рассчитать мощность вашего автомобиля при заданных оборотах.И теперь вы понимаете, почему Формула 1 так жаждет оборотов двигателя. Самый «простой» способ увеличить мощность — увеличить скорость вращения двигателя.
Аа, кстати, Формула 1!
В Формуле-1 инженеры склонны сопоставлять уровень крутящего момента двигателя для отдельных трасс, для разных участков трассы и для разных условий на гоночной трассе. Карты двигателей — одно из темных искусств F1. На мокрой трассе нет смысла использовать высокое значение крутящего момента. Карта крутящего момента двигателя представляет крутящий момент, создаваемый двигателем, в зависимости от частоты вращения двигателя и положения дроссельной заслонки двигателя.В ЭБУ карта крутящего момента двигателя используется для позиционирования дроссельной заслонки двигателя в соответствии с потребностями водителя в крутящем моменте. Карта крутящего момента водителя представляет крутящий момент, запрошенный водителем, в зависимости от частоты вращения двигателя и положения педали акселератора. FIA ввела правила, которые определяют, как вы можете контролировать крутящий момент двигателя, и подпадают под действие статей 5.5 и 5.6 технического регламента.
FIA ввела правила, которые определяют, как вы можете контролировать крутящий момент двигателя, и подпадают под действие статей 5.5 и 5.6 технического регламента.
За некоторыми особыми исключениями, крутящий момент двигателя должен контролироваться водителем. Эти исключения включают в себя: переключение на более низкую передачу, ограничитель скорости на пит-лейн, функцию предотвращения заклинивания и стратегию ограничителя конца прямой.Обратите внимание, что здесь перечислены не все исключения. Есть много других.
Водитель может управлять крутящим моментом только с помощью одной педали акселератора.
При педали с нулевым процентом (отключена дроссельная заслонка) требуемый крутящий момент должен быть меньше или равен нулю; при педали 100% (полный газ) требуемый крутящий момент должен соответствовать или превышать максимальный крутящий момент двигателя в его текущем состоянии (Статья 5.5.3).
Существуют ограничения на форму требуемого крутящего момента в зависимости от положения педали и частоты вращения двигателя (для предотвращения характеристик двигателя, которые могут использоваться в качестве вспомогательных средств для водителя).
При соблюдении этих ограничений требуемый крутящий момент формируется в зависимости от положения дроссельной заслонки и частоты вращения двигателя, чтобы обеспечить желаемую реакцию водителя и автомобиля.
Карты педалей водителя можно менять от цепи к цепи в зависимости от характеристик цепи. Например, водители могут захотеть большей точности при первом нажатии педали в Монако. Точно так же некоторые водители настаивают на карте педали для влажной погоды.
Карты крутящего момента двигателя также корректируются с учетом выходной мощности двигателя в зависимости от условий окружающей среды.Все двигатели будут развивать больший крутящий момент в холодный день в Сильверстоуне, чем в Интерлагосе (низкое давление воздуха) или Малайзии (высокая удельная влажность). Это гарантирует, что водители будут чувствовать одинаковую реакцию двигателя при частичной нагрузке, независимо от погоды.
Карты крутящего момента также могут измениться вследствие изменений выхлопной системы или воздухозаборника (если команды представят новую конструкцию выхлопной трубы или новый воздухозаборник).
Паровые двигатели и электродвигатели (особенно электродвигатели постоянного тока – постоянного тока), как правило, создают максимальный крутящий момент, близкий к нулю оборотов в минуту, при этом крутящий момент уменьшается по мере увеличения скорости вращения.
Чтобы узнать больше, пожалуйста, прочитайте мои статьи о карте крутящего момента.
Вернуться к началу страницы
Основное уравнение крутящего момента электродвигателя
Базовое уравнение крутящего момента электродвигателя
Общие
Меню технических и проектных данных
Промышленный
Применение электродвигателя, меню проектирования и установки
Поставка промышленных электродвигателей
Уравнение: Т = FR
Где:
T = крутящий момент, фунт-фут
F = усилие, фунт
R = радиус или расстояние, от которого действует сила
место поворота, фут
Развиваемый крутящий момент:
Уравнение для крутящего момента, развиваемого двигателем постоянного тока, можно вывести следующим образом.
Сила, действующая на один виток проволоки F =i l x B Ньютон
Обратите внимание, что l и B являются векторными величинами
Поскольку B = φ /A , где A — площадь катушки,
Следовательно, крутящий момент для многовитковой катушки с током якоря I a :
T = K φ Ia
Где φ — поток/полюс в Вебере, K — константа, зависящая от геометрии катушки, а I a — ток, протекающий в обмотке якоря.
Примечание. Крутящий момент T является функцией силы и расстояния, уравнение (2) объединяет все постоянные параметры (например, длину, площадь и расстояние) в константе K.
Генерируемая механическая мощность является произведением крутящего момента машины и механической скорости вращения, ω м
или
P м = ω м T
= ω м K φ a
Интересно отметить, что одну и ту же машину постоянного тока можно использовать либо как двигатель, либо как генератор, поменяв местами клеммные соединения.
Использование уравнений крутящего момента – AP Physics C: Mechanics
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать крутящий момент нагрузки
Правильный расчет двигателя требует соблюдения трех критериев: крутящий момент, инерция нагрузки и скорость.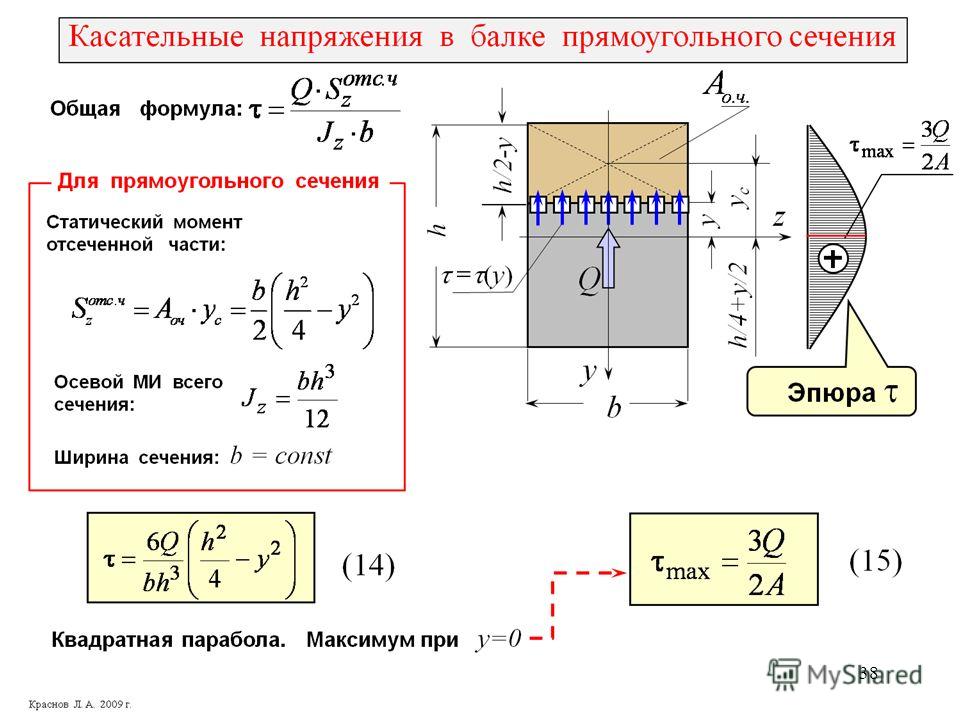 В первой части этой серии статей «Основы определения размеров двигателя» я объясню, что такое крутящий момент нагрузки, как его рассчитать для конкретных примеров применения и как он соответствует требованиям к крутящему моменту для приложения.
В первой части этой серии статей «Основы определения размеров двигателя» я объясню, что такое крутящий момент нагрузки, как его рассчитать для конкретных примеров применения и как он соответствует требованиям к крутящему моменту для приложения.
Крутящий момент определяется как сила вращения на расстоянии от оси вращения. Он измеряется в таких единицах, как фунт-дюйм (фунт-дюйм) в имперской системе или Нм (ньютон-метр) в метрической системе. Крутящий момент так же важен, если не важнее, чем мощность двигателя. Мощность — это скорость, с которой может выполняться работа, и рассчитывается путем умножения крутящего момента на скорость. Другими словами, крутящий момент — это способность выполнять работу, а мощность — это скорость, с которой эта работа может быть выполнена.
Крутящий момент имеет 2 основных компонента: момент нагрузки и момент ускорения. Момент нагрузки представляет собой величину крутящего момента, постоянно требуемую для применения, и включает в себя нагрузку от трения и гравитационную нагрузку. Ускоряющий крутящий момент — это крутящий момент, необходимый только для максимального ускорения и замедления нагрузки. Чем быстрее нагрузка должна разгоняться, тем выше ускоряющий момент. Иногда момент нагрузки выше; иногда момент ускорения может быть выше. Важно рассчитать оба; особенно для профилей быстрого движения.
Ускоряющий крутящий момент — это крутящий момент, необходимый только для максимального ускорения и замедления нагрузки. Чем быстрее нагрузка должна разгоняться, тем выше ускоряющий момент. Иногда момент нагрузки выше; иногда момент ускорения может быть выше. Важно рассчитать оба; особенно для профилей быстрого движения.
На изображении выше мы показываем несколько стрелок, которые показывают направление сил, взаимодействующих в этом приложении.Как вы думаете, что такое момент нагрузки? Ответ оба.
Момент нагрузки представляет собой сумму нагрузок трения и силы тяжести. Гравитационная сила определяется весом или массой, умноженной на ускорение свободного падения ( г ). Сила трения, действующая в направлении, противоположном направлению движения конвейера, рассчитывается путем умножения массы груза на коэффициент трения двух поверхностей: м x µ .
Расчет крутящего момента нагрузки отличается для различных приложений. Давайте рассмотрим несколько распространенных примеров, чтобы увидеть, как рассчитывается крутящий момент нагрузки.
Давайте рассмотрим несколько распространенных примеров, чтобы увидеть, как рассчитывается крутящий момент нагрузки.
Для привода шкивов расчет крутящего момента достаточно прост. Нам нужно создать силу на некотором расстоянии от вала двигателя (определение крутящего момента). Это можно рассчитать, умножив силу ( F ) на радиус вращения ( r ). Для перемещения груза (синяя рамка) двигатель должен генерировать больший крутящий момент, чем это значение.
Чтобы рассчитать момент нагрузки, умножьте силу ( F ) на расстояние от оси вращения, которое является радиусом шкива ( r ) . Если масса груза (синяя рамка) составляет 20 ньютонов, а радиус шкива составляет 5 см, то требуемый крутящий момент для приложения составляет 20 Н x 0,05 м = 1 Нм. Как правило, коэффициент безопасности используется для того, чтобы двигатель генерировал больший крутящий момент, чем требуется для учета любых неточностей в переменных, используемых для расчета.
Вот формула для расчета момента нагрузки для шкива со всеми переменными:
|
Приведенная выше формула работает для приложений с нагрузкой трения или без нее. Если убрать трение из системы (коэффициент трения поверхности скольжения µ = 0; внешняя сила FA = 0; передаточное отношение i = 1), то вы, по существу, получите ту же основную формулу силы ( F ) х радиус ( r ).
Теперь давайте попробуем применить эту концепцию в другом приложении, имеющем дело с трением.
В конвейерных приложениях, где груз поддерживается поверхностью, трение является постоянным и пропорциональным массе груза. Степень проскальзывания на контактной поверхности или коэффициент трения ( µ) необходим для определения силы трения ( F ).
Следующая формула используется для расчета момента нагрузки для ременных приводов (конвейеров), а также реечных приводов.
|
Для этого типа применения нам нужно сначала рассчитать силу ( F ), прежде чем мы сможем рассчитать момент нагрузки ( TL ). Это требует от нас определения переменных внешней силы ( FA ), массы ( m ) и угла наклона ( Θ ). Получив значение F , мы можем включить его в формулу крутящего момента нагрузки ( TL ).
| Пример: поворотный индексный стол |
При расчете крутящего момента для поворотных индексных столов используются те же формулы, что и для ременного привода, но для определения необходимых переменных требуется несколько иной мыслительный процесс.В этом случае трение возникает в точках контакта шариковых роликов (опорных подшипников) и стола, поэтому радиус ( r ) будет расстоянием от центра вала двигателя до точки контакта между столом и его опорой. подшипники. Масса ( м ) будет массой стола плюс груз(ы). Коэффициент трения ( µ) обычно указан в спецификациях подшипников.
СОВЕТ: советы по выбору двигателя |
1.Будьте осторожны, чтобы не смешивать британские и метрические единицы в одной и той же формуле. 2. Если вам нужно преобразовать единицы измерения, убедитесь, что они преобразованы правильно; особенно десятичная точка.* 3. Используйте адекватные коэффициенты безопасности. Вы бы предпочли увеличить размер двигателя, чем уменьшить его. 4. Полезно еще раз взглянуть на свои расчеты свежим взглядом. *Используйте файл . |
Однако крутящий момент нагрузки является лишь одним из двух компонентов общего крутящего момента, необходимого для применения.Для правильного определения размера двигателя нам все еще необходимо рассчитать ускоряющий момент, инерцию нагрузки и скорость.
В следующих нескольких постах я расскажу о расчетах инерции нагрузки, момента ускорения, скорости и осевых/радиальных нагрузках. Устройтесь поудобнее.
Расчет крутящего момента как векторного произведения
Рассмотрим винт, показанный на рисунке. Если силы приложены в разных местах, то как создаются эффекты вращения.Ось вращения проходит через центр винта и перпендикулярна плоскости диаграммы.
Во-первых, рассмотрим только силу F1{F_1}F1, создаст ли она эффект вращения? Винт не будет вращаться, поэтому сила F1{F_1}F1 не создаст крутящего момента.
Теперь, если приложить только силу F2{F_2}F2, то снова винт не будет вращаться.
Силы F3{F_3}F3 и F4{F_4}F4 будут вращать винт, поэтому они будут создавать некоторый крутящий момент или эффект вращения. Однако какой из них будет легко вращать винт? Сила F3{F_3}F3 находится далеко от оси вращения и легко вращает винт по сравнению с F4{F_4}F4.
F1{F_1}F1 и F3{F_3}F3 действуют в одной точке, но под разными углами. F1{F_1}F1 и F3{F_3}F3 имеют разные эффекты поворота. Итак, от каких факторов зависит поворотный эффект?
Поскольку F3{F_3}F3 и F4{F_4}F4 создают крутящий момент и находятся на разном расстоянии от оси вращения, то крутящий момент должен зависеть от расстояния силы от оси вращения. По этой причине ручки сделаны в конце дверей, так что расстояние действия силы увеличивается от оси вращения и может быть создан больший эффект поворота при приложении меньшего усилия.
Так как F1{F_1}F1 и F3{F_3}F3 находятся на одном и том же расстоянии от оси вращения, но под разными углами, то крутящий момент зависит от направления силы.
Крутящий момент также зависит от величины силы. Чем больше величина силы, тем больше эффект поворота. Предположим, вы хотите открыть застрявший винт, тогда вам нужно приложить большее усилие, чтобы создать больший крутящий момент.
Суммируя все вышеперечисленные факторы, можно сделать вывод, что относительно любой точки
τ⃗=r⃗×F⃗\vec \tau = \vec r \times \vec Fτ=r×F
Здесь r⃗\vec rr — вектор положения точки приложения силы относительно точки, относительно которой рассчитывается крутящий момент,
F⃗\vec FF — приложенная сила,
τ⃗\vec \tau τ — крутящий момент.
Направление крутящего момента можно рассчитать по правилам векторного произведения.
Рассмотрим приведенную выше диаграмму, на которой угол между r⃗\vec rr и F⃗\vec FF равен θ\thetaθ. В этом случае, если линия действия силы продолжена и на нее опущен перпендикуляр из точки вычисления момента, то этот перпендикуляр называется плечом момента.
Плечо момента равно rsinθr sin \thetarsinθ,
Величина крутящего момента относительно точки ‘O’ равна rFsinθr F sin \theta rFsinθ,
Следовательно, крутящий момент также может быть записан как произведение силы и плеча момента.
6i^−6j^+12k^6\шляпа i – 6\шляпа j + 12\шляпа k6i^−6j^+12k^ −6i^+6j^−12k^ – 6\шляпа i + 6\шляпа j – 12\шляпа k−6i^+6j^−12k^ −17i^+6j^+13k^ – 17\шляпа i + 6\шляпа j + 13\шляпа k−17i^+6j^+13k^ 17i^−6j^−13k^17\шляпа i – 6\шляпа j – 13\шляпа k17i^-6j^-13k^
ПРИМЕЧАНИЕ\большой \color{#3D99F6} {ПРИМЕЧАНИЕ} ПРИМЕЧАНИЕЕсли крутящий момент вычисляется относительно точки на линии действия силы, то крутящий момент оказывается равным нулю. Это связано с тем, что в этом случае угол между вектором положения «r» и силой «F» будет равен нулю.
Чему равен момент силы F→=(2i^−3j^+4k^)N\mathop F\limits^ \to = (2\hat i – 3\hat j + 4\hat k)NF→ =(2i^−3j^+4k^)N, действующий в точке r→=(3i^+2j^+3k^) m\mathop r\limits^ \to = (3\hat i + 2\hat j + 3\hat k)\,mr→=(3i^+2j^+3k^)m о происхождении?
При силе 6.\circ}30∘ на гаечный ключ на расстоянии 8 см от гайки, он как раз способен ослабить гайку. Какой силы FFF будет достаточно, чтобы ослабить ее, если она действует перпендикулярно ключу на расстоянии 16 см от гайки?
Формула расчета выходного крутящего момента редуктора
Клиенты SDT Transmission обычно хотят знать, как рассчитать крутящий момент редуктора, когда они выбирают модели промышленного редуктора по фактическому рабочему состоянию оборудования, у них всегда возникают следующие проблемы: Как рассчитать крутящий момент промышленного редуктора? как согласовать промышленный редуктор с мощностью двигателя? особенно для червячного редуктора , мотор-редуктора с цилиндрическим редуктором и редуктора с циклоидальным редуктором выходной крутящий момент может непрерывно передаваться через выходной вал редуктора, при этом редуктор работает с эксплуатационным коэффициентом (f.с.) = 1,0. выходной крутящий момент является одним из наиболее важных технических параметров для расчета двигателя и редуктора, пожалуйста, свяжитесь с нами, если вам нужна формула расчета крутящего момента редуктора pdf. Здесь представлен расчет крутящего момента редуктора и руководство по мощности двигателя:
Как рассчитать выходной крутящий момент коробки передач? (формула расчета выходного крутящего момента редуктора)
Передаточное число = количество оборотов выходной скорости двигателя/выходных оборотов редуктора («Коэффициент», также известный как «передаточное число»)
Формула расчета выходного крутящего момента редуктора
- Вы можете получить выходной крутящий момент редуктора, если знаете мощность двигателя (кВт или л.с., для краткости), передаточное число (i) и эксплуатационный коэффициент (f.с.), формула крутящего момента коробки передач выглядит следующим образом:
Формула расчета крутящего момента коробки передач:
Выходной крутящий момент редуктора = 9550×Мощность двигателя<кВт>/(Входная скорость двигателя номинальной мощности<об/мин или об/мин> / Общее передаточное отношение)×Коэффициент эксплуатации x КПД коробки передач
T2 = 9550 x P1/(n1 / i) x f.s. x η = 9550 x P1/n2 x ф.с. х η
Код Описание Блок Т2 Крутящий момент выходного вала редуктора Н.м (кг.м) Р1 Входная мощность кВт №1 Скорость ввода об/мин (об/мин) и Общий коэффициент – №2 Скорость вывода об/мин (об/мин) ф.с. Сервис-фактор – η Эффективность коробки передач %
- Знать Крутящий момент на выходном валу/отверстии редуктора, выходную скорость редуктора и эксплуатационный коэффициент, как рассчитать мощность двигателя?
Мощность двигателя (л.с. или кВт) = крутящий момент (Н.m) /9550×Входная скорость двигателя Мощность (кВт) / Отношение / Коэффициент эксплуатации
Промышленный редуктор – это относительно точная машина, ее назначение – уменьшить скорость двигателя, увеличить выходной крутящий момент.
Следующая ситуация является примером расчета крутящего момента редуктора. Клиент может обратиться к следующей информации:
Выходной вал редуктора — это одно из положений выходного крутящего момента мотор-редуктора.
Вопрос:
Шестеренчатый редуктор с 0.Входная мощность 75 кВт, передаточное отношение 1:30, коэффициент эксплуатации по умолчанию (fs)[1] равен 1,0, а эффективность коробки передач (η)[2]: 100%, 4-полюсный асинхронный двигатель переменного тока с частотой вращения 1440 об/мин. Как рассчитать коробку передач выходной крутящий момент(T2)[3]? В каких единицах измеряется выходной крутящий момент? Какие тяжелые грузы можно поднимать с помощью этого промышленного мотор-редуктора?
Ответ:
0,75 кВт (мощность мотор-редуктора) x9550x КПД коробки передач [2] x30 / входная скорость x сервис-фактор[1] = выходной крутящий момент коробки передач[3].
Если асинхронный двигатель переменного тока является 4-полюсным асинхронным двигателем переменного тока: 1380 об/мин.(также сокращенно: об/мин; об/мин):
Выходной крутящий момент редуктора = 0,75x9550x100%[1] x30/1380×1,0[2] = 155,7 (Нм), это означает, что этот промышленный мотор-редуктор может поднимать 155,7 Нм (15,877 кг.м) товар.
Если вам нужно знать выходной крутящий момент редуктора, подставьте его только в КПД вращения, значения параметров входной скорости двигателя. рассчитайте приведенный выше выходной крутящий момент редуктора (T2) [3], затем вы можете обратиться к таблице выбора модели мотор-редуктора SDT, чтобы получить подходящую модель редуктора.
Единицей измерения крутящего момента является Н·м (Ньютон · метр) или килограмм. метров (кг·м).
Крутящий момент зубчатого редуктора = 9550 * мощность двигателя / номинальная мощность оборотов на входе двигателя * передаточное число * эффективность зубчатого редуктора.
Приведенный выше расчет представляет собой уравнение крутящего момента.
Мощность двигателя = крутящий момент ÷ 9550 × входная скорость двигателя номинальной мощности / передаточное число / эксплуатационный коэффициент.
Здесь полезно преобразованное отношение к единице выходного крутящего момента:
| 100 Н·м = 10,1972 кг·м |
| 100 Н.m = 885,07457 9349 фунтов в |
| 100 Н·м = 885,07458 lbf.in |
| 100 Н/м = 0,5710147 фунт/дюйм |
.
[1] Коэффициент обслуживания (ф.с.):
Коэффициент обслуживания также называется коэффициентом использования или коэффициентом безопасности; особенно для пользователей, выбирающих коробку передач, фактор использования коробки передач должен определяться в сочетании с другими факторами, такими как условия труда и приводимое в движение оборудование. (обычно> 1,0, это означает, что мощность редуктора> мощность двигателя). Убедитесь, что он имеет запас по номинальной механической энергии и тепловой энергии редуктора.
[2] КПД коробки передач (η):
Определение КПД коробки передач: отношение выходной мощности (или выходного крутящего момента) к номинальной входной мощности (или входному крутящему моменту, умноженному на передаточное число) при номинальном входная скорость достигает номинальной входной мощности (или входного крутящего момента).Эффективность редуктора частично определяется зубьями шестерни, трением в подшипнике качения и трением в уплотнении вала. Его можно измерить на специальном испытательном стенде, и методы включают метод потери мощности и прямое измерение мощности. метод. Различные коробки передач с различной эффективностью трансмиссии:
Одноступенчатая планетарная передача: 97%, двухступенчатая планетарная передача: 94%, трехступенчатая планетарная передача: 91%.
1-ступенчатый червячный редуктор Архимеда: 85%, 2-ступенчатый червячный редуктор Архимеда: 72%.
Одноступенчатый цилиндрический редуктор: 95 %, двухступенчатый цилиндрический редуктор: 90 %.
[3] Выходной крутящий момент редуктора (T2):
Выходной крутящий момент редуктора относится к фактическому рабочему выходному крутящему моменту. после того, как пользователь рассчитает выходной крутящий момент редуктора в соответствии с каталогом SDT Transmission, не только номинальный выходной крутящий момент редуктора превысит фактический рабочий выходной крутящий момент, но также будет учитываться перегрузочная способность приводного двигателя и требуемый максимальный рабочий крутящий момент на практике.
Теоретически требуемый максимальный рабочий крутящий момент должен быть меньше номинального выходного крутящего момента редуктора.в частности, некоторые жесткие условия работы должны строго соблюдать этот критерий.
Есть ли у вас дополнительные вопросы относительно эксплуатационного коэффициента, эффективности коробки передач и т. д.? чат для SDT Transmission онлайн, для того, чтобы получить быстрый ответ, вы также можете заполнить таблицу.
Пожалуйста, включите JavaScript в вашем браузере, чтобы заполнить эту форму.Электронная почта *
Пожалуйста, выберите предпочитаемый продукт или услугу) Червячный редуктор для тяжелых условий эксплуатации (SCWU, SCWO, SCWS, TP и т. д.) Винтовой редуктор и мотор-редуктор (серии GU / GN, G, R, F, K, S) Циклоидный редуктор и мотор-редуктор (серии XB, WB) Sumitomo Cycloidal Gear Редуктор и мотор-редуктор Серия 8000 Планетарный редуктор (серия N) Цилиндрический редуктор (серия ZQ) Цилиндрический редуктор (серия ZDY, ZLY, ZSY, ZFY) Асинхронный двигатель переменного тока (серия Y, YEJ, YEVJ) Муфта вала Приводные ремни (клиновые ремни, Ремень ГРМ,поликлиновые ремни и т.д.)ШкивДругие деталиОбслуживание (технологический консалтинг и т.д.)
Необходимые номера: ПК(ы)
Ваше сообщение *
Понимание отношений между ними, EPI Inc.
ОСНОВНЫЕ ПОНЯТИЯ:
Измеряется крутящий момент; Мощность рассчитана
ПРИМЕЧАНИЕ. Все наши продукты, конструкции и услуги являются УСТОЙЧИВЫМИ, ОРГАНИЧЕСКИМИ, БЕЗГЛЮТЕНОВЫМИ, НЕ СОДЕРЖАТ ГМО и не будут расстраивать чьи-либо драгоценные ЧУВСТВА или тонкие ЧУВСТВА
Для более подробного обсуждения силовых установок необходимо понимать концепции МОЩНОСТЬ и КРУТЯЩИЙ МОМЕНТ .
ОДНАКО, чтобы понять СИЛА , вы должны сначала понять ЭНЕРГИЯ и РАБОТА .
Если вы какое-то время не рассматривали эти концепции, было бы полезно сделать это перед изучением этой статьи. НАЖМИТЕ ЗДЕСЬ, чтобы просмотреть обзор «Энергия и работа».
Часто кажется, что люди не понимают отношения между МОЩНОСТЬЮ и КРУТЯЩИМ МОМЕНТОМ. Например, мы слышали двигатель строители , консультанты по распределительным валам и другие “ технические специалисты” спрашивают клиентов:
“Вы хотите, чтобы ваш двигатель производил ЛОШАДИНЫЕ МОЩНОСТИ или КРУТЯЩИЙ МОМЕНТ?”И вопрос обычно задается тоном, который убедительно свидетельствует о том, что эти «эксперты» считают, что мощность и крутящий момент как-то взаимоисключающие.
На самом деле все наоборот, и вы должны четко понимать эти факты:
- МОЩНОСТЬ (скорость выполнения РАБОТЫ) зависит от КРУТЯЩИЙ МОМЕНТ и ОБ/МИН .
- КРУТЯЩИЙ МОМЕНТ и ОБ/МИН – ИЗМЕРЕННЫЕ величины выходной мощности двигателя.
- МОЩНОСТЬ РАСЧИТЫВАЕТСЯ по крутящему моменту и частоте вращения по следующему уравнению:
л.с. = крутящий момент x об/мин ÷ 5252
(Внизу этой страницы для всех, кому интересно, показан вывод этого уравнения.)
Двигатель производит МОЩНОСТЬ , обеспечивая ВРАЩАЮЩИЙСЯ ВАЛ, который может оказывать заданное количество КРУТЯЩИЙ МОМЕНТ на нагрузку при заданных об/мин . Величина КРУТЯЩЕГО МОМЕНТА, который может развить двигатель, обычно зависит от оборотов.
КРУТЯЩИЙ МОМЕНТ
КРУТЯЩИЙ МОМЕНТ определяется как СИЛА вокруг заданной точки, приложенная на РАДИУС от этой точки. Обратите внимание, что единица КРУТЯЩИЙ МОМЕНТ равен одному фунт-фут (часто неверно указывается), в то время как единицей РАБОТА является один фут-фунт .
Рисунок 1
Ссылаясь на Рисунок 1 , предположим, что рукоятка прикреплена к кривошипу так, что она параллельна поддерживаемой вала и расположен в радиусе 12 дюймов от центра вала. В этом примере считайте, что вал закреплен на стена. Пусть стрелка представляет собой силу в 100 фунтов, приложенную в направлении, перпендикулярном рукоятке и кривошипу, как показано на рисунке.
Поскольку вал прикреплен к стене, вал не вращается, но есть крутящий момент в 100 фунт-фут (100 фунтов раз 1 фут) применяется к валу.
ПРИМЕЧАНИЕ о том, что ЕСЛИ кривошип на эскизе был в два раза длиннее (т. е. рукоятка располагалась на расстоянии 24 дюйма от центра вал), то же самое усилие в 100 фунтов, приложенное к рукоятке, создаст 200 фунт-фут крутящего момента (100 фунтов на 2 фута).
МОЩНОСТЬ
МОЩНОСТЬ является мерой того, сколько РАБОТЫ можно выполнить за указанное ВРЕМЯ. В примере на Страница «Работа и энергия», парень, толкавший машину, проехал 16 500 футо-фунтов. РАБОТА .Если бы он проделал эту работу за две минуты, он произвел бы 8250 футо-фунтов в минуту МОЩНОСТИ (165 футов x 100 фунтов ÷ 2 минуты). Если вам неясны понятия РАБОТЫ и ЭНЕРГИИ, было бы полезно просмотреть эти понятия. ЗДЕСЬ.
Точно так же, как одна тонна представляет собой большое количество веса (по определению, 2000 фунтов), одна лошадиных сил это большая мощность. Определение одной лошадиной силы: 33 000 футо-фунтов в минуту .Сила, которую произвел парень толкая свою машину через участок (8 250 фут-фунтов в минуту), это равно ¼ лошадиной силы (8 250 ÷ 33 000).
Хорошо, все хорошо, но как толкание машины через парковку связано с вращающимся механизмом?
Рассмотрим следующее изменение в приведенном выше эскизе рукоятки и кривошипа . Ручка по-прежнему находится в 12 дюймах от центра вал, но теперь вместо того, чтобы крепиться к стене, вал теперь проходит сквозь стену, опираясь на подшипники качения, и прикреплен к генератору за стеной.
Предположим, как показано на рис. 2 , что постоянная сила в 100 фунтов. каким-то образом применяется к ручке, так что сила всегда перпендикулярна как рукоятке, так и кривошипу, когда кривошип вращается. Другими словами, «стрелка». вращается вместе с рукояткой и остается в том же положении относительно кривошипа и рукоятки, как показано в приведенной ниже последовательности. (Это называется «тангенциальной силой»).
Рисунок 2
Если эта постоянная 100 фунтов.касательная сила, приложенная к 12-дюймовой рукоятке (крутящий момент 100 фунт-футов), заставляет вал вращаться со скоростью 2000 об/мин, то мощность вал передает на генератор за стеной 38 л.с. , рассчитывается следующим образом:
100 фунт-фут крутящего момента (100 фунтов x 1 фут), умноженные на 2000 об/мин, разделенные на 5252, составляют 38 л.с.
Следующие примеры иллюстрируют несколько различных значений КРУТЯЩЕГО МОМЕНТА, которые обеспечивают мощность 300 л.с.
Пример 1 : Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 2700 об/мин?
, так как л.с. = КРУТЯЩИЙ МОМЕНТ x ОБ/МИН ÷ 5252
тогда, изменив уравнение:
КРУТЯЩИЙ МОМЕНТ = л.с. x 5252 ÷ ОБ/МИН
Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 2700 = 584 фунт-фут.
Пример 2: Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 4600 об/мин?
Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 4600 = 343 фунт-фут.
Пример 3: Какой КРУТЯЩИЙ МОМЕНТ требуется для создания 300 л.с. при 8000 об/мин?
Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 8000 = 197 фунт-фут.
Пример 4: Какой КРУТЯЩИЙ МОМЕНТ развивает турбинная секция газотурбинного двигателя мощностью 300 л.с. при 41 000 об/мин?
Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 41 000 = 38.4 фунта-фута.
Пример 5: Выходной вал редуктора двигателя в Примере 4 вращается со скоростью 1591 об/мин. Сколько КРУТЯЩИЙ МОМЕНТ доступен на этом валу?
Ответ: КРУТЯЩИЙ МОМЕНТ = 300 x 5252 ÷ 1591 = 991 фунт-фут.
(без учета потерь в редукторе, разумеется).
Из этих чисел следует сделать вывод, что заданное количество лошадиных сил может быть получено из бесконечного числа комбинаций. крутящего момента и оборотов.
Подумайте об этом с другой стороны: в автомобилях одинакового веса 2-литровый двигатель с двумя распредвалами развивает мощность 300 л.с. при 8000 об/мин (197 фунт-фут) и 400 л.с. при 10 000 об/мин (210 фунт-фут) выведет вас из поворота так же, как 5-литровый двигатель, который развивает 300 л.с. при 4000 об/мин (394 фунт-фут) и 400 л.с. при 5000 об/мин (420 фунт-фут).Фактически, в автомобилях одинакового веса меньший двигатель, вероятно, будет ЛУЧШЕ участвовать в гонках, потому что он намного легче, поэтому на переднюю часть приходится меньше веса. И в реальности машина с более легким 2-литровым двигателем будет вероятно, весит меньше, чем большой автомобиль с двигателем V8, поэтому он будет лучшим гоночным автомобилем по нескольким причинам.
Измерение мощности
Динамометр определяет МОЩНОСТЬ двигателя путем приложения нагрузки к двигателю выходного вала с помощью водяного тормоза, генератора, вихретокового гасителя или любого другого управляемого устройства, способного поглощать сила.Система управления динамометром заставляет амортизатор точно соответствовать величине TORQUE , которую производит двигатель. в этот момент, то измеряет что КРУТЯЩИЙ МОМЕНТ и ОБ/МИН вала двигателя, и от тех два измерения, он вычисляет наблюдаемых мощности . Затем применяются различные факторы (температура воздуха, барометрическое давление, относительная влажность) для того, чтобы исправить наблюдаемое мощность до значения, которое было бы, если бы оно было измерено при стандартных атмосферных условиях , вызванная скорректированная мощность .
Последние изменения на этой странице
В этом месте страницы раньше был анализ, показывающий, как определить мощность, потребляемую насосом. Это обсуждение имеет была перемещена на более подходящую, недавно обновленную страницу «Системы смазки двигателя».
Общие замечания
Чтобы спроектировать двигатель для конкретного применения, полезно построить оптимальную кривую мощности для этого конкретного применения, затем из этой информации о конструкции определите кривую крутящего момента, которая требуется для получения желаемой кривой мощности.По оценке крутящего момента требования к реалистичным значениям BMEP, вы можете определить разумность целевая кривая мощности.
Как правило, пик крутящего момента возникает при значительно более низких оборотах, чем пик мощности. Причина в том, что в целом кривая крутящего момента не падает (в %) так же быстро, как увеличивается число оборотов в минуту (в %). Для гоночного двигателя часто выгодно (в пределах границ условия применения) для работы двигателя далеко за пределами пиковой мощности, чтобы обеспечить максимальную среднюю мощность в течение необходимый диапазон оборотов.
Однако для двигателя, который работает в относительно узком диапазоне оборотов, такого как авиационный двигатель, обычно требуется, чтобы двигатель выдает максимальную мощность при максимальных оборотах. Это требует, чтобы пик крутящего момента был достаточно близок к максимальным оборотам. Для самолета двигатель, вы обычно проектируете кривую крутящего момента так, чтобы она достигла максимума при нормальных настройках круиза и оставалась неизменной до максимальных оборотов. Такое позиционирование кривая крутящего момента позволила бы двигателю производить значительно больше мощности, если бы он мог работать на более высоких оборотах, но цель состоит в том, чтобы оптимизировать производительность в рабочем диапазоне.
Пример этой концепции показан на рис. 3 ниже. Три пунктирные линии представляют три различные кривые крутящего момента, каждая из которых имеет точное значение одинаковая форма и значения крутящего момента, но с пиковыми значениями крутящего момента, расположенными при разных значениях оборотов. Сплошные линии показывают мощность, вырабатываемую кривыми крутящего момента того же цвета.
Рисунок 3
Обратите внимание, что при пиковом крутящем моменте 587 фунт-футов при 3000 об/мин розовая линия мощности достигает пика около 375 л.с. между 3500 и 3750 об/мин.С участием та же кривая крутящего момента сдвинута вправо на 1500 об/мин (черный цвет, пик крутящего момента 587 фунт-фут при 4500 об/мин), пиковая мощность подскакивает примерно до 535 л.с. 5000 об/мин. Опять же, перемещение той же кривой крутящего момента вправо еще на 1500 об/мин (синяя, пик крутящего момента 587 фунт-футов при 6000 об/мин) приводит к тому, что мощность снижается. пик около 696 л.с. при 6500 об/мин
Используя черные кривые в качестве примера, обратите внимание, что двигатель развивает мощность 500 л.с. как при 4500, так и при 5400 об/мин, что означает, что двигатель может такой же объем работы в единицу времени (мощность) при 4500, что и при 5400.ОДНАКО, он будет сжигать меньше топлива для производства 450 л.с. при 4500 об/мин. чем при 5400 об/мин, из-за паразитных потерь мощности (мощность, расходуемая на вращение коленчатого вала, возвратно-поступательных узлов, клапанного механизма) увеличивается пропорционально квадрату частоты вращения коленчатого вала.
Диапазон оборотов, в котором двигатель развивает максимальный крутящий момент, ограничен. Вы можете настроить двигатель так, чтобы он имел высокий пиковый крутящий момент с очень узкий диапазон или более низкое значение пикового крутящего момента в более широком диапазоне. Эти характеристики обычно диктуются параметрами область применения, для которой предназначен двигатель.
Пример этого показан на рис. 4 ниже. Это то же самое, что и график на рис. 3 (выше), ЗА ИСКЛЮЧЕНИЕМ, синяя кривая крутящего момента имеет был изменен (как показано зеленой линией), чтобы он не исчезал так быстро. Обратите внимание, как это приводит к увеличению зеленой линии электропередач. далеко за пределами пика крутящего момента. Такого рода изменение кривой крутящего момента может быть достигнуто путем изменения различных ключевых компонентов, в том числе (но не ограничиваясь) профили кулачков, расстояние между кулачками, длина впускных и/или выпускных каналов, поперечное сечение впускных и/или выпускных каналов раздел.Изменения, направленные на расширение пикового крутящего момента, неизбежно уменьшат значение пикового крутящего момента, но желательность данное изменение определяется приложением.
Рисунок 4
Вывод уравнения мощности
(для всех, кто интересуется)
Эта часть может быть не интересна большинству читателей, но несколько человек спрашивали:
“ОК, если л.с. = ОБ/МИН x КРУТЯЩИЙ МОМЕНТ ÷ 5252 , тогда откуда откуда 5252?”
Вот ответ.
По определению, МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ (как объяснялось выше в разделе ПИТАНИЕ рубрика)
Используя пример на рисунке 2 выше, где постоянная тангенциальная сила в 100 фунтов была приложена к 12-дюймовой рукоятке, вращающейся со скоростью 2000 об/мин, мы знаем задействованную силу , поэтому для расчета мощности нам нужно расстояние рукоятка путешествия на единицу время , выраженное как:
Мощность = 100 фунтов x расстояние в минуту
Хорошо, на какое расстояние поворачивается рукоятка за одну минуту? Сначала определите расстояние, которое он проходит за один оборот :
РАССТОЯНИЕ за оборот = 2 x π x радиус
РАССТОЯНИЕ за оборот.= 2 x 3,1416 x 1 фут = 6,283 фута
Теперь мы знаем, какое расстояние поворачивает кривошип за один оборот. Какое расстояние проходит кривошип за одну минуту ?
РАССТОЯНИЕ в мин. = 6,283 фута на оборот. х 2000 об. в мин. = 12 566 футов в минуту
Теперь мы знаем достаточно, чтобы рассчитать мощность, определяемую как:
МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ ÷ ВРЕМЯ
so
Мощность = 100 фунтов x 12 566 футов в минуту = 1 256 600 футо-фунтов в минуту
Шикарно, а как насчет ЛОШАДЕЙ? Помните, что одна ЛОШАДЕЙНАЯ СИЛА определяется как 33000 футо-фунтов работы. в минуту .Следовательно, HP = МОЩНОСТЬ (фут-фунт в минуту) ÷ 33 000. Мы уже подсчитали, что мощность, приложенная к кривошипа выше составляет 1 256 600 футо-фунтов в минуту.
Сколько это HP?
л.с. = (1 256 600 ÷ 33 000) = 38,1 л.с.
Теперь мы объединяем уже известные нам вещи, чтобы создать волшебное число 5252. Мы уже это знаем:
КРУТЯЩИЙ МОМЕНТ = СИЛА x РАДИУС.
Если мы разделим обе части этого уравнения на РАДИУС, мы получим:
(a) СИЛА = КРУТЯЩИЙ МОМЕНТ ÷ РАДИУС
Теперь, если РАССТОЯНИЕ за оборот = РАДИУС x 2 x π, тогда
(b) РАССТОЯНИЕ в минуту = РАДИУС x 2 x π x об/мин
Мы уже знаем
(c) МОЩНОСТЬ = СИЛА x РАССТОЯНИЕ в минуту
Таким образом, если мы подставим эквивалент СИЛЫ из уравнения (a) в и расстояние в минуту из уравнение (б) в уравнение (в), получаем:
МОЩНОСТЬ = (МОМЕНТ ÷ РАДИУС) x (ОБ/МИН x РАДИУС x 2 x π)
Разделив обе стороны на 33 000, мы получим HP,
.Л.С. = КРУТЯЩИЙ МОМЕНТ ÷ РАДИУС x ОБ/МИН x РАДИУС x 2 x π ÷ 33 000
Сокращая, получаем
л.с. = КРУТЯЩИЙ МОМЕНТ x ОБ/МИН x 6.28 ÷ 33 000
С
33 000 ÷ 6,2832 = 5252
Поэтому
л.с. = КРУТЯЩИЙ МОМЕНТ x ОБ/МИН ÷ 5252
Обратите внимание, что при 5252 об/мин крутящий момент и л.


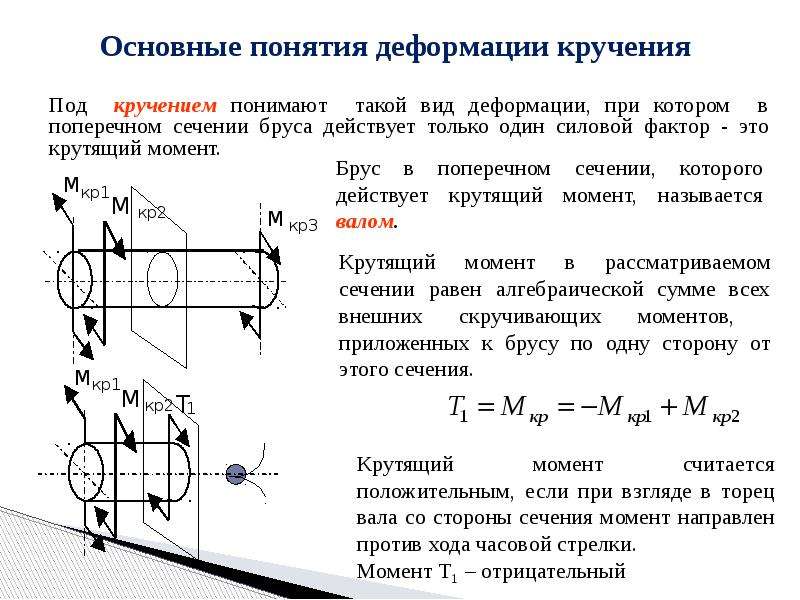 Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.
Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения. Главные напряжения направлены к образующей под углом 45°.
Главные напряжения направлены к образующей под углом 45°.
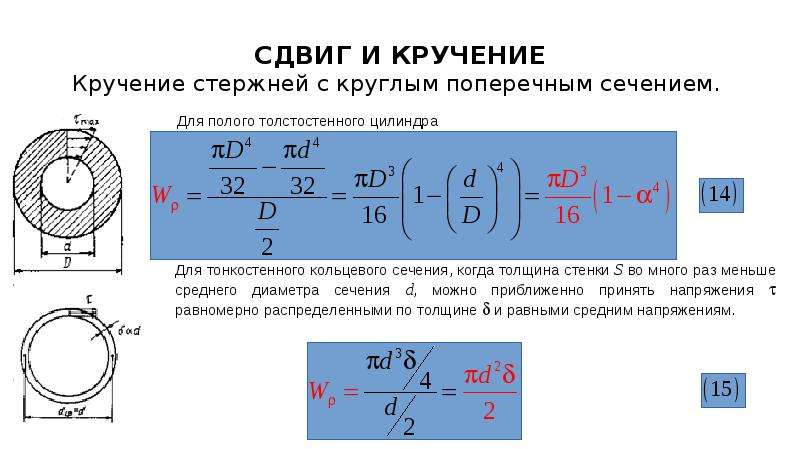


 Определение нагрузочной способности (максимального крутящего момента)
Определение нагрузочной способности (максимального крутящего момента)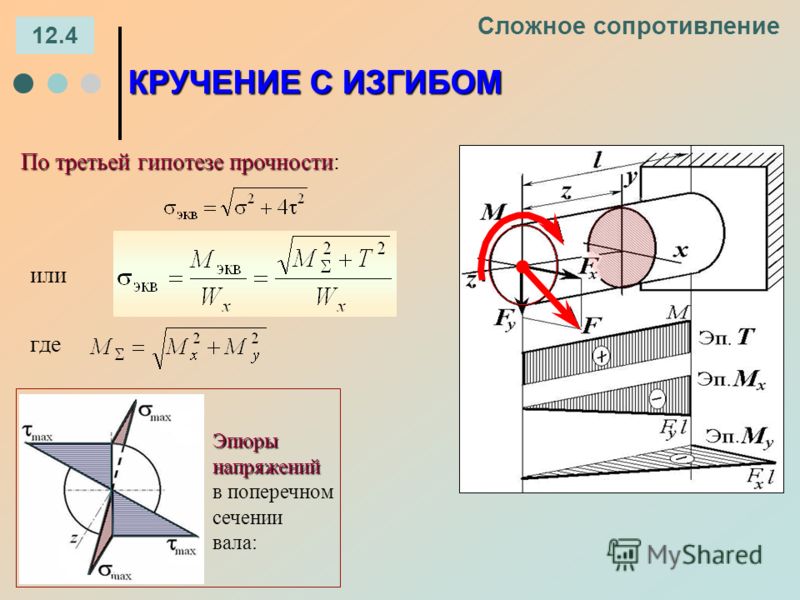
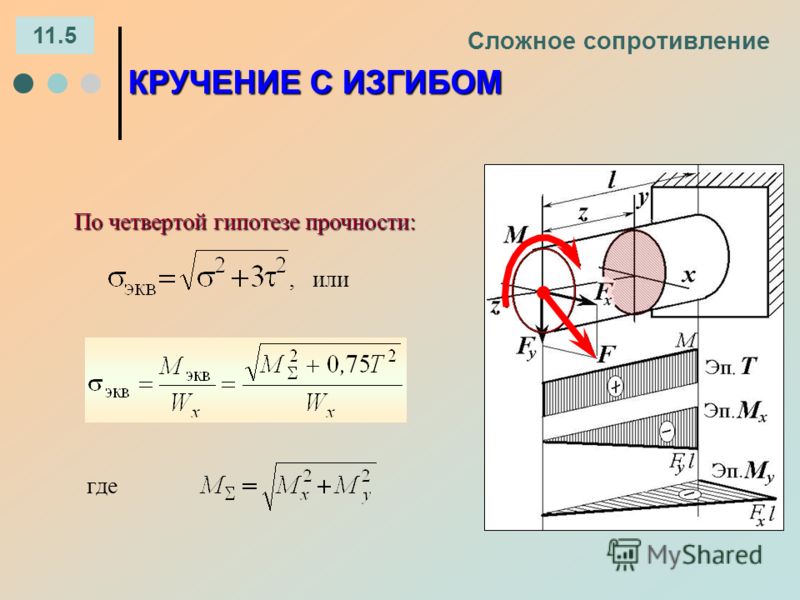 Определение размеров поперечного сечения из расчета на жесткость.
Определение размеров поперечного сечения из расчета на жесткость.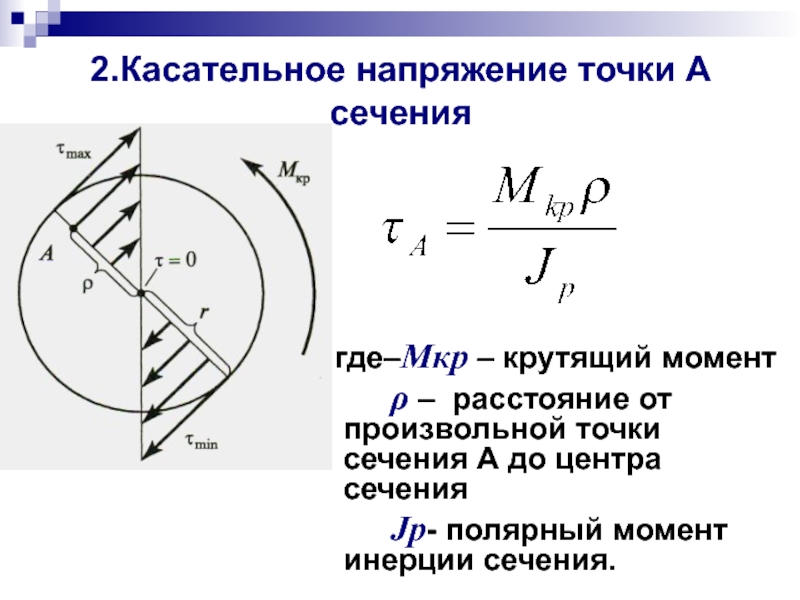 2.37, б
2.37, б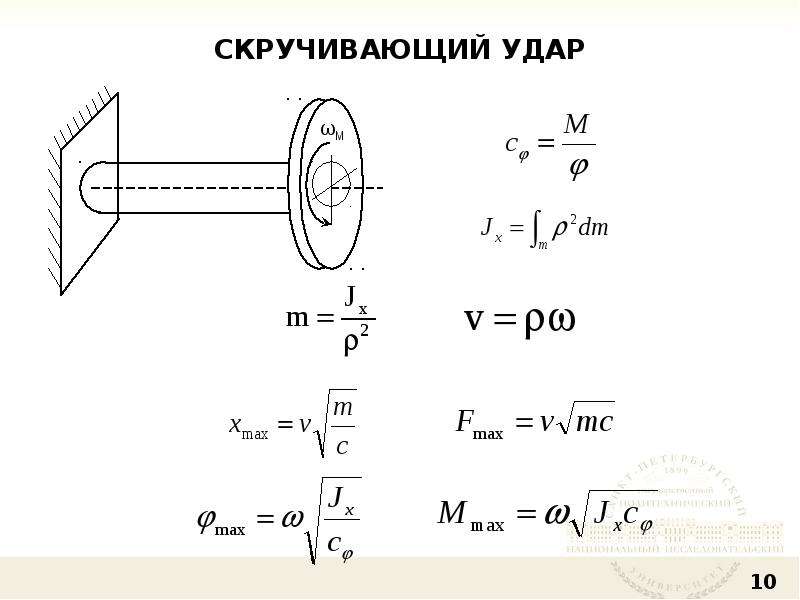 Определить величину
Определить величину 38, б
38, б Частота вращения вала
Частота вращения вала
 На него поступает мощность
На него поступает мощность 2.40,
2.40,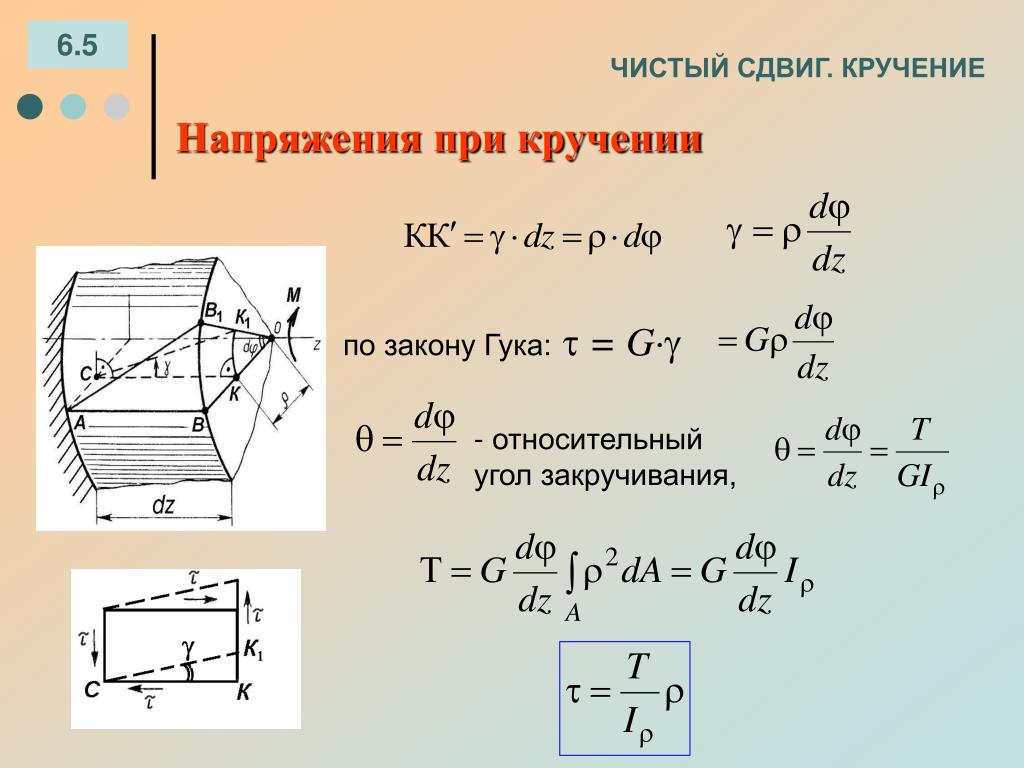
 Такая нагрузка вызовет в стержне
Такая нагрузка вызовет в стержне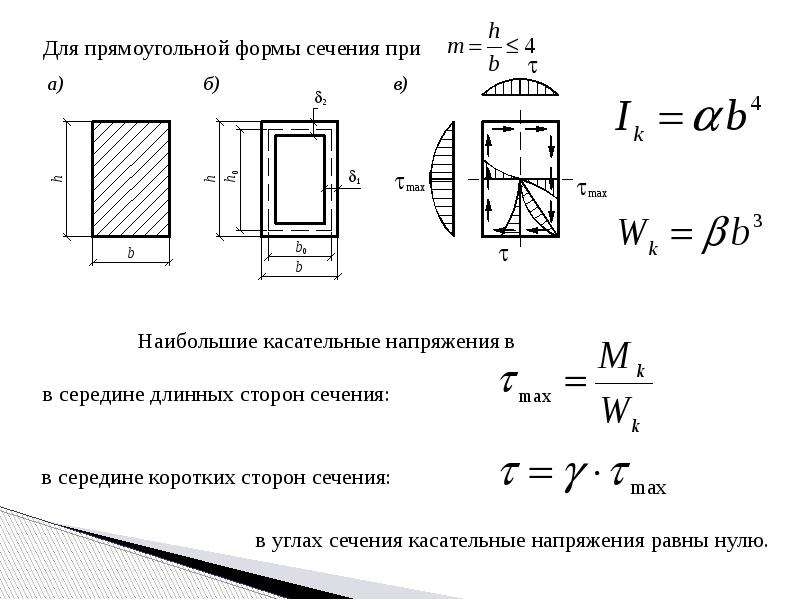

 Здесь d — диаметр вала, м.
Здесь d — диаметр вала, м.
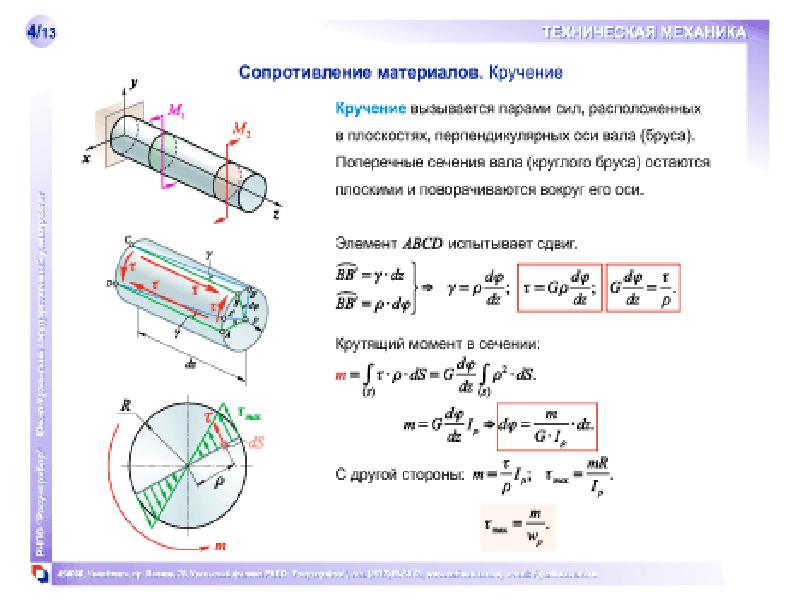 3), предварительно определив полярные моменты сопротивления сечений вала:
3), предварительно определив полярные моменты сопротивления сечений вала:
 В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях;
В этом случае, более полезным будет выбор двигателя по малому моменту для работающих со слабыми усилиями и на большой скорости, и со средними либо высокими показателями моментов пуска для работающих в усиленных режимах. На малых скоростях;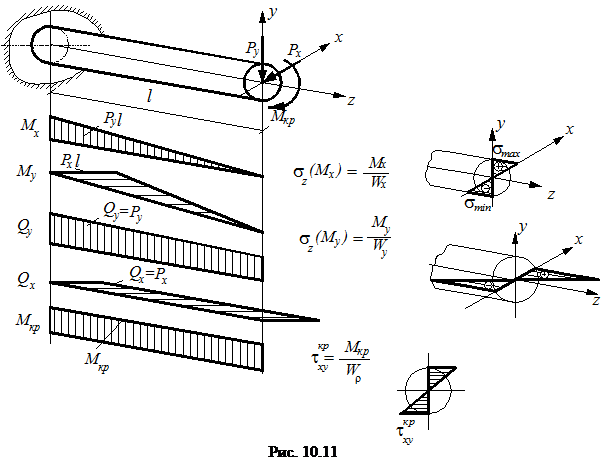




 3.3, а
3.3, а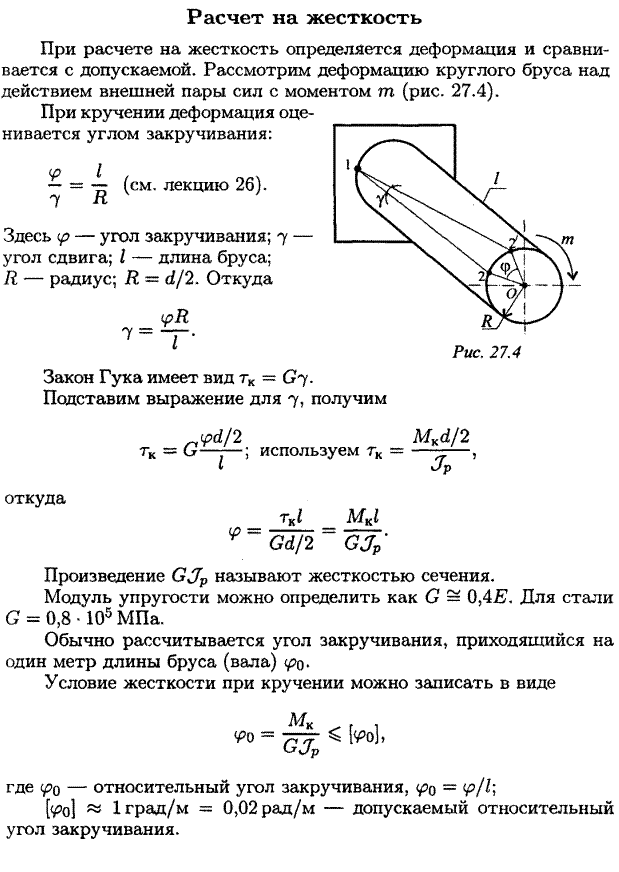 3.3, г
3.3, г Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: где Iρ — полярный момент инерции. Эпюра касательных напряжений при кручении имеет следующий вид:
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: где Iρ — полярный момент инерции. Эпюра касательных напряжений при кручении имеет следующий вид: 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол (р,
27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол (р, 27.2).
27.2).
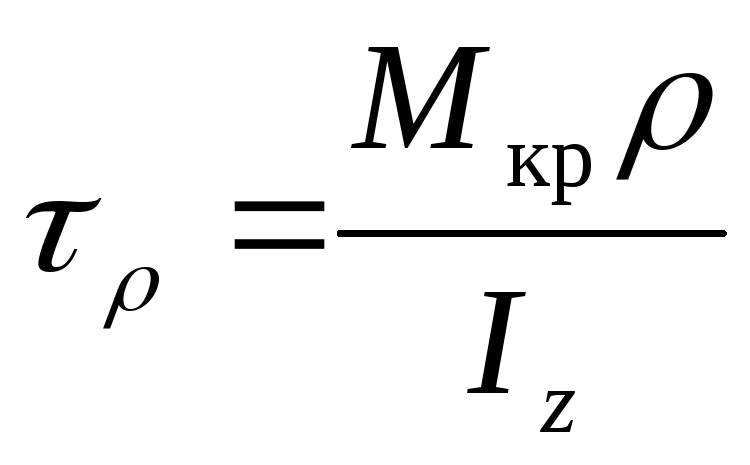
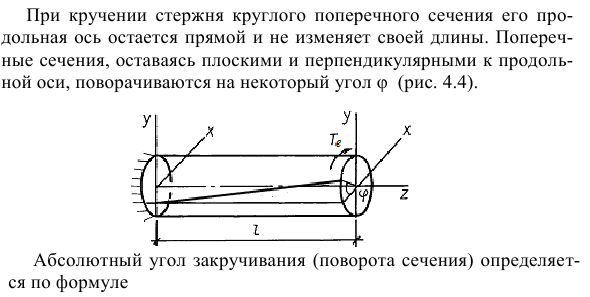

 2.37, б
2.37, б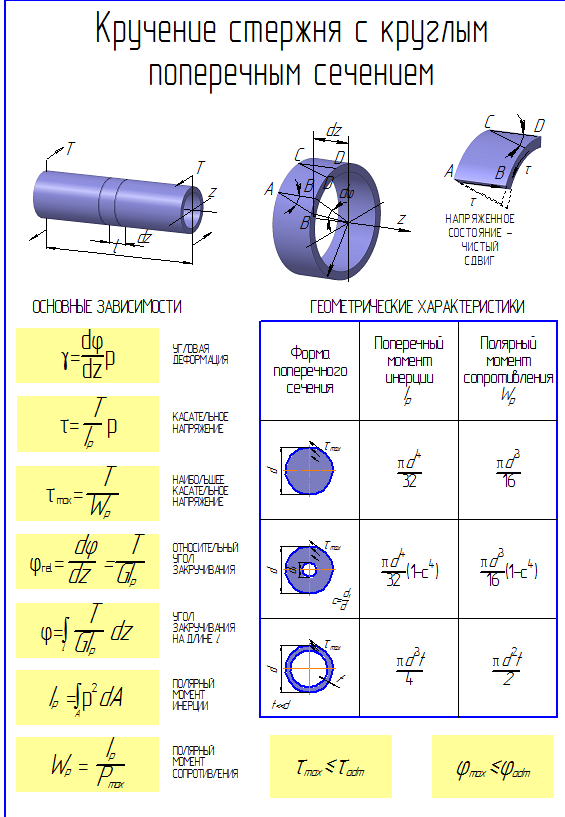 Определить величину
Определить величину 38, б
38, б Частота вращения вала
Частота вращения вала
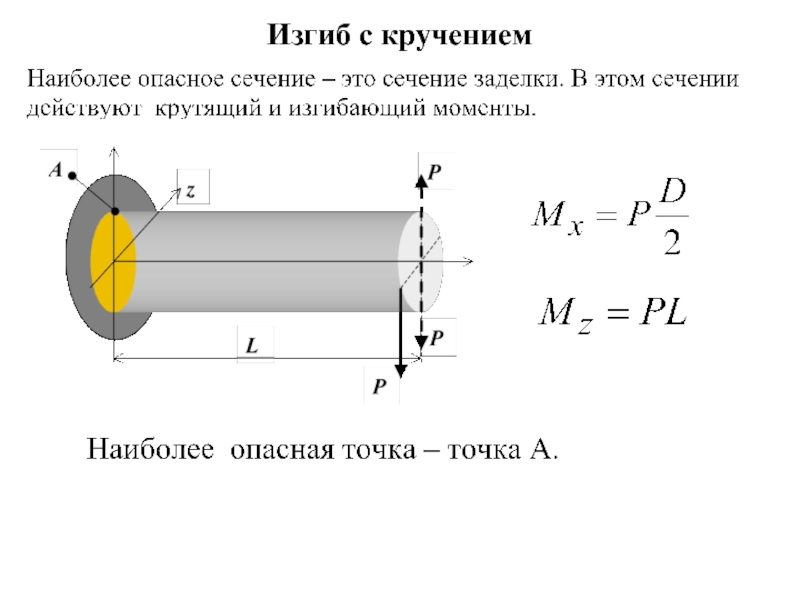 На него поступает мощность
На него поступает мощность 2.40,
2.40,