Формула момента: Момент силы — урок. Физика, 7 класс.

Формула расчета момента инерции – Центрсельстрой

Моменты инерции распространенных форм

Что такое момент инерции?

Момент инерцииназываемый также моментом инерции массы или угловой массой, (единицы СИ кг м2) — это мера сопротивления объекта изменению скорости вращения. Это вращательный аналог массы. То есть, это инерция жесткого вращающегося тела по отношению к его вращению.
Момент инерции играет во вращательной динамике практически ту же роль, что и масса в основной динамике, определяя связь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также некоторыми другими величинами. Хотя для многих ситуаций достаточно простой скалярной обработки, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как вращающиеся вершины и движение гироскопа.
Для обозначения момента инерции обычно используется символ I и иногда J.
Момент инерции объекта относительно данной оси описывает, насколько трудно изменить его угловое движение относительно этой оси. Например, рассмотрим два диска (A и B) одинаковой массы. Диск А имеет больший радиус, чем диск В. Если предположить, что толщина и распределение массы равномерны, то для ускорения диска А (изменения его угловой скорости) требуется больше усилий, поскольку его масса распределена дальше от оси вращения: масса, находящаяся дальше от оси, должна для данной угловой скорости двигаться быстрее, чем масса, находящаяся ближе. В этом случае диск A имеет больший момент инерции, чем диск B.
Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, которая не требует знания оси вращения. Скалярная форма I (часто называемая просто «моментом инерции») позволяет кратко проанализировать многие простые проблемы в динамике вращения, такие как скатывание объектов по наклонной плоскости и поведение шкивов.
Например, хотя блок любой формы будет скользить вниз по наклонной плоскости с одинаковой скоростью, катящиеся объекты могут спускаться с разной скоростью, в зависимости от их моментов инерции. Обруч будет спускаться медленнее, чем сплошной диск равной массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения и, следовательно, должна двигаться быстрее, если обруч катится с той же угловой скоростью.
Однако для (более сложных) задач, в которых ось вращения может меняться, скалярный метод неадекватен, и необходимо использовать тензорный метод (хотя в особых ситуациях возможны сокращения). Примеры, требующие такого обращения, включают гироскопы, вершины и даже спутники — все объекты, чья центровка может меняться.
Момент инерции не следует путать с полярным моментом инерции, который является мерой способности объекта сопротивляться кручению (скручиванию).

Формула момента инерции:

Простая формула момента инерции любого объекта, будь то точечная масса или 3D-структура, дается следующим образом:

где
dm — масса бесконечно малой части тела
и r — (перпендикулярное) расстояние точечной массы до оси вращения.

Подробный анализ

(Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется следующим образом

I является аддитивным. Таким образом, для твердого тела, состоящего из N точечных масс mi с расстояниями ri до оси вращения, общий I равен сумме моментов инерции точечных масс:

Для твердого тела, описываемого непрерывной функцией плотности массы ?(r), I вокруг известной оси может быть вычислена путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки тела до оси вращения:

V — объем, занимаемый объектом.
? — функция пространственной плотности объекта, и

координаты точки внутри тела.

Диаграмма для расчета I диска. Здесь k — 1/2, а r — радиус, используемый при определении момента.
Исходя только из анализа размеров, I неточечного объекта должна иметь вид:

M — масса
R — радиус объекта от центра масс (в некоторых случаях вместо него используется длина объекта).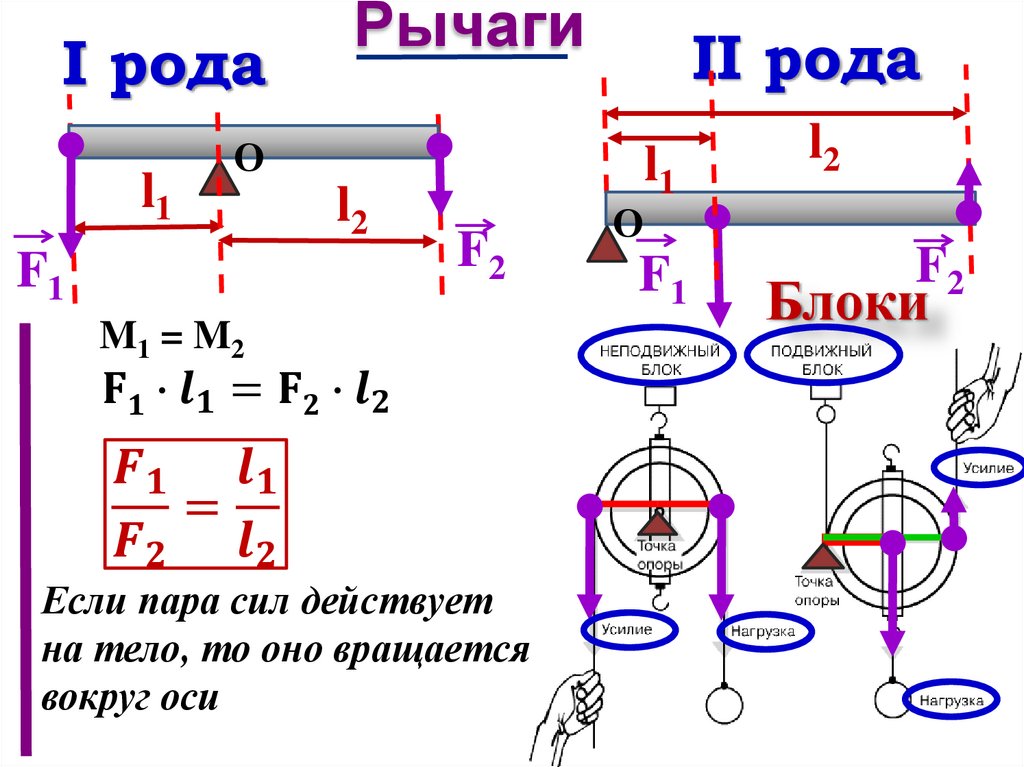
k — безразмерная постоянная, называемая константой инерции, которая изменяется в зависимости от рассматриваемого объекта.

Инерционные константы используются для учета различий в размещении массы от центра вращения. Примеры включают:
k = 1, тонкое кольцо или тонкостенный цилиндр вокруг своего центра,
k = 2/5, твердая сфера вокруг своего центра
k = 1/2, твердый цилиндр или диск вокруг своего центра.

Теорема о параллельных осях

После того как момент инерции вычислен для вращения вокруг центра масс твердого тела, его можно удобно пересчитать и для всех параллельных осей вращения, не прибегая к формальному определению. Если ось вращения смещена на расстояние R от оси центра масс (например, вращение диска вокруг точки на его периферии, а не через центр), то смещенный и центральный моменты инерции связаны следующим образом:

Эта теорема также известна как правило параллельных осей и является частным случаем теоремы Штейнера о параллельных осях.

Теорема о перпендикулярных осях

Теорему о перпендикулярных осях для плоских объектов можно продемонстрировать, рассмотрев вклад в трехосные моменты инерции от произвольного элемента массы. Из момента массы точки, вклады в каждый из осевых моментов инерции составляют

Составные тела

Если тело может быть разложено (физически или концептуально) на несколько составных частей, то момент инерции тела вокруг данной оси получается суммированием моментов инерции каждой составной части вокруг той же заданной оси.

Моменты инерции распространенных форм

Читайте далее:

• Испытание маятника на кручение металлической проволоки.
• Испытание маятника на кручение металлической проволоки.
• Что такое потенциальная функция скорости и функция потока?.
• Что такое формула Чези для открытых каналов? Как определить постоянную Чези?.
• Метод распределения моментов в структурном анализе.
• ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОМПРЕССИОННЫХ ЭЛЕМЕНТОВ.
• Теория линии текучести для проектирования перекрытий — допущения, методы анализа.

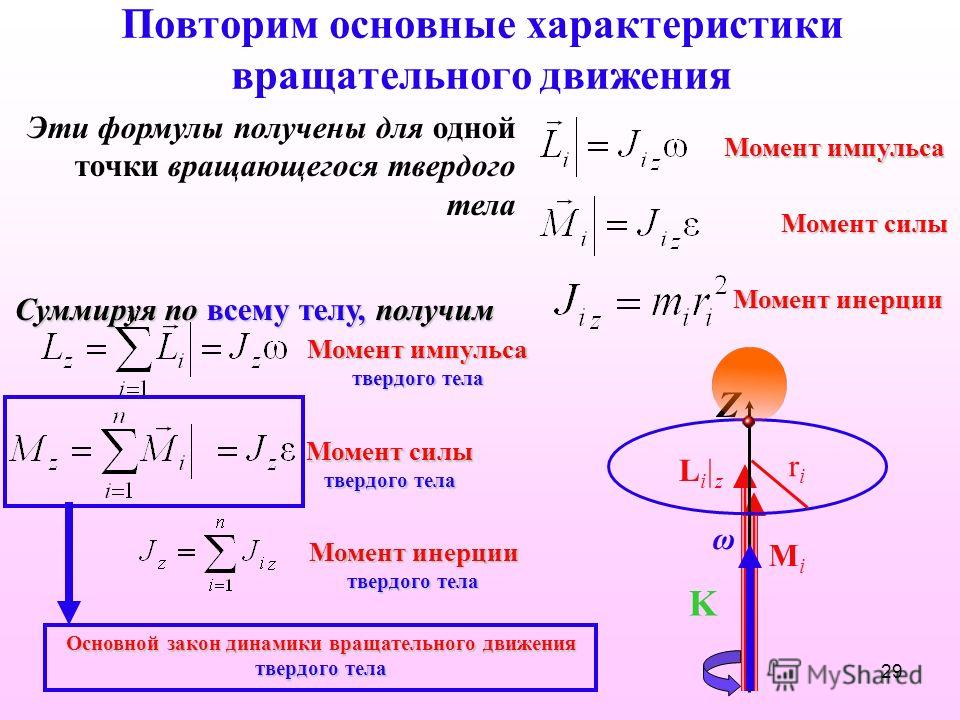
Момент силы

Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.

Обозначение: M, m или M(F).

Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]

Аналогом момента силы является момент пары сил.

Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение

Момент определяется как произведение силы F на плечо h:

M(F)=F×h

Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.

Наш короткий видеоурок про момент силы с примерами:

Другие видео

Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.

Пример момента силы

Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.

Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h3>h2).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

Рассмотрим порядок определения плеча h момента:

Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

Сила расположена перпендикулярно оси стержня

Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.

То момент силы F относительно точки A:

М_A=F×AB

Сила расположена под углом к оси стержня

В случае, если сила F приложена под углом α к оси балки

Момент силы относительно точки B:

M_B=F×cosα×AB

Известно расстояние от точки до линии действия силы

Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)

Момент силы относительно точки B:

M_B=F×h

---

См. также:

• Примеры решения задач >
• Момент силы относительно точки
• Момент силы относительно оси

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)
• Инженерная механика (инжмех)

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Помощь с решением

---

Поиск формул и решений задач

Изгибающий момент: лучшие уравнения, которые нужно знать (бесплатный калькулятор)

В этой статье мы обсудим концепции, связанные с изгибающим моментом. Мы также предоставляем уравнения и калькуляторы для распространенных конфигураций балок.

Почему важен изгибающий момент?

Конструкция конструкций учитывает воздействие нагрузки. Поэтому для сохранения устойчивости конструкций решающее значение имеет сопротивление изгибающему моменту . Примерами нагрузок могут быть, например, динамическая нагрузка (люди или объекты в здании), статическая нагрузка (вес самой конструкции) и нагрузки от окружающей среды (снеговая нагрузка, ветровая нагрузка и землетрясения). Повреждение может произойти из-за изгиба, когда напряжение изгиба превышает предел прочности элемента.

Грузоподъемность в зависимости от спроса

Постоянные и временные нагрузки действуют на конструкции одновременно, изменяя взаимодействие всех их компонентов. В результате, проектируя структуру для обеспечения оптимальной устойчивости, инженеры должны учитывать и то, и другое. Способность балки выдерживать нагрузку — это вычисление, которое помогает определить общую прочность конструкции здания. Поскольку ни один материал не может выдержать бесконечную нагрузку, инженеры рассчитывают «изгибающий момент» с учетом внешних сил .

Внешние силы

Три силы влияют на расчетные параметры конструкции нагрузок:

• Сжатие происходит, когда частицы вещества прижимаются друг к другу, укорачивая или сжимая их. Сжатие обычно применяется сверху конструкции. Узнайте больше о сжатии и его последствиях в этой статье: Потеря устойчивости колонны
• Растяжение — это полная противоположность сжатия; при растяжении материал тянется силами тяги. Балка находится под растягивающей нагрузкой, когда балка выходит из строя в верхней части.
• Сила скручивания, действующая на конструктивную часть, известна как кручение.

Вышеупомянутые три напряжения всегда присутствуют в конструкциях. Например, предположим, что вы прогуливаетесь по второму этажу дома. Затем ваш вес будет сжимать балки, поддерживающие пол. Следовательно, балки вверху сжимаются, а внизу растягиваются.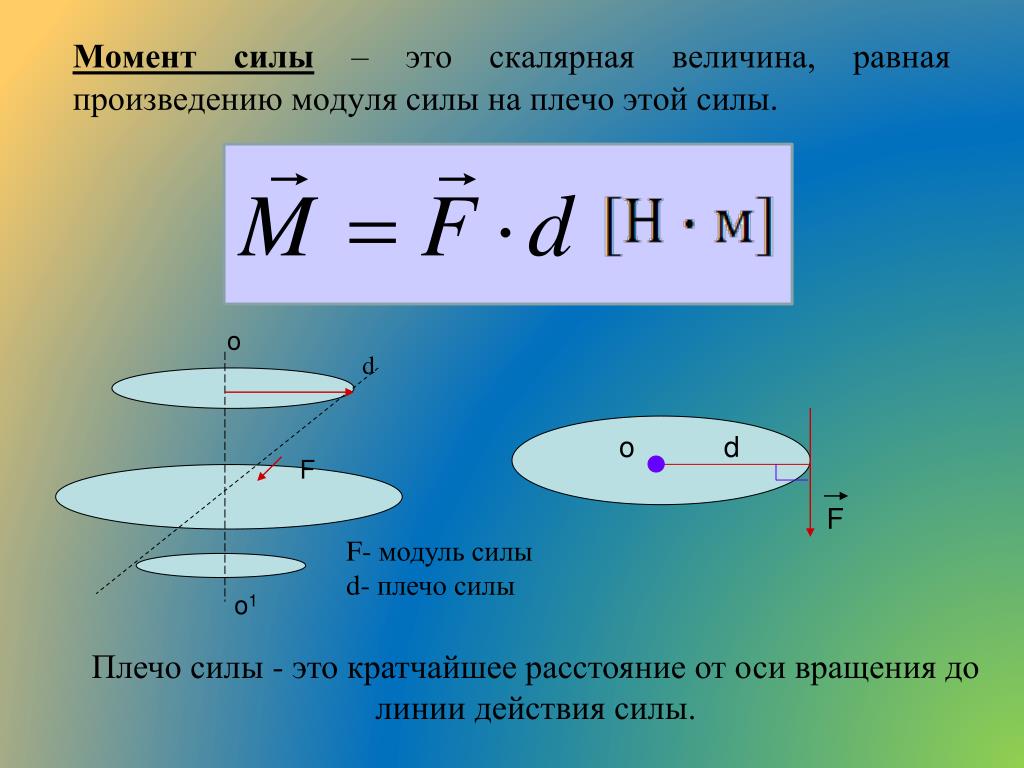 Это создает изгибающий момент. Кроме того, срезное полотно удерживает балки вместе. В заключение, структура дома должна быть в состоянии сбалансировать все эти нагрузки, чтобы сохранить структурную целостность.

Что такое изгибающий момент?

Мера эффекта изгиба из-за приложенной к элементу конструкции поперечной силы называется изгибающим моментом. Таким образом, в проектировании конструкций изгибающий момент является важным элементом при проектировании конструкций. В противном случае было бы трудно понять поведение элементов конструкции при приложении поперечной нагрузки. Как упоминалось ранее, конструкция конструкции удерживает максимальные пределы изгиба конструкции в допустимых пределах. Однако при превышении пределов изгиба или сдвига конструкция не сможет сохранить свою устойчивость и в конечном итоге приведет к ее разрушению.

Изгибающие моменты, визуализированные на балке, подвергнутой двухосному изгибу.

Как рассчитывается изгибающий момент

Когда поперечная сила прикладывается к секции балки, возникающие напряжения называются напряжениями изгиба. Следовательно, приложенные силы вызывают изгибающий момент, который обычно измеряется как сила x расстояние (кН-м). При измерении изгиба сила должна быть перпендикулярна плечу момента . Балка является наиболее распространенным конструктивным элементом, подверженным изгибающим моментам, так как под нагрузкой она может изгибаться в любой точке по своей длине. Несмотря на различия в процессах, балка может разрушиться из-за касательных напряжений до разрушения изгиба. В этом случае изгибающая сила заставит балку вращаться вокруг точки поворота, если точка поворота не ограничена должным образом. Таким образом, точка, в которой возникает максимальный изгибающий момент, важна для расчета конструкции на изгиб.

Вывод уравнения изгибающего момента

Чтобы понять полный контекст изгибающих моментов, мы должны изучить поперечное сечение балки при изгибе.

Дискретная полоса напряжения изгиба

Иллюстрация распределения напряжения по сечению при изгибе. Источник: Университет Аризоны

Из рисунка видно, что внутренние напряжения статически эквивалентны внешним силам и моментам. Во-первых, рассмотрим силу dF , действующую на полосу площадью дА . Развиваемое напряжение σ будет равно

Следовательно, момент M будет задан как

Здесь y — расстояние силы от нейтральной оси (т. на луче). Следовательно, чтобы получить максимальное напряжение в крайней точке волокна, fb , мы можем использовать тригонометрический прием:

Напряжения изгибающего момента, возникающие в поперечном сечении.

Из подобия треугольников на рисунке выше мы можем получить

Преобразование вышеприведенного уравнения

Где c — расстояние от нейтральной оси до вершины поперечного сечения, fbmax — максимальное напряжение в крайней точке волокна, а σ — изгибные напряжения на полосе на расстоянии.

Интегрирование напряжения изгиба

Теперь мы можем подставить это в первое уравнение. Однако в начале вывода уравнения предполагалась одна полоса поперечного сечения. Чтобы включить все сечение, берется интегрирование;

Здесь мы определяем, что определение второго момента площади I можно использовать для упрощения уравнения.

Переставить для fbmax (Напряжение при изгибе)

Таким образом, напряжение fb на любом расстоянии, y от нейтральной оси будет

Мы также можем написать

I сечение 9000s Y .

Допущения

Обратите внимание, что приведенный выше вывод уравнений изгибающего момента основан на следующих допущениях:

1. Во-первых, балка является линейной и имеет однородную площадь поперечного сечения до приложения напряжений.
2. Во-вторых, изгибающий момент возникает внутри продольной плоскости симметрии балки.
3. В-третьих, балка подвергается чистому изгибу (изгибающий момент не изменяется по длине).
4. Наконец, материал, используемый в балке, является однородным и изотропным.

Понравился ли вам этот пост? Подпишитесь, и каждый месяц мы будем присылать вам еще больше таких замечательных постов.

Уравнения изгибающего момента

Разделы ниже содержат конфигурацию балки вместе с приложенной нагрузкой и формулами для расчета максимального изгибающего момента .

Консоли

В этом подразделе мы рассмотрим различные конфигурации нагрузки консольных балок.

Консоль – Точечная нагрузка на конце

Защемленная балка с вертикальной точечной нагрузкой на конце будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.

Уравнение и диаграмма

Диаграмма изгибающего момента консоли – точечная нагрузка на конце

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной нагрузке P в конце.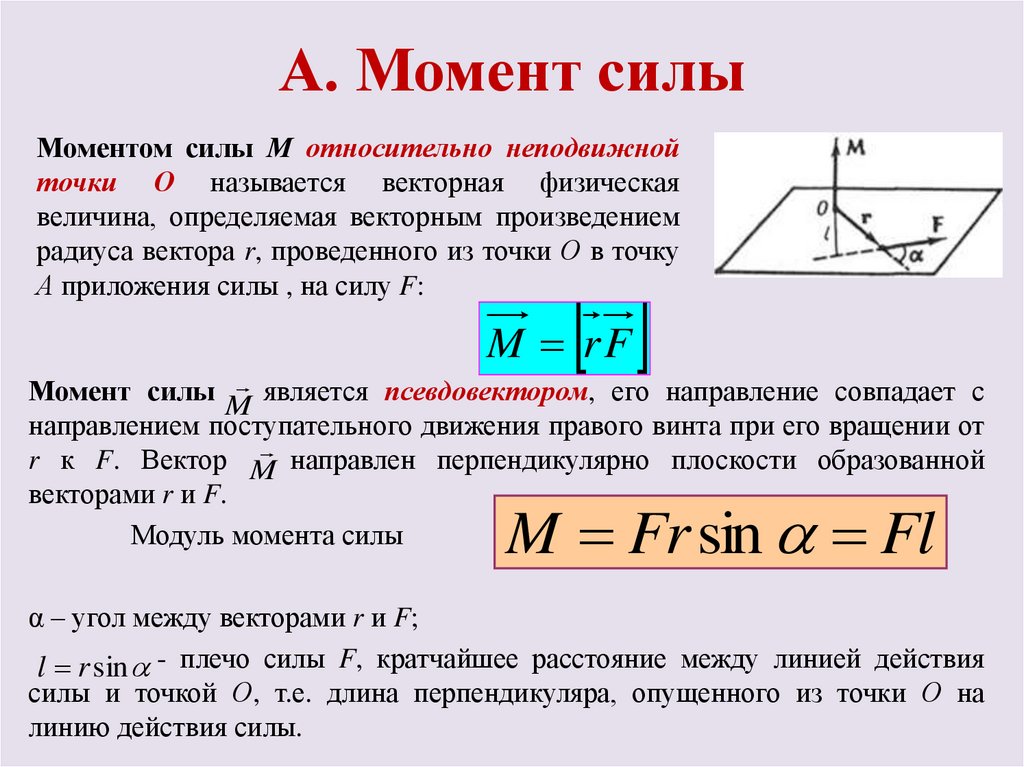

Консоль – равномерно распределенная нагрузка

Как и в приведенной выше конфигурации, защемленная балка с равномерно распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.

Уравнение и диаграмма

Диаграмма изгибающего момента консоли – равномерно распределенная нагрузка

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной равномерно распределенной нагрузке q .

Консоль – треугольная распределенная нагрузка

Как и в приведенной выше конфигурации, защемленная балка с треугольной распределенной нагрузкой будет иметь максимальный момент на опоре. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.

Уравнение и диаграмма

Диаграмма изгибающего момента консольной балки – треугольная распределенная нагрузка

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой точечной треугольной распределенной нагрузке q .

Консоль – конечный момент

Защемленная балка с моментной нагрузкой на конце будет иметь постоянный момент по всей балке. Чтобы проиллюстрировать это, см. диаграмму моментов и уравнение ниже.

Уравнение и диаграмма

Диаграмма изгибающего момента Консоль – конечный момент

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента консольной балки длиной L , подвергаемой мгновенной нагрузке M0 в конец.

Просто поддерживаемые

В этом подразделе мы рассмотрим различные конфигурации нагрузки свободно опертых балок. Другими словами, балки с одним концом на штифтах, а другой конец на ролике.

Просто поддерживаемая – промежуточная нагрузка

Теперь, если мы рассмотрим свободно опертые балки, общая конфигурация – это конфигурация с точечной нагрузкой на расстоянии a от первой опоры.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто опертая – промежуточная нагрузка

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки общей длиной

a + b , подверженной точечная нагрузка P расположен на расстоянии a от опоры.

Ф:
а:
б:

Простая опора — центральная точечная нагрузка

Просто опертая балка с точечной нагрузкой в ​​центре. Максимальный момент возникает там, где приложена точечная нагрузка.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто опертая – центральная нагрузка

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подвергаемой точечной нагрузке P в центре.

Просто опертая – две точечные нагрузки на равном расстоянии от опор

Просто опертая балка с двумя точечными нагрузками на равном расстоянии от опор. Максимальный момент возникает между двумя точечными нагрузками.

Уравнение и диаграмма

Диаграмма изгибающего момента для свободно опертой балки – две точечные нагрузки на равном расстоянии от опор

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L две точечные нагрузки на равном расстоянии и от опор.

Просто опертая – равномерно распределенная нагрузка

Просто опертая балка с равномерно распределенной нагрузкой. Максимальный момент возникает в центре балки.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто опертая – равномерно распределенная нагрузка

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подвергаемой равномерно распределенной нагрузке нагрузка q .

Просто опертая – момент на каждой опоре

Просто опертая балка с двухточечной моментной нагрузкой на каждом конце. Момент постоянен по длине балки.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто опертая – момент на каждой опоре

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной действию двух моментов нагрузки М0 на концах.

Просто опертая – момент на одной опоре

Просто опертая балка с моментной нагрузкой на одну опору. Диаграмма момента имеет треугольную форму, где максимальный момент возникает там, где приложен момент.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто поддерживаемая – момент на одной опоре

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту нагрузка M0 на одном конце.

Просто опертая, момент в средней точке

Свободно опертая балка с мгновенной нагрузкой в ​​центре. Максимальный момент будет в центре.

Уравнение и диаграмма

Диаграмма изгибающего момента Просто поддерживаемая, момент в средней точке

Калькулятор

Следуя приведенному выше уравнению, используйте этот калькулятор для расчета максимального момента свободно опертой балки длиной L , подверженной одному моменту нагрузки M0 в центре.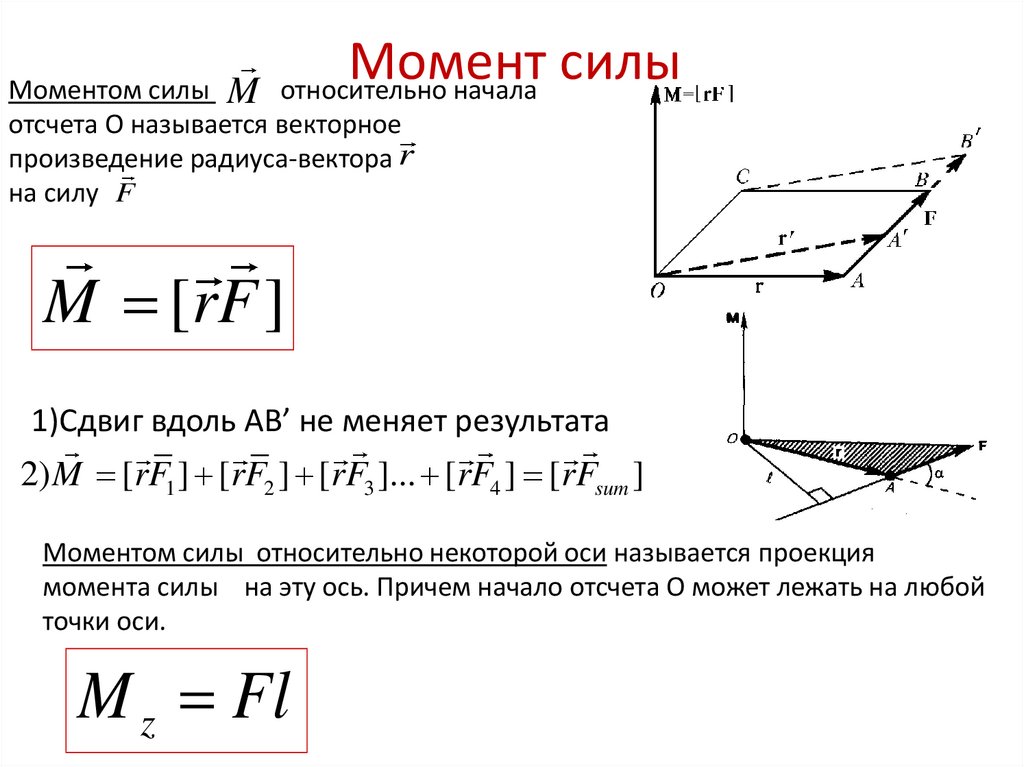

Заключение по изгибающему моменту

В заключение, изгибающий момент — это реакция, возникающая в элементе конструкции, когда на него действует внешняя сила или момент, вызывающий его изгиб. Балка является наиболее типичным или простейшим элементом конструкции, подверженным действию изгибающих моментов.

Чтобы проиллюстрировать это далее, рассмотрим момент (силу) на локте. Как упоминалось ранее в статье, момент прямо пропорционален плечу рычага. Точно так же он играет важную роль в определении параметров конструкции консольных конструкций. Если момент превышает расчетную прочность конструкции или любого другого компонента из-за чрезмерной нагрузки, она может разрушиться. Разрушение башен Всемирного торгового центра произошло из-за увеличения количества соединений, вызванных сильным жаром пожаров. При изменении моментов в конструкции передача усилий на другие элементы, соединения и узлы общей системы становится неуправляемой, что может привести к отказу.

Наконец, в настоящее время инженеры проектируют конструкции с помощью программного обеспечения для получения точных и быстрых результатов. Например, Tribby3d — облачное программное обеспечение для загрузки конструкций. Используя tribby3d, инженеры могут легко рассчитать площади притоков и нагрузку на элементы различных типов, таких как колонны и стены. Затем результаты можно экспортировать в различные выходные файлы, такие как Excel и AutoCAD.

Tribby3d — это облачное инженерное программное обеспечение, которое может вычислять загрузку элементов.

Связанные статьи

Моменты и функции генерации моментов

Моменты и функции генерации моментов

---

Мы используем MathJax

Измерения центральной тенденции и дисперсии являются двумя наиболее распространенными способами суммирования признаков. распределения вероятностей. Ожидаемое значение и дисперсия — две обычно используемые меры. Другой особенности, которые можно обобщить, включают асимметрию и эксцесс. Все четыре меры являются примеры математической величины, называемой моментом. 94$

Функции генерации момента

Так как каждый момент является ожидаемым значением, а определение ожидаемого значения включает либо сумма (в дискретном случае) или интеграл (в непрерывном случае), казалось бы, вычисление моментов может быть утомительным.