Формула момента силы в физике
Содержание:
- Определение и формула момента силы
- Момент силы относительно оси
- Главный момент сил
- Основной закон динамики вращательного движения
- Единицы измерения момента силы
- Примеры решения задач
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$
На рис.1 точка О и вектор силы (
$\bar{F}$)и радиус – вектор
$\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы
($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы
выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор
$\bar{M}$ создают правовинтовую систему.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$
где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$
где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$
где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.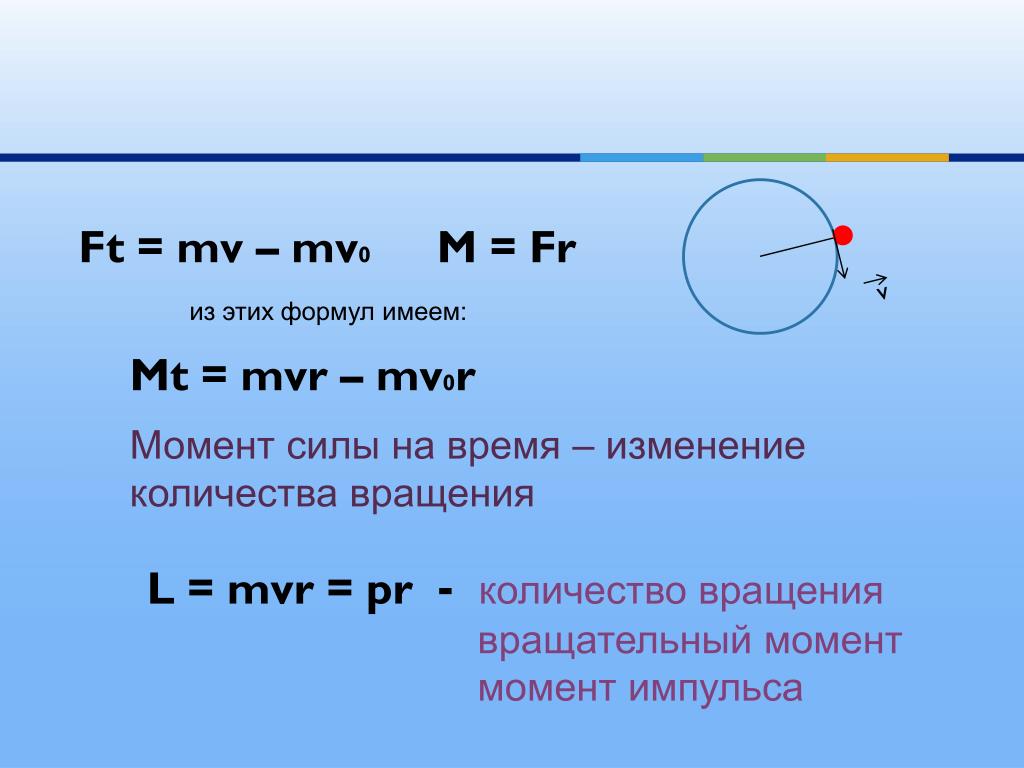
Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$
Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Момент силы, формулы
Определение 1
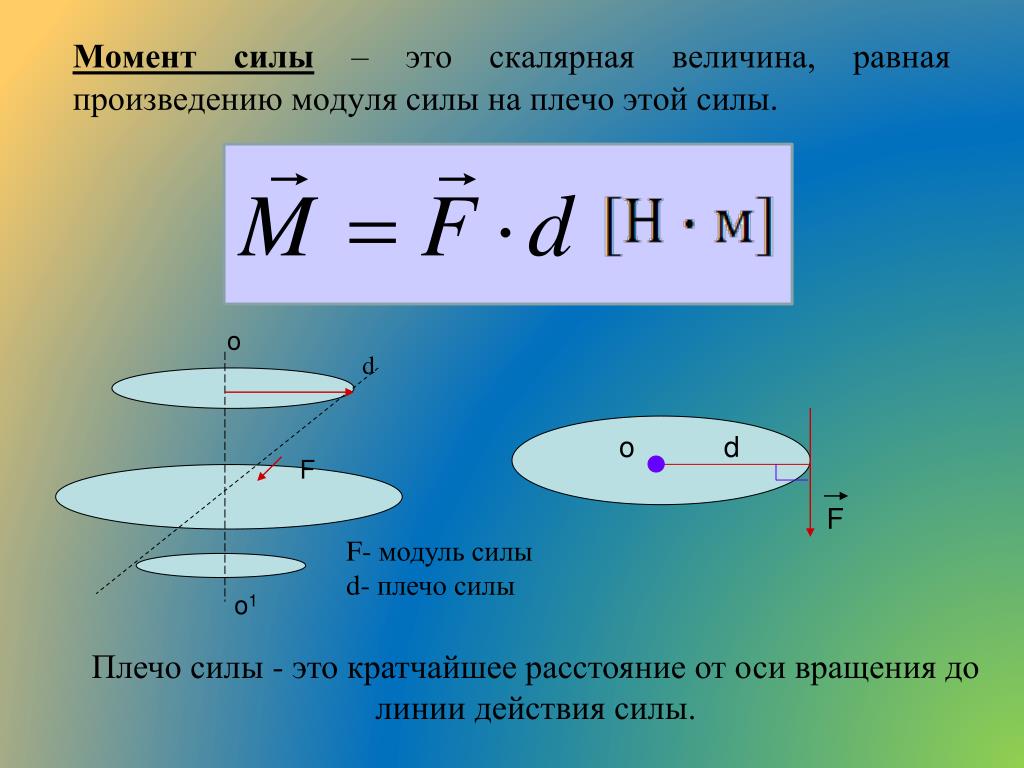
Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.
Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.
Момент силы выступает характеристикой вращательного воздействия силы на твердое тело. Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.
В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).
Понятие момента силы
Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.
Замечание 1
В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.
К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:
$\vec {M}=\vec{r}\vec{F}$, где:
- $\vec {F}$ представляет силу, воздействующая на частицу,
- $\vec {r}$ является радиусом вектора частицы.
В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н•м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:
$E = M\theta $, где:
- $E$ представляет энергию;
- $M$ считается вращающимся моментом;
- $\theta $ будет углом в радианах.
Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.
Формулы расчета момента силы
Интересным в физике является вычисление момента силы в поле, производимого по формуле:
$\vec{M} = \vec{M_1}\vec{F}$, где:
- $\vec{M_1}$ считается моментом рычага;
- $\vec{F}$ представляет величину действующей силы.
Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину.
При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:
$\vec{T}=\vec{r}\vec{F}$
При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.
$P = \vec {M}\omega $
В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы— в ньютон-метрах. При этом угловая скорость определяется в радианах в секунду.
Момент нескольких сил
Замечание 2
При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия. Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).
В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.
Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.
$M={FL_1+FL-2} = F{L_1+L_2}=FL$
В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.
Что такое момент?
Что такое момент?
Что такое момент?
Момент силы
является мерой его стремления заставить тело вращаться вокруг определенной
точка или ось.
Представьте, что два человека толкают дверь за ручку с противоположных сторон.
Если оба они толкают с одинаковой силой, то возникает состояние
равновесие. Если бы кто-нибудь из них вдруг отскочил от двери,
толчок другого человека больше не будет иметь никакого противодействия, и дверь
отмахивался бы. Человек, который все еще толкал дверь, создал
момент.
Элементы момента
Величина момента силы, действующей относительно точки или оси, равна
прямо пропорционально расстоянию силы от точки или оси.
Он определяется как произведение силы (F) и плеча момента (d).
плечо момента или плечо рычага — это перпендикулярное расстояние между
линия действия силы и центр моментов.
Момент = Сила x Расстояние или M = (F)(d)
Центр моментов может быть фактической точкой, относительно которой сила вызывает вращение. Это также может быть точка отсчета или ось, вокруг которой сила может рассматриваться как вызывающая вращение. Это не имеет значения, пока поскольку конкретная точка всегда принимается за точку отсчета. Последний случай гораздо более распространенная ситуация в задачах проектирования конструкций.
Момент выражается в футо-фунтах, тысячах футов,
ньютон-метры или килоньютон-метры. Момент тоже имеет смысл; по часовой стрелке
вращение вокруг центра моментов будет считаться положительным моментом;
а вращение против часовой стрелки вокруг центра моментов будет считаться
отрицательный. Самый распространенный способ выразить момент —
В примере показано, как гаечный ключ крепится к гайке.
Момент относительно точки C
Плечо момента для расчета момента вокруг точки C составляет 12 дюймов.
величина момента относительно точки C равна 12 дюймам, умноженным на силу
100 фунтов, чтобы дать общий момент 1200 дюймов-фунтов (или 100 фут-фунтов).
Рычаг момента (d) = 12 дюймов
Величина (F) = 100 фунтов
Момент = M = 100 фунтов x 12 дюймов = 1200 дюйм-фунтов
Точно так же мы можем найти моменты относительно любой точки пространства.
| Момент @ | А | Б | D |
| Моментный рычаг | 8 дюймов | 2 дюйма | 0 дюймов |
| Величина F | 100 фунтов | 100 фунтов | 100 фунтов |
| Общий момент | 800 дюйм-фунтов | 200 фунтов стерлингов | 0 дюймы-фунты |
Момент вызывает вращение вокруг точки или оси.
Если момент
быть взято около точки благодаря силе F, то для того, чтобы на момент развиться,
линия действия не может проходить через эту точку. Если линия действия
проходит через эту точку, момент равен нулю, потому что величина
плечо момента равно нулю. Так было с точкой D в предыдущем гаечном ключе.
проблема. Суммарный момент равен нулю, потому что плечо момента также равно нулю.
В качестве другого примера предположим, что сила в 200 фунтов приложена к
ключ, как указано. Момент силы в 200 фунтов, приложенной в точке С, равен нулю.
потому что:
M = F x d = 200 фунтов x 0 дюймов = 0 дюймов-фунтов
Другими словами, сила в 200 фунтов не вызывает ключ для вращения гайки. Можно было бы увеличить величину силы пока болт окончательно не сломался (разрушение при сдвиге).
Момент вокруг точек X, Y и Z также будет равен нулю, потому что они также
лежат на линии действия.
Момент также можно рассматривать как результат действия сил, отклоняющихся от
прямая линия, проведенная между точкой загрузки системы и ее опорами.
В этом случае синяя сила является эксцентрической силой. Для того, чтобы оно достигло
основание колонны, она должна делать обход через балку. Чем больше
объезд, тем больше момент. Наиболее эффективные структурные системы
иметь наименьшее количество обходных путей. Это будет обсуждаться более
подробно в Лекции 37 и
более поздние курсы.
Есть случаи, когда проще рассчитать моменты компоненты силы вокруг определенной точки, чем вычислить момент самой силы. Возможно, определение перпендикуляра расстояние действия силы сложнее, чем определение перпендикуляра расстояние компонентов силы. Момент нескольких сил о точка — это просто алгебраическая сумма составляющих их моментов относительно тот же пункт. При сложении моментов составляющих необходимо принимать большие заботиться о том, чтобы соответствовать смыслу каждого момента. Часто это благоразумно отметить смысл рядом с моментом, когда берутся за такие задачи.
Комбинированный
Моменты
Моменты
на балке
Типичные ошибки
При добавлении моментов компонентов необходимо проявлять большую осторожность, чтобы быть последовательными со смыслом каждого момента.
Часто целесообразно отметить следующий смысл
к моменту, когда берутся за такие задачи.
Часто задаваемые вопросы
Любая трудность с вычислением момента обычно связана с одним из
следующее:
- Центр моментов установлен неправильно или четко понял.
- Предполагаемое плечо момента не является ПЕРПЕНДИКУЛЯРНЫМ расстоянием между линия действия силы и центр моментов.
- Направление или направление вращения было проигнорировано или неправильно понято.
Вопросы для размышления
Какой момент относительно точки B и точки D для обоих случаев
показано в примере с ключом выше? Как можно добавить расширение в
конец гаечного ключа поможет отвернуть ржавый болт? Какие структурные системы
будет иметь наименьшее количество «обходных путей»?
Проблемы
Соответствующие материалы
Шеффер, Р.Э. Элементарные конструкции для архитекторов и строителей.
стр. 33-39.
Copyright © 1995, 1996 Крис Х. Любкеман и Дональд Петинг
Copyright © 1996, 1997, 1998 Крис Х. Любкеман
Счет, математика и статистика — Набор академических навыков
Моменты (механика)
ContentsToggle Main Menu 1 Моменты 2 Рабочий пример: нахождение момента 3 Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 4 Рабочий пример: тела покоятся в равновесии
Моменты
Вращающее действие силы на тело, на которое она действует, измеряется моментом силы.
Момент силы зависит от величины силы и расстояния от оси вращения.
Момент силы относительно точки равен (величине силы) $\times$ (перпендикулярному расстоянию линии действия силы от точки).
Когда на тело действует несколько сил, моменты относительно точки могут складываться, если задано положительное направление (по часовой стрелке или против часовой стрелки) и учитывается для каждого момента. 9{\circ}), \\ &= 64,241\mathrm{Нм} \text{ (до 3д.
п.).} \end{align} Момент силы измеряется в ньютон-метрах $\mathrm{Н м }$, поэтому момент $F$ относительно $P$ равен $64,241\mathrm{Nm}$.
Сумма моментов
На схеме показан набор сил, действующих на световой стержень. Вычислите сумму моментов относительно точки $P$.
Решение
Каждая сила уже перпендикулярна точке $P$.
Момент силы $6\mathrm{N}$ равен $6 \times 2 = 12 \mathrm{N m}$ против часовой стрелки.
Момент силы $14\mathrm{N}$ равен $14 \times 2 = 28 \mathrm{N m}$ по часовой стрелке.
Момент силы $5\mathrm{N}$ равен $5 \times (2+3) = 25 \mathrm{Nm}$ против часовой стрелки.
Всего по часовой стрелке $= 28 \mathrm{N m}$ и всего против часовой стрелки $= 37 \mathrm{Nm}$. Следовательно, сумма моментов равна $37 – 28 = 9 \mathrm{Nm}$ против часовой стрелки. Поскольку сумма против часовой стрелки была больше, мы выбрали против часовой стрелки в качестве положительного направления.
Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 9{\circ}), \\ & = 66,684 \mathrm{Nm} \text{ против часовой стрелки (3 д.
п.).} \end{align} Рабочий пример: Тела, находящиеся в равновесии
Нахождение нормальных реакций
Предположим, что имеется однородный стержень длины $9\mathrm{m}$ и веса $30\mathrm{N}$. Он опирается на опору $X$ одним концом и опору $Y$, которая находится на расстоянии $5\mathrm{m}$ от опоры $X$. Рассчитайте величину реакции на каждой из опор.
Решение
Мы можем нарисовать диаграмму, показывающую все действующие силы.
Вес стержня будет действовать в его центре масс – так как это однородный стержень, вес действует в средней точке. Стержень находится в равновесии, поэтому суммарные силы, действующие вверх, будут равны суммарным силам, действующим вниз, когда мы разрешим вертикально. \begin{equation} R_X + R_Y = 30. \end{equation} Рассмотрим моменты относительно точки $X$, мы имеем, что моменты по часовой стрелке будут равны моментам против часовой стрелки, поэтому \begin{align} 30 \times 4.5 & = R_Y \times ( 4,5 + 0,5), \\ 135 & = 5R_Y, \\ 27 \mathrm{N} & = R_Y.
\end{align} Теперь мы можем использовать это значение, чтобы найти $R_X$ \begin{align} R_X + R_Y & = 30, \\ R _ X & = 30 – 27, \\ & = 3 \mathrm{N}. \end{align} Следовательно, реакция в точке $X$ равна $3 \mathrm{N}$, а реакция в точке $Y$ равна $27\mathrm{N}$.
Нахождение центра масс неоднородного тела
Предположим, что имеется неоднородный стержень $AB$ длины $10\mathrm{m}$ и веса $15\mathrm{N}$. Он находится в горизонтальном положении и опирается на опоры в точках $C$ и $D$. Расстояние $A C = 3m$ и $AD = 7m$. Величина реакции при $C$ в четыре раза превышает величину реакции при $D$. Найдите расстояние от центра масс стержня до $A$.
Решение
Мы можем нарисовать диаграмму, показывающую все действующие силы.
Здесь мы предположили, что центр масс действует в точке $x$ m из точки $A$. Поскольку стержень не является однородным, мы не можем сказать, что центр масс находится в середине стержня. Разрешаем по вертикали \begin{align} 4R + R & = 15, \\ 5R & = 15, \\ R & = 3.